Prediction of mechanical properties of steel fibre-reinforced concrete under elevated temperature using artificial neural network techniques (ann)

This study investigates the mechanical performance of Steel Fibre-Reinforced Concrete (SFRC) subjected to elevated temperatures using artificial neural network (ANN) modeling. While existing literature mainly emphasizes the prediction of compressive strength, limited efforts have been made to predict other key mechanical properties under thermal stress. A comprehensive ANN framework was developed to simultaneously predict compressive strength, flexural strength, split tensile strength, and bond strength. The model was trained and validated using 967 experimental datasets encompassing a wide range of concrete mix designs and exposure conditions. The ANN architecture employed fully connected feedforward networks with ReLU activation in hidden layers and was individually optimized for each target parameter. The ANN model exhibited high predictive accuracy, with R² values of 0.85 (RMSE = 6.25 N/mm²) for compressive strength, 0.88 (RMSE = 5.74 N/mm²) for split tensile strength, 0.86 (RMSE = 6.18 N/mm²) for flexural strength, and 0.86 (RMSE = 6.08 N/mm²) for bond strength. These outcomes affirm the model's robustness in capturing complex nonlinear interactions between constituent materials, elevated temperature exposure, and mechanical behaviour. The proposed ANN-based framework provides an efficient and unified tool for predicting multiple mechanical properties of SFRC under thermal loading, requiring just 10 minutes for full analysis. This advancement fills a critical research gap and offers practical insights for the structural design of concrete in high-temperature environments.

1 Introduction

Concrete is a crucial component in the construction and infrastructure industries, playing a vital role in determining the performance of engineering projects. However, concrete structures are often subjected to various environmental factors that can compromise their structural integrity over time. The addition of discontinuous fibres to concrete has been recognized as a method to enhance its structural performance due to their bridging effect (Shafighfard et al., 2021; Shafighfard et al., 2019). Fibres were first introduced into concrete mixes nearly a century ago, and today, four main types are commonly used: glass, natural, synthetic, and steel fibres (Hossain et al., 2019; Shahjalal et al., 2020; Shahjalal et al., 2021). Glass fibres were initially employed for architectural applications but faced limitations due to durability concerns (Hwang et al., 2013). Natural fibres are often preferred in less developed regions due to their cost-effectiveness, although their performance compared to steel fibres has been questioned. Some studies have indicated that even a small amount of synthetic fibres can positively impact concrete properties (Majdzadeh et al., 2006; Greenough and Nehdi, 2008). Steel fibres are commonly chosen by designers for their superior ability to withstand tensile pressures compared to concrete. The use of Steel Fibre-Reinforced Concrete (SFRC) has gained popularity worldwide as it enhances the performance of reinforced concrete members (Salehian and Barros, 2017; Venkateshwaran and Tan, 2018). Consequently, concrete with added fibres exhibits superior impact resistance, toughness, compressive strength, tensile strength, and crack resistance compared to conventional concrete. However, exposure to high temperatures can lead to degradation in the performance of these materials due to physical and chemical changes induced by heating, which affect their mechanical properties (Dong et al., 2022). Thus, studying the mechanical properties of Fibre-Reinforced Concrete (FRC) at high temperatures is essential for enabling appropriate design considerations and ensuring structural integrity.

In the realm of cementitious composite materials, steel and polypropylene fibres are prevalent choices. Steel fibres maintain their stability under high temperatures, while polypropylene fibres exhibit a low melting point (Wu et al., 2022). Research by Serrano et al. (2016) and Nili et al. (2018) emphasizes that the combination of supplementary cementitious materials (SCM) and steel fibres significantly influences the performance of Fibre-Reinforced Concrete (FRC) under elevated temperatures. Moreover, the aspect ratio and orientation of reinforced fibres, as highlighted by Tahenni et al. (2021) and Nana et al. (2021), play pivotal roles in determining the structural integrity of FRC concrete. Concrete strength also contributes significantly to its resistance against high temperatures. Mahmood et al. (2022) examined the effect of various grading of soil on the compressive strength of cement grout treated with a water-reducing polymer. Further, Mahmood et al. (2021) developed several mathematical models, including Linear Regression (LR), Nonlinear Regression (NLR), multilinear regression (MLR), artificial neural networks (ANN), and the M5P-tree algorithm, were developed to predict the compressive strength of cement-grouted sand considering variables such as sand particle size, water-to-cement ratio (w/c), polymer content, and curing duration. Kodur (2000) points out that high-strength concrete may be more susceptible to spalling and possess lower fire resistance compared to low-strength concrete due to its reduced permeability and higher strength. The assessment of mechanical properties of FRC materials under varying conditions, including high temperatures, is essential for exploring their potential applications (Babalola et al., 2021). However, conducting experimental tests on FRC constructions poses challenges due to the time and costs involved in test preparation, execution, and material requirements. In recent years, the focus has shifted towards developing highly accurate prediction models using Machine Learning (ML) methodologies to estimate concrete strength. Machine learning techniques have emerged as reliable tools for computer modelling, particularly artificial neural networks which demonstrate robust pattern recognition capabilities as demonstrated by Priddy and Keller (2005). Furthermore, the thermal behaviour prediction of SFRC requires specialized adaptation of these techniques according to (Wu et al., 2020). For instance, Kang et al. (2021) employed ML algorithms like linear regressor, lasso regressor, ridge regressor, K-Nearest Neighbor (KNN) regressor, decision tree regressor, random forest regressor, AdaBoost regressor, gradient boost regressor, and XGBoost regressor to predict the compressive and flexural strength of Steel Fibre-Reinforced Concrete (SFRC). Thus, the literature underscores the importance of fibre types, supplementary cementitious materials, fibre aspect ratio, and concrete strength in dictating the performance of FRC at high temperatures. Additionally, ML methodologies offer promising avenues for accurately predicting concrete strength, thereby facilitating the design and evaluation of FRC structures. Continued research in this direction holds the potential to enhance the understanding and application of FRC in various engineering contexts, contributing to the advancement of construction practices and infrastructure resilience.

A dataset containing 200 experimental results for both compressive and flexural strength served as the basis for numerous investigations into Steel Fibre-Reinforced Concrete (SFRC). Mahesh and Sathyan (2022) utilized Artificial Neural Networks (ANN) to predict SFRC’s compressive strength and elastic modulus, leveraging 140 and 158 datasets, respectively. Their ANN model achieved remarkable predictive accuracy, boasting regression coefficient values of 0.96 and 0.97. Similarly, Khan et al. (2022) explored Machine Learning (ML) algorithms such as random forest regressor, gradient boost regressor, and XGBoost regressor to forecast SFRC compressive strength. Notably, the Random Forest (RF) regressor yielded an accurate prediction with an R² value of 0.96. Zheng et al. (2022) employed ML methodologies including Gradient Boosting (GB), gradient boost regressor, and XGBoost regressor to predict SFRC’s flexural strength. Their study highlighted the efficacy of the Gradient Boosting (GB) model, which achieved an R² value of 0.96 in accurately predicting flexural strength. Awolusi et al. (2019) employed ANN and a genetic algorithm to estimate SFRC’s compressive strength, favouring the ANN model over the genetic approach due to its superior performance. Rahman et al. (2021) investigated 11 ML models to predict SFRC beam shear strength, with the XGBoost model demonstrating an 85% accuracy in predicting shear strength. Hossain et al. (2017) developed an ANN model to predict SFRC beam shear strength, achieving an impressive accuracy level of approximately 96%. Shende et al. (2022) developed an ANN simulation to forecast SFRC strength using five significant input parameters. Hossain et al. (2023) developed ANN models based on 762 experimental data points and 12 input variables to predict compressive strength. Pazouki and Pourghorban (2022) explored Radial Basis Function Neural Network (RBFNN), artificial neural network, and adaptive-neuro fuzzy inference system approaches to predict SFRC’s compressive strength. Abubakar et al. (2020) employed the support vector machine to model and predict High Strength Concrete (HSC) compressive strength with steel fibre addition. Shafighfard et al. (2022) predicted SFRC compressive strength exposed to high temperatures using data from 307 experiments conducted between 2000 and 2022. Alyousef et al. (2023) utilized novel ML techniques, including Adaptive Neuro-Fuzzy Inference Systems (ANFIS), Artificial Neural Networks (ANN), and Gene Expression Programming (GEP), achieving a correlation coefficient (R) of 0.962 for ANN in predicting SFRC compressive strength at high temperatures.

The exploration of relationships between inputs and outputs using machine learning (ML) models has transformed the approach to addressing regression problems (Samuel, 2000; Challagulla et al., 2021; Asteris et al., 2022; Wang et al., 2023; Wang et al. 2024; Wang et al. 2025). Over the past few decades, a variety of innovative ML prediction techniques have emerged, with Artificial Neural Networks (ANNs) standing out prominently. ANNs, a subset of artificial intelligence, have gained widespread acceptance for modelling human actions (Saridemir et al., 2009). Unlike traditional prediction models requiring periodic updates to coefficients and equations when new data slightly deviates from the original dataset, ANNs offer greater flexibility. They don’t rely on specific equation forms but instead adapt to an abundance of input and output data. ANNs excel in adapting to new data, continuously retraining to accommodate changes (Lee, 2003). Additionally, ANNs effectively capture latent non-linear patterns within complex datasets through the utilization of non-linear activation functions. This enables them to identify intricate relationships among various elements by encoding data through connection weights, addressing issues arising from a lack of theoretical concepts (Graupe, 2013; Khan et al., 2018). Acikgenc et al. (2015) and Ramkumar et al. (2020) underscored the significant potential of ANNs in predicting concrete mix composition in SFRC. In recent years, ANN models have increasingly replaced conventional linear regression models in predicting the mechanical properties of concrete.

The application of Machine Learning (ML) techniques for predicting the mechanical properties of Steel Fibre-Reinforced Concrete (SFRC) has gained attention, particularly in estimating compressive, flexural, and split tensile strengths. However, despite its potential, the utilization of ML methods in enhancing SFRC concrete estimation is still limited. One of the main hurdles to wider ML adoption in this domain is the acquisition of comprehensive datasets, especially considering multiple variables such as temperature, fibre volume fraction, heating rate, and aspect ratio. Only a few studies, such as those conducted by Shafighfard et al. (2021), Chen et al. (2021), and Alyousef et al. (2023), have explored the impact of temperature and employed ML algorithms to forecast the composite strength of Fibre-Reinforced Concrete (FRC) at elevated temperatures. It is widely recognized that elevated temperatures have a significant effect on the mechanical properties of SFRC (Xiong and Liew, 2015). However, the prediction model for temperature effect on compressive strength of SFRC was scarce. Acknowledging the critical influence of temperature on SFRC mechanical properties, this study aims to develop a prediction model using Artificial Neural Network (ANN) to estimate the mechanical behaviour of SFRC exposed to elevated temperatures. By focusing on ANN modelling, this research aims to address the gap in the literature and contribute to advancing SFRC technology for practical applications, particularly in scenarios involving high-temperature environments.

This manuscript is organized as follows: Section 2 discusses the significance of the research, highlighting the importance of accurately predicting the mechanical behaviour of Steel Fibre-Reinforced Concrete (SFRC) exposed to elevated temperatures. Section 3 presents the materials and methodology adopted, including the experimental design and the development of the Artificial Neural Network (ANN) model. Section 4 provides a detailed presentation and discussion of the results obtained, emphasizing the predictive performance of the ANN model. Finally, Section 5 summarizes the key conclusions drawn from the study.

2 Research significance

The existing research has primarily focused on using machine learning techniques to predict the compressive strength of SFRC at elevated temperatures. However, it is of paramount importance to underscore that this research focus has predominantly excluded the prediction of various other critical mechanical properties, including but not limited to split tensile strength, flexural strength and bond strength. These mechanical attributes are pivotal in comprehensively assessing the performance and stability of SFRC under high-temperature environments. In light of the aforementioned research gap, the present study has been undertaken with the primary objective of rectifying these limitations. To achieve this goal, the experimental data gathered through a systematic and comprehensive experimental program. The dataset encompasses a broad spectrum of conditions characteristic of the elevated temperatures encountered by SFRC structures during their service life. Advanced statistical and machine learning techniques were then employed to formulate precise predictive models. These models are not only capable of estimating the compressive strength of SFRC under elevated temperature conditions but also extend their predictive capabilities to encompass the split tensile strength, flexural strength and bond strength.

3 Materials and methodology

The primary goal of this study is to construct a predictive model for Steel Fibre-Reinforced Concrete (SFRC) capable of estimating its compressive strength, split tensile strength, flexural strength, and bond strength under elevated temperatures. By focusing on the mechanical properties of SFRC in high-temperature environments, this research aim to bridge a gap in the current literature and contribute to a better understanding of SFRC behaviour under such conditions.

3.1 Materials

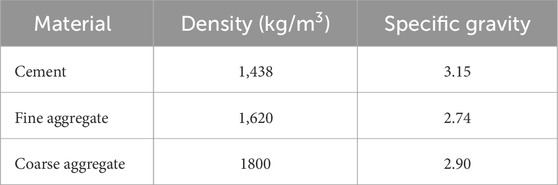
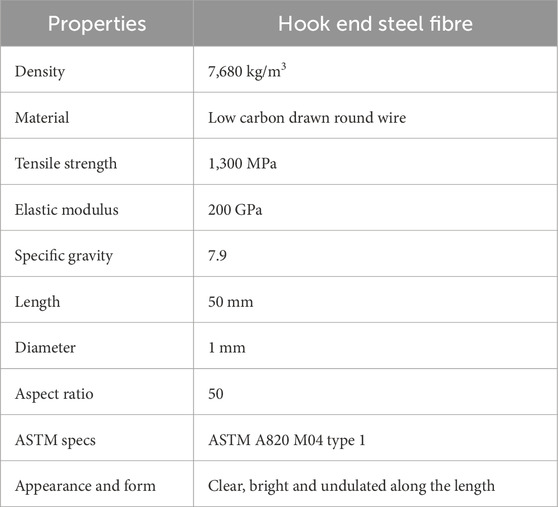
The mechanical properties, including compressive strength, split tensile strength, flexural strength and bond strength of SFRC with M20, M30 and M40 grades at elevated temperatures, were determined through experimental testing. The obtained results were used as input for creating predictive models. The cement used adhered to OPC 53 grade standards as per IS: 12269 (2015). Natural river sand, conforming to the zone-II specifications outlined in IS: 383 (1970), was used as the fine aggregate. The coarse aggregate comprised granite stones with a maximum size of 20 mm. Table 1 provides information on the density and specific gravity of the cement, fine aggregate and coarse aggregate. The inclusion of steel fibres in the concrete mix aimed to reduce cracking and enhance the concrete durability. Specifically, hook-end steel fibre were employed, known for their wavy configuration along their length added as volume fraction of 0.5 as shown in Figure 1. This unique shape improves the bond between the fibres and the concrete matrix, further enhancing the concrete’s mechanical properties. Table 2 outlines various properties of the steel fibre.

Table 1

Table 1. Material properties.

Figure 1

Figure 1. Steel fibre.

Table 2

Table 2. Properties of steel fibre.

3.2 Experimental investigation

Concrete specimens, including a Cube, Cylinder, and Prism, underwent casting and subsequent testing to assess the compressive strength, split tensile strength, flexural strength, and bond strength of Steel Fibre-Reinforced Concrete (SFRC) under elevated temperatures. This experimental procedure adhered to the standards outlined in IS: 516-1959 and IS: 5816-1959. After casting, the concrete samples were subjected to a 28-day curing process in a tank to achieve optimal strength. Upon completion of the curing period, the specimens were removed from the tank and allowed to air-dry for 24 h before laboratory testing. To evaluate the mechanical properties of the concrete under elevated temperatures, a specialized test setup was devised, as illustrated in Figure 2. The furnace employed an Iron-Chromium-Aluminium alloy heating element, with ceramic fibre and insulated bricks providing insulation against the generated heat. The furnace casing, constructed from high-quality mild steel, was capable of withstanding temperatures up to 1,200°C. The specimens were exposed to temperatures of 80°C, 120°C, and 200°C for a duration of 6 h. After reaching the desired temperature, the furnace was deactivated, allowing for natural air cooling. Subsequently, the specimens were left to return to room temperature. Following thermal exposure, the compressive strength, split tensile strength, flexural strength, and bond strength of the specimens were determined through standard testing procedures.

Figure 2

Figure 2. Testing specimen under various furnace temperatures: 80°C, 120°C and 200°C. (a) Cube specimen. (b) Cylinder specimen. (c) Prism specimens.

The average compressive strengths of M20, M30, and M40 grade concrete without steel fibres at ambient temperature were 27.88 N/mm², 35.15 N/mm², and 42.75 N/mm², respectively. When exposed to elevated temperatures, these values dropped to 23.66 N/mm² for M20, 29.52 N/mm² for M30, and 35.66 N/mm² for M40, corresponding to reductions of 15.3%, 16%, and 16.58%, respectively. Similarly, the average split tensile strengths at ambient temperature were recorded as 3.66 N/mm² (M20), 4.67 N/mm² (M30), and 5.94 N/mm² (M40), while under elevated temperatures, the values decreased to 2.41 N/mm², 3.34 N/mm², and 4.37 N/mm², representing strength losses of 34.15% for M20, 28.47% for M30, and 26.4% for M40. Furthermore, the average flexural strengths at ambient conditions were 3.61 N/mm² for M20, 5.92 N/mm² for M30, and 6.85 N/mm² for M40. Under elevated temperature, these reduced to 2.78 N/mm², 3.72 N/mm², and 4.55 N/mm², showing a decline of 22.99%, 37.16%, and 33.57% for M20, M30, and M40 concrete, respectively.

3.3 Methodology

3.3.1 Building the dataset

This process involves the collection of data from various sources and its careful compilation. To create machine learning models, the dataset must undergo pre-processing to select the relevant data for use. While numerous researchers have conducted machine learning predictions for concrete strength, there have been relatively few studies focused on developing machine learning models specifically for SFRC at high temperatures. Constructing SFRC machine learning models to predict compressive strength, split tensile strength, flexural strength and bond strength necessitates a novel dataset specifically tailored to SFRC at elevated temperatures. Consequently, experimental data was employed to construct the machine learning models.

3.3.2 Data pre-processing

Sorting out the missing values is crucial before standardizing the dataset for model development in order to correctly identify and arrange the obtained data. After the dataset was created, it was divided into two groups as training and testing dataset. A training set is the first and is used to train models. The second is the testing set. The machine-learning model is trained using the training set, and the testing set is used to compare the results to those predicted. In this study, the ratio between the training set and the test set was 80:20. In order to prevent data leaking, scaling is carried out after the training and testing sets have been divided (Oey et al., 2020). Because the ranges and units of the values are different, the data for each value were scaled to a conventional normal distribution. Standard Scaler, a scikit-learn function that sets the mean to zero and the standard deviation to one was used to rescale the model.

3.3.3 Selection of model

An artificial neural network is a computational model composed of neurons, activation functions, connection weights and bias (Priddy and Keller, 2005). The mathematical representation of a basic artificial neuron is as follows:

$Y=f\left(\sum wX+b\right)$

where $X$ is the input vector; $Y$ is the output; $f$ is an activation function; $w$ is the weight vector and b is the bias. The neuron may be viewed as a linear feature map with an adjustable weight matrix.

As depicted in Figure 3, the ANN model comprises multiple interconnected layers of artificial neurons. Each artificial neuron in every layer is fully connected to every neuron in the immediately preceding and subsequent layers through associated weights. Consequently, each neuron in the model receives input signals from all neurons in the preceding layer. Weights play a crucial role in illustrating how input values from the preceding layer influence the processing elements and these weights can be adjusted to achieve the desired output. In the ANN model, data flows unidirectionally from the input layer to the output layer. The learning process is geared towards minimizing the disparity between actual and output values. During the learning phase, the ANN has the capacity to adapt its model based on the significant information traversing through the network. Artificial neural networks find applications in modeling complex relationships, building upon established architectures described by (Priddy and Keller, 2005). Specifically for high-temperature conditions, the input layer configuration follows recommendations from (Wu et al., 2020) to account for thermal degradation effects.

Figure 3

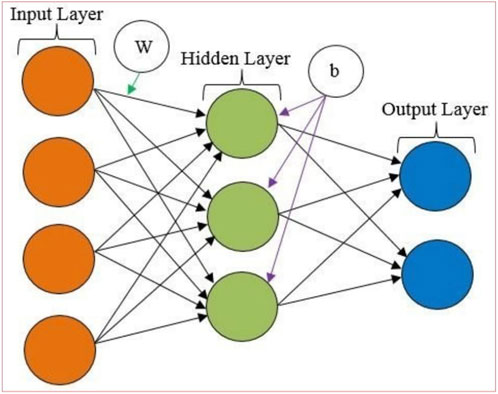
Figure 3. ANN General architecture of ANN (Kavya et al., 2022).

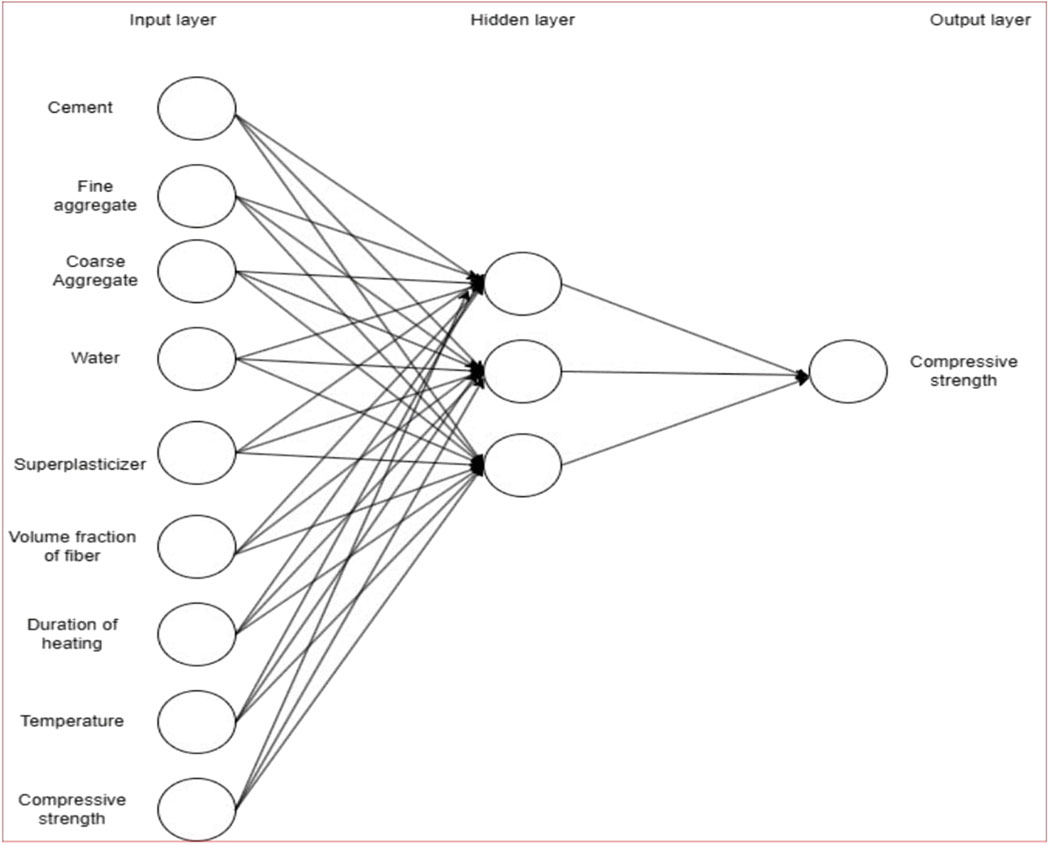
The ANN models developed in this study for predicting compressive strength, split tensile strength, flexural strength and bond strength are presented in Figures 4–7. Specifically, ANN model-1, as shown in Figure 4, is designed to predict the compressive strength of SFRC after exposure to high temperatures. This model is a fully connected feedforward neural network consisting of one input layer, one hidden layer, and one output layer. The hidden layer comprises three nodes activated by the ReLU activation function. The primary advantage of ReLU is its introduction of non-linearity to the model, which enables neural networks to learn complex patterns in data (Sharma et al., 2017).

Figure 4

Figure 4. ANN model-1.

Figure 5

Figure 5. ANN model-2.

Figure 6

Figure 6. ANN model-3.

Figure 7

Figure 7. ANN model-4.

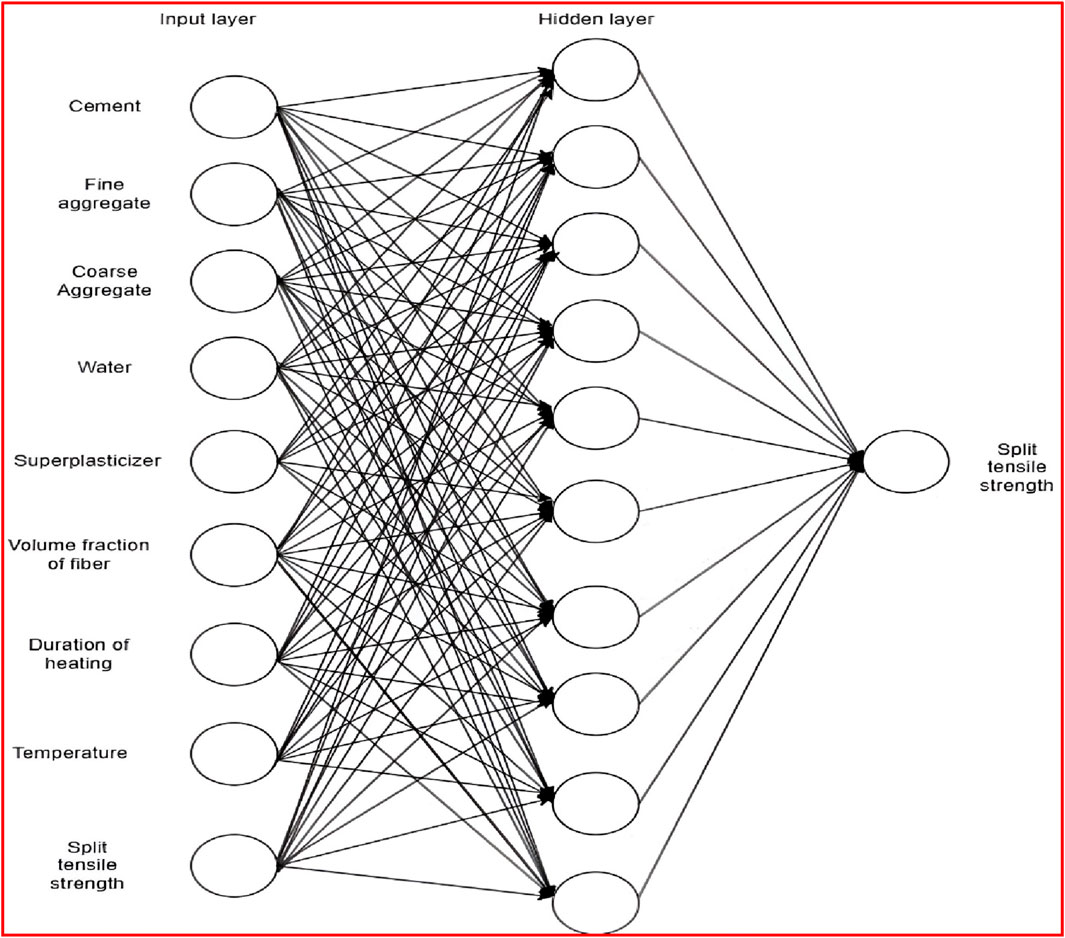
The ANN model-2 depicted in Figure 5, is specifically developed to predict the split tensile strength of SFRC after exposure to elevated temperatures. This model adopts a fully connected feedforward neural network architecture, which includes one input layer, one hidden layer, and one output layer. The hidden layer is composed of ten nodes activated by the Rectified Linear Unit (ReLU) activation function.

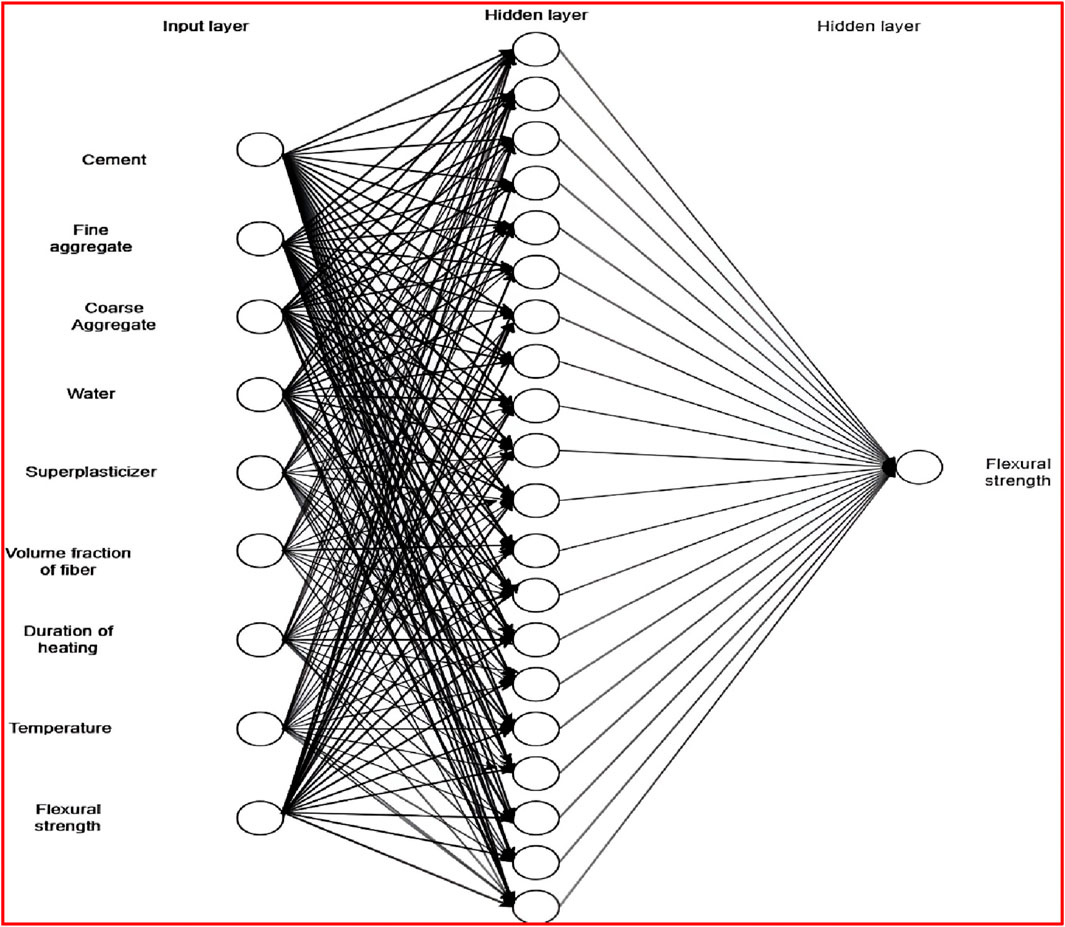
The ANN model-3 as illustrated in Figure 6, is developed for predicting the flexural strength of SFRC after exposure to high temperatures. This model employs a fully connected feedforward neural network architecture, consisting of one input layer, one hidden layer and one output layer. The hidden layer is composed of twenty nodes activated by the Rectified Linear Unit (ReLU) activation function.

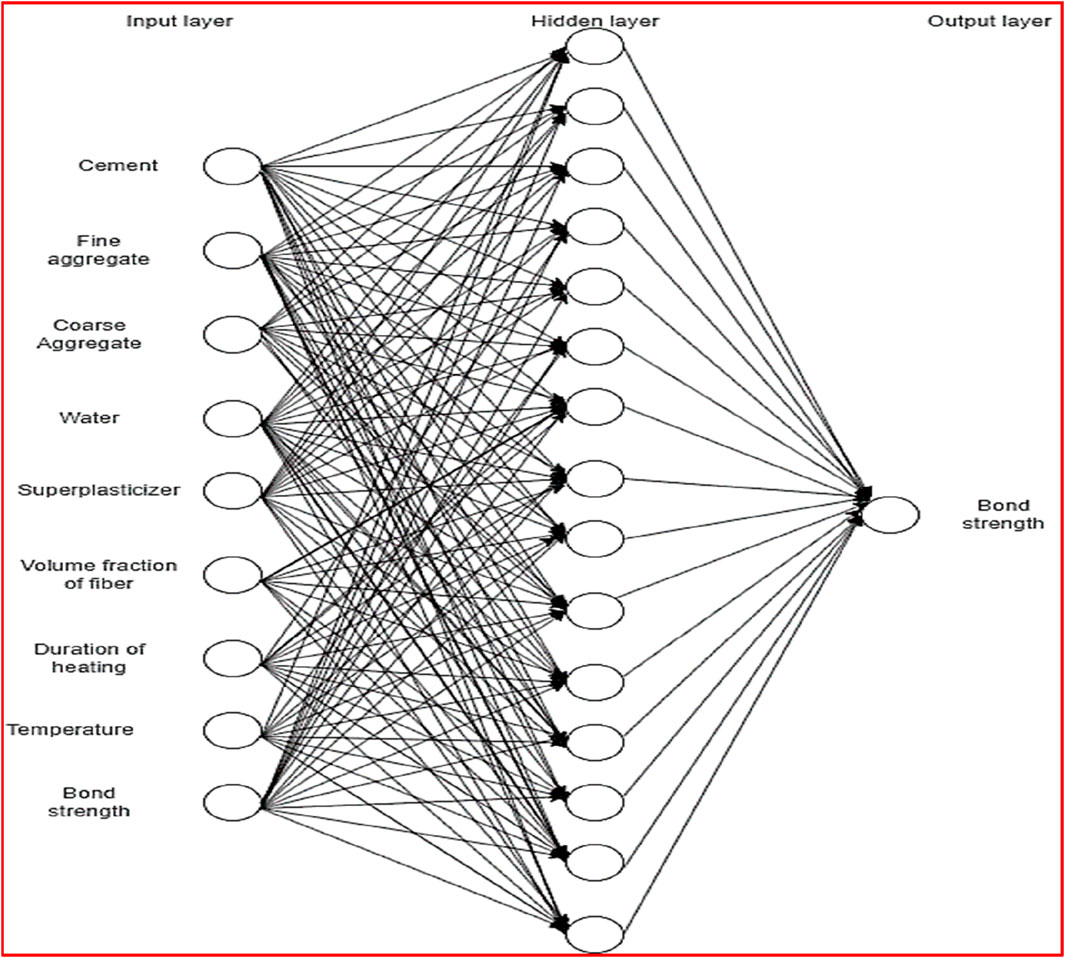
The ANN model-4, as depicted in Figure 7 has been specifically designed to predict the bond strength of SFRC after exposure to elevated temperatures. This model utilizes a fully connected feedforward neural network architecture, comprising one input layer, one hidden layer, and one output layer. Within the hidden layer, there are fifteen nodes activated by the Rectified Linear Unit (ReLU) activation function. In this hidden layer, the input data undergoes processing and transformation into a new representation through the use of a set of weights and biases. The ReLU activation function is applied element-wise to the output of each neuron within these layers. ReLU is favoured for its computational efficiency and its ability to mitigate the vanishing gradient problem, a challenge that can arise with other activation functions such as sigmoid or tanh (Wang et al., 2019; Szandala, 2021).

3.3.4 Training the model

The ANN prediction model was developed using the Python platform. To train the model, 80% of the sample data was utilized and the training process was completed after 1,000 epochs. Subsequently, the prediction model underwent testing using the remaining 20% of the sample data. Throughout the training phase, the model was optimized to minimize the mean squared error loss, employing the Adam optimizer. The prediction results generated by the ANN model were then compared to the actual experimental results from the test sample.

3.3.5 Evaluation of model

The developed models were compared with each other, and the selection of the best-performing algorithm was based on performance metrics such as the fitting coefficient (R²), Root Mean Square Error (RMSE), and Mean Absolute Error (MAE).

3.4 Description of dataset

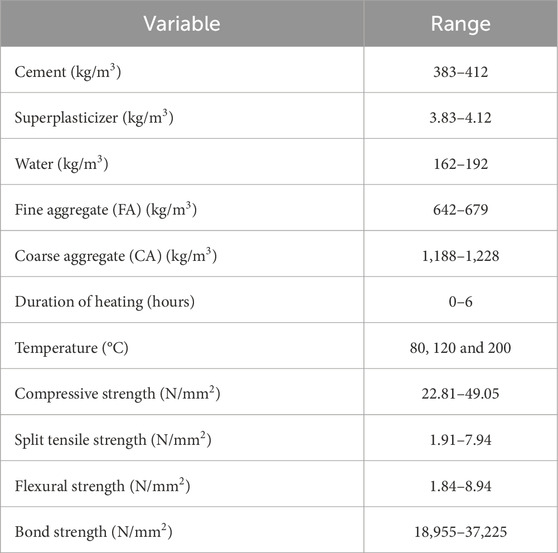
A dataset consisting of 967 concrete mixtures was experimentally developed concrete mixes as well as concrete mixes reported in the existing studies, involving varying proportions of cement, fine aggregate, coarse aggregate, water, superplasticizer, volume fraction of fibres, duration of heating and temperature were used. This dataset encompasses 9 input variables and 1 output variable for each model and their respective ranges can be found in Table 3. The input variables include cement, superplasticizer, water, steel fibre, fine aggregate, coarse aggregate, age, as well as concrete properties like compressive strength, split tensile strength, flexural strength and bond strength. The output variable encompasses compressive strength, split tensile strength, flexural strength and bond strength, all measured at 28 days.

Table 3

Table 3. Variables.

4 Results and discussions

The implementation aimed to assess the model’s performance in predicting the mechanical properties of SFRC concrete under elevated temperatures. This modeling task was treated as a regression problem within a machine learning framework. The process of training the model took place using Python language. Data analysis and model development were carried out utilizing the Python programming language on the Kaggle platform.

4.1 Statistical characteristics of the dataset

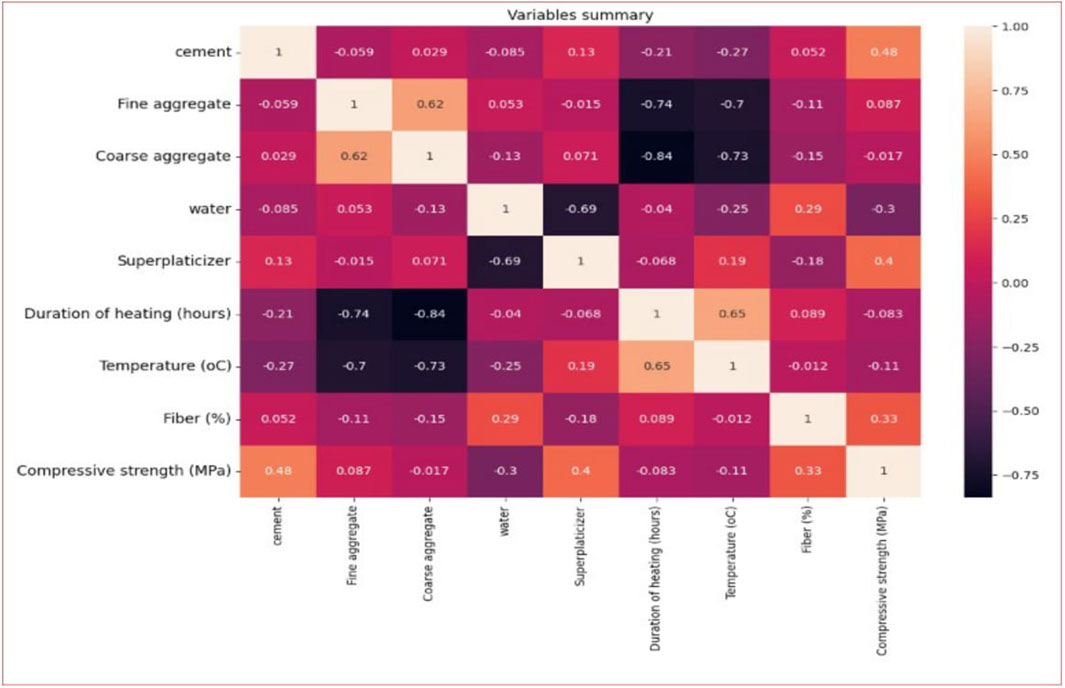
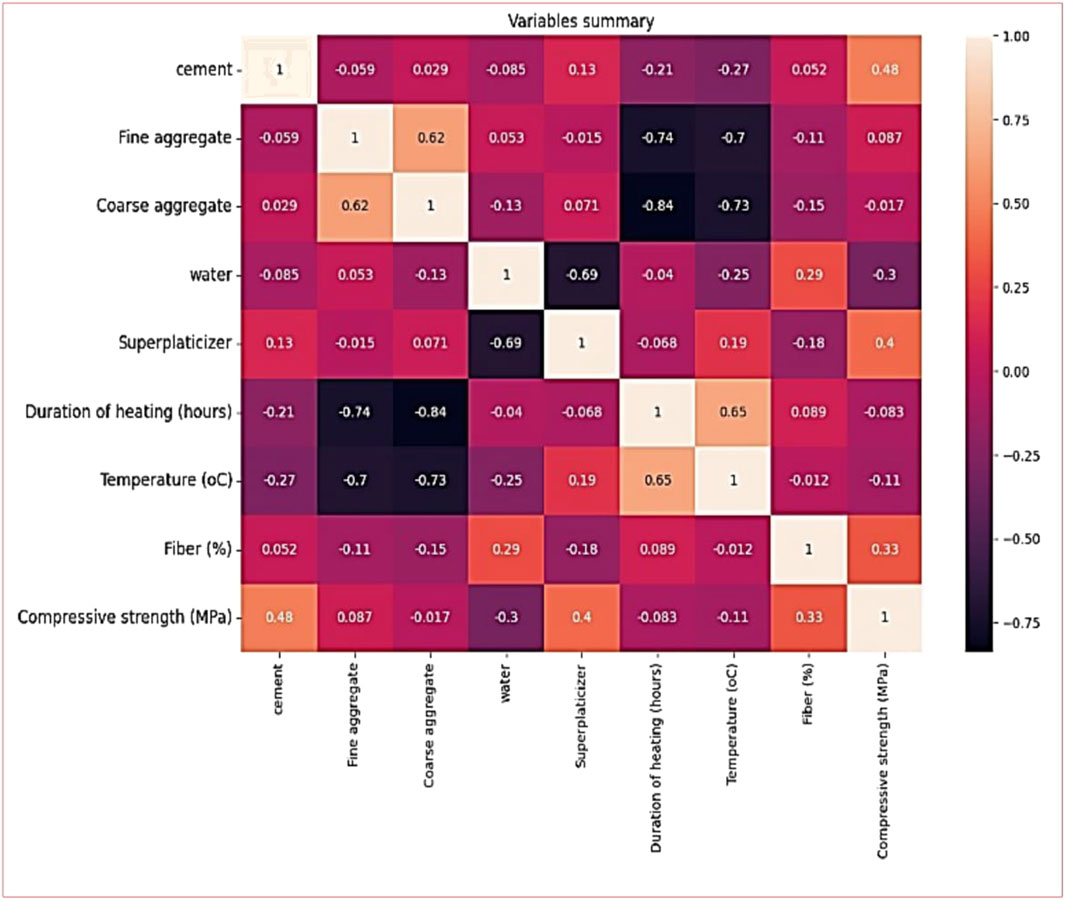
Figure 8 depicts the correlation between the input and output variables of Model-1. The graph clearly illustrates a complex, non-linear relationship between compressive strength and multiple input variables. Notably, there is a negative correlation observed, indicating that an increase in one variable is associated with a decrease in another. Furthermore, it was observed that variables such as cement, fine aggregate, superplasticizer, and volume fraction of fibre exhibit a positive correlation with compressive strength. This suggests that an increase in the quantity of these variables leads to higher compressive strength in the concrete. In contrast, coarse aggregate, water, duration of heating and temperature show a negative correlation with concrete compressive strength, indicating that an increase in their quantity results in a reduction in the compressive strength of the concrete. These similar results also obtained by Alyousef et al. (2023).

Figure 8

Figure 8. Correlation between two variables of model-1.

Figure 9 illustrates the correlation between the input and output variables of model-2. It is evident from the graph that there exists a complex, non-linear correlation between split tensile strength and multiple input variables. Additionally, there is a negative correlation observed, where an increase in one variable is related to a decrease in another. Notably, it was observed that fine aggregate and duration of heating exhibit a positive correlation with split tensile strength, suggesting that an increase in their quantity leads to an increase in split tensile strength. Conversely, cement, coarse aggregate, water, superplasticizer, volume fraction of fibre and temperature show a negative correlation with split tensile strength, indicating that an increase in their quantity results in a reduction in split tensile strength of the concrete.

Figure 9

Figure 9. Correlation between two variables of model-2.

Figure 10 illustrates the correlation between the input and output variables of model-3. It is evident from the graph that there exists a complex, non-linear correlation between flexural strength and multiple input variables. Additionally, there is a negative correlation observed, where an increase in one variable is related to a decrease in another. Notably, it was observed that fine aggregate, coarse aggregate, water and duration of heating exhibit a positive correlation with flexural strength, suggesting that an increase in their quantity leads to an increase in flexural strength. Conversely, cement, superplasticizer, volume fraction of steel fibre and temperature show a negative correlation with flexural strength, indicating that an increase in their quantity results in a reduction in flexural strength of the concrete.

Figure 10

Figure 10. Correlation between two variables of model-3.

Figure 11 illustrates the correlation between the input and output variables of model-4. It is evident from the graph that there exists a complex, non-linear correlation between bond strength and multiple input variables. The negative correlation also observed, where an increase in one variable is related to a decrease in another. Notably, it was observed that fine aggregate, coarse aggregate, water and duration of heating exhibit a positive correlation with bond strength, suggesting that an increase in their quantity leads to an increase in bond strength. Conversely, cement, superplasticizer, volume fraction of steel fibre and temperature show a negative correlation with bond strength, indicating that an increase in their quantity can decreases the bond strength.

Figure 11

Figure 11. Correlation between two variables of model-4.

4.2 Prediction outputs

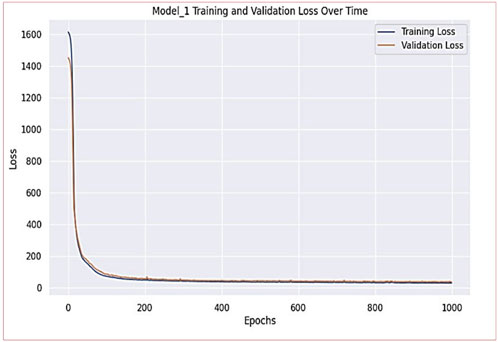
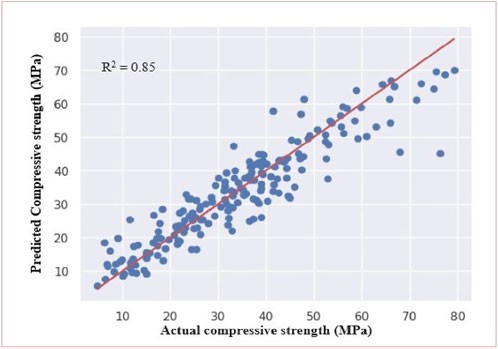
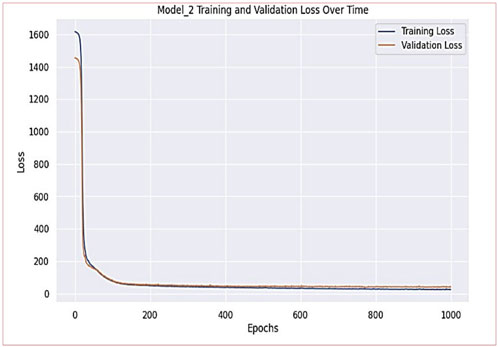
The proposed ANN model achieved a performance level (R²) of 0.85 in the prediction of the compressive strength of SFRC at elevated temperatures. The model also demonstrated Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) values of 6.25 N/mm² and 4.54 N/mm² respectively. Figure 12 presents the training and validation loss for model-1. Figure 13 presents a comparison between the predicted compressive strength from the proposed ANN model and the experimental compressive strength. The exceptional accuracy of the ANN predictions is evident as they consistently align closely with the diagonal line. This alignment is most striking when considering the compressive values, where the ANN predictions closely match the actual compressive values. This robust alignment underscores the ANN model’s ability to effectively capture the complex non-linear relationship between input and output variables. Consequently, this study establishes that the ANN model is proficient in estimating how temperature impacts the compressive strength of SFRC.

Figure 12

Figure 12. Training and validation loss for model-1.

Figure 13

Figure 13. Precited vs. Actual compressive strength.

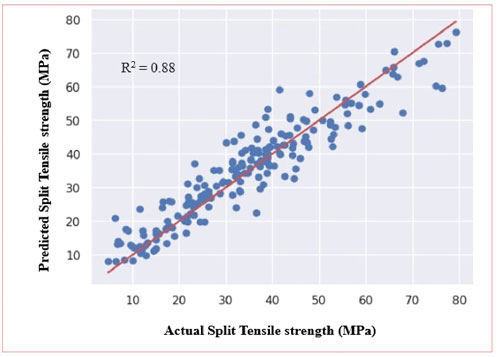
The proposed ANN model achieved a performance level (R²) of 0.88 in the prediction of the split tensile strength of SFRC at elevated temperatures. The model also demonstrated Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) values of 5.74 N/mm² and 4.30 N/mm² respectively. Figure 14 presents the training and validation loss for model-2. Figure 15 presents a comparison between the predicted split tensile strength from the proposed ANN model and the experimental split tensile strength. The enhanced accuracy of ANN predictions becomes evident as each point predicted by the ANN aligns closely with the diagonal line, particularly noticeable in the case of predicted split tensile strength values, which closely mirror the actual values. This clear alignment underscores the ANN model’s aptitude for capturing the complex non-linear relationship between input and output variables. Consequently, it is evident that the ANN model holds the potential to estimate the impact of temperature on the split tensile strength of SFRC.

Figure 14

Figure 14. Training and validation loss for model-2.

Figure 15

Figure 15. Precited vs. Actual split tensile strength.

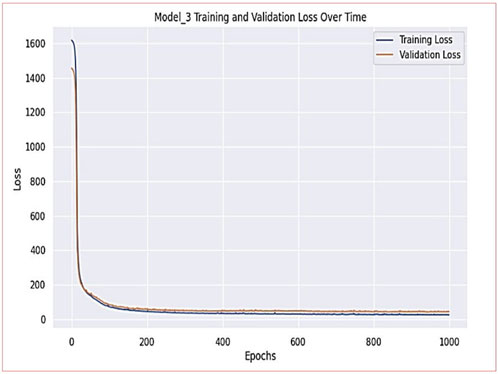
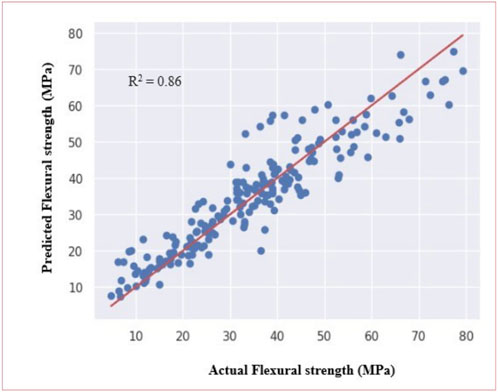
The proposed ANN model achieved a performance level (R²) of 0.86 in the prediction of the flexural strength of SFRC at elevated temperatures. The model also demonstrated Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) values of 6.18 N/mm² and 4.55 N/mm² respectively. Figure 16 presents the training and validation loss for model-3. Figure 17 presents a comparison between the predicted flexural strength from the proposed ANN model and the experimental flexural strength. The superior accuracy of ANN predictions is clearly demonstrated by the close alignment of each ANN-predicted point with the diagonal line. This alignment is particularly conspicuous when considering the predicted flexural strength values, which closely resemble the actual values. This observation underscores the ANN model’s effectiveness in capturing the complex non-linear relationship between input and output variables. Consequently, it is evident that the ANN model has the capacity to accurately estimate the influence of temperature on the flexural strength of SFRC.

Figure 16

Figure 16. Training and validation loss for model-3.

Figure 17

Figure 17. Precited vs. Actual flexural strength.

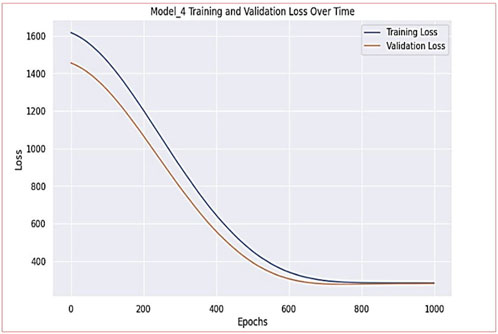
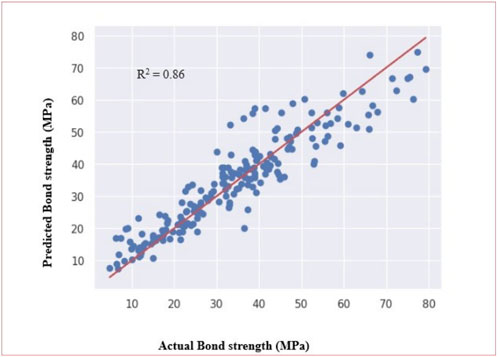
The proposed ANN model achieved a performance level (R²) of 0.86 in the prediction of the bond strength of SFRC at elevated temperatures. The model also demonstrated Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) values of 6.08 N/mm² and 4.71 N/mm² respectively. Figure 18 presents the training and validation loss for model-4. Figure 19 presents a comparison between the predicted bond strength from the proposed ANN model and the experimental bond strength. During the estimation of bond strength using the proposed ANN model, it was observed that a significant portion of the predicted points fell within a 10% margin of the line representing perfect agreement. This clear alignment underscores that the bond strength values predicted by the ANN closely corresponded to the actual bond strength values. This observation serves as compelling evidence of the ANN model’s capability to effectively capture the intricate non-linear connection between input and output variables. Consequently, it was established that the ANN model possesses the capacity to accurately estimate the influence of temperature on the bond strength of SFRC.

Figure 18

Figure 18. Training and validation loss for model-4.

Figure 19

Figure 19. Precited vs. Actual bond strength.

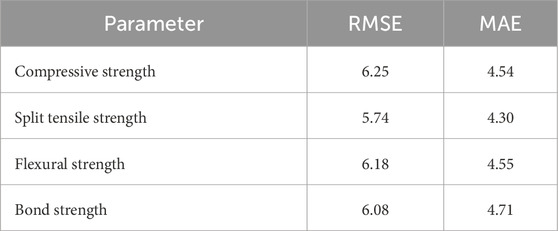
The RMSE value for compressive strength, split tensile strength, flexural strength and bond strength was 6.25, 5.74, 6.18 and 6.08 as presented in Table 4. The MAE for compressive strength, split tensile strength, flexural strength and bond strength was 4.54, 4.30, 4.55 and 4.71. About 70% of the samples show an error of less than 10%, indicating a good correlation between the ANN model predictions results and the experimental results, which validates the suitability of the proposed ANN model for predicting the compressive, split tensile, flexural strengths and bond strength of SFRC. Alyousef et al. (2023) reported that Multiple Linear regression (MLR) model effectively predicts the compressive strength of the SFRC after exposed to high temperature with MAE of 26.31 and RMSE of 32.43. Compared to Multiple Linear regression (MLR) developed by Alyousef et al. (2023), the developed ANN effectively predicts the compressive strength with less errors. The RMSE and MAE value of the proposed ANN model was 80% and 82.74% lesser than the existing MLR model.

Table 4

Table 4. Errors.

In the evaluation of various strength parameters, including compressive strength, split tensile strength, flexural strength and bond strength, RMSE and MAE values were computed to assess the accuracy of predictive models or measurement techniques. Among these parameters, split tensile strength emerged as the most accurately predicted or measured, with the lowest RMSE (5.74) and MAE (4.30) values, indicating minimal errors when compared to actual values. Conversely, compressive strength exhibited the highest RMSE (6.25) and flexural strength had the highest MAE (4.55), suggesting slightly larger deviations from the true values in these cases. The evaluation of these parameters provides valuable insights into the performance and reliability of predictive models or measurement methodologies, aiding in quality control and decision-making processes. The model demonstrated exceptional predictive capability, surpassing traditional analytical methods documented in (Priddy and Keller, 2005) while confirming the temperature-strength correlation patterns identified by (Wu et al., 2020).

The emergence of the developed ANN prediction model for concrete strength represents a significant advancement in the field of construction and materials engineering. One notable feature that sets the developed model apart is its remarkable efficiency, with the entire prediction process taking a mere 10 min to execute as shown in Figure 20. This rapid processing time holds immense practical significance. In industries where time is often of the essence, such as construction and infrastructure development, swift access to critical information can lead to substantial cost savings and improved project timelines. Traditional methods of concrete strength prediction, including time-consuming laboratory tests can be laborious and time-intensive.

Figure 20

Figure 20. Time taken.

In contrast, the ANN model streamlines this process, providing engineers and stakeholders with quick and reliable insights into concrete strength. Furthermore, the ability of the model to generate concrete strength predictions in a matter of minutes demonstrates its computational prowess. It showcases the potential of artificial neural networks to efficiently process vast amounts of data and perform complex calculations with exceptional speed. This not only enhances decision-making processes but also opens up avenues for real-time monitoring and quality control in construction projects. The 10-min runtime of this ANN prediction model is a demonstrates to its practicality, efficiency and transformative potential in the field of concrete strength prediction and construction management.

5 Conclusion

Elevated temperatures can substantially compromise the strength of concrete structures, rendering them vulnerable to failures. Utilizing an Artificial Neural Network (ANN) model can provide predictions of concrete behaviour under such conditions, enabling more accurate safety assessments and improved structural designs. This is of utmost importance, especially in critical infrastructure contexts such as bridges, buildings and nuclear power plants. The primary objective of this study is to develop a predictive model for assessing the compressive strength, split tensile strength, flexural strength and bond strength of SFRC after exposure to high temperatures.

• The proposed ANN model achieved a R² of 0.85 in predicting SFRC compressive strength at high temperatures, with RMSE and MAE values of 6.25 N/mm² and 4.54 N/mm² respectively. The RMSE and MAE value of the proposed ANN model was 80% and 82.74% lesser than the existing MLR model.

• The presented ANN model successfully achieved an R² value of 0.88 when predicting the split tensile strength of SFRC at elevated temperatures. Additionally, it yielded RMSE and MAE values of 5.74 N/mm² and 4.30 N/mm², respectively.

• The proposed ANN model achieved an R² value of 0.85 when predicting SFRC flexural strength at elevated temperatures. Additionally, it resulted in RMSE and MAE values of 6.18 N/mm² and 4.55 N/mm², respectively.

• The proposed ANN model demonstrated a performance level, as measured by an R² value of 0.86, in predicting the bond strength of SFRC at elevated temperatures. It also yielded RMSE and MAE values of 6.08 N/mm² and 4.71 N/mm², respectively.

• Incorporating temperature and heating duration as primary input parameters, this study yielded noteworthy findings. The results unveiled a substantial influence of heating duration on split tensile strength, flexural strength and bond strength. In contrast, the impact of heating duration on compressive strength was observed to be more limited and of a milder nature.

• The presented model requires only 10 min for performing the prediction.

This study focuses on the development of a predictive model for the mechanical properties of SFRC under elevated temperature conditions. The created model accurately forecasts compressive strength, split tensile strength, flexural strength, and bond strength, demonstrating minimal errors. Future improvements in model precision can be achieved through the utilization of metaheuristic algorithms.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Ethics statement

The studies involving humans were approved by GP and SS, Department of Civil Engineering, Faculty of Engineering and Technology, SRM Institute of Science and Technology, Kattankulathur-603203, Tamil Nadu, India. Email: cHJlbWt1bWdAc3JtaXN0LmVkdS5pbg==, c2VudGhpbHMxMEBzcm1pc3QuZWR1Lmlu. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author contributions

GP: Visualization, Formal Analysis, Data curation, Methodology, Writing – review and editing, Software, Conceptualization, Investigation, Writing – original draft. SS: Software, Investigation, Methodology, Writing – review and editing, Supervision, Funding acquisition, Conceptualization, Writing – original draft, Formal Analysis, Data curation, Visualization, Validation, Resources, Project administration.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2025.1610115/full#supplementary-material

References

Abubakar, A. U., Kau, K. A., Hassan, M., and Tabra, M. S. (2020). Prediction of compressive strength in high strength concrete with steel fiber addition using support vector machine algorithm. Sustain. Struct. Mater. An Int. J. 3 (1), 25–36. doi:10.26392/SSM.2020.03.01.025

CrossRef Full Text | Google Scholar

Acikgenc, M., Ulas, M., and Alyamaç, K. E. (2015). Using an artificial neural network to predict mix compositions of steel fiber-reinforced concrete. Arabian J. Sci. Eng. 40, 407–419. doi:10.1007/s13369-014-1549-x

CrossRef Full Text | Google Scholar

Alyousef, R., Rehman, M. F., Khan, M., Fawad, M., Khan, A. U., Hassan, A. M., et al. (2023). Machine learning-driven predictive models for compressive strength of steel fiber reinforced concrete subjected to high temperatures. Case Stud. Constr. Mater. 19, e02418. doi:10.1016/j.cscm.2023.e02418

CrossRef Full Text | Google Scholar

Asteris, P. G., Gavriilaki, E., Touloumenidou, T., Koravou, E. E., Koutra, M., Papayanni, P. G., et al. (2022). Genetic prediction of ICU hospitalization and mortality in COVID-19 patients using artificial neural networks. J. Cell. Mol. Med. 26 (5), 1445–1455. doi:10.1111/jcmm.17098

PubMed Abstract | CrossRef Full Text | Google Scholar

Awolusi, T. F., Oke, O. L., Akinkurolere, O. O., Sojobi, A. O., and Aluko, O. G. (2019). Performance comparison of neural network training algorithms in the modeling properties of steel fiber reinforced concrete. Heliyon 5 (1), e01115. doi:10.1016/j.heliyon.2018.e01115

PubMed Abstract | CrossRef Full Text | Google Scholar

Babalola, O. E., Awoyera, P. O., Le, D. H., and Romero, L. B. (2021). A review of residual strength properties of normal and high strength concrete exposed to elevated temperatures: impact of materials modification on behaviour of concrete composite. Constr. Build. Mater. 296, 123448. doi:10.1016/j.conbuildmat.2021.123448

CrossRef Full Text | Google Scholar

Challagulla, S. P., Parimi, C., Pradeep, S., and Farsangi, E. N. (2021). Estimation of dynamic design parameters for buildings with multiple sliding non-structural elements using machine learning. Int. J. Struct. Eng. 11 (2), 147–172. doi:10.1504/ijstructe.2021.114262

CrossRef Full Text | Google Scholar

Chen, H., Yang, J., and Chen, X. (2021). A convolution-based deep learning approach for estimating compressive strength of fiber reinforced concrete at elevated temperatures. Constr. Build. Mater. 313, 125437. doi:10.1016/j.conbuildmat.2021.125437

CrossRef Full Text | Google Scholar

Dong, J. F., Wang, Q. Y., Guan, Z. W., and Chai, H. K. (2022). High-temperature behaviour of basalt fibre reinforced concrete made with recycled aggregates from earthquake waste. J. Build. Eng. 48, 103895. doi:10.1016/j.jobe.2021.103895

CrossRef Full Text | Google Scholar

Graupe, D. (2013). Principles of artificial neural networks. World Sci. 7. doi:10.1142/8868

CrossRef Full Text | Google Scholar

Greenough, T., and Nehdi, M. (2008). Shear behavior of fiber-reinforced self-consolidating concrete slender beams. ACI Mater. J. 105 (5), 468–477.

Google Scholar

Hossain, F. Z., Shahjalal, M., Islam, K., Tiznobaik, M., and Alam, M. S. (2019). Mechanical properties of recycled aggregate concrete containing crumb rubber and polypropylene fiber. Constr. Build. Mater. 225, 983–996. doi:10.1016/j.conbuildmat.2019.07.245

CrossRef Full Text | Google Scholar

Hossain, K. M., Gladson, L. R., and Anwar, M. S. (2017). Modeling shear strength of medium-to ultra-high-strength steel fiber-reinforced concrete beams using artificial neural network. Neural Comput. Appl. 28, 1119–1130. doi:10.1007/s00521-016-2417-2

CrossRef Full Text | Google Scholar

Hossain, M. M., Uddin, M. N., and Hossain, M. A. S. (2023). Prediction of compressive strength ultra-high steel fiber reinforced concrete (UHSFRC) using artificial neural networks (ANNs). Mater. Today Proc. doi:10.1016/j.matpr.2023.02.409

CrossRef Full Text | Google Scholar

Hwang, J. H., Lee, D. H., Kim, K. S., Ju, H., and Seo, S. Y. (2013). Evaluation of shear performance of steel fibre reinforced concrete beams using a modified smeared-truss model. Mag. Concr. Res. 65 (5), 283–296. doi:10.1680/macr.12.00009

CrossRef Full Text | Google Scholar

Kang, M. C., Yoo, D. Y., and Gupta, R. (2021). Machine learning-based prediction for compressive and flexural strengths of steel fiber-reinforced concrete. Constr. Build. Mater. 266, 121117. doi:10.1016/j.conbuildmat.2020.121117

CrossRef Full Text | Google Scholar

Kavya, B. R., Sureshchandra, H. S., Prashantha, S. J., and Shrikanth, A. S. (2022). Prediction of mechanical properties of steel fiber-reinforced concrete using CNN. Jordan J. Civ. Eng. 16 (2).

Google Scholar

Khan, K., Ahmad, W., Amin, M. N., Ahmad, A., Nazar, S., and Alabdullah, A. A. (2022). Compressive strength estimation of steel-fiber-reinforced concrete and raw material interactions using advanced algorithms. Polymers 14 (15), 3065. doi:10.3390/polym14153065

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, S., Rahmani, H., Shah, S. A. A., Bennamoun, M., Medioni, G., and Dickinson, S. (2018). A guide to convolutional neural networks for computer vision. Morgan and Claypool Publ. 8 (1), 1–207. doi:10.2200/S00822ED1V01Y201712COV015

CrossRef Full Text | Google Scholar

Kodur, V. K. R. (2000). “Spalling in high strength concrete exposed to fire: concerns, causes, critical parameters and cures,” in Advanced technology in structural engineering, 1–9.

Google Scholar

Lee, S. C. (2003). Prediction of concrete strength using artificial neural networks. Eng. Struct. 25 (7), 849–857. doi:10.1016/s0141-0296(03)00004-x

CrossRef Full Text | Google Scholar

Mahesh, R. R., and Sathyan, D. (2022). Modelling the hardened properties of steel fiber reinforced concrete using ANN. Mater. Today Proc. 49, 2081–2089. doi:10.1016/j.matpr.2021.08.311

CrossRef Full Text | Google Scholar

Mahmood, W., Mohammed, A. S., Asteris, P. G., Kurda, R., and Armaghani, D. J. (2022). Modeling flexural and compressive strengths behaviour of cement-grouted sands modified with water reducer polymer. Appl. Sci. 12 (3), 1016. doi:10.3390/app12031016

CrossRef Full Text | Google Scholar

Mahmood, W., Mohammed, A. S., Sihag, P., Asteris, P. G., and Ahmed, H. (2021). Interpreting the experimental results of compressive strength of hand-mixed cement-grouted sands using various mathematical approaches. Archives Civ. Mech. Eng. 22 (1), 19. doi:10.1007/s43452-021-00341-0

CrossRef Full Text | Google Scholar

Majdzadeh, F., Soleimani, S. M., and Banthia, N. (2006). Shear strength of reinforced concrete beams with a fiber concrete matrix. Can. J. Civ. Eng. 33 (6), 726–734. doi:10.1139/l05-118

CrossRef Full Text | Google Scholar

Nana, W. S. A., Tran, H. V., Goubin, T., Kubisztal, G., Bennani, A., and Bui, T. T. (2021). Behaviour of macro-synthetic fibers reinforced concrete: experimental, numerical and design code investigations. Structures 32. 1271–1286. doi:10.1016/j.istruc.2021.03.080

CrossRef Full Text | Google Scholar

Nili, M., Azarioon, A., Danesh, A., and Deihimi, A. (2018). Experimental study and modeling of fiber volume effects on frost resistance of fiber reinforced concrete. Int. J. Civ. Eng. 16, 263–272. doi:10.1007/s40999-016-0122-2

CrossRef Full Text | Google Scholar

Oey, T., Jones, S., Bullard, J. W., and Sant, G. (2020). Machine learning can predict setting behavior and strength evolution of hydrating cement systems. J. Am. Ceram. Soc. 103 (1), 480–490. doi:10.1111/jace.16706

CrossRef Full Text | Google Scholar

Pazouki, G., and Pourghorban, A. (2022). Anticipation of the compressive strength of steel fiber-reinforced concrete by different types of artificial intelligence methods. Struct. Concr. 23 (6), 3834–3848. doi:10.1002/suco.202100776

CrossRef Full Text | Google Scholar

Priddy, K. L., and Keller, P. E. (2005). Artificial neural networks: an introduction, 68. Bellingham, WA: SPIE press.

Google Scholar

Rahman, J., Ahmed, K. S., Khan, N. I., Islam, K., and Mangalathu, S. (2021). Data-driven shear strength prediction of steel fiber reinforced concrete beams using machine learning approach. Eng. Struct. 233, 111743. doi:10.1016/j.engstruct.2020.111743

CrossRef Full Text | Google Scholar

Ramkumar, K. B., Rajkumar, P. K., Ahmmad, S. N., and Jegan, M. (2020). A review on performance of self-compacting concrete–use of mineral admixtures and steel fibres with artificial neural network application. Constr. Build. Mater. 261, 120215. doi:10.1016/j.conbuildmat.2020.120215

CrossRef Full Text | Google Scholar

Salehian, H., and Barros, J. A. (2017). Prediction of the load carrying capacity of elevated steel fibre reinforced concrete slabs. Compos. Struct. 170, 169–191. doi:10.1016/j.compstruct.2017.03.002

CrossRef Full Text | Google Scholar

Samuel, A. L. (2000). Some studies in machine learning using the game of checkers. IBM J. Res. Dev. 44 (1.2), 206–226. doi:10.1147/rd.441.0206

CrossRef Full Text | Google Scholar

Sarıdemir, M., Topçu, İ. B., Özcan, F., and Severcan, M. H. (2009). Prediction of long-term effects of GGBFS on compressive strength of concrete by artificial neural networks and fuzzy logic. Constr. Build. Mater. 23 (3), 1279–1286. doi:10.1016/j.conbuildmat.2008.07.021

CrossRef Full Text | Google Scholar

Serrano, R., Cobo, A., Prieto, M. I., and de las Nieves González, M. (2016). Analysis of fire resistance of concrete with polypropylene or steel fibers. Constr. Build. Mater. 122, 302–309. doi:10.1016/j.conbuildmat.2016.06.055

CrossRef Full Text | Google Scholar

Shafighfard, T., Bagherzadeh, F., Rizi, R. A., and Yoo, D. Y. (2022). Data-driven compressive strength prediction of steel fiber reinforced concrete (SFRC) subjected to elevated temperatures using stacked machine learning algorithms. J. Mater. Res. Technol. 21, 3777–3794. doi:10.1016/j.jmrt.2022.10.153

CrossRef Full Text | Google Scholar

Shafighfard, T., Cender, T. A., and Demir, E. (2021). Additive manufacturing of compliance optimized variable stiffness composites through short fiber alignment along curvilinear paths. Addit. Manuf. 37, 101728. doi:10.1016/j.addma.2020.101728

CrossRef Full Text | Google Scholar

Shafighfard, T., Demir, E., and Yildiz, M. (2019). Design of fiber-reinforced variable-stiffness composites for different open-hole geometries with fiber continuity and curvature constraints. Compos. Struct. 226, 111280. doi:10.1016/j.compstruct.2019.111280

CrossRef Full Text | Google Scholar

Shahjalal, M., Islam, K., Ahmed, K. S., Tamanna, K., and Alam, M. S. (2020). “Mechanical characterization of rubberized fiber reinforced recycled aggregate concrete for bridge barriers,” in IABSE-JSCE joint conference on advances in bridge engineering-IV (Dhaka Bangladesh).

Google Scholar

Shahjalal, M., Islam, K., Rahman, J., Ahmed, K. S., Karim, M. R., and Billah, A. M. (2021). Flexural response of fiber reinforced concrete beams with waste tires rubber and recycled aggregate. J. Clean. Prod. 278, 123842. doi:10.1016/j.jclepro.2020.123842

CrossRef Full Text | Google Scholar

Sharma, S., Sharma, S., and Athaiya, A. (2017). Activation functions in neural networks. Towards Data Sci. 6 (12), 310–316. doi:10.33564/ijeast.2020.v04i12.054

CrossRef Full Text | Google Scholar

Shende, A. M., Yadav, K. P., and Pande, A. M. (2022). “Artificial neural network (ANN) models for prediction of steel fibre-reinforced concrete strength,” in Recent advancements in civil engineering: select proceedings of ACE 2020 (Singapore: Springer), 223–230.

CrossRef Full Text | Google Scholar

Szandała, T. (2021). Review and comparison of commonly used activation functions for deep neural networks. Bio-inspired neurocomputing, 203–224. doi:10.1007/978-981-15-5495-7_11

CrossRef Full Text | Google Scholar

Tahenni, T., Bouziadi, F., Boulekbache, B., and Amziane, S. (2021). Experimental and numerical investigation of the effect of steel fibres on the deflection behaviour of reinforced concrete beams without stirrups. Structures 33, 1603–1619. doi:10.1016/j.istruc.2021.05.005

CrossRef Full Text | Google Scholar

Venkateshwaran, A., and Tan, K. H. (2018). Arching action in steel fiber-reinforced concrete flat slabs. ACI Struct. J. 115 (6). doi:10.14359/51702447

CrossRef Full Text | Google Scholar

Wang, S., Wu, R., Gong, F., Xia, J., Zhao, Y., and Zeng, B. (2025). Service life evaluation of marine concrete structures considering spatial and temporal characteristics: a framework based on multi training-MCS-NLS. Eng. Struct. 322, 119193. doi:10.1016/j.engstruct.2024.119193

CrossRef Full Text | Google Scholar

Wang, S., Xia, P., Gong, F., Zeng, Q., Chen, K., and Zhao, Y. (2024). Multi objective optimization of recycled aggregate concrete based on explainable machine learning. J. Clean. Prod. 445, 141045. doi:10.1016/j.jclepro.2024.141045

CrossRef Full Text | Google Scholar

Wang, S., Xia, P., Wang, Z., Meng, T., and Gong, F. (2023). Intelligent mix design of recycled brick aggregate concrete based on swarm intelligence. J. Build. Eng. 71, 106508. doi:10.1016/j.jobe.2023.106508

CrossRef Full Text | Google Scholar

Wang, X., Qin, Y., Wang, Y., Xiang, S., and Chen, H. (2019). ReLTanh: an activation function with vanishing gradient resistance for SAE-based DNNs and its application to rotating machinery fault diagnosis. Neurocomputing 363, 88–98. doi:10.1016/j.neucom.2019.07.017

CrossRef Full Text | Google Scholar

Wu, H., Lin, X., and Zhou, A. (2020). A review of mechanical properties of fibre reinforced concrete at elevated temperatures. Cem. Concr. Res. 135, 106117. doi:10.1016/j.cemconres.2020.106117

CrossRef Full Text | Google Scholar

Xiong, M. X., and Liew, J. R. (2015). Spalling behavior and residual resistance of fibre reinforced ultra-high-performance concrete after exposure to high temperatures. Mater. Construcción 65 (320), e071. doi:10.3989/mc.2015.00715

CrossRef Full Text | Google Scholar

Zheng, D., Wu, R., Sufian, M., Kahla, N. B., Atig, M., Deifalla, A. F., et al. (2022). Flexural strength prediction of steel fiber-reinforced concrete using artificial intelligence. Materials 15 (15), 5194. doi:10.3390/ma15155194

PubMed Abstract | CrossRef Full Text | Google Scholar