Extremum information transfer over networks for remote estimation and distributed learning

1 Introduction

The importance of distributed systems cannot be overstated in the current technological paradigm. Many modern systems, such as sensor networks, robotic teams and multi-core microprocessors, are designed from the ground up to be distributed. Other systems are inherently distributed such as social networks, vehicular networks, micro-grids and the internet of things. Due to the overwhelming availability of inexpensive sensing devices and storage, a high volume of data can be easily generated and stored locally. The combination of a data rich world and high computing power of today has provided many exciting developments such as the new wave (a tsunami¹ might be a more appropriate term) of artificial intelligence algorithms and applications in virtually every existing technological field.

However, distributed systems are special. Because they are designed to work together, they must communicate to coordinate actions to solve a common problem. Anyone who has ever worked on the same project with a large group of people can attest that the key for successfully completing it is to communicate as much and as often as possible. Communication networks used to exchange information in a distributed system are often limited. This feature leads to many difficulties that prevent the system from achieving its full performance: 1. every robot/sensor/machine/device/human in the system has access to a lot more data than it is able to transmit; thus, the agents operate under incomplete information for the most part; 2. communication, more specifically wireless communication, consumes a lot of power, which limits not only how often an agent can communicate, but also the signal to noise ratio one is able to use for each transmission; 3. the agents are distributed; thus, they may operate without synchrony due to random delays, clock-drift or a complete absence of a reference signal. These three issues lead to inefficiencies that are inherent to the optimal design of distributed systems and lead to a wealth of under-explored research problems at the interface of communication, control and optimization.

First, we focus on fundamental issues when the agents in a network system have more information to transmit than what the communication link can support. We formulate a canonical problem that leads to the notion of max-scheduling, in which the transmitter only sends the extremum information (in an appropriate sense) to the receiver. The principle learned from this problem formulation and solution extends to many other variants such as unicast and broadcast networks, and a transmitter with an energy harvesting battery, among others. Of utmost importance is the notion of ranking information sources in a list and transmitting only the top-K entries from the list, when the channel can only support K sources. In the second part of the paper, we study how we can decentralize the top-K principle based on a probabilistic threshold strategy, and by means of a strategy based on distributed estimation over a local communication network. Then, we show that the problem of finding the top-K observations in the network can be mapped into an optimization problem, called quantile inference; that problem admits a natural distributed implementation.

Finally, we turn our attention to another fundamental problem in networked information processing. Suppose that an agent has many neighbors, but at any given time can only communicate with one. Which neighbor should this agent talk to? We address this question in the context of distributed learning, and we introduce the notion of max-dissent, where an agent communicates with the neighbor with the largest distance between their states. Similarly to the situation discussed in the first part of the paper, there is a fundamental principle here that emerges from the communication constraint, which reinforces the notion that communicating extremum information is beneficial to the overall goal of the system. We summarize this principle as follows: When an agent is faced with the choice of what to transmit and/or with whom to communicate, the agent should rank information based on a criterion, and choose the top element(s), and transmit information based on that ranking.

The main goal of this paper is to systematically review the notion of extremum information and algorithms to compute it in centralized and distributed settings. The main advantage of using extremum information compared to other algorithms is that it often leads in substantial improvements in performance and convergence speed. This paper contains several examples of such improvements. However, the gains in performance and convergence rate obtained from using extremum information come at a price, which is the communication overhead required to compute the extremum information. Moreover, the implementation of this principle is not always straightforward, and still poses challenges. We suggest several possible ways of overcoming these practical difficulties as future research topics at the end of the paper.

1.1 Related literature

Multi-agent systems are defined as a collection of many decision making units that collaborate to perform a complex task, that would be infeasible to complete by any single agent (Olfati-Saber et al., 2007). There is an incredible number of applications that can be modeled as multi-agent systems. The most classical examples of such systems are wireless sensor networks and robotic networks. These are engineered systems, where the components are jointly designed to facilitate collaboration. Many non-engineered systems are multi-agent. For example, economic networks, and bacterial colonies can also be understood and analyzed through that lens. Many such systems coordinate actions by sharing information over a communication network, and communication is often imperfect. Issues such as noise, delay, quantization, packet-drops, and limited connectivity may prevent a distributed system from emulating a centralized unit.

One particular type of “communication imperfection” is caused by interference. Broadly speaking, interference happens due to the superposition (e.g., in time or frequency) of two or more signals, such that the receiver is not able to distinguish what information was embedded in the original waveforms. There are many ways to model interference and there exist many significant results in the field of information theory on the fundamental limits of interference channels (El Gamal and Kim, 2011). Our focus herein is not to tackle the capacity of the interference channel, but instead, we look at interference as a limit on the number of communication packets/sources that can be simultaneously supported over a link in the network. In order to address this problem, we see communication as a commodity, with the links having a predetermined capacity, which we denote by K ≥ 1.

Therefore, if we specify that a link has capacity K, we mean that the link supports up to K concurrent packets (by any number of transmitters and receivers). For example, if more than K packets are simultaneously transmitted by any combination of agents (e.g., K + 1 agents transmitting one packet each, or one agent transmitting K + 1 packets, etc.) a communication failure occurs, and a collision is declared (Vasconcelos and Martins, 2017; Vasconcelos and Martins, 2019). Therefore, the communication constraint imposes a strategic behavior at the transmitters: if every agent communicates a packet at the same time all the time, and there are more than K agents, collisions will occur all of the time, and no packets will go through the channel. The agents need to be selective in what they transmit to the receiver. In other words, the agents need to be strategic (Farokhi et al., 2016). Similarly, if one agent has more than K packets to communicate at any given time, a few packets may need to be discarded. The question is, what to discard, and how to implement such a policy. The answer to this fundamental question is one of the centerpieces of this article.

The idea of selecting the most relevant observations from a larger set is a well-studied problem in control and signal processing (Joshi and Boyd, 2008; Moon and Başar, 2017; Hashemi et al., 2020). These results rely on knowledge of the statistical model of the sensed data, and often result in sensor selection policies which are not data-driven. In a different class of problems, data is transmitted over a network when its magnitude surpasses a certain threshold (Yun et al., 2023; Soleymani and Gündüz, 2023; Lipsa and Martins, 2011; Imer and Basar, 2010, and references therein). Such event-based policies are interesting because they allow the channel to be used only when the data is relevant, i.e., it is worth to transmit it, otherwise the transmitter should remain silent. In a similar fashion, when the transmitter has access to many data sources and needs to decide which one to send, the optimal policy requires comparisons among the sources to determine which one is the most relevant. In this case, the comparison is not against a threshold, although a threshold can be used as a proxy to determined the most relevant observation, as we will discuss later. Another body of work relates the notion of Age of Information (AoI) (Yates et al., 2021) and the event-based scheduling of multiple information sources (Chen et al., 2021). While there might exist a connection between these, it is still unclear how AoI relates to the notion of extremum information.

Finally, the notion of dissent is a topic of interest in models of information dissemination over social networks (Acemoglu et al., 2010; Liu et al., 2018; Mei et al., 2022; Zhang et al., 2022). However, there has been limited work on using dissent to produce beneficial results in distributed settings. Our idea is to instead of avoiding agents with whom we disagree, we use them to reduce the overall disagreement in the network. We do that by making allowing them to communicate and average their measurements. The maximal dissent gossip algorithm introduced by Verma et al. (2023) can also be interpreted as extremum information. Furthermore, it reveals an intuitive principle in distributed information processing that shows that to expedite collectively learning, we should enable the agents with largest disagreement to come to a consensus at every time step.

1.2 Paper organization

The paper is organized into three main parts. In the first part, we introduce a canonical remote estimation problem that leads to the max-scheduling principle for independent Gaussian information sources. We then proceed to discuss a similar principle when the source distributions are unknown, but restricting ourselves to the class of linear estimators. Such a scheme is effective even when the probabilistic model for the source is not available to the system designer. At the end of the first part, we make the case for a generalized version of max-scheduling called the Top-K scheduling. In the second part of the paper, we begin to study how to distribute the Top-K strategy by using threshold strategies and then allow for local communication among the agents, ultimately leading to a distributed optimization problem. In the last part of the paper, we present a second principle called max-dissent, which is extremely useful in the context of distributed learning. In every section, we discuss the implementation challenges and provide a few suggestions to overcome them. We conclude the paper with pointers to open problems and our perspective for future work on these problems.

2 The max-scheduling principle for remote estimation

Consider the following prototypical problem shown in Figure 1: there are two sensors communicating with one remote receiver. The sensors measure two different physical quantities modeled by possibly correlated Gaussian random variables. The receiver is interested in obtaining both, however, the communication link can only allow for the transmission of one the sensors at a time. Our goal as a system designer is to ascribe to the transmitter and the receiver a pair of policies that jointly optimize a common performance metric. We can understand this system in two ways: 1. this is a system where all of the information is available at a single node, but due to internal constraints (heterogeneous sensing modalities, or incompatibilities at the level of packet generation) the agent is not allowed to combine the information into a single packet for transmission; 2. the performance of this system serves as a lower bound on the performance of a decentralized system communicating over a collision channel, and scheduling what gets transmitted at every time slot to avoid collisions (Vasconcelos and Mitra, 2020).

Figure 1

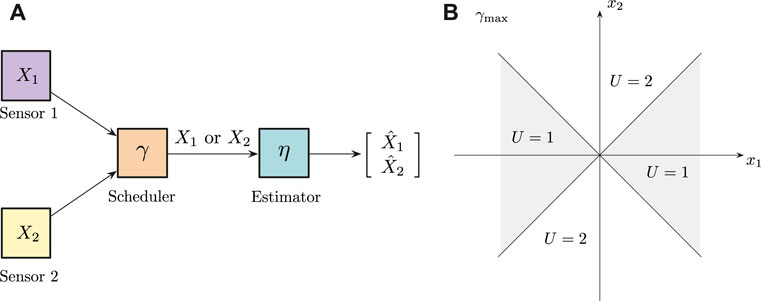
Figure 1. (A) Observation-driven sensor scheduling system with two sensors, one scheduler and one receiver. (B) Decision regions corresponding to the Max-scheduling policy, γ_max.

Mathematically, suppose that $X_i\sim \mathcal{N}(0,{\sigma }_i^2)$, i ∈ {1, 2}, and assume that all sources have stationary statistics. At a given time, the scheduler observes one realization of X₁ and X₂ decides using a scheduling policy, whether X₁ or X₂ will be transmitted to the destination. One crucial aspect of our setup that distinguishes it from the field of information theory, is that the communication happens in real time, i.e., we do not make our decisions based on observing blocks of data, which would necessarily incur communication delays. A scheduling policy is a map from the observation space ${\mathbb{R}}^2$ to the set {1, 2}. Let the decision variable be U ∈ {1, 2}, which is computed according to

$U=\gamma \left(X_1,X_2\right).(1)$

Based on U, the information sent over the channel is determined as follows:

$Y=\left\{\begin{array}{cc}\left(1,X_1\right),\hfill & \text{if}U=1\hfill \\ \left(2,X_2\right),\hfill & \text{if}U=2,\hfill \end{array}\right.(2)$

where the index in front of the information variable is important since the receiver needs to know which information source generated the real number observed in the packet, i.e., it indicates the origin of the communication packet.

At the destination, the receiver implements an estimation policy, which attempts to reconstruct both sources based on the observation received over the link, Y. We define η as such estimation policy, and the estimates are computed as follows:

$\left[\begin{array}{c}\hfill {\widehat{X}}_1\hfill \\ \hfill {\widehat{X}}_2\hfill \end{array}\right]=\eta \left(Y\right).(3)$

From the designer’s perspective, the optimization problem that we are interested in solving is the following:

$\underset{\left(\gamma ,\eta \right)\in \mathrm{\Gamma }\times \mathrm{H}}{\min }\mathbf{E}\left[{\left(X_1-{\widehat{X}}_1\right)}^2+{\left(X_2-{\widehat{X}}_2\right)}^2\right],(4)$

where Γ and H are the spaces of all admissible scheduling and estimation policies, respectively.

2.1 Solving the scheduling problem

Although this problem admits a very simple description, obtaining the jointly optimal solution in closed form is often intractable due to the fact that a convex parametrization for the objective in terms of γ and (or) η is not available. Even when the estimator is constrained to the class of piece-wise affine functions, the resulting optimization problem turns out to be non-convex. For general nonlinear estimation policies such as the minimum mean-squared error estimation, the problem becomes infinite dimensional in addition to being non-convex, which further complicates our analysis. The curious reader is referred to (Vasconcelos et al., 2020; Vasconcelos and Mitra, 2020) for a detailed explanation of this issue.

There are two alternatives to address these difficulties: 1. we may relax the formulation from jointly optimal to the so-called, person-by-person optimal (PBPO) solution (Yüksel and Başar, 2013); 2. we may constrain the estimator to be piece-wise affine and deal with the non-convexity using alternative global optimization techniques. In the following subsections, we address each of these cases.

2.1.1 Game theoretic approach

The optimization problem can be understood as a signaling game (Akyol et al., 2016) between two players, the transmitter and the receiver. The players have the same objective function, but their information patterns differ. In a signaling game, the transmitter’s decision affects the information pattern of the receiver, creating an intricate dependency between their policies, which lead to challenging problems with often counter-intuitive results. In general, the concept of joint optimality is much stronger than the notion of a PBPO solution, because every jointly optimal pair of policies is PBPO, but the reverse is not necessarily true. Therefore, instead of requiring joint optimality, we settle for a PBPO solution.

To find a PBPO solution for this problem, we use a guess-and-verify method. In other words, we first conjecture that a specific pair of policies γ^⋆, η^⋆ is PBPO, and we show that the transmitter policy γ^⋆ is optimal for the receiver policy η^⋆ and vice versa.

Our starting point is what we called the max-scheduling policy (Vasconcelos and Mitra, 2020), which is defined as follows:

${\gamma }_{\max }\left(x_1,x_2\right)\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\left\{\begin{array}{cc}1,\hfill & |x_1|\ge |x_2|\hfill \\ 2,\hfill & \text{otherwise}.\hfill \end{array}\right.(5)$

In its essence, max-scheduling is a greedy policy that selects the observation that will reduce the expected error by the largest amount possible. On the receiver end, we know that the optimal estimation policy will always be the conditional expectation of the random variables X₁ and X₂, given what the scheduler has transmitted. The interesting factor here is that if the transmitter is using the max-scheduling policy, the receiver automatically knows that the magnitude of the non-transmitted source is upper-bounded by the magnitude of the transmitted observation. For example, suppose that the receiver observes Y = (2, x₂) over the channel. The receiver immediately learns that X₂ = x₂ and that

$-|x_2|<X_1<|x_2|.(6)$

Therefore, the optimal estimate of X₁ given Y = (2, x₂) is

${\widehat{X}}_1=\mathbf{E}\left[X_1\mid -x_2<X_1<x_2\right].(7)$

From the symmetry of the Gaussian density of X₁ around its mean μ₁ = 0, the conditional expectation above is simply equal to 0, leading to what we call the mean-estimation policy, which is given by:

${\eta }_{\text{mean}}\left(1,x_1\right)=\left[\begin{array}{c}\hfill x_1\hfill \\ \hfill 0\hfill \end{array}\right]\text{and}{\eta }_{\text{mean}}\left(2,x_2\right)=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill x_2\hfill \end{array}\right].(8)$

It turns out that by fixing the estimation policy to be η_mean, the optimal transmission policy is exactly equal to the max-scheduling policy γ_max. Thereby establishing a pair of policies from which the agents do not have an incentive to deviate. In the literature, a pair or policies that satisfies this property is often called a person-by-person optimal policy, which in the game-theoretic literature is referred to as a Nash equilibrium (Hespanha, 2017). The following result was obtained in (Vasconcelos and Mitra, 2020), and to the best of our knowledge, it is the first occurrence of the solution in the literature:

If X₁ and X₂ are independent with arbitrary variances, or correlated with the same variance, zero mean Gaussian random variables, (γ_max, η_mean) is a person-by-person optimal strategy for the observation-driven sensor scheduling problem.

To illustrate the benefit of using an observation-driven policy rather than a scheduling policy based solely on the statistics of the sources, consider the following scenario. Suppose the scheduler uses a policy which ignores the realization of the observed data, and always sends the observation with the largest variance. This is a reasonable policy, since the random variable with the largest variance will also lead to large magnitude observations. We refer to that policy as open-loop because it is not adapted to the variables X₁ and X₂. We denote the open-loop policy by γ_open.

The performance of max-scheduling and mean-estimation is given by

$\mathcal{J}\left({\gamma }_{\max },{\eta }_{\text{mean}}\right)=\mathbf{E}\left[\min \left\{X_1^2,X_2^2\right\}\right],(9)$

while the performance of the open-loop policy is given by

$\mathcal{J}\left({\gamma }_{\text{open}},{\eta }_{\text{mean}}\right)=\min \left\{{\sigma }_1^2,{\sigma }_2^2\right\}.(10)$

Since $\min \{x_1^2,x_2^2\}$ is a concave function of x₁, x₂, Eqs 9, 10 are related via Jensen’s inequality as:

$\mathcal{J}\left({\gamma }_{\max },{\eta }_{\text{mean}}\right)\le \mathcal{J}\left({\gamma }_{\text{open}},{\eta }_{\text{mean}}\right).(11)$

Figure 2 below shows the gap between the open-loop strategy and the observation-driven strategy for a fixed value of ${\sigma }_2^2=1$. The difference between these two curves is the so-called value-of-information (VoI) (Soleymani et al., 2022; Soleymani et al., 2023). The VoI corresponds to how much one can gain from making optimal use of information available to the scheduler relative to policies that are oblivious to this information.

Figure 2

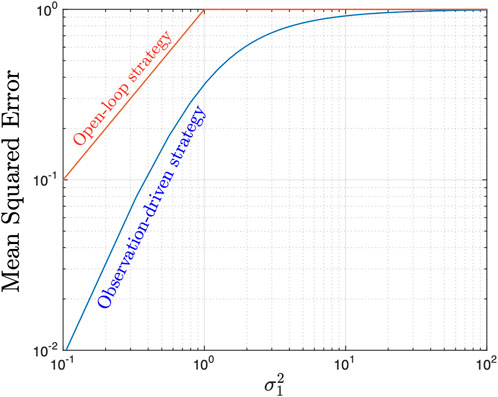
Figure 2. Mean-squared estimation error for the open-loop strategy and the PBPO max-scheduling strategy for two independent Gaussian sources with variances ${\sigma }_1^2$ (variable) and ${\sigma }_2^2=1$ (fixed). The gap between these curves is the VoI for the observation-driven sensor scheduling problem.

2.1.2 Switched-linear estimator approach

The drawback from using the person-by-person optimality approach is the inability to guarantee that other solution pairs with even better performance do or do not exist. For example, there is no systematic way to obtain other solution pairs using the guess-and-verify method. One way to deal with that difficulty is to use another suboptimal approach that allows for systematic analysis and design. Constraining the estimator to lie within the class of switched linear estimators, we obtain a very interesting class of optimization problems with appealing properties known as difference-of-convex programs (Nouiehed et al., 2019).

Suppose that when the estimator receives Y = (1, x₁), instead of computing the conditional expectation of X₂ (a non-linear estimate), the estimator uses a linear function to do so, i.e.,

${\widehat{X}}_2=a_1{x}_1.(12)$

Similarly, the estimator outputs

${\widehat{X}}_1=a_2{x}_2,(13)$

when it receives Y = (2, x₂). More precisely, the switched-linear estimation strategy is given by

${\eta }_{\left(a_1,a_2\right)}^{\text{linear}}\left(1,x_1\right)=\left[\begin{array}{c}\hfill x_1\hfill \\ \hfill a_2{x}_2\hfill \end{array}\right]\text{and}{\eta }_{\left(a_1,a_2\right)}^{\text{linear}}\left(2,x_2\right)=\left[\begin{array}{c}\hfill a_1{x}_1\hfill \\ \hfill x_2\hfill \end{array}\right].(14)$

The two variables $(a_1,a_2)\in {\mathbb{R}}^2$ parameterize this estimation strategy, and consequently also fix the optimal scheduling strategy, which is:

${\gamma }_{\left(a_1,a_2\right)}^{\star }=\left\{\begin{array}{cc}1,\hfill & \text{if}|x_2-a_1{x}_1|\le |x_1-a_2{x}_2|\hfill \\ 2,\hfill & \text{otherwise.}\hfill \end{array}\right.(15)$

Using this pair of policies, we obtain the following objective function:

$\tilde{\mathcal{J}}\left(a_1,a_2\right)\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\mathcal{J}\left({\gamma }_{\left(a_1,a_2\right)}^{\star },{\eta }_{\left(a_1,a_2\right)}^{\text{linear}}\right)=\mathbf{E}\left[\min \left\{{\left(X_1-a_2{X}_2\right)}^2,{\left(X_2-a_1{X}_1\right)}^2\right\}\right].(16)$

Therefore, the minimizers of $\tilde{\mathcal{J}}$ define the optimal switched-linear mean-squared error estimator. We are interested in solving the following unconstrained optimization problem:

$\left(a_1^{\star },a_2^{\star }\right)=\arg \underset{\left(a_1,a_2\right)\in {\mathbb{R}}^2}{\min }\tilde{\mathcal{J}}\left(a_1,a_2\right).(17)$

Due to the fact that the point-wise minimum of quadratic functions is not convex, at first glance, this objective function seems problematic. However, using a very simple algebraic trick, we can obtain the following representation as a difference-of-convex (DC) functions:

$\tilde{\mathcal{J}}\left(a_1,a_2\right)=\mathbf{E}\left[{\left(X_1-a_2{X}_2\right)}^2+{\left(X_2-a_1{X}_1\right)}^2\right]-\mathbf{E}\left[\max \left\{{\left(X_1-a_2{X}_2\right)}^2,{\left(X_2-a_1{X}_1\right)}^2\right\}\right].(18)$

The DC representation allows for a heuristic algorithm known as the Convex-Concave Procedure (CCP) (Yuille and Rangarajan, 2003). The same algorithm is also called Sequential Convex Programming (Lipp and Boyd, 2016) and Difference-of-Convex Programming Algorithm (DCA) (Ahn et al., 2017). The idea of the algorithm is very simple: to replace the second term of the DC decomposition with an affine approximation at a point, and solve the resulting convex optimization problem, obtaining an upper bound for the solution of the original problem.

The CCP is appealing for three reasons: (1) the sequence of points generated using CCP is guaranteed to converge to a local minimum of the objective function. There is no need for additional convergence analysis, and we do not need to use a diminishing step-size gradient descent algorithm, whose convergence is often slow, and not always guaranteed; (2) the resulting algorithm only requires the computation of a sub-gradient of the second term in the DC decomposition (see Eq. 20 below), and, in our case, there is no need to solve the additional convex optimization problem; and (3) CCP admits a data-driven implementation, which is important in applications where the probability density function of the variables X₁ and X₂ is unknown (Vasconcelos and Mitra, 2021).

2.1.3 Optimization algorithm

The algorithm is described by the following dynamical system, where $\left(a_1^{(k)},a_2^{(k)}\right)$ denotes a pair of estimator parameters at the kth iteration, and the constants ${\sigma }_1^2,{\sigma }_2^2$ and ρ are the variances and correlation for the two Gaussian sources X₁ and X₂:

$\left[\begin{array}{c}\hfill a_1^{\left(k+1\right)}\hfill \\ \hfill a_2^{\left(k+1\right)}\hfill \end{array}\right]=\frac{1}{2}\left[\begin{array}{cc}\hfill \frac{1}{{\sigma }_2^2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{{\sigma }_1^2}\hfill \end{array}\right]g\left(a_1^{\left(k\right)},a_2^{\left(k\right)}\right)+\rho \left[\begin{array}{c}\hfill {\sigma }_1/{\sigma }_2\hfill \\ \hfill {\sigma }_2/{\sigma }_1\hfill \end{array}\right],(19)$

where

$g\left(a_1,a_2\right)=-2\mathbf{E}\left[\begin{array}{c}\hfill \left(X_1-a_1{X}_2\right)X_2\mathbf{1}\left(|X_1-a_1{X}_2|\ge |X_2-a_2{X}_1|\right)\hfill \\ \hfill \left(X_2-a_2{X}_1\right)X_1\mathbf{1}\left(|X_1-a_1{X}_2|<|X_2-a_2{X}_1|\right)\hfill \end{array}\right].(20)$

The recursion above is guaranteed to converge to a point $(a_1^{\star },a_2^{\star })\in {\mathbb{R}}^2$, which is a locally optimal solution of Eq. 17. Notice that in this method we are not constrained by the dimension, independence, or correlation with identical variances between the two random variables X₁ and X₂. A very important observation that distinguishes this algorithm from standard stochastic gradient descent, is the fact that it does not require a diminishing step-size for convergence. This property leads to swift convergence to a locally optimal estimator, which is important in applications where the sources have higher dimensions, and if the source statistics change often, such that the estimator has to be updated by the designer with a high frequency.

Consider, for example, the scheduling of two Gaussian variables with variances ${\sigma }_1^2=1$, ${\sigma }_2^2=1.5$ and correlation coefficient ρ = 0.5. Since $\tilde{\mathcal{J}}$ is a function over ${\mathbb{R}}^2$ (in this illustrative example), we can visualize the optimization landscape, which is shown in Figure 3, where we can clearly observe the lack of convexity. There is a unique minimum, and therefore there are no spurious local minima for this set of parameters. It remains an open problem to determine whether the objective function in Eq. 17 has any spurious local minima or not for other parameter configurations and other distributions.

Figure 3

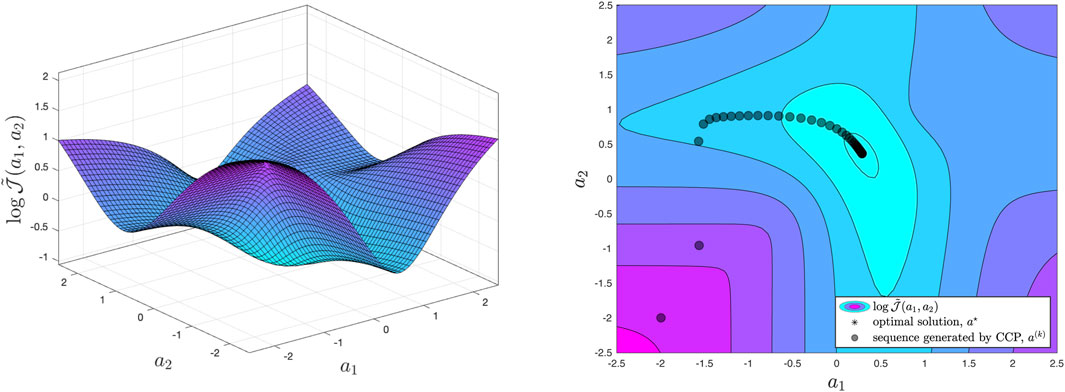
Figure 3. Non-convex optimization landscape for the scheduling problem with switched linear estimators. On the right we can visualize a sequence of points generated by the CCP applied to our problem. The sequence converges to a locally optimal solution, which is also globally optimal.

2.2 Practical considerations

The basic scheduling problem that we have discussed here is the simplest non-trivial instance of observation-driven scheduling. Since its inception, other more sophisticated versions of the problem have also been considered. Vasconcelos et al. (2020) studied the scheduling problem when the transmitter has an energy harvesting battery (Nayyar et al., 2013a). That version of the problem adds multiple layers of complexity to the basic formulation. Most notably, the presence of a battery introduces a temporal dependence between the stages of a sequential scheduling of i.i.d. sources and the optimal max-scheduling policy includes a time-varying threshold which controls if the scheduler will transmit any of the observations to the receiver at all. To obtain that result, (Vasconcelos et al., 2020), resorts to the coordinator approach (Nayyar et al., 2013b), which is a technique that can be used to solve decentralized stochastic control problems with non-classical information patterns (Yüksel and Başar, 2013).

Our basic problem formulation also admits data-driven solutions in the following sense. Suppose that the system designer does not know what is the probability distribution of the underlying sources, but has access to M data samples: ${\{x_1(k),x_2(k)\}}_{k=1}^M$. For example, the agent may only know that the data comes from a single distribution and that it is independent and identically distributed. In Vasconcelos and Mitra (2021), it was shown that this problem can be related to statistical learning (Vapnik, 1999; Tsiamis et al., 2022). We showed that the policies are learnable, i.e., that as the number of samples in the designer’s data set grows, the optimal solution to the data-driven version of CCP converges to the optimal solution of the original stochastic optimization problem. The data-driven approximation is based on empirical risk minimization, and by using CCP, we just need to estimate a sub-gradient similar to the one in Eq. 20 but replacing the expectation by its sample average, and the variances and the correlation coefficient, by their respective estimates. There are many advantages of using this method, with the most important being that it works for any joint probability distribution. The price that we pay when using this approach is that we are restricting our estimators to be linear (a similar version of the algorithm can be easily obtained by letting the estimators be affine functions). Therefore, there may be other nonlinear estimators that provide a better performance. However, as we have established, there are no known systematic methods to search for them.

3 Decentralization of max-scheduling for remote estimation–distributed top-K strategies

A natural extension of the problem described in the previous section involves N zero mean independent Gaussian sources being scheduled over a channel with capacity K < N. Using the lessons learned from max-scheduling, we may also show that given a set of independent observations from sources ${\{X_i\}}_{i=1}^N$, a person-by-person optimal strategy is for the scheduler to always transmit the K largest ones. Notice that, the indices of the sources scheduled for transmission change with every realization. To that end, consider the following partial ordering: x_[1] ≥ x_[2] ≥⋯ ≥ x_[N], where x_[i] ≥ x_[j] if and only if |x_[i]|≥|x_[j]|. A top-K scheduling strategy requires us to reorder all of the observations according to their magnitude and transmit ${\{([i],x_{[i]})\}}_{i=1}^K$ to the estimator. If all of the information is available at a centralized location, we are essentially done. However, more often than not, the observed data is distributed over many nodes in a network. It is often helpful to think that the network is comprised of many interconnected servers, each one with a local data set. Max-scheduling provides us with a general principle that tells us which observations should be communicated, but if the data is distributed across the aforementioned network, how can we determine which nodes/servers are holding the top-K measurements?

3.1 Thresholding strategies

First, let us assume that local communication among the nodes in the network is not available. For instance, the nodes are not allowed to talk to each other because there is no peer-to-peer infrastructure, or due to privacy concerns. However, the nodes can communicate with a common gateway or base-station by means of a channel with capacity K. One way to determine if a node i has a large observation is to use a correspondingly large threshold T_i. The ith node decides to transmit if the magnitude of its observation is larger than T_i, i.e.,

$U_i=\left\{\begin{array}{cc}1\hfill & \text{if}|X_i|>T_i\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}\right.(21)$

where U_i = 1 denotes transmission and U_i = 0 denotes no transmission. By adjusting T_i, we control the individual node’s probability of transmission and therefore the system’s performance. Assume that we are interested in large scale systems with possibly hundreds of nodes observing distinct i.i.d. sources. Due to the symmetry in the probabilistic model, it is natural to assume that all of the nodes use a single threshold, T. The objective then is to find T such that the normalized mean-squared error (NMSE) is minimized, i.e.,

${\mathcal{J}}_{N,K}\left(T\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N}\mathbf{E}\left[{\left(X_i-{\widehat{X}}_i\right)}^2\right].(22)$

The underlying constraint here is that if more than K sensors communicate, there will be a collision and the transmitted packets will be lost. Zhang et al. (2022) shows that when the sources have a symmetric and unimodal probability density function (e.g., Gaussian, Laplace, etc.), the objective function is quasi-convex in T, which means that there exist very efficient numerical methods to find T^⋆ (Agrawal and Boyd, 2020). Moreover, when compared to the centralized strategy, the performance of the decentralized thresholding strategy is reasonably close to the lower bound given by the centralized top-K scheduler, denoted by ${\mathcal{J}}^L$ as seen in Figure 4.

Figure 4

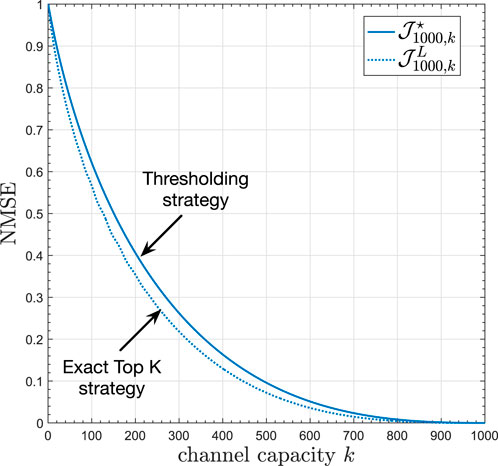
Figure 4. Decentralized vs Centralized Top-K strategies for N =1,000 Gaussian sources with zero mean and unit variance. Reprinted with permission from IEEE, “Distributed Remote Estimation Over the Collision Channel With and Without Local Communication” by Xu Zhang; Marcos M. Vasconcelos; Wei Cui and Urbashi Mitra, licensed under 5743970328454, IEEE.

3.2 Distributed inference of the Kth order statistics

Due to the loss of information resulting from collisions in the previous section, to bridge the gap between the decentralized and the centralized performance curves in Figure 4, we must introduce local communication among the agents. There are two ways of achieving this goal: every agent sharing all of its observations with its neighbors, in which case every sensor must store in its memory everything it has received and update its top-K list, or to compute an estimate of the Kth ordered statistics using distributed optimization, which is the focus of this section.

3.2.1 Problem definition

Consider the setup where data is collected over a sensor network with N nodes. Each node in the network has a subset of the dataset and for the reasons discussed in the previous section, a remote data collector can only receive a limited number) of packets from the sensors. As we have argued, if the data is zero-mean, independent and identically distributed, and the goal is to minimize the mean-squared error, we know that a PBPO strategy is to transmit the measurements corresponding to the K largest magnitudes. To that end, each sensor exchanges messages with its neighbors in a peer-to-peer fashion to decide who is going to transmit and who is going to stay silent, when the opportunity to communicate with the destination occurs. A depiction of an example scenario with a mobile fusion center is provided in Figure 5.

Figure 5

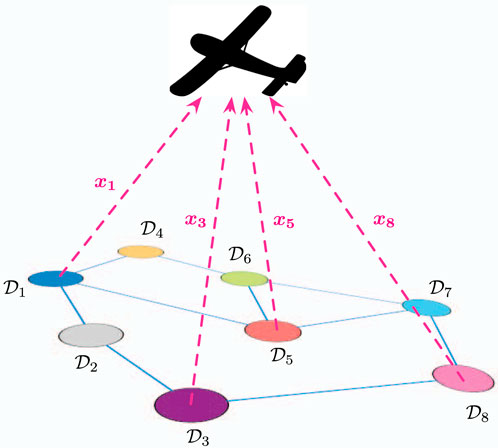
Figure 5. Remote estimation of distributed sensing data with local communications. Here, a sensor network on the ground can communicate locally, before uploading their data to a remote collection point, depicted here by a drone. Here, we model the uplink from the sensors to the drone via a collision channel with capacity K < N.

The problem is: design an efficient distributed algorithm to compute a threshold T^⋆ ∈ (x_[k], x_[k+1]) such that each node determines if it is going to transmit any of its observations or not.

For simplicity, assume that each sensor has exactly one data point. The extension to larger local data sets is relatively straightforward, although it may lead to multiple transmissions by the same node should it have more than one of the K largest data points. This has exactly the same structure of the previous strategy, except that here exactly the K largest points are transmitted, making optimal use of the capacity of the collision channel. This allow us to obtain the best possible performance, at the expense of local communication.

3.3 A solution via distributed sample quantile inference

The trick to find the Kth largest measurement over a network is to compute an appropriate sample quantile for the empirical distribution of data stored over the nodes in the network. We begin by relating the problem of computing the top-K observations with quantile inference (Koenker and Hallock, 2001), which is a convex optimization problem. Even though convex problems can be solved very efficiently in a centralized server, its distributed implementation over a network can still be quite slow if the network has a very large number of nodes.

Consider a collection of N agents [N] = {1, … , N}, interconnected by a time-invariant, undirected, communication graph $\mathcal{G}=([N],\mathcal{E})$, where $\mathcal{E}\subset [N]\times [N]$ denotes the set of edges between nodes. Each agent holds a non-negative real number, which corresponds to the magnitude, i.e., the absolute value of measurement. Let $z_i\in \mathbb{R}$ be the data of the ith agent. The goal of the team of agents is to determine in a distributed fashion the K agents holding the top-K largest data points.

At first, one may be inclined to consider the following strategy: Each agent keeps a list of K entries in its memory. At time t each agent sends this list to its neighbors. At time t + 1, every agent updates its list with by selecting the top-K received data and discarding the rest. Each agent sorts its list and repeats. While this simple scheme converges to the top-K results in finite time, it has two main drawbacks. First, it requires noiseless communication channels of K real numbers per channel use. Even the slightest amount of noise will cause the algorithm to diverge. Second, it requires a memory with size K. If $K\sim \mathcal{O}(N)$, the communication and storage requirements will quickly turn the cost of finding the top-K observations across the network prohibitive.

On the other hand, this problem can be conveniently cast into the framework of distributed convex optimization, and admits an implementation where a single real number is exchanged and a single unit of memory is updated at each time. Furthermore, this algorithm is robust to the presence of noise. Here we present the version of the algorithm for the noiseless case found in (Zhang et al., 2022). A related algorithm designed to handle noisy communications can be found in (Zhang and Vasconcelos, 2023b). Consider the problem of inferring the sample quantile from the data set containing all of the agents’ individual data points $\mathcal{D}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}{\{z_i\}}_{i=1}^N$. Let $\widehat{F}(\xi ;\mathcal{D})$ denote the empirical cumulative distribution function of the data set $\mathcal{D}$, defined as:

$\widehat{F}\left(\xi ;\mathcal{D}\right)\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\frac{1}{N}{\displaystyle \sum _{i=1}^N}\mathbb{1}\left(z_i\le \xi \right).(23)$

Let p ∈ (0, 1). The (sample) p-quantile is defined as

${\theta }_p\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\inf \left\{\xi \left|\widehat{F}\left(\xi ;\mathcal{D}\right)\ge p\right.\right\}.(24)$

A classic result in quantile regression (Koenker, 2005) relates the p-quantile of $\mathcal{D}$ to the solution of the following optimization problem

${\theta }_p=\arg \underset{\xi \in \mathbb{R}}{\min }{\displaystyle \sum _{i=1}^N}{\rho }_p\left(z_i-\xi \right),\text{where}{\rho }_p\left(x\right)\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\left\{\begin{array}{cc}\left(p-1\right)x\hfill & \text{if}x<0\hfill \\ px\hfill & \text{if}x\ge 0.\hfill \end{array}\right.(25)$

Let the local functions of the ith node be defined as $f_i(\xi )\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}{\rho }_p(z_i-\xi )$, which are called the score functions, and the objective be defined as the aggregate score function $f(\xi )\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}{\displaystyle {\sum }_{i=1}^N}{f}_i(\xi ),$ then the sample quantile is the solution of the following distributed optimization problem:

${\theta }_p=\arg \underset{\xi \in \mathbb{R}}{\min }f\left(\xi \right)=\arg \underset{\xi \in \mathbb{R}}{\min }{\displaystyle \sum _{i=1}^N}{f}_i\left(\xi \right).(26)$

A few noteworthy aspects of Eq. 26 are: (1) this is a convex optimization problem; (2) the objective function is non-smooth; (3) the local functions have bounded sub-gradients:

$|g_i\left(\xi \right)|\le \max \left\{p,1-p\right\}\le 1,g_i\in \partial f_i;(27)$

and finally, (4) the p-quantile, θ_p, belongs to the data set $\mathcal{D}$, for any parameter $p\in \mathcal{P}$, where

$\mathcal{P}\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\left(\mathrm{0,1}\right)\backslash \left\{\frac{1}{N},\dots ,\frac{N-1}{N}\right\}.(28)$

This framework can be used to compute many statistics of interest. For example, to compute the maximum (K = 1), let p ∈ (1 − 1/N, 1). To compute the minimum (K = N), let p ∈ (0, 1/N). Provided the number of samples in $\mathcal{D}$ is odd, to compute the median, set $p\in \left((N-1)/2N,(N+1)/2N\right)$. In general, if we would like to find the Kth largest element of $\mathcal{D}$, then

$p\in \left(\frac{N-K}{N},\frac{N-K+1}{N}\right).(29)$

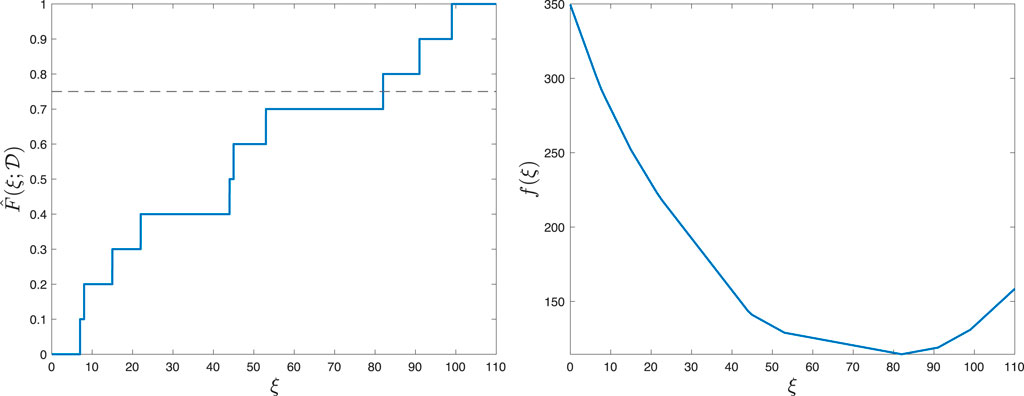
In Figure 6 (left), we display an example of an empirical CDF for a dataset $\mathcal{D}$ with N=10 samples, where the dashed line represents the chosen value of $p$ that should be used to compute the quantile corresponding to select the $K=3$ largest numbers from $\mathcal{D}$. In Figure 6 (right), we show the associated convex objective function whose optimal solution gives us the desired quantile that should be used as a threshold.

Figure 6

Figure 6. Empirical CDF and aggregate score function for N =10 and K =3.

3.3.1 The algorithm

Based on the desired value of K, set p to lie in the interval in (29). Let w_i(t) denote the local estimate of z_[K] by the ith node at time t. Set w_i (0) = z_i, i ∈ [N]. Finally, let η(t) be a deterministic diminishing step-size sequence, square summable but not summable, e.g., η(t) = α/t^0.51. On the tth round of local communication, we perform the following iteration:

$w_i\left(t+1\right)=w_i\left(t\right)+{\displaystyle \sum _{j\in {\mathcal{N}}_i}}\frac{1}{\max \left\{d_i,d_j\right\}}\left(w_j\left(t\right)-w_i\left(t\right)\right)-\eta \left(t\right)s_i\left(z_i,w_i\left(t\right)\right),(30)$

where

$s_i\left(z_i,w_i\left(t\right)\right)\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\left\{\begin{array}{cc}1-p,\hfill & z_i<w_i\left(t\right)\hfill \\ -p,\hfill & z_i\ge w_i\left(t\right).\hfill \end{array}\right.(31)$

Zhang et al. (2022) showed that if all the nodes adhere to this algorithm, it converges to z_[K] as t → ∞. However, due to the diminishing step-size sequence, the convergence is often slow, and this may lead to a large delay and communication overhead. Accelerating this algorithm is still an open problem for investigation.

3.4 Practical considerations

To use the top-K inference in conjunction with the remote estimation system, we compute the transmit decisions at time t as follows:

$u_i\left(t\right)=\left\{\begin{array}{cc}1\hfill & |x_i|\ge w_i\left(t\right)\hfill \\ 0\hfill & \text{otherwise.}\hfill \end{array}\right.(32)$

and the instantaneous cost of using this strategy is given by

$\mathcal{J}\left(\mathbf{x},\mathbf{u}\left(t\right)\right)=\left\{\begin{array}{cc}\frac{1}{N}{\displaystyle {\sum }_{i=1}^N}{x}_i^2\left(1-u_i\left(t\right)\right)\hfill & \text{if}{\displaystyle {\sum }_{i=1}^N}{u}_i\left(t\right)\le K\hfill \\ \frac{1}{N}{\displaystyle {\sum }_{i=1}^N}{x}_i^2\hfill & \text{otherwise.}\hfill \end{array}\right.(33)$

When the top-K algorithm converges, the instantaneous cost yields the lowest cost possible. However, the performance can be quite poor before the local estimates approach z_[K] within a close enough range. One way to mitigate that issue is to combine the two approaches in this section as follows: Initially, the nodes communicate with the goal of estimating the variance of the distribution using a simple distributed averaging algorithm. This simple algorithm converges swiftly because it does not require a diminishing step-size. Based on that estimate, we compute the optimal threshold T^⋆ for the problem without local communication, which is quasi-convex (provided the data distribution is unimodal and continuous) and can be efficiently solved. Finally, we use T^⋆ as an initial condition for the distributed quantile estimator. This 3-step procedure works remarkably well, accelerating the convergence to the minimum instantaneous cost by hundreds of iterations. The performance of this scheme can be visualized in Figure 7. Furthermore, it has the additional advantage of being robust to distribution shifts (Tibshirani et al., 2019).

Figure 7

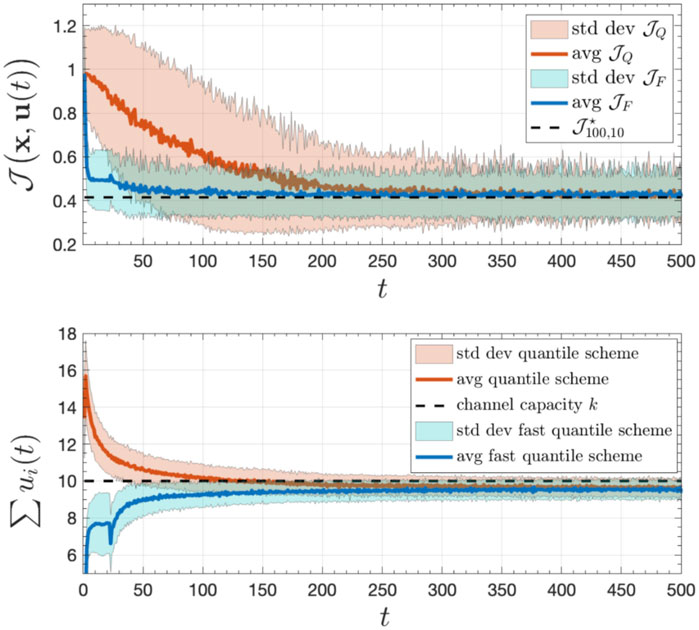
Figure 7. Hybrid data-driven scheme for distributed remote inference with averaging followed by quantile inference for a system with N =100 nodes and collision channel of capacity K =10. The curve labeled as ${\mathcal{J}}_Q$ corresponds to the strategy based on pure quantile inference, and the one labeled as ${\mathcal{J}}_F$ corresponds to its faster implementation using the 3-step procedure described herein. Reprinted with permission from IEEE, “Distributed Remote Estimation Over the Collision Channel With and Without Local Communication” by Xu Zhang; Marcos M. Vasconcelos; Wei Cui and Urbashi Mitra, licensed under 5743970328454, IEEE.

The distributed algorithm considered in this section assumes that the network is time-invariant and undirected. In practice, these assumptions are often violated. However, a similar version of the algorithm also can be implemented over time-varying directed graphs, under the appropriate technical assumptions required for convergence in that case (Nedić and Olshevsky, 2015). An important research direction, is regarding the possibility of having a network compromised by malicious agents (Shang, 2023) or events that may cause some agents to misbehave (Ballotta et al., 2023). In this case, it is not clear what is the distributed Top-K algorithm that should be implemented, and this is an interesting area for further research. Figure 8 summarizes and compares the existing results and techniques for extremum information in the context of remote estimation.

Figure 8

Figure 8. Comparison of extremum information results and techniques for different system architectures for remote estimation.

4 Max-dissent and extremum information exchange in distributed optimization

In the previous sections, we discussed the important role of extremum information, i.e., observations, data, or measurements, in problems of remote estimation. In this section, we shift gears and consider a different application: distributed convex optimization. In such applications, nodes exchange messages with the goal of optimizing an aggregate objective function,

$f\left(x\right)\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}{\displaystyle \sum _{i=1}^N}{f}_i\left(x\right),(34)$

where each f_i is available at node i. Moreover, the nodes are not allowed to share the function with its neighbors. This assumption is sometimes attributed to privacy, but it reality it can be that each local function may depend to local data sets which may themselves be too large, or perhaps to valuable to share, in addition to the privacy concerns. Distributed optimization is a large research area with a rich history dating back to seminal work of Tsitsiklis et al. (1986). Revitalized by Nedić and Ozdaglar (2009) and many others, this research area continues to be relevant due to the abundant number of existing distributed Machine Learning applications, and the fact that in general it is not viable to consolidate all the data stored at local nodes in a single server to solve a centralized optimization problem (Nedić, 2020).

Within this context, we asked the following question: if a node is forced to choose only one of its neighbors to communicate, which one should it be? This question is closely related to the problem discussed in the previous sections, and surprisingly, the answer aligns with our previous findings: we should talk to the agent who disagrees with us the most. In this section, we will provide intuition as to why this is the case and how it would work in practice.

4.1 Max-dissent gossiping algorithms

Before we discuss the notion of how to chose an informative neighbor in the context of distributed optimization, we need to introduce the notion of a gossip algorithm (Shah, 2009). Gossiping is a class of asynchronous algorithms with its origins in computer science, where a node in a network randomly “awakes” and interacts with one of its neighbors. The type of interaction depends on what is the overall goal of the network, which could be, for example, spreading a rumor or information (hence the moniker “gossip”). In distributed optimization, gossiping is typically used as an averaging mechanism: two nodes exchange their local variables and compute the average of those two numbers reaching a local average consensus, that propagates over the network as the process continues.

One crucial detail that it is often overlooked is how a node that has just woken up should choose with whom to gossip. Traditionally, a node selects one of its neighbors uniformly at random. While this seems to be a fair choice, it does not necessarily lead to the best possible convergence properties. Let the state of the network system at time k, the local information available at each of the N nodes, i.e., x(k) = [x₁(k), …, x_N(k)]. Between time k and k + 1, node i wakes up, and chooses $j\in {\mathcal{N}}_i$ to average its state with. Consider, for example, as an “instantaneous optimality measure” the sample variance of the of the vector x(k), $\mathrm{V}\mathrm{a}\mathrm{r}\left(x(k)\right)$².The closer this value is to 0, the more concentrated the vector is around its average, our desired goal. Therefore, we should be always looking for the maximal possible reduction in the sample variance, and that happens when the node i gossips with the node that is most distant from x_i(k), leading to the notion of the local max-dissent edge:

$\mathrm{V}\mathrm{a}\mathrm{r}\left(x\left(k\right)\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(x_i\left(k\right)-\mathrm{A}\mathrm{v}\mathrm{g}\left(x\left(k\right)\right)\right)}^2,(35)$

where $\mathrm{A}\mathrm{v}\mathrm{g}\left(x(k)\right)$ is the sample average.

$e_i^{\star }\left(k\right)=\left(i,\arg \underset{j\in {\mathcal{N}}_i}{\max }\Vert x_j\left(k\right)-x_i\left(k\right)\Vert \right).(36)$

One may argue that instead of letting a random node wake up and gossip with its max-dissent neighbor, we may select the edge over the entire graph. This defines the global max-dissent edge, i.e.,

$e^{\star }\left(k\right)=\arg \underset{\left(i,j\right)\in \mathcal{E}}{\max }\Vert x_j\left(k\right)-x_i\left(k\right)\Vert .(37)$

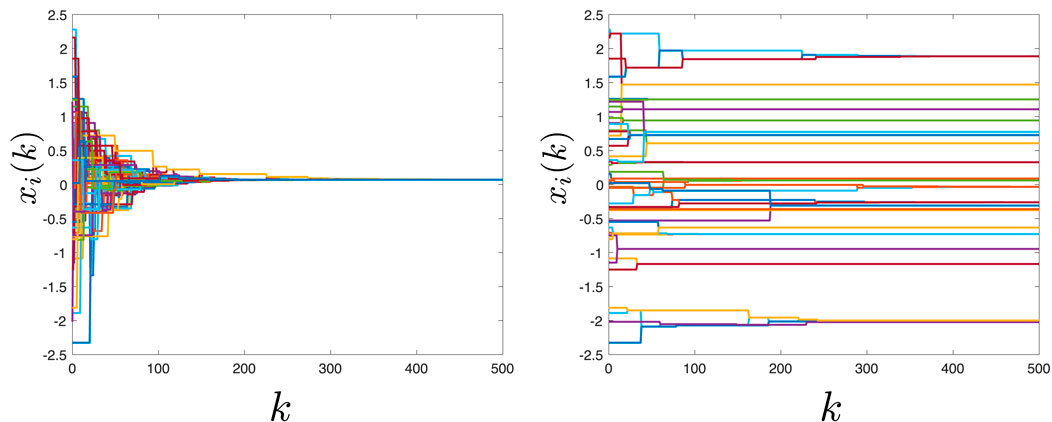
The selection of the agents with the largest disagreement leads to the largest possible reduction in the variance at time k. This greedy approach does not necessarily yield an overall faster convergence rate and the proof that this scheme is the optimal neighbor selection policy overall possible state-dependent gossiping algorithms is still a challenging open problem. However, this heuristic shows a consistent improvement over all of the asynchronous state-independent gossiping algorithms we have examined. Figure 9 illustrates the convergence of these three schemes for a graph sampled from the Erdös-Rényi ensemble with N = 200 nodes and edge probability p = 0.01. Figure 10 shows an example of how the three Gossip algorithms considered herein compare in terms of reduction in the variance of the state vector x(t) after one iteration. Random Gossip consistently shows a slowest convergence compared to local and global max-dissent gossip. Notice global max-dissent gossip requires a full order of magnitude less iterations to achieve the same level of performance of random gossip. This substantial gain in convergence may lead to much longer deployments, and overall increase in productivity if the system is used to perform other distributed tasks.

Figure 9

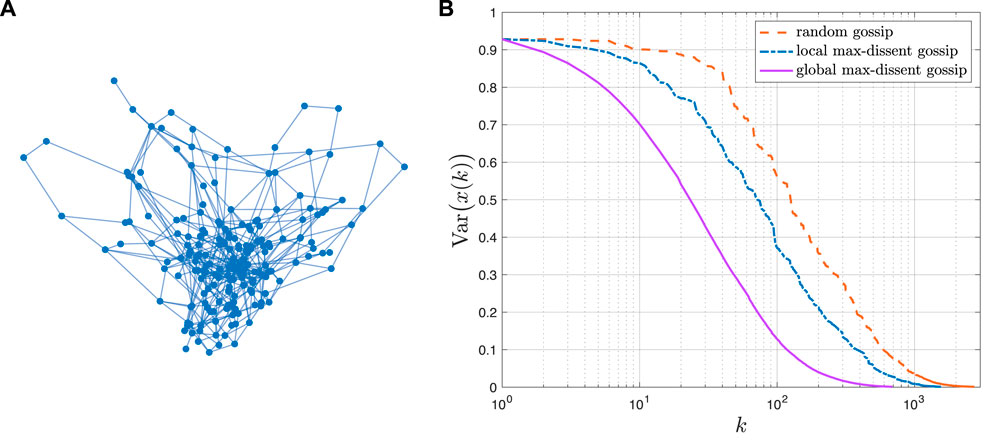
Figure 9. (A) Erdös-Rényi graph with N =200 nodes. (B) Example of convergence for three Gossip algorithms: random gossip, local max-dissent gossip and global max-dissent gossip regarding the instantaneous objective function $\mathrm{V}\mathrm{a}\mathrm{r}\left(x(k)\right)$.

Figure 10

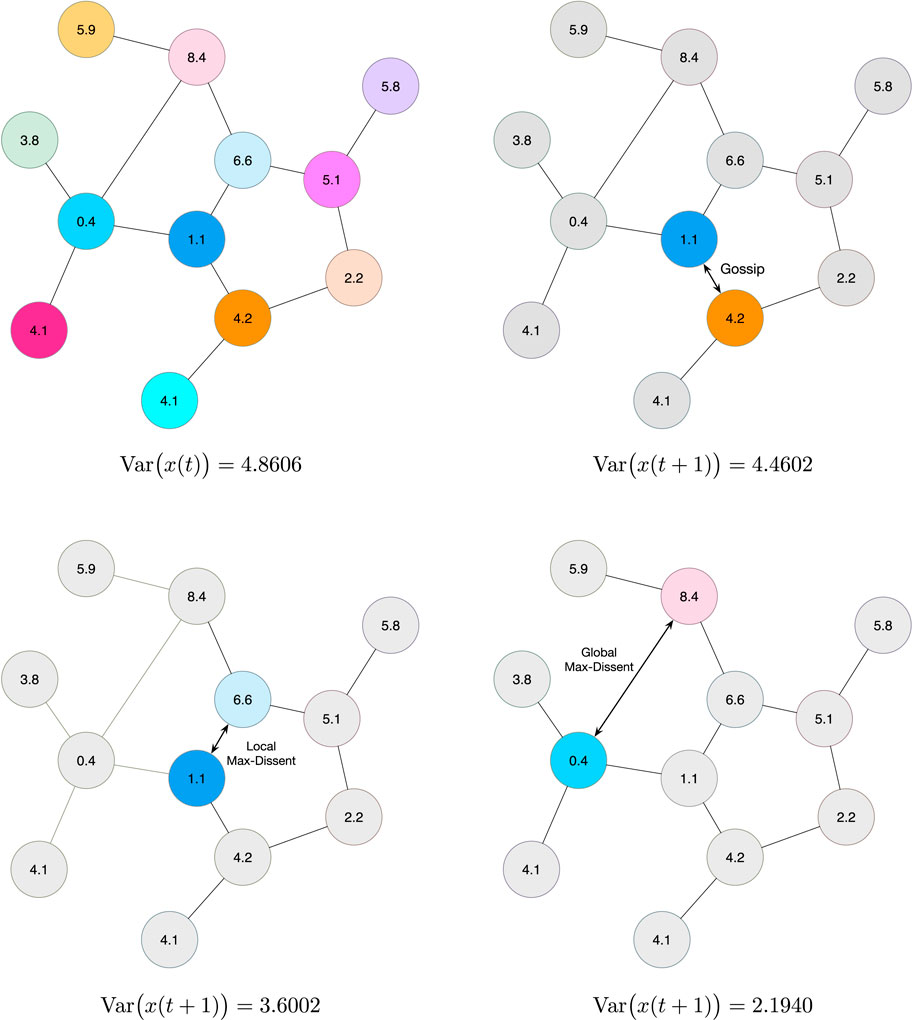
Figure 10. Example of the three Gossip algorithms: random gossip, local-max gossip and global max-gossip regarding the instantaneous objective function $\mathrm{V}\mathrm{a}\mathrm{r}\left(x(t)\right)$.

4.2 A state-dependent subgradient method and its analysis

There are many algorithms for distributed optimization, and any attempt to summarize it in this section would be a futile exercise. We refer the interested reader to the excellent survey by Yang et al. (2019). Instead, we adopt the class of algorithms originally proposed in (Nedić and Ozdaglar, 2009). In classical sub-gradient algorithms/methods, we have

$\mathbf{W}\left(k+1\right)=\mathbf{A}\left(k\right)\mathbf{X}\left(k\right),(38)$

where X(k) is a matrix whose columns are the local estimates of the optimal solutions to the objective function in Eq. 34 at time k. The matrix A(k) is a time-varying, random averaging matrix. After an iteration of averaging, each agent in the network takes a step of size α(k + 1) in the direction of its local subgradient computed at its local value ${\mathbf{w}}_i(k+1)={\left[\mathbf{W}(k+1)\right]}_i$. Collectively, the system state evolves as:

$\mathbf{X}\left(k+1\right)=\mathbf{W}\left(k+1\right)-\alpha \left(k+1\right)\mathbf{G}\left(k+1\right),(39)$

where G is the matrix whose columns are subgradients of the local functions at the local estimates at time k + 1. Notice that the matrix A(k) is not state-dependent, e.g., random gossip, and that leads to more tractable convergence analysis to the optimal solution of the problem under the appropriate technical conditions.

Suppose now that the agents would like to use information about the state when choosing who they are going to gossip with. In other words, the averaging matrix in Eq. 38 becomes a function of X(k):

$\mathbf{W}\left(k+1\right)=\mathbf{A}\left(k,\mathbf{X}\left(k\right)\right)\mathbf{X}\left(k\right).(40)$

The literature on such algorithms is scarce, and the available techniques are quite complex. We refer to (Lobel et al., 2011; Etesami and Başar, 2015; Alaviani and Elia, 2021) for previous work in state-dependent averaging in various contexts. In the past works, the emphasis was placed on the vector x_i(k) being the position of the ith agent at time k. Consider for example, applications in robotics where the agents may be trying to find an optimal configuration in the environment that optimizes an aggregate objective function on the basis of local information (Cortes et al., 2004), or perhaps, the placement of mobile wireless base stations in a geographic area (Mozaffari et al., 2017). Another application where the state may be related to position is optimal sensor placement in the Internet of Things (Firouzabadi and Martins, 2008). It is natural to assume that in such applications, the agents that are closer should communicate more frequently, due to the communication channels having a higher signal to noise ratio. For example, Lobel et al. (2011) use a probabilistic state-dependent model of gossiping between a pair of agents (i, j) defined as:

$\mathbf{P}\left({\mathbf{A}}_{ij}\left(k\right)>0\mid \mathbf{X}\left(k\right)=\bar{\mathbf{X}}\right)\ge \min \left\{\delta ,\frac{K}{\Vert {\bar{\mathbf{x}}}_i-{\bar{\mathbf{x}}}_j{\Vert }_2^C}\right\},(41)$

where K, C are positive constants and $\delta \in \left(\left.\mathrm{0,1}\right]\right.$. We highlight two properties of the probabilistic model above: (1) closer nodes have a higher chance of gossiping; and (2) two nodes that are far apart always have a nonzero probability of communicating, including the two nodes corresponding to the max-dissent edge.

If only the agents who are closer to each other were allowed to communicate, that would lead to an echochamber, a social network phenomenon where individuals with the same opinion reinforce each others beliefs and opinions. Echochambers have the opposite effect of what Max-dissent has: they do not lead to convergence as it can be seen in Figure 11.

Figure 11

Figure 11. Convergence of Max-Dissent vs Divergence of Echochambers.

If echochambers do not work, how can we explain the convergence of algorithms such as the one considered in (Lobel et al., 2011)? The key to answering this question is to realize that when there is a non-zero probability of gossiping with one of your max-dissent neighbors, over time this non-zero probability leads to a contraction in expectation of the Lyapunov function for the state dependent averaging algorithm. To study that phenomenon, Verma et al. (2023) established the following property for the state dependent averaging matrix for the different algorithms considered herein:

$\mathbf{E}{\left[\mathbf{A}{\left(k,\mathbf{X}\left(k\right)\right)}^T\mathbf{A}\left(k,\mathbf{X}\left(k\right)\right)\mid {\mathcal{F}}_k\right]}_{i^{\star }{j}^{\star }}\ge \delta =\left\{\begin{array}{cc}\frac{1}{N{\max }_i|{\mathcal{N}}_i|}\hfill & \text{random\hspace{0.17em}gossip}\hfill \\ \frac{1}{N}\hfill & \text{local\hspace{0.17em}max\hspace{0.17em}gossip}\hfill \\ \frac{1}{2}\hfill & \text{global\hspace{0.17em}max\hspace{0.17em}gossip},\hfill \end{array}\right.(42)$

where ${\mathcal{F}}_k$ is a filtration at time k (Cinlar, 2011).

If the value of δ in Eq. 42 is large, the two neighbors in the graph with largest disagreement will gossip more often. Not surprisingly, this increased gossiping leads to larger contractions on the Lyapunov function used to measure the empirical variance of the states of the network system. While it is possible to prove that schemes such as max-dissent converge, establishing its exact convergence rate is challenging. A detailed analysis can be found in (Verma et al., 2023).

A more easily computable and intuitive piece of evidence of the benefits of state-dependent averaging can be obtained by looking at the contraction factor. The contraction factor, λ, quantifies the expected decrease in the Lyapunov function $V\left(\mathbf{X}\right)$, i.e.,

$\mathbf{E}\left[V\left(\mathbf{X}\left(k+1\right)\right)\mid {\mathcal{F}}_k\right]\le \lambda V\left(\mathbf{X}\left(k\right)\right).(43)$

Moreover, it can be precisely characterized and is given by:

$\lambda =1-\frac{2\delta }{\left(N-1\right)\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}{\left(\mathcal{G}\right)}^2},(44)$

where δ depends on the averaging algorithm as specified in Eq. 42. The larger the δ, the larger the contraction and the best possible δ for a single pair of nodes engaging in gossip is obtained via global max-dissent.

4.3 Practical considerations

The benefit of having two agents with the largest possible disagreement exchanging information seems clear and intuitive. However, the implementation of the max-dissent mechanism is not trivial. Let us start by discussing local max-dissent. When a node wakes up, before it decides who it will gossip with, it must compare its state with the states of its neighbors. This requires the nodes in the neighborhood to share information before the gossiping starts, which leads to a communication overhead that is absent in random gossiping. Therefore, the gains in convergence come at the expense of communication overhead.

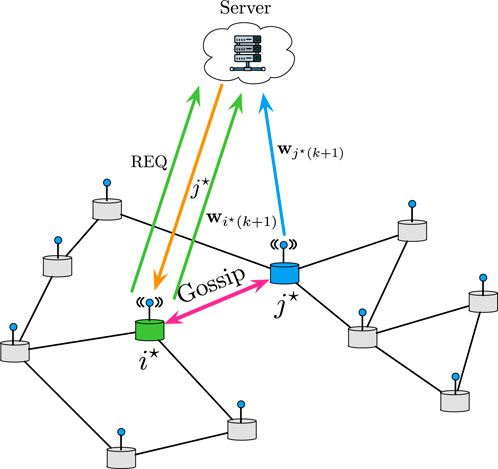
One way to address this issue is to create a two-layer network infrastructure where the agents post their current states to a trusted server as they change. When a node wakes up, instead of pulling information from the neighbors, it asks the server which one of its neighbors it should gossip with. The server is in charge of computing the max-dissent edge, and not the nodes. That also preserves privacy in the state variables of the other non-gossiping agents. This architecture is summarized in the diagram of Figure 12.

Figure 12

Figure 12. Two-layer federated architecture for state dependent gossiping algorithms.

A two-layer federated architecture (Reisizadeh et al., 2020; Kairouz et al., 2021; Wang et al., 2021, and references therein) would also be able to implement global-max gossip, where an intermediate server determines which agents should gossip in the network at every time. It is important to note that this differs from having a centralized server solve the optimization problem, because the local functions remain local information at the nodes and are never exchanged. The communication overhead is also kept under control because at every time, only one pair of nodes update their variables and communicate with the server, and the entire neighborhood does not need to communicate. In both cases, the additional cost comes from having to implement a secure centralized server to which the information is posted. Figure 13 summarizes the existing results for extremum information in the context of distributed learning.

Figure 13

Figure 13. Comparison of gossip algorithms depending on the level of extremum information used. The communication overhead assumes that a real number is encoded using 32 bits. The number of bits per iteration required to implement global max dissent is unknown.

5 Perspectives for future work

Transmitting information strategically based on the value of the observations and the state offers many benefits such as better performance, optimal resource allocation (e.g., spectrum and battery power), as well as potentially speeding up convergence in distributed systems. However, there is a wealth of open problems related to the multi-faceted nature of the problem. Herein, we discuss a subset of them related to privacy and security, distributed learning and applications in the spread of information in social-networks.

5.1 Max-scheduling of information for remote estimation under privacy constraints

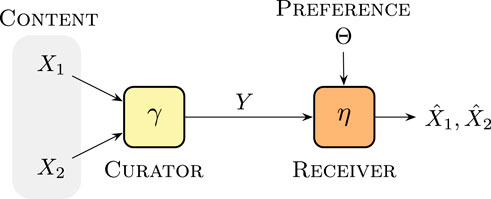
In the setup introduced by Vasconcelos and Mitra (2020), the receiver is indifferent about which of the sources it observes. However, this is rarely the case in practice. A more sensible model should account for different optimality metrics when the receiver has a bias towards a source. Here is a possible model for this situation: Let Θ be a random variable distributed on the interval [0,1]. This variable is private to the receiver. Then, the objective function for the designer is:

$\mathcal{J}\left(\gamma ,\eta \right)=\mathbf{E}\left[\mathrm{\Theta }{\left(X_1-{\widehat{X}}_1\right)}^2+\left(1-\mathrm{\Theta }\right){\left(X_2-{\widehat{X}}_2\right)}^2\right].(45)$

This scenario is considered in the block diagram of Figure 14, where the curator plays the role of the scheduler. This seems to be only a minor modification on the problem. However, there is more to the problem than one might notice at first glance. One major difference is that the objective functions in the ensuing game are now misaligned. That is because the receiving agent observes the realization of its preference, i.e., Θ = θ, whereas the transmitter only has a belief on Θ, i.e., its probability density function, π_Θ. A second aspect is that with the increased asymmetry in information patterns between the transmitter and the receiver, we now have a potential incentive for the receiver to communicate with the transmitter. For example, whether is bias is towards X₁, i.e., Θ > 1/2, or towards X₂, i.e., Θ < 1/2.

Figure 14

Figure 14. Data curation with privacy constraints.

The signaling aspect to the problem is completely new, and has not been studied. It is also possible to extend this setup using statistical learning techniques, similar to the ones used in (Vasconcelos and Mitra, 2021). However, new scheduling strategies would also need to incorporate the private data sequence ${\{{\theta }_k\}}_{k=1}^N$ in non trivial ways, especially if there is interaction between the transmitter and receiver. Suppose that the transmitter acts first and then collects feedback about θ_k, building a better belief on π_Θ. Then not only the sequence of scheduling decision have the role to minimize the expected distortion, but also to learn what the probability distribution of Θ is, turning this into a stochastic bandit problem (Bubeck and Cesa-Bianchi, 2012).

5.2 Using neural networks to learn the optimal estimators for the max-scheduling policies

In Vasconcelos and Mitra (2021), a suboptimal approach to replace the MMSE estimator, which is nonlinear, with a linear function led to the DC decomposition and an efficient data-driven optimization algorithm. We may be interested in using a parameterizable class of nonlinear functions to approximate the MMSE estimator instead. For example, by choosing neural networks, we might approximate the optimal estimators, and this approach would allow us to trade-off the complexity of the architecture with the residual approximation error (Tabuada and Gharesifard, 2023). A few open questions are: Can we exploit the structure and obtain efficient algorithms such as CCP for an estimation policy implemented by a neural network? Can we do better than stochastic gradient descent? Do these suboptimal solutions reveal anything about the elusive MMSE estimator and its associated max-scheduling policy?

5.3 Characterizing the robustness of decentralized and distributed top-K strategies

The algorithms used to find the top-K observations across a multi-agent network rely on the unrealistic assumption that the data is identically distributed. In (Zhang et al., 2022), an example showed by means of a random perturbation approach, that even if the distributions are not the same across sensors, using the policy designed as if a single distribution generated the entire data set does not lead to a significant loss in performance. In fact, this approach can be quite robust to perturbations of the probabilistic model. However, a complete analysis of this robustness margin is still lacking.

Another important observation is the robustness with respect to the family of distributions. An example in (Zhang et al., 2022) shows that if the system is designed under the assumption that the data is Gaussian distributed, it may perform extremely well for other distributions, such as Laplace. The hypothesis is that provided that the distance between the distributions under an appropriate metric such as the symmetric Kullback-Liebler divergence (Csiszar and Shields, 2004) is within a reasonable margin, the degradation in performance is bounded. This notion is akin to the notion of estimating a Lipschitz constant for a function, where the input is our distribution and the output is the performance of the system designed for that distribution. The question is how to quantify this Lipschitz constant or at least to obtain a good bound for it. Such results are important is many fields, in particular in Machine Learning, where there is an important class of problems related to the so-called distribution shift via conformal prediction (Tibshirani et al., 2019).

5.4 Adversarial settings in max-dissent algorithms

While multi-agent network systems are typically robust to node failures and other disturbances, they are extremely vulnerable to cyber-attacks. Such vulnerabilities are exacerbated if the agent share information over a low-power wide-area network, which is the case in most practical applications (Zhang and Vasconcelos, 2023a, and references therein). Therefore, securing distributed systems is an important research topic, that includes enabling resilience to adversarial agents in distributed optimization (Sundaram and Gharesifard, 2018; Zhao et al., 2019).

Max-dissent algorithms are particularly susceptible to nodes behaving maliciously. When operating without the aid of a server, an adversarial nodes may launch a data spoofing attack by flat out lying about their states, making them always very large and leading to them being selected in a local max-dissent algorithm with a much higher probability than other nodes. Thus, skewing the result to a point that does not correspond to the optimal for the legitimate agents. In a similar context, Mitra et al. (2021) studied a clever way to discard information received by agents in a distributed non-Bayesian learning setting: assuming there exists a limited number of malicious agents connected to every legitimate node, each node then ignores the neighbors that have opinions that are too distant or too close from their own. A similar approach was used in (Chattopadhyay and Mitra, 2019) to improve the performance of a Kalman filter with multiple sensors subject to false data-injection attacks.

The approach of discarding discrepant nodes is effective in a network system where the gossiping nodes are not chosen based on their state. However, the implementation of this principle in a max-dissent algorithm would eventually rule out the max-dissent neighbors, leading to a conundrum for the system designer as well as the attacker, as to what strategy should be used. If each node has at most one malicious neighbor, occasionally selecting the second most dissenting neighbor might help the system achieve robustness, but would lead to some degradation in convergence rate.

The cyber-attack issues when there is a server involved is somewhat mitigated, because the server would be able to notice any unusual behaviors by some agents in the network. For example, when an agent reports a state that has not changed significantly after a few times it has been selected to gossip, this node may than be ignored all together by the server in future iterations. The federated architecture is still vulnerable to other types of attacks, since it fundamentally depends on the server to operate, if for any reason the server ceases to work, the entire system is at risk. Therefore, in addition to having an additional implementation cost due to the server, there needs to be an additional cyber-infrastructure cost to protect the server to possible attacks. The most detrimental attack, could be, for example, if instead of selecting the max-dissent node, the server selects the min-dissent (echochamber) leading to the worst possible convergence performance of the entire optimization process.

6 Final remarks

Distributed processing of information over networks to support decision-making and control is an area with more open problems than solutions. There are numerous research opportunities that extend beyond the traditional goals in communication networks, which typically focus on maximizing data rates between information sources and their corresponding receivers. Furthermore, in this paper, we have illustrated several examples of new principles that emerge in control and estimation when the transmitter faces communication constraints, requiring choices about what and with whom to communicate. These principles revolve around the notion of extremum information and give rise to a wide array of challenges, only a few of which have been discussed here. In particular, we have focused on the problem of identifying and computing extremum information in the context of remote estimation when different network architectures are available. We have also identified max-dissent as a version of extremum information in the context of distributed learning, and argued that when an agent must choose who to talk to, it should choose the agent with largest disagreement within its neighborhood. We strongly believe that similar themes will continue to emerge, and the concept of extremum information transfer for control and learning will play an important role in many of the current applications and those yet to be invented.

Author contributions

MV: Conceptualization, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing–original draft. UM: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Validation, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The work of UM was partially sponsored by NSF under grants CCF-1817200, CCF-2008927 and CCF-2200221; ARO under grant W911NF1910269; ONR under grants 503400-78050 and N00014-15-1-2550.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Tsunami [noun] a very large sea wave, caused by an underwater earthquake or a volcanic eruption, that can cause a lot of destruction when it hits land–Cambridge Dictionary.

²The sample variance is defined as:

References

Acemoglu, D., Ozdaglar, A., and ParandehGheibi, A. (2010). Spread of (mis) information in social networks. Games Econ. Behav. 70, 194–227. doi:10.1016/j.geb.2010.01.005

CrossRef Full Text | Google Scholar

Agrawal, A., and Boyd, S. (2020). Disciplined quasiconvex programming. Optim. Lett. 14, 1643–1657. doi:10.1007/s11590-020-01561-8

CrossRef Full Text | Google Scholar

Ahn, M., Pang, J.-S., and Xin, J. (2017). Difference-of-convex learning: directional stationarity, optimality, and sparsity. SIAM J. Optim. 27, 1637–1665. doi:10.1137/16m1084754

CrossRef Full Text | Google Scholar

Akyol, E., Langbort, C., and Başar, T. (2017). Information-theoretic approach to strategic communication as a hierarchical game. Proc. IEEE 105, 205–218. doi:10.1109/jproc.2016.2575858

CrossRef Full Text | Google Scholar

Alaviani, S. S., and Elia, N. (2021). Distributed convex optimization with state-dependent (social) interactions and time-varying topologies. IEEE Trans. Signal Process. 69, 2611–2624. doi:10.1109/tsp.2021.3070223

CrossRef Full Text | Google Scholar

Ballotta, L., Como, G., Shamma, J. S., and Schenato, L. (2023). Can competition outperform collaboration? the role of misbehaving agents. IEEE Trans. Automatic Control 1, 1–16. doi:10.1109/TAC.2023.3329850

CrossRef Full Text | Google Scholar

Bubeck, S., and Cesa-Bianchi, N. (2012). Regret analysis of stochastic and nonstochastic multi-armed bandit problems. Found. Trends® Mach. Learn. 5, 1–122. doi:10.1561/2200000024

CrossRef Full Text | Google Scholar

Chattopadhyay, A., and Mitra, U. (2020). Security against false data-injection attack in cyber-physical systems. IEEE Trans. Control Netw. Syst. 7, 1015–1027. doi:10.1109/tcns.2019.2927594

CrossRef Full Text | Google Scholar

Chen, X., Liao, X., and Bidokhti, S. S. (2021). “Real-time sampling and estimation on random access channels: Age of information and beyond,” in IEEE INFOCOM 2021 - IEEE Conference on Computer Communications, Vancouver, BC, Canada, 10-13 May 2021 (IEEE). doi:10.1109/INFOCOM42981.2021.9488702

CrossRef Full Text | Google Scholar

Cinlar, E. (2011). Probability and stochastics. New York, NY: Springer.

Google Scholar

Cortes, J., Martinez, S., Karatas, T., and Bullo, F. (2004). Coverage control for mobile sensing networks. IEEE Trans. robotics Automation 20, 243–255. doi:10.1109/tra.2004.824698

CrossRef Full Text | Google Scholar

Csiszar, I., and Shields, P. C. (2004). Information theory and statistics: a tutorial. Found. Trends™ Commun. Inf. Theory 1, 417–528. doi:10.1561/0100000004

CrossRef Full Text | Google Scholar

El Gamal, A., and Kim, Y.-H. (2011). Network information theory. Cambridge: Cambridge University Press.

Google Scholar

Etesami, S. R., and Başar, T. (2015). Game-theoretic analysis of the Hegselmann-Krause model for opinion dynamics in finite dimensions. IEEE Trans. Automatic Control 60, 1886–1897. doi:10.1109/tac.2015.2394954

CrossRef Full Text | Google Scholar

Farokhi, F., Teixeira, A. M., and Langbort, C. (2017). Estimation with strategic sensors. IEEE Trans. Automatic Control 62, 724–739. doi:10.1109/tac.2016.2571779

CrossRef Full Text | Google Scholar

Firouzabadi, S., and Martins, N. C. (2008). “Optimal node placement in wireless networks,” in 2008 3rd international symposium on communications, control and signal processing, Malta, March 12–14, 2008, 960–965. doi:10.1109/ISCCSP.2008.4537362

CrossRef Full Text | Google Scholar

Hashemi, A., Ghasemi, M., Vikalo, H., and Topcu, U. (2021). Randomized greedy sensor selection: leveraging weak submodularity. IEEE Trans. Automatic Control 66, 199–212. doi:10.1109/tac.2020.2980924

CrossRef Full Text | Google Scholar

Hespanha, J. P. (2017). Noncooperative game theory: an introduction for engineers and computer scientists. Princeton: Princeton University Press.

Google Scholar

Imer, O. C., and Basar, T. (2010). Optimal estimation with limited measurements. Int. J. Syst. Control Commun. 2, 5–29. doi:10.1504/ijscc.2010.031156

CrossRef Full Text | Google Scholar

Joshi, S., and Boyd, S. (2009). Sensor selection via convex optimization. IEEE Trans. Signal Process. 57, 451–462. doi:10.1109/tsp.2008.2007095

CrossRef Full Text | Google Scholar

Kairouz, P., McMahan, H. B., Avent, B., Bellet, A., Bennis, M., Nitin Bhagoji, A., et al. (2021). Advances and open problems in federated learning. Found. Trends® Mach. Learn. 14, 1–210. doi:10.1561/2200000083

CrossRef Full Text | Google Scholar

Koenker, R. (2005). Quantile regression. Cambridge: Cambridge University Press. Econometric Society Monographs.

Google Scholar

Koenker, R., and Hallock, K. F. (2001). Quantile regression. J. Econ. Perspect. 15, 143–156. doi:10.1257/jep.15.4.143

CrossRef Full Text | Google Scholar

Lipp, T., and Boyd, S. (2016). Variations and extension of the convex-concave procedure. Optim. Eng. 17, 263–287. doi:10.1007/s11081-015-9294-x

CrossRef Full Text | Google Scholar

Lipsa, G. M., and Martins, N. C. (2011). Remote state estimation with communication costs for first-order lti systems. IEEE Trans. Automatic Control 56, 2013–2025. doi:10.1109/TAC.2011.2139370

CrossRef Full Text | Google Scholar

Liu, J., Ye, M., Anderson, B. D., Basar, T., and Nedic, A. (2018). “Discrete-time polar opinion dynamics with heterogeneous individuals,” in IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17-19 December 2018 (IEEE), 1694–1699.

CrossRef Full Text | Google Scholar

Lobel, I., Ozdaglar, A., and Feijer, D. (2011). Distributed multi-agent optimization with state-dependent communication. Math. Program. 129, 255–284. doi:10.1007/s10107-011-0467-x

CrossRef Full Text | Google Scholar

Mei, W., Hendrickx, J. M., Chen, G., Bullo, F., and Dörfler, F. (2022). Convergence, consensus and dissensus in the weighted-median opinion dynamics. arXiv preprint arXiv:2212.08808.

Google Scholar

Mitra, A., Richards, J. A., and Sundaram, S. (2021). A new approach to distributed hypothesis testing and non-bayesian learning: improved learning rate and byzantine resilience. IEEE Trans. Automatic Control 66, 4084–4100. doi:10.1109/tac.2020.3033126

CrossRef Full Text | Google Scholar

Moon, J., and Başar, T. (2017). Static optimal sensor selection via linear integer programming: the orthogonal case. IEEE Signal Process. Lett. 24, 953–957. doi:10.1109/lsp.2017.2698465

CrossRef Full Text | Google Scholar

Mozaffari, M., Saad, W., Bennis, M., and Debbah, M. (2017). Mobile unmanned aerial vehicles (uavs) for energy-efficient internet of things communications. IEEE Trans. Wirel. Commun. 16, 7574–7589. doi:10.1109/twc.2017.2751045

CrossRef Full Text | Google Scholar

Nayyar, A., Başar, T., Teneketzis, D., and Veeravalli, V. V. (2013a). Optimal strategies for communication and remote estimation with an energy harvesting sensor. IEEE Trans. Automatic Control 58, 2246–2260. doi:10.1109/tac.2013.2254615

CrossRef Full Text | Google Scholar

Nayyar, A., Mahajan, A., and Teneketzis, D. (2013b). Decentralized stochastic control with partial history sharing: a common information approach. IEEE Trans. Automatic Control 58, 1644–1658. doi:10.1109/tac.2013.2239000

CrossRef Full Text | Google Scholar

Nedić, A. (2020). Distributed gradient methods for convex machine learning problems in networks: distributed optimization. IEEE Signal Process. Mag. 37, 92–101. doi:10.1109/msp.2020.2975210

CrossRef Full Text | Google Scholar

Nedić, A., and Olshevsky, A. (2015). Distributed optimization over time-varying directed graphs. IEEE Trans. Automatic Control 60, 601–615. doi:10.1109/TAC.2014.2364096

CrossRef Full Text | Google Scholar

Nedić, A., and Ozdaglar, A. (2009). Distributed subgradient methods for multi-agent optimization. IEEE Trans. Automatic Control 54, 48–61. doi:10.1109/tac.2008.2009515

CrossRef Full Text | Google Scholar

Nouiehed, M., Pang, J.-S., and Razaviyayn, M. (2019). On the pervasiveness of difference-convexity in optimization and statistics. Math. Program. 174, 195–222. doi:10.1007/s10107-018-1286-0

CrossRef Full Text | Google Scholar

Olfati-Saber, R., Fax, J. A., and Murray, R. M. (2007). Consensus and cooperation in networked multi-agent systems. Proc. IEEE 95, 215–233. doi:10.1109/jproc.2006.887293

CrossRef Full Text | Google Scholar

Reisizadeh, A., Mokhtari, A., Hassani, H., Jadbabaie, A., and Pedarsani, R. (2020). Proceedings of the twenty third international conference on artificial intelligence and statistics. PMLR 108, 2021–2031.

Google Scholar

Shah, D. (2007). Gossip algorithms. Found. Trends® Netw. 3, 1–125. doi:10.1561/1300000014

CrossRef Full Text | Google Scholar

Shang, Y. (2023). Resilient vector consensus over random dynamic networks under mobile malicious attacks. Comput. J. 2023, 1–11. doi:10.1093/comjnl/bxad043

CrossRef Full Text | Google Scholar

Soleymani, T., Baras, J. S., and Hirche, S. (2022). Value of information in feedback control: quantification. IEEE Trans. Automatic Control 67, 3730–3737. doi:10.1109/tac.2021.3113472

CrossRef Full Text | Google Scholar

Soleymani, T., Baras, J. S., Hirche, S., and Johansson, K. H. (2023). Value of information in feedback control: global optimality. IEEE Trans. Automatic Control 68, 3641–3647. doi:10.1109/tac.2022.3194125

CrossRef Full Text | Google Scholar

Soleymani, T., and Gündüz, D. (2023). State estimation over broadcast and multi-access channels in an unreliable regime. arXiv preprint arXiv:2308.16085.

Google Scholar

Sundaram, S., and Gharesifard, B. (2019). Distributed optimization under adversarial nodes. IEEE Trans. Automatic Control 64, 1063–1076. doi:10.1109/tac.2018.2836919

CrossRef Full Text | Google Scholar

Tabuada, P., and Gharesifard, B. (2023). Universal approximation power of deep residual neural networks through the lens of control. IEEE Trans. Automatic Control 68, 2715–2728. doi:10.1109/tac.2022.3190051

CrossRef Full Text | Google Scholar

Tibshirani, R. J., Foygel Barber, R., Candes, E., and Ramdas, A. (2019). “Conformal prediction under covariate shift,” in Advances in neural information processing systems. Editors H. Wallach, H. Larochelle, A. Beygelzimer, A. Buc, E. Fox, and R. Garnett (Curran Associates, Inc.) 32. Available at: https://proceedings.neurips.cc/paper_files/paper/2019/file/8fb21ee7a2207526da55a679f0332de2-Paper.pdf.

Google Scholar

Tsiamis, A., Ziemann, I., Matni, N., and Pappas, G. J. (2022). Statistical learning theory for control: a finite sample perspective. arXiv preprint arXiv:2209.05423.

Google Scholar

Tsitsiklis, J., Bertsekas, D., and Athans, M. (1986). Distributed asynchronous deterministic and stochastic gradient optimization algorithms. IEEE Trans. Automatic Control 31, 803–812. doi:10.1109/tac.1986.1104412

CrossRef Full Text | Google Scholar

Vapnik, V. (1999). The nature of statistical learning theory. 2nd Edition. New York, NY: Springer, 314. doi:10.1007/978-1-4757-3264-1

CrossRef Full Text | Google Scholar

Vasconcelos, M. M., Gagrani, M., Nayyar, A., and Mitra, U. (2020). Optimal scheduling strategy for networked estimation with energy harvesting. IEEE Trans. Control Netw. Syst. 7, 1723–1735. doi:10.1109/tcns.2020.2997191

CrossRef Full Text | Google Scholar

Vasconcelos, M. M., and Martins, N. C. (2017). Optimal estimation over the collision channel. IEEE Trans. Automatic Control 62, 321–336. doi:10.1109/tac.2016.2558644

CrossRef Full Text | Google Scholar

Vasconcelos, M. M., and Martins, N. C. (2019). Optimal remote estimation of discrete random variables over the collision channel. IEEE Trans. Automatic Control 64, 1519–1534. doi:10.1109/tac.2018.2854888

CrossRef Full Text | Google Scholar

Vasconcelos, M. M., and Mitra, U. (2020). Observation-driven scheduling for remote estimation of two Gaussian random variables. IEEE Trans. Control Netw. Syst. 7, 232–244. doi:10.1109/tcns.2019.2900864

CrossRef Full Text | Google Scholar

Vasconcelos, M. M., and Mitra, U. (2021). Data-driven sensor scheduling for remote estimation in wireless networks. IEEE Trans. Control Netw. Syst. 8, 725–737. doi:10.1109/tcns.2021.3050136

CrossRef Full Text | Google Scholar

Verma, A., Vasconcelos, M. M., Mitra, U., and Touri, B. (2023). Maximal dissent: a state-dependent way to agree in distributed convex optimization. IEEE Trans. Control Netw. Syst. 10, 1783–1795. doi:10.1109/tcns.2023.3240332

CrossRef Full Text | Google Scholar

Wang, J., Charles, Z., Xu, Z., Joshi, G., McMahan, H. B., Al-Shedivat, M., et al. (2021). A field guide to federated optimization. arXiv preprint arXiv:2107.06917.

Google Scholar

Yang, T., Yi, X., Wu, J., Yuan, Y., Wu, D., Meng, Z., et al. (2019). A survey of distributed optimization. Annu. Rev. Control 47, 278–305. doi:10.1016/j.arcontrol.2019.05.006

CrossRef Full Text | Google Scholar

Yates, R. D., Sun, Y., Brown, D. R., Kaul, S. K., Modiano, E., and Ulukus, S. (2021). Age of information: an introduction and survey. IEEE J. Sel. Areas Commun. 39, 1183–1210. doi:10.1109/JSAC.2021.3065072

CrossRef Full Text | Google Scholar

Yuille, A. L., and Rangarajan, A. (2003). The concave-convex procedure. Neural Comput. 15, 915–936. doi:10.1162/08997660360581958

PubMed Abstract | CrossRef Full Text | Google Scholar

Yüksel, S., and Başar, T. (2013). “Stabilization and optimization under information constraints,” in Stochastic networked control cystems. (New York, NY: Birkhäuser), XVIII, 482. 1st Edition. doi:10.1007/978-1-4614-7085-4

CrossRef Full Text | Google Scholar

Yun, J., Eryilmaz, A., Moon, J., and Joo, C. (2023). Remote estimation for dynamic iot sources under sublinear communication costs. IEEE/ACM Trans. Netw. 2023, 1–13. doi:10.1109/tnet.2023.3314506

CrossRef Full Text | Google Scholar

Zhang, X., and Vasconcelos, M. M. (2023a). Robust one-shot estimation over shared networks in the presence of denial-of-service attacks. arXiv preprint arXiv:2302.14689.

Google Scholar

Zhang, X., and Vasconcelos, M. M. (2023b). Proceedings of The 5th annual learning for dynamics and control conference. PMLR 211, 813–824.

Google Scholar

Zhang, Z., Al-Abri, S., and Zhang, F. (2022). Opinion dynamics on the sphere for stable consensus and stable bipartite dissensus. IFAC-PapersOnLine 55, 288–293. doi:10.1016/j.ifacol.2022.07.274

CrossRef Full Text | Google Scholar

Zhao, C., He, J., and Wang, Q.-G. (2020). Resilient distributed optimization algorithm against adversarial attacks. IEEE Trans. Automatic Control 65, 4308–4315. doi:10.1109/tac.2019.2954363

CrossRef Full Text | Google Scholar