- 1Physics Department, Technical University of Munich, Munich, Germany
- 2Max Planck Institute for Chemical Physics of Solids, Dresden, Germany
- 3Center for Correlated Matter, Zhejiang University, Hangzhou, China
The tetragonal heavy-fermion metal YbRh2Si2 orders antiferromagnetically at TN = 70 mK and exhibits an unconventional quantum critical point (QCP) of Kondo-destroying type at BN = 60 mT, for the magnetic field applied within the basal (a, b) plane. Ultra-low-temperature magnetization and heat-capacity measurements at very low fields indicate that the 4f-electronic antiferromagnetic (AF) order is strongly suppressed by a nuclear-dominated hybrid order (“A-phase”) at TA ≤ 2.3 mK, such that quantum critical fluctuations develop at B ≈ 0 (Schuberth et al., Science, 2016, 351, 485–488). This enables the onset of heavy-fermion superconductivity (Tc = 2 mK) which appears to be suppressed by the primary antiferromagnetic order at elevated temperatures. Measurements of the Meissner effect reveal bulk superconductivity, with Tc decreasing under applied field to Tc < 1 mK at B > 20 mT. The observation of a weak but distinct superconducting shielding signal at a temperature as high as 10 mK suggests the formation of insulated random islands with emergent A-phase order and superconductivity. Upon cooling, the shielding signal increases almost linearly in temperature, indicating a growth of the islands which eventually percolate at T ≈ 6.5 mK. Recent electrical-resistivity results by Nguyen et al. (Nat. Commun., 2021, 12, 4341) confirm the existence of superconductivity in YbRh2Si2 at ultra-low temperatures. The combination of the results of Schuberth et al. (2016) and Nguyen et al. (2021) at ultra-low temperatures below BN, along with those previously established at higher temperatures in the paramagnetic state, provide compelling evidence that the Kondo-destruction quantum criticality robustly drives unconventional superconductivity.
1 Kondo-Destroying, Field-Induced Quantum Critical Point
Lanthanide-based intermetallic compounds showing heavy-fermion phenomena are well understood within the framework of the Kondo lattice (Wirth and Steglich, 2016). The localized open 4f-shells of such materials are characterized by a distinct hierarchy of fundamental energy scales, the local Coulomb repulsion and Hund’s rule energies, spin-orbit coupling, crystal-field splitting, Kondo screening including excited crystal-field states at an elevated temperature, where the formation of hybridized 4f-bands starts to be recognized in ARPES measurements (Chen et al., 2017), as well as Kondo screening of the lowest-lying crystal-field-derived Kramers doublet (kBTK). As illustrated below, the single-ion Kondo temperature TK was found to be identical to Tcoh (Ernst et al., 2011; Seiro et al., 2018) where spatial coherence among 4f-shells sets in as seen in transport measurements.
The onsite Kondo screening competes with the inter-site magnetic Ruderman–Kittel–Kasuya-Yosida (RKKY) interaction. While predominant Kondo screening results in a paramagnetic heavy-fermion ground state, a dominant RKKY interaction causes magnetic, most frequently antiferromagnetic (AF), order. For a substantial number of these heavy-fermion metals the Kondo screening turns out to almost exactly cancel the RKKY interaction. In this situation, a continuous transition may exist at T = 0 between the heavy-fermion and the AF phase. This continuous quantum phase transition or quantum critical point (QCP) can be tuned by a non-thermal control parameter, e.g., pressure or magnetic field (Stewart, 2001; von Löhneysen et al., 2007; Gegenwart et al., 2008; Sachdev, 2011).
YbRh2Si2 is a prototypical heavy-fermion metal (Köhler et al., 2008; Ernst et al., 2011) which orders antiferromagnetically at a Néel temperature TN = 70 mK (Trovarelli et al., 2000). Because of a strong magnetic anisotropy the critical field BN at which AF order smoothly disappears is only 60 mT when the field is applied within the basal tetragonal (a, b) plane, i.e., it is more than ten times lower compared to BN ∥ c (Gegenwart et al., 2002). The staggered moment was shown to be very small, μAF ≈ 0.002 μB (Ishida et al., 2003). Both the low-temperature paramagnetic (B > BN) and AF phases (B < BN) behave as heavy Fermi liquids (Gegenwart et al., 2002) whereas a funnel-shaped quantum critical regime in the B–T phase diagram (Figure 1) with non-Fermi-liquid properties is centered at the critical field BN. The AF phase transition is of second order to the lowest temperature (20 mK) accessible in magnetostriction measurements (Gegenwart et al., 2007); the crossover between the paramagnetic Fermi liquid and the non-Fermi-liquid phase turns out to be quite broad. The sub-linear white T*(B) crossover line in Figure 1 was constructed by the midpoints of thermally broadened jumps in both the longitudinal magneto-resistivity and the isothermally measured initial normal Hall coefficient (Paschen et al., 2004; Friedemann et al., 2010). They agree satisfactorily with the locations of distinct anomalies in the field dependence of both the isothermal DC magnetization and magnetostriction as well as in the temperature dependence of the AC susceptibility measured at fixed magnetic field (Gegenwart et al., 2007). T*(B) indicates a crossover between a small Fermi volume (“small Fermi surface”) at low fields and a large one at elevated fields. The crossover width (grey shaded region) turns out to be proportional to T. The QCP at BN(T = 0) is of an unconventional “local” (instead of itinerant) variety, which may be called a “partial Mott” or Kondo-destroying QCP. It is characterized by a dynamical spin susceptibility with frequency-over-temperature scaling and a fractional exponent in the singular parts of both the frequency and temperature dependences (Coleman et al., 2001; Si et al., 2001) as observed by inelastic neutron scattering on both UCu5−xPdx (Aronson et al., 1995) and CeCu6−xAux (Schröder et al., 2000). The latter material (von Löhneysen et al., 1994) as well as CeRhIn5 (Shishido et al., 2005; Park et al., 2006) are also prototypical heavy-fermion metals exhibiting a local QCP.
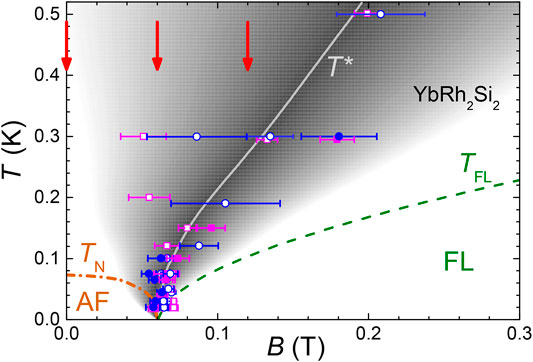
FIGURE 1. Temperature–magnetic field phase diagram of YbRh2Si2 for B ⊥ c. The symbols mark the results from Hall and magnetoresistance measurements on two different samples from which the Fermi surface crossover temperature T*-line is estimated (Friedemann et al., 2010). The grey scale visualizes the slope of isothermal magnetoresistance. Orange and green dashed lines indicate the Néel temperature TN and the crossover temperature TFL below which AF order and Fermi liquid behavior are observed, respectively. Red arrows indicate B = 0, BN and 2BN, respectively. Figure adapted from Wirth and Steglich (2016).
Figure 2 displays the thermal evolution at low temperatures of both the (Sommerfeld) coefficient of the 4f-derived part of the specific heat, γ = Cel/T = C4f/T (Figure 2A), and the electrical resistivity measured on an YbRh2Si2 single crystal with a low residual resistivity of about 0.5 μΩ cm (Figure 2B), at B = 0, BN and 2BN, respectively (see red arrows in Figure 1). The behavior of a heavy Fermi liquid in both the AF and low-temperature paramagnetic phase is clearly resolved by a huge constant γ-value (Figure 2A) and a pronounced T2-dependence in ρ(T) (Figure 2B). Very peculiarly, the Fermi liquid in the AF phase (with small Fermi surface as T → 0) is considerably heavier than the Fermi liquid in the paramagnetic phase (with large Fermi surface). Approaching the QCP at B = BN by cooling to below 0.3 K, one finds that γ(T) diverges following a power-law dependence with a critical exponent of
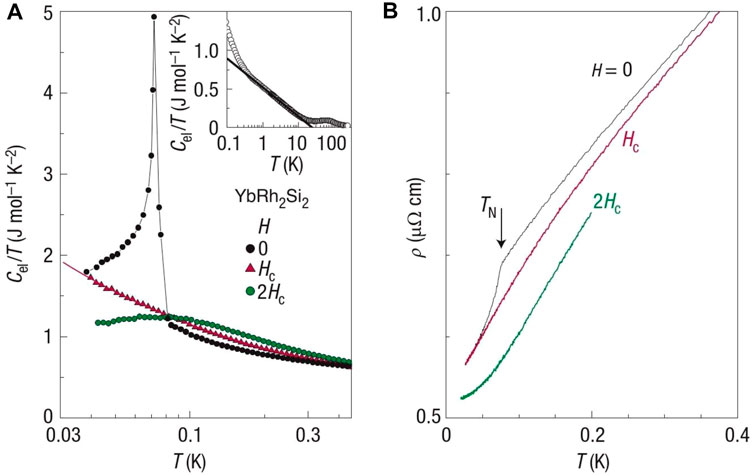
FIGURE 2. (A) Sommerfeld coefficient of the electronic specific heat and (B) electrical resistivity vs temperature T at B = 0, BN and 2BN for a YbRh2Si2 single crystal with RRR = 150. Inset in (A) shows the Sommerfeld coefficient at BN = 60 mT between 0.1 K and room temperature. Reproduced from Gegenwart et al. (2008).
One of the important techniques that provides new insight into such correlation-driven phenomena is scanning tunneling spectroscopy (STS) with its unique ability to give local, atomically resolved information that relates to the one-particle Green’s function (Kirchner et al., 2020). However, one of the prerequisites for successful STS measurements is the preparation and perpetuation of clean sample surfaces. Fortunately, YbRh2Si2 can be cleaved nicely perpendicular to the c-axis in ultra-high vacuum (UHV) and at low temperatures of about 20 K providing atomically flat surface areas of often several hundreds of nanometers in extent. Such surfaces not only evidence the excellent sample quality (inset to Figure 3A), they even allow to analyze the defects to be mostly caused by Rh-atoms on Si sites (Wirth et al., 2012).
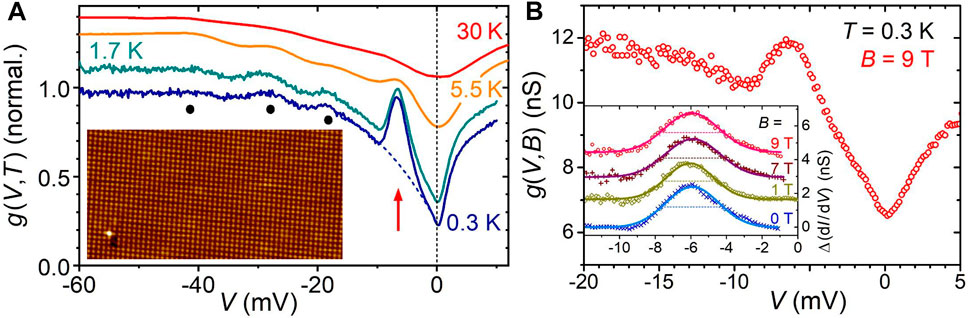
FIGURE 3. Tunneling conductance g(V, T, B) on Si-terminated YbRh2Si2. (A) Data obtained at different temperatures and B = 0. g(V, T)-values are normalized at V = −80 mV and offset for clarity. The −6 meV-peak evolving at low T is marked by a red arrow; the parabola background for peak analysis at T = 0.3 K is shown as a dashed line. Black dots indicate features resulting from crystalline electric field splitting of the Yb 4f multiplet. Inset: Topography visualizing the excellent surface quality (area: 20 × 10 nm2, V = 100 mV, I = 0.6 nA). (B) Exemplary in-field data at T = 0.3 K and B = 9 T (∥ c). Inset: Data (markers) after background subtraction with corresponding Gaussian fits (lines). A reduced width (full width at half maximum, dashed lines) of the Gaussian at B = 1 T can be recognized. All figure parts adapted from Seiro et al. (2018).
We here focus on predominantly encountered Si-terminated surfaces. In case of such surfaces, the Kondo-active Yb atoms are located in the fourth-to-topmost layer which prevents a reduced screening of the Yb local moments at the surface (Alexandrov et al., 2015) and ensures a predominant study of bulk properties by STS. The latter is clearly evidenced by the observation of crystal field excitations in the tunneling spectra (Ernst et al., 2011) at energies in excellent agreement with inelastic neutron scattering data (Stockert et al., 2006b) (black dots in Figure 3A). Moreover, Si-terminated surfaces promote predominant tunneling into the conduction band as compared to the 4f quasiparticle states and thereby simplify the analysis of the obtained spectra as co-tunneling can be neglected (Ernst et al., 2011; Kirchner et al., 2020). In this simplified picture, the successive formation of the single-ion Kondo effect upon lowering the temperature results primarily in a modification of the density of states of the conduction band seen as a strong decrease of the tunneling conductance g (V, T) for V small enough to not break up the quasiparticles. This process is observed to commence at around 100 K and coincides with the onset of local Kondo screening involving excited crystalline electric field levels as concluded from entropy estimates (Custers et al., 2003). Upon cooling to below the single-ion Kondo temperature TK ≃ 25 K the 4f electrons condense into the Kramers doublet ground state and the Kondo lattice develops. This is reflected in the STS data, Figure 3A, by the strong development of a peak at around −6 meV. Notably, the position in energy of this peak does not depend on temperature.
The relation of this −6 meV-peak to the Kondo lattice is supported by calculations: Results of a multi-level finite-U non-crossing approximation (Ernst et al., 2011) which does not consider intersite Kondo correlations captures the temperature evolution of the zero-bias conductance dip remarkably well but provides no indication for a peak at −6 meV. Conversely, renormalized band structure calculations (Zwicknagl, 2011) which treats the fully renormalized Kondo lattice ground state finds a partially developed hybridization gap at slightly smaller energy in the quasiparticle density of states (which is complementary to the here measured density of states of the conduction band within the Kondo regime).
Albeit this Kondo lattice peak sets in at around TK, i.e., Tcoh ≈ TK as mentioned above, it only slowly increases in height down to about 3 K
STS was also conducted at 0.3 K for magnetic fields applied B ∥ c, see exemplary data for B = 9 T in Figure 3B. It should be noted that renormalized band structure calculations (Zwicknagl, 2011) predict a smooth quasiparticle disintegration up to well above 30 T in YbRh2Si2 while AF order is already suppressed at B ≈ 0.6 T for B ∥ c. The position in energy of the Kondo lattice signature peak at −6 meV is not influenced by applying a magnetic field, further supporting its attribution. After background subtraction it can be well fitted by a Gaussian, cf. inset of Figure 3B. The width of the Gaussian fit is somewhat reduced at B = 1 T compared to peak widths at zero field and at several Tesla. Here we note that a field magnitude of 1 T is close to the T*-line (cf. Figure 1) for T = 0.3 K and B ∥ c. Therefore, the reduced peak width at B = 1 T is consistent with a reduced quasiparticle weight related to quantum criticality, see also Figure 4C. However, these STS data on their own do not allow to distinguish between different scenarios for quantum criticality and should be extended to lower temperatures.
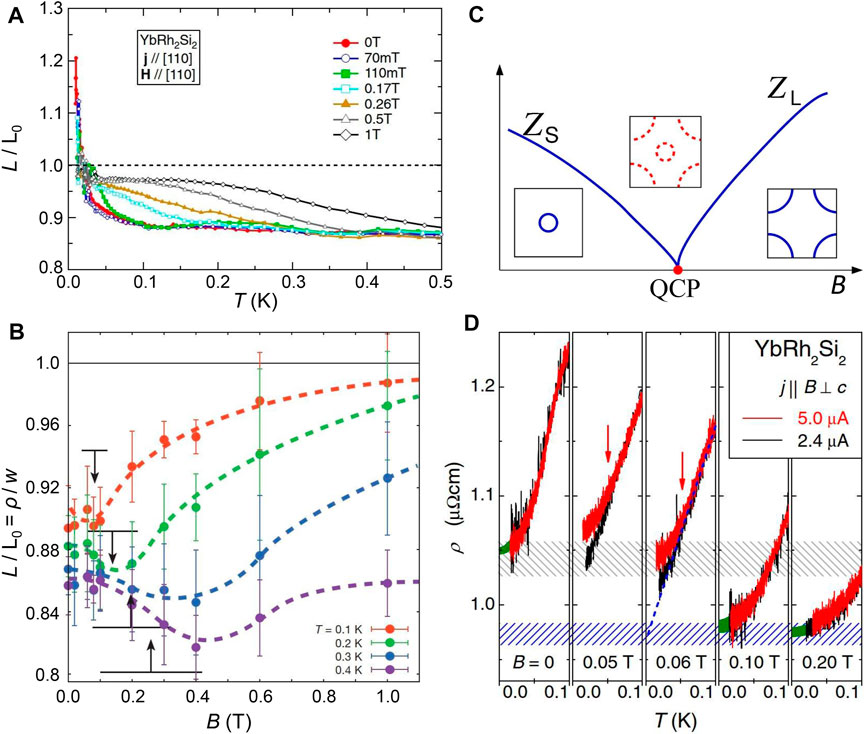
FIGURE 4. (A) Lorenz ratio L(T)/L0 vs. T for an YbRh2Si2 single crystal at B = 0 and at various finite fields B ⊥ c. Reproduced with permission from Pourret et al. (2014), Copyright (2014) The Physical Society of Japan. (B) L(T)/L0 vs. B (⊥ c) isotherms, T ≥ 0.1 K (paramagnetic regime, purely electronic heat transport, no bosonic contribution to κ). Reproduced from Pfau et al. (2012). (C) Schematic sketch showing coexistence of small and large Fermi surfaces. Reproduced from Pfau et al. (2012). (D) BN = 0.059 T. Black (small j): no heating. B = 0, [ρ(T) −ρ01] = A1T2; B = 0.2 T, [ρ(T) −ρ02] = A2T2 (extrapolations to T = 0 shown in green) with ρ01 > ρ02 (different carrier densities, small vs. large FS). A1 > A2 (Figure 2B). B = 0.05 T
Consequently, the question concerning the nature of the “local” QCP in YbRh2Si2 and the associated critical excitations remains. To answer this question, combined thermal and electrical transport investigations on YbRh2Si2 single crystals were carried out down to 25 mK at zero field, close to BN and up to B = 1 T (≫ BN) (Pfau et al., 2012). Subsequently, Pourret et al. (2014) were able to extend such measurements down to even 8 mK. The main quantity to study in this context is the Lorenz number L = ρκ/T, where ρ is the electrical resistivity and κ the thermal conductivity. By defining the thermal resistivity as w = L0T/κ, with
Very different phenomena can cause a violation of this law: 1) Fermionic excitations like spinons, i.e., charge-neutral heat carriers, may lead to L(T → 0)/L0 > 1. This was indeed concluded from measurements on, e.g., LiCuVO4 (Parfen’eva et al., 2004). 2) Alternatively, an enhanced w(T) can lead to L/L0 < 1, as frequently observed at finite temperature with dominating inelastic scatterings of the charge carriers, like the ones from acoustic phonons. In the zero-temperature limit, however, inelastic scatterings have to disappear. To our knowledge, before 2012 this latter kind of violation of the Wiedemann-Franz law, L(T → 0)/L0 < 1, has never been convincingly established. For example, for the quasi-two-dimensional (2D) heavy-fermion metal CeCoIn5, where an AF QCP was suspected (Singh et al., 2007; Zaum et al., 2011) but not identified, L(T)/L0 was extrapolated to about 0.8 as T → 0 for c-axis transport at B ≈ Bc2 ≈ 5 T, while it approaches L(T)/L0 ≈ 1 for in-plane (⊥ c) transport (Tanatar et al., 2007). This result was ascribed to the action of anisotropic spin fluctuations, although as T → 0, spin fluctuations as bosonic excitations must disappear as well. Subsequently, the observations by Tanatar et al. could be consistently explained within the framework of quasi-2D transport (Smith and McKenzie, 2008).
In the following, we describe the violation of the Wiedemann-Franz law in YbRh2Si2 with the aid of Figure 4, see also (Smidman et al., 2018). As shown in Figure 4A at B = 0 and 0.07 T, L(T)/L0 ≈ 0.87 in an extended temperature window (0.1 K
Several groups have reported very similar experimental data compared with those by Pfau et al. (2012), but questioned the interpretation sketched above. The key problem is the correct treatment of the bosonic term κm(T). This term was just ignored by Machida et al. (2013); Reid et al. (2014), i.e., here the measured thermal conductivity was erroneously regarded as the electronic contribution in the whole low-temperature range of the experiments, down to 40 mK. On the other hand, Taupin et al. (2015), who gave a detailed interpretation of the data previously published by Pourret et al. (2014), consider κm(T) to set in at a temperature as low as 30 mK, although the data (Pourret et al., 2014) clearly prove this to occur already at about 0.1 K (Figure 4A). Therefore, on extrapolating the data to T = 0 from just above 30 mK where κm(T) dominates, they miss the intrinsic value Lel(T → 0)/L0 ≈ 0.9 and instead obtain accidently
In Figure 4D, the conclusions drawn from the heat-conduction study discussed above are nicely confirmed by results of measurements of the electrical resistivity (Lausberg, 2013). Close to the critical field BN = 59 mT and at sufficiently low temperatures, the sample under investigation becomes heated by a moderate current due to its deteriorated heat conductivity. No heating is observed when applying a low enough current. Away from BN, in the AF phase at B = 0 as well as in the paramagnetic phase at 0.1 and 0.2 T, the resistivity follows the Fermi liquid-type T2-dependence, independent of the size of the here investigated currents. Upon approaching BN from either side, at the lowest accessible temperatures “strange-metal” behavior, characteristic of the local QCP, is observed at low current. If these linear T-dependences of ρ(T) obtained at 2.4 μA are extrapolated to T = 0, ρ(T) ends up at very different values of the residual resistivity. In particular, the so extrapolated ρ0 values match nicely with those obtained by extrapolating the Fermi liquid-type T2-dependences of ρ(T) found at B = 0 and way above BN, respectively. We consider this jump in ρ0 as a direct visualization of the abrupt change in the charge-carrier density of YbRh2Si2 on field tuning through the Kondo-destroying QCP.
2 Competition Between Nuclear and Primary 4f-Electronic Order, Emergence of Hybrid A-Phase and Superconductivity
When YbRh2Si2 single crystals were investigated by resistivity measurements at T > 10 mK, and specific-heat as well as susceptibility measurements at T > 18 mK, no superconductivity could be detected (Custers et al., 2003). The most natural explanation for this is that superconductivity becomes suppressed by the AF order which forms at TN = 70 mK. To find out whether superconductivity in YbRh2Si2 shows up at T ≤ 10 mK, magnetization, susceptibility and specific-heat measurements have been carried out down to temperatures as low as 0.8 mK by using a nuclear demagnetization cryostat providing a base temperature of 400 μK (Schuberth et al., 2016). Here, a total of five different single crystals was investigated. In Figure 5A, the temperature dependence of the field-cooled (fc) DC-magnetization, measured at a magnetic field of 0.09 mT, reveals two phase-transition anomalies at TN ≈ 70 mK and TA (Tc)
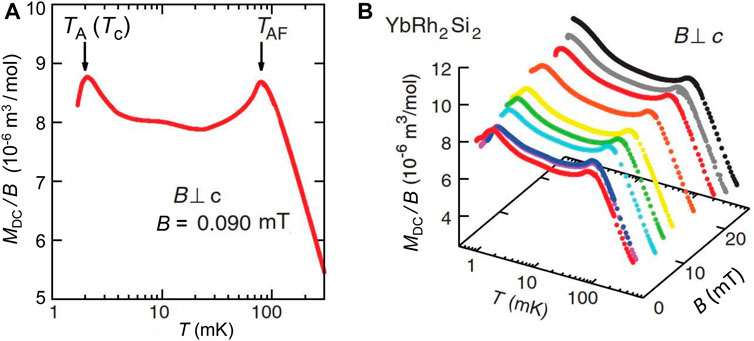
FIGURE 5. Field-cooled (fc) DC magnetization MDC, normalized at 1.1 mT, in dependence on temperature T for magnetic field B ⊥ c. After cooling the sample at the magnetic measuring field B to below 1 mK, the magnetization curve was taken on the warmup of the nuclear stage. (A) B = 0.090 mT. (B) B ≤ 23 mT. Reproduced from Schuberth et al. (2016).
Figure 6A displays the zero-field-cooled (zfc-) and fc-MDC(T) curves taken up to B = 0.418 mT in a specially shielded setup (different from the one used to obtain the data of Figure 5). The data registered at the lowest field, B = 0.012 mT, illustrate how the experiment was performed: one starts at T > 10 mK by cooling the sample in zero field to the lowest temperature, T = 0.8 mK. Then, the field is applied and the zfc curve is recorded on warming to above 10 mK. Cooling again with field applied yields the fc curve. The zfc-MDC(T) curve, which separates abruptly from the fc curve at T ≈ 10 mK, indicates a shielding signal which is increasing almost linearly upon cooling and assumes a value of not more than 20% just above Tc = 2 mK. This is followed by a sharp, pronounced drop at Tc and a robust diamagnetic response at T ≤ 1 mK. These data are well reproduced by the results of the AC susceptibility obtained under nearly zero-field conditions, Figure 6B. In the χAC(T) data partial shielding below T ≈ 10 mK and the AF phase transition at TN ≈ 70 mK are resolved as well.
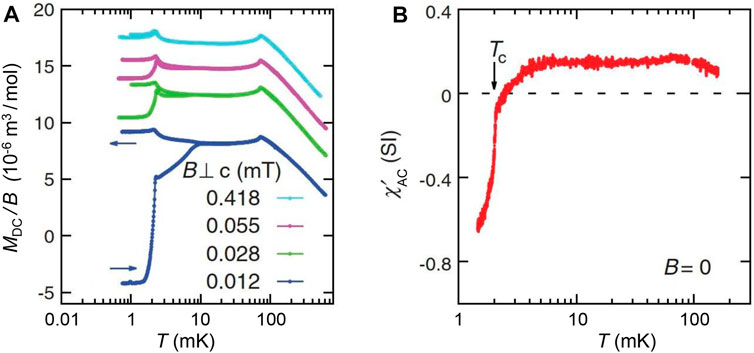
FIGURE 6. (A) fc- and zfc-MDC(T) curves, normalized to 1.1 mT and offset for the sake of clarity, between 0.012 and 0.418 mT. The data were taken in a special measuring cell which allowed for the compensation of the earth field to obtain a smallest magnetic measuring field of 0.012 mT. Note that the vertical scale is larger by more than a factor of 5 compared to that in Figure 5A. (B) Real part of the AC susceptibility
We now turn to the peak in the fc-MDC(T) curve at 2 mK which reveals a pronounced decline ΔM of about 0.075 μB per Yb down to 0.8 mK (Figure 5A). As will be discussed below, about 25% of this decline on the low-T side of the 2 mK-peak should be attributed to the onset of the nuclear-4f electronic hybrid “A-phase”, leaving about 75% of this being due to the Meissner effect. This corresponds to a Meissner volume amounting to only about 2% of the full shielding signal which seems to be quite a small value; however, owing to vortex pinning this is typical for bulk type-II superconductors. After destroying the pinning centers by powdering and subsequent annealing, the sample should exhibit a substantially increased Meissner volume when measured below the lower critical field Bc1, see, e.g., Steglich et al. (1979); Rauchschwalbe et al. (1982). As also inferred from Figure 6A, the shielding signal in zfc-MDC(T) has become extremely weak at a field as low as 0.418 mT, cf. the discussion below. By contrast, the jump in fc-MDC(T), ΔM, is robust, hinting at the existence of bulk superconductivity with Tc ≥ 0.8 mK up to B ≤ 23 mT, see Figure 5B.
The coefficient of the molar spin specific heat, δC(T)/T, obtained after subtracting a huge nuclear quadrupolar contribution (for B = 0) from the raw data taken at 2.4 mT, is shown below 6 mK in Figure 7A. δC(T) mainly consists of the contributions by the Yb-derived nuclear spins (S = 1/2 for 171Yb ions with a natural abundance of 14.3% as well as S = 5/2 for 173Yb ions with 16.1% abundance). Note that neither the 100Rh nor the 29Si nuclear spins contribute to the specific heat above T = 1 mK, because they assume their full Zeeman entropies already below this temperature. In addition to the nuclear spin contributions, there is a small one by the 4f-electronic spins, C4f(T). Since the effect of a magnetic field on the nuclear quadrupole contribution is only of higher order, one can use these δC(T)/T data, subtracted by C4f(T)/T, to estimate the molar Yb-derived nuclear spin entropy SI,Yb(T) (for B = 2.4 mT). Clearly seen in Figure 7A is a huge, broadened phase-transition anomaly of mean-field type. The latter can be replaced, under conservation of entropy, by a jump which yields a phase transition temperature of TA = 2 mK (at B = 2.4 mT) and a jump height ΔC/TA of
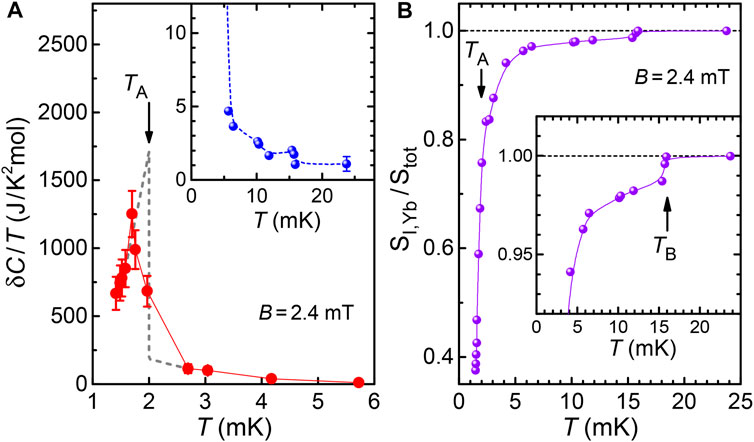
FIGURE 7. (A) Molar spin specific heat of YbRh2Si2 in an external magnetic field B = 2.4 mT plotted as δC/T vs. T at T < 6 mK. The data were obtained by the common heat-pulse as well as the relaxation methods with the fc-MDC(T) dependence of YbRh2Si2 used as an internal thermometer. In the latter case, the heat capacity
The temperature-magnetic field phase diagram in Figure 8 indicates the various low-T, low-B phases of YbRh2Si2, i.e., the primary AF phase (blue dots and dashed line), the so-called “B-phase” (light blue shading), the A-phase and superconductivity whose transition temperatures are closely spaced and jointly displayed by the red dots, designating the positions of the low-temperature peaks in fc-MDC(T), see Figure 5. The green symbol at B = 0 represents the superconducting phase transition observed in χAC(T), and the yellow ones, partly hidden by the former, denote the positions of the pronounced shielding signals registered at very low fields by zfc-MDC(T) (Figure 6A). These latter transition temperatures are plotted as a function of field in the inset, yielding the absolute initial slope of the upper critical field curve at T = Tc,
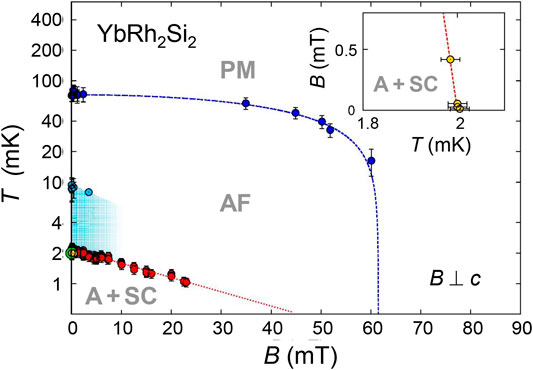
FIGURE 8. Phase diagram of YbRh2Si2. Dark blue dots and line: boundary of the primary AF order. Light blue dots and shaded area: partial superconducting shielding in previously labelled “B-phase”, i.e., in insulated droplets of A-phase which form below TB ≈ 16 mK, see text. Red data points: Position of low-T peak in fc-MDC(B), see Figure 5. Green circle: superconducting Tc at B = 0 from χAC(T), see Figure 6B. Yellow circles: superconducting Tc from zfc-MDC(T), Figure 6A, blown up in the inset to illustrate the huge absolute value of the initial slope of Bc2(T) at Tc,
One can derive the effective g-factor of the A-phase, geff ≃ 0.051, from the ratio of the transition temperature TA(B = 0) = 2.3 mK and the critical field BA(T → 0) ≃ 45 mT (Figure 8). Using the in-plane 4f-g-factor of YbRh2Si2, g4f = 3.5 (Sichelschmidt et al., 2003), one finds the A-phase to represent hybrid AF order comprising a dominant (≃ 98.5%) nuclear component and a tiny 4f-electronic component of ≃ 1.5%, with a staggered moment of mJ ≃ 0.018 μB. This is obtained with the aid of the (T → 0) saturation moment, 1.24 μB, as estimated from a Curie-Weiss fit to the fc-magnetization data taken in the paramagnetic regime at an external field of 10.1 mT, see Figure 9. The staggered moment mJ exceeds significantly that of the primary AF phase, mAF ≈ 0.002 μB (Ishida et al., 2003) which may explain the “re-entrant AF order” at very low temperatures as reported by Saunders (2018) based on measurements of Nyquist noise. We note that a pure nuclear phase transition would not be resolved in our magnetization measurements because of the very small nuclear moment. Therefore, one can state that the 2 mK-peak in fc-MDC(T) originates in the tiny 4f-component of the hybrid A-phase (and additionally, to a larger part in the Meissner signal of the superconducting transition), while the huge anomaly in the specific-heat coefficient shown in Figure 7A is only due to the Yb-derived nuclear spin states. We infer from the red data points shown in Figure 8 and the results of Figure 5B that the existence range for bulk superconductivity is most likely extended to fields in excess of 23 mT where the values of Tc are below 0.8 mK.
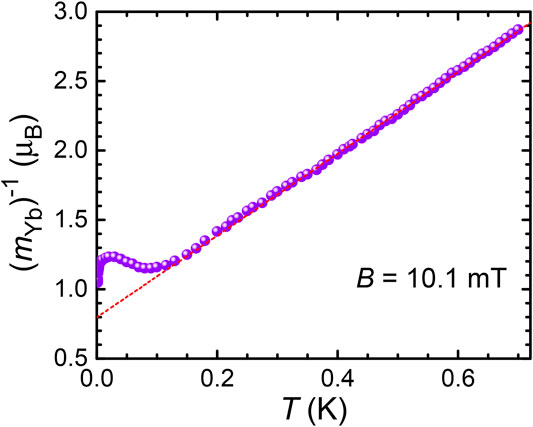
FIGURE 9. Curie Weiss fit, μB/mYb vs temperature at B = 10.1 mT. For T → 0 a saturation moment msat = 1.24 μB is estimated. The Weiss temperature θ ≈ − 0.27 K agrees well with the result reported by Custers et al. (2003) and illustrates dominant AF correlations at low temperature (Hamann et al., 2019).
Measurements of the electrical resistivity at ultra-low temperatures are extremely difficult in view of the unavoidable contact resistances which may easily heat up the sample. Recently, Nguyen et al. were successful in performing such measurements on YbRh2Si2 single crystals down to 0.5 mK (Nguyen et al., 2021). Figure 10 reproduces their results on a pristine sample of YbRh2Si2 (A, C) as well as on a single crystal with nominally 100 at% of 174Yb ions which do not carry nuclear spins (denoted as 174YbRh2Si2 in B, D). This latter sample had been prepared and intensively studied by Knebel et al. (2006). For both single crystals the onset of the primary AF order at TN = 70 mK is resolved, see Figures 10A,B, as is the superconducting transition with a (mid-point) Tc = 7.9 mK, following an onset at ≃ 9 mK for the YbRh2Si2 crystal and an onset at about 5 mK for the 174YbRh2Si2 crystal (Figures 10C,D). Within the resolution of the experiments, the resistivity reaches ρ = 0 at about 6.5 mK for the former sample (Figure 10C). In case of the nominally nuclear-spin free 174YbRh2Si2 sample, the onset of superconductivity at 5 mK is followed by a broadened 75% decrease of ρ(T), which starts to decline in a substantially steeper fashion at about 1 mK, without reaching zero at the low-T limit of 0.5 mK, suggesting ρ = 0 at around 0.3–0.4 mK (Figure 10D). Under external magnetic field the transitions are shifted to lower temperatures. As shown in Figure 10C, for the YbRh2Si2 sample, the transition is broadened at B = 11 mT, and zero resistivity is achieved at T ≈ 2 mK. Even at B = 60 mT a residual, very broad and incomplete transition is recognized. The initial Tc(B) dependence is found to be relatively steep, implying an absolute initial slope of |B′c2| ≃ 4.4 T/K. The field dependence of Tc becomes flatter above B ≈ 11 mT. The finite-field data for the 174YbRh2Si2 sample displayed in Figure 10D show a field-induced reduction of the temperature range of the broad initial decline in ρ(T). In addition, the temperature of 0.3–0.4 mK at which ρ(T) is likely to vanish, appears to be almost independent of field up to B = 30 mT.
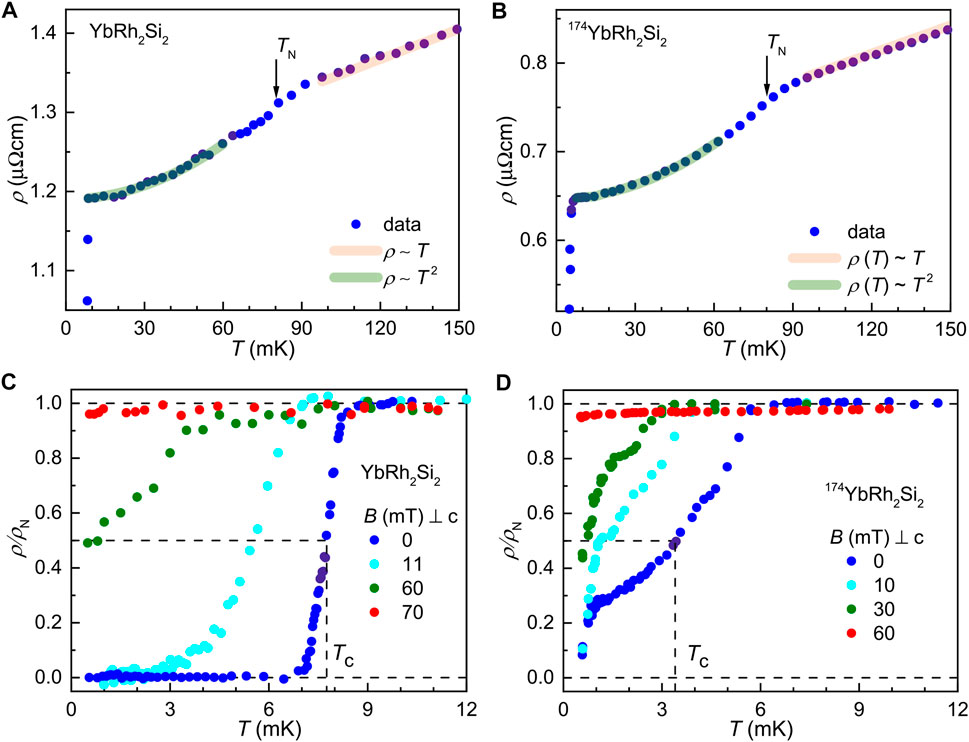
FIGURE 10. Electrical resistivity as a function of temperature for (A), (C) YbRh2Si2 and (B), (D) 174YbRh2Si2 at B = 0 and various applied fields. Reproduced from Nguyen et al. (2021) under a Creative Commons Attribution 4.0 International License. Copyright 2021, The Authors, published by Springer Nature.
To put these new results in perspective, we wish to note that resistive transitions (at Tc,ρ) commonly probe percolative superconductivity, with ρ(T) reaching zero when the first percolating path through the sample is formed. On the other hand, both χAC(T) (with Tc,χ) and zfc-MDC(T) provide shielding signals due to “networks of screening currents” in the sample surface. The thermodynamic (bulk-) Tc is obtained through transitions in the specific heat and/or the Meissner effect as measured by fc-MDC(T) (with Tc,M). For inhomogeneous superconductors one frequently finds Tc,ρ > Tc,χ > Tc,M. In case of the Ce-based 115-superconductors with anisotropic transport owing to the delicate interplay of competition and coexistence between superconductivity and AF order, an exotic type of percolative (“textured”) superconductivity has been reported (Park et al., 2012). For CeIrIn5, the thermodynamic Tc probed via specific heat is 0.4 K, while Tc,ρ = 1.2 K (Petrovic et al., 2001).
In the YbRh2Si2 sample, the onset of superconductivity at very low fields is observed at almost the same Tc,ρ ≈ 8 mK in measurements of both the electrical resistivity (Nguyen et al., 2021) and Nyquist noise (Saunders, 2018). In this exceptional case Tc,ρ, and even the onset temperature of the resistive transition, is smaller than Tc,χ ≈ 10 mK. The resistivity study yields an absolute initial slope of Bc2(T) at Tc,
Concerning the 174YbRh2Si2 sample, we believe that 1) it contains a low, but finite, concentration of residual Yb ions with nuclear spins which give rise to a weakened hybrid A-phase order and, thus, weakened superconductivity, and 2) YbRh2Si2 free of nuclear spins would not be a superconductor, at least near B = 0. To check this, future studies of superconductivity of YbRh2Si2 samples with enriched 174Yb isotope should be assisted by high-precision mass spectrometry, which is required to determine the amount of residual nuclear spins.
A three-component Landau theory was applied in Schuberth et al. (2016) to explain the development of two subsequent AF phase transitions at TN and TA. (Assuming two components, one would obtain only one phase transition). This theoretical treatment was based on the empirical knowledge that the 4f-electronic spin susceptibility χ4f(Q) is highly anisotropic, exhibiting maxima at two wave vectors, QAF and Q = 0, and giving rise to the primary AF order and ferromagnetic correlations (Gegenwart et al., 2005), respectively.
It is, therefore, natural to assume that a peak in χ4f(Q) exists at yet another finite wave vector Q1, different from QAF. Along Q1, the RKKY interaction generates an order parameter ΦJ among the 4f-electronic spins and simultaneously an order parameter ΦI among the Yb-derived nuclear spins. According to the size of the effective g-factor discussed above, ΦI must be much larger than ΦJ. As ΦJ and ΦI exist at the same wave vector Q1, they are coupled bilinearly via − λ ΦJΦI, where the coupling parameter λ ≈ 25 mK is related to the hyperfine coupling constant Ahf by λ ∼ Ahf ≈ 100 T/μB. As a result, one finds the transition temperature of the nuclear-dominated hybrid A-phase
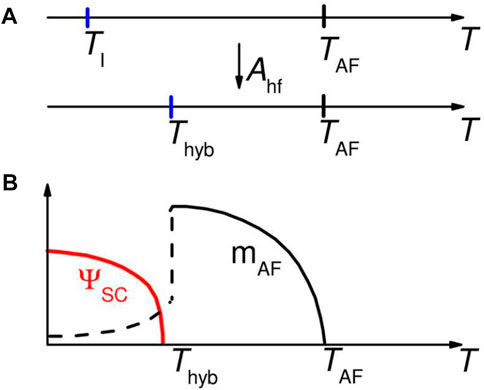
FIGURE 11. Three component Landau theory: Phase transitions at TAF and Thyb. (A) Sketch of the two phase transitions associated with electronic and nuclear spin orders. (Top line) Without any hyperfine coupling (Ahf), the electronic and nuclear spins are ordered at TAF and TI, respectively. (Bottom line) With hyperfine coupling, TAF is not affected, but a hybrid nuclear and electronic spin order is induced at Thyb ≫ TI. (B) Temperature evolution of the primary electronic spin order parameter (mAF) and the superconducting order parameter ΨSC. ΨSC is developed when mAF is suppressed by the formation of hybrid nuclear and electronic spin order directly below Thyb. Reproduced from Schuberth et al. (2016).
As this Landau theory is a mean-field theory, it does not treat short-range order. However, unique nuclear short-range order, as visualized by a significant temperature dependence of the nuclear spin entropy (Figure 7B), apparently exists up to at least 16 mK and generates the nucleation of superconductivity at T ≃ 10 mK (Figure 6A). In reality, as was inferred from Figure 5A, the staggered magnetization of the primary AF phase, mAF, starts to decrease already at 20 mK, rather than at T = Thyb. As suggested in Figure 11, mAF(T) continues to decrease below Thyb and may well vanish as T → 0. This means, the QCP is located at (or very close to) zero external magnetic field. Interestingly, the transition from the primary AF order to superconductivity is of first order (Schuberth et al., 2016), similar to what was found for single-crystalline A/S-type CeCu2Si2 (Stockert et al., 2006a).
In the following we summarize, and offer a—possibly oversimplified—explanation of, the multitude of puzzling results achieved by the previous magnetic and calorimetric as well as the recent resistive measurements:
1) Superconductivity in YbRh2Si2 apparently exists in a wide field range almost up to BA = 45 mT, with the maximum Tc occurring at B = 0 (Schuberth et al., 2016).
2) The T-dependence of fc-MDC(T) displayed in Figure 5A demonstrates that the staggered moment, mAF, of the primary order starts to decrease already at about 20 mK, which is close to the temperature associated with the strength of the local Yb hyperfine interaction (25 mK). In addition, a significant T-dependence of the Yb-derived nuclear spin entropy, SI,Yb(T), is observed up to TB ≈ 16 mK, where a distinct anomaly is visible in Figure 7. The latter is associated with a rather sharp removal of a tiny fraction of about 1.5% of Stot, the full value of SI,Yb(T) at high temperatures. This can be ascribed to a corresponding small fraction of the Yb-derived nuclear spins which interact with the mean hyperfine field induced by the 4f-electron spins (Schuberth et al., 2016) to create random and insulated A-phase regions which must be growing upon lowering the temperature.
3) The simultaneous onset of both a weak, but distinct shielding signal (Figure 6) and a pronounced decline in the absolute slope of fc MDC(T) (Figure 5A) at T ≈ 10 mK are interpreted as manifesting the nucleation of superconductivity.
4) The network of superconducting islands turns out to be extremely fragile as the shielding signal is suppressed already by a very small external magnetic field (Figure 6A).
5) Upon further cooling, the resistivity reaches zero at about 6.5 mK. This can be reconciled with the above results in terms of the onset of superconducting percolation as mentioned before. The percolation initiates a considerably increasing strength of A-phase short-range order as illustrated by a pronounced increase of fc-MDC(T) below 5 mK (Figure 5A) and corroborated by a significant removal of the Yb-derived nuclear spin entropy from its maximum value Stot (at T > TB) by 26% on cooling the sample down to TA (Figure 7B). Remarkably, the shielding signal due to the network of superconducting islands in the sample surface does not exceed 20% when cooling from T ≈ 10 mK to T ≥ TA, the temperature range previously called “B-phase”, cf. Figure 8.
6) At TA (= 2.3 mK as B → 0, see Schuberth et al. (2016)), a second-order phase transition into long-range A-phase order takes place (Figure 7A). The ordering of the Yb nuclear spins reaches a level of more than 60% already at 1.5 mK, see Figure 7B. Nuclear-dominated hybrid order at elevated magnetic fields has yet to be confirmed by future measurements of the specific heat. This should clarify whether the A-phase exists up to BA ≃ 45 mT, as indicated by the dotted red line in the phase diagram of Figure 8, or even up to the quantum critical field BN = 60 mT, as suggested by the new resistivity results of Nguyen et al. (2021), Figure 10. In the latter case, we conjecture the existence of not just two QCPs at B = BN (vanishing of the primary AF order due to the applied magnetic field) and at B = 0 (due to the competing A-phase). Rather, a phase boundary TA(B) spanning the whole field range B < BN would exist and most likely establish a quantum critical line between these two QCPs.
7) From the magnetization measurements (Schuberth et al., 2016), bulk superconductivity emerges at Tc = 2 mK (Figures 5A, 6A), slightly below TA. Future fc-MDC(T) measurements on annealed powder samples below the lower critical field Bc1 are needed to confirm that bulk superconductivity indeed exists well below Tc,ρ at magnetic fields up to B ≃ BA.
We should welcome future work by other groups to cross-check the above reasoning.
The new resistivity study by Nguyen et al. (2021) suggests the existence of two separate superconducting regimes, at low and elevated fields, respectively. In view of the preceding discussion, we cannot concur with the proposal by Nguyen et al. that, at least in the low-field regime, Cooper pairing in YbRh2Si2 is mediated by the critical fluctuations of the field-induced QCP at BN: For, here the primary AF order is apparently suppressed by the competing nuclear order, allowing a quantum critical line to be established. Therefore, it is natural to consider the associated quantum critical fluctuations at very low fields being the driving force for the formation of Cooper pairs.
The origin of the superconductivity at elevated fields remains to be resolved. If here, the existence of the nuclear-dominated hybrid A-phase can be proven by future specific-heat experiments, the Cooper-pairing mechanism emphasized above in the low-field regime will most likely be operating as well. An alternative scenario proposed by Nguyen et al. (2021) neglects the competition between the nuclear and primary 4f-electronic orders and instead implies, as mentioned before, that the quantum critical fluctuations associated with the field-induced QCP at BN = 60 mT bring about the formation of superconductivity. As these critical fluctuations would be strongly impeded by the pair-breaking applied magnetic field, the competition between the field-induced quantum criticality and the destructive action of the magnetic field on the Cooper pairs causes a maximum Tc to occur well below BN. Nguyen et al. (2021) propose that superconductivity at elevated field may be of the spin-triplet variety. While this would not have been a surprise had the quantum criticality been of nearly ferromagnetic (and conventional) type (Li et al., 2019), how could spin-triplet pairing develop for Kondo-destroying type AF quantum criticality as is the case in YbRh2Si2? Insights into this question have come from theoretical studies near a Kondo-destroying QCP in antiferromagnetically coupled Kondo models (Hu et al., 2021b): They showed that significant Ising anisotropy, as it effectively arises under an external magnetic field in the easy-plane antiferromagnetically correlated YbRh2Si2, makes the spin-triplet pairing competitive.
3 Perspective
The discovery of superconductivity in YbRh2Si2 at ultra-low temperatures opens up new dimensions. It expands the horizon of ultra-low temperature physics towards strongly correlated electronic matter in solids and conversely, it determines a new area of heavy-fermion physics by reaching down to ultra-low temperatures.
Up to now, heavy-fermion superconductivity has been detected in more than fifty f-electron compounds. Despite the fact that, compared with PuCoGa5, exhibiting the record-high Tc of 18.5 K (Sarrao et al., 2002), YbRh2Si2 shows a transition temperature which is lower by almost four decades, this may be called “high Tc”—in the sense that Tc is limited by an enormously high ordering temperature of nuclear spins. This nuclear order paves the way for the superconductivity, not by actively helping in the Cooper-pair formation, rather by destroying the 4f-electronic order below TN = 70 mK, which appears to be extremely hostile to superconductivity. The apparent competition between the nuclear and the 4f-electronic orders results in an AF QCP at, or very close to, B = 0. Most likely, the latter—like its field-induced counterpart at B = BN—is of the “local” type, as inferred from the B = 0 results of electrical and thermal transport as well as specific-heat measurements in the paramagnetic state as presented in Section 1.
The ultra-low temperature work on YbRh2Si2 strongly supports the notion that superconductivity robustly develops in the vicinity of such a “partial-Mott” QCP, as has been theoretically derived in Kondo-lattice models for a Kondo-destroying QCP (Hu et al., 2021a) and experimentally evidenced from de Haas-van Alphen studies in high magnetic fields (Shishido et al., 2005) and transport measurements (Park et al., 2006) on pressurized CeRhIn5. Therefore, the results on these two compounds provide the long-sought (Maple et al., 2004) link between unconventional superconductivity in heavy-fermion metals (Pfleiderer, 2009) and that occurring near a true Mott metal-insulator transition, e.g., in the cuprates (Lee et al., 2006) and organic charge-transfer salts (Kanoda, 2008).
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
SW acknowledges support by the Deutsche Forschungsgemeinschaft through WI 1324/5-1.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We are grateful for conversations with Manuel Brando, Ang Cai, Lei Chen, Piers Coleman, Haoyu Hu, Stefan Lausberg, Silke Paschen, John Saunders, Rong Yu and in particular Qimiao Si for his insightful comments.
References
Alexandrov, V., Coleman, P., and Erten, O. (2015). Kondo Breakdown in Topological Kondo Insulators. Phys. Rev. Lett. 114, 177202. doi:10.1103/physrevlett.114.177202
Aronson, M. C., Osborn, R., Robinson, R. A., Lynn, J. W., Chau, R., Seaman, C. L., et al. (1995). Non-Fermi-Liquid Scaling of the Magnetic Response in UCu5−xPdx(x=1,1.5). Phys. Rev. Lett. 75, 725–728. doi:10.1103/physrevlett.75.725
Assmus, W., Herrmann, M., Rauchschwalbe, U., Riegel, S., Lieke, W., Spille, H., et al. (1984). Superconductivity in CeCu2Si2 Single Crystals. Phys. Rev. Lett. 52, 469–472. doi:10.1103/physrevlett.52.469
Chen, Q. Y., Xu, D. F., Niu, X. H., Peng, R., Xu, H. C., Wen, C. H. P., et al. (2018). Band Dependent Interlayer f-Electron Hybridization in CeRhIn5. Phys. Rev. Lett. 120, 066403. doi:10.1103/PhysRevLett.120.066403
Chen, Q. Y., Xu, D. F., Niu, X. H., Jiang, J., Peng, R., Xu, H. C., et al. (2017). Direct Observation of How the Heavy-Fermion State Develops in CeCoIn5. Phys. Rev. B 96, 045107. doi:10.1103/physrevb.96.045107
Coleman, P., Anderson, P. W., and Ramakrishnan, T. V. (1985). Theory for the Anomalous Hall Constant of Mixed-Valence Systems. Phys. Rev. Lett. 55, 414–417. doi:10.1103/physrevlett.55.414
Coleman, P., Pépin, C., Si, Q., and Ramazashvili, R. (2001). How Do Fermi liquids get heavy and die? J. Phys. Condens. Matter 13, R723–R738. doi:10.1088/0953-8984/13/35/202
Custers, J., Gegenwart, P., Wilhelm, H., Neumaier, K., Tokiwa, Y., Trovarelli, O., et al. (2003). The Break-Up of Heavy Electrons at a Quantum Critical Point. Nature 424, 524–527. doi:10.1038/nature01774
Dong, J. K., Tokiwa, Y., Bud’ko, S. L., Canfield, P. C., and Gegenwart, P. (2013). Anomalous Reduction of the Lorenz Ratio at the Quantum Critical Point in YbAgGe. Phys. Rev. Lett. 110, 176402. doi:10.1103/physrevlett.110.176402
Ernst, S., Kirchner, S., Krellner, C., Geibel, C., Zwicknagl, G., Steglich, F., et al. (2011). Emerging Local Kondo Screening and Spatial Coherence in the Heavy-Fermion Metal YbRh2Si2. Nature 474, 362–366. doi:10.1038/nature10148
Friedemann, S., Oeschler, N., Wirth, S., Krellner, C., Geibel, C., Steglich, F., et al. (2010). Fermi-Surface Collapse and Dynamical Scaling Near a Quantum-Critical Point. Proc. Natl. Acad. Sci. U.S.A. 107, 14547–14551. doi:10.1073/pnas.1009202107
Gegenwart, P., Custers, J., Geibel, C., Neumaier, K., Tayama, T., Tenya, K., et al. (2002). Magnetic-field Induced Quantum Critical Point in YbRh2Si2. Phys. Rev. Lett. 89, 056402. doi:10.1103/physrevlett.89.056402
Gegenwart, P., Custers, J., Tokiwa, Y., Geibel, C., and Steglich, F. (2005). Ferromagnetic Quantum Critical Fluctuations in YbRh2(Si0.95Ge0.05)2. Phys. Rev. Lett. 94, 076402. doi:10.1103/physrevlett.94.076402
Gegenwart, P., Westerkamp, T., Krellner, C., Tokiwa, Y., Paschen, S., Geibel, C., et al. (2007). Multiple Energy Scales at a Quantum Critical Point. Science 315, 969–971. doi:10.1126/science.1136020
Gegenwart, P., Si, Q., and Steglich, F. (2008). Quantum Criticality in Heavy-Fermion Metals. Nat. Phys 4, 186–197. doi:10.1038/nphys892
Hamann, S., Zhang, J., Jang, D., Hannaske, A., Steinke, L., Lausberg, S., et al. (2019). Evolution from Ferromagnetism to Antiferromagnetism in Yb(Rh1−xCox)2Si2. Phys. Rev. Lett. 122, 077202. doi:10.1103/physrevlett.122.077202
Hartmann, S., Oeschler, N., Krellner, C., Geibel, C., Paschen, S., and Steglich, F. (2010). Thermopower Evidence for an Abrupt Fermi Surface Change at the Quantum Critical Point of YbRh2Si2. Phys. Rev. Lett. 104, 096401. doi:10.1103/physrevlett.104.096401
Hu, H., Cai, A., Chen, L., Deng, L., Pixley, J. H., Ingersent, K., et al. (2021a). Unconventional Superconductivity from Fermi Surface Fluctuations in Strongly Correlated Metals. arXiv:2109.13224.
Hu, H., Cai, A., Chen, L., and Si, Q. (2021b). Spin-Singlet and Spin-Triplet Pairing Correlations in Antiferromagnetically Coupled Kondo Systems. arXiv:2109.12794.
Ishida, K., MacLaughlin, D. E., Young, B.-L., Okamoto, K., Kawasaki, Y., Kitaoka, Y., et al. (2003). Low-temperature Magnetic Order and Spin Dynamics in YbRh2Si2. Phys. Rev. B 68, 184401. doi:10.1103/physrevb.68.184401
Kanoda, K. (2008). “Mott Transition and Superconductivity in quasi-2D Organic Conductors,” in The Physics of Organic Superconductors and Conductors. Editor A. Lebed (Berlin, Heidelberg: Springer-Verlag), 623–642. doi:10.1007/978-3-540-76672-8_22
Kirchner, S., Paschen, S., Chen, Q., Wirth, S., Feng, D., Thompson, J. D., et al. (2020). Heavy Electron Quantum Criticality and Single-Particle Spectroscopy. Rev. Mod. Phys. 92, 011002. doi:10.1103/revmodphys.92.011002
Knebel, G., Boursier, R., Hassinger, E., Lapertot, G., G. Niklowitz, P., Pourret, A., et al. (2006). Localization of 4f State in YbRh2Si2 under Magnetic Field and High Pressure: Comparison with CeRh2Si2. J. Phys. Soc. Jpn. 75, 114709. doi:10.1143/jpsj.75.114709
Köhler, U., Oeschler, N., Steglich, F., Maquilon, S., and Fisk, Z. (2008). Energy Scales of Lu1−xYbxRh2Si2 by Means of Thermopower Investigations. Phys. Rev. B 77, 104412.
Lausberg, S. (2013). Quantum Criticality in Ferromagnetic Correlated Ce- and Yb-Based Heavy Fermion Systems (In German) (Germany: Technical University Dresden). Ph.D. thesis.
Lee, P. A., Nagaosa, N., and Wen, X.-G. (2006). Doping a Mott Insulator: Physics of High-Temperature Superconductivity. Rev. Mod. Phys. 78, 17–85. doi:10.1103/revmodphys.78.17
Li, Y., Wang, Q., Xu, Y., Xie, W., and Yang, F. Y. (2019). Nearly Degenerate px + ipy and
Machida, Y., Tomokuni, K., Izawa, K., Lapertot, G., Knebel, G., Brison, J.-P., et al. (2013). Verification of the Wiedemann-Franz Law in YbRh2Si2 at a Quantum Critical Point. Phys. Rev. Lett. 110, 236402. doi:10.1103/physrevlett.110.236402
Maple, M. B., Bauer, E. D., Zapf, V. S., and Wosnitza, J. (2004). “Unconventional Superconductivity in Novel Materials,” in The Physics of Superconductors. Editors K. H. Bennemann, and J. B. Ketterson (Berlin, Heidelberg: Springer), II, 555–730. doi:10.1007/978-3-642-18914-2_8
Nguyen, D. H., Sidorenko, A., Taupin, M., Knebel, G., Lapertot, G., Schuberth, E., et al. (2021). Superconductivity in an Extreme Strange Metal. Nat. Commun. 12, 4341. doi:10.1038/s41467-021-24670-z
Parfen’eva, L. S., Smirnov, I. A., Misiorek, H., Mucha, J., Jezowski, A., Prokof’ev, A. V., et al. (2004). Spinon Thermal Conductivity of (CuO2)-Spin Chains in LiCuVO4. Phys. Solid State. 46, 357–363. doi:10.1134/1.1649437
Park, T., Lee, H., Martin, I., Lu, X., Sidorov, V. A., Gofryk, K., et al. (2012). Textured Superconducting Phase in the Heavy Fermion CeRhIn5. Phys. Rev. Lett. 108, 077003. doi:10.1103/PhysRevLett.108.077003
Park, T., Ronning, F., Yuan, H. Q., Salamon, M. B., Movshovich, R., Sarrao, J. L., et al. (2006). Hidden Magnetism and Quantum Criticality in the Heavy Fermion Superconductor CeRhIn5. Nature 440, 65–68. doi:10.1038/nature04571
Paschen, S., Lühmann, T., Wirth, S., Gegenwart, P., Trovarelli, O., Geibel, C., et al. (2004). Hall-effect Evolution across a Heavy-Fermion Quantum Critical Point. Nature 432, 881–885. doi:10.1038/nature03129
Petrovic, C., Movshovich, R., Jaime, M., Pagliuso, P. G., Hundley, M. F., Sarrao, J. L., et al. (2001). A New Heavy-Fermion Superconductor CeIrIn5 : A Relative of the Cuprates? Europhys. Lett. 53, 354–359. doi:10.1209/epl/i2001-00161-8
Pfau, H., Hartmann, S., Stockert, U., Sun, P., Lausberg, S., Brando, M., et al. (2012). Thermal and Electrical Transport across a Magnetic Quantum Critical Point. Nature 484, 493–497. doi:10.1038/nature11072
Pfleiderer, C. (2009). Superconducting Phases of f-Electron Compounds. Rev. Mod. Phys. 81, 1551–1624. doi:10.1103/revmodphys.81.1551
Pourret, A., Aoki, D., Boukahil, M., Brison, J.-P., Knafo, W., Knebel, G., et al. (2014). Quantum Criticality and Lifshitz Transition in the Ising System CeRu2Si2: Comparison with YbRh2Si2. J. Phys. Soc. Jpn. 83, 061002. doi:10.7566/jpsj.83.061002
Rauchschwalbe, U., Lieke, W., Bredl, C. D., Steglich, F., Aarts, J., Martini, K. M., et al. (1982). Critical Fields of the “Heavy-Fermion” Superconductor CeCu2Si2. Phys. Rev. Lett. 49, 1448–1451. doi:10.1103/physrevlett.49.1448
Reid, J.-P., Tanatar, M. A., Daou, R., Hu, R., Petrovic, C., and Taillefer, L. (2014). Wiedemann-Franz Law and Non-Vanishing Temperature Scale across the Field-Tuned Quantum Critical Point of YbRh2Si2. Phys. Rev. B 89, 045130. doi:10.1103/physrevb.89.045130
Sarrao, J. L., Morales, L. A., Thompson, J. D., Scott, B. L., Stewart, G. R., Wastin, F., et al. (2002). Plutonium-based Superconductivity with a Transition Temperature above 18 K. Nature 420, 297–299. doi:10.1038/nature01212
Saunders, J. (2018). “Superconductivity in YbRh2Si2: Electrical Transport and Noise Experiments,” in Invited Talk at 12th Intern. Conf. on Materials and Mechanisms of Superconductivity (M2S 2018), Beijing, China, August 19–24, 2018.
Schröder, A., Aeppli, G., Coldea, R., Adams, M., Stockert, O., v. Löhneysen, H., et al. (2000). Onset of Antiferromagnetism in Heavy-Fermion Metals. Nature 407, 351–355. doi:10.1038/35030039
Schuberth, E., Tippmann, M., Steinke, L., Lausberg, S., Steppke, A., Brando, M., et al. (2016). Emergence of Superconductivity in the Canonical Heavy-Electron Metal YbRh2Si2. Science 351, 485–488. doi:10.1126/science.aaa9733
Seiro, S., Jiao, L., Kirchner, S., Hartmann, S., Friedemann, S., Krellner, C., et al. (2018). Evolution of the Kondo Lattice and Non-Fermi Liquid Excitations in a Heavy-Fermion Metal. Nat. Commun. 9, 3324. doi:10.1038/s41467-018-05801-5
Shishido, H., Settai, R., Harima, H., and Ōnuki, Y. (2005). A Drastic Change of the Fermi Surface at a Critical Pressure in CeRhIn5: dHvA Study under Pressure. J. Phys. Soc. Jpn. 74, 1103–1106. doi:10.1143/jpsj.74.1103
Si, Q., Rabello, S., Ingersent, K., and Smith, J. L. (2001). Locally Critical Quantum Phase Transitions in Strongly Correlated Metals. Nature 413, 804–808. doi:10.1038/35101507
Sichelschmidt, J., Ivanshin, V. A., Ferstl, J., Geibel, C., and Steglich, F. (2003). Low Temperature Electron Spin Resonance of the Kondo Ion in a Heavy Fermion Metal: YbRh2Si2. Phys. Rev. Lett. 91, 156401. doi:10.1103/physrevlett.91.156401
Singh, S., Capan, C., Nicklas, M., Rams, M., Gladun, A., Lee, H., et al. (2007). Probing the Quantum Critical Behavior of CeCoIn5 via Hall Effect Measurements. Phys. Rev. Lett. 98, 057001. doi:10.1103/PhysRevLett.98.057001
Smidman, M., Stockert, O., Arndt, J., Pang, G. M., Jiao, L., Yuan, H. Q., et al. (2018). Interplay between Unconventional Superconductivity and Heavy-Fermion Quantum Criticality: CeCu2Si2 versus YbRh2Si2. Philos. Mag. 98, 2930–2963. doi:10.1080/14786435.2018.1511070
Smith, M. F., and McKenzie, R. H. (2008). Apparent Violation of the Wiedemann-Franz Law Near a Magnetic Field Tuned Metal-Antiferromagnetic Quantum Critical Point. Phys. Rev. Lett. 101, 266403. doi:10.1103/physrevlett.101.266403
Steglich, F., Aarts, J., Bredl, C. D., Lieke, W., Meschede, D., Franz, W., et al. (1979). Superconductivity in the Presence of Strong Pauli Paramagnetism: CeCu2Si2. Phys. Rev. Lett. 43, 1892–1896. doi:10.1103/physrevlett.43.1892
Steglich, F., Pfau, H., Lausberg, S., Hamann, S., Sun, P., Stockert, U., et al. (2014). Evidence of a Kondo Destroying Quantum Critical Point in YbRh2Si2. J. Phys. Soc. Jpn. 83, 061001. doi:10.7566/jpsj.83.061001
Stewart, G. R. (2001). Non-Fermi-Liquid Behavior in d- and f-Electron Metals. Rev. Mod. Phys. 73, 797–855. ibid. 78, 743-753 (2006). doi:10.1103/RevModPhys.73.797
Stockert, O., Andreica, D., Amato, A., Jeevan, H. S., Geibel, C., and Steglich, F. (2006a). Magnetic Order and Superconductivity in Single-Crystalline CeCu2Si2. Physica B: Condensed Matter 374-375, 167–170. doi:10.1016/j.physb.2005.11.043
Stockert, O., Koza, M. M., Ferstl, J., Murani, A. P., Geibel, C., and Steglich, F. (2006b). Crystalline Electric Field Excitations of the Non-Fermi-Liquid YbRh2Si2. Physica B: Condensed Matter 378-380, 157–158. doi:10.1016/j.physb.2006.01.059
Sun, P., and Steglich, F. (2013). Nernst Effect: Evidence of Local Kondo Scattering in Heavy Fermions. Phys. Rev. Lett. 110, 216408. doi:10.1103/physrevlett.110.216408
Tanatar, M. A., Paglione, J., Petrovic, C., and Taillefer, L. (2007). Anisotropic Violation of the Wiedemann-Franz Law at a Quantum Critical Point. Science 316, 1320–1322. doi:10.1126/science.1140762
Taupin, M., Knebel, G., Matsuda, T. D., Lapertot, G., Machida, Y., Izawa, K., et al. (2015). Thermal Conductivity through the Quantum Critical Point in YbRh2Si2 at Very Low Temperature. Phys. Rev. Lett. 115, 046402. doi:10.1103/physrevlett.115.046402
Trovarelli, O., Geibel, C., Mederle, S., Langhammer, C., Grosche, F. M., Gegenwart, P., et al. (2000). YbRh2Si2: Pronounced Non-Fermi-Liquid Effects above a Low-Lying Magnetic Phase Transition. Phys. Rev. Lett. 85, 626–629. doi:10.1103/physrevlett.85.626
von Löhneysen, H., Pietrus, T., Portisch, G., Schlager, H. G., Schröder, A., Sieck, M., et al. (1994). Non-Fermi-Liquid Behavior in a Heavy-Fermion Alloy at a Magnetic Instability. Phys. Rev. Lett. 72, 3262–3265. doi:10.1103/PhysRevLett.72.3262
von Löhneysen, H., Rosch, A., Vojta, M., and Wölfle, P. (2007). Fermi-Liquid Instabilities at Magnetic Quantum Phase Transitions. Rev. Mod. Phys. 79, 1015–1075.
Westerkamp, T. (2009). Quantum Phase Transitions in the Heavy Fermion Systems Yb(Rh1−xMx)2Si2 and CePd1−xRhx(in German) (Germany: Technical University Dresden). Ph.D. thesis.
Wirth, S., Ernst, S., Cardoso-Gil, R., Borrmann, H., Seiro, S., Krellner, C., et al. (2012). Structural Investigations on YbRh2Si2: from the Atomic to the Macroscopic Length Scale. J. Phys. Condens. Matter 24, 294203. doi:10.1088/0953-8984/24/29/294203
Wirth, S., and Steglich, F. (2016). Exploring Heavy Fermions from Macroscopic to Microscopic Length Scales. Nat. Rev. Mater. 1, 16051. doi:10.1038/natrevmats.2016.51
Wölfle, P., and Abrahams, E. (2011). Quasiparticles beyond the Fermi Liquid and Heavy Fermion Criticality. Phys. Rev. B 84, 041101. (R). doi:10.1103/physrevb.84.041101
Zaum, S., Grube, K., Schäfer, R., Bauer, E. D., Thompson, J. D., and von Löhneysen, H. (2011). Towards the Identification of a Quantum Critical Line in the (p, B) Phase Diagram of CeCoIn5 with Thermal-Expansion Measurements. Phys. Rev. Lett. 106, 087003. doi:10.1103/PhysRevLett.106.087003
Keywords: heavy fermion, superconductivity, quantum criticality, Kondo destruction, nuclear order
Citation: Schuberth E, Wirth S and Steglich F (2022) Nuclear-Order-Induced Quantum Criticality and Heavy-Fermion Superconductivity at Ultra-low Temperatures in YbRh2Si2. Front. Electron. Mater. 2:869495. doi: 10.3389/femat.2022.869495
Received: 04 February 2022; Accepted: 01 March 2022;
Published: 17 May 2022.
Edited by:
Jeffrey W. Lynn, National Institute of Standards and Technology (NIST), United StatesReviewed by:
Hyunsoo Kim, Missouri University of Science and Technology, United StatesHuixia Luo, Sun Yat-Sen University, China
Copyright © 2022 Schuberth, Wirth and Steglich. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Frank Steglich, c3RlZ2xpY2hAY3Bmcy5tcGcuZGU=
 Erwin Schuberth1
Erwin Schuberth1 Steffen Wirth
Steffen Wirth