- 1Max Planck Institute for Chemical Physics of Solids, Dresden, Germany
- 2Physics Department, Technical University Munich, Munich, Germany
CeRh2As2 is a rare unconventional superconductor (Tc = 0.26 K) characterized by two adjacent superconducting phases for a magnetic field H‖c-axis of the tetragonal crystal structure. Antiferromagnetic order, quadrupole-density-wave order (T0 = 0.4 K) and the proximity of this material to a quantum-critical point have also been reported: The coexistence of these phenomena with superconductivity is currently under discussion. Here, we present thermal conductivity and electrical resistivity measurements on a single crystal of CeRh2As2 between 60 mK and 200 K and in magnetic fields (H‖c) up to 8 T. Extrapolation of our normal-state data to zero temperature validates the Wiedemann-Franz law within the error bars. The T dependence of the thermal conductivity κ(T) shows a pronounced drop below Tc which is also field dependent and thus interpreted as the signature of superconductivity. However, the large residual resistivity and the lack of sharp anomalies in κ(T) at the expected transition temperatures clearly indicate that samples of much higher purity are required to gain more information about the superconducting gap structure.
1 Introduction
CeRh2As2 is a newly discovered unconventional heavy-fermion superconductor with Tc = 0.26 K (Khim et al., 2021). Two different superconducting states occur when the magnetic field H is applied along the crystallographic c axis, as shown in the H − T phase diagram in Figure 1A. The low-field superconducting state SC1 changes into the high-field superconducting state SC2 at μ0H⋆ ≈ 4 T. At this field the Tc-vs-H phase boundary line shows a sharp kink. Remarkably, the SC2 state has an extremely large upper critical field μ0Hc2 = 14 T limited by orbital pair breaking. For fields applied within the basal plane H ⊥ c only the SC1 state exists and is Pauli limited with an upper critical field μ0Hc2 = 2 T. This field still exceeds the BCS Pauli limit by a factor of 4. The anisotropy of Hc2 and the superconducting phase diagrams were explained by a model based on the crystal symmetry: The tetragonal CaBe2Ge2-type structure of CeRh2As2 is globally centrosymmetric but breaks inversion symmetry locally at the Ce site. As a consequence, Rashba spin-orbit coupling arises with alternating sign in the two adjacent Ce layers. In this picture, SC1 is identified as an even-parity superconducting state and SC2 as an odd-parity superconducting state (Khim et al., 2021; Cavanagh et al., 2022). The angle dependence of the critical fields agrees with this interpretation (Landaeta et al., 2022). A recent theoretical work hypothesizes that odd SC2 might also exist for H ⊥ c but is suppressed by impurities. By contrast, the even SC1 phase is robust to impurities (Möckli and Ramires, 2021a). Experimentally, the sensitivity to impurities has not been investigated systematically. Further theoretical investigations cover different options for the superconducting order parameters (Skurativska et al., 2021; Möckli and Ramires, 2021b,a; Nogaki et al., 2021; Schertenleib et al., 2021) and a normal-state Lifshitz transition with field (Ptok et al., 2021).
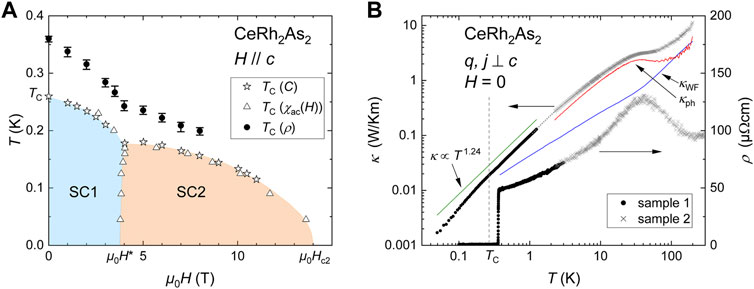
FIGURE 1. (A) Superconducting phase diagram of CeRh2As2 for H//c. The values of Tc at the phase boundaries estimated from specific-heat and field-dependent ac susceptibility measurements are reproduced from Ref. Khim et al. (2021). In addition, we show Tc determined from our resistivity measurements as the temperature at which ρ drops to 50% of the normal-state value. Error bars indicate the transition width. (B) Temperature dependence of the thermal conductivity κ(T) and of the electrical resistivity ρ(T) of CeRh2As2. The low-T and high-T data have been measured on two different samples using two different setups. The dotted line, which connects the high-T and low-T κ(T) data, is a guide to the eye. The bulk Tc estimated from specific-heat measurements is marked by a dashed vertical line. Estimates of the electron and phonon contributions to the thermal conductivity, determined as explained in the text, are shown. The green line emphasizes that κ ∝ T1.24 between 1.2 K and Tc.
The behavior in the normal state is also unconventional and complex. It mainly originates from two key properties of CeRh2As2: Its vicinity to a quantum-critical point and the unusual situation in which the energy difference between the two lowest-lying crystal-electric-field doublets of the Ce3+ ions is comparable to the Kondo temperature (TK ≈ 30 K) of this material. The first property is evidenced by the large increase of the specific heat, C(T)/T ∝ T−0.6, towards low temperatures, very low ordering temperatures and the presence of superconductivity (Khim et al., 2021; Hafner et al., 2022). Furthermore, a non-Fermi-liquid behavior is observed in resistivity,
Many details of the normal-state and superconducting properties of CeRh2As2 are unsettled up to now. For example, little is known about the superconducting gap structure and the presence or absence of nodes. The only available information is from muon spin resonance experiments: The weak T dependence of the superconducting relaxation rate for T → 0 points to a gap structure with point-like nodes or a full gap (Khim, 2022). This motivated us to study the thermal conductivity κ which depends sensitively on the available heat carriers and on the relevant scattering processes. In the past, measurements of κ have been applied successfully to study the gap structure of unconventional superconductors (Izawa et al., 2005; Dong et al., 2010; Shakeripour et al., 2010; Reid et al., 2012). So, this technique might be able to reveal differences in the gap structure of the two superconducting states in CeRh2As2. Another fundamental relation that can be verified by these experiments is the Wiedemann-Franz law. A violation of this law in the T = 0 limit would provide a direct proof for the breakdown of the quasiparticles picture, as it has been proposed for systems at a quantum-critical point (Podolsky et al., 2007; Tanatar et al., 2007; Kim and Pépin, 2009; Pfau et al., 2012; Taupin et al., 2015). In order to obtain a comprehensive picture about the heat transport in CeRh2As2, we measured κ in a large T range, between 60 mK and 200 K, which covers Tc, T0 as well as TK. At low temperatures, we also studied the magnetic-field dependence with fields H‖c up to 8 T across the transition field H⋆ between SC1 and SC2. We supplement these investigations by electrical resistivity measurements and a comparison of our data with the Sommerfeld coefficient C/T (T → 0).
Our measurements reveal no clear anomalies in the thermal conductivity as a function of temperature at the phase transition temperatures Tc and T0, probably due to scattering from defects in our sample. A crude extrapolation to T = 0 of the Lorenz ratio from above 0.4 K confirms the validity of the Wiedemann-Franz law within the error bars. Superconductivity induces a pronounced drop of κ(T)/T below Tc that shifts with magnetic field as expected from the behavior of Hc2. However, better samples are needed to obtain clear information about the gap structure.
2 Methods and Experimental Details
We measured the low-temperature thermal conductivity κ(T) and the electrical resistivity ρ(T) of single-crystalline CeRh2As2 between T = 60 mK and 1.2 K and for magnetic fields up to 8 T. Both, the heat current and the electrical current were applied within the ab-plane of the crystal, while the magnetic field was applied parallel to the c axis. A second sample was used to extend zero-field measurements to about 300 K. Thermal conductivity measurements in our setups require samples with a minimum length of about 1.5 mm. We cut bar-shaped samples with dimensions of approximately 2 × 0.5 × 0.1 mm3 from appropriate crystals.
Low-temperature measurements were performed in a dilution refrigerator using a home-made setup. The thermal conductivity was measured by a four-point steady-state method using two RuOx thermometers and a resistive heater. The sample thermometers were calibrated in-situ for each temperature sweep against a field-calibrated thermometer at the cold bath. The field was always changed at high temperature in the normal state of the sample. The electrical resistivity was determined by an ac technique. κ and ρ were obtained in subsequent measurements using the same contacts.
High-T measurements were performed in a commercial Physical Property Measurement System (PPMS from Quantum Design) using a modified sample holder for the thermal transport option suitable for small single crystals [(Stockert et al., 2017) which contains a photo of part of the setup]. Due to the considerable contact width compared to the sample dimensions, the uncertainty of the geometry factor of the high-temperature measurement is relatively large. Instead, the geometry factor chosen for sample 2 in Figure 1B was determined by matching low- and high-T κ and ρ data. It agrees with the geometry factor from sample size and contact separation within the uncertainty, i.e., a difference of 20% between the two geometry factors. For T > 200 K, the measured thermal conductivity strongly increases due to thermal radiation losses. Therefore, we neither show nor discuss κ-data in this T range.
3 Results
3.1 Zero-Field Thermal and Electrical Transport Between 2 K and 200 K
Figure 1B shows the thermal conductivity of CeRh2As2 between 200 K and 60 mK. For comparison, we also plot the electrical resistivity ρ(T) between 300 K and 100 mK, which reflects the behavior previously observed in other samples (Khim et al., 2021). In this section, we only focus on data above 2K. κ(T) decreases monotonously with decreasing temperature. A plateau is reached at around 40 K. On the contrary, the resistivity ρ(T) increases with decreasing temperature due to Kondo scattering. At TK ≈ 30 K a maximum is reached. Towards lower T, ρ(T) decreases due to the onset of coherence and thermal depopulation of the excited crystal-electric-field levels. The residual resistivity ratio of our crystals ρ(300 K)/ρ(0.4 K) ≈ 2 is rather small and comparable to the one measured previously (Khim et al. (2021). The smaller absolute values of ρ(0.4 K) in Ref. Hafner et al. (2022), which were obtained on very small crystals from the same batch as that investigated in Ref. Khim et al. (2021), are probably due to uncertainties in estimating the geometry factor. Characterization measurements of ρ(T) on a large number of CeRh2As2 crystals for other experiments confirm that a room temperature resistivity of 100 μΩcm is a reasonable value for the material (Semeniuk (2022)).
From the data in Figure 1B it is not directly clear whether the plateau in κ(T) is related to the maximum in ρ(T) or not. We can, however, consider that the thermal conductivity of standard nonmagnetic metals is the sum of two contributions, namely that of phonons (κph) and that of charge carriers (κel). A rough estimate of κel can be obtained from the electrical resistivity by simply assuming that the Wiedemann-Franz law is valid. In this case, κel ≈ κWF = L0T/ρ with the Lorenz constant
Qualitatively, the temperature dependence of κph can be understood as follows: Starting from low T, κph of clean materials initially increases with increasing phonon density. Upon further heating, phonon-phonon interactions become more relevant with allowed Umklapp scattering, and κph starts to decrease again. Therefore, κph usually exhibits a maximum at intermediate temperatures. The exact temperature dependence of κph as well as the magnitude and position of the maximum depend on the relevant scattering processes and the purity of the material. Our crystals exhibit rather large residual resistivities with ρ(300 K)/ρ(0.4 K) ≈ 2 indicative of a considerable number of scattering centers. This may be the reason for the absence of a more pronounced maximum in κph(T). A weak T dependence of κph without pronounced maximum is typical of Ce-based heavy-fermion compounds, and has been observed, e.g., in CeCu2Si2 (Franz et al., 1978), CeCu2 (Gratz et al., 1985), CeAl2 (Bauer et al., 1986), CeCu4Al (Falkowski and Kowalczyk, 2011), Ce(Ni1−xCux)2Si2 (Toliński et al., 2013), and CeRh2Ga2 (Anand et al., 2017).
Between 2 K and 10 K, in CeRh2As2, the inelastic scattering of charge carriers below the Kondo coherence maximum and the non-Fermi-liquid behavior observed at low-T lead to a larger uncertainty of estimating the phonon thermal conductivity via the Wiedemann-Franz law. Lacking a better method, we nevertheless continue in the same way. The estimated phonon thermal conductivity of CeRh2As2 in that temperature range exhibits roughly a linear temperature dependence, κph(T) ∝ T, which may be somewhat surprising. In a very simple picture κph is expected to follow a T3-function. This type of behavior can be derived within the Boltzmann formalism assuming a momentum- and T-independent phonon mean free path and velocity. However, the situation in real materials is much more complicated. Different types of scattering mechanisms lead to other temperature dependencies. For instance, scattering of phonons from electrons and dislocations may result in κph ∝ T2 [Ziman (1960)] and phonon specular reflection results in an exponent between 2 and 3 (Li et al., 2008). A linear-in-T dependence of κph has also been found and ascribed to the existence of dislocation networks (Kapoor et al., 1974; Franz et al., 1978). A quasi-linear-in-T behavior was found in the above mentioned Ce-based heavy-fermion compounds CeCu4Al (Falkowski and Kowalczyk, 2011) and CeRh2Ga2 (Anand et al., 2017).
We would like to emphasize, that the unusual T dependence of κph cannot be explained solely by uncertainties of estimating κel via the Wiedemann-Franz law. Since κel amounts to at most 30% of the total thermal conductivity at 2 K, the T-dependence of κph will not change dramatically, e.g., from linear to quadratic, as long as deviations of the experimental Lorenz number Lel = ρκel/T from L0 are small and weakly T-dependent. A direct determination of Lel is difficult, since it requires accurate separation of κ into phonon and an electron contributions. The only example of a Ce system where this was done in the relevant T range is La1−xCexAl2 with Lel/L0 at most 1.25 (Moeser and Steglich, 1975). Assuming a similar Lorenz ratio for CeRh2As2 would enhance the electronic contribution to κ only moderately to at most 40% at 2 K, which is too small to change the T dependence of κph fundamentally.
3.2 Zero-Field Thermal and Electrical Transport Below 2 K
Now we take a look at the low-T behavior of ρ(T) and κ(T) in zero magnetic field summarized in Figure 2A. The resistivity shows the superconducting transition at 0.36 K. This temperature is larger than the bulk Tc = 0.26 K determined from specific heat, as shown in Figure 1A. This is probably due to defect-mediated percolation superconductivity (Khim et al., 2021). Importantly, Figure 1A demonstrates how the suppression of the superconducting transition in ρ(T) with magnetic field follows the behavior of the bulk Tc, thus excluding the possibility of a superconducting impurity phase. The low-temperature normal-state resistivity exhibits a rather unusual temperature dependence,
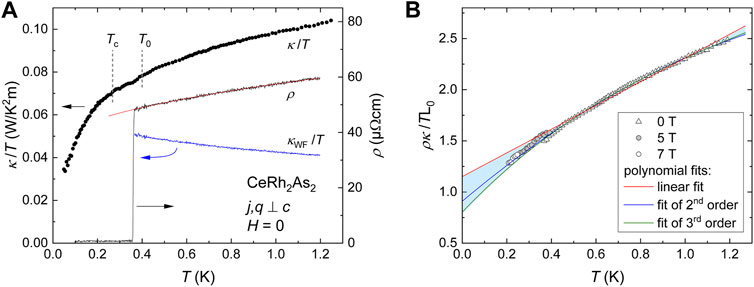
FIGURE 2. (A) T dependence of the thermal conductivity of CeRh2As2 plotted as κ(T)/T vs. T and compared to electrical resistivity ρ(T) measured using the same contacts. A fit
3.3 Wiedemann-Franz Law
In the temperature range below 2 K, the electronic contribution to the thermal conductivity becomes increasingly relevant (see a comparison of κ/T and κWF/T in Figure 2A). Normally, the Wiedermann-Franz law is studied and established for the electronic contribution to thermal conductivity, i.e., L = ρκel/T, which can tell us if scattering processes have different effects on thermal and electrical transport of charge carriers (Jaoui et al., 2021). In the zero-temperature limit L = L0 is expected in a normal metal where the Wiedemann-Franz law should be fulfilled, but might be violated near a quantum-critical point (Podolsky et al., 2007; Tanatar et al., 2007; Kim and Pépin, 2009; Pfau et al., 2012; Taupin et al., 2015). However, as described above, we are not able to determine and remove κph from κ to extract the pure electronic contribution. Therefore, we use a different approach. We calculate the Lorenz ratio L = ρκ/T taking the total thermal conductivity and normalize it by the Lorenz constant L0. This ratio is also expected to reach unity in the zero-temperature limit if the Wiedemann-Franz law is fulfilled, since κph goes to zero.
Figure 2B shows the normalized Lorenz ratio L/L0 for CeRh2As2 in the T range below 1.2 K. L/L0 is well above one but decreases towards one with decreasing T. Most likely, the phonon contribution to κ is still considerable in this temperature range in our material. Due to the onset of superconductivity, our calculation of L/L0 in zero field is limited to temperatures above 0.36 K. These data mainly reflect the behavior of CeRh2As2 above T0, but an influence of the transition at T0 = 0.4 K cannot be excluded. Therefore, and because of the unusual temperature dependencies of κ and ρ, any extrapolation of the data to 0 K goes along with large uncertainties. As rough attempts we show polynomial fits up to 3rd order for T > 0.4 K, without any physical reasoning. A linear fit does not describe the data well and extrapolates to L/L0 = 1.2. Polynomials of higher order better fit the data and extrapolate to values of L/L0 < 1. The corresponding fits are shown as lines Figure 2B. Using only part of the data range for fitting slightly changes the results. Nevertheless, as long as we use at least the data up to 1 K, all fits fall in the range shaded in blue in Figure 2B, which is roughly limited by the linear fit and the polynom of 3rd order on the whole data set below 1.2 K. Within the error bars of our analysis, L/L0 extrapolates to one at T → 0 as expected for a Fermi liquid. However, moderate deviations from this ideal value cannot be excluded due to the limited T range for the data extrapolation.
A more accurate evaluation of L/L0 in the unordered state might be achieved in magnetic fields if we assume that the only effect of the magnetic field is to suppress both T0 and Tc without changing the paramagnetic state. Therefore, we also show L/L0 in 5 and 7 T at lower T for comparison in Figure 2B. At these fields, the T0 order should be completely suppressed and hence the Wiedemann-Franz law in the paramagnetic state is tested. These data points follow the extrapolation of the zero-field curve. At this point we would also like to mention, that application of a magnetic field perpendicular to c would not increase the T range for evaluation of L/L0 in the paramagnetic state. Though Tc is suppressed much more rapidly in that case, T0 increases with field (Hafner et al., 2022) and thus further reduces the useful temperature range. In contrast, it would allow a test of the Wiedemann-Franz law in the T0 ordered state.
In the strict sense, concluding a validity or violation of the Wiedemann-Franz law from L/L0 in the zero-T limit is not reasonable without quantifying what would be a relevant deviation from unity. Over the past years many systems have been claimed to show a huge violation exceeding in some cases L/L0 = 10, although not always in the zero-T limit. Such large deviations, e.g., in the Luttinger liquid candidate Li0.9Mo6O17 (Wakeham et al., 2011), are excluded for CeRh2As2. However, as discussed in detail in Ref. (Lavasani et al., 2019) the Wiedemann-Franz law may be violated also due to trivial reasons, e.g., residual inelastic scattering in the investigated T range or bipolar conduction. For a better comparability we take a look at the Lorenz ratio in the zero-T limit in strongly correlated systems showing non-Fermi-liquid behavior close to a quantum-critical point: A rather low value of L/L0 ≈ 0.5 is observed in CeCoIn5 right at its field-induced quantum critical point (Tanatar et al., 2007). A much weaker reduction of L/L0 ≈ 0.92 is reported for YbAgGe (Dong et al., 2013). By contrast, L/L0 ≈ 1 for CeNi2Ge2 (Kambe et al., 1999), β-YbAlB4 (Sutherland et al., 2015), and Sr3Ru2O7 (Ronning et al., 2006), within the experimental uncertainties of 10%, 3%, and 5%, respectively. The difficulties in confirming a violation of the Wiedemann-Franz-law are most obvious for YbRh2Si2 (Taupin et al., 2015). Depending on the extrapolation of the data to 0 K, this material is either claimed to show a reduced value L/L0 ≈ 0.9 (Pfau et al., 2012) or no deviation from unity (Machida et al., 2013; Reid et al., 2014). This example demonstrates that a confirmation of a violation of the Wiedemann-Franz-law at lowest T is not trivial. Concerning CeRh2As2, a large violation as in CeCoIn5 is well beyond our uncertainty and can be excluded, while smaller deviations of about 10% as in YbAgGe and possibly in YbRh2Si2 are still possible within the resolution of our experiment.
3.4 Magnetic Field Dependence
In order to clarify whether the low-temperature downward bending of κ/T at roughly 0.2 K is related to superconductivity, we studied the influence of magnetic fields H up to 8 T parallel to the c axis. Figure 3A shows κ(T)/T in various fields. Above 0.5 K we find an almost field-independent behavior. The change of κ/T with field is less than 3% and below the resolution of our measurement. This negligible field dependence is consistent with the weak magnetoresistance for charge transport (Hafner et al., 2022). No field dependence is expected from phonon transport, as well. Below about
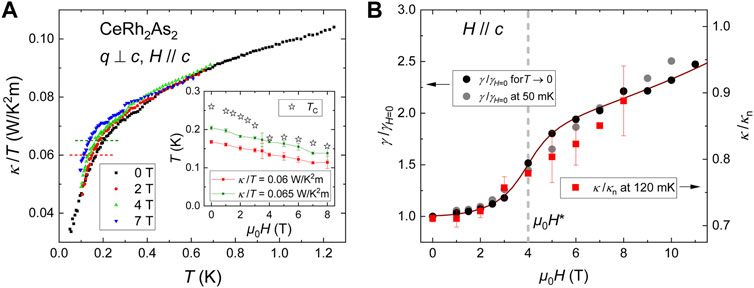
FIGURE 3. (A) Main plot: Thermal conductivity of CeRh2As2 divided by temperature in various magnetic fields. The dashed lines indicate cuts at constant κ/T, which are used for the inset. Inset: The stars indicate the field dependence of Tc taken from Ref. Khim et al. (2021) and are compared with points taken from our data at constant κ/T. (B) Field dependence of the thermal conductivity at 120 mK normalized to the value in the normal state, κ/κn. For comparison, the field dependence of the specific heat coefficient γ = C/T taken at constant T = 50 mK and extrapolated for T → 0, normalized to the value at H = 0, is plotted. The continuous line is a guide to the eye. The dashed perpendicular line marks the transition field μ0H⋆ between SC1 and SC2.
In summary, the impact of the superconducting transition at Tc on κ(T) of CeRh2As2 in our experiments is weak, probably due to residual states which contribute to thermal transport, despite the condensation of quasiparticles into the superconducting state. In the trivial case, such states are defects, which cause the presence of normal quasiparticles. A systematic study on Sr2RuO4 shows a broadening of the superconducting transition in κ(T) with increasing impurity concentration (Suzuki et al., 2002). A similar trend is seen in type-I, elemental superconductors (Hulm, 1949). In CeIrIn5, a heavy-fermion superconductor, κ/T (T < Tc) shows a peak. With disorder, the peak disappears and becomes a downward bend from the normal-state value at Tc (Shakeripour et al., 2010). So, measurements on CeRh2As2 samples of higher purity are definitively required to study the influence of superconductivity on κ(T) in more detail.
The temperature dependence of κ(T) in the temperature range below Tc provides information about the gap structure. For instance, an exponential T dependence indicates a full superconducting gap whereas a power-law-behavior points to the presence of nodes. As a consequence, the extrapolation of the thermal conductivity κ/T towards T = 0 will be finite if the superconducting gap has nodes, but it will be zero if the gap is finite everywhere on the Fermi surface (Shakeripour et al., 2010).
The magnetic field dependence also depends on the superconducting gap structure. The field dependence of thermal conductivity and specific heat in a superconductor in the zero-temperature limit is comparable if scattering of the quasiparticles with vortices can be neglected. Both quantities are sensitive to the increase of the density of states of the normal states inside the vortex core—resulting in a linear increase in field—and to the Volovik effect (Volovik, 1993) which can lead to different field dependencies depending on the pairing state (Bang, 2010), for example the famous
At low magnetic fields, γ/γH=0 increases very slowly with field, a behavior typical of s-wave superconductivity (Shakeripour et al., 2010). This is in agreement with results of the penetration depth obtained from muon-spin-resonance experiments, where a nearly-full-gap temperature dependence was observed (Khim, 2022). Around H⋆, a stronger increase occurs, followed by another region with weak, almost linear field dependence. The overall behavior for data points at 50 mK and in the zero-T limit is similar, with a slightly steeper increase for T → 0 around H⋆. The field dependence of κ roughly follows the one of γ with a small slope at low H and a larger one around H⋆ when going from SC1 to SC2. Measurements at higher fields and lower T are required to confirm that this change in slope is really due to the transition between the two superconducting phases.
4 Summary and Conclusion
In this manuscript we have presented the thermal conductivity and electrical resistivity of single-crystalline CeRh2As2 between 60 mK and 200 K. The high-temperature behavior is typical for a Ce-based Kondo-lattice system with the thermal conductivity dominated by phonons and the electrical resistivity governed by Kondo scattering and crystal-electric-field excitations. By contrast, the temperature dependence between 60 mK and 1.2 K of both quantities does not follow the expected behavior for a Fermi liquid. Within the uncertainties of our data and analysis, the data fulfill the Wiedemann-Franz law in the T = 0 limit. No sharp anomalies are detected by the thermal conductivity at the expected phase transition temperatures, Tc and T0, seen in thermodynamic and resistivity measurements, but a downward bending of κ/T at low temperature appears to be due to superconductivity. In fact, as expected, this feature shifts to lower temperatures when magnetic fields are applied along the c axis. It seems that impurities in our sample and associated scattering hide the putative sharp features expected for both phase transitions. Hence, better sample quality is required to obtain clear information about the superconducting gap structure via thermal conductivity.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
SK grew the samples. US carried out the high-temperature measurements and the low-temperature field calibration. SO carried out the low-temperature experiments. US and SO analyzed the data with input from EH. JB and MB measured and analysed the specific heat. US and EH wrote the manuscript with input from all coauthors.
Funding
The research environment in Dresden benefits from the DFG Excellence Cluster Complexity and Topology in Quantum Matter (ct.qmat). We acknowledge funding from the Physics of Quantum Materials department and the research group “Physics of Unconventional Metals and Superconductors (PUMAS)” by the Max Planck Society. EH acknowledges support from the German Science Foundation (DFG) through Grant GE 602/4-1 Fermi-NESt.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Christoph Geibel and Louis Taillefer for useful comments about the manuscript.
References
Anand, V. K., Adroja, D. T., Bhattacharyya, A., Klemke, B., and Lake, B. (2017). Kondo Lattice Heavy Fermion Behavior in CeRh2Ga2. J. Phys. Condens. Matter 29, 135601. doi:10.1088/1361-648X/aa5b5d
Bang, Y. (2010). Volovik Effect in the ± s-Wave State for the Iron-Based Superconductors. Phys. Rev. Lett. 104, 217001. doi:10.1103/PhysRevLett.104.217001
Bauer, E., Gratz, E., and Adam, G. (1986). Thermal Conductivity of REAl2 compounds (RE = Rare Earth). J. Phys. F: Met. Phys. 16, 493–506. doi:10.1088/0305-4608/16/4/013
Cavanagh, D. C., Shishidou, T., Weinert, M., Brydon, P. M. R., and Agterberg, D. F. (2022). Nonsymmorphic Symmetry and Field-Driven Odd-Parity Pairing in CeRh2As2. Phys. Rev. B 105, L020505. doi:10.1103/PhysRevB.105.L020505
Custers, J., Gegenwart, P., Wilhelm, H., Neumaier, K., Tokiwa, Y., Trovarelli, O., et al. (2003). The Break-Up of Heavy Electrons at a Quantum Critical Point. Nature 424, 524–527. doi:10.1038/nature01774
Dong, J. K., Tokiwa, Y., Bud’ko, S. L., Canfield, P. C., and Gegenwart, P. (2013). Anomalous Reduction of the Lorenz Ratio at the Quantum Critical Point in YbAgGe. Phys. Rev. Lett. 110, 176402. doi:10.1103/PhysRevLett.110.176402
Dong, J. K., Zhou, S. Y., Guan, T. Y., Zhang, H., Dai, Y. F., Qiu, X., et al. (2010). Quantum Criticality and Nodal Superconductivity in the FeAs-Based Superconductor KFe2As2. Phys. Rev. Lett. 104, 087005. doi:10.1103/PhysRevLett.104.087005
Falkowski, M., and Kowalczyk, A. (2011). Thermopower and Thermal Conductivity of Kondo Lattice CeCu4Al. J. Appl. Phys. 110, 043709. doi:10.1063/1.3624748
Franz, W., Grießel, A., Steglich, F., and Wohlleben, D. (1978). Transport Properties of LaCu2Si2 and CeCu2Si2 between 1.5K and 300K. Z. Physik B 31, 7–17. doi:10.1007/bf01320122
Gratz, E., Bauer, E., Barbara, B., Zemirli, S., Steglich, F., Bredl, C. D., et al. (1985). CeCu2: A New Kondo Lattice Showing Magnetic Order. J. Phys. F: Met. Phys. 15, 1975–1986. doi:10.1088/0305-4608/15/9/015
Hafner, D., Khanenko, P., Eljaouhari, E.-O., Küchler, R., Banda, J., Bannor, N., et al. (2022). Possible Quadrupole Density Wave in the Superconducting Kondo Lattice CeRh2As2. Phys. Rev. X 12, 011023. doi:10.1103/PhysRevX.12.011023
Hulm, J. K. (1949). Thermal Conductivity of Superconductors. Nature 163, 368–369. doi:10.1038/163368a0
Izawa, K., Kasahara, Y., Matsuda, Y., Behnia, K., Yasuda, T., Settai, R., et al. (2005). Line Nodes in the Superconducting Gap Function of Noncentrosymmetric CePt3Si. Phys. Rev. Lett. 94, 197002. doi:10.1103/PhysRevLett.94.197002
Jaoui, A., Fauqué, B., and Behnia, K. (2021). Thermal Resistivity and Hydrodynamics of the Degenerate Electron Fluid in Antimony. Nat. Commun. 12, 195. doi:10.1038/s41467-020-20420-9
Kadowaki, K., and Woods, S. B. (1986). Universal Relationship of the Resistivity and Specific Heat in Heavy-Fermion Compounds. Solid State. Commun. 58, 507–509. doi:10.1016/0038-1098(86)90785-4
Kambe, S., Suderow, H., Fukuhara, T., Flouquet, J., and Takimoto, T. (1999). Spin-Fluctuation Mediated Thermal Conductivity Around the Magnetic Instability of CeNi2Ge2. J. Low. Temp Phys. 117, 101–112. doi:10.1023/A:1021865906745
Kapoor, A., Rowlands, J. A., and Woods, S. B. (1974). Lattice Thermal Conductivity of Cold-Worked Noble-Metal Alloys between 0.5 and 4 K. Phys. Rev. B 9, 1223–1229. doi:10.1103/PhysRevB.9.1223
Khim, S., Landaeta, J. F., Banda, J., Bannor, N., Brando, M., Brydon, P. M. R., et al. (2021). Field-induced Transition within the Superconducting State of CeRh2As2. Science 373, 1012–1016. doi:10.1126/science.abe7518
Kibune, M., Kitagawa, S., Kinjo, K., Ogata, S., Manago, M., Taniguchi, T., et al. (2022). Observation of Antiferromagnetic Order as Odd-Parity Multipoles inside the Superconducting Phase in CeRh2As2. Phys. Rev. Lett. 128, 057002. doi:10.1103/PhysRevLett.128.057002
Kim, K.-S., and Pépin, C. (2009). Violation of the Wiedemann-Franz Law at the Kondo Breakdown Quantum Critical Point. Phys. Rev. Lett. 102, 156404. doi:10.1103/PhysRevLett.102.156404
Landaeta, J. F., Khanenko, P., Cavanagh, D. C., Geibel, C., Khim, S., Mishra, S., et al. (2022). Field-Angle Dependence Reveals Odd-Parity Superconductivity in CeRh2As2. To be published.
Lavasani, A., Bulmash, D., and Das Sarma, S. (2019). Wiedemann-Franz Law and Fermi Liquids. Phys. Rev. B 99, 085104. doi:10.1103/PhysRevB.99.085104
Li, S. Y., Bonnemaison, J.-B., Payeur, A., Fournier, P., Wang, C. H., Chen, X. H., et al. (2008). Low-Temperature Phonon Thermal Conductivity of Single-Crystalline Nd2CuO4: Effects of Sample Size and Surface Roughness. Phys. Rev. B 77, 134501. doi:10.1103/PhysRevB.77.134501
Machida, Y., Tomokuni, K., Izawa, K., Lapertot, G., Knebel, G., Brison, J.-P., et al. (2013). Verification of the Wiedemann-Franz Law in YbRh2Si2 at a Quantum Critical Point. Phys. Rev. Lett. 110, 236402. doi:10.1103/PhysRevLett.110.236402
Möckli, D., and Ramires, A. (2021a). Superconductivity in Disordered Locally Noncentrosymmetric Materials: An Application to CeRh2As2. Phys. Rev. B 104, 134517. doi:10.1103/PhysRevB.104.134517
Möckli, D., and Ramires, A. (2021b). Two Scenarios for Superconductivity in CeRh2As2. Phys. Rev. Res. 3, 023204. doi:10.1103/PhysRevResearch.3.023204
Moeser, J. H., and Steglich, F. (1975). Kondo Anomalies of Heat Conductivity and Lorenz Ratio in Normal State (La,Ce)Al2. Z. Physik B 21, 165–170. doi:10.1007/bf01322247
Nogaki, K., Daido, A., Ishizuka, J., and Yanase, Y. (2021). Topological Crystalline Superconductivity in Locally Noncentrosymmetric CeRh2As2. Phys. Rev. Res. 3, L032071. doi:10.1103/PhysRevResearch.3.L032071
Pfau, H., Hartmann, S., Stockert, U., Sun, P., Lausberg, S., Brando, M., et al. (2012). Thermal and Electrical Transport across a Magnetic Quantum Critical Point. Nature 484, 493–497. doi:10.1038/nature11072
Podolsky, D., Vishwanath, A., Moore, J., and Sachdev, S. (2007). Thermoelectric Transport Near Pair Breaking Quantum Phase Transition Out of d-Wave Superconductivity. Phys. Rev. B 75, 014520. doi:10.1103/PhysRevB.75.014520
Ptok, A., Kapcia, K. J., Jochym, P. T., Łażewski, J., Oleś, A. M., and Piekarz, P. (2021). Electronic and Dynamical Properties of CeRh2As2 : Role of Rh2As2 Layers and Expected Orbital Order. Phys. Rev. B 104, L041109. doi:10.1103/PhysRevB.104.L041109
Reid, J.-P., Tanatar, M. A., Daou, R., Hu, R., Petrovic, C., and Taillefer, L. (2014). Wiedemann-Franz Law and Nonvanishing Temperature Scale across the Field-Tuned Quantum Critical point of YbRh2Si2. Phys. Rev. B 89, 045130. doi:10.1103/PhysRevB.89.045130
Reid, J.-P., Tanatar, M. A., Juneau-Fecteau, A., Gordon, R. T., de Cotret, S. R., Doiron-Leyraud, N., et al. (2012). Universal Heat Conduction in the Iron Arsenide Superconductor KFe2As2: Evidence of a d-Wave State. Phys. Rev. Lett. 109, 087001. doi:10.1103/PhysRevLett.109.087001
Ronning, F., Hill, R. W., Sutherland, M., Hawthorn, D. G., Tanatar, M. A., Paglione, J., et al. (2006). Thermal Conductivity in the Vicinity of the Quantum Critical End Point in Sr3Ru2O7. Phys. Rev. Lett. 97, 067005. doi:10.1103/PhysRevLett.97.067005
Schertenleib, E. G., Fischer, M. H., and Sigrist, M. (2021). Unusual H−T Phase Diagram of CeRh2As2 : The Role of Staggered Noncentrosymmetricity. Phys. Rev. Res. 3, 023179. doi:10.1103/PhysRevResearch.3.023179
Shakeripour, H., Tanatar, M. A., Petrovic, C., and Taillefer, L. (2010). Universal Heat Conduction and Nodal gap Structure of the Heavy-Fermion superconductor CeIrIn5. Phys. Rev. B 82, 184531. doi:10.1103/PhysRevB.82.184531
Skurativska, A., Sigrist, M., and Fischer, M. H. (2021). Spin Response and Topology of a Staggered-Rashba Superconductor. Phys. Rev. Res. 3, 033133. doi:10.1103/PhysRevResearch.3.033133
Stockert, U., dos Reis, R. D., Ajeesh, M. O., Watzman, S. J., Schmidt, M., Shekhar, C., et al. (2017). Thermopower and Thermal Conductivity in the Weyl Semimetal NbP. J. Phys. Condens. Matter 29, 325701. doi:10.1088/1361-648X/aa7a3b
Sutherland, M. L., O'Farrell, E. C. T., Toews, W. H., Dunn, J., Kuga, K., Nakatsuji, S., et al. (2015). Intact Quasiparticles at an Unconventional Quantum Critical Point. Phys. Rev. B 92, 041114(R). doi:10.1103/PhysRevB.92.041114
Suzuki, M., Tanatar, M. A., Kikugawa, N., Mao, Z. Q., Maeno, Y., and Ishiguro, T. (2002). Universal Heat Transport in Sr2RuO4. Phys. Rev. Lett. 88, 227004. doi:10.1103/PhysRevLett.88.227004
Tanatar, M. A., Paglione, J., Petrovic, C., and Taillefer, L. (2007). Anisotropic Violation of the Wiedemann-Franz Law at a Quantum Critical Point. Science 316, 1320–1322. doi:10.1126/science.1140762
Taupin, M., Knebel, G., Matsuda, T. D., Lapertot, G., Machida, Y., Izawa, K., et al. (2015). Thermal Conductivity through the Quantum Critical Point in YbRh2Si2 at Very Low Temperature. Phys. Rev. Lett. 115, 046402. doi:10.1103/PhysRevLett.115.046402
Toliński, T., Synoradzki, K., Koterlyn, M., and Yasnitskii, R. (2013). Competing Energy Scales in the Compounds Ce(Ni1−xCux)2(Si2). J. Alloys Compd. 580, 512.
Volovik, G. E. (1993). Superconductivity with Lines of Gap Nodes: Density of States in the Vortex. JETP 58, 469. doi:10.1126/science.1140762
Wakeham, N., Bangura, A. F., Xu, X., Mercure, J.-F., Greenblatt, M., and Hussey, N. E. (2011). Gross Violation of the Wiedemann-Franz Law in a Quasi-One-Dimensional Conductor. Nat. Commun. 2, 396. doi:10.1038/ncomms1406
Keywords: superconductivity, low temperature, heavy fermion, local inversion-symmetry breaking, thermal conductivity, Wiedemann-Franz law
Citation: Onishi S, Stockert U, Khim S, Banda J, Brando M and Hassinger E (2022) Low-Temperature Thermal Conductivity of the Two-Phase Superconductor CeRh2As2. Front. Electron. Mater. 2:880579. doi: 10.3389/femat.2022.880579
Received: 21 February 2022; Accepted: 06 April 2022;
Published: 29 April 2022.
Edited by:
Jeffrey W. Lynn, National Institute of Standards and Technology (NIST), United StatesReviewed by:
Joe Thompson, Los Alamos National Laboratory (DOE), United StatesJohn Tranquada, Brookhaven National Laboratory (DOE), United States
Copyright © 2022 Onishi, Stockert, Khim, Banda, Brando and Hassinger. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Elena Hassinger, ZWxlbmEuaGFzc2luZ2VyQGNwZnMubXBnLmRl
 Seita Onishi
Seita Onishi Ulrike Stockert
Ulrike Stockert Seunghyun Khim
Seunghyun Khim Jacintha Banda1
Jacintha Banda1 Manuel Brando
Manuel Brando Elena Hassinger
Elena Hassinger