Anisotropy of the T vs. H phase diagram and the HO/LMAFM phase boundary in URu2−xFexSi2

The correlated f-electron compound URu₂Si₂ exhibits superconductivity (SC) with a critical temperature T_c = 1.5 K that coexists with the “hidden order” (HO) phase that forms below a characteristic temperature T₀ = 17.5 K. The SC of URu₂Si₂ appears to be spin singlet chiral SC with d-wave order parameter symmetry, and the pairing of SCing electrons may involve spin excitations of the HO phase. Electrical resistance R measurements were performed on single crystal specimens of URu_2−xFe_xSi₂ with increasing x throughout the transition from the HO phase to the large moment antiferromagnetic LMAFM phase in high magnetic fields H oriented at various angles θ with respect to the tetragonal c-axis. Measurements of R(θ) at H = 20, 33, 40, and 45 T were conducted in the temperature range 0.33 ≤ T ≤ 20 K and showed θ-dependent behavior in the various phase transitions of URu_2−xFe_xSi₂ (HO, LMAFM, spin density wave, Fermi surface reconstruction, etc.). These phase transitions, as functions of T, H, and θ are plotted in a phase diagram of T vs. H//c = Hcosθ for multiple values of x and show that H//c, not θ is a tuning parameter of the URu_2−xFe_xSi₂ system throughout all Fe concentrations, as previously found by Scheereret al. for the URu₂Si₂ parent compound.

1 Introduction

The heavy fermion superconductor (SCor) URu₂Si₂ has attracted an enormous amount of interest among correlated electron materials because of the wealth of extraordinary phases and phenomena it harbors in the phase space of atomic substituent composition x, pressure P, and magnetic field H. Two of these phases, the so-called “hidden order” (HO) phase and the unconventional superconducting (SCing) phase, are of particular interest and appear to be interrelated. Researchers have been especially intrigued by the HO phase, since the features in its transport, thermal and magnetic properties are prominent but its order pB27arameter has not been identified after more than 3–1/2 decades of research on URu₂Si₂ based materials (Mydosh and Oppeneer, 2011; Mydosh and Oppeneer, 2014; Mydosh et al., 2020). The superconductivity (SC) is also unique and appears to be spin singlet chiral SC with d-wave order parameter symmetry in which the pairing of SCing electrons may involve spin excitations of the HO phase.

We note that the HO phase of URu₂Si₂ has been studied extensively by means of various types of physical properties measurements via tuning of non-thermal parameters such as P (McElfresh et al., 1987; Butch et al., 2010; Hassinger et al., 2010), H (Jo et al., 2007) and x, in, for example, URu_2−xM_xSi₂ (where M = Fe (Kanchanavatee et al., 2011), Os (Kanchanavatee et al., 2017), Re (Bauer et al., 2005; Butch and Maple, 2009), etc.), U_1−xTh_xRu₂Si₂ (de la Torre et al., 1992), and URu₂Si_2−xP_x (Gallagher et al., 2016). In the present study, we have focused on URu_2−xFe_xSi₂ in magnetic fields H oriented at angles θ with respect to the tetragonal c-axis, where the tuning parameters are x, H and θ. This study complements a study of the URu₂Si₂ parent compound involving the tuning parameters H and θ by Scheereret al. (Scheerer et al., 2012; Scheerer et al., 2014).

Early experiments–HO and SC: partial gapping scenario

In the earliest experiments on URu₂Si₂, features in the electrical resistivity ρ(T), magnetic susceptibility χ(T), and specific heat C(T) were observed at a temperature T₀ = 17.5 K, signaling a transition to an ordered state, followed by a SCing transition at a critical temperature T_c = 1.5 K (Palstra et al., 1985; Maple et al., 1986; Schlabitz et al., 1986). It was noted that the anomalies in these properties at T₀ are reminiscent of a charge or spin density wave (CDW or SDW) transition (Maple et al., 1986). Analysis of the electronic specific heat led to the proposal of a “partial gapping” scenario in which the phase that develops below T₀ forms a gap of about 100 K over about 40% of the Fermi surface (FS) (Maple et al., 1986). The value of the gap was derived from the exponential T-dependence of the BCS-like mean field anomaly in the electronic specific heat below T₀, while the amount of the FS that is gapped was estimated from the reduction in the electronic specific heat coefficient γ as T → 0 K relative to its value above T₀, where γ is assumed to be proportional to the density of states (N (E_F)) at the Fermi level (E_F). The energy gap has been measured using various spectroscopic techniques and found to be close to the value estimated from the specific heat anomaly (Mydosh and Oppeneer, 2014). The remainder of the FS is gapped by the SC that occurs below T_c.

Temperature vs. pressure phase diagram: HO–LMAFM phase transition

Experiments on URu₂Si₂ under pressure have provided important clues about the HO phase and its relation to the SCing phase, as well as to other phases. Upon application of pressure, there is a first order phase transition from the HO phase to a large moment antiferromagnetic (LMAFM) phase and a concomitant suppression of the SCing phase where T_c approaches 0 K near ∼ 8 kbar, the critical pressure where the HO-LMAFM transition occurs at very low temperature (Butch et al., 2010). The SCing phase appears to coexist with the HO phase and be suppressed by the LMAFM phase (Hassinger et al., 2008; Butch et al., 2010), suggesting that the pairing of SCing electrons may be associated with particular types of spin excitations which are present in the HO phase but absent in the LMAFM phase.

The application of high pressure reveals that the phase boundary between the paramagnetic (PM) and HO/LMAFM phases increases with P in the HO phase, exhibits a kink at 15 kbar, the critical pressure (P_c) where the HO-LMAFM transition occurs, and increases with P with a larger slope in the LMAFM region. The concomitant increase of T₀ and decrease of T_c with P is consistent with an increase of the area of the FS gapped by the HO phase at the expense of the FS area gapped by the SC (Maple et al., 1986; McElfresh et al., 1987). The “partial gapping scenario” can be described by the theory of Bilbro and McMillan (Bilbro, 1976), extended to include SC and SDW order by Machida (Machida, 1981), in terms of a relation between T₀, T_c and the fraction of the FS gapped by the HO (Maple et al., 1986; Fisher et al., 1990; Jeffries et al., 2007; Jeffries et al., 2008). On the other hand, models based on the localized character of the U 5f electrons in URu₂Si₂ have been proposed that are consistent with certain aspects of HO and other phenomena. Ironically, the richness of the phenomena found in URu₂Si₂ and the challenge of developing a fundamental understanding of the underlying physics are associated with the admixture of localized U 5f and itinerant electron states in this system. A review of the large amount of research that has been carried out on URu₂Si₂, including experiments on chemically substituted URu₂Si₂ systems and the latest theoretical developments, can be found in a series of reviews by Mydosh, Openeer and Riseborough (Mydosh and Oppeneer, 2011; Mydosh and Oppeneer, 2014; Mydosh et al., 2020).

Superconducting phase

The nature of the SC that occurs below 1.5 K has also attracted great interest. A series of complementary experiments has provided a picture in which the SCing phase of URu₂Si₂ is unconventional and appears to be spin singlet, d-wave SC, with chiral k_z (k_x + ik_y) order parameter symmetry, in which the SCing gap has a horizontal line node at k_z = 0 and point nodes at k_x = k_y = 0 (Mydosh et al., 2020). While the SCing state of URu₂Si₂ seems to be well established experimentally, the underlying interactions responsible for this SCing pairing state have not yet been established. However, as noted above, insofar as the unconventional SCing phase of URu₂Si₂ resides within and coexists with the HO phase and is suppressed by the LMAFM phase, the SCing electron pairing would seem to involve special types of spin excitations within the HO phase that are not present in the LMAFM phase. Interestingly, a theory of magnetic exciton mediated SC in URu₂Si₂ has been proposed by Kusunose (Kusunose, 2012) based on the Ising-like collective modes in the HO phase (Altarawneh et al., 2011; Altarawneh et al., 2012) that lead to chiral d-wave singlet pairing with E_g symmetry. The Ising character of the spin resonance modes is an essential ingredient that explains the strong anisotropy of the upper critical field H_c2(T) (Ohkuni et al., 1999)

Substitutional studies

In 2011, our group reported that the substitution of isoelectronic Fe (Kanchanavatee et al., 2011) for Ru in URu₂Si₂ generates a T vs. x phase diagram, where x is the Fe concentration, that is reminiscent of the T vs. P phase diagram for pure URu₂Si₂ (Butch et al., 2010). We noted that substitution of Fe for Ru yields a reduction in the unit cell volume similar to that obtained under pressure at the critical concentration x_c = 0.15 or pressure P_c = 1.5 GPa at which the HO-LMAFM transition occurs. This led us to suggest that substitution of Fe could generate a “chemical pressure” P_ch = (x/x_c)P_c = (P_c/x_c)x = (10 GPa)x that drives the HO-LMAFM transition.

Subsequent studies of the URu_2−xFe_xSi₂ system under pressure revealed that increases in x and P induce the HO-LMAFM phase transition in an additive manner; i.e., x_c*(P) = x_c–(x_c/P_c)P = 0.15–0.1 (GPa)⁻¹P (Wolowiec et al., 2016). Later it was shown that the substitution of isoelectronic Os for Ru yields a T vs. x phase diagram similar to that obtained for Fe substitution, even though the substitution of Os corresponds to an increase of the unit cell volume, or “negative” chemical pressure (Kanchanavatee et al., 2014). Studies of the URu_2−xOs_xSi₂ system under pressure revealed that increasing both x and P are additive in inducing the HO-LMAFM transition for Os substitution, just like Fe substitutions (Wolowiec et al., 2021). An analysis of the increase in the hybridization of the U 5f states and the transition metal d-states upon substitution of Fe and Os for Ru in URu_2−xM_xSi₂ (M = Fe, Os) suggested that the transition from HO to the LMAFM order is primarily driven by the increase in hybridization due to partial replacement of Ru 4d states with Fe 3d and Os 5d states which enhances and over compensates for the effects of positive or negative chemical pressure for Fe and Os substitutions, respectively.

Since the substitution of Fe and Os for Ru in URu₂Si₂ has the same effect as the application of pressure in driving the HO-LMAFM transition, the substitutional route has the attractive feature that measurements which are difficult to perform on URu₂Si₂ under pressure in the HO and LMAFM phases can instead be performed on URu_2−xM_xSi₂ (M = Fe, Os) compounds at atmospheric pressure to achieve the same objective. Also, the LMAFM phase in URu₂Si₂ accessed by applying pressure (Jeffries et al., 2007; Jo et al., 2007; Hassinger et al., 2010) and substituting Fe for Ru (Kanchanavatee et al., 2011; Das et al., 2015; Ran et al., 2016) is especially intriguing due to the similarities between the HO and LMAFM phases (e.g., electronic structure, effective masses, c-axis wave vector downfolding). This motivated our group to undertake a study of the HO and LMAFM phases in URu_2−xFe_xSi₂ under the “effective pressure” associated with Fe substitution in high magnetic fields up to 60 T applied along the c-axis at the National High Magnetic Field Laboratory (NHMFL) facilities at Florida State University (FSU) and Los Alamos National Laboratory (LANL) (Ran et al., 2017). The R(T,H) measurements in high magnetic fields yielded some spectacular 2D T vs. H phase diagrams for various values of x and a 3D T vs. H and x phase diagram shown in the “EXPERIMENTAL RESULTS” section.

The R(T,H) measurements on the URu₂Si₂ parent compound reveal a rich and complex T vs. H phase diagram similar to that previously reported by Kim et al. (2003) and Jaime et al. (2002). The HO transition temperature T₀ and temperature T* where the magnetoresistance changes from positive to negative are suppressed towards 0 K near 35 T and in the vicinity of a metamagnetic transition at ∼38 T (Kim et al., 2003). Between ∼33 T and ∼39 T, there is a cascade of exotic phases, one of which is an incommensurate SDW, and non-Fermi liquid behavior where ρ(T) ≈ AT^∼1.3 (Kim et al., 2003). Regions within the T vs. H phase diagrams contain HO, re-entrant HO (HO*), LMAFM phases and a change in Fermi surface geometry. These phase diagrams reveal the appearance of a “re-entrant” hidden order (HO*) phase as a large magnetic field was applied at low temperatures in the LMAFM phase (Harrison et al., 2003; Aoki et al., 2010; Ran et al., 2017). With the continuing efforts to understand the underlying physics of the HO, it would be useful to probe the field-induced transition between the HO and the LMAFM phases for several values of x in URu_2−xFe_xSi₂.

Scheerer et al. (Scheerer et al., 2012) reported measurements of the electrical resistivity of URu₂Si₂ in high magnetic fields applied at an angle θ with respect to the c-axis and characterized the various phase transitions of URu₂Si₂ as a function of θ. The ultimate finding was that the observed θ-dependent behavior of the T vs. H phase diagram of URu₂Si₂ is actually a reflection of the phase transitions depending on the magnetic field projection onto the c-axis, where H//c = Hcosθ. This study showed that neither H nor θ independently are tuning parameters of URu₂Si₂, but instead H//c is the tuning parameter, possibly due to the symmetry of the g-factor of URu₂Si₂ (Ohkuni et al., 1999; Altarawneh et al., 2011).

Our primary motivation for the research described herein was to study the θ-dependent behavior of R at larger H, lower T, and for several values of x in the URu_2−xFe_xSi₂ system. We wanted to determine whether H//c, which is a tuning parameter for x = 0, remains a tuning parameter over the full range of Fe concentrations, x, throughout the HO phase and into the LMAFM phase. Additionally, these measurements can probe the transition between LMAFM and HO* (“re-entrant HO”), as well as potentially allowing one to distinguish the closely-related LMAFM and HO ground states from one another. These objectives can be explored by constructing a T vs. H phase diagram for URu_2−xFe_xSi₂, as presented in the work by Ranet al. (Ran et al., 2017), but with variation of θ. Our construction of the URu_2−xFe_xSi₂ phase diagram with varying T, H, and θ, not only confirmed the results for URu₂Si₂ presented by Scheerer et al. (Scheerer et al., 2012), but also showed that H//c, as opposed to θ, was a tuning parameter that extended throughout all x in the URu_2−xFe_xSi₂ system.

2 Experimental results

Electrical transport measurements on single crystals of URu_2−xFe_xSi₂ were made in high magnetic fields using a 65 T pulsed-field magnet at National High Magnetic Field Lab (NHMFL), Los Alamos, NM and the 45 T dc hybrid magnet at NHMFL, Tallahassee, FL. The electrical transport properties of the single crystals, with cleaved surfaces perpendicular to the c-axis, were measured using a standard four-wire technique in the ab-plane, where voltage was measured in the same direction as current. The magnetic field, H, is applied at an angle, θ, to the c-axis, such that θ = 0 represents H//c and θ = 90° represents H//ab Rotation is performed in-situ using a cryogenic goniometer (Willis et al., 2020). Figure 1 shows a depiction of this setup at both facilities.

FIGURE 1

FIGURE 1. Graphic of the sample rotation in a vertical magnetic field representing the experimental setup at both the Pulsed Field facility at LANL and the DC Field facility at FSU.

2.1 Angular-dependence of magnetoresistance in URu₂Si₂

Measurements of the electrical transport properties of URu₂Si₂ were taken under a pulsed field of μ₀H_max = 65 T directed at various angles 0 ≤ θ ≤ 90° for T = 1.5, 10, and 13 K. The results of these measurements are presented in Figures 2A–C. Electrical resistance, R, of URu₂Si₂ is measured as H is pulsed to 65 T, and several features associated with phase transitions appear at various values of H_phase, dependent on T and θ. For fixed T, the θ-dependent behavior as θ → 90° shows these transitions being shifted to higher fields, suggesting strong correlation between H_phase and θ, where θ = 90° makes these transitions impossible to observe. We follow this idea by using the trigonometric relation, cos θ, which represents the projection of H onto the c-axis, and can reduce the scaling of H by cos θ on the bottom panels of Figures 2D–F to determine if the transitions observed in URu₂Si₂ are dependent on H//c. This reduced scaling, based on the geometry of the setup, shows that the transitions observed in URu₂Si₂ are indeed solely dependent on the application of magnetic field along the c-axis. Despite a very large μ₀H up to 65 T being applied in the ab-plane, there is no deviation from this behavior. These results confirm the findings of Scheerer et al. and give strong indication that not only the HO, but all phases (Fermi surface reconstruction, SDW, etc.) in URu₂Si₂ are only susceptible to H applied along the c axis, suggesting that the magnetic properties of the 5f-electrons are linked to the Fermi surface (Scheerer et al., 2012).

FIGURE 2

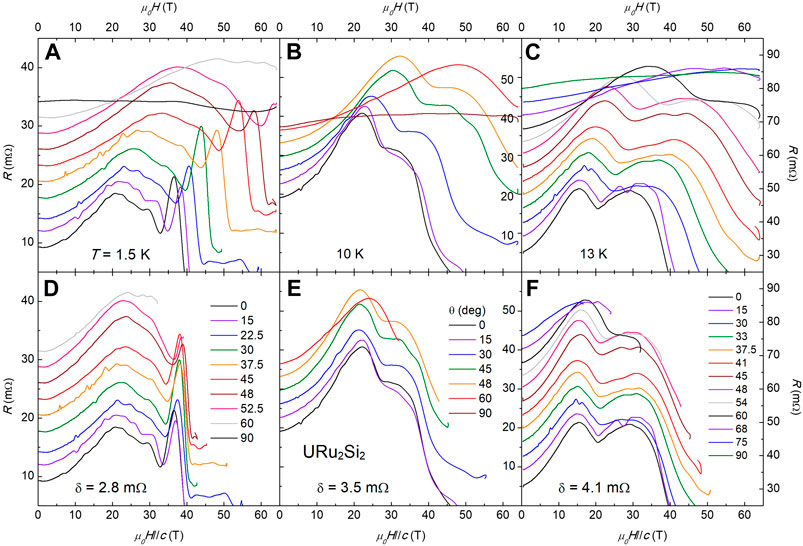
FIGURE 2. (A–C) Resistance, R, vs. magnetic field, H, of URu₂Si₂ at multiple angles θ for T = 1.5, 10, and 13 K, respectively. (D–F) Resistance curves from (A–C) plotted versus the projection of the magnetic field onto the c-axis of URu₂Si₂, H//c, where H//c = H cos θ. The behavior of magnetoresistance in URu₂Si₂ appears to only depend on H//c, consistent with Scheerer et al. (Scheerer et al., 2012).

2.2 Angular dependence of magnetoresistance in URu_2−xFe_xSi₂

Measurements of R vs. θ were performed on URu_2−xFe_xSi₂ in the 45 T hybrid magnet at NHMFL to characterize the angular symmetry of R(θ) at higher fields and across the phase diagram for URu_2−xFe_xSi₂ constructed by Ran et al. (2017). Measurements on R(θ) were made as θ was swept through the range 0 ≤ θ ≤ 180° for fixed magnetic fields μ₀H = 20, 33, 40, and 45 T at multiple temperatures above and below the HO and LMAFM transitions in URu_2−xFe_xSi₂ for selected x. The data taken for this measurement on x = 0.2 at μ₀H = 45 T are shown in Figure 3 as an example.

FIGURE 3

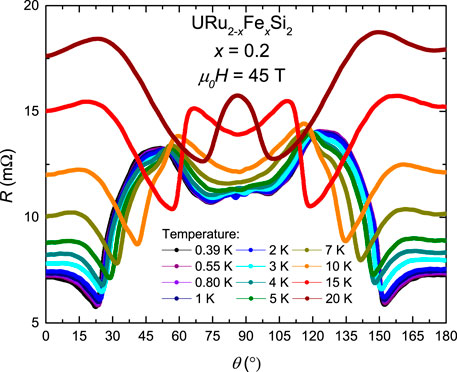
FIGURE 3. Selected R vs. θ curves at selected temperatures for x = 0.2 with the applied field magnitude of μ₀H = 45 T. Features that develop at high fields represent phase transitions occurring at θ_c (T, H).

The features in R(θ) are actually representative of phase transitions. This explanation utilizes the knowledge that the T vs. H phase diagram for URu₂Si₂ does not explicitly depend on the angle, but instead on the projection of H onto the c-axis, as shown by Scheerer et al. (Scheerer et al., 2012) and confirmed in the prior discussion in this manuscript using an independent, but similar experiment on URu₂Si₂. Much like in Figure 2, where the magnetic field sweeps of R(H) at several θ were reduced to a system of just R vs. H//c, a reduction of parameters can be attempted where θ is converted to H//c using the magnitude of the field (45 T, for Figure 3) and the relation H//c = H cos θ. This conversion is shown for a single R vs. θ dataset in Figure 4, with x-axis values of θ being converted to H//c and shown on the top x-axis. Using the first angular derivative of resistance, dR/dθ, the features in R(θ) can be more easily identified at specific θ and H//c, as shown by the red line in Figure 4.

FIGURE 4

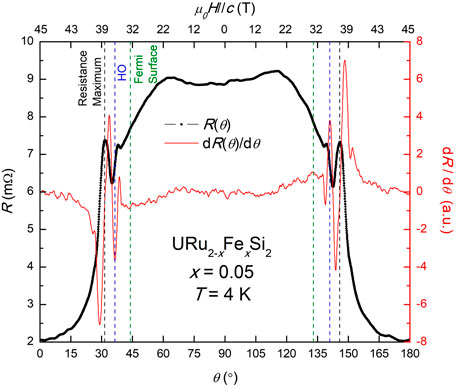
FIGURE 4. Single R vs. θ curve (black) for x = 0.05 at T = 4 K with its angular derivative dR/dθ as an overlay (red). Sharp features in the derivative data at specific values of θ can be converted to H//c (top x-axis). This reduction of H and θ into H//c shows that these features actually correspond to phase transitions which were previously mapped out by Ran et al. (2017).

The features, identified by sharp peaks in dR/dθ, were plotted in phase diagrams for all T and H, for several x, with no guidance from prior studies. The phase diagrams constructed from these data are shown in Figure 5. The newly constructed phase diagrams bear a remarkable resemblance to the phase diagrams explored by Ran et al. (2017) shown in Figure 6, suggesting that, like in URu₂Si₂, the T vs. H phase diagrams for URu_2−xFe_xSi₂ are strictly dependent on H//c and exhibit no angle-dependent behavior. Overlap in the T vs. H//c phase diagram confirms no angle-dependence of the phases by noting that an increase in field magnitude H does not change the anisotropy. This is particularly insightful, as one would expect that perhaps the LMAFM phase of URu_2−xFe_xSi₂ could be perturbed by a large magnetic field being applied along the ab-plane. Instead, it is shown that, no matter the Fe concentration of URu_2−xFe_xSi₂, all field-induced phase transitions in this system happen along the c-axis and may be closely intertwined. Further, the inability to show a difference in the anisotropy between the HO and LMAFM phases using this measurement technique represents a significant finding.

FIGURE 5

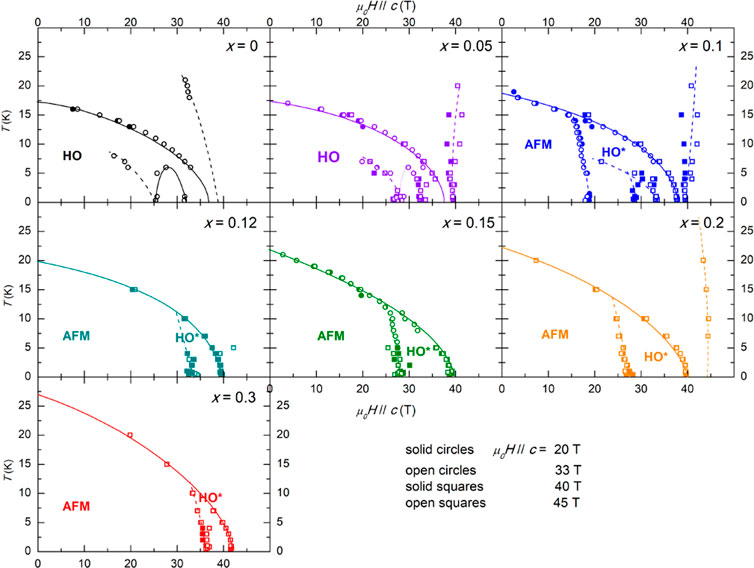
FIGURE 5. A T vs. H//c phase diagram is constructed for several x using extracted values of θ(T, H) from various R(θ) curves using the method shown in Figure 4. The phase diagrams presented show a striking similarity to what was mapped out by Ran et al. (2017) suggesting that various phases in URu_2−xFe_xSi₂ only depend on H on the c-axis.

FIGURE 6

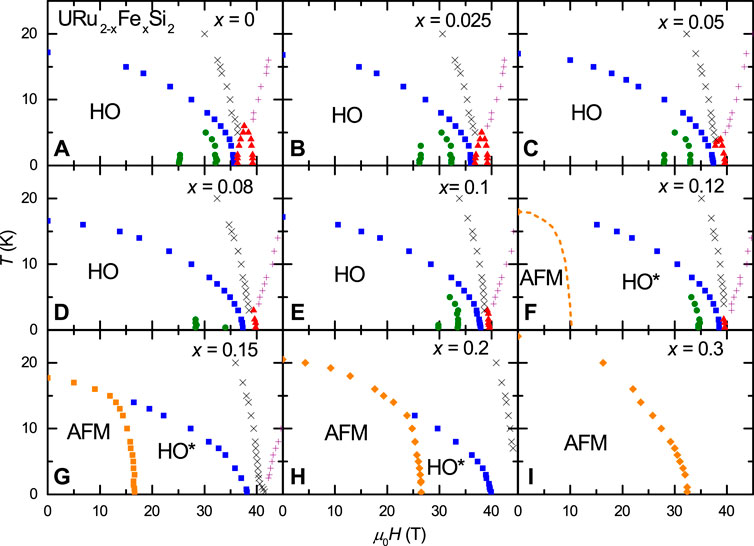
FIGURE 6. The T vs. H phase diagrams for URu₂-xFe_xSi₂ (A–I) in Ran et al. (2017). H was applied along the c-axis.

In the phase diagram we show, for samples with Fe concentration x ≥ 0.1, that the LMAFM ground state undergoes a transition into re-entrant HO as H is increased, which is expected from prior studies on re-entrant HO in URu_2−xFe_xSi₂ (Ran et al., 2017). Since our measurements yielded a large amount of data in a T vs. H, x phase diagram, and the reduction of θ and H into H//c provides redundancies in this phase diagram, we can thoroughly explore the phase boundary between LMAFM and HO*. One such visualization is presented in Figure 7, where, for x = 0.1 at μ₀H = 33 T, we can show the signatures of the LMAFM and HO* transitions in dR/dθ. As expected, at higher temperatures, there is only a LMAFM phase before making a transition into the PM state, but as the temperature is lowered, a transition to HO* is observed at high fields.

FIGURE 7

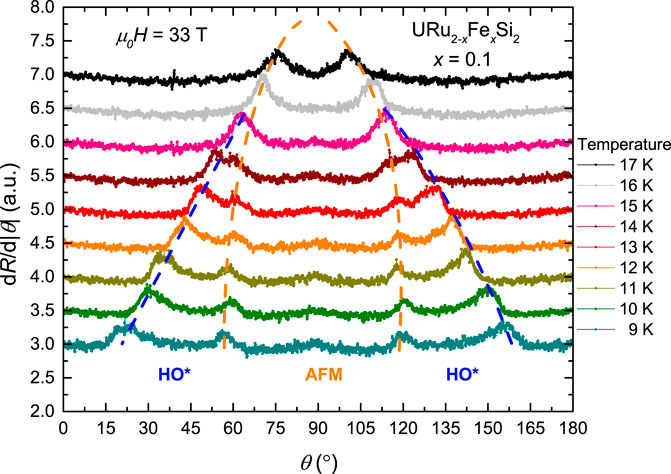
FIGURE 7. Demonstration of the LMAFM and HO* signatures in the dR/dθ data for x = 0.1 at μ₀H = 33 T as HO* develops at lower temperatures. This picture is consistent with the idea that the LMAFM phase is interrupting the larger HO phase.

The interesting behavior shown in Figure 7 is the smooth nature of the transition from the PM state to HO* or LMAFM as a function of T. The PM state boundary traces out continuously with T from the LMAFM to the HO* phases for the Fe concentrations where both phases are observed. The transition between LMAFM and HO* is very abrupt, however, and its behavior may lend insight into the nature of the LMAFM phase. A possible scenario is that the substitution of Fe is actually “interrupting” the HO phase, rather than a separate re-entrant HO phase “growing out” of the LMAFM ground state. This idea may be supported by characterizing the shape of the outer boundary of the phase diagrams: HO for x = 0 and 0.05, LMAFM + HO* for x = 0.1, 0.12, 0.15, 0.2, and 0.3, and LMAFM for presumably x > 0.3. This characterization is presented in Figure 8, much like what was done by Ran et al. (2017) where the phase boundaries are normalized to one at the T and H endpoints, such that the qualitative behavior of the boundary can be observed and characterized according to Eq. 1. Using this fitting of the curvature, the data can be organized into essentially 3 clusters. The first cluster, where fitting parameter n = 1.8, is the same as observed by Ran et al. (2017), and applies to x = 0, 0.05, and 0.1 where HO is the dominant phase. The second cluster represents a flatter boundary where LMAFM is the dominant phase and n = 1.45 for x = 0.15, 0.2, and 0.3. This suppression of n may be related to the fact that T₀ increases significantly between x = 0.1 and 0.15. The final cluster is a more general grouping where this boundary was mapped out to where H₀ = H_LMAFM, instead of the usual H_HO. As discussed, the LMAFM phase cuts into the HO phase rather abruptly, yielding a phase boundary which is not smooth and therefore cannot be cleanly described by Eq. 1.

${\left(T/T_0\right)}^n+{\left(H/H_0\right)}^n=1(1)$

FIGURE 8

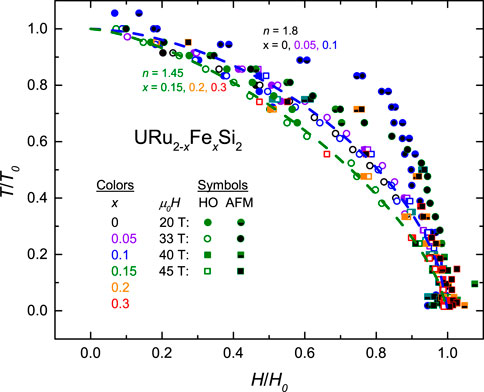
FIGURE 8. Normalized T/T₀ vs. H/H₀ phase boundary for both LMAFM and HO(*) phases for all x and H. Curvature of this boundary is analyzed using Eq. 1, showing two clusters for the HO(*) phases: n = 1.8 for x = 0, 0.05, and 0.1 where HO is the dominant phase and n = 1.45 for x = 0.15, 0.2, and 0.3 where LMAFM is the dominant phase. As expected, the AFM boundary does not fit into this smooth curve due to the abrupt nature of the transition into HO*.

Further visualization of the behavior of the LMAFM/HO* to PM state boundary is provided in the 3D phase diagram shown in Figure 9, with the color of the data points corresponding to the various phases in URu_2−xFe_xSi₂. For comparison, the 3D phase diagram of URu_2−xFe_xSi₂ with magnetic fields applied parallel to the c-axis is presented in Figure 10. The transition from the PM state to LMAFM/HO* follows a continuous boundary with x, whereas the HO* to LMAFM boundary cuts in abruptly. This LMAFM to HO* transition “wedge” in the 3D phase diagram cuts in at an angle such that it eventually converges with the HO* boundary at x ≥ 0.3, but near x = 0.1, this boundary rapidly disappears as the URu_2−xFe_xSi₂ system moves into a HO-only regime. The 3D phase diagram reflects the possible explanation that Fe-substitution leads to an abrupt interruption of the HO phase via introduction of the LMAFM phase at μ₀H = 0 T. As Fe continues to be substituted into URu_2−xFe_xSi₂, the space in the phase diagram previously occupied by the HO phase is quickly replaced by LMAFM. One can picture a tall “dome” of LMAFM growing into a large “bubble” of HO in this 3D phase diagram. While no angular-dependent behavior is clearly observed in this phase diagram, the data collected from our measurements show a more detailed picture of the interaction between the LMAFM and HO phases in the URu_2−xFe_xSi₂ system.

FIGURE 9

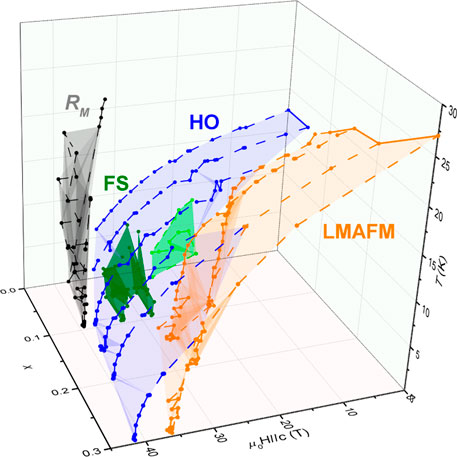
FIGURE 9. 3D phase diagram combining all of the 2D phase diagrams from Figure 5, except for x = 0.12, due to likely discrepancy in the Fe concentration. In 3D space, the joint LMAFM-HO boundary appears to curve smoothly in a consistent matter, with the only variation being where the AFM phase cuts in at higher T based on x.

FIGURE 10

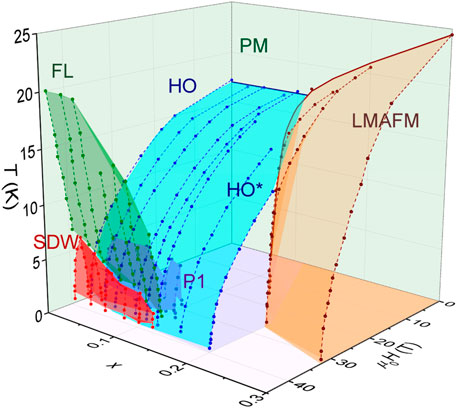
FIGURE 10. 3D phase diagram from Ran et al. (2017). SDW: spin density wave; P1: possible new phase in low field; FL: field induced recovery of the normal metallic phase. Note the similarities especially in PM-HO-LMAFM phase boundaries between this figure with H//c and Figure 9.

3 Concluding remarks

We performed a series of measurements on URu_2−xFe_xSi₂ in order to characterize the T vs. H phase diagram as a function of θ, the angle between H and the c-axis, in order to better understand the nature of the HO and LMAFM phases, which was initially explored in URu₂Si₂ (Kanchanavatee et al., 2017). We show that these two studies actually probe the same phenomenon, which is that the phases in the T vs. H phase diagram are strictly dependent on the magnetic field applied along the c-axis, H//c. The reduction of these two seemingly independent problems to a single phenomenon was allowed when magnetoresistance R(H) curves at various θ for fixed T could be understood as being independent of θ by converting H into its c-axis projection, such that H//c = H cos θ. This characterization of the phases as a function of H//c was initially provided by Scheerer et al. (Scheerer et al., 2012) and then separately verified with our own measurements on URu₂Si₂. By applying this technique to the study of the substitutional system in URu_2−xFe_xSi₂, the phase diagram behavior could be reduced by converting values of θ at fixed H to an equivalent H//c. After construction of the 2D phase diagram for several x, we found recovery of the original 2D phase diagrams constructed by Ran et al. (2017), where H was strictly parallel to c, suggesting that, despite large H being applied along the ab-plane, potentially causing perturbations to the T vs. H phase diagram, the various phases in URu_2−xFe_xSi₂ are resistant to magnetic fields H//ab, and that phenomena such as HO, LMAFM, Fermi surface reconstruction, SDW, etc. are all exclusively dependent on H//c. This suggests that these various phases are closely related to one another, with H//c, and not H or θ, being a non-thermal tuning parameter. Further, we can continue to observe the x-dependence of these various phases in URu_2−xFe_xSi₂ to provide further insight into their nature, particularly the HO and LMAFM order. By studying the characteristics of the various phase boundaries, we can actually imagine an explanation of the relationship between HO, HO*, and LMAFM, where LMAFM interrupts the continuous HO phase, as a potential alternative explanation to the idea that re-entrant HO* grows out of LMAFM at high fields. Thus, this study potentially offers two new insights into URu_2−xFe_xSi₂: 1) not only in the parent compound URu₂Si₂ are the phases solely dependent on H//c (Scheerer et al., 2012), but this is also true for URu_2−xFe_xSi₂ despite the introduction of LMAFM via Fe-substitution (this also provides a clear explanation for the observed “symmetry” in R(θ) for μ₀H ≥ 0 T) (Kanchanavatee et al., 2017) and 2) we provide an additional visualization of the T vs. H phase diagram for several values of x, allowing for an alternative explanation of the interaction between HO and LMAFM induced via Fe-substitution.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://osf.io/puy6j/?view_only=953de102b00f49adaa7e184aedd91ecb, OSF.

Author contributions

NP and MBM designed research; NP, SR, DG, YL, JS, FFB, REB, and MBM performed research; NP, YD, and MBM wrote the paper; all coauthors provided input into the paper.

Funding

Research at UCSD was supported by the NNSA through the U.S. DOE under Grant No. DE-NA0002909 (measurements in high magnetic fields), by the DOE under Grant No. DEFG02-04-ER46105 (single crystal growth), and by the NSF under Grant No. DMR 1206553 (sample characterization). A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation Cooperative Agreement Nos. DMR-1157490 and DMR-1644779, the State of Florida and the Department of Energy (DOE). JS acknowledges support from the DOE BES program Science at 100 T, which permitted the design and construction of much of the specialised equipment used in the high-field studies. This research was also funded in part by a QuantEmX grant from ICAM and the Gordon and Betty Moore Foundation through Grant No. GBMF5305 to Hector D. Rosales.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Altarawneh, M. M., Harrison, N., Sebastian, S. E., Balicas, L., Tobash, P. H., Thompson, J. D., et al. (2011). Sequential spin polarization of the fermi surface pockets in URu₂Si₂ and its implications for the hidden order. Phys. Rev. Lett. 106, 146403. doi:10.1103/physrevlett.106.146403

PubMed Abstract | CrossRef Full Text | Google Scholar

Altarawneh, M. M., Harrison, N., Li, G., Balicas, L., Tobash, P. H., Ronning, F., et al. (2012). Superconducting pairs with extreme uniaxial anisotropy in URu₂Si₂. Phys. Rev. Lett. 108, 066407. doi:10.1103/physrevlett.108.066407

PubMed Abstract | CrossRef Full Text | Google Scholar

Aoki, D., Bourdarot, F., Hassinger, E., Knebel, G., Miyake, A., Raymond, S., et al. (2010). Field re-entrant hidden-order phase under pressure in URu₂Si₂. J. Phys. Condens. Matter 22, 164205. doi:10.1088/0953-8984/22/16/164205

PubMed Abstract | CrossRef Full Text | Google Scholar

Bauer, E. D., Zapf, V. S., Ho, P.-C., Butch, N. P., Freeman, E. J., Sirvent, C., et al. (2005). Non-Fermi-liquid behavior within the ferromagnetic phase in URu₂-xRe_xSi₂. Phys. Rev. Lett. 94, 046401. doi:10.1103/physrevlett.94.046401

PubMed Abstract | CrossRef Full Text | Google Scholar

Bilbro, G. (1976). Theoretical model of superconductivity and the martensitic transformation in A15 compounds. Phys. Rev. B 14, 1887–1892. doi:10.1103/physrevb.14.1887

CrossRef Full Text | Google Scholar

Butch, N. P., and Maple, M. B. (2009). Evolution of critical scaling behavior near a ferromagnetic quantum phase transition. Phys. Rev. Lett. 103, 076404.

PubMed Abstract | CrossRef Full Text | Google Scholar

Butch, N. P., Jeffries, J. R., Chi, S., Leão, J. B., Lynn, J. W., and Maple, M. B. (2010). Antiferromagnetic critical pressure in URu₂ Si₂ under hydrostatic conditions. Phys. Rev. B 82, 060408(R). doi:10.1103/physrevb.82.060408

CrossRef Full Text | Google Scholar

Das, P., Kanchanavatee, N., Helton, J. S., Huang, K., Baumbach, R. E., Bauer, E. D., et al. (2015). Chemical pressure tuning of URu₂Si₂via isoelectronic substitution of Ru with Fe. Phys. Rev. B 91, 085122.

CrossRef Full Text | Google Scholar

de la Torre, A. L., Visani, P., Dalichaouch, Y., Lee, B., and Maple, M. B. (1992). Th-Doped URu₂Si₂: Influence of "Kondo holes" on coexisting superconductivity and magnetism. Phys. B Condens. Matter 179, 208–214. doi:10.1016/0921-4526(92)90018-n

CrossRef Full Text | Google Scholar

Fisher, R. A., Kim, S., Wu, Y., Phillips, N. E., McElfresh, M. S., Torikachvili, M. S., et al. (1990). Specific heat of URu₂Si₂: Effect of pressure and magnetic field on the magnetic and superconducting transitions. Phys. B Condens. Matter 163, 419–423. doi:10.1016/0921-4526(90)90229-n

CrossRef Full Text | Google Scholar

Gallagher, A., Chen, K.-W., Moir, C. M., Cary, S. K., Kametani, F., Kikugawa, N., et al. (2016). Unfolding the physics of URu₂Si₂ through silicon to phosphorus substitution. Nat. Commun. 7, 10712. doi:10.1038/ncomms10712

PubMed Abstract | CrossRef Full Text | Google Scholar

Harrison, N., Jaime, M., and Mydosh, J. (2003). Reentrant hidden order at a metamagnetic quantum critical end point. Phys. Rev. Lett. 90, 096402. doi:10.1103/physrevlett.90.096402

PubMed Abstract | CrossRef Full Text | Google Scholar

Hassinger, E., Knebel, G., Izawa, K., Lejay, P., Salce, B., and Flouquet, J. (2008). Temperature-pressure phase diagram of URu₂Si₂ from resistivity measurements and ac calorimetry: Hidden order and Fermi-surface nesting. Phys. Rev. B 77, 115117. doi:10.1103/physrevb.77.115117

CrossRef Full Text | Google Scholar

Hassinger, E., Knebel, G., Matsuda, T. D., Aoki, D., Taufour, V., and Flouquet, J. (2010). Similarity of the fermi surface in the hidden order state and in the antiferromagnetic state of URu₂Si₂. Phys. Rev. Lett. 105, 216409. doi:10.1103/physrevlett.105.216409

PubMed Abstract | CrossRef Full Text | Google Scholar

Jaime, M., Kim, K. H., Jorge, G., McCall, S., and Mydosh, J. A. (2002). High magnetic field studies of the hidden order transition in URu₂Si₂. Phys. Rev. Lett. 89, 287201. doi:10.1103/physrevlett.89.287201

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeffries, J. R., Butch, N. P., Yukich, B. T., and Maple, M. B. (2008). The evolution of the ordered states of single-crystal URu₂Si₂ under pressure. J. Phys. Condens. Matter 20, 095225. doi:10.1088/0953-8984/20/9/095225

CrossRef Full Text | Google Scholar

Jeffries, J. R., Butch, N. P., Yukich, B. T., and Maple, M. B. (2007). Competing ordered phases in URu₂Si₂: Hydrostatic pressure and rhenium substitution. Phys. Rev. Lett. 99, 217207. doi:10.1103/physrevlett.99.217207

PubMed Abstract | CrossRef Full Text | Google Scholar

Jo, Y., Balicas, L., Capan, C., Behnia, K., Lejay, P., Flouquet, J., et al. (2007). Field-induced fermi surface reconstruction and adiabatic continuity between antiferromagnetism and the hidden-order state in URu₂Si₂. Phys. Rev. Lett. 98, 166404. doi:10.1103/physrevlett.98.166404

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanchanavatee, N., Janoschek, M., Baumbach, R. E., Hamlin, J. J., Zocco, D. A., Huang, K., et al. (2011). Twofold enhancement of the hidden-order/large-moment antiferromagnetic phase boundary in the URu2−xFexSi2 system. Phys. Rev. B 84, 245122. doi:10.1103/physrevb.84.245122

CrossRef Full Text | Google Scholar

Kanchanavatee, N., Janoschek, M., Huang, K., White, B. D., Riseborough, P. S., Balatsky, A. V., et al. (2017). Emergence of higher order rotational symmetry in the hidden order phase of URu₂Si₂. Philos. Mag. 97, 144–154. doi:10.1080/14786435.2016.1235294

CrossRef Full Text | Google Scholar

Kanchanavatee, N., White, B. D., Burnett, V. W., and Maple, M. B. (2014). Enhancement of the hidden order/large moment antiferromagnetic transition temperature in the URu₂−xOs_xSi₂ system. Philos. Mag. 94, 3681–3690. doi:10.1080/14786435.2014.886022

CrossRef Full Text | Google Scholar

Kim, K. H., Harrison, N., Jaime, M., Boebinger, G. S., and Mydosh, J. A. (2003). Magnetic-field-induced quantum critical point and competing order parameters in URu₂Si₂. Phys. Rev. Lett. 91, 256401. doi:10.1103/physrevlett.91.256401

PubMed Abstract | CrossRef Full Text | Google Scholar

Kusunose, H. (2012). Magnetic exciton mediated superconductivity in the hidden-order phase of URu₂Si₂. J. Phys. Soc. Jpn. 81, 023704. doi:10.1143/jpsj.81.023704

CrossRef Full Text | Google Scholar

Machida, K. (1981). Spin density wave and superconductivity in highly anisotropic materials. J. Phys. Soc. Jpn. 50, 2195–2202. doi:10.1143/jpsj.50.2195

CrossRef Full Text | Google Scholar

Maple, M. B., Chen, J. W., Dalichaouch, Y., Kohara, T., Rossel, C., Torikachvili, M. S., et al. (1986). Partially gapped Fermi surface in the heavy-electron superconductor URu₂Si₂. Phys. Rev. Lett. 56, 185–188. doi:10.1103/physrevlett.56.185

PubMed Abstract | CrossRef Full Text | Google Scholar

McElfresh, M. W., Thompson, J. D., Willis, J. O., Maple, M. B., Kohara, T., and Torikachvili, M. S. (1987). Effect of pressure on competing electronic correlations in the heavy-electron system URu₂Si₂. Phys. Rev. B 35, 43–47. doi:10.1103/physrevb.35.43

PubMed Abstract | CrossRef Full Text | Google Scholar

Mydosh, J., Oppeneer, P. M., and Riseborough, P. (2020). Hidden order and beyond: An experimental-theoretical overview of the multifaceted behavior of URu₂Si₂. J. Phys. Condens. Matter 32, 143002. doi:10.1088/1361-648x/ab5eba

PubMed Abstract | CrossRef Full Text | Google Scholar

Mydosh, J. A., and Oppeneer, P. M. (2011). Colloquium: Hidden order, superconductivity, and magnetism: The unsolved case of URu₂Si₂. Rev. Mod. Phys. 83, 1301–1322. doi:10.1103/revmodphys.83.1301

CrossRef Full Text | Google Scholar

Mydosh, J. A., and Oppeneer, P. M. (2014). Hidden order behaviour in URu₂Si₂ (A critical review of the status of hidden order in 2014). Philos. Mag. 94, 3642–3662. doi:10.1080/14786435.2014.916428

CrossRef Full Text | Google Scholar

Ohkuni, H., Inada, Y., Tokiwa, Y., Sakurai, K., Settai, R., Honma, T., et al. (1999). Fermi surface properties and de Haas-van Alphen oscillation in both the normal and superconducting mixed states of URu₂Si₂. Philos. Mag. B 79, 1045–1077. doi:10.1080/014186399256916

CrossRef Full Text | Google Scholar

Palstra, T. T. M., Menovsky, A. A., van den Berg, J., Dirkmaat, A. J., Kes, P. H., Nieuwenhuys, G. J., et al. (1985). Superconducting and magnetic transitions in the heavy-fermion system URu₂Si₂. Phys. Rev. Lett. 55, 2727–2730. doi:10.1103/physrevlett.55.2727

PubMed Abstract | CrossRef Full Text | Google Scholar

Ran, S., Jeon, I., Pouse, N., Breindel, A. J., Kanchanavatee, N., Huang, K., et al. (2017). Phase diagram of URu₂- x Fe_x Si₂ in high magnetic fields. Proc. Natl. Acad. Sci. U.S.A. 114, 9826–9831. doi:10.1073/pnas.1710192114

PubMed Abstract | CrossRef Full Text | Google Scholar

Ran, S., Wolowiec, C. T., Jeon, I., Pouse, N., Kanchanavatee, N., White, B. D., et al. (2016). Phase diagram and thermal expansion measurements on the system URu₂−xFe_x Si₂. Proc. Natl. Acad. Sci. U.S.A. 113, 13348–13353. doi:10.1073/pnas.1616542113

PubMed Abstract | CrossRef Full Text | Google Scholar

Scheerer, G. W., Knafo, W., Aoki, D., and Flouquet, J. (2012). Angular dependence of the high-magnetic-field phase diagram of URu₂Si₂. J. Phys. Soc. Jpn. 81, SB005. doi:10.1143/jpsjs.81sb.sb005

CrossRef Full Text | Google Scholar

Scheerer, G. W., Knafo, W., Aoki, D., Nardone, M., Zitouni, A., Béard, J., et al. (2014). Fermi surface in the hidden-order state of URu₂Si₂ under intense pulsed magnetic fields up to 81 T. Phys. Rev. B 89, 165107. doi:10.1103/physrevb.89.165107

CrossRef Full Text | Google Scholar

Schlabitz, W., Baumann, J., Pollit, B., Rauchschwalbe, U., Mayer, H. M., Ahlheim, U., et al. (1986). Superconductivity and magnetic order in a strongly interacting fermi-system: URu₂Si₂. Z. Phys. B - Condens. Matter 62, 171–177. doi:10.1007/bf01323427

CrossRef Full Text | Google Scholar

Willis, X., Ding, X., Singleton, J., and Balakirev, F. F. (2020). Cryogenic goniometer for measurements in pulsed magnetic fields fabricated via additive manufacturing technique. Rev. Sci. Instrum. 91 (3), 036102.

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolowiec, C. T., Kanchanavatee, N., Huang, K., Ran, S., and Maple, M. B. (2016). Evolution of critical pressure with increasing Fe substitution in the heavy-fermion system URu₂−xFe_xSi₂. Phys. Rev. B 94, 085145. doi:10.1103/physrevb.94.085145

CrossRef Full Text | Google Scholar

Wolowiec, C. T., Kanchanavatee, N., Huang, K., Ran, S., Breindel, A. J., Pouse, N., et al. (2021). Isoelectronic perturbations to f-d-electron hybridization and the enhancement of hidden order in URu₂ Si₂. Proc. Natl. Acad. Sci. 118, e2026591118. doi:10.1073/pnas.2026591118

CrossRef Full Text | Google Scholar