The State Change Per Cycle Map: a novel system-theoretic analysis tool for periodically-driven ReRAM cells

Memristive devices are the subject of extensive studies nowadays. While the Dynamic Route Map is a powerful tool for analyzing the response of first-order memristors under DC stimuli, the development of an equivalent tool for investigating the response of these devices to AC stimuli is still an open question. Recently, Pershin and Slipko introduced a graphic method, which we name Time Average State Dynamic Route (TA-SDR), applicable to study first-order memristors subject to periodic rectangular pulse train-based stimuli. In this paper we introduce an alternative investigation tool, referred to as State Change Per Cycle Map (SCPCM), which is applicable in these very same scenarios. The novel analysis technique, inspired by the work of the French mathematician Henri Poincaré, reduces the investigation of a first-order non-autonomous continuous-time system to a simpler study of a first-order discrete-time map. A State Change Per Cycle Map defines precisely how the stimulus modulates each of the admissible device memory states over one input cycle. It is derivable either by means of numerical simulations, where a model for the ReRAM cell is available, or experimentally, in the case where the device memory state is accessible. While the predictive capability of a TA-SDR is limited to those case studies, where the AC periodic voltage signal applied across the device induces negligible changes in the respective memory state over each cycle, the conclusions drawn by analyzing a SCPCM have general validity, irrespective of the properties of the stimulus. The advantages of the novel analysis method for periodically driven ReRAM cells over the classical TA-SDR tool are highlighted through a number of case studies, some of which reveal the interesting capability of the ReRAM cell to display multiple oscillatory operating modes upon periodic stimulation via trains with a suitable number of SET and RESET pulses per period.

1 Introduction

Over the past few years, in view of a probable and inevitable impending end of the Moore era, the scientific community has been focusing with ever-growing fervor on the exploration of novel device and data processing concepts to enable sustainable progress in integrated circuit (IC) design in the years to come, especially when shrinking CMOS transistor dimensions shall no longer represent a viable option. Among the various alternatives, disruptive two-terminal nano-devices, generally called memory-resistors, or memristors (Chua, 2018) for short, in which the resistance depends upon at least one state variable, have caught the eye of the international scientific community for their potential to enable a revolutionary paradigm shift in the operating principles of computing machines (Zhang et al., 2020), which, mimicking the behavior of energy-efficient biological neural networks, may potentially outperform state-of-the-art data processing structures that suffer from the well-known limitations of classical von-Neumann architecture. With their unique capability to combine multiple functionalities within a single nanoscale physical volume, non-volatile memristors may be alternatively used to perform a calculation, including the measurement of a signal under monitoring, or to store data, which allows the hardware implementation of innovative area-, time-, and energy-efficient information management paradigms for Artificial Intelligence (AI) applications, e.g., in-memory-sensing and in-memory-computing, but cannot be run nowadays on conventional computing structures, which are fabricated purely using Complementary Metal Oxide Semiconductor (CMOS) technology.

Memristors from the non-volatile class (Ielmini and Waser, 2016) may be programmed at significantly high rates as many times as state-of-the-art high-performance data storage units, consuming very little power while switching between distinct resistance levels and retaining information encoded in some state, under zero input, for a very long time; as required in practical applications nowadays. Furthermore, while densely packed across crossbar arrays, stacked on top of standard CMOS circuitry by exploiting the natural availability of metal-insulator-metal layers along the third dimension in IC fabrication processes, they allow efficient use of the available area, endowing the resulting hybrid hardware platforms with add-on capabilities as compared to conventional technical systems. For example, non-volatile memristors enable the processing elements of standard cellular dynamic arrays to perform memory operations without the need for additional data storage units (Ascoli et al., 2021b).Interestingly, memristors may do much more. Certain resistance switching memories (Ascoli et al., 2021a), unable to store data, are attracting an increasing interest in both academia and industry for their extraordinary capability to act as sources of infinitesimal energy under suitable polarization, analogous to the ion channels in biological neuronal membranes. The adoption of these volatile memristor realizations in circuit and system design opens the opportunity to synthesize Cellular Neural Networks (CNNs) (Ascoli et al., 2022b; Ascoli et al., 2022c), mimicking closely biological systems, which may enable a better understanding of their complex bifurcation phenomena, as well as the design of ground-breaking computing machines, including spike-based computing Cellular Automata (CAs) (Pickett and Williams, 2013), which, operating according to bio-inspired principles, promise to approach the information management efficiency of the human brain. Given the potential of memristors for the electronics of the future, endowing the circuit designer’s toolkit with predictive yet simple models of non-volatile and volatile memristors, while facilitating the accessibility of the general community to their physical realizations, which would allow their usability in academic lab environments, is crucially necessary for advancement of the knowledge base, which would ultimately convince industry partners to invest massively in memristive nanotechnologies.

In parallel to modelling activities, another fundamental area of research regards the development of system-theoretic analysis techniques for exploration of the complex dynamics of these intrinsically nonlinear nano-devices. While the Dynamic Route Map¹ (DRM) (Chua, 2018) is a reference graphic tool for studying the response of first-order memristors to DC excitations, an equivalent methodology for investigating its behavior under AC stimuli is not yet available.

In (Pershin and Slipko, 2019a), Pershin and Slipko studied the time evolution of the mean value of the memory state of a non-volatile Resistive Random Access Memory (ReRAM) cell (Yang et al., 2010), manufactured at Hewlett Packard (HP) Labs, under appropriately weak AC periodic rectangular pulse-based stimulation, by applying a time averaging-based approximation (Strogatz, 2015) of its mathematical description (Strachan et al., 2013). The application of this method—see also (Pershin and Slipko, 2019b) for more details—resulted in the introduction of a powerful graphic tool, enabling to infer that the level around which the memory state, initiated from a predefined initial condition, would be found to oscillate asymptotically. Here, we coin the name Time Average State Dynamic Route (TA-SDR) for such a precious analysis tool. The time averaging methodology has been recently adopted in (Messaris et al., 2023) to study the response of the aforementioned ReRAM cell to high-frequency AC periodic stimuli, which resulted in the introduction of a new strategy for programming its memory content.

In this paper, we introduce a new valuable graphic tool, which we name State Change Per Cycle Map, SCPCM for short, inspired by the Poincaré Map technique (Ascoli et al., 2005), enabling the exploration of the response of a second-order continuous-time system, corresponding to a resistance switching memory cell with scalar state variables under periodic forcing, through the simpler study of a one-dimensional discrete-time system. The derivation of a SCPCM calls for the acquirement of a data series. Each recording, which requires the run of an experiment, in the case where accessibility to the device memory state is possible, or a numerical simulation where a reliable model for the ReRAM cell is available, quantitatively defines the change in the device memory state from a prescribed initial condition over one input cycle. Spacing the initial conditions uniformly across the admissible range and then plotting each of the recordings versus the respective initial condition, a map is finally obtained by means of a suitable interpolation method. Remarkably, each fixed point of this one-dimensional discrete-time system, i.e., the abscissa of any crossing of the graph of the SCPCM with the horizontal axis, indicating an initial condition, which the stimulus maps onto itself from cycle to cycle, corresponds to a possible oscillatory mode for the periodically driven ReRAM cell. The oscillatory solution for the device memory state is then asymptotically stable (unstable) if the slope of the graph of the SCPCM is found to be negative (positive) at the fixed point under focus.

While the predictive capability of a TA-SDR is restricted to those case studies in which the amplitude and frequency of the input signal stimulating the ReRAM cell are set in such a way to induce small changes in its memory state over each cycle², a SCPCM has general applicability, irrespective of the characteristics of the excitation signal. This paper introduces the fundamentals of the novel system-theoretic method for the investigation of first-order ReRAM cells under periodic excitation, highlighting its advantages over the standard TA-SDR graphic tool through a number of illustrative examples, some of which unveil the interesting capability of the ReRAM cell to exhibit multiple steady-state oscillatory behaviors under the application of pulse trains featuring a suitable number of pulses per cycle between its terminals.

With regard to the structure of the manuscript, a brief review of the Strachan model, capturing the nonlinear dynamics of the ReRAM cell from HP Labs, and constituting the object of the investigations in this research study, is provided in section 2. The novel system-theoretic method for exploring the response of a first-order memristor to periodic excitations is presented in section 3, which begins with a short introduction to the classical technique introduced by Pershin and Slipko for the same purpose, revolving around a time averaging-based approximation of the Strachan model. Section 4 derives the SCPCM and the TA-SDR for a number of ReRAM cell excitation scenarios, comparing their predictions, which clearly reveals the superior capability of the proposed analysis tool. Conclusions are finally drafted in section 5.

2 Memristor model

The memristor model under study was first developed by Strachan et al. (Strachan et al., 2013) in 2013 to capture the nonlinear dynamics of a ReRAM cell (Yang et al., 2010) manufactured at HP Labs and composed of a nearly stoichiometric tantalum oxide Ta₂O_5−x thin film sandwiched between two metal electrodes, one made of tantalum (Ta) and one of platinum (Pt). Strachan modelled this nano-device as a first-order voltage-controlled extended memristor (Chua, 2018) with the DAE set.

$\dot{x}=g\left(x,v\right),\text{and}(1)$

$i=G\left(x,v\right)\cdot v,(2)$

where a dot over a variable denotes its time differentiation, while v (i) stands for the voltage (current) falling between (flowing through) its terminals, whereas x represents the memory state variable, which is physically associated to the most conductive volume fraction of the Ta₂O_5−x film, being tunable, by means of stimulation, across a limited, closed range referred to as its existence domain $\mathcal{D}$ and defined as [x_min, x_max], with x_min = 0, and x_max = 1. The ODE 1) governs the time course of the memory state x, when a voltage drops across the memristor³. It is also referred to as the state equation (SE). Its right hand side, referred to as the state evolution function, here reads

$g\left(x,v\right)=g_{\text{SET}}\left(x,v\right)\cdot \text{step}\left(v\right)+g_{\text{RESET}}\left(x,v\right)\cdot \text{step}\left(-v\right).(3)$

Here, the adoption of the Heaviside function step (⋅) allows to capture the asymmetry between the SET and RESET resistance switching dynamics. In fact, with p = i ⋅ v denoting the instantaneous power dissipated in the memristor while it is subject to some excitation, the state evolution function g (x, v) reduces either to the form

$g_{\text{SET}}\left(x,v\right)=B\cdot \sinh \left(\frac{v}{{\sigma }_{\text{SET}}}\right)\cdot \exp \left(-\frac{x^2}{x_{\text{SET}}^2}\right)\cdot \exp \left(\frac{p}{{\sigma }_p}\right),(4)$

during a SET transition, i.e., for v > 0V, or to the form

$g_{\text{RESET}}\left(x,v\right)=A\cdot \sinh \left(\frac{v}{{\sigma }_{\text{RESET}}}\right)\cdot \exp \left(-\frac{x_{\text{RESET}}^2}{x^2}\right)\cdot \exp \left(\frac{1}{1+\beta \cdot p}\right),(5)$

during a RESET transition⁴, i.e., for v < 0V. Eq. 2 models the electronic transport across the nano-structure. Here G (x, v), standing for the memductance function, is expressed by

$G\left(x,v\right)=G_m\cdot x+a\cdot \exp \left(b\cdot \sqrt{|v|}\right)\cdot \left(1-x\right).(6)$

The values of the parameters in Strachan model Equations 6 and 4, and 5 (Strachan et al., 2013), as fitted to the Ta₂O_5−x memristor nano-device under focus here (Ascoli et al., 2016c), are listed in Table 1.

TABLE 1

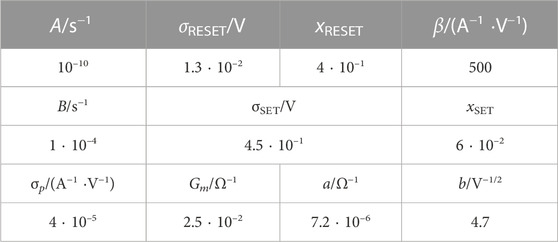
TABLE 1. Values assigned to the parameters in the Strachan DAE set (Strachan et al., 2013) so as to match the static and dynamic properties of a Ta₂O_5−x resistance switching memory from HP Labs (Ascoli et al., 2016c).

Back in 2016, powerful circuit- and system-theoretic methods applied to the Strachan model enabled to uncover a previously unknown dynamical phenomenon (Ascoli et al., 2016c) emerging in the nano-structure under both DC and AC periodic excitations, known⁵ as Fading Memory (Boyd and Chua, 1985), and explored extensively in the literature since then, e.g., in (Messaris et al., 2023) and, earlier, in (Ascoli et al., 2018) as well as in (Ascoli et al., 2022a).

3 Exploring the nonlinear dynamics of periodically-driven memristors

While an accurate graphic tool, namely, the DRM (Chua, 2018), was conceptualized for studying the response of first-order memristors to DC inputs, there is no homologous method for exploring the nonlinear behavior of these devices under AC stimuli. Under the assumption that, over each T-long cycle, a voltage signal applied across the aforementioned ReRAM cell (Yang et al., 2010) from HP Labs is null for most of the time, except within two brief temporal intervals of duration τ₊ and τ₋, where it respectively consists of a rectangular pulse of positive SET and a negative RESET amplitude, in turn V₊ and V₋, a graphic tool was recently introduced in (Pershin and Slipko, 2019a) for predicting the mean value of the oscillatory waveform of the device memory state for any given initial condition, on the basis of the Strachan model reviewed in section 2. We refer to such a tool as Time Average State Dynamic Route (TA-SDR). Unless otherwise stated, the investigations described in this manuscript assume AC periodic stimuli, which are generalized versions of the rectangular pulse train-based inputs employed in the study (Pershin and Slipko, 2019a) from Pershin and Slipko. First of all, given that the memristor is insensitive to zero input signals, each excitation waveform from the class considered in our research is never let vanish. Moreover, within each cycle, an AC periodic stimulus is here composed of P SET positive and N RESET negative rectangular pulses, as schematically depicted in Figure 1B. The total number of pulses in the input waveform per period is Q = P + N. The ith positive pulse features a height V_+,i and a width τ_+,i (i ∈ {1, 2, … , P}). The jth negative pulse features a height V_−,j and a width τ_−,j (j ∈ {1, 2, … , N}). The period of the stimulus is then T = τ_+,1 + τ_+,2 + ⋯ + τ_+,P + τ_−,1 + τ_−,2 + ⋯ + τ_−,N.

FIGURE 1

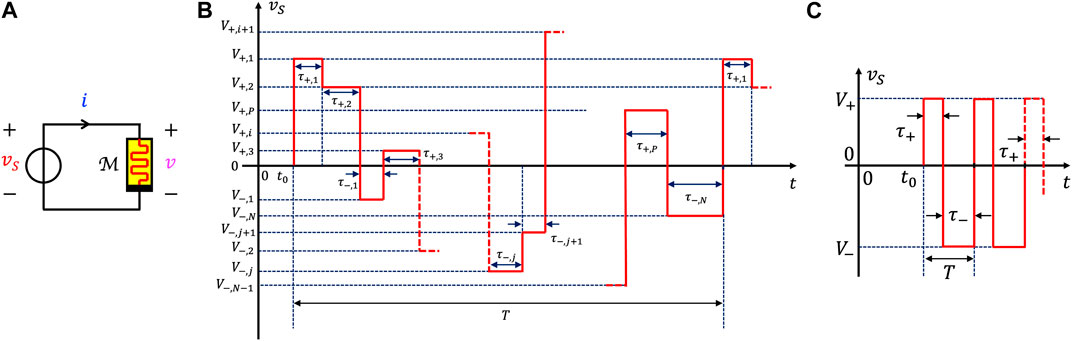
FIGURE 1. Circuit set-up (A) for the exploration of the response of the memristor $\mathcal{M}$ from HP Labs to AC periodic stimuli. (B) A rectangular pulse train-based voltage stimulus with P positive and N negative rectangular pulses per period. The characterization of an AC periodic input from this class calls for the specification of the heights and widths of the positive pulses, i.e., the collection of pairs (V_+,i, τ_+,i) for i ∈{1,2,… , P}, as well as of the heights and widths of the negative pulses, i.e., the collection of pairs (V_−,j, τ_−,j) for j ∈{1,2,… , N}. (C) Rectangular pulse train excitation signal, featuring one SET (p =1) and one RESET (N =1) pulse per cycle (Q =2), adapted from the stimulus employed by Pershin and Slipko by simply excluding from each period those intervals where no signal was applied across the ReRAM cell in the interesting study reported in (Pershin and Slipko, 2019a). A stimulus of this kind is identifiable via the tuple (V₊, τ₊, V₋, τ₋). In both plots (B) and (C), t₀ indicates an arbitrary time instant at which the voltage stimulus v_S is first applied across the nanostructure.

Consequently, any stimulus of this kind can be simply described by the associated parameter tuple (V_+,1, τ_+,1, … , V_+,P, τ_+,P, V_−,1, τ_−,1, … , V_−,N, τ_−,N). Crafting the pulse train with just two pulses per cycle, as in the study from Pershin and Slipko, the memory state of the ReRAM cell across which it is applied may be found to undergo one of at most two different locally stable limit-cycle oscillations after transients decay to zero (Pershin and Slipko, 2019a), depending upon its initial condition. On the other hand, increasing Q past 2, the periodically driven memristor may be endowed with a number of distinct oscillatory modes progressively larger than 2 at steady state, as revealed later on in section 4. Let us now briefly review the standard analysis tool proposed by Pershin and Slipko for investigating the nonlinear dynamics of periodically forced memristors.

3.1 The Time Average State Dynamic Route

By shaping the AC periodic voltage stimulus from Figure 1A in such a way that it would induce small changes in the memory state of the ReRAM cell (Messaris et al., 2023) across which it is applied over each cycle, precious insights into the response of the memristive device may be gained from the⁶ Time Average State Equation (TA-SE). Let us define the mean value of the memory state⁷ of the periodically driven ReRAM cell at any given time t ≥ t₀, with t₀ denoting the time instant at which the stimulus from Figure 1A is first applied between the device terminals, as

$\bar{x}\left(t\right)=\frac{1}{T}\cdot {\int }_{t^{\prime }=t}^{t^{\prime }=t+T}x\left(t^{\prime }\right)d{t}^{\prime }.(7)$

Employing the Leibniz integral formula, and making use of Equations 1–3, the derivative of the time average state with respect to the time may be expressed via

$\dot{\stackrel{̄}{x}}\left(t\right)=\frac{x\left(t+T\right)-x\left(t\right)}{T}=\frac{1}{T}\cdot {\int }_{t^{\prime }=t}^{t^{\prime }=t+T}g\left(x\left(t^{\prime }\right),v\left(t^{\prime }\right)\right)d{t}^{\prime }(8)$

$=\frac{1}{T}\cdot \sum _{k=1}^{k=Q}{\int }_{t^{\prime }=t_{k-1}}^{t^{\prime }=t_k}g\left(x\left(t^{\prime }\right),V_k\right)d{t}^{\prime },(9)$

where τ_k ∈ {τ_+,1, τ_+,2, … , τ_+,P, τ_−,1, τ_−,2, … , τ_−,N}, V_k ∈ {V_+,1, V_+,2, … , V_+,P, V_−,1, V_−,2, … , V_−,N}, and t_k = t_k−1 + τ_k. Now, invoking the aforementioned hypothesis on the input shape, it is assumed that replacing the memory state by its time average in each of the Q integrands from Equation 9 does not introduce a noticeable error in the resulting approximation (Messaris et al., 2023). The TA-SE is then cast in the form (Pershin and Slipko, 2019a)

$\dot{\stackrel{̄}{x}}\approx {\dot{\stackrel{̄}{x}}}_{\text{SET}}+{\dot{\stackrel{̄}{x}}}_{\text{RESET}},(10)$

where the explicit dependence of the left hand side upon the time has been omitted, while.

${\dot{\stackrel{̄}{x}}}_{\text{SET}}=\frac{1}{T}\cdot \sum _{i=1}^{i=P}{g}_{\text{SET}}\left(\bar{x},V_{+,i}\right)\cdot {\tau }_{+,i},\text{and}(11)$

${\dot{\stackrel{̄}{x}}}_{\text{RESET}}=\frac{1}{T}\cdot \sum _{j=1}^{j=N}{g}_{\text{RESET}}\left(\bar{x},V_{-,j}\right)\cdot {\tau }_{-,j}(12)$

May be respectively referred to as SET and RESET TA-SE components, given the sign invariance of the state evolution function 1) in the memristor model under focus. For Q = 2, with P = N = 1 (refer to Figure 1C), the formulas for the SET and RESET TA-SE components reduce to.

${\dot{\stackrel{̄}{x}}}_{\text{SET}}=\frac{1}{T}\cdot g_{\text{SET}}\left(\bar{x},V_{+}\right)\cdot {\tau }_{+},\text{and}(13)$

${\dot{\stackrel{̄}{x}}}_{\text{RESET}}=\frac{1}{T}\cdot g_{\text{RESET}}\left(\bar{x},V_{-}\right)\cdot {\tau }_{-}(14)$

where (V₊, τ₊) and (V₋, τ₋) are the positive SET and negative RESET pulse height-width pairs, respectively (Pershin and Slipko, 2019a). Importantly, a TA-SE is strictly associated to a given stimulus as well as to a specific model. The formulation in Equation 10 provides an approximation for the ODE, which governs the time evolution of the time average state of the ReRAM cell under a particular periodic input belonging to the class illustrated in Figure 1B, and on the basis of the Strachan model (Strachan et al., 2013). As sketched qualitatively through an exemplary blue (red) trace in Figure 2A, plotting the right hand side of Equation 11 ((12)) versus the time average state, which is constrained to assume values in the closed set $\mathcal{D}$ in all circumstances, the graph of the SET (RESET) TA-SDR component is found to lie completely within the first (fourth) quadrant. Arrows pointing toward the east (the west) are drawn on top of the blue (red) trace to indicate how the SET (RESET) dynamics induce a progressive increase (decrease) in the time average state over any τ_k-long time interval, over which a positive (negative) voltage pulse of height V_k falls across the ReRAM cell within any input cycle. Plotting the modulus of the SET (RESET) TA-SE component versus the time average state while keeping an eastward (westward) direction for the arrows on the respective locus, as depicted in Figure 2B, extracted as an illustrative example from plot a) of the same figure, is definitely more insightful. In fact, the direction of motion of the time average state from any value it can possibly have at some given time may be more easily inferred from this graph than from the visual representation from which it was derived. If, at the time of interest, the ordinate of the SET (RESET) locus is higher than the ordinate of the RESET (SET) locus at the abscissa, corresponding to the running value of the time average state, then the latter shall be subject to an increment (a decrement) thereafter. Moreover, the intersections between the SET and RESET loci in this graphical representation identify the locations of the possible equilibria for the associated TA-SE (10). A TA-SE equilibrium ${\bar{x}}_{eq}$ is asymptotically stable if and only if the time average state moves toward the east (west) to its left (right) (Ascoli et al., 2022a). If, on the other hand, the time average state moves toward the west (east) to its left (right), ${\bar{x}}_{eq}$ is unstable. As it is common in the theory of nonlinear dynamics (Strogatz, 2015), in this paper, a stable (an unstable) equilibrium is marked as a filled (hollow) circle, as shown in the exemplary illustration of Figure 2B. An alternative way to explore the dynamics of the time average state, under the application of a voltage stimulus from the class of Figure 1B across the ReRAM cell, involves plotting directly the right hand side of the TA-SE (10), which we call time average state evolution function, versus the time average state itself. This locus is in fact the Time Average State Dynamic Route (TA-SDR) associated with the AC periodic excitation under consideration. Since the TA-SE adds up the SET and RESET TA-SE components in modulus and sign, a TA-SDR is endowed with arrows pointing to the east (west) on the upper (lower) half of the $\dot{\stackrel{̄}{x}}$ versus $\bar{x}$ plane, as depicted in Figure 2C, which is derived as an exemplary case study from plot a) of the same figure. While the arrows superimposed upon a TA-SDR indicate the polarity of the change about to occur in the time average state after it attains a certain value at a given time instant, each crossing of the locus with the horizontal axis identifies an admissible equilibrium ${\bar{x}}_{eq}$ for the associated TA-SE. Here, ${\bar{x}}_{eq}$ is asymptotically stable (unstable) if the slope of the TA-SDR is negative (positive) at its location. The derivation of a TA-SDR is straightforward, as it merely requires to plot the right hand side of Equation 10. This precious graphic tool allows a quick estimate for the level around which the memory state, initially set to some predefined value x₀ ≜ x (t₀), is bound to oscillate asymptotically under the application of an AC periodic rectangular pulse train voltage stimulus across the ReRAM cell. Specifically, computing the time average state via Equation 7 for t = t₀, which requires preliminarily solving the ODE 1) over the first input cycle, i.e., across the time interval [t₀, t₀ + T], a value for ${\bar{x}}_0\triangleq \bar{x}(t_0)$ is first determined. This then allows the derivation of the initial condition for the trajectory point $(\bar{x},\dot{\stackrel{̄}{x}})$ along the relevant TA-SDR, enabling to infer the dynamics of the time average state thereafter. The next section introduces a novel system-theoretic technique, which, different to the TA-SDR analysis method, enables studying the response of the periodically driven ReRAM cell also in the case where the voltage stimulus, falling between its terminals, induces significant changes in the respective memory state over each cycle.

FIGURE 2

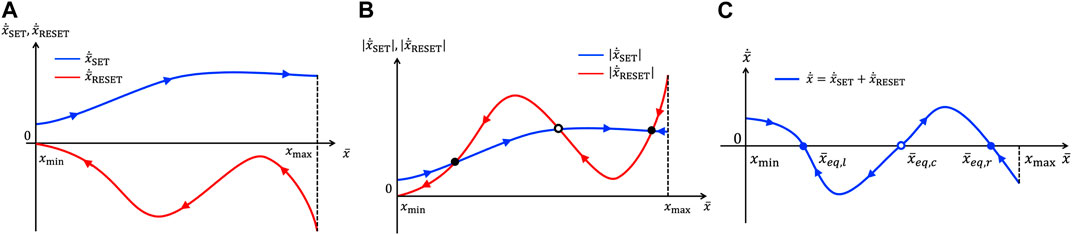
FIGURE 2. Visualization of exemplary graphs, enabling studying the response of the time average state of the ReRAM cell to the application of a specific AC periodic voltage stimulus belonging to the class illustrated in Figure 1B between its terminals, as shown in plot (a) of the same figure. Here, x_min =0 and x_max =1, in agreement with the Strachan memristor model. (A) Loci of the SET $\dot{\stackrel{̄}{x}}{|}_{\mathit{SET}}$ (blue trace) and RESET $\dot{\stackrel{̄}{x}}{|}_{\mathit{RESET}}$ (red trace) TA-SE components versus the time average state $\bar{x}$. (B) Loci of the moduli of the SET $|\dot{\stackrel{̄}{x}}{|}_{\mathit{SET}}|$ (blue trace) and RESET $|\dot{\stackrel{̄}{x}}{|}_{\mathit{RESET}}|$ (red trace) TA-SE components versus the time average state $\bar{x}$. In both plots (A) and (B), arrows along the blue (red) trace reveal how the physical mechanisms, which underlie the SET (RESET) resistance switching process, and set in as a positive (negative) pulse voltage falls of height V_k across the ReRAM cell, induce a progressive increase (decrease) in the time average state $\bar{x}$ of the device over its temporal duration of length τ_k (refer to Eq. 9 for the significance of V_k and τ_k). (C) Locus of the right hand side of the TA-SE (10) versus the time average state, denoting the TA-SDR associated with the stimulus under focus. The time average state evolves from west to east (from east to west) on the upper (lower) half of the $\dot{\stackrel{̄}{x}}$ versus $\bar{x}$ plane. In this illustrative case study, the TA-SE (10) is assumed to admit two locally stable equilibria, specifically ${\bar{x}}_l$ and ${\bar{x}}_r$ (an unstable equilibrium, namely, ${\bar{x}}_c$), as indicated by the appearance of two filled circles (of a hollow circle) at their locations (at its location), in both plots (B) and (C). This is the simplest form of local fading memory (Ascoli et al., 2016a; Ascoli et al., 2016b), also referred to as bi-stability (Ascoli et al., 2022a). It has been recently discovered in the periodically driven HP Ta₂O_5−x nano-device through a bifurcation analysis (Pershin and Slipko, 2019a) of the Strachan model (see also case study 2 in section 4.1). As anticipated earlier, the ReRAM cell may display a higher number of possible steady-state oscillatory operating modes when driven by a pulse train voltage stimulus composed of more than 2 pulses per cycle, as revealed in case study 3 from section 4.1.

3.2 The State Change Per Cycle Map: a novel system-theoretic tool for exploring the response of a ReRAM cell to any AC periodic stimulus

The novel graphic tool to be introduced and discussed shortly is inspired by the Poincaré Map Technique (Ascoli et al., 2005), a powerful analysis method from the theory of nonlinear dynamics. Let us then provide a pedagogical introduction to this precious investigation method, first introduced by the French mathematician Jules Henri Poincaré (1854–1912).

B.1 The Poincaré Map.The Poincaré Map Technique enables one to study the nonlinear dynamics of an nth-order continuous-time system through the investigation of a simpler (n − 1)-dimensional discrete-time one. This analysis tool requires a preliminary choice for an (n − 1)-dimensional sub-space, called Poincaré section, here indicated as Π.

Let us first assume the nth-order continuous-time system to be autonomous⁸. Its state vector is denoted here as $\mathbf{x}\triangleq {[x_1,x_2,\dots x_n]}^{\text{T}}\in {\mathbb{R}}^n$, where the scalar variables x₁, x₂, …, x_n span the system state space. Assume Π to be defined as $x_i=h(\tilde{\mathbf{x}})$, with i conveniently chosen from the set {1, 2, … , n} and $\tilde{\mathbf{x}}\in {\mathbb{R}}^{n-1}$ denoting a state sub-vector, which includes all components of x except for x_i. Let the ODE $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ govern the time evolution of the state vector. This equation is numerically solved from the time instant $t=t_0\in {\mathbb{R}}_{\ge 0}$ for any initial condition ${\mathbf{x}}_{\mathbf{0}}={[x_{\mathrm{1,0}},x_{\mathrm{2,0}},\dots x_{i,0},\dots x_{n,0}]}^{\text{T}}\triangleq \mathbf{x}(t_0)={[x_1(t_0),x_2(t_0),\dots x_i(t_0),\dots x_n(t_0)]}^{\text{T}}$ from a set $\{{\mathbf{x}}_{\mathbf{0}}^{(1)},{\mathbf{x}}_{\mathbf{0}}^{(2)},\dots ,{\mathbf{x}}_{\mathbf{0}}^{(J)}\}$ of large cardinality J, and, in each case, the successive returns of the state-space trajectory on the Poincaré sub-space Π are recorded in terms of the state sub-vector $\tilde{\mathbf{x}}$. In particular, denoting the kth Poincaré return point $(k\in {\mathbb{N}}_{>0})$ in the jth simulation run (j ∈ {1, 2, … , J}) as ${\tilde{\mathbf{x}}}_{\mathbf{k}}^{(j)}\triangleq {\tilde{\mathbf{x}}}^{(j)}(t_k^{(j)})$, a data series of the form ${\tilde{\mathbf{x}}}_{\mathbf{1}}^{(j)},{\tilde{\mathbf{x}}}_{\mathbf{2}}^{(j)},\dots$ may be numerically determined for the jth initial condition⁹ ${\mathbf{x}}_{\mathbf{0}}^{(j)}$. By numerical interpolation methods, it is then possible to derive an (n − 1)-dimensional discrete-time system, known as a Poincaré map, and defined as $\tilde{\mathbf{x}}(k+1)\triangleq \mathcal{P}(\tilde{\mathbf{x}}(k))$, which predicts how the vector field of the original nth-order continuous-time system transforms any return point $\tilde{\mathbf{x}}(k)$ in Π onto a subsequent return point $\tilde{\mathbf{x}}(k+1)$ in Π.

Focusing now on the class of case studies our periodically driven ReRAM cell falls into, let us consider an nth-order non-autonomous¹⁰ continuous-time system with state vector $\mathbf{x}\triangleq {[x_1,x_2,\dots ,x_n]}^{\text{T}}\in {\mathbb{R}}^n$. Assume an ODE in the form¹¹ $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},t)$ to dictate the nonlinear dynamics of the state vector. In particular, let the nth-order non-autonomous continuous-time system be driven by an AC periodic excitation, as it is in the case for the ReRAM cell under consideration in our research study. In order to derive the Poincaré map under these circumstances, samples of the state vector, which solves the nth-order non-autonomous ODE, are first recorded successively at regular T-long time intervals, where T is the period of the stimulus for each initial condition from a set $\{{\mathbf{x}}_{\mathbf{0}}^{(1)},{\mathbf{x}}_{\mathbf{0}}^{(2)},\dots ,{\mathbf{x}}_{\mathbf{0}}^{(J)}\}$ of large cardinality J. Specifically, indicating the kth $(k\in {\mathbb{N}}_{\ge 0})$ sample in the jth simulation run (j ∈ {1, 2, … , J}) as ${\mathbf{x}}_{\mathbf{k}}^{(j)}\triangleq {\mathbf{x}}^{(j)}(t_0+k\cdot T)$, a data series of the form ${\mathbf{x}}_{\mathbf{0}}^{(j)},{\mathbf{x}}_{\mathbf{1}}^{(j)},{\mathbf{x}}_{\mathbf{2}}^{(j)},\dots$ is then obtained for each of the J iterations. The application of numerical interpolation methods allows then the derivation of an n-dimensional Poincaré map $\mathbf{x}(k+1)=\mathcal{P}(\mathbf{x}(k))$, which enables the prediction of the value x (k + 1), which the state vector of the original nth-order non-autonomous continuous-time system attains from any admissible value x(k) from the respective existence domain, after a T-long time interval, due to the AC periodic excitation.

Studying a Poincaré map allows one to gain precious insights on the nonlinear dynamics of the original continuous-time system, whether the latter be autonomous or non-autonomous. Our ReRAM cell is a first-order system. The Poincaré map of a first-order system under periodic stimulation reduces to the one-dimensional form $x(k+1)=\mathcal{P}(x(k))$, where $\mathcal{P}:\mathbb{R}\to \mathbb{R}$ is a scalar function and $k\in {\mathbb{N}}_{\ge 0}$. Figure 3A shows a graph of the Poincaré map (magenta trace) associated to the very same case study explored in Figure 2. The identity map, defined as $x(k+1)={\mathcal{P}}_I(x(k))\triangleq x(k)$, is also plotted along with the map of interest in this figure (black trace). This enables one to infer the sequence of return points x (1), x (2), … of the map $x(k+1)={\mathcal{P}}_I(x(k))\triangleq x(k)$ from any initial condition x (0) by graphic inspection of the associated cobweb plot ((Ascoli et al., 2005; Strogatz, 2015)). The following remark explains how to derive a cobweb plot, which is also known as Verhulst diagram, from an arbitrary initial condition.

FIGURE 3

FIGURE 3. (A) Magenta curve: exemplary illustration of a Poincaré map $x(k+1)=\mathcal{P}(x(k))$. Black line: graph of the identity map $x(k+1)={\mathcal{P}}_I(x(k))$. The intersections between the curve and the diagonal line identify a triplet of fixed points, specifically $\{x_l^{*},x_c^{*},x_r^{*}\}$, for the one-dimensional discrete-time system. Four cobweb trajectories (Ascoli et al., 2005) are also depicted here to determine the sequence of return points from each of four distinct initial conditions (see the red, blue, green, and violet traces). Inspecting the zigzag trajectories, it is clear that in this pedagogical example, the fixed points $x_l^{*}$ and $x_r^{*}$ are asymptotically stable. Their basins of attraction are separated by the unstable fixed point $x_c^{*}$. The location of each of the two stable fixed points (of the unstable fixed point) is indicated by means of a filled (hollow) circle, in line with the typical convention in the Theory of Nonlinear Dynamics (Pershin and Slipko, 2019a). (B) Magenta curve: graph of the SCPCM corresponding to the x (k +1) versus x(k) locus from plot (a). It is constructed by plotting Δx (k +1; k), as formulated in equation 15, against x(k). A sequence of return points x (1), x (2),…of the Poincaré map from a given initial condition x (0) may be derived easily from the graph of the SCPCM. In fact, for any value of $k\in {\mathbb{N}}_{\ge 0}$, x (k +1) may be obtained by adding the ordinate Δx (k +1; k) of the point of intersection between the graph of the SCPCM and a vertical line through the point (x(k),0). This geometric method is applied here only for one of the four initial conditions from plot (a) so as to avoid clutter. Despite the SCPCM representing a discrete-time system, arrows are superimposed upon the respective curve to indicate the direction along which the return points of the associated Poincaré map progress with increments in the iteration number. The intersections between the graph of the SCPCM and the horizontal axis identify all the admissible fixed points of the associated Poincaré map. A zero crossing of the locus of Δx (k +1; k) versus x(k) indicates an asymptotically stable (an unstable) fixed point for the Poincaré map if the slope of the graph of the SCPCM is negative (positive) at its location. The direction of the arrows appearing along this curve in the neighborhood of the zero crossing are also indicative of its stability properties. In both plots (a) and (b), x_min =0 and x_max =1, while a filled (hollow) circle marker is employed to mark a stable (an unstable) fixed point of the Poincaré map under focus.

Remark 1. Given a one-dimensional Poincaré map $\mathcal{P}:\mathbb{R}\to \mathbb{R}$, its graphic representation consists of the locus of $\mathcal{P}(x(k))$ versus x(k). The graph of the identity map $x(k+1)={\mathcal{P}}_I(x(k))$ is a line forming a 45° angle with the horizontal axis as it crosses it in the origin. A cobweb plot associated with a given initial condition x (0) is a zigzag trajectory, which may be derived by iterating a sequence of steps (refer to the exemplary blue-colored trace in Figure 3A). For m = 1, where m indicates the iteration number, the following operations are carried out:

1. Find the point on the graph of the map of interest with abscissa x₀. The ordinate of this point is $x(1)\triangleq \mathcal{P}(x(0))$.

2. Draw an horizontal line from this point to the graph of the identity map. The horizontal and diagonal lines meet at the point (x (1), x (1)).

3. A vertical line drawn through this point is found to intersect the graph of the map of interest at a location with coordinates (x (1), x (2)), where $x(2)\triangleq \mathcal{P}(x(1))$.

For m ≥ 2, only steps 2 and 3 from the above list are performed in the same order as in the first iteration, with x(j) in place of x (1), and $x(j+1)\triangleq \mathcal{P}(x(j))$ in place of x (2). This iterative procedure allows one to determine the sequence of return points x (1), x (2), … of the map $x(k+1)=\mathcal{P}(x(k))$ from any initial condition x (0) of interest. Importantly, the sequence of return points can be read either on the horizontal or on the vertical axis of the x (k + 1) versus x(k) plane, in correspondence with the abscissas or the ordinates of the points where the zigzag trajectory of interest meets the diagonal line, respectively.

Given a generic map $\mathbf{x}(k+1)=\mathcal{P}(\mathbf{x}(k))$, with $\mathcal{P}:{\mathbb{R}}^n\to {\mathbb{R}}^n$, it is said to admit a fixed point at x(k) = x* if and only if ${\mathbf{x}}^{*}=\mathcal{P}({\mathbf{x}}^{*})$ (Strogatz, 2015). Thus any intersection between the graph of the map of interest and the diagonal line, denoting the locus of x (k + 1) = x(k) versus x(k), indicates a possible fixed point for the one-dimensional discrete-time system $x(k+1)=\mathcal{P}(x(k))$. Importantly, the progressive bidirectional convergence (divergence) of a sequence of Poincaré return points to a fixed point¹² ${\mathbf{x}}^{*}=\mathcal{P}({\mathbf{x}}^{*})$ (Ascoli et al., 2005), as inferable through the inspection of a couple of cobweb plots, initiated one to the left and one to the right of the fixed point itself, indicates the existence of a stable (an unstable) periodic attractor for the original continuous-time system. With reference to the pedagogical illustration of Figure 3A, both the red and the blue (both the green and the violet) cobweb plots asymptotically converge toward the leftmost (rightmost) fixed point $x_l^{*}$ $(x_r^{*})$ of the map. The stability of the two fixed points of the map reveals the emergence of bi-stability in the oscillatory response of the periodically forced first-order continuous-time system. In particular, depending upon the initial condition, the ODE of the continuous-time system shall admit one of two admissible oscillatory solutions after transients vanish. At the end of each input cycle, the value attained by the first (latter) of these steady-state solutions shall indeed be $x_l^{*}$ $(x_r^{*})$.

B.2 The State Change Per Cycle Map.In some cases, especially for stimulus parameter settings whereby the memory state undergoes negligible changes over each input cycle across its entire existence domain $\mathcal{D}$, which definitely ensures the accuracy of the approximation of the memory state with its time average in each integrand function from Equation 9, the visualization of cobweb trajectories on the x (k + 1) versus x(k) plane is difficult since the graph of the Poincaré map is found to deviate very little from the diagonal line illustrating the identity map (see for example, Figure 4D referring to case study 1 in section 4.1). We then introduce a variant of the Poincaré map, named State Change Per Cycle Map (SCPCM), revealing the net change Δx (k + 1; k) that the memory state x experiences over the (k + 1)^th input cycle, depending upon its value x(k) at the end of the kth input cycle for $k\in {\mathbb{N}}_{\ge 0}$. In fact, the SCPCM may be directly retrieved from the Poincaré map via

$\mathrm{\Delta }x\left(k+1;k\right)\triangleq x\left(k+1\right)-x\left(k\right)=\mathcal{P}\left(x\left(k\right)\right)-x\left(k\right).(15)$

FIGURE 4

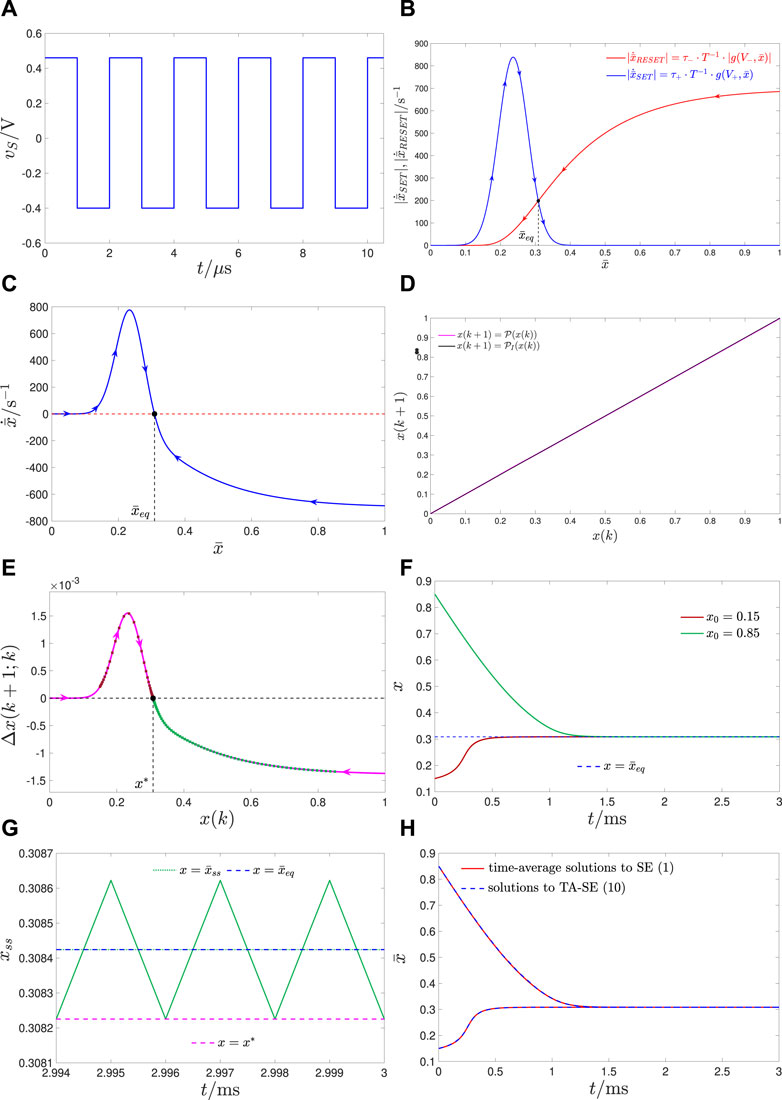
FIGURE 4. Case study 4.1.1 on the input-induced ReRAM cell mono-stability: (A) Voltage waveform generated by the AC periodic source v_S across the memristor (see Figure 1A). With reference to the stimulus parameters defined in Figure 1C, the first SET and second RESET rectangular pulses in the input pulse doublet within each cycle feature height-width pairs (V₊, τ₊)=(0.46V,1 µs) and (V₋, τ₋)=(−0.4V,1 µs), respectively. Here, the input period T is equal to 2μs and t = t₀=0s. (B) Blue (Red) trace: graph of the SET (RESET) TA-SE component versus the time average state. As indicated by the arrows on the first (latter) trace, the SET (RESET) dynamics, active as the positive (negative) pulse stimulates the device, determine a progressive increase (decrease) in the time average state. The TA-SE (10), tailored to this input, features a single equilibrium at ${\bar{x}}_{eq}=0.3084$. The SET (RESET) TA-SE component is higher than the RESET (SET) TA-SE component to the left (right) of this equilibrium, revealing its stability, as indicated by the filled circle appearing at the crossing between the blue and the red traces, which is standard in the Theory of Nonlinear Dynamics (Strogatz, 2015). (C) Blue trace: TA-SDR associated with the stimulus in plot (a). Arrows superimposed on the blue trace point to the east (west) on the upper (lower) half plane, indicating a progressive increase (decrease) in the time average state therein. (D) Magenta trace: graph of the Poincaré map $x(k+1)=\mathcal{P}(x(k))$ of the first-order non-autonomous continuous-time DAE system (1)–(2), with g (x, v) expressed by Eqs 3, 4, and 5, G (x, v) described by equation 6, and v ≡ v_S, where v_S is illustrated in plot (A). Black trace: graph of the identity map $x(k+1)={\mathcal{P}}_I(x(k))$. In this case study, the graph of the Poincaré map is found to stretch at very close proximity to the diagonal line as it revolves around it, complicating the visualization of zigzag trajectories, which are thus omitted from plot (D). (E) Magenta trace: graph of the SCPCM associated with the input in (A). The eastward (westward) direction of the arrows appearing along the magenta trace in the upper (lower) half plane indicate a progressive increase (decrease) in the sequence of return points of the Poincaré map therein. The Poincaré map admits one globally asymptotically stable fixed point at x*=0.3082. A filled circle marks the location of this stable fixed point, as is common practice in the Theory of Nonlinear Dynamics. (F) Brown (Green) trace: solution to the SE (1) for x₀=0.15 (x₀=0.85). The ReRAM cell has fading memory under the stimulus in plot (A). The dashed horizontal blue line indicates the state value denoting the only equilibrium for the TA-SE. Sampling the state solution for x₀=0.15 (x₀=0.85) from t = t₀ at regular 10⋅ T-long time intervals, i.e., at t = t₀+ k ⋅10⋅ T, with $k\in {\mathbb{N}}_{\ge 0}$, and then plotting Δx (k +1; k) versus x(k) for each k results in the sequence of brown (green) squares, superimposed along the magenta curve of plot (C) and converging asymptotically toward the point (x*,0). (G) Zoom-in view of the green-colored waveform from plot (D) across a steady-state time interval. Here, x_ss stands for the steady-state part of the data series of the memory state x. In this example, the TA-SDR prediction for the time average state (refer to the blue line) agrees rather well with the time average of the steady-state solution to the SE (1) (see the green line in dotted line style). The absolute error between ${\bar{x}}_{ss}$ and ${\bar{x}}_{eq}$, i.e., $|{\bar{x}}_{ss}-{\bar{x}}_{eq}|$ is as low as 5.9816⋅10^–8. The magenta line indicates the location of the Poincaré map fixed point, which coincides with the value assumed by the solution to the SE (1) for any initial condition at the end of each input cycle, after the transient phase is over, providing evidence for the accuracy of the novel system-theoretic analysis tool. (H) Bottom (top) red trace: time average of the solution to the SE (1) from the initial condition x₀=0.15(0.85). The first cycle in each simulation is discarded, i.e., the respective trace is plotted only thereafter. Bottom (top) blue trace: solution to the TA-SE (10) obtained upon setting the initial condition ${\bar{x}}_0$ to the result of the computation of the time average of the solution to the ODE (1) for x₀=0.15(0.85) across the time interval [0, T].

With reference to Figure 3, the magenta trace in plot b) qualitatively depicts the locus of Δx (k + 1; k) versus x(k), which corresponds to the Poincaré map from plot a). The magenta trace shows the graph of an exemplary SCPCM, characterizing the oscillatory response of the ReRAM cell to the periodic stimulation envisaged in the pedagogical case study from Figure 2. The same information, extracted from the Poincaré map, may be retrieved from the associated SCPCM. For example, the sequence of return points x (1), x (2), …, associated with a given initial condition x (0), may be easily inferred from Equation 15, given that x (k + 1) = x(k) + Δx (k + 1; k), $k\in {\mathbb{N}}_{\ge 0}$. They lie along the horizontal axis of the plane, hosting the graph of the SCPCM. In fact, for each k value in ${\mathbb{N}}_{\ge 0}$, the (k + 1)^th return point x (k + 1) may be obtained by adding to the abscissa x(k), representing the kth return point, the ordinate Δ(k + 1; k) of the point of intersection between the graph of the SCPCM and the vertical line passing through the point (x(k), 0). For example, the abscissas of the blue squares in Figure 3B represent the return points associated with the initial condition of the blue cobweb trajectory in plot a) of the same figure.

Remark 2. A time-efficient approach to derive the graph of the SCPCM of the ReRAM cell under the application of any given AC periodic stimulus between its terminals, either experimentally, in the case where the device memory state is physically accessible, or numerically, where a predictive model for the nonlinear dynamics of the non-volatile memristor is available, envisages the following steps. Preliminarily, a set of regularly spaced values $\{x_0^{(1)},x_0^{(2)},\dots ,x_0^{(J)}\}$ for the initial condition x₀ ≡ x (t₀) for the memory state would be picked from the respective existence domain $\mathcal{D}$. For each of the specified initial conditions, the AC periodic voltage stimulus of interest would then be applied across the non-volatile memristor over a T-long time span only. At the end of the test, associated with the jth initial condition (j ∈ {1, 2, … , J}), the value $x_T^{(j)}\equiv x^{(j)}(t_0+T)$ for the memory state would be recorded, as well as the change $\mathrm{\Delta }{x}^{(j)}(T;0)\equiv x_T^{(j)}-x_0^{(j)}$ in the memory state itself over the single input cycle, which would allow plotting of the point $(x_0^{(j)},\mathrm{\Delta }{x}^{(j)}(T;0))$ on the plane, reserved for accommodating the graph of the SCPCM. Applying a suitable interpolation method to the sequence of points collected from the series of J tests, a numerical approximation for the graph of the SCPCM of interest would be finally derived. With such an approach, one could in principle rename the horizontal and vertical axes of the plane hosting the graph of the SCPCM, associated with a certain periodic stimulation of the ReRAM cell, as x₀ and Δx (T; 0), respectively.

4 Application of the theory

This section, composed of two sub-sections, shall provide strong evidence for the significance of the novel analysis tool for the investigation of the response of an arbitrary first-order ReRAM cell to AC periodic stimuli of any kind. In the first subsection 4.1, the properties of the pulse train stimulus, applied across the particular memristor under focus in this manuscript, are carefully set (Messaris et al., 2023) so as to guarantee a small change in the respective memory state per cycle, which is the conditio sine qua non, to endow the TA-SDR investigation tool with a good predictive capability. In the second subsection 4.2, scenarios where either the pulse train stimulus or a triangular wave induces non-negligible changes in the device memory state per cycle shall be investigated, revealing the general applicability of the proposed system-theoretic technique to explore the nonlinear dynamics of the periodically driven ReRAM cell.

4.1 From mono-stability to multi-stability

In the three case studies¹³ discussed in this sub-section, the pulse train stimulus shall be respectively crafted in such a way to induce mono-stability, bi-stability, and tri-stability in the oscillatory dynamics of the non-volatile memristor from HP Labs (refer to Figure 4; Figure 5; Figure 6, respectively).

FIGURE 5

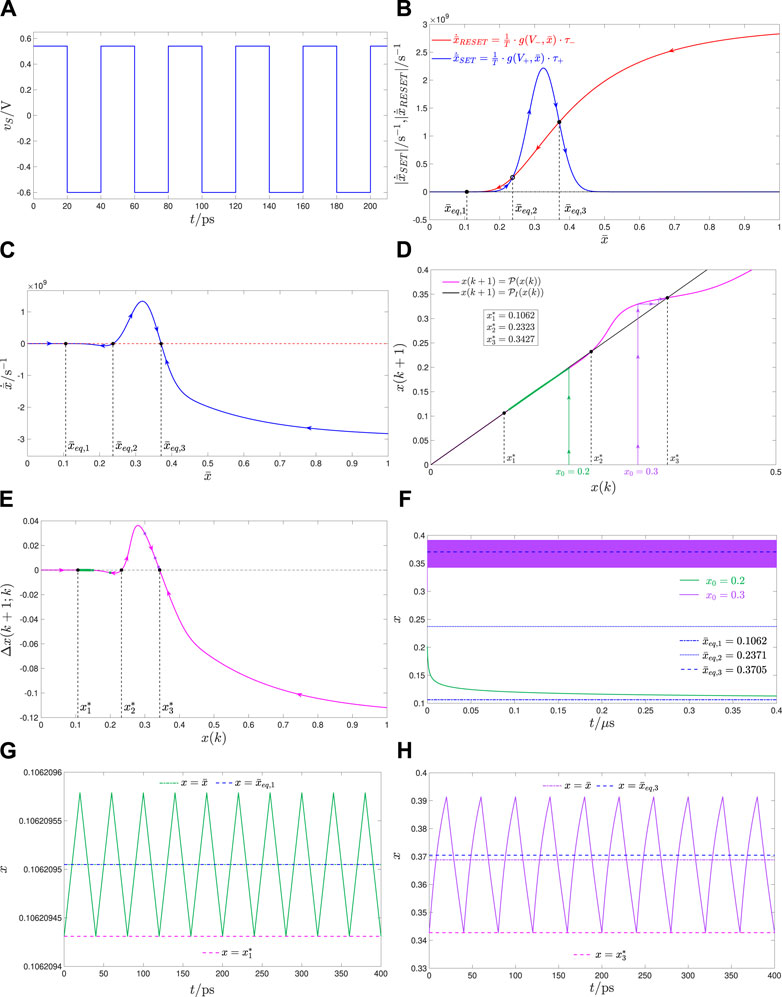
FIGURE 5. Case study 4.1.2 on the input-induced ReRAM cell bi-stability: (A) Rectangular pulse train-based voltage stimulus v_S for the ReRAM cell in the test circuit of Figure 1A. With reference to plot (c) in the same figure, the tuple defining the input signal is here (V₊, τ₊, V₋, τ₋)=(+0.54 V,20 ps,−0.6 V,20 ps). The input period is then T = τ₊+ τ₋=40 ps. Here, t = t₀=0s. (B) Blue (red) trace: locus of $|{\dot{\stackrel{̄}{x}}}_{\mathit{SET}}|$ $(|{\dot{\stackrel{̄}{x}}}_{\mathit{RESET}}|)$ versus $\bar{x}$ for the specified ReRAM cell excitation scenario. The TA-SE admits here three equilibria, specifically ${\bar{x}}_{eq,1}=0.1062$, ${\bar{x}}_{eq,2}=0.2371$, and ${\bar{x}}_{eq,3}=0.3705$. The SET (RESET) component is higher than the RESET (SET) one to the left (right) of each of the outer equilibria, revealing their stability. The opposite holds true for the inner equilibrium, which is thus unstable. The unstable equilibrium (stable equilibria) is (are) marked with a hollow circle (filled circles), according to typical convention in the Theory of Nonlinear Dynamics (Strogatz, 2015). (C) Blue trace: TA-SDR, dictating the dynamics of the time average state under the above-specified pulse train-based memristor stimulation. The slope of the TA-SDR is negative (positive) at the leftmost and rightmost TA-SE equilibria (at the inner TA-SE equilibrium), confirming their asymptotic stability (its instability). (D) Magenta trace: graph of the Poincaré map associated with the given ReRAM cell excitation scenario. Black trace: graph of the identity map. (E) Graph of the SCPCM for the periodically forced non-volatile memristor from HP Labs. Three are the fixed points of the Poincaré map, namely, $x_1^{*}=0.1062$, $x_2^{*}=0.2323$, and $x_3^{*}=0.3427$. Clearly, inspecting the slope of the magenta curve, the intermediate one (the outer ones) is unstable (are asymptotically stable), which is indicated by marking its location (their locations) using a hollow circle (using filled circles), as is common in the Theory of Nonlinear Dynamics (Strogatz, 2015). (F) Green (Violet) trace: Device memory state over time as recorded in a transient simulation of the test circuit of Figure 1A under the periodic excitation from plot (a) for x₀=0.2 (x₀=0.3). The ReRAM cell exhibits the simplest form of local fading memory, i.e., bi-stability under the effects of such a stimulus. The dash-dotted, dotted, and dashed horizontal blue lines respectively indicate the state values representing the leftmost, intermediate, and rightmost equilibria, respectively, for the TA-SE. This case study is adapted from the one illustrated in Figure 4 from (Pershin and Slipko, 2019a). While here the stimulus is simply a square wave with an offset, the excitation signal assumed by Pershin and Slipko featured a longer period, being null for most of the time except for two non-consecutive time intervals of lengths τ₊ and τ₋, accommodating a SET and a RESET pulse of heights V₊ and V₋, respectively. The green (violet) zigzag trajectory in plot (d), derived from the numerical solution with initial condition x₀=0.2 (x₀=0.3), illustrated in plot (f), reveals the monotonically decreasing (monotonically increasing) sequence of return points of the Poincaré map. As expected, the first (latter) cobweb plot approaches the leftmost (rightmost) fixed point of the map. Referring now to plot (e), the samples of the waveform of the memory state, recorded at 100⋅ T-long time intervals (at the end of each input period) from t = t₀ in the transient simulation for x₀=0.2 (x₀=0.3), may be extracted from the monotonically decreasing (monotonically increasing) abscissas of the green (violet) squares as they progress toward $(x_1^{*},0)$ $((x_3^{*},0))$. (G) ((H)) Time course of the solution to the SE (1) of the periodically forced ReRAM cell when the initial condition is set to the leftmost (rightmost) fixed point of the Poincaré map. In plot (E) ((F)), the memristor never experiences transient phenomena. Moreover, as indicated by the dashed horizontal magenta line, the leftmost (rightmost) fixed point $x_1^{*}$ ($x_3^{*}$) of the Poincaré map corresponds to the minimum of the oscillation in the memory state initiated from the same fixed point. Finally, the dashed horizontal blue line shows how the leftmost (rightmost) equilibrium ${\bar{x}}_{eq,1}$ $({\bar{x}}_{eq,3})$ of the TA-SE accurately predicts the level $\bar{x}$, around which the solution of the SE oscillates, as indicated by the dash-dotted green (violet) line. With reference to plot (g) ((h)), the absolute error between $\bar{x}$ and ${\bar{x}}_{eq,1}$ $({\bar{x}}_{eq,3})$, i.e., $|\bar{x}-{\bar{x}}_{e{q}_1}|$ $(|\bar{x}-{\bar{x}}_{eq,3}|)$, is as low as 7.3538⋅10^–14 (1.6580⋅10^–3).

FIGURE 6

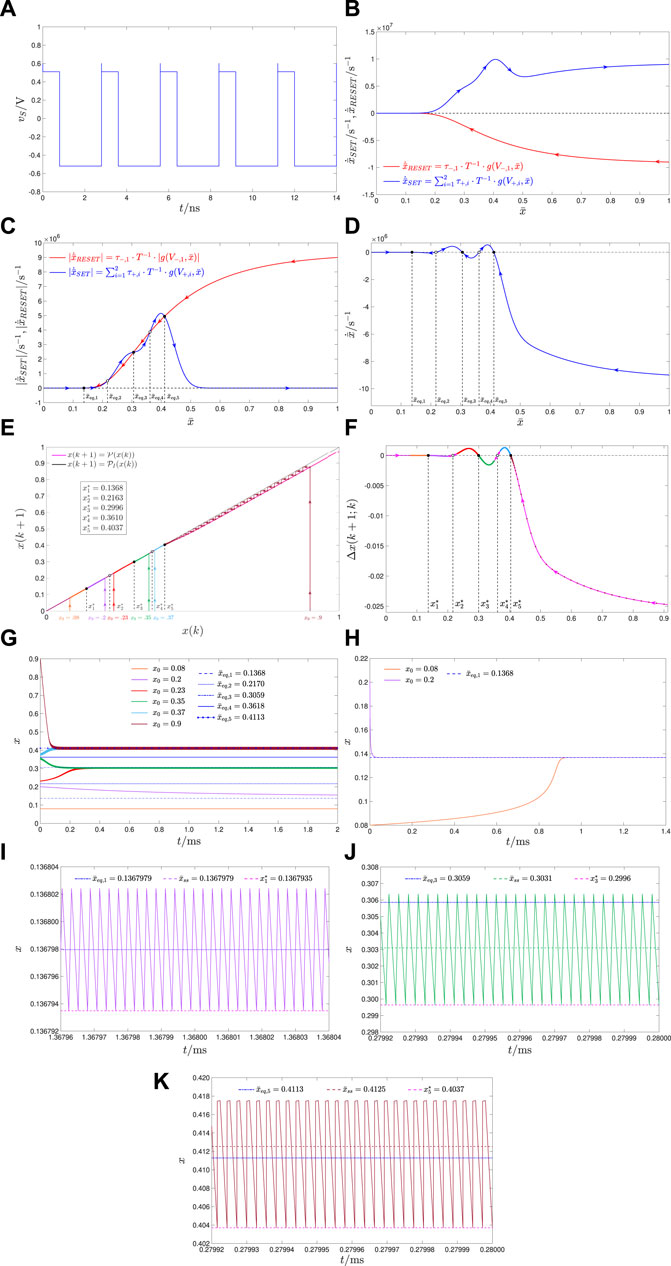
FIGURE 6. Case study 4.1.3 on the input-induced ReRAM cell tri-stability: (A) Time waveform of a pulse train-based voltage signal, which, stimulating the ReRAM cell, as illustrated in the circuit of Figure 1A, induces the emergence of a more interesting form of local fading memory, namely, tri-stability, across its physical stack. The input belongs to the class of Figure 1B, being composed of Q =3 consecutive pulses per cycle. The first, second, and third pulse in each cycle of the pulse train feature heights V_+,1=0.6V, V_+,2=0.51V, and V_−,1=−0.52V, and widths τ_+,1=3⋅10⁻¹⁹s, τ_+,2=0.8⋅10⁻⁹s, and τ_−,1=2⋅10⁻⁹s, respectively. Thus, here, p =2 and N =1. Moreover, the input period amounts to T = τ_+,1+ τ_+,2+ τ_+,3=2.8 ns, while t₀=0s. (B) Blue (Red) trace: graph of the SET (RESET) TA-SE component ${\dot{\stackrel{̄}{x}}}_{\mathit{SET}}$ $({\dot{\stackrel{̄}{x}}}_{\mathit{RESET}})$ versus the time average state $\bar{x}$. (C) Blue (Red) trace: graph of the modulus of the SET (RESET) TA-SE component $|{\dot{\stackrel{̄}{x}}}_{\mathit{SET}}|$ $(|{\dot{\stackrel{̄}{x}}}_{\mathit{RESET}}|)$ versus the time average state $\bar{x}$. The crossings between the blue and red traces reveal the existence of five equilibria for the TA-SE, specifically, ${\bar{x}}_{eq,1}=0.1368$, ${\bar{x}}_{eq,2}=0.2170$, ${\bar{x}}_{eq,3}=0.3059$, ${\bar{x}}_{eq,4}=0.3618$, and ${\bar{x}}_{eq,5}=0.4113$. Those labelled by means of odd (even) numbers are asymptotically stable (unstable). In both plots (b) and (c), arrows along the blue (red) traces point toward the east (west), indicating a progressive increase (decrease) in the time average state under the effects of the physical mechanisms, which underlie a SET (RESET) resistance switching process and set in as a positive (negative) pulse voltage fall across the ReRAM cell. (D) Blue trace: Locus of the time average state evolution function versus the time average state for the specified ReRAM cell excitation scenario. The competition between the counteractive SET and RESET dynamics shall determine either an increase or a decrease in the time average state over a given input cycle, depending upon the value, which the time average state itself holds at the end of the previous input cycle, as inferable from the direction of the arrows along the TA-SDR in its neighborhood. (E) Magenta trace: graph of the Poincaré map $x(k+1)=\mathcal{P}(x(k))$ in the case study under focus. Black trace: graph of the identity map $x(k+1)={\mathcal{P}}_I(x(k))$. The Poincaré map provides the value x (k +1), which the memory state x is bound to attain at the end of the (k +1)^th input cycle, given any possible value $x(k)\in \mathcal{D}$, which it may ever hold at the end of the kth input cycle $(k\in {\mathbb{N}}_{\ge 0})$. The two maps share the same return point at five occasions, specifically at $x_1^{*}=0.1368$, differing from ${\bar{x}}_{eq,1}$ at the sixth decimal point only, at $x_2^{*}=0.2163$, at $x_3^{*}=0.2996$, at $x_4^{*}=0.3610$, and at $x_5^{*}=0.4037$. (F) Magenta trace: Graph illustrating the net change $\mathrm{\Delta }x(k+1;k)=\mathcal{P}(x(k))-x(k)$ that the memory state x is bound to undergo over the (k +1)^th input cycle, given any value $x(k)\in \mathcal{D}$, it may ever assume at the end of the kth input cycle $(k\in {\mathbb{N}}_{\ge 0})$. (G) Numerical simulations of the Strachan DAE set under the excitation signal from plot (A), uncovering the progressive approach of the memory state x toward one of three admissible oscillatory waveforms, depending upon the initial condition. In the jth simulation run, the initial condition x₀ for the device memory state x is set to the jth value $x_0^{(j)}$ in the set {0.08,0.2,0.23,0.35,0.37,0.9} (j ∈{1,2,3,4,5,6}). The jth color from the set {orange, violet, red, green, cyan, brown} is assigned to the trace, which is initiated from the jth initial condition (j ∈{1,2,3,4,5,6}). While the solutions from the last four initial conditions in the aforementioned set attain the steady state well before the end of the 2μs-long simulation, this is not the case for the other two solutions, whose transient behaviors are much longer, as may be evinced from plot (H), illustrating their asymptotic convergence to a common oscillation. The cobweb plots, extracted from the solutions initiated from the last four initial conditions in plot (G) and from the solutions initiated from the first two initial conditions in plot (H), are illustrated using the aforementioned color convention in plot (E), revealing the stability (instability) of the Poincaré map fixed points labelled via odd (even) numbers. For j ∈{1,2,3,4} (j ∈5,6), the sequence of Poincaré return points from the jth initial condition may be read from the abscissas of the squares, which are laid over the graph of the SCPCM in plot (F), feature the same color as the associated DAE set solution in plot (G) ((H)), and show the discrete-time evolution of the trajectory point (x^(j)(k), Δx^(j) (k +1; k) for each $k\in {\mathbb{N}}_{\ge 0}$. (I), and (J) ((K)): Zoom-in view of the DAE set solutions (solution) initiated in turn from the second and fourth (initiated from the sixth) initial condition from the earlier-specified set, as illustrated respectively through a violet and green trace in plot (G)) (as illustrated through a brown trace in plot (G), over an 80μs-long steady-state time interval. The absolute error between the mean value of the state solution from plot (I) (J), and (K) and the first, third, and fifth TA-SE equilibrium, respectively, is in turn as low as 9.9632⋅10^–11, 2.7604⋅10^–3, and 1.2362⋅10^–3. The first, third, and fifth map fixed point match accurately the minimum of the oscillation from plot (I), (J), and (K), respectively.

Remark 3. Remarkably, as shown in the last figure, a more elaborate variant of the pulse train adopted in the study from Pershin and Slipko in (Pershin and Slipko, 2019a) allows one to endow the ReRAM cell with tri-stability. A systematic method enabling one to induce the emergence of a predefined number of oscillatory dynamical phenomena in the nano-device under pulse train stimulation, including an interesting discussion on potential applications, is about to appear shortly in (Ascoli et al., 2023).

4.2 On the general applicability of the SCPCM analysis tool

In the examples to follow, the stimulus applied across the ReRAM cell induces major changes in its memory state over each cycle. In these circumstances, the time averaging-based approximation of the Strachan model loses reliability, and, consequently, the predictions of the standard TA-SDR analysis tool are either prone to error (refer to the case study illustrated in Figure 7) or completely wrong (see the case studies in Figure 8; Figure 9). On the other hand, as revealed in Figures 7–9, the SCPCM investigation tool enables accurate estimation of both the number and the stability properties of the possible oscillatory modes for the periodically driven non-volatile memristor, irrespective of the input characteristics. Last but not least, and very importantly, the SCPCM tool is also applicable in scenarios where the ReRAM cell is stimulated via AC periodic stimuli other than the pulse trains considered so far, as demonstrated in the final case study illustrated in Figure 10, which provides further evidence for the superior performance of the novel system-theoretic technique over the standard TA-SDR method.

FIGURE 7

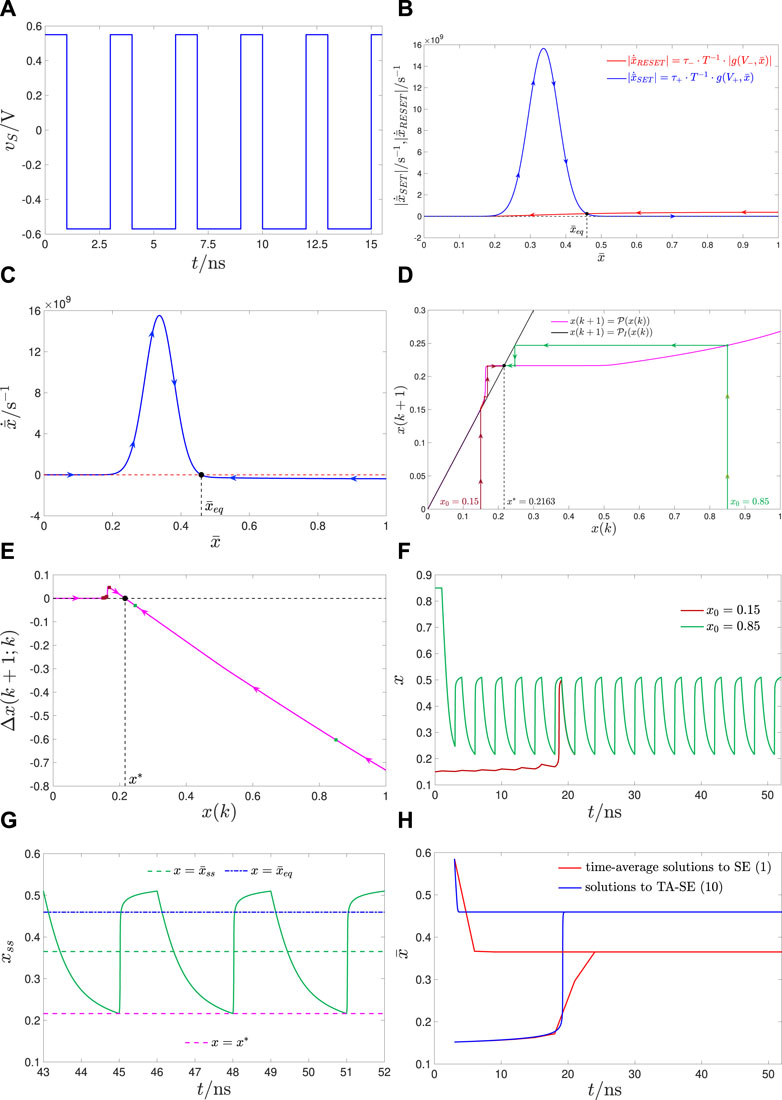
FIGURE 7. Case study 4.2.1 on the SCPCM accuracy in predicting the asymptotic memristor response upon large state excursions per input cycle: (A) Time course of the voltage signal v_S, acting as an AC periodic stimulus for the ReRAM cell in the circuit of Figure 1A. The first SET and second RESET pulses, which, as sketched in plot (c) from the same figure, compose the excitation waveform in each cycle, of duration T = τ₊+ τ₋=3ns, have height-width pairs (V₊, τ₊)=(0.55V,1ns) and (V₋, τ₋)=(−0.57V,2ns), respectively. Here, t₀=0s. (B) Blue (Red) trace: locus of $|{\dot{\stackrel{̄}{x}}}_{\mathit{SET}}|$ $(|{\dot{\stackrel{̄}{x}}}_{\mathit{RESET}}|)$ versus $\bar{x}$ for the input from plot (a). Here, the TA-SE (10) admits a globally asymptotically stable equilibrium at ${\bar{x}}_{eq}=0.4596$. (C) Blue trace: TA-SDR associated with the above-specified ReRAM cell excitation scenario. (D) Magenta trace: graph of the Poincaré map $x(k+1)=\mathcal{P}(x(k))$ of the memristive system upon excitation via the AC periodic voltage signal from plot (a). Black line: plot of the identity map $x(k+1)={\mathcal{P}}_I(x(k))$. The Poincaré map admits here a globally asymptotically stable fixed point at x*=0.2163. (E) Magenta trace: graph of the SCPCM corresponding to the Poincaré map. (F) Brown (Green) trace: time waveform of the solution to the SE (1) for x₀=0.15 (x₀=0.85), revealing the emergence of global input-induced history erase effects (Ascoli et al., 2016c) across the ReRAM cell. The green (brown) cobweb plots in plot (d) show the sequence of samples of the SE solution with initial condition x₀=0.15 (x₀=0.85) at regular T-long time intervals from t = t₀. The series of brown (green) squares, lying along the magenta-colored graph of the SCPCM from plot (e), is obtained upon recording the state value at the end of each period from the beginning of the transient simulation, where x₀ is set to 0.15(0.85). (G) Close-up view of the time course of the memory state initiated from 0.85 over a steady-state time interval. The top green line in dashed line style, indicating the time average of the steady-state solution x_ss to the SE, is rather distant from the blue line, showing the TA-SE equilibrium x_eq. In fact, for the input parameter setting in this case study, approximating the state with its time average within each integrand from Eq. 9 introduces a non-negligible error. The absolute error between ${\bar{x}}_{ss}$ and x_eq is in fact as large as 9.4408⋅10^–2. On the other hand, as shown by the magenta line, the Poincaré map fixed point corresponds to the value attained by the memory state, irrespective of the initial condition, at the end of each input period after transients decay to zero, demonstrating the infallibility of the SCPCM analysis method. (H) Bottom (Top) red trace: Time average of the solution to the SE (1) for x₀=0.15 (x₀=0.85). The traces are shown from the end of the first input cycle. Bottom (Top) blue trace: solution to the TA-SE (10), resulting from choosing as initial condition ${\bar{x}}_0$ the time average of the solution to the ODE (1) from the initial condition x₀=0.15 (x₀=0.85) across the first input period. Clearly, comparing this simulation result to its counterpart in case study 4.1.1—refer to Figure 4H—here, the time averaging method is not as reliable as in the earlier example.

FIGURE 8

FIGURE 8. Case study 4.2.2 on the SCPCM accuracy in predicting the number (here, 1) of admissible and stable memristor oscillatory modes upon large state excursions per input cycle: (A) Time waveform of the AC periodic voltage signal applied across the ReRAM cell in the test circuit of Figure 1A. With reference to plot (C) from the same figure, v_S is unequivocally identified through the tuple (V₊, τ₊, V₋, τ₋)=(0.52 V,15⋅10⁻³s,−0.58 V,2⋅10⁻³s). The input period is T = τ₊+ τ₋=17⋅10⁻³s. Once again, t₀=0s. (B) Blue trace: TA-SDR associated with the pulse train-based stimulus from plot (A). The TA-SE (10) admits here three equilibria, of which the outer ones, specifically ${\bar{x}}_{eq,1}=0.1237$ and ${\bar{x}}_{eq,3}=0.3212$, are locally stable, while the intermediate one, i.e., ${\bar{x}}_{eq,2}=0.2249$, is unstable. Here, the TA-SDR tool is unable to predict the monostable oscillatory dynamics of the periodically driven ReRAM cell. (C) Magenta trace: Graph of the Poincaré map for the case study under consideration. Black trace: graph of the identity map. Here, the Poincaré map features one globally asymptotically stable fixed point at x*=0.0862. (D) Magenta trace: Graph of the SCPCM extracted from the Poincaré map. (E) Brown (Green) trace: Time course of the memory state of the non-volatile memristor driven by the pulse train depicted in plot (A) from the first (second) initial condition x₀ in the set {0.04,0.6}. Clearly, the input from this example may determine very large changes in the memory state per cycle. The only fixed point x* of the Poincaré map matches the value attained by either of the two solutions at the end of each cycle after transients decay to zero. A brown (green)-colored cobweb plot, showing the discrete-time evolution of the Poincaré return points from x₀=0.04 (x₀=0.6), as extracted from the respective state solution in plot (E), is shown in plot (C). In either case, the sequence of return points of the Poincaré map converges rather quickly to its globally asymptotically stable fixed point x*. A brown (green) square is marked along the magenta curve in plot (D) at the abscissa, corresponding to the sample of the state solution initiated in plot (E) from x₀=0.04 (x₀=0.6) at the end of each input cycle, from the very beginning of the corresponding numerical simulation. (F) Bottom (Top) red trace: Time average of the solution to the ODE (1) from the initial condition x₀=0.04 (x₀=0.6). The traces are displayed from the end of the first input cycle. Bottom (Top) blue trace: solution to the TA-SE (10), resulting from setting the initial condition ${\bar{x}}_0$ to the time average of the solution to the ODE 1 for x₀=0.04 (x₀=0.6) across the time interval [0, T].

FIGURE 9

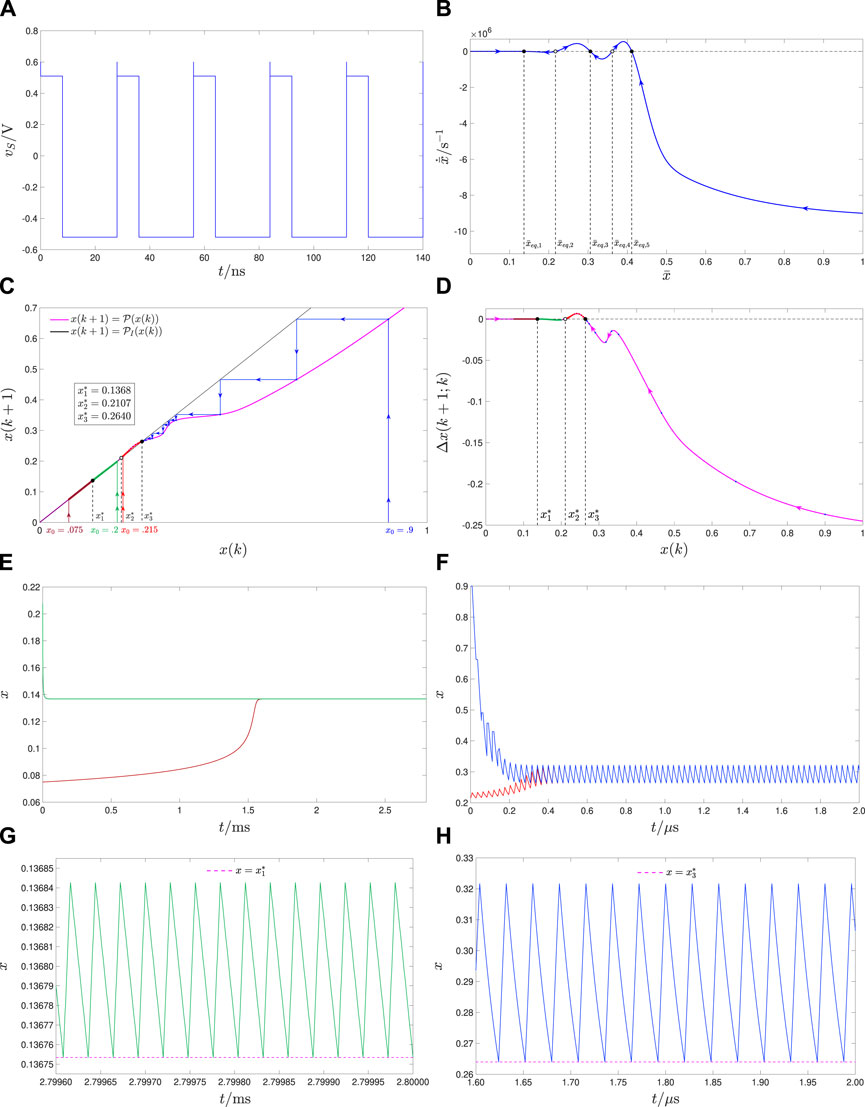
FIGURE 9. Case study 4.2.3 on the SCPCM accuracy in predicting the number (here, 2) of admissible and stable memristor oscillatory modes upon large state excursions per input cycle: (A) Time evolution of the pulse train-based voltage signal, which stimulates the ReRAM cell in the circuit from Figure 1A. With reference to plot (B) from the same figure, three are the pulses, which the train accommodates over each cycle, i.e., Q =3 here. The height-width pairs of the pulses are (V_+,1, τ_+,1)=(0.6 V,3⋅10^–18 s) (V_+,2, τ_+,2)=(0.51 V,8⋅10^–9 s), and (V_−,1, τ_−,1)=(−0.52 V,20⋅10^–9 s) (thus p =2, and N =1). The input period is then T = τ_+,1+ τ_+,2+ τ_−,1=28⋅10⁻⁹s, whereas t₀=0s. (B) Blue trace: TA-SDR of the memristive system in the periodic stimulation scenario illustrated in plot (A). In this example, five are the equilibria of the TA-SE (10), namely, ${\bar{x}}_{eq,1}=0.1368$, ${\bar{x}}_{eq,2}=0.2170$, ${\bar{x}}_{eq,3}=0.3059$, ${\bar{x}}_{eq,4}=0.3618$, and ${\bar{x}}_{eq,5}=0.4113$, of which those labelled by means of odd (even) numbers are locally asymptotically stable (unstable). Here, the time averaging method predicts the existence of three possible oscillatory modes for the periodically driven ReRAM cell, which, however, truly exhibits a bistable oscillatory response to the earlier specified pulse stimulus. (C) Magenta trace: locus of $x(k+1)=\mathcal{P}(x(k))$ versus x(k) for the case study under focus. The fixed points of the Poincaré map are $x_1^{*}=0.1368$, $x_2^{*}=0.2107$, and $x_3^{*}=0.2640$, of which the outer ones (the intermediate one) are locally asymptotically stable (is unstable). (D) Magenta trace: graph of the SCPCM associated with the Poincaré map. (E) Brown (Green) trace: state solution of the ODE (1), employing the state evolution function reported in (3), from the initial condition x₀=0.075 (x₀=0.2). The stepwise approach of the Poincaré return point from the first (latter) initial condition toward $x_1^{*}$ is illustrated by the brown (green) zigzag trajectory in plot (C). The monotonically increasing (monotonically decreasing) abscissas of the brown (green) squares lying along the locus of Δx (k +1; k) versus x(k) in plot (D) correspond to the sequence of samples extracted from the ODE solution initiated from x₀=0.075 (x₀=0.2) at regular one-cycle-long time intervals from t = t₀. (F) Red (Blue) trace: solution to the Strachan state equation from the initial condition x₀=0.215 (x₀=0.9). The red (blue) zigzag trajectory in plot (c) reveals the progressive convergence of the sequence of Poincaré return points from the first (latter) initial condition toward $x_3^{*}$. The whole sequence of Poincaré return points from x₀=0.215 (x₀=0.9) can also be read from the monotonically increasing (monotonically decreasing) abscissas of the red (blue) squares superimposed on the graph of the SCPCM in plot (D). (G) ((H)) Time waveform of the device memory state, as resulting from the numerical simulation of the Strachan ODE from the initial condition x₀=0.075 (x₀=0.215)—refer to plot (E) ((F))—over a 0.4μs-long steady-state time window. As may be inferred by inspecting plots (G) and (H), the SCPCM analysis tool accurately predicts the bistable dynamics of the periodically forced ReRAM cell, detecting the value that the respective memory state attains at the end of each input cycle after transients decay to zero, for each of its two possible oscillatory solutions.

FIGURE 10

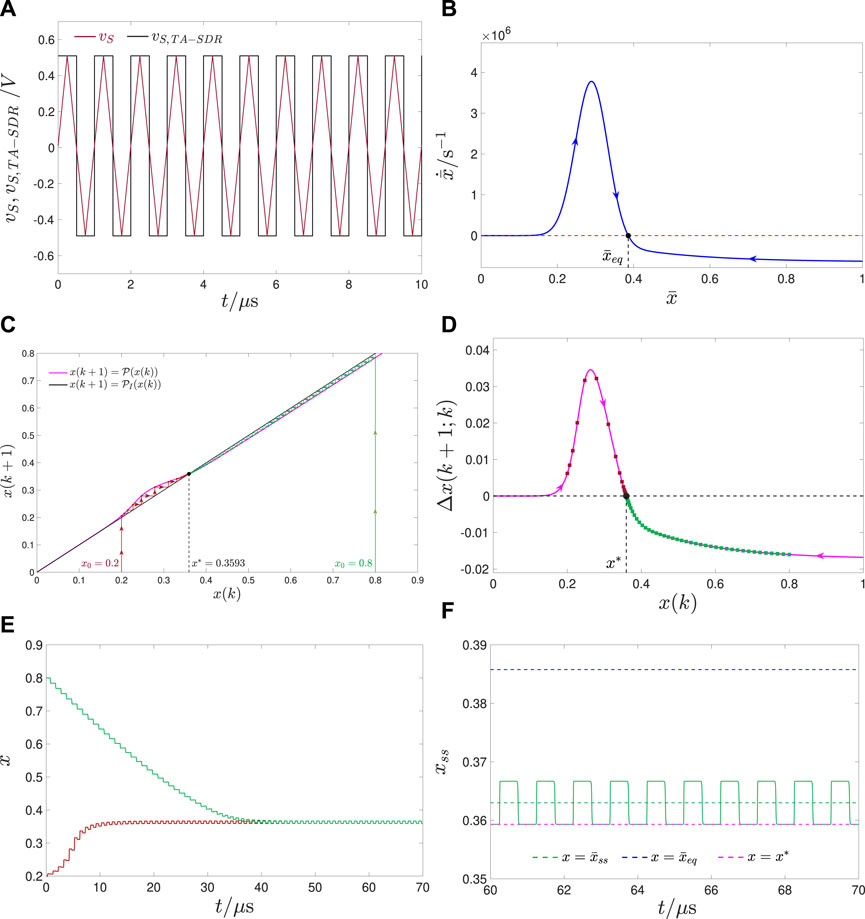
FIGURE 10. Case study 4.2.4 on the input-agnostic SCPCM predictive capability: (A) Magenta trace: AC periodic triangular voltage waveform v_S, featuring amplitude V =0.5V, offset V₀=0.01V, and period T =1⋅10⁻⁶s, and let fall across the ReRAM cell from t₀=0s in the test circuit from Figure 1A. Black trace: Pulse train-based voltage signal v_S,TA−SDR, employed as an approximation of the triangular wave stimulus, so as to enable the application of the TA-SDR analysis tool in this case study. The pulse train falls into the class depicted in Figure 1C, accommodating two pulses per cycle, specifically first a SET one of height V₊=0.51 V and width τ₊=5.1⋅10⁻⁷s, and then a RESET one of height V₋=−0.49 V and width τ₋=4.9⋅10⁻⁷s. (B) Blue trace: TA-SDR of the ReRAM cell under the assumption that the pulse train-based voltage waveform v_S,TA−SDR from plot (A) falls between its terminals. The TA-SE (10) admits one globally asymptotically stable equilibrium at ${\bar{x}}_{eq}=0.3858$. Here, the TA-SDR analysis tool properly predicts the existence of one and only one possible oscillatory operating mode for the non-autonomous memristive system. However, its estimate for the level around which the memory state is bound to revolve at steady state, irrespective of its initial condition, is rather off from the actual value. (C) Magenta trace: graph of the Poincaré map of the ReRAM cell under the specified triangular wave-based periodic stimulation. The map admits one globally asymptotically stable fixed point at x*=0.3593, where it assumes the same value as the identity map, appearing as a diagonal line that forms a 45° angle with the horizontal axis in the origin. (D) Magenta trace: locus of Δx (k +1; k) versus x(k), as extracted from the Poincaré map. (E) Brown (green) trace: Time evolution of the memory state from the initial condition x₀=0.2 (x₀=0.8) toward the unique oscillatory steady-state solution, which the SE (1) admits under the application of the earlier-defined triangular voltage waveform across the ReRAM cell. Plot (C) shows the discrete-time evolution of the Poincaré return point from the first (latter) initial condition through a brown (green) cobweb plot. The monotonically increasing (monotonically decreasing) abscissas of the brown (green) squares along the magenta trace in plot (D) correspond to the sequence of return points, which stepwise approach the only fixed point x* of the Poincaré map from the initial condition x₀=0.2 (x₀=0.8). (F) Unique steady-state oscillation in the memory state, as retrieved from the green trace in plot (E). While the fixed point x* of the Poincaré map matches the minimum of the steady-state time waveform x_ss of the memory state, the absolute error between the mean value ${\bar{x}}_{ss}$ of this very same signal and the TA-SE equilibrium ${\bar{x}}_{eq}$ is rather noticeable here, amounting to 0.0228.

4.3 Discussion

Comparing the TA-SDR and SCPCM analysis methods, the technique from Pershin and Slipko, revolving around a time averaging approximation of the device model, is trustworthy only in excitation scenarios where approximating the memory state of the periodically forced ReRAM cell with its time average in each input cycle is reasonable, whereas the tool proposed in this manuscript, relying strictly on the true un-approximated switching kinetics of the memory state, enables one to accurately explore the response of a first-order memristor to any kind of AC periodic stimulation. Provided physical measurements of the memory state of a device were feasible, the SCPCM tool more naturally lends itself to experimental validation. In fact, acquiring a TA-SDR in the lab would be cumbersome as it would preliminarily require estimation of the time derivative of the state across its existence domain under the application, across the ReRAM cell of each DC voltage from a set, including the heights of all the pulses and composing the input train over each cycle according to Equations 10 and 11, and 12. However, upon availability of a predictive device model, the derivation of a TA-SDR is computationally inexpensive, as it merely requires plotting the time average state evolution function versus the time average state, while the acquirement of a SCPCM envisages the run of a number of numerical simulations. A couple of important observations should be made at this point in regard to the examples from case studies 4.1.3 and 4.2.3. They call for the use of rather small input pulse widths. To the best of our knowledge, no instrumentation tool available nowadays would be capable of producing a pulse with a temporal width of the order of 10⁻¹⁹s in a practical experiment. As a result, future research efforts shall be devoted to the development of a strategy that allows increasing the minimum input pulse width without jeopardizing the device response of interest. Perhaps some adaptation of the simple experimental set-up shown in Figure 1A shall allow us to resolve the issue; however, its design might take a long time and is reserved for a future publication. It is important to remark, however, the theoretical relevance of these two examples, granted that the Strachan model is capable of predicting the nonlinear dynamics of the HP Ta₂O_5−x nano-device with high accuracy, as demonstrated in the seminal work (Ascoli et al., 2016c) in the past. In fact, as established by the TA-SE (10), each pulse contributes to the device time average kinetics as an additive term, appearing on the right hand side of the same equation and consisting of the product between the ratio between its time duration and the input period and the value of the time average state evolution function, evaluated at the voltage level and corresponding to the pulse amplitude, as shown in (11) and 12 for the SET and RESET cases, respectively. Therefore, even if a pulse has a rather short temporal width, it may still have a significant impact on the device time average dynamics because this is also affected by the range of values assumed by the time average state evolution function for the DC level corresponding to the pulse amplitude across the domain of existence of the device state (for the Strachan model, such a range can span several orders of magnitudes and its upper bound may be as high as 10³⁵s⁻¹ for a voltage level of just 0.7V, as shown in Fig. 15a) from (Demirkol et al., 2022)). On the basis of these observations, were it possible 1 day in the near future to avail of instrumentation tools capable to generate pulses of temporal widths on the order of 10⁻¹⁹s, the theoretically sound predictions from examples 4.1.3 and 4.2.3 could be experimentally tested. Furthermore, it is fair and worthy to mention that the unique opportunity offered by the analysis technique from Pershin and Slipko to decompose the time average state evolution function into SET and RESET components, allows the development of a system-theoretic procedure, enabling the setting of number, heights, and widths of the pulses within each period of a train stimulus so as to endow the ReRAM cell with as many locally stable steady-state oscillatory modes as desired, as discussed in (Ascoli et al., 2023). Here, the SCPCM tool can be used for verification purposes, so as to validate the theoretical predictions drawn from the TA-SDR analysis. Finally, with an outlook on other research works planned in our agenda, the evaluation of the transient dynamics of a non-volatile memristor ((Slipko and Pershin, 2019; Slipko and Pershin, 2021)) toward the respective asymptotic behavior in response to a given stimulus is worthy of consideration, especially in view of an in-depth evaluation of the practical feasibility of a potential exploitation of its peculiar features, including, in relation to the work presented in this manuscript, its global and local fading memory properties.

5 Conclusion

While the response of a first-order ReRAM cell may be completely characterized by means of a standard Dynamic Route Map analysis (Ascoli et al., 2022a), no homologous tool has ever been introduced for exploring the nonlinear dynamics of a memristive nanodevice of this kind under any AC excitation. In order to fill this gap in the literature, Pershin and Slipko (Pershin and Slipko, 2019a) recently proposed a new insightful method, which revolves around a time averaging-based approximation of the mathematical description of a first-order memristive device, and is applicable in scenarios where the memristive device itself is driven by pulse train-based stimuli (refer to (Pershin and Slipko, 2019b) for more insights). As shown in (Pershin and Slipko, 2019a), when applied to the predictive model (Strachan et al., 2013) of a first-order ReRAM cell from Hewlett Packard (HP) Labs, this method, which we call Time Average State Dynamic Route, enables one to infer the time evolution of the mean value of the device memory state under the assumption that the pulse train-based voltage stimulus, falling across the non-volatile memristor, induces small changes in the memory state itself over each cycle. In order for such an assumption to hold true, the amplitudes of the pulses included over each cycle in the waveform of the AC periodic stimulus, as well as the input frequency, must be carefully chosen, as thoroughly explained in (Messaris et al., 2023). A ReRAM cell is typically excited by pulse trains; therefore, the Time Average State Dynamic Route enables us to investigate its behavior for a very important class of case studies. However, this tool is not rigorously applicable to studying the device response to other AC periodic excitations. Motivated by the necessity to derive a more general analysis method for periodically driven ReRAM cells, this manuscript introduces a novel system-theoretic tool, referred to as State Change Per Cycle Map, which is inspired by the Poincaré Map technique, and is applicable in all case studies where an arbitrarily shaped AC periodic signal stimulates a first-order device of this kind. The new tool enables one to infer the change that the device memory state undergoes during one complete cycle of the stimulus from any of its admissible values. In particular, it allows us to determine the number and stability properties of all the possible oscillatory modes of the periodically driven nano-device, which is effectively a second-order autonomous continuous-time system, through the investigation of a simpler one-dimensional discrete-time one (Ascoli et al., 2005). Light is shed on the significance and general applicability of the proposed system-theoretic tool through the analysis of a number of illustrative case studies. The State Change Per Cycle Map technique could be employed to explore a time- and energy-efficient approach to program a ReRAM cell. An in-depth study of this kind could allow the synthesis of a look-up table, which would provide the most appropriate characteristics of a suitable AC periodic stimulus for programming a ReRAM cell from a given initial state into a desired final one within the shortest time and at the lowest possible energy cost. Last but not least, the manuscript reveals, for the first time, how applying, across the ReRAM cell, a pulse train more elaborate than the stimulus employed in the study from Pershin and Slipko may induce the asymptotic convergence of the respective memory state toward any of a number of locally stable oscillatory waveforms larger than two, depending upon the initial condition (see (Ascoli et al., 2023) for more details). This research study contributes to laying the foundations of memristor theory, providing the research community with a new, powerful analysis tool to unlock the full potential of memristive nanotechnologies for the electronics of the future.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AA and NS conceived the theoretical framework, and wrote the manuscript. AA, NS, IM, and ASD performed the numerical simulations to validate the theory. RT, and LC supported the research work, providing precious suggestions, and constructive comments. All authors contributed to the article and approved the submitted version.

Funding

LC is supported in part by USA Air Force Office of Scientific Research (AFOSR) grant number FA 9550-18-1-0016.

Acknowledgments

The authors wish to thank the Editor and the Reviewers for the highly-professional constructive criticism, which helped us to improve considerably the manuscript relative to its original version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Referring, without loss of generality, to a voltage-controlled first-order memristor, with Differential Algebraic Equation (DAE) set (1)–(2), its DRM is a family of State Dynamic Routes (SDRs), each of which visualizes the time derivative $\dot{x}$ of the device state x versus the device state x itself under a specific DC voltage stimulus v = V (Chua, 2018). When lying in the upper (lower) half plane, a SDR is endowed with arrows, pointing eastward (westward), which reveal the progressive increase (decrease) in the memory state under a given bias input. At each state value $x=\bar{x}$, where a SDR crosses the horizontal axis with negative (positive) slope, the Ordinary Differential Equation (ODE) 1) admits an asymptotically stable (unstable) equilibrium for v = V.

²The interested reader is invited to consult (Messaris et al., 2023) for more details on the constraints to be enforced on the ReRAM stimulus for the application of the time averaging method to its mathematical description to deliver reliable predictions for the time evolution of the mean value of the respective memory state from a given initial condition.

³If v = 0, the memory state x of an analogue non-volatile memristor such as the one under consideration in this study, is motionless.

⁴The state evolution function g(x, v) in Eq. 1 is said to be sign-invariant (Chua, 2018), since it features the same sign as the voltage, falling across the memristor, irrespective of the state variable value.

⁵A system is said to have Fading Memory on a given input if it exhibits a unique asymptotic behavior, irrespective of the initial condition, as it is exposed to its stimulation. In case, on the other hand, a forced system may feature one of a set of distinct operating modes, at the end of the transient phase, depending upon the initial state, it is said to have Local Fading Memory on the respective stimulus. Input-induced fading memory effects were first discovered in a ReRAM cell from HP Labs back in 2016. As revealed more recently (Ascoli et al., 2023), under suitable stimulation the very same non-volatile memristor may experience local fading memory, endowing the ReRAM cell with an interesting multi-modal operating capability, which may be leveraged for application purposes.

⁶The TA-SE is an ODE, which predicts rather well the dynamical evolution of the time average of the state of a first-order memristor under pulse train stimulation, provided the input is shaped in such a way so as to trigger a rather slow device response over each period. Despite the fact that Pershin and Slipko did not coin a name for this ODE, they should be credited for its introduction in the bifurcation analysis of the Strachan DAE set (Strachan et al., 2013) reported in (Pershin and Slipko, 2019a). The TA-SE was recently employed in (Messaris et al., 2023) to study the response of the non-volatile memristor from HP Labs to high-frequency AC periodic excitations.

⁷For simplicity, the mean value of the memory state is referred to as time average state in the remainder of the paper.

⁸A nth-order continuous-time system is said to be autonomous if no input signal drives its dynamics, which are then only controlled by means of the initial conditions assigned to its n state variables.

⁹The sequence of time instants $\{t_1^{(j)},t_2^{(j)},\dots \}$ is monotonically increasing. If the jth initial condition is chosen on the Poincaré section Π, then $t_1^{(j)}\equiv t_0$ holds true, which implies ${\tilde{\mathbf{x}}}_{\mathbf{1}}^{(j)}\equiv {\tilde{\mathbf{x}}}_{\mathbf{0}}^{(j)}$, where ${\tilde{\mathbf{x}}}_{\mathbf{0}}^{(j)}$ includes all components of ${\mathbf{x}}_{\mathbf{0}}^{(j)}$ except for the ith one $x_{i,0}^{(j)}$.

¹⁰An nth-order continuous-time system is said to be non-autonomous if some input signal controls its dynamics.

¹¹An nth-order non-autonomous ODE of the form $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},t)$ can be converted into an equivalent (n + 1)^th-order autonomous one, combining $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},x_{n+1})$ with ${\dot{x}}_{n+1}=1$, where the time variable assumes the role of an additional state via y_n+1 ≜ t. The application of the Poincaré map technique then allows investigation of this (n + 1)^th-order autonomous continuous-time system through the simpler study of an n-dimensional discrete-time one.

¹²With f′(⋅) denoting the derivative of a function $f:\mathbb{R}\to \mathbb{R}$ with respect to its argument, the fixed point x* of a map $x(k+1)=\mathcal{P}(x(k))$ is said to be stable (unstable) if and only if $|{\mathcal{P}}^{\prime }(x(k)){|}_{x(k)=x^{*}}|<(>)1$, i.e., if the modulus of the slope of the graph of the map at the fixed point is smaller (larger) than the unitary slope of the diagonal line (Strogatz, 2015).

¹³Without loss of generality, in each of the AC periodic stimuli shown in Figures 4A, 5A, 6A, the sequence of pulses included in the train over each cycle is arranged in such a way to accommodate only one RESET pulse featuring a negative height at its very end. As a result, inspecting the behavior of the device, evolving from a certain initial condition in response to any of these excitation signals, the sample of the memory state at the end of each input period, after transients decay to zero, coincides with the minimum of the asymptotic oscillatory solution to the periodically driven continuous-time ODE 1), adapted to the Strachan state evolution function, expressed by Eqs 3, 4, and 5. In each of these ReRAM cell excitation scenarios, a stable (an unstable) fixed point x* for the relevant one-dimensional discrete-time system $x(k+1)=\mathcal{P}(x(k))$ corresponds to the minimum value of a stable (of an unstable) steady-state oscillation in the device memory state.

References

Ascoli, A., Demirkol, A. S., Tetzlaff, R., and Chua, L. O. (2022b). Edge of chaos is sine qua non for turing instability. IEEE Trans. Circuits Systems-I (TCAS-I) Regul. Pap. 69 (11), 4596–4609. doi:10.1109/tcsi.2022.3194465

CrossRef Full Text | Google Scholar

Ascoli, A., Demirkol, A. S., Tetzlaff, R., and Chua, L. O. (2022c). Edge of chaos theory resolves smale paradox. IEEE Trans. Circuits Systems-I (TCAS-I) Regul. Pap. 69 (3), 1252–1265. doi:10.1109/tcsi.2021.3133627

CrossRef Full Text | Google Scholar

Ascoli, A., Demirkol, A. S., Tetzlaff, R., Slesazeck, S., Mikolajick, T., and Chua, L. O. (2021a). On local activity and edge of chaos in a NaMLab memristor. Front. Neurosci. 15 (651452), 651452. doi:10.3389/fnins.2021.651452

PubMed Abstract | CrossRef Full Text | Google Scholar

Ascoli, A., Mahon, A., and Feely, O. (2005). Nonlinear dynamics of first- and second-order log-domain circuits. IEEE Trans. Circuits Systems-I (TCAS-I) Regul. Pap. 52 (7), 1372–1381. doi:10.1109/tcsi.2005.851715

CrossRef Full Text | Google Scholar

Ascoli, A., Menzel, S., Rana, V., Kempen, T., Messaris, I., Demirkol, A. S., et al. (2022a). A deep study of resistance switching phenomena in TaOx ReRAM cells: system-theoretic dynamic Route map analysis and experimental verification. Adv. Electron. Mater., 8 (8), 2200182. doi:10.1002/aelm.202200182

CrossRef Full Text | Google Scholar

Ascoli, A., Schmitt, N., Messaris, I., Demirkol, A. S., Tetzlaff, R., Strachan, J. P., et al. (2023). “Multistability in the response of a ReRAM cell from Hewlett packard labs to pulse train stimulation,” in IEEE trans. On circuits and systems–I: Regular papers (TCAS-I) (IEEE), in preparation.

Google Scholar

Ascoli, A., Tetzlaff, R., Chua, L. O., Strachan, J. P., and Williams, R. S. (2016c). History erase effect in a non-volatile memristor. IEEE Trans. Circuits Systems–I (TCAS–I) Regul. Pap. 63 (3), 389–400. doi:10.1109/tcsi.2016.2525043

CrossRef Full Text | Google Scholar

Ascoli, A., Tetzlaff, R., and Chua, L. O. (2016a). The first ever real bistable memristors–Part I: theoretical insights on local fading memory. IEEE Trans. Circuits Systems–II Express Briefs 63 (12), 1091–1095. doi:10.1109/tcsii.2016.2604567

CrossRef Full Text | Google Scholar

Ascoli, A., Tetzlaff, R., and Chua, L. O. (2016b). The first ever real bistable memristors–Part II: design and analysis of a local fading memory system. IEEE Trans. Circuits Systems–II Express Briefs 63 (12), 1096–1100. doi:10.1109/tcsii.2016.2613560

CrossRef Full Text | Google Scholar

Ascoli, A., Tetzlaff, R., Kang, S. M., and Chua, L. O. (2021b). System-theoretic methods for designing bio-inspired mem-computing memristor cellular nonlinear networks. Front. Nanotechnol. 3 (633026), 33. doi:10.3389/fnano.2021.633026

CrossRef Full Text | Google Scholar

Ascoli, A., Tetzlaff, R., and Menzel, S. (2018). Exploring the dynamics of real-world memristors on the basis of circuit theoretic model predictions. IEEE Circuits Syst. Mag. 18 (2), 48–76. doi:10.1109/mcas.2018.2821760

CrossRef Full Text | Google Scholar

Boyd, S., and Chua, L. O. (1985). Fading memory and the problem of approximating nonlinear operators with Volterra series. IEEE Trans. Circuits Syst. 32 (11), 1150–1161. doi:10.1109/tcs.1985.1085649

CrossRef Full Text | Google Scholar

Chua, L. O. (2018). Five non-volatile memristor enigmas solved. Appl. Phys. A 124 (563), 563. doi:10.1007/s00339-018-1971-0

CrossRef Full Text | Google Scholar

Demirkol, A. S., Ascoli, A., Messaris, I., Al Chawa, M. M., Chua, L. O., and Tetzlaff, R. (2022). A compact and continuous reformulation of the strachan TaOx memristor model with improved numerical stability. IEEE Trans. Circuits Systems-I Regul. Pap. 69 (3), 1266–1277. doi:10.1109/tcsi.2021.3132278

CrossRef Full Text | Google Scholar

Ielmini, D., and Waser, R. (2016). Resistive switching: From fundamentals of nanoionic redox processes to memristive device applications. first edition. Weinheim, Germany: Wiley VCH.

Google Scholar

Messaris, I., Ascoli, A., Demirkol, A. S., and Tetzlaff, R. (2023). High frequency response of non-volatile memristors. IEEE Trans. Circuits Systems-I (TCAS-I) Regul. Pap. 70 (2), 566–578. doi:10.1109/tcsi.2022.3219368

CrossRef Full Text | Google Scholar

Pershin, Y. V., and Slipko, V. A. (2019a). Bifurcation analysis of a TaO memristor model. J. Phys. D Appl. Phys. 52 (50), 505304. doi:10.1088/1361-6463/ab4537

CrossRef Full Text | Google Scholar

Pershin, Y. V., and Slipko, V. A. (2019b). Dynamical attractors of memristors and their networks. Europhys. Lett. (EPL) 125 (2), 20002. doi:10.1209/0295-5075/125/20002

CrossRef Full Text | Google Scholar

Pickett, M. D., and Williams, R. S. (2013). Phase transitions enable computational universality in neuristor-based cellular automata. Nanotechnology 24 (38), 384002. doi:10.1088/0957-4484/24/38/384002

PubMed Abstract | CrossRef Full Text | Google Scholar

Slipko, V. A., and Pershin, Y. V. (2021). Importance of the window function choice for the predictive modelling of memristors. Trans. Circuits Syst. II Express Briefs 68 (6), 2167–2171. doi:10.1109/tcsii.2019.2906295

CrossRef Full Text | Google Scholar

Slipko, V. A., and Pershin, Y. V. (2019). Transient dynamics of pulse-driven memristors in the presence of a stable fixed point. Phys. E Low-dimensional Syst. Nanostructures 114 (113561), 113561. doi:10.1016/j.physe.2019.113561

CrossRef Full Text | Google Scholar

Strachan, J. P., Torrezan, A. C., Miao, F., Pickett, M. D., Yang, J. J., Yi, W., et al. (2013). State dynamics and modeling of Tantalum oxide memristors. IEEE Trans. Electron Devices 60 (7), 2194–2202. doi:10.1109/ted.2013.2264476

CrossRef Full Text | Google Scholar

Strogatz, S. H. (2015). Nonlinear dynamics and chaos: With applications to physics, biology, chemistry, and engineering. second edition. Boulder, Colorado, United States: Westview Press.

Google Scholar

Yang, J. J., Zhang, M. X., Strachan, J. P., Miao, F., Pickett, M. D., Kelley, R. D., et al. (2010). High switching endurance in TaOx memristive devices. Appl. Phys. Lett. 97 (23), 232102. doi:10.1063/1.3524521

CrossRef Full Text | Google Scholar

Zhang, Y., Wang, Z., Zhu, J., Yang, Y., Rao, M., Song, W., et al. (2020). Brain-inspired computing with memristors: challenges in devices, circuits, and systems. Appl. Phys. Rev. 7 (1), 011308. doi:10.1063/1.5124027

CrossRef Full Text | Google Scholar