Electromagnetic response of disordered superconducting cavities

We present the results for the resonant frequency shift and quality factor of disordered niobium (Nb) superconducting radio-frequency cavities driven out of equilibrium by the resonant microwave field. The theory is based on the non-equilibrium theory of superconductivity for the current response to the electromagnetic field at the vacuum–metal interface. We are able to accurately predict the observed frequency shifts with a precision of order fractions of kHz over the full temperature range 0 < T ≤ T_c, including the negative frequency shift anomalies that are observed very near T_c. The origin of these anomalies is shown to be the competition between the normal metal skin depth and the London penetration depth, which diverges as $T\to T_c^{-}$. An analytical approximation to the full current response, valid for |T − T_c|≪ T_c, accounts for the negative frequency shift near T_c. The non-monotonic dependence of the quality factor on the quasiparticle scattering rate is related to the pair-breaking effect of disorder on the superfluid fraction and, thus, the London penetration depth.

1 Introduction

Superconducting radio-frequency (SRF) cavities made of niobium are a key technology for high-energy particle accelerators. Material processes such as nitrogen infusion combined with heat treatments have led to significant improvements in the cavity quality factor now of order Q ≈ 2 × 10¹¹, as well as increased accelerating gradients now approaching 50 MV/m (Grassellino et al., 2013; Grassellino et al., 2017). High-Q SRF cavities provide a novel platform as sensors for rare events, e.g., as detectors for photon–photon scattering at microwave frequencies mediated by virtual electron–positron pairs or by pseudo-scalar axions (Bogorad et al., 2019; Gao and Harnik, 2021). High-Q SRF cavities have also been proposed as exceptional resonators for quantum memory with photon lifetimes exceeding T₁ ≈ 2 sec and as quantum processors (Romanenko et al., 2020). The performance of these cavities, for both accelerator applications or as quantum devices, is sensitive to the surface screening currents and the impact of surface and bulk disorder on the current response (Gurevich and Kubo, 2017; Ngampruetikorn and Sauls, 2019; Sauls, 2022; Ueki et al., 2022). The sensitivity of the screening current to disorder is highlighted by measurements of the frequency shift of N-doped niobium (Nb) SRF cavities as a function of temperature, for four cavities with frequencies f = 0.65, 1.3, 2.6, 3.9 GHz (Bafia et al., 2021). All four cavities show a negative frequency shift confined to a narrow range of temperatures near the transition temperature T_c, followed by a rapid rise to a positive frequency shift that saturates at low temperature. The non-monotonic temperature dependence (“anomaly”) of the negative shift of the resonant frequency of the cavity just below T_c, i.e., δf = f_s(T) − f_n (T_c), for |T − T_c|≪ T_c is sensitive to surface treatment and to disorder in the region of the screening currents (Bafia et al., 2021). A similar anomaly in the frequency shift just below T_c was reported previously for Nb coupled to a tunnel-diode oscillator operating at f ≈ 10 MHz (Varmazis et al., 1975). In addition, analysis of the surface impedance data of Nb embedded in a cylindrical copper cavity (Klein et al., 1994) implies a negative shift in the resonance frequency shift at f = 60 GHz (Ueki et al., 2022). Thus, the resonance frequency of oscillators made of, or coupled to, superconducting Nb exhibits a negative shift anomaly for resonant frequencies spanning nearly four orders of magnitude, albeit in all cases with hf ≪ 2Δ(0) ≈ 3.6 k_BT_c. Nevertheless, the temperature of the maximum negative shift and the magnitude of the negative frequency shift depend on both frequency, ω, and disorder, the latter parametrized by the quasiparticle-impurity mean scattering time, τ.

Ueki et al. (2022) developed the theory for the complex surface impedance Z_s = R_s + iX_s and its connection to the resonant frequency and quality factor of SRF cavities based on Slater’s approach to solving Maxwell’s equations for enclosed electromagnetic cavities (Slater, 1946) in terms of surface and volume responses of the cavity wall and dielectric medium within the cavity, which, in our case, is N-doped superconducting Nb for the cavity wall and vacuum for the dielectric medium.

In this report, we derive an equation for the complex eigenfrequency for the lowest transverse magnetic (TM) mode of a cylindrical RF cavity including the penetration of the EM field and its confinement by the normal and superconducting currents in the vicinity of the vacuum–metal interface. The current response is obtained from the Keldysh formulation of the quasiclassical theory of superconductivity (Rainer and Sauls, 1994). The resulting eigenvalue equation is straightforward to solve numerically, as well as analytically in certain limits. From the complex eigenvalue equation, we calculate both the quality factor, Q, and the frequency shift, δf, of the cavity as a function of cavity geometry, fundamental frequency, ω, temperature, T, and material properties of the superconductor such as T_c and scattering rate from the disorder potential, 1/τ. Here, we report the results based on the low-field linear response limit for the screening current at microwave frequencies. The main results are as follows: 1) the eigenvalue equation for the fundamental mode of an SRF cavity based on our theory of the superconducting state of disordered Nb (Zarea et al., 2022), 2) theoretical results for δf as a function of temperature for disordered Nb and the quantitative comparison with experimental results reported for an N-doped Nb SRF cavity, 3) an approximate analytical result for the non-monotonic, negative frequency shift “anomaly” that is a characteristic of sufficiently disordered SRF cavities for temperatures very close to T_c, and 4) non-monotonic dependence of Q as a function of the mean quasiparticle-impurity scattering rate, 1/τ, with a maximum near τ ∼ ℏ/2πk_BT_c, i.e., the pair formation timescale.

2 Current response of an SRF cavity

SRF cavities are open quantum systems in which photons in a single mode are coupled to the environment of a superconducting metal, normal electrons, Cooper pairs, phonons, embedded impurities, and two-level defects, which confines the photons within the cavity for relatively long timescales, T₁ ≃ 1 s, for Nb SRF cavities with f ≃GHz and Q ≃ 10¹¹. The penetration of the EM field into the superconductor also shifts the resonant frequency of the cavity by δf ∼ 0.1 − 50 kHz. It is possible to predict the magnitude and the variations of the resonant frequency and quality factor of Nb-based SRF cavities with remarkable precision.

We first solve Maxwell’s equations for the EM field with the constitutive equation for the screening current response to a transverse EM field within the superconductor.

$\mathbf{\text{J}}\left(\mathbf{\text{r}},t\right)=-\frac{c}{4\pi }{\int }_{-\infty }^{t}d{t}^{\prime }K\left(t-t^{\prime }\right)\mathbf{\text{A}}\left(\mathbf{\text{r}},t^{\prime }\right),(1)$

where K (t − t′) = 0 for t − t′ < 0 is the retarded response function. For the analysis in this report, we assume there is sufficient disorder that the current response to A(r,t) can be evaluated in the local limit. Thus, the Ampère–Maxwell equation for the EM field in the superconductor becomes

$\left(\frac{1}{c^2}{\partial }_t^2-{\nabla }^2\right)\mathbf{\text{A}}\left(\mathbf{\text{r}},t\right)=-{\int }_{-\infty }^{t}d{t}^{\prime }K\left(t-t^{\prime }\right)\mathbf{\text{A}}\left(\mathbf{\text{r}},t^{\prime }\right),(2)$

where we work in the gauge ∇ ⋅ A = 0 for a purely transverse EM field. Inside the cavity, A(r,t) satisfies the wave equation in vacuum. Thus, to obtain the full solution for the EM field in the cavity and the surface region of the cavity walls, we must solve the free-field wave equation and Eq. 2 with the boundary condition for the continuity of A and the normal derivative at the vacuum–superconductor interface. For a resonant mode of frequency ω, Eq. 2 reduces to

$\left({\nabla }^2+\frac{{\omega }^2}{c^2}-K\left(\omega \right)\right)\mathbf{\text{A}}\left(\mathbf{\text{r}},\omega \right)=0,(3)$

where K(ω) is the Fourier transform of the retarded current response function appearing in Eq. 1.

2.1 Keldysh response function

The linear response function K(q,ω) for superconductors subjected to excitation by an electromagnetic field is calculated using Keldysh’s formulation of non-equilibrium response in the quasiclassical approximation (Rainer and Sauls, 1994). The current response depends on the frequency and wavevector, ω and q, of the electromagnetic field within the metal and includes the condensate response (supercurrent) and the dissipative response of unbound quasiparticles scattered by the random potential with scattering rate, 1/τ. The other important internal timescale is the pair formation time, τ₀ ≡ ℏ/2πk_BT_c, and the corresponding ballistic pair correlation length is ξ₀ = v_fτ₀ = ℏv_f/2πk_BT_c. For pure Nb, the pair correlation length and London penetration depth are comparable, ${\xi }_0\approx {\lambda }_{{\text{L}}_0}\simeq 33\text{nm}$. However, disorder leads to a finite mean free path for quasiparticles, ℓ = v_fτ, converting ballistic motion to diffusive motion, and, thus, a reduction in the pair correlation length. Disorder is also pair breaking, particularly in the presence of screening currents, resulting in a reduction of the superfluid density, n_s. Thus, the London penetration depth, ${\lambda }_{\text{L}}\propto 1/\sqrt{n_s}$, increases due to scattering by the random potential.

For the analysis reported here, we consider the long-wavelength (“local”) limit, q ≲ 1/λ_L ≪ 1/ξ₀, for the current response, which is achieved in Nb when the mean scattering time is comparable to the pair formation time, τ ∼ τ₀. This level of disorder leads to weak suppression of T_c, a reduction in the superconducting coherence length, ξ, and an increase in the London penetration depth such that λ ≫ ξ. In this limit, the screening current is determined by the local value of the electromagnetic field, and we can set q = 0 in the current response function. The result is given by (Rainer and Sauls, 1994)

$\begin{array}{cc}\hfill K\left(\omega ;\tau ,T\right)& =\frac{\pi {\sigma }_{\text{D}}}{i{c}^2\tau }{\int }_{-\infty }^{+\infty }dϵ\left\{\tanh \left(\frac{ϵ-\omega /2}{2T}\right)\frac{1}{D_{+}^R+D_{-}^R+1/\tau }\left(\frac{{ϵ}^2+{\mathrm{\Delta }}^2-{\omega }^2/4}{D_{+}^R{D}_{-}^R}+1\right)\right.\hfill \\ \hfill & -\tanh \left(\frac{ϵ+\omega /2}{2T}\right)\frac{1}{D_{+}^A+D_{-}^A+1/\tau }\left(\frac{{ϵ}^2+{\mathrm{\Delta }}^2-{\omega }^2/4}{D_{+}^A{D}_{-}^A}+1\right)\hfill \\ \hfill & +\left.\left[\tanh \left(\frac{ϵ+\omega /2}{2T}\right)-\tanh \left(\frac{ϵ-\omega /2}{2T}\right)\right]\frac{1}{D_{+}^R+D_{-}^A+1/\tau }\left(\frac{{ϵ}^2+{\mathrm{\Delta }}^2-{\omega }^2/4}{D_{+}^R{D}_{-}^A}+1\right)\right\},\hfill \end{array}(4)$

where ${\sigma }_{\text{D}}=\frac{2}{3}{N}_f{e}^2{v}_f^2\tau =n{e}^2\tau /m^{*}$ is the Drude result for the d.c. conductivity for charge e quasiparticles, with Fermi velocity, v_f, Fermi momentum, p_f, and density of states, $N_f=\frac{3}{2}n/p_f{v}_f$, where n is the electron density and m* = p_f/v_f is the quasiparticle effective mass. The denominators in Eq. 4 are defined by

$D_{\pm }^{R/A}\equiv \sqrt{{\mathrm{\Delta }}^2-{\left(ϵ\pm \omega /2\pm i\delta \right)}^2}(5)$

and are retarded (advanced) functions defined by the analytic continuation to the real axis indicated by +i δ (−i δ) and δ → 0⁺. The response function K(ω) is directly related to the bulk microwave conductivity.

$\sigma ={\sigma }_1+i{\sigma }_2=i\frac{c^2}{4\pi \omega }K\left(\omega \right),(6)$

where σ₁ = Re σ(ω) and σ₂(ω) = Im σ(ω) are the real and imaginary parts of the a.c. conductivity, respectively. In the normal state, Δ → 0, the conductivity, σ(ω), defined by Eqs 4, 6 reduces to

${\sigma }_n\left(\omega \right)=\frac{{\sigma }_{\text{D}}}{1-i\omega \tau }.(7)$

Superconductivity leads to significant changes in the cavity resonance frequency, as well as the quality factor, that are sensitive to disorder and temperature, which we calculate to predict and analyze experimental data using Eqs 3–5 and boundary conditions for the EM field at the vacuum–metal interface.

2.2 Cylindrical cavities

SRF cavities for accelerator applications adopt the Tesla geometry, i.e., axially symmetric with an oval shape designed in part to eliminate sharp corners which are sources of field emission (Padamsee et al., 2008). Here, we consider cylindrical cavities of radius R and length L. This model is chosen in order to simply our theoretical analysis, in particular, in implementing the boundary conditions on the EM field for the lowest TM mode at the vacuum–metal interface. The theoretical results depend on the response function, the local boundary conditions on the field at the vacuum–metal interface, and an overall geometric factor, G. The latter geometric factor depends on the field distribution within the geometry of the cavity and is independent of the temperature and material properties of the cavity walls. Thus, we correct our result obtained using the TM₀₁₀ mode of the cylindrical cavity by replacing the value of G for the cylindrical cavity with the geometric factor computed for the lowest TM mode of the Tesla cavity.

For the cylindrical cavity, the lowest frequency TM resonance is the TM₀₁₀ mode with the vector potential along the cylinder axis $\mathbf{\text{A}}(\mathbf{\text{r}},\omega )=A_0{J}_0(\omega \rho /c)\widehat{\mathbf{\text{z}}}$ in the gauge ∇ ⋅ A = 0. The Fourier component of the electric field is axial, $\mathbf{\text{E}}(\mathbf{\text{r}},\omega )=(i\omega /c)A_0{J}_0(\omega \rho /c)\widehat{\mathbf{\text{z}}}$, and the magnetic field circulates azimuthally, $\mathbf{\text{B}}(\mathbf{\text{r}},\omega )=A_0(\omega /c)J_1(\omega \rho /c)\widehat{\mathit{\phi }}$. J₀(x) (J₁(x)) is the cylindrical Bessel function of order n = 0 (n = 1). The perfect conductor boundary condition, $\widehat{\mathbf{\text{n}}}\times \mathbf{\text{E}}{|}_S=0$, where $\widehat{\mathbf{\text{n}}}$ is a local unit vector normal to any point on the surface, S, determines the field distribution in the interior to the cavity and the eigenfrequency of the cavity based on the cavity geometry. In particular, we have J₀ (ωR/c) = 0 and, thus, a resonant frequency of ω = x₀₁c/R, where x₀₁ ≃ 2.405 is the first zero of J₀(x). The electric field is the maximum along the axis of the cavity and vanishes on the cylinder wall, while the magnetic field vanishes along the axis of the cavity and is maximum on the cylinder wall, $B_{\text{max}}=\mathcal{C}{A}_{0}R$, where $\mathcal{C}\equiv x_{01}{J}_1(x_{01})\simeq 1.248$. The geometric factor for a cylindrical cavity of length L and radius R reduces to (Padamsee et al., 2008)

$G=Z_0\left(\omega /c\right)\frac{{\int }_V{d}^{3}r|\mathbf{\text{B}}\left(\mathbf{\text{r}},\omega \right){|}^2}{{\int }_{S}dS|\mathbf{\text{B}}\left({\mathbf{\text{r}}}_S,\omega \right){|}^2}=Z_0\frac{x_{01}}{2}\frac{L}{L+R},(8)$

where Z₀ = 4π/c ≈ 377 Ω is the vacuum impedance.

However, for a vacuum–superconductor interface, the vector potential, and, thus, a tangential electric field as well as a tangential magnetic field, penetrates into the superconductor, but is confined to the interface within a distance of order the London penetration depth, of order λ_L ≃ 50 nm for moderately disordered Nb. The penetration of the field over distance scales of order λ_L ≪ R leads to a small shift in the resonance frequency, δω, which depends on the material properties of the superconductor via the current response function K(ω). Penetration of the electric field into the superconductor also leads to the dissipation of the microwave field by quasiparticles scattering from the interface and from the random distribution of impurities, thus limiting the quality factor, Q.

Both δω and Q are determined by an eigenvalue equation obtained from the boundary conditions on the vector potential and its derivative at the vacuum–superconductor interface. In particular, for the TM₀₁₀ mode on the vacuum side, $A(\rho )=A_0{J}_0(\frac{\omega }{c}\rho )$. However, on the superconducting side, the confinement of the field to distances of order λ_L ≪ R allows us to neglect the curvature of the interface. Thus, for ρ ≥ R, we obtain $A(\rho )=A_0^{\prime }\exp \{-\mathrm{\Lambda }(\omega )(\rho -R)\}$, where $\mathrm{\Lambda }(\omega )\equiv \sqrt{K(\omega )-{(\omega /c)}^2}$. The ratio of the two boundary conditions reduces to

$\mathrm{\Lambda }\left(\varpi \right)=\sqrt{K\left(\varpi \right)-{\left(\varpi /c\right)}^2}=\left(\frac{\varpi }{c}\right)\frac{J_1\left(\varpi R/c\right)}{J_0\left(\varpi R/c\right)},(9)$

where J₁(x) = −dJ₀(x)/dx. It should be noted that the response function is in general a complex function of ω, which is analytic in the upper half of the complex frequency plane; thus, ω → ϖ, with Im ϖ > 0. Equation 9 is the key equation for the complex eigenfrequency, ϖ, that determines the resonance frequency, the penetration depth, and the quality factor, all of which become functions of temperature, disorder, and frequency. The results reported here support and agree with our analysis of disordered SRF cavities based on Slater’s method (Ueki et al., 2022).

2.3 Field penetration and frequency shifts

Before presenting the numerical results for the frequency shift and quality factor of disordered SRF cavities, we discuss the physics underlying the dependence of the cavity resonance frequency on disorder and temperature in both the normal and superconducting states.

In the limit ωτ ≪ 1, σ_n ≃ σ_D determines the dissipation of microwave power and the penetration depth of the EM field in the normal metal. In particular, on the metallic side of the vacuum–metal interface (x > 0),

$A_n\left(x,\omega \right)=A_0\text{Re}{e}^{iq\left(\omega \right)x},(10)$

where $q(\omega )=\sqrt{i4\pi {\sigma }_{\text{D}}\omega }/c=(1+i)/\delta (\omega )$ with

$\delta \left(\omega \right)\equiv c/\sqrt{2\pi {\sigma }_{\text{D}}\omega }=\frac{{\lambda }_{{\text{L}}_0}}{\sqrt{\omega \tau /2}}.(11)$

It should be noted that ${\lambda }_{{\text{L}}_0}=c/{\omega }_p$ is the clean limit result for the London penetration depth at zero temperature, defined here in terms of the plasma frequency, ${\omega }_p\equiv \sqrt{\frac{8\pi }{3}{N}_f{e}^2{v}_f^2}$. The penetration of the EM field in the normal metal is then given by

${\lambda }_n=\frac{1}{A_0}{\int }_0^{\infty }dx{A}_n\left(x,\omega \right)=\text{Re}\left(\frac{i}{q\left(\omega \right)}\right)=\frac{\delta \left(\omega \right)}{2}.(12)$

In the superconducting state, $A_s(x,\omega )=A_0{e}^{-x/{\lambda }_{\text{L}}}$, and thus, the penetration depth of the EM field is given by the London length

${\lambda }_s=\frac{1}{A_0}{\int }_0^{\infty }dx{A}_s\left(x,\omega \right)={\lambda }_{\text{L}}.(13)$

For pure Nb, we adopt the values of ${\lambda }_{{\text{L}}_0}\simeq 33\text{nm}$, $T_{c_0}=9.33\text{K}$, and Δ₀ = 1.55 meV in Table 1 (Zarea et al., 2022). Here, we consider N-doped Nb SRF cavities with fundamental frequency f = ω/2π = 1.3 GHz and a transition temperature of T_c = 9.0 K (Bafia et al., 2021). The combination of quasiparticle scattering by non-magnetic impurities and gap anisotropy leads to pair breaking and accounts for the suppression of T_c with a quasiparticle scattering rate of τ ≈ 2 × 10⁻¹³ sec [c.f. Fig. 12 of the work of Zarea et al. (2022)]. Thus, ωτ ≃ 1.6 × 10⁻³ ≪ 1 as we assumed. The normal metal penetration depth with this level of disorder is then λ_n ≈ 910 nm. Disorder also suppresses the superfluid fraction, n_s/n ≈ 0.4, and, thus, increases the zero-temperature London penetration depth to λ_L ≈ 52 nm. For the f = 1.3 GHz TM₀₁₀ mode of a cylindrical cavity, the radius is R = 8.83 cm. Thus, the difference in the penetration depth of the EM field for the normal and superconducting states implies a maximum increase in the cavity resonance frequency of order δf ≈ f (λ_n − λ_s)/R ≈ 12.6 kHz, which is close to the maximum frequency shift for an N-doped Nb Tesla SRF cavity with f = 1.3 GHz, i.e., δf_expt ≃ 12.5 kHz (Bafia et al., 2021). The geometric factor for an f = 1.3 GHz cylindrical cavity with δf = 12.6 kHz and radius R = 8.83 cm corresponds to G_cyl = 268 Ω, and thus, L ≃ 1.44 R compared to G_Tesla = 270 Ω.

TABLE 1

TABLE 1. Material parameters for pure niobium. It should be noted that ${\tau }_0=\hslash /2\pi k_{\text{B}}{T}_{c_0}$, ξ₀ = v_fτ₀, ${\lambda }_{{\text{L}}_0}=c/{\omega }_p$, and Δ₀ is the strong-coupling gap for pure Nb (Zarea et al., 2022).

Although the maximum shift is positive, very near T_c, the cavity resonance frequency exhibits a negative frequency shift of order δf ≳ − 1 kHz over a narrow temperature range near T_c [c.f. Fig. 4 of the work of Ueki et al. (2022)]. This anomaly can be qualitatively understood based on the divergence of the London penetration depth as T → T_c, i.e., ${\lambda }_{\text{L}}(T)={\lambda }_{\text{L}}/\sqrt{1-T/T_c}$. Thus, the temperature window over which the frequency shift is expected to be negative is $|\mathrm{\Delta }T|/T_c<{({\lambda }_{\text{L}}/{\lambda }_n)}^2\approx 3.3\times 10^{-3}$, which is in rough agreement with the experimentally observed width of the temperature anomaly of |ΔT|/T_c|_expt ≃ 3.8 × 10⁻³ at f = 1.3 GHz [c.f. Fig. 4 of the work of Ueki et al. (2022)]. More detailed and accurate analysis of the temperature dependence of the cavity resonance and quality factor, as well as an approximate analytical formula for the frequency anomaly very near T_c, is given in the following.

2.4 Impedance, resistance, and reactance

The EM response of cavity resonators, as well as 2D co-planar waveguide resonators, is often expressed in terms of the complex surface impedance, Z(ω). For SRF cavities, the surface impedance resulting from the response of screening currents in the superconductor is defined by the ratio of the tangential fields at the interface.

$Z/Z_0\equiv E_{\Vert }\left(R\right)/H_{\Vert }\left(R\right)=\frac{J_0\left(\varpi R/c\right)}{J_1\left(\varpi R/c\right)}=\frac{\varpi }{c}\mathrm{\Lambda }{\left(\varpi \right)}^{-1}.(14)$

Thus, the solution to the boundary value problem, Eq. 9, directly determines the complex impedance. Equations 6, 9, 15 give Z(ω) directly in terms of the complex conductivity

$Z=Z_0\sqrt{\frac{\omega }{4\pi i\sigma \left(\omega \right)}},(15)$

and thus, $Z_s/Z_n=\sqrt{{\sigma }_n(\omega )/{\sigma }_s(\omega )}$. This result is valid in the limit c/ω ≫ λ_s,n, which is well satisfied for SRF cavities at GHz frequencies. The real and imaginary parts of Z_s/n = R_s/n − iX_s/n are the surface resistance and surface reactance of the metal in the superconducting (s) and normal (n) states, respectively. For SRF cavities in the normal state with a moderate level of disorder, we have ωτ ≪ 1, in which case σ_1n ≃ σ_D and σ_2n ≃ (ωτ)σ_D ≪ σ_1n. Thus,

$X_n\simeq R_n\simeq Z_0\sqrt{\omega /8\pi {\sigma }_{\text{D}}}.(16)$

The change in the reactance upon cooling through superconducting transition generates a shift in the resonance frequency,

$\delta f\equiv f_s-f_n=\frac{f}{2G}\left(X_n-X_s\right),(17)$

while the surface resistance below T_c determines the quality factor.

$Q_s=\frac{G}{R_s},(18)$

where G is the geometric factor of the cavity, which is given for the TM₀₁₀ mode of a cylindrical cavity by Eq. 8.

2.5 Quality factor

The effects of disorder on quality factor Q are important for the development of SRF cavities for both accelerator and quantum applications. Both the quality factor and resonance frequency of the cavity can be calculated directly from Eqs 4, 9. In particular, for a cylindrical cavity of radius R, Eq. 9 reduces to

$\frac{1}{Q}=\frac{2}{R}\text{Im}\left\{\frac{1}{\sqrt{K\left(\omega \right)}}\right\},(19)$

$\delta \omega =-\frac{\omega }{R}\text{Re}\left\{\frac{1}{\sqrt{K\left(\omega \right)}}\right\}(20)$

in the limit δω ≪ ω and ω/Q ≪ ω, where the complex eigenvalue defined by the solution of Eq. 9 is written as ϖ ≡ ω + δω − iω/2Q, with ω = x₀₁c/R being the TM₀₁₀ mode frequency of the ideal cavity.

Figure 1 shows the dependence of Q on the quasiparticle scattering time in units of τ_Δ ≡ ℏ/2πΔ(T) for an f = 2.6GHz Nb SRF cavity at T = 0.2T_c. Thus, in the local limit, i.e., sufficient disorder such that λ_L ≫ ξ, the maximum Q occurs for intermediate disorder with τ ∼ τ_Δ. Indeed the non-monotonic dependence of Q on τ is due to the pair-breaking suppression of the superfluid fraction, n_s ∝ 1/λ², by quasiparticle-impurity scattering. For strong disorder, τ ≪ τ_Δ, the quality factor drops rapidly and approaches the Q of the normal state for τ → 0. In the clean limit τ → ∞, the local approximation for the current response function breaks down for Nb. This is not an issue for the current state-of-the-art SRF cavities for accelerator applications, but it may be relevant to consider ultra-purity cavity technology for quantum sensors and processors, the case in which non-local electrodynamics of SRF cavities will be relevant.

FIGURE 1

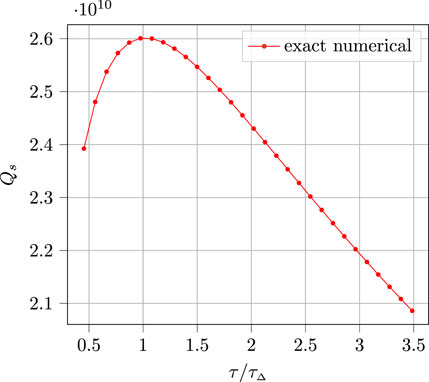
FIGURE 1. Theoretical result for the quality factor Q_s at T/T_c = 0.2 as a function of the quasiparticle scattering time in units of τ_Δ, for an f = 2.6GHz cavity.

3 Comparison of theory & experiment

Here, we compare our results and analysis with the measurements reported for N-doped Nb SRF cavities in the work of Bafia et al. (2021). The authors also provided measurements of T_c and the normal-state surface resistance, R_n, for Tesla cavities with mode frequencies of f = {0.65, 1.3, 2.6, 3.9} GHz. When comparing the theory with the experimental data from Tesla cavities, we rescale the magnitudes of δf and Q by replacing G for the cylindrical cavity with the numerically calculated value of G for the Tesla cavity (Bafia et al., 2021; Ueki et al., 2022).

Figure 2 shows the temperature dependence of the frequency shift of an f = 2.6 GHz cavity relative to the resonant frequency in the normal state just above T_c. The black symbols are the experimental data from the work of Bafia et al. (2021). The calculated frequency shift is the solid red line. The theoretical curve corresponds to a quasiparticle scattering time of τ = 2.57 × 10⁻¹³ sec (τ = 1.963 τ₀). This result is in reasonable agreement with the value of τ obtained from the reported normal-state surface resistance for the same cavity. We estimate τ from R_n using Eq. 16 and the relations between Drude conductivity, the plasma frequency, and the zero-temperature London penetration depth in the clean limit (c.f. Table 2) to give

$\tau =\pi f{\left(\frac{{\lambda }_{{\text{L}}_0}}{c}\frac{Z_0}{R_n}\right)}^2.(21)$

FIGURE 2

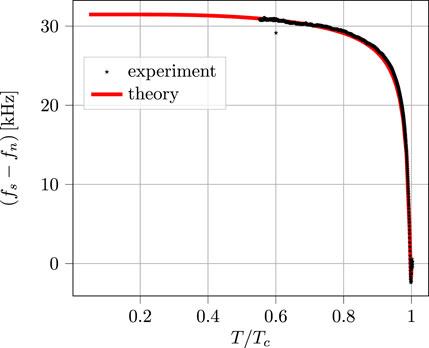
FIGURE 2. Frequency shift δf = f_s − f_n as a function of temperature for a cavity with fundamental frequency f = 2.6GHz. The data (black symbols) are from the work of Bafia et al. (2021). The theoretical result (red line), based on Eqs 4, 9, corresponds to a quasiparticle scattering rate of τ = 0.257 ps. The negative shift close to T_c should be noted.

TABLE 2

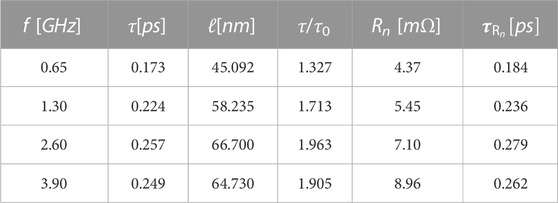
TABLE 2. Material parameters for different cavities. The second column is the scattering time that gives the best fit of theory to experiment. The values of R_n were provided by D. Bafia [private communication].

Bafia et al. (2021) reported R_n ≃ 7.1 × 10⁻³Ω, which gives τ = 0.28 ps, compared to the value of τ = 0.26 ps obtained from our fit to the temperature-dependent frequency shift. It is worth noting that there is no single value of the quasiparticle-impurity scattering rate, 1/τ, because the disorder is inhomogeneously distributed in the cavity walls. This fact is reflected in the distribution of values of T_c measured at different locations on the cavity (Bafia et al., 2021). We analyzed the effects of inhomogeneity of 1/τ and, thus, T_c, on the frequency shift and quality factor in the work of Ueki et al. (2022). The value of 1/τ we obtain here from our fit to δf(T,τ) is in excellent agreement with the mean of the probability distribution ρ(1/τ) for the 2.6 GHz N-doped Nb cavity (Ueki et al., 2022). The results for other N-doped Nb cavities are summarized and discussed in detail in the work of Ueki et al. (2022) [c.f. Table 3 therein].

3.1 Anomalous frequency shift

Figure 2 shows the negative frequency shift very close to T_c, which is expanded in Figure 3. The region of negative frequency shift is where the London penetration depth, ${\lambda }_{\text{L}}(T)\approx {\lambda }_{\text{L}}/\sqrt{1-T/T_c}$, exceeds the normal-state penetration depth, λ_n. The experimental data are reasonably well described by theory, given the fact that the scattering time τ was fit to the full temperature-dependent shift.

FIGURE 3

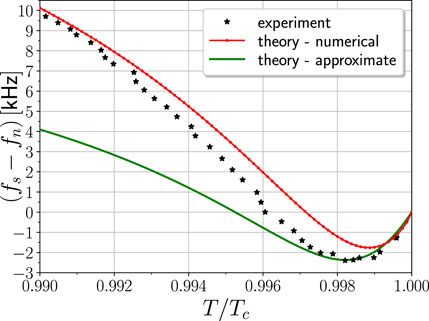
FIGURE 3. Experimental data for the frequency shift of the 2.6 GHz cavity near T_c are the black symbols. The minimum frequency shift is −2.39 kHz at T = 0.9982 T_c and extends over a temperature window of |ΔT| ≈ 4 × 10⁻³ T_c. The theoretical result based on the best fit to the full temperature dependence of the frequency shift is the red line. The green line is the approximate theoretical result based on the leading terms in the current response function as a function of t = 1 − T/T_c with the constraint ℏω ≪ 2Δ(T) for the same scattering time, τ = 0.257 ps.

Here, we provide an approximate analytic expression for the response function and the frequency shift anomaly near T_c. From Eq. 6, it should be noted that the real part of the current response function in Eq. 4 is proportional to the out-of-phase component of conductivity, and thus, the penetration depth in the superconducting state is

$\text{Re}K\left(\omega \right)=\frac{4\pi \omega }{c^2}{\sigma }_2\left(\omega \right)\underset{T\to T_c^{-}}{\overset{\hslash \omega \ll 2\mathrm{\Delta }\left(T\right)}{\to }}\frac{1}{{\lambda }_{\text{L}}{\left(T,\tau \right)}^2},(22)$

where ${\lambda }_{\text{L}}(T,\tau )\simeq {\lambda }_{\text{L}}/\sqrt{1-T/T_c}$ for T ≲ T_c. The imaginary part of K(ω) is proportional to the dissipative component of conductivity.

$\text{Im}K\left(\omega \right)=-\frac{4\pi \omega }{c^2}{\sigma }_1\left(\omega \right)\underset{T\to T_c^{-}}{\overset{\hslash \omega \ll 2\mathrm{\Delta }\left(T\right)}{\to }}-\frac{1}{2{\lambda }_{\text{n}}{\left(\omega ,\tau \right)}^2},(23)$

with λ_n (ω, τ) given by Eqs 11, 12; i.e., we drop corrections of order ${(\mathrm{\Delta }(T)/\pi T_c)}^2$ to the normal-state Drude conductivity.

Thus, for temperatures just below the superconducting transition, but still below the pair-breaking continuum, ℏω ≪ 2Δ(T), we obtain an approximate analytic form for the frequency shift and quality factor using Eq. 9 in the limit δω/ω ≪ 1 and 1/Q ≪ 1. In particular, the frequency shift of the superconductor relative to the ideal cavity frequency for |T − T_c|≪ T_c becomes

$\delta f_s=-\frac{f}{R_{\text{eff}}}\text{Re}\left\{{\left(\frac{1}{{\lambda }_{\text{L}}{\left(T,\tau \right)}^2}-\frac{i}{2{\lambda }_n{\left(\omega ,\tau \right)}^2}\right)}^{-\frac{1}{2}}\right\},(24)$

where R_eff = R G_Tesla/G_cyl and R is the radius of a cylindrical SRF cavity with a TM₀₁₀ mode frequency of f = 2.6 GHz. The corresponding shift for the normal metallic state just above T_c is δf_n = −(f/R_eff) λ_n. Thus, the observable frequency shift of the superconducting cavity relative to the normal state is δf = δf_s − δf_n. This approximate result reproduces the negative frequency shift near T_c, including a good estimate of the temperature and a minimum value of the negative frequency shift, but deviates from the full theory as the temperature drops further. Thus, the origin of the negative shift is the competition between the large normal-state penetration depth for disordered Nb and the London penetration depth which competes with λ_n only as $T\to T_c^{-}$.

4 Conclusion

The theoretical results for the frequency shift and quality factor, as well as the suppression of T_c and superfluid density by disorder, can provide powerful analysis tools for characterizing disorders in SRF cavities for both accelerator and detector applications.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

MZ: formal analysis, investigation, software, visualization, writing–original draft, and writing–review and editing. HU: formal analysis, investigation, software, and writing–review and editing. JS: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, Superconducting Quantum Materials and Systems Center (SQMS) under contract number DE-AC02-07CH11359.

Acknowledgments

The authors thank Daniel Bafia, Anna Grassellino, Alex Romanenko, and John Zasadzinski for discussions on their results on N-doped Nb SRF cavities and for their motivation during this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that they were editorial board members of Frontiers at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bafia, D., Grassellino, A., Checchin, M., Zasadzinski, J., and Romanenko, A. (2021). The anomalous resonant frequency variation of microwave superconducting Niobium cavities near T_c. e-print arXiv:2103.10601.

Google Scholar

Bogorad, Z., Hook, A., Kahn, Y., and Soreq, Y. (2019). Probing Axionlike particles and the Axiverse with superconducting radio-frequency cavities. Phys. Rev. Lett. 123, 021801. doi:10.1103/physrevlett.123.021801

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, C., and Harnik, R. (2021). Axion searches with two superconducting radio-frequency cavities. J. High. Energ. Phys. 2021, 53. doi:10.1007/jhep07(2021)053

CrossRef Full Text | Google Scholar

Grassellino, A., Romanenko, A., Sergatskov, D., Melnychuk, O., Trenikhina, Y., Crawford, A., et al. (2013). Nitrogen and argon doping of niobium for superconducting radio frequency cavities: A pathway to highly efficient accelerating structures. Supercond. Sci. Technol. 26, 102001. doi:10.1088/0953-2048/26/10/102001

CrossRef Full Text | Google Scholar

Grassellino, A., Romanenko, A., Trenikhina, Y., Checchin, M., Martinello, M., Melnychuk, O. S., et al. (2017). Unprecedented quality factors at accelerating gradients up to 45 MVm⁻¹ in niobium superconducting resonators via low temperature nitrogen infusion. Supercond. Sci. Tech. 30, 094004. doi:10.1088/1361-6668/aa7afe

CrossRef Full Text | Google Scholar

Gurevich, A., and Kubo, T. (2017). Surface impedance and optimum surface resistance of a superconductor with an imperfect surface. Phys. Rev. B 96, 184515. doi:10.1103/physrevb.96.184515

CrossRef Full Text | Google Scholar

Klein, O., Nicol, E. J., Holczer, K., and Grüner, G. (1994). Conductivity coherence factors in the conventional superconductors Nb and Pb. Phys. Rev. B 50, 6307–6316. doi:10.1103/physrevb.50.6307

PubMed Abstract | CrossRef Full Text | Google Scholar

Ngampruetikorn, V., and Sauls, J. A. (2019). Effect of inhomogeneous surface disorder on the superheating field of superconducting RF cavities. Phys. Rev. Res. 1, 012015(R). doi:10.1103/physrevresearch.1.012015

CrossRef Full Text | Google Scholar

Padamsee, H., Knobloch, J., and Hays, T. (2008). RF superconductivity for accelerators. John Wiley and Sons, Inc., 1–515.

Google Scholar

Rainer, D., and Sauls, J. A. (1994). “Strong-coupling theory of superconductivity,” in Superconductivity: From basic physics to New developments (Singapore: World Scientific), 45–78. arXiv: https://arxiv.org/abs/1809.05264.

Google Scholar

Romanenko, A., Pilipenko, R., Zorzetti, S., Frolov, D., Awida, M., Belomestnykh, S., et al. (2020). Three-dimensional superconducting resonators at T < 20 mK with photon lifetimes up to τ = 2 s. Phys. Rev. Appl. 13, 034032. doi:10.1103/physrevapplied.13.034032

CrossRef Full Text | Google Scholar

Sauls, J. A. (2022). Theory of disordered superconductors with applications to nonlinear current response. Prog. Theor. Exp. Phys. 2022, 033I03. doi:10.1093/ptep/ptac034

CrossRef Full Text | Google Scholar

Slater, J. C. (1946). Microwave Electronics. Rev. Mod. Phys. 18, 441–512. doi:10.1103/revmodphys.18.441

CrossRef Full Text | Google Scholar

Ueki, H., Zarea, M., and Sauls, J. A. (2022). The frequency shift and Q of disordered superconducting RF cavities. Phys. Rev. Res. submitted, 1. doi:10.48550/arXiv.2207.14236

CrossRef Full Text | Google Scholar

Varmazis, C., Hook, J. R., Sandiford, D. J., and Strongin, M. (1975). Inductive transition of niobium and tantalum in the 10-MHz range. II. The peak in the inductive skin depth for T just less than T_c. Phys. Rev. B 11, 3354–3361. doi:10.1103/physrevb.11.3354

CrossRef Full Text | Google Scholar

Zarea, M., Ueki, H., and Sauls, J. A. (2022). Effects of anisotropy and disorder on the superconducting properties of Niobium. arXiv 2201.07403.

Google Scholar