Toward Human-Centered Design of Automated Vehicles: A Naturalistic Brake Policy

Introduction

While safety is the ultimate goal in designing Connected and Automated Vehicles (CAVs), current automotive safety standards fail to explicitly define rules and regulations that ensure the safety of CAVs or those interacting with such vehicles. Even though some companies adhere to available standards in their vehicles (e.g., GM/Cruise Automation considered ISO-26262 functional safety standard in the vehicle design), the state-of-the-practice in CAV safety analysis is focused on actual and simulated miles driven. All existing companies (even traditional automotive OEMs) asses their safety records based on the total miles driven and the number of crashes and disengagement events (i.e., any interference in the vehicle’s decision-making and/or maneuver by the safety driver). In a recent study, however, Intel/Mobileye showed the infeasibility of such an approach and the need for 10⁹ h of testing to reach human-level driving safety after each software/hardware update (Shalev-Shwartz et al., 2017). Considering that CAV development goal is to form better than human drivers, the overall testing time should be much higher to ensure reliable and safe driving-related decisions (Shalev-Shwartz et al., 2017). Moreover, most high-risk instances are rare and might not occur during typical driving and testing efforts. Unfortunately, the factors that potentially contribute to such critical safety issues are not well-studied, and the current measures of safety (i.e., miles driven and crashes/disengagement events) do not provide any insight into the nature of those crashes and near-crashes. Therefore, developing preventive measures and design guidelines require an alternate approach.

The key factor in providing a reliable assessment of safety risks in mixed traffic environments with both traditional vehicles and CAVs is to identify the risk factors that contribute to crashes and near-crashes involving CAVs and human-driven vehicles. Understanding these underlying factors is critical to ensure safety during the testing and deployment phases of the CAV technology.

An existing hypothesis is that the primary reason behind human-CAV crashes is a potential mismatch between CAVs’ braking patterns and the expectations of surrounding human drivers (e.g., the 3-s stopping rule built-in to CAVs, vs. rolling stops performed by human drivers). The primary motivation toward formulating this hypothesis is a recently published study by Waymo indicating that their CAVs are designed based on defensive driving standards; however, human drivers do not always follow/expect such behaviors (Waymo, LLC, 2017). Such instances can lead to crashes/near-crashes; for instance, from August 2016 to February 2017, 18 out of 26 crashes involving CAVs in California involved a CAV that was rear-ended by a human driver at an intersection (State of California Department of Motor Vehicles, 2017). As driving uniformity is a significant factor in safety, a major challenge in autonomous driving is to achieve human-like driving behavior while staying within safety bounds (Kuderer et al., 2015; Zhu et al., 2018; Xu et al., 2020).

Through investigating the above hypothesis, the present study aims to bring critical knowledge from traffic analysis to develop a systematic and scalable approach to assess the safety of CAVs as an improvement to the state-of-the-practice in CAV safety analysis in mixed environments. Investigating the feasibility of developing a systematic evaluation approach, the present study particularly focuses on the rear-end crashes at urban intersections. According to the California Department of Motor Vehicles, these crashes are the most common CAV recorded crashes in California (Favarò et al., 2017; State of California Department of Motor Vehicles, 2017). The findings of this study are expected to facilitate the development of higher levels of vehicle automation by providing guidelines to prevent rear-end crashes caused by potential mismatches between CAVs and humans’ braking strategies. Moreover, the findings of this paper can lead to a fair assessment of the current state-of-the-art in vehicle automation safety.

Accordingly, the focus of this study is threefold: 1) to learn human drivers’ braking behavior when approaching an intersection under different driving conditions, 2) to compare humans’ braking behavior to that of CAVs under corresponding conditions, and 3) to propose a deceleration profile for CAVs comparable to human drivers’ braking pattern while ensuring safety and efficiency of the braking maneuver.

The remainder of this paper is organized as follows: Section Background presents a review of the previous studies. The data collection process and data description are presented next followed by a detailed description of the proposed methodologies and modeling results to characterize humans’ and CAVs’ braking behaviors. Finally, the paper is concluded with a summary of the findings and future research needs.

Background

The majority of studies on developing a connected, automated driving environment are based on the assumption that all vehicles are equipped with required communication systems (Wei et al., 2013; Pueboobpaphan et al., 2010). However, despite the rapid development of CAVs, such an environment is not foreseen in the near future. According to De La Fortelle et al. (2014), traditional vehicles are predicted to predominate for decades. It is expected that by 2030, nearly 50% of vehicles will still be operated by human drivers. It is, therefore, of paramount importance to equip CAVs with the required technologies that enable them to safely and efficiently operate in mixed traffic environments with both human actors and automated vehicles (Rahmati et al., 2020). CAVs in such environments need to understand humans’ driving behavior and also act in a way that is safe and yet expected by surrounding human drivers. Any mismatch between humans’ and CAVs’ driving strategies can potentially lead to unsafe driving instances (Wei et al., 2013). Thus, the key to achieving a reliable and safe human-CAV collaboration is to understand and characterize humans’ driving decisions and translate them into CAVs’ decision logic (Rahmati and Talebpour 2017).

The review of the previous research studies reveals several papers that have focused on modeling humans’ driving behavior under different driving conditions. It has been shown that a better understanding of different driving behaviors allows for more appropriate safety policies, and possibly leads to greater effectiveness in reducing traffic incidents (Luo and Guo 2006; Rudenko et al., 2020). In light of this, Dabiri and Abbas (2018) aimed at modeling drivers’ car-following behavior based on the Gradient Boosting of Regression Tree (GBRT) technique. The proposed model has been trained by trajectory-based features, including vehicles’ relative location, speed, and acceleration. The test results indicated a promising performance of the GBRT algorithm in modeling the motion characteristics of two successive vehicles. Similarly, Yang et al. (2017)) conducted a study on the recognition of different driving behaviors for a simulated car-following scenario. Using K-means and Support Vector Machine (SVM) classifiers, five groups of driving behavior were categorized using driving data. In another study, Wang et al. (2018) also used hidden Markov Models (HMMs) combined with Gaussian mixture models to predict the tendency of a driver to brake in a car-following platform.

Several studies have also focused on understanding and modeling humans’ driving decisions at intersections. A significant portion of driving behavior analysis at intersections has alluded to modeling drivers’ direction choices. Amsalu et al. (2015), for example, investigated the actions taken by drivers at intersections using a hybrid-state system (HSS), where the decisions of the driver and vehicle dynamics are modeled as discrete-state and continuous-state systems, respectively. A multi-class SVM model was then proposed to predict drivers’ intentions. In another study, Aoude et al. (2012) developed algorithms to classify drivers’ behavior at intersections as either compliant or violating using SVM and HMMs techniques. Some researchers have also studied drivers’ intention and decision-making when approaching a yellow indication. For example, Elhenawy et al. (2015) have used AI techniques including adaptive boosting (Ada-boost), Artificial Neural Networks (ANNs), and SVMs to model drivers’ stop/go behavior at the yellow indication. In another study, Hoehener et al. (2015) investigated drivers’ dilemma when the traffic light changes to yellow. Using an ANN model based on Gaussian process theory, they introduced an upper bound for the crossing probability in the proposed situation.

While modeling humans’ driving behavior has been the subject of several studies, only a few have focused on incorporating such behavior into CAVs’ decision making to alleviate the potential mismatch in humans’ and CAVs’ driving behaviors. More promising in this regard is a study by Kuderer et al. (2015), who have developed a reinforcement learning process to model individual driving behavior based on the observed driving style of each individual. The model is then used to compute trajectories online during autonomous driving tasks. In another study, Hao et al. (2016) implemented a car-following model for CAVs that imitates the car-following behavior of a human driver. The proposed fuzzy logic-based model is validated using NGSIM data, and the results indicated an acceptable similarity between the actual and simulated trajectories of the follower vehicle. In a recent study, Emuna et al. (2020) have introduced a model-free, deep reinforcement learning approach for autonomous driving in mixed environments that is able to imitate the behavior of an expert human driver. Human-like driving patterns were generated and evaluated by simulating a static obstacle avoidance task on a two-way highway. In a recent field experiment, Rahmati et al. investigated humans’ car-following behavior in interaction with surrounding human-driven and automated vehicles (Rahmati et al., 2019). Results indicated that humans feel more comfortable following an automated vehicle and tend to drive closer to their leader even though they were not aware if it is a human-driven or automated vehicle. In another study, Naumann et al. (2020) have studied the utilization of different cost function structures to imitate humans’ behavior under different driving scenarios. They have then proposed an inverse reinforcement learning algorithm to learn the optimum cost function weights based on the observed human behavior in three different scenarios.

The above list is by no means a comprehensive one, and there are many studies that have focused on modeling the interactions between CAVs and human drivers. However, while crash records indicate the importance of such analysis to ensure safe CAV operation at intersections, a review of previous studies indicates that only a limited number of research efforts have investigated the need for cooperative human-CAV braking when approaching an intersection. The majority of the studies on CAVs’ driving pattern analysis at intersections have focused on predicting drivers’ decisions regarding which direction to go (Dresner and Stone 2007; Rahmati and Talebpour 2017; Qian et al., 2014; Talebpour et al., 2015). Focusing on CAVs’ most frequent crashes (i.e., being rear-ended by human drivers when stopping at intersections), the present study aims at approximating the braking behavior of human drivers at intersections and proposing a safe and human-like braking profile for CAVs. Considering that the braking decisions can be influenced by the existence of a proceeding vehicle, it is necessary to distinguish the associated braking profiles under the following driving conditions: 1) if the target vehicle is the first in line to stop (free-flow braking behavior), and 2) if there are other vehicles between the target vehicle and the stop line (car-following braking behavior). The proposed models are expected to alleviate the mismatch between human drivers’ expectations and CAVs’ decision making, and potentially prevent CAVs from being rear-ended in mixed driving environments. This study is an initial step toward developing a systematic guideline for vehicle automation safety via providing insights into the nature of most frequent CAV crashes.

Data

Drivers’ speed pattern has been known as one of the main descriptors used to understand and model humans’ driving behavior under different traffic conditions (Eboli et al., 2017). Drivers’ speed choices are linked to their characteristics and speed variations are often treated as an indicator of the driving behavior. Today, thanks to the technologies like the high-precision kinematic Global Positioning System (GPS), speed patterns can be accurately analyzed to identify different driving behavior. Inspired by previous research, the present study has designed an experiment to collect data on humans’ real-world braking patterns at urban intersections. For the purpose of the study, human drivers’ instantaneous speeds are recorded when stopping at an intersection. The associated speed patterns are then used to analyze humans’ braking decisions under car-following and free-flow driving conditions. The following section explains the data collection experiment.

To record the required data, a field test is conducted using an autonomous Chevrolet Bolt EV. Data is collected on four different days and by eight drivers that were asked to drive the vehicle through a pre-specified test track at Texas A&M University System RELLIS Campus in Bryan, Texas. Drivers consisted of two female and six male college students between the ages of 20–35 and all had a valid driver’s license. The speed limit on the test route was 30 mph. There were multiple stop signs behind which drivers stopped, and their trajectory data were recorded using a high-precision GPS/IMU system installed on the vehicle.

Real-world experience suggests that the existence of a proceeding vehicle often affects drivers’ breaking profile before reaching a full stop. Accordingly, each stopping scenario in this field experiment is labeled as either car-following or free-flow driving condition based on the presence of any proceeding vehicle between the target vehicle and the stop line of the intersection. Figure 1 illustrates a schematic of the data collection scenarios.

FIGURE 1

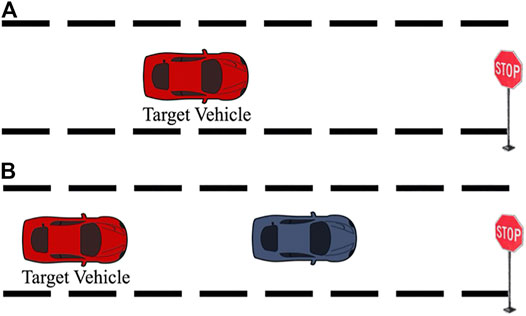
FIGURE 1. Schematic of the data collection scenarios: (A) free flow, and (B) car-following conditions.

The final dataset contains the time, location, and instantaneous speeds of the target vehicle (and its leader in car-following scenarios) measured in increments of 0.1 s. A total of 213 observations (each representing a stopping scenario at an intersection) were collected, among which 62 braking scenarios were recorded under the car-following condition, and the remaining 151 stops were associated with the free-flow condition. Once different braking scenarios were identified, the braking pattern 10 s before reaching a full stop was extracted for each scenario. The final database, therefore, includes vehicles’ speed data 10 s before reaching a complete stop along with the associated driving condition for each of the 213 braking scenarios. The collected data (raw and processed) is available through the University of Illinois at Urbana-Champaign website (smartctlab.web.illinois.edu).

Methodology and Results

As alluded to, the focus of the present study is to investigate CAVs’ rear-end collisions at intersections in mixed traffic environments. The hypothesis set forth to justify these crashes is the potential mismatch between the braking pattern of humans and that of CAVs. The first step in testing this hypothesis is then to understand and model humans’ braking behavior when stopping at intersections in urban settings. Potential differences in humans’ decision making under different driving scenarios should also be taken into account when preparing CAVs to operate in mixed traffic environments.

Real-world experience suggests that the existence of a proceeding vehicle often affects drivers’ breaking profile before reaching a full stop. In light of this, the following section is dedicated to learning and capturing potential differences in humans’ braking decisions under two scenarios; 1) free-flow and 2) car-following driving conditions.

Humans’ Braking Behavior

The present study utilizes supervised learning techniques to classify humans’ deceleration patterns based on the potential differences in their braking decisions (speed profiles) under each driving scenario. A relatively high classification accuracy would lend support to the existence of distinguishable differences in drivers’ free-flow and car-following braking strategies, which, therefore, should be learned and translated into CAVs’ decision-making logic.

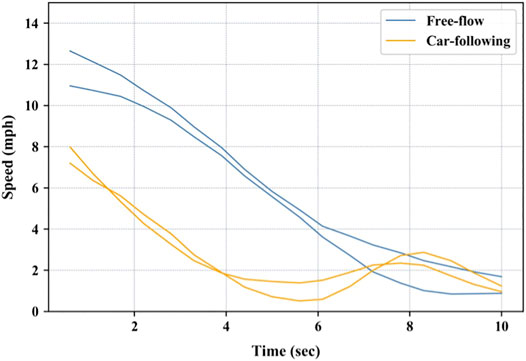
Figure 2 illustrates an example of drivers’ speed pattern over the 10-s period before reaching a full stop for the two classes of braking scenarios. Note that in order to avoid clutter, only four samples (two stopping scenarios for each class) are indicated in the figure. It can be observed that despite the overall decreasing pattern in both scenarios, the car-following braking profile consists of consecutive deceleration and acceleration maneuvers during the 10-s interval, while braking under the free-flow condition follows a smoother pattern. A lower average speed is also observable for car-following scenarios compared to the free-flow braking profiles.

FIGURE 2

FIGURE 2. Speed patterns under two different driving conditions.

Two approaches are adopted to analyze the associated speed time series under each driving condition. The first approach is dedicated to extracting features from the time series and using them with normal supervised learning techniques. The second approach, on the other hand, directly uses the speed time series to investigate potential differences using series-specific classifiers.

Summarized Time Series Classification

In this method, the provided speed time series are summarized into variables that can properly capture the associated braking pattern under the car-following or free-flow driving conditions. The idea is to reduce the dimensionality of the data while retaining its key features. Accordingly, the more relevant features selected, the better the algorithm learns and thus can generate more realistic results. After investigating multiple descriptors, the speed time series are summarized by vehicles’ average speed, maximum acceleration/deceleration rate, and minimum acceleration/deceleration rate. The importance of these descriptors in modeling driving behaviors has also been pointed out in previous studies (Eboli et al., 2017; Dabiri and Abbas 2018). The selected variables are then used to train models that classify humans’ braking patterns under free-flow and car-following conditions. Eq. 1 represents a general formulation of the proposed classifiers.

$\mathit{y}\mathrm{=}\mathit{f}\left(U_{\text{mean}}, a_{\min }, a_{\max }\right),(1)$

where $y$ is a binary variable equal to 1 for car-following and 0 for the free-flow condition; and $U_{\text{mean}}$, $a_{\min }$, and $a_{\max }$, respectively, denote the average speed, minimum acceleration/deceleration rate, and maximum acceleration/deceleration rate of the vehicle during the 10-s interval before reaching the full stop.

To better analyze human drivers’ braking decisions under car-following and free-flow conditions, two AI techniques are adopted:

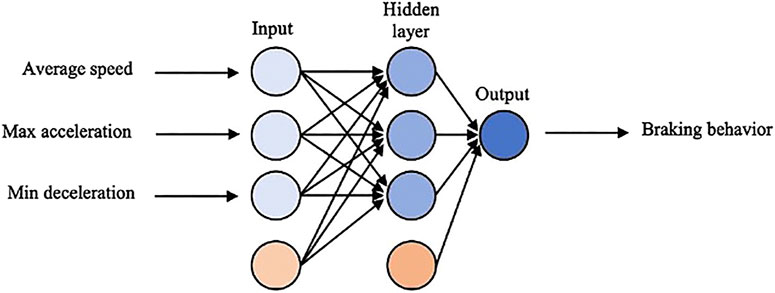
Multi-Layer Perceptron: MLP (or Artificial Neural Network- ANN) is a supervised learning algorithm consisting of at least three layers of nodes that learn a non-linear function for classification or regression. The main difference between the MLP algorithm and logistic regression is the existence of a few non-linear layers between the input and output layers, called hidden layers. Learning occurs through backpropagation, where the connecting weights on the network get updated based on the error between the resulted and expected outcome for each input.

Figure 3 illustrates the structure of the proposed ANN model for classifying human drivers’ braking behavior. The input layer consists of three nodes for vehicle’s average speed, maximum acceleration/deceleration rate, and minimum acceleration/deceleration rate, as well as a bias node (i.e. a trainable constant value). The output layer is a single node for the class of braking behavior. To determine the structure of the model, a grid search algorithm is developed to tune model hyperparameters based on the performance of the classifier, while avoiding overfitting. Accordingly, several models are created using all possible combinations of model parameters selected from a manually specified subset, and the set of parameter values corresponding to the model with minimum classification error is selected. Based on the results, an ANN model with one hidden layer including three nodes and a bias node is designed for the purpose of this study. Also, “Relu” and “Sigmoid” activation functions are considered for the hidden and output layers, respectively.

FIGURE 3

FIGURE 3. Structure of the proposed ANN classifier.

Support Vector Machine: SVM is another well-known supervised learning algorithm used for classification and regression analysis and outlier detection. SVM is, in essence, a linear model that can solve linear and non-linear classifiaction problems. The key idea of the algorithm is to generate a line that separates the training data into classes such that the line’s distance to the closest data point in each class is maximized. When the classes are not linearly separable, the algorithm transforms the data into a higher-dimensional space and formally defines a separative hyperplane to classify the new examples. This transformation is handled using a set of mathematical functions defined as the kernel. After developing a grid search algorithm to evaluate the performance of the model under different kernel functions, the RBF kernel is selected for the proposed SVM classifier.

Given the set of features extracted from the speed profiles during the braking maneuver, along with the corresponding driving condition at each scenario, the ANN and SVM models are trained to learn drivers’ braking behaviors and classify them into the car-following and free-flow categories. The classifiers are then compared based on their performance in capturing potential differences in drivers’ braking patterns at intersections.

Table 1 presents the model evaluation results based on the precision and recall values, as well as the F1 scores as a tradeoff between these two measures (note that the MLPClassifier from “Scikit-learn platform” and the SVC package in Python were used to train and test the proposed ANN and SVM classifiers, respectively).

TABLE 1

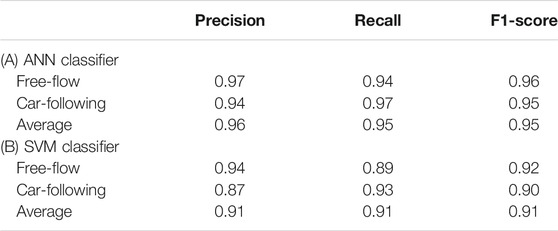
TABLE 1. Classifying Humans’ Free-flow and Car-following Braking Behavior using Summarized Time Series: (A) ANN, and (B) SVM.

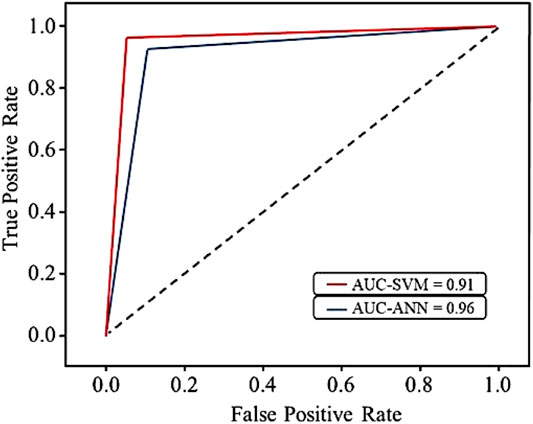
To better illustrate and compare the performance of the adopted classifiers, the Receiver Operating Characteristics (ROC) curves are also plotted for the proposed ANN and SVM models (Figure 4). ROC curves are used to visualize model performance by plotting the associated true-positive rate as a function of the false-positive rate. The Area Under the Curve (AUC) indicates how well the model classifies each category, where larger AUC values indicate a higher classification accuracy.

FIGURE 4

FIGURE 4. Receiver Operating Characteristics (ROC) curves for the ANN and SVM models.

The analysis of the results presented in Figure 4 and Table 1 provides evidence on humans’ different braking patterns under the free-flow and car-flowing driving scenarios. Indeed, the high F1-score values of 0.95 and 0.91 for the ANN and SVM models, respectively, indicate that the proposed AI techniques can effectively learn and distinguish differences in humans’ braking behavior under each driving scenario, suggesting that humans have different braking strategies when approaching an intersection under free-flow and car-flowing driving conditions.

Univariate Time Series Classification

Reducing the dimensionality of the time series data using its key features creates an approximate representation of the speed profiles which may not provide enough insights into the nature of potential differences in humans braking behavior. To further investigate human drivers’ braking decisions when approaching intersections under different conditions, time series-specific classifiers are adopted where the associated speed patterns are directly passed to the models. The present study utilizes the “sktime” Python toolbox developed for machine learning with time series and panel data (Löning et al., 2019). Three different classifiers are selected for this study:

1) K-Nearest-Neighbor (KNN) algorithm; a commonly used distance-based time series classifier that uses the dynamic time wrapping method to measure similarities between time series (Löning et al., 2019).

2) Time Series Forest Classifier (TSF); a variation of the standard random forest algorithm that uses randomized time series segmentation and feature selection based on a combination of entropy gain and distance to the nearest feature value (Deng et al., 2013).

3) Proximity Forests (PF); an ensemble of randomized proximity trees that branch on another exemplar time series based on their similarities (Lucas et al., 2019). The distance measure at each node is randomly selected from 11 distance measures including the Euclidian Distance and different Dynamic Time Wrapping methods.

Table 2 presents the classification results for the speed profiles under free-flow and car-following scenarios using the aforementioned classifiers. It can be observed that the proposed classifiers provide slightly lower performance compared to the proposed ANN and SVM structures in the previous section. Nevertheless, all three classifiers have resulted in a high F1-score value of at least 0.8.

TABLE 2

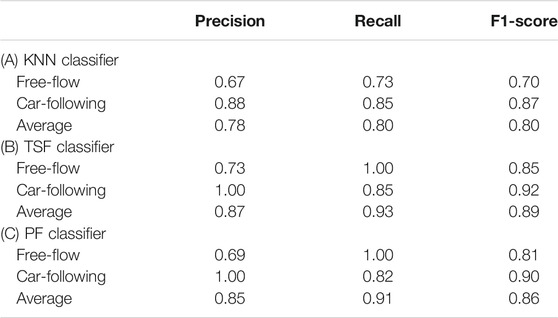
TABLE 2. Classifying Humans’ Free-flow and Car-following Braking Behavior using Univariate Time Series Classifiers: (A) KNN, (B) TSF, and (C) PF Classifiers.

The analyses indeed lend support to the premise that human drivers implement different braking maneuvers depending on the existence of a proceeding vehicle. Such findings justify dedicated braking rules in CAVs’ decision logic under free-flow and car-following driving conditions to ensure safe and human-like braking maneuvers by CAVs in mixed traffic environments.

On the next step toward investigating the hypothesis of the mismatch between humans’ and CAVs’ deceleration profile at intersections, the CAV braking pattern is simulated using the state of practice in vehicle automation safety guidelines. Resulted profiles are then compared to those of humans under corresponding driving conditions. It should be noted that the proposed ANN classifier in the previous section is selected for the rest of the analysis as it results in slightly higher accuracy in classifying different braking patterns.

Connected and Automated Vehicles’ Braking Behavior

In this section, CAVs’ braking behavior under free-flow and car-following conditions are first simulated using the proposed models in the literature. Then, potential differences in humans’ and CAVs’ braking decisions are investigated under corresponding driving scenarios.

Connected and Automated Vehicle Braking Under Free-Flow Conditions

Safety, efficiency, and comfort play significant roles in defining CAV braking rules at urban intersections. Under a free-flow condition where there is no other preceding vehicle, CAVs can choose comfortable and efficient deceleration rates and follow a smooth braking maneuver until reaching a full stop. High deceleration rates can result in dangerous situations for both the CAV and its potential followers, while small decelerations fail to meet system efficiency requirements. Accordingly, a constant deceleration rate of 1.5 m/s² (∼5 ft/s²) is selected as CAVs’ braking rule under free-flow driving conditions. This deceleration rate accommodates smooth and comfortable braking maneuvers by the vehicle, as suggested in (Wu et al., 2009). A braking profile is thus simulated for CAVs using 1.5 m/s² (∼5 ft/s²) constant deceleration when approaching an intersection under the free-flow driving condition.

Connected and Automated Vehicle Braking Under Car-Following Conditions

CAVs’ car-following behavior has been the subject of several studies during the past decades. A promising study in this regard is the deterministic acceleration model developed by Talebpour and Mahmassani (2016). They have developed a comprehensive microscopic simulation framework that uses different models to capture the interactive behavior between human drivers and CAVs, considering different levels of connectivity. The present study adopts a similar approach to simulate the braking decisions made by CAVs at intersections under car-following driving conditions.

In their study, Talebpour and Mahmassani modeled CAVs car-following behavior by determining the maximum safe speed for the follower based on two main assumptions:

1) Autonomous vehicles can only monitor the vehicles in their sensor detection range. Thus, the speed of the follower CAV should be low enough to be able to reach a full stop in case of confronting a stopped vehicle immediately out of the boundary of the sensor detection range.

2) If the CAV is following another vehicle detected by its sensors, it should be able to reach a full stop if the leader decides to stop with the maximum deceleration rate.

Considering a platoon of vehicles, the safe speed profile for the follower CAV can then be modeled using the following equations:

$\begin{array}{l}\Delta {\mathit{x}}_{\mathit{n}}=\left({\mathit{x}}_{\mathit{n}-1}-{\mathit{x}}_{\mathit{n}}-{\mathit{l}}_{\mathit{n}-1}\right)+{\mathit{v}}_{\mathit{n}-1}\mathit{\tau }+\frac{{\mathit{v}}_{\mathit{n}}^2}{2{\mathit{a}}_{\mathit{n}}^{\mathit{decc}}},\\ \Delta \mathit{x}=\min \left\{\text{Sensor}\text{Detection}\text{Range},\Delta x_n\right\},\\ {\mathit{v}}_{\max }=\sqrt{-2{\mathit{a}}_{\mathit{i}}^{\mathit{decc}}\Delta \mathit{x}},\end{array}(2)$

where $v_{\max }$ is the maximum safe speed, $x_n$ is the location of vehicle $n$ (follower CAV), $l_{n-1}$ is the length of vehicle n − 1 (leader), $v_{n-1}$ represents the speed of the leader, $\tau$ is the reaction time of vehicle $n$, and $a_n^{decc}$ represents the maximum deceleration rate for vehicle $n$.

The acceleration rate of the CAV at every decision points is then computed using the following equation (Shalev-Shwartz et al., 2017):

$\begin{array}{l}{\mathit{a}}_{\mathit{n}}^{\mathit{d}}\left(\mathit{t}\right)={\mathit{k}}_{\mathit{a}}{\mathit{a}}_{\mathit{n}-1}\left(\mathit{t}-\mathit{\tau }\right)+{\mathit{k}}_{\mathit{v}}\left({\mathit{v}}_{\mathit{n}-1}\left(\mathit{t}-\mathit{\tau }\right)-{\mathit{v}}_{\mathit{n}}\left(\mathit{t}-\mathit{\tau }\right)\right)+{\mathit{k}}_{\mathit{d}}\left({\mathit{S}}_{\mathit{n}}\left(\mathit{t}-\mathit{\tau }\right)-{\mathit{S}}_{\mathit{ref}}\right),\\ S_{ref}=\max \left\{S_{\min }, S_{system}, S_{safe}\right\},\\ {\mathit{S}}_{\mathit{safe}}=\frac{{\mathit{v}}_{\mathit{n}-1}^2}{2}\left(\frac{1}{{\mathit{a}}_{\mathit{n}}^{\mathit{decc}}}-\frac{1}{{\mathit{a}}_{\text{n}-1}^{\mathit{decc}}}\right),\\ {\mathit{S}}_{\mathit{system}}={\mathit{v}}_{\mathit{n}}\mathit{\tau ,}\end{array}(3)$

where $a_n^d\left(t\right)$ represents the acceleration rate of vehicle $n$, $S_n$ is the spacing between the vehicles, $S_{\min }$ is the minimum distance that is set to 2.0 m in this study, and $k_a$, $k_v$, and $k_d$ are model parameters to be estimated. Finally, the implemented acceleration in CAV navigation systems can be computed as:

${\mathit{a}}_{\mathit{n}}\left(\mathit{t}\right)=\mathit{min}\left({\mathit{a}}_{\mathit{n}}^{\mathit{d}}\left(\mathit{t}\right),\mathit{ }\mathit{k}{\mathit{v}}_{\mathit{max}}-{\mathit{v}}_{\mathit{n}}\left(t\right)\right)(4)$

where $k$ is the model parameter to be estimated. Using the deterministic acceleration model represented by Eq. 4, a braking profile is simulated for CAVs under car-following driving conditions. Note that the following parameter values are selected for the purpose of this study: $k$= 0.1, $k_{a }$= 1.0, $k_{v }$= 0.58, and $k_{d }$= 1.0.

Comparing Humans’ and Connected and Automated Vehicles’ Braking Behaviors

After simulating CAV’s driving behaviors under free-flow and car-following scenarios, a similar ANN architecture with the same input information is adopted to investigate potential differences in braking maneuvers executed by human drivers and CAVs under the same driving conditions. The proposed ANN framework is trained to capture potential differences in humans’ and CAVs’ braking patterns under a specific driving condition, and then classify an unseen test braking pattern to belong to a human driver or a CAV. A high classification accuracy can then illustrate a significant difference in the braking decisions made by humans and CAVs under similar driving conditions. Table 3 presents the classification results for each of the free-flow and car-following driving conditions.

TABLE 3

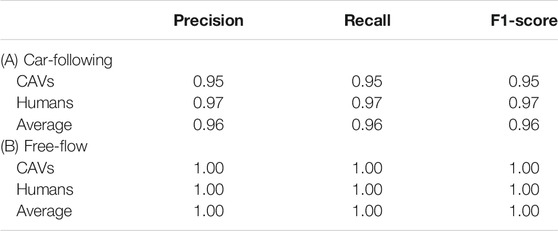
TABLE 3. Classifying humans’ and CAVs’ braking behavior under different driving conditions using the ANN classifier.

Analysis of the results presented in Table 3 indicates that the proposed ANN model is able to accurately classify test braking patterns into human and CAV categories based on the differences in their profiles. Substantially high F1-score values for both the car-following (F1-score = 0.96) and free-flow scenarios (F1-score = 1.0) suggest significant differences in humans’ and CAVs’ braking decisions under the same driving conditions, which can then be captured and learned via common AI techniques. These findings would lend support to the idea that CAVs do not brake the way humans do and expect. Such mismatch in humans’ and CAVs’ braking patterns can lead to high-risk situations in mixed traffic environments and happen to be a potential reason for CAVs’ rear-end collisions at urban intersections. Indeed, existing CAV braking rules may result in unexpected braking decisions from humans’ perspective and potentially cause CAVs to be hit by a follower human-driven vehicle. These findings justify the need for a human-like and yet safe CAV braking profile that ensures appropriate human-CAV cooperation when stopping at interactions in mixed environments. The rest of the sections deals with designing a novel decision modeling framework for CAV braking that meets these criteria.

Designing a Connected and Automated Vehicle Braking Profile

This section aims at generating a safe braking pattern for CAVs based on the observed behavior of human drivers under free-flow and car-following driving conditions. Different deterministic and stochastic modeling frameworks have been adopted to model humans’ driving behavior in different scenarios. The major challenge posed by most deterministic approaches is centered around capturing the existing uncertainties in humans’ decision-making (Sadigh et al., 2014). Stochastic techniques, on the other hand, are known for their ability to capture the heterogeneity in individual agents and, therefore, can better reflect humans’ real-world behavior.

Markov Decision Process (MDP) is one of the well-known stochastic frameworks employed for decision modeling in uncertain domains. MDPs are powerful analytical tools that allow agents to determine the ideal behavior within an environment. A quick literature review indicates multiple applications of MDPs for modeling driver behavior under different traffic scenarios (Morris and Trivedi 2008; Sathyanarayana et al., 2008; Berndt and Dietmayer 2009; Osipychev et al., 2015; Chae et al., 2017). The present study puts forward an MDP-based modeling framework to design a safe and human-like braking profile for CAVs in mixed traffic environments. The solution of the proposed MDP model can be implemented in the form of a look-up table that can satisfy real-time requirements of autonomous driving without high computational complexities.

Markov Decision Process

Identifying the optimum decision in uncertain domains is a major challenge in probabilistic modeling. MDP is a random process used to optimize a sequential decision-making problem by maximizing agents’ total rewards (Russell and Peter 2016). A common MDP is defined by:

1) States, $S_t$; represent the condition of the system at time t.

2) Actions, $A_{s }$; a set of possible action at state $s\in S_t$, where executing each action can result in either the same or a different state $\left(s^{\prime }\in S_{t+1}\right)$. The Markov property asserts that the future state of a process depends only on the current state, overlooking the future and past states (Gagniuc 2017).

3) Transition probability, $T\left(S_t , S_{t+1},a_t\right)=P\left(S_{t+1}|S_t ,a_t\right)$; the probability that action $a_s$ in state $s\in S_t$ results in state $s^{\prime }\in S_{t+1}$.

4) Rewards, $R\left(s,a\right)$; represents the long-term reward received when transferring from state $s\in S_t$ to states $s^{\prime }\in S_{t+1}$ as the result of executing action $a_s$.

The goal of the MDP process is to determine actions that maximize the cumulative rewards over the whole process. MDP solution is often represented by a policy, $\pi : S_t\to A_t$ , that specify the optimum action that an agent should take at each state in order to maximize its overall payoff.

A common approach used to solve an MDP problem is the value iteration algorithm. The method defines a value function $q(s, a)$ to measure how rewarding an action is in a particular state. Eq. 5 represents the value function defined at any state under policy $\pi$ (Sutton and Barto 2018):

${\mathit{q}}_{\mathit{\pi }}\left(\mathit{s},\mathit{a}\right)\doteq {\mathbb{E}}_{\mathit{\pi }}\left[{\mathit{G}}_{\mathit{t}}|{\mathit{S}}_{\mathit{t}}=\mathit{s},{\mathit{A}}_{\mathit{t}}=\mathit{a}\right]={\mathbb{E}}_{\mathit{\pi }}\left[{\displaystyle \sum }_{\mathit{k}=0}^{\infty }{\mathit{\gamma }}^{\mathit{k}}{\mathit{R}}_{\mathit{t}+\mathit{k}+1}|{\mathit{S}}_{\mathit{t}}=\mathit{s},{\mathit{A}}_{\mathit{t}}=\mathit{a}\right],(5)$

where $\gamma$ is a discount factor that asserts the priority of the immediate action rewards over future rewards and is set to 0.9 for this study. The optimal policy, denoted by $\left({\pi }^{\ast }\right)$, is then the policy that generates the maximum expected value. In other words, the optimum policy at each state denotes the agent’s best action for which the optimal value function will be achieved. The optimal action-value function ($q^{\ast }$), also known as the Bellman optimality equation, is defined as follows (Sutton and Barto 2018):

${\mathit{q}}_{\mathit{*}}\left(\mathit{s},\mathit{a}\right)\doteq \underset{\mathit{\pi }}{\max }{\mathit{q}}_{\mathit{\pi }}\left(\mathit{s},\mathit{a}\right)={\Sigma }_{s\mathrm{\prime }r}p\left({\mathit{s}}^{\mathit{\prime }},\mathit{r}\text{|}\mathit{s},\mathit{a}\right)\left[\mathit{r}+\mathit{\gamma }\underset{{\mathit{a}}^{\mathit{\prime }}}{\max }{\mathit{q}}_{\mathit{*}}\left({\mathit{s}}^{\mathit{\prime }},{\mathit{a}}^{\mathit{\prime }}\right)\right](6)$

The Bellman optimality equation results in a unique solution. Each state has a Bellman equation with an unknown utility. An MDP problem with n states will thus result in n nonlinear equations with n unknowns. Literature suggests several approaches to solve the Bellman optimality equation (Christopher 1992; Russell and Peter 2016). The value iteration approach is one of the well-known methods which starts with some initial values for each state and updates them based on Eq. 5. The process continues until all state values reach a steady number. The assigned allowable error between successive values defines the stopping criteria. The final values are then set as the optimal decisions proposed by the Markov process. Note that utilizing the aforementioned method requires knowledge about transition probabilities. Accordingly, this study utilizes empirical data to estimate these probabilities. While other methods exist that can solve the Markov process without knowing the transition probabilities and/or reward [e.g., Q-Learning (Huang and Haskell 2017; Shah and Vivek 2018)], these methods require much larger datasets that is not available to the researchers. Accordingly, this study assumes that the calculated transition probability distributions represent the actual transition probabilities. Since this study is considered a proof-of-concept for the brake profile design problem, such an assumption can be considered reasonable.

Considering the problem of designing a CAV braking profile in MDP terminology, the autonomous braking system should select an appropriate braking action in each state such that the resulting braking profile meets surrounding human drivers’ expectations without sacrificing safety. States in such systems should reflect the factors that affect CAV braking under corresponding driving conditions. The following sections provide a detailed description of the proposed MDP model for designing a braking profile for CAVs in mixed environments.

Connected and Automated Vehicle Braking Profile Under Free-Flow Driving Condition

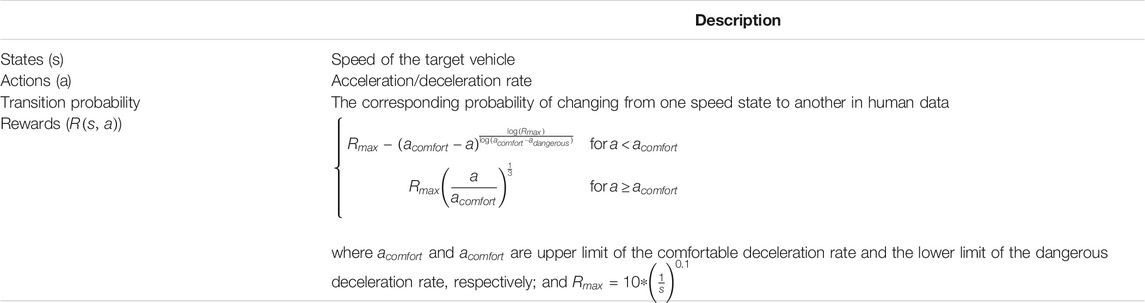
Table 4 summarizes the structure of the proposed MDP model for designing a CAV braking profile under free-flow driving condition. The following describes the components of the MDP problem in more details.

TABLE 4

TABLE 4. Proposed MDP structure to design a CAV braking profile under free-flow driving condition.

States: Real-world observations suggest that when there is no other car between the target vehicle and the upcoming intersection, the vehicle speed plays a major role in driver’s braking decisions. Accordingly, in designing a CAV braking profile under free-flow driving conditions using an MDP structure, states are defined to be the speed of the target vehicle.

Analyzing the collected vehicle trajectories under free-flow driving conditions, vehicle speeds are divided into groups (bins) based on the initial speed of the vehicle 10 s before reaching a full stop. Considering that the initial speeds in the dataset range from 7 to 17 m/s, five bins are generated with the interval of 2 m/s. Then, at each bin, vehicle speeds are categorized into 17 states, where speeds in range (s-1, s] fall into state “s” (s = 1, 2, 17 m/s).

Actions: Actions of the system are defined as the different acceleration/deceleration rates that might be selected by the vehicle at each state. Based on the collected dataset, available actions at each state encompass 34 acceleration/deceleration rates, equally-spaced in the range [−3 m/s², 3 m/s²]. The proposed range also includes the maximum comfortable acceleration/deceleration rate suggested in the literature (Wu et al., 2009). Note that the states and actions of the system are defined such that any recorded speed value is covered by exactly one state in the implemented MDP structure.

Transition Probability: As alluded to, the main contribution of the present study is to design a CAV braking profile that is compatible with human expectations. To meet this objective, the transition probabilities between the states in the proposed MDP problem are estimated based on human drivers’ real-world braking decisions. Accordingly, the probability of changing from one speed state to another is calculated for human drivers using the collected dataset. These probabilities are then set to be the corresponding transition probabilities in the MDP model. The procedure can ensure human-like accelerations/deceleration maneuvers in the solution profile generated by the proposed Markov decision modeling framework for modeling CAV braking in mixed environments.

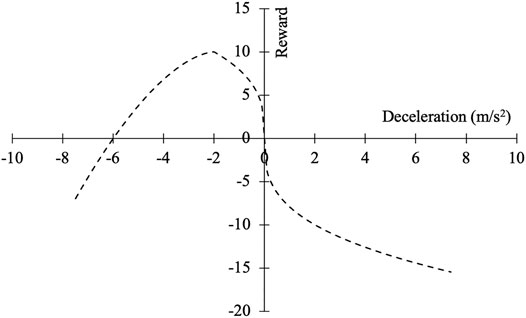
Rewards: The final step in defining the MDP structure is to formulate a reward system that in each state favors the actions which result in more satisfactory conditions. The satisfaction criterion is defined based on the present state (speed) of the agent as well as the convenience level of the acceleration/deceleration maneuver. The ultimate goal is then to guide the agent toward the terminal state, i.e., reaching the speed of zero at the intersection. The penalty for each state is, therefore, proportional to the distance from the terminal state. On the other hand, the associated reward of each action depends on its deviation from the comfortable deceleration rate ($a_{comfort}$). In this study, the upper limit of the comfortable deceleration rate and the lower limit of the dangerous deceleration rate ($a_{dangerous}$) are considered to be 2 m/s² and 6 m/s², respectively. Based on the above discussion, the proposed reward function $R(s,a)$ for action $a$ at state $s$ is computed according to equation 7, where $R_{\max }=10\ast {\left(1/s\right)}^{0.1}$. Figure 5 indicates the reward distribution for a sample terminal state.

$\mathit{R}\left(\mathit{s},\mathit{a}\right)=\{\begin{array}{cc}{\mathit{R}}_{\mathit{max}}-{\left({\mathit{a}}_{\mathit{comfort}}-\mathit{a}\right)}^{\frac{\log \left({\mathit{R}}_{\mathit{max}}\right)}{\log \left({\mathit{a}}_{\mathit{comfort}}-{\mathit{a}}_{\mathit{dangerous}}\right)}},& \text{for}a<{\mathit{a}}_{\mathit{comfort}},\\ {\mathit{R}}_{\mathit{max}}{\left(\frac{\mathit{a}}{{\mathit{a}}_{\mathit{comfort}}}\right)}^{\frac{1}{3}},& for a\ge {\mathit{a}}_{\mathit{comfort}}.\end{array}(7)$

FIGURE 5

FIGURE 5. Reward distribution for actions at the terminal state.

With the states, actions, transition probabilities, and reward system described above, an MDP structure is developed and optimized using the value iteration procedure with stopping criteria of 0.001 for change in q values. Note that other stopping criteria (e.g., no change in action at each decision point) might result in a different outcome. Exploring such differences are, however, beyond the scope of this paper as this paper serves as a proof-of-concept for the CAV brake profile design. The resulted best policy provided the optimum action (acceleration/deceleration rate) that can be adopted by CAVs at each speed state when approaching an intersection. Based on these findings, a decision framework is designed for CAVs braking under free-flow driving conditions in mixed environments such that: 1) it follows the guideline for safe and comfortable braking maneuvers at intersections, and 2) favors human-like braking decisions observed in real-world contexts.

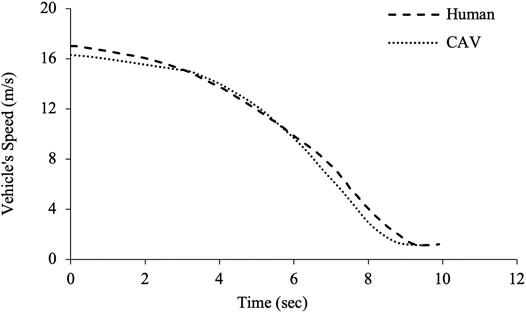
Figure 6 illustrates a sample CAV free-flow braking profile generated by the proposed MDP structure for the initial speed bin (15–17] m/s, along with a sample free-flow braking profile executed by a human driver in the dataset. Visual analysis indicates smooth braking maneuvers along with promising similarities between the two braking patterns, which can, in turn, alleviate the existing mismatch between the way humans and CAVs stop at intersections.

FIGURE 6

FIGURE 6. Humans’ and the proposed CAV braking profiles under free-flow driving condition.

To further evaluate the proposed MDP structure, specialized statistical methods are also adopted to compare the observed deceleration trajectories of human drivers and the corresponding CAV braking profile. In light of this, simulated and actual speed time series are separately analyzed using the Auto-Regressive Integrated Moving Average (ARIMA) model. ARIMA is one of the most common tools in analyzing time series data used to understand various aspects and the inherent nature of time series. The model explains a given time series based on the idea that the information in past values of the series is sufficient to predict future points. The null hypothesis set forth here is that there is no statistically significant difference between the ARIMA models fitted to the observed and simulated braking profiles.

Three distinct terms are used to characterize an ARIMA model and determine the required number of model parameters to account for the auto-regressive, integrated, and moving average components. A grid search algorithm is developed to select optimal values of these terms based on the Akaike Information Criterion (AIC). Table 5 presents the ARIMA modeling results fitted to the human and CAV braking profiles illustrated in Figure 6.

TABLE 5

TABLE 5. ARIMA model results for (A) human, and (B) simulated CAV braking profiles under free-following driving condition.

Referring to the coefficient tables, it can be observed that the estimated values of the corresponding model parameters are fairly close to each other. From a statistical perspective, the estimated parameter values for the ARIMA model of the simulated CAV profile (ar.L1.D and ar.L2.D) fall into the associated 95% confidence interval of the corresponding parameters in the ARIMA model of humans. In other words, there is no evidence of statistically significant differences between the time series models constructed to describe the given human and CAV braking patterns, being 95% confident. These findings suggest that the proposed MDP structure is capable of generating a safe human-like braking profile for CAVs’ real-time operation in mixed traffic environments.

Connected and Automated Vehicle Braking Profile Under Car-Following Driving Condition

Table 6 summarizes the structure of the proposed MDP model for designing a CAV braking profile under the car-following driving condition. The following describes the components of the MDP problem in more details.

TABLE 6

TABLE 6. Proposed MDP structure to design a CAV braking profile under car-following driving condition.

States: In the previous section, vehicles’ speed was considered as the main factor affecting drivers’ braking decisions under the free-flow driving condition. For the car-following scenario, however, drivers’ decisions hinges on several dominant factors, including the speed of the target and leader vehicles as well as their relative distance. Therefore, it is crucial to consider these factors when defining the current state of the agent in the proposed MDP model for CAVs’ braking in car-following scenarios. Considering the speed data recorded 10 s before reaching a full stop, vehicle speeds (for both follower and leader vehicles) are categorized into 17 states (similar to the categories defined for the free-flow condition). The observed distances between the leader and follower vehicles in the data are also categorized into 29 states, where distances between (d-1, d] fall into category “d.” The final state is then defined as a vector of the follower vehicle’s speed, the leader vehicle’s speed, and the relative distance between the leader and follower.

Actions: Similar to the previous section, actions are defined as the possible acceleration/deceleration rates that might be selected by the target CAV at each state. Analyzing the collected data on human braking, available actions to the driver in the proposed MDP problem include 34 acceleration/deceleration rates equally-spaced in range [−3, 3] (m/s²).

Transition Probability: Similar to the free-flow scenario, the recorded data on human drivers’ braking decisions in real-world contexts is used to estimate the transition probabilities between the states to ensure a human-like deceleration profile.

Rewards: For the car-following scenario, rewards are formulated based on the deviation of the relative distance between vehicles from the safe braking distance at any given state. The inputs of the reward function include the current state of the follower vehicle, along with the braking action of the leader vehicle at that state. The latter is predicted using the best braking profile generated by the proposed MDP model for free-follow braking. As suggested by Luo et al. (Luo et al., 2011), the safe distance $d_{safe}$ between vehicles is defined as the distance that assures the safety of the braking maneuver by preventing rear-end vehicle collisions and is computed using the following equation:

${\mathit{d}}_{\mathit{safe}}=\{\begin{array}{cc}{\mathit{V}}_{\mathit{f}}{\mathit{t}}_{\mathit{r}}+\frac{\left({\mathit{V}}_{\mathit{f}}-{\mathit{V}}_{\mathit{l}}\right){\mathit{t}}_{\mathit{b}}}{2}+\frac{{{\displaystyle \mathit{v}}}_{\mathit{f}}^{\mathit{2}}}{2{\mathit{a}}_{\mathit{f}}}-\frac{{{\displaystyle \mathit{v}}}_{\mathit{l}}^{\mathit{2}}}{2{\mathit{a}}_{\mathit{l}}}+{\mathit{d}}_{\mathit{final}},& \text{for}{\mathit{V}}_{\mathit{f}}\ge {\mathit{V}}_{\mathit{l}}\\ {\mathit{V}}_{\mathit{f}}\left(t_r+t_b\right)+\frac{2{\mathit{V}}_{\mathit{l}}{\mathit{V}}_{\mathit{f}}-2{{\displaystyle \mathit{v}}}_{\mathit{f}}^{\mathit{2}}-{{\displaystyle \mathit{v}}}_{\mathit{l}}^{\mathit{2}}}{2{\mathit{a}}_{\mathit{l}}}+\frac{{{\displaystyle \mathit{v}}}_{\mathit{f}}^{\mathit{2}}}{2{\mathit{a}}_{\mathit{l}}}+\frac{{\mathit{V}}_{\mathit{l}}{\mathit{t}}_{\mathit{b}}}{2}+{\mathit{d}}_{\mathit{final}}& \text{for}{\mathit{V}}_{\mathit{f}}<{\mathit{V}}_{\mathit{l}}\end{array}(8)$

where $V_{f }$, $V_{l }$, $a_{f }$, and $a_l$ denote the follower and leader vehicles’ speed and acceleration/deceleration rates, respectively; $t_r$ and $t_b$ are drivers’ reaction and braking times which are approximately [0.8–1.0] and [0.1–0.2] seconds, respectively; and $d_{final}$ is the required safe distance when vehicles stop (usually [2–5] meters).

Actions that result in shorter distances than $d_{safe}$ will get high penalties in the proposed MDP structure. To avoid harsh braking maneuvers, actions leading to longer distances are also subject to penalties. In contrast, those that keep the two vehicles at a reasonable safe distance will receive higher rewards. Considering the above criteria, the reward function associated with action $a$ at a given state $s$ is formulated as follows;

$\mathit{R}\left(\mathit{s},\mathit{a}\right)=\mathit{ }0.1\mathit{*}{\mathit{d}}_{\mathit{safe}}-{\left({\mathit{d}}_{\mathit{safe}}-\mathit{ }\mathit{d}\left(\mathit{s},\mathit{a}\right)\right)}^2(9)$

where $d\left(s,a\right)$ is the resulted distance between the vehicles if action $a$ is taken by the follower CAV. This function perfectly assigns penalties and rewards to the follower vehicle’s actions keeping the braking maneuver within a safe as well as comfortable deceleration range.

Similar to the free-flow scenario and considering the proposed states, actions, transition probabilities, and reward structure, an MDP model is developed and optimized using the value iteration procedure with the stopping criteria of 0.001 for change in q values. The resulted best policy then identifies the optimum braking actions (acceleration/deceleration rates) at each state under a car-following driving scenario.

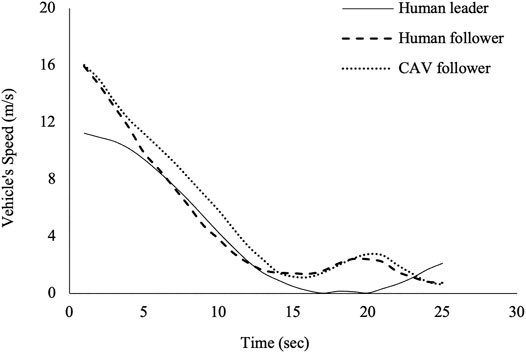
The MDP solution can be represented in the form of a look-up table where an optimum action is suggested for each condition (state) that the vehicle might experience. In a connected, automated driving environment, CAVs can accurately measure their own speed, the leader’s speed, and the distance to the leader, and in turn, determine their current state when approaching an intersection under a car-following driving scenario. Corresponding optimum acceleration/deceleration rate can then be selected based on the best policy table provided by the MDP model. Similar to the free-flow condition, a deceleration profile can then be designed for CAV braking under car-following conditions based on humans’ braking decisions in real-world context while meeting safe and comfortable braking criteria. Figure 7 illustrates a sample car-following braking profile generated for CAVs, along with the real-world behavior of the follower and leader vehicles extracted from the data. Initial analysis of the results reveals promising similarities among the proposed CAV braking profile and the actual deceleration pattern of the corresponding human follower.

FIGURE 7

FIGURE 7. Car-following braking profile generated from the observations and MDP model.

Similar to the free-flow condition, separate ARIMA models are fitted to the human and CAV series illustrated in Figure 7 in order to identify the best model to describe the characteristics of each profile. Table 7 presents the associated results. Adopting a 95% confidence level, it can be shown that there is no statistically significant evidence to reject the null hypothesis of using similar ARIMA models to describe the given human and CAV braking profiles.

TABLE 7

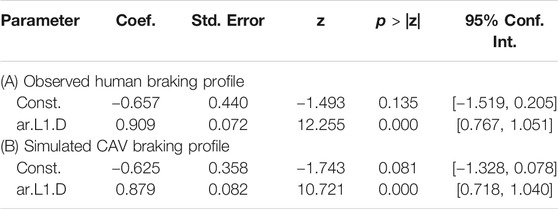
TABLE 7. ARIMA model results for (A) Human, and (B) Simulated CAV braking profiles under car-following driving condition.

These findings indeed suggest that the proposed MDP modeling framework can properly approximate the decision-making procedure of human drivers when stopping at intersections. Incorporating such a framework in CAV navigation algorithms is therefore expected to relieve the existing mismatch between humans’ and CAVs’ deceleration patterns and potentially prevent the frequently-observed rear-end crashes in mixed traffic environments.

Conclusion

While safety considerations play a crucial role in designing connected and automated vehicles, current measures of safety do not provide enough insight into the nature of CAV crashes. CAV safety analysis and crash records during the testing phase indicate that CAVs are frequently involved in rear-end collisions caused by human drivers when stopping at intersections. The mismatch between CAVs’ defined braking decisions and humans’ expectations is considered to be one of the core hypotheses in justifying these crashes. To test this hypothesis, the present study aims at modeling human drivers’ braking behavior at intersections under different driving conditions and translate the findings into CAVs’ decision logic.

Data is collected from human drivers’ braking behavior at intersections using Texas A&M’s automated Chevy Bolt EV. Artificial Intelligence techniques are then used to model and predict drivers’ braking behavior under car-following and free-flow driving conditions. Strong evidence on the difference in braking patterns of human drivers under these driving conditions, justified dedicated braking rules for CAV deceleration under each scenario. In the next step, humans’ braking decisions are compared to that of CAVs’ under corresponding driving conditions. The results indicated notably large differences in humans’ and CAVs’ braking patterns, confirming the need for designing a safe braking pattern for CAVs that is more human-like.

The main contribution of the present study is to propose a decision modeling framework for CAV braking in mixed traffic environments. To this end, a Markov Decision Process (MDP) is developed to generate a braking profile based on human drivers’ real-world behavior while incorporating the required criteria for a safe and comfortable braking maneuver. States of the system reflect the factors that affect drivers’ braking decisions at intersections, and actions are defined as possible acceleration/deceleration rates that can be executed by the target vehicle at each state. The transition probabilities for each action are then computed using the frequency of the associated acceleration/deceleration rate selected by human drivers in corresponding conditions. Reward functions are also defined to favor safe, efficient, and comfortable deceleration maneuvers.

The resulting best policy by the proposed MDP model provides a human-like and yet safe braking profile for CAV braking under each of the aforementioned driving conditions. Simulation results in both conditions indicated a relatively high performance of the designed CAV profile in approximating humans’ braking decisions at intersections.

The findings of this study are expected to facilitate the development of higher levels of vehicle automation by providing guidelines to prevent human-CAV rear-end collisions that are caused by the potential mismatch between CAVs’ braking behavior and humans’ expectations. Larger datasets that cover a broader range of vehicle speeds and relative distances are required to generalize the designed braking profiles for CAVs in mixed traffic environments. Further analysis using more data from human-driven vehicles is also necessary to better capture the heterogeneity in individual braking decisions. Modeling CAVs’ braking behavior under different driving conditions, for example, a platoon of three or more vehicles, different speed limits, and different weather conditions are left for future studies.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors upon request.

Author Contributions

The authors confirm contribution to the paper as follows: study conception and design: YR, AT; data collection: YR, AT, and AA; analysis and interpretation of results: YR, AA, MT, and AT; draft manuscript preparation: YR, AA, MT, and AT. All authors reviewed the results and approved the final version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Amsalu, S. B., Homaifar, A., Afghah, F., Ramyar, S., and Kurt, Arda. (2015). Driver Behavior Modeling Near Intersections Using Support Vector Machines Based on Statistical Feature Extraction. Intelligent Vehicles SymposiumIV. 2015. IEEE. doi:10.1109/ivs.2015.7225857

CrossRef Full Text

Aoude, G. S., Desaraju, V. R., Stephens, L. H., and How, J. P. (2012). Driver Behavior Classification at Intersections and Validation on Large Naturalistic Data Set. IEEE Trans. Intell. Transport. Syst. 13 (2), 724–736. doi:10.1109/tits.2011.2179537

CrossRef Full Text | Google Scholar

Berndt, H., and Dietmayer, K. (2009). “Driver Intention Inference with Vehicle Onboard Sensors,” in 2009 IEEE International Conference on Vehicular Electronics and Safety (ICVES), 11–12. Nov. 2009

Google Scholar

Chae, H., Kang, C. M., Kim, B., Kim, J., Chung, C. C., and Choi, J. W. (2017). “Autonomous Braking System via Deep Reinforcement Learning,” in 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), 16–19. Oct. 2017.

Google Scholar

Christopher, J. C. H. (1992). Watkins and Peter Dayan. Q-Learning. Mach. Learn. 8 (3), 279–292.

Dabiri, S., and Abbas, M. (2018). Evaluation of the Gradient Boosting of Regression Trees Method on Estimating the Car Following Behavior. arXiv preprint arXiv. 1804, 04954. doi:10.1177/0361198118772689

Google Scholar

De La Fortelle, A., Qian, X., Diemer, S., Grégoire, J., Moutarde, F., Bonnabel, S., et al. (2014). Network of Automated Vehicles: The AutoNet 2030 Vision. 21st World Congress on Intelligent Transport Systems.

Google Scholar

Deng, H., Runger, G., Tuv, E., and Vladimir, M. (2013). A Time Series forest for Classification and Feature Extraction. Inf. Sci. 239, 142–153. doi:10.1016/j.ins.2013.02.030

CrossRef Full Text | Google Scholar

Dresner, K. M., and Stone, P. (2007). Sharing the Road: Autonomous Vehicles Meet Human Drivers. IJCAI 7, 1263–1268.

Google Scholar

Eboli, L., Guido, G., Mazzulla, G., Pungillo, G., and Pungillo, R. (2017). Investigating Car Users' Driving Behaviour through Speed Analysis. Promet. 29 (2), 193–202. doi:10.7307/ptt.v29i2.2117

CrossRef Full Text | Google Scholar

Elhenawy, M., Jahangiri, A., Rakha, H. A., and El-Shawarby, I. (2015). "Modeling Driver Stop/run Behavior at the Onset of a Yellow Indication Considering Driver Run Tendency and Roadway Surface Conditions". Accid. Anal. Prev. 83, 90–100. doi:10.1016/j.aap.2015.06.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Emuna, R., Borowsky, A., and Biess, A. (2020). Deep Reinforcement Learning for Human-like Driving Policies in Collision Avoidance Tasks of Self-Driving Cars. arXiv preprint arXiv 2006, 04218.

Google Scholar

Favarò, F. M., Nader, N., O Eurich, S., Tripp, M., and Varadaraju, N. (2017). Examining Accident Reports Involving Autonomous Vehicles in California. PLoS one. 12 (9), e0184952. doi:10.1371/journal.pone.0184952

PubMed Abstract | CrossRef Full Text | Google Scholar

Gagniuc, P. A. (2017). Markov Chains: From Theory to Implementation and Experimentation. John Wiley & Sons, 256. doi:10.1002/9781119387596

CrossRef Full Text

Hao, H., Ma, W., and Xu, H. (2016). A Fuzzy Logic-Based Multi-Agent Car-Following Model. Transportation Res. C: Emerging Tech. 69, 477–496. doi:10.1016/j.trc.2015.09.014

CrossRef Full Text | Google Scholar

Hoehener, D., Green, P. A., and Domitilla Del Vecchio, (2015). Stochastic Hybrid Models for Predicting the Behavior of Drivers Facing the Yellow-Light-Dilemma. Am. Control. Conf. (Acc) 2015, 3348–3354. doi:10.1109/acc.2015.7171849

CrossRef Full Text | Google Scholar

Huang, W., and Haskell, W. B. (2017). “Risk-aware Q-Learning for Markov Decision Processes,” in 2017 IEEE 56th Annual Conference on Decision and Control (CDC). doi:10.1109/cdc.2017.8264388

CrossRef Full Text | Google Scholar

Kuderer, M., Gulati, S., and Burgard, W. (2015). “Learning Driving Styles for Autonomous Vehicles from Demonstration,” in Robotics and Automation (ICRA), 2015 IEEE International Conference on. doi:10.1109/icra.2015.7139555

CrossRef Full Text | Google Scholar

Löning, M., Anthony, B., Ganesh, S., Kazakov, V., Lines, J., and Király, F. J. (2019). Sktime: A Unified Interface for Machine Learning with Time Series. arXiv preprint arXiv 1909, 07872. doi:10.1109/ACCESS.2019.2914675

Google Scholar

Lucas, B., Shifaz, A., Pelletier, C., O’Neill, L., Zaidi, N., Goethals, B., et al. (2019). Proximity forest: an Effective and Scalable Distance-Based Classifier for Time Series. Data Min Knowl Disc. 33 (3), 607–635. doi:10.1007/s10618-019-00617-3

CrossRef Full Text | Google Scholar

Luo, Q., Xun, L., Cao, Z., and Huang, Y. (2011). “Simulation Analysis and Study on Car-Following Safety Distance Model Based on Braking Process of Leading Vehicle,” in 2011 9th World Congress on Intelligent Control and Automation, 21–25. June 2011

Google Scholar

Luo, Y., and Guo, X. (2006). “Driving Behavior Analysis Applying Driving Behavior in the AHS,” in Intelligent Transportation Systems Conference, 2006. ITSC'06 (IEEE)

Google Scholar

Morris, B. T., and Trivedi, M. M. (2008). Learning, Modeling, and Classification of Vehicle Track Patterns from Live Video. IEEE Trans. Intell. Transport. Syst. 9 (3), 425–437. doi:10.1109/TITS.2008.922970

CrossRef Full Text | Google Scholar

Naumann, M., Sun, L., Zhan, W., and Tomizuka, M (2020). Analyzing the Suitability of Cost Functions for Explaining and Imitating Human Driving Behavior Based on Inverse Reinforcement Learning. 2020 IEEE International Conference on Robotics and Automation (ICRA). doi:10.1109/icra40945.2020.9196795

CrossRef Full Text | Google Scholar

Osipychev, D., Tran, D., Sheng, W., Chowdhary, G., and Zeng, R. (2015). “Proactive MDP-Based Collision Avoidance Algorithm for Autonomous Cars,” in 2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), 8-12 June 2015. doi:10.1109/cyber.2015.7288078

CrossRef Full Text | Google Scholar

Pueboobpaphan, R., Liu, F., and Bart van Arem, (2010). “The Impacts of a Communication Based Merging Assistant on Traffic Flows of Manual and Equipped Vehicles at an On-Ramp Using Traffic Flow Simulation,” in Intelligent Transportation Systems (ITSC), 2010 13th International IEEE Conference on. doi:10.1109/itsc.2010.5625245

CrossRef Full Text | Google Scholar

Qian, X., Gregoire, J., Moutarde, F., and De La Fortelle, A. (2014). “Priority-based Coordination of Autonomous and Legacy Vehicles at Intersection,” in Intelligent Transportation Systems (ITSC), 2014 IEEE 17th International Conference on. doi:10.1109/itsc.2014.6957845

CrossRef Full Text | Google Scholar

Rahmati, Y., Talebpour, A., Mittal, A., and James, F. (2020). Game Theory-Based Framework for Modeling Human–Vehicle Interactions on the Road. Transportation Res. Rec. 2674, 0361198120931513. doi:10.1177/0361198120931513

Google Scholar

Rahmati, Y., and Talebpour, A. (2017). “Towards a Collaborative Connected, Automated Driving Environment: A Game Theory Based Decision Framework for Unprotected Left Turn Maneuvers,” in Intelligent Vehicles Symposium (IV), 2017 (IEEE). doi:10.1109/ivs.2017.7995894

CrossRef Full Text | Google Scholar

Rahmati, Y., Khajeh Hosseini, M., Talebpour, A., Swain, B., and Nelson, C. (2019). Influence of Autonomous Vehicles on Car-Following Behavior of Human Drivers. Transportation Res. Rec. 2673 (12), 367–379. doi:10.1177/0361198119862628

CrossRef Full Text | Google Scholar

Rudenko, A., Palmieri, L., Herman, M., Kitani, K. M., Gavrila, D. M., and Arras, K. O. (2020). Human Motion Trajectory Prediction: A Survey. Int. J. Robotics Res. 39 (8), 895–935. doi:10.1177/0278364920917446

CrossRef Full Text | Google Scholar

Russell, S. J., and Peter, N. (2016). Artificial Intelligence: A Modern Approach. Malaysia: Pearson Education Limited.

Sadigh, D., Driggs-Campbell, K., Alberto, P., Li, W., Shia, V., Bajcsy, R., et al. (2014). “Data-driven Probabilistic Modeling and Verification of Human Driver Behavior,” in 2014 AAAI Spring Symposium Series. doi:10.1145/2566468.2576851

CrossRef Full Text | Google Scholar

Sathyanarayana, A., Boyraz, P., and Hansen, J. H. L. (2008). "Driver Behavior Analysis and Route Recognition by Hidden Markov Models". 2008 IEEE Int. Conf. Vehicular Electronics Saf. 22–24. doi:10.1109/ICVES.2008.4640874

Google Scholar

Shah, S. M., and Borkar, V. S. (2018). Q-learning for Markov Decision Processes with a Satisfiability Criterion. Syst. Control. Lett. 113, 45–51. doi:10.1016/j.sysconle.2018.01.003

CrossRef Full Text | Google Scholar

Shalev-Shwartz, S., Shammah, S., and Shashua, A. (2017). On a Formal Model of Safe and Scalable Self-Driving Cars. arXiv preprint arXiv 1708, 06374.

Google Scholar

State of California Department of Motor Vehicles (2017). Report of Traffic Accident Involving an Autonomous Vehicle (OL 316). Available at: https://www.dmv.ca.gov/portal/dmv/detail/vr/autonomous/autonomousveh_ol316+.

Sutton, R. S., and Barto, A. G. (2018). Reinforcement Learning, Second Edition: An Introduction Adaptive Computation and Machine Learning series. MIT press, 552.

Talebpour, A., Mahmassani, H. S., and Hamdar, S. H. (2015). Modeling Lane-Changing Behavior in a Connected Environment: A Game Theory Approach. Transportation Res. Proced. 7, 420–440. doi:10.1016/j.trpro.2015.06.022

CrossRef Full Text | Google Scholar

Talebpour, A., and Mahmassani, H. S. (2016). Influence of Connected and Autonomous Vehicles on Traffic Flow Stability and Throughput. Transportation Res. Part C: Emerging Tech. 71, 143–163. doi:10.1016/j.trc.2016.07.007

CrossRef Full Text | Google Scholar

Wang, W., Xi, J., and Ding, Z. (2018). Learning and Inferring a Driver's Braking Action in Car-Following Scenarios. arXiv preprint arXiv 1801, 03905. doi:10.1109/TVT.2018.2793889

Google Scholar

Waymo, LLC (2017). Waymo Safety Report: On the Road to Fully Self-Driving. Available at: https://waymo.com/safetyreport/.

Wei, J., Dolan, J. M., and Litkouhi, B. (2013). “Autonomous Vehicle Social Behavior for Highway Entrance Ramp Management,” in Intelligent Vehicles Symposium (IV) (IEEE), 2013. doi:10.1109/ivs.2013.6629471

CrossRef Full Text | Google Scholar

Wu, Z., Liu, Y., and Pan, G. (2009). A Smart Car Control Model for Brake Comfort Based on Car Following. IEEE Trans. Intell. Transportation Syst. 10 (1), 42–46. doi:10.1109/TITS.2008.2006777

CrossRef Full Text | Google Scholar

Xu, D., Ding, Z., Xu, H., Zhao, H., Moze, M., Aioun, F., et al. (2020). Learning from Naturalistic Driving Data for Human-like Autonomous Highway Driving. IEEE Trans. Intell. Transportation Syst., 1-14. doi:10.1109/tits.2020.3001131

CrossRef Full Text | Google Scholar

Yang, L., Ma, R., Zhang, H. M., Guan, W., and Jiang, S. (2017). Driving Behavior Recognition Using EEG Data from a Simulated Car-Following experiment. Accid. Anal. Prev. 116, 30-40. doi:10.1016/j.aap.2017.11.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, M., Wang, X., and Wang, Y. (2018). Human-like Autonomous Car-Following Model with Deep Reinforcement Learning. Transportation Res. C: emerging Tech. 97, 348–368. doi:10.1016/j.trc.2018.10.024

CrossRef Full Text | Google Scholar