A novel mixed-integer programming approach for the aircraft landing problem

1 Introduction

The aviation industry is of crucial importance for transportation of passengers, logistics and commerce in our globalized world. Although travel numbers have considerably declined in the past two years due to the COVID-19 pandemic, the International Air Transport Association (IATA) expects these numbers to constantly grow in the near future. According to its most likely scenario, the industry will fully recover from the negative pandemic effects by 2024 (IATA, 2022). EUROCONTROL’s recent aviation outlook published in 2022 expects an average increase in flights across Europe by 1.2% per annum. This forecast implies that the number of flights will have increased by 44% by 2050 compared to 2019 (EUROCONTROL, 2022). In view of these trends, busy hub airports need to urgently address the congestion problem in order to guarantee smooth air traffic. One possibility is to expand the existing capacities through building new runways. However, this solution might be inappropriate or even infeasible because of economic, environmental, political or other issues. Another more promising approach is improvement of air traffic management (ATM) based on more efficient aircraft sequencing and scheduling (ASS).

While the ASS problem aims at simultaneous management of all in- and outbound flights, the aircraft take-off problem (ATP) and the aircraft landing problem (ALP) consider only departing or arriving aircraft, respectively. Since this paper places particular emphasis on the ALP, it is hereinafter considered in a detailed manner. To solve this problem for all aircraft entering the radar range of an airport (approximately 45–60 min from the destination), it is necessary to sequence all flights, to determine the landing time of each aircraft and to assign it to a runway if there are multiple ones.

To date, most air traffic controllers rely on the First-Come-First-Served (FCFS) strategy for dealing with the ALP. This concept provides a landing sequence based on the estimated time of arrival (ETA) of each aircraft, which is normally computed by a decision support tool. However, sequencing based on the FCFS concept has not proven to be the best one with respect to different criteria as, for example, maximum runway throughput or minimum average delay (Bennell et al., 2011).

In literature, different solution approaches have been extensively investigated. They can be mainly divided into exact and heuristic/metaheuristic methods. Exact solution techniques comprise:

• Dynamic Programming, which was first proposed by (Dear, 1976) and (Psaraftis, 1978) followed by (Chandran and Balakrishnan, 2007; Lee and Balakrishnan, 2008; Balakrishnan and Chandran, 2010; Briskorn and Stolletz, 2013; Lieder et al., 2015)

• Mixed-Integer Programming (MIP) preferred by (Beasley et al., 2000; Wen et al., 2005; Furini et al., 2012; Briskorn and Stolletz, 2013; Kim et al., 2014; Pohl et al., 2021)

Heuristic and metaheuristic approaches represent other powerful methods for solving the ALP. While authors of (Bianco et al., 2006; Faye, 2015; Shi et al., 2019; Ikli et al., 2021b) make use of heuristics, others decide in favor of metaheuristic methods. Some of them are listed below with the corresponding references:

• Genetic algorithms – (Beasley et al., 2001; Hu and Chen, 2005; Hu and Di Paolo, 2009; Yu et al., 2011)

• Tabu search – (Furini et al., 2015)

• Ant colony optimization – (Bencheikh et al., 2011; Xu, 2017)

• Variable Neighborhood Descent – (Salehipour et al., 2009)

In addition, see (Pinol and Beasley, 2006) for integrated scatter search and bionomic algorithms or (Bencheikh et al., 2009) for combination of both genetic and ant colony optimization algorithms.

Since the ALP is known to be NP-hard, most of the recent works concentrate on heuristic/metaheuristic approaches, which provide high-quality results in reasonable time (Ikli et al., 2021a). However, this paper proposes an exact and highly efficient solution technique for the ALP formulated as a Mixed-Integer Linear Program (MILP). In contrast to many other works, our method delivers almost optimal solutions also for large datasets (up to 90 aircraft and 4 runways) in low computational time thanks to improved modeling.

The remainder of this paper is structured as follows. It starts with the exact problem formulation and its mathematical modeling. In Section 3, numerical results obtained for four different airports are presented and analyzed. A summary and an outlook are given in the end.

2 Problem formulation

This section is devoted to the formulation of the ALP as an MILP. The first part highlights the setting of the problem including the exploited objective function and constraints. In the second part, the mathematical model used within the framework of this paper is presented. Its advantages are discussed in detail in the last part of this section.

2.1 Setting

Throughout this work, we denote by N the total number of aircraft approaching an airport, which can be tracked by an airport’s radar, and the corresponding index set by $\mathcal{N}=\{1,\dots ,N\}$. The total number of runways is denoted by K with the corresponding index set $\mathcal{K}=\{1,\dots ,K\}$. When dealing with the ALP, the aim is to assign a landing time t_i, $i\in \mathcal{N}$, and a runway $k\in \mathcal{K}$ to each aircraft $i\in \mathcal{N}$ taking into account corresponding penalty terms such that the total cost for all aircraft is minimal, and all necessary constraints are satisfied.

For the sake of a better overview, all quantities and variables used in this paper are given in Table 1.

TABLE 1

TABLE 1. Quantities and variables introduced in this paper.

2.1.1 Objective function

As indicated in (Bennell et al., 2011), there are many different objectives depending on the fact whose preferences are taken into consideration. From the airline’s perspective, it might be desirable to minimize total fuel costs or overall passenger delays, while air traffic controllers might be more interested in maximizing the runway throughput or minimizing their workload. Some objectives may be contradictory, wherefore decision makers need to find good trade-offs. The interested reader is referred to (Lee and Balakrishnan, 2008; Bennell et al., 2011; Ikli et al., 2021a) for more details.

This work makes use of a common objective function that prioritizes interests of air controllers by minimizing the sum of weighted deviations from the target (planned) landing times T_i, $i\in \mathcal{N}$.

2.1.2 Constraints

For reasons of safety and fairness, the following essential constraints are incorporated into our model:

• Arrival time windows: After having reached the radar range of an airport, an aircraft can accelerate to a certain extent and therefore arrive earlier at the destination than estimated. On the other hand, an aircraft might slow down before landing to its minimum speed (e.g. because of some unforeseen difficulties or events), which might result in a delay. Note that every landing aircraft is assumed to fly directly to the runway assigned to it, which implies that there are no go-rounds. Thus, the actual time of arrival is bounded from below and above by the earliest and latest landing times E_i and L_i, respectively.

• Separation requirements: Each aircraft causes chaotic wake turbulence flows, which can heavily influence other aircraft on the same runway. Therefore, certain separation times between two successive aircraft have to be included into the model. The International Civil Aviation Organisation (ICAO) has divided all aircraft in three main categories depending on their maximum take-off mass: heavy (H), medium (M) and light (L). The minimum separation time depends on the category of both the leading and the trailing aircraft. The exact times are indicated in Table 2.

• Constrained-Position Shifting (CPS): This constraint defines the maximum possible deviation from the FCFS or another nominal order. The maximum position shifting is denoted by m and is typically less or equal to four in many applications (Chandran and Balakrishnan, 2007; Balakrishnan and Chandran, 2010; Ikli et al., 2021b). CPS is included to guarantee equity between aircraft and to reduce the problem complexity and thus the workload of air traffic controllers in the terminal area, which is in general a very dynamic environment.

TABLE 2

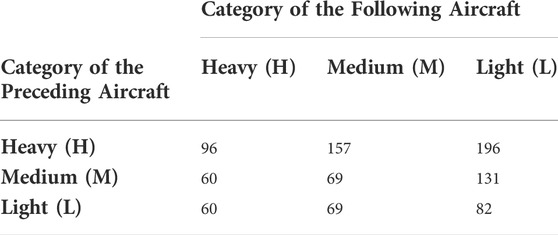
TABLE 2. Separation matrix indicating separation time in seconds between different aircraft categories.

2.2 Mixed-integer program formulation

Before we formulate the ALP as an MILP and explain the choice of constraints, let us first introduce two sets of binary (decision) variables needed for our model. In order to formulate a problem, which can be solved in reasonable time, it is essential to keep the number of binary variables as small as possible. In contrast to (Kim et al., 2014; Lieder et al., 2015; Ikli et al., 2021b), we have considerably less decision variables, namely the scheduling variables

$w_{ij}=\left\{\begin{array}{cc}1\hfill & \text{if\hspace{0.17em}aircraft\hspace{0.17em}}i\text{\hspace{0.17em}lands\hspace{0.17em}before\hspace{0.17em}aircraft\hspace{0.17em}}j,\hfill \\ 0\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e},\hfill \end{array}\right.$

and the allocation variables

$x_{ik}=\left\{\begin{array}{cc}1\hfill & \text{if\hspace{0.17em}aircraft\hspace{0.17em}}i\text{\hspace{0.17em}is\hspace{0.17em}allocated\hspace{0.17em}to\hspace{0.17em}runway\hspace{0.17em}}k,\hfill \\ 0\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}\right.$

Note that a detailed discussion on the advantages of our formulation is given in Section 2.3. The MIP reads as follows

$\mathrm{m}\mathrm{i}\mathrm{n}\sum _{i=1}^N\left[c_i^{-}\underset{t_i^{-}}{\underbrace{\mathrm{m}\mathrm{a}\mathrm{x}\left(0,T_i-t_i\right)}}+c_i^{+}\underset{t_i^{+}}{\underbrace{\mathrm{m}\mathrm{a}\mathrm{x}\left(0,t_i-T_i\right)}}\right](1)$

subject to

$t_i=T_i-t_i^{-}+t_i^{+}i\in \mathcal{N},(2)$

$t_i+S_{ij}-t_j\le M\left(1-w_{ij}\right)+M\left(1-x_{ik}\right)+M\left(1-x_{jk}\right)i<j,i,j\in \mathcal{N},k\in \mathcal{K},(3)$

$t_j+S_{ji}-t_i\le M{w}_{ij}+M\left(1-x_{ik}\right)+M\left(1-x_{jk}\right)i<j,i,j\in \mathcal{N},k\in \mathcal{K},(4)$

$\sum _{k=1}^K{x}_{ik}=1i\in \mathcal{N},(5)$

$E_i\le t_i\le L_{i}i\in \mathcal{N},(6)$

$t_i\le t_{j}i+m<j,(7)$

$i\in \mathcal{N}\backslash \left\{N-m,\dots ,N\right\},$

$t_i^{-}\ge 0i\in \mathcal{N},(8)$

$t_i^{+}\ge 0i\in \mathcal{N},(9)$

$w_{ij}\in \left\{\mathrm{0,1}\right\}i<j,i,j\in \mathcal{N},(10)$

$x_{ik}\in \left\{\mathrm{0,1}\right\}i\in \mathcal{N},k\in \mathcal{K}.(11)$

The most important constraints in the problem above are constraints (3) and (4), which cover both scheduling of aircraft and their allocation to runways. Note that inequality (3) becomes active only if binary variables w_ij, x_ik and x_jk are equal to one meaning that aircraft i lands before aircraft j, and both aircraft land on the same runway. In this case, the inequality reads as

$t_i+S_{ij}\le t_j$

indicating that minimum separation time S_ij has to be ensured between two landing aircraft i and j. In case when at least one of those binary variables is not equal to one, the inequality is not active due to the large constant M. An analogous argument holds for constraint (4).

Let us also briefly comment on the other constraints. Equalities (2) are auxiliary expressions that linearize the objective function. Constraints (5) guarantee that each aircraft lands only on one runway. Inequalities (6) correspond to time-window constraints, while inequalities (7) represent the CPS constraints (see an example below). Inequalities (8) and (9) ensure that auxiliary variables are non-negative, whereas (10) and (11) represent integrality conditions.

Next, let us give a detailed explanation of the CPS-constraints (7) to clarify their formulation. Note that these constraints are incorporated into the model to guarantee that the landing order of an aircraft deviates from the FCFS or another nominal order at most by m. Suppose that N = 6, $\mathcal{N}=\{1,\dots ,6\}$ and m = 2 and that $i\in \mathcal{N}$ already indicates a specific landing order of an aircraft (e.g. FCFS). For this setting, it holds $\mathcal{N}$∖{N − m, … , N} = {1, 2, 3}. For i = 1, condition i + m < j then yields index pairs (i, j) = (1, 4), (i, j) = (1, 5) and (i, j) = (1, 6). A similar argument holds for i = 2 and i = 3. Hence, the folowing conditions have to be satisfied:

• i = 1: t₁ ≤ t₄, t₁ ≤ t₅ and t₁ ≤ t₆

• i = 2: t₂ ≤ t₅ and t₂ ≤ t₆

• i = 3: t₃ ≤ t₆

To be more precise, these constraints ensure that in the case with N = 6 and m = 2 aircraft 1 does not overtake aircraft 4, 5 and 6 before landing. Similarly, aircraft 2 has to land before aircraft 5 and 6, while aircraft 3 is not allowed to overtake aircraft 6 in the terminal area.

2.3 Complexity reduction compared to other formulations

Number of binary (integer in general case) variables in an MILP is a bottleneck for finding an optimal solution in reasonable time (which can be any time less than a minute in our application example). Even obtaining a solution within some given tolerance, e.g. 5%, might be very challenging if the number of binary variables is large. For instance, if one uses the branch-and-bound algorithm for solving an MILP, the number of linear problems that have to be solved in the worst case is

$2^{\#allbinaryvariables}.$

For that reason, binary variables have to be carefully chosen when modeling the ALP.

So far, many works as, e.g. (Kim et al., 2014; Lieder et al., 2015; Ikli et al., 2021b), have exploited an MIP-model with three sets of integer variables. For comparison, the exact model used by (Ikli et al., 2021b) can be found in Supplementary Appendix A.

Compared to this modeling approach, our model contains only two sets of binary variables, namely the scheduling variables w_ij and the allocation variables x_ik. The difference in this number is linear in K (number of runways) and quadratic in N (number of aircraft). This important modification does not only simplify the implementation process, but also reduces computational time significantly, see next section.

3 Numerical results

In order to validate the proposed model, we performed a large number of numerical tests with different input data. All computations were performed on an Intel quad-core i5 1.0 GHz processor using GUROBI MIP-solver (Gurobi Optimization LLC, 2020), which exploits the branch-and-bound algorithm, see, e.g. (Winston and Goldberg, 2004).

For numerical experiments, data provided in (Rachelson, 2019) were used for Paris-Orly airport, whereas mock schedules were created for three other airports, namely Munich, Frankfurt and Atlanta. These schedules include planned time of arrival for each aircraft, its category and penalty cost (here it is assumed that $c_i^{-}=c_i^{+}$, $i\in \mathcal{N}$). For Munich airport, see Table 3, these values can be found in columns “planned”, “category” and “cost”, respectively. Note that our experiments were performed during the COVID-19 pandemic that is why the input data for the experiments are not real. However, the landing aircraft density corresponds to its real density in the pre- and post-pandemic times.

TABLE 3

TABLE 3. Optimal schedule for Munich airport with N = 40 aircraft landing between 07:00:00 and 08:00:00 on K = 2 runways.

Before the numerical results are discussed, let us briefly take a look at real-world data generation, namely ETA and landing time bounds. To generate an ETA, a random number generated from $\mathcal{N}(\mathrm{0,300})s$ is added to a planned time of arrival. The earliest landing time E_i is calculated by subtracting 120 s from the corresponding ETA. The latest landing time L_i is linearly dependent on the distance to the destination airport. Note that enlarging the bounds does not significantly affect the solver runtime.

For each of four airports introduced above, 10 experiments were run with and without a minimum branch-and-bound gap limit of 5%, see Tables 4 and 5, respectively. This gap essentially shows the relation between the worst and the best possible solution in terms of the objective function value. If this gap gets less than a given minimum, the algorithm terminates, see (Winston and Goldberg, 2004) for more information. Note that the branch-and-bound gap is not equal to the actual relative error. For instance, if the gap is equal to 5%, the relative error in this case can be less than 2%. The time limit in both cases was 60 seconds. For all airports, the maximum position shifting m was set to two, and different numbers of approaching aircraft and runways (less or equal to the actual one) were chosen, namely 40 and 2, 40 and 2, 60 and 3, and 90 and 4 for Paris-Orly, Munich, Frankfurt and Atlanta airports, respectively. An example of an optimal schedule for Munich airport is given in Table 3. Figure 1 visualizes these results for both runways. Note that optimal schedules for three other airports can be found in Supplementary Appendix B.

TABLE 4

TABLE 4. Solver runtimes in seconds and corresponding branch-and-bound gaps with a predefined 5% gap and time budget of 60 s.

TABLE 5

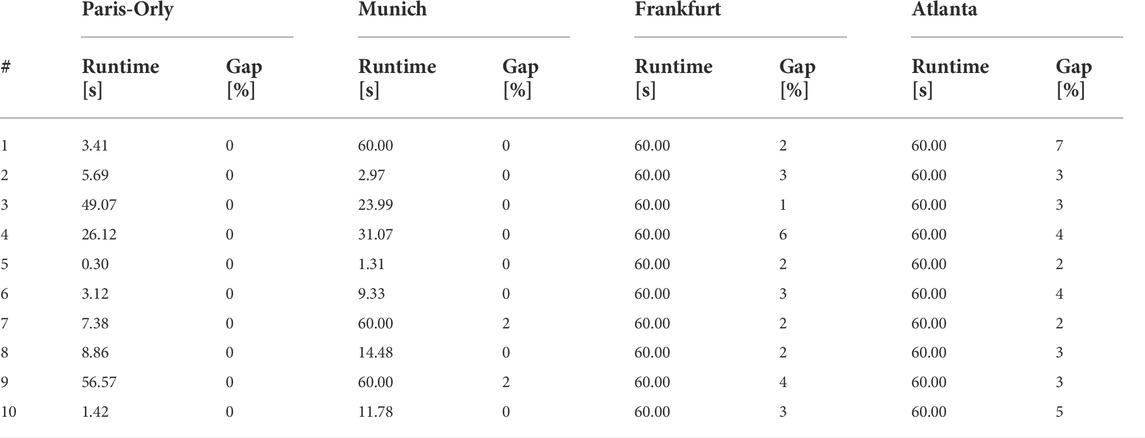
TABLE 5. Solver runtimes in seconds and corresponding branch-and-bound gaps with no predefined gap and time budget of 60 s.

FIGURE 1

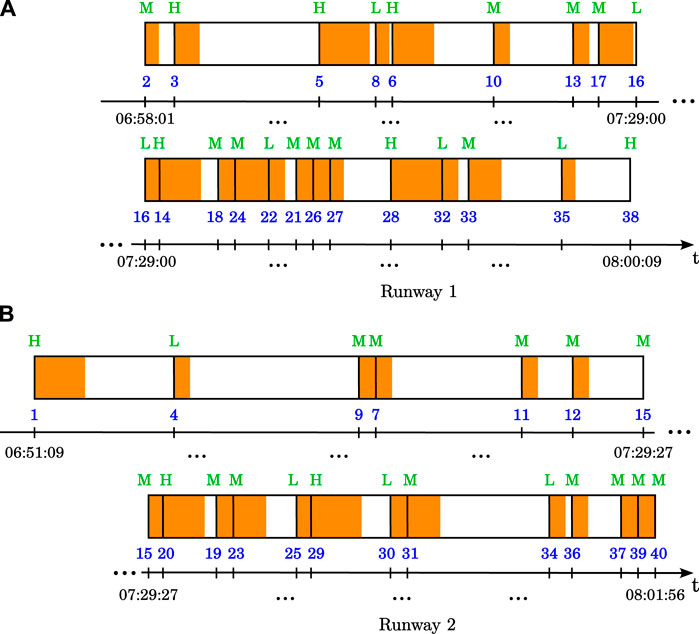
FIGURE 1. Optimal schedule for Munich airport for all aircraft landing on runway 1 (A) and runway 2 (B) between 07:00:00 and 08:00:00. In green: category of the aircarft, in blue: number of the aircraft, in orange: minimum separation time, in white: runway idle time.

The experiments justify the fact that a reasonable solution can be found using our method within a minute even for bigger airports. Only in two simulations, the solver did not find a solution within the branch-and-bound gap of 5%, but a very close one. Moreover, by comparing Tables 4 and 5, it can be seen that seeking for a solution with a corresponding branch-and-bound gap less than 5% might significantly increase the computation time, but not the solution quality.

In order to investigate advantages of optimal scheduling over the FCFS order, the average values of the corresponding objective functions were computed after 100 optimization experiments. The exact results are given in Table 6. It is remarkable that even for such big airports as Atlanta the optimal schedule provided by the solver can improve the values of the objective function by nearly 40% compared to the FCFS heuristics.

TABLE 6

TABLE 6. Comparison of optimal schedules with the FCFS heuristics for different airports.

As to results achieved in other works, (Faye, 2015) reported that the ALP with 44 planes and 2 runways was solved by the exact approach in 20,7 s, while the heuristic method needed between 132,7 and 166,7 s for finding a solution of a large-sized problem with 100 aircraft and 4 runways (see Table 3, S7 and Table 5, L1 in that reference). Results indicated by (Ikli et al., 2021b) show that their optimistic planning approach handles well small- to medium-sized aircraft landing problems with a single runway. However, computational time increases drastically when it comes, e.g. to 2-CPS problems with 30 aircraft. In this particular case, an exact solution can be found within approximately 750 s. To compare our approach with that presented in (Ikli et al., 2021b), experiments for Paris-Orly airport were run for the same setting with N = 30, K = 1 and m ∈ {2, … , 6}. The obtained results are presented in Table 7.

TABLE 7

TABLE 7. Performance of the solver for Paris-Orly airport with N = 30 aircraft landing on one runway for different CPS-numbers.

4 Conclusion

In this paper, an exact method was proposed to obtain an optimal landing sequence by determining landing times for each aircraft within the radar range of an airport and by allocating them to some available runway. The problem was modeled as a mixed-integer linear program with a reduced number of integer variables in contrast to many other previous works. The objective function was chosen such that the total deviation from the target landing times is minimized, and the required constraints as, for example, minimum separation time and CPS are satisfied. For simulations, we exploited the GUROBI MIP-solver based on the branch-and-bound algorithm. Numerical computations performed for four different airports (Paris-Orly, Munich, Frankfurt and Atlanta) demonstrate that the presented problem’s formulation is a suitable approach for achieving near-optimal results in reasonable time.

Possible extensions of our method include integration of a multi-objective function with the aim of finding a good compromise for different stakeholders or incorporation of uncertainties encountered in the terminal area into the model.

Data availability statement

The raw data supporting the conclusion of this article can be provided by the authors upon request.

Author contributions

In the underlying work, SR and MG formulated the novel mixed-integer model of the problem. SR and VN implemented the problem and performed the numerical experiments. Moreover, VN did a literature survey and found possible model extensions.

Funding

This material is based upon work supported, inter alia, by dtec.bw–Digitalization and Technology Research Center of the Bundeswehr [MissionLab] and by the Air Force Office of Scientific Research, Air Force Materiel Command, USAF, under Award No. FA8655-20-1-7026. We acknowledge financial support by Universität der Bundeswehr München. Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the author(s) and do not necessarily reflect the views of the funders.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/ffutr.2022.968957/full#supplementary-material

References

Balakrishnan, H., and Chandran, B. G. (2010). Algorithms for scheduling runway operations under constrained position shifting. Operations Res. 58, 1650–1665. doi:10.1287/opre.1100.0869

CrossRef Full Text | Google Scholar

Beasley, J. E., Krishnamoorthy, M., Sharaiha, Y. M., and Abramson, D. (2000). Scheduling aircraft landings—The static case. Transp. Sci. 34, 180–197. doi:10.1287/trsc.34.2.180.12302

CrossRef Full Text | Google Scholar

Beasley, J. E., Sonander, J., and Havelock, P. (2001). Scheduling aircraft landings at London heathrow using a population heuristic. J. Operational Res. Soc. 52, 483–493. doi:10.1057/palgrave.jors.2601129

CrossRef Full Text | Google Scholar

Bencheikh, G., Boukachour, J., Khoukhi, F., and Alaoui, A. (2009). Hybrid method for aircraft landing scheduling based on a job shop formulation. Int. J. Comput. Sci. Netw. Secur. 9, 78–88.

Google Scholar

Bencheikh, G., Boukachour, J., and Alaoui, A. E. H. (2011). Improved ant colony algorithm to solve the aircraft landing problem. Int. J. Comput. Theory Eng. 3, 224–233. doi:10.7763/ijcte.2011.v3.309

CrossRef Full Text | Google Scholar

Bennell, J. A., Mesgarpour, M., and Potts, C. N. (2011). Airport runway scheduling. J. Oper. Res. 9, 115–138. doi:10.1007/s10288-011-0172-x

CrossRef Full Text | Google Scholar

Bianco, L., Dell’Olmo, P., and Giordani, S. (2006). Scheduling models for air traffic control in terminal areas. J. Sched. 9, 223–253. doi:10.1007/s10951-006-6779-7

CrossRef Full Text | Google Scholar

Briskorn, D., and Stolletz, R. (2013). Aircraft landing problems with aircraft classes. J. Sched. 17, 31–45. doi:10.1007/s10951-013-0337-x

CrossRef Full Text | Google Scholar

Chandran, B. G., and Balakrishnan, H. (2007). “A dynamic programming algorithm for robust runway scheduling,” in 2007 American Control Conference, 1161–1166.

CrossRef Full Text | Google Scholar

Dear, R. G. (1976). The dynamic scheduling of aircraft in the near terminal area. Cambridge, Massachusetts: Ph.D. thesis, Massachusetts Institute of Technology.

Google Scholar

[Dataset] Rachelson, E. (2019). Alp instances. Available at: https://pagespro.isae-supaero.fr/emmanuel-rachelson/alp-instances.html?lang=fr (Accessed 02 12, 2022).

Google Scholar

[Dataset] Gurobi Optimization LLC (2020). Gurobi optimizer reference manual. Available at: https://www.gurobi.com/wp-content/plugins/hd_documentations/documentation/9.1/refman.pdf (Accessed 0210, 2022).

Google Scholar

[Dataset] IATA (2022). Air passenger numbers to recover in 2024. Available at: https://www.iata.org/en/pressroom/2022-releases/2022-03-01-01/(Accessed 04 25, 2022).

Google Scholar

[Dataset] EUROCONTROL (2022). Aviation outlook 2050. Available at: https://www.eurocontrol.int/sites/default/files/2022-04/eurocontrol-aviation-outlook-2050-report.pdf (Accessed 05 03, 2022).

Google Scholar

Faye, A. (2015). Solving the aircraft landing problem with time discretization approach. Eur. J. Operational Res. 242, 1028–1038. doi:10.1016/j.ejor.2014.10.064

CrossRef Full Text | Google Scholar

Furini, F., Persiani, C. A., and Toth, P. (2012). “Aircraft sequencing problems via a rolling horizon algorithm,” in Lecture notes in computer science (Springer Berlin Heidelberg), 273–284. doi:10.1007/978-3-642-32147-4_25

CrossRef Full Text | Google Scholar

Furini, F., Kidd, M., Persiani, C., and Toth, P. (2015). Improved rolling horizon approaches to the aircraft sequencing problem. J. Sched. 18, 435–447. doi:10.1007/s10951-014-0415-8

CrossRef Full Text | Google Scholar

Hu, X.-B., and Chen, W.-H. (2005). Genetic algorithm based on receding horizon control for arrival sequencing and scheduling. Eng. Appl. Artif. Intell. 18, 633–642. doi:10.1016/j.engappai.2004.11.012

CrossRef Full Text | Google Scholar

Hu, X.-B., and Di Paolo, E. (2009). An efficient genetic algorithm with uniform crossover for air traffic control. Comput. Operations Res. 36, 245–259. doi:10.1016/j.cor.2007.09.005

CrossRef Full Text | Google Scholar

Ikli, S., Mancel, C., Mongeau, M., Olive, X., and Rachelson, E. (2021a). The aircraft runway scheduling problem: A survey. Comput. Operations Res. 132, 105336. doi:10.1016/j.cor.2021.105336

CrossRef Full Text | Google Scholar

Ikli, S., Mancel, C., Mongeau, M., Olive, X., and Rachelson, E. (2021b). “An optimistic planning approach for the aircraft landing problem,” in Lecture notes in electrical engineering (Springer Singapore), 173–188. doi:10.1007/978-981-33-4669-7_10

CrossRef Full Text | Google Scholar

Kim, B., Li, L., and Clarke, J.-P. (2014). Runway assignments that minimize terminal airspace and airport surface emissions. J. Guid. Control, Dyn. 37, 789–798. doi:10.2514/1.61829

CrossRef Full Text | Google Scholar

Lee, H., and Balakrishnan, H. (2008). A study of tradeoffs in scheduling terminal-area operations. Proc. IEEE 96, 2081–2095. doi:10.1109/JPROC.2008.2006145

CrossRef Full Text | Google Scholar

Lieder, A., Briskorn, D., and Stolletz, R. (2015). A dynamic programming approach for the aircraft landing problem with aircraft classes. Eur. J. Operational Res. 243, 61–69. doi:10.1016/j.ejor.2014.11.027

CrossRef Full Text | Google Scholar

Pinol, H., and Beasley, J. (2006). Scatter search and bionomic algorithms for the aircraft landing problem. Eur. J. Operational Res. 171, 439–462. doi:10.1016/j.ejor.2004.09.040

CrossRef Full Text | Google Scholar

Pohl, M., Kolisch, R., and Schiffer, M. (2021). Runway scheduling during winter operations. Omega 102, 102325. doi:10.1016/j.omega.2020.102325

CrossRef Full Text | Google Scholar

Psaraftis, H. N. (1978). A dynamic programming approach to the aircraft sequencing problem. Tech. rep. Cambridge, Massachusetts: Massachusetts Institute of Technology.

Google Scholar

Salehipour, A., Naeni, L., and Kazemipoor, H. (2009). Scheduling aircraft landings by applying a variable neighborhood descent algorithm: Runway-dependent landing time case. J. Appl. Operational Res. 1, 39–49.

Google Scholar

Shi, W., Jiang, S., Liang, X., and Zhou, N. (2019). A heuristic algorithm for solving the aircraft landing scheduling problem with a landing sequence division. IEICE Trans. Fundam. E102.A, 966–973. doi:10.1587/transfun.e102.a.966

CrossRef Full Text | Google Scholar

Wen, M., Larsen, J., and Clausen, J. (2005). An exact algorithm for aircraft landing problem.

Google Scholar

Winston, W., and Goldberg, J. (2004). Operations research: Applications and algorithms. Belmont, CA: Thomson Brooks/Cole.

Google Scholar

Xu, B. (2017). An efficient ant colony algorithm based on wake-vortex modeling method for aircraft scheduling problem. J. Comput. Appl. Math. 317, 157–170. doi:10.1016/j.cam.2016.11.043

CrossRef Full Text | Google Scholar

Yu, S.-P., Cao, X.-B., and Zhang, J. (2011). A real-time schedule method for aircraft landing scheduling problem based on cellular automation. Appl. Soft Comput. 11, 3485–3493. doi:10.1016/j.asoc.2011.01.022

CrossRef Full Text | Google Scholar