- Station d’Amélioration Génétique Animale, Institut National de la Recherche Agronomique, Castanet-Tolosan, France
Many of the models used to optimize selection processes in livestock make the assumption that the population is of infinite size and are built on deterministic equations. The finite size case should however be considered explicitly when selection involves one identified gene. Indeed, drift can cause the loss of a favorable allele if its initial frequency is low. In this paper, a stochastic approach was developed to simultaneously optimize selection on two traits in a limited size population: a quantitative trait with underlying polygenic variation and a monogenic trait. We outline the interests of considering the limited size of the population in stochastic modeling with a simple example. Such stochastic models raise some technical problems (uncertain convergence to the maximum, computational burden) which could obliterate their usefulness as compared to simpler but approximate deterministic models which can be used when the population size is large. By way of this simple example, we show the feasibility of the optimization of this type of model using a genetic algorithm and demonstrate its interest compared with the corresponding deterministic model which assumes that the population is of infinite size.
Introduction
Marker- or gene-assisted selection (MAS/GAS) was demonstrated to be more efficient than classical selection schemes for traits which are lowly heritable or difficult and/or expensive to measure (Lande and Thompson, 1990; Meuwissen and van Arendonk, 1992; Dekkers and van Arendonk, 1998). Hereafter, a classical selection scheme is defined as a breeding plan where candidates are sorted according to polygenic estimated breeding values (EBV) only (i.e., without considering known genotypic information for some QTLs or identified genes). The superiority of GAS/MAS has been demonstrated on the short term (Gibson, 1994; Meuwissen and Goddard, 1996; Larzul et al., 1997; Spelman and van Arendonk, 1997; Pong-Wong and Woolliams, 1998) but these results were not always confirmed on the long term, one reason being unfavorable linkage disequilibrium between the major locus and the polygenic background created by the selection (Gibson, 1994; Verrier, 2001).
Several procedures to optimize selection with overlapping generations have been proposed and include an optimal control approach (Dekkers and Chakraborty, 2001; Chakraborty et al., 2002), sequential quadratic programming (SQP, Manfredi et al., 1998) or a genetic algorithm (Costard et al., 2009). Costard et al. (2009) developed a mathematical approach to simultaneously optimize the selection on two traits: a quantitative trait with underlying polygenic variation and a monogenic trait (GAS). They proposed to maximize the frequency of the favorable genotype for the monogenic trait (e.g., resistance to a disease) while minimizing the loss of genetic progress on the polygenic trait.
In GAS modeling, as the selection process is dynamic, the best decision at time t + 1 depends on the values of the state variables at time t, and it is needed to simultaneously optimize the whole set of decision variables across time. In other words, optimization results in a set of decisions which vary across time when the population state changes, especially for the genotype frequency of the identified gene.
The models that are used to optimize the selection process in livestock usually make the assumption that the population is of infinite size. Few studies took into account the variability of the response due to finite population size, mostly in the context of a co-optimization of genetic gain and rate of inbreeding, in the classical selection scheme situation (Meuwissen, 1997; Villanueva et al., 2006; Pong-Wong and Woolliams, 2007). The finite size case has clearly to be considered when selection involves an identified gene. Indeed, it is likely that a favorable but rare allele may disappear due to drift. This case was addressed by Fournet et al. (1997), Meuwissen and Sonesson (2004), Villanueva et al. (2006).
As described by Sanchez et al. (2006), two approaches were invented to describe the selection process to be optimized: the “path method” which gives the QTL favorable allele frequency path during this process, and the “weighting method” which aggregates, with appropriate weights, the polygenic and QTL breeding values. The first approach was followed by Meuwissen and Sonesson (2004), Sanchez et al. (2006), Liu and Wooliams (2010) in the finite population size context.
In this study, we address the question of the optimization of a two traits MAS scheme that takes into account the response variability due to finite population size. The first trait was supposed to be purely polygenic, the secondary trait, monogenic. Our selection is similar to weighing method. To this aim, we extended the deterministic model of Costard et al. (2009).
Our modeling has some similarities with the Meuwissen and Sonesson (2004) “ANNEAL” scheme. This scheme used the simulated annealing algorithm to optimize the path of the QTL allele frequencies which maximizes a mean of 10 estimations of the final genetic gain under an optimum contribution selection plan. However, as quoted by the authors, sampling errors made estimating this mean genetic gain made it hard for ANNEAL to find the optimal path.
Beyond the description of an alternative stochastic model, the objective of this paper was to demonstrate the feasibility and relevance of a dynamic stochastic selection optimization when large numbers of replicates are used to estimate the objective function. Following our previous choice (Costard et al., 2009) the Genetic Algorithm was chosen as the optimization method.
Model Framework
Before entering in the detail of a simple stochastic model in order to provide proof of concept, we describe in this introductory section why and how our new stochastic approach differs from the previously published deterministic approaches.
The Deterministic Approach
The model proposed by Costard et al. (2009) was developed to optimize (1) selection of candidates after evaluation of their breeding value for a main polygenic trait and for a secondary monogenic trait, and (2) mating between selected individuals. The gene affecting the secondary trait was supposed biallelic, the first allele being favorable. As any other deterministic selection model, the Costard et al. (2009) model is a set of equations that include fixed parameters, decision variables (e.g., selection rate), and state variables. Table 1 gives a list of those elements. State variables were statistics which described classes of individuals that shared the same characteristics across the population, i.e., sex s, age a, genotype g for a gene to be selected and category c (e.g., elite vs. non-elite for mating males and females). The state of a class was described by its relative frequency and by its polygenic trait means value. Equations modeled the time evolution of the state variables with respect to natural (ageing or death) and artificial (selection) phenomena with discrete steps.
The values of the state variables at time t + 1 depended on state variables and the values of parameters at time t as well as the values of decision variables corresponding to the applied decision between times t and t + 1. The objective function was the frequency of the favorable genotype in reproducers born in the last year of the selection process, an implicit function of the parameters and variables of the model.
A most essential feature of this type of modeling is that the evolution of the state variables is unique for each set of parameters and decision variable values. On the other hand, the objective function is algebraically expressed as a combination of all those elements (parameters, decision, and state variables). Thus, to a given set of decision variable corresponds a unique set of state variable and a single value of the objective function. The decision variables were selection rates based on genetic values (EBV) for the polygenic trait of individuals belonging to key classes of candidates (defined by specific value of s, a, and c) in the population. (Note that mating probabilities between elite individuals according to their genotype were also introduced in the model). Optimization provided the EBV selection rates qsacgt that should be applied to candidates from the key class Csacg with genotype g at time t, given the constraint that the mean selection rate across the three genotypes (for a biallelic gene), must be equal to a fixed qsac.
It must be noted that other decision variables could have been used without affecting the meaning of the model: an EBV threshold value λsacgt above which candidates could be selected, or the addition of a penalty term θsacgt to the EBV.
Proposed Stochastic Approach
In the case where the population size is finite, one must take into account the variability, due to the stochastic nature of the model, of possible states at time t + 1 resulting from a decision taken at time t. This variability generates three specific phenomena.
Firstly, the relationship between the parameters, decision, and state variables (elementary statistics on the EBV and distribution of the genotype among the elements of the population), must be adapted, for instance using order statistics. However, the modeling problem quickly becomes inextricable when the number of classes and cycles of selection increases. A simple approach is to consider the individuals, rather than their classes, as the elements of the model. For example, if the number of 4-year-old elite males is limited to five individuals, the three elements of the corresponding model (three classes defined by the possible genotypes for a biallelic gene) will be replaced by five elements (the five individuals sharing the same sex, age, and category), but each possessing its own state defined by its genotype and polygenic value.
It must be emphasized that, with this stochastic modeling approach, the decision variables (rates, thresholds or penalties: qsacgt, λsacgt, ou θsacgt) are not equivalent, only the penalty terms being easily applicable.
Secondly, the value of the objective function corresponding to a set of decision variables is not unique. When individuals are used as the elements of the model then the selection process can be simulated easily, the distribution of possible responses can be obtained, and the expectation of the objective function distribution can therefore be estimated (rather than algebraically derived), for any set of decisions.
Thirdly, the search for the optimal selection process should take into account the possible events to come: a decision taken at time t will be optimal only if the set of following events weighted by their probabilities are considered. These probabilities depend on the decisions to be optimized at time t + 1, t + 2, …, T. Thus the rule used in the deterministic model (simultaneous optimization of the whole set of decision variables across time in order to deal with the fact that the best decision at time t + 1 depends on the state variables values at time t) is not practically applicable. For instance, dynamic programming, although often used in this framework, cannot be applied in our particular case where the state variables are numerous continuous variables and not just a few discrete variables.
In the deterministic models proposed by Chakraborty et al., 2002, Dekkers and Chakraborty (2001), Manfredi et al. (1998), and Costard et al. (2009), the decision variables (e.g., the penalties λsacgt) were optimized for each key class of candidates. Since this procedure is not applicable in the present stochastic model for the reason given above, we propose to focus optimization on a simplified framework. The penalties will be defined as constant (invariable with the time t) functions of genotype frequency distribution and compared, the optimization thus being reduced to a two-step procedure: (i) the choice of the function (e.g., a constant value, a linear combination of genotype frequencies in new born females etc.) and (ii) optimization of the coefficient of the function.
To summarize, we propose the following approach: the population is analyzed with simple elements, i.e., individuals characterized by their sex, age, category (elite/non-elite). Their state is defined by their genotype g and their polygenic value m (these state variables replace the genotype frequencies and polygenic mean values of classes in the deterministic model).
1. Selection is optimized by choosing the penalties to be added to the EBV. These penalties vary according to the genotype of the identified gene and possibly according to the genotype frequencies when applying the penalty.
2. For a given set of penalties, the evolution of the population is simulated many times in order to obtain the distribution of the state variables.
3. The objective function is a composite statistic of the distribution, at some stage in the selection process (e.g., the last year) and across elements of the models defined by a given characteristic (e.g., the 1-year-old females), of the genotypes for the gene affecting the secondary trait and of the polygenic values for the main trait.
Besides the computational time inherent to any stochastic approach, the proposed approach can be invalidated for two reasons:
1. All numerical optimization procedures are based on the evaluation of differences between the values of the objective function obtained for a decision variables vector and which become closer and closer to each other as the optimum is nearly reached. If the estimation errors for the objective function are of the same order as these variations, then convergence toward an optimum would be impossible.
2. We cannot exclude that the approximate solutions given by a simpler deterministic model were sufficient if one is solely interested in distribution expectations.
In this study, our aim is to show that our proposed approach is feasible and efficient using a simple example. We will then illustrate how this approach can be used to choose amongst different selection methods.
Materials and Methods
Proof Model
In most livestock populations, only the number of males is small. Our illustrative model is therefore composite, as the population elements are individuals for the males and classes for the females. Consequently, the state variables which characterize these elements are the genotype gj and the polygenic value mj for each male, the genotypic frequency fs,a,c,t,g and the mean polygenic value μs,a,c,t,g for each class of females (s = 2).
To facilitate the proof of concept, the selection scheme is extremely simplified. There is no female selection, the male selection is performed in one step (Ns selected candidates amongst N candidates), and we include random mating, non-overlapping generations and constant genetic variability across time. We use the notations of Costard et al. (2009) with appropriate modifications to take into account the finite male population size.
Renewal of the female population
The genotypic frequency and the mean polygenic values of the new generation (a = 1, c = 1) at time t are defined as:
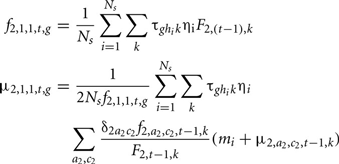
where 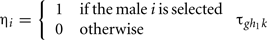 is the probability that the progeny has a genotype g given that the parents have the genotypes k (dam) and hi (sire i). F2, t−1, k is the probability that the dam has a genotype k, defined by:
is the probability that the progeny has a genotype g given that the parents have the genotypes k (dam) and hi (sire i). F2, t−1, k is the probability that the dam has a genotype k, defined by:
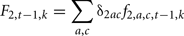
Where δ2ac is the proportion of females of age a and class c.
Renewal of the male population
We randomly simulated the genotype gi = g and the polygenic value mi of the sire i (i = 1…N), which is the progeny of the sire j of genotype hj, and of polygenic value mj. The genotype was simulated from multinomial distribution with the parameters 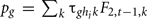 (g = 1, 2, 3). The polygenic value was sampled from normal distribution with constant variance and expectation
(g = 1, 2, 3). The polygenic value was sampled from normal distribution with constant variance and expectation
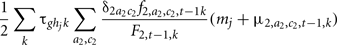
Selection of reproducers
For the generation t, an index I(j,t)=mj+c(t,hj) was assigned to each male candidate j. This index is a linear combination of the individual’s polygenic value mj and a weight c(t,hj), which is function of its genotype hj (as the favorable genotype was chosen to be the first one (hj = 1), the weights c(t, 2) and c(t, 3) must be considered as penalties and are expected to be generally negative). The Ns males with the largest index values I(j,t) were selected amongst the N candidates to renew the population.
The weight formulation c(t,hj) can be optimized. For example, a selection uniquely based on the main polygenic trait is obtained using the index I(j,t)=mj Conversely, the criterion I(j,t)=c(t,hj) corresponds to a selection that is only based on the secondary trait. Generally, the coefficients c(t,hj) can be constant or depend on generation t population characteristics such as genotypic frequencies for the males and/or females. Optimization of the selection of reproducers, and therefore of the selection process first consists in choosing the type of weights, and then in determining the best values to be assigned to decision variables for each type of weight. In our proof model, three types of weight and indexes (I1, I2, I3), which correspond to respectively 10, 6, and 2 decision variables were compared:
1. Weights c(t,hj) can be a linear combination of the genotypic frequencies for males and females in the population at generation t:
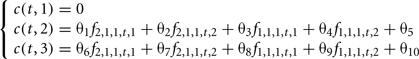
The 10 parameters to be optimized are in this case θ1,…,θ10.
2. The information about male genotypic frequencies can be neglected as they have a low economical impact for the production given their small population size.
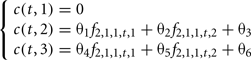
The six parameters to be optimized are θ1, θ2, θ3, θ4, θ5, θ6.
3. Lastly, the third type of weight is the simplest case where the coefficients c(t, hj) are constant for any generation t:
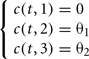
In this particular case, there are only two parameters to optimize θ1, θ2.
Objective function
To facilitate the comparison between the stochastic and deterministic models, the objective function to be maximized was the expectation of a composite function which describes the population state at the end of the selection process for the secondary trait (favorable female genotype frequency) and for the main trait (deviation from the maximally achievable genetic progress):
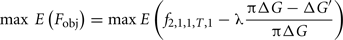
where ΔG′ is the genetic progress achieved on the main trait for the simultaneous selection on both traits, ΔG is the genetic progress that would have been achieved without selection on the secondary trait and 1 − π is the accepted fraction of genetic progress loss (if, for instance, we accept only a maximal reduction of the genetic progress of 5% on the main trait when putting some selection pressure on the secondary trait, then π = 0.95 and the term (πΔG − ΔG′)/(πΔG) will constraint ΔG′ to being not too far below πΔG, the λ coefficient allowing a control of the constraint (higher λ, stronger the constraint)). As in Costard et al. (2009), a genetic algorithm was used to optimize the objective function with constraints.
Simplified Deterministic Model
In order to evaluate the usefulness of the stochastic approach, as compared to a much simpler deterministic approach, the model of Costard et al. (2009) was simplified to fit into the stochastic model framework described above. For any generation, selection of males was performed with a constant rate W111 as in Costard et al. (2009). The characteristics of the selected males, genotypic frequencies and polygenic values were obtained as follows:
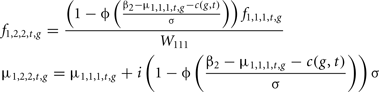
Where β2 is the selection threshold, Φ(β) the Normal cumulative distribution function and i(q) the selction intensity corresponding to a q selection rate.
Mating between the selected males and the females was performed randomly. The genotypic frequency and the mean polygenic value of the progeny were:
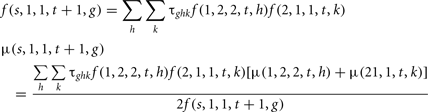
Numerical Application
The population consists of a large number of females and N = 10 males, amongst which the Ns = 5 best ranked males according to their index were selected. Following this selection, males and females were mated in a panmictic way with identical male contribution (one male gives two male progenies for each generation). This process is iterated over T generations (5, 10, 15, 20) and simulated 1000 times. The initial frequencies for the three considered genotypes (g = 1,2,3) are respectively 20, 50, and 30%. The genetic variance is equal to σ2g = 36. In this example, the coefficient λ is set to an arbitrary value of 5.
Results
Feasibility of the approach: does the genetic algorithm converge toward the maximum in the stochastic model?
We compared the results obtained using the genetic algorithm with those obtained by a grid search for the third index I3 with two decision variables (θ1,θ2). Three different cases were tested with 5, 10, and 15 generations and a maximum loss of progress of 10%. Both approaches gave similar results (Table 2). Results were slightly better with the genetic algorithm (higher values of the objective function). These results could be explained by the imprecise step of the grid search (0.2) and by the limited number of simulations (1000). Therefore, for this selection scheme, global optimization using a stochastic modeling approach seems feasible with a genetic algorithm.
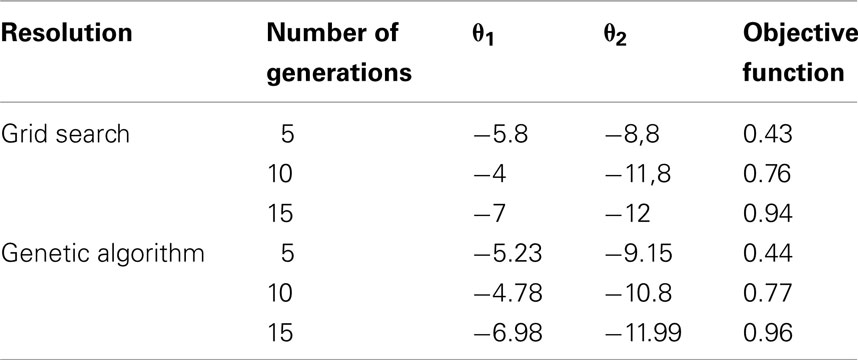
Table 2. Optimized weights (θ1 and θ2) of the unfavorable genotypes in the selection index and objective function obtained with the grid search and the genetic algorithm with a maximum loss of progress of 10%.
Superiority of the Stochastic Model Compared to the Deterministic Model
Table 3 displays the optimization of the deterministic model given the different configurations: 5, 10, 15, and 20 generations, 10% maximum loss of genetic progress or no constraint on the loss. The values of the objective function obtained with the deterministic model are in general greater or equal to those obtained with the stochastic model. These results were logical as the deterministic model did not consider the depressing effect of random sampling on mean distributions (the convergence, increasing the population size, of the stochastic model toward the deterministic one was checked, result not shown). The finite population size therefore has a noticeable effect on the outcome of selection. The (negative) optimal values predicted for the coefficients θ1,θ2 obtained without constraint on the loss of genetic progress were very low for both stochastic and deterministic model. However, these values strongly increase (in absolute terms) when a constraint on the loss of genetic progress is imposed. In addition, under this constraint, the values of the coefficients θ1,θ2 were very close for both models. At the optimum, the heterozygous genotype is less penalized than the unfavorable homozygous genotype (θ2 < θ2). The ratio between these weights vary between 0.34 and 0.83, mostly within [0.4,0.6], showing that the penalty is not far to be proportional to the number of unfavorable alleles.
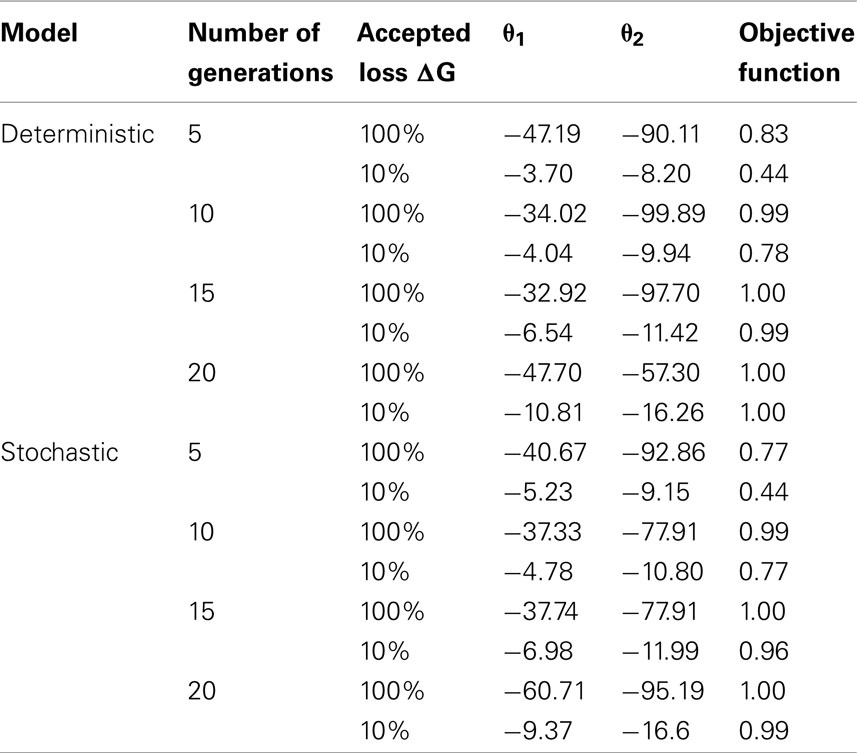
Table 3. Results obtained with the optimization of the deterministic and the stochastic models with the optimized weights (θ1 and θ2) of the unfavorable genotypes in the selection index and the objective function for different configurations: number of generation cycles, percentage of tolerated loss of genetic progress.
In order to assess the difference in prediction between the two models, simulations were performed with the stochastic model using values of the coefficients θ1,θ2 obtained with the optimization of the stochastic model (“stochastic coefficients”) and values obtained with the optimization of the deterministic model (“deterministic coefficients”; Table 4).
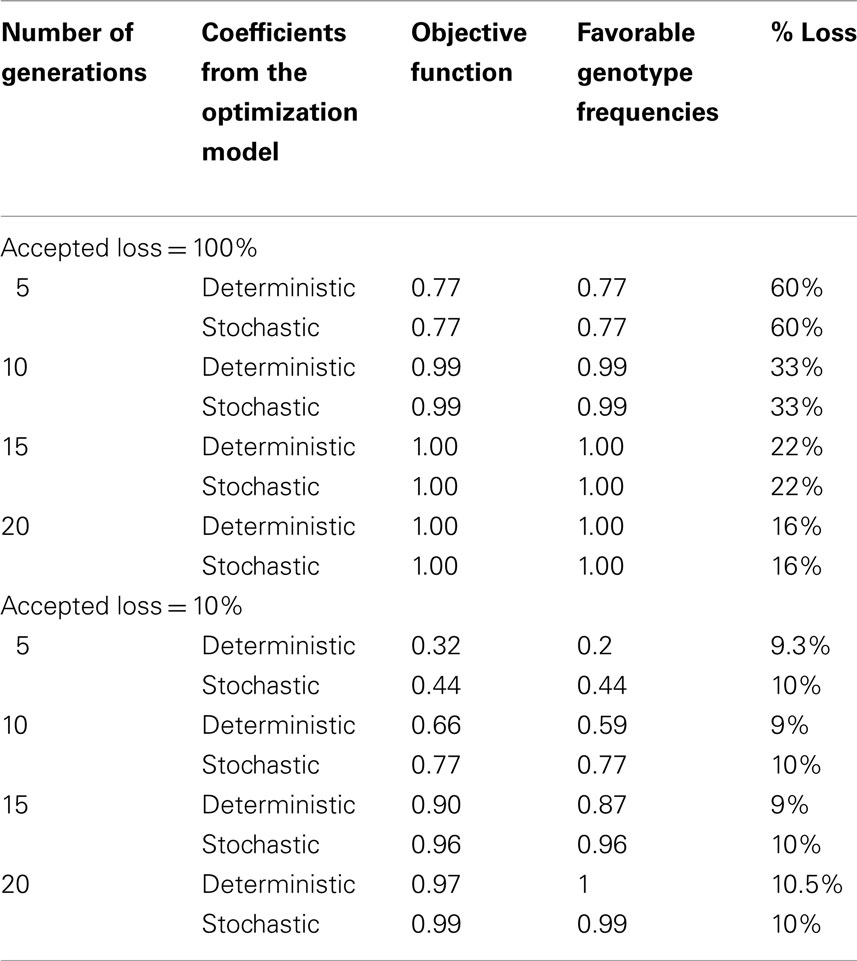
Table 4. Results obtained with different values of coefficients in the stochastic model: coefficients from the optimization of the stochastic model and coefficients from the optimization of the deterministic model.
In the case where no constraint was imposed on genetic progress, use of a stochastic model is not justified as the results obtained with both models were identical.
In the case where a constraint was imposed, there was a significant difference between the outputs of the stochastic model using stochastic or deterministic coefficients (p < 0.001): the value of the objective function of the stochastic model was smaller when using the deterministic coefficients compared to the stochastic coefficient, whatever the number of generations, with a lower loss of genetic progress but much lower favorable genotypic frequency in females. The stochastic model performed significantly better the deterministic model.
Application of the Stochastic Model to Choose a Selection Criterion
The stochastic model was evaluated with different indexes I1, I2, I3 on 5, 10, 15, and 20 generations, with different values of accepted genetic progress loss: 5, 10, and 100%. Table 5 shows that the values of the optimized objective function were similar for all indexes. Therefore, taking into account the population structure with I1, I2 does not seem useful. In our setting with non-overlapping generations and a one-step selection of males, the I3 index is sufficient.
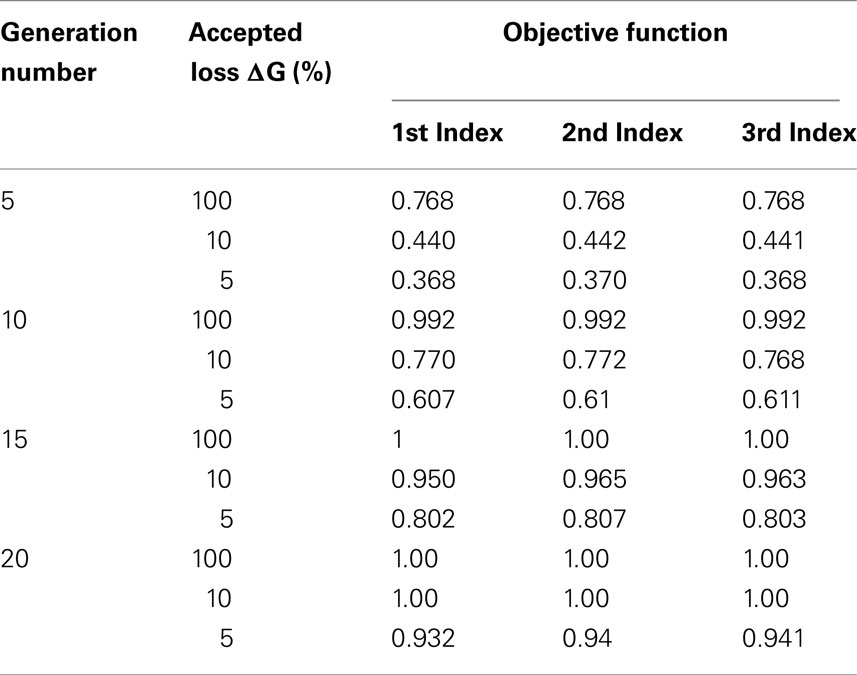
Table 5. Objective function values obtained with the different indexes for 5, 10, 15, and 20 generations, 5, 10, and 100% of loss of genetic progress.
Regarding the coefficient values θ1, θ2 for the index I3 and the different configurations tested, the coefficients assigned to the males of genotype 2 and 3 were negative (Table 3). The coefficient assigned to genotype 2 was less penalizing than the one assigned to genotype 3.
Discussion and Conclusion
To our knowledge, this paper is the first evaluation of a stochastic dynamic model for GAS using a genetic algorithm. This approach was developed to deal with selection in small populations where drift plays an important role. To avoid useless numerical complications, this model was evaluated in a very simple situation. We have been able to demonstrate that this new approach is feasible and useful.
The feasibility of the optimization with a stochastic modeling approach using a genetic algorithm was validated through a grid search in a very simple framework.
The comparison of the deterministic and stochastic models demonstrated that in populations of limited size, a deterministic model, which assumes that the population is very large, overestimates the genetic progress and produces suboptimal selection criteria. In the small example studied (Table 4), the frequency of the favorable genotype reached in the short term (five generations) was inferior to 50% of its optimal value obtained with the stochastic model. The optimal selection strategy thus obtained with the stochastic approach could not be obtained with a deterministic model.
The dynamic stochastic approach may be used to optimize and compare selection alternatives. Basic illustration was provided and showed that the simplest decision criteria were as good as those obtained with a selection criterion that takes into account the genotypic structure of the population, such as genotypic frequency for females and/or males. However, our framework was restricted to non-overlapping generations and the selection of the males was performed in only one step. The generalization of the results obtained should therefore be taken with caution.
It would be interesting to evaluate the model in more complex frameworks. For example, the “best” males could be kept during several generations, or the uses of several selection steps for both females and males could also be considered. It would also be interesting to take into account the evolution of the genetic variance across generations. Finally, in the specific setting of a finite population size of reproducers, considering the relationship matrix between the individuals may help minimizing the inbreeding rate and maintaining a genetic diversity.
In this stochastic approach, the empirical distributions of the objective function and its components (e.g., the polygenic gain, the genotypic frequency in different classes of animal, etc.) are produced. In our demonstration, we focused only on the expectation of the objective function expectation. Modification of the criteria, such as the maximization of the objective function expectation with a constraint on variance, would be straight-forward.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Midi Pyrénées Région is gratefully acknowledged for partly granting A. Costard-Devalle
References
Chakraborty, R., Moreau, L., and Dekkers, J. C. M. (2002). A method to optimize selection on multiple identified quantitative trait loci. Genet. Sel. Evol. 34, 145–170.
Costard, A. D., Vitezica, Z. G., Moreno, C. R., and Elsen, J. M. (2009). A dynamic deterministic model to optimize a multiple-trait selection scheme. J. Anim. Sci. 87, 885–894.
Dekkers, J. C. M., and Chakraborty, R. (2001). Potential gain from optimizing multigeneration selection on an identified quantitative trait locus. J. Anim. Sci. 79, 2975–2990.
Dekkers, J. C. M., and van Arendonk, J. A. M. (1998). Optimizing selection for quantitative traits with information on an identified locus in outbred populations. Genet. Resour. Crop Evol. 71, 257–275.
Fournet, F., Elsen, J. M., Barbieri, M. E., and Manfredi, E. (1997). Effect of including major gene information in mass selection: a stochastic simulation in a small population. Genet. Sel. Evol. 29, 35–56.
Gibson, J. P. (1994). “Short term gain at the expense of long term response with selection of identified loci,” in 5th World Congress of Genetics Applied to Livestock Production, Guelph, ON, 201–204.
Lande, R., and Thompson, R. (1990). Efficiency marker assisted selection in the improvement of quantitative traits. Genetics 124, 743–756.
Larzul, R., Manfredi, E., and Elsen, J. M. (1997). Potential gain from including major gene information in breeding value estimation. Genet. Sel. Evol. 29, 161–184.
Liu, A. Y. H., and Wooliams, J. A. (2010). Continuous approximations for optimizing allele trajectories. Genet. Res. Camb. 92, 157–166.
Manfredi, E., Barbieri, M., Fournet, F., and Elsen, J. M. (1998). A dynamic deterministic model to evaluate breeding strategies under mixed inheritance. Genet. Sel. Evol. 30, 127–148.
Meuwissen, T. H. (1997). Maximizing the response of selection with a predefined rate of inbreeding. J. Anim. Sci. 75, 934–940.
Meuwissen, T. H., and van Arendonk, J. A. M. (1992). Potential improvements in rate of genetic gain from marker-assisted selection in dairy cattle breeding schemes. J. Dairy Sci. 75, 1651–1659.
Meuwissen, T. H. E., and Goddard, M. E. (1996). The use of marker haplotypes in animal breeding schemes. Genet. Sel. Evol. 28, 161–176.
Meuwissen, T. H. E., and Sonesson, A. K. (2004). Genotype-assisted optimum contribution selection to maximize selection response over a specified time period. Genet. Res. Camb. 84, 109-1–109-6.
Pong-Wong, R., and Woolliams, J. A. (1998). Response to mass selection when an identified major gene is segregating. Genet. Sel. Evol. 30, 313–337.
Pong-Wong, R., and Woolliams, J. A. (2007). Optimisation of contribution of candidate parents to maximise genetic gain and restricting inbreeding using semidefinite programming. Genet. Sel. Evol. 39, 3–25.
Sanchez, L., Caballero, A., and Santiago, E. (2006). Palliating the impact of fixation of a major gene on the genetic variation of artificially selected polygenes. Genet. Res. Camb. 88, 105–118.
Spelman, R. J., and van Arendonk, J. A. M. (1997). Effect of inaccurate parameter estimates on genetic response to marker-assisted selection in an outbred population. J. Dairy Sci. 80, 3399–3410.
Verrier, E. (2001). Marker assisted selection for the improvement of two antagonistic traits under mixed inheritance. Genet. Sel. Evol. 33, 17–38.
Keywords: gene-assisted selection, optimization, small population, genetic algorithm, stochastic model
Citation: Costard AD and Elsen J-M (2011) Optimization of gene-assisted selection in small-sized populations: comparison of deterministic and stochastic approaches. Front. Gene. 2:40. doi: 10.3389/fgene.2011.00040
Received: 29 March 2011; Accepted: 21 June 2011;
Published online: 21 July 2011.
Edited by:
Steve Bishop, University of Edinburgh, UKReviewed by:
Andrea B. Doeschl-Wilson, University of Edinburgh, UKKathryn Kemper, University of Melbourne, Australia
Piter Bijma, Wageningen University, Netherlands
Copyright: © 2011 Costard and Elsen. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Jean-Michel Elsen, Station d’Amélioration Génétique Animale, Institut National de la Recherche Agronomique, 31326 Castanet-Tolosan, France. e-mail:amVhbi1taWNoZWwuZWxzZW5AdG91bG91c2UuaW5yYS5mcg==
 Anne D. Costard
Anne D. Costard
