- 1 Department of Biostatistics, University of Alabama at Birmingham, Birmingham, AL, USA
- 2 Department of Statistics, Kansas State University, Manhattan, KS, USA
- 3 Department of Epidemiology and Statistics, Case Western Reserve University, Cleveland, OH, USA
Several authors have acknowledged that testing mediational hypotheses between treatments, genes, physiological measures, and behaviors may substantially advance our understanding of how these associations operate. In psychiatric research, the costs of measuring the putative mediator or the outcome can be prohibitive. Extreme sampling designs have been validated as methods for reducing study costs by increasing power per subject measured on the more expensive variable when assessing bivariate relationships. However, there exist concerns about how missing data can potentially bias the results. Additionally, most mediation analysis techniques presuppose the joint measurement of mediators and outcomes for all subjects. There have been limited methodological developments for techniques that can evaluate putative mediators in studies that have employed extreme sampling, resulting in missing data. We demonstrate that extreme (selective) sampling strategies can be beneficial in the context of mediation analyses. Handling the missing data with maximum likelihood (ML) resulted in minimal power loss and unbiased parameter estimates. We must be cautious, though, in recommending the ML approach for extreme sampling designs because it yielded inflated Type 1 error rates under some null conditions. Yet, the use of extreme sampling designs and methods to handle the resultant missing data presents a viable research strategy.
Introduction
Mediation analysis has a long history (MacCorquodale and Meehl, 1948) and currently is a very popular topic in a variety of research disciplines, including psychology, sociology, education, health behavior, and program evaluation. Although mediation analysis has not received as much attention outside of the behavioral sciences, Stoltenberg et al. (2002) acknowledged that testing mediational hypotheses between treatments, genes, biochemical or physiological measures, and behaviors may substantially advance our understanding of how these associations operate. Furthermore, there has been growing interest in examining the pathways that mediate the effects of many causal factors (e.g., experimental treatments, genetic polymorphisms) on psychiatric, neurological, and behavioral outcomes. For example, the serotonin transporter gene has been investigated in relation to anxiety-related personality traits (Lesch et al., 1996), clinical depression (Hauser et al., 2003), smoking behavior (Munafò et al., 2004), and alcohol consumption (Hammoumi et al., 1999).
The investigation of mediation involving genetic factors often requires the definition of intermediate phenotypes of theoretical interest, which may be behavioral or neurobiological in nature. The intermediate phenotype concept also represents a strategy for characterizing neural systems affected by risk gene variants to describe quantitative mechanisms of brain functioning in psychiatric diseases. Although the term “endophenotype” was originally used to elucidate more general psychological processes (Meyer-Lindenberg and Weinberger, 2006), it is currently used to describe risk factors or intermediate biological phenotypes that mediate genetic effects (Gottesman and Gould, 2003). For example, impaired response inhibition has been proposed as a cognitive endophenotype (i.e., mediator) for genetic associations to ADHD (Slaats-Willemse et al., 2003), while measures of deficits in sustained attention (Chen and Faraone, 2000) and visual performance (Cornblatt and Malhotra, 2001) have received considerable attention as mediators of genetic effects in the schizophrenia literature. In a review of findings concerning the genetic effects in mediation, Veling (2008) noted that genetic factors have been studied as mediators in many areas of psychiatry. For example, there is growing evidence that psychosis-associated environmental exposures, at critical developmental stages, may result in long-lasting epigenetic alterations that impact on the neurobiological processes involved in many pathologies. Specifically, Rutten and Mill (2009) report indirect evidence suggesting a potential major role for epigenetic mechanisms in mediating the affect of childhood trauma on certain psychoses.
One of the most popular approaches for assessing mediation involves fitting a sequence of linear regression equations (Baron and Kenny, 1986). Let Yi denote the outcome (i.e., MRI measure or oxidative damage of brain tissue) for individual i, Zi an intermediate (potential mediator) variable, and Xi a potential causal factor of interest (e.g., treatment vs. control) for individual i. In standardized notation (i.e., all variables have zero mean and unit variance), the three separate linear models can be expressed as:

where the uppercase A, B, C, and C′ represent unknown fixed regression parameters estimated by lowercase sample coefficients (a, b, c, and c′), and the errors (εs) for each model are assumed to be normally distributed, uncorrelated, and to have mean zero and constant variance. Baron and Kenny (1986) and Judd and Kenny (1981) have discussed four steps in establishing whether the intermediate variable Z is to be considered a mediator:
Step 1: Demonstrate that the potential causal factor, X, is associated with the outcome, Y (Regression model 1; Reject H0: C = 0).
Step 2: Demonstrate that the potential causal factor, X, is associated with the intermediate variable, Z (Regression model 2; Reject H0: A = 0). This step essentially involves treating the mediator as if it were an outcome variable, which has led to some statistical concerns about Z being both a fixed and a random effect (Bauer et al., 2006).
Step 3: The mediator and the outcome may be associated because they are both caused by X; therefore, one must demonstrate that the mediator (Z) affects the outcome variable (Y) while statistically controlling for X (Regression model 3; Reject H0: B = 0).
Step 4: Demonstrate that the direct (adjusted) effect of X on Y controlling for Z (C′) is significantly smaller than the total (unadjusted) effect of X on Y (C).
The effects in both Steps 3 and 4 are estimated in regression model 3. If all four of these steps are met and H0: C′ = 0 is rejected, then the data are consistent with the hypothesis that variable Z partially mediates the X–Y relationship. If H0: C′ = 0 is not rejected, then complete mediation is indicated. Currently, dozens of tests for mediation have been proposed with no consensus on which is best (Mackinnon et al., 2002; Albert, 2008). Methods that test whether the association between X and Y is significantly smaller when Z is controlled in order to assess mediation do not require the X–Y relationship to be non-significant (MacKinnon et al., 1995). We will focus on the “four step” approach to testing partial mediation [i.e., mediation leads to a significant reduction in X–Y relationship (c − c′)].
In psychiatric research, sometimes the costs of measuring the putative mediator (Z) or the outcome (Y) can be prohibitively large or can only be measured after the organism has died. For example, some cognitive functioning measures (e.g., motor skill tasks) can be measured inexpensively and without harming the subject. Some measures associated with cognitive decline (e.g., oxidative damage of specific brain tissues) may require the researchers to wait for the subject to die. This is also true of tissue-specific gene expression and gene-methylation measurements. Also, if the outcome is a terminal measure, the researchers may refrain from sacrificing all the subjects in order to collect more longitudinal data or to examine treatment or genetic effects on late-life outcomes or lifespan. Similarly, some brain function measures could be prohibitively expensive for a large number of subjects (e.g., MRI assessments).
Extreme sampling designs have been used to reduce study costs by increasing power per subject measured on the more expensive variable (Feldt, 1961; Alf and Abrahams, 1975; Abrahams and Alf, 1978; Allison et al., 1998), which has also created concerns about how missing data potentially affects the reliability and power of the statistical results (Beasley et al., 2004; Preacher et al., 2005). Most mediation analysis techniques presuppose the joint measurement of mediators and outcomes for all subjects, apart from limited missing data (i.e., complete-case data). There have been limited methodological developments for techniques that can evaluate putative mediators in studies that have employed extreme sampling designs because obtaining certain measurements is prohibitively costly.
How to select subjects for obtaining measurements is the initial challenge in using selective sampling to reduce study costs (i.e., which subjects to measure on the expensive variable). One approach would be random selection in which case the missing data (i.e., subjects not measured) are missing-completely at-random (MCAR). For the MCAR mechanism to be valid, the probability of missingness is not a function of any variable, whether measured or not. Another approach would be to employ extreme sampling [e.g., measure organisms on the mediator (Z) and then select organisms with extreme values of Z to measure on Y]. This would no longer meet the MCAR condition; however, this missingness would satisfy the missing-at-random (MAR) criteria (see Little and Rubin, 2002). When data are MAR, data for any specific variable are missing as a function of the other measured variables.
By selecting subjects from both tails of a distribution (i.e., subjects with high or low values), two-tailed extreme sampling generally increases the expected correlation between expensive (or terminal) measures and other variables (Allison et al., 1998) and thereby incidentally increases statistical power per subject. However, there is a trade-off between (a) increasing the correlation through extreme sampling and (b) reducing the overall statistical power due to the reduction in sample size (Beasley et al., 2004). Taris and Kompier (2006) concluded that extreme-groups analysis may grossly bias meditational effects in the context of a longitudinal design. Similarly, Maxwell and Cole (2007) conducted simulation studies and found that cross-sectional estimates of the direct effect of X on Y, the indirect effect of X on Y through Z, and the proportion of the total effect mediated by Z were highly misleading. D:TarisandKompier’s:2006] results are based on existing datasets and not on simulations; thus, it is unclear whether their recommendations are based on bias created by using cross-sectional estimates of a longitudinal mediation process, bias created by the missing data in an extreme sampling design, or artifacts in their data.
Motivating Example
In this paper, we will focus on the “four step” approach to testing partial mediation in a two-group (e.g., Selenium vs. Placebo) experimental design where extreme sampling is based on a supposed mediator (Z) with no missing data that is used to select cases for measuring the outcome (Y) that has missing values due to it being too expensive to measure. For example, Selenium is thought to protect the brain from oxidative damage in various models of neuro-degeneration (see Ishrat et al., (2009 for murine model). In this case, assigning subjects to treatment conditions (e.g., Selenium vs. Placebo) and measuring the epigenetic pathways response (Z) after a certain number weeks is relatively inexpensive compared to collecting brain imaging measures of cognitive function via MRI (see Figure 1).
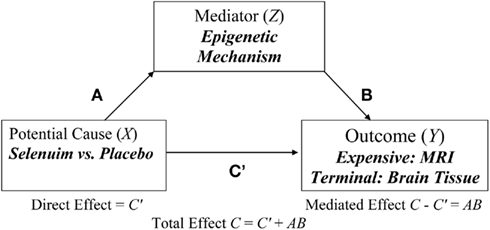
Figure 1. Hypothetical example of an epigenetic mechanism (Z) mediating the effect of selenium (X) on an expensive (MRI) or terminal (brain tissue) outcome (Y).
To illustrate, Table 1 presents a small hypothetical dataset with N = 24 cases. In the data, X is a effect-code representing the independent variable with Selenium coded as −1 and Placebo coded as 1. Z is the mediator (e.g., epigenetic pathway), and Y is the outcome variable. Step 1 of the Baron and Kenney approach to assessing mediation was met and showed a statistically significant total effect [c = 0.5765; t(22) = 3.31; p = 0.0032]. Step 2 is also met with a significant relationship between X and Z [a = 0.5165; t(22) = 2.83; p = 0.0098]. Step 3 is also satisfied, where the mediator (Z) is significantly related to the outcome variable (Y) while statistically controlling for X [b = 0.7074; t(21) = 5.06; p < 0.0001]. Regression model 3 results also indicates mediation because the relationship of X to Y is no longer significant with Z in the model [c′ = 0.2112; t(21) = 1.51; p = 0.1456]. The mediated effect is (c − c′) = (0.5765 − 0.2112) = 0.3653. The McGuigan and Langholtz (1998) test for differences in coefficients was also statistically significant [t(21) = 2.50; p = 0.0205]; thus, Step 4 was also confirmed and one would conclude that Z mediates the effect of X on Y.
Table 1 also demonstrates three strategies for selectively sampling subjects to reduce study costs. In the first sampling strategy, subjects were ranked according to their Z value and every other Y value was coded as missing (Half). Retaining every other value ensures that missingness on Y is not systematically related to Z, which mimics a MCAR condition with 50% missing data. In the second sampling strategy, subjects were ranked according to their Z value and Y values between the 75th and 25th percentiles of Z were coded as missing (Z), which is a symmetric two-tailed extreme sampling design that mimics a MAR condition with 50% missing data. In the third sampling strategy, specimens were ranked according to their Z value and those above the 75th percentile that were also assigned to the Placebo condition (X = 1) or below the 25th percentile that were also assigned to the Selenium group (X = −1) were retained while the remaining individuals had their Y measurements coded as missing (Z|X). This again mimics a MAR condition with approximately 50% missing data. Although optimal thresholds for extreme sampling designs depend on many factors (Fowler, 1992; Preacher et al., 2005), the quartile sampling approach is the most common in extreme sampling designs (see Discussion).
For any of the three sampling schemes, listwise deletion (LD), as implemented in most statistical software, will drastically reduce the sample size for regression models 1 and 3. Furthermore, the missing data must be MCAR for LD to yield valid results (Little and Rubin, 2002). Thus, mediation analyses using LD potentially affects the parameter estimates of the B, C, and C′; and therefore the decisions in Steps 1 and 3. Although the results for the a coefficient from Step 2 will not necessarily change because neither Z nor X has missing data (pairwise deletion would likely be utilized in an experimental setting), LD will have an effect on the X–Z relationship when Regression Model 3 is conducted. The McGuigan and Langholtz (1998) test is based on the difference in c and c′ coefficients and the SE for this test is based on a composite of the SE in Models 1 and 3; therefore, using this test to evaluate Step 4 will be affected by LD of missing data. The expectation–maximization (EM) algorithm is a method for obtaining maximum likelihood (ML) estimates in the presence of missing data, based on the assumption that the missingness mechanism is at least MAR, but not necessarily MCAR (Little and Rubin, 2002), and should produce unbiased estimates.
Table 2 shows the results from the analyses using LD and ML based on the three sampling strategies performed on the data in Table 1. As can be seen, for Half, LD and ML slightly overestimate the c and c′ coefficients and slightly underestimate the b coefficient. Additionally, LD should have lower statistical power due to the missing data, leading the researcher to conclude that a mediating relationship does not exist. However, ML does have the statistical power to recognize significant mediation. For the Z Quartile sampling scheme, LD again suffers from into little power while ML is sufficiently powered. The Z|X Quartile sampling scheme yielded very unusual results in that the mediation reversed and the effect of X on Y was larger after including Z in Regression Model 3. As seen in Table 2, the c and c′ coefficients were overestimated by both LD and ML. Further, the b coefficient was negative for both methods even though the relationship was strong and positive in the Full data analysis. It is difficult to discern whether these analyses represent the properties of LD, ML, or the selective sampling schemes. These results may simply be an artifact of these methods applied to one relatively small dataset. Therefore, we conducted a simulation study to further investigate the properties of these methods.
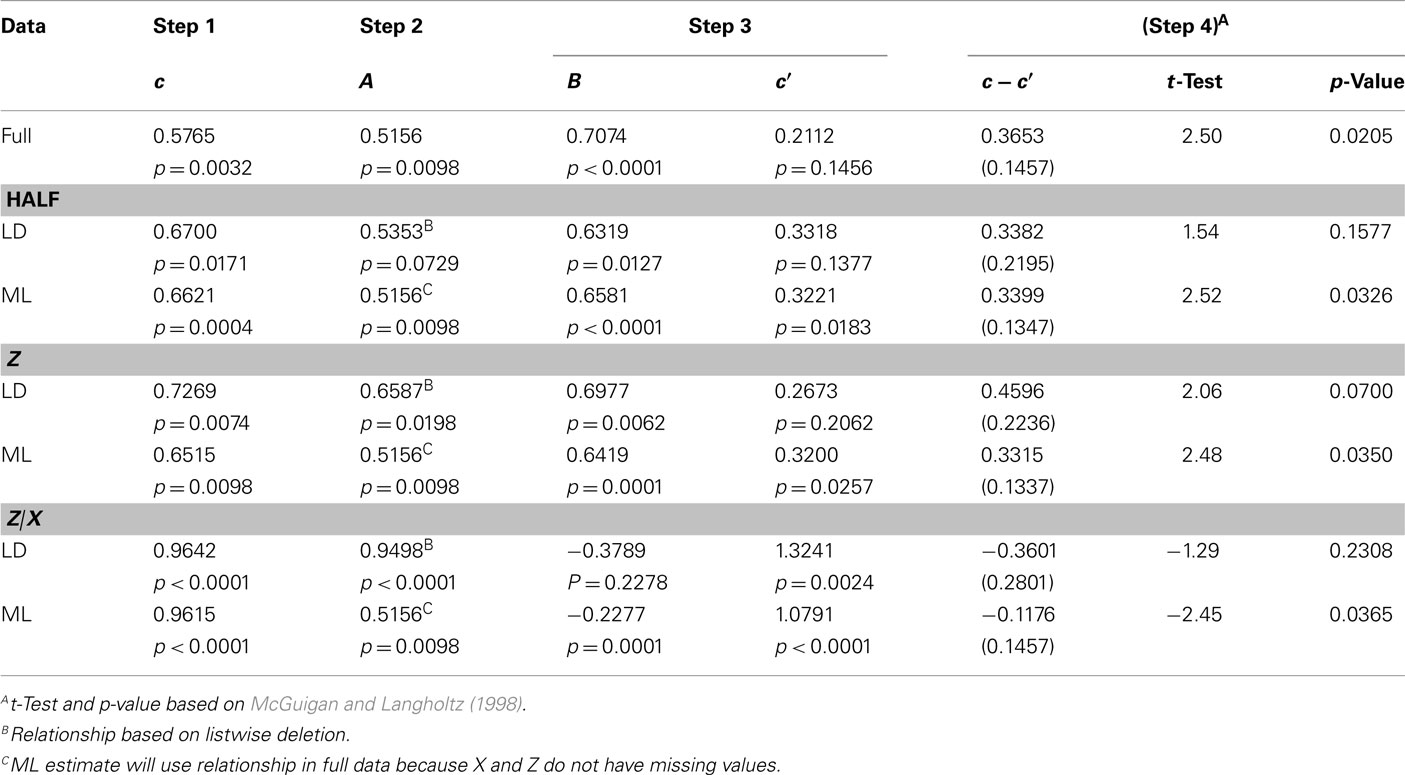
Table 2. Results from analyses of data in Table 1 using listwise deletion (LD) and maximum likelihood (ML) based the three sampling strategies.
Materials and Methods
We simulated a hypothetical experiment comparing the effects of two randomized conditions (e.g., Selenium and Placebo). The relationship between X (dichotomous predictor) and Y (continuous outcome) is partially mediated by Z (continuous variable). Using R 2.12.0 (www.r-project.org), data were simulated across multiple conditions. We varied the complete-case sample size of N = 24, 50, 100, 300, or 500. The causal factor (X) was generated as a dichotomous variable (0,1) with equal samples sizes n0 = n1 = N/2, which was then standardized to have a zero mean and unit variance. The relationship of X to the mediator (Z) was imposed as: Z = AX + σAε; where A = 0, 0.1, 0.3, or 0.5 is the parameter from Eq. 2; 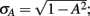 and ε is a random normal variable with zero mean and unit variance. The partial relationships of X and Z to Y were generated as: Y = C′X + BZ + σYε, where B = 0, 0.1, 0.3, or 0.5 and C′ (fixed at 0.5) are parameters from Eq. 3;
and ε is a random normal variable with zero mean and unit variance. The partial relationships of X and Z to Y were generated as: Y = C′X + BZ + σYε, where B = 0, 0.1, 0.3, or 0.5 and C′ (fixed at 0.5) are parameters from Eq. 3;  and ε is a random normal variable with zero mean and unit variance.
and ε is a random normal variable with zero mean and unit variance.
Analyses of the three sampling strategies described above were compared to analyses of the Full dataset. Across all analyses, subjects had complete-case data for the X and Z measurements while the three sampling strategies resulted in some subjects not being measured on Y. For each of the three sampling strategies, data were analyzed using two approaches. First, subjects without complete-case data were removed from further analyses (i.e., LD), which should yield unbiased results under the MCAR (Half) sampling strategy. For the Half and Z Quartiles sampling strategies, LD reduced the dataset by 50%. For the Z|X Quartiles strategy, LD resulted in a dataset that was slightly less than half the original size on average. In the second analysis approach, the deleted Y values were imputed with the ML approach using the R package mvnmle with the default settings. Because the data were MAR by design, ML, as opposed to LD, should provide unbiased parameter estimates with maximal statistical power (Little and Rubin, 2002).
To test partial mediation, we used the four step approach (i.e., all four steps must be satisfied to reject the null of no mediation at a significance level of α = 0.05). We used a regression approach to test Steps 1 through 3. To test the fourth step, we define c as the sample estimate of the total (unadjusted) effect of X on Y and c′ as the sample estimate of the direct (adjusted) effect of X on Y. We used the test suggested in McGuigan and Langholtz (1998). This approach tests whether the association between X and Y is significantly smaller when Z is controlled, but does not require the X–Y relationship to be non-significant (zero), and thus is a test of partial mediation rather than complete mediation (MacKinnon et al., 1995). The R package mvnmle provides ML estimates for a mean vector and covariance matrix; therefore, the estimated covariance matrix was converted to a correlation matrix and all ML based tests were computed from the estimated correlation matrix.
To obtain Type I and II error rates, we ran 1,000 Monte Carlo simulations for each of the 560 combinations of five sample sizes (complete-case; N = 24, 50, 100, 300, 500) × 4 X–Z correlations (A = 0, 0.1, 0.3, 0.5) × 4 Z–Y correlations (B = 0, 0.1, 0.3, 0.5 parameters) × 7 (missing data/sampling strategy; Full; LD-Half; LD-Z; LD-Z|X; ML-Half; ML-Z; ML-Z|X) factorial design. For all simulations, the X–Y correlations (C) were fixed at 0.5. With 1,000 replicates, the SE for empirical Type I error rates at α = 0.05 is 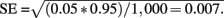 Thus, between-method differences in Type I error rates as small as 1.4% should be easily detectable. For Type II errors, the SE is maximized at 50% power, which yields a SE = 0.016. Thus, power rates differences of 3.2% should be discernable. A supplemental simulation with 10,000 replicates for a complete-case sample size of N = 500 was conducted to evaluate the bias and accuracy of the parameter estimates and to calculate the SD of these estimates.
Thus, between-method differences in Type I error rates as small as 1.4% should be easily detectable. For Type II errors, the SE is maximized at 50% power, which yields a SE = 0.016. Thus, power rates differences of 3.2% should be discernable. A supplemental simulation with 10,000 replicates for a complete-case sample size of N = 500 was conducted to evaluate the bias and accuracy of the parameter estimates and to calculate the SD of these estimates.
Results
Even though the simulated data were generated in standardized format, when missing data are handled using LD or ML, the resultant sample means and variances are no longer expected to be 0 and 1, respectively. Furthermore, all regression based tests and the test for mediation can be expressed in terms of bivariate and partial correlations (MacKinnon et al., 1995). Therefore, Tables 3 and 4 report all pairwise bivariate and partial correlations in order to examine bias in the parameter estimates (italicized estimates differ from the Full estimates). These correlations were averaged over 10,000 replications with a complete-case sample size of N = 500. The SD of these parameter estimates are displayed in parentheses and are underlined if they differ from the Full estimates. In all cases, analyses of the Full dataset are expected to represent the most accurate estimates.
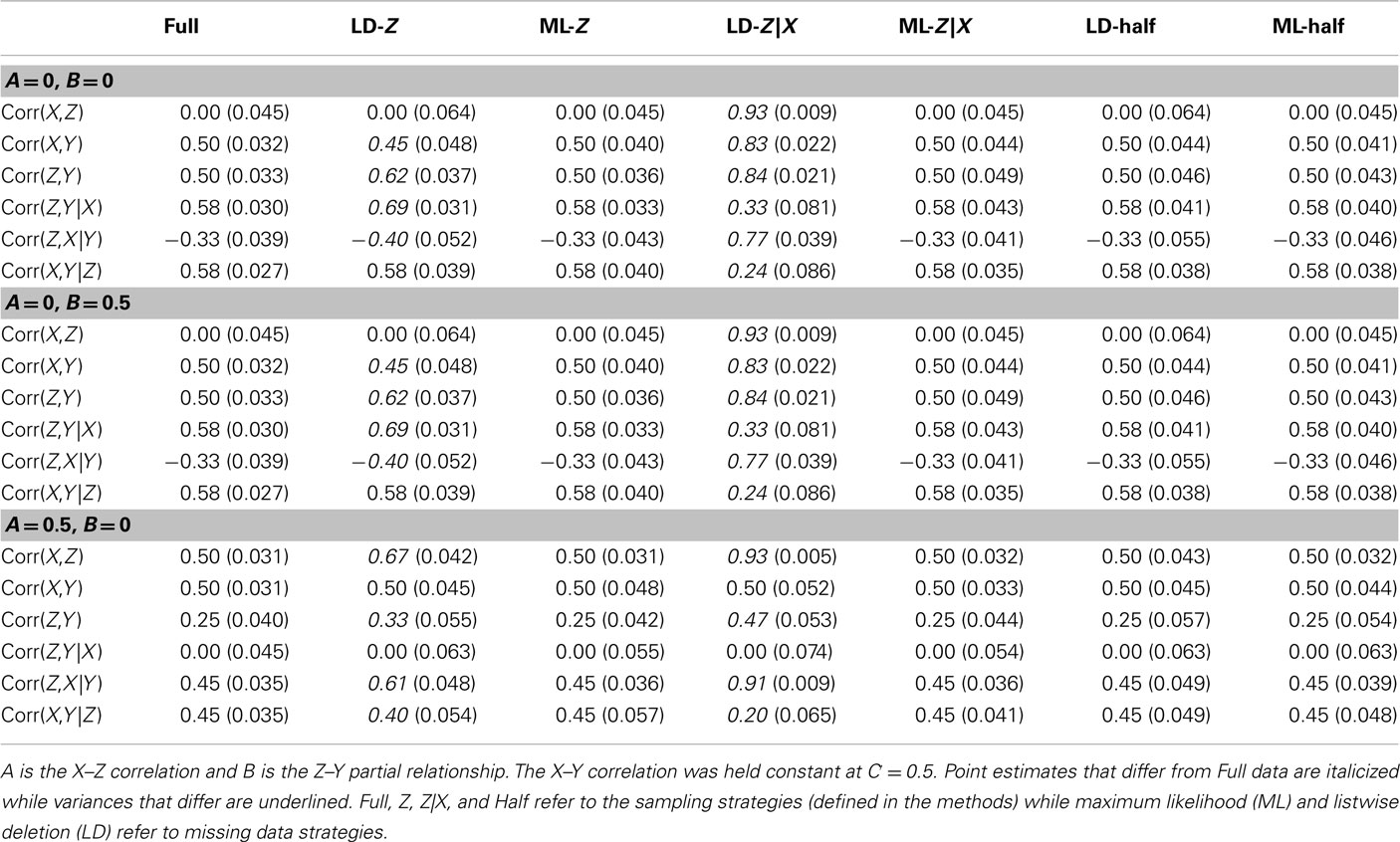
Table 3. Estimates and their SD for correlations and partial correlations across various null situations (N = 500).
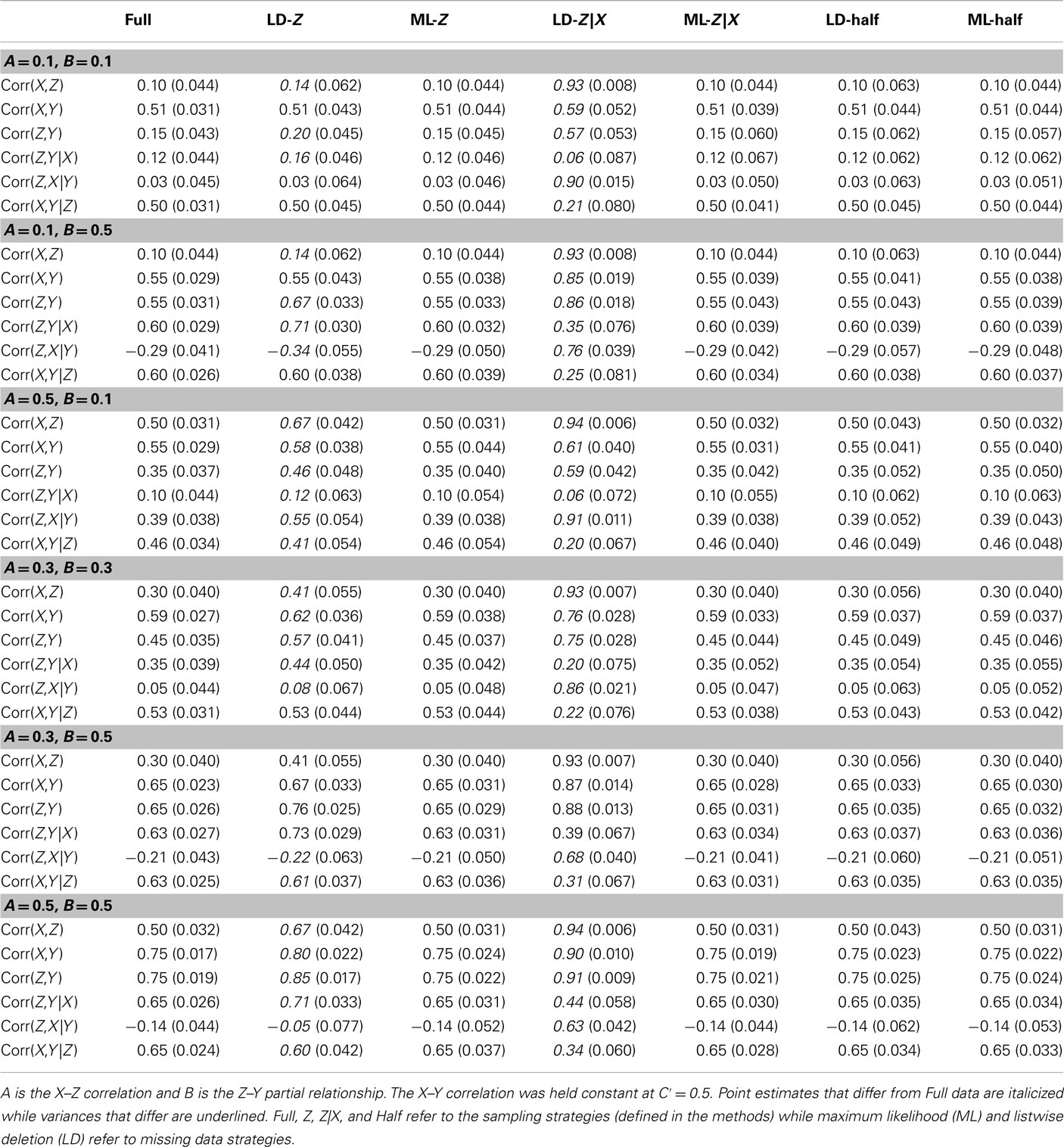
Table 4. Estimates and their SD for correlations and partial correlations across various mediation (non-null) situations (N = 500).
Tables 3 and 4 demonstrate that LD generally results in biased parameter estimates (except for the Half approach). ML generated unbiased parameter estimates across all strategies and correlations. SD of the estimates were generally higher in all sampling schemes, although the inflations were generally minimal. The Z|X approach that used LD to handle the missing data exhibited lower SD for some correlation measurements, although the bias inherent in the method negates such benefits.
Type 1 Error
Regardless of the C′ parameter, which was fixed at 0.5 in these simulations, mediation does not occur when either the A or B (or both) parameters equal zero (i.e., mediation null hypothesis is true). Figure 2 shows the Type 1 error rate for testing the null hypothesis of no mediation under three null conditions. The vertical axes are focused on a range near the nominal significance level (α = 0.05) in order to evaluate the validity of Type 1 error rates. That is, values substantially above 0.05 clearly do not maintain a valid Type 1 error rate and may not appear in the Figures. The horizontal axes display the sample size of the expensive (or terminal measure), not the complete-case sample size (N). Thus, the analyses for the Full data are based on approximately twice the sample size as the other analyses.
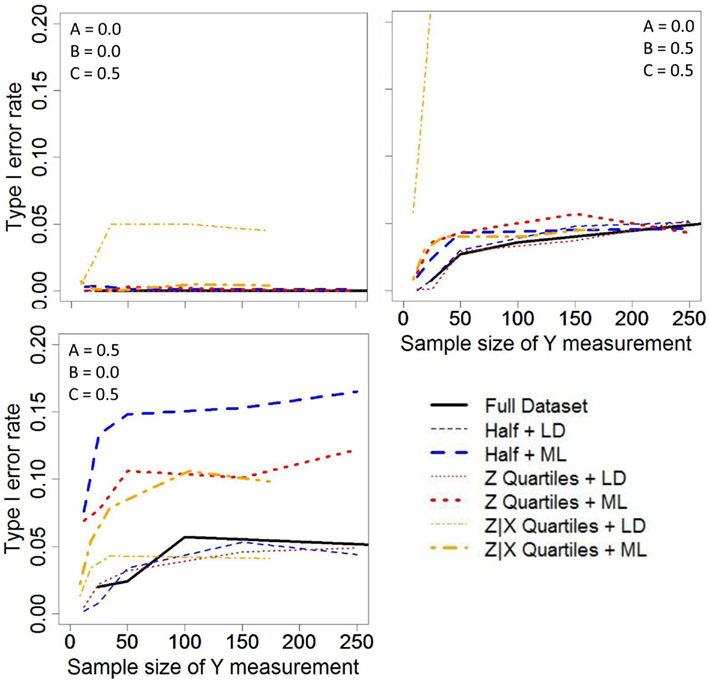
Figure 2. Type I error rates for the various sampling strategies across different correlation structures. Sampling strategies with listwise deletion (LD) are represented with thin lines while maximum likelihood estimates are thick lines.
In the condition where both the A and B parameters were null (Figure 2 upper-left panel), the Type 1 error rates for the four step test of mediation were suppressed substantially below the nominal significance level of α = 0.05, except for LD of the Y data missing from the Z|X sampling process which had Type 1 error rates around the α = 0.05 criterion. In the condition where A was null and the B parameter was non-zero (Figure 2 upper-right panel), the Type 1 error rates were generally maintained around the nominal significance level of α = 0.05. However, LD of the Y data missing from the Z|X sampling process yielded Type 1 error rates greatly exceeding 0.05, even with smaller sample sizes, and thus these results do not fully appear on Figure 2 (upper-right panel).
In the condition where B was null and the A parameter was non-zero (Figure 2 lower-left panel), the Type 1 error rates for the four step test of mediation were generally maintained around the nominal significance level of α = 0.05 for the Full dataset and for analyses that employed LD. However, the use of the ML procedure to handle the missing data yielded inflated Type 1 error rates. In examining Table 3 (third panel), one can see that the estimated correlations are not biased; however, any bivariate or partial correlation related to Y, which had missing data and thus involved ML, had higher SDs. This increase in the variability of the parameter estimates resulted in more than expected extreme values in the sample estimates and thus led to more than the expected number of rejections at Steps 3 and 4 of mediation testing. Interestingly, in this situation, LD yielded extremely biased estimates of the correlations, yet did not result in inflated Type 1 error rates.
Statistical Power
The estimated power rates of the sampling schemes are depicted in Figure 3. Because of the inflated Type I error rates for Z|X Quartiles sampling with LD, the power estimates are not presented. This is supported by Table 4 which shows extreme bias and inflated SDs for many estimates of the bivariate and partial correlations for the LD-Z|X approach. As in Figure 2, the sample size presented on the horizontal axis of Figure 3 was based on the number subjects that were measured for the expensive variable (Y), making it possible for the Half, Z Quartiles, and Z|X Quartiles sampling schemes to have more per subject power than the Full dataset approach. To elaborate, the per subject power for the LD of the Half (MCAR) sampling scheme was nearly identical to that of the Full data analysis, which was expected given that this is basically equivalent to randomly deleting half of the cases. Across all of the A and B relationships examined, LD of the Z quartile sampling (LD-Z) resulted in slightly higher per subject power as compared to analyses of the Full data; however, LD (LD-Half; LD-Z) resulted in lower power compared to ML. The power of the Z Quartile and Half approaches were similar when ML was used to handle missing data and provide covariance estimates. However, one must be cautious in interpreting the power advantages of the ML approach since this method inflated Type 1 error rates under a certain null condition.
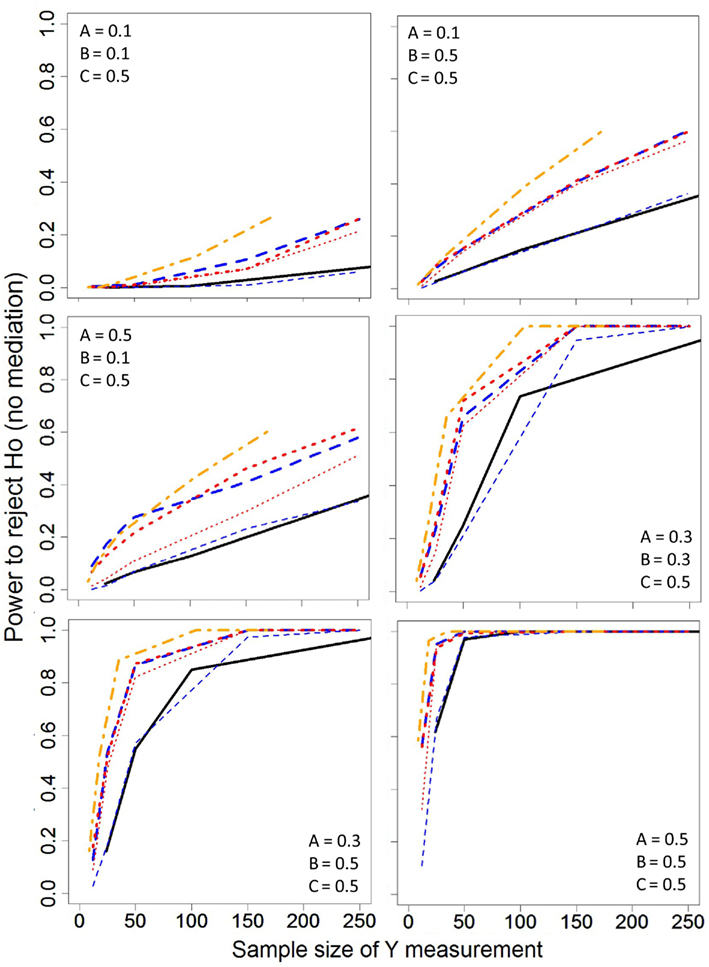
Figure 3. Statistical power estimates for the various sampling strategies across different correlation structures. Line specifications are the same as in Figure 2.
Discussion
We evaluated the performance of extreme sampling methods in the context of mediation analyses. To handle the missing data caused by extreme sampling, we employed two approaches; LD and ML estimation. When LD was used to handle missing data, as expected, only the Half dataset sampling (LD-Half) yielded unbiased parameter estimates (Table 3) and valid Type 1 error rates (Figure 2) across all of the null conditions examined, because this was the only sampling condition that met MCAR criteria. LD resulted is biased parameter estimates when combined with either extreme sampling strategy (i.e., Z Quartile or Z|X Quartile) because these approaches do not meet MCAR criteria. The Z Quartile given X approach produced the most biased estimates (Table 3) as well as elevated Type I error rates (Figure 2). Specifically, when the B and C′ parameters equaled 0.5 and the A = 0, LD-Z|X had Type 1 error rates greatly exceeding the α = 0.05 criterion. Although LD yielded biased estimates (Table 3) with the Z Quartile sampling approach, the Type I error rates were minimally elevated (Figure 2). Therefore, LD may be considered a valid approach for testing mediation (i.e., maintaining the appropriate false positive rate) when the Z Quartile extreme sampling approach (LD-Z) is used. Furthermore, the power for LD-Z exceeded the power of LD under the Half (MCAR) sampling scheme, provided more per subject power than analyzing the Full data, and had similar power to the ML approach to missing data in some conditions (see Figure 3). Thus, LD-Z has potential as a way to enhance per subject power in order to reduce study cost; however, the coefficients in terms of the amount of mediation will be biased (see Table 3).
When missing data were handled using ML, all sampling strategies produced unbiased parameter estimates (Table 3). Despite the estimates being correct on average, elevated variances among these estimates were seen for at least one of the correlations examined (Table 3) across all of the null models. Importantly, for all sampling strategies when the A and C′ parameters were 0.5 and the B parameter was 0, the increase in the variability of the parameter estimates produced by ML resulted in more than the expected amount of extreme values in the sample estimates and resulted elevated Type 1 error rates. The difference in this situation compared to the others is that the elevated variance in parameter estimates led to more than the expected number of rejections at Steps 3 and 4 of mediation testing. In the other situations, the parameter estimates corresponding to Steps 3 and 4 did not exhibit elevated variances. To determine if this was restricted to ML, we reran these analyses using multiple imputation and observed the similar results (not shown). In the other null situations examined, ML did not produce elevated Type I error rates (Figure 2).
While we have focused on the four step approach, another common approach to demonstrating mediation is the product rule, in which mediation is tested by multiplying the parameter estimates of A and B (i.e., a and b), while controlling for X. It has been noted that the four step approach suffers from multiplicity problems, yielding lower power and Type I error rates compared to the produce rule approach (Mackinnon et al., 2002). Additional simulations using the product rule approach and the Sobel (1982) product test confirmed this notion (results not shown), although the increase in statistical power was generally small (less than 5%). Importantly, the product test also suffered elevated Type I error rates when A = 0.5, B = 0.0, and C′ = 0.5 under the same conditions that were problematic for the four step approach. Therefore, both the four step and product rule approaches to testing mediation will have similar problem with maintaining the appropriate false positive rate if missing data are handled using ML, especially when the independent variable (X) is strongly related to the mediator (Z) and outcome (Y), but the mediator is not related to the outcome.
Overall, our results show that extreme (selective) sampling strategies can be beneficial in the context of mediation analyses. There are many possible modifications to extreme sampling that were not addressed. For example, extreme samples need not be equal in size (i.e., asymmetric sampling) or cover the same range of scores. D’Agostino and Cureton (1975) showed that, assuming normality, the optimal percentage of symmetric extreme sampling approaches 21% as correlations become large. However, statistical power is maximized when the percentage sampled from each tail is somewhere between 25 and 27% for moderate to small correlations (Feldt, 1961) and that these sampling percentages maximize power over a remarkably wide range of population correlation structures and distributional shapes (Fowler, 1992). Thus, the quartile sampling approach has become common in extreme sampling designs.
In the situations examined, handling the missing data due to extreme sampling with ML resulted in minimal power loss and unbiased parameter estimates. LD is an acceptable alternative when the missing data mechanism is MCAR (Half approach), but it produces biased parameter estimates in the other sampling situations and yields less power than ML even if the missing data are MCAR. Yet, we must be cautious in recommending ML for extreme sampling designs because this resulted in Type 1 error rate inflation under some null conditions. While we have presented specific examples of hypothesized mediation relationships, these results should be applicable to any situation that satisfies multivariate normality. ML should be applicable under MCAR, MAR, and multivariate normality regardless of sample size. However, smaller sample sizes make evaluating these assumptions difficult. Furthermore, ML and imputation methods are known to be adversely affected by non-normality, especially when sample sizes are small or the rate of missingness is high (Yucel and Demirtas, 2010). Extreme sampling can impose a large amount of missing data by design; therefore, extreme sampling percentages larger that 25% may help ameliorate problems due to small sample size and non-normality, even though they may not optimize per subject power. In conclusion, we demonstrate that using extreme sampling presents a worthy research strategy. Extreme sampling presents an attractive approach to enhance statistical power by using the information in the data to its maximal amount. Based on our results, we would suggest the Half approach combined with LD. This results in slightly less power that ML, but the parameter estimates are also unbiased and the Type I error rates are controlled.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Supported in part by NIH grants T32HL072757, P60AR048095, and P30DK056336. The opinions expressed are those of the authors and not necessarily the NIH or any other organization with which the authors are affiliated.
References
Abrahams, N. M., and Alf, E. F. (1978). Relative costs and statistical power in the extreme groups approach. Psychometrika 4, 11–17.
Alf, E. F., and Abrahams, N. M. (1975). The use of extreme groups in assessing relationships. Psychometrika 40, 563–572.
Allison, D. B., Heo, M., Schork, N. J., Wong, S. L., and Elston, R. C. (1998). Extreme selection strategies in gene mapping studies of oligogenic quantitative traits do not always increase power. Hum. Hered. 48, 97–107.
Baron, R. M., and Kenny, D. A. (1986). The moderator-mediator variable distinction in social psychological research: conceptual, strategic and statistical considerations. J. Pers. Soc. Psychol. 51, 1173–1182.
Bauer, D. J., Preacher, K. J., and Gil, K. M. (2006). Conceptualizing and testing random indirect effects and moderated mediation in multilevel models: new procedures and recommendations. Psychol. Methods 11, 142–163.
Beasley, T. M., Yang, D., Yi, N., Bullard, D. C., Amos, C. I., Xu, S., and Allison, D. B. (2004). Joint tests for quantitative trait loci in experimental crosses. Genet. Sel. Evol. 36, 601–619.
Chen, W. J., and Faraone, S. V. (2000). Sustained attention deficits as markers of genetic susceptibility to schizophrenia. Am. J. Med. Genet. 97, 52–57.
Cornblatt, B. A., and Malhotra, A. K. (2001). Impaired attention as an endophenotype for molecular genetic studies of schizophrenia. Am. J. Med. Genet. 105, 11–15.
D’Agostino, R. B., and Cureton, E. E. (1975). The 27 percent rule revisited. Educ. Psychol. Meas. 35, 47–50.
Feldt, L. S. (1961). The use of extreme groups to test for the presence of a relationship. Psychometrika 26, 307–316.
Fowler, R. L. (1992). Using the extreme groups strategy when measures are not normally distributed. Appl. Psychol. Meas. 16, 249–259.
Gottesman, I. I., and Gould, T. D. (2003). The endophenotype concept in psychiatry: etymology and strategic intentions. Am. J. Psychol. 160, 636–645.
Hammoumi, S., Payen, A., Favre, J. D., Balmes, J. L., Benard, J. Y., Husson, M., Ferrand, J. P., Martin, J. P., and Daoust, M. (1999). Does the short variant of the serotonin transporter linked polymorphic region constitute a marker of alcohol dependence? Alcohol 17, 107–112.
Hauser, J., Leszczynska, A., Samochowiec, J., Czerski, P. M., Ostapowicz, A., Chlopocka, M., Horodnicki, J., and Rybakowski, J. K. (2003). Association analysis of the insertion/deletion polymorphism in serotonin transporter gene in patients with affective disorder. Eur. Psychol. 18, 129–132.
Ishrat, T., Parveen, K., Khan, M. M., Khuwaja, G., Khan, M. B., Yousuf, S., Ahmad, A., Shrivastav, P., and Islam, F. (2009). Selenium prevents cognitive decline and oxidative damage in rat model of streptozotocin-induced experimental dementia of Alzheimer’s type. Brain Res. 1281, 117–127.
Judd, C. M., and Kenny, D. A. (1981). Process analysis: estimating mediation in treatment evaluations. Eval. Rev. 5, 602–619.
Lesch, K. P., Bengel, D., Heils, A., Sabol, S. Z., Greenberg, B., Petri, S., Benjamin, J., Muller, C. R., Hamer, D. H., and Murphy, D. L. (1996). Association of anxiety-related traits with a polymorphism in the serotonin transporter gene regulatory region. Science 274, 1527–1531.
Little, R. J. A., and Rubin, D. B. (2002). Statistical Analysis with Missing Data. New York: John Wiley.
MacCorquodale, K., and Meehl, P. E. (1948). On a distinction between hypothetical constructs and intervening variables. Psychol. Rev. 55, 95–107.
Mackinnon, D., Lockwood, C., Hoffman, J., West, S., and Sheets, V. (2002). A comparison of methods to test mediated and other intervening variable effects. Psychol. Methods 7, 83–104.
MacKinnon, D., Warsi, G., and Dwyer, J. (1995). A simulation study of mediated effect measures. Multivariate Behav. Res. 30, 41–62.
Maxwell, S. E., and Cole, D. A. (2007). Bias in cross-sectional analyses of longitudinal mediation. Psychol. Methods 12, 23–44.
McGuigan, K., and Langholtz, B. (1998). A note on testing mediation paths using ordinary least-squares regression. [Unpublished note].
Meyer-Lindenberg, A., and Weinberger, D. R. (2006). Intermediate phenotypes and genetic mechanisms of psychiatric disorders. Nat. Rev. Neurosci. 7, 818–827.
Munafò, M. R., Clark, T. G., Johnstone, E. C., Murphy, M. F. G., and Walton, R. (2004). The genetic basis for smoking behaviour: a systematic review and meta-analysis. Nicotine Tob. Res. 6, 583–598.
Preacher, K. J., Rucker, D. D., MacCallum, R. C., and Nicewander, W. A. (2005). Use of the extreme groups approach: a critical reexamination and new recommendations. Psychol. Methods 10, 178–192.
Rutten, B. P. F., and Mill, J. (2009). Epigenetic mediation of environmental influences in major. Schizophr. Bull. 35, 1045–1056.
Slaats-Willemse, D., Swaab-Barneveld, H., De Sonneville, L., Van Der Meulen, E., and Buitelaar, J. (2003). Deficient response inhibition as a cognitive endophenotype of ADHD. J. Am. Acad. Child Adolesc. Psychiatry 42, 1242–1248.
Sobel, M. E. (1982). “Asymptotic confidence intervals for indirect effects in structural equation models,” in Sociological Methodology, ed. S. Leinhardt (San Francisco: Jossey-Bass), 290–312.
Stoltenberg, S. F., Twitchell, G. R., Hanna, G. L., Cook, E. H., Fitzgerald, H. E., Zucker, R. A., and Little, K. Y. (2002). Serotonin transporter promoter polymorphism, peripheral indexes of serotonin function, and personality measures in families with alcoholism. Am. J. Med. Genet. 114, 230–234.
Taris, T. W., and Kompier, M. (2006). Games researchers play. Extreme group analysis and mediation analysis in longitudinal occupational health research. Scand. J. Work Environ. Health 32, 463–472.
Veling, W. (2008). Genetic mediation of the link between schizophrenia and cannabis use. Psychiatry 7, 511–515.
Keywords: mediation, extreme sampling, missing data, terminal measures
Citation: Makowsky R, Beasley TM, Gadbury GL, Albert JM, Kennedy RE and Allison DB (2011) Validity and power of missing data imputation for extreme sampling and terminal measures designs in mediation analysis. Front. Gene. 2:75. doi: 10.3389/fgene.2011.00075
Received: 06 July 2011; Paper pending published: 01 August 2011;
Accepted: 07 October 2011; Published online: 31 October 2011.
Edited by:
Evgeny Ivanovich Rogaev, University of Massachusetts Medical School, USAReviewed by:
Marleen H. M. De Moor, VU University Amsterdam, NetherlandsAndre Scherag, University of Duisburg-Essen, Germany
Copyright: © 2011 Makowsky, Beasley, Gadbury, Albert, Kennedy and Allison. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: T. Mark Beasley, Section on Statistical Genetics, Department of Biostatistics, University of Alabama at Birmingham, 1530 3rd Avenue South, Birmingham, AL 35294, USA. e-mail:bWJlYXNsZXlAdWFiLmVkdQ==

 T. Mark Beasley1*
T. Mark Beasley1*