- 1 Department of Mathematics, Tandy School of Computer Science, University of Tulsa, Tulsa, OK, USA
- 2 Department of Biostatistical Sciences, Wake Forest School of Medicine, Winston-Salem, NC, USA
There is growing evidence that much more of the genome than previously thought is required to explain the heritability of complex phenotypes. Recent studies have demonstrated that numerous common variants from across the genome explain portions of genetic variability, spawning various avenues of research directed at explaining the remaining heritability. This polygenic structure is also the motivation for the growing application of pathway and gene set enrichment techniques, which have yielded promising results. These findings suggest that the coordination of genes in pathways that are known to occur at the gene regulatory level also can be detected at the population level. Although genes in these networks interact in complex ways, most population studies have focused on the additive contribution of common variants and the potential of rare variants to explain additional variation. In this brief review, we discuss the potential to explain additional genetic variation through the agglomeration of multiple gene–gene interactions as well as main effects of common variants in terms of a network paradigm. Just as is the case for single-locus contributions, we expect each gene–gene interaction edge in the network to have a small effect, but these effects may be reinforced through hubs and other connectivity structures in the network. We discuss some of the opportunities and challenges of network methods for analyzing genome-wide association studies (GWAS) such as the study of hubs and motifs, and integrating other types of variation and environmental interactions. Such network approaches may unveil hidden variation in GWAS, improve understanding of mechanisms of disease, and possibly fit into a network paradigm of evolutionary genetics.
Introduction
It has long been appreciated that the regulation of biological processes involves a complex orchestration of genes in networks. However, typical analytic frameworks for genome-wide association studies (GWAS) have assumed a simplified genetic architecture, largely considering independent additive contributions to genetic risk. While recent studies have supported a large contribution of additive genetic variance to complex traits (Yang et al., 2010; Lee et al., 2011a), “missing heritability” remains, which has led to a range of potential explanations (Eichler et al., 2010). One such explanation is the existence of epistatic (gene by gene) effects, which are, in fact, not precluded even in the presence of sizeable additive genetic variance (Hill et al., 2008). In this opinion and review, we propose that there is room for additional mining of datasets generated in the GWAS era using a paradigm of networks that aggregate gene–gene interactions and main effects. We argue that network approaches may have utility not only for discovery, but also for further characterizing relationships with genetic effects that may have been identified through standard analytic means.
The recognition that numerous genetic variants may act in concert to modulate disease susceptibility has led to the development of gene set enrichment and pathway approaches (Torkamani et al., 2008; Shi et al., 2009; Liu et al., 2010). The small but consistent effect of many SNPs in gene sets suggests evidence at the population level of the coordination of genes known to interact through particular biological pathways. Gene set enrichment approaches are able to identify these coordination effects despite typically relying on small effect single-marker association evidence. Gene–gene interaction effects also show small effect sizes, but evidence for coordination from main effects suggests that the aggregation of gene–gene interactions and main effects in epistasis networks may lead to even more consistent pathway enrichment.
Epistasis networks may also be used to test the hypothesis of a network paradigm of evolution and disease susceptibility. A recent study comparing the connectivity changes of Arabidopsis networks following gene duplication events suggests a possible model of evolution acting at the level of the interactome network (Dreze et al., 2011). These studies suggest improved understanding of disease susceptibility may be achieved by conceptualizing the genotype to phenotype mapping as a network of coupled gene–gene interactions and main effects. We refer to these as genetic association interaction networks (GAIN) or epistasis networks; however, the networks we describe model main effects as well as epistasis.
In a recent GAIN analysis of a study of the immune response to smallpox vaccine, we identified a new association in the RXRA gene reflecting a large number of gene–gene interactions (Davis et al., 2010). We refer to such findings colloquially as “Kevin Bacon” variants in Figure 1 after the ability to connect other actors to him in a few jumps in a network constructed by shared movie credit. Such variants may be important to a phenotype, not because of their individual effect, but because of their overall influence in modulating the effect of other variants. Another analogy from popular culture is Lady Gaga, who has over one million Twitter followers. Even a small perturbation from such a node may have a large downstream effect due to a cascade through the subnetworks of followers.
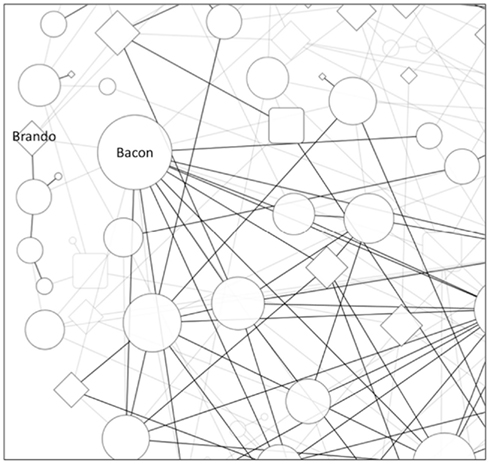
Figure 1. Epistasis network from a hypothetical GWAS. Edges represent small gene–gene interactions between SNPs. Gray nodes and edges have weaker interactions. Circle nodes represent SNPs that do not have a significant main effect. The diamond nodes represent significant main effect association. The size of the node is proportional to its number of connections. The Brando node would be easily found by a standard single-locus statistic, but the Kevin Bacon node would only be revealed by an epistasis network approach due to its many small gene–gene interactions. The epistasis network may also be useful for identifying new mechanisms for known effects, such as the connection of the Brando node to the pathway represented by the subnetwork below it.
Returning to acting as an analogy, “Marlon Brando” variants (the usual target of the GWAS approach) may or may not have a large network centrality, but are deemed important because of their individual (main) effect. Examples of “Marlon Brando” variants could include the CYP2C9 and VKOR1C polymorphisms involved in warfarin metabolism (Limdi et al., 2010), the wealth of human leukocyte antigen (HLA) alleles associated with immunologic phenotypes (Lechler and Warrens, 2000; Blackwell et al., 2009), or APOL1 variants associated with kidney disease in African-Americans (Genovese et al., 2010). While the majority of variants identified to date do not exhibit such individually strong effects, most are only likely in linkage disequilibrium (LD) with causal alleles; given that the GWAS approach relies upon tagSNPs to efficiently span the entire genome. Thus, there is an expectation that additional Brando SNPs (presumably functional variants tied to more penetrant phenotypic effects) will be found by fine-mapping experiments (such as the Immunochip for autoimmune disorders (Trynka et al., 2011), trans-racial mapping (Rosenberg et al., 2010; Teo et al., 2010), and through the proliferation of next-generation sequencing. Recent studies incorporating next-generation sequencing in age-related macular degeneration (Raychaudhuri et al., 2011) and inflammatory bowel disease (Rivas et al., 2011) have provided initial evidence consistent with this expectation.
However, when considering the issue of the “missing heritability,” it is important to remember that causal variants are expected to occur at lower frequencies compared to the tagSNPs that have been identified thus far (Visscher et al., 2011). Therefore, the existence of stronger effects will be offset to an unknown extent by a lower prevalence of causal alleles, potentially restricting the total variability that will be explained at the population level. It seems unlikely that identifying less frequent, causal alleles will immediately fill the missing heritability void, suggesting that complementary approaches, such as understanding variation in a network context, could have important implications in biological mechanistic research and translational medicine. For example, even for well-known genetic factors such as HLA, there is a growing recognition of epistatic considerations, such as the interplay between HLA class I polymorphisms and the killer cell immunoglobulin receptor (KIR) gene complex within the context of infectious disease, autoimmune disorders, cancer, and bone marrow transplantation outcomes (Kulkarni et al., 2008; Cooley et al., 2010). Thus, network analysis is not restricted to discovery. Even in cases where there are known genetic effects, network analysis provides an opportunity to more fully characterize the genetic etiology by identifying the full network of interactions with known susceptibility variants.
Network Approaches for GWAS
The focus of this review is on empirical network approaches, where connections are based on gene–gene interactions (epistasis) estimated from GWAS data. However, we pause to mention prior knowledge networks (PKNs), such as ingenuity pathway analysis (www.ingenuity.com), which represent the most popular network analysis approach applied to GWAS to date (Burgner et al., 2009). Similar to gene set enrichment approaches, PKNs typically utilize statistical measures of marginal association to select genes to include in a putative network, with connections then constructed from various knowledge bases including protein–protein interactions (PPIs), co-occurrence in literature mining, or co-expression in microarray experiments. For example, the approach in (Lee et al., 2011b) uses evidence from PKNs based on selected candidate pathways combined with odds ratios from GWAS in order to boost the importance of neglected genes. Prior knowledge based strategies have also been used to focus searches for epistatic effects in multiple sclerosis (Bush et al., 2011) and bipolar disorder (Moskvina et al., 2011). Interestingly, Moskvina et al. (2011) found that a prioritization strategy did not lead to an enrichment of replicable statistical interactions, suggesting a large risk of false positive associations. These contrasting results could reflect the issue that connections are typically defined independently of the environmental/disease context; leading to differences in performance as a function of the particular trait under study. While the knowledge bases for PKNs are constantly improving in quality and scope, there is likely a need for empirical network approaches that are able to account for the conditional dependence of gene connections on the specific disease under study. For example, in studies of infection or vaccination, it is reasonable to hypothesize that genetic effects in networks may be dependent on the particular antigenic perturbation.
There has been a growth in the use of pathway-based approaches to GWAS to shed light on biological processes and identify new candidate disease genes. These approaches identify enriched pathways from a broader set of significant genes rather than focus only on a few of the most significant SNPs. For example, pathway-based approaches and pathway clustering have identified important processes in breast cancer (Torkamani et al., 2008; Menashe et al., 2010) and in the diseases from the WTCCC GWAS (Torkamani et al., 2008). However, these approaches rank genes based on single-marker association evidence. We propose that such pathway-based approaches to GWAS may benefit from the prioritization of genes based on the aggregation of gene–gene interactions as well as single-locus effects. A data-driven epistasis network approach may increase the discovery of enriched disease-specific pathways and new candidate gene targets in GWAS over single-locus prioritization alone. Using gene–gene interaction networks in this way may require some modifications to pathway analysis because enrichment scores typically rely on permutation to determine the statistical significance of enrichment, and data-driven networks are much more computationally intensive than single-locus calculations.
Data-Driven Epistasis Networks
Previous data-driven network approaches for GWAS have used Shannon information theory for epistasis calculations and network construction (Jakulin and Bratko, 2004; Moore et al., 2006; McKinney et al., 2009; Davis et al., 2010). However, casting the network in the widely used statistical framework of a general linear model (GLM) has some advantages over information theory. For example, use of a GLM framework provides the flexibility to handle environmental covariates, longitudinal data, missing data, censoring, and cluster structure (e.g., family studies) through the inclusion of appropriate random effects. As an example, we present a likelihood ratio test of association between disease and a genetic locus, allowing for the possibility that the genetic effect may be modified by another genetic factor. This illustration is for case–control data, but it is straightforward to develop similar tests for non-dichotomous phenotypes and other designs (e.g., family studies).
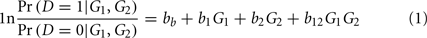
The coefficient bb gives the baseline risk of disease and coefficients b1 and b2 correct for main effects in the interaction regression model. For defining gene–gene edge weights b12 in the GAIN matrix, we are interested in the b12 regression coefficients that are statistically different from zero. The statistical framework also allows false discovery rate (FDR) procedures to be applied to correct for multiple gene–gene hypotheses. FDR would be a more computationally efficient procedure than the permutation approached used in McKinney et al. (2009) to reduce false interaction information-based edges. The diagonal element bii of the GAIN is simply the main effect regression coefficient without interactions. Additional terms may be added to the regression equation to define interactions between other factors, such as environment or gene expression, to create a heterogeneous network or to correct for these factors. Heterogeneous interaction networks represent an important frontier in genetics because they may improve our understanding of the interplay between genetic and environmental modifiers of susceptibility.
Influential SNPS in Networks
Once an epistasis graph like Figure 1 is calculated, one may identify the most influential or central SNPs or other factors in the network. Such SNP hubs in the disease-specific network may be potential targets for therapy or diagnostics, and the rankings may be used for a more sensitive pathway enrichment analysis. Various measures of node centrality have been proposed, with one of the most powerful and computationally tractable being eigenvector centrality – the basis of Google’s PageRank (Page et al., 1999). Eigenvector centrality calculates the steady state eigenvector of a Markov transition matrix whose elements represent the probability to move from one node to another. We recently designed a transition matrix method based on the main effects and interactions in GAIN and an eigenvector centrality algorithm we call SNPrank (Davis et al., 2010). In a disease risk interaction network, the network is specific to the disease (context sensitive), and each node and edge contains information about disease risk.
The SNPrank transition matrix T (Eq. 2) is constructed from the GAIN network B, with elements bij. The diagonal of B captures main (Brando) effects, while the off diagonals represent gene–gene and/or gene-environment interactions (Bacon) effects. The factors dj (the node degree) and Tr(B) (the trace of B) normalize T to a stochastic matrix. The elements of B could be calculated using approaches such as information theory or from coefficients of statistical models. Simple recursion is used to compute T’s steady-state eigenvector, whose elements are the rankings of each node. The interaction term bij in (Eq. 2) also includes self-interactions or main effects when i = j. In contrast, Google’s PageRank does not permit self-interactions because this would represent a website including links to itself and would artificially inflate the site’s importance. (Eq. 2) includes a parameter γ, typically chosen close to 1 so that the main effect is not overwhelmed by the potentially large number of gene–gene interactions a SNP may have. We find γ in the range [0.8, 0.9] gives the highest internal consistency of the SNPrank scores, which we estimate by splitting data randomly into halves and calculating the Kendall Tau (Kendall, 1938) rank correlation of the SNPranks. We typically set γ to 0.85; however, γ = 1 is also a reasonable simplification to (Eq. 2). The parameter γ can also be used to blend prior knowledge from canonical pathways or protein–protein interactions.
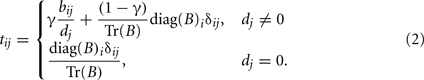
A helpful way to conceptualize the way the algorithm scores the importance of genes is to think of the SNPrank centrality algorithm as simulating ants that follow paths through the network that have the most disease risk information, either due to gene–gene interactions or main effects encoded in the edges and nodes of the network. More pheromones are deposited at more frequently visited genetic or environmental nodes, and the amount of pheromone is proportional to the rank score of the node. The steady state eigenvector, v (eigenvalue λ = 1), of the SNPrank transition matrix is given by Tv = v, where the elements of v are the SNPrank score of each SNP. The elements of v represent a probability field, and, thus, it is possible to use quantile plots and similar approaches to identify SNPs with SNPranks that deviate from a uniform probability distribution. One can also see from the eigenvalue equation that the SNPrank importance of the ith SNP, vi, is influenced by the entire network:

In other words, the SNPrank of the ith SNP is a function of all interaction coefficients bij (j ≠ i), the main effect (self interaction), bii, of the ith SNP, and the recursively estimated importance of each SNP vj (j ≠ i). This approach does not include pure higher order interactions, like three-way etc. but when ranking an individual SNP, this approach models the interaction with every other SNP in the network and the SNP’s main effect.
Power and Validation of Networks
An important point for future research is the extent to which network approaches offer improved statistical power to detect complex genetic effects. In the case of PKNs, power critically depends on the extent to which a particular dataset fits with the current state of biological knowledge. Similar to a correctly constructed informative prior distribution in Bayesian modeling, PKNs will have an advantage in situations where the data is congruent with prior expectations. In contrast, the power for empirical approaches like SNPrank is somewhat less clear. Much of this is due to limitations in simulation methodology, as it is currently difficult to generate datasets with a complex and “realistic” latent structure. While some inroads have been made (Himmelstein et al., 2011), because approaches to characterize complex effects are in their infancy, it is also not clear what constitutes a realistic level of complexity. Therefore, it is imperative that advancements in network methodologies be pursued in tandem with research into appropriate simulation frameworks. We do note, however, that approaches like SNPrank operate on network representation typically defined in a pair-wise fashion. Therefore, they implicitly inherit some of the features of the approach used to construct this pair-wise representation, whether based on information theory, statistical modeling, or other approaches (Cordell, 2009). The power of network approaches thus could be improved by finding the best approach or combination of approaches for detecting pair-wise interactions (Ritchie et al., 2001; Fan et al., 2011). In addition to this inheritance, SNPrank may also boost power to detect associations by aggregating numerous interactions and main effects (Selinger-Leneman et al., 2003).
Other statistical challenges include replication of network models and the effect of LD. Strategies for replication of a single SNP are well accepted (Kraft et al., 2009), but the replication strategy for a network is less obvious because of the complex entanglement of all SNPs in the network. One level of replication would be to test for replication of a gene set in an independent cohort based on gene set enrichment from the network prioritization. LD is another area that requires further investigation because the common strategy of LD pruning could run the risk of excluding interactions. Finally, both of these issues simultaneously become pertinent within the context of comparisons across racial/ethnic populations (Teo et al., 2010) as differential patterns of LD could complicate the interpretation of edges connecting specific haplotype tagging variants.
Conclusion
Pathway and gene set enrichment approaches have demonstrated the utility of aggregating information from many moderate-sized single-locus effects. While such approaches assume implicitly that the targeted genetic architecture reflects a complex interacting system, the prioritization of genes for enrichment typically relies on single-locus effects. We propose network models of GWAS data, built up from many single-locus and gene–gene interactions. We anticipate systems level network approaches to GWAS will reveal new mechanisms and improve our understanding of the complex relationship between genotypes and phenotypes. However, there are numerous statistical and bioinformatics challenges that remain to be addressed to realize this systems level understanding.
The two network approaches for GWAS discussed in this brief review – prior knowledge and gene–gene interaction – each have their own advantages. PKNs are able to leverage information from different scales, such as PPI or gene co-expression, though these data sources may lack specificity to the disease under study. Specificity could be achieved by calculating the interaction between genes conditional on the phenotype at hand. Thus, the best approach may be to integrate prior knowledge with epistasis networks, perhaps through a Bayesian formalism. As the biological connections of PKNs and canonical pathways continue to improve in specificity, the integration of these networks with new interactions discovered in empirical networks will likely be a powerful combination.
Previous data-driven epistasis networks have modeled interactions with Shannon information theory measures because of the computational efficiency and power to detect interactions. An advantage of regression-based empirical networks is the ability to incorporate variation from other data types (gene expression, methylation, copy number), covariates, and environmental factors. Another open question is how much of the missing heritability is explained by network/epistatic effects. Answering such questions will require the development of statistical models that provide a coherent predictive mechanism based on a highly interacting network.
There is also a methodological need for tools to construct and understand features of empirical networks, such as subnetwork motifs, hubs, and node degree distributions. One well-studied degree distribution is the power law, which corresponds to the notion of a small world network (Bassett and Bullmore, 2006). It remains to be seen whether the degree distribution of epistasis networks exhibits a power law and how LD would affect the degree distribution. A power law edge distribution of small world networks implies that most nodes have a small number of edges, but there are a few nodes with a large number of connections (hubs). The small world property allows one to traverse from one node to any other in relatively few steps and the network is robust to random attack or mutation. However, a targeted intervention of a hub could have a strong therapeutic effect.
The need for the application and development of algorithms for characterizing networks is not unique to genomics. The importance of network concepts and algorithms is recognized throughout biology, notably in neuroscience where there is current interest in resting-state functional connectivity networks from fMRI data (Braun et al., 2011). Thus, there is an opportunity to adapt methods and integrate data from other domains for genomic data. Both data from brain connectivity and gene network analysis for other genomic data seem to exhibit characteristics of small world networks (Barabasi and Oltvai, 2004), and it will be important to determine whether this is also reflected in the structure of GWAS data.
Evolution occurs in the context of a complex network of interconnected genes and pathways. We are in the early stages of understanding how the network of epistatic and main effects synthesizes with biological networks and pathways. Knowledge of hubs, centralities and other properties of disease risk epistasis networks provide a new path toward identifying critical nodes in the network that may act as therapeutic targets or disease risk predictors. And a data-driven interaction network paradigm of GWAS and deeper sequencing may lead to new insights into the mechanisms of evolution and complexity.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by NIH Grants no. K25 AI-64625 (PI: B. A. McKinney), R56 AI-80932 (PI: B. A. McKinney). Dr. McKinney is also supported by the William K. Warren foundation.
References
Barabasi, A. L., and Oltvai, Z. N. (2004). Network biology: understanding the cell’s functional organization. Nat. Rev. Genet. 5, 101–113.
Blackwell, J. M., Jamieson, S. E., and Burgner, D. (2009). HLA and infectious diseases. Clin. Microbiol. Rev. 22, 370–385.
Braun, U., Plichta, M. M., Esslinger, C., Sauer, C., Haddad, L., Grimm, O., Mier, D., Mohnke, S., Heinz, A., Erk, S., Walter, H., Seiferth, N., Kirsch, P., and Meyer-Lindenberg, A. (2011). Test-retest reliability of resting-state connectivity network characteristics using fMRI and graph theoretical measures. Neuroimage 59, 1404–1412.
Burgner, D., Davila, S., Breunis, W. B., Ng, S. B., Li, Y., Bonnard, C., Ling, L., Wright, V. J., Thalamuthu, A., Odam, M., Shimizu, C., Burns, J. C., Levin, M., Kuijpers, T. W., Hibberd, M. L., and International Kawasaki Disease Genetics Consortium. (2009). A genome-wide association study identifies novel and functionally related susceptibility loci for kawasaki disease. PLoS Genet. 5, e1000319. doi:10.1371/journal.pgen.1000319
Bush, W. S., McCauley, J. L., DeJager, P. L., Dudek, S. M., Hafler, D. A., Gibson, R. A., Matthews, P. M., Kappos, L., Naegelin, Y., Polman, C. H., Hauser, S. L., Oksenberg, J., Haines, J. L., Ritchie, M. D., and International Multiple Sclerosis Genetics Consortium. (2011). A knowledge-driven interaction analysis reveals potential neurodegenerative mechanism of multiple sclerosis susceptibility. Genes Immun. 12, 335–340.
Cooley, S., Weisdorf, D. J., Guethlein, L. A., Klein, J. P., Wang, T., Le, C. T., Marsh, S. G., Geraghty, D., Spellman, S., Haagenson, M. D., Ladner, M., Trachtenberg, E., Parham, P., and Miller, J. S. (2010). Donor selection for natural killer cell receptor genes leads to superior survival after unrelated transplantation for acute myelogenous leukemia. Blood 116, 2411–2419.
Cordell, H. J. (2009). Detecting gene-gene interactions that underlie human diseases. Nat. Rev. Genet. 10, 392–404.
Davis, N. A., Crowe, J. E. Jr., Pajewski, N. M., and McKinney, B. A. (2010). Surfing a genetic association interaction network to identify modulators of antibody response to smallpox vaccine. Genes Immun. 11, 630–636.
Dreze, M., Carvunis, A. R., Charloteaux, B., Galli, M., Pevzner, S. J., Tasan, M., Ahn, Y.-Y., Balumuri, P., Barabasi, A.-L., Bautista, V., Braun, P., Byrdsong, D., Chen, H., Chesnut, J. D., Cusick, M. E., Dangl, J. L., de los Reyes, C., Dricot, A., Duarte, M., Ecker, J. R., Fan, C., Gai, L., Gebreab, F., Ghoshal, G., Gilles, P., Gutierrez, B. J., Hao, T., Hill, D. E., Kim, C. J., Kim, R. C., Lurin, C., MacWilliams, A., Matrubutham, U., Milenkovic, T., Mirchandani, J., Monachello, D., Moore Jonathan, D., Mukhtar, M. S., Olivares, E., Patnaik, S., Poulin, M. M., Przulj, N., Quan, R., Rabello, S., Ramaswamy, G., Reichert, P., Rietman, E. A., Rolland, T., Romero, V., Roth, F. P., Santhanam, B., Schmitz, R. J., Shinn, P., Spooner, W., Stein, J., Swamilingiah, G. M., Tam, S., Vandenhaute, J., Vidal, M., Waaijers, S., Ware, D., Weiner, E. M., Wu, S., and Yazaki, J. (2011) Evidence for network evolution in an Arabidopsis interactome map. Science 333, 601–607.
Eichler, E. E., Flint, J., Gibson, G., Kong, A., Leal, S. M., Moore, J. H., and Nadeau, J. H. (2010). Missing heritability and strategies for finding the underlying causes of complex disease. Nat. Rev. Genet. 11, 446–450.
Fan, R., Zhong, M., Wang, S., Zhang, Y., Andrew, A., Karagas, M., Chen, H., Amos, C. I., Xiong, M., and Moore, J. H. (2011). Entropy-based information gain approaches to detect and to characterize gene-gene and gene-environment interactions/correlations of complex diseases. Genet. Epidemiol. 35, 706–721.
Genovese, G., Friedman, D. J., Ross, M. D., Lecordier, L., Uzureau, P., Freedman, B. I., Bowden, D. W., Langefeld, C. D., Oleksyk, T. K., Uscinski Knob, A. L., Bernhardy, A. J., Hicks, P. J., Nelson, G. W., Vanhollebeke, B., Winkler, C. A., Kopp, J. B., Pays, E., and Pollak, M. R. (2010). Association of trypanolytic ApoL1 variants with kidney disease in African Americans. Science 329, 841–845.
Hill, W. G., Goddard, M. E., and Visscher, P. M. (2008). Data and theory point to mainly additive genetic variance for complex traits. PLoS Genet. 4, e1000008. doi:10.1371/journal.pgen.1000008
Himmelstein, D. S., Greene, C. S., and Moore, J. H. (2011). Evolving hard problems: generating human genetics datasets with a complex etiology. BioData Min. 4, 21.
Jakulin, A., and Bratko, I. (2004). “Testing the significance of attribute interactions,” in Proceedings of the 21st International Conference on Machine Learning (ICML-2004), eds R. Greiner, and D. Schuurmans (Banff: ACM Press), 409–416.
Kraft, P., Zeggini, E., and Ioannidis, J. P. (2009). Replication in genome-wide association studies. Stat. Sci. 24, 561–573.
Kulkarni, S., Martin, M. P., and Carrington, M. (2008). The Yin and Yang of HLA and KIR in human disease. Semin. Immunol. 20, 343–352.
Lee, S. H., Wray, N. R., Goddard, M. E., and Visscher, P. M. (2011a). Estimating missing heritability for disease from genome-wide association studies. Am. J. Hum. Genet. 88, 294–305.
Lee, I., Blom, U. M., Wang, P. I., Shim, J. E., and Marcotte, E. M. (2011b). Prioritizing candidate disease genes by network-based boosting of genome-wide association data. Genome Res. 21, 1109–1121.
Limdi, N. A., Wadelius, M., Cavallari, L., Eriksson, N., Crawford, D. C., Lee, M. T., Chen, C. H., Motsinger-Reif, A., Sagreiya, H., Liu, N., Wu, A. H., Gage, B. F., Jorgensen, A., Pirmohamed, M., Shin, J. G., Suarez-Kurtz, G., Kimmel, S. E., Johnson, J. A., Klein, T. E., Wagner, M. J., and International Warfarin Pharmacogenetics Consortium. (2010). Warfarin pharmacogenetics: a single VKORC1 polymorphism is predictive of dose across 3 racial groups. Blood 115, 3827–3834.
Liu, J. Z., McRae, A. F., Nyholt, D. R., Medland, S. E., Wray, N. R., Brown, K. M., AMFS Investigators, Hayward, N. K., Montgomery, G. W., Visscher, P. M., Martin, N. G., and Macgregor, S. (2010). A versatile gene-based test for genome-wide association studies. Am. J. Hum. Genet. 87, 139–145.
McKinney, B. A., Crowe, J. E., Guo, J., and Tian, D. (2009). Capturing the spectrum of interaction effects in genetic association studies by simulated evaporative cooling network analysis. PLoS Genet. 5, e1000432. doi:10.1371/journal.pgen.1000432
Menashe, I., Maeder, D., Garcia-Closas, M., Figueroa, J. D., Bhattacharjee, S., Rotunno, M., Kraft, P., Hunter, D. J., Chanock, S. J., Rosenberg, P. S., and Chatterjee, N. (2010). Pathway analysis of breast cancer genome-wide association study highlights three pathways and one canonical signaling cascade. Cancer Res. 70, 4453–4459.
Moore, J. H., Gilbert, J. C., Tsai, C. T., Chiang, F. T., Holden, T., Barney, N., and White, B. C. (2006). A flexible computational framework for detecting, characterizing, and interpreting statistical patterns of epistasis in genetic studies of human disease susceptibility. J. Theor. Biol. 241, 252–261.
Moskvina, V., Craddock, N., Muller-Myhsok, B., Kam-Thong, T., Green, E., Holmans, P., Owen, M. J., and O’Donovan, M. C. (2011). An examination of single nucleotide polymorphism selection prioritization strategies for tests of gene-gene interaction. Biol. Psychiatry 70, 198–203.
Page, L., Brin, S., Motwani, R., and Winograd, T. (1999). The PageRank Citation Ranking: Bringing Order to the Web. Technical Report, Stanford InfoLab, 1–17.
Raychaudhuri, S., Iartchouk, O., Chin, K., Tan, P. L., Tai, A. K., Ripke, S., Gowrisankar, S., Vemuri, S., Montgomery, K., Yu, Y., Reynolds, R., Zack, D. J., Campochiaro, B., Campochiaro, P., Katsanis, N., Daly, M. J., and Seddon, J. M. (2011). A rare penetrant mutation in CFH confers high risk of age-related macular degeneration. Nat. Genet. 43, 1232–1236.
Ritchie, M. D., Hahn, L. W., Roodi, N., Bailey, L. R., Dupont, W. D., Parl, F. F., and Moore, J. H. (2001). Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. Am. J. Hum. Genet. 69, 138–147.
Rivas, M. A., Beaudoin, M., Gardet, A., Stevens, C., Sharma, Y., Zhang, C. K., Boucher, G., Ripke, S., Ellinghaus, D., Burtt, N., Fennell, T., Kirby, A., Latiano, A., Goyette, P., Green, T., Halfvarson, J., Haritunians, T., Korn, J. M., Kuruvilla, F., Lagacé, C., Neale, B., Lo, K. S., Schumm, P., Törkvist, L., National Institute of Diabetes and Digestive Kidney Diseases Inflammatory Bowel Disease Genetics Consortium (NIDDK IBDGC), United Kingdom Inflammatory Bowel Disease Genetics Consortium, International Inflammatory Bowel Disease Genetics Consortium, Dubinsky, M. C., Brant, S. R., Silverberg, M. S., Duerr, R. H., Altshuler, D., Gabriel, S., Lettre, G., Franke, A., D’Amato, M., McGovern, D. P., Cho, J. H., Rioux, J. D., Xavier, R. J., and Daly, M. J. (2011) Deep sequencing of GWAS loci identifies independent rare variants associated with inflammatory bowel disease. Nat Genet. 43, 1066–1073.
Rosenberg, N. A., Huang, L., Jewett, E. M., Szpiech, Z. A., Jankovic, I., and Boehnke, M. (2010). Genome-wide association studies in diverse populations. Nat. Rev. Genet. 11, 356–366.
Selinger-Leneman, H., Genin, E., Norris, J. M., and Khlat, M. (2003). Does accounting for gene-environment (GxE) interaction increase the power to detect the effect of a gene in a multifactorial disease? Genet. Epidemiol. 24, 200–207.
Shi, J., Levinson, D. F., Duan, J., Sanders, A. R., Zheng, Y., Pe’er, I., Dudbridge, F., Holmans, P. A., Whittemore, A. S., Mowry, B. J., Olincy, A., Amin, F., Cloninger, C. R., Silverman, J. M., Buccola, N. G., Byerley, W. F., Black, D. W., Crowe, R. R., Oksenberg, J. R., Mirel, D. B., Kendler, K. S., Freedman, R., and Gejman, P. V. (2009). Common variants on chromosome 6p22.1 are associated with schizophrenia. Nature 460, 753–757.
Teo, Y. Y., Small, K. S., and Kwiatkowski, D. P. (2010). Methodological challenges of genome-wide association analysis in Africa. Nat. Rev. Genet. 11, 149–160.
Torkamani, A., Topol, E. J., and Schork, N. J. (2008). Pathway analysis of seven common diseases assessed by genome-wide association. Genomics 92, 265–272.
Trynka, G., Hunt, K. A., Bockett, N. A., Romanos, J., Mistry, V., Szperl, A., Bakker, S. F., Bardella, M. T., Bhaw-Rosun, L., Castillejo, G., de la Concha, E. G., de Almeida, R. C., Dias, K. R., van Diemen, C. C., Dubois, P. C., Duerr, R. H., Edkins, S., Franke, L., Fransen, K., Gutierrez, J., Heap, G. A., Hrdlickova, B., Hunt, S., Izurieta, L. P., Izzo, V., Joosten, L. A., Langford, C., Mazzilli, M. C., Mein, C. A., Midah, V., Mitrovic, M., Mora, B., Morelli, M., Nutland, S., Núñez, C., Onengut-Gumuscu, S., Pearce, K., Platteel, M., Polanco, I., Potter, S., Ribes-Koninckx, C., Ricaño-Ponce, I., Rich, S. S., Rybak, A., Santiago, J. L., Senapati, S., Sood, A., Szajewska, H., Troncone, R., Varadé, J., Wallace, C., Wolters, V. M., Zhernakova, A., Spanish Consortium on the Genetics of Coeliac Disease (CEGEC), Prevent CD Study Group, Wellcome Trust Case Control Consortium (WTCCC), Thelma, B. K., Cukrowska, B., Urcelay, E., Bilbao, J. R., Mearin, M. L., Barisani, D., Barrett, J. C., Plagnol, V., Deloukas, P., Wijmenga, C., and van Heel, D. A. (2011) Dense genotyping identifies and localizes multiple common and rare variant association signals in celiac disease. Nat. Genet. 43, 1193–1201.
Visscher, P. M., Goddard, M. E., Derks, E. M., and Wray, N. R. (2011). Evidence-based psychiatric genetics, AKA the false dichotomy between common and rare variant hypotheses. Mol. Psychiatry 14. doi:10.1038/mp.2011.65. [Epub ahead of print].
Keywords: epistasis network, genetic association interaction network, missing heritability
Citation: McKinney BA and Pajewski NM (2012) Six degrees of epistasis: statistical network models for GWAS. Front. Gene. 2:109. doi: 10.3389/fgene.2011.00109
Received: 03 October 2011;
Paper pending published: 21 November 2011;
Accepted: 22 December 2011;
Published online: 12 January 2012.
Edited by:
Frank Emmert-Streib, Queen’s University Belfast, UKReviewed by:
Andrew DeWan, Yale School of Public Health, USAMarylyn D. Ritchie, The Pennsylvania State University, USA
Copyright: © 2012 McKinney and Pajewski. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License , which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: B. A. McKinney, Department of Mathematics, Tandy School of Computer Science, University of Tulsa, Rayzor Hall, 800 South Tucker Drive, Tulsa, OK 74104, USA. e-mail:YnJldHQubWNraW5uZXlAZ21haWwuY29t
