- Center Leo Apostel, Vrije Universiteit Brussel, Brussels, Belgium
Robustness has been studied through the analysis of data sets, simulations, and a variety of experimental techniques that each have their own limitations but together confirm the ubiquity of biological robustness. Recent trends suggest that different types of perturbation (e.g., mutational, environmental) are commonly stabilized by similar mechanisms, and system sensitivities often display a long-tailed distribution with relatively few perturbations representing the majority of sensitivities. Conceptual paradigms from network theory, control theory, complexity science, and natural selection have been used to understand robustness, however each paradigm has a limited scope of applicability and there has been little discussion of the conditions that determine this scope or the relationships between paradigms. Systems properties such as modularity, bow-tie architectures, degeneracy, and other topological features are often positively associated with robust traits, however common underlying mechanisms are rarely mentioned. For instance, many system properties support robustness through functional redundancy or through response diversity with responses regulated by competitive exclusion and cooperative facilitation. Moreover, few studies compare and contrast alternative strategies for achieving robustness such as homeostasis, adaptive plasticity, environment shaping, and environment tracking. These strategies share similarities in their utilization of adaptive and self-organization processes that are not well appreciated yet might be suggestive of reusable building blocks for generating robust behavior.
Introduction
Life is able to withstand internal and external fluctuations at various frequencies and timescales. Genetic mutations, localized stochastic fluctuations in molecular concentrations, loss of structural integrity (e.g., trauma), infectious diseases, endogenous threats such as cancer, temperature fluctuations, altered species interactions, and regime shifts in the physical environment are just some examples of these disturbances. Many biological systems have an intrinsic capacity to maintain specific functions or traits when exposed to particular perturbations and have thus been described as being robust. Trait robustness is pervasive in biology throughout at all organizational levels including protein folding, gene expression, metabolic flux, physiological homeostasis, development, organism survival, species persistence, and ecological resilience (Holling, 2001; de Visser et al., 2003; Kitano, 2007).
Research into the mechanisms, trade-offs, and evolution of robustness is changing our understanding of molecular, evolutionary, and systems biology. To many biologists, robustness is ubiquitous and essential because proteins, cells, biochemical networks, immune systems, organisms, and natural populations exist within changing and sometimes novel conditions under which the maintenance of satisfactory performance will determine persistence or function. Evolutionary biologists are interested in mutational robustness because it deconstrains evolution at the molecular level (Cowen and Lindquist, 2005; Bloom et al., 2006; McBride et al., 2008) and at other levels of biological organization (Babajide et al., 1997; Aldana et al., 2007; Ciliberti et al., 2007; Wagner, 2008; Whitacre and Bender, 2010a). Recent studies suggest that mutational robustness is also important to the adaptive diversification of populations because it allows cryptic genetic variation (CGV) to accumulate in populations that can subsequently be co-opted or exapted for rapid evolution in novel environments (Hayden et al., 2011; Whitacre and Atamas, submitted). In systems biology, robustness provides a measure of model plausibility because only an exceedingly small fraction of model instantiations will display the robust expression patterns observed in real biological networks. As a result, a model’s robustness provides information that can guide the development of realistic biochemical network simulations (Morohashi et al., 2002). Rare instances of extreme fragility sometimes reveal insights into evolutionary history, system function, and the performance–complexity–cost trade-offs that are sometimes associated with robustness (Csete and Doyle, 2004; Stelling et al., 2004a,b; Chandra et al., 2011). In other cases, fragilities have little to do with the organism traits. For instance, environmental changes such as habitat fragmentation and lost resources as well as ecological properties such as food web structure can introduce large disturbances that cause local extinctions yet do not reflect poorly on any particular phenotype (Raup, 1992; Bak and Paczuski, 1995; Green et al., 2000).
Background
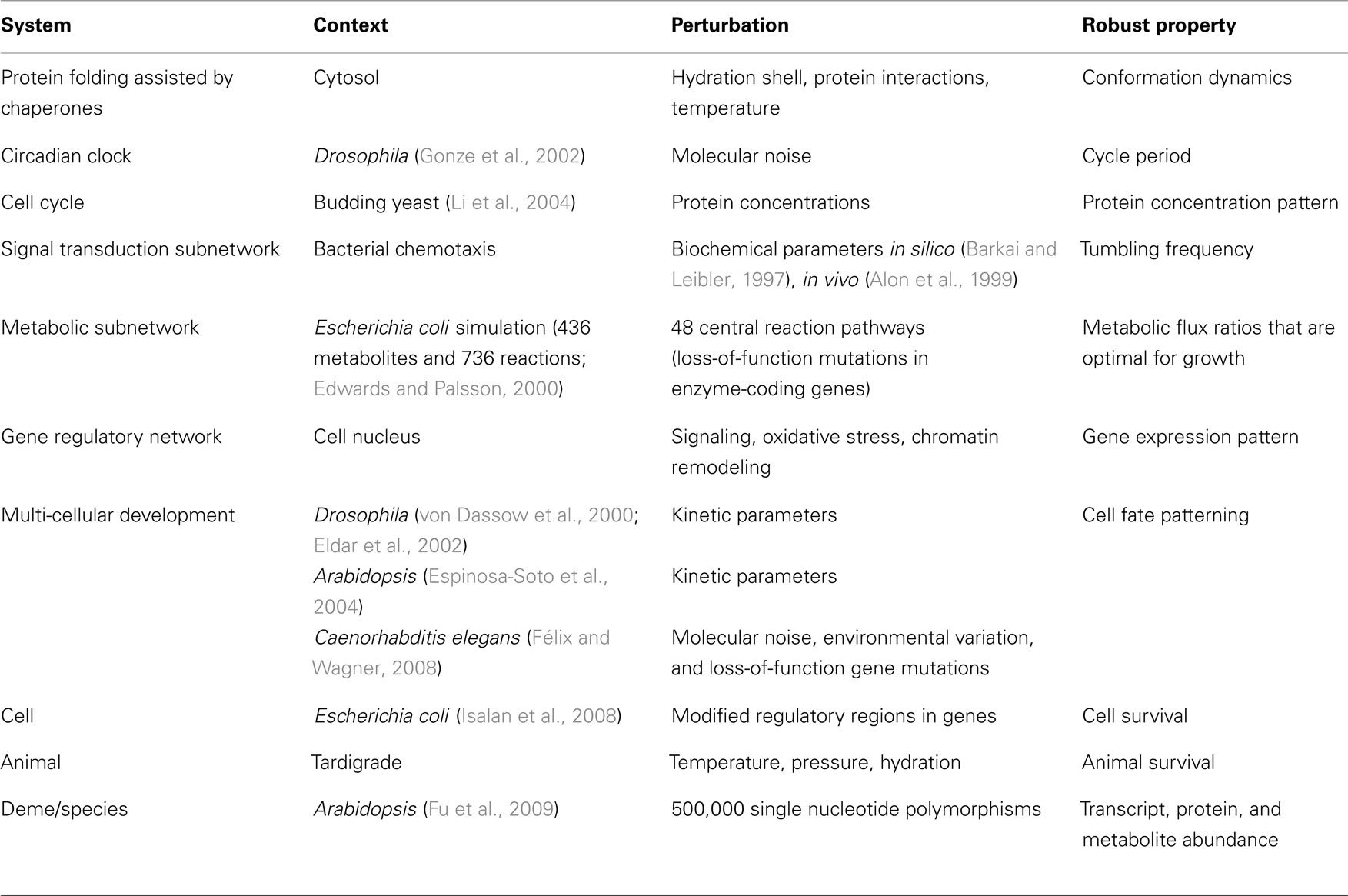
Robustness arises in many aspects of gene expression from single gene output, to expression patterns in a single cell (Li et al., 2004), to expression patterns of differentiating cells during development (Scharloo, 1991; von Dassow et al., 2000; Eldar et al., 2002; Espinosa-Soto et al., 2004; Félix and Wagner, 2008). It is also observed in large signaling networks (Barkai and Leibler, 1997; Alon et al., 1999), metabolic networks (Edwards and Palsson, 2000; Shinar and Feinberg, 2010), neural networks (Jahnke et al., 2009), and in smaller biochemical networks involved in bacteria chemotaxis (Barkai and Leibler, 1997; Alon et al., 1999) and circadian rhythm (Gonze et al., 2002). Table 1 provides a representative sampling of the extensive literature that has been devoted to these topics.
Robustness is studied using a patchwork of tools that each have their own limitations. A growing number of studies develop discrete agent-based simulation models – with component relationships defined by extant knowledge and parameters determined from biological datasets – to evaluate robustness in silico. Simulations can provide a systematic analysis of perturbations that might be orders of magnitude too numerous to directly evaluate and it can allow researchers to probe specific perturbations that are difficult to introduce in biological experiments. Simulations have undoubtedly contributed to progress in systems biology, however models must be used with a good understanding of their limitations. Developing a good model is a challenging exercise because it requires an accurate mapping between the digital genotype and analog phenotype for a given level of phenotypic organization in addition to an appropriate parameterization of the environmental space (Savageau et al., 2009).
Simulation studies also generally assume an equivalence between fitness and the stability of a phenotypic manifestation, thus neglecting the contextual multi-functionality of many biological networks and the importance of adaptive phenotypic plasticity to the robustness of an organism fitness (see Pathways Toward Robustness). The systematic characterization of the robust operating conditions for a function and the environmental cues that drive transitions to alternative functions is an important open problem in the study of systems robustness. Studies progressing along these lines have so far estimated convex regions of environmental conditions for which a functional output is stabilized. Methods for this type of analysis include stochastic sampling of robust parameter volumes, random walks in parameter space, and use of models that facilitate an estimation of the boundaries of robust parameter regions (Coelho et al., 2009).
Importantly, the number of degrees of freedom for model development are often enormous, and many model instantiations can generate similar behavior within specific environments (many to one mapping), thus making model overfitting a serious problem and the scientific merit of any result greatly dependent on experimental validation. Consequently, it is becoming common practice to validate simulation results using a smaller set of biological experiments that test unexpected or noteworthy predictions from the model. Finally, all studies evaluate robustness by exposing a system, or a model of the system, to a small set of perturbations. However because robustness is contingent on the perturbations considered (see Box 1), caution is needed when making generalizations that extend beyond the perturbations tested in a study.
Box 1. Defining robustness.
As stated by Alderson and Doyle (2010), “a (property) of a (system) is robust if it is (invariant) with respect to a (set of perturbations).” The conclusions from studying robustness will therefore depend on how each element in the square brackets is defined. An example of this contingency is seen in the conditional existence of genetic neutrality. For instance, populations in their native habitat can harbor considerable genetic diversity with minor quantitative trait differences amongst individuals, i.e., the phenotype is largely robust to these particular genetic variants. However, exposing the population to new environments can reveal phenotypic differences and a lower degree of observed mutational robustness; a phenomenon known as CGV (Gibson and Dworkin, 2004). In other words, the mutational robustness apparent in a population depends on the traits measured, the environments considered, and the genetic background.
Studies introducing perturbations to actual biological networks have employed a variety of techniques. For instance, a study by Isalan et al. (2008) developed a method for evaluating the robustness of cellular fitness toward modifications in genetic regulation. They constructed 598 recombinations of promoters (including regulatory regions) that were combined with copies of different transcription factor genes in Escherichia coli and then added to the wild-type genetic background. Isalan et al. found that 95% of these modified gene interaction networks were tolerated by the bacteria and some conferred selective advantages in particular environments. While prior studies reported high robustness from gene knockout in a number of genomically complex species, this study provided the first evidence of high tolerance and evolvability toward heritable regulatory modifications.
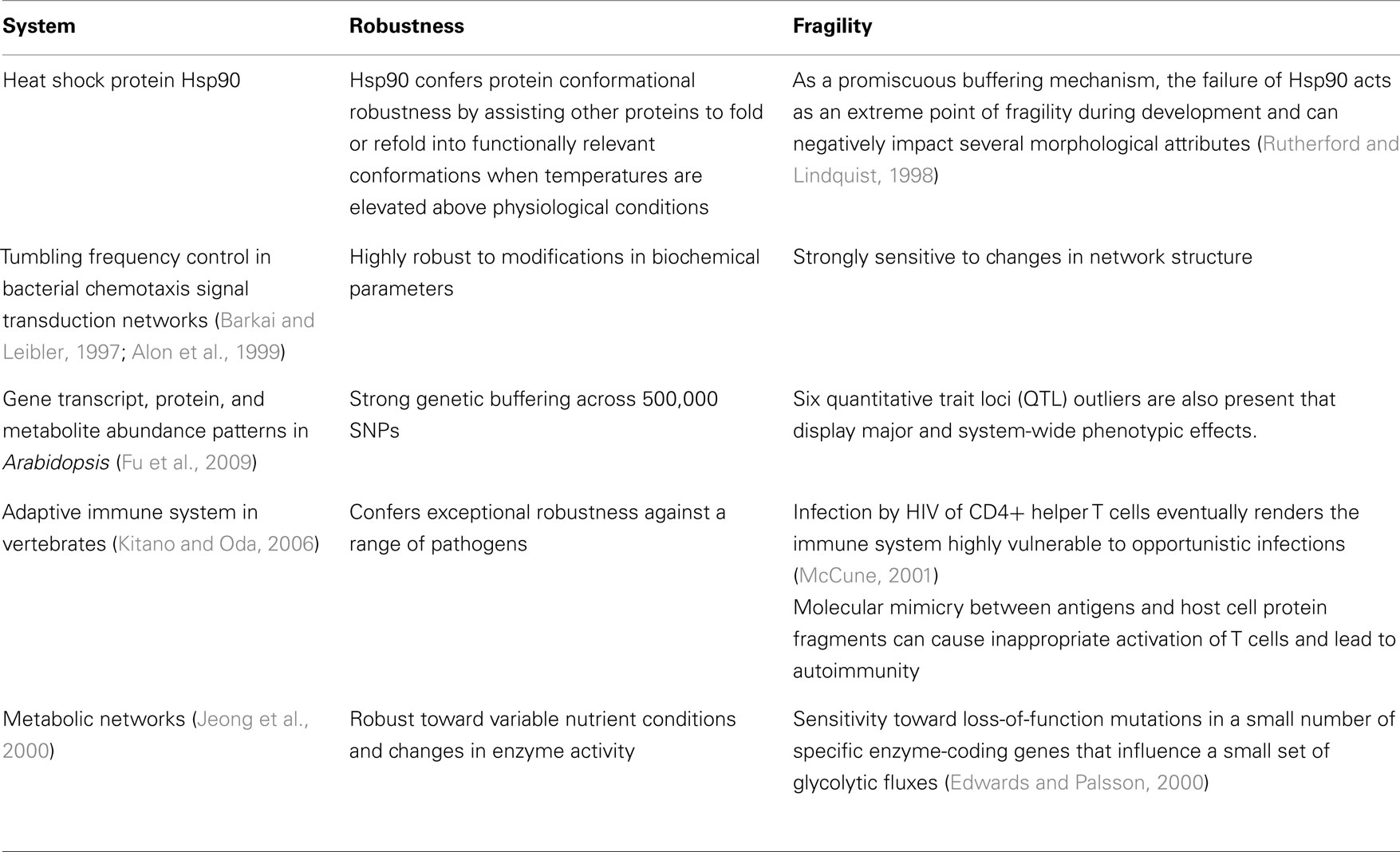
Other studies systematically evaluated robustness in situ. For instance in a comprehensive study by Fu et al. (2009), they profiled 162 lines of Arabidopsis for variation in transcript, protein, and metabolite abundance and found widespread genetic buffering from expressed gene to complex phenotypic trait. The widespread buffering of most of the 500,000 SNPs studied was accompanied by only six quantitative trait loci (QTL) outliers that displayed relatively large and system-wide phenotypic effects. In isolation, labeling these outliers as inconsequential artifacts seems reasonable, however studies of gene expression (Featherstone and Broadie, 2002; Fu et al., 2009), the immune system (Kitano and Oda, 2006; Stromberg and Carlson, 2006), protein chaperones (Rutherford and Lindquist, 1998), metabolic networks (Stelling et al., 2002), and circadian clocks (Stelling et al., 2004b) have similarly reported that exceptionally robust biological systems often harbor rare yet devastating fragilities (see Table 2). The theory of Highly Optimized Tolerance proposes that these rare yet devastating fragilities arise from fundamental trade-offs between robustness, complexity, and performance (Carlson and Doyle, 2002). As discussed in Section “Mechanisms,” such trade-offs might originate from the organization of biological networks into bow-tie architectures.
Cell Fate Patterning
There is a long history of studying canalization in development (e.g., Waddington, 1942; Scharloo, 1991), however some recent studies of cell fate patterning also have important implications to the study of robustness. In a study by von Dassow and colleagues, empirical observations were used to construct an ODE model of the segment polarity network of Drosophila, which was then validated by demonstrating that the model mimics several aspects of network function. In analyzing the model, they reported gene expression patterns that were robust to kinetic parameters even when varied by an order of magnitude or more (von Dassow et al., 2000). Unexpectedly, the network typically maintained key functional outputs even when values for all 48 model parameters were selected randomly (within biologically plausible ranges; von Dassow et al., 2000). Similar findings have since been reported in models of Arabidopsis (Espinosa-Soto et al., 2004) and in other biological networks, suggesting that evolution generally establishes networks with exceptional robustness toward mutations.
Another study of cell fate patterning modeled developmental patterning in Drosophila that is guided by morphogen gradients and feedback loops that buffer against fluctuations in gene dosage and expression (Eldar et al., 2002). From studying contributing factors in the model’s robustness, they predicted that the gradient of a particular morphogen, bone morphogenic protein, would need to be buffered through the localized storage of excess signaling molecules and they confirmed these model predictions with biological experiments. The robustness of early cell fate patterning has also been reported for several model organisms. For instance in experiments reviewed in Félix and Wagner (2008), the spatial pattern of vulval cell fates during development in the nematode Caenorhabditis elegans is reported as being highly robust to molecular noise, environmental variation, and loss-of-function gene mutations (Félix and Wagner, 2008) and interestingly, this patterning is largely conserved across species within the family Rhabditidae despite large differences in the mechanistic details that underly cell fate patterning for each species (Félix and Wagner, 2008). As reviewed by Kirschner and Gerhart (1998), numerous developmental traits have been conserved across related species yet at the same time evolution has been deconstrained to construct these traits through distinct pathways.
Metabolic Networks
Metabolic flux-balance analysis (FBA) is a standard technique for estimating the maximum rate of biomass production for specific nutrient inputs and has become a standard tool for estimating metabolic network robustness toward the elimination of individual chemical reactions. These eliminations correspond with loss-of-function mutations in enzyme-coding genes and thus provide rough estimations of mutational robustness for this subset of the genome. In Edwards and Palsson (2000) they use FBA to study metabolic network models of E. coli K-12 comprised of 436 metabolites and 736 reactions. They evaluate the effects on cell growth from individually eliminating 48 central reactions related to glycolysis, the pentose phosphate pathway, and the tricarboxylic acid cycle. They find that only seven of these reactions are essential to cell growth and that the ability to obtain optimal conditions (i.e., the metabolic flux ratios that optimize biosynthetic demands for growth) is robust toward large changes in flux for most of these essential reactions although robustness diminishes quickly for perturbations in a few glycolytic fluxes (Edwards and Palsson, 2000). Their computational predictions matched experimental data for only 86% of cases, however Wagner (2005) has suggested that there might be plausible explanations to account for some of these discrepancies.
In a study by Smart et al. (2008) they use an alternative (topological) technique for estimating cascading failures in metabolic network models of E. coli, Saccharomyces cerevisiae, Staphylococcus aureus, and Methanosarcina barkeri. Perturbations involved the complete removal of a single enzyme and its associated reactions from a metabolic network, while network sensitivity was characterized by the extent that such perturbations can cause the “knockout” of additional reactions. Metabolite viability was defined based on a topological flux-balance (TFB) criterion, which requires that each metabolite participate in at least one generating and one consuming reaction. The study also defines two network motifs that are important in the analysis; rigid clusters and non-rigid branches. Rigid clusters correspond with non-branching metabolic pathways, i.e., the loss of any single reaction in the pathway causes all pathway metabolites to fail the TBF criterion. Non-rigid branching motifs represent alternative (i.e., degenerate; Whitacre, 2010) reaction pathways and thus influence the boundaries of rigid clusters. In Smart et al. (2008) they show that the rigid and branching motifs in metabolic networks are non-randomly organized to reduce the presence of large rigid clusters and thereby reduce the likelihood of large cascading failures. To demonstrate that motif organization was a major contributor to network robustness, they compare biological data sets to null models generated by randomly switching pairs of edges in each metabolic network. The development of suitable null models is an open research topic and a very important one because the null model defines the point of reference from which conclusions are drawn. In the study by Smart et al. (2008), the null models are simple to generate yet are able to randomize motif organizational structure while preserving important topological properties that would otherwise act as potential confounding factors such as distributions of node degree, degree-in, degree-out, and in–out degree correlations.
In a study by Stelling et al. (2002) they analyze the metabolic network of E. coli using a “control-effective” flux analysis that evaluates the extent that individual reaction pathways contribute toward efficient and flexible operation of the entire network. Using this analysis technique they were able to accurately predict metabolic network phenotypes that are accessible through genetic mutations. Although computationally more demanding, control-effective flux analysis provides advantages over FBA because it does not require linear and steady state approximations in order to determine the optimal flux vector and importantly, it is able to model the important contribution of pathway flexibility toward the robustness of metabolic network outputs.
Other Biochemical Networks
Robustness has been studied in a number of other biochemical networks. In models of the cell cycle regulatory network of budding yeast for instance, the sequence of cellular states associated with the cell cycle was determined to be a global attractor for the dynamics of the network and is robust to perturbations in the concentrations of most proteins (Li et al., 2004). Simple circadian clock models for Drosophila have also been found to produce a circadian rhythm that is highly robust toward stochastic noise (Gonze et al., 2002). Simulation experiments on models of bacterial chemotactic signal transduction networks have similarly found that the key functionality of this signaling network (control of tumbling frequency) is robust to biochemical parameters (Barkai and Leibler, 1997); findings that were later confirmed in biological experiments (Alon et al., 1999).
Mechanisms
While a full accounting of biological robustness remains elusive; both in terms of the mechanisms by which robustness is achieved and the forces that have caused robustness to grow over evolutionary time, there has been progress in uncovering systems principles that contribute to robustness across biological disciplines (Fontana and Schuster, 1998; Kitami and Nadeau, 2002; Conant and Wagner, 2004; Wilhelm et al., 2004; Gómez-Gardenes et al., 2005; Braendle and Félix, 2008; Félix and Wagner, 2008; Levin and Lubchenco, 2008; Szollosi and Derenyi, 2009). For instance, trait robustness has been found to spontaneously arise from the presence of coupled feedback loops within signaling and gene regulatory networks (GRN). Similar forms of distributed robustness have been shown to arise from the topological properties of mass-action networks (Shinar and Feinberg, 2010) as well as in reentrant neural circuitry (Edelman, 1993) where local stability is further enhanced when neural connections exhibit high inhibition:activation ratios and moderate to fast synaptic response times (Jahnke et al., 2009). Robustness is also sometimes attributed to modularity in RNA and protein folding (Ancel and Fontana, 2000), to local environment shaping/control enacted by protein chaperones (Rutherford, 2000), and is supported indirectly from the stochasticity of dynamics occurring during multi-cellular development (Kupiec, 1997) or within a single cell’s interactome (Feinerman et al., 2008). Robustness arising from local functional redundancy in genes and metabolic pathways (Edelman and Gally, 2001; Ma and Zeng, 2003) can also reappear as distributed forms of robustness at higher organizational levels when degenerate pathways are organized into nested bow-tie architectures (Ma and Zeng, 2003; Csete and Doyle, 2004) and when degenerate ensembles are organized into buffering networks (Whitacre and Bender, 2010b). Robustness also commonly arises from saturation effects as seen in the sensitivity of reaction flux toward enzymes with high catalytic activity. Because of the asymptotic relationship between metabolic flux and enzyme activity (Figure 1), mutations that reduce enzyme activity typically have only a small influence on reaction flux (Meiklejohn and Hartl, 2002). Such robustness can be compounded by the existence of multiple high activity enzymes positioned serially within a metabolic pathway (Kacser and Burns, 1981, 1995).
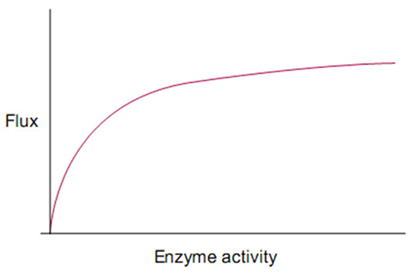
Figure 1. Saturation kinetics: the hyperbolic relationship between enzyme activity and reaction rate.
At present it remains unclear how discipline-specific properties relate to one another and whether more fundamental mechanisms underpin robustness across these contexts. Although universal mechanisms are difficult to uncover, many of these properties share similarities in how they influence the generation and regulation of system response options. In particular, and as highlighted throughout this section, response options often take the form of functional redundancy or response diversity, and the regulation of responses typically arises through competitive exclusion or cooperative facilitation.
Functional Redundancy and Response Diversity
Functional redundancy – multiple elements with similar functions or similar effects on a trait –supports canalization during development (Edelman and Gally, 2001), robustness toward loss-of-function mutations (Wagner, 2005), and robustness toward stochastic fluctuations. Functional redundancy does not require identical (isomorphic) elements and instead often arises between molecular species, developmental pathways, and organisms that are redundant only within particular contexts (Edelman and Gally, 2001). In other words, the elements can be structurally unique and only contingently similar in function: a property known as degeneracy (Edelman and Gally, 2001; see Figure 2). Due to structural differences, degenerate components often harbor unique vulnerabilities in their implementation of a functional role. Degeneracy there by facilitates a natural form of bet-hedging that enables biological functions to be achieved in a variety of ways meaning for instance that a targeted attack such as a specific inhibitor is less likely to present a risk to all functionally related components at once (Tian et al., 2011). For example in glioblastoma cancers, therapies targeting the EGF receptor are thwarted by the co-activation of alternate receptor tyrosine kinases (RTK) that have partial functional overlap with the EGF receptor (and are therefore degenerate), but are not targeted by the specific EGF receptor inhibitor (Huang et al., 2007; Stommel et al., 2007). In S. cerevisiae, the adhesins gene family expresses proteins that typically play unique roles during development, yet can perform each other’s functions when expression levels are altered (Guo et al., 2000). Such context-dependent similarity in functions/traits among diverse units of an ensemble, and, reciprocally, context-dependent dissimilarity of redundant units, is common in biology. It can be observed at the molecular and cellular levels of gene regulation, in proteins of every functional class (e.g., enzymatic, structural, or regulatory; Atamas, 2005), in protein complex assemblies (Kurakin, 2009); also in ontogenesis (see Newman, 1994, p. 14), the nervous system (Edelman and Gally, 2001), metabolic pathways (Csete and Doyle, 2004), and in cell signaling (Ozaki and Leonard, 2002). In short, degeneracy is a common and basic contributor to regulatory and structural robustness.
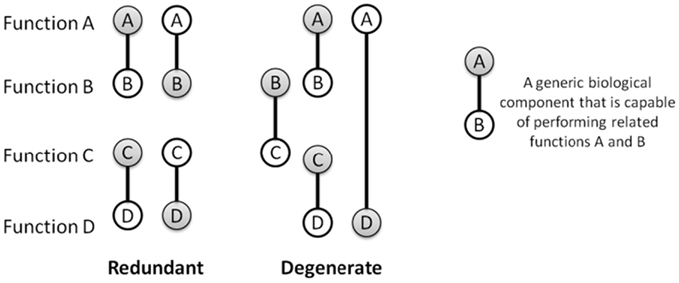
Figure 2. Biological components such as proteins, complexes, circuits, and pathways, often display a range of closely related functions. Some of these functions sometimes partially overlap with other components, i.e., they are degenerate. This is illustrated using bi-functional components that are either (purely) redundant, i.e., perfectly identical in functional capabilities, or degenerate, i.e., diverse in their bi-functionality while also having overlap in one of their functions (partial redundancy). Node shading indicates a functional role that is invoked within a particular environmental context.
Feedback and Regulatory Complexity
Activation and inhibition are basic regulatory interactions that influence the robustness of almost any quantitative trait. Underlying these interactions are simple physical processes including competitive exclusion (e.g., competition for binding sites, foraging competition amongst species) and cooperative facilitation (e.g., regulated recruitment of molecular species, facilitative species–species interactions). The activation of single regulatory effects is often dependent upon local conditions (e.g., the presence of a competitor or inducing factor, the scarcity of a resource). The large numbers of distinct, contextually active, regulatory effects make it impossible to reduce the origins of trait robustness into simple sets of independent processes despite the rather simple mechanistic origins of biological robustness.
Some studies have however attempted to decompose system behavior and reveal modular control circuits of biological robustness. The study of bacterial chemotaxis has become a popular model system in the search for rational regulatory control paradigms that can account for the robustness of a biochemical network. For instance, in Levchenko and Iglesias (2002) they report evidence that the robustness of eukaryotic cells in following chemo-attractant gradients arises through a simple positive feedback controller. A related study investigated models of bacterial chemotaxis signal transduction networks (Barkai and Leibler, 1997) and it was later predicted that the observed robustness in tumbling frequency control under continued stimulation is the result of an integral feedback control system that is embedded in the biological network (Yi et al., 2000). Integral feedback is a basic control method that is seen for instance in the well-studied PID (proportional, integral, derivative) controller. While integral feedback provides a valid explanation for the robustness of their model (Barkai and Leibler, 1997), upon closer examination, it was later argued by Stelling et al. (2004a) that much of the robustness of the real network is instead conferred through nested and partially overlapping feedback loops that are not easily deconstructed into isolated, single reference point, controllers.
In contrast to research programs that attempt to deconstruct biological robustness, others have studied system properties that promote the emergence of robustness through a system’s self-organization. Robust regulatory control can spontaneously emerge in networks of positively and negatively reinforcing regulatory interactions with several studies reporting widespread links between robustness and regulatory complexity (Kauffman, 1969, 1993; Siegal and Bergman, 2002; Martin and Wagner, 2008). For instance, in simulations of GRN, Siegal and Bergman (2002) found gene expression patterns became more robust as the number of regulatory connections in the network is randomly increased. This and other studies have shown that robustness can emerge in GRN models without direct selection for robustness, thus suggesting that the origins of trait robustness could preclude their fitness benefits and their selective conservation in evolution.
Early studies by Kauffman (1969, 1993) investigated similar questions surrounding complexity, robustness, and evolvability using random Boolean network models of gene regulation. In these models, Kauffman (1990) found that network stability improves if the average number of regulatory factors is increased for each gene or if regulatory interactions become more redundant, thereby providing one plausible explanation for positive associations between regulatory complexity and robustness. From a related perspective, it has been proposed that the contingency of regulatory effects within dense regulatory networks results in numerous weak associations that together stabilize biological networks. Such diffuse regulatory control has been proposed to explain stable flux patterns in metabolic networks (Csermely, 2004), meta-stable organization of protein interaction networks (Whitacre and Bender, 2010b) as well as cohesion in social networks (Granovetter, 1973) and ecosystems (McCann et al., 1998; Berlow, 1999).
The role of regulatory complexity is also arguably observed in the relationship between physiological homeostasis and the integration of biological subsystems within the body. For instance, multiple organ dysfunction syndrome (MODS) – a leading cause of death in intensive care units –causes widespread inflammation in locations that are remote from the initial inciting event. Studies have found that patients with MODS have increased regularity in physiological time series measurements (e.g., electrocardiogram signals), which is likely to reflect a decoupling in the cross-regulation of organ systems (Buchman, 2002). Similar decoupling of organs has been found to occur from severe brain injury, aging, and during septic shock where decoupling is also reversed during recovery (Buchman, 2002).
In the examples discussed, regulatory control is distributed amongst many genes, enzymes, circuits, and pathways where the modification of one regulating factor is compensated for by other contingently activated factors of roughly similar effect. In other words, there is partial redundancy or degeneracy within these distributed control networks. Simulations have suggested that this degeneracy may widely contribute to the robustness of regulatory network expression patterns (Tononi et al., 1999; Csermely, 2004; Whitacre and Bender, 2010b, in press).
Robust Architectures
Several network structural motifs and statistical topological properties have been reported to be positively associated with the robustness of biological networks. The attention of the scientific community has been particularly drawn toward evidence that the organization of biological systems into a scale-free network (SFN) is a major contributor to biological robustness (Kitano, 2002). Concisely stated, SFN are networks in which the degree distribution of node connectivity can be approximated by a power law. A number of studies have reported the presence of SFN in biological networks with follow-up studies suggesting that this topological feature is significant to structural robustness or integrity. Integrity is measured by the proportion of nodes that remain members of a single connected network after the removal of a single node and its associated links. Assuming that a network is static, it can be proven that the integrity of a SFN is robust to the loss of randomly selected nodes, which typically have low connectivity, yet is fragile to the removal of highly connected hubs. Thus it was speculated that the robust-yet-fragile (RYF) nature of many biological systems (see Background) might originate from their SFN topology. Because SFN topologies can emerge in protein interaction networks using gene duplication and divergence algorithms (Solé et al., 2002; Pastor-Satorras et al., 2003), it thus would seem plausible that RYF is a basic feature of life and has a partly non-adaptive origin, e.g., in the neutral evolution of genome complexity (Force et al., 2005; Lynch, 2007).
A number of studies using abstract models have claimed that a SFN topology will improve the efficiency of technological systems such as power grids and communication networks, increase the spread of ideas and diseases in a society, and provide robustness to biological networks (but also, see Alderson and Doyle, 2010). For instance, in Featherstone and Broadie (2002) the so called “gene expression network” (network where gene interactions are defined based on whether the loss of one gene’s function influences the expression of another gene) in yeast meets the conditions of a scale-free topology, which arguably explains the high levels of phenotypic robustness (>95%) that they observed in yeast subjected to single point mutations. A somewhat related study found that protein–protein interaction networks are also scale-free and importantly, that there generally exists a positive association between the degree of a protein (i.e., its promiscuity) and the phenotypic effects from mutating the gene expressing that protein (Jeong et al., 2001).
Metabolic networks meet the conditions of a scale-free topology (Jeong et al., 2000) and also display a power law distribution of reaction fluxes where the most connected metabolites tend to have the greatest flux (Almaas et al., 2004). However, subsequent analysis has found that metabolic networks also exhibit a modular hierarchical structure (Ravasz et al., 2002) that is possibly better described as being “scale-rich,” i.e., most topological features are unique to specific levels of system granularity (Tanaka, 2005). Instead of being random instances of gene duplication and divergence (Solé et al., 2002; Pastor-Satorras et al., 2003) or “rich get richer” paradigms of SFN evolution (Barabási and Albert, 1999), biological networks instead appear to consist of unique SFN representations that are notable for the abundance of so called “nested bow-ties” (Ma and Zeng, 2003; Csete and Doyle, 2004) with RYF features that are unique to each systems context. Bow-tie architectures are increasingly being described as an important contributor to network robustness and interestingly are replete with structural manifestations of functional redundancy and degeneracy (Tieri et al., 2010).
A bow-tie architecture – where many inputs are fed into a central core that is the unutilized to produce many distinct outputs – is believed to contribute to the robustness of many biological networks and may provide an alternative explanation for the rare yet devastating fragilities of biological systems (see Figure 3) (Csete and Doyle, 2004). In metabolism, the bow-tie architecture provides a formal description of the large “fan in” of catabolized nutrients that produce a small number of activated carriers (e.g., ATP, NADH) and precursor metabolites (the “knot” of the bow-tie), that then “fan out” in the synthesis of numerous building blocks (e.g., nucleotides, sugars, amino acids) and eventually larger macromolecules. This architecture provides exceptional robustness toward variable nutrient inputs through the many degenerate metabolic pathways that can be used to produce a few common building blocks (Csete and Doyle, 2004). As a simple example of this degeneracy, glucose metabolism can take place by either glycolysis or the pentose phosphate pathway. Although these pathways can substitute for each other if necessary, the sum of their metabolic effects is not the same (Sauer et al., 2004).
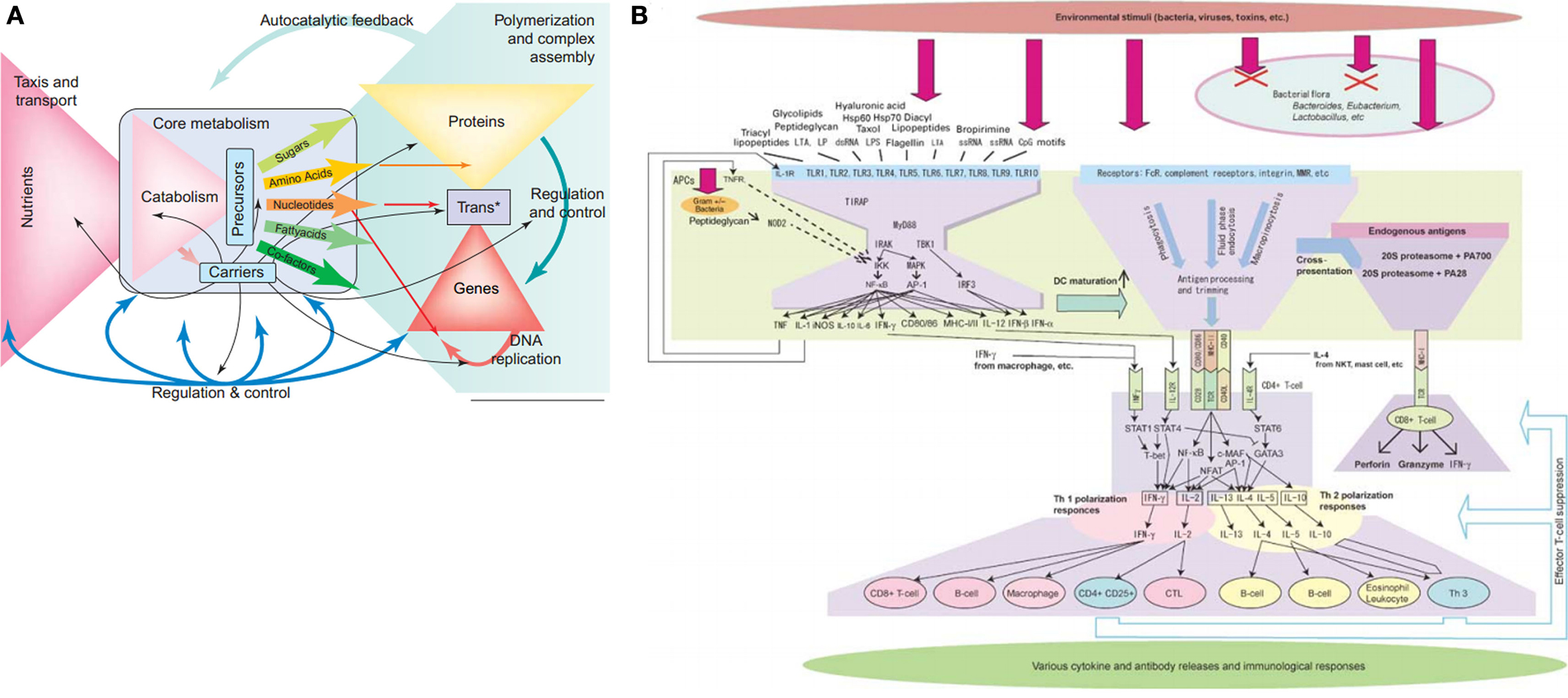
Figure 3. Bow-tie network architecture of metabolism (reprinted from Csete and Doyle, 2004) and the immune system (reprinted from Kitano and Oda, 2006).
The core of the bow-tie architecture is generally seen as its Achilles heel: if sufficiently perturbed or hijacked for alternative uses then catastrophic failure is likely (Ma and Zeng, 2003; Csete and Doyle, 2004). On the other hand, creating such catastrophic perturbations is not easy. Core components can be synthesized with great flexibility at high levels of flux and the hypothetical modification or removal of dynamically constructed core components may require multiple enzymatic modifications or large perturbations. In Isalan et al. (2008) for instance, E. coli survival was surprisingly robust to the addition of new regulatory regions in practically all hubs of the scale-free bacterial gene regulatory network. For nested bow-ties in the immune system (Tieri et al., 2010), even the targeted attack of the CD4+ cell hubby HIV requires a large and sustained assault before the system degrades to an immune-compromised state. One reason that points of fragility are still fairly robust is that they are regulated and protected from damaging disturbances by strategies that utilize environmental regulation, homeostatic regulation, steric inhibition, and others (see Pathways Toward Robustness). However once a network is successfully hijacked, as seen for instance in cancerous tumors, the resulting maladaptive state may inherit pre-existing robust mechanisms and acquire additional robust attributes that are difficult to reverse or destroy (Kitano, 2004a).
Conceptualizing Robust System Dynamics
On the fringes (or forefront) of biological sciences, there has been progress in understanding the theoretical basis by which robustness evolves and emerges. In theory, robustness is high when there exists a sufficient repertoire of actions to counter perturbations (Ashby’s Law of Requisite Variety; Ashby, 1964) and when a system’s memory, regulatory organization, or structural bias will elicit particular responses to particular perturbations that stabilize the measured trait (e.g., see Heylighen and Joslyn, 2001). Biological responses are not deterministically bijective (i.e., characterized by a one-to-one mapping between perturbation and response) and instead proceed through a concurrent stochastic process that can sometimes be conceptualized as exploratory behavior but in other cases is more accurately described as a process of self-organization (Kirschner and Gerhart, 1998).
Exploratory Behavior
Exploratory behavior reliably transforms pseudo-random variations into robust end states. To do this, exploratory behavior involves repeated selection over a repertoire of subsystem states that are each elaborations of previously selected states. Exploratory behavior thus requires one subsystem or process that generates options and another subsystem that selects options that are to be retained and expanded upon. Selection may occur through activation and reinforcement of options (positive selection) or inhibition and constraint of options (negative selection). In addition to genetic evolution, there are a variety of biological systems that exhibit this type of exploratory behavior (Kirschner and Gerhart, 1998).
Immune system
During positive/negative selection of immature T cells in the thymus, immature thymocytes stochastically recombine gene segments involved in the expression of alpha and beta chains of the T cell receptor (TCR) resulting in a large variety of possible TCR affinities. The thymus selects from this repertoire using apoptotic checkpoints that utilize both positive and negative selection processes. Positive thymic selection allows cell maturation in only a subset of thymocytes that meet TCR-driven activation requirements for effective scanning of antigen presenting cell surfaces. Negative selection in the thymus prevents cell maturation of thymocytes that are inappropriately activated by endogenous protein fragments. After maturation, subsequent rounds of selection are also imposed on mature cytotoxic T cells through the adaptive immune response. In particular, positive selection activates a small set of the T cell repertoire based on recognition of foreign antigens and co-activation by regulatory T cells, resulting in the clonal expansion of a small set of activated cells (see Figure 4). The result of these stages of variation and selection is typically a repertoire of immune cells that as a group are highly robust at recognizing the presence of dangerous pathogens (Whitacre et al., 2012).
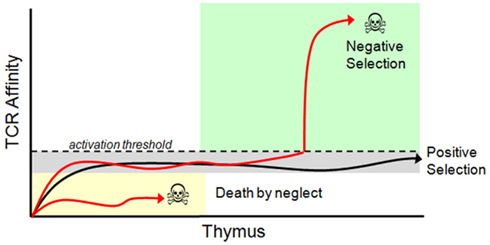
Figure 4. Thymic selection of T cells. Immature T cells (called thymocytes) enter the thymic cortex and undergo differentiation. During this time TCR re-arrangement occurs until an active TCR is expressed along with both the CD4 and CD8 co-receptors. Those thymocytes that have a functional TCR and survive commit to a single positive (SP) state (SP thymocytes express either CD4 or CD8, but not both), and migrate to the thymic medulla. Here, SP thymocytes systematically scan medullary thymic epithelial cells and dendritic cells presenting self-peptides in their MHC molecules. During the SP thymocyte stage, any thymocyte that expresses a TCR that has an above threshold affinity to self-peptides undergoes apoptosis and dies. Surviving thymocytes eventually exit the thymus and enter the periphery as mature, naïve T cells. Positive and negative selection is determined by TCR affinity to their peptide/MHC ligand. Once a TCR is expressed on the cell surface it immediately begins interacting with MHC molecules presenting self-peptides. Functional TCR’s generate a basal signal output that, although insufficient to cross the activation threshold, is still necessary for thymocyte survival. TCR’s that cannot recognize peptide/MHC complexes ultimately die by neglect. Surviving thymocytes then migrate to the thymic medulla where they are exposed to self-antigen. Any TCR that reacts with a self-peptide with too high of an affinity will induce T cell activation and apoptosis. Only thymocytes with a functional TCR, which is competent to trigger low-level signaling but does not cross the activation threshold to self-peptides, is positively selected and permitted to exit the thymus. Modified from Whitacre et al. (2012).
Microtubule spindle formation
During morphogenesis of the microtubule (MT) cytoskeleton, spindle MTs bind to the kinetochores of chromosomes and mediate chromosome segregation toward spindle poles. Location of the chromosomes by MT takes place through an exploratory process involving stochastic polymerization and depolymerization of MT in random directions, with spindle directions (positively) selected in instances where MT fortuitously interacts with a kinetochore and is stabilized by surface proteins. This exploratory process robustly achieves a functional end state under different initial arrangements, different numbers of chromosomes, and different morphologies of the cell (Kirschner and Gerhart, 1998).
Other examples of exploratory behavior supporting robustness can be found throughout biology, for instance: in cellular differentiation, proliferation, and apoptosis during development; chemotaxis and cell motility; the formation of neural connections and vascular growth during development (Edelman, 1987); behavioral adaptation in complex species such as predator avoidance, habitat tracking, and adaptive foraging; adaptive social behaviors such as ant foraging, the honey bee “waggle dance,” and termite nest building; and the somatic evolution of cancer cells during the development of therapy resistance (Tian et al., 2011).
Self-Organization and Emergence
Functional robustness is achieved through system responses that are invoked by environmental cues. In some cases, the process of response development can be modeled as an exploratory process that is akin to Darwinian evolution or as a simple feedback control loop. In other cases, it is difficult to clearly distinguish between the elements being varied in the system and the elements imposing selection over the repertoire of variant states. Instead, many components both influence and respond to their local microenvironment, each regulating the other and together forming an emergent response to environmental perturbations that cannot be neatly decomposed into a conceptually simple controller or exploratory search paradigm. When robustness arises in such a manner, systems theorists generally refer to the system as being self-organized or say that the system exhibits emergent properties, i.e., stable properties spontaneously arise without a clear selection process that matches stochastic variations with environmental cues. While every robust expression pattern in biology can be classified as involving one or a combination of adaptive and self-organizing paradigms, the intuitive relationships between these paradigms discussed here are rarely if ever mentioned in the literature.
Self-organization of robust expression patterns is observed in all complex biological networks including gene expression, signaling networks, and metabolism. While many studies focus attention on small molecular circuits where feedback loops are easily defined, at the system level these feedback loops cannot be decomposed to reveal a logical conceptualization of system dynamics. For many biological systems, exploratory and self-organizing processes interact at different organizational levels of the system. In microtubule spindle formation for instance, regulatory recruitment between macromolecules drives microtubule assembly (self-organization) and less frequent acts of positive activation by the local environment (selection) determine those microtubules that remain and are elaborated upon. Self-assembly combined with less frequent external positive/negative selection is common in the dynamic construction and deconstruction of many molecular assemblies, temporary scaffolding structures, and cellular compartments (Kirschner and Gerhart, 1998). While environmental cues often initiate assembly or provide stimulation that prevents disassembly, the actual assembly process involves numerous regulatory actions distributed throughout the system and thus is best described as a process of self-organization.
Pathways Toward Robustness
For the viability of an organism to be robust, it would seem that the phenotype needs to be regulated. In some cases, this requires maintaining trait stability despite variability of the environment (e.g., developmental canalization in multi-cellular eukaryotes; Waddington, 1942, 1953), while in others it requires the adaptation of traits toward a modified environment, e.g., adaptive phenotypic plasticity (see Figure 5) (Kitano, 2004b; Pfennig et al., 2010). Although rarely discussed, phenotypic regulation is not the only means by which robustness can be achieved. Alternatively, organisms and biological subsystems can exert influence on their surroundings to reduce exposure to damaging perturbations or to track resources that are relevant to system function. Here I discuss underlying similarities between four different strategies for achieving robustness: (1) adaptive phenotypic plasticity (modifying traits); (2) homeostasis (enforcing trait stability); (3) environment shaping (modifying the environment); (4) environment tracking (enforcing environment stability).
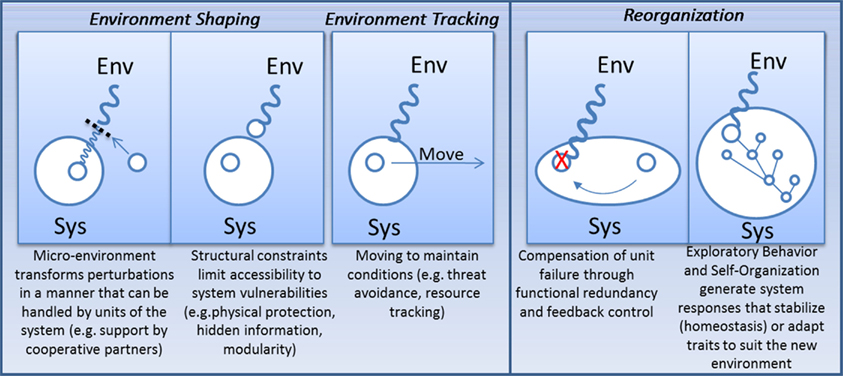
Figure 5. Four responses to environmental stress: regulate the environment so fragilities are not accessed/revealed; move to new environments where performance can be maintained; adapt system response to the environment in order to robustly maintain traits or adapt traits in order to preserve organism fitness.
Homeostasis and Adaptive Phenotypic Plasticity
Organisms often respond to changing conditions by changing their own states; both those externally expressed (i.e., phenotype) and those internal to the organism, in order to maintain fitness (Figure 6). In either case, a regulated response is guided by information from the environment to stabilize or modify traits in a manner that robustly preserves viability of the organism under changing conditions. Homeostasis – the stabilizing regulation of internal states – preserves traits through regulatory responses and actions that buffer internal stresses through the altered usage of internal components. Adaptive phenotypic plasticity, on the other hand, preserves fitness through regulated responses that modify higher level traits to match a changing environment. Homeostasis and adaptive phenotypic plasticity thus reflect the same basic phenomena viewed from different perspectives (see Figure 6).
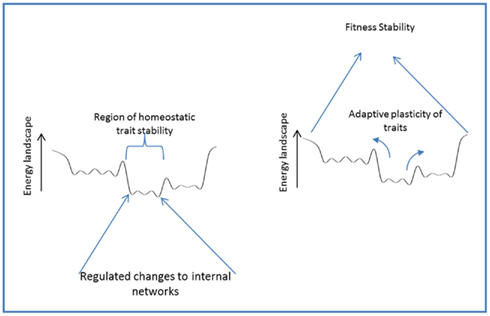
Figure 6. Homeostasis and adaptive phenotypic plasticity: different perspectives of a similar phenomena.
Plasticity is a generic property of phenotypic expression that derives from the phenotype’s dependency on the environment. The more specific term adaptive plasticity is reserved for genetically evolved regulation of phenotypic change (e.g., physiological, behavioral) that supports organism survival under a transient stress or altered environment. Adaptive plasticity can also sometimes support survival through reduced functionality, as illustrated in the remarkable behavior of microscopic tardigrades. By transitioning to a nearly suspended metabolic state (Crowe and Crowe, 2000), tardigrades can persist for years under tremendous extremes in temperature (−200, 150°C; Jönsson et al., 2008), pressure (0, 1200 atm; Seki and Toyoshima, 1998; Jönsson et al., 2008), dehydration (Guidetti and Jönsson, 2002), and direct solar radiation (Jönsson et al., 2008).
Adaptive phenotypic plasticity is prevalent in biological networks. Many networks contribute to multiple functions that only benefit to fitness in specific environmental contexts. Thus a network’s contribution to organism fitness can depend on its ability to reliably transition between distinct functions depending on context. This is seen in small inducible-catabolic and repressible-biosynthetic circuits (Wall et al., 2004) and in various threshold-activated functions involving genetic switches, activation potential in neurons, and analog-to-digital signal processing (Harding and Hancock, 2008).
Context-dependent changes in function are also important to networks involved in multi-cellular development. For instance, the Hox gene network plays an important role in patterning of the main anteroposterior body axis and also in the patterning of the vertebrate limb. The network is presented with different regulatory inputs within these different embryonic regions, resulting in distinct gene expression outputs that influence cell development differently in the two contexts. Similarly, Drosophila segment polarity genes (e.g., wingless, engrailed, hedgehog) contribute to early segmentation but also play important roles later in the development of the fly’s wing. As a further demonstration of adaptive plasticity in segment polarity networks, Ingolia (2004) demonstrated that the robustness of cell pattern formation in Drosophila relies on so called bistability; the ability of gene expression to exhibit multiple stable expression states that emerge depending on the local environment and history of the cell. In short, the robustness of development relies on the robustness of a small number of gene expression states (homeostasis) as well as the context-dependent transition between these expression states (adaptive plasticity).
In a study of a gene regulatory network model, Martin and Wagner (2008) examined whether the robustness of distinct functions is constrained in multi-functional networks. Although increasing the number of functions for a network was found to exponentially constrain the number of viable network architectures, they found that the robustness of one network function was generally uncorrelated with the robustness of another. At least for the experimental conditions tested, Martin and Wagner demonstrated that network structures with multiple highly robust functions could readily be discovered through a process of gradual evolution. For other in silico studies, analyzing results to account for the interplay between homeostasis and adaptive plasticity remains an unresolved challenge (see Background).
Environment Tracking
Movement within the environment alters the perturbations a system is exposed to and can improve robustness, e.g., by avoiding dangerous conditions or reliably acquiring important resources. More generally, environment tracking can help to ensure that suitable phenotype-environment pairings are preserved. Common forms of environmental tracking include chemotaxis, migration, seed dispersal, predator avoidance (Kondoh, 2007), and adaptive foraging (Kondoh, 2003). Evolution can also facilitate environment tracking through changes to life history traits such as the timing of reproduction (e.g., seasonal flowering and seeding times), hibernation, and the duration of development (Hamrick and Godt, 1996).
Environment Regulation/Shaping
Robustness is typically discussed as occurring through regulation of the phenotype. However many biological systems also regulate their environments in ways that influence the types and frequencies of perturbations experienced and thus the robustness of these systems. For instance, many species actively shape their environments through niche construction (Odling-Smee et al., 1996; Day et al., 2003), environment simplification (West-Eberhard, 2003, 2005), behavioral and genetic coevolution (Agrawal, 2001), parental inheritance (Jablonka et al., 1995; Uller, 2008), and cultural inheritance (Dawkins, 1983; Dennett, 1995). The ability to create environmental conditions when needed instead of depending on the environment has a direct influence on the range of viable habitats but is rarely discussed as a mechanism for achieving biological robustness. While humans are the most remarkable users of environment shaping, the extent that this occurs in other species is impressive (Laland and Sterelny, 2006). Transformation of the environment is so important in biology and evolution that Dawkins devoted a popular science book to this topic and dubbed such phenomenon as the extended phenotype (Dawkins, 1999).
Environment shaping occurs at the molecular level as well. One well-studied example of environment shaping is seen in protein chaperones and particularly, the heat shock protein Hsp90 (Rutherford and Lindquist, 1998; Rutherford, 2003). Heat shock proteins assist other proteins to fold or refold into functionally relevant conformations when temperatures are elevated above physiological conditions and thus confer protein conformational robustness. Studies on Drosophila and Arabidopsis have shown that Hsp90 also contributes to phenotypic robustness and canalizes a broad range of morphological attributes (Rutherford and Lindquist, 1998). However, while Hsp90 suppresses phenotypic variation under normal conditions, its function can be overwhelmed by environmental stress resulting in a substantial subsequent loss of phenotypic robustness. As an important buffering mechanism, the failure of this component thus acts as an extreme point of fragility during development.
Environment shaping often involves physical changes to the environment that alter the accessibility of system vulnerabilities as is seen in niche construction activities such as nest building. At the molecular level, steric inhibition prevents certain ligands from docking to the active site of a macromolecule while membrane structures throughout the body prevent dangerous molecules and pathogens from perturbing internal networks.
The four pathways described in this section can be related to one another by their usage of exploratory and self-organizing paradigms discussed in the previous section. With environment tracking, heterogeneity in the environment is sampled and selected through an exploratory process. Adaptive phenotypic plasticity involves self-organized responses to environmental change that were previously selected and genetically assimilated through evolution. In other words, relatively rapid self-organization within an organism’s lifetime is shaped slowly over time through exploratory genetic evolution. Similarly, homeostasis constitutes a prototypical self-organization process that is selectively modified over long periods of time based on the benefits and costs to organism fitness. Environment shaping extends control beyond system boundaries using behaviors that are either learned in a lifetime (exploratory) or evolved over generations.
Discussion
Insights into biological robustness may also be important outside of biology. At the moment, control engineers optimize system homeostasis using PID controllers and Kalman filters while design engineers design systems with well controlled environments that avoid damaging perturbations or that include fail-safe protection against catastrophic failure. In organization science and manufacturing, operational variability is minimized using frameworks that systematically reduce endogenous variability such as six sigma. These heuristics and control-theoretic principles are successful within predictable environmental conditions, however they are considerably less successful in volatile environments that occasionally introduce novel stresses. Novel stresses are by definition not predictable, thus the flexibility needed to achieve robustness cannot be entirely pre-specified based on the anticipation of future stresses: a common assumption in engineering and organization science. Instead, properties such as flexibility, response diversity, and functional redundancy must emerge on demand or arise through adaptive processes that do not require foresight. Alternatively, if flexibility only arises in the places where designers perceive future need, then a system’s ability to accommodate novel design conditions will be limited by the designer’s foresight, e.g., their ability to predict plausible future environments. These challenges of adaptive robustness are becoming increasingly important to engineers due to the growing number of technological domains where volatility and novel disturbances cannot be avoided (Crawford, 1992; Millson et al., 1992; Griffin, 1993; Page, 1993; Bettis and Hitt, 1995; Walter, 2005; Waldner, 2008).
Insights into the emergent and exploratory robustness of biological systems are being studied within non-biological domains with the goal of translating some of these concepts into new engineering design principles. As highlighted throughout this review, degeneracy is a common source of robustness across different biological disciplines. Degeneracy is also a system property that can be clearly articulated and defined for any system comprising functionally versatile elements (Figure 2; Table 3). Because these requirements transcend biological contexts, several research programs have begun exploring how the degeneracy concept can be translated into design principles for the realization of more flexible and resilient systems in non-biological disciplines (Randles et al., 2010; Whitacre et al., 2010, in press; Frei and Whitacre, in press). For instance, in defense capability simulations, it has been shown that fleets of military field vehicles with high degeneracy in task capabilities can improve operational robustness within anticipated mission scenarios yet at the strategic level provide exceptional design and organizational adaptability for responding to unanticipated challenges (Bender and Whitacre, 2011; Whitacre et al., in press). Other studies have looked at how the degeneracy concept can be used in the design of more flexible manufacturing and assembly systems (Frei and Whitacre, in press), the design of more flexible behaviors in swarm robotics (Whitacre and Bender, in press), and for improving the performance of population-based dynamic optimization algorithms (Whitacre et al., 2010). Others are using the concept to understand the requisite conditions for embodied (Fernandez-Leon, 2011) and simulated artificial life (Mendao et al., 2007; Kerkstra and Scha, 2008; Clark et al., 2011).
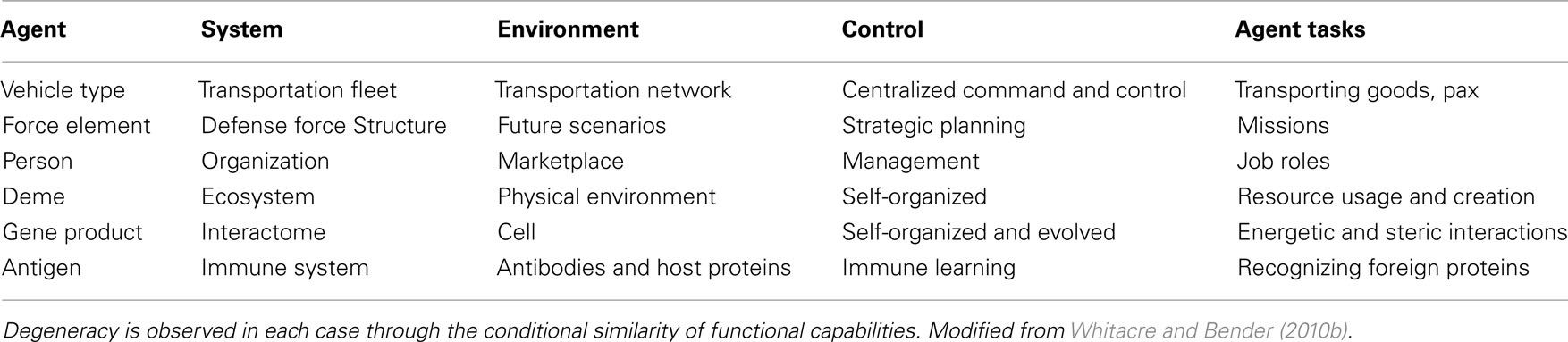
Table 3. System classes where components (agents) are multi-functional and have functions that can partially overlap with other agents.
Conclusion
Robustness is a ubiquitous feature of biological networks. A number of fields have contributed to our understanding of robustness including control theory, network theory, complexity science, and evolution. With the wide range of tools and principles used to probe biological robustness, it has been difficult to determine how these concepts relate to each another. This review has attempted to integrate studies of robustness in systems biology with an emphasis on systems principles that transcend specific disciplines and that might be fundamental to the robustness of biological networks.
According to Ashby’s Law of requisite variety, the variety of system responses provides an upper limit on the variety of conditions toward which a system can be robust. This upper limit is not necessarily an active constraint however because many natural perturbations can be suppressed by the same response, i.e., the perturbations are congruent (see Meiklejohn and Hartl, 2002; de Visser et al., 2003; Lehner, 2010). Ashby’s Law formalizes a well-known rule of robustness; namely that different perturbations often require different counter responses. In addition to response variety, robustness also requires the regulation of responses in order to achieve compatibility with each perturbation encountered (e.g., see Heylighen and Joslyn, 2001). For systems that display exploratory behavior, the generation of variety and the regulation of variety occurs in mostly separate subsystems. One subsystem generates new elaborations of its previous self (e.g., heritable variants) while the other subsystem imposes positive or negative selection on the variants expressed, thereby dictating what manifestations of phenotypic expression are elaborated upon. When the variety of perturbations and responses is greatly restricted, e.g., each arises over a single dimension, and when there is a single reference point for stability, it sometimes becomes possible to conceptualize robustness using feedback control models. However it is more often the case that robustness cannot be modeled by either control-theoretic or adaptive paradigms and instead emerges through a process of self-organization. A self-organizing process differs from adaptive behavior in that the system cannot be neatly decomposed into distinct sets of components responsible for generating and regulating responses. Instead, components mutually influence and respond to their local microenvironment. Considerable research has been devoted toward uncovering system principles that explain how robustness becomes distributed over a self-organizing interconnected system. This article has proposed that many of these systems properties are related to basic mechanisms involving functional redundancy, response diversity, and degeneracy.
Robustness involves a matching between system and environment. Distinct pathways for achieving this matching are differentiated in this review based on whether regulated changes take place in the system or the environment. The four pathways described – homeostasis, adaptive phenotypic plasticity, environment tracking, and environment shaping – can also be distinguished by the manner in which adaptive and self-organizing processes are integrated to achieve robustness. As highlighted throughout this review, adaptive and self-organizing processes both contribute to the robustness of many biological networks. Multi-scale models that can capture both adaptive and self-organizing processes would provide an important technological step forward in simulation-based research, however research on this topic has only just begun within the context of abstract artificial life models, e.g., (Whitacre et al., 2010, in press; Jin and Meng, 2011; Meng et al., 2011). Formal models and methods for analyzing both homeostasis and adaptive plasticity are also lacking and their development would represent an important milestone. Achieving this milestone requires new efficient methods for systematically probing and characterizing attractor basins (of a system’s phenotypic expression) along with the efficient and systematic exploration of perturbations (i.e., environmental cues) that are responsible for initiating adaptive transitions between phenotypic attractors.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Agrawal, A. A. (2001). Phenotypic plasticity in the interactions and evolution of species. Science 294, 321–326.
Aldana, M., Balleza, E., Kauffman, S., and Resendiz, O. (2007). Robustness and evolvability in genetic regulatory networks. J. Theor. Biol. 245, 433–448.
Alderson, D. L., and Doyle, J. C. (2010). Contrasting views of complexity and their implications for network-centric infrastructures. IEEE Trans. Syst. Man Cybern. A Syst. Hum. 40, 839–852.
Almaas, E., Kovács, B., Vicsek, T., Oltvai, Z. N., and Barabási, A. L. (2004). Global organization of metabolic fluxes in the bacterium Escherichia coli. Nature 427, 839–843.
Alon, U., Surette, M. G., Barkai, N., and Leibler, S. (1999). Robustness in bacterial chemotaxis. Nature 397, 168–171.
Ancel, L. W., and Fontana, W. (2000). Plasticity, evolvability, and modularity in RNA. J. Exp. Zool. 288, 242–283.
Babajide, A., Hofacker, I. L., Sippl, M. J., and Stadler, P. F. (1997). Neutral networks in protein space: a computational study based on knowledge-based potentials of mean force. Fold. Des. 2, 261–269.
Bak, P., and Paczuski, M. (1995). Complexity, contingency, and criticality. Proc. Natl. Acad. Sci. U.S.A. 92, 6689–6696.
Barabási, A. L., and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512.
Bender, A., and Whitacre, J. M. (2011). “Emergent flexibility as a strategy for addressing long-term planning uncertainty,” in NATO Risk-Based Planning Conference, Salisbury.
Berlow, E. L. (1999). Strong effects of weak interactions in ecological communities. Nature 398, 330–334.
Bloom, J. D., Labthavikul, S. T., Otey, C. R., and Arnold, F. H. (2006). Protein stability promotes evolvability. Proc. Natl. Acad. Sci. U.S.A. 103, 5869.
Braendle, C., and Félix, M. A. (2008). Plasticity and errors of a robust developmental system in different environments. Dev. Cell 15, 714–724.
Carlson, J. M., and Doyle, J. (2002). Complexity and robustness. Proc. Natl. Acad. Sci. U.S.A. 99, 2538–2545.
Chandra, F. A., Buzi, G., and Doyle, J. C. (2011). Glycolytic oscillations and limits on robust efficiency. Science 333, 187.
Ciliberti, S., Martin, O. C., and Wagner, A. (2007). Innovation and robustness in complex regulatory gene networks. Proc. Natl. Acad. Sci. U.S.A. 104, 13591–13596.
Clark, E., Nellis, A., Hickinbotham, S., Stepney, S., Clarke, T., Pay, M., and Young, P. (2011). “Degeneracy enriches artificial chemistry binding systems,” in European Conference on Artificial Life, Paris.
Coelho, P. M. B. M., Salvador, A., and Savageau, M. A. (2009). Quantifying global tolerance of biochemical systems: design implications for moiety-transfer cycles. PLoS Comput. Biol. 5, e1000319. doi: 10.1371/journal.pcbi.1000319
Conant, G. C., and Wagner, A. (2004). Duplicate genes and robustness to transient gene knock-downs in Caenorhabditis elegans. Proc. Biol. Sci. 271, 89–96.
Cowen, L. E., and Lindquist, S. (2005). Hsp90 potentiates the rapid evolution of new traits: drug resistance in diverse fungi. Science 309, 2185.
Crawford, M. (1992). The hidden costs of accelerated product development. J. Prod. Innov. Manag. 9, 188–199.
Crowe, J. H., and Crowe, L. M. (2000). Preservation of mammalian cells-learning nature’s tricks. Nat. Biotechnol. 18, 145.
Csermely, P. (2004). Strong links are important, but weak links stabilize them. Trends Biochem. Sci. 29, 331–334.
Dawkins, R. (1983). “Universal Darwinism,” in Evolution from Molecules to Man, ed. D. S. Bendall (Cambridge University Press), 202.
Day, R., Laland, K. N., and Odling-Smee, F. J. (2003). Rethinking adaptation. Perspect. Biol. Med. 46, 80–95.
de Visser, J., Hermisson, J., Wagner, G. P., Ancel Meyers, L., Bagheri-Chaichian, H., Blanchard, J. L., Chao, L., Cheverud, J. M., Elena, S. F., Fontana, W., Gibson, G., Hansen, T. F., Krakauer, D., Lewontin, R. C., Ofria, C., Rice, S. H., von Dassow, G., Wagner, A., and Whitlock, M. C. (2003). Perspective: evolution and detection of genetic robustness. Evolution 57, 1959–1972.
Edelman, G. (1987). Neural Darwinism: The Theory of Neuronal Group Selection. New York: Basic Books.
Edelman, G. M. (1993). Neural Darwinism: selection and reentrant signaling in higher brain function. Neuron 10, 115–125.
Edelman, G. M., and Gally, J. A. (2001). Degeneracy and complexity in biological systems. Proc. Natl. Acad. Sci. U.S.A. 98, 13763–13768.
Edwards, J. S., and Palsson, B. O. (2000). Robustness analysis of the Escherichia coli metabolic network. Biotechnol. Prog. 16, 927–939.
Eldar, A., Dorfman, R., Weiss, D., Ashe, H., Shilo, B. Z., and Barkai, N. (2002). Robustness of the BMP morphogen gradient in Drosophila embryonic patterning. Nature 419, 304–308.
Espinosa-Soto, C., Padilla-Longoria, P., and Alvarez-Buylla, E. R. (2004). A gene regulatory network model for cell-fate determination during Arabidopsis thaliana flower development that is robust and recovers experimental gene expression profiles. Plant Cell 16, 2923.
Featherstone, D., and Broadie, K. (2002). Wrestling with pleiotropy: genomic and topological analysis of the yeast gene expression network. Bioessays 24, 267–274.
Feinerman, O., Veiga, J., Dorfman, J. R., Germain, R. N., and Altan-Bonnet, G. (2008). Variability and robustness in T cell activation from regulated heterogeneity in protein levels. Science 321, 1081.
Félix, M. A., and Wagner, A. (2008). Robustness and evolution: concepts, insights and challenges from a developmental model system. Heredity 100, 132–140.
Fernandez-Leon, J. A. (2011). Behavioural Robustness and the Distributed Mechanisms Hypothesis. D.Phil. Ph.D. thesis, University of Sussex.
Fontana, W., and Schuster, P. (1998). Continuity in evolution: on the nature of transitions. Science 280, 1451–1455.
Force, A., Cresko, W. A., Pickett, F. B., Proulx, S. R., Amemiya, C., and Lynch, M. (2005). The origin of subfunctions and modular gene regulation. Genetics 170, 433–446.
Frei, R., and Whitacre, J. M. (in press). Degeneracy and networked buffering: principles for supporting emergent evolvability in agile manufacturing systems. J. Nat. Comput.
Fu, J., Keurentjes, J. J., Bouwmeester, H., America, T., Verstappen, F. W., Ward, J. L., Beale, M. H., de Vos, R. C., Dijkstra, M., Scheltema, R. A., Johannes, F., Koornneef, M., Vreugdenhil, D., Breitling, R., and Jansen, R. C. (2009). System-wide molecular evidence for phenotypic buffering in Arabidopsis. Nat. Genet. 41, 166–167.
Gibson, G., and Dworkin, I. (2004). Uncovering cryptic genetic variation. Nat. Rev. Genet. 5, 681–690.
Gómez-Gardenes, J., Moreno, Y., and Floría, L. M. (2005). On the robustness of complex heterogeneous gene expression networks. Biophys. Chem. 115, 225–228.
Gonze, D., Halloy, J., and Goldbeter, A. (2002). Robustness of circadian rhythms with respect to molecular noise. Proc. Natl. Acad. Sci. U.S.A. 99, 673.
Green, D. G., Newth, D., and Kirley, M. G. (2000). “Connectivity and catastrophe-towards a general theory of evolution,” in Artificial Life VII: Proceedings of the Seventh International Conference, 153–161.
Griffin, A. (1993). Metrics for measuring product development cycle time. J. Prod. Innov. Manag. 10, 112–125.
Guidetti, R., and Jönsson, K. I. (2002). Long-term anhydrobiotic survival in semi-terrestrial micrometazoans. J. Zool. 257, 181–187.
Guo, B., Styles, C. A., Feng, Q., and Fink, G. R. (2000). A Saccharomyces gene family involved in invasive growth, cell-cell adhesion, and mating. Proc. Natl. Acad. Sci. U.S.A. 97, 12158–12163.
Hamrick, J., and Godt, M. (1996). Effects of life history traits on genetic diversity in plant species. Philos. Trans. R. Soc. Lond. B Biol. Sci. 351, 1291–1298.
Harding, A., and Hancock, J. F. (2008). Ras nanoclusters: combining digital and analog signaling. Cell Cycle 7, 127–134.
Hayden, E. J., Ferrada, E., and Wagner, A. (2011). Cryptic genetic variation promotes rapid evolutionary adaptation in an RNA enzyme. Nature 474, 92–97.
Heylighen, F., and Joslyn, C. (2001). Cybernetics and second order cybernetics. Encyclopedia Phys. Sci. Technol. 4, 155–170.
Holling, C. S. (2001). Understanding the complexity of economic, ecological, and social systems. Ecosystems 4, 390–405.
Huang, P. H., Mukasa, A., Bonavia, R., Flynn, R. A., Brewer, Z. E., Cavenee, W. K., Furnari, F. B., and White, F. M. (2007). Quantitative analysis of EGFRvIII cellular signaling networks reveals a combinatorial therapeutic strategy for glioblastoma. Proc. Natl. Acad. Sci. 104, 12867.
Ingolia, N. T. (2004). Topology and robustness in the Drosophila segment polarity network. PLoS Biol. 2, e123. doi: 10.1371/journal.pbio.0020123
Isalan, M., Lemerle, C., Michalodimitrakis, K., Horn, C., Beltrao, P., Raineri, E., Garriga-Canut, M., and Serrano, L. (2008). Evolvability and hierarchy in rewired bacterial gene networks. Nature 452, 840–845.
Jablonka, E., Oborny, B., Molnár, I., Kisdi, E., Hofbauer, J., and Czárán, T. (1995). The adaptive advantage of phenotypic memory in changing environments. Philos. Trans. R. Soc. Lond. B Biol. Sci. 350, 133–141.
Jahnke, S., Memmesheimer, R. M., and Timme, M. (2009). How chaotic is the balanced state? Front. Comput. Neurosci. 3:13. doi: 10.3389/neuro.10.013.2009
Jeong, H., Mason, S. P., Barabási, A. L., and Oltvai, Z. N. (2001). Lethality and centrality in protein networks. Nature 411, 41–42.
Jeong, H., Tombor, B., Albert, R., Oltvai, Z. N., and Barabási, A. L. (2000). The large-scale organization of metabolic networks. Nature 407, 651–654.
Jin, Y., and Meng, Y. (2011). Morphogenetic robotics: an emerging new field in developmental robotics. IEEE Trans. Syst. Man Cybern. C Appl. Rev. 41, 145–160.
Jönsson, K. I., Rabbow, E., Schill, R. O., Harms-Ringdahl, M., and Rettberg, P. (2008). Tardigrades survive exposure to space in low Earth orbit. Curr. Biol. 18, R729–R731.
Kauffman, S. A. (1969). Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 22, 437–467.
Kauffman, S. A. (1990). Requirements for evolvability in complex systems: orderly components and frozen dynamics. Physica D 42, 135–152.
Kauffman, S. A. (1993). The Origins of Order: Self-Organization and Selection in Evolution. Oxford University Press.
Kerkstra, S., and Scha, I. R. (2008). Evolution and the Genotype-Phenotype Map. Masters thesis, University of Amsterdam.
Kitami, T., and Nadeau, J. H. (2002). Biochemical networking contributes more to genetic buffering in human and mouse metabolic pathways than does gene duplication. Nat. Genet. 32, 191–194.
Kitano, H. (2004a). Cancer as a robust system: implications for anticancer therapy. Nat. Rev. Cancer 4, 227–235.
Kitano, H., and Oda, K. (2006). Robustness trade-offs and host-microbial symbiosis in the immune system. Mol. Syst. Biol. 2, 2006.0022.
Kondoh, M. (2003). Foraging adaptation and the relationship between food-web complexity and stability. Science 299, 1388.
Kondoh, M. (2007). Anti-predator defence and the complexity–stability relationship of food webs. Proc. Biol. Sci. 274, 1617.
Kupiec, J. J. (1997). A Darwinian theory for the origin of cellular differentiation. Mol. Gen. Genet. 255, 201–208.
Kurakin, A. (2009). Scale-free flow of life: on the biology, economics, and physics of the cell. Theor. Biol. Med. Model. 6.
Laland, K., and Sterelny, K. (2006). Perspective: seven reasons (not) to neglect niche construction. Evolution 1751–1762.
Lehner, B. (2010). Genes confer similar robustness to environmental, stochastic, and genetic perturbations in yeast. PLoS ONE 5, e9035. doi: 10.1371/journal.pone.0009035
Levchenko, A., and Iglesias, P. (2002). Models of eukaryotic gradient sensing: application to chemotaxis of amoebae and neutrophils. Biophys. J. 82, 50–63.
Levin, S., and Lubchenco, J. (2008). Resilience, robustness, and marine ecosystem-based management. Bioscience 58, 27–32.
Li, F., Long, T., Lu, Y., Ouyang, Q., and Tang, C. (2004). The yeast cell-cycle network is robustly designed. Proc. Natl. Acad. Sci. U.S.A. 101, 4781–4786.
Lynch, M. (2007). The frailty of adaptive hypotheses for the origins of organismal complexity. Proc. Natl. Acad. Sci. U.S.A. 104, 8597.
Ma, H. W., and Zeng, A. P. (2003). The connectivity structure, giant strong component and centrality of metabolic networks. Bioinformatics 19, 1423–1430.
Martin, O., and Wagner, A. (2008). Multifunctionality and robustness trade-offs in model genetic circuits. Biophys. J. 94, 2927–2937.
McBride, R. C., Ogbunugafor, C. B., and Turner, P. E. (2008). Robustness promotes evolvability of thermotolerance in an RNA virus. BMC Evol. Biol. 8, 231. doi: 10.1186/1471-2148-8–231
McCann, K., Hastings, A., and Huxel, G. R. (1998). Weak trophic interactions and the balance of nature. Nature 395, 794–798.
Meiklejohn, C. D., and Hartl, D. L. (2002). A single mode of canalization. Trends Ecol. Evol. (Amst.) 17, 468–473.
Mendao, M., Timmis, J., Andrews, P. S., and Davies, M. (2007). “The immune system in pieces: computational lessons from degeneracy in the immune system,” in IEEE Symposium on Foundations of Computational Intelligence, 2007, 394–400.
Meng, Y., Zhang, Y., and Jin, Y. (2011). Autonomous self-reconfiguration of modular robots by evolving a hierarchical mechanochemical model. IEEE Comput. Intell. Mag. 6, 43–54.
Millson, M. R., Raj, S. P., and Wilemon, D. (1992). A survey of major approaches for accelerating new product development. J. Prod. Innov. Manag. 9, 53–69.
Morohashi, M., Winn, A. E., Borisuk, M. T., Bolouri, H., Doyle, J., and Kitano, H. (2002). Robustness as a measure of plausibility in models of biochemical networks. J. Theor. Biol. 216, 19–30.
Newman, S. A. (1994). Generic physical mechanisms of tissue morphogenesis: a common basis for development and evolution. J. Evol. Biol. 7, 467–488.
Odling-Smee, F., Laland, K. N., and Feldman, M. W. (1996). Niche construction. Am. Nat. 147, 641–648.
Ozaki, K., and Leonard, W. J. (2002). Cytokine and cytokine receptor pleiotropy and redundancy. J. Biol. Chem. 277, 29355.
Page, A. L. (1993). Assessing new product development practices and performance: establishing crucial norms. J. Prod. Innov. Manag. 10, 273–290.
Pastor-Satorras, R., Smith, E., and Solé, R. V. (2003). Evolving protein interaction networks through gene duplication. J. Theor. Biol. 222, 199–210.
Pfennig, D. W., Wund, M. A., Snell-Rood, E. C., Cruickshank, T., Schlichting, C. D., and Moczek, A. P. (2010). Phenotypic plasticity’s impacts on diversification and speciation. Trends Ecol. Evol. (Amst.) 25, 459–467.
Randles, M., Lamb, D., Odat, E., and Taleb-Bendiab, A. (2010). Distributed redundancy and robustness in complex systems. J. Comput. Syst. Sci. 77, 293–304.
Ravasz, E., Somera, A. L., Mongru, D. A., Oltvai, Z. N., and Barabási, A. L. (2002). Hierarchical organization of modularity in metabolic networks. Science 297, 1551–1555.
Rutherford, S. L. (2000). From genotype to phenotype: buffering mechanisms and the storage of genetic information. Bioessays 22, 1095–1105.
Rutherford, S. L. (2003). Between genotype and phenotype: protein chaperones and evolvability. Nat. Rev. Genet. 4, 263.
Rutherford, S. L., and Lindquist, S. (1998). Hsp90 as a capacitor for morphological evolution. Nature 336–342.
Sauer, U., Canonaco, F., Heri, S., Perrenoud, A., and Fischer, E. (2004). The soluble and membrane-bound transhydrogenases UdhA and PntAB have divergent functions in NADPH metabolism of Escherichia coli. J. Biol. Chem. 279, 6613.
Savageau, M. A., Coelho, P. M., Fasani, R. A., Tolla, D. A., and Salvador, A. (2009). Phenotypes and tolerances in the design space of biochemical systems. Proc. Natl. Acad. Sci. U.S.A. 106, 6435.
Shinar, G., and Feinberg, M. (2010). Structural sources of robustness in biochemical reaction networks. Science 327, 1389.
Siegal, M. L., and Bergman, A. (2002). Waddington’s canalization revisited: developmental stability and evolution. Proc. Natl. Acad. Sci. U.S.A. 99, 10528–10532.
Smart, A., Amaral, L. A., and Ottino, J. M. (2008). Cascading failure and robustness in metabolic networks. Proc. Natl. Acad. Sci. 105, 13223.
Solé, R. V., Pastor-Satorras, R., Smith, E., and Kepler, T. B. (2002). A model of large-scale proteome evolution. Adv. Complex Syst. 5, 43–54.
Stelling, J., Klamt, S., Bettenbrock, K., Schuster, S., and Gilles, E. D. (2002). Metabolic network structure determines key aspects of functionality and regulation. Nature 420, 190–193.
Stelling, J., Sauer, U., Szallasi, Z., Doyle, F. J. III, and Doyle, J. (2004a). Robustness of cellular functions. Cell 118, 675–685.
Stelling, J., Gilles, E. D., and Doyle, F. J. III. (2004b). Robustness properties of circadian clock architectures. Proc. Natl. Acad. Sci. U.S.A. 101, 13210.
Stommel, J. M., Kimmelman, A. C., Ying, H., Nabioullin, R., Ponugoti, A. H., Wiedemeyer, R., Stegh, A. H., Bradner, J. E., Ligon, K. L., Brennan, C., Chin, L., and DePinho, R. A. (2007). Coactivation of receptor tyrosine kinases affects the response of tumor cells to targeted therapies. Science 318, 287.
Stromberg, S. P., and Carlson, J. (2006). Robustness and fragility in immunosenescence. PLoS Comput. Biol. 2, e160. doi: 10.1371/journal.pcbi.0020160
Szollosi, G. J., and Derenyi, I. (2009). Congruent Evolution of Genetic and Environmental Robustness in Micro-RNA. Mol. Biol. Evol. 26, 867.
Tian, T., Olson, S., Whitacre, J. M., and Harding, A. (2011). The origins of cancer robustness and evolvability. Integr. Biol. (Camb.) 3, 17–30.
Tieri, P., Grignolio, A., Zaikin, A., Mishto, M., Remondini, D., Castellani, G. C., and Franceschi, C. (2010). Network, degeneracy and bow tie integrating paradigms and architectures to grasp the complexity of the immune system. Theor. Biol. Med. Model. 7, 32.
Tononi, G., Sporns, O., and Edelman, G. M. (1999). Measures of degeneracy and redundancy in biological networks. Proc. Natl. Acad. Sci. U.S.A. 96, 3257–3262.
Uller, T. (2008). Developmental plasticity and the evolution of parental effects. Trends Ecol. Evol. (Amst.) 23, 432–438.
von Dassow, G., Meir, E., Munro, E. M., and Odell, G. M. (2000). The segment polarity network is a robust developmental module. Nature 406, 188–192.
Waddington, C. H. (1942). Canalization of development and the inheritance of acquired characters. Nature 150, 563.
Wagner, A. (2005). Distributed robustness versus redundancy as causes of mutational robustness. Bioessays 27, 176–188.
Wagner, A. (2008). Robustness and evolvability: a paradox resolved. Proc. R. Soc. Lond. B Biol. Sci. 275, 91–100.
Wall, M. E., Hlavacek, W. S., and Savageau, M. A. (2004). Design of gene circuits: lessons from bacteria. Nat. Rev. Genet. 5, 34–42.
West-Eberhard, M. (2005). Developmental plasticity and the origin of species differences. Proc. Natl. Acad. Sci. U.S.A. 102, 6543.
Whitacre, J. M. (2010). Degeneracy: a link between evolvability, robustness and complexity in biological systems. Theor. Biol. Med. Model. 7.
Whitacre, J. M., and Bender, A. (2010a). Degeneracy: a design principle for achieving robustness and evolvability. J. Theor. Biol. 263, 143–153.
Whitacre, J. M., and Bender, A. (2010b). Networked buffering: a basic mechanism for distributed robustness in complex adaptive systems. Theor. Biol. Med. Model. 7.
Whitacre, J. M., and Bender, A. (in press). Pervasive flexibility in living technologies through degeneracy based design. Artif. Life.
Whitacre, J. M., Lin, J., and Harding, A. (2012). T cell adaptive immunity proceeds through environment-induced adaptation from the exposure of cryptic genetic variation. Front. Genet. 3:5. doi: 10.3389/fgene.2012.00005
Whitacre, J. M., Rohlfshagen, P., Bender, A., and Yao, X. (in press). Evolutionary mechanics: new engineering principles for the emergence of flexibility in a dynamic and uncertain world. Nat. Comp.
Whitacre, J. M., Rohlfshagen, P., Yao, X., and Bender, A. (2010). “The role of degenerate robustness in the evolvability of multi-agent systems in dynamic environments,” in PPSN XI, Krakow, 284–293.
Wilhelm, T., Behre, J., and Schuster, S. (2004). Analysis of structural robustness of metabolic networks. Syst. Biol. (Stevenage) 1, 114–120.
Keywords: biochemical networks, homeostasis, canalization, degeneracy, evolution, bow-tie, redundancy, robustness
Citation: Whitacre JM (2012) Biological robustness: paradigms, mechanisms, and systems principles. Front. Gene. 3:67. doi: 10.3389/fgene.2012.00067
Received: 05 January 2012; Accepted: 05 April 2012;
Published online: 11 May 2012.
Edited by:
Aristotle A. Chatziioannou, National Hellenic Research Foundation, GreeceReviewed by:
Scott H. Harrison, North Carolina A&T State University, USAEleftherios Pilalis, National Hellenic Research Foundation, Greece
Copyright: © 2012 Whitacre. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: James Michael Whitacre, Center Leo Apostel, Vrije Universiteit Brussel, Krijgskundestraat 33 1160 Brussels, Belgium. e-mail:andoaXRhY3JlNzlAZ21haWwuY29t