- 1 Center for Statistical Genetics, The Pennsylvania State University, Hershey, PA, USA
- 2 Department of Statistics, The Pennsylvania State University, State College, PA, USA
- 3 Division of Public Health Sciences, Fred Hutchinson Cancer Research Center, Seattle, WA, USA
The growing evidence that cancer originates from stem cells (SC) holds a great promise to eliminate this disease by designing specific drug therapies for removing cancer SC. Translation of this knowledge into predictive tests for the clinic is hampered due to the lack of methods to discriminate cancer SC from non-cancer SC. Here, we address this issue by describing a conceptual strategy for identifying the genetic origins of cancer SC. The strategy incorporates a high-dimensional group of differential equations that characterizes the proliferation, differentiation, and reprogramming of cancer SC in a dynamic cellular and molecular system. The deployment of robust mathematical models will help uncover and explain many still unknown aspects of cell behavior, tissue function, and network organization related to the formation and division of cancer SC. The statistical method developed allows biologically meaningful hypotheses about the genetic control mechanisms of carcinogenesis and metastasis to be tested in a quantitative manner.
Introduction
Human cancers grow from stem cells (SC) in the way that healthy organs do (Dick, 2003; Dontu et al., 2003; Alison, 2005; Brown et al., 2007; Lobo et al., 2007; Baumann et al., 2008; Visvader and Lindeman, 2008). This discovery, or hypothesis, has refreshed our hope to eliminate these fatal diseases. A stem cell is one that, when it divides, produces two unequal daughters. While one remains a stem cell, the other differentiates into a diverse range of specialized cell types. There is emerging evidence that cancer formation may follow a similar mechanism of cell division (Lapidot et al., 1994; Al-Hajj et al., 2003; Singh et al., 2004). In breast and brain tumors, for example, a minority population of cancer SC has the ability to self-renew, whereas the majority of cancer cells have limited or no ability to proliferate. Because cancer SC may drive the growth and spread of the tumor, the prevention of a malignant tumor can be made possible by designing specific drugs that destroy those mother cells (Clarke and Fuller, 2006). However, current cancer-killing therapies are not able to distinguish cancer SC from malignant cells. If only the descendants of the non-stem-cell daughters are removed or destroyed, the tumor will continue to return. For this reason, the primary step toward the effective control and prevention (and even eradication) of cancers is the prospective identification and characterization of cancer SC, followed by the removal of targeted cancer SC by developing specified drug therapies.
The distinction between stem cancer cells and non-stem cancer cells has been a highly challenging issue, but can be made possible through a profound understanding of the differences in their origin, property, and function (Lobo et al., 2007). Modern life sciences, such as molecular biology, genomics, biomedicine, or oncology, are powerful for understanding the genetic and molecular mechanisms of carcinogenesis and the complexity of its progress and dynamics based on experimental and clinical observations. The past decade has witnessed a vital development in high-dimensional genetic, genomic, and proteomic technologies that have led to the availability of an enormous amount of data (Clarke et al., 2008). For example, high-throughput single nucleotide polymorphism (SNP) analysis can yield hundreds of thousands of polymorphic markers for a single specimen. Gene microarray techniques, such as Affymetrix, allow concurrent measurements on numerous mRNA transcripts. Dimensionality can be even larger in proteomic studies using the ProteinChip System. These data provide invaluable resources to detect and define expression patterns for the phenotypes of complex traits or diseases (Khan et al., 2001; Bhanot et al., 2005) and predict a potential clinical outcome of patients after a particular drug therapy (Ayers et al., 2004; Lopez-Rios et al., 2006; Ganly et al., 2007).
In another different world, tremendous progress has been made in mathematical modeling of complex biological processes and cell differentiating mechanisms (Anderson and Quaranta, 2008; Piotrowska et al., 2008). Mathematical models and numerical simulations can uncover and explain many still unknown aspects of cell behavior, tissue function, and network organization. Models based on fundamental biological and developmental mechanisms can gain comprehensive insights and formulate predictions that cannot be derived from experiments or statistical data alone. Over the past decade, countless mathematical models have been developed to describe tumor growth, ranging from simple temporal population dynamic models to fully three-dimensional spatiotemproal models (Araujo and McElwain, 2006). The application of differential equations to the specification of the proliferation and differentiation of normal SC and cancer SC has now attracted considerable attention of mathematicians and computer scientists (Adimy et al., 2008; Piotrowska et al., 2008).
However, there is currently a serious lack in the intrinsic integration of genetic, genomic and proteomic data with sophisticated mathematical models built on biological principles. Although simple statistical analysis of these data is helpful for studying the structure and function of selected signaling pathways, proteins, and drugs, it does not reveal a general dynamics and complexity of the problem and the “engine” that drives the whole biochemical machinery even in case of single cell (Piotrowska et al., 2008). An increasing recognition has been articulated about the incorporation of interdisciplinary dialogs to understand complicated cell mechanisms, network regulation, and tissue physiology. The central theme of such so-called systems biology approaches (Khalil and Hill, 2005) is to identify genes, proteins, and signaling pathways that have a functional role in the formation and expression of cancer SC by combining quantitative experimental data with mathematical modeling and computer simulation.
The objective of this article is to present a conceptual strategy for identifying genes and proteins or their expression patterns that are linked with the formation, proliferation, and programming of cancer SC. A quantitative framework will be formulated to characterize the differences in the genetic origin and biological properties between normal SC and cancerous SC, providing applied geneticists, clinical doctors, and health professionals with experimental designs and analytical tools to extract predictive information from their seemingly “chaotic” data.
Defining the Genetic Architecture of Cancer
Recent advances in technology, which lead to genomic, proteomic and metabomic data collection on the human genome, now provide a powerful means of defining the genetic architecture of cancer cells. The development of any methodologies for mapping cancer genes should be based on the philosophical link of these omic data with the proliferation and differentiation of cancer SC through mathematical, statistical and engineering approaches. Below, we review several aspects that comprise the genetic architecture of cancer pathways.
From Genetic Mapping to Genetic Haplotyping
For complex traits like cancer, genetic mapping is a powerful approach for illustrating their genetic architecture (Lander and Botstein, 1989; Anholt and Mackay, 2004; Li and Wu, 2010). This approach dissects complex traits into individual quantitative trait loci (QTLs) and maps them on the gnome. However, a QTL detected by traditional markers may contain multiple genes that operate in a collective way, thus it is not possible to study the DNA structure, organization, and function of a QTL. A more accurate and useful approach to characterizing the underlying genetic variants is to directly analyze DNA sequences, known as quantitative trait nucleotides (QTNs), using SNPs. If a string of DNA sequence, or haplotype, for a QTN is known to increase disease risk, this risk can be intervened by inhibiting the expression of this haplotype with specialized drugs. The control of this disease can be made more efficient if all such DNA sequences are identified throughout the entire genome. This possibility has increased dramatically with the construction of the haplotype map, or “HapMap” by SNPs (The International HapMap Constortium, 2007).
Statistical models for detecting the haplotype effects of a QTN have been derived for continuous (Liu et al., 2004; Lin and Huang, 2007) and binary traits (Cui et al., 2007). The main idea of haplotyping models is to discern the difference between unobservable diplotypes (i.e., a pair of haplotypes) from an observable unphased SNP genotype. For example, a double heterozygous genotype, AaBb, can be formed by either diplotype AB|ab or Ab|aB where | is used to separate the paternally or maternally derived haplotype. These two diplotypes, although genetically identical, can be differently responsive to cancer risk. Haplotype models allow the separation of diplotypes in the genetic control of cancer (see Liu et al., 2004).
From Genetic Actions to Genetic Interactions
Most current approaches for cancer gene identification allow the characterization of small numbers of genes or proteins involved in cancer susceptibility. These approaches are often insufficient to study the molecular mechanisms of neoplastic processes. Cancer is a complex trait involving a network of genes that interact in a coordinated manner. These so-called genetic interactions or epistasis occur when the action of one gene measured through a molecular, cellular, or organism phenotype is modified by one or more other genes. To date, genetic interactions remain largely unknown on a large-scale in human systems. Previous reviews and assays gave excellent descriptions of the role of genetic interactions in understanding phenotypic variability (Hartman et al., 2001; Lehner et al., 2006; Boone et al., 2007). The study of genetic interactions will not only help better understand cancer susceptibility and progression, but also, and most importantly, develop novel anticancer treatments.
From Mendelian Inheritance to Genetic Imprinting
Each copy of a gene, called an allele, instructs a particular task to be conducted in the cells of the body. These instructions expressed through a genetic code, i.e., a sequence of nucleotide in the DNA, guide the cells to yield a protein. In each cell of the body, there are two copies for each gene carried on a pair of maternal and paternal chromosomes, respectively. According to Mendelian inheritance, the information contained in the maternal and paternal copies of the gene is equally utilized by the cells to produce proteins. However, for certain genes, their alleles are expressed only when they transmits to a progeny through the sperm or egg. This phenomenon is called “genetic imprinting” that describes the expression of a gene relying on the paternal or maternal origin of an allele (Wilkins and Haig, 2003; Reik and Lewis, 2005; Jirtle and Skinner, 2007). Epigenetic marks that influence the expression of genes by switching the genetic information on and off may be one of the important mechanisms for genetic imprinting (Feinberg and Tycko, 2004; Sha, 2008). The imprinting modification process may be reversible in the next generation. Increasing recognition has been made that genetic imprinting plays a pivotal role in the initiation of cancer through various molecular mechanisms (Feinberg and Tycko, 2004; Secko, 2005; Sasaki and Matsui, 2008).
From Gene Mutation to Aneuploidy
Human cancer cells frequently possess large-scale chromosomal rearrangements due to chromosomal instability (CIN) or gene mutation. CIN makes whole chromosomes or large fractions of chromosomes gained or lost during cell division, resulting in an imbalance in the number of chromosomes per cell (aneuploidy), and an enhanced rate of loss of heterozygosity. Thus, the “aneuploidy hypothesis of cancer” (Stock and Bialy, 2002) proposes that the main differences between normal and abnormal (cancer) cells result from the number of genes rather than the types of genes differentially expressed, as opposed to the “gene-mutation hypothesis” (Jallepalli and Lengauer, 2001; Greenman et al., 2007; Li et al., 2010b).
Gene mutation has been a dominant hypothesis for explaining the genetics of cancer (Greenman et al., 2007), although aneuploidy was proposed to cause cancer over 100 years ago. However, growing evidence supports a role for aneuploidy in the genetic underpinning of cancer (Stock and Bialy, 2002). According to extensive work by Duesberg and his group, aneuploidy offers a simple, coherent explanation of all cancer-specific phenotypes (Duesberg, 2007; Duesberg et al., 2007). It is concluded that when aneuploidy exceeds a certain threshold it is sufficient to cause all cancer-specific phenotypes. This aneuploidy mechanism of phenotype alteration is independent of gene mutation. With a continuous confirmation of the aneuploidy hypothesis, it is crucial to quantify the genetic effects of aneuploidy loci on cancer susceptibility with the genetic data collected from the cancer genome project (Li et al., 2010a).
From Genomics to Proteomics
With the advent of large-scale functional proteomic data (Clarke et al., 2008), additional mechanistic insights into neoplasia can be gleaned. Whole-genome association studies for cancer risk variants and somatic mutation screening projects will only provide a “part lists” of cancer genes. Transcript analyses have identified expression profiles that provide accurate prognoses for cancer patients (Fan et al., 2006). Currently, systematic mapping of protein–protein interactions leads to the birth of the so-called “interactome” mapping projects. This will elucidate the wiring diagram of protein associations in cells (Rual et al., 2005; Stelzl et al., 2005; Cohen et al., 2008). These types of genes and/or protein (gene/protein) functional relationships can be modeled together to provide better understanding and predict molecular mechanisms of neoplasia (Barabasi and Oltvai, 2004; Rhodes and Chinnaiyan, 2005; Pujana et al., 2007).
From Studying High-Order Phenotypes to Modeling Mechanistic Pathways
The final phenotypes of cancer size and shape are formed through a series of biological pathways. The existing strategies for genetic mapping, including functional mapping, aimed to map a biological process (Wu and Lin, 2006; Das and Wu, 2008; Li and Wu, 2010), are based directly on these high-order phenotypes, neglecting the biological, biochemical, and metabolic pathways that underlies the phenotypes. By regarding cancer formation and growth as a dynamic system, biochemical networks in the system consist of chemical reactions, such as association, dissociation, degradation, and synthesis (Clayton et al., 2006; Hopkins, 2008). The dynamics of biochemical networks follow the rules of mechanics as well as rules governed by their own ability to organize movement and biological functions. Because a biological system is far more complex than a physical system of inert matter, we need a higher level of analysis to tackle such complexity. Mathematical models using kinetic theory may represent a way to deal with such complexity, allowing an understanding of phenomena of non-equilibrium statistical mechanics (Goldbeter, 2002). The models for system dynamics are related to the generalized Boltzmann equation, describing the population dynamics of several interacting elements (kinetic population models).
A set of non-linear ordinary or time delay differential equations have been derived to model the biological pathways and interactions between cells and between cell and surrounding environment. Biological and mechanistic behaviors of the biochemical network can be described by solving the non-linear parameters that define the differential equations. Thus, the incorporation of differential equations into genetic mapping can provide a coherent framework with which to characterize genes and the patterns of gene expression involved in mechanistic pathways.
From Mathematic Modeling to Statistical Solution
Numerical approaches have been derived to estimate parameters for non-linear differential equations (Feng and Navaratna, 2007). Theoretical investigations of parameter estimation have been available in the applied mathematical literature (Beretta and Kuang, 2002). Increased interest has been received in the integration of statistical modeling and simulation with differential equations to study dynamic systems. In statistics, differential equations can be estimated by non-linear least squares approaches. More recently, with the availability of observational data for dynamic processes, there is a pressing need on developing more powerful statistical methods for estimating the parameter defining differential equations with noisy measurements. Ramsay et al. (2007) provided such a statistical method by combining a modified data smoothing method and the generalization of profiled estimation. The accuracy and coverage properties of parameter estimates from the new method were examined by simulation studies.
From Gene–Gene Interactions to Genome–Genome Interactions
Cancer arises from sporadic gene mutations, but its growth and spread will be affected by both genes from the normal and cancer genomes (Araujo and McElwain, 2006; de Araujo et al., 2008). These two different systems of genes operate interactively or epistatically to alter the course of cancer growth (de Araujo et al., 2008). Shortly after the completion of the human genome sequencing, the cancer genome is being sequenced (Kaiser, 2005). The data from these two types of genomes will provide tremendous resources for characterizing the patterns and organization of genome–genome interactions in cancer susceptibility. More recently, an interactive model has been developed to study genetic interactions of DNA sequences (or haplotypes) between host and cancer genes responsible for cancer risk using quantitative genetic principles (Li and Wu, 2009). The model is founded on a commonly used genetic association design in which a sample of related or unrelated patients is randomly drawn from a natural human population. Each patient is typed for SNPs on normal and cancer cells and measured for cancer susceptibility. The model provides a general procedure for testing the distribution of haplotypes constructed by SNPs from host and cancer genes and the linkage disequilibria of different orders among the SNPs. The model also formulates a series of testable hypotheses about the effects of host genes, cancer genes, and their interactions on cancer susceptibility.
Li and Wu’s (2009) model can be extended to detect imprinted loci based on a random set of three-generation families from a natural population by using genotyped SNPs. This design provides a pathway for characterizing the effects of imprinted genes on a complex disease at different generations and testing transgenerational changes of imprinted effects (Youngson and Whitelaw, 2008; Li et al., 2011b). The design is integrated with population and cytogenetic principles of gene segregation and transmission from the previous generation to the next.
Currently used genome-wide association studies (GWAS) allow the scan of functional or causal polymorphisms from 300,000 to 1 million SNPs (Pearson and Manolio, 2008). Genetic mapping has developed to a point at which a comprehensive analysis of all the markers that cover the genetic map of the genome can be performed to search for the chromosomal distribution of all possible QTLs or QTNs. Some basic work in GWAS of QTLs has been initiated in recent years, although it is still full of challenges. Several statistical models for analyzing all SNPs through lasso and other variable selection approaches have been developed (Li et al., 2011a). These models shrink the effects of most SNPs toward zero to provide sparse estimates of whole-genome associations.
Modeling Dynamic Genetic Control
Mathematical models have been increasingly used to describe the population dynamics of cancer SC and their differentiation into cancer cells (Solyani et al., 1995; Ganguly and Puri, 2006; Enderling et al., 2007; Adimy et al., 2008; Michor, 2008; Piotrowska et al., 2008). There is strong evidence that genes due to mutations in normal SC are involved in the regulation of the self-renewal of cancer SC for cancers (Al-Hajj and Clarke, 2004; Clarke, 2004). Statistical models are needed to map those genes from mathematical aspects of cancer SC.
Ordinary Differential Equations (ODE)
A large system of non-linear ordinary differential equations (ODE) has been derived to the self-renewing capacity of cancer SC (Ganguly and Puri, 2006; Piotrowska et al., 2008). These equations were founded on the principle according to which cancers result from mutations in normal SC, early progenitor (EP) cells and even mature cells (MC). The model for brain cancer cells by Ganguly and Puri (2006) defines seven main types of cells – SC, EP cells, late progenitor (LP) cells, MC, abnormal stem cells (SCA), abnormal early progenitor cells (EPA), and abnormal progeny (AP; tumor) cells. Each cell type is considered as a separate model compartment, whose cell population growth is modeled by considering individual rate expressions (Figure 1). SCs can self-renew with a probability PSC, in which both daughter cells retain stem cell features, or differentiate and transfer to the EP compartment. Stem cell DNA may mutate during the replication with probability MSC by which the daughter cell inheriting the mutated gene is transferred into the SCA population. EP cells, as well as EPA cells, experience only a limited number (K) of self-renewal steps. Thus, cells with identical self-renewal capacity are grouped into K sub-compartments, although cells belonging to the kth (k = 1, …, K) compartment cannot self-renew any more. If EPk cells undergo cell division, they self-renew into a subgroup EPk + 1 with a given probability PEP, which is assumed to be equal for all subpopulations. The same is true for EPAk which self-renews into EPAk + 1 with a probability PEP,A. Dividing cells that do not supply the EPi + 1 or EPAi + 1 compartment differentiate into LP or AP (in case of abnormal cells) cells, respectively. Furthermore, at each division EPi cells are subject to mutations as defined by mutation probability MEP, which is assumed to be identical for each EPi compartment. Naturally, the AP compartment is supplied by EPA cells. Finally, cells that reach the MC or AP compartment die due to apoptosis (Piotrowska et al., 2008).
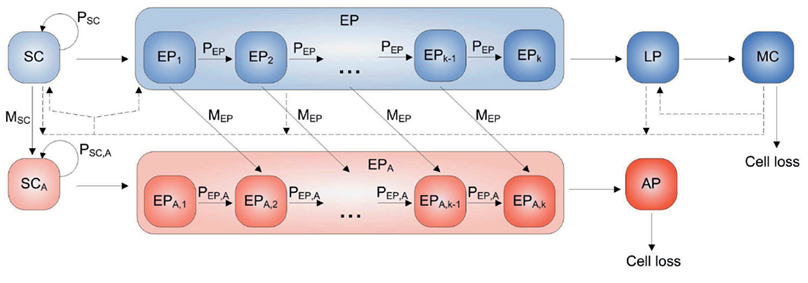
Figure 1. A diagram for multi-compartment blocks shown to derive a system of ordinary differential Eq.(1; Ganguly and Puri, 2006; Piotrowska et al., 2008). The EP cells and EPA cells are each split into K sub-compartments that contain an identical type of cells, which differ only in the number of times they have undergone self-renewal. The direct transition from one compartment to another one and feedback interaction loops are indicated by the solid and dash lines, respectively. Adapted from Piotrowska et al. (2008).
Ganguly and Puri (2006) described the rates of joint changes of different types of cell populations by a system of differential equations expressed as
where N. is the number of cells; ωSC, ωEP, and ωLP are the cell division rates with SC, EP, and LP compartments, respectively; PSC = PSC(NSC, NEP, NLP, NMC) ∈ [Pmin,SC, Pmax,SC] is the self-renewal probability; Zin is the factor by which the efflux from the EP compartment is amplified as soon as the cells enter the LP compartment; is the efflux from the LP compartment, i.e., the generation rate of MC, where Zout is the factor by which the cells are further amplified immediately before leaving the LP compartment; ω0,MC is the cell death or apoptotic rate; is the outflux of abnormal EP cells; and ω0,AP is the AP cell death or apoptotic rate. Cell populations in the EP and EPA compartments are determined by the output equations and , respectively.
Cell division rates ωSC = (αSC/τSC)ln2, ωEP = (αEP/τEP)ln2, and ωLP = (αLP/τLP)ln2 depend on the mitotic fraction (α) and the cell cycle time (τ), i.e., the time required to complete a full cycle of cell division. The total time τLP spent by a cell in the LP compartment is the sum of the cell generation time (τg= τLP/αLPln2) and the cell maturation time τm. The two factors Zin and Zout are selected such that Zin × Zout = 2n, where Zin = (2n – 1)τg/τLP + 2nτm/τLP and n is the number of stages of cell division of the LP compartment before transforming into MC. All in all, the dynamic system of cancer formation from cancer SC can be quantified by the group of ODEs (1) with a set of parameters, cell cycle times (τSC, τEP, τLP), cell maturation time for LP compartment τm, self-renewal probabilities (PSC, PEP), mitotic fractions (αSC, αEP, αLP), number of EP cell self-renewals K, the number of mitotic cycles n, and death rates (ω0,MC, ω0,AP), and the probabilities of occurrence of oncogenic mutations during DNA transcription (MSC, MEP).
The solution of these differential equations is not known in closed, analytic form, and hence must be computed approximately by means of algorithms and software from numerical mathematics and scientific computing. Savcenco (2009) proposed a multirate time stepping technique for a system of ODEs. This method uses large time steps for slowly varying components, and small steps for rapidly varying ones. Numerical experiments confirm that the efficiency of time integration methods can be significantly improved by using multirate methods.
Given the fact that there is a substantial variability in cancer formation from cancer SC, we integrate the differential Eq. (1) into a genetic mapping framework (Fu et al., 2010; Luo et al., 2010). By estimating ODE parameters for individual genotypes at a (or a set of) SNP, we can test whether there exist significant loci associated with the capacity of cancer SC to develop into malignant cancers and how these significant loci affect various proliferation and apoptotic processes within different cell compartments. Consider a QTL with three genotypes AA, Aa, and aa bearing ODE parameters (τSC, τEP, τLP; τm; PSC, PEP; αSC, αEP, αLP; K; n; ω0,MC, ω0,AP; MSC, MEP) = (8 h, 8 h, 8 h; 40 h; 0.5, 0.5; 0.4, 0.4; 0.35, 5; 6; 0.01, 0.01; 0.6, 0.6), (9 h, 9 h, 9 h; 45 h; 0.45, 0.45; 0.5, 0.45, 0.45; 6; 7; 0.02, 0.02; 0.5, 0.5), and (7 h, 8 h, 9 h; 40 h; 0.45, 0.3; 0.4, 0.45, 0.5; 7; 7; 0.03, 0.03; 0.65, 0.65), respectively. Figure 2 provides the dynamic behavior of each cell type separately for different QTL genotypes. The integrated mapping models allow the formulation of numerous biologically meaningful hypothesis tests about the genetic control of each pathway in the system.
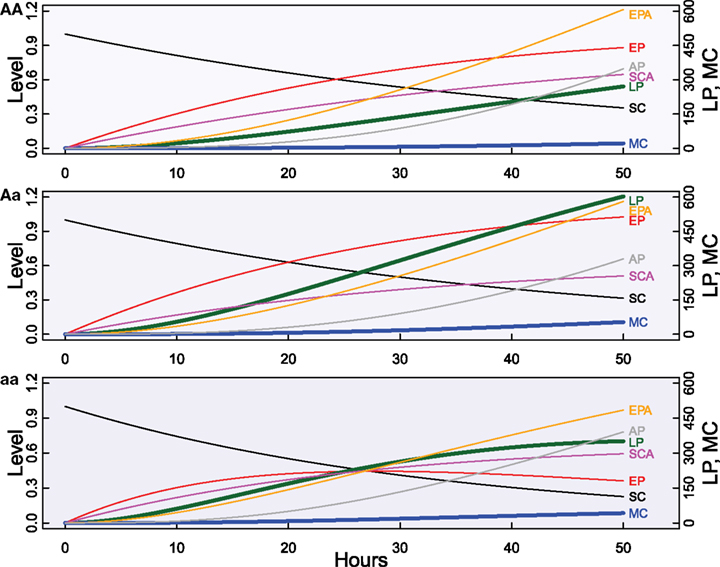
Figure 2. Genetic differences in the dynamic behavior of a cancer stem cell-initiating system composed of seven biological aspects (SC, EP, LP, MC, SCA, EPA, and AP) of cell proliferation characterized by ODEs (1) at a gene having genotypes AA, Aa, and aa.
Delay Differential Equations (DDE)
All blood cells arise from a common origin in the bone marrow, the hematopoietic SC. These SC can differentiate into one of three major cell lines: the leukocytes, the platelets, and the erythrocytes. Because of genetic mutations, the hematopoietic SC become leukemia SC, endowed with the capacity to self-renew and to generate many leukaemic blasts (Viale et al., 2009). Mackey and colleagues (Colijn and Mackey, 2005a,b; Piotrowska et al., 2008) published a series of quantitative models that specify four distinct compartments representing the hematopoietic SC and the circulating leukocytes, platelets, and erythrocytes. Typically all of the three differentiated cell types have the same oscillation period, but the relation of the oscillation mean and amplitude to the normal levels is variable. Due to chronic features of these cells, a system of delay differential equations (DDEs) has been derived to specify the dynamics of the system. A number of mathematicians studied the stability properties of these delay non-linear differential equations and identified the supercritical Hopf bifurcation and a saddle–node bifurcation of limit circles (Bernard et al., 2003; Kirk et al., 2008). It is concluded that the major cause of the oscillation in cyclic neutropenia is an increase rate of apoptosis of neutrophil precursors leading to a destabilization of hematopoietic stem cell compartments (Crauste, 2006; Feng and Navaratna, 2007; Verdugo and Rand, 2008).
We studied the influences of different DDE parameters on the period and amplitude of oscillations if a specific set of DDEs is given (Fu et al., 2011), which helps to obtain a solution of the DDEs. In Fu et al. (2011), we have developed a framework for incorporating DDEs into the functional mapping of a periodic system (Liu et al., 2007). This framework can be readily extended to study the genetic mapping of chronic myelogenous leukemia by incorporating Colijn and Mackey’s (2005a,b) DDEs. As shown in Wu et al. (2004), the genetic control mechanisms for the biochemical connections between differentiated cells and SC will formulated in a quantitative and testable ways.
Systems Mapping
Systems mapping is a computational model that views a complex phenotype as a dynamic system, dissects it into its underlying components, coordinates different components in terms of biological laws through mathematical equations, and maps specific genes that mediate each component and its connection with other components (Wu et al., 2011). As a bottom–top model, systems approach can identify specific QTLs that govern the developmental interactions of various components giving rise to the function and behavior of the system. By estimating and testing mathematical parameters that specify the system, systems mapping enables the prediction or alteration of the physiological status of a phenotype based on the underlying genetic control mechanisms.
Mixture model
Systems mapping embeds a system of differential equations, like (1), into a genetic mapping setting constructed by a segregating population. Genetic mapping uses a mixture model-based likelihood to estimate genotype-specific parameters by assuming J QTL genotypes. For the mapping population of n members with marker information (M) and phenotypic data for different types of cancer SC (Y), we formulate the likelihood as
where Y i = (Y1i,…, Y7i) is the phenotypic vector for individual i containing seven types of cancer SC, SC (Y1), EP (Y2), LP (Y3), MC (Y4), SC (Y5), EPA (Y6), AP (Y7) [see (1)], whose kth type is a time-dependent vector measured at T time points, i.e., Y k = (Yk(1), …, Yk(T)) (k = 1, …, 7); ωj|i is the mixture proportion representing the conditional probability of QTL genotype j given the marker genotype of individual j; and fj(Y i;Θ j,Ψ) is a multivariate normal distribution with expected mean vector for individual i that belongs to QTL genotype j,
and covariance matrix
with Σk being a (T × T) covariance matrix for cell type k and Σkk′ = ΣTk’k being a (T × T) covariance matrix between cell types k and k′.
Traditional approaches estimate every element in (3) and (4), but systems mapping specifies and models vector μ j|i by ODE parameters Θ j and covariance matrix Σ by Ψ. Next, we show how to model and estimate ωj|i, Θ j, and Ψ.
Architectural and dynamic modeling
Mixture proportion ωj|i relates to the pattern of QTL segregation whose optimal description relies on the genetic architecture of phenotypic traits. In the preceding section, we review several key aspects of the genetic architecture of cancer SC, which can embedded into systems mapping (2). ωj|i can be expressed at the individual locus level or haplotype level (Liu et al., 2004), and can be used to model genetic main effects or epistatic interactions that occur within and between genomes (Li and Wu, 2009). ωj|i can also consider genetic imprinting and epigenetic effects by incorporating the parental information of mapping individuals. In particular, genetic causes of cancer, like gene mutation or aneuploidy, can be tested through ωj|i, providing a way to test the hypothesis of cancer formation.
The dynamic behavior of cancer phenotypes can be described by various differential equations. We have incorporated commonly used mathematical tools, like the Runge–Kutta fourth order algorithm, to provide the estimates of mathematical parameters for individual QTL genotypes contained within a mixture-model framework (Fu et al., 2010). Mathematical solution for delay differential equations has been discussed and used to map clock genes for a biological system (Fu et al., 2011). For longitudinal data, we can use structural approaches to model the covariance matrix for longitudinal traits (Zimmerman and Nunez-Anton, 2001; Zhao et al., 2005; Yap et al., 2009). These approaches include (1) parametric stationary, (2) parametric non-stationary, (3) non-parametric, and (4) semiparametric models. Each of these approaches has advantages and disadvantages in computing efficiency, flexibility, and power.
Numerical simulation
We performed a simple simulation studies to test the statistical behavior of systems mapping for cancer SC. Fu et al. (2010) provided much more detailed information about the test and validation of systems mapping. The simulation assumes a mapping population of different heritabilities at a middle stage of cancer stem cell growth. Consider a SNP marker which is associated with a putative QTL (with three genotypes AA, Aa, and aa) through linkage disequilibrium (LD). Given allele frequencies of the marker and QTL and their LD, joint marker and phenotypic data were simulated. The genotypic mean vectors were modeled by ODE (1) using parameters Θ j = (τSCj, τEPj, τLPj; τmj; PSCj, PEPj; αSCj, αEPj, αLPj; Kj; nj; ω0,MCj, ω0,APj; MSCj, MEPj), whereas the covariance matrix was structured by the first-order autoregressive [AR(1)] model with correlation and variance parameters for cell type k, Ψ k= (ρ, σ2). We assume no residual correlation between different cell types.
Tables 1 and 2 provide the results about the estimates of ODE parameters for individual QTL genotypes and covariance-structural parameters, along with marker and QTL segregation parameters. The parameters for marker and QTL allele frequencies and LD can well be estimated, although missing QTL information is inferred using the mixture model. The AR(1) parameters can also well be estimated, partly because of their simple structure for covariance modeling. The precision of ODE parameter estimation heavily rely on heritability and sample size. For a modest heritability (say 0.1), some ODE parameters, like τLP, in a small group of QTL genotype (aa) were not precisely estimated (Table 1). Given its allele frequency 0.3, the number of genotype aa is less than 50. However, when heritability increases to 0.4, all ODE parameters including ones in small-sized genotype aa can be reasonably estimated (Table 2). The results from the simulation study suggest that the increase of trait heritability through reducing phenotyping errors is an important measure for improving the precision of parameter estimation.
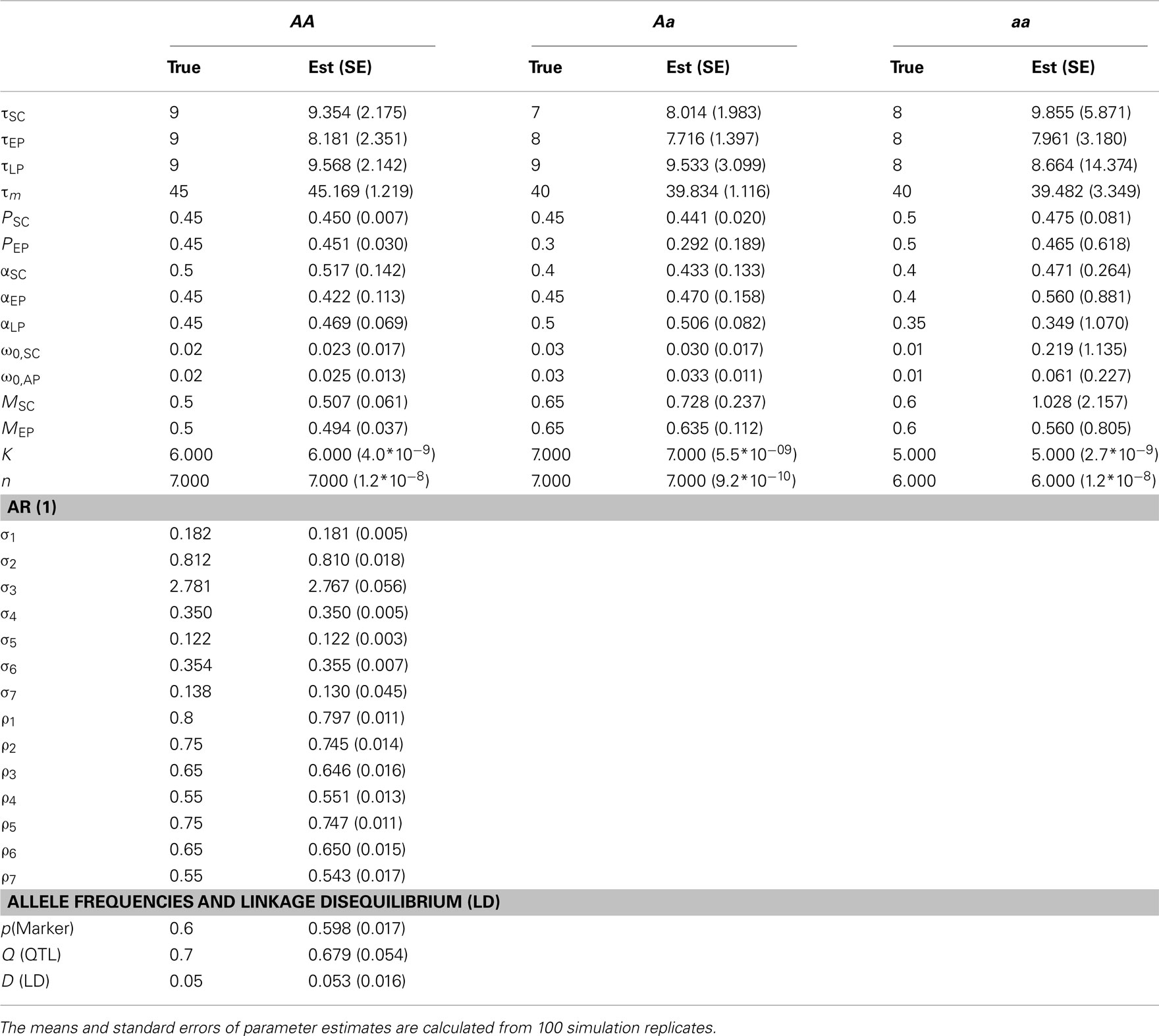
Table 1. The estimation of parameters by a dynamic model for mapping cancer stem cell proliferation from a simulated mapping population of 500 individuals by assuming heritability H2= 0.1.
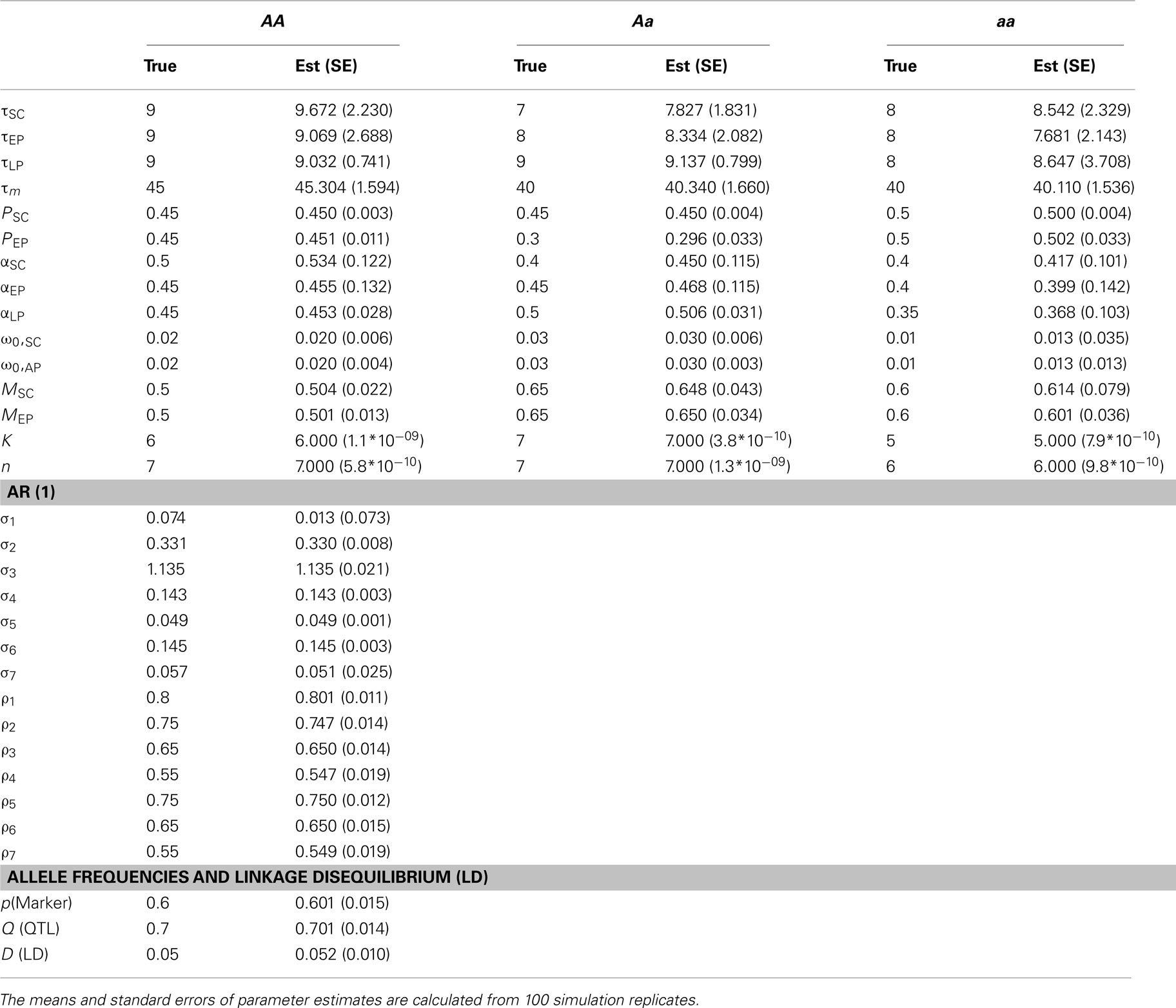
Table 2. The estimation of parameters by a dynamic model for mapping cancer stem cell proliferation from a simulated mapping population of 500 individuals by assuming heritability H2= 0.4.
Discussion
Tremendous investments have been made on cancer genome projects in order to make a complete landscape of mutations in tumors accessible. Although the importance of cataloging genome variations is well recognized, there are obvious difficulties in bridging the gaps between high-throughput sequencing information and molecular mechanisms of cancer evolution. In this article, we argue that the integration of functional and systems mapping (Wu and Lin, 2006; Li and Wu, 2010; Wu et al., 2011) with mathematical models for describing the origin and proliferation of cancer SC (Colijn and Mackey, 2005a,b; Ganguly and Puri, 2006; Enderling et al., 2007; Adimy et al., 2008; Michor, 2008; Piotrowska et al., 2008) may shed light on a better understanding of cancer genetics. We particularly emphasize the importance of integrating the latest discoveries of cancer genetics in a diversity of areas from haplotype effects to gene mutation or aneuploidy to genetic imprinting into statistical functional mapping models.
We have constructed a general framework for modeling the genetic control of the dynamics of cancer stem cell populations based on the general characterization of a tumor. The model uses specific differential equation parameters to describe different stages of tumor progression and test the magnitude and patterns of genetic effects on the proliferation of cancer SC. The model should be extended to model differences in proliferation dynamics of normal SC and cancer SC, which facilitates the diagnosis of cancer initiation and malignant progression from individuals’ genetic information.
The model allows the target of cancer SC based on genetic data. By coupling with “omics” data, the model may offer additional therapeutic window for success in disease elimination. Also, mathematical modeling of gene regulatory networks in cancer SC may provide insight into the underlying mechanism for disease prevention and for the provision of novel insight into new therapeutic formulations. A more sophisticated model that takes into account multi-step processes with several feedback functions and therapeutic responses of cancer interventions would be very beneficial in future studies.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work is partly supported by NIH/UL1RR0330184.
References
Adimy, M., Angulo, O., Crauste, F., and Lopez-Marcos, J. C. (2008). Numerical integration of a mathematical model of hematopoietic stem cell dynamics. Comput. Math. Appl. 56, 594–560.
Al-Hajj, M., Wicha, M. S., Benito-Hernandez, A., Morrison, S. J., and Clarke, M. F. (2003). Prospective identification of tumorigenic breast cancer cells. Proc. Natl. Acad. Sci. U.S.A. 100, 3983–3988.
Alison, M. R. (2005). Liver stem cells: implications for hepatocarcinogenesis. Stem Cell. Rev. 1, 253–260.
Anderson, A. R. A., and Quaranta, V. (2008). Integrative mathematical oncology. Nat. Rev. Cancer 8, 227–233.
Anholt, R. R., and Mackay, T. F. C. (2004). Quantitative genetic analyses of complex behaviours in Drosophila. Nat. Rev. Genet. 5, 838–849.
Araujo, R. P., and McElwain, D. L. S. (2006). The role of mechanical host-tumour interactions in the collapse of tumour blood vessels and tumour growth dynamics. J. Theor. Biol. 238, 817–827.
Ayers, M., Symmans, W. F., Stec, J., Damokosh, A. I., Clark, E., Hess, K., Lecocke, M., Metivier, J., Booser, D., Ibrahim, N., Valero, V., Royce, M., Arun, B., Whitman, G., Ross, J., Sneige, N., Hortobagyi, G. N., and Pusztai, L. (2004). Gene expression profiles predict complete pathologic response to neoadjuvant paclitaxel and fluorouracil, doxorubicin, and cyclophosphamide chemotherapy in breast cancer. J. Clin. Oncol. 22, 2284–2293.
Barabasi, A. L., and Oltvai, Z. N. (2004). Network biology: understanding the cell’s functional organization. Nat. Rev. Genet. 5, 101–113.
Baumann, M., Krause, M., and Hill, R. (2008). Exploring the role of cancer stem cells in radioresistance. Nat. Rev. Cancer 8, 545–554.
Beretta, E., and Kuang, Y. (2002). Geometric stability switch criteria in delay differential systems with delay dependent parameters. SIAM J. Math. Anal. 33, 1144–1165.
Bernard, S., Belair, J., and Mackey, M. (2003). Oscillations in cyclical neutropenia: New evidence based on mathematical modeling. J. Theor. Biol. 223, 283–298.
Bhanot, G., Alexe, G., Levine, A. J., and Stolovitzky, G. (2005). Robust diagnosis of non-Hodgkin lymphoma phenotypes validated on gene expression data from different laboratories. Genome Inform. 16, 233–244.
Boone, C., Bussey, H., and Andrews, B. J. (2007). Exploring genetic interactions and networks with yeast. Nat. Rev. Genet. 8, 437–449.
Brown, M. D., Gilmore, P. E., Hart, C. A., Samuel, J. D., Ramani, V. A., George, N. J., and Clarke, N. W. (2007). Characterization of benign and malignant prostate epithelial Hoechst 33342 side populations. Prostate 67, 1384–1396.
Clarke, R., Ressom, H. W., Wang, A., Xuan, J., Liu, M. C., Gehan, E. A., and Wang, Y. (2008). The properties of high-dimensional data spaces: implications for exploring gene and protein expression data. Nat. Rev. Cancer 8, 37–49.
Clayton, T. A., Lindon, J. C., Cloarec, O., Antti, H., Charuel, C., Hanton, G., Provost, J.-P., Le Net, J.-L., Baker, D., Walley, R. J., Everett, J. R., and Nicholson, J. K. (2006). Pharmacometabonomic phenotyping and personalized drug treatment. Nature 440, 1073–1077.
Cohen, A. A., Geva-Zatorsky, N., Eden, E., Frenkel-Morgenstern, M., Issaeva, I., Sigal, A., Milo, R., Cohen-Saidon, C., Liron, Y., Kam, Z., Cohen, L., Danon, T., Perzov, N., and Alon, U. (2008). Dynamic proteomics of individual cancer cells in response to a drug. Science 322, 1511–1516.
Colijn, C., and Mackey, M. C. (2005a). A mathematical model of hematopoiesis: periodic chronic myelogenous leukemia, part I. J. Theor. Biol. 237, 117–132.
Colijn, C., and Mackey, M. C. (2005b). A mathematical model of hematopoiesis: cyclical neutropenia, part II. J. Theor. Biol. 237, 133–146.
Crauste, F. (2006). Global asymptotic stability and Hopf bifurcation for a blood cell production model. Math. Biosci. Eng. 3, 325–346.
Cui, Y. H., Sun, K. L., Fan, X., and Wu, R. L. (2007). Mapping nucleotide sequences that encode complex binary disease traits with HapMap. Curr. Genomics 8, 307–322.
Das, K., and Wu, R. L. (2008). A statistical model for the identification of genes governing the incidence of cancer with age. Theor. Biol. Med. Model. 5, 7.
de Araujo, S. P. S., Maciag, P. C., Ribeiro, K. B., Petzl-Erler, M. L., Franco, E. L., and Villa, L. L. (2008). Interaction between polymorphisms of the human leukocyte antigen and HPV-16 variants on the risk of invasive cervical cancer. BMC Cancer 8, 246.
Dick, J. E. (2003). Breast cancer stem cells revealed. Proc. Natl. Acad. Sci. U.S.A. 100, 3547–3549.
Dontu, G., Al-Hajj, M., Abdallah, W. M., Clarke, M. F., and Wicha, M. S. (2003). Stem cells in normal breast development and breast cancer. Cell Prolif. 36, 59–72.
Duesberg, P., Li, R., Fabarius, A., and Hehlmann, R. (2007). Orders of magnitude change in phenotype rate caused by mutation. Cell. Oncol. 29, 71–72.
Enderling, H., Chaplain, M. A., Anderson, A. R., and Vaidya, J. S. (2007). A mathematical model of breast cancer development, local treatment and recurrence. J. Theor. Biol. 246, 245–259.
Fan, C., Oh, D. S., Wessels, L., Weigelt, B., Nuyten, D. S., Nobel, A. B., van’t Veer, L. J., and Perou, C. M. (2006). Concordance among gene-expression-based predictors for breast cancer. N. Engl. J. Med. 355, 560–569.
Feinberg, A. P., and Tycko, B. (2004). The history of cancer epigenetics. Nat. Rev. Cancer 4, 143–153.
Feng, P., and Navaratna, M. (2007). Modelling periodic oscillations during somitogenesis. Math. Biosci. Eng. 4, 661–673.
Fu, G. F., Luo, J., Berg, A., Wang, Z., Li, J. H., Das, K., Li, R., and Wu, R. L. (2010). A dynamic model for functional mapping of biological rhythms. J. Biol. Dyn. 4, 1–10.
Fu, G. F., Wang, Z., Li, J. H., and Wu, R. L. (2011). A mathematical framework for functional mapping of complex phenotypes using delay differential equations. J. Theor. Biol. 289, 206–216.
Ganguly, R., and Puri, I. K. (2006). Mathematical model for the cancer stem cell hypothesis. Cell Prolif. 39, 3–14.
Ganly, I., Talbot, S., Maghami, E., Viale, A., Pfister, D., Olshen, A. B., Shah, J. P., Socci, N., and Singh, B. (2007). Identification of angiogenesis/metastases genes predicting chemoradiotherapy response in patients with laryngopharyngeal carcinoma. J. Clin. Oncol. 25, 1369–1376.
Greenman, C., Stephens, P., Smith, R., Dalgliesh, G. L., Hunter, C., Bignell, G., Davies, H., Teague, J., Butler, A., Stevens, C., Edkins, S., O’Meara, S., Vastrik, I., Schmidt, E. E., Avis, T., Barthorpe, S., Bhamra, G., Buck, G., Choudhury, B., Clements, J., Cole, J., Dicks, E., Forbes, S., Gray, K., Halliday, K., Harrison, R., Hills, K., Hinton, J., Jenkinson, A., Jones, D., Menzies, A., Mironenko, T., Perry, J., Raine, K., Richardson, D., Shepherd, R., Small, A., Tofts, C., Varian, J., Webb, T., West, S., Widaa, S., Yates, A., Cahill, D. P., Louis, D. N., Goldstraw, P., Nicholson, A. G., Brasseur, F., Looijenga, L., Weber, B. L., Chiew, Y. E., DeFazio, A., Greaves, M. F., Green, A. R., Campbell, P., Birney, E., Easton, D. F., Chenevix-Trench, G., Tan, M. H., Khoo, S. K., Teh, B. T., Yuen, S. T., Leung, S. Y., Wooster, R., Futreal, P. A., and Stratton, M. R.. (2007). Patterns of somatic mutation in human cancer genomes. Nature 446, 153–158.
Hartman, J. L., Garvik, B., and Hartwell, L. (2001). Principles for the buffering of genetic variation. Science 291, 1001–1004.
Hopkins, A. L. (2008). Network pharmacology: the next paradigm in drug discovery. Nat. Chem. Biol. 4, 682–690.
Jallepalli, P. V., and Lengauer, C. (2001). Chromosome segregation and cancer: Cutting through the mystery. Nat. Rev. Cancer 1, 109–117.
Jirtle, R. L., and Skinner, M. K. (2007). Environmental epigenomics and disease susceptibility. Nat. Rev. Genet. 8, 253–262.
Khan, J., Wei, J. S., Ringnr, M., Saal, L. H., Ladanyi, M., Westermann, F., Berthold, F., Schwab, M., Antonescu, C. R., Peterson, C., and Meltzer, P. S. (2001). Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nat. Med. 7, 673–679.
Kirk, P. D. W., Toni, T., and Stumpf, M. P. H. (2008). Parameter inference for biochemical systems that undergo a Hopf bifurcation. Biophys. J. 95, 540–549.
Lander, E. S., and Botstein, D. (1989). Mapping Mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 121, 185–199.
Lapidot, T., Sirard, C., Vormoor, J., Murdoch, B., Hoang, T., Caceres-Cortes, J., Minden, M., Paterson, B., Caligiuri, M. A., and Dick, J. E. (1994). A cell initiating human acute myeloid leukaemia after transplantation into SCID mice. Nature 17, 645–648.
Lehner, B., Crombie, C., Tischler, J., Fortunato, A., and Fraser, A. G. (2006). Systematic mapping of genetic interactions in Caenorhabditis elegans identifies common modifiers of diverse signaling pathways. Nat. Genet. 38, 896–903.
Li, J. H., Das, K., Fu, G. F., Li, R., and Wu, R. L. (2011a). Bayesian lasso for genome-wide association studies. Bioinformatics 27, 516–523.
Li, Y., Berg, A., Wu, L. R., Chen, G., and Wu, R. L. (2010a). Modeling the aneuoploidy control of cancer. BMC Cancer 10, 346.
Li, Y., Guo, Y. Q., Hou, W., Chang, M., Liao, D. P., and Wu, R. L. (2011b). A statistical design for testing transgenerational genomic imprinting in natural human populations. PLoS ONE 6, e16858.
Li, Y., Ma, C. M., Wang, Z., Chen, G., Ahn, A., Lazarus, P., and Wu, R. L. (2010b). A disequilibrium model for detecting somatic mutations causing cancer. J. Theor. Biol. 165, 218–224.
Li, Y., and Wu, R. L. (2009). Modeling host-cancer genetic interactions with multilocus sequence data. J. Comput. Sci. Syst. Biol. 2, 24–43.
Lin, D. Y., and Huang, B. E. (2007). The use of inferred haplotypes in downstream analyses. Am. J. Hum. Genet. 80, 577–579.
Liu, T., Johnson, J. A., Casella, G., and Wu, R. L. (2004). Sequencing complex diseases with HapMap. Genetics 168, 503–511.
Liu, T., Liu, X. L., Chen, Y. M., and Wu, R. L. (2007). A unifying differential equation model for functional genetic mapping of circadian rhythms. Theor. Biol. Med. Model. 4, 5.
Lobo, N. A., Shimono, Y., Qian, D., and Clarke, M. F. (2007). The biology of cancer stem cells. Annu. Rev. Cell Dev. Biol. 23, 675–699.
Lopez-Rios, F., Chuai, S., Flores, R., Shimizu, S., Ohno, T., Wakahara, K., Illei, P. B., Hussain, S., Krug, L., Zakowski, M. F., Rusch, V., Olshen, A. B., and Ladanyi, M. (2006). Global gene expression profiling of pleural mesotheliomas: overexpression of aurora kinases and P16/CDKN2A deletion as prognostic factors and critical evaluation of microarray-based prognostic prediction. Cancer Res. 66, 2970–2979.
Luo, J. T., Hager, W. W., and Wu, R. L. (2010). A differential equation model for functional mapping of a virus-cell dynamic system. J. Math. Biol. 65, 1–15.
Pearson, T. A., and Manolio, T. A. (2008). How to interpret a genome-wide association study. J. Am. Med. Assoc. 299, 1335–1344.
Piotrowska, M. J., Enderling, H., an der Heiden, U., and Mackey, M. C. (2008). “Mathematical modeling of stem cells related to cancer,” in Cancer and Stem Cells, eds T. Dittmar, and K. S. Zanker (New York: Nova Science Publishers), 11–35.
Pujana, M. A., Han, J. D., Starita, L. M., Stevens, K. N., Tewari, M., Ahn JS Rennert, G., Moreno, V., Kirchhoff, T., Gold, B., Assmann, V., Elshamy, W. M., Rual, J. F., Levine, D., Rozek, L. S., Gelman, R. S., Gunsalus, K. C., Greenberg, R. A., Sobhian, B., Bertin, N., Venkatesan, K., Ayivi-Guedehoussou, N., Solé, X., Hernández, P., Lázaro, C., Nathanson, K. L., Weber, B. L., Cusick, M. E., Hill, D. E., Offit, K., Livingston, D. M., Gruber, S. B., Parvin, J. D., and Vidal, M. (2007). Network modeling links breast cancer susceptibility and centrosome dysfunction. Nat. Genet. 39, 1338–1349.
Ramsay, J. O., Hooker, G., Campbell, D., and Cao, J. G. (2007). Parameter estimation for differential equations: a generalized smoothing approach (with discussion). J. R. Stat. Soc. B 69, 741–796.
Reik, W., and Lewis, A. (2005). Co-evolution of X-chromosome inactivation and imprinting in mammals. Nat. Rev. Genet. 6, 403–410.
Rhodes, D. R., and Chinnaiyan, A. M. (2005). Integrative analysis of the cancer transcriptome. Nat. Genet. 37: S31–S37.
Rual, J. F., Venkatesan, K., Hao, T., Hirozane-Kishikawa, T., Dricot, A., Li N Berriz, G. F., Gibbons, F. D., Dreze, M., Ayivi-Guedehoussou, N., Klitgord, N., Simon, C., Boxem, M., Milstein, S., Rosenberg, J., Goldberg, D. S., Zhang, L. V., Wong, S. L., Franklin, G., Li, S., Albala, J. S., Lim, J., Fraughton, C., Llamosas, E., Cevik, S., Bex, C., Lamesch, P., Sikorski, R. S., Vandenhaute, J., Zoghbi, H. Y., Smolyar, A., Bosak, S., Sequerra, R., Doucette-Stamm, L., Cusick, M. E., Hill, D. E., Roth, F. P., and Vidal, M. (2005). Towards a proteome-scale map of the human protein-protein interaction network. Nature 437, 1173–1178.
Sasaki, H., and Matsui, Y. (2008). Epigenetic events in mammalian germ-cell development: reprogramming and beyond. Nat. Rev. Genet. 2008, 129–140.
Savcenco, V. (2009). Construction of a multirate RODAS method for stiff ODEs. J. Comput. Appl. Math. 225, 323–337.
Sha, K. (2008). A mechanistic view of genomic imprinting. Annu. Rev. Genomics Hum. Genet. 9, 197–216.
Singh, S. K., Hawkins, C., Clarke, I. D., Squire, J. A., Bayani, J., Hide, T., Henkelman, R. M., Cusimano, M. D., and Dirks, P. B. (2004). Identification of human brain tumour initiating cells. Nature 432, 396–401.
Solyani, G. I., Berezetskaya, N. M., Bulkiewicz, R. I., and Kulik, G. I. (1995). Different growth patterns of a cancer cell population as a function of its starting growth characteristics. Analysis by mathematical modelling. Cell Prolif. 28, 263–278.
Stelzl, U., Worm, U., Lalowski, M., Haenig, C., Brembeck, F. H., Goehler H Stroedicke, M., Zenkner, M., Schoenherr, A., Koeppen, S., Timm, J., Mintzlaff, S., Abraham, C., Bock, N., Kietzmann, S., Goedde, A., Toksoez, E., Droege, A., Krobitsch, S., Korn, B., Birchmeier, W., Lehrach, H., and Wanker, E. E. (2005). A human protein-protein interaction network: a resource for annotating the proteome. Cell 122, 957–968.
The International HapMap Constortium. (2007). A second generation human haplotype map of over 3.1 million SNPs. Nature 449, 851–862.
Verdugo, A., and Rand, R. (2008). Hopf bifurcation in a DDE model of gene expression. Commun. Nonlinear Sci. Numer. Simul. 13, 235–242.
Viale, A., De Franco, F., Orleth, A., Cambiaghi, V., Giuliani, V., Bossi, D., Ronchini, C., Ronzoni, S., Muradore, I., Monestiroli, S., Gobbi, A., Alcalay, M., Minucci, S., and Pelicci, P. G. (2009). Cell-cycle restriction limits DNA damage and maintains self-renewal of leukaemia stem cells. Nature 457, 51–56.
Visvader, J. E., and Lindeman, G. J. (2008). Cancer stem cells in solid tumours: accumulating evidence and unresolved questions. Nat. Rev. Cancer 8, 755–768.
Wilkins, J. F., and Haig, D. (2003). What good is genomic imprinting: The function of parent-specific gene expression. Nat. Rev. Genet. 4, 359–368.
Wu, R., Cao, J., Huang, Z., Wang, Z., Gai, J., and Vallejos, E. (2011). Systems mapping: how to improve the genetic mapping of complex traits through design principles of biological systems. BMC sys. biol. 5, 84–94.
Wu, R. L., and Lin, M. (2006). Functional mapping – how to map and study the genetic architecture of dynamic complex traits. Nat. Rev. Genet. 7, 229–237.
Wu, R. L., Ma, C. X., Lin, M., and Casella, G. (2004). A general framework for analyzing the genetic architecture of developmental characteristics. Genetics 166, 1541–1551.
Yap, J. S., Fan, J., and Wu, R. L. (2009). Nonparametric modeling of covariance structure in functional mapping of quantitative trait loci. Biometrics 65, 1068–1077.
Youngson, N. A., and Whitelaw, E. (2008). Transgenerational epigenetic effects. Annu. Rev. Genomics Hum. Genet. 9, 233–257.
Zhao, W., Chen, Y. Q., Casella, G., Cheverud, J. M., and Wu, R. L. (2005). A nonstationary model for functional mapping of complex traits. Bioinformatics 21, 2469–2477.
Keywords: differential equation, cancer stem cell, statistical model, genetic architecture
Citation: Wang Z, Liu J, Wang J, Wang Y, Wang N, Li Y, Li R and Wu R (2012) Dynamic modeling of genes controlling cancer stem cell proliferation. Front. Gene. 3:84. doi: 10.3389/fgene.2012.00084
Received: 11 January 2012; Accepted: 26 April 2012;
Published online: 22 May 2012.
Edited by:
Lin S. Chen, The University of Chicago, USAReviewed by:
Qianying Liu, University of Chicago, USACopyright: © 2012 Wang, Liu, Wang, Wang, Wang, Li, Li and Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Rongling Wu, Center for Statistical Genetics, The Pennsylvania State University, Hershey, PA 17033, USA. e-mail:cnd1QHBocy5wc3UuZWR1



 Yaqun Wang2
Yaqun Wang2
