- 1 The University of Queensland, Queensland Brain Institute, Brisbane, QLD, Australia
- 2 Department of Psychiatry, University of Minnesota, Minneapolis, MN, USA
- 3 Department of Psychology, University of Minnesota, Minneapolis, MN, USA
Estimates of heritability of psychiatric disorders quantify the genetic contribution to their etiology. Estimation of these parameters requires affected status on probands and their family members. Traditionally, heritabilities have been estimated from families ascertained from specific hospital registers, but accumulating sufficient numbers of families can be difficult. Larger sample sizes are achievable from national registries, but calculation of heritability from individual level data from these data sets is accompanied by other problems. Here, we use published summary data from a national population-based cohort of >2.6 million persons in Denmark to estimate heritabilities of schizophrenia, bipolar disorder, and major depressive disorder (MDD). The summary data comprised cumulative incidences up to 52 years of age for schizophrenia and bipolar disorder and up to 51 years for MDD in offspring where either one or both parents were diagnosed with one of these disorders. Estimates of the heritabilities of the liability to developing schizophrenia, bipolar disorder, and MDD are 0.67 (95% confidence interval (CI) 0.64–0.71), 0.62 (95% CI 0.58–0.65), and 0.32 (95% CI 0.30–0.34) respectively. The estimates may be inflated by common environmental effects, but despite this, they are somewhat lower for schizophrenia and bipolar disorder than those estimated from contemporary twin samples. The lower estimates may reflect the diverse environments (including diagnostic interpretation) that contribute to national data, compared to twin/family studies. Our estimates are similar to those estimated previously from national data of Sweden, and they may be more representative of the international samples brought together for large-scale genome-wide association studies. We investigated the estimation of genetic correlations from these data. We used simulation to conclude that estimates may not be interpretable and so report them only in the Section “Appendix.”
Introduction
Twin and family studies of schizophrenia, bipolar disorder, and major depressive disorder (MDD) have demonstrated a major genetic contribution to the etiology of these common complex disorders (Sullivan et al., 2000; McGuffin et al., 2003; Kirov and Owen, 2009), and this contribution is quantified through estimates of heritability to their liability. The current generation of genome-wide association studies (GWAS) have identified specific variants, both common and rare, associated with these disorders (Purcell et al., 2009; Ripke et al., 2011; Sklar et al., 2011; Psychiatric GWAS Consortium for Major Depressive Disorder, 2012), but together these explain only a fraction of the heritability identified from family studies (Visscher et al., 2012). The puzzle of this so-called “missing heritability” (Maher, 2008) is not limited to neuropsychiatric disorders, but is a characteristic of studies of almost all complex genetic traits, diseases, and disorders. One contributing explanation may be overestimation of heritabilities from twin and family studies.
Just as estimates of heritability benchmark the maximum contribution to the variance we expect to achieve through direct interrogation at the molecular level, genetic correlations benchmark the relationship between disorders. Estimates of heritabilities and genetic correlations of liability, although quite simple in theory (Visscher et al., 2008), depend on estimates of lifetime probabilities of disease in relatives of affected individuals and from the total population from which they are drawn. Quantifying the genetic contribution to disease is achieved by assuming the liability threshold model (Falconer, 1965); under this model, liability to disease (which includes both genetic and environmental effects) is considered to be normally distributed, with affected individuals being those with liabilities greater than the threshold that truncates the proportion with the disorder in the population. The liability model can be shown to be exchangeable with a wide range of other models that are also consistent with empirical data (Slatkin, 2008), but its parameterization makes it the model of choice for theoretical and applied studies. This liability threshold model was first applied to schizophrenia psychopathology by Gottesman and Shields (1967) having consulted with Douglas Falconer in 1965 in Edinburgh on the validity of their extrapolations to psychiatric diseases. Many estimates of heritability have been made from twin samples or extended family studies (reviewed for schizophrenia; Cardno and Gottesman, 2000; Sullivan et al., 2003). A limitation of these studies is that families ascertained from specific hospital registers may not be a representative sample of the population used to get overall probability rates (Kendler et al., 1995), for example if different diagnostic criteria are used for the family sample compared to the total reference population. Further, family samples tend to be small implying large sampling variances, and rates may be biased upward if there are any ascertainment biases (Odegard, 1963; Guo, 1998) or if diagnoses of family members are more highly correlated than if family members presented at different hospitals. These problems can be overcome by using national data, where available, such as in a Swedish study comprising over nine million individuals from over two million families which represented all individuals born between 1932 and 2002 and all hospital records since 1973 (Lichtenstein et al., 2009).
However, use of national registries brings its own problems (Mortensen et al., 2010) from routinely recorded clinical diagnoses collected into dynamic data-bases of records necessarily censored given the age structure of the population and varying ages of onset for the disorders. The Swedish study (Lichtenstein et al., 2009) matched schizophrenia and bipolar probands on age and sex with unaffected controls as a way to overcome problems of censored data. In that study, estimates of heritabilities and genetic correlations were achieved through development of generalized linear mixed models for binary bivariate data applied to individual level data (Yip et al., 2008). Their estimates of heritabilities were lower than those traditionally quoted for schizophrenia [0.64 (95% confidence interval (CI) 0.62–0.68) vs. 0.81 (95% CI 0.73–0.90); Sullivan et al., 2003] and bipolar disorder [0.59 (95% CI 0.56–0.62) vs. 0.85 (95% CI 0.73–0.93); McGuffin et al., 2003]. As a stand-alone study, it is difficult to evaluate the importance of these differences, but estimates of heritability from national data may be of most relevance to the international samples brought together in large GWAS studies.
Another study that used national data to investigate increased risks of schizophrenia and bipolar in offspring of affected parents was the study from Denmark of Gottesman et al. (2010), which particularly focused on a rare sample of offspring with two affected parents. To account for censorship in lifetime estimates of probability of disease, they calculated the increased risks of disease from cumulative incidences of disease across ages, well into their risk periods. Analysis of these records accounting for censorship in a mixed model framework to estimate genetic parameters would be complex. The framework of the liability model, as proposed by Falconer (1965), is of estimation of heritability from recurrence risk to relatives estimated from the population, even though at the time such population estimates were not available. Here, we implement that framework to provide estimates of heritability for psychiatric disorders from nationally collected records. We use population summary statistics, i.e., cumulative incidences from the large Danish study (>2.6 million records) to estimate heritabilities of schizophrenia, bipolar disorder, and MDD. To demonstrate the validity of the approach we apply these methods to the summary statistics from the Swedish study and show that the resulting estimates of heritability agree well with their estimates derived from full data modeling (Lichtenstein et al., 2009). Originally, our interest was to use the Danish summary data to estimate the genetic correlation between schizophrenia and bipolar disorder and, between schizophrenia and MDD, since few studies have been able to quantify this relationship. We explored this aim, but using simulation to represent important characteristics of the summary data available, we concluded that the estimates could not be considered reliable and so report them only in the Section “Appendix.”
Materials and Methods
Description of Data Generating Published Summary Statistics
We use the summary statistics calculated from population-based cohort reported in Gottesman et al. (2010). Briefly, the cohort comprises all persons born in Denmark, alive in 1968 or born between 1969 and 1996 who could be linked to their parents through the Civil Registration System (N = 2,685,301). Those who had ever received diagnoses of schizophrenia or bipolar affective disorder or unipolar depressive disorder from a psychiatric facility between April 1 1970 and January 1 2007 were identified from the Psychiatric Central Register according to diagnoses at discharge from admissions to all inpatient facilities and from out-patient treatment facilities for admissions from 1995 onward. All admissions in Denmark are contained in the register, as there are no private psychiatric inpatient or outpatient units (Gottesman et al., 2010). Diagnostic classification was based on the International Classification of Disease, Eighth Revision (ICD-8) from 1966 to 1993 and on the 10th revision (ICD-10) since then (Gottesman et al., 2010). Here we use the nomenclature of MDD rather than unipolar depressive disorder. Those discharged more than once with different diagnoses were counted in more than one diagnostic group after unsuccessful trials with alternative ascertainments (Gottesman et al., 2010).
Cumulative Incidences
The incidence of psychiatric admission was calculated from the number of new cases occurring for each age in the cohort members. Gottesman et al. (2010) reported cumulative incidences up to a maximum of age 52 for schizophrenia and bipolar disorder, an age well into the accepted risk period for these disorders. Cumulative incidences were based on the Nelson–Aalen estimator, which is a cumulative hazard rate function appropriate for censored and incomplete data. The cumulative incidences to age 52 can be interpreted as the proportion of people in the population who have/will received a diagnosis by age 52 (Gottesman et al., 2010). Cumulative incidences were calculated for different cohorts including: the general population (no restriction on psychiatric diagnosis of parents), and the offspring of parents where one or both parents had a psychiatric diagnosis. The number of unique parent couples (counted only once) was 1,278,977, some of whom had more than one offspring. Here we utilize the cumulative incidences to estimate genetic parameters. For MDD, the authors of Gottesman et al. (2010) provided estimates of the cumulative incidences up to a maximum of age 51, unpublished results from their preliminary analyses. Gottesman et al. (2010) showed that cumulative incidences had plateaued by age 52 for schizophrenia, but they were still rising for bipolar disorder.
Methods for Estimation of Heritabilities, Genetic Correlations, and Their Standard Errors
We adapted the methods of Falconer (1965) and Reich et al. (1972) to estimate heritabilities of schizophrenia, bipolar disorder, and MDD (, , and , respectively), the genetic correlation between disorders and their standard errors. These methods are based on the liability threshold model in which a normal distribution of liability is assumed to underlie affection status and those affected have liability that surpasses a critical threshold. The liability is unobserved but the threshold can be determined from normal distribution theory given the proportion of the population that are affected in their lifetime. The proportions affected in the population and in relatives of those affected are used to estimate heritability of liability (Falconer and Mackay, 1996; Lynch and Walsh, 1998). Here we use cumulative incidence to 52 or 51 years as estimates of the proportion of the population that are affected in their lifetime. Critical assumptions associated with these widely used methods are discussed below. Corrections for non-normality in the relatives are negligible (Lynch and Walsh, 1998) and are not considered here. We estimate twice: from the prevalence of schizophrenia in offspring where one parent has schizophrenia and from the prevalence of schizophrenia in offspring where both parents had schizophrenia; and likewise for bipolar disorder and MDD. We obtain overall estimates by weighting the individual estimates by the inverse of their sampling variances. Full derivations are provided in the Section “Appendix.”
Simulation to Investigate Estimates from Genetic Correlations from the Danish Summary Data
In the Danish summary data used in our analysis, those discharged more than once with different diagnoses were counted in more than one diagnostic group, a non-hierarchical approach. It is widely recognized that many patients do not have disorders that conform to discrete diagnostic classes (Craddock and Owen, 2007) and that some individuals may be truly co-morbid. None-the-less long-term stable diagnoses are considered more reliable than first episode diagnosis (Bromet et al., 2011). Laursen et al. (2009) reported the frequency of individuals receiving multiple diagnoses within their lifetime using the Danish registry data (>2.5 million persons born in Denmark after 1954). From their Table 1, of 16,890 first admissions of bipolar disorder, schizophrenia, or schizoaffective disorder, we calculate that 2.8% of the 12,458 with a final diagnosis of schizophrenia had also been diagnosed with bipolar disorder and 7.1% of the 3,862 with a final diagnosis of bipolar disorder had also been diagnosed with schizophrenia. Also, 4.9% of those who ever received a diagnosis of schizophrenia and 15% of those who ever received a diagnosis of bipolar disorder also received a diagnosis of the other disorder. These raw estimates do not account for censoring (i.e., some individuals may not have yet received their stable diagnosis) and so may be underestimates. We were concerned that the counting of individuals across multiple diagnostic classes (double counting) could bias the estimates of genetic parameters, particularly genetic correlations. The impact of misdiagnosis on estimates of genetic parameters has been explored before (Kendler, 1987; Wray et al., 2012), but these studies assumed individuals were counted in a single, possibly incorrect, diagnostic class. We extended the simulation of (Wray et al., 2012) to consider individuals being counted in more than one diagnostic class. We simulated 100,000 nuclear pedigrees of two parents and one child under a liability threshold model for two independent disorders (i.e., genetic correlation zero). The input parameters were heritabilities and prevalence rates of the two disorders. We also specified the probability of an individual affected with disorder A, also being diagnosed with disorder B, and vice versa. According to these rates, a proportion of cases were randomly assigned affected status for the other disorder. Within the simulation we estimated the heritabilities and genetic correlation based on prevalence diagnosis rates in the parents and in the offspring of affected parents. True simulation parameters were set so that estimated prevalence rates and heritabilities matched those from the empirical results. We repeated each simulation scenario 100 times to achieve approximate 95% CIs (5th and 95th percentile simulation results) on the estimates.
Results
Validation of Methods
To check the validity of our methods of estimating genetic parameters from summary data, we used the Swedish population prevalences and recurrence risk ratios listed in Lichtenstein et al. (2009) to estimate the genetic parameters. We compared these estimates to their estimates based on mixed model methodology that used individual level data (Table 1). Our estimates compared to the published estimates were: 0.64 (95% CI 0.61–0.67) vs. 0.64 (95% CI 0.62–0.68) for and 0.56 (95% CI 0.54–0.58) vs. 0.59 (95% CI 0.56–0.62) for . The overlapping confidence intervals between these estimates justified our approach, recognizing that the good agreement partly reflects that the full partitioning of variance analyses in the original study found only estimates of common environmental variance to be significant but small 0.045 (95% CI 0.044–0.074) for schizophrenia and 0.034 (95% CI 0.023–0.062) for bipolar disorder.
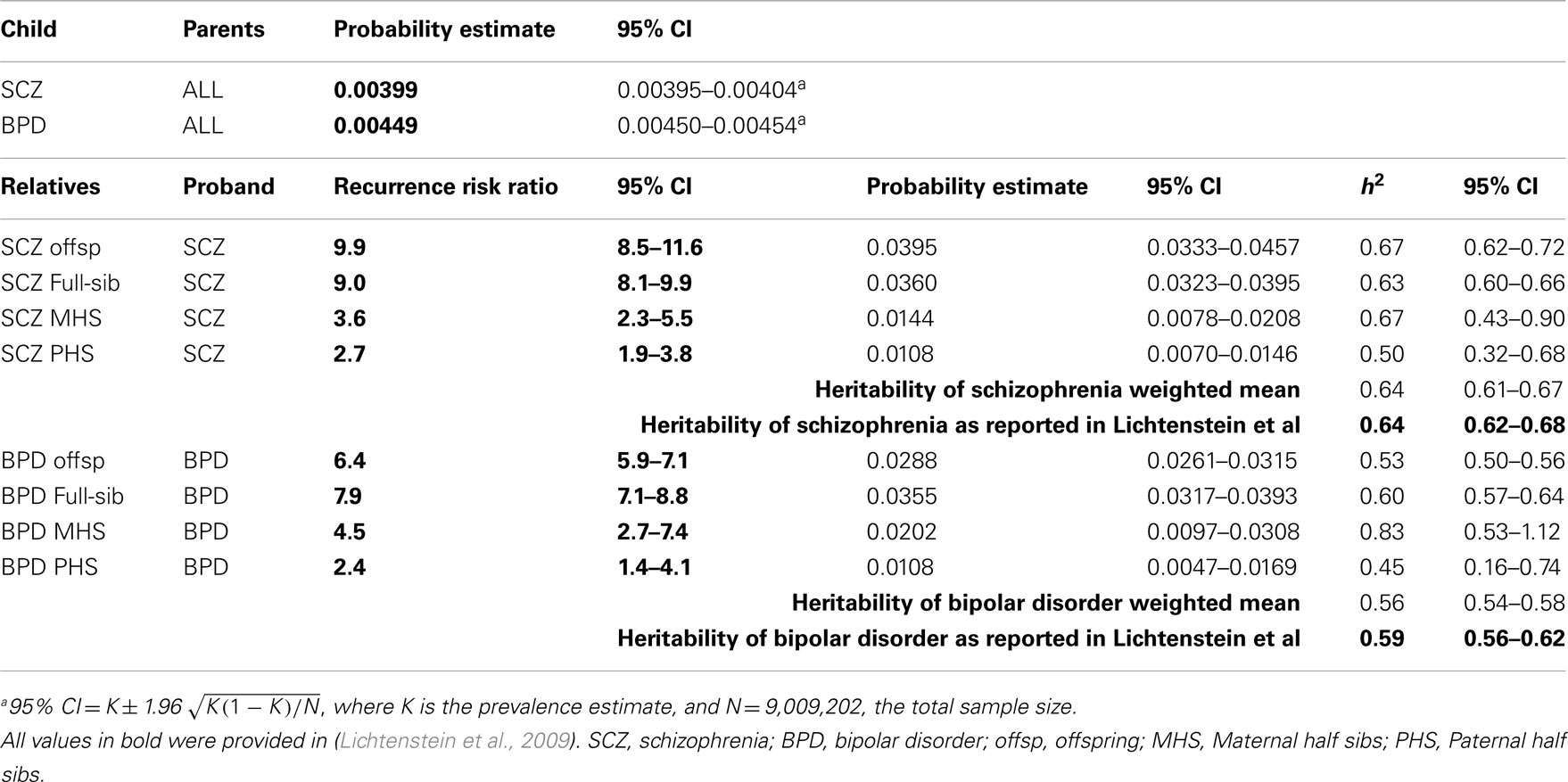
Table 1. Validation of approach: estimation of heritabilities using probability estimates and recurrence risk ratios presented in Lichtenstein et al. (2009).
Estimates of Heritability
Using the cumulative incidences of disease to age 52 estimated from national records of Denmark, we calculate to be 0.67 (95% CI 0.64–0.71), to be 0.62 (95% CI 0.58–0.65), and to be 0.32 (95% CI 0.30–0.34; Table 2). For both MDD and bipolar disorder the heritability estimated from disorder probabilities in offspring with both parents affected was slightly higher than when only one parent was affected, a pattern that might be consistent with confounding of common environmental effects or non-additive genetic effects, but the estimates were not significantly different. For schizophrenia the estimate of heritability when both parents were affected was less than when only one parent was affected, but not significantly so.
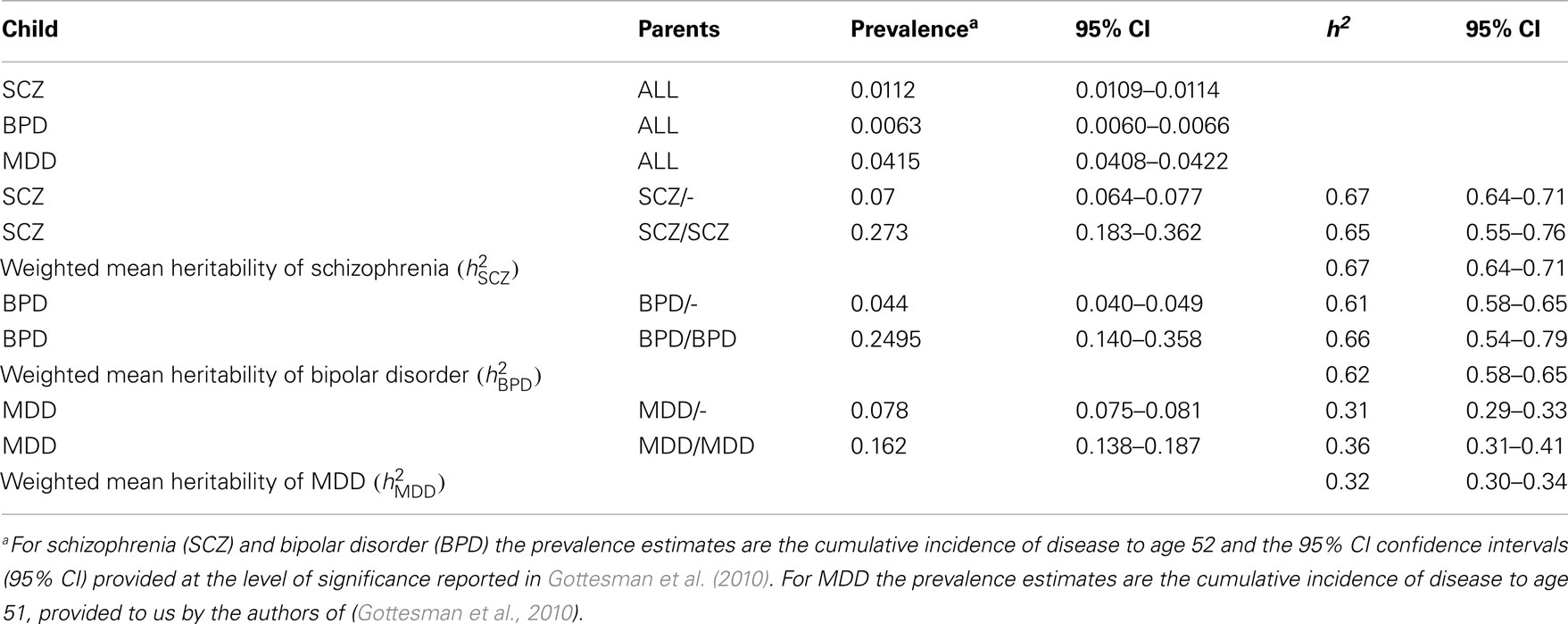
Table 2. Estimates of heritabilities based on the data presented in Gottesman et al. (2010).
Using Simulation to Explore Estimation of Genetic Correlation
Our calculations are based on the summary statistics estimated from the Danish National Register in which individuals were included in more than one diagnostic class if their hospital discharge records across their lifetime reflected multiple diagnoses. We used simulation to explore the impact of including a proportion of individuals in more than one diagnostic class (one true and one misdiagnosed) on estimates of heritabilities and genetic correlation for schizophrenia and bipolar disorder (Table 3). Without misdiagnosis, the simulation returned estimated heritabilities and genetic correlation that matched the simulation parameters (Table 3 row 1), as expected. With misdiagnosis rates of 2.7% for schizophrenia and 7.1% for bipolar disorder (chosen to match our estimates calculated from; Laursen et al., 2009) true heritabilities were slightly higher (and true prevalence rates slightly lower) than those estimated, but not dramatically so. However, in line with results of (Wray et al., 2012), the misdiagnosis and double counting generated an estimated genetic correlation was 0.17 (Table 3 row 2), even though the true correlation was set to zero. This scenario also resulted in 7.0% of those with a diagnosis of schizophrenia and 12.5% of those with a diagnosis of bipolar disorder also having a diagnosis of schizophrenia. Recognizing that the misdiagnosis rates calculated from (Laursen et al., 2009) data may underestimate dual diagnosis rate as some cases may not yet have achieved their final diagnosis, we repeated the simulations with misdiagnosis rates increased twofold. These extreme misdiagnosis rates generated an estimated genetic correlation of 0.31 when the true correlation was zero (Table 3 row 3) and again reflected slightly higher true heritabilities. The simulations also confirmed that the 95% CI for the genetic correlations are considerably wider than those for heritabilities. We conclude from these simulations that our estimates of heritability from the Danish summary data may be slightly lower than the true values as a result of the double counting of individuals across diagnostic classes, but not considerably so. We also concluded that the estimates of genetic correlation are consistent with a true underlying positive genetic correlation between both schizophrenia and bipolar disorder and schizophrenia and MDD, the double counting, and other assumptions would make estimates of genetic correlation from the Danish summary data impossible to interpret, and so report them only in the Section “Appendix.”
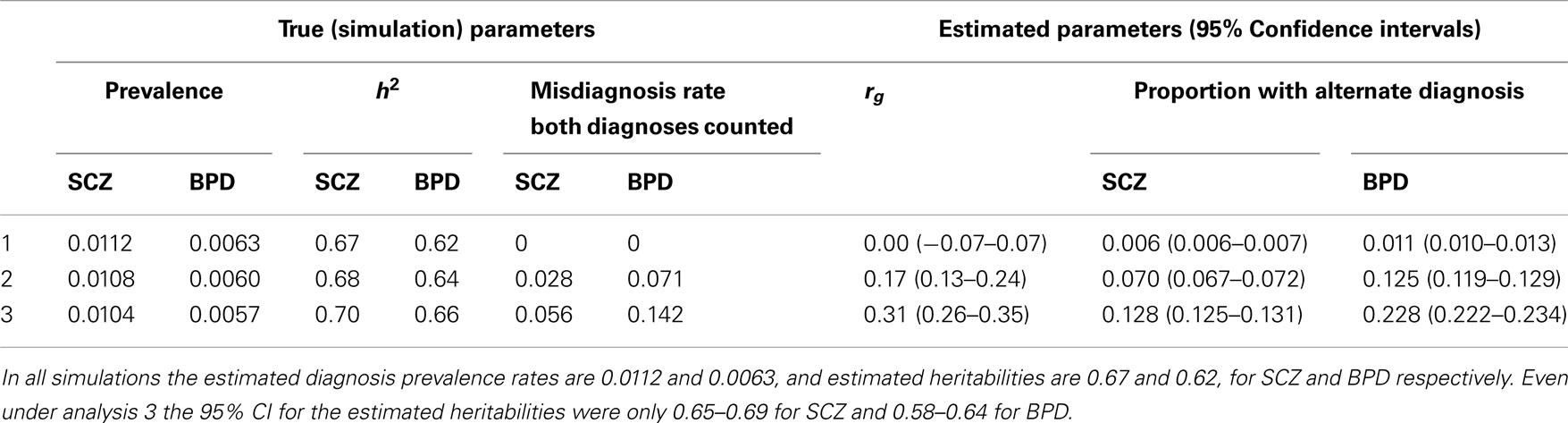
Table 3. Simulation results: simulation parameters were selected to generate estimated diagnosis prevalence rates and heritabilities that match empirical estimates for schizophrenia (SCZ) and bipolar disorder (BPD).
Discussion
Heritabilities of schizophrenia, bipolar disorder, and MDD estimated from published summary data from Danish national records are (95% CI 0.64–0.71), (95% CI 0.58–0.65), and (95% CI 0.30–0.34; Table 2). The estimates of heritability are low compared to the estimates commonly quoted for schizophrenia [0.81 (95% CI 0.73–0.90); Sullivan et al., 2003] and bipolar disorder [0.85 (95% CI 0.73–0.93); McGuffin et al., 2003] but are similar to the estimates from the Swedish study of national records (Lichtenstein et al., 2009): 0.64 (95% CI 0.62–0.68) for schizophrenia and 0.59 (95% CI 0.56–0.62) for bipolar disorder. Lower estimates from national samples may reflect an effect of averaging across “nosological environments” such as diagnostic interpretation, which is likely to be more homogeneous in within-hospital twin studies than in national data. The ever-increasing size of samples used in GWAS necessarily combine cohorts with different collection protocols (e.g., diagnostic criteria and their local applications), and therefore, the lower estimates of heritability may be more representative of population samples. The estimate of heritability for MDD is in line with the estimate from a meta-analysis of twin studies [0.37 (95% CI 0.31–0.42); Sullivan et al., 2000] where many of the contributing estimates were from very large community samples of twins. Lewis et al. (2010) argued that major depression cases ascertained through clinical contact are more severe and tend to have stronger genetic contribution than cases diagnosed by lay interviewers in the general population since the heritability of MDD from a large hospital sample ranged from 0.48 to 0.75 [depending on the model fitted to the 177 twin pairs (McGuffin et al., 1996)]. The MDD cases contributing to the summary data used here are recorded from psychiatric in- and out-patient units and so may be considered severe, in which case our estimate of heritability for MDD is also lower than those estimated from data collected from limited hospital environments.
Despite a classification system that considers schizophrenia and bipolar disorder to be distinct, this dichotomy has long been questioned by empirical observations (Craddock and Owen, 2005; Craddock et al., 2006; Van Snellenberg and de Candia, 2009) which includes the relatively common occurrence of cases with a mix of mood and psychotic symptoms and families with multiple cases of both disorders (Pope and Yurgeluntodd, 1990; Blackwood et al., 2001; McGuffin et al., 2003; Cardno et al., 2012). Molecular studies support a partially shared genetic etiology of bipolar disorder and schizophrenia (Moskvina et al., 2009; Purcell et al., 2009), but only few studies (to our knowledge) have directly estimated the genetic correlation between schizophrenia and bipolar disorder (Yip et al., 2008; Lichtenstein et al., 2009; or schizophrenic and mania syndromes; Cardno et al., 2002). Depression is frequently co-morbid with schizophrenia, for example 31% of 90 patients with a stable diagnosis of schizophrenia were found to qualify for a diagnosis of depression (Majadas et al., 2012). However, overlapping symptoms of disorders does not necessarily imply a shared genetic etiology (Klein and Riso, 1993; Neale and Kendler, 1995). Increased risks for MDD in relatives of those with schizophrenia have been reported, e.g., (Maier et al., 1993; Varma et al., 1997; Mortensen et al., 2010), but it is difficult to separate the impact of shared environment from the genetic components, since psychiatric disorders impact on the lives of family members. We were unable to identify studies that had estimated the genetic correlation between schizophrenia and major depression. For these reasons we were motivated to estimate genetic correlations between schizophrenia and both bipolar disorder and MDD. However, the collation of the Danish summary data counted individuals in multiple diagnosis categories if their hospital discharge records offered different diagnoses over time. Misdiagnosis between disorders inflates estimates of genetic correlations (Wray et al., 2012). Using simulation we found that this double counting of diagnoses could generate marginal underestimates of heritability (by up to 4%), but could generate considerable overestimates of the genetic correlation when the true genetic correlation is zero. We believe that the empirical estimates are consistent with a positive genetic correlation between both schizophrenia and bipolar disorder and between schizophrenia and MDD, but concluded that the estimates of genetic/familial correlations from these summary data could be misleading and so report them only in the Section “Appendix.”
Assumptions and Limitations
Our analysis required a number of important assumptions and our results must be interpreted with caution recognizing the inherent limitations of our study, as in most studies estimating genetic parameters. Firstly, we have assumed the Falconer liability model for disease. This model is particularly suited to an etiology of many underlying risk factors and is used in all other studies estimating heritability from binary disease records, and results from GWAS provide no evidence to reject this model (Purcell et al., 2009; Lee et al., 2012). Secondly, we have assumed that increased risk to relatives reflects only genetic factors and have ignored common environmental factors, therefore our estimates of heritability, strictly speaking, are estimates of familial transmission. However, published estimates of variance attributable to a common family environment suggest that these effects are small (McGue et al., 1983; Sullivan et al., 2000, 2003), as discussed above. Since we are not able to account for common family environment our estimates of heritability may be slightly inflated, but even so, our estimates are lower than those usually reported for schizophrenia and bipolar disorder. Thirdly, as in all other studies using close relatives, non-additive (epistatic) genetic effects may inflate the estimates attributed to additive genetic effects. Fourthly, we have used estimates of cumulative incidences at 52 years as the estimates of lifetime probability of disease. We note that although the cumulative incidences had plateaued by age 52 for schizophrenia they were still rising for bipolar disorder. For MDD cumulative incidences are also likely to increase beyond 51 years. Therefore, incidences cumulated to older ages may impact on our results but since we have used the same definition across all cohorts the impact on the estimates of genetic parameters will be limited. Fifthly, changes in diagnostic practice over time may impact estimates of cumulative incidence in offspring compared to parents and hence bias estimates. Sixthly, as discussed above, misdiagnosis between disorders could result in our estimates of heritability being slightly lower than true values in the population, but that this cannot account for the difference between our estimates and the higher estimates reported from twin studies. Lastly, in our use of the liability threshold model we have assumed that genetic liability variance is constant across generations. Specifically, we ignored the reduced fertility of those with both bipolar disorder (Baron et al., 1982) and schizophrenia (Svensson et al., 2007); for example using the Danish registry data Laursen and Munk-Olsen (2010) estimated that the relative risk of having a child for women with hospital admissions for schizophrenia, bipolar disorder, and MDD compared to individuals never admitted with any psychiatric diagnosis were was 0.18 (95% CI 0.17,0.20), 0.36 (95% CI 0.33–0.40) and 0.57 (95% CI 0.55,0.60), respectively. Reduced fertility and fecundity could reduce genetic variance from one generation to the next. However, we have also ignored assortative mating which would increase genetic variance across generations. Assortative mating can be calculated from the data provided in the Danish study (Gottesman et al., 2010) as a relative risk to spouse of 2.13 for schizophrenia and 1.09 for bipolar disorder, much less than the estimate reported in the Swedish national cohort ∼8 for schizophrenia (Lichtenstein et al., 2006). Accurate modeling of genetic variance across generations would require good estimates of fertility, fecundity, assortative mating, and a net decrease/increase in genetic variance could imply decrease/increase in lifetime probability of disease. Without better empirical data it seems reasonable to assume that these forces on genetic variance balance each other and to assume equality of parameters across generations, as in other studies.
Conclusions
We provide estimates of heritabilities derived from cumulative incidences estimated from the National Danish Registry of over 2.6 million individuals. Only one other study has published genetic parameters from national data (a Swedish study; Lichtenstein et al., 2009). Our estimates of heritability for schizophrenia and bipolar disorder, like theirs, are lower than the traditionally quoted estimates, which are based on small samples of relatives (usually twins) usually from single hospital environments. Our estimates may be more relevant to the large samples that make up the consortia that underpin the current generation of GWAS (Cichon et al., 2009).
Estimates of increased risk to disease in relatives, which are straightforward in principle, are difficult to collect in practice. Here we show that cumulative incidence summary statistics calculated from national data can be used to estimate heritabilities. Evidence for a shared genetic etiology between disorders could make important contributions to psychiatric nosology. However, very large cohorts of twin and family samples, ascertained without bias and recorded for multiple disorders would be needed to estimate the genetic correlation between disorders. Not surprisingly, such studies are difficult to achieve (Cardno et al., 2012) and hence are limited. The use of regional or national data seems the only way to achieve sufficient sample sizes, but these data sets have their own challenges. Here, we were not able to estimate genetic correlations that we considered reliable. The new era of genome-wide genotype data provides perhaps our best hope of understanding the shared etiology of psychiatric disorders (Lee et al., 2011). Such estimates are derived using independently collected cases and controls for the two disorders and estimates are based on such distant relatives that contamination by shared environmental factors seems unlikely.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We gratefully acknowledge the contribution made by Drs Laursen, Bertelsen, and Mortensen the co-authors of Gottesman et al. (2010) in generating the data which forms the basis of our calculations and for providing the unpublished MDD results. We thank Dr Bertelsen for valuable comments on the manuscript, and we thank Ken Kendler for discussions about the validity of the estimates of genetic correlations from these data. We acknowledge funding from the Australian National Health and Medical Research Council (grant 613608) and the Australian Research Council (FT0991360) to Naomi R Wray, the Stanley Medical Research Institute, and the Gralnick Prize for Severe Mental Illness from the American Psychological Foundation and the Lieber Prize for Outstanding Schizophrenia Research from NARSAD to Irving I Gottesman.
References
Baron, M., Risch, N., and Mendlewicz, J. (1982). Differential fertility in bipolar affective-illness. J. Affect. Disord. 4, 103–112.
Blackwood, D. H. R., Fordyce, A., Walker, M. T., St Clair, D. M., Porteous, D. J., and Muir, W. J. (2001). Schizophrenia and affective disorders – cosegregation with a translocation at chromosome 1q42 that directly disrupts brain-expressed genes: clinical and P300 findings in a family. Am. J. Hum. Genet. 69, 428–433.
Bromet, E. J., Kotov, R., Fochtmann, L. J., Carlson, G. A., Tanenberg-Karant, M., Ruggero, C., and Chang, S. W. (2011). Diagnostic shifts during the decade following first admission for psychosis. Am. J. Psychiatry 168, 1186–1194.
Cardno, A. G., and Gottesman, I. I. (2000). Twin studies of schizophrenia: from bow-and-arrow concordances to star wars Mx and functional genomics. Am. J. Med. Genet. 97, 12–17.
Cardno, A. G., Rijsdijk, F. V., Sham, P. C., Murray, R. M., and McGuffin, P. (2002). A twin study of genetic relationships between psychotic symptoms. Am. J. Psychiatry 159, 539–545.
Cardno, A. G., Rijsdijk, F. V., West, R. M., Gottesman, II Craddock, N., Murray, R. M., and McGuffin, P. (2012). A twin study of schizoaffective-mania, schizoaffective-depression, and other psychotic syndromes. Am. J. Med. Genet. B Neuropsychiatr. Genet. 159B, 172–182.
Cichon, S., Craddock, N., Daly, M., Faraone, S. V., Gejman, P. V., Kelsoe, J., Lehner, T., Levinson, D. F., Moran, A., Sklar, P., Sullivan, P. F., and Psychiatric, G. C. S. (2009). A framework for interpreting genome-wide association studies of psychiatric disorders The Psychiatric GWAS Consortium Steering Committee. Mol. Psychiatry 14, 10–17.
Craddock, N., O’Donovan, M. C., and Owen, M. J. (2006). Genes for schizophrenia and bipolar disorder? Implications for psychiatric nosology. Schizophr. Bull. 32, 9–16.
Craddock, N., and Owen, M. J. (2005). The beginning of the end for the Kraepelinian dichotomy. Br. J. Psychiatry 186, 364–366.
Craddock, N., and Owen, M. J. (2007). Rethinking psychosis: the disadvantages of a dichotomous classification now outweigh the advantages. World Psychiatry 6, 20–27.
Falconer, D. S. (1965). The inheritance of liability to certain diseases, estimated from the incidence among relatives. Ann. Hum. Genet. 29, 51–71.
Falconer, D. S., and MacKay, T. F. C. (1996). Introduction to Quantitative Genetics. Harlow: Longman.
Gottesman, I. I., Laursen, T. M., Bertelsen, A., and Mortensen, P. B. (2010). Severe mental disorders in offspring with 2 psychiatrically ill parents. Arch. Gen. Psychiatry 67, 252–257.
Gottesman, I. I., and Shields, J. (1967). A polygenic theory of schizophrenia. Proc. Natl. Acad. Sci. U.S.A. 58, 199.
Guo, S. W. (1998). Inflation of sibling recurrence-risk ratio, due to ascertainment bias and/or overreporting. Am. J. Hum. Genet. 63, 252–258.
Kendler, K. S. (1987). The impact of diagnostic misclassification on the pattern of familial aggregation and coaggregation of psychiatric illness. J. Psychiatr. Res. 21, 55–91.
Kendler, K. S., Pedersen, N. L., Neale, M. C., and Mathe, A. A. (1995). A pilot Swedish twin study of affective-illness including hospital-ascertained and population-ascertained subsample – results of model-fitting. Behav. Genet. 25, 217–232.
Kirov, G. K., and Owen, M. J. (2009). “Genetics of schizophrenia,” in Comtemporary Textbook of Psychiatry, eds B. J. Sadock, V. A. Sadock and P. Ruiz (Philadelphia: Lippincott Williams & Wilkins), 1462–1474.
Klein, D. N., and Riso, L. P. (1993). “Psychiatric disorders: problems of boundaries and comorbidity,” in Basic Issues in Pscyhopathology, ed. C. G. Costello (New York: Guilford Press), 19–66.
Laursen, T. M., Agerbo, E., and Pedersen, C. B. (2009). Bipolar disorder, schizoaffective disorder, and schizophrenia overlap: a new comorbidity index. J. Clin. Psychiatry 79, 1432–1438.
Laursen, T. M., and Munk-Olsen, T. (2010). Reproductive patterns in psychotic patients. Schizophr. Res. 121, 234–240.
Lee, S. H., DeCandia, T. R., Ripke, S. R., and Yang, J. T.S.P.G.A.S. Consortium T.I.S. Consortium T.M.G.o.S. Consortium Sullivan, P. F., Goddard, M. E., Keller, M. C., Visscher, P. M., and Wray, N. R. (2012). Estimating the proportion of variation in susceptibility to schizophrenia captured by common SNPs. Nat. Genet. 44, 247–250.
Lee, S. H., Wray, N. R., Goddard, M. E., and Visscher, P. M. (2011). Estimating missing heritability for disease from genome-wide association studies. Am. J. Hum. Genet. 88, 294–305.
Lewis, C. M., Ng, M. Y., Butler, A. W., Cohen-Woods, S., Uher, R., Pirlo, K., Weale, M. E., Schosser, A., Paredes, U. M., Rivera, M., Craddock, N., Owen, M. J., Jones, L., Jones, I., Korszun, A., Aitchison, K. J., Shi, J., Quinn, J. P., Mackenzie, A., Vollenweider, P., Waeber, G., Heath, S., Lathrop, M., Muglia, P., Barnes, M. R., Whittaker, J. C., Tozzi, F., Holsboer, F., Preisig, M., Farmer, A. E., Breen, G., Craig, I. W., and McGuffin, P. (2010). Genome-wide association study of major recurrent depression in the U.K. population. Am. J. Psychiatry 167, 949–957.
Lichtenstein, P., Bjork, C., Hultman, C. M., Scolnick, E., Sklar, P., and Sullivan, P. F. (2006). Recurrence risks for schizophrenia in a Swedish National Cohort. Psychol. Med. 36, 1417–1425.
Lichtenstein, P., Yip, B. H., Bjork, C., Pawitan, Y., Cannon, T. D., Sullivan, P. F., and Hultman, C. M. (2009). Common genetic determinants of schizophrenia and bipolar disorder in Swedish families: a population-based study. Lancet 373, 234–239.
Lynch, M., and Walsh, B. (1998). Genetics and Analysis of Quantitative Traits. Sunderland, MA: Sinauer Associates.
Maier, W., Lichtermann, D., Minges, J., Hallmayer, J., Heun, R., Benkert, O., and Levinson, D. F. (1993). Continuity and discontinuity of affective-disorders and schizophrenia – results of a controlled family study. Arch. Gen. Psychiatry 50, 871–883.
Majadas, S., Olivares, J., Galan, J., and Diez, T. (2012). Prevalence of depression and its relationship with other clinical characteristics in a sample of patients with stable schizophrenia. Compr. Psychiatry 53, 145–151.
McGue, M., Gottesman, II and Rao, D. C. (1983). The transmission of schizophrenia under a multifactorial model. Am. J. Hum. Genet. 35, 1161–1178.
McGuffin, P., Rijsdijk, F., Andrew, M., Sham, P., Katz, R., and Cardno, A. (2003). The heritability of bipolar affective disorder and the genetic relationship to unipolar depression. Arch. Gen. Psychiatry 60, 497–502.
McGuffin, P., Katz, R., Watkins, S., and Rutherford, J. (1996). A hospital-based twin register of the heritability of DSM-IV unipolar depression. Arch. Gen. Psychiatry 53, 129–136.
Mortensen, P. B., Pedersen, M. G., and Pedersen, C. B. (2010). Psychiatric family history and schizophrenia risk in Denmark: which mental disorders are relevant? Psychol. Med. 40, 201–210.
Moskvina, V., Craddock, N., Holmans, P., Nikolov, I., Pahwa, J. S., Green, E., Owen, M. J., and O’Donovan, M. C. (2009). Gene-wide analyses of genome-wide association data sets: evidence for multiple common risk alleles for schizophrenia and bipolar disorder and for overlap in genetic risk. Mol. Psychiatry 14, 252–260.
Neale, M. C., and Kendler, K. S. (1995). Models of comorbidity for multifactorial disorders. Am. J. Hum. Genet. 57, 935–953.
Odegard, O. (1963). Psychiatric disease entities in light of a genetic investigation. Acta Psychiatr. Scand. 39(Suppl. 169), 94–104.
Pope, H. G., and Yurgeluntodd, D. (1990). Schizophrenic individuals with bipolar 1st-degree relatives – analysis of 2 pedigrees. J. Clin. Psychiatry 51, 97–101.
Psychiatric GWAS Consortium for Major Depressive Disorder. (2012). A mega-analysis of genome-wide association studies for major depressive disorder. Mol. Psychiatry. doi:10.1038/mp.2012.21. [Epub ahead of print].
Purcell, S. M., Wray, N. R., Stone, J. L., Visscher, P. M., O’Donovan, M. C., Sullivan, P. F., Sklar, P., Ruderfer, D. M., McQuillin, A., Morris, D. W., O’Dushlaine, C. T., Corvin, A., Holmans, P. A., Macgregor, S., Gurling, H., Blackwood, D. H. R., Craddock, N. J., Gill, M., Hultman, C. M., Kirov, G. K., Lichtenstein, P., Muir, W. J., Owen, M. J., Pato, C. N., Scolnick, E. M., St Clair, D., Williams, N. M., Georgieva, L., Nikolov, I., Norton, N., Williams, H., Toncheva, D., Milanova, V., Thelander, E. F., Sullivan, P., Kenny, E., Quinn, E. M., Choudhury, K., Datta, S., Pimm, J., Thirumalai, S., Puri, V., Krasucki, R., Lawrence, J., Quested, D., Bass, N., Crombie, C., Fraser, G., Kuan, S. L., Walker, N., McGhee, K. A., Pickard, B., Malloy, P., Maclean, A. W., Van Beck, M., Pato, M. T., Medeiros, H., Middleton, F., Carvalho, C., Morley, C., Fanous, A., Conti, D., Knowles, J. A., Ferreira, C. P., Macedo, A., Azevedo, M. H., Kirby, A. N., Ferreira, M. A. R., Daly, M. J., Chambert, K., Kuruvilla, F., Gabriel, S. B., Ardlie, K., and Moran, J. L. (2009). Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature 460, 748–752.
Reich, T., James, J. W., and Morris, C. A. (1972). The use of multiple thresholds in determining the mode of transmission of semi-continuous traits. Ann. Hum. Genet. 36, 163–184.
Ripke, S., Sanders, A. R., Kendler, K. S., Levinson, D. F., Sklar, P., Holmans, P. A., Lin, D. Y., Duan, J., Ophoff, R. A., Andreassen, O. A., Scolnick, E., Cichon, S., St Clair, D., Corvin, A., Gurling, H., Werge, T., Rujescu, D., Blackwood, D. H., Pato, C. N., Malhotra, A. K., Purcell, S., Dudbridge, F., Neale, B. M., Rossin, L., Visscher, P. M., Posthuma, D., Ruderfer, D. M., Fanous, A., Stefansson, H., Steinberg, S., Mowry, B. J., Golimbet, V., De Hert, M., Jonsson, E. G., Bitter, I., Pietilainen, O. P., Collier, D. A., Tosato, S., Agartz, I., Albus, M., Alexander, M., Amdur, R. L., Amin, F., Bass, N., Bergen, S. E., Black, D. W., Borglum, A. D., Brown, M. A., Bruggeman, R., Buccola, N. G., Byerley, W. F., Cahn, W., Cantor, R. M., Carr, V. J., Catts, S. V., Choudhury, K., Cloninger, C. R., Cormican, P., Craddock, N., Danoy, P. A., Datta, S., de Haan, L., Demontis, D., Dikeos, D., Djurovic, S., Donnelly, P., Donohoe, G., Duong, L., Dwyer, S., Fink-Jensen, A., Freedman, R., Freimer, N. B., Friedl, M., Georgieva, L., Giegling, I., Gill, M., Glenthoj, B., Godard, S., Hamshere, M., Hansen, M., Hansen, T., Hartmann, A. M., Henskens, F. A., Hougaard, D. M., Hultman, C. M., Ingason, A., Jablensky, A. V., Jakobsen, K. D., Jay, M., Jurgens, G., Kahn, R. S., Keller, M. C., Kenis, G., Kenny, E., Kim, Y., Kirov, G. K., Konnerth, H., Konte, B., Krabbendam, L., Krasucki, R., Lasseter, V. K., Laurent, C., Lawrence, J., Lencz, T., Lerer, F. B., Liang, K. Y., Lichtenstein, P., Lieberman, J. A., Linszen, D. H., Lönnqvist, J., Loughland, C. M., Maclean, A. W., Maher, B. S., Maier, W., Mallet, J., Malloy, P., Mattheisen, M., Mattingsdal, M., McGhee, K. A., McGrath, J. J., McIntosh, A., McLean, D. E., McQuillin, A., Melle, I., Michie, P. T., Milanova, V., Morris, D. W., Mors, O., Mortensen, P. B., Moskvina, V., Muglia, P., Myin-Germeys, I., Nertney, D. A., Nestadt, G., Nielsen, J., Nikolov, I., Nordentoft, M., Norton, N., Nöthen, M. M., O’Dushlaine, C. T., Olincy, A., Olsen, L., O’Neill, F. A., Orntoft, T. F., Owen, M. J., Pantelis, C., Papadimitriou, G., Pato, M. T., Peltonen, L., Petursson, H., Pickard, B., Pimm, J., Pulver, A. E., Puri, V., Quested, D., Quinn, E. M., Rasmussen, H. B., Réthelyi, J. M., Ribble, R., Rietschel, M., Riley, B. P., Ruggeri, M., Schall, U., Schulze, T. G., Schwab, S. G., Scott, R. J., Shi, J., Sigurdsson, E., Silverman, J. M., Spencer, C. C., Stefansson, K., Strange, A., Strengman, E., Stroup, T. S., Suvisaari, J., Terenius, L., Thirumalai, S., Thygesen, J. H., Timm, S., Toncheva, D., van den Oord, E., van Os, J., van Winkel, R., Veldink, J., Walsh, D., Wang, A. G., Wiersma, D., Wildenauer, D. B., Williams, H. J., Williams, N. M., Wormley, B., Zammit, S., Sullivan, P. F., O’Donovan, M. C., Daly, M. J., and Gejman, P. V. Schizophrenia Psychiatric Genome-Wide Association Study (GWAS) Consortium. (2011). Genome-wide association study identifies five new schizophrenia loci. Nat. Genet. 43, 969–976.
Sklar, P., Ripke, S., Scott, L. J., Andreassen, O. A., Cichon, S., Craddock, N., Edenberg, H. J., Nurnberger, J. I., Rietschel, M. Jr., Blackwood, D., Corvin, A., Flickinger, M., Guan, W., Mattingsdal, M., McQuillin, A., Kwan, P., Wienker, T. F., Daly, M., Dudbridge, F., Holmans, P. A., Lin, D., Burmeister, M., Greenwood, T. A., Hamshere, M. L., Muglia, P., Smith, E. N., Zandi, P. P., Nievergelt, C. M., McKinney, R., Shilling, P. D., Schork, N. J., Bloss, C. S., Foroud, T., Koller, D. L., Gershon, E. S., Liu, C., Badner, J. A., Scheftner, W. A., Lawson, W. B., Nwulia, E. A., Hipolito, M., Coryell, W., Rice, J., Byerley, W., McMahon, F. J., Schulze, T. G., Berrettini, W., Lohoff, F. W., Potash, J. B., Mahon, P. B., McInnis, M. G., Zollner, S., Zhang, P., Craig, D. W., Szelinger, S., Barrett, T. B., Breuer, R., Meier, S., Strohmaier, J., Witt, S. H., Tozzi, F., Farmer, A., McGuffin, P., Strauss, J., Xu, W., Kennedy, J. L., Vincent, J. B., Matthews, K., Day, R., Ferreira, M. A., O’Dushlaine, C., Perlis, R., Raychaudhuri, S., Ruderfer, D., Hyoun, P. L., Smoller, J. W., Li, J., Absher, D., Thompson, R. C., Meng, F. G., Schatzberg, A. F., Bunney, W. E., Barchas, J. D., Jones, E. G., Watson, S. J., Myers, R. M., Akil, H., Boehnke, M., Chambert, K., Moran, J., Scolnick, E., Djurovic, S., Melle, I., Morken, G., Gill, M., Morris, D., Quinn, E., Muhleisen, T. W., Degenhardt, F. A., Mattheisen, M., Schumacher, J., Maier, W., Steffens, M., Propping, P., Nöthen, M. M., Anjorin, A., Bass, N., Gurling, H., Kandaswamy, R., Lawrence, J., McGhee, K., McIntosh, A., McLean, A. W., Muir, W. J., Pickard, B. S., Breen, G., St Clair, D., Caesar, S., Gordon-Smith, K., Jones, L., Fraser, C., Green, E. K., Grozeva, D., Jones, I. R., Kirov, G., Moskvina, V., Nikolov, I., O’Donovan, M. C., Owen, M. J., Collier, D. A., Elkin, A., Williamson, R., Young, A. H., Ferrier, I. N., Stefansson, K., Stefansson, H., Thornorgeirsson, T., Steinberg, S., Gustafsson, O., Bergen, S. E., Nimgaonkar, V., Hultman, C., Landén, M., Lichtenstein, P., Sullivan, P., Schalling, M., Osby, U., Backlund, L., Frisén, L., Langstrom, N., Jamain, S., Leboyer, M., Etain, B., Bellivier, F., Petursson, H., Sigur Sson, E., Müller-Mysok, B., Lucae, S., Schwarz, M., Schofield, P. R., Martin, N., Montgomery, G. W., Lathrop, M., Oskarsson, H., Bauer, M., Wright, A., Mitchell, P. B., Hautzinger, M., Reif, A., Kelsoe, J. R., Purcell, S. M., Psychiatric GWAS Consortium Bipolar Disorder Working Group. (2011). Large-scale genome-wide association analysis of bipolar disorder identifies a new susceptibility locus near ODZ4. Nat. Genet. 43, 977–983.
Sullivan, P. F., Kendler, K. S., and Neale, M. C. (2003). Schizophrenia as a complex trait – evidence from a meta-analysis of twin studies. Arch. Gen. Psychiatry 60, 1187–1192.
Sullivan, P. F., Neale, M. C., and Kendler, K. S. (2000). Genetic epidemiology of major depression: review and meta-analysis. Am. J. Psychiatry 157, 1552–1562.
Svensson, A. C., Lichtenstein, P., Sandin, S., and Hultman, C. M. (2007). Fertility of first-degree relatives of patients with schizophrenia: a three generation perspective. Schizophr. Res. 91, 238–245.
Van Snellenberg, J. X., and de Candia, T. (2009). Meta-analytic evidence for familial coaggregation of schizophrenia and bipolar disorder. Arch. Gen. Psychiatry 66, 748–755.
Varma, S. L., Zain, A. M., and Singh, S. (1997). Psychiatric morbidity in the first-degree relatives of schizophrenic patients. Am. J. Med. Genet. 74, 7–11.
Visscher, P. M., Goddard, M. E., Derks, E. M., and Wray, N. R. (2012). Evidence-based psychiatric genetics, AKA the false dichotomy between common and rare variant hypotheses. Mol. Psychiatry 17, 474–485.
Visscher, P. M., Hill, W. G., and Wray, N. R. (2008). Heritability in the genomics era – concepts and misconceptions. Nat. Rev. Genet. 9, 255–266.
Wray, N. R., Lee, S. H., and Kendler, K. S. (2012). Impact of diagnostic misclassification on estimation of genetic correlations using genome-wide genotypes. Eur. J. Hum. Genet. 20, 668–674.
Yip, B. H., Bjork, C., Lichtenstein, P., Hultman, C. M., and Pawitan, Y. (2008). Covariance component models for multivariate binary traits in family data analysis. Stat. Med. 27, 1086–1105.
Appendix
Estimation of Heritabilities and Genetic Correlations
(I) Relatives are affected with the same disorder as probands.
We define K as the lifetime probability of disease (or prevalence of a disease) in the population. Under the liability threshold model, those with phenotypic liability, Z ∼ N(0,1), greater than the threshold T are diseased such that distribution p(Z > T) = K. Falconer (1965) in his Model 1 showed that the threshold in relatives (TR) is expected to be
where aR is the additive genetic relationship between the relatives i is the mean liability of the diseased group in the population, calculated as i = y/K where y is the height of the normal curve at threshold T. Since TR can be calculated from the observed probability of disease in the relatives, KR (and KR > K, therefore TR < T), heritability can be estimated as
Falconer (1965) derived the approximate standard error of the estimate of the heritability,
where the variance of the estimate of the truncation threshold is V(T) = K2/y2 and likewise for V(TR).
Reich et al. (1972), showed that although Eq. A1 accounts for the mean liability of the relative group given the affected probands, it does not account for the reduced variance in this group compared to the general population which results from the conditioning on the proband disease status. Therefore, the equality in Eq. A1 needs to be standardized to return it to a N(0,1) distribution,
Rearrangement of this equation provides an estimate of the heritability of liability based on the directly measurable parameters of population prevalence of disease (K) and the recurrence risk ratio in relatives λR = KR/K.
We use Eq. A4 for estimation of heritability and Eq. A2 for estimation of an approximate standard error (using the h2 from Eq. A4 for situations where the relatives and probands have the same disorder and the cohort of relatives are associated with only one affected proband. These methods are generalized for different circumstances below (II)–(V).
(II) Offspring affected and both parents affected – offspring and parents have the same disorder
s.e from Eq. A2 with aR set to 1.
(III) Relatives have one disease (c) probands have another (f).
We assumed that the heritability of diseases c and f are and respectively, and the genetic correlation between them is rcf, then eqs A3 and A4 generalize to
(IV) Offspring have one disorder (c) and both parents have the same but other disorder (f).
and s.e (rcf hc hf) as Eq. A5 but with aR set equal to 1. Since the scenario is relatively rare the resulting estimates have high standard errors and so have little impact on a weighted average with the estimate from a single affected parent.
(V) Offspring have disorder (c), one parent also has disorder c but the other parent has another disorder (f).
In this case
Solving for rcf hc hf creates and expression dependent on so estimates of genetic correlation from this type of data have not been achieved.
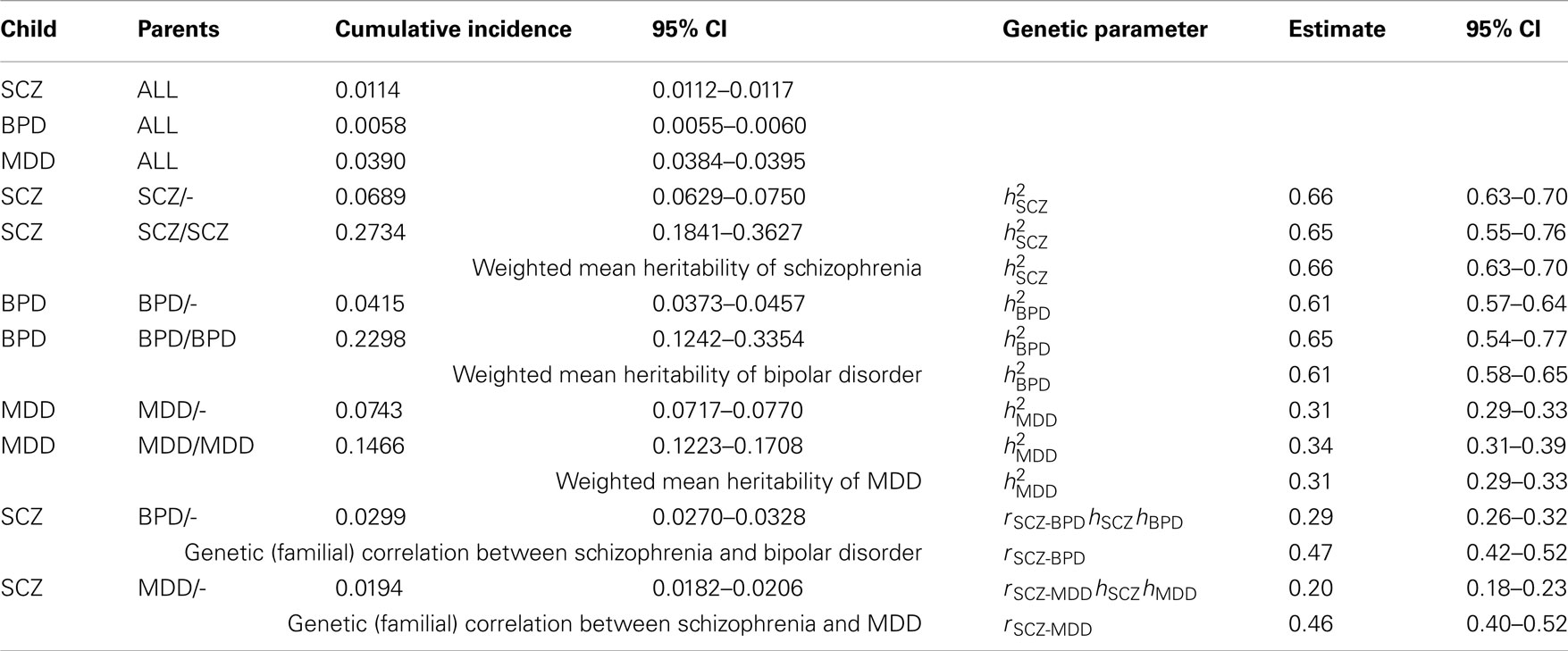
Table A1. Estimates of genetic parameters using cumulative incidences to age 51 estimated from national records of the Danish population.
Confidence Intervals of Ratios
95% CI of recurrence risk ratio calculated from 95% CI of numerator (x1 ± s1) and denominator (x2 ± s2):
Weighting by Sampling Variance
When there are n estimates of the same parameter, i.e., x1.. xn each with standard error si for i = 1,…n. Then the overall estimate x ± s weights the different estimates by their sampling variance,
Estimates of Genetic Correlations
For completeness, we provide the estimates of genetic correlations calculated from the Danish summary data. Based on our simulation results these estimates are consistent with a genetic correlation greater than zero. However, we believe it is not possible to separate out the impact of the double counting of diagnoses. In addition, these estimates may be inflated by contributions of common environmental factors. For these reasons we do not consider the estimates to be reliable.
Firstly, for comparison the estimate of the genetic correlation between schizophrenia and bipolar disorder reported in the Swedish study (Lichtenstein et al., 2009) was 0.60 (no 95% CI reported), whereas based on the summary statistics from that study we estimated the genetic correlation to be 0.47 (95% CI 0.42–0.52).
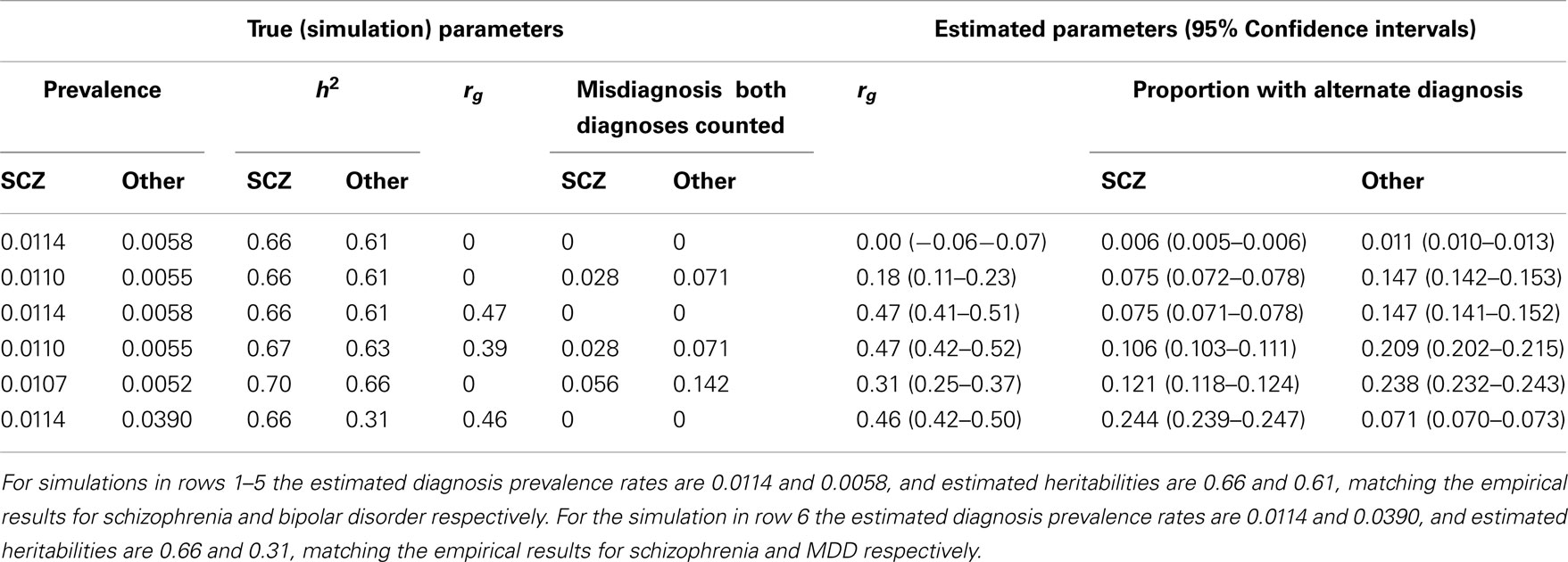
Table A2. Simulation results with simulation parameters selected to generate estimated diagnosis prevalence rates and heritabilities based on cumulative incidences up to 51 years.
In preliminary analyses for the Gottesman et al. (2010) article the authors calculated cumulative incidences up to age 51 and for a different (but overlapping) set of relative types. Here we use the previously unpublished estimates to age 51 because, firstly, this set allowed us to estimate the genetic correlation between schizophrenia and MDD, which was not possible from the published estimates. Secondly, while the published results allowed us to estimate the genetic correlation between schizophrenia and bipolar disorder the estimates were based on cumulative incidence of one disorder in children where both parents had the other disorder. In contrast, the unpublished results allowed us to estimate this genetic correlation from cumulative incidence of schizophrenia in children where one parent has bipolar disorder; since this event is more prevalent the resulting estimate of the genetic correlation has a lower standard error. Results are presented in Table A1.
Simulations that generate prevalence rates and heritabilities consistent with the empirical estimates based on the summary data to age 51 years are presented in Table A2. Simulation scenario in row 3 shows that in the absence of random misdiagnosis but with a true genetic correlation of 0.47 between schizophrenia and bipolar disorder, that 7.5% of those with a diagnosis of schizophrenia and 14.7% of those with a diagnosis of bipolar disorder would qualify also for the diagnosis of the other disorder, demonstrating that dual diagnosis is consistent with a positive correlation between the disorders. Simulation scenarios in rows 4 and 5 consider the genetic correlation resulting under random misdiagnosis/double counting of disorders. Simulation scenario 6 shows the parallel scenario to the row 3 simulation, but is based on empirical estimates for schizophrenia and MDD. A true genetic correlation that matches the empirical estimate of 0.42, was consistent with 24% of those with schizophrenia and 7.1% of those diagnosed with major depression would also be diagnosed with the other disorder. In simulations, we were unable to generate the empirical estimate of the genetic correlation by manipulating the misdiagnosis rate and heritability of schizophrenia while assuming the true genetic correlation and the MDD misdiagnosis rate to be zero. However, to report 0.42 as the genetic correlation between SCZ and MDD would be misleading as we cannot disentangle contributions of the effects of common environment.
Keywords: Danish National Registry, cumulative incidence, risk to relatives
Citation: Wray NR and Gottesman II (2012) Using summary data from the Danish National Registers to estimate heritabilities for schizophrenia, bipolar disorder, and major depressive disorder. Front. Gene. 3:118. doi: 10.3389/fgene.2012.00118
Received: 20 April 2012; Accepted: 07 June 2012;
Published online: 02 July 2012.
Edited by:
Ellen W. Demerath, University of Minnesota, USAReviewed by:
Audrey C. Choh, Wright State University, USAPaul Lichtenstein, Karolinska Institutet, Sweden
Alastair Cardno, University of Leeds, UK
Copyright: © 2012 Wray and Gottesman. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Naomi R. Wray, The University of Queensland, Queensland Brain Institute, Building 79, St Lucia, Brisbane, QLD 4072, Australia. e-mail:bmFvbWkud3JheUB1cS5lZHUuYXU=

