Monotonicity is a key feature of genotype-phenotype maps

It was recently shown that monotone gene action, i.e., order-preservation between allele content and corresponding genotypic values in the mapping from genotypes to phenotypes, is a prerequisite for achieving a predictable parent-offspring relationship across the whole allele frequency spectrum. Here we test the consequential prediction that the design principles underlying gene regulatory networks are likely to generate highly monotone genotype-phenotype maps. To this end we present two measures of the monotonicity of a genotype-phenotype map, one based on allele substitution effects, and the other based on isotonic regression. We apply these measures to genotype-phenotype maps emerging from simulations of 1881 different 3-gene regulatory networks. We confirm that in general, genotype-phenotype maps are indeed highly monotonic across network types. However, regulatory motifs involving incoherent feedforward or positive feedback, as well as pleiotropy in the mapping between genotypes and gene regulatory parameters, are clearly predisposed for generating non-monotonicity. We present analytical results confirming these deep connections between molecular regulatory architecture and monotonicity properties of the genotype-phenotype map. These connections seem to be beyond reach by the classical distinction between additive and non-additive gene action.

Introduction

Quantitative genetics is the major theoretical foundation for genetic studies in production biology, evolutionary biology, and biomedicine. A core concept in quantitative genetics is the genotypic value, the mean observed phenotype for a given genotype. It constitutes the basis for the genotype-to-phenotype (GP) map concept. The shape of a given GP map is typically described by the classical gene action terms: additivity, dominance, and epistasis. Together with genotype frequencies in a given population, the GP map is the basis for decomposing observed phenotypic variance into environmental variance and genetic variance components including additive variance, dominance variance and epistatic variance. This provides the basis for a very successful theory when it comes to predicting selection response and breeding values (Falconer and Mackay, 1996; Lynch and Walsh, 1998) and more recent statistical genetics methods for mapping Quantitative Trait Loci (QTL) (Neale et al., 2008). Quantitative genetics thus provides a mature machinery for predicting the population level consequences of a given GP map, but in order to understand several generic genetic phenomena there is a stated need for new tools for disclosing how the shape of the GP map is determined by underlying biology (Jaeger et al., 2012; Moore, 2012; Gjuvsland et al., 2013).

One such phenomenon is the resemblance between parents and offspring. An explanation in quantitative genetic terms is that the additive variance (V_A) makes up a substantial part of the phenotypic (V_P) and genetic variance (V_G). Hill et al. (2008) showed that in populations with extreme allele frequencies, high V_A/V_G ratios will arise regardless of the shape of the GP map. However, for populations with intermediate allele frequencies a much wider range of V_A/V_G ratios is observed (Wang et al., 2013). In such populations, high V_A/V_G ratios cannot be fully accounted for without considering properties of the GP map. Gjuvsland et al. (2011) showed that a key feature of GP maps that give high ratios of additive to genotypic variance (V_A/V_G), is a monotone (or order-preserving) relation between gene content (the number of alleles of a given type) and phenotype. This led to the hypothesis that the regulatory circuitry of sexually reproducing organisms predominantly predisposes for highly monotone genotype-phenotype maps.

Here we address the above hypothesis by a two-step approach. First we provide methods and software tools for measuring monotonicity of generic GP maps (i.e., sets of genotypic values). Then we use these tools on the data generated by an extensive simulation study of a broad collection of gene regulatory network models. In these network models the steady state expression levels serve as phenotypes and genetic variation is introduced through parameters describing maximal production rates and the shape of the gene regulation function. Such causally cohesive genotype-phenotype (cGP) models [see Gjuvsland et al. (2013) and references therein] allow us to identify relationships between regulatory network architecture and properties of the resulting GP maps.

Our results confirm the prediction that the GP maps arising from a wide range of gene regulatory network motifs are in general highly monotone. In addition we show through numerical as well as mathematical analysis that regulatory motifs involving incoherent feed-forward or positive feedback stand out in their capacity to generate non-monotonicity. These relationships between molecular regulatory architecture and properties of the genotype-phenotype map—of substantial relevance to functional genomics in general—are beyond reach by the standard distinction between additive and non-additive gene action.

Our approach can be applied to cGP models of a wide range of biological systems at any level of model complexity. It opens for a systematic study of the monotonicity properties of molecular regulatory structures underlying the whole spectrum of physiological regulation. This suggests that the concept of monotonicity of GP maps can be used to build theory about heredity phrased in terms of molecular mechanism, something which standard genetic concepts and approaches appear to be incapable of.

Models and Methods

Background on Monotonicity of GP Maps

To ease understanding we provide a brief recapitulation of the concept of monotonicity (or order-preservation) in GP maps introduced in (Gjuvsland et al., 2011). We consider a diploid genetic model with N biallelic loci (alleles indexed 1 and 2) underlying a quantitative phenotype. A genotype at a single locus k is denoted by g_k ∈ {11, 12, 22}. In the case of two loci k and l there are 9 possible genotypes g_kl = g_kg_l ∈ {1111, 1112, 1122, 1211, …, 2212, 2222}. The general N loci genotype space Γ contains 3^N genotypes g₁g₂ … g_N (in condensed notation g_1:N) constructed by concatenating single locus genotypes, Γ = {g₁g₂ … g_N | g_k ∈ {11, 12, 22}, k = 1, 2, …, N}. For any locus k, the genotypic background, i.e., the allele composition of all loci except k, is g^(k) = g₁g₂ … g_{k − 1} g_{k + 1} … g_N = g_{1: k − 1} g_{k + 1: N}. For example, if N = 4 then g⁽²⁾ = 112212 means that the genotypes of locus 1, 3, and 4 are 11, 22, and 12, respectively. We use the straightforward notation g₁ g₂ … g_{k − 1} 11g_{k + 1} … g_N = g_{1:k − 1} 11g_{k + 1: N} to indicate a genotype where g_k = 11 while the background genotype is arbitrary. We will also use the compressed notation 11g^(k) (or generally g_kg^(k)).

We use the 2-allele content (i.e., the number of 2-alleles) of genotypes to define a partial order on the genotype space Γ (see Figure 1, left panel for an illustration). For a particular locus k we order the three genotypes sharing the same background genotype g_{1: k − 1} g_{k + 1: N} as follows,

$\begin{array}{cc}{g}_{1:k-1}11g_{k+1:N}<g_{1:k-1}12g_{k+1:N}<g_{1:k-1}22g_{k+1:N}& (1)\end{array}$

FIGURE 1

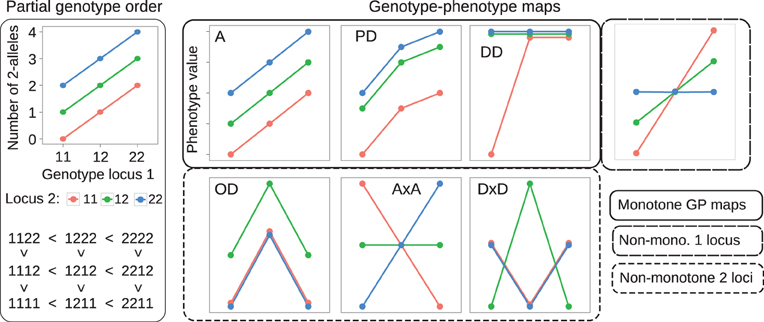
Figure 1. Examples of partial genotype order and genotype-phenotype maps. Left panel: The allele content defines a partial order on genotype space. A two-locus example is shown. The plot at the top displays the genotype at locus 1 (x-axis) and locus 2 (color) vs. the total number of 2-alleles (y-axis) in the two-locus genotype. The resulting partial ordering of genotypes is shown below. Right panel: Each lineplot shows the 9 genotypic values (y-axis) for a single GP map, coding of genotype are the same as in the left panel. GP maps that preserve the partial order of genotypes are called monotone. Examples shown are an intra- and interlocus additive map (A), a map showing partial dominance at both loci (PD), and duplicate dominant (DD) epistasis (see Table 1 in Phillips, 1998). GP maps that break the partial order of genotypes are called non-monotone, examples shown are pure overdominance at both loci (OD), additive-by-additive epistasis (A × A) and dominance-by-dominance epistasis (D × D). The rightmost plot shows a GP map that is monotone w.r.t. locus 1, but non-monotone w.r.t. locus 2.

We call this the partial genotype order relative to locus k, and it defines a strict partial order on Γ.

A genotype-phenotype map is a mapping G that assigns to each genotype g ∈ Γ a real-valued genotypic value G(g) (the mean trait value for a given genotype). We define monotonicity of G in terms of how it transforms the partial genotype order to the algebraic order of the genotypic values G(g). Without loss of generality we assume that the allele indexes at each locus have been chosen such that G(1111 … 11) is the smallest of all homozygote genotypic values. We call a genotype-phenotype map G monotone or order-preserving with respect to locus k if it preserves the partial genotype order relative to locus k, i.e., if,

$\begin{array}{cc}\begin{array}{l}G(g_{1:k-1}11g_{k+1:N})\le G(g_{1:k-1}12g_{k+1:N})\\ \le G(g_{1:k-1}22g_{k+1:N})\end{array}& (2)\end{array}$

for all genetic backgrounds of locus k. By allowing non-strict inequalities we include GP maps showing complete dominance and complete magnitude epistasis (Weinreich et al., 2005) in the class of order-preserving GP maps. Conversely we call a GP map non-monotone or order-breaking with respect to locus k if it does not preserve the partial genotype order relative to locus k for all backgrounds. Figure 1 (right panel) shows classical dominance and epistasis patterns, categorized into monotone and non-monotone GP maps.

Statistical Decomposition of Genotype-Phenotype Maps

Given a genotype-phenotype map G as described above and a corresponding vector of genotype frequencies f in a population, quantitative genetic provides methods for orthogonal decomposition of genotypic values and resulting genetic variance in the population into additive and non-additive (dominance and epistasis) components (Lynch and Walsh, 1998). We performed such statistical decomposition with the function linearGPmapanalysis in the R package noia (http://cran.r-project.org/package=noia; Le Rouzic and Alvarez-Castro, 2008) version 0.94.1. We assumed an idealized population where all genotype frequencies are equal (1/3^N). In such a hypothetical population the NOIA (Alvarez-Castro and Carlborg, 2007) statistical and functional formulations and the unweighted regression model proposed by Cheverud and Routman (1995) are equivalent. Furthermore, the decomposition of genotypic values is equivalent to decomposing G into a sum of additive and non-additive GP maps, and the genetic variance in this case is simply the variance of the 3^N genotypic values in G. We used the NOIA statistical formulation to decompose a GP map G into its additive and non-additive components, and computed the ratio of additive to total genetic variance V_A/V_G as a measure of how well the additive component describes the original GP map. In case of the illustrative GP maps depicted in Figure 1, this gives V_A/V_G = 1 for the fully additive GP map A, and V_A/V_G = 0 for the pure overdominance (OD) and the pure epistasis (Cheverud and Routman, 1996) maps A × A and D × D.

Gene Regulatory Network Models

Gene expression in eukaryotes is controlled through gene regulatory networks involving numerous regulatory mechanisms [see e.g., Latchman (2005), for details]. Modeling of such gene regulatory networks is well-established, and available modeling frameworks range from coarse-grained descriptions of the topology of genome-wide networks to very detailed mechanistic models describing the dynamics of small networks (De Jong, 2002; Schlitt and Brazma, 2007; Karlebach and Shamir, 2008). In line with a large number of authors we used ordinary differential equations (ODEs) to study a family of generic gene regulatory network models containing three diploid genes X₁, X₂, and X₃, organized as a regulatory system where the rate of expression of each gene can be regulated by the expression level of one or both of the other genes. The wiring of the system is described by a 3 × 3 connectivity matrix A with elements A_kl ∈ {−1, 0, 1}. The signs of the elements of A describe the mode of regulation, A_kl = 0 indicates that X_l is not a regulator of X_k, if A_kl = 1 then X_l is an activator of X_k, and if A_kl = −1 then X_l is a repressor of X_k. Gene regulatory systems are often laid out visually as signed directed graphs. There is a one-to-one correspondence between a connectivity matrix and a signed directed graph, two examples are illustrated in Figure 4. We used the sigmoid formalism (Mestl et al., 1995; Plahte et al., 1998) in the diploid form (Omholt et al., 2000) where the expression the two alleles of gene k is described by the following ODEs,

$\begin{array}{cc}\begin{array}{l}{\dot{x}}_{k1}={\alpha }_{k1}{R}_{k1}(y_1,y_2,y_3)-{\gamma }_{k1}{x}_{k1},\\ {\dot{x}}_{k2}={\alpha }_{k2}{R}_{k2}(y_1,y_2,y_3)-{\gamma }_{k2}{x}_{k2},\\ y_k=x_{k1}+x_{k2},k=1,2,3.\end{array}& (3)\end{array}$

Here α_ki is the maximal production rate for allele i of gene X_k, γ_ki is the decay rate, while R_ki is the gene regulation function (dose-response function). If X_k has no regulators, we assume production is always switched on i.e., R_ki = 1. If X_k has a single regulator X_l, the gene regulation function is given as R_ki(y_l) = S(y_l, θ_lki, p_lki), where S(y, θ, p) = y^p/(y^p + θ^p) if X_l is an activator and S(y, θ, p) = 1 − y^p/(y^p + θ^p) if it is a repressor. In both cases the parameter θ_lki gives the amount of regulator needed to get 50% of maximal production rate, and p_lki determines the steepness of the response. In the case of two regulators X_l and X_j we set R_ki(y_l, y_j) = S(y_l, θ_lki, p_lki)S(y_j, θ_jki, p_jki), corresponding to the Boolean AND function. Modeling transcription regulation by means of Hill functions and Boolean composition has a long tradition in modeling of gene regulation and is widely used.

With three genes and up to two regulators per gene the number of possible connectivity matrices is 6859. We further required that the system is connected, and that X₃ is downstream to both X₁ and X₂ so either X₁ and X₂ both regulate X₃ directly (A₃₁A₃₂ ≠ 0), or one of them regulates X₃ directly and the other one indirectly (A₃₁A₁₂ ≠ 0 or A₃₂A₂₁ ≠ 0). This reduces the number of distinct connectivity matrices to 3724. Finally, we identified pairs of matrices that are symmetric with respect to interchanging X₁ and X₂ and picked just one matrix from each pair. The resulting 1881 connectivity matrices were used for our gene regulatory simulations.

Identifying Feedback Loops and Feedforward Motifs

Feedback and feedforward motifs appear recurrently as regulatory building blocks in transcription networks across all living organisms. These network motifs have several characteristic features (Alon, 2007), negative feedback can for example accommodate fast transcriptional responses and homeostasis, while positive feedbacks are utilized as biological switches. We went through all 1881 gene regulatory models and extracted information about their feedback and feedforward loop characteristics from their connectivity matrices. For each system we computed three autoregulatory feedback loop products FL₁ = A₁₁, FL₂ = A₂₂, FL₃ = A₃₃, three two-gene feedback loop products: FL₁₂ = A₂₁A₁₂, FL₁₃ = A₃₁ A₁₃, FL₂₃ = A₂₃ A₃₂ and two three-gene feedback loop products: FL₁₂₃ = A₃₂ A₂₁ A₁₃, FL₂₁₃ = A₃₁ A₁₂A₂₃. Non-zero loop products indicate that the system contains the corresponding feedback loop, and the sign of the loop product gives the sign of the feedback loop. We also computed the products for two feedforward motifs: FFL₃₂ = A₃₂(A₃₁ A₁₂), FFL₃₁ = A₃₁ (A₃₂A₂₁). Again non-zero products indicate that the system contains the corresponding feedforward motif, a positive value corresponds to a coherent feedforward while a negative value indicates incoherent feedforward. Figure 4 depicts the connectivity matrix and the signed digraphs of a system with a positive feedback loop as well as a system with incoherent feedforward. Spreadsheet S1 contains adjacency matrices and loop products for all 1881 motifs.

Gene Regulatory Network Simulations

The simulation were performed with the Python package cgptoolbox (http://github.com/jonovik/cgptoolbox), using the sigmoidmodel submodule, which contains an implementation of the gene regulatory network model (Equation 3) and the connectivity matrix A. A similar simulation setup is found in Gjuvsland et al. (2011) together with a discussion of gene regulation functions and the genotype-parameter map in molecular terms. We compared two different types of genotype-to-parameter maps:

• Genotype to parameter map without pleiotropy: biallelic genotypic variation for all three loci was introduced through the maximal production rates α_ki. For each Monte Carlo simulation the allelic parameter values were sampled from U(100, 200).
• Genotype to parameter map with pleiotropy: allelic parameter values were sampled for maximal production rates α_ki (sampled from U(100, 200)), regulation thresholds θ_lki (sampled from U(20, 40)), and regulation steepnesses p_lki (sampled from U(1, 10)).

All decay rates γ_ki were set equal to 10. We assembled parameter sets for all 27 diploid genotypes, and for each genotypic parameter set the system of Equation 3 was integrated numerically until convergence to a stable state. The equilibrium value of y₃ was recorded as phenotype. Datasets where the system failed to converge for one or more genotypes were discarded. For each of the 1881 motifs we performed 1000 Monte Carlo simulations.

Some Monte Carlo simulations lead to very little phenotypic variation, in the sense that the span between the largest and smallest of the 27 genotypic values was small. In order to avoid artifacts arising from the numeric ODE solver tolerance, these essentially flat GP maps were discarded. Further analysis of monotonicity and variance components were only performed on GP maps where the absolute range (maximum genotypic value – minimum genotypic value) and relative range (absolute range/mean genotypic value) were both > 0.01.

Results

Measuring Monotonicity of GP Maps

In the following we present two numerical measures for quantifying monotonicity in a GP map G with N biallelic loci. The first quantifies the monotonicity for individual loci by comparing negative and positive allele substitution effects before weighting the individual loci into an overall measure. The second utilizes isotonic regression to quantify the distance between G and the closest fully monotone GP map.

Measure 1: quantifying non-monotonicity by substitution effects

We first develop a measure of monotonicity based on the effects of substituting a single allele at locus k,

$\begin{array}{cc}\begin{array}{l}{s}^1(g^{(k)})=G(g_{1:k-1}22g_{k+1:N})-G(g_{1:k-1}12g_{k+1:N}),\\ s^2(g^{(k)})=G(g_{1:k-1}12g_{k+1:N})-G(g_{1:k-1}11g_{k+1:N}),\end{array}& (4)\end{array}$

while keeping the background genotype g^(k) = g_{1: k + 1}g_{k + 1: N} fixed. Monotonicity as defined by Equation 2 is equivalent to sⁱ (g^(k)) ≥ 0 for i = 1, 2 across all genetic backgrounds of locus k. By taking into account also the magnitude of the substitution effects we can quantify the deviation from strict monotonicity. We start with the set S^k = {sⁱ(g^(k))} of single allele substitution effects for locus k for i = 1, 2 and across all genotypic backgrounds g^(k). The total number of elements in S^k thus becomes 2· 3^{N − 1}, and we split the set into two disjoint subsets reflecting their sign; S^k₊ = {sⁱ(g^(k)) ∈ S^k | sⁱ (g^(k)) > 0} and S^k₋ = {sⁱ (g^(k)) ∈ S^k | sⁱ (g^(k)) < 0}. We compute the sum of positive substitution effects and the sum of absolute values of negative substitution effects,

$\begin{array}{cc}{P}_k={\displaystyle \sum _{S_{+}^k}{s}^i}(g^{(k)}),& (5)\end{array}$

$N_k={\displaystyle \sum _{S_{-}^k}\left|s^i(g^{(k)})\right|},$

and let T_k = P_k + N_k denote the overall sum of absolute substitution effects. We then define the degree to which the GP map G is monotone with respect to locus k by,

$\begin{array}{cc}{m}_k=\frac{|P_k-N_k|}{T_k}=\frac{\left|{\displaystyle \sum _{g^{(k)}}\left(s^1(g^{(k)})+s^2(g^{(k)})\right)}\right|}{{\displaystyle \sum _{g^{(k)}}\left(|s^1(g^{(k)})|+|s^2(g^{(k)})|\right)}}.& (6)\end{array}$

The absolute value in the numerator ensures that the measure m_k is invariant with respect to the choice of indexes for the two alleles of locus k. Interchanging the numbering of the alleles leads to the mappings s¹ (g^(k)) ↦ −s²(g^(k)), s²(g^(k)) ↦ −s¹ (g^(k)), which leaves the value of m_k unchanged. By the triangle inequality m_k ≤ 1. If m_k = 1, then G is monotonic with respect to locus k, whereas m_k < 1 implies that G is order-breaking w.r.t. locus k. If m_k = 0, then the positive substitution effects equal the negative substitution effects in magnitude and we say that G is completely order-breaking w.r.t. locus k. This measure distinguishes well between the monotone and non-monotone maps in Figure 1. Clearly m₁ = m₂ = 1 for the additive map (A) and GP maps showing partial dominance and duplicate dominance epistasis. In contrast, m₁ = m₂ = 0 for the maps showing pure OD and pure epistasis (A × A and D × D).

In order to quantify the overall monotonicity of the GP map G we introduce the degree of monotonicity (m) which is a weighted mean of all m_k, where the weights reflect the relative effect size of the loci in terms of T_k,

$\begin{array}{cc}m=\frac{{\displaystyle \sum _{k=1}^N{m}_k}{T}_k}{{\displaystyle \sum _{k=1}^N{T}_k}}.& (7)\end{array}$

As shown in Figure 3A, the degree of monotonicity is accordingly 1 for the monotone maps in Figure 1 while it is 0 for the pure OD and pure epistasis maps. This definition of degree of monotonicity allows us to establish a vocabulary that is analogous to the classification of single locus dominance; i.e., a GP map is called monotone if m = 1, (partially) non-monotone if m < 1 and purely non-monotone if m = 0.

For example, the degree of monotonicity of the GP map published by Cheverud and Routman (1995), with two loci underlying 10-week body-weight (in grams) at 10 weeks in a mouse F₂ cross, may be computed as follows. After renaming the two loci (B → 1, A → 2) and indexing alleles to conform to our notation, the nine genotypic values (Table 1 in (Cheverud and Routman, 1995)) are G(1111) = 31.23, G(1112) = 34.13, G(1122) = 33.82, G(1211) = 34.89, G(1212) = 35.90, G(1222) = 36.53, G(2211) = 34.12, G(2212) = 37.95, and G(2222) = 36.84. From the line plot of this GP map (Figure 2, left panel) we find that the GP map is non-monotone with respect to both loci. Locus 1 shows marginal OD for the 11 genotype of locus 2 and locus 2 shows marginal OD for the 11 and 22 genotypes of locus 1. To compute the degree of monotonicity, we start with the set of single allele substitution effects for locus 1, S¹ = {3.66, −0.77, 1.77, 2.05, 2.71, 0.31}, and divide this into sets of negative S¹₋ = {−0.77} and positive effects S¹₊ = {3.66, 1.77, 2.05, 2.71, 0.31}. The sum N₁ of elements in S¹₊ is 10.50 and P₁ the sum of absolute values of elements in S¹₋ is 0.77, which gives T₁ = P₁ + N₁ = 11.27. From Equation 6 it follows that m₁ = 0.86. Similarly, the sets of substitution effects for locus 2 are S²₋ = {−1.11, −0.31} and S²₊ = {3.83, 0.63, 1.01, 2.90}. This gives, N₂ = 1.42, P₂ = 8.37, T₂ = 9.79, and m₂ = 0.71. Inserting values for both loci into Equation 7, the degree of monotonicity (m) of this GP map is calculated to be 0.79. This value concords well with the visual observation (Figure 2, left panel) that it does not deviate substantially from a purely monotone map.

FIGURE 2

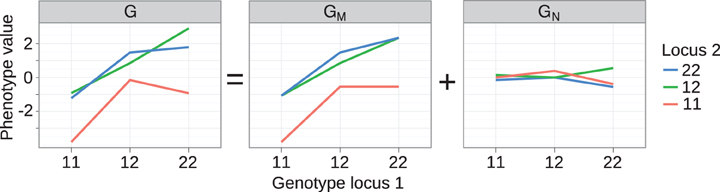
Figure 2. Decomposition of genotype-phenotye map into monotone and non-monotone components. Left panel: Genotype-phenotype map G for two loci underlying 10-week body-weight at 10 weeks in a mouse F₂ cross. The GP map shown here is equivalent to the one in the original publication [see Figure 3A in Cheverud and Routman (1995)], but we have changed indexing of loci and alleles for consistency with the notation used here. The GP map G is decomposed with isotonic regression into a (middle panel) monotone component G_M and a (right panel) non-monotone component G_N.

For random GP maps (randomly sampled genotypic values as in (Gjuvsland et al., 2011)) there is a strong positive correlation between the degree of monotonicity and the size of the additive component (V_A/V_G) (Figure 3A). A similar relationship was observed for three-locus random GP maps (Figure A1A). All GP maps in Figure 3A with m < 0.1 have V_A/V_G < 0.1. At the other end of the spectrum there is much more variation, for instance the most extreme completely monotone map (the duplicate dominant factors DD) has V_A/V_G as low as 0.375.

FIGURE 3

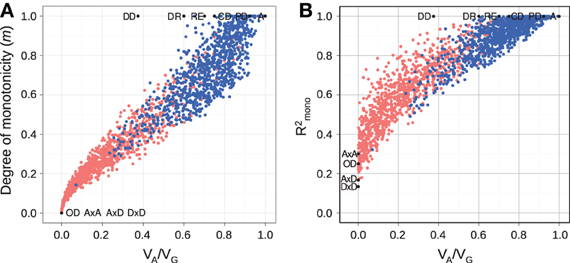
Figure 3. Measures of monotonicity vs. additivity of GP maps. Scatterplots showing V_A/V_G from unweighted regression vs. (A) degree of monotonicity (m) and (B) R²_mono from isotonic regression. Black dots correspond to the maps shown in Figure 1 together with additive-by-dominance epistasis (A × D), a map with two loci showing complete dominance (CD) and two classical epistasis types from Table 1 in Phillips (1998); duplicate recessive genes (DR) and recessive epistasis (RE). Red dots show 1000 random two-locus GP maps, while blue dots show the same 1000 GP maps after rearranging genotypic values to introduce order-preservation for 1 locus [see Model and Methods in Gjuvsland et al. (2011)].

Measure 2: quantifying monotonicity by isotonic regression

This measure quantifies the monotonicity of a particular GP map G in terms of the least-squares distance to the closest monotone map. We build on the mathematical notation introduced in section “Background on monotonicity of GP maps” where Γ is the genotype space for N biallelic loci and a GP map is a function that assigns a real-valued genotypic value G(g) to each genotype g in Γ. For any particular GP map G, we identify the monotone component of G as the map G_M which minimizes the residual variance var(G − G_M), i.e., G_M is the monotone GP map which is closest to G in the least-squares sense. For a given G the monotone component G_M is unique (Barlow and Brunk, 1972) and can be computed numerically by isotonic regression (Leeuw et al., 2009) of G subject to the partial ordering of genotypes defined in Equation 1. Furthermore, the residual G_N is orthogonal to G_M in the sense that ∑_{g ∈ Γ} G_M (g)G_N (g) = 0. This allows the orthogonal decomposition,

$\begin{array}{cc}G=G_M+G_N,& \left(8\right)\end{array}$

of a genotype-phenotype map into a monotone component G_M and a non-monotone component G_N such that var(G) = var(G_M) + var(G_N). The orthogonality property allows us to measure monotonicity of G in terms of the coefficient of determination R²_mono of the isotonic regression given by the ratio R²_mono = var(G_M)/var(G). In the case that G itself is monotone for all loci we have R²_mono = 1, while order-breaking for one or more loci will result in R²_mono < 1.

The isotonic regression approach can be illustrated in a straightforward way on the two-locus GP map provided by Cheverud and Routman (1995) (see text above and left panel of Figure 2). The partial ordering of genotypes defined by Equation 1 is illustrated in Figure 1 (left panel). By isotone regression (Leeuw et al., 2009) on this partial genotype ordering, the original GP map is decomposed into a monotone and a non-monotone component (Figure 2, middle and right panels), and the coefficient of determination (R²_mono) is 0.97.

Our simulation results for random GP maps show that R²_mono is positively correlated to the size of the additive component (Figure 3B for two-locus GPs maps and Figure A1B for three-locus GP maps) and that for a given V_A/V_G the lower bound for R²_mono is close to a straight line from (0, 0.2) to (1, 1). However, due to the search for the closest monotone GP map, R²_mono will not become zero even for purely overdominant or purely epistatic maps. As shown in Figure A2, the two monotonicity measures are highly correlated.

An R package for studying monotonicity in GP maps

We developed an R package gpmap for studying functional properties of GP maps. The package takes GP maps in the form of vectors of genotypic values as input, and provides functions for (i) determining whether the map is order-breaking or order-preserving w.r.t. any given locus, (ii) the degree of monotonicity m, (iii) R²_mono using isotonic regression from the isotone package (Leeuw et al., 2009), and (iv) plots of the original and decomposed GP maps. Code example 1 (Box 1) below illustrates the usage and functionality of the gpmap package. The package is available from CRAN http://cran.r-project.org/package=gpmap under GPLv3.

Box 1

Box 1. Code example 1.

Monotonicity in GP Maps Arising from Gene Regulatory Networks

To search for generic relationships between monotonicity and regulatory network structure, we used the above measures of monotonicity to characterize GP maps emerging from the gene regulatory network models (see Models and Methods). Based on earlier results (Gjuvsland et al., 2007, 2011; Wang et al., 2013) we hypothesized that incoherent feed forward (Figure 4, right panel) or positive feedback (Figure 4, left panel) would be necessary in order to obtain highly order-breaking GP maps, and we characterized all 1881 networks in terms of these two properties. Table 1 shows the number of motifs falling into the resulting four categories. We summarized the number of Monte Carlo simulations where all genotypic parameter sets gave convergence to a stable steady state, and where the resulting GP maps were not essentially flat (see Models and Methods for details). Motifs with less than 100 usable GP maps were discarded from further analysis. For the genotype-to-parameter maps without pleiotropy (in the sense that genetic variation at one locus influences only a single parameter, see Model and Methods) 868 motifs were discarded, while for the genotype-to-parameter map with pleiotropy (genetic variation at one locus influences three parameters) 791 motifs were discarded. All (but one) discarded motifs contained at least one positive feedback loop (Table 1). A plausible explanation for this is that many motifs with positive feedback loops have a stable steady state at, or very close to 0 for one or more state variables regardless of parameter values, and this leads to essentially flat GP maps.

FIGURE 4

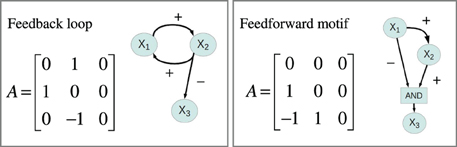
Figure 4. Connectivity matrices and signed directed graphs. Connectivity matrix A and the corresponding signed directed graph for two of the 1881 systems in the simulation study. The left panel depicts the connectivity matrix and the signed digraph of a system with a positive feedback loop between X₁ and X₂ while the right panel shows a system with incoherent feedforward from X₁ to X₃.

TABLE 1

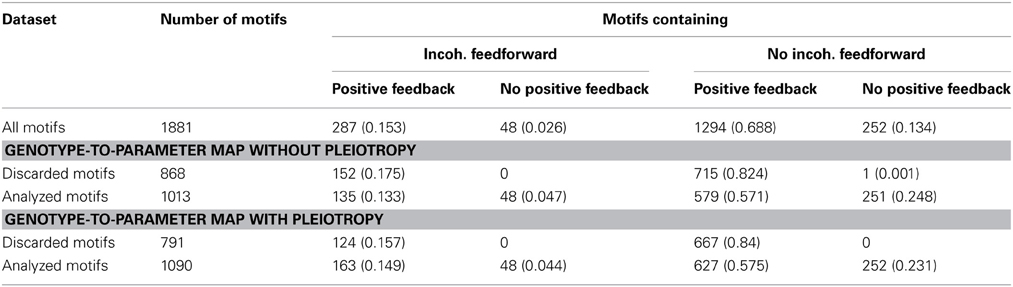
Table 1. Frequencies (proportion of row total in parenthesis) of incoherent feedforward and positive feedback loops in subsets of the 1881 studied motifs.

The introduction of pleiotropy in the genotype to parameter map has a marked effect on the monotonicity characteristics of the associated GP map (Figure 5). When genetic variation at a locus X_i affects only its maximal production rate the GP maps come out as highly monotone (Figure 5A), with a large majority being fully monotone or order-breaking for just a single locus. When genetic variation at locus X_i affects the threshold and steepness of the dose-response curve in addition to the maximal production rate (pleiotropy in the genotype-to-parameter map), the majority of GP maps still show order-breaking either for no loci or just one locus (Figure 5B). But a considerable number of GP maps are in this case order-breaking for two or three loci. Furthermore, by dividing the motifs into the four groups given in Table 1 it is evident that the regulatory anatomy of a network determines its predisposition for non-monotonicity in its associated GP map. Presence of incoherent feedforward or positive feedback loops appears to be prerequisites for the majority of the observed non-monotonic GP maps.

FIGURE 5

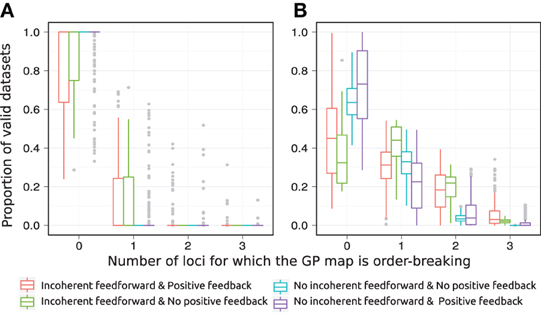
Figure 5. Order-breaking in motifs containing a single feedforward loop. Summary of order-breaking for all motifs for which at least 100 (out of 1000) Monte Carlo simulations lead to GP maps with non-negligible variation (see Models and Methods section “Gene regulatory network simulations,” for detailed criteria). Results are shown for 1013 motifs with a genotype-to-parameter map without pleiotropy (A) and 1090 motifs with a genotype-to-parameter map with pleiotropy (B). Colors indicate classes of motifs based on the presence/absence of incoherent feedforward and positive feedback loops, see Table 1 for the number of motifs in each class. A single boxplot summarizes, for all motifs in the given class, the proportion of the GP maps (y-axis) that are order-breaking with respect to a given number of loci (x-axis). For example, consider the red box at x = 0 in panel (A). This boxplot contains results for motifs with both incoherent feedforward and positive feedback and from Table 1 we find that the red boxplot summarizes results for 135 motifs. From the y-axis we find that at least half (box median at y = 1) of these 135 motifs result in only monotone GP maps, while for the most extreme (end of whisker) of the 135 motifs only 25% of the GP maps are monotone. Similarly, the cyan box is compressed into a line at x = 0, y = 1 indicating that all 251 motifs that lack both incoherent feedforward and positive feedback result in only monotone GP maps.

The class of motifs lacking both incoherent feedforward and positive feedback contains very few order-breaking GP maps, and with no pleiotropy in the genotype-to-parameter map we observe only fully order-preserving GP maps for this class (cyan in Figure 5A). In the Appendix we generalize this to an arbitrary number of nodes and formally prove that without pleiotropy in the genotype-to-parameter map, the presence of incoherent feedforward or positive feedback is indeed a necessary condition for non-monotone GP maps to arise from networks with monotone gene regulation functions.

The introduction of pleiotropy in the genotype-to-parameter map increases the frequency of order-breaking GP maps substantially (Figure 5B). Motifs lacking both incoherent feedforward and positive feedback may in this case lead to GP maps that are order-breaking for one or two loci, but never for all three loci. Using isotonic regression to quantify the overall monotonicity of the GP maps reinforces the finding that incoherent feedforward and positive feedback predispose for non-monotonicity (Figure 6). Figure 6 also shows that for all classes of motifs the majority of GP maps are fully monotone, while the most non-monotone GP maps (lowest R²_mono values) are observed for motifs with positive feedback. The differences between classes of motifs are also evident when inspecting the additivity of GP maps (Figure A3), but since monotone GP maps can still be non-additive, the patterns are much more blurred than for monotonicity.

FIGURE 6

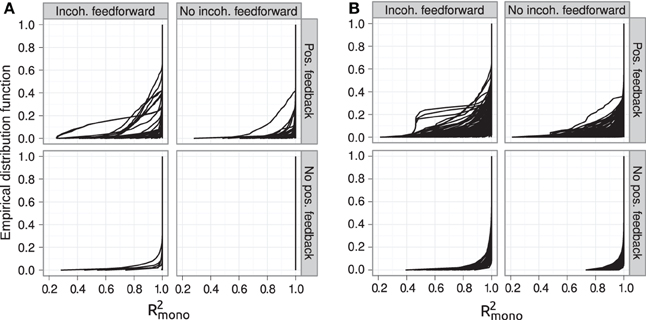
Figure 6. Empirical distribution functions for R²_mono. Summary of R²_mono values from isotone regression for all motifs for which at least 100 (out of 1000) Monte Carlo simulations lead to GP maps with non-negligible phenotypic variation (see Models and Methods section “Gene regulatory network simulations,” for detailed criteria). Results are shown for 1013 motifs with a genotype-to-parameter map without pleiotropy (A) and 1090 motifs with a genotype-to-parameter map with pleiotropy (B). Each panel is divided into 4 subplots containing classes of motifs based on the presence/absence of incoherent feedforward and positive feedback loops, see Table 1 for the number of motifs in each class. Each curve shows, for a single motif, the empirical distribution function value (y-axis) of R²_mono for all GP maps (x-axis).

Discussion

Fisher's (1918) regression on gene content and the concepts derived from this, such as additive effects and dominance deviation, provide the theoretical basis for most of quantitative genetics (Falconer and Mackay, 1996; Lynch and Walsh, 1998). By regressing on gene content, including the extensions by Cockerham (1954), the genotype-phenotype map is decomposed into additive, dominant, and epistatic components. The use of gene content or the number (0, 1, or 2) of alleles with a particular index in a genotype implies the same partial ordering of genotype space as defined in Equation 1. Thus, our proposed definition of monotonicity of GP maps, and in particular the use of isotonic regression to quantify monotonicity, may be viewed as a relaxation of the linearity assumption underlying current quantitative genetics theory. In this perspective the positive correlation between monotonicity and additivity (Figure 3) is expected.

We have addressed GP maps with 2 and 3 loci as we considered an in-depth study of the properties of GP maps with higher number of loci to be outside the scope of this study. Some general observations can be made, though. Since m is a weighted average, the m_k of major loci (i.e., for which T_k is large relative to ∑ T_k) will tend to dominate. For instance, in a case with a single major locus showing monotone gene action and several minor loci showing order-breaking, the GP map will overall be close to monotone (m close to 1). Conversely, order-preservation in a number of minor loci would have little influence on m if major loci have strongly non-monotone gene action. Isotonic regression gives an overall measure of monotonicity of a GP map, but provides no locus-specific measures corresponding to m_k. Similar to the case for m, the gene action of major loci will have high influence on the value of R²_mono.

The observation that monotonicity is an important property of GP maps is in principle not new. For a single locus, non-monotone gene action appears in the form of over- or under-dominance, while complete and partial dominance as well as additivity exemplify monotone gene action. Weinreich et al. (2005) distinguished between sign epistasis and magnitude epistasis and showed that sign epistasis limits the number of mutational trajectories to higher fitness. As sign epistasis reflects a non-monotone GP relationship and magnitude epistasis reflects a monotone one, this insight concords with our results. A similar distinction has been proposed (Wang et al., 2010) for statistical interactions where removable interactions are those that can be removed by a monotone transformation of the phenotype scale, while non-monotonicity in the GP map leads to essential interactions. Wu et al. (2009) developed a method to screen for and test the significance of essential interaction in genome-wide association studies. Isotonic regression has also recently been applied to link genotype and phenotype data (Beerenwinkel et al., 2011; Luss et al., 2012). Our treatment of monotonicity is more general than these earlier works in three major ways. First, we deal with monotonicity of the GP map as a whole rather than either intra-locus (dominance vs. overdominance) or inter-locus (magnitude vs. sign epistasis and removable vs. essential interactions). Second, where the earlier treatments have focused on classifying the type of gene action, we make use of quantitative measures of monotonicity. Third, our approach combining the concept of monotonicity with cGP models opens a direct link between genetics and the theory of dynamical systems in the wide sense.

Monotonicity is a property of the GP map separate from the allele frequencies, making it a physiological (Cheverud and Routman, 1995) or functional (Hansen and Wagner, 2001) descriptor rather than a statistical one. The distinction between physiological and statistical epistasis has lead to much debate (Phillips, 2008). Zeng et al. (2005) argued the distinction was unnecessary and potentially misleading. Although their arguments around orthogonality and variance components are valid, our results demonstrate very clearly that describing the properties of the GP map without reference to any particular study population is essential if we want to connect quantitative genetics with regulatory biology.

It is clear from our results that positive feedback and incoherent feedforward promote non-monotonicity. The clear-cut differences in monotonicity between different classes of regulatory networks, combined with the strong correlation between monotonicity and additivity of GP maps, appear therefore to explain the findings that regulatory systems with positive feedback give considerably more statistical epistasis than those without (Gjuvsland et al., 2007; Wang et al., 2013). Even though both incoherent feedforward and positive feedback predispose for non-monotone GP maps, the underlying mechanisms are different for the two regulatory motifs. In the case of incoherent feedforward the sum of direct and indirect effects may result in a non-monotone dose-response relationship (Kaplan et al., 2008). That positive feedback loops can give non-monotonicity is intuitively less clear, but in the Appendix we show both results analytically. Positive feedback predisposes for multiple steady states, and order-breaking might also emerge from different genotypes corresponding to different states. It should be noted, however that positive feedback is only a necessary condition for multistationarity (Plahte et al., 1995), and a positive loop in the connectivity matrix A of a system is not necessarily active at any point during the time course of the system.

Without any restrictions on the connectivity of a three-gene system there are 3⁹ = 19, 683 possible distinct networks. The main restriction we imposed (see Models and Methods for details) was a maximum of two regulators per gene, which allowed us to use Boolean gene regulation functions already established in the sigmoid formalism (Plahte et al., 1998). Other model formalisms allowing an arbitrary number of regulators are also available (Wagner, 1994, 1996; Siegal and Bergman, 2002) and could be extended to diploid forms and used in later studies.

Although this study has focused on gene regulatory networks, the concept of monotone gene action applies to the propagation of genetic variation across the whole physiological hierarchy. One may therefore systematically use the concepts and methods presented here to study the order-preserving and order-breaking properties of genotype-phenotype mappings that are associated with any regulatory structure amenable for mathematical modeling. Through this it will be possible to make a wide-ranging survey of which regulatory anatomies promote monotonicity and which promote non-monotonicity. We foresee that this classification may become instrumental for predicting how phenotypic effects of genetic variation propagate across generations in sexually reproducing populations.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: http://www.frontiersin.org/journal/10.3389/fgene.2013.00216/abstract

Spreadsheet S1 | Excel spreadsheet with connectivity matrices and loop products for all 1881 gene regulatory networks.

References

Alon, U. (2007). Network motifs: theory and experimental approaches. Nat. Rev. Genet. 8, 450–461. doi: 10.1038/nrg2102

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Alvarez-Castro, J. M., and Carlborg, Ö. (2007). A unified model for functional and statistical epistasis and its application in QTL analysis. Genetics 176, 1151–1167. doi: 10.1534/genetics.106.067348

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Barlow, R. E., and Brunk, H. D. (1972). The isotonic regression problem and its dual. J. the Am. Stat. Assoc. 67, 140–147. doi: 10.1080/01621459.1972.10481216

CrossRef Full Text

Beerenwinkel, N., Knupfer, P., and Tresch, A. (2011). Learning monotonic genotype-phenotype maps. Stat. Appl. Genet. Mol. Biol. 10:3. doi: 10.2202/1544-6115.1603

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cheverud, J. M., and Routman, E. J. (1995). Epistasis and its contribution to genetic variance components. Genetics 139, 1455–1461.

Pubmed Abstract | Pubmed Full Text

Cheverud, J. M., and Routman, E. J. (1996). Epistasis as a source of increased additive genetic variance at population bottlenecks. Evolution 50, 1042–1051. doi: 10.2307/2410645

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cockerham, C. C. (1954). An extension of the concept of partitioning hereditary variances for analysis of covariances among relatives when epistasis is present. Genetics 39, 859–882.

Pubmed Abstract | Pubmed Full Text

De Jong, H. (2002). Modeling and simulation of genetic regulatory systems: a literature review. J. Comput. Biol. 9, 67–103. doi: 10.1089/10665270252833208

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Falconer, D. S., and Mackay, T. F. C. (1996). Introduction to Quantitative Genetics. Harlow: Longman Group.

Fisher, R. A. (1918). The correlation between relatives on the supposition of Mendelian inheritance. Trans. R. Soc. Edinb. 52, 399–433. doi: 10.1017/S0080456800012163

CrossRef Full Text

Gjuvsland, A. B., Hayes, B. J., Omholt, S. W., and Carlborg, Ö. (2007). Statistical epistasis is a generic feature of gene regulatory networks. Genetics 175, 411–420. doi: 10.1534/genetics.106.058859

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gjuvsland, A. B., Vik, J. O., Beard, D. A., Hunter, P. J., and Omholt, S. W. (2013). Bridging the genotype-phenotype gap: what does it take? J. Physiol. 591, 2055–2066. doi: 10.1113/jphysiol.2012.248864

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gjuvsland, A. B., Vik, J. O., Woolliams, J. A., and Omholt, S. W. (2011). Order-preserving principles underlying genotype-phenotype maps ensure high additive proportions of genetic variance. J. Evol. Biol. 24, 2269–2279. doi: 10.1111/j.1420-9101.2011.02358.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hansen, T. F., and Wagner, G. P. (2001). Modeling genetic architecture: a multilinear theory of gene interaction. Theor. Popul. Biol. 59, 61–86. doi: 10.1006/tpbi.2000.1508

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hill, W. G., Goddard, M. E., and Visscher, P. M. (2008). Data and theory point to mainly additive genetic variance for complex traits. PLoS Genet. 4:e1000008. doi: 10.1371/journal.pgen.1000008

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jaeger, J., Irons, D., and Monk, N. (2012). The inheritance of process: a dynamical systems approach. J. Exp. Zool. B Mol. Dev. Evol. 318, 591–612. doi: 10.1002/jez.b.22468

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kaplan, S., Bren, A., Dekel, E., and Alon, U. (2008). The incoherent feed-forward loop can generate non-monotonic input functions for genes. Mol. Syst. Biol. 4, 203. doi: 10.1038/msb.2008.43

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Karlebach, G., and Shamir, R. (2008). Modelling and analysis of gene regulatory networks. Nat. Rev. Mol. Cell Biol. 9, 770–780. doi: 10.1038/nrm2503

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Latchman, D. (2005). Gene Regulation: a Eukaryotic Perspective. New York, NY: Taylor and Francis.

Le Rouzic, A., and Alvarez-Castro, J. M. (2008). Estimation of genetic effects and genotype-phenotype maps. Evol. Bioinformatics 4, 225–235. doi: 10.4137/EBO.S756. Available online at: http://www.la-press.com/estimation-of-genetic-effects-and-genotype-phenotype-maps-article-a887

CrossRef Full Text

Leeuw, J. D., Hornik, K., and Mair, P. (2009). Isotone optimization in R: pool-adjacent-violators algorithm (PAVA) and active set methods. J. Stat. Softw. 32, 1–24.

Luss, R., Rosset, S., and Shahar, M. (2012). Efficient regularized isotonic regression with application to gene–gene interaction search. Ann. Appl. Stat. 6, 253–283. doi: 10.1214/11-AOAS504

CrossRef Full Text

Lynch, M., and Walsh, B. (1998). Genetics and Analysis of Quantitative Traits. Sunderland, MA: Sinauer Associates.

Mestl, T., Plahte, E., and Omholt, S. W. (1995). A mathematical framework for describing and analysing gene regulatory networks. J. Theor. Biol. 176, 291–300. doi: 10.1006/jtbi.1995.0199

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Moore, A. (2012). Towards the new evolutionary synthesis: gene regulatory networks as information integrators. Bioessays 34, 87–87. doi: 10.1002/bies.201290000

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Neale, B. M., Ferreira, M. A. R., Medland, S. E., and Posthuma, D. (eds.). (2008). Statistical Genetics: Gene Mapping through Linkage and Association. New York, NY: Taylor and Francis Group.

Omholt, S. W., Plahte, E., Øyehaug, L., and Xiang, K. F. (2000). Gene regulatory networks generating the phenomena of additivity, dominance and epistasis. Genetics 155, 969–980.

Pubmed Abstract | Pubmed Full Text

Phillips, P. C. (1998). The language of gene interaction. Genetics 149, 1167–1171.

Pubmed Abstract | Pubmed Full Text

Phillips, P. C. (2008). Epistasis - the essential role of gene interactions in the structure and evolution of genetic systems. Nat. Rev. Genet. 9, 855–867. doi: 10.1038/nrg2452

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Plahte, E., Mestl, T., and Omholt, S. W. (1995). Feedback loops, stability and multistationarity in dynamical systems. J. Biol. Syst. 3, 409–413. doi: 10.1142/S0218339095000381

CrossRef Full Text

Plahte, E., Mestl, T., and Omholt, S. W. (1998). A methodological basis for description and analysis of systems with complex switch-like interactions. J. Math. Biol. 36, 321–348. doi: 10.1007/s002850050103

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schlitt, T., and Brazma, A. (2007). Current approaches to gene regulatory network modelling. BMC Bioinformatics 8(Suppl. 6):S9. doi: 10.1186/1471-2105-8-S6-S9

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Siegal, M. L., and Bergman, A. (2002). Waddington's canalization revisited: developmental stability and evolution. Proc. Natl. Acad. Sci. U.S.A. 99, 10528–10532. doi: 10.1073/pnas.102303999

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wagner, A. (1994). Evolution of gene networks by gene duplications: a mathematical model and its implications on genome organization. Proc. Natl. Acad. Sci. U.S.A. 91, 4387–4391. doi: 10.1073/pnas.91.10.4387

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wagner, A. (1996). Does evolutionary plasticity evolve? Evolution 50, 1008–1023. doi: 10.2307/2410642

CrossRef Full Text

Wang, X., Elston, R. C., and Zhu, X. (2010). The meaning of interaction. Hum. Hered. 70, 269–277. doi: 10.1159/000321967

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wang, Y., Vik, J. O., Omholt, S. W., and Gjuvsland, A. B. (2013). Effect of regulatory architecture on broad versus narrow sense heritability. PLoS Comput. Biol. 9:e1003053. doi: 10.1371/journal.pcbi.1003053

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Weinreich, D. M., Watson, R. A., and Chao, L. (2005). Perspective: sign epistasis and genetic constraint on evolutionary trajectories. Evolution 59, 1165–1174. doi: 10.1554/04-272

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wu, C., Zhang, H., Liu, X., Dewan, A., Dubrow, R., Ying, Z., et al. (2009). Detecting essential and removable interactions in genome-wide association studies. Stat. Interface 2, 161–170. doi: 10.4310/SII.2009.v2.n2.a6

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zeng, Z. B., Wang, T., and Zou, W. (2005). Modeling quantitative trait loci and interpretation of models. Genetics 169, 1711–1725. doi: 10.1534/genetics.104.035857

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Appendix

In this appendix we complement the simulation studies in the main text with some analytic results for GP maps emerging from ODE models of gene regulatory networks. We study a generalization of the gene network model in Equation (3) with an arbitrary number of loci and monotone gene regulation functions, but restrict the analysis to genotype-parameter maps without pleiotropy. In particular, we show that (i) if there are no positive feedback loops and no incoherent feedforward loops in the network, the resulting GP maps are always monotone, (ii) a positive feedback loop or an incoherent feedforward loop may lead to non-monotone GP maps. The results hold for phenotypes given as the stable concentration of the product of one of the genes, and under certain restrictions also for phenotypes given as a function of one or several stable gene product concentrations that is monotonic with respect to each of its arguments.

Gene Network Model

We consider a dynamic system consisting of n mutually interacting diploid loci X_j, j ∈ N = {1, …, n}, regulating each other's expression. The time dependent output of X_j is denoted z_j, and we define z = [z₁, z₂, …, z_n]. It goes without saying that z_j in general depends on the genotypes of all the genes even though we will not always state this explicitly.

For a given genotype g = g_jg^(j) = a_jb_jg^(j), where g_j ∈ {11, 12, 22} denotes the genotype and a_j, b_j ∈ 1, 2 denote the indexes of the two alleles of locus X_j, the equations of motion for X_j are

$\begin{array}{cc}\begin{array}{l}{\dot{z}}_j^1={\alpha }_j^{a_j}{r}_j^{a_j}(z)-{\gamma }_j^{a_j}{z}_j^1,\\ {\dot{z}}_j^2={\alpha }_j^{b_j}{r}_j^{b_j}(z)-{\gamma }_j^{b_j}{z}_j^2,\\ z_j=z_j^1+z_j^2,\end{array}& \left(\text{A}1\right)\end{array}$

where z¹_j and z²_j are the time-dependent outputs of the two homologous copies of X_j. The two allele rate functions r¹_j(z) and r²_j(z) have range [0, 1] so that α¹_j and α²_j represent the maximum production rates of the two alleles. We assume that all dose-response functions in Equation (A1) are differentiable and monotonic with respect to each of its arguments, and that for each j, k, the signs of ∂r¹_j/∂x_k and ∂r²_j/∂x_k in the stable point x are equal. This model generalizes Eq. (3) to an arbitrary number of loci and a broader class of gene regulation functions.

In the following we are only concerned with the steady states of Equation (A1), and assume for simplicity that they have just a single stable equilibrium point. Solving the equilibrium conditions of Equation (A1) with respect to z¹_j and z²_j and adding gives

$\begin{array}{cc}{f}_j(x)={\mu }_j^{a_j}{r}_i^{a_j}(x)+{\mu }_j^{b_j}{r}_j^{b_j}(x)-x_j=0,j\in N,& \left(\text{A}2\right)\end{array}$

where x = [x1, …, xn] is the stable point, μaij = αajj/γajj and μbjj = αbjj/γbjj. Since our definition of monotonicity of GP maps does not depend on the numbering of alleles, we will without loss of generality assume μ1j ≤ μ2j for all j.

The network architecture can be read out from the structure of the system's Jacobian matrix in the stable state x. We define the elements of the Jacobian J for the set of functions f_j defined in Equation (A2) by

$\begin{array}{cc}{J}_{jk}=J_{jk}(g)=\frac{\partial f_j(x)}{\partial x_k},j,k\in N.& \left(\text{A}3\right)\end{array}$

To the Jacobian J it is customary to assign a signed directed graph in which each locus X_k is represented by a node X_k, and in which there is an arc from X_j to X_k if and only if J_kj ≠ 0, its sign given by the sign of J_kj. A chain from X_j to X_k is a set of arcs in leading from X_j to X_k in which all intermediate nodes are visited only once. The sign of a chain is equal to the product of the signs of the J_ij corresponding to the arcs in the chain. If there is a chain from X_i to X_j and also a chain from X_j to X_i through a disjoint set of nodes, the two chains constitute a proper feedback loop (FBL). To each FBL is associated a loop product L which is the product of the Jacobian elements corresponding to all the arcs in the loop. The sign of the loop is given by the sign of L. Two chains from X_j to X_i, i ≠ j, with only the endpoint nodes in common, constitute a feedforward loop (FFL). If the two chains have opposite signs, the FFL is incoherent (IFFL), otherwise it is coherent (CFFL).

The system's phenotype could be any scalar quantity defined by its equilibrium value x. In the following we assume the genotype-phenotype map G(g) = x_q(g), q ∈ N, for a given and fixed q, and investigate the monotonicity properties of G(g_kg^(k)) with respect to genetic variation in any locus X_k for different backgrounds g^(k). In the following sections we analyse the causes of order-breaking in G in the restricted case in which there is only genetic variation in μ¹_k and μ²_k, not in the shape of the dose-response functions r¹_k and r²_k, implying r¹_k(x) = r²_k(x) = r_k(x). This is what we mean by a genotype-to-parameter map without pleoitropy.

In the next sections we prove the following result:

Proposition 1. Assume all rate functions in Equation (A1) are monotonic and that G is the mapping from g to x_q for some fixed q so that x_q(g) is the phenotype. If there is no feedback loop (FBL) and no feedforward loop (FFL) anywhere in the network corresponding to the system Equation (A1), then necessarily m_k = 1 for all k. If the system contains either a single FFL or a single FBL, then G may be non-monotone for some x_k if the FFL is positive or the FBL is incoherent, but if the FBL is negative or the FFL is coherent, no order breaking can occur for any x_k.

At the end of this note we show that under some reasonable conditions this result is also valid for more general phenotypes depending on more than one x_q.

Networks Without Loops

We first consider networks containing no feedforward loop and no feedback loop. In these networks there is at most one chain from one node to another, and of course no autoregulatory loops. If there is a chain from X_j to X_k, there is no chain from X_k to X_j. Any node is either unregulated (constitutively expressed) or regulated by one or several other nodes.

We first prove a useful lemma.

Lemma 1. If x_l(11g^(j)) ≤ x_l(12g^(j)) ≤ x_l(22g^(j)) for any j and l and there is an arc X_l → X_m with positive sign and no other chain from X_l → X_m, then also x_m(11g^(j)) ≤ x_m(12g^(j)) ≤ x_m(22g^(j)). If the sign of the arc is negative, then x_m(11g^(j)) ≥ x_m(12g^(j)) ≥ x_m(22g^(j)).

Proof. Suppressing the explicit dependence on other genes that are not affected by genetic variation in X_j, we have

$\begin{array}{cc}\begin{array}{l}{x}_m(11g^{(j)})=2{\mu }_m^1{r}_m(x_l(11g^{(j)})),\\ x_m(12g^{(j)})=({\mu }_m^1+{\mu }_m^2)r_m(x_l(12g^{(j)})),\\ x_m(22g^{(j)})=2{\mu }_m^2{r}_m(x_l(22g^{(j)})).\end{array}& \left(\text{A}4\right)\end{array}$

Now, r_m is monotonic by assumption. If it is monotonically increasing,

$\begin{array}{cc}\begin{array}{l}{x}_m(12g^{(j)})\ge ({\mu }_m^1+{\mu }_m^2)r_m(x_l(11g^{(j)}))\ge x_m(11g^{(j)}),\\ x_m(22g^{(j)})\ge 2{\mu }_m^2{r}_m(x_l(12g^{(j)}))\ge x_m(12g^{(j)}),\end{array}& \left(\text{A}5\right)\end{array}$

from which the assertion follows. If r_m is monotonically decreasing, we find the same relations with the inequality signs reversed.        □

If there is no chain from X_j to X_q, genetic variation in X_j will not be reflected in G, i.e. G(11g^(j)) = G(12g^(j)) = G(22g^(j)), and by definition does not give order-breaking. Then assume X_j is upstream relative to X_q and that the chain from X_j to X_q is positive. We first let X_j be an unregulated node with no predecessor. Then

$\begin{array}{cc}\begin{array}{l}{x}_j(11g^{(j)})=2{\mu }_j^1,\\ x_j(12g^{(j)})={\mu }_j^1+{\mu }_j^2,\\ x_j(22g^{(j)})=2{\mu }_j^2,\end{array}& \left(\text{A}6\right)\end{array}$

because r¹_j = r²_j = 1. From this it follows that x_j(11g^(j)) ≤ x_j(12g^(j)) ≤ x_j(22g^(j)).

Repeated use of Lemma 1 leads eventually to x_q(11g^(j)) ≤ x_q(12g^(j)) ≤ x_q(22g^(j)), irrespective of the genotypic background of X_j. If the chain from X_j to X_q is negative, the argument goes in the same way, but then x_q(11g^(j)) ≥ x_q(12g^(j)) ≥ x_q(22g^(j)). The above argument can be carried out in the same way if X_j is not top-stream. It follows that in a network without FFBs and FFLs and where genetic variation is restricted to μ¹_k and μ²_k, the genotype-phenotype map G(g) = x_q(g) cannot be order-breaking.

Networks with a Feedback Loop

In this section we investigate the effects of feedback loops on the degree of monotonicity. Assuming monotonic dose-response functions and non-pleiotropic genetic variation, we show that a positive feedback loop may lead to order breaking, while negative feedback loops never do. We consider a network in which there is no FFL and a single FBL with X_q as one of its members and X_k is upstream of the loop.

Lemma 2. Consider a network with n nodes for which all dose-response functions are monotonic and there is only genetic variation in μ¹_k and μ²_k. Asssume there is a chain from X_k to X₁, that X₁, but not X_k, is member of a FBL with m nodes, and that there is no other FBL and no FFL in the system. If X_q is in the loop, let the loop be X₁ → X₂ → … → X_q → … → X_m → X₁. If the FBL is positive, there may be order-breaking in X_q due to genetic variation in X_k, but no order-breaking can occur if the loop is negative. If X_q is downstream of the loop, the same result applies.

Proof. With a single FBL and no FFL there is at most one directed path from any node X_i to any other node X_j, and if there is a path from X_i to X_j, there is no return path from X_j to X_i if either X_i or X_j is not part of the FBL. We first consider the dependence of x₁ on x_k. The direct regulators of node X₁ are X_m and X_l, the latter being the last but one node in the chain from X_k to X₁. In Plahte et al. (2013) we introduced the propagation functions x_j = p_jk(x_k) which express the effect on x_j of genetic variation in X_k. An important property of p_jk is that it can be derived from all the equilibrium conditions Equation (A2) except the equation for f_k. This implies that the effects on X_j of genotypic variation in X_k are only expressed in terms of the variations in x_k, while the parameters expressing the genotype of X_k do not enter into the function p_jk.

We then have x_l = p_lk(x_k) and x_m = p_m1(x₁). To make it easier to use the results in Plahte et al. (2013) we rewrite the equilibrium condition Equation (A2) as

$\begin{array}{cc}{R}_j(x)-{\gamma }_j{x}_j=0,& \left(\text{A}7\right)\end{array}$

where γj > 0. In the following, the Jacobian refers to this set of equations, which has the same root and the same functional dependencies between the variables as the original set. The signs of the partial derivatives of Rj are the same as for rajj and rbjj. The equilibrium condition for X1 is then

$\begin{array}{cc}{\gamma }_1{x}_1=R_1(p_{lk}(x_k),p_{m1}(x_1))).& \left(\text{A}8\right)\end{array}$

This equation defines x₁ as a function of x_k in an open domain around the equilibrium point and with a derivative that can be computed by implicit differentiation, i.e.

$\begin{array}{cc}{\gamma }_1\frac{\text{d}{x}_1}{\text{d}{x}_k}=\frac{\partial R_1}{\partial x_l}{q}_{lk}+\frac{\partial R_1}{\partial x_m}{q}_{m1}\frac{\text{d}{x}_1}{\text{d}{x}_k},& \left(\text{A}9\right)\end{array}$

where q_ij = p′_ij is the derivative of p_ij for all i, j.

From Lemma 1 it follows that there is no order breaking in X_l, in other words, q_lk has a fixed sign. Consider then q_m1. There is just a single chain from X₁ to X_m, and Equation (13) in Plahte et al. (2013) gives

$\begin{array}{cc}{q}_{m1}(x_1)={(-1)}^{m-1}\frac{D_{VV}{C}_U}{D^{(11)}}.& \left(\text{A}10\right)\end{array}$

Here U is the set of nodes in this chain, C_U is its chain product, i.e. the product of the Jacobian elements corresponding to the arcs in the chain, V = N \ U, D⁽¹¹⁾ is the subdeterminant of J with row 1 and column 1 deleted, and D_VV is the subdeterminant of J composed of the rows and columns V. Because there is no feedback loop among the nodes represented in D⁽¹¹⁾ and D_VV, only the diagonal degradation terms contribute to these two determinants. Hence D⁽¹¹⁾ = (−1)^{n − 1} ∏_{i ≠ 1} γ_i. Similarly, D_VV = (−1)^{n − m} ∏_{i ∈ V} γ_i, giving q_ml = γ₁C_U/Γ_U, where Γ_U = ∏_{i ∈ U} γ_i. Finally, we note that P = (∂ R₁/∂ x_m)C_U is the loop product of the loop.

Solving Equation (A9) with respect to dx₁/dx_k and using all these expressions lead to

$\begin{array}{cc}{\gamma }_1\frac{\text{d}{x}_1}{\text{d}{x}_k}=\frac{{\Gamma }_U}{{\Gamma }_U-P}\frac{\partial x_1}{\partial x_l}{q}_{1k}.& \left(\text{A}11\right)\end{array}$

The sign of ∂x₁/∂x_l is independent of the genotype of X_k and the sign of q_1k is fixed. Genotypic variation in X_k may change the magnitude of P, but its sign is fixed because all Jacobi elements have fixed sign independent of the system parameters. Thus, genotypic variation in X_k does not alter the sign of dx₁/dx_k if the loop is negative (P < 0), while for a positive loop the sign of Γ_U − P may switch. In the latter case, an increase in x_k due to genetic variation in X_k may increase x₁ in some cases and decrease it in others, leading to order breaking. As there is only a single chain from X₁ to X_q, no order breaking in X₁ implies no order breaking in X_q, while order breaking in X₁ may propagate to X_q. The same result follows if X_q is downstream a node in the loop because order breaking in this node may propagate to X_q.    □

Feedforward Loops (FFLs)

A feedforward loop (FFL) is a motif in the network in which there are two different chains C₁ and C₂ from one particular node to another particular node. To each chain C_i is associated a chain product P_i defined as the product of the Jacobian elements corresponding to the arcs in C_i. If P₁ and P₂ have equal signs, the FFL is coherent, otherwise it is incoherent.

In a network with a single feedforward loop and no feedback loops we now investigate the effect on G(g) = x_q(x_k(g)) of genetic variation in X_k for varying background g^(k). Our starting point is again Equation (A7). We first let X_k and X_q be the initial and terminal nodes in the FFL. The two chains C₁ and C₂ leading from X_k to X_q comprise ρ₁ and ρ₂ nodes including X_k and X_q, respectively. Let the set of nodes in C₁ and C₂ be X_U1 and X_U2, respectively, where U₁ and U₂ are the corresponding subsets of N, and let V₁ and V₂ be their complements.

Roughly speaking, the derivative of the propagation function p_qk(x_k) can be expressed as a sum of terms, each term corresponding to one of the chains leading from X_k to X_q (Plahte et al., 2013). To the chain C_i is assigned the chain weight w_i given by

$\begin{array}{cc}{w}_i={(-1)}^{{\rho }_i-1}\frac{D_{V_i{V}_i}}{D^{(kk)}},i=1,2,& \left(\text{A}12\right)\end{array}$

where D_ViVi is the Jacobian subdeterminant for the nodes not included in C_i, and D^(kk) is the Jacobian subdeterminant for all nodes except X_k. Because there are two chains from X_k to X_q, the derivative of p_qk is a sum of two terms:

$\begin{array}{cc}\frac{\text{d}{p}_{qk}}{\text{d}{x}_k}=w_1{P}_1+w_2{P}_2,& \left(\text{A}13\right)\end{array}$

where P₁ and P₂ are the two chain products, and w₁ and w₂ their weights (Plahte et al., 2013). When there is no feedback loop in the system, only the diagonal elements in J stemming from the term −γ_i x_i in Equation (A7) contribute to the determinants D_ViVi and D^(kk):

$\begin{array}{cc}\begin{array}{l}{D}_{V_i{V}_i}={(-1)}^{n-{\rho }_i}{\displaystyle \prod _{j\in V_i}{\gamma }_j},\\ D^{(kk)}={(-1)}^{n-1}{\displaystyle \prod _{j\ne k}{\gamma }_j}.\end{array}& \left(\text{A}14\right)\end{array}$

Altogether this gives

$\begin{array}{cc}\frac{\text{d}{x}_q}{\text{d}{x}_k}=\frac{\text{d}{p}_{qk}}{\text{d}{x}_k}=\frac{{\gamma }_k}{{\Gamma }_1}{P}_1+\frac{{\gamma }_k}{{\Gamma }_2}{P}_2,& \left(\text{A}15\right)\end{array}$

where Γ₁ and Γ₂ are the products of the γ_j in the two chains, respectively. The chain products P₁ and P₂ depend on the genotype g_k of X_k as well as on the genotypic background g^(k), but their signs S₁ and S₂ are invariant under genotypic variation. It is easy to see that a negative autoregulatory loop, which is a common feature in gene regulatory networks, would not invalidate the conclusion, but a positive autoregulatory loop might.

If the FFL is incoherent, P₁ and P₂ have opposite signs, implying that the sign of dx_q/dx_k may vary. If the FFL is coherent, however, no order-breaking can occur.

If X_k is upstream relative to the initial node X_init of the FFL, it follows from the above section on networks without loops that there will be no order-breaking in X_init, and the above argument is still valid.

More General Phenotypes

In real life, relevant phenotypes are not direct gene products, but rather functions of the concentrations of one or several gene products. Let the phenotype G(g) be a function of x_U(g), G = h(x_U(g)), where U is a subset of N, and assume that for any u ∈ U, ∂h/∂x_u has fixed sign for all genotypes. To analyse this case we extend the original system Equation (A2) to

$\begin{array}{cc}\begin{array}{l}{\mu }_i^{a_i}{r}_i^{a_i}(x(g))+{\mu }_i^{b_i}{r}_i^{b_i}(x(g))-x_i(g)=0,i=1,\dots ,n,\\ h(x_U(g))-x_{n+1}=0,\end{array}& \left(\text{A}16\right)\end{array}$

and apply our above results to this system, in which G(g) = x_{n + 1}(g), i.e. q = n + 1. If there are two nodes among X_U which have a common predecessor X_k, then there will exist two chains from X_k to X_{n + 1}. These two chains constitute a feedforward loop with X_{n + 1} as final node. If this FFL is incoherent, order breaking due to genetic variation in X_k may occur even if there is no order breaking in the original system comprising the nodes X₁, …, X_n. If the FFL is coherent, order breaking only occurs if it occurs in the original system.

References

Plahte, E., Gjuvsland, A. B., and Omholt, S. W. (2013). Propagation of genetic variation in gene regulatory networks. Phys. D 256–257, 7–20. doi: 10.1016/j.physd.2013.04.002

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

FIGURE A1

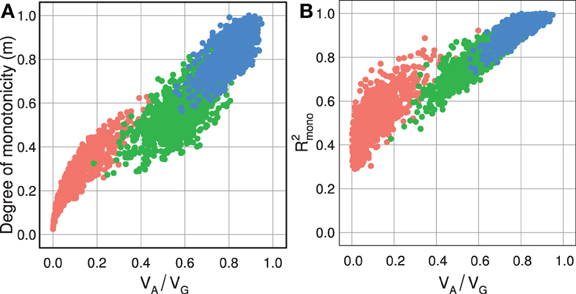
Figure A1. Measures of monotonicity vs. additivity of GP maps with three loci. Scatterplots showing V_A/V_G from unweighted regression vs. (A) degree of monotonicity (m) and (B) R²_mono. Red dots show 1000 random three-locus GP maps, blue dots show the same 1000 GP maps after sorting to introduce order-preservation for 1 locus while green dots show the same 1000 GP maps after sorting to introduce order-preservation for 2 loci [see Model and Methods in Gjuvsland et al. (2011)].

FIGURE A2

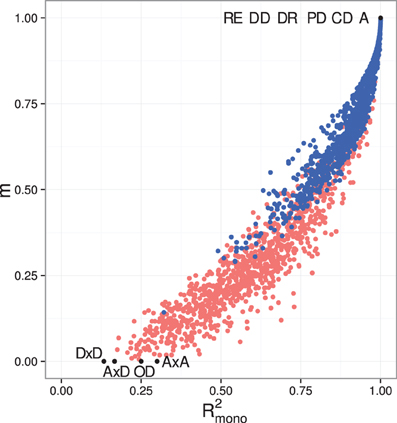
Figure A2. Comparing measures of monotonicity GP maps. Scatterplots showing degree of monotonicity (m) vs. R²_mono. Black dots correspond to the maps shown in Figure 1. Red dots show 1000 random two-locus GP maps, while blue dots show the same 1000 GP maps after sorting to introduce order-preservation for 1 locus [see Model and Methods in Gjuvsland et al. (2011)].

FIGURE A3

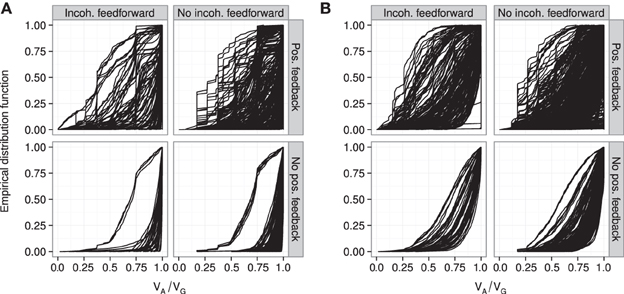
Figure A3. Empirical distribution functions for additivity of GP maps. Summary of V_A/V_G from unweighted regression for all motifs for which at least 100 (out of 1000) Monte Carlo simulations lead to GP maps with non-negligible phenotypic variation (see Models and Methods section “Gene regulatory network simulations,” for detailed criteria). Results are shown for 1013 motifs with a genotype-to-parameter map without pleiotropy (A) and1090 motifs with a genotype-to-parameter map with pleiotropy (B). Each panel is divided into 4 subplots containing classes of motifs based on the presence/absence of incoherent feedforward and positive feedback loops, see Table 1 for the number of motifs in each class. Each curve shows, for a single motif, the empirical distribution function value (y-axis) of V_A/V_G from unweighted regression for all GP maps (x-axis).