- 1Department of Pediatrics, Research Development and Clinical Investigation, Children's Mercy Hospital, Kansas City, MO, USA
- 2Department of Pediatrics, University of Missouri-Kansas City, Kansas City, MO, USA
- 3Department of Informatic Medicine and Personalized Health, University of Missouri-Kansas City, Kansas City, MO, USA
- 4Department of Pediatrics, Clinical Pharmacology and Therapeutic Innovation, Children's Mercy Hospital, Kansas City, MO, USA
- 5Department of Statistics and Probability, Michigan State University, East Lansing, MI, USA
Rapid developments in molecular technology have yielded a large amount of high throughput genetic data to understand the mechanism for complex traits. The increase of genetic variants requires hundreds and thousands of statistical tests to be performed simultaneously in analysis, which poses a challenge to control the overall Type I error rate. Combining p-values from multiple hypothesis testing has shown promise for aggregating effects in high-dimensional genetic data analysis. Several p-value combining methods have been developed and applied to genetic data; see Dai et al. (2012b) for a comprehensive review. However, there is a lack of investigations conducted for dependent genetic data, especially for weighted p-value combining methods. Single nucleotide polymorphisms (SNPs) are often correlated due to linkage disequilibrium (LD). Other genetic data, including variants from next generation sequencing, gene expression levels measured by microarray, protein and DNA methylation data, etc. also contain complex correlation structures. Ignoring correlation structures among genetic variants may lead to severe inflation of Type I error rates for omnibus testing of p-values. In this work, we propose modifications to the Lancaster procedure by taking the correlation structure among p-values into account. The weight function in the Lancaster procedure allows meaningful biological information to be incorporated into the statistical analysis, which can increase the power of the statistical testing and/or remove the bias in the process. Extensive empirical assessments demonstrate that the modified Lancaster procedure largely reduces the Type I error rates due to correlation among p-values, and retains considerable power to detect signals among p-values. We applied our method to reassess published renal transplant data, and identified a novel association between B cell pathways and allograft tolerance.
Introduction
Rapid developments in molecular technology have created high throughput data in search of genetic variants associated with complex traits. As the cost of experiments goes down, the amount of data that can be generated, and the resulting complexity of statistical analysis required to interpret the data goes up. The increase of genetic variants requires more statistical testing to be performed simultaneously, which poses a challenge to control the genome wide Type I error rate. False discovery rate (FDR) and its extended methods have been proposed to adjust p-values in multiple tests in order to control the genome wide Type I error (Benjamini and Hochberg, 1995; Cheng and Pounds, 2007). However, in large-scale hypothesis testing, these methods often require very a large sample size to maintain power of detecting risk factors.
The global test (also named omnibus test) of p-values can combine evidence and turn dimensionality from a curse into rich information. From a systems biology perspective, genes, cells, tissues, and organs function as a system through metabolic networks and cell signaling networks. In non-Mendelian inheritance patterns, such as complex disorders, a subset of genetic variants may jointly confer moderate effects in mediating molecular activities. As a result, signals may not be significant in single marker-single trait analysis, but many such values from related genes might provide valuable information on gene function and regulation. For instance, in pathway analysis (Khatri et al., 2012) and gene set enrichment analysis (Subramanian et al., 2005), multiple genes that work together to serve a particular biological function are often analyzed jointly as a gene set. Several pathway repositories, such as the Kyoto Encyclopedia of Genes and Genomes (KEGG) (Kanehisa et al., 2004), PANTHER classification system for protein sequence data (Nikolsky and Bryant, 2009), and Reactome pathways in humans (Matthews et al., 2009) have been established, and are continually being updated. For non-Mendelian diseases and complex traits, identification of isolated genetic variants is insufficient to summarize the complex association with disease. The “most-significant SNPs/genes” approach often detects variants with small effect sizes and odds ratios ranging between 1.3 and 2 (Wacholder et al., 2004). Therefore, integrating information from pathways, gene sets, and networks will provide useful information in understanding the gene regulation mechanism. Furthermore, filtration techniques can be integrated with global testing of p-values to remove sets of genetic variants that are not related to traits, and thereby reduce the dimensionality of the data (Dai and Charnigo, 2008; Dai et al., 2012a).
The global test of p-values evaluates the pattern (distribution) of p-values instead of selecting p-values less than an arbitrary threshold. Therefore, this method has the potential to identify multiple genes with small effects. If we assume that all individual tests are independent and arise from genetic variants with no effects, then p-values are identically and independently distributed as Uniform (0, 1). Taking this as a null hypothesis for the pattern of p-values in the global test, one can assess whether p-values, especially small p-values, are generated by chance. The global test of p-values is robust and can be applied to p-values from varying statistical models including t-tests, analysis of variance (ANOVA), linear mixed models, and so forth. Multiple simulation studies and case studies have demonstrated that this approach usually has sufficient power to detect signals of genetic association from a group of genes. For instance, Peng et al. (2010) has assessed Fisher's combination test and Sidak's combination test, Sime's combination test and the FDR method using 13 published genome wide association studies (GWAS), and the results indicate that combined p-value approaches can identify biologically meaningful pathways associated with the disease susceptibility. A review of methods of global test of p-values, developmental trends and their application to genetic data analysis has been presented by (Dai et al., 2012b).
One category of global tests of p-values involves combining p-values in the form of ∑iH(pi), where p-values might first be transformed by a function H. So far, several statistical methods have been developed to combine p-values. Let pi(i = 1,2, …, n) be independent p-values obtained from n hypothesis tests. Under the null hypothesis (H0) that p-values follow a Uniform (0, 1) distribution, Fisher (1932) shows that −2 ln (pi) follows a chi-square distribution with 2n degrees of freedom. For a one sided test with a nominal error rate of α, one can reject the null hypothesis when the test statistics exceeds the (1 − α)*100% percentile of χ22n. Stouffer (Stouffer et al., 1949) proposed a z-test by transforming p-values to standard normal variables, i.e., , where Φ−1 is the inverse Cumulative Distribution Function (CDF) for N(0, 1). Under the null hypothesis, the z-test statistic follows N(0, 1).
Although there is no consensus regarding the most powerful method of combining p-values, Littell and Folks (1971, 1973) demonstrated that the Fisher's method of combining independent tests is asymptotically Bahadur efficient (Bahadur, 1967). Subsequently, weighting schemes have been incorporated into the Fisher's method and the z-test. Lancaster (1961) generalized the Fisher method by converting independent p-values to chi-square variables with wi degrees of freedom and he showed that , d = ∑iwi under H0, where γ−1(wi/2,2) is the inverse CDF of Gamma distribution. Mosteller and Bush (1954) proposed a weighted z-test, which follows N(0,1) under H0.
In a separate paper, we have proved that the Lancaster procedure achieves the optimal Bahadur efficiency. We further demonstrated that the Lancaster procedure yields higher Bahadur efficiency than the weighted z-test. The Bahadur efficiency ratio gives the limiting ratio of sample sizes required by two statistics to attain an equally small significance level. Thus, Bahadur efficiency is an important method to compare test statistics. From the perspective of Bahadur efficiency, the Lancaster procedure asymptotically requires a relatively smaller sample size than other weighted p-value combining methods. This prompted us to focus on modification of the Lancaster procedure for correlated genetic data in this work.
Although the Fisher's method and Lancaster procedure both achieve the optimal Bahadur efficiency, the Lancaster procedure is more general and can be viewed as a generalized Fisher's method with weighting functions. There are three advantages to carefully select appropriate weight functions in genetic data analysis. Firstly, weight functions allow incorporation of prior biological information. Genetic data are complex and can be measured from different sources. Thus, weight functions can be used as a tool to incorporate meaningful information from different sources in order to interpret and derive biological insight from gene expression profiles. (Wu and Lin, 2009) provides a review of statistical methods for analysis of microarray data by incorporating prior biological knowledge using gene sets and biological pathways, which consist of groups of biologically similar genes. They show that the use of prior knowledge has led to a better understanding of the biological mechanisms underlying phenotypic responses. Secondly, weight functions can be used to remove bias. For instance, larger genes may contain more probes and/or SNPs. Therefore, larger genes will exert a stronger influence on the p-value combining methods as compared to smaller genes (Wang et al., 2007). To avoid this bias, one can consider a weight function to adjust for gene size when combining p-values. We will illustrate this approach in sections Empirical Assessments and Case Study: Renal Transplant Tolerance Data. Thirdly, as suggested by Benjamini and Hochberg (1997), Genovese et al. (2006), procedures that assign weights positively associated with the underlying alternative hypotheses will usually improve power. Therefore, one needs to carefully choose an appropriate weight function, either based on the biological knowledge, or by statistical hypotheses. An arbitrary weight is inappropriate for the Lancaster procedure.
In this work, we will provide modifications to the Lancaster procedure to accommodate correlation structures among p-values. The proposed method provides a generalization to the Fisher's method with a weight function and can be used in pathway analysis and gene sets enrichment analysis for a variety of genetic data including microarray gene expression data, GWAS data, and next generation sequencing data. In essence, investigators first dissect genetic variants by biological functions or prior knowledge, then combine the p-values from these gene sets to identify whether a proportion of genetic variants are associated with traits.
Correlated Lancaster Procedures
In this section, we allow p-values to be correlated. Consider a Lancaster test statistic where γ−1(wi /2,2) is the inverse CDF of Gamma distribution with a shape parameter wi /2 and a scale parameter 2. This transformation converts pi ~ Uniform(0,1) to a chi-square distribution, i.e., γ−1(wi /2, 2) (1 − pi) ~ χ2wi where χ2wi is a chi-square distribution with wi >0 degree(s) of freedom. The parameter wi serves as a weight function to adjust the individual p-values. When p-values are independent, T has an exact chi-square distribution with degrees of freedom.
For correlated p-values, does not follow . The distribution of T does not have an explicit analytical form. To address this issue, we consider a Satterthwaite approximation by approximating a scaled T statistic with a new chi-square distribution (Li et al., 2011). Let cT ≈ χ2v where c > 0 is a scalar and v > 0 is the degree of freedom for the approximated chi-square distribution. Note that
where takes the correlations among p-values into account.
We propose the following five approaches to approximate the distribution of T. In approximation (A), we use the Satterthwaite method to match the mean and variance of cT and χ2v, and then solve the equations to derive c and v. Koziol (1996) have proposed multiple methods to approximate the Lancaster procedure, but these approximations require the assumption of independence. In approximation (B)–(E), we extend the work of Koziol (1996) to correlated data by first approximating cT with χ2v then approximating χ2v using varying methods.
• TA approximation.
Correlation among p-values is taken into consideration, and then Satterthwaite's approximation is used (Patnaik, 1949) to derive new degrees of freedom:
• TB approximation.
cT is first approximated by χ2v, followed by Fisher's approximation (Fisher, 1922) to χ2v:
• Tc approximation.
After approximating cT by χ2v, the Wilson–Hilferty approximation is performed (Wilson and Hilferty, 1931) to derive χ2v.
• TD approximation.
Approximate cT by χ2v, followed by the Cornish–Fisher expansion (Fisher and Cornish, 1960) to χ2v. Let xα denote the α-percentage point of the standard normal distribution, that is, Φ(xα) = α. It follows that the corresponding percentage point for is given by
• TE approximation.
Approximate cT by χ2v then perform saddle point approximation (Lugannani and Rice, 1980) to χ2v. Let . Then Pr (YE ≤ y) = Φ (ay) − ϕ(by−1 − ay−1) for y≠ 1 and , where , and K(t) = −0.5log (1 − 2t), and ty = (y − 1)/2y.
When the covariance ρij is unknown, one can use the permutation approach to estimate ρij by shuffling the phenotype variable among subjects. For the kth permutation (k = 1,2, …,m), we keep the genetic variants within the subject to preserve the correlation structure, then randomly assign the phenotype variable to subjects. Individual hypothesis testing can be done on all n genetic variants separately to generate the p-value vector pk = (pk1, pk2,… pkn)t. The permutation is repeated m = 1000 times, and ρij is estimated from (p1, p2, … pm).
The accuracy of the five approximate distributions to the correlated Lancaster procedure is then assessed using p-values with varying correlation structures. We consider six different types of correlation structures, including fixed and random compound symmetric as well as random positive definite variance-covariance structures for Σ. Let I be an identity matrix, be a vector of 1 s, ⊗ be the Kronecker product, and superscript t be the transposition. In Cases I–V, let Σ = Block ⊗ I20 be compound symmetric variance matrices with 20 blocks of size 5 where . We vary ρ over two fixed values with ρ = 0.3 for moderate dependence and ρ = 0.6 for strong dependence. In addition, we simulate random correlation coefficients from beta and uniform distributions, i.e., ρ ~ β(0.3, 1.5) and ρ ~ uniform(−0.2, 0.2), which ensures that 20 variance blocks have distinct correlation coefficients ρ within Σ. More generally, we consider random positive definite correlation matrices Σ that vary across samples and simulation runs.
The quantile-quantile (Q-Q) plot assessing the accuracy of the proposed methods when the correlation coefficient ρ = 0.3 is shown in Figure 1. For clarity, the Lancaster statistic T that combines n p-values is renamed as TLancastern in Figure 1. For the original Lancaster procedure under the independence assumption, the general trend of the Q-Q plot is flatter than the reference line y = x, indicating the limiting distribution for the test statistic in the original Lancaster procedure is less dispersed than the distribution of TLancastern under correlation structures. As a result, the original Lancaster procedure will have severely inflated Type I errors. In contrast, the five approximations (TA, …, TE) match the underlying distribution of TLancastern. For data with stronger internal correlation, TA, TD, and TE better approximate TLancastern. The Q-Q plots under other correlation structures are similar to Figure 1. To save space, these similar results are not shown, but can be provided upon request.
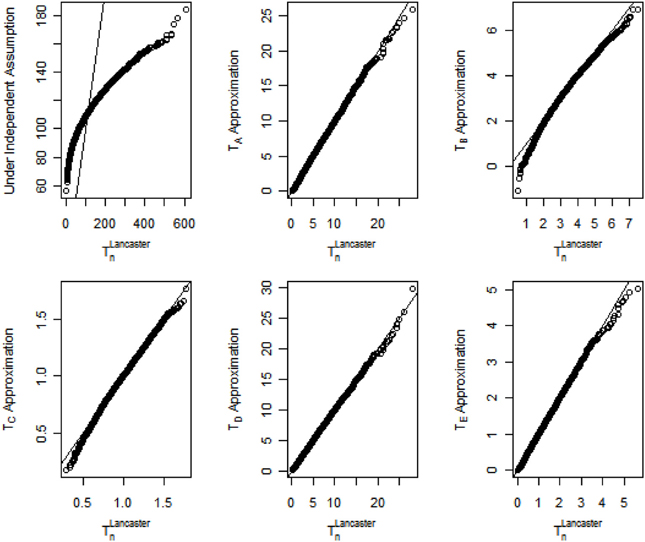
Figure 1. Q-Q plots for distributions of the Lancaster statistic when p-values are correlated with correlation coefficient ρ = 0.3.
Empirical Assessments
We assess the Type I error rates and power for the proposed correlated Lancaster procedures and compare them to the independent Lancaster procedure (Lancaster, 1961). SNPs from a pathway of haploid GWAS are simulated using linkage disequilibrium (LD) (Li et al., 2011). Let q1 and q2 be the minor allele frequencies (MAFs) at loci 1 and 2. Assuming Hardy–Weinberg equilibrium, the genotype at locus 1 can be randomly generated using a binomial distribution. Given the distribution of SNP at locus 1, one can simulate the genotype at locus 2. To do so, let D be a measure of LD. Then the conditional probability for the genotype at locus 2 given the genotype at locus 1 can be expressed as P(A|B) = [qA qB + D]/qB, P(a|B) = [(1 − qA)qB −D]/qB, P(A|b) = [qA (1 − qB)−D]/(1 − qB), and P(a|b) = [(1 − qA)(1 − qB)+D]/(1 − qB) where A and B represent the minor alleles at the two loci. For a diploid genome, similar idea can be applied and the simulation details can be found at Cui et al. (2008). We simulate a pathway with 5 genes with varying numbers of SNPs in each gene listed in parenthesis i.e., G1(12), G2(8), G3(5), G4(3), G5(2). The MAF of each SNP was set to be 0.3. We simulate different levels of LD for SNPs from the same gene with D = 0, 1.5, 2, and uniform(0, maximum of LD). The variable D = 0, 1.5, and 2 suggests no LD, moderate LD, and very strong LD among SNPs with the corresponding correlation R = 0, 0.71, and 0.95. Six scenarios for disease susceptibility (p) are simulated
- Case I: ln (p/(1 − p)) = β1 G1, 2 +β2 G1, 5 +β3 G1, 7 +β4 G1, 8 +β5 G1, 12.
- Case II: ln (p/(1 − p)) = β1 G2, 2 +β2 G2, 4 +β3 G2, 6 +β4 G3, 2 +β5 G3, 3.
- Case III: ln (p/(1 − p)) = β1 G3, 2 +β2 G3, 4 +β3 G4, 1 +β4 G4, 3 +β5 G5, 1.
- Case IV: ln (p/(1 − p)) = β1 G1, 1 +β2 G1, 3 +β3 G1, 7 +β4 G1, 8 G1, 10 G1, 11 +β5 G1, 12.
- Case V: ln (p/(1 − p)) = β1 G3, 1 +β2 G3, 3 +β3 G4, 2 +β4 G3, 2 G3,4 +β5 G4, 3 G5, 1.
- Case VI: ln (p/(1 − p)) = β1 G1, 2 +β2 G2, 2 +β3 G3, 3 +β4 G5, 2 +β5 G1, 5 G1,7 +β6 G3, 3 G5, 1.
Weight functions can be used to remove potential bias when combining p-values. Wang et al. (2007) and others have noted that larger genes contain more probes and/or SNPs. Therefore, larger genes may exert a stronger influence on the p-value combining methods compared to smaller genes. To avoid this bias, we set the weight function is the number of SNPs in the ith gene. When ni = 1, γ−1(wi /2, 2) (1−pi) transforms p-value into a variable with χ22 distribution.
We simulate data with sample sizes n = 200 (Tables 1, 4) and n = 400 (Tables 2, 3), respectively. For simplicity, we assume the same effect size for all of the regression coefficients. For each set of data, we perform the original and modified Lancaster procedures to assess the pathway data by combining p-values from individual tests. We set nominal error rate to be 0.05. The simulation is repeated 1000 times.
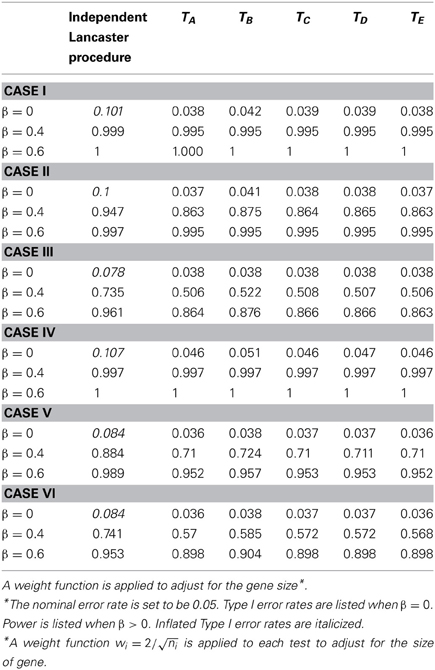
Table 1. Type I error and power for independent Lancaster Procedure and five approximations to correlated Lancaster Procedures when sample size = 200 and linkage disequilibrium D = 0.15.
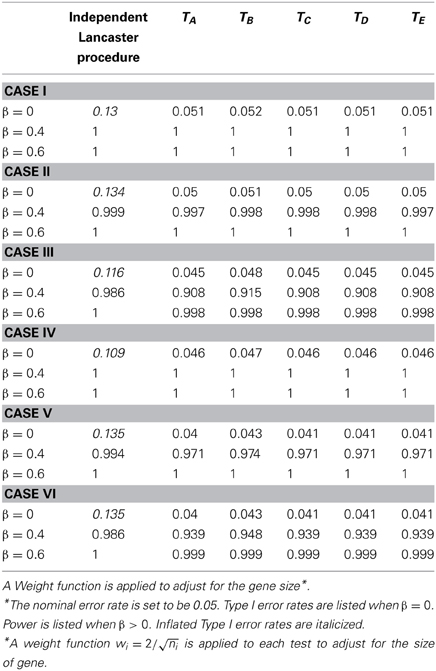
Table 2. Type I error and power for independent Lancaster Procedure and five approximations to correlated Lancaster Procedures when sample size = 400 and linkage disequilibrium D = 0.20.
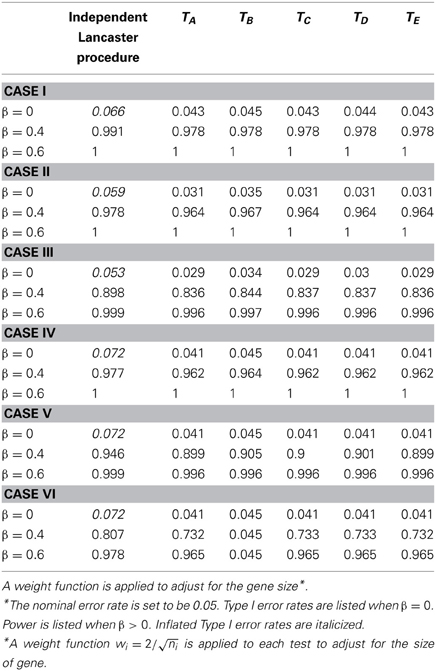
Table 3. Type I error and power for independent Lancaster Procedure and five approximations to correlated Lancaster Procedures when sample size = 400 and linkage disequilibrium D = 0.15.
Due to LD, SNPs from the same gene are correlated. We first assess the Type I error rate of the test statistics by testing H0:β1 = … = β6 = 0. As shown in Tables 1, 2, the Type I error rate for the original Lancaster procedure is inflated (>0.05) for all of the six cases. In contrast, five modified Lancaster procedures (TA − TE) have well controlled Type I error rates (<0.05).
The power of all test statistics was compared for regression coefficient values set at β = 0.4 and β = 0.6, respectively. The results in Tables 1, 2 suggest strong and comparable power among the modified Lancaster procedures. In most simulated cases, the proposed methods have more than 80% power to detect β = 0.4. When the effect size increases to β = 0.6, the power of proposed methods increases to 90% or above. Also the power of these tests improves as sample size increases from n = 200 to n = 400.
We simulate different levels of LD for SNPs with D = 0, 1.5, 2, and uniform(0, maximum of LD). To save the space, we only show the results for D = 1.5 (Table 3) and D = 2 (Tables 1, 2). Our findings show that the inflation of Type I error rate for the original Lancaster procedure gets severe when LD is strong (Tables 1, 2). The modified Lancaster procedures (TA − TE) have well-controlled Type I error rates and power for both moderate and strong LD (Tables 1–3).
In Table 4, we assess the performance of all tests without a weighting function. We then compare the results in Table 4 (without a weight function) vs. Table 1 (with a weight function). All other simulation parameters are held the same in Tables 1, 4. We note that the original Lancaster procedure without a weighting function (Table 4) tends to have higher Type I error rates than the original Lancaster procedure with a weighting function (Table 1). For modified tests (TA − TE), the power is increased when a weighting function is used. This confirms that an appropriate weight function is beneficial to the Lancaster procedure.
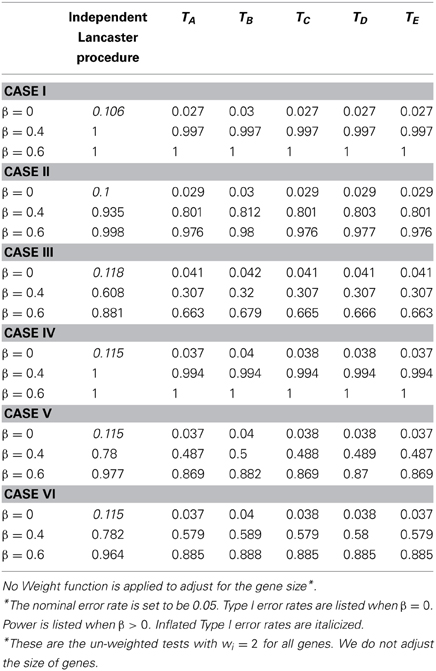
Table 4. Type I error and power for independent Lancaster Procedure and five approximations to correlated Lancaster Procedures when sample size = 200 and linkage disequilibrium D = 0.20.
Case Study: Renal Transplant Tolerance Data
We revisited a kidney transplant data first collected and analyzed by Newell et al. (2010). Data were downloaded from the GEO website with ID = GDS4266 (http://www.ncbi.nlm.nih.gov/sites/GDSbrowser?acc=GDS4266). A group of tolerant renal transplant recipients (Tolerant, n = 19), as defined by stable graft function in the absence of immunosuppression for more than 1 year, were compared to subjects with stable graft function who were receiving standard immunotherapy (SI, n = 27) as well as to a group of healthy controls (Control, n = 12). Gene expression profiles of whole-blood total RNA from all subjects were measured by microarray. The goal of the study was to identify genetic variants associated with long-term allograft survival without the requirement for continuous immunosuppression, a condition known as allograft tolerance. Newell et al. (2010) performed statistical analysis to identify differentially expressed genes between the SI group and the Tolerant group. The results revealed a critical role for B cells in regulating alloimmunity, and provided a candidate set of genes for wider-scale screening of renal transplant recipients. However, no comprehensive pathway analysis was conducted by this group (Newell et al., 2010).
To further understand molecular mechanisms underlying renal allograft tolerance, we have applied the modified Lancaster procedure to this dataset to identify candidate cellular pathways. Gene expression levels were normalized using Robust Multichip Average (rma) preprocessing methodology, which included background subtraction, quantile normalization, and summarization via median-polish.
Gene expression levels were summarized for a total of 54,675 probes from 21,049 genes. Expression levels were compared among three groups using the Bioconductor “Limma” package. Three pair wise comparisons were conducted, including: SI vs. Control, SI vs. Tolerant, and Tolerant vs. Control. Then three comparisons were combined into one F-test. This is equivalent to a One-Way ANOVA for each gene except that the residual mean squares have been moderated across genes. P-values from multiple hypothesis testing were adjusted by FDR (Benjamini and Hochberg, 1995). Our results of differentially expressed genes are consistent with the previous published work. See Newell et al. (2010) for the gene analysis findings.
Although (Newell et al., 2010) identified a set of differentially expressed genes, our analysis demonstrates that these significant genes have small effect sizes with fold changes <1.5. Therefore, a limited number of individual genes in the absence of a biological context is inadequate to explain the total variation of allograft tolerance among renal transplant patients.
To address this issue, we performed the modified Lancaster procedure (TA) as described in Section Correlated Lancaster Procedures to combine p-values from pathways. Combining p-values allows us to integrate small effects in pathway and gain the power of statistical testing. A total of 1454 Gene Ontology human pathway gene sets were analyzed. The size of pathways ranged from 9 genes to 2131 genes, with a median of 27 genes per pathway. Also, the number of probes per gene was highly variable. In order to map genes to pathways, we removed genes without gene symbols from the analysis. Among 21,049 genes with gene symbols, approximately 48% (n = 10161) of genes were interrogated with a single probe, 26% (n = 5389) of genes were queried using 2 probes, 14% (n = 2842) of genes were assessed by 3 probes. There were 3 or more probes for each on the remaining genes (range: 4–17). This finding indicates that larger genes would have more p-values and a stronger impact to pathway analysis. To prevent this bias, we set the weight function as swhere ni is the number of probes for the ith gene.
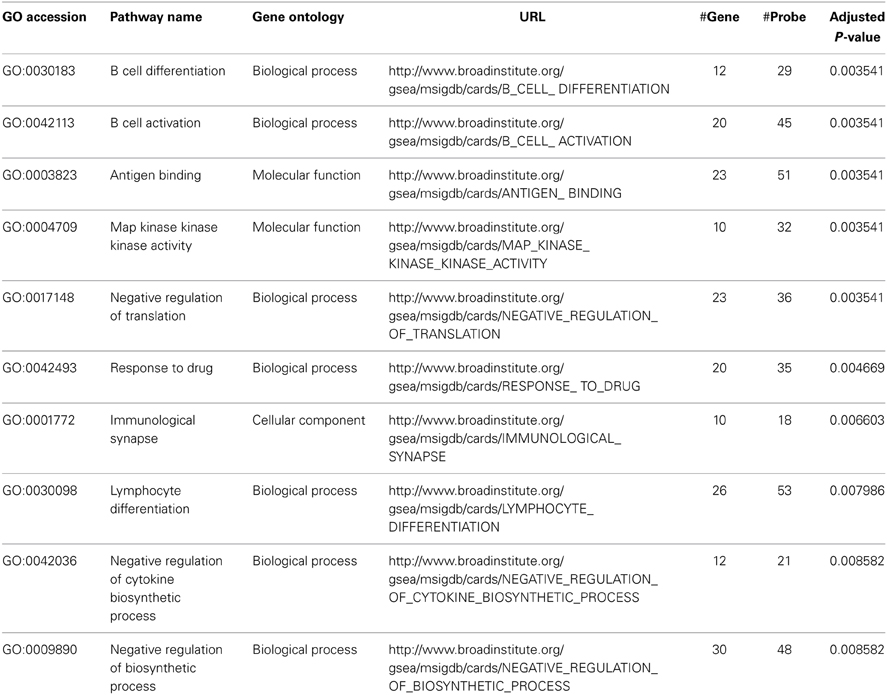
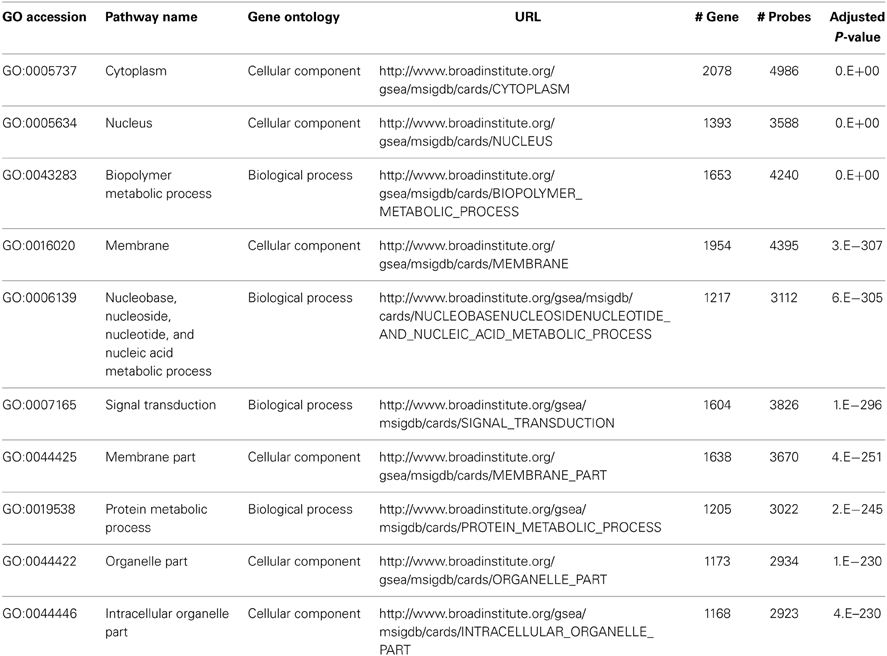
We performed pathway analysis for the One-Way ANOVA test and three pair wise comparisons. The top 10 significant pathways based on the One-Way ANOVA test are listed in Table 5. The top two pathways, B cell differentiation (GO:0030183) and B cell activation (GO:0042113), confirm the signature of B cell involvement described by Newell et al. (2010). Furthermore, we identified other pathways related to B cell activation and function. These include antigen binding (GO:0003823), map kinase kinase kinase activity (GO:0004709) and lymphocyte differentiation (GO:0030098). These pathways are biologically consistent with the proposed role of B-lymphocytes in renal transplant tolerance reported by Newell et al. In contrast, when we performed the traditional Fisher's method without considering correlation structures (LD) within pathways or applying a weighting function to compensate for variability in the number of probes per gene, the result was a list of larger pathways, some containing >1000 genes, describing more general cellular processes and not specifically related to immune functions (See Table 6, #gene and #probe). Furthermore, when comparing the SI group and the Control group, the traditional method identified 1078 significant pathways while our proposed method narrowed the list down to 64 significant pathways (adjusted p-value <0.05). The increase in number of significant pathways identified by the traditional approach is primarily due to false positive discovery, and is consistent with the inflation of Type I error rate as presented in Section Empirical Assessments. Thus, by accounting for correlation structures (LD) within pathways and the number of probes per gene, our proposed method minimized identification of larger, non-specific cellular processes pathways, and instead revealed more focused and functionally relevant biological pathways implicating a role for a humoral immune response in immunotolerance to renal transplants (See Table 5, #gene and #probe).
Discussion and Conclusions
Modifications to the Lancaster procedure are proposed to take correlations among p-values into account. Extensive simulation studies show that the original Lancaster procedure has inflated Type I error rates due to correlation among p-values. By using permutation approach to estimate the correlation among p-values, the proposed methods have well-controlled Type I error rates and maintain strong power to detect signals related to SNPs in pathways.
Among five proposed approximation methods (TA, …, TE), the Satterthwaite approximation (TA) is the most computationally efficient. Other approximation methods (TB, …, TE) are based on the Satterthwaite approximation. Therefore, we recommend using the Satterthwaite approximation (TA) as the standard procedure to modify the Lancaster procedure. Among other approximation methods, simulation results in Section Correlated Lancaster Procedures show that, for data with stronger internal correlation, TD and TE have better approximation than TB and TC. Our simulation study and the case study further provide evidence that TD tends to have slightly higher power than the Satterthwaite approximation TA. The R code for five approximation is posted at http://d.web.umkc.edu/daih/.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank two reviewers for their constructive comments, which helped us improve the manuscript. This work was supported in part by NSF grant DMS-1209112 (to Yuehua Cui).
References
Bahadur, R. R. (1967). Rates of convergence of estimates and test statistics. Ann. Math. Stat. 38, 303–324. doi: 10.1214/aoms/1177698949
Benjamini, Y., and Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. B 57, 289–833. doi: 10.2307/2346101
Benjamini, Y., and Hochberg, Y. (1997). Multiple hypothesis testing with weights. Scand. J. Stat. 24, 407–417. doi: 10.1111/1467-9469.00072
Cheng, C., and Pounds, S. (2007). False discovery rate paradigms for statistical analyses of microarray gene expression data. Bioinformation 1, 436–446. doi: 10.6026/97320630001436
Cui, Y., Kang, G., Sun, K., Qian, M., Romero, R., and Fu, W. (2008). Gene-centric genomewide association study via entropy. Genetics 179, 637–650. doi: 10.1534/genetics.107.082370
Dai, H., Bhandary, M., Becker, M. L., Leeder, S. J., Gaedigk, R., and Motsinger-Reif, A. A. (2012a). Global tests of p-values for multifactor dimensionality reduction models in selection of optimal number of target genes. BioData Min. 5:3. doi: 10.1186/1756-0381-5-3
Dai, H., Charnigo, R., Srivastava, T., Talebizadeh, Z., and Ye, S. (2012b). Integrating P-values for genetic and genomic data analysis. J. Biom. Biostat. 3:e117. doi: 10.4172/2155-6180.1000e117
Dai, H., and Charnigo, R. (2008). Omnibus testing and gene filtration in microarray data analysis. J. Appl. Stat. 35, 31–47. doi: 10.1080/02664760701683528
Fisher, R. A. (1922). On the interpretation of x2 from contingency tables and calculation of p. J. R. Stat. Soc. A 85, 87–94. doi: 10.2307/2340521
Fisher, R. A., and Cornish, E. A. (1960). The percentile points of distributions having known cumulants. Technometrics 2, 209–225. doi: 10.1080/00401706.1960.10489895
Genovese, C. R., Roeder, K., and Wasserman, L. (2006). False discovery control with p-value weighting. Biometrika 93, 509–524. doi: 10.1093/biomet/93.3.509
Kanehisa, M., Goto, S., Kawashima, S., Okuno, Y., and Hattori, M. (2004). The KEGG resource for deciphering the genome. Nucleic Acids Res. 32, D277–D280. doi: 10.1093/nar/gkh063
Khatri, P., Sirota, M., and Butte, A. J. (2012). Ten years of pathway analysis: current approaches and outstanding challenges. PLoS Comput. Biol. 8:e1002375. doi: 10.1371/journal.pcbi.1002375
Koziol, J. A. (1996). A note on Lancaster's procedure for the combination of independent events. Biom. J. 38, 653–660. doi: 10.1002/bimj.4710380603
Lancaster, H. D. (1961). The combination of probabilities: an application of orthonomral functions. Aust. J. Stat. 3, 20–33. doi: 10.1111/j.1467-842X.1961.tb00058.x
Li, S., Williams, B. L., and Cui, Y. (2011). A combined p-value approach to infer pathway regulations in eQTL mapping. Stat. Interface 4, 389–402. doi: 10.4310/SII.2011.v4.n3.a13
Littell, R. C., and Folks, J. L. (1971). Asymptotic optimality of Fisher's method of combining independent tests. J. Am. Stat. Assoc. 66, 802–806. doi: 10.1080/01621459.1971.10482347
Littell, R. C., and Folks, J. L. (1973). Asymptotic optimality of Fisher's method of combining independent tests. II. J. Am. Stat. Assoc. 68, 193–194. doi: 10.1080/01621459.1973.10481362
Lugannani, R., and Rice, S. O. (1980). Saddlepoint approximation for the sum of independent random variables. Adv. Appl. Probab. 12, 475–490. doi: 10.2307/1426607
Matthews, L., Gopinath, G., Gillespie, M., Caudy, M., Croft, D., de Bono, B., et al. (2009). Reactome knowledgebase of human biological pathways and processes. Nucleic Acids Res. 37, D619–D622. doi: 10.1093/nar/gkn863
Mosteller, F., and Bush, R. R. (1954). Selected quantitative technique. Handb. Soc. Psychol. 1, 289–334.
Newell, K. A., Asare, A., Kirk, A. D., Gisler, T. D., Bourcier, K., Suthanthiran, M., et al. (2010). Identification of a B cell signature associated with renal transplant tolerance in humans. J. Clin. Invest. 120, 1836–1847. doi: 10.1172/JCI39933
Nikolsky, Y., and Bryant, J. (2009). Protein networks and pathway analysis. Preface. Methods Mol. Biol. 563, v–vii. doi: 10.1007/978-1-60761-175-2
Patnaik, P. B. (1949). The non-central x2 - and F - distributions and their applications. Biometrika 36, 202–232.
Peng, G., Luo, L., Siu, H., Zhu, Y., Hu, P., Hong, S., et al. (2010). Gene and pathway-based second-wave analysis of genome-wide association studies. Eur. J. Hum. Genet. 18, 111–117. doi: 10.1038/ejhg.2009.115
Stouffer, S., DeVinney, L., and Suchmen, E. (1949). The American Solder: Adjustment during Army Life. Vol. 1. Princeton, NJ: Princeton University Press.
Subramanian, A., Tamayo, P., Mootha, V. K., Mukherjee, S., Ebert, B. L., Gillette, M. A., et al. (2005). Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. U.S.A. 102, 15545–15550. doi: 10.1073/pnas.0506580102
Wacholder, S., Chanock, S., Garcia-Closas, M., El Ghormli, L., and Rothman, N. (2004). Assessing the probability that a positive report is false: an approach for molecular epidemiology studies. J. Natl. Cancer Inst. 96, 434–442. doi: 10.1093/jnci/djh075
Wang, K., Li, M., and Bucan, M. (2007). Pathway-based approaches for analysis of genomewide association studies. Am. J. Hum. Genet. 81, 1278–1283. doi: 10.1086/522374
Wilson, E. B., and Hilferty, M. M. (1931). The distribution of chi-square. Proc. Natl. Acad. Sci. U.S.A. 17, 684–688. doi: 10.1073/pnas.17.12.684
Keywords: generalized Fisher method (Lancaster procedure), weight function, correlated p-values, multiple hypothesis testing, high dimensional genetic data
Citation: Dai H, Leeder JS and Cui Y (2014) A modified generalized Fisher method for combining probabilities from dependent tests. Front. Genet. 5:32. doi: 10.3389/fgene.2014.00032
Received: 05 November 2013; Accepted: 27 January 2014;
Published online: 20 February 2014.
Edited by:
José M. Álvarez-Castro, Universidade de Santiago de Compostela, SpainReviewed by:
Wei Hou, Stony Brook University, USAJ. Concepcion Loredo-Osti, Memorial University, Canada
Copyright © 2014 Dai, Leeder and Cui. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hongying Dai, Department of Pediatrics, Research Development and Clinical Investigation, Children's Mercy Hospital, 2401 Gillham Road, Kansas City, MO 64108, USA e-mail:aGRhaUBjbWguZWR1
 Hongying Dai
Hongying Dai J. Steven Leeder
J. Steven Leeder Yuehua Cui
Yuehua Cui