- 1Genus plc, Hendersonville, TN, USA
- 2Department of Animal and Dairy Science, University of Georgia, Athens, GA, USA
- 3Instituto Nacional de Investigación Agropecuaria, INIA Las Brujas, Mejoramiento Genético Animal, Canelones, Uruguay
- 4Institut National de la Recherche Agronomique, UR631 Station d'Amélioration Génétique des Animaux, Castanet-Tolosan, France
- 5Department of Animal Science, Iowa State University, Ames, IA, USA
- 6Département de Sciences Animales, Ecole Nationale Superieure Agronomique de Toulouse, Université de Toulouse, Castanet-Tolosan, France
- 7Cobb-Vantress Inc., Siloam Springs, AR, USA
- 8Department of Animal Science, Purdue University, West Lafayette, IN, USA
The purpose of this study was to compare results obtained from various methodologies for genome-wide association studies, when applied to real data, in terms of number and commonality of regions identified and their genetic variance explained, computational speed, and possible pitfalls in interpretations of results. Methodologies include: two iteratively reweighted single-step genomic BLUP procedures (ssGWAS1 and ssGWAS2), a single-marker model (CGWAS), and BayesB. The ssGWAS methods utilize genomic breeding values (GEBVs) based on combined pedigree, genomic and phenotypic information, while CGWAS and BayesB only utilize phenotypes from genotyped animals or pseudo-phenotypes. In this study, ssGWAS was performed by converting GEBVs to SNP marker effects. Unequal variances for markers were incorporated for calculating weights into a new genomic relationship matrix. SNP weights were refined iteratively. The data was body weight at 6 weeks on 274,776 broiler chickens, of which 4553 were genotyped using a 60 k SNP chip. Comparison of genomic regions was based on genetic variances explained by local SNP regions (20 SNPs). After 3 iterations, the noise was greatly reduced for ssGWAS1 and results are similar to that of CGWAS, with 4 out of the top 10 regions in common. In contrast, for BayesB, the plot was dominated by a single region explaining 23.1% of the genetic variance. This same region was found by ssGWAS1 with the same rank, but the amount of genetic variation attributed to the region was only 3%. These findings emphasize the need for caution when comparing and interpreting results from various methods, and highlight that detected associations, and strength of association, strongly depends on methodologies and details of implementations. BayesB appears to overly shrink regions to zero, while overestimating the amount of genetic variation attributed to the remaining SNP effects. The real world is most likely a compromise between methods and remains to be determined.
Introduction
Genome-wide association analysis (GWAS) is an efficient way to discover QTLs associated with phenotypes. A common method for GWAS is to sequentially fit all SNPs one at a time as a fixed effect in a mixed model that includes the pedigree or genomic relationship matrix to control for polygenic background effects (Meyer and Tier, 2012; Xie et al., 2012). Another method utilizes all markers simultaneously using a Bayesian framework (Abasht et al., 2009). If the phenotypes used in these analyses are BLUP estimates of breeding values, both methods may have severe limitations. When much of the phenotypic information is on ungenotyped animals, the BLUP estimates need to be de-regressed (DP) (Garrick et al., 2009), which can lead to biases and losses of accuracy (Vitezica et al., 2011; Ricard et al., 2013). Calculation of DP relies on accuracies of estimated breeding values. For large data sets, such accuracies cannot be computed directly and need to be approximated and for complex models and data structures, such approximations may be poor or unavailable (Sanchez et al., 2008).
An alternative GWAS approach was recently proposed by Wang et al. (2012) where all genotypes, observed phenotypes and pedigree information are jointly considered in one step (ssGBLUP), and thus allows the use of any model, and all relationships simultaneously. With this approach, all SNPs are considered simultaneously along with all phenotypes from those genotyped and ungenotyped. The latter is accomplished by augmenting the genomic relationships with traditional pedigree relationships (Aguilar et al., 2010). With this approach GWAS is accomplished by converting the estimated breeding values (GEBVs) obtained from ssGBLUP to marker effects and marker weights, which are then used in an iterative approach to update solutions. The theoretical advantage of this method is that it uses all phenotypic information for which either the pedigree or marker effects are known, and can be used for any model for which BLUP estimates of breeding values can be obtained (Wang et al., 2012). GWAS by ssGBLUP can be called ssGWAS. Dikmen et al. (2013) applied ssGWAS for identification of QTLs for rectal temperature during heat stress in Holsteins using a model with many effects.
Wang et al. (2012) examined the efficiency of the ssGWAS method by simulation. In those simulations, ssGWAS achieved the highest correlation between QTL effect and the sum of 8 adjacent SNP effects as compared to BayesB (Habier et al., 2011) or classical GWAS (Meyer and Tier, 2012), while at the same time was faster and simpler to apply than other methods. However, simulated data may not reflect true world genetic architectures, such as LD patterns, allelic effect distributions, and number of loci affecting the trait, which may affect the comparisons. The objective of this study was to compare the same three GWAS methods using real data to detect QTLs for body weight at 6 weeks (BW6) in broiler chickens.
Materials and Methods
Animal Care and Use Committee approval was not obtained for this study because the data were obtained from an existing database.
Data
Body weights at 6 weeks (BW6) for broiler chickens were provided by Cobb-Vantress Inc. (Siloam Springs, AR) for a dam line across 5 generations (G1, G2 G3, G4, and G5). The total number of animals with phenotypes was 274,776, and the average BW6 was 2.40 ± 0.33 kg. Complete pedigrees were available for all individuals. For generations G1–G4, 4732 broilers were genotyped with 57,636 SNP markers on a SNP panel across the whole genome developed by Groenen et al. (2011).
Quality control (QC) procedures were applied to remove genotyped individuals with pedigree errors and SNP genotypes that were either monomorphic, or displaced segregation distortion according to Wiggans et al. (2010) with methodology by Aguilar et al. (2011). After QC, 179 birds were removed for pedigree errors and 4553 birds (2205 in G1, 737 in G2, 818 in G3, 793 in G4) with 40,615 autosomal SNPs remained in the data set. Moreover, the number of SNP loci with missing genotypes reduced from 29.8 to 0.32%.
Models and Computation
Single-step genomic association study
The ssGWAS method is a modification of BLUP with the numerator relationship matrix A−1 matrix replaced by H−1 (Aguilar et al., 2010):
where A22 is a numerator relationship matrix for genotyped animals and G is a genomic relationship matrix. The genomic matrix can be created following Vanraden (2008) as:
where Z is a matrix of gene content adjusted for allele frequencies, D is a weight matrix for SNP (initially D = I), and q is a weighting factor. The weighting factor can be derived either based on SNP frequencies (Vanraden, 2008), or by ensuring that the average diagonal in G is close to that of A22 (Vitezica et al., 2011). The latter method was used in this study. Briefly, SNP effects and weights for GWAS were be derived as follows (Wang et al., 2012):
- Let D = I in the first step.
- Calculate G = ZDZ′q.
- Calculate GEBVs for entire data set using ssGBLUP.
- Convert GEBVs to SNP effects (û): û = qDZ′(ZDZ′q)−1â, where â is the GEBVs of animals which were also genotyped.
- Calculate weight for each SNP: di = û2i2pi(1−pi), where i is the i-th SNP.
- Normalize SNP weights to remain the total genetic variance constant.
- Loop to 2. (ssGWAS1) or 4. (ssGWAS2).
SNP weights were calculated iteratively either looping through steps 4–6 (ssGWAS1) or through steps 2–6 (ssGWAS2). Iterations with both scenarios increase weights of SNP with large effects and decrease those with small effects, essentially regressing them to the mean. Experiences with simulated data using ssGBLUP (Wang et al., 2012) and of a similar method based on GBLUP (Sun et al., 2012; Zhang et al., 2012) indicated that ssGWAS1 was more suitable for identification of SNPs with the largest effects while ssGWAS2 was superior for more accurate GEBVs.
Percentage of genetic variance explained by i-th region has been calculated as below:
Where ai is genetic value of the i-th region that consists of contiguous 20 SNPs, σ2a is the total genetic variance, Zj is vector of gene content of the j-th SNP for all individuals, and ûj is marker effect of the j-th SNP within the i-th region.
Computations
For analyses, we applied an animal model with fixed effects of sex and contemporary group and random effects for additive animal and maternal permanent environment. Variance components were estimated by REML based on all the individuals in the pedigree. All analyses for REML, BLUP and ssGWAS were run using the BLUPF90 software (Misztal et al., 2002; Aguilar et al., 2011). For BayesB and CGWAS methods, DP were created from BLUP estimates of EBVs as pseudo-observations, following Garrick et al. (2009) assuming that 0.1 of the genetic variance was not accounted for by SNPs, as in Ostersen et al. (2011). GWAS was then performed using three alternative methods. The first method of ssGWAS was run for five iterations with both ssGWAS1 and ssGWAS2 options. The second method of CGWAS was implemented in WOMBAT (Meyer and Tier, 2012). The third method, BayesB was implemented in GenSel (Habier et al., 2011) with π = 0.9. Estimates of genotypic and residual variances from REML were used as priors in BayesB, which followed a scaled inverse Chi-squared distribution with default parameters used in GenSel. The use of the default parameter π = 0.9 was due to failure for convergence of π estimation based on BayesCπ after 100,000 iterations. A Monte Carlo Markov Chain was completed for 51,000 rounds with Gibbs sampling, of which the first 1000 rounds were discarded as burn-in. Within each Gibbs sample cycle, Metropolis-Hastings samples were run for 10 iterations. Because WOMBAT and GenSel are not able to incorporate missing genotypes, missing SNPs were replaced by their average value for that locus.
Results were compared based on the proportion of total variance explained by the SNP. However, such estimates based on single-SNP were found to be noisy from all the methods due to the high ratio between the number of SNPs and the number of genotyped individuals. Therefore, non-overlapping windows of 20 consecutive SNPs were used to present results in Manhattan plots, instead of single locus. The methods were also compared based on the top 10 ranking windows for genetic variance explained by that window.
The methods were additionally compared in terms of predicted GEBVs. For ssGWAS, GEBVs were obtained directly, whereas for CGWAS and BayesB, GEBVs were calculated as the sum of estimated SNP effects for each genotyped individual. For comparison of accuracy of phenotypic BLUP and ssGWAS, realized accuracies were computed for ssGWAS1 and ssGWAS2, as the ratio of predictive ability over the square root of heritability according to Legarra et al. (2008).
Results and Discussion
Genetic Estimations
Variance components, calculated from regular phenotypic BLUP based on all individuals in the data set, for maternal permanent environmental, additive and residual variances, were respectively 0.20, 1.14, and 3.88. The estimated heritability of BW6 was 0.22, which was similar to earlier estimates using the same trait (Chen et al., 2011).
Table 1 includes correlations between EBV (obtained from regular BLUP) and GEBVs for genotyped individuals; solutions for GEBVs in ssGWAS1 do not change between iterations, and they are the same as the first iteration in ssGWAS2 (ssGWAS2/1). The correlations between EBVand GEBVs for ssGWAS2 in the first and second iterations, and BayesB, were all ≤0.9; while for CGWAS, and ssGWAS with 3 or more iterations, the correlations were <0.9. As SNP effects are calculated in CGWAS individually, estimates for closely linked SNP were similar, which results in correlated residual and is likely to cause problems due to double counting. The decline in correlations after 2 iterations implies the estimates were over-regressing, resulting in lower accuracy.
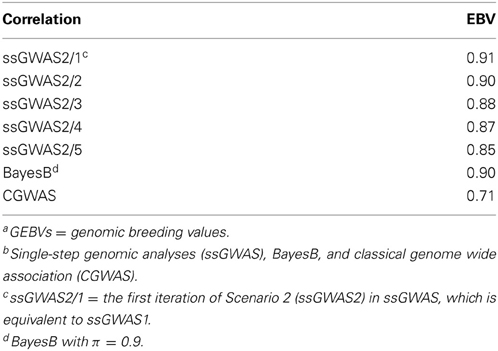
Table 1. Correlations of EBV obtained from regular BLUP and GEBVsa obtained from three approachesb for genotyped individuals.
Table 2 gives realized accuracies of EBV estimated using phenotypic BLUP and GEBVs estimated using ssGWAS. For these data, the accuracy was maximized by the second iteration (ssGWAS2/2), then declined after the third iteration (ssGWAS2/3). For GBLUP, Sun et al. (2012) added a constant in the equation to calculate SNP variance, mimicking the structure of such formulas in REML. Subsequently, the accuracy reached plateau but did not decline with iterations. In our studies, involving such a constant (results not shown), the accuracy did not improve over ssGWAS2/2 with the original formula. Further, adding a constant makes identification of top QTL more difficult (Sun et al., 2011).

Table 2. Comparison of accuracies of EBV obtained from regular BLUP and GEBVsa from ssGWAS2b with up to 5 iterations.
QTL Mapping
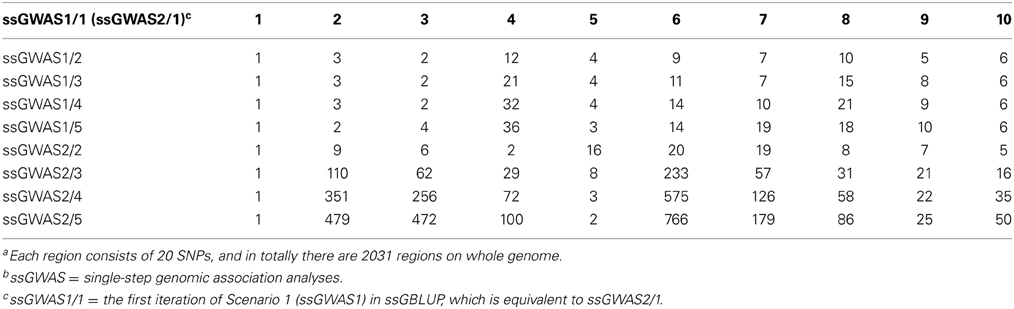
Figures 1–4 show plots of genetic variances accounted for by windows of 20 contiguous SNPs within a chromosome, based on different methods. Windows were neither overlapping nor repetitive. Chromosomes were differentiated by different shades. In total, there were 2031 regions, with an average chromosomal length of 0.45 Mbp.
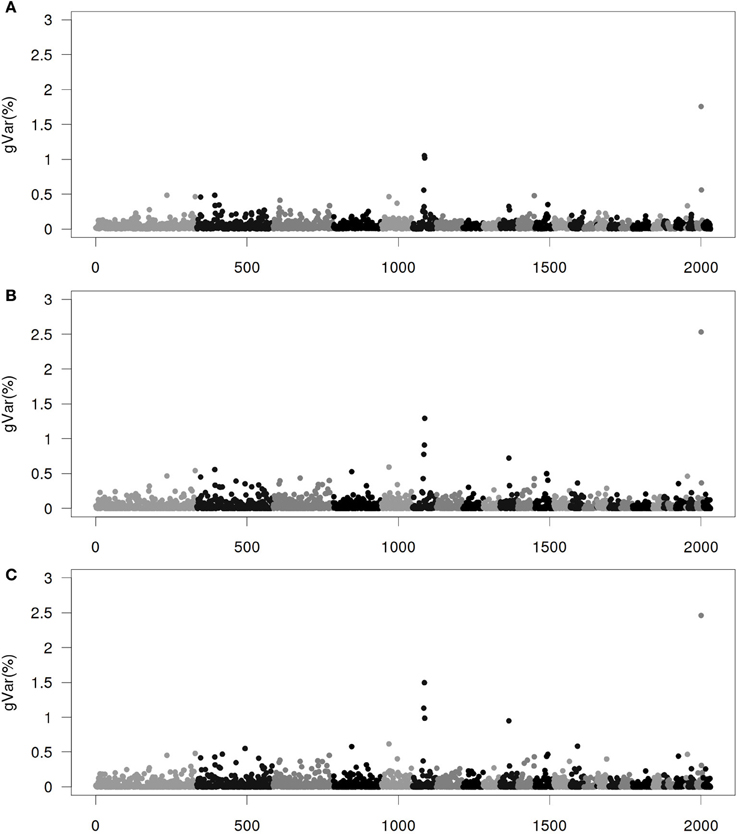
Figure 1. Proportion of genetic variance of 20-SNP region under the Senarios 1 (ssGWAS1) of extended single-step genomic BLUP (ssGBLUP). (A) The first iteration (ssGWAS1/1). (B) The third iteration (ssGWAS1/3). (C) The fifth iteration (ssGWAS1/5). The x-axis represents region location of 20 SNPs. The y-axis represents the proportion of genetic variance of each region.
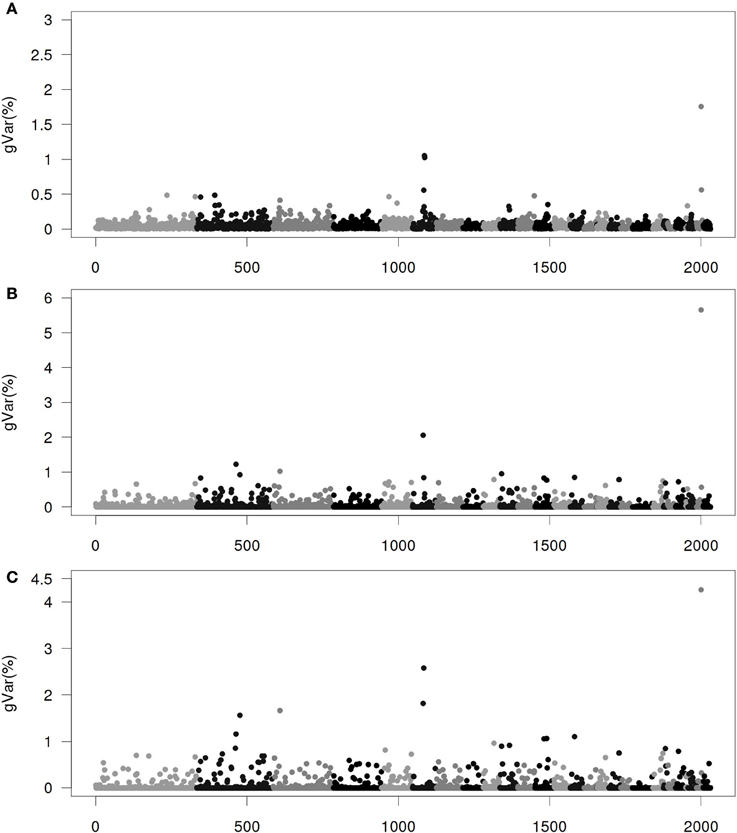
Figure 2. Proportion of genetic variance of 20-SNP region under the Senarios 2 (ssGWAS2) of extended single-step genomic BLUP (ssGBLUP). (A) The first iteration (ssGWAS2/1). (B) The third iteration (ssGWAS2/3). (C) The fifth iteration (ssGWAS2/5). The x-axis represents region location of 20 SNPs. The y-axis represents the proportion of genetic variance of each region.
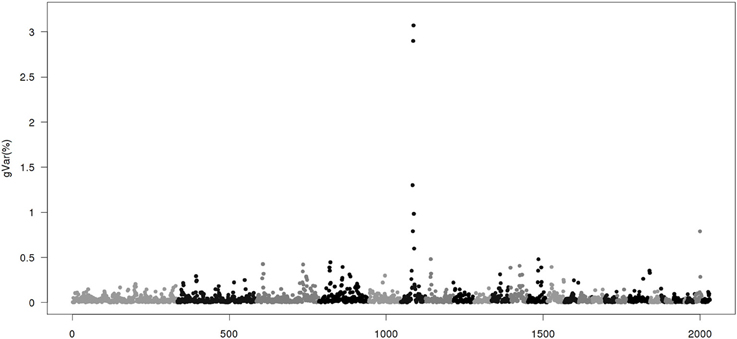
Figure 3. Proportion of genetic variance of 20-SNP region using classical genome wide association studies (CGWAS) implemented by WOMBAT. The x-axis represents region location of 20 SNPs. The y-axis represents the proportion of genetic variance of each region.
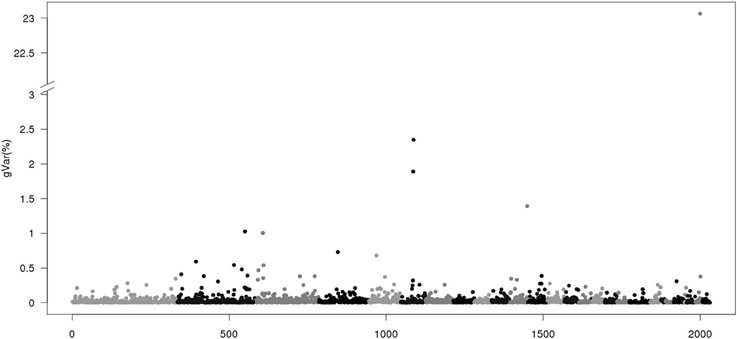
Figure 4. Proportion of genetic variance of 20-SNP region using BayesB with π = 0.9 implemented by GenSel. The x-axis represents region location of 20 SNPs. The y-axis represents the proportion of genetic variance of each region.
Figure 1 shows plots by ssGWAS1/1, ssGWAS1/3, and ssGWAS1/5, which indicate iteration 1, 3, and 5 using ssGWAS1, which derives weights and solely iterates on SNPs. On one hand, as the iterations progress, the plots became less noisy, and the peaks associated with the largest regions become more distinct. On the other hand, the iterations caused some re-rankings of the top regions (Table 3). The simulation studied by Sun et al. (2011) indicated that a few iterations similar to ssGWAS1 provided the most accurate identification of the top QTLs.
Figure 2 shows plots by ssGWAS2/1, ssGWAS2/3, and ssGWAS2/5 iterating on both SNPs and GEBVs. Please note that the plots for ssGWAS1/1 and ssGWAS2/1 are identical. Compared with ssGWAS1, “thinning” in ssGWAS2 is more rapid. The plot of ssGWAS2/3 clearly points to many distinct regions, while the plot in ssGWAS1/3 seems less so. Note that the accuracy of GEBVs peaked at ssGWAS2/2 to ssGWAS2/3 and declined thereafter, suggesting that plots of ssGWAS2/2 and ssGWAS2/3 are also the most accurate depictions of where the most important regions are.
Figure 3 gives results from the CGWAS method. With this method, more peaks were found than from ssGWAS. However, the two largest regions remained the same as ssGWAS1/1-ssGWAS1/5. The presence of many more peaks in CGWAS than the other methods is most likely a result of strongly linked regions resulting in false positive (Shen et al., 2013).
Figure 4 gives results for the BayesB method. The plot is dominated by a few large regions, with all the other regions representing much smaller variances ≤2.5%. Methods like BayesB are strongly influenced by priors (Van Hulzen et al., 2012), and particularly by the percentage of SNPs assumed to have null effect (π). Studies on the number of genes influencing a quantitative effect estimate the number of <500 (Otto and Jones, 2000; Hayes and Goddard, 2001). Here, we assume that 10% of all SNPs (>4000) have effects. However, some of the alleles are rare variants that are not fully captured by medium or even high density SNP panels (Vinkhuyzen et al., 2012). For populations with small effective size, gains in GEBVs over EBVs in genomic selection are partly due to accounting for major genes, and partly for superior genetic relationships among animals. Fitting single chromosome in a genomic evaluation resulted in 86% of accuracy of GEBVs from using SNPs on all 26 chromosomes (Daetwyler et al., 2012). As the relationship information is replicated on all chromosomes but the QTL effects are not, the majority of large SNP effects may be due to specific population structure and not due to QTLs.
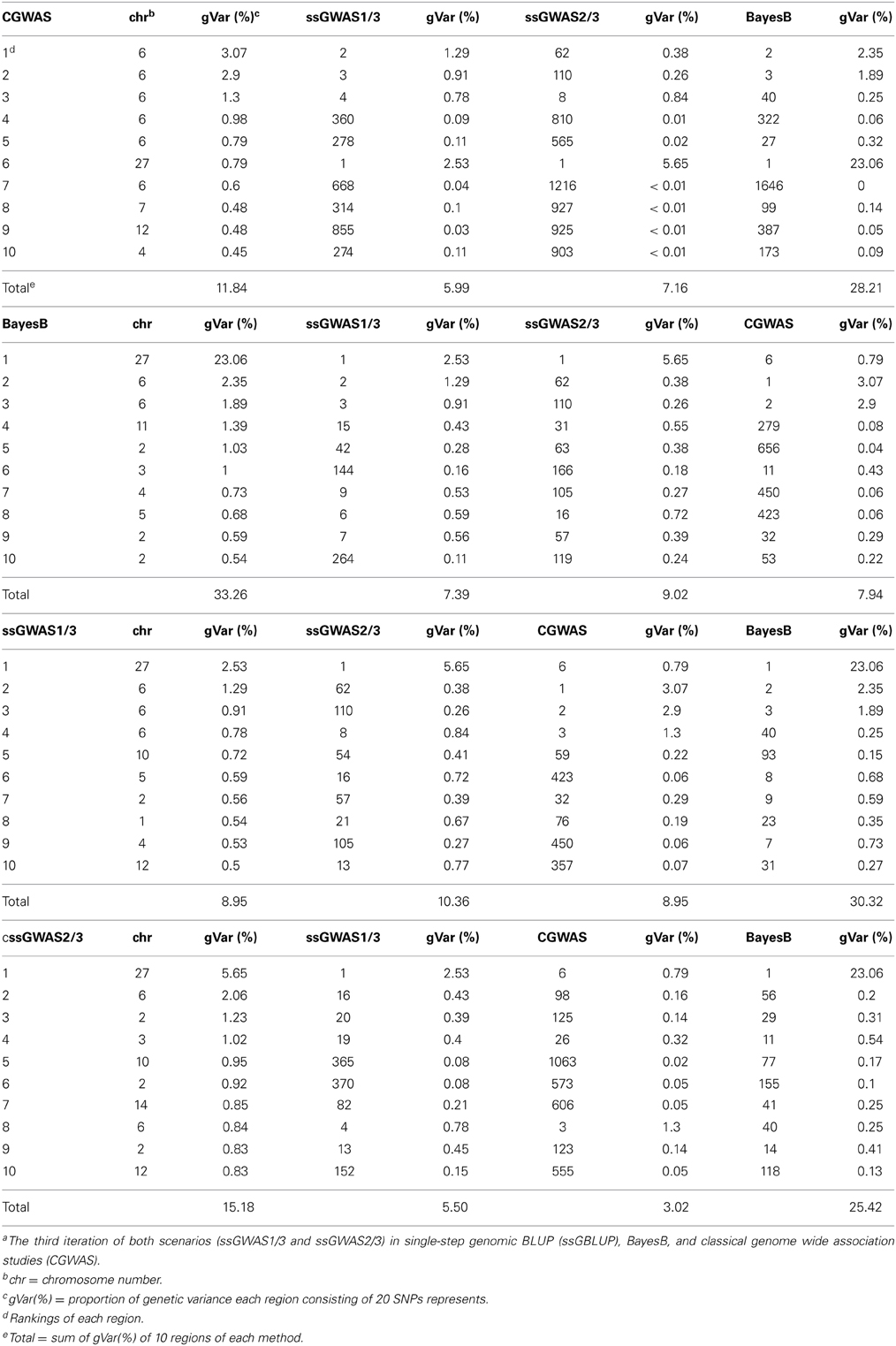
Table 4 shows chromosomal positions and fraction of variances explained by the top 10 regions of the 4 methods: CGWAS, BayesB, ssGWAS1 and ssGWAS2. For ssGWAS1/3 and BayesB, the regions that accounted for the largest genetic variance were on chromosome 27 and identical, but accounted for vastly different amounts of genetic variance: 2.53 and 23.06%, respectively. The order of magnitude difference in genetic variance accounted for by the methods, even though the regions were the same, is due to how total genetic variance is accounted for by the methods. BayesB partitioned all the genetic variance to 10% of the SNPs while ssGWAS partitions the genetic variance among all SNPs. Thus, ssGWAS has more SNPs to distribute the same amount of genetic variance.
Among the top 10 regions in ssGWAS1/3, there were 2, 4, and 6 regions respectively in common with ssGWAS2/3, CGWAS, and BayesB. In contrast, for the top 10 regions in BayesB, there were 6, 1, and 3 in common, respectively, with ssGWAS1/3, ssGWAS2/3 and CGWAS. Among the top 10 regions in CGWAS, there were 4, 3, 2, in common with ssGWAS1/ 3, BayesB, and ssGWAS2/3. Thus, in general, the rankings of top 10 regions were similar between ssGWAS (ssGWAS1 and ssGWAS2) and BayesB. The re-rankings in CGWAS was greater compared with the other methods. Additionally, the fraction of explained variance varied greatly among methods. Because of the way BayesB partitions variances among a fraction of the total SNPs, it is expected that BayesB will always assign a greater proportion of genetic variance to a SNP in any GWAS comparison.
The comparison between ssGBLUP and CGWAS is more direct. Part of the reason that CGWAS accounts for less genetic variance than ssGWAS may be because CGWAS does not take into account all relationships among subjects but only for genotyped individuals, which might lead to detection of spurious associations due to incompleteness (Kang et al., 2010). BayesB and CGWAS are also dependent on the choice of parameters and accuracy of deregression (Garrick et al., 2009; Van Hulzen et al., 2012), while ssGWAS1 or ssGWAS2 include all available relationships, and deregression is not necessary. Zeng et al. (2012) and Wang et al. (2012) examined a few methods for GWAS using simulated data sets, and both indicated that all methods were able to identify the same top few regions. However, few regions were common among methods in this study suggesting that simulations do not capture the complexities of real data and highlight the need to do comparisons using real data.
Many studies have looked at QTLs or chromosomal regions in chicken for body weight. For example, Rowe et al. (2006) looked for QTLs for 40-day body weight in Cobb-Vantress chickens. They found that chromosomal segments could explain up to 4% phenotypic variation (PV) on chromosomes 1, 4, and 5. Podisi et al. (2013) looked at body weight and gains at different ages for broiler-layer crosses. For body weight at 6 weeks, they identified several QTLs on chromosomes 1–4, 6, 8, 11, and 13 explaining >1.4% PV; the largest QTL was on chromosome 4 and explained 6.0% PV. Neither study found an important QTL on chromosome 27. The large proportion of explained variance could be due to simple models of analyses.
Considerations
Windows were defined with fixed numbers of SNPs (i.e., 20), which might not match every pattern of haplotype blocks. Thus, over- or under-estimation of window variances were possible. Moreover, window variances were calculated based on SNP effects at each locus, which probably contains estimation errors, and translates into more variation in results for ssGWAS2. The noise due to the estimation process could be reduced by using sliding average values for SNP windows rather than point estimates.
Results showed that interpretation of GWAS using BayesB can be misleading. BayesB is based on a mixture model of those SNPs that explain genetic variance and those that do not (π). While the proportion of SNPs that explains genetic variance may become small, the total genetic variance remains constant, and is thus distributed among fewer SNPs resulting in what appears to be an inflated estimate of genetic variation accounted for by a SNP.
Every methodology for GWAS has a weakness. The ssGWAS1 method seems a more useful methodology compared with CGWAS and BayesB when a large number of phenotyped subjects are not genotyped, and obtaining deregressed proofs is difficult or impossible. A limitation of ssGWAS is that the number of iterations is dictated by heuristics at this time. Additional studies (unpublished) indicate that GWAS accuracy with ssGWAS1 is maximized at 2–4 iterations, with a single iteration creating noisy plots, and with more iterations suppressing signals from smaller QTLs. Another weakness of ssGWAS1 is the inability to determine the significance level. Possibilities to address this issue are the permutation test (Churchill and Doerge, 1994), or normalizing each SNP solution to a t-like statistic (McClure et al., 2012). The latter could be difficult to apply to a region including multiple SNPs. Future research may determine the level of significance in ssGWAS1 or ssGWAS2, e.g., following ideas by Garcia-Cortes and Sorensen (2001), where the estimation variances are obtained by sampling.
Computing Time
In this study, BayesB and CGWAS required DP which included running a regular BLUP, computing accuracies, and creating deregressed proofs. Omitting those procedures, GenSel required 17 h 13 min and WOMBAT required ~6 min. The very fast computing time in WOMBAT is due to precomputing matrices for prediction, so that computation for an additional marker takes very little time. Traditional algorithms were about 100 times slower for a population with about 1000 animals and 4000 SNP (Meyer and Tier, 2012). The ssGWAS methods were applied directly to the phenotypes without DP, and took about 15 min per iteration.
Conclusion
This study compares genomic evaluation and association results between different methods: ssGWAS1, ssGWAS2, CGWAS, and BayesB. Because this was real data and the true values are unknown, it is not possible to conclude which method was most accurate for GWAS, but similarity between BayesB and ssGWAS1 was shown in various aspects. CGWAS was the most different but also found the greatest number of signals. The latter could be due to false positives. Advantages of using ssGWAS includes: (1) no pseudo values are required, (2) complex modeling and multiple-traits are possible, and (3) computing is fast and implementation is simple.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This study was partially funded by USDA, NRICGP grant 2009-65205, and Binational Agricultural Research and Development Fund (BARD) Research Project IS-4394-11R. We appreciate Cobb-Vantress Inc. (Siloam Springs, AR) for access to the data for this study.
References
Abasht, B., Sandford, E., Arango, J., Settar, P., Fulton, J. E., O'sullivan, N. P., et al. (2009). Extent and consistency of linkage disequilibrium and identification of DNA markers for production and egg quality traits in commercial layer chicken populations. BMC Genomics 10(Suppl. 2):S2. doi: 10.1186/1471-2164-10-S2-S2
Aguilar, I., Misztal, I., Johnson, D. L., Legarra, A., Tsuruta, S., and Lawlor, T. J. (2010). Hot topic: a unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J. Dairy Sci. 93, 743–752. doi: 10.3168/jds.2009-2730
Aguilar, I., Misztal, I., Legarra, A., and Tsuruta, S. (2011). Efficient computation of the genomic relationship matrix and other matrices used in single-step evaluation. J. Anim. Breed. Genet. 128, 422–428. doi: 10.1111/j.1439-0388.2010.00912.x
Chen, C. Y., Misztal, I., Aguilar, I., Legarra, A., and Muir, W. M. (2011). Effect of different genomic relationship matrices on accuracy and scale. J. Anim. Sci. 89, 2673–2679. doi: 10.2527/jas.2010-3555
Churchill, G. A., and Doerge, R. W. (1994). Empirical threshold values for quantitative trait mapping. Genetics 138, 963–971.
Daetwyler, H. D., Kemper, K. E., Van Der Werf, J. H., and Hayes, B. J. (2012). Components of the accuracy of genomic prediction in a multi-breed sheep population. J. Anim. Sci. 90, 3375–3384. doi: 10.2527/jas.2011-4557
Dikmen, S., Cole, J. B., Null, D. J., and Hansen, P. J. (2013). Genome-wide association mapping for identification of quantitative trait loci for rectal temperature during heat stress in Holstein cattle. PLoS ONE 8:e69202. doi: 10.1371/journal.pone.0069202
Garcia-Cortes, L. A., and Sorensen, D. (2001). Alternative implementations of Monte Carlo EM algorithms for likelihood inferences. Genet. Sel. Evol. 33, 443–452. doi: 10.1051/gse:2001106
Garrick, D. J., Taylor, J. F., and Fernando, R. L. (2009). Deregressing estimated breeding values and weighting information for genomic regression analyses. Genet. Sel. Evol. 41, 55. doi: 10.1186/1297-9686-41-55
Groenen, M. A., Megens, H. J., Zare, Y., Warren, W. C., Hillier, L. W., Crooijmans, R. P., et al. (2011). The development and characterization of a 60K SNP chip for chicken. BMC Genomics 12:274. doi: 10.1186/1471-2164-12-274
Habier, D., Fernando, R. L., Kizilkaya, K., and Garrick, D. J. (2011). Extension of the bayesian alphabet for genomic selection. BMC Bioinformatics 12:186. doi: 10.1186/1471-2105-12-186
Hayes, B., and Goddard, M. E. (2001). The distribution of the effects of genes affecting quantitative traits in livestock. Genet. Sel. Evol. 33, 209–229. doi: 10.1186/1297-9686-33-3-209
Kang, H. M., Sul, J. H., Service, S. K., Zaitlen, N. A., Kong, S. Y., Freimer, N. B., et al. (2010). Variance component model to account for sample structure in genome-wide association studies. Nat. Genet. 42, 348–354. doi: 10.1038/ng.548
Legarra, A., Robert-Granié, C., Manfredi, E., and Elsen, J. M. (2008). Performance of genomic selection in mice. Genetics 180, 611–618. doi: 10.1534/genetics.108.088575
McClure, M. C., Ramey, H. R., Rolf, M. M., Mckay, S. D., Decker, J. E., Chapple, R. H., et al. (2012). Genome-wide association analysis for quantitative trait loci influencing Warner-Bratzler shear force in five taurine cattle breeds. Anim. Genet. 43, 662–673. doi: 10.1111/j.1365-2052.2012.02323.x
Meyer, K., and Tier, B. (2012). “SNP Snappy”: a strategy for fast genome-wide association studies fitting a full mixed model. Genetics 190, 275–277. doi: 10.1534/genetics.111.134841
Misztal, I., Tsuruta, S., Strabel, T., Auvray, B., Druet, T., and Lee, D. H. (2002). “BLUPF90 and related programs (BGF90),” in Proceedings of the 7th World Congress on Genetics Applied to Livestock Production. Vol. 28, (Montpellier: INRA), 21–22.
Ostersen, T., Christensen, O. F., Henryon, M., Nielsen, B., Su, G., and Madsen, P. (2011). Deregressed EBV as the response variable yield more reliable genomic predictions than traditional EBV in pure-bred pigs. Genet. Sel. Evol. 43, 38. doi: 10.1186/1297-9686-43-38
Otto, S. P., and Jones, C. D. (2000). Detecting the undetected: estimating the total number of loci underlying a quantitative trait. Genetics 156, 2093–2107.
Podisi, B. K., Knott, S. A., Burt, D. W., and Hocking, P. M. (2013). Comparative analysis of quantitative trait loci for body weight, growth rate and growth curve parameters from 3 to 72 weeks of age in female chickens of a broiler-layer cross. BMC Genet. 14:22. doi: 10.1186/1471-2156-14-22
Ricard, A., Danvy, S., and Legarra, A. (2013). Computation of deregressed proofs for genomic selection when own phenotypes exist with an application in French show-jumping horses. J. Anim. Sci. 91, 1076–1085. doi: 10.2527/jas.2012-5256
Rowe, S. J., Windsor, D., Haley, C. S., Burt, D. W., Hocking, P. M., Griffin, H., et al. (2006). QTL analysis of body weight and conformation score in commercial broiler chickens using variance component and half-sib analyses. Anim. Genet. 37, 269–272. doi: 10.1111/j.1365-2052.2006.01424.x
Sanchez, J. P., Misztal, I., and Bertrand, J. K. (2008). Evaluation of methods for computing approximate accuracies of predicted breeding values in maternal random regression models for growth traits in beef cattle. J. Anim. Sci. 86, 1057–1066. doi: 10.2527/jas.2007-0398
Shen, X., Alam, M., Fikse, F., and Ronnegard, L. (2013). A novel generalized ridge regression method for quantitative genetics. Genetics 193, 1255–1268. doi: 10.1534/genetics.112.146720
Sun, X., Fernando, R. L., Garrick, D. J., and Dekkers, J. C. M. (2011). An iterative approach for efficient calculation of breeding values and genome-wide association analysis using weighted genomic BLUP. J. Anim. Sci. 89(E-Suppl. 2), 28 (Abstr.).
Sun, X., Qu, L., Garrick, D. J., Dekkers, J. C., and Fernando, R. L. (2012). A fast EM algorithm for BayesA-like prediction of genomic breeding values. PLoS ONE 7:e49157. doi: 10.1371/journal.pone.0049157
Van Hulzen, K. J., Schopen, G. C., Van Arendonk, J. A., Nielen, M., Koets, A. P., Schrooten, C., et al. (2012). Genome-wide association study to identify chromosomal regions associated with antibody response to Mycobacterium avium subspecies paratuberculosis in milk of Dutch Holstein-Friesians. J. Dairy Sci. 95, 2740–2748. doi: 10.3168/jds.2011-5005
Vanraden, P. M. (2008). Efficient methods to compute genomic predictions. J. Dairy Sci. 91, 4414–4423. doi: 10.3168/jds.2007-0980
Vinkhuyzen, A. A., Pedersen, N. L., Yang, J., Lee, S. H., Magnusson, P. K., Iacono, W. G., et al. (2012). Common SNPs explain some of the variation in the personality dimensions of neuroticism and extraversion. Transl Psychiatry 2, e102. doi: 10.1038/tp.2012.27
Vitezica, Z. G., Aguilar, I., Misztal, I., and Legarra, A. (2011). Bias in genomic predictions for populations under selection. Genet. Res. 93, 357–366. doi: 10.1017/S001667231100022X
Wang, H., Misztal, I., Aguilar, I., Legarra, A., and Muir, W. M. (2012). Genome-wide association mapping including phenotypes from relatives without genotypes. Genet. Res. 94, 73–83. doi: 10.1017/S0016672312000274
Wiggans, G. R., Vanraden, P. M., Bacheller, L. R., Tooker, M. E., Hutchison, J. L., Cooper, T. A., et al. (2010). Selection and management of DNA markers for use in genomic evaluation. J. Dairy Sci. 93, 2287–2292. doi: 10.3168/jds.2009-2773
Xie, L., Luo, C., Zhang, C., Zhang, R., Tang, J., Nie, Q., et al. (2012). Genome-wide association study identified a narrow chromosome 1 region associated with chicken growth traits. PLoS ONE 7:e30910. doi: 10.1371/journal.pone.0030910
Zeng, J., Pszczola, M., Wolc, A., Strabel, T., Fernando, R. L., Garrick, D. J., et al. (2012). Genomic breeding value prediction and QTL mapping of QTLMAS2011 data using Bayesian and GBLUP methods. BMC Proc. 6(Suppl 2):S7. doi: 10.1186/1753-6561-6-S2-S7
Keywords: body weight, broiler chicken, genome-wide association, ssGWAS, BayesB, association mapping
Citation: Wang H, Misztal I, Aguilar I, Legarra A, Fernando RL, Vitezica Z, Okimoto R, Wing T, Hawken R and Muir WM (2014) Genome-wide association mapping including phenotypes from relatives without genotypes in a single-step (ssGWAS) for 6-week body weight in broiler chickens. Front. Genet. 5:134. doi: 10.3389/fgene.2014.00134
Received: 03 March 2014; Paper pending published: 04 April 2014;
Accepted: 25 April 2014; Published online: 20 May 2014.
Edited by:
Martien Groenen, Wageningen University, NetherlandsReviewed by:
Juan Steibel, Michigan State University, USADan Nonneman, United States Department of Agriculture/Agricultural Research Service, USA
Copyright © 2014 Wang, Misztal, Aguilar, Legarra, Fernando, Vitezica, Okimoto, Wing, Hawken and Muir. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Huiyu Wang, Genus plc, 100 Bluegrass Commons Blvd, Hendersonville, TN 37075, USA e-mail:am95LmtpbmdAZ2VudXNwbGMuY29t
 Huiyu Wang
Huiyu Wang Ignacy Misztal
Ignacy Misztal Ignacio Aguilar
Ignacio Aguilar Andres Legarra
Andres Legarra Rohan L. Fernando
Rohan L. Fernando Zulma Vitezica
Zulma Vitezica Ron Okimoto
Ron Okimoto Terry Wing
Terry Wing Rachel Hawken7
Rachel Hawken7 William M. Muir
William M. Muir