- 1Computational Biology and Machine Learning Laboratory, Faculty of Medicine, Health and Life Sciences, Center for Cancer Research and Cell Biology, School of Medicine, Dentistry and Biomedical Sciences, Queen's University Belfast, Belfast, UK
- 2Institute for Bioinformatics and Translational Research, UMIT, Hall in Tyrol, Austria
- 3Bioinformatics and Computational Genomics Laboratory, Princess Margaret Cancer Centre, University Health Network, Toronto, ON, Canada
In this paper, we shed light on approaches that are currently used to infer networks from gene expression data with respect to their biological meaning. As we will show, the biological interpretation of these networks depends on the chosen theoretical perspective. For this reason, we distinguish a statistical perspective from a mathematical modeling perspective and elaborate their differences and implications. Our results indicate the imperative need for a genomic network ontology in order to avoid increasing confusion about the biological interpretation of inferred networks, which can be even enhanced by approaches that integrate multiple data sets, respectively, data types.
1. Introduction
The post-genomic era possesses considerable challenges for the development of novel data analysis approaches. A reason for this necessity stems from the fact that in order to conduct a sensible data analysis, a method and the data from a unit that needs to fit optimally together, in order to extract the maximal amount of robust information from the data set. However, high-throughput technologies used in genomics generate data with novel characteristics for which, usually, no off-the-shelf methods are available. This is especially true for approaches that aim to infer large-scale networks from gene expression data (Friedman, 2004; Wille et al., 2004; Zhang et al., 2012).
The purpose of our manuscript is to untangle two distinct but related perspectives that are currently, in our opinion, inadvertently mixed-up in the literature. Specifically, in this paper, we focus exclusively on methods for “obtaining” networks from gene expression data and two opposing concepts from which methods are derived. We call the first concept category the statistical perspective (Stats P) and the second the mathematical modeling perspective (Math MP). In the following, we, first, define what we mean by a statistical and mathematical modeling perspective, second, we compare them with each other to show that they have complementary purposes and meanings and, third, we provide an explanation of possible sources for this confusion. Finally, we suggest a potential solution to avoid future antilogies by establishing a genomics network ontology.
Overall, the goal of this paper is to provide conceptual clarity in the interdisciplinary area of network inference from high-throughput data, because with the anticipated availability of novel high-throughput technologies, e.g., on the single-gene level or from imaging technologies, the inference of regulatory networks from the integration of such data types will become increasingly important. Hence, this problem could dramatically accelerate if not tackled in its early phase.
2. Statistical Perspective
The first perspective we describe in this paper is the statistical perspective. By this we mean any approach that applies a statistical inference method to a gene expression data set in order to draw conclusions about the biochemical interactions between genes and gene products without requiring further constraints or assumptions, e.g., regarding the underlying biological mechanisms. The result of such an approach can be used to make predictions about the interactions of genes and gene products for constructing a network representation of the biochemical interactions. For reasons of clarity, we provide an explicit definition for the resulting network.
Definition 1. A network that has been inferred from gene expression data by the application of a statistical inference method is called a “gene regulatory network.” In this network, nodes correspond to genes or gene products and edges correspond to biochemical interactions of any type. The network can be directed or undirected.
For this definition, we used the term gene regulatory network (GRN) because it is frequently used (Wang et al., 2006; Hecker et al., 2009). However, for reasons of completeness, we would like to note that in the literature, there are also various alternative notations used instead of GRN (Haibe-Kains and Emmert-Streib, 2014), but for the following discussion the nomenclature is not of relevance.
2.1. Purpose of the Statistical Perspective
From the above definition one can see that a statistical perspective is very general as it does not require biological information of any kind about the underlying mechanisms within a biological cell. Instead, biological information can be gained from the inference process about the biochemical interactions.
Now, the question is what type(s) of biochemical interaction(s) can be identified by statistical network inference methods? The answer to this question is actually only partially given by the data type used for the inference. Since the inference is based on gene expression data, which provide information about the abundance of mRNAs only rather than binding information of, e.g., a transcription factor to a promoter region or protein-protein binding, gene regulatory networks defined in the above sense provide information about general regulatory interactions between regulators and their potential targets; gene-gene interactions, and potential protein-protein interactions (e.g., in a complex) (de Matos Simoes et al., 2013). In other words, if a network inference method predicts the interaction between two genes or gene products then there is no systematic way to find out which particular biochemical interaction type this is, due to the nature of gene expression data. Hence, this is not a shortcoming of any network inference method, but the data themselves.
In brief, the purpose of the statistical perspective is to make predictions regarding the presence of interactions and directions of interactions within gene regulatory networks. However, such a method or its components are not required to have a meaningful biological interpretation (in contrast, see Section 3.1) in the sense that these emulate, e.g., a biological process.
2.2. Methods for Inferring Gene Regulatory Networks
There are many examples where such networks have been studied (Margolin et al., 2006; Werhli et al., 2006; Meyer et al., 2008; Stolovitzky et al., 2009; Emmert-Streib et al., 2012); see Table 1 for a brief overview of some widely used methods. All of these methods have in common that they estimate statistical independence relations for random variables, by different inference approaches, to construct a GRN component-wise.
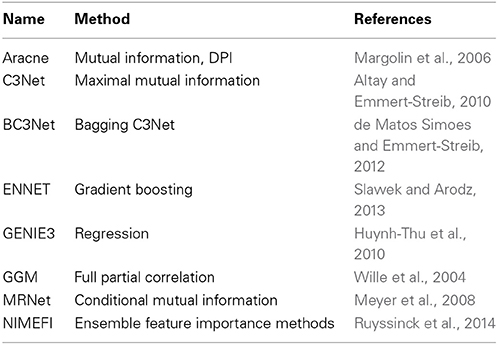
Table 1. A brief overview of statistical network inference methods that have been introduced in recent years (first column) and the key methods (second column) on which the inference algorithms are based on to estimate interactions.
2.3. Who uses the Statistical Perspective
The statistical perspective is the preferred approach in computational biology, computational genomics, biostatistics and bioinformatics, where the goal is to extract (infer) information from a given data set to predict population aspects of its.
3. Mathematical Modeling Perspective
In a molecular biological context, which is our focus, the mathematical modeling perspective aims to provide a realistic model for the transcription of DNA into RNA and the translation of RNA into proteins. However, there are also simpler models that focus on the former part only. In general, the detail level of such models varies considerably (see Section 3.2).
3.1. Purpose of the Modeling Perspective
The purpose of the mathematical modeling perspective is to increase our understanding of dynamical properties of a system and to derive behavioral features thereof that can then be used for making predictions about a natural system. This is possible because, usually, such a system is meant to form a mechanistic model of a natural (biological) system or process. Seminal models in this context are for instance the model of a neuron (Hodgkin and Huxley, 1952), a heart (NOBLE, 1960) or enzyme kinetics (Schnell and Mendoza, 1997). Simply put, the purpose of a mathematical model is to emulate a natural system as good as possible with respect to its dynamical activity. Additionally, even its components have a meaningful biological interpretation.
3.2. Methods to Model Transcription Regulation
Over the last years, many different models have been introduced to model the transcription regulation of genes (Gardner and Faith, 2005; Karlebach and Shamir, 2008; Ribeiro, 2008). These models vary on, e.g., the level of their detail complexity, the closeness to biological reality or the time complexity of the simulations.
Among the first and simplest approaches to models of GRNs are Boolean Networks and Probabilistic Boolean Networks (Kauffman, 1993; Shmulevich et al., 2002); see Table 2. These models assume a discrete activity level of genes, which can be either on (1) or off (0). For this reason such models are called logical models. Discrete Boolean Networks and Probabilistic Boolean Networks provide a simplistic representation of the transcriptional activity rather than a detailed biological formulation of molecular processes.
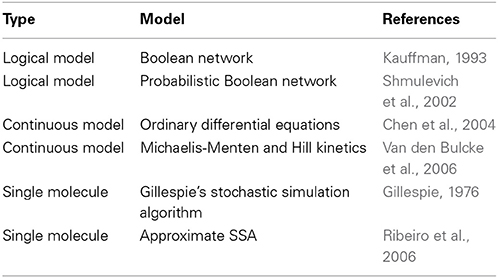
Table 2. A brief overview of some mathematical modeling methods that are used to model the transcription regulation of genes.
Models allowing to simulate a continuous gene activity dynamics are, e.g., systems of coupled ordinary differential equations (ODEs) or the Gillespie's stochastic simulation algorithm (SSA). Different models in this category can be distinguished based on the biological details that are modeled. The two major model categories focus either on transcription regulation or transcription and translation events. Hence, the latter model type is closest with respect to the phenomenologically observable biological mechanisms. Another difference between these models is if the average activity of a population of cells is simulated or the activity of a single cell (Ribeiro et al., 2006; Kandhavelu et al., 2012).
3.3. Who uses the Mathematical Modeling Perspective
The mathematical modeling perspective is very popular in mathematical biology, theoretical biology, systems biology, biochemistry and biophysics.
4. Comparison of the Two Perspectives
In Figure 1, we show a schematic overview and a comparison of the statistical perspective (red box) and the mathematical modeling perspective (blue box), discussed individually in the previous sections.
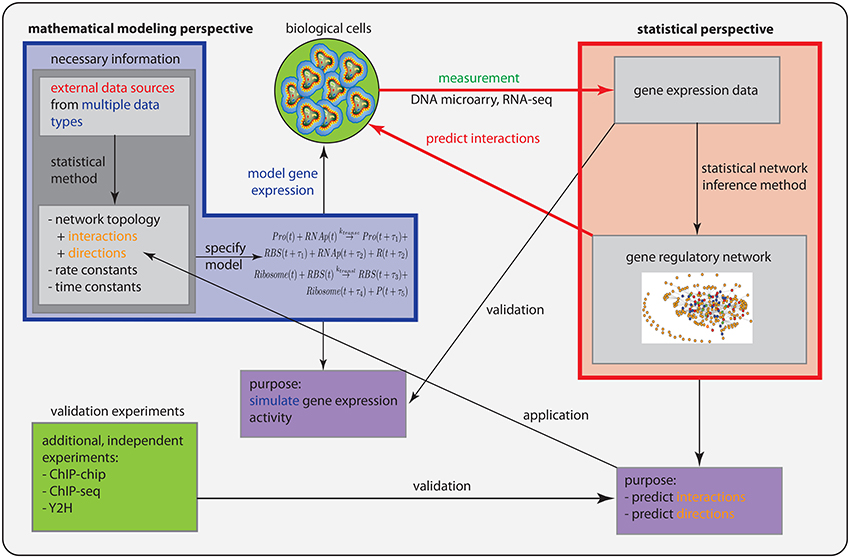
Figure 1. Schematic comparison of the statistical perspective (red) and the mathematical modeling perspective (blue).
However, there are three important differences. (1) Prior information: From a statistical perspective, there is no prior information required in addition to a gene expression data set to conduct an analysis. In contrast, in order to specify a mathematical model, information about the connectivity of the genes is needed and also the parameter values for the rate and time constants. (2) Purpose: The purpose of both perspectives is different. Whereas the goal of a statistical approach is to predict interactions between genes and gene products, and potentially their directionality (not all methods try to do this), the purpose for a mathematical model is to simulate gene expression levels. (3) Validation: From the former points, there results an immediate consequence for the validation of the models. In order to validate predicted interactions, additional data from different data types are needed that provide direct information about biochemical binding activity. For instance, information about the protein-DNA binding from ChIP-chip or ChIP-seq experiments can be used to identify interactions between transcription factors and regulated genes. Also, proteomics data, e.g., from Y2H experiments, provide information about protein binding and protein complex formation that can be used in this respect. In contrast, mathematical modeling approaches are validated by gene expression data. In Table 3, we show a summary of these differences.
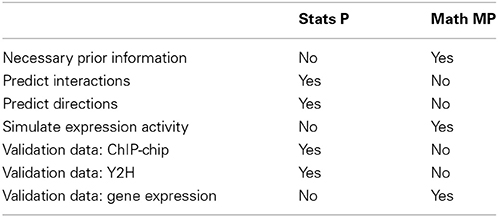
Table 3. Comparison of properties, features and requirements of statistical and mathematical models that fall under the category statistical perspective (Stat P) and mathematical modeling perspective (Math MP).
5. The Theoretical Perspective Matters Practically
In the following, we make an attempt for explaining the unfortunate amalgamation of the statistical perspective and the mathematical modeling perspective that might form sources for confusions and provide also some examples from the literature.
First, the interdisciplinary character of the problem to infer networks from gene expression data provides such a source by itself. The reason for this is that different subject areas have a different educational focus toward either the statistical perspective (computational biology—see Section 2.3), or the mathematical modeling perspective (mathematical biology—see Section 3.3). Hence, there is a natural plurality of complementary perspectives in this field that can get entangled easily.
Second, some early papers in this field presented in review articles methods from a statistical perspective and the mathematical modeling perspective side-by-side, which might have given the misleading impression that there is actually no difference between both (D'haeseleer et al., 2000; Gardner and Faith, 2005). These influences can be also observed in more recent review papers following the same structure (Bansal and di Bernardo, 2007; Hecker et al., 2009; Chai et al., 2014). Furthermore, there are research papers that contributed to this impression (Hoon et al., 2003). However, we would like to point out that there are also positive examples were this misleading presentation has been avoided, essentially, by focusing on one perspective only (de Jong, 2002; Kim et al., 2003; Markowetz and Spang, 2007; Karlebach and Shamir, 2008; Emmert-Streib et al., 2012).
In our opinion, the very best example to understand the imperative need for a clear distinction of both perspectives is given if one asks for the meaning of networks inferred from gene expression data. Because the answer is: It depends on your perspective. The explanation of this, forms our third example.
Suppose, you assume a mathematical modeling perspective and you use a model that emulates transcription regulation without consideration of a protein level. In this case, one concludes that the inferred network corresponds to a transcription regulation network. On the other hand, if you assume a statistical perspective using any of the algorithms listed in Table 1, the meaning of this network is a mixture of a transcription regulation network and a protein interaction network (Gardner and Faith, 2005; de Matos Simoes et al., 2013); as we will see below.
The crucial question is, how can it happen that we get from the same gene expression data set networks with different (but overlapping) meaning? The reason for this is that not the data alone define the meaning of an inferred network, but the combination of the data and the method. Specifically, the mathematical modeling perspective requires us to define a biological model with a well-defined biological meaning, whereas the statistical perspective does not. Instead, all methods in Table 1 estimate statistical independence relations (Emmert-Streib et al., 2012), because this is required to estimate causal relations (Pearl, 2000). Unfortunately, a statistical independence relation cannot be equated with either “transcription regulation” or “protein-protein interaction,” because it is not a model of reality (biology), but a statistical model.
So far, we established that in the former case a network is a transcriptional regulatory network but are still lacking a meaning in the latter case. However, this gap can be naturally filled by thinking one step further addressing the question of network validation. Here by network validation we mean that we compare an inferred network with an experimentally determined biological network. By using transcriptional regulatory networks and protein interaction networks it has been shown that a network inferred from a statistical perspective contains a significant number of interactions of both types (de Matos Simoes et al., 2013). Hence, such a network is a mixture of a transcriptional regulatory network and a protein interaction network. This is of course not a surprise but has already been discussed before (Gardner and Faith, 2005).
For reasons of clarity, we add a fourth example, discussing a question that we encountered frequently in various arguments. The question is, how can a network whose interactions are a composition of transcription regulations and protein interactions provide a valid model of the biology system? The answer is, such a network does not aim to be a biological model by itself, but it aims to be a statistical model that allows to make predictions about constituting parts of the biological system (see Table 1 for the purpose of the statistical perspective and the mathematical modeling perspective).
6. Subjective Objectivity
We waited until this point in our paper to provide an explanation for our chosen terminology, i.e., why we prefer the term “perspective” over, e.g., “formalism” to denote the two conceptual categories—statistical perspective and mathematical modeling perspective—because based on the arguments presented above, this is easy to understand now. A “perspective” is commonly associated with an individual point of view, which can be perceived as subjective. On the other hand, a “formalism” appears to be objective. In science, one strives for objectivity, but every assumption one makes is subjective by nature. Hence, despite the fact that any statistical formalism and any mathematical modeling formalism is fully objective, the selection process itself to pick either one of the formalisms is subjective. From this, it appears very natural to chose “perspective” over “formalism” to indicate explicitly that despite of the objectivity of the two formalisms the resulting interpretation depends on the selection too; as we have seen in our discussion above.
7. A Genomics Ontology for Inferred Networks
Due to the expected increase in the next years with respect to more data, but also novel biotechnologies to generate further high-throughput data types, we are facing an urgent need to organize the vocabulary for inferred networks. Specifically, data integration becomes more and more important implying that from 7 different data types different network types can be inferred using two different data types only, whereas integrating three data types gives already different network types. Considering the fact that the method itself has also an influence on the meaning of such networks it is easy to imagine that there are immense problems waiting for us to be addressed in order to avoid mounting confusion in this area. For this reason, we suggest to establish a genomics network ontology that provides a systematic vocabulary for networks inferred from biological, biomedical and clinical omics data.
8. Conclusion
The purpose of our paper was to generate awareness for the important distinction between a statistical perspective and a mathematical modeling perspective when inferring networks from gene expression data. However, this is only one of many epistemological problems we are currently facing in genomics (Dougherty, 2008) generated by the intricate interplay between large-scale high-throughput data and mathematical inference procedures. We hope that such problems receive more appreciation in the future because their neglection can lead to disastrous effects, especially when entering translational research (Dougherty, 2009).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
We would like to thank Ricardo de Matos Simoes and Shailesh Tripathi for fruitful discussions.
Funding
Frank Emmert-Streib thanks the Engineering and Physical Research Council (EPSRC EP/H048871/1) for support. Matthias Dehmer thanks the Austrian Science Funds for supporting this work (project P26142). Matthias Dehmer also gratefully acknowledges funding from the Standortagentur Tirol (formerly Tiroler Zukunftsstiftung).
References
Altay, G., and Emmert-Streib, F. (2010). Inferring the conservative causal core of gene regulatory networks. BMC Syst. Biol. 4:132. doi: 10.1186/1752-0509-4-132
Bansal, M., and di Bernardo, D. (2007). Inference of gene networks from temporal gene expression profiles. IET Syst. Biol. 1, 306–312. doi: 10.1049/iet-syb:20060079
Chai, L. E., Loh, S. K., Low, S. T., Mohamad, M. S., Deris, S., and Zakaria, Z. (2014). A review on the computational approaches for gene regulatory network construction. Comput. Biol. Med. 48, 55–65. doi: 10.1016/j.compbiomed.2014.02.011
Chen, K. C., Calzone, L., Csikasz-Nagy, A., Cross, F. R., Novak, B., and Tyson, J. J. (2004). Integrative analysis of cell cycle control in budding yeast. Mol. Biol. Cell 15, 3841–3862. doi: 10.1091/mbc.E03-11-0794
D'haeseleer, P., Liang, S., and Somogyi, R. (2000). Genetic network inference: from co-expression clustering to reverse engineering. Bioinformatics 16, 707–726. doi: 10.1093/bioinformatics/16.8.707
de Jong, H. (2002). Modeling and simulation of genetic regulatory systems: a literature review. J. Comput. Biol. 9, 67–103. doi: 10.1089/10665270252833208
de Matos Simoes, R., Dehmer, M., and Emmert-Streib, F. (2013). Interfacing cellular networks of S. cerevisiae and E. coli: connecting dynamic and genetic information. BMC Genomics 14:324. doi: 10.1186/1471-2164-14-324
de Matos Simoes, R., and Emmert-Streib, F. (2012). Bagging statistical network inference from large-scale gene expression data. PLoS ONE 7:e33624. doi: 10.1371/journal.pone.0033624
Dougherty, E. R. (2008). On the epistemological crisis in genomics. Curr. Genomics 9, 69–79. doi: 10.2174/138920208784139546
Dougherty, E. R. (2009). Translational science: epistemology and the investigative process. Curr. Genomics 10, 102–109. doi: 10.2174/138920209787847005
Emmert-Streib, F., Glazko, G., Altay, G., and de Matos Simoes, R. (2012). Statistical inference and reverse engineering of gene regulatory networks from observational expression data. Front. Genet. 3:8. doi: 10.3389/fgene.2012.00008
Friedman, N. (2004). Inferring cellular networks using probabilistic graphical models. Science 303, 799–805. doi: 10.1126/science.1094068
Gardner, T. S., and Faith, J. J. (2005). Reverse-engineering transcription control networks. Phys. Life Rev. 2, 65–88. doi: 10.1016/j.plrev.2005.01.001
Gillespie, D. (1976). A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22, 403–434. doi: 10.1016/0021-9991(76)90041-3
Haibe-Kains, B., and Emmert-Streib, F. (2014). Quantitative assessment and validation of network inference methods in bioinformatics. Front. Genet. 5:221. doi: 10.3389/fgene.2014.00221
Hecker, M., Lambeck, S., Toepfer, S., van Someren, E., and Guthke, R. (2009). Gene regulatory network inference: data integration in dynamic models - A review. Biosystems 96, 86–103. doi: 10.1016/j.biosystems.2008.12.004
Hodgkin, A., and Huxley, A. (1952). A quantitative description of the membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544.
Hoon, M. D., Imoto, S., and Miyano, S. (2003). Inferring gene regulatory networks from time-ordered gene expression data of bacillus subtilis using differential equations. Pac. Symp. Biocomput 2003, 17–28.
Huynh-Thu, V. A., Irrthum, A., Wehenkel, L., and Geurts, P. (2010). Inferring regulatory networks from expression data using tree-based methods. PLoS ONE 5:e12776. doi: 10.1371/journal.pone.0012776
Kandhavelu, M., Häkkinen, A., Yli-Harja, O., and Ribeiro, A. S. (2012). Single-molecule dynamics of transcription of the lar promoter. Phys. Biol. 9:026004. doi: 10.1088/1478-3975/9/2/026004
Karlebach, G., and Shamir, R. (2008). Modelling and analysis of gene regulatory networks. Nat. Rev. Mol. Cell Biol. 9 770–780. doi: 10.1038/nrm2503
Kauffman, S. (1993). Origins of Order: Self-Organization and Selection in Evolution. New York, NY: Oxford University Press.
Kim, S. Y., Imoto, S., and Miyano, S. (2003). Inferring gene networks from time series microarray data using dynamic bayesian networks. Brief. Bioinform. 4, 228–235. doi: 10.1093/bib/4.3.228
Margolin, A., Nemenman, I., Basso, K., Wiggins, C., and Stolovitzky, G. (2006). ARACNE: an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinformatics 7(Suppl. 1):S7. doi: 10.1186/1471-2105-7-S1-S7
Markowetz, F., and Spang, R. (2007). Inferring cellular networks–a review. BMC Bioinformatics 8(Suppl. 6):S5. doi: 10.1186/1471-2105-8-S6-S5
Meyer, P., Lafitte, F., and Bontempi, G. (2008). minet: a R/Bioconductor package for inferring large transcriptional networks using mutual information. BMC Bioinformatics 9:461. doi: 10.1186/1471-2105-9-461
NOBLE, D. (1960). Cardiac action and pacemaker potentials based on the Hodgkin-Huxley equations. Nature 188, 495–497. doi: 10.1038/188495b0
Pearl, J. (2000). Causality: Models, Reasoning, and Inference New York, NY: Cambridge University Press.
Ribeiro, A. (2008). “A model of genetic networks with delayed stochastic dynamics,” in Analysis of Microarray Data: A Network-based Approach, eds F. Emmert-Streib and M. Dehmer (Weinheim; Chichester: Wiley-VCH), 169–204.
Ribeiro, A., Zhu, R., and Kauffman, S. (2006). A general modeling strategy for gene regulatory networks with stochastic dynamics. J. Comput. Biol. 13, 1630–1639. doi: 10.1089/cmb.2006.13.1630
Ruyssinck, J., Huynh-Thu, V. A., Geurts, P., Dhaene, T., Demeester, P., and Saeys, Y. (2014). Nimefi: gene regulatory network inference using multiple ensemble feature importance algorithms. PLoS ONE 9:e92709. doi: 10.1371/journal.pone.0092709
Schnell, S., and Mendoza, C. (1997). Closed form solution for time-dependent enzyme kinetics. J. Theor. Biol. 187, 207–212. doi: 10.1006/jtbi.1997.0425
Shmulevich, I., Dougherty, E. R., Kim, S., and Zhang, W. (2002). Probabilistic boolean networks: a rule-based uncertainty model for gene regulatory networks. Bioinformatics 18, 261–274. doi: 10.1093/bioinformatics/18.2.261
Slawek, J., and Arodz, T. (2013). ENNET: inferring large gene regulatory networks from expression data using gradient boosting. BMC Syst. Biol. 7:106. doi: 10.1186/1752-0509-7-106
Stolovitzky, G., Prill, R., and Califano, A. (2009). Lessons from the DREAM 2 challenges. Ann. N.Y. Acad. Sci. 1158, 159–195. doi: 10.1111/j.1749-6632.2009.04497.x
Van den Bulcke, T., Van Leemput, K., Naudts, B., van Remortel, P., Ma, H., Verschoren, A., et al. (2006). SynTReN: a generator of synthetic gene expression data for design and analysis of structure learning algorithms. BMC Bioinformatics 7:43. doi: 10.1186/1471-2105-7-43
Wang, Y., Joshi, T., Zhang, X.-S., Xu, D., and Chen, L. (2006). Inferring gene regulatory networks from multiple microarray datasets. Bioinformatics 22, 2413–2420. doi: 10.1093/bioinformatics/btl396
Werhli, A., Grzegorczyk, M., and Husmeier, D. (2006). Comparative evaluation of reverse engineering gene regulatory networks with relevance networks, graphical gaussian models and bayesian networks. Bioinformatics 22, 2523–2531. doi: 10.1093/bioinformatics/btl391
Wille, A., Zimmermann, P., Vranova, E., Furholz, A., Laule, O., Bleuler, S., et al. (2004). Sparse graphical gaussian modeling of the isoprenoid gene network in arabidopsis thaliana. Genome Biol. 5:R92. doi: 10.1186/gb-2004-5-11-r92
Keywords: gene regulatory networks, computational genomics, statistical inference, mathematical modeling, systems biology, epistemology, genomics network ontology
Citation: Emmert-Streib F, Dehmer M and Haibe-Kains B (2014) Untangling statistical and biological models to understand network inference: the need for a genomics network ontology. Front. Genet. 5:299. doi: 10.3389/fgene.2014.00299
Received: 28 June 2014; Accepted: 12 August 2014;
Published online: 29 August 2014.
Edited by:
Hong-Wen Deng, Tulane University, New Orleans, USACopyright © 2014 Emmert-Streib, Dehmer and Haibe-Kains. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Frank Emmert-Streib, Computational Biology and Machine Learning Laboratory, Faculty of Medicine, Health and Life Sciences, Center for Cancer Research and Cell Biology, School of Medicine, Dentistry and Biomedical Sciences, Queen's University Belfast, 97 Lisburn Road, BT9 7JL Belfast, UK e-mail:dkBiaW8tY29tcGxleGl0eS5jb20=
 Frank Emmert-Streib
Frank Emmert-Streib Matthias Dehmer
Matthias Dehmer Benjamin Haibe-Kains
Benjamin Haibe-Kains