Abstract
Effective population size (Ne) is a key population genetic parameter that describes the amount of genetic drift in a population. Estimating Ne has been subject to much research over the last 80 years. Methods to estimate Ne from linkage disequilibrium (LD) were developed ~40 years ago but depend on the availability of large amounts of genetic marker data that only the most recent advances in DNA technology have made available. Here we introduce SNeP, a multithreaded tool to perform the estimate of Ne using LD using the standard PLINK input file format (.ped and.map files) or by using LD values calculated using other software. Through SNeP the user can apply several corrections to take account of sample size, mutation, phasing, and recombination rate. Each variable involved in the computation such as the binning parameters or the chromosomes to include in the analysis can be modified. When applied to published datasets, SNeP produced results closely comparable with those obtained in the original studies. The use of SNeP to estimate Ne trends can improve understanding of population demography in the recent past, provided a sufficient number of SNPs and their physical position in the genome are available. Binaries for the most common operating systems are available at https://sourceforge.net/projects/snepnetrends/.
Introduction
Effective population size (Ne) is an important genetic parameter that estimates the amount of genetic drift in a population, and has been described as the size of an idealized Wright–Fisher population expected to yield the same value of a given genetic parameter as in the population under study (Crow and Kimura, 1970). Ne sizes can be influenced by fluctuations in census population size (Nc), by the breeding sex ratio and the variance in reproductive success.
Ne estimation can be achieved using approaches that fall into three methodological categories: demographic, pedigree-based, or marker-based (Flury et al., 2010). Pedigree data have been traditionally used to obtain Ne estimates in livestock. However, reliable estimates of Ne depend on the pedigree being complete. This state of knowledge is feasible in some domestic populations, the demographic parameters of which have been accurately monitored for a sufficiently large number of generations. However, in practice, the applicability of this approach remains limited to a few cases involving highly managed breeds (Flury et al., 2010; Uimari and Tapio, 2011). One solution to overcome the limitation of an incomplete pedigree is to estimate the recent trend in Ne using genomic data. Several authors have recognized that Ne could be estimated from information on linkage disequilibrium (LD) (Sved, 1971; Hill, 1981). LD describes the non-random association of alleles in different loci as a function of the recombination rate between the physical positions of the loci in the genome. However, LD signatures can also result from demographic processes such as admixture and genetic drift (Wright, 1943; Wang, 2005), or through processes such as “hitchhiking” during selective sweeps (Smith and Haigh, 1974) or background selection (Charlesworth et al., 1997). In such scenarios alleles at different loci become associated independently of their proximity in the genome. Assuming that a population is closed and panmictic, the LD value calculated between neutral unlinked loci depends exclusively on genetic drift (Sved, 1971; Hill, 1981). This occurrence can be used to predict Ne due to the known relationship between the variance in LD (calculated using allele frequencies) and effective population size (Hill, 1981).
Recent advances in genotyping technology (e.g., using SNP bead arrays with tens of thousands of DNA probes) have enabled the collection of vast amounts of genome-wide linkage data ideal for estimating Ne in livestock and humans among others (e.g., Tenesa et al., 2007; de Roos et al., 2008; Corbin et al., 2010; Uimari and Tapio, 2011; Kijas et al., 2012). However, a software tool that enables estimation of Ne from LD is lacking, and researchers currently rely on a combination of tools to manipulate data, infer LD, and tend to use bespoke scripts to perform the appropriate calculations and estimate Ne.
Here we describe SNeP, a software tool that allows the estimation of Ne trends across generation using SNP data that corrects for sample size, phasing and recombination rate.
Materials and methods
The method SNeP uses to calculate LD depends on the availability of phased data. When the phase is known the user can select Hill and Robertson (1968) squared correlation coefficient that makes use of haplotype frequencies to define LD between each pair of loci (Equation 1). However, in the absence of a known phase, squared Pearson's product-moment correlation coefficient between pairs of loci can be selected. While these two approaches are not the same, they are highly comparable (McEvoy et al., 2011): where pA and pB are respectively the frequencies of alleles A and B at two separate loci (X, Y) measured for n individuals, pAB is the frequency of the haplotype with alleles A and B in the population studied, X and Y are the mean genotype frequencies for the first and second locus respectively, Xi is the genotype of individual i at the first locus and Yi is the genotype of individual i at the second locus. Equation (2) correlates the genotypic allele counts instead of the haplotype frequencies and is not influenced by double heterozygotes (this approach results in the same estimates as the --r2 option in PLINK).
SNeP estimates the historic effective population size based on the relationship between r2, Ne, and c (recombination rate), (Equation 3—Sved, 1971), and enabling users to include corrections for sample size and uncertainty of the gametic phase (Equation 4—Weir and Hill, 1980): where n is the number of individual sampled, β = 2 when the gametic phase is known and β = 1 if instead the phase is not known.
Several approximations are used to infer the recombination rate using the physical distance (δ) between two loci as a reference and translating it into linkage distance (d), which is usually described as Mb(δ) ≈ cM(d). For small values of d the latter approximation is valid, but for larger values of d the probability of multiple recombination events and interference increases, moreover the relationship between map distance and recombination rate is not linear, as the maximum recombination rate possible is 0.5. Thus, unless using very short δ, the approximation d ≈ c is not ideal (Corbin et al., 2012). We therefore implemented mapping functions to translate the estimated d into c, following Haldane (1919), Kosambi (1943), Sved (1971), and Sved and Feldman (1973). Initially SNeP infers d for each pair of SNPs as directly proportional to δ according to d = kδ where k is a user defined recombination rate value (default value is 10−8 as in Mb = cM). The inferred value of δ can then be subjected to one of the available mapping functions if required by the user.
Solving Equation (3) for Ne and including all the corrections described, allows the prediction of Ne from LD data using (Corbin et al., 2012): where Nt is the effective population size t generations ago calculated as t = (2f(ct))−1 (Hayes et al., 2003), ct is the recombination rate defined for a specific physical distance between markers and optionally adjusted with the mapping functions mentioned above, r2adj is the LD value adjusted for sample size and α:= {1, 2, 2.2} is a correction for the occurrence of mutations (Ohta and Kimura, 1971). Therefore, LD over greater recombinant distances is informative on recent Ne while shorter distances provide information on more distant times in the past. A binning system is implemented in order to obtain averaged r2 values that reflect LD for specific inter-locus distances. The binning system implemented uses the following formula to define the minimum and maximum values for each bin: Where bi (ℕ1) is the ith bin of the total number of bins (totBins), minD, and maxD are respectively the minimum and the maximum distance between SNPs and x is a positive real number (ℝ0) When x equals 1, the distribution of distances between the bins is linear and each bin has the same distance range. For larger values of x the distribution of distances changes allowing a larger range on the last bins and a smaller range on the first bins. Varying this parameter allows the user to have a sufficient number of pairwise comparisons to contribute to the final Ne estimate for each bin.
Example application
We tested SNeP with two published datasets that had been previously used to describe trends in Ne over time using LD, Bos indicus [54,436 SNPs of 423 East African Shorthorn Zebu (SHZ)–Mbole-Kariuki et al., 2014, data available at Dryad Digital Repository: doi:10.5061/dryad.bc598.] and Ovis aries [49,034 SNPs genotyped in 24 Swiss White Alpine (SWA), 24 Swiss Black-Brown Mountain sheep (SBS), 24 Valais Blacknose sheep (VBS), 23 Valais Red sheep (VRS), 24 Swiss Mirror sheep (SMS) and 24 Bundner Oberländer sheep (BOS)–Burren et al., 2014]. The r2 estimates for the cattle datasets were obtained by the authors using GenABLE (Aulchenko et al., 2007) using a minimum allele frequency (MAF) < 0.01 and adjusting the recombination rate using Haldane's mapping function (Haldane, 1919). The r2 estimates of the sheep data were calculated by the authors using PLINK-1.07 (Purcell et al., 2007), with a MAF < 0.05 and no further corrections. For both autosomal datasets r2 estimates where corrected for sample size using equation (4) with β = 2. For these comparative analyses the SNeP command line included the same parameters used for the published data apart from the r2 estimates, calculated through genotype count and the use of SNeP's novel binning strategy.
Results
SNeP is a multithreaded application developed in C++ and binaries for the most common operating systems (Windows, OSX, and Linux) can be downloaded from https://sourceforge.net/projects/snepnetrends/. The binaries are accompanied by a manual describing the step-by-step use of SNeP to infer trends in Ne as described here. SNeP produces an output file with tab delimited columns showing the following for each bin that was used to estimate Ne: the number of generations in the past that the bin corresponds to (e.g., 50 generations ago), the corresponding Ne estimate, the average distance between each pair of SNPs in the bin, the average r2 and the standard deviation of r2 in the bin, and the number of SNPs used to calculate r2 in the bin. This file can be easily imported in Microsoft Excel, R or other software to plot the results. The plots shown here (Figures 1, 3) correspond to the columns of generations ago and Ne from the output file. The column with the r2 standard deviation is provided for users to inspect the variance in the Ne estimate in each bin, particularly for those bins reflecting older time estimates and which are less reliable as the number of SNPs used to estimate r2 becomes smaller.
Figure 1
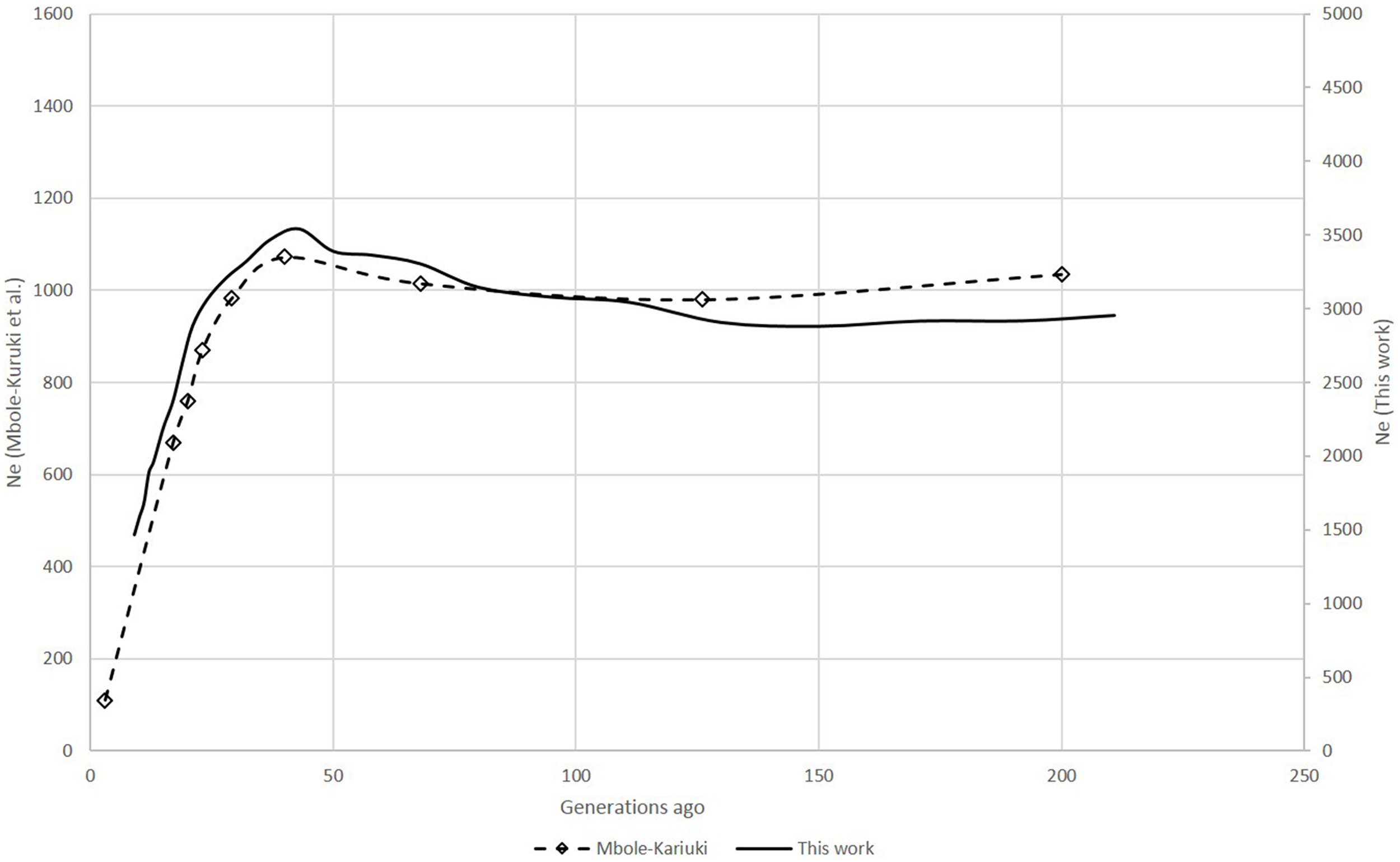
Comparison of Ne trends of six Swiss sheep breeds according to Burren et al. (2014) (dashed lines) and this work (solid lines).
The format required for the input files is the standard PLINK format (ped and map files) (Purcell et al., 2007). SNeP allows the users to either calculate LD on the data as described above, or use a custom precalculated LD matrix to estimate Ne using Equation (5).
The software interface allows the user to control all parameters of the analysis, e.g., the distance range between SNPs in bp, and the set of chromosomes used in the analysis (e.g., 20–23). Additionally, SNeP includes the option to choose a MAF threshold (default 0.05), as it has been shown that accounting for MAF results in unbiased r2 estimates irrespective of sample size (Sved et al., 2008). SNeP's multithreaded architecture allows fast computation of large datasets (we tested up to ~100K SNPs for a single chromosome), for example the BOS data described here was analyzed with one processor in 2′43″, the use of two processors reduced the time to 1′43″, four processors reduced the analysis time to 1′05″.
Zebu example
For the zebu analysis, the shapes of the Ne curves obtained with SNeP and their published data trends showed the same trajectory with a smooth decline until around 150 generations ago, followed by an expansion with a peak around 40 generations ago and ending in a steep decline on the most recent generations (Figure 1). However, while the trends in both curves were the same, the two approaches resulted in different Ne estimates, with SNeP's values being approximately three-fold larger than those in the original paper. While we attempted to use the authors' parameters in our analyses, some differences were inevitable, i.e., the original publication of the cattle data estimated r2 with a different approach to that implemented in SNeP. Analyses with SNeP were based on genotypes, while the original analysis was based on inferred two locus haplotypes, which results in the published data showing an expected r2 of 0.32 at the minimum distance, while our estimates was 0.23. Similarly, Mbole-Kariuki et al. (2014) obtained a background level r2 = 0.013 around 2 Mb, while our estimate at the same distance was 0.0035 (data not shown). Consequently, as our estimates of LD were consistently smaller than Mbole-Kariuki et al. (2014) it is expected that our Ne estimates should be larger. While this observation highlights the importance of a careful choice of the parameters and their thresholds, it is important to highlight that although the absolute magnitude of the Ne values is different, the trends are almost identical.
Swiss sheep example
The six Swiss sheep breeds analyzed with SNeP produced comparable results with those from the original paper (Figure 2), with mostly overlapping Ne trend curves (Figure 3). However, the general trend in Ne showed a decline toward the present. SNeP produced slightly larger values of Ne for the more distant past (700–800 generations). This is due to the different binning system used in SNeP, which allows the user to obtain a more even distribution of pairwise comparisons within each bin (i.e., the number of SNP pairwise comparisons within each bin is comparable). For the time span extending beyond 400 generations ago, Burren et al. (2014) used only three bins in their analysis (centered at 400, 667, and 2000 generations ago) while for the same time span SNeP used 5 bins with a number of pairwise comparisons dependent to the range defined with formulae 6a,b. Consequently, Burren and colleagues' approach ends with a higher density of data describing the most recent generations than describing the oldest generations. Therefore, the use of fewer bins tends to increase the presence of smaller values of Ne in each bin, consequently lowering the average Ne value for each bin. The Ne values for the recent past, compared at the 29th generation in the past, gave very similar results. The largest difference (50) was obtained for the SBS breed.
Figure 2
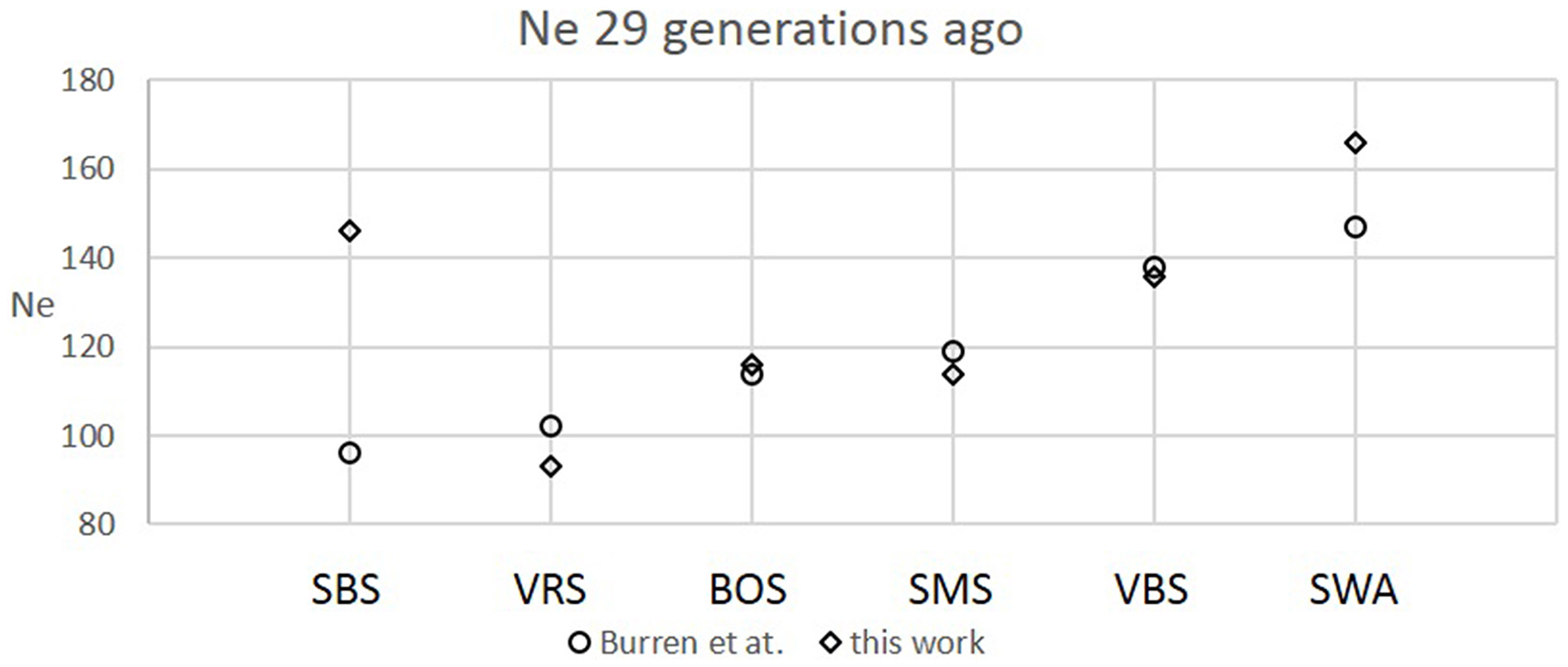
Comparison between recent Ne values calculated at the 29th generation in this work and Burren et al. (2014) for six Swiss sheep breeds.
Figure 3
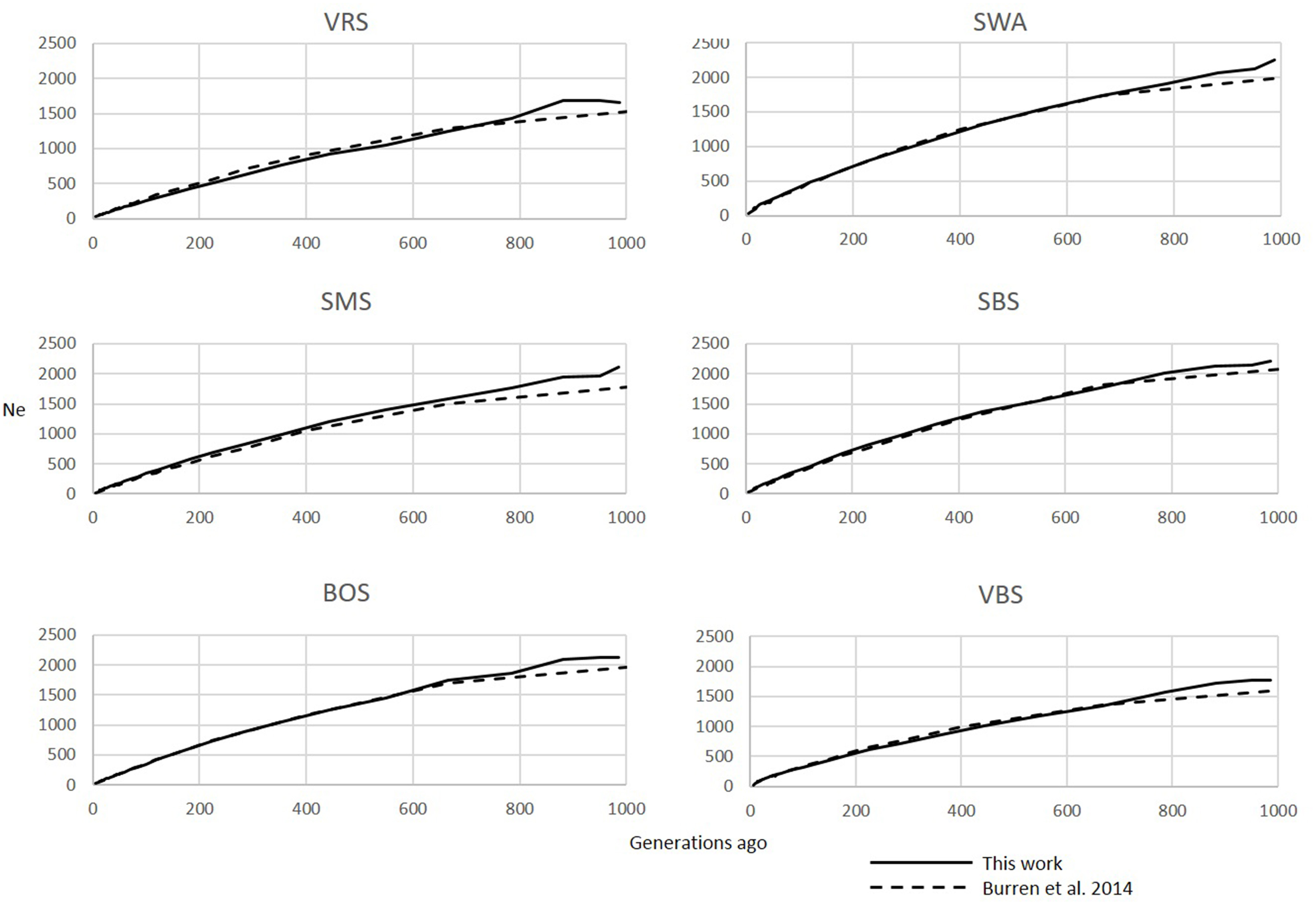
Comparison of Ne trends for the last 250 generations in the SHZ data obtained by Mbole-Kariuki et al. (2014) (dashed line) and using SNeP (solid line).
Discussion
Analysis of Ne using LD data was first demonstrated 40 years ago, and has been applied, developed and improved since (Sved, 1971; Hayes et al., 2003; Tenesa et al., 2007; de Roos et al., 2008; Corbin et al., 2012; Sved et al., 2013). The traditionally small number of SNPs analyzed is no longer a limitation, since SNP Chips comprise an extremely large number of SNPs, available in a short time and at a reasonable price. This has boosted the use of the method, which has been applied to humans (Tenesa et al., 2007; McEvoy et al., 2011) as well as to several domesticated species (England et al., 2006; Uimari and Tapio, 2011; Corbin et al., 2012; Kijas et al., 2012). Along with these improvements, methodological limitations have become apparent and have been addressed here, with the majority of the efforts pointing to the correct estimation of recent Ne. Yet, the quantitative value of the estimate is highly dependent on sample size, the type of LD estimation and the binning process (Waples and Do, 2008; Corbin et al., 2012), while its qualitative pattern depends more on the genetic information than on data manipulation.
So far this method has been applied using a variety of software, no standardized approach exists to bin the results and each study has applied a more or less arbitrary approach, e.g., binning for generation classes in the past (Corbin et al., 2012), binning for distance classes with a constant range for each bin (Kijas et al., 2012) or binning per distance classes in a linear fashion but with larger bins for the more recent time points (Burren et al., 2014). To our knowledge the only software available that estimate Ne through LD is NeEstimator (Do et al., 2014), an upgraded version of the former LDNE (Waples and Do, 2008) allowing the analysis of large dataset (as 50k SNPChip). Importantly, while SNeP focuses on estimating historical Ne trends, NeEstimator's aim is to produce contemporary unbiased Ne estimates, the latter should therefore be considered as a complementary tool while investigating demography through LD.
We used SNeP to analyze two datasets where the method was previously applied. The results we obtained for the sheep data were both quantitatively and qualitatively comparable with those obtained by Burren et al. (2014), while for the Zebu data we obtained a Ne trend estimate that closely matched that of Mbole-Kariuki et al. (2014) although our point estimates of Ne were larger than those described for the data (Mbole-Kariuki et al., 2014). The discrepancy between these two results reflects that Burren and colleagues produced their r2 estimates using PLINK (the standard software for large scale SNP data manipulation) which uses the same approach used to estimate r2 by SNeP, while Mbole-Kariuki et al. followed Hao et al. (2007) for r2 estimation. The use of different estimates for LD is critical for the quantitative aspect of the Ne curve, where due to the hyperbolic correlation between Ne and r2, a decrease in r2 on its range closer to 0 can lead to a very large change in Ne estimates, while differences in estimates are less significant when the r2 value is high, i.e., closer to 1. Therefore, although in one of the datasets the Ne values where substantially different, in both cases the Ne curves overlapped with those originally published.
As already suggested by other authors, the reliability of the quantitative estimates obtained with this method must be taken with caution, especially for Ne values related to the most recent and the oldest generations (Corbin et al., 2012) because for recent generations, large values of c are involved, not fitting the theoretical implications that Hayes proposed to estimate a variable Ne over time (Hayes et al., 2003). Estimates for the oldest generations might also be unreliable as coalescent theory shows that no SNP can be reliably sampled after 4Ne generations in the past (Corbin et al., 2012). Further, Ne estimates, and especially those related to generations further in the past, are strongly affected by data manipulation factors, such as the choice of MAF and alpha values. Additionally, the binning strategy applied can interfere with the general precision of the method, for example where an insufficient number of pairwise comparisons are used to populate each bin.
One of the applications of method is to compare breed demographies. In this case the shape of the Ne curves would be the optimal tool to differentiate different demographic histories, more than their numerical values, by using them as a potential demographic fingerprint for that breed or species, yet taking into consideration that mutation, migration, and selection can influence the Ne estimation through LD (Waples and Do, 2010). Additionally, careful consideration of the data analyzed with SNeP (and other software to estimate Ne) is very important, as the presence of confounding factors such as admixture, may result in biased estimates of Ne (Orozco-terWengel and Bruford, 2014).
The aim of SNeP is therefore to provide a fast and reliable tool to apply LD methods to estimate Ne using high throughput genotypic data in a more consistent way. It allows two different r2 estimation approaches plus the option of using r2 estimates from external software. The use of SNeP does not overcome the limits of the method and the theory behind it, yet it allows the user to apply the theory using all corrections suggested to date.
Statements
Author contributions
MB conceived and wrote the software and the manuscript. MB, MT, and POtW tested the software and performed the analyses. MT, POtW, and MWB revised the manuscript. All authors approved the final manuscript.
Acknowledgments
We thank Christine Flury for providing the sheep data and for useful discussion. We also thank the two reviewers for useful suggestions to improve this paper. MB was supported by the program Master and Back (Regione Sardegna).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1
AulchenkoY. S.RipkeS.IsaacsA.van DuijnC. M. (2007). GenABEL: an R library for genome-wide association analysis. Bioinformatics23, 1294–1296. 10.1093/bioinformatics/btm108
2
BurrenA.Signer-HaslerH.NeuditschkoM.TetensJ.KijasJ. W.DrögemüllerC.et al. (2014). Fine-scale population structure analysis of seven local Swiss sheep breeds using genome-wide SNP data. Anim. Genet. Resour. 55, 67–76. 10.1017/S2078633614000253
3
CharlesworthB.NordborgM.CharlesworthD. (1997). The effects of local selection, balanced polymorphism and background selection on equilibrium patterns of genetic diversity in subdivided populations. Genet. Res. 70, 155–174. 10.1017/S0016672397002954
4
CorbinL. J.BlottS. C.SwinburneJ. E.VaudinM.BishopS. C.WoolliamsJ. A. (2010). Linkage disequilibrium and historical effective population size in the Thoroughbred horse. Anim. Genet. 41(Suppl. 2), 8–15. 10.1111/j.1365-2052.2010.02092.x
5
CorbinL. J.LiuA. Y. H.BishopS. C.WoolliamsJ. A. (2012). Estimation of historical effective population size using linkage disequilibria with marker data. J. Anim. Breed. Genet. 129, 257–270. 10.1111/j.1439-0388.2012.01003.x
6
CrowJ. F.KimuraM. (1970). An Introduction to Population Genetics Theory. New York, NY: Harper and Row.
7
de RoosA. P. W.HayesB. J.SpelmanR. J.GoddardM. E. (2008). Linkage disequilibrium and persistence of phase in Holstein-Friesian, Jersey and Angus cattle. Genetics179, 1503–1512. 10.1534/genetics.107.084301
8
DoC.WaplesR. S.PeelD.MacbethG. M.TillettB. J.OvendenJ. R. (2014). NeEstimator v2: re-implementation of software for the estimation of contemporary effective population size (Ne) from genetic data. Mol. Ecol. Resour. 14, 209–214. 10.1111/1755-0998.12157
9
EnglandP. R.CornuetJ.-M.BerthierP.TallmonD. A.LuikartG. (2006). Estimating effective population size from linkage disequilibrium: severe bias in small samples. Conserv. Genet. 7, 303–308. 10.1007/s10592-005-9103-8
10
FluryC.TapioM.SonstegardT.DrögemüllerC.LeebT.SimianerH.et al. (2010). Effective population size of an indigenous Swiss cattle breed estimated from linkage disequilibrium. J. Anim. Breed. Genet. 127, 339–347. 10.1111/j.1439-0388.2010.00862.x
11
HaldaneJ. B. S. (1919). The combination of linkage values, and the calculation of distances between the loci of linked factors. J. Genet. 8, 299–309.
12
HaoK.DiX.CawleyS. (2007). LdCompare: rapid computation of single- and multiple-marker r2 and genetic coverage. Bioinformatics23, 252–254. 10.1093/bioinformatics/btl574
13
HayesB. J.VisscherP. M.McPartlanH. C.GoddardM. E. (2003). Novel multilocus measure of linkage disequilibrium to estimate past effective population size. Genome Res. 13, 635–643. 10.1101/gr.387103
14
HillW. G. (1981). Estimation of effective population size from data on linkage disequilibrium. Genet. Res. 38, 209–216. 10.1017/S0016672300020553
15
HillW. G.RobertsonA. (1968). Linkage Disequilibrium in Finite Populations. Theor. Appl. Genet. 38, 226–231. 10.1007/BF01245622
16
KijasJ. W.LenstraJ. A.HayesB. J.BoitardS.Porto NetoL. R.San CristobalM.et al. (2012). Genome-wide analysis of the world's sheep breeds reveals high levels of historic mixture and strong recent selection. PLoS Biol. 10:e1001258. 10.1371/journal.pbio.1001258
17
KosambiD. D. (1943). The estimation of map distances from recombination values. Ann. Eugen. 12, 172–175. 10.1111/j.1469-1809.1943.tb02321.x
18
Mbole-KariukiM. N.SonstegardT.OrthA.ThumbiS. M.BronsvoortB. M. D. C.KiaraH.et al. (2014). Genome-wide analysis reveals the ancient and recent admixture history of East African Shorthorn Zebu from Western Kenya. Heredity113, 297–305. 10.1038/hdy.2014.31
19
McEvoyB. P.PowellJ. E.GoddardM. E.VisscherP. M. (2011). Human population dispersal “Out of Africa” estimated from linkage disequilibrium and allele frequencies of SNPs. Genome Res. 21, 821–829. 10.1101/gr.119636.110
20
OhtaT.KimuraM. (1971). Linkage disequilibrium between two segregating nucleotide sites under the steady flux of mutations in a finite population. Genetics68, 571–580.
21
Orozco-terWengelP.BrufordM. W. (2014). Mixed signals from hybrid genomes. Mol. Ecol. 23, 3941–3943. 10.1111/mec.12863
22
PurcellS.NealeB.Todd-BrownK.ThomasL.FerreiraM. A. R.BenderD.et al. (2007). PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81, 559–575. 10.1086/519795
23
SmithJ. M.HaighJ. (1974). The hitch-hiking effect of a favourable gene. Genet. Res. 23, 23–35. 10.1017/S0016672300014634
24
SvedJ. A. (1971). Linkage disequilibrium and homozygosity of chromosome segments in finite populations. Theor. Popul. Biol. 141, 125–141. 10.1016/0040-5809(71)90011-6
25
SvedJ. A.CameronE. C.GilchristA. S. (2013). Estimating effective population size from linkage disequilibrium between unlinked loci: theory and application to fruit fly outbreak populations. PLoS ONE8:e69078. 10.1371/journal.pone.0069078
26
SvedJ. A.FeldmanM. W. (1973). Correlation and probability methods for one and two loci. Theor. Popul. Biol. 4, 129–132. 10.1016/0040-5809(73)90008-7
27
SvedJ. A.McRaeA. F.VisscherP. M. (2008). Divergence between human populations estimated from linkage disequilibrium. Am. J. Hum. Genet. 83, 737–743. 10.1016/j.ajhg.2008.10.019
28
TenesaA.NavarroP.HayesB. J.DuffyD. L.ClarkeG. M.GoddardM. E.et al. (2007). Recent human effective population size estimated from linkage disequilibrium. Genome Res. 17, 520–526. 10.1101/gr.6023607
29
UimariP.TapioM. (2011). Extent of linkage disequilibrium and effective population size in Finnish Landrace and Finnish Yorkshire pig breeds. J. Anim. Sci. 89, 609–614. 10.2527/jas.2010-3249
30
WangJ. (2005). Estimation of effective population sizes from data on genetic markers. Philos. Trans. R. Soc. Lond. B Biol. Sci. 360, 1395–1409. 10.1098/rstb.2005.1682
31
WaplesR. S.DoC. (2008). LDNE: a program for estimating effective population size from data on linkage disequilibrium. Mol. Ecol. Resour. 8, 753–756. 10.1111/j.1755-0998.2007.02061.x
32
WaplesR. S.DoC. (2010). Linkage disequilibrium estimates of contemporary Ne using highly variable genetic markers: a largely untapped resource for applied conservation and evolution. Evol. Appl. 3, 244–262. 10.1111/j.1752-4571.2009.00104.x
33
WeirB. S.HillW. G. (1980). Effect of mating structure on variation in linkage disequilibrium. Genetics95, 477–488.
34
WrightS. (1943). Isolation by distance. Genetics28, 114–138.
Summary
Keywords
effective population size, linkage disequilibrium, SNPChip, demography, large scale genotyping
Citation
Barbato M, Orozco-terWengel P, Tapio M and Bruford MW (2015) SNeP: a tool to estimate trends in recent effective population size trajectories using genome-wide SNP data. Front. Genet. 6:109. doi: 10.3389/fgene.2015.00109
Received
15 November 2014
Accepted
03 March 2015
Published
20 March 2015
Volume
6 - 2015
Edited by
Paolo Ajmone Marsan, Università Cattolica del Sacro Cuore, Italy
Reviewed by
David MacHugh, University College Dublin, Ireland; Yuri Tani Utsunomiya, Universidade Estadual Paulista(UNESP), Brazil
Copyright
© 2015 Barbato, Orozco-terWengel, Tapio and Bruford.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mario Barbato, School of Biosciences, Cardiff University, Sir Martin Evans Building, Museum Avenue CF10 3AX Cardiff, UK barbatom@cardiff.ac.uk
This article was submitted to Livestock Genomics, a section of the journal Frontiers in Genetics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.