- Institute of Molecular Pathology and Immunology of the University of Porto, Porto, Portugal
Substitution models of evolution describe the process of genetic variation through fixed mutations and constitute the basis of the evolutionary analysis at the molecular level. Almost 40 years after the development of first substitution models, highly sophisticated, and data-specific substitution models continue emerging with the aim of better mimicking real evolutionary processes. Here I describe current trends in substitution models of DNA, codon and amino acid sequence evolution, including advantages and pitfalls of the most popular models. The perspective concludes that despite the large number of currently available substitution models, further research is required for more realistic modeling, especially for DNA coding and amino acid data. Additionally, the development of more accurate complex models should be coupled with new implementations and improvements of methods and frameworks for substitution model selection and downstream evolutionary analysis.
Introduction
Substitution models of evolution describe the rates of change of fixed mutations among sequences and constitute the basis of the evolutionary analysis of genetic data at the molecular level. Although, the first substitution models that corrected the effects of multiple replacements were documented a long time ago (Jukes and Cantor, 1969; Dayhoff et al., 1978; Kimura, 1980), they were not applied in evolutionary analysis until much later when they were implemented in phylogenetic software packages based on maximum-likelihood (ML) methods (Felsenstein, 1991; Swofford, 1993). Then, it was noted that substitution model misspecification might bias phylogenetic inferences (Posada and Crandall, 2001; Minin et al., 2003; Lemmon and Moriarty, 2004). As a consequence, the selection of the best-fit substitution model became an essential stage in the pipeline of phylogenetic inference (Posada and Crandall, 1998, 2001), which also increased the popularity of substitution models in phylogenetics.
Nowadays, substitution models are routinely used in diverse areas of evolutionary biology. A large number of substitution models exist and new models are emerging to mimic the evolution of particularly complex real datasets. Nevertheless, recent studies suggest that there is still room for improving the commonly used substitution models (e.g., Keane et al., 2006).
This perspective provides an overview on the trends of substitution models of DNA, codon and amino acid evolution, including goals, and pitfalls of well-established substitution models. It also discusses directions for future research in substitution models of evolution and the establishment of complex substitution models as an essential step for phylogenetic inference.
Trends in DNA Substitution Models
The first and simplest model to mimic the DNA substitution process was described by Jukes and Cantor (JC) (1969). This model considers one rate of change between all nucleotides and equal nucleotide frequencies. However, changes between bases with equal chemical nature (transitions) are more common than changes between bases with different chemical structure (transversions) because the replacement of a similar structure is more likely in terms of molecular energy. Moreover, the genetic code allows for more transitions than transversions without amino acid replacement (Kimura, 1980; Collins and Jukes, 1994). Motivated by this evidence, Kimura (1980) presented the two-parameter model (K80), where the rates of change differ between transitions and transversions. Similarly, Felsenstein (1981) (F81) extended the JC model to include different nucleotide frequencies, which can also appear as a consequence of the physicochemical properties of nucleotides and the operation of natural selection. A number of models were later developed by incorporating extensions to those original models [i.e., HKY (Hasegawa et al., 1985) and SYM (Zharkikh, 1994)]. Following this trend, the most complex model, the general time-reversible model (GTR; Tavaré, 1986), incorporates different rates for every change and different nucleotide frequencies. In addition, a proportion of invariable sites (+I) (Shoemaker and Fitch, 1989) and/or rate of variation across sites (+G) (Yang, 1994) can be incorporated into any model. For technical details about these parametric DNA substitution models the reader is referred to the following reviews (Liò and Goldman, 1998; Felsenstein, 2004).
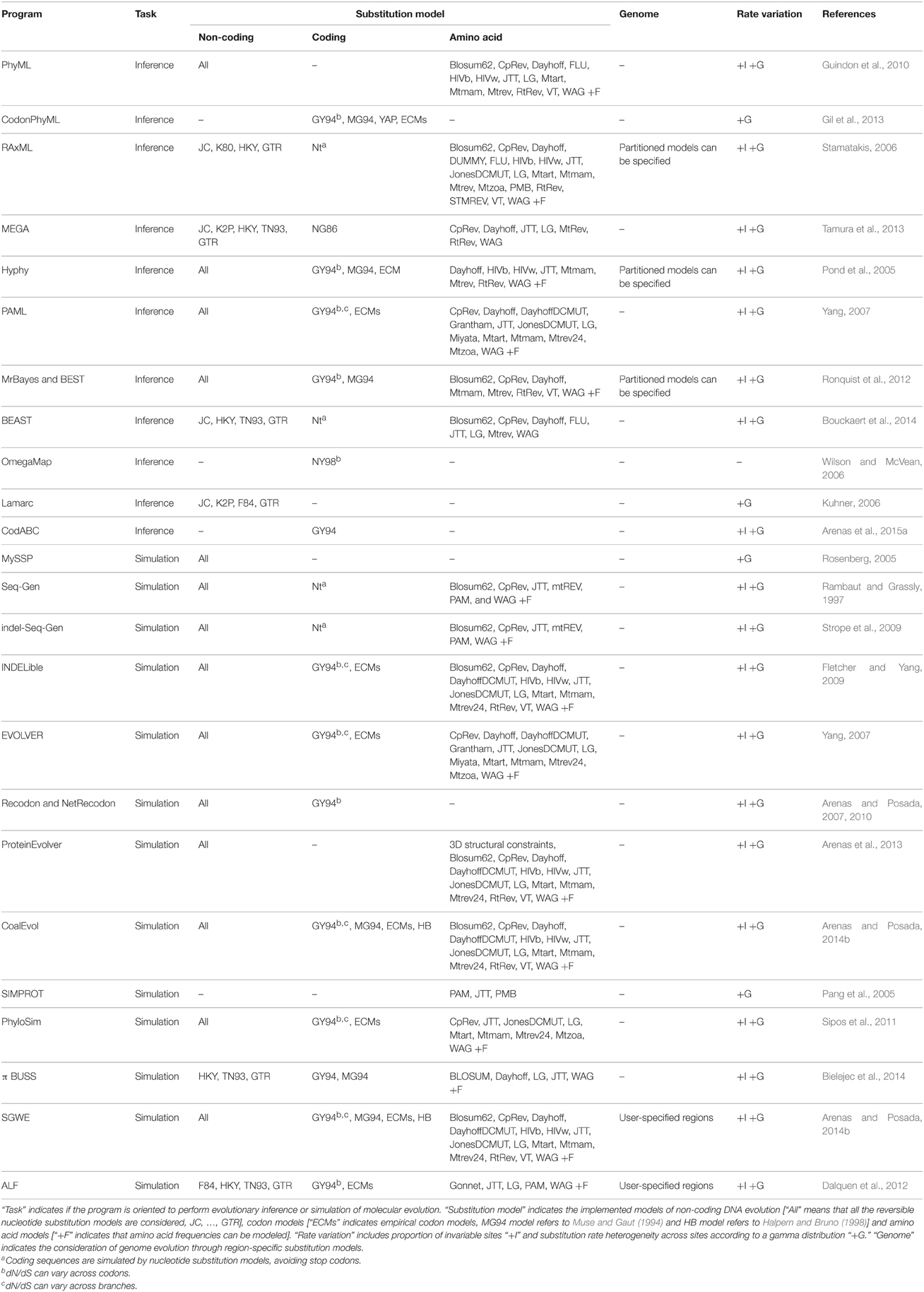
The stationary, reversible and homogeneous DNA substitution models derived from all possible combinations (equal/different rates of change and frequencies, with/without +G and/or +I; more than 1600 models) have already been defined, and are currently implemented in some phylogenetic programs (e.g., Darriba et al., 2012; Arenas and Posada, 2014b), see also Table 1. However, despite the large number of available DNA substitution models, the GTR +G +I model usually fits real data better than the other (simpler) alternative models (Sumner et al., 2012b), suggesting that the evolutionary process is very complex. Importantly, the GTR model presents undesirable mathematical properties [i.e., the multiplication of two GTR matrices does not return another GTR matrix (Sumner et al., 2012a)] for its application as a Markov model in phylogenetics (see Gatto et al., 2006; Sumner et al., 2012a,b). Indeed, the frequent selection of the most complex substitution model may suggest that more complex models could improve the fitting to real data (e.g., Jayaswal et al., 2011).
In order to improve the fitting to real data, current trends in the development of DNA substitution models involve non-reversible (asymmetric) and non-stationary (nucleotide composition can change over time) matrices (e.g., Boussau and Gouy, 2006; Jayaswal et al., 2011), or even consider neighbor interactions (Lunter and Hein, 2004), that can lead to more accurate phylogenetic inferences (Boussau and Gouy, 2006; Kaehler et al., 2015). However, these models have not been implemented yet in the most popular phylogenetic software packages due to their implicit complexity. In addition to the proposal of novel substitution models, future research should also address the implementation of these complex models in methods and programs for substitution model choice and phylogenetic inference.
Trends in Codon Substitution Models
Sites within codons evolve at different rates and, consequently, they should not be equally treated (Shapiro et al., 2006). Indeed, considering molecular evolution at the codon level allows us to incorporate more realistic evolutionary patterns for each codon position. Actually, evolutionary inferences based on the modeling of codon evolution are more robust than those derived from empirical amino acid models (Benner et al., 1994; Seo and Kishino, 2008).
Interestingly, mutations at the codon level can be classified as synonymous (silent) and non-synonymous (amino-acid replacing), which provides a measure of selective pressure at the molecular level (molecular adaptation). Then, the first codon substitution models included the non-synonymous and synonymous substitution rates, dN and dS respectively (Muse and Gaut, 1994), or the dN/dS ratio (Goldman and Yang, 1994). Despite the large number of (frequently ignored) considerations that should be made for the analysis and interpretation of dN/dS [i.e., dN/dS at the codon level can be biased if recombination is ignored (Anisimova et al., 2003; Arenas and Posada, 2010, 2014a) or if nucleotide frequencies vary across sites (Arenas and Posada, 2014b) and dN/dS should be estimated from samples of different populations (Kryazhimskiy and Plotkin, 2008; Pellissier, 2015)], dN/dS is commonly estimated in evolutionary biology for testing hypothesis related to selective pressure (e.g., Yang and Bielawski, 2000; Perez-Losada et al., 2009, 2011; Lopes et al., 2014; Arenas, 2015b; Arenas et al., 2015b; Lopez-Bueno et al., 2015). dN/dS >1 indicates that substitutions in the protein-coding gene were enriched for those that altered the amino acids states, suggesting diversifying (positive) selection. By contrast, dN/dS < 1 and dN/dS = 1 can be interpreted as purifying (negative) selection and neutral evolution, respectively.
Additional codon models have been proposed in order to better fit particular codon datasets. The GY94 codon model (Goldman and Yang, 1994) was extended to consider different nucleotide models (e.g., GTR; Kosakovsky Pond and Frost, 2005; Pond and Frost, 2005; Pond and Muse, 2005; Arenas and Posada, 2014b), dN/dS variation across sites (Yang et al., 2000; Anisimova et al., 2001; Kosakovsky Pond and Frost, 2005; Yang, 2007) and across branches (e.g., Pond and Frost, 2005; Yang, 2007; Dutheil et al., 2012). Other codon models implement information about the physicochemical properties of the encoded amino acids (Wong et al., 2006). Additionally, several empirical codon models—based on large databases of coding data—have been proposed (Schneider et al., 2005; Doron-Faigenboim and Pupko, 2007; Kosiol et al., 2007) and also codon models that consider codon bias (McVean and Charlesworth, 1999; Nielsen et al., 2007; Yang and Nielsen, 2008) or the effects of different GC contents (Misawa, 2011). Here, a promising trend is the emergence of mutation-selection models (e.g., Halpern and Bruno, 1998; Yang and Nielsen, 2008; Rodrigue et al., 2010) that attempt to integrate complex selection patterns into the mutation process and that outperform simple neutral models (Lawrie et al., 2011). Note that the interplay of mutational biases and weak selection can be complex, where constrained sites can evolve faster than neutral sites (McVean and Charlesworth, 1999; Lawrie et al., 2011). The consideration of these effects in substitution models of evolution can improve the identification of functional regions and the fitting to the data (Lawrie et al., 2011). For technical aspects on codon models the reader is referred to Anisimova and Kosiol (2009) and Cannarozzi and Schneider (2012).
Therefore, codon models allow us to perform accurate evolutionary analysis and to explore signatures of molecular adaptation. However, a problematic technical aspect regarding the implementation of these models is their large exchangeability matrices (61 × 61, note that stop codons are excluded). As a consequence, large amounts of data are needed to generate statistically well-supported empirical codon matrices and the computational burden is heavy. Fortunately, research on codon-based algorithm optimization is already generating new evolutionary tools to simulate (e.g., Fletcher and Yang, 2009; Arenas, 2012; Arenas and Posada, 2012) and analyze (e.g., Pond et al., 2005; Gil et al., 2013; Arenas et al., 2015a; Zoller et al., 2015) codon evolution (see Table 1), although further work is still required in this regard (e.g., the implementation of parallel computing of probability matrices).
The future of codon models will probably be related to the development of more complex models to better fit real data. In this concern, in addition to the development of new empirical models, codon models may follow two interesting trends. First, the consideration of heterogeneity along the sequence and over time, where different sites/regions and time periods could evolve under different models (Arenas, 2015a; Zoller et al., 2015). Note that these partition schemes can be very realistic, for example by considering different models for coding and non-coding regions. Moreover, it is known that codon models based on different codon frequencies across sites can bias dN/dS estimates (Arenas and Posada, 2014b), and Zoller et al. (2015) recently found that a two-partition codon model resolves a phylogeny better than a one-partition codon model. Consequently, methods and software to identify the best codon substitution model for particular codon regions (i.e., following Bao et al., 2008; Delport et al., 2010) and time periods are demanded. A second trend may be the consideration of structural information of proteins in codon models. Information derived from the protein function and from the protein folding stability [i.e., considering energy functions (Grahnen et al., 2011; Liberles et al., 2012; Arenas et al., 2015c)] of the encoded proteins could be considered in codon models. However, these implementations would require large computational costs if the protein structure varies with time or if more than one protein structure is needed to represent the encoded proteins of the dataset.
Trends in Amino Acid Substitution Models
Substitution models of amino acid evolution intend to mimic the evolution of protein data, which is crucial for testing a variety of hypotheses such as selection toward novel proteins (e.g., Fares et al., 2002), rate of protein evolution (e.g., Alvarez-Ponce and Fares, 2012), role of protein function on protein evolution (e.g., Liberles et al., 2011), evolutionary aspects of protein-protein interaction networks (e.g., Alvarez-Ponce and Fares, 2012), multiple sequence alignment based on protein evolution (Zhao and Sacan, 2015), or phylogenetic tree and ancestral protein reconstructions (e.g., Perez-Jimenez et al., 2011). Substitution models of amino acid evolution can be classified in two major groups: (i) empirical models—based on large protein databases—[e.g., CpRev (Adachi et al., 2000), Dayhoff (Dayhoff et al., 1978), DayhoffDCMUT (Kosiol and Goldman, 2005), HIVb (Nickle et al., 2007), HIVw (Nickle et al., 2007), JTT (Jones et al., 1992), JonesDCMUT (Kosiol and Goldman, 2005), LG (Le and Gascuel, 2008), Mtart (Abascal et al., 2007), Mtmam (Yang et al., 1998), Mtrev24 (Adachi and Hasegawa, 1996), RtRev (Dimmic et al., 2002), VT (Müller and Vingron, 2000), WAG (Whelan and Goldman, 2001), see Table 1 for their implementation in phylogenetic software], and (ii) parametric models—based on parameters that describe protein evolution—(Rastogi et al., 2006; Liberles et al., 2012).
An empirical amino acid substitution model consists of a 20 × 20 matrix of exchangeability rates and 20 amino acid frequencies. This simplicity (compared to other amino acid models such as those based on structural constraints) leads to advantages but also pitfalls. Empirical models can be incorporated into the commonly used likelihood functions implemented in the standard phylogenetic software by assuming site-independence (all sites evolve under the same model). Heterogeneous evolution can also be modeled by specifying different empirical models for different partitions (i.e., sites or domains) of the protein sequence (Halpern and Bruno, 1998; Lartillot and Philippe, 2004; Zoller and Schneider, 2013). However, a given real dataset may not be properly represented by any of the currently available empirical models. For example, Keane et al. (2006) found that the best fitting empirical model for two large proteobacteria and archaea protein datasets was originally derived from retroviral Pol proteins.
In order to provide an alternative to empirical models, constraints on the protein folding have been considered to generate parametric amino acid substitution models that have led to significant improvements (with respect to empirical models) when fitting real data (e.g., Taverna and Goldstein, 2000; Parisi and Echave, 2005; Goldstein, 2011; Grahnen et al., 2011; Wilke, 2012; Arenas et al., 2013, 2015c; Bordner and Mittelmann, 2013). However, these models are not well-established yet in the evolutionary analysis of protein data because the commonly used evolutionary frameworks implement likelihood functions that cannot deal with site-dependence. Consequently, a current trend in structurally constrained substitution models is to generate site-specific matrices that can be incorporated into common phylogenetic frameworks (Arenas et al., 2015c).
New empirical models are emerging to represent protein families (e.g., Cox and Foster, 2013); similarly, new parametric models are appearing to account for different evolutionary processes across sites and over time—covarion models—(Usmanova et al., 2015), epistatic fitness landscapes (Usmanova et al., 2015), or complex structural constraints (Bordner and Mittelmann, 2013; Arenas et al., 2015c). Nevertheless, the large variety and complexity of current amino acid substitution models cause problems when implemented. As noted, complex amino acid models (such as those based on protein folding stability) are not established yet in popular phylogenetic software due to their implicit complexity. In addition, the user often restricts the candidate substitution models to those empirical models implemented in common substitution model choice programs (e.g., Abascal et al., 2005), which may lead to severe incongruences (Keane et al., 2006).
Therefore, although current research on amino acid substitution models is providing more sophisticated models, these models are usually not applied by evolutionary biologists because they are not implemented in evolutionary frameworks and, consequently, these models are often forgotten. In order to consider complex substitution models in model selection and in evolutionary analysis, an alternative strategy can be the approximate Bayesian computation (ABC) approach (Beaumont, 2010; Csilléry et al., 2010; Sunnaker et al., 2013; Lopes et al., 2014; Arenas, 2015a). Basically, simulated data under different complex models are contrasted with real data through multiple regression adjustments to identify the model that best fits the real data, and to estimate the parameter values of the model corresponding to the studied dataset (see Lopes et al., 2014 for an example of ABC using complex codon models).
Conclusions
The modeling of genome evolution is nowadays important in population genomics and phylogenomics (Kumar et al., 2012; Librado et al., 2014). In that regard, as noted above, a variety of substitution models are known to mimic the evolution of coding and non-coding data. Importantly, the evolutionary process may differ between genomic regions because molecular evolution is often highly heterogeneous (Shapiro et al., 2006; Bofkin and Goldman, 2007; Arbiza et al., 2011) and, consequently, genome evolution should be mimicked with specific substitution models for each genomic region (Arbiza et al., 2011; Dalquen et al., 2012; Arenas and Posada, 2014b), see software implementation of partition models in Table 1. However, there is a need for methods to identify the regions that can better fit with a single substitution model. A strategy to perform this task could emulate genetic algorithms for the detection of recombination breakpoints based on phylogenetic tree incongruence (Fitch and Goodman, 1991; Grassly and Holmes, 1997; Kosakovsky Pond et al., 2006) assuming that different substitution models can also lead to significant signatures of phylogenetic tree incongruence (Minin et al., 2003; Lemmon and Moriarty, 2004). Then, these partitioning schemes could be evaluated with tools such as PartitionFinder (Lanfear et al., 2012). Additionally, a realistic modeling may involve not only region-specific models, but also branch-specific models (Ho, 2009). However, in practice only large datasets could provide sufficient statistical support for identifying the best models at those levels.
It seems clear that future research on substitution models of evolution will involve the development of more sophisticated and realistic substitution models. For example, the increasing amount of genomic data will probably require, in addition to partitioning, the development of complex mixture models where each site/region can be modeled with more than one substitution model. Concomitantly, efforts are needed to design and implement more robust methods to evaluate, compare and apply these complex substitution models.
Funding
This work was supported by the Portuguese Government through the FCT Starting Grant IF/00955/2014.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I want to thank Frontiers in Evolutionary and Population Genetics for the invitation to contribute with this inaugural perspective article derived from my new role in the journal as Associate Editor. I thank Marcos Pérez-Losada, at The George Washington University (USA), for helpful comments. I also thank three reviewers for insightful comments.
References
Abascal, F., Posada, D., and Zardoya, R. (2007). MtArt: a new model of amino acid replacement for arthropoda. Mol. Biol. Evol. 24, 1–5. doi: 10.1093/molbev/msl136
Abascal, F., Zardoya, R., and Posada, D. (2005). ProtTest: selection of best-fit models of protein evolution. Bioinformatics 21, 2104–2105. doi: 10.1093/bioinformatics/bti263
Adachi, J., and Hasegawa, M. (1996). MOLPHY version 2.3: programs for molecular phylogenetics based in maximum likelihood. Comp. Sci. Monogr. 28, 1–150.
Adachi, J., Waddell, P. J., Martin, W., and Hasegawa, M. (2000). Plastid genome phylogeny and a model of amino acid substitution for proteins encoded by chloroplast DNA. J. Mol. Evol. 50, 348–358. doi: 10.1007/s002399910038
Alvarez-Ponce, D., and Fares, M. A. (2012). Evolutionary rate and duplicability in the Arabidopsis thaliana protein-protein interaction network. Genome Biol. Evol. 4, 1263–1274. doi: 10.1093/gbe/evs101
Anisimova, M., Bielawski, J. P., and Yang, Z. (2001). Accuracy and power of the likelihood ratio test in detecting adaptive molecular evolution. Mol. Biol. Evol. 18, 1585–1592. doi: 10.1093/oxfordjournals.molbev.a003945
Anisimova, M., and Kosiol, C. (2009). Investigating protein-coding sequence evolution with probabilistic codon substitution models. Mol. Biol. Evol. 26, 255–271. doi: 10.1093/molbev/msn232
Anisimova, M., Nielsen, R., and Yang, Z. (2003). Effect of recombination on the accuracy of the likelihood method for detecting positive selection at amino acid sites. Genetics 164, 1229–1236. Available online at: http://www.genetics.org/content/164/3/1229.long
Arbiza, L., Patricio, M., Dopazo, H., and Posada, D. (2011). Genome-wide heterogeneity of nucleotide substitution model fit. Genome Biol. Evol. 3, 896–908. doi: 10.1093/gbe/evr080
Arenas, M., Dos Santos, H. G., Posada, D., and Bastolla, U. (2013). Protein evolution along phylogenetic histories under structurally constrained substitution models. Bioinformatics 29, 3020–3028. doi: 10.1093/bioinformatics/btt530
Arenas, M., Lopes, J. S., Beaumont, M. A., and Posada, D. (2015a). CodABC: a computational framework to coestimate recombination, substitution, and molecular adaptation rates by approximate bayesian computation. Mol. Biol. Evol. 32, 1109–1112. doi: 10.1093/molbev/msu411
Arenas, M., Lorenzo-Redondo, R., and Lopez-Galindez, C. (2015b). Influence of mutation and recombination on HIV-1 in vitro fitness recovery. Mol. Phylogenet. Evol. 94, 264–270. doi: 10.1016/j.ympev.2015.09.001
Arenas, M., and Posada, D. (2007). Recodon: coalescent simulation of coding DNA sequences with recombination, migration and demography. BMC Bioinformatics 8:458. doi: 10.1186/1471-2105-8-458
Arenas, M., and Posada, D. (2010). Coalescent simulation of intracodon recombination. Genetics 184, 429–437. doi: 10.1534/genetics.109.109736
Arenas, M., and Posada, D. (2012). “Simulation of coding sequence evolution,” in Codon Evolution, eds G. M. Cannarozzi and A. Schneider (Oxford: Oxford University Press), 126–132.
Arenas, M., and Posada, D. (2014a). “The influence of recombination on the estimation of selection from coding sequence alignments,” in Natural Selection: Methods and Applications, ed M. A. Fares (Boca Raton, FL: CRC Press/Taylor & Francis), 112–125.
Arenas, M., and Posada, D. (2014b). Simulation of genome-wide evolution under heterogeneous substitution models and complex multispecies coalescent Histories. Mol. Biol. Evol. 31, 1295–1301. doi: 10.1093/molbev/msu078
Arenas, M., Sánchez-Cobos, A., and Bastolla, U. (2015c). Maximum likelihood phylogenetic inference with selection on protein folding stability. Mol. Biol. Evol. 32, 2195–2207. doi: 10.1093/molbev/msv085
Arenas, M. (2012). Simulation of molecular data under diverse evolutionary scenarios. PLoS Comput. Biol. 8:e1002495. doi: 10.1371/journal.pcbi.1002495
Arenas, M. (2015a). Advances in computer simulation of genome evolution: toward more realistic evolutionary genomics analysis by approximate bayesian computation. J. Mol. Evol. 80, 189–192. doi: 10.1007/s00239-015-9673-0
Arenas, M. (2015b). Genetic consequences of antiviral therapy on HIV-1. Comput. Math. Methods Med. 2015, 9. doi: 10.1155/2015/395826
Bao, L., Gu, H., Dunn, K. A., and Bielawski, J. P. (2008). Likelihood-based clustering (LiBaC) for codon models, a method for grouping sites according to similarities in the underlying process of evolution. Mol. Biol. Evol. 25, 1995–2007. doi: 10.1093/molbev/msn145
Beaumont, M. A. (2010). Approximate Bayesian computation in evolution and ecology. Annu. Rev. Ecol. Evol. Syst. 41, 379–405. doi: 10.1146/annurev-ecolsys-102209-144621
Benner, S. A., Cohen, M. A., and Gonnet, G. H. (1994). Amino acid substitution during functionally constrained divergent evolution of protein sequences. Protein Eng. 7, 1323–1332. doi: 10.1093/protein/7.11.1323
Bielejec, F., Lemey, P., Carvalho, L. M., Baele, G., Rambaut, A., and Suchard, M. A. (2014). piBUSS: a parallel BEAST/BEAGLE utility for sequence simulation under complex evolutionary scenarios. BMC Bioinformatics 15:133. doi: 10.1186/1471-2105-15-133
Bofkin, L., and Goldman, N. (2007). Variation in evolutionary processes at different codon positions. Mol. Biol. Evol. 24, 513–521. doi: 10.1093/molbev/msl178
Bordner, A. J., and Mittelmann, H. D. (2013). A new formulation of protein evolutionary models that account for structural constraints. Mol. Biol. Evol. 31, 736–749. doi: 10.1093/molbev/mst240
Bouckaert, R., Heled, J., Kühnert, D., Vaughan, T., Wu, C. H., Xie, D., et al. (2014). BEAST 2: a software platform for Bayesian evolutionary analysis. PLoS Comput. Biol. 10:e1003537. doi: 10.1371/journal.pcbi.1003537
Boussau, B., and Gouy, M. (2006). Efficient likelihood computations with nonreversible models of evolution. Syst. Biol. 55, 756–768. doi: 10.1080/10635150600975218
Collins, D. W., and Jukes, T. H. (1994). Rates of transition and transversion in coding sequences since the human-rodent divergence. Genomics 20, 386–396. doi: 10.1006/geno.1994.1192
Cox, C. J., and Foster, P. G. (2013). A 20-state empirical amino-acid substitution model for green plant chloroplasts. Mol. Phylogenet. Evol. 68, 218–220. doi: 10.1016/j.ympev.2013.03.030
Csilléry, K., Blum, M. G., Gaggiotti, O. E., and François, O. (2010). Approximate Bayesian Computation (ABC) in practice. Trends Ecol. Evol. 25, 410–418. doi: 10.1016/j.tree.2010.04.001
Dalquen, D. A., Anisimova, M., Gonnet, G. H., and Dessimoz, C. (2012). ALF–a simulation framework for genome evolution. Mol. Biol. Evol. 29, 1115–1123. doi: 10.1093/molbev/msr268
Darriba, D., Taboada, G. L., Doallo, R., and Posada, D. (2012). jModelTest 2: more models, new heuristics and parallel computing. Nat. Methods 9, 772. doi: 10.1038/nmeth.2109
Dayhoff, M. O., Schwartz, R. M., and Orcutt, B. C. (1978). “A model of evolutionary change in proteins,” in Atlas of Protein Sequence and Structure, ed M. O. Dayhoff (Washington, DC: National Biomedical Research Foundation), 345–352.
Delport, W., Scheffler, K., Botha, G., Gravenor, M. B., Muse, S. V., and Kosakovsky Pond, S. L. (2010). CodonTest: modeling amino acid substitution preferences in coding sequences. PLoS Comput Biol 6:e1000885. doi: 10.1371/journal.pcbi.1000885
Dimmic, M. W., Rest, J. S., Mindell, D. P., and Goldstein, R. A. (2002). rtREV: an amino acid substitution matrix for inference of retrovirus and reverse transcriptase phylogeny. J. Mol. Evol. 55, 65–73. doi: 10.1007/s00239-001-2304-y
Doron-Faigenboim, A., and Pupko, T. (2007). A combined empirical and mechanistic codon model. Mol. Biol. Evol. 24, 388–397. doi: 10.1093/molbev/msl175
Dutheil, J. Y., Galtier, N., Romiguier, J., Douzery, E. J., Ranwez, V., and Boussau, B. (2012). Efficient selection of branch-specific models of sequence evolution. Mol. Biol. Evol. 29, 1861–1874. doi: 10.1093/molbev/mss059
Fares, M. A., Barrio, E., Sabater-Muñoz, B., and Moya, A. (2002). The evolution of the heat-shock protein GroEL from Buchnera, the primary endosymbiont of aphids, is governed by positive selection. Mol. Biol. Evol. 19, 1162–1170. doi: 10.1093/oxfordjournals.molbev.a004174
Felsenstein, J. (1981). Evolutionary trees from DNA sequences: a maximum likelihood approach. J. Mol. Evol. 17, 368–376. doi: 10.1007/BF01734359
Felsenstein, J. (1991). PHYLIP: Phylogenetic Inference Package, 3.4 Edn. Seattle, WA: University of Washington.
Fitch, D. H. A., and Goodman, M. (1991). Phylogenetic scanning: a computer assisted algorithm for mapping gene conversions and othe recombinational events. CABIOS 7, 207–215. doi: 10.1093/bioinformatics/7.2.207
Fletcher, W., and Yang, Z. (2009). INDELible: a flexible simulator of biological sequence evolution. Mol. Biol. Evol. 26, 1879–1888. doi: 10.1093/molbev/msp098
Gatto, L., Catanzaro, D., and Milinkovitch, M. C. (2006). Assessing the applicability of the GTR nucleotide substitution model through simulations. Evol. Bioinform. Online 2, 145–155. Available online at: http://www.la-press.com/assessing-the-applicability-of-the-gtr-nucleotide-substitution-model-t-article-a145
Gil, M., Zanetti, M. S., Zoller, S., and Anisimova, M. (2013). CodonPhyML: fast maximum likelihood phylogeny estimation under codon substitution models. Mol. Biol. Evol. 30, 1270–1280. doi: 10.1093/molbev/mst034
Goldman, N., and Yang, Z. (1994). A codon-based model of nucleotide substitution for protein-coding DNA sequences. Mol. Biol. Evol. 11, 725–736.
Goldstein, R. A. (2011). The evolution and evolutionary consequences of marginal thermostability in proteins. Proteins 79, 1396–1407. doi: 10.1002/prot.22964
Grahnen, J. A., Nandakumar, P., Kubelka, J., and Liberles, D. A. (2011). Biophysical and structural considerations for protein sequence evolution. BMC Evol. Biol. 11:361. doi: 10.1186/1471-2148-11-361
Grassly, N. C., and Holmes, E. C. (1997). A likelihood method for the detection of selection and recombination using nucleotide sequences. Mol. Biol. Evol. 14, 239–247. doi: 10.1093/oxfordjournals.molbev.a025760
Guindon, S., Dufayard, J. F., Lefort, V., Anisimova, M., Hordijk, W., and Gascuel, O. (2010). New algorithms and methods to estimate maximum-likelihood phylogenies: assessing the performance of PhyML 3.0. Syst. Biol. 59, 307–321. doi: 10.1093/sysbio/syq010
Halpern, A. L., and Bruno, W. J. (1998). Evolutionary distances for protein-coding sequences: modeling site-specific residue frequencies. Mol. Biol. Evol. 15, 910–917. doi: 10.1093/oxfordjournals.molbev.a025995
Hasegawa, M., Kishino, H., and Yano, T. (1985). Dating the human-ape splitting by a molecular clock of mitochondrial DNA. J. Mol. Evol. 22, 160–174. doi: 10.1007/BF02101694
Ho, S. Y. (2009). An examination of phylogenetic models of substitution rate variation among lineages. Biol. Lett. 5, 421–424. doi: 10.1098/rsbl.2008.0729
Jayaswal, V., Jermiin, L. S., Poladian, L., and Robinson, J. (2011). Two stationary nonhomogeneous Markov models of nucleotide sequence evolution. Syst. Biol. 60, 74–86. doi: 10.1093/sysbio/syq076
Jones, D. T., Taylor, W. R., and Thornton, J. M. (1992). The rapid generation of mutation data matrices from protein sequences. Comput. Appl. Biosci. 8, 275–282. doi: 10.1093/bioinformatics/8.3.275
Jukes, T. H., and Cantor, C. R. (1969). “Evolution of protein molecules,” in Mammalian Protein Metabolism, ed H. M. Munro (New York, NY: Academic Press), 21–132.
Kaehler, B. D., Yap, V. B., Zhang, R., and Huttley, G. A. (2015). Genetic distance for a general non-stationary markov substitution process. Syst. Biol. 64, 281–293. doi: 10.1093/sysbio/syu106
Keane, T. M., Creevey, C. J., Pentony, M. M., Naughton, T. J., and Mclnerney, J. O. (2006). Assessment of methods for amino acid matrix selection and their use on empirical data shows that ad hoc assumptions for choice of matrix are not justified. BMC Evol. Biol. 6:29. doi: 10.1186/1471-2148-6-29
Kimura, M. (1980). A simple method for estimating evolutionary rate of base substitutions through comparative studies of nucleotide sequences. J. Mol. Evol. 16, 111–120. doi: 10.1007/BF01731581
Kosakovsky Pond, S. L., and Frost, S. D. (2005). Not so different after all: a comparison of methods for detecting amino Acid sites under selection. Mol. Biol. Evol. 22, 1208–1222. doi: 10.1093/molbev/msi105
Kosakovsky Pond, S. L., Posada, D., Gravenor, M. B., Woelk, C. H., and Frost, S. D. (2006). Automated phylogenetic detection of recombination using a genetic algorithm. Mol. Biol. Evol. 23, 1891–1901. doi: 10.1093/molbev/msl051
Kosiol, C., and Goldman, N. (2005). Different versions of the Dayhoff rate matrix. Mol. Biol. Evol. 22, 193–199. doi: 10.1093/molbev/msi005
Kosiol, C., Holmes, I., and Goldman, N. (2007). An empirical codon model for protein sequence evolution. Mol. Biol. Evol. 24, 1464–1479. doi: 10.1093/molbev/msm064
Kryazhimskiy, S., and Plotkin, J. B. (2008). The population genetics of dN/dS. PLoS Genet. 4:e1000304. doi: 10.1371/journal.pgen.1000304
Kuhner, M. K. (2006). LAMARC 2.0: maximum likelihood and Bayesian estimation of population parameters. Bioinformatics 22, 768–770. doi: 10.1093/bioinformatics/btk051
Kumar, S., Filipski, A. J., Battistuzzi, F. U., Kosakovsky Pond, S. L., and Tamura, K. (2012). Statistics and truth in phylogenomics. Mol. Biol. Evol. 29, 457–472. doi: 10.1093/molbev/msr202
Lanfear, R., Calcott, B., Ho, S. Y., and Guindon, S. (2012). Partitionfinder: combined selection of partitioning schemes and substitution models for phylogenetic analyses. Mol. Biol. Evol. 29, 1695–1701. doi: 10.1093/molbev/mss020
Lartillot, N., and Philippe, H. (2004). A Bayesian mixture model for across-site heterogeneities in the amino-acid replacement process. Mol. Biol. Evol. 21, 1095–1109. doi: 10.1093/molbev/msh112
Lawrie, D. S., Petrov, D. A., and Messer, P. W. (2011). Faster than neutral evolution of constrained sequences: the complex interplay of mutational biases and weak selection. Genome Biol. Evol. 3, 383–395. doi: 10.1093/gbe/evr032
Le, S. Q., and Gascuel, O. (2008). An improved general amino acid replacement matrix. Mol. Biol. Evol. 25, 1307–1320. doi: 10.1093/molbev/msn067
Lemmon, A. R., and Moriarty, E. C. (2004). The importance of proper model assumption in bayesian phylogenetics. Syst. Biol. 53, 265–277. doi: 10.1080/10635150490423520
Liò, P., and Goldman, N. (1998). Models of molecular evolution and phylogeny. Genome Res. 8, 1233–1244.
Liberles, D. A., Teichmann, S. A., Bahar, I., Bastolla, U., Bloom, J., Bornberg-Bauer, E., et al. (2012). The interface of protein structure, protein biophysics, and molecular evolution. Protein Sci. 21, 769–785. doi: 10.1002/pro.2071
Liberles, D. A., Tisdell, M. D., and Grahnen, J. A. (2011). Binding constraints on the evolution of enzymes and signalling proteins: the important role of negative pleiotropy. Proc. Biol. Sci. 278, 1930–1935. doi: 10.1098/rspb.2010.2637
Librado, P., Vieira, F. G., Sánchez-Gracia, A., Kolokotronis, S. O., and Rozas, J. (2014). Mycobacterial phylogenomics: an enhanced method for gene turnover analysis reveals uneven levels of gene gain and loss among species and gene families. Genome Biol. Evol. 6, 1454–1465. doi: 10.1093/gbe/evu117
Lopes, J. S., Arenas, M., Posada, D., and Beaumont, M. A. (2014). Coestimation of recombination, substitution and molecular adaptation rates by approximate Bayesian computation. Heredity 112, 255–264. doi: 10.1038/hdy.2013.101
López-Bueno, A., Rastrojo, A., Peiro, R., Arenas, M., and Alcami, A. (2015). Ecological connectivity shapes quasispecies structure of RNA viruses in an Antarctic lake. Mol. Ecol. 24, 4812–4825. doi: 10.1111/mec.13321
Lunter, G., and Hein, J. (2004). A nucleotide substitution model with nearest-neighbour interactions. Bioinformatics 20(Suppl. 1), i216–i223. doi: 10.1093/bioinformatics/bth901
McVean, G. A., and Charlesworth, B. (1999). A population genetic model for the evolution of synonymous codon usage: patterns and predictions. Genet. Res. Camb. 74, 145–158. doi: 10.1017/S0016672399003912
Minin, V., Abdo, Z., Joyce, P., and Sullivan, J. (2003). Performance-based selection of likelihood models for phylogeny estimation. Syst. Biol. 52, 674–683. doi: 10.1080/10635150390235494
Misawa, K. (2011). A codon substitution model that incorporates the effect of the GC contents, the gene density and the density of CpG islands of human chromosomes. BMC Genomics 12:397. doi: 10.1186/1471-2164-12-397
Muller, T., and Vingron, M. (2000). Modeling amino acid replacement. J. Comput. Biol. 7, 761–776. doi: 10.1089/10665270050514918
Muse, S. V., and Gaut, B. S. (1994). A likelihood approach for comparing synonymous and nonsynonymous nucleotide substitution rates, with application to the chloroplast genome. Mol. Biol. Evol. 11, 715–724.
Nickle, D. C., Heath, L., Jensen, M. A., Gilbert, P. B., Mullins, J. I., and Kosakovsky Pond, S. L. (2007). HIV-specific probabilistic models of protein evolution. PLoS ONE 2:e503. doi: 10.1371/journal.pone.0000503
Nielsen, R., Bauer Dumont, V. L., Hubisz, M. J., and Aquadro, C. F. (2007). Maximum likelihood estimation of ancestral codon usage bias parameters in Drosophila. Mol. Biol. Evol. 24, 228–235. doi: 10.1093/molbev/msl146
Pang, A., Smith, A. D., Nuin, P. A., and Tillier, E. R. (2005). SIMPROT: using an empirically determined indel distribution in simulations of protein evolution. BMC Bioinformatics 6:236. doi: 10.1186/1471-2105-6-236
Parisi, G., and Echave, J. (2005). Generality of the structurally constrained protein evolution model: assessment on representatives of the four main fold classes. Gene 345, 45–53. doi: 10.1016/j.gene.2004.11.025
Pellissier, L. (2015). Stability and the competition-dispersal trade-off as drivers of speciation and biodiversity gradients. Front. Ecol. Evolution 3:52. doi: 10.3389/fevo.2015.00052
Perez-Jimenez, R., Inglés-Prieto, A., Zhao, Z. M., Sanchez-Romero, I., Alegre-Cebollada, J., Kosuri, P., et al. (2011). Single-molecule paleoenzymology probes the chemistry of resurrected enzymes. Nat. Struct. Mol. Biol. 18, 592–596. doi: 10.1038/nsmb.2020
Perez-Losada, M., Jobes, D. V., Sinangil, F., Crandall, K. A., Arenas, M., Posada, D., et al. (2011). Phylodynamics of HIV-1 from a phase III AIDS vaccine trial in Bangkok, Thailand. PLoS ONE 6:e16902. doi: 10.1371/journal.pone.0016902
Perez-Losada, M., Posada, D., Arenas, M., Jobes, D. V., Sinangil, F., Berman, P. W., et al. (2009). Ethnic differences in the adaptation rate of HIV gp120 from a vaccine trial. Retrovirology 6:67. doi: 10.1186/1742-4690-6-67
Pond, S. K., and Muse, S. V. (2005). Site-to-site variation of synonymous substitution rates. Mol. Biol. Evol. 22, 2375–2385. doi: 10.1093/molbev/msi232
Pond, S. L., and Frost, S. D. (2005). A genetic algorithm approach to detecting lineage-specific variation in selection pressure. Mol. Biol. Evol. 22, 478–485. doi: 10.1093/molbev/msi031
Pond, S. L., Frost, S. D., and Muse, S. V. (2005). HYPHY: hypothesis testing using phylogenies. Bioinformatics 21, 676–679. doi: 10.1093/bioinformatics/bti079
Posada, D., and Crandall, K. A. (1998). Modeltest: testing the model of DNA substitution. Bioinformatics 14, 817–818. doi: 10.1093/bioinformatics/14.9.817
Posada, D., and Crandall, K. A. (2001). Selecting the best-fit model of nucleotide substitution. Syst. Biol. 50, 580–601. doi: 10.1080/106351501750435121
Rambaut, A., and Grassly, N. C. (1997). Seq-Gen: an application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Comput. Appl. Biosciences 13, 235–238. doi: 10.1093/bioinformatics/13.3.235
Rastogi, S., Reuter, N., and Liberles, D. A. (2006). Evaluation of models for the evolution of protein sequences and functions under structural constraint. Biophys. Chem. 124, 134–144. doi: 10.1016/j.bpc.2006.06.008
Rodrigue, N., Philippe, H., and Lartillot, N. (2010). Mutation-selection models of coding sequence evolution with site-heterogeneous amino acid fitness profiles. Proc. Natl. Acad. Sci. U.S.A. 107, 4629–4634. doi: 10.1073/pnas.0910915107
Ronquist, F., Teslenko, M., Van Der Mark, P., Ayres, D. L., Darling, A., Höhna, S., et al. (2012). MrBayes 3.2: efficient Bayesian phylogenetic inference and model choice across a large model space. Syst. Biol. 61, 539–542. doi: 10.1093/sysbio/sys029
Rosenberg, M. S. (2005). MySSP: non-stationary evolutionary sequence simulation, including indels. Evol. Bioinform. Online 1, 81–83. Available online at: http://www.la-press.com/myssp-non-stationary-evolutionary-sequence-simulation-including-indels-article-a185
Schneider, A., Cannarozzi, G. M., and Gonnet, G. H. (2005). Empirical codon substitution matrix. BMC Bioinformatics 6:134. doi: 10.1186/1471-2105-6-134
Seo, T. K., and Kishino, H. (2008). Synonymous substitutions substantially improve evolutionary inference from highly diverged proteins. Syst. Biol. 57, 367–377. doi: 10.1080/10635150802158670
Shapiro, B., Rambaut, A., and Drummond, A. J. (2006). Choosing appropriate substitution models for the phylogenetic analysis of protein-coding sequences. Mol. Biol. Evol. 23, 7–9. doi: 10.1093/molbev/msj021
Shoemaker, J. S., and Fitch, W. M. (1989). Evidence from nuclear sequences that invariable sites should be considered when sequence divergence is calculated. Mol. Biol. Evol. 6, 270–289.
Sipos, B., Massingham, T., Jordan, G. E., and Goldman, N. (2011). PhyloSim - Monte Carlo simulation of sequence evolution in the R statistical computing environment. BMC Bioinformatics 12:104. doi: 10.1186/1471-2105-12-104
Stamatakis, A. (2006). RAxML-VI-HPC: maximum likelihood-based phylogenetic analyses with thousands of taxa and mixed models. Bioinformatics 22, 2688–2690. doi: 10.1093/bioinformatics/btl446
Strope, C. L., Abel, K., Scott, S. D., and Moriyama, E. N. (2009). Biological sequence simulation for testing complex evolutionary hypotheses: indel-Seq-Gen version 2.0. Mol. Biol. Evol. 26, 2581–2593. doi: 10.1093/molbev/msp174
Sumner, J. G., Fernandez-Sanchez, J., and Jarvis, P. D. (2012a). Lie Markov models. J. Theor. Biol. 298, 16–31. doi: 10.1016/j.jtbi.2011.12.017
Sumner, J. G., Jarvis, P. D., Fernández-Sánchez, J., Kaine, B. T., Woodhams, M. D., and Holland, B. R. (2012b). Is the general time-reversible model bad for molecular phylogenetics? Syst. Biol. 61, 1069–1074. doi: 10.1093/sysbio/sys042
Sunnaker, M., Busetto, A. G., Numminen, E., Corander, J., Foll, M., and Dessimoz, C. (2013). Approximate Bayesian computation. PLoS Comput. Biol. 9:e1002803. doi: 10.1371/journal.pcbi.1002803
Swofford, D. L. (1993). PAUP: Phylogenetic Analysis Using Parsimony, 3.1.1 Edn. Washington, DC: Smithsonian Institution.
Tamura, K., Stecher, G., Peterson, D., Filipski, A., and Kumar, S. (2013). MEGA6: molecular evolutionary genetics analysis version 6.0. Mol. Biol. Evol. 30, 2725–2729. doi: 10.1093/molbev/mst197
Tavaré, S. (1986). “Some probabilistic and statistical problems in the analysis of DNA sequences,” in Some Mathematical Questions in Biology - DNA Sequence Analysis, ed R. M. Miura (Providence, RI: Amer Math Soc), 57–86.
Taverna, D. M., and Goldstein, R. A. (2000). The distribution of structures in evolving protein populations. Biopolymers 53, 1–8. doi: 10.1002/(SICI)1097-0282(200001)53:1<1::AID-BIP1>3.0.CO;2-X. Available online at: http://onlinelibrary.wiley.com/doi/10.1002/%28SICI%291097-0282%28200001%2953:1%3C1::AID-BIP1%3E3.0.CO;2-X/abstract
Usmanova, D. R., Ferretti, L., Povolotskaya, I. S., Vlasov, P. K., and Kondrashov, F. A. (2015). A model of substitution trajectories in sequence space and long-term protein evolution. Mol. Biol. Evol. 32, 542–554. doi: 10.1093/molbev/msu318
Whelan, S., and Goldman, N. (2001). A general empirical model of protein evolution derived from multiple protein families using a maximum-likelihood approach. Mol. Biol. Evol. 18, 691–699. doi: 10.1093/oxfordjournals.molbev.a003851
Wilke, C. O. (2012). Bringing molecules back into molecular evolution. PLoS Comput. Biol. 8:e1002572. doi: 10.1371/journal.pcbi.1002572
Wilson, D. J., and McVean, G. (2006). Estimating diversifying selection and functional constraint in the presence of recombination. Genetics 172, 1411–1425. doi: 10.1534/genetics.105.044917
Wong, W. S., Sainudiin, R., and Nielsen, R. (2006). Identification of physicochemical selective pressure on protein encoding nucleotide sequences. BMC Bioinformatics 7:148. doi: 10.1186/1471-2105-7-148
Yang, Z., and Bielawsky, J. P. (2000). Statistical methods for detecting molecular adaptation. Trends Ecol. Evol. 15, 496–503. doi: 10.1016/S0169-5347(00)01994-7
Yang, Z., and Nielsen, R. (2008). Mutation-selection models of codon substitution and their use to estimate selective strengths on codon usage. Mol. Biol. Evol. 25, 568–579. doi: 10.1093/molbev/msm284
Yang, Z., Nielsen, R., Goldman, N., and Pedersen, A.-M. K. (2000). Codon-substitution models for heterogeneous selection pressure at amino acid sites. Genetics 155, 431–449. Available online at: http://www.genetics.org/content/155/1/431.long
Yang, Z., Nielsen, R., and Hasegawa, M. (1998). Models of amino acid substitution and applications to mitochondrial protein evolution. Mol. Biol. Evol. 15, 1600–1611. doi: 10.1093/oxfordjournals.molbev.a025888
Yang, Z. (1994). Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J. Mol. Evol. 39, 306–314. doi: 10.1007/BF00160154
Yang, Z. (2007). PAML 4: phylogenetic analysis by maximum likelihood. Mol. Biol. Evol. 24, 1586–1591. doi: 10.1093/molbev/msm088
Zhao, C., and Sacan, A. (2015). UniAlign: protein structure alignment meets evolution. Bioinformatics 31, 3139–3146. doi: 10.1093/bioinformatics/btv354
Zharkikh, A. (1994). Estimation of evolutionary distances between nucleotide sequences. J. Mol. Evol. 39, 315–329. doi: 10.1007/BF00160155
Zoller, S., Boskova, V., and Anisimova, M. (2015). Maximum-likelihood tree estimation using codon substitution models with multiple partitions. Mol. Biol. Evol. 32, 2208–2216. doi: 10.1093/molbev/msv097
Keywords: substitution model, molecular evolution, model selection, molecular adaptation, phylogenetics, phylogenomics
Citation: Arenas M (2015) Trends in substitution models of molecular evolution. Front. Genet. 6:319. doi: 10.3389/fgene.2015.00319
Received: 27 July 2015; Accepted: 09 October 2015;
Published: 26 October 2015.
Edited by:
James J. Cai, Texas A&M University, USAReviewed by:
Benjamin Callahan, Stanford University, USADavid S. Lawrie, Stanford University, USA
Russell Alan Hermansen, Temple University, USA
Copyright © 2015 Arenas. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Miguel Arenas, bWFyZW5hc0BpcGF0aW11cC5wdA==
 Miguel Arenas
Miguel Arenas