- 1Department of Computing, Informatics Institute of Technology, University of Westminster, Colombo, Sri Lanka
- 2Department of Microbiology, Bioinformatics Infrastructure Facility, Vidyasagar University, Midnapore, India
- 3Bioinformatics, Bioclues Organization, Hyderabad, India
- 4Environmental Health Institute, National Environment Agency, Singapore, Singapore
- 5Molecular Biology and Genetics, Quantitative Genetics and Genomics, Aarhus University, Tjele, Denmark
- 6Bioinformatics, Bioinformatics Organization, Hudson, MA, USA
Data mining and pattern recognition methods reveal interesting findings in genetic studies, especially on how the genetic makeup is associated with inherited diseases. Although researchers have proposed various data mining models for biomedical approaches, there remains a challenge in accurately prioritizing the single nucleotide polymorphisms (SNP) associated with the disease. In this commentary, we review the state-of-art data mining and pattern recognition models for identifying inherited diseases and deliberate the need of binary classification- and scoring-based prioritization methods in determining causal variants. While we discuss the pros and cons associated with these methods known, we argue that the gene prioritization methods and the protein interaction (PPI) methods in conjunction with the K nearest neighbors' could be used in accurately categorizing the genetic factors in disease causation.
Introduction
Many human diseases that have a causative association with genetic components are called as inherited diseases. Recent advances have significantly improved our understanding on diseases and inherited factors that play an important role in the disease paradigm (Schrodi et al., 2014). While it is a challenging task to identify the variants associated with inherited diseases through wet-lab based techniques, there is a need to find the causal effects of genetic changes associated with inherited diseases such as Autism, Schizophrenia, Bipolar disorder, etc. However, due to the complexity of the human genome, information from traditional methods such as human pedigree analysis has been in demand. In humans, as crosses cannot be performed due to ethical reasons, genealogical records need to be scrutinized to distinguish autosomal diseases from other forms of inherited diseases like X-linked diseases. Conversely, animals have been employed as models to ascertain factors linking to such diseases and causal mutations. From these studies, the pedigree or genealogy trees are interpreted to understand concurrent pairs of phenotypes for the diseasome studies. Such phenotypic studies would further allow us to understand the inheritance patterns of a disease associated with genetic polymorphism.
In the recent-past, there is a great deal of information outlying the genes associated with polymorphisms in relation to single nucleotide polymorphisms (SNP), genetic variants, multi nucleotide polymorphisms (MNP), quantitative trait loci (QTL), gene ontology (GO), and protein-protein interactions (PPI) or association and transcriptomic datasets coming from RNA-Seq data (Costa et al., 2013; Schrodi et al., 2014). Nevertheless, the genetic variation can be best seen with the intragenic/intronic regions or those that are non-coding or non-regulatory in nature. As most of the sequences associated with non-coding or non-regulatory regions, especially miRNAs, are highly conserved, it would be difficult to find the SNPs associated with them and their principal component part of diseasome studies is debated. Although the root cause for such genetic models could be studied by patterns associated with these polymorphisms, there remains a challenge on how these models are essential for understanding different data types.
Performance of the SNP Based Approaches for Identifying Inherited Diseases
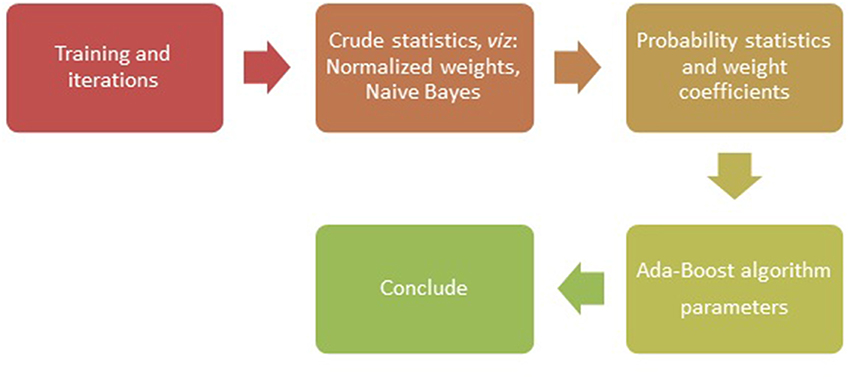
With the SNPs as genetic variants (Jiaxin et al., 2010), traditional classification methods and novel data mining techniques were explored to show effectiveness of different algorithms in identifying the disease association (Jiang et al., 2007). The SNPs located within protein coding regions can be further categorized into synonymous and non-synonymous SNPs (nsSNPs). A synonymous SNP does not alter the protein sequence, whereas the non-synonymous substitutions potentially affect protein function that may result in diseases (Yates and Sternberg, 2013). In methods used for classification and machine learning, the nsSNPs have been known to serve as better candidates, for example in studies involving binary classification with ensemble learning approach (Breiman, 1999). The methods such as AdaBoost (Figure 1), Random forest, L2boosting, stochastic gradient regression are known to fall short of classification methods such as decision tree and support vector machines (Jiaxin et al., 2010; Benso et al., 2013).
The five ensemble learning approaches and two classification methods are briefly tabulated in Table 1. Essentially, the following three categories of data are integrated to identify disease-causing SNPs of statistical significance: (a) annotations of nsSNPs extracted from the Swiss-Prot database (Consortium, 2010), (b) annotation of the protein families and structural domains extracted from Pfam database (Finn et al., 2006), and (c) a domain-domain interaction network obtained from the DOMINE (Raghavachari et al., 2008) and the InterDom database (Ng et al., 2003). From our preliminary observations, when we test all the classifiers against the above data, they seem to perform well in disease causing nsSNPs against regular nsSNPs. However, when comparing only four pre-set evaluation criteria, we find them to have significant differences from the random situations (Figure 2). The performance of approaches in identifying SNPs associated with diseases is measured by accuracy of the prediction (ACC), proportion of correctly classified cases (Horn et al., 2003), the area under receiver operating characteristic (ROC) curve (also called AUC), understating the prediction power of a given classification method, the balanced error rate (BER), and Matthew's correlation coefficient (MCC) which represents the prediction power under a certain decision threshold considering the biased and unbiased samples. Generally, smaller the BER, larger are the ACC and MCC. These methods have been reviewed elsewhere and are in agreement with the datum that Logit boost algorithm is the best method (Jiaxin et al., 2010). Results of the decision tree are distinguished more from other ensemble classifiers; BER of the decision tree is higher than other classifiers. The performance wise arrangement of the classifiers are L2boosting < stochastic gradient regression < SVM < Adaboost < random forest tree < logitboosts (Jiaxin et al., 2010). These methods for prioritizing candidates are based on the integrated use of two-sequence conservation features and methods such as domain-domain interaction networks. The bioinformatics based methods such as PolyPhen (Ramensky et al., 2002), SIFT (Ng and Henikoff, 2003), KBAC (Liu and Leal, 2010), and MSRV (Jiang et al., 2007) along with binary classification methods provide limited information in prioritizing disease-associated nsSNPs when compared to multiple sequence alignment (MSA) methods (Rui and Jiaxin, 2011) which extracts conserved protein sequences underlying the mutation.
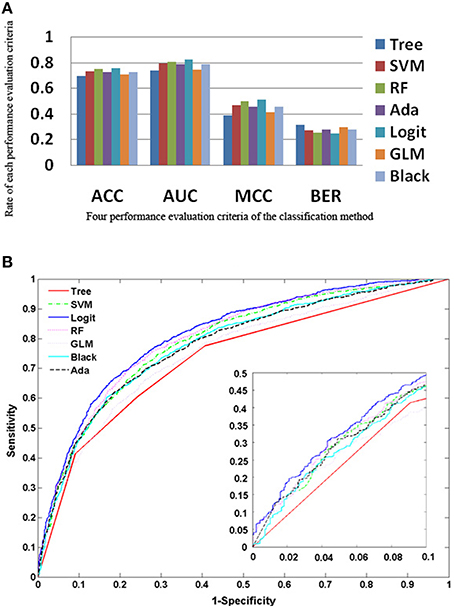
Figure 2. Performance of the approaches as explained from the methods (A) Rate of performance evaluation comparison of the each classification methods; the accuracy of the prediction (ACC); the area under the receiver operating characteristic (ROC) curve (AUC); the balanced error rate (BER) and the Matthews' correlation coefficient (MCC). (B) Performance of the 7 approaches based on the true positive rate vs. false positive rate.
To overcome this limitation, we introduced methods that integrate conservation properties of amino acids and domains harbored calculated association score (Rui and Jiaxin, 2011). A brief description is given below.
Calculation of Similarity Scores between nsSNPs
The purpose of using following equations is to measure the similarity scores between a single pair of nsSNPs, first getting an nsSNP and the corresponding amino acid substitution occurring at a certain position. The probability of occurrence of the original amino acid (Porg) is calculated at a similar position of the protein super family. For this purpose, the Pfam database is used to extract the multiple sequence alignment (MSA) of the query protein to find the number of occurrences of the original amino acid at the corresponding position of the alignment and then to divide the number of occurrences by the number of proteins in the alignment (Rui and Jiaxin, 2011).
First Equation corresponds to probability of occurrence of the original amino acid (Porg).
Second Equation corresponds to probability of occurrence of the substituted amino acid (Psub).
Third Equation corresponds to calculation of diffusion kernel of the domain-domain interaction network
Prioritization of Candidate nsSNPs
After calculating the single pairwise similarity measure of nsSNPs, the prioritization of a set of candidate nsSNPs is done by “guilt-by-association principle” (Altshuler et al., 2000). The association score for a candidate nsSNPs as the mean similarity value between the nsSNP and all seed nsSNPs is calculated using
where c is a candidate nsSNP, A(c) is the association score and S(d) the set of seed nsSNPs from query disease d.
Integrating Multiple Ranks
The multiple ranking lists obtained from guilt-by-association principle is applied to each data sources. Here, an altered Stouffer's Z-score method is provided to integrate the ranks and to obtain a single ranking list.
The integrated Z-score is made by adding up their corresponding Z-scores as following equation. Finally, they are re-ranked according to the integrated Z-scores in decreasing order to obtain the integrated ranking list.
We argue that there are certain limitations in this approach, as it is a choice for extracting conserved protein domains using the Pfam database. To overcome the problem of identifying the variants, few other sequence alignment tools such as BLAST or PSIBLAST can be used to extract sequence conservation features (Altschul et al., 1997) which highlight the mutations in genome regions such as transcriptional-factor binding sites or promoter regions (Jiaxin et al., 2010; Rui and Jiaxin, 2011). While a binary classification solution such as Logitboost is found to be a more accurate classification algorithm, it is fully dependent on the multiple sequence alignment. However, combining the multiple sequence analysis and domain-domain interaction method is a better method to identify nsSNPs associated with diseases. Further enhancement of domain-domain interaction models would allow us to evaluate the functional similarity between two genes and their products. These data sources contain gene expression profile, gene ontology annotations, PPI.
Combination of SNP Methods Attributing to Inherited Diseases
With SNPs and other clinical conditions contributing to a wide range of inherited diseases (Fiaschi et al., 2009), a general framework has been proposed to find variants for pre-eclampsia, a progressive disorder that occurs during pregnancy and soon after the birth, affecting both the mother and the baby (Roberts et al., 1989). Mutated risk genes, genetic, and environmental factors are thought to be of key importance in such diseases (Risch and Merikangas, 1996; Liangcai et al., 2008). Further methods have been proposed to analyze risk pathway of the bipolar disorder (BD; Hirschfeld et al., 2003). Keeping in view of the fact that detection of associations between human genetic variant and their phenotypic involvement is a significant challenge in understanding genetic basis of inherited diseases in humans (Wu et al., 2014), various methods, viz. ID3 (Breiman et al., 1999), ADTree (Freund and Mason, 1999), and C4.5 (Quinlan, 1993) have been recognized. Most of the current systems, however, predict associations between nsSNPs and diseases based on features obtained from only protein sequences and/or structure information, and do not provide details about which specific disease is associated with nsSNPs. Further, to evaluate combination of methodologies, analysis of the disease association of the SNPs and environmental factors in the KEGG pathways can be done through which we could represent the SNP networks of molecular wiring diagrams, in addition to mapping genes to the reaction and interactions (Kanehisa and Goto, 2000; Liangcai et al., 2008). There are few major steps of calculating disease risks which focus on genetic factors involved in the relationship between multiple genes and the diseases, but also the metabolic environment factors between genes and pathways. This can be further achieved by calculating the two RS scores and by prioritizing the pathways. The RS measures are integrated according to condition-dependent theory, and the association between the biological pathways and the complex disease is established through sorts of genes. The measurements algorithm, viz. a SNP Pathway based Association Method (SPAM) is briefed as follows (also see Figure 3) (Liangcai et al., 2008).
Or
Here, RS (D, pi) is the relationship scoring between pathway pi and the disease D, N is the number of gene clusters on pathway pi and d(GSj, pi) reveals the complexity of gene cluster GSj on pathway pi. m is the number of genes with p < 0.05. M is the count of all genes on pathway pi.
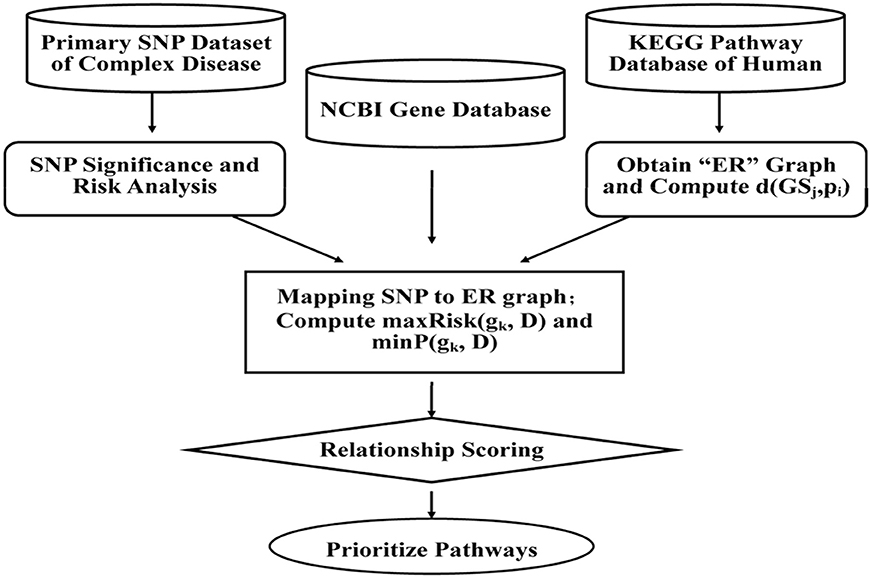
Figure 3. A SNP pathway based Association Method (SPAM): First step is SNP significance analysis and the corresponding risk calculation. Data of case and control for each and risk ratio is calculated from relationships between the SNP and complex diseases. The second step is reconstruction of KEGG pathway and analysis of the reconstructed network attribution. As per the format, KEGG pathway represents a network where a node represents metabolite and one edge represents some enzyme or a gene cluster. The third step involves screening of SNPs and mapping of SNPs to reconstructed network (Hoh and Ott, 2003). The fourth step is calculation of the two integrated measurements of RS scoring and prioritizing the pathway.
While comparing our method (SNPs analysis) with earlier stated methods, we argue that other methods are effective only in detecting partially known genetic or unknown genetic bases and are used for analyzing queried protein sequences. To overcome this limitation, PSI-BLAST (Altschul et al., 1997) or COBALT (Papadopoulos and Agarwala, 2007) enables feature selection methods. Family history related data can additionally be used to infer performance of the proposed solution (Fiaschi et al., 2009), in addition to feature selection entities such as transcriptional and promoter regions (Liangcai et al., 2008; Wu et al., 2014). Whereas the combination methods explain more originality of how SNPs specific to diseases can be analyzed, KEGG pathways are useful to scrutinize other environment factors with SNP data. The phenotype data associated with diseases and its threshold values are used to transform categorical data into Boolean ones (Fiaschi et al., 2009) which helps in machine learning. However, it must be done judiciously as selection may significantly affect the accuracy of the solution. Wu et al. (2014) argue that Canberra distance (Emran and Ye, 2001) algorithm is the best to calculate distance between pairwise nsSNPs but in some cases, the same distance may be inferred between two similar pairs in the dataset as it is hard to classify or to associate with the particular diseases.
Given the numbers of diseased gene prioritization generated by wet lab techniques serve as a major impediment in human genetics, bringing a multi-faceted approach for diagnostics and treatment (Arrais and Oliveira, 2010) for diseases such as autism (Kim et al., 2000), schizophrenia (Jingchun et al., 2008) and diabetes should be strategically prioritized. That said, the similarity between all strategies is the use of “guilt-by-association” concept where the most relevant candidates will be the ones that are similar to the genes already known to be linked to the biological process of interest. Graph based models for gene-disease prioritization consider biomedical terms such as genes, pathways, homologies, ontologies, gene expression data and literature in ascertaining the model (Arrais and Oliveira, 2010). The previous gene-disease prioritization models have been built using gene related concepts to construct the questions over biomedical databases and to create ranked list of genes. Following this, from MeSH (Xu and Li, 2006), the statistical and knowledge based combining data from gene ontology and MeSH (Raghavachari et al., 2008) apart from probabilistic methods, viz. Hyper-Induced Topic Search (HITS; Kleinberg, 1999) and PageRank (Page et al., 1999) have been very useful. However, the above methods lagged by annotation coverage and tend for large biases.
PPI Networks and Inherited Diseases
The availability of human genome-wide PPI data has opened a wide outlook for discovering inherited disease genes by studying topological features in PPI networks (Xu and Li, 2006). Keeping in view of the fact that studies on proteins and their interactions are important to understand their dynamic roles for identification of inherited, and to a certain extent rare immunological disorders, mapping the disease specific genes (for example genes related to schizophrenia) into the whole human interaction network and then the extraction of related sub networks can throw light on the cellular mechanisms and biological processes related to the inherited disease (Jingchun et al., 2008). The sequence based features have previously been exploited and found that in many cases there are significant differences between genes responsible for human hereditary disease and those not known to be involved in diseases (Xu and Li, 2006). Genes associated with a human disease preferentially interacted with other disease-causing genes, suggesting that heritable disease-genes might share some topological features in the PPIs network when compared to the non-diseased genes (Gandhi et al., 2006). We further argue that similar genes are obtained with human PPI datasets from Online Predicted Human Integration Database (OPID; Brown and Jurisica, 2005) employing K-nearest neighbor (KNN) algorithm for classification. The KNN algorithm is a simple and yet a powerful non parametric classification algorithm (Franke et al., 2006) with an effective performance. With rapid enhancement in quantity and quality of human interaction and phenotypic data, the performance and utility of this approach to detect novel disease-genes should improve further as we come to the end of the post-genomic era. We have earlier proposed a classification scoring method to validate the interaction mapping between such proteins and calculated the total reliability score (TRS) using machine learning algorithms (Suravajhala and Sundararajan, 2012). The accuracy of six point classification model was found to be 81.08% on multilayer perception of neural network which, if used based on such approaches, could have identified causal SNPs toward development of molecular markers. In the recent-past, the PPI database is also used as a knowledge base with a set of known disease-related genes that is utilized with linkage analysis in prioritizing the best candidates. From our previous discussions, we argue that the main advantage of the probabilistic knowledge model is that it reduces the prioritization error by 6% when compared to already published methods. These studies based on the relatedness to known diseases or closely related disease processes, however, remain a challenge in prioritizing loner or isolated genes with no known relationships between two nodes in the network. The solution for prioritizing loosely connected disease genes with other genes has previously been proposed by Fang et al. (Fang et al., 2014) (Figure 4) which uses network diffusion and rank concordance (NDRC). In addition, they found that genes related to complex diseases are divided into several modules associated with different disease phenotypes. First, they built the network without removing the insignificant genes from the network, while the second one was based on the Diffusion Rank (DR) algorithm (Yang et al., 2007). The NDRC simulates the heat diffusion process where information flows from the known disease genes of related disease and propagates over the PPI network with noisy data as a problem to prioritize disease genes (Li et al., 2009; Wang et al., 2009; Fang et al., 2014). Multiple kernels learning (KML) and N dimensional order statistic (NDOS) methods were found to be handling noisy data effectively. Two strategies are relatively known, one to search for a kernel that would best represent all the information available using a convex optimization method, known as semi-definite programming (SDP; Lanckriet et al., 2004; De Bie et al., 2007) which simultaneously optimizes parameters for one-class SVM and tests genes ranked by the one-class SVM. In the second strategy, all test genes were first ranked using one-class SVM with an individual data source and then, N-dimensional order statistics was used to combine these rank lists into one rank list (Lanckriet et al., 2004). For gene ontology and sequence data, we argue that the kernel with higher weight may not have much influence in discerning the SNPs. Different machine learning algorithms as described are used for prioritizing SNPs and proven to be effective especially SVMs with higher performance than the random forest. A comparative study was carried out by Tranchevent et al. (2010) on prioritizing tools. The authors recommended genes to diseases (G2D) as a good tool for providing an ordered list of candidate genes in the peak regions (Perez-Iratxeta et al., 2002). In conclusion, SVM can be applied to the gene prioritizing process with ontology association as it encompasses enrichment based feature selection processes in identification of inherited diseases (He and Jiang, 2012; Xie et al., 2012). Nevertheless, feature selection method and integrating more data sources like semantic and phenotype similarity profiling between diseases and genes could build better prediction ability.
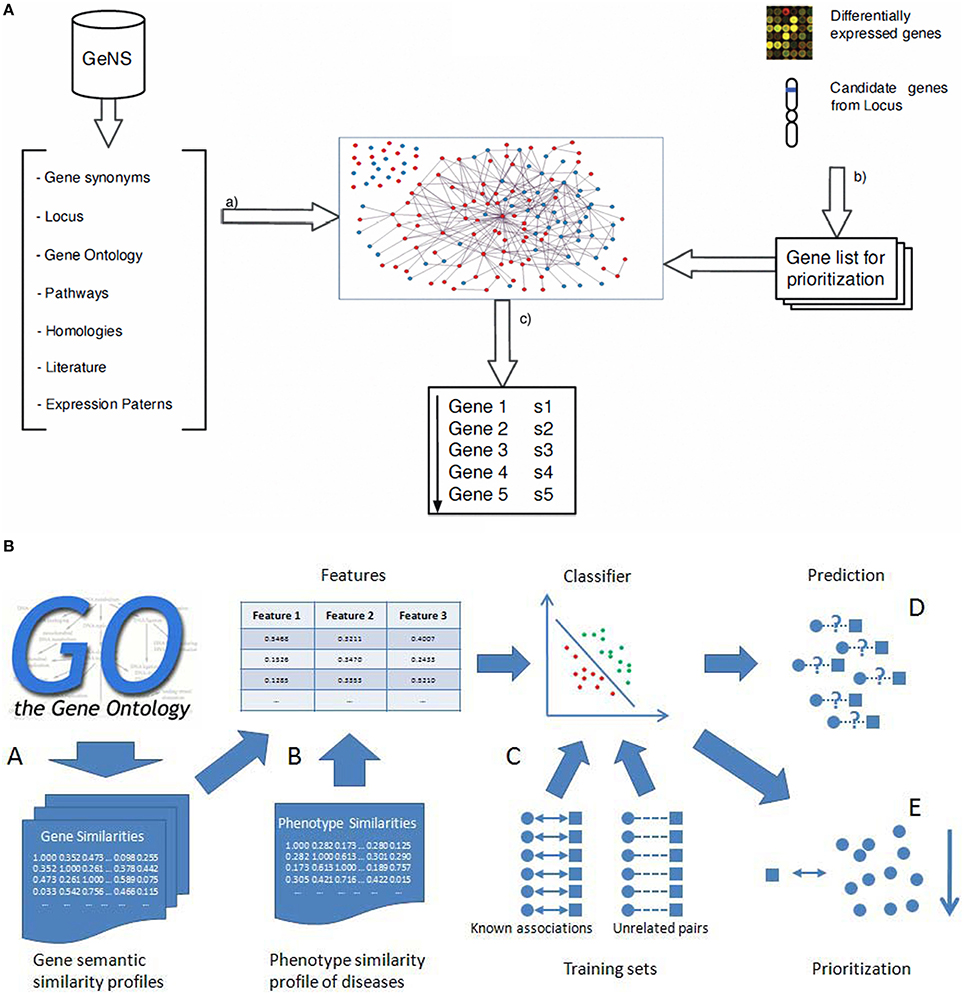
Figure 4. Gene prioritization methods. (A) (a) Entities and their relations are retrieved from the source databases which are then filtered, sorted and disambiguated to create the graph. From gene expression studies or positional studies or GO, a list of genes are obtained for prioritization (Arrais and Oliveira, 2010) (b) Calculation of the gene semantic similarity scores to obtain the three gene similarity profiles; (B) Combining the three gene similarity profiles and the phenotype similarity profile to calculate three dimensional features for classification; (C) Training classifier using the known associations and sufficient unrelated gene-disease pairs as training sets; (D) Prediction of disease-gene associations; (E) Prioritization of candidate genes (He and Jiang, 2012).
Conclusions
Most of the inherited diseases are caused by SNP variants and research findings on causal SNPs are becoming prominent. During the last few years, the multitude of research showcasing SNPs and other methodologies has come up in identifying the candidates for inherited diseases. From this commentary, we reason out that identification of SNPs has generally been considered as a binary classification problem, although, there are a host of methods, viz. support vector machine tools, random forest methods, gene prioritization methods that are used for scoring and calculating genes truly associated with the inherited diseases. Among the classifiers, KNN is known to be the most best performing algorithm for the analysis of inherited diseases based on PPI network. As human PPIs grow in post-genomic era, a promising source for discovering such disease genes could herald a need to understand the rigorous algorithms behind such approaches. As researchers use different cross validation methods to prove accuracy, efficiency, and the appropriation, a conceptualized framework for identification of inherited diseases would be promising. With deluge of human genomic data containing SNPs and PPI, there remains this challenge.
Author Contributions
LI and AA made the initial survey and validation of studies, PD, VS, and PS discussed and mentored the graduate students toward their virtual project, JV advised and guided the review, PS and JV proofread the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Dr. Chanditha Hapuarachchi, Environmental Health Institute, National Environment Agency, Singapore for his final version of the proof-read of the manuscript.
References
Altschul, S. F., Madden, T. L., Schäffer, A. A., Zhang, J., Zhang, Z., Miller, W., et al. (1997). Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 25, 3389–3402. doi: 10.1093/nar/25.17.3389
Altshuler, D., Daly, M., and Kruglyak, L. (2000). Guilt by association. Nat. Genet. 26, 135–137. doi: 10.1038/79839
Arrais, J. P., and Oliveira, J. L. (2010). “Gene-disease prioritization through biomedical networks,” in 2010 10th IEEE International Conference on Information Technology and Applications in Biomedicine (ITAB) (Corfu), 1–4.
Benso, A., Di Carlo, S., Ur Rehman, H., Politano, G., Savino, A., and Suravajhala, P. (2013). A combined approach for genome wide protein function annotation/prediction. Proteome Sci. 11 (Suppl. 1):S1. doi: 10.1186/1477-5956-11-S1-S1
Breiman, L. (1999). Using Adaptive Bagging to Debias Regressions. Technical Report 547, Statistics Department UCB.
Breiman, L., Friedman, J. H., Olshen, R. A., and Stone, C. J. (1999). Classification and Regression Trees. New York, NY: CRC Press.
Brown, K. R., and Jurisica, I. (2005). Online predicted human interaction database. Bioinformatics 21, 2076–2082. doi: 10.1093/bioinformatics/bti273
Consortium, T. U. (2010). The Universal Protein Resource (UniProt) in 2010. Nucleic Acids Res. 38, D142–D148. doi: 10.1093/nar/gkp846
Cortes, C., and Vapnik, V. (1995). Support-vector networks. Mach. Learn. 20, 273–297. doi: 10.1007/BF00994018
Costa, V., Aprile, M., Esposito, R., and Ciccodicola, A. (2013). RNA-Seq and human complex diseases: recent accomplishments and future perspectives. Eur. J. Hum. Genet. 21, 134–142. doi: 10.1038/ejhg.2012.129
De Bie, T., Tranchevent, L.-C., Van Oeffelen, L. M., and Moreau, Y. (2007). Kernel-based data fusion for gene prioritization. Bioinformatics 23, i125–i132. doi: 10.1093/bioinformatics/btm187
Emran, S. M., and Ye, N. (2001). “Robustness of canberra metric in computer intrusion detection,” in Proceedings of the IEEE Workshop on Information Assurance and Security (West Point, NY: Citeseer).
Fang, M., Hu, X., He, T., Wang, Y., Zhao, J., Shen, X., et al. (2014). “Prioritizing disease-causing genes based on network diffusion and rank concordance,” in IEEE International Conference on Bioinformatics and Biomedicine (BIBM) (Belfast), 242–247.
Fiaschi, L., Garibaldi, J. M., and Krasnogor, N. (2009). “A framework for the application of decision trees to the analysis of SNPs data,” in IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology, CIBCB'09 (Nashville, TN), 106–113.
Finn, R. D., Mistry, J., Schuster-Böckler, B., Griffiths-Jones, S., Hollich, V., Lassmann, T., et al. (2006). Pfam: clans, web tools and services. Nucleic Acids Res. 34, D247–D251. doi: 10.1093/nar/gkj149
Franke, L., Bakel, H. V., Fokkens, L., De Jong, E. D., Egmont-Petersen, M., and Wijmenga, C. (2006). Reconstruction of a functional human gene network, with an application for prioritizing positional candidate genes. Am. J. Hum. Genetics 78, 1011–1025. doi: 10.1086/504300
Freund, Y., and Mason, L. (1999). “The alternating decision tree learning algorithm,” in ICML 99 Proceedings of the Sixteenth International Conference on Machine Learning (Montreal, QC), 124–133.
Friedman, J., Hastie, T., and Tibshirani, R. (2000). Additive logistic regression: a statistical view of boosting (with discussion and a rejoinder by the authors). Ann. Statis. 28, 337–407. doi: 10.1214/aos/1016218223
Gandhi, T., Zhong, J., Mathivanan, S., Karthick, L., Chandrika, K., Mohan, S. S., et al. (2006). Analysis of the human protein interactome and comparison with yeast, worm and fly interaction datasets. Nat. Genet. 38, 285–293. doi: 10.1038/ng1747
He, P., and Jiang, R. (2012). “Integrating multiple gene semantic similarity profiles to infer disease genes,” in 31st Chinese Control Conference (CCC) (Hefei), 7420–7425.
Hirschfeld, R. M. A., Lewis, L., and Vornik, L. A. (2003). Perceptions and impact of bipolar disorder: how far have we really come? Results of the National Depressive and Manic-Depressive Association 2000 survey of individuals with bipolar disorder. J. Clini. Psychiatry 64, 161–174. doi: 10.4088/JCP.v64n0209
Hoh, J., and Ott, J. (2003). Mathematical multi-locus approaches to localizing complex human trait genes. Nat. Rev. Genet. 4, 701–709. doi: 10.1038/nrg1155
Horn, W., Shahar, Y., Lindberg, G., Andreassen, S., and Wyatt, J. (2003). “Artificial intelligence in medicine,” in Joint European Conference on Artificial Intelligence in Medicine and Medical Decision Making, AIMDM'99 (Aalborg), Springer.
Jiang, R., Yang, H., Zhou, L., Kuo, C. C. J., Sun, F., and Chen, T. (2007). Sequence-based prioritization of nonsynonymous single-nucleotide polymorphisms for the study of disease mutations. Am. J. Hum. Genetics 81, 346–360. doi: 10.1086/519747
Jiaxin, W., Wangshu, Z., and Rui, J. (2010). “Comparative study of ensemble learning approaches in the identification of disease mutations,” in International Conference on Biomedical Engineering and Informatics (BMEI) (Yantai), 2306–2310.
Jingchun, S., Leng, H., and Zhongming, Z. (2008). “Schizophrenia genes: characteristics of function and protein interaction networks,” in International Conference on BioMedical Engineering and Informatics, 2008. BMEI 2008 (Sanya), 437–441.
Kanehisa, M., and Goto, S. (2000). KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 28, 27–30. doi: 10.1093/nar/28.1.27
Kim, J. A., Szatmari, P., Bryson, S. E., Streiner, D. L., and Wilson, F. J. (2000). The prevalence of anxiety and mood problems among children with autism and asperger syndrome. Autism 4, 117–132. doi: 10.1177/1362361300004002002
Kleinberg, J. M. (1999). Authoritative sources in a hyperlinked environment. J. ACM 46, 604–632. doi: 10.1145/324133.324140
Lanckriet, G. R., De Bie, T., Cristianini, N., Jordan, M. I., and Noble, W. S. (2004). A statistical framework for genomic data fusion. Bioinformatics 20, 2626–2635. doi: 10.1093/bioinformatics/bth294
Li, Y., Patra, J. C., and Sun, J. (2009). “A new method to combine heterogeneous data sources for candidate gene prioritization,” in Ninth IEEE International Conference on IEEE Bioinformatics and BioEngineering, BIBE'09 (Taichung), 123–129.
Liangcai, Z., Lina, C., Yan, Z., Liangde, X., Yukui, S., Qian, W., et al. (2008). “A SNP and KEGG based approach to mine risk pathways associated with bipolar disorder,” in Fourth International Conference on Natural Computation, 2008. ICNC'08 (Jinan), 34–38.
Liu, D. J., and Leal, S. M. (2010). A novel adaptive method for the analysis of next-generation sequencing data to detect complex trait associations with rare variants due to gene main effects and interactions. PLoS Genet. 6:e1001156. doi: 10.1371/journal.pgen.1001156
Ng, P. C., and Henikoff, S. (2003). SIFT: predicting amino acid changes that affect protein function. Nucleic Acids Res. 31, 3812–3814. doi: 10.1093/nar/gkg509
Ng, S.-K., Zhang, Z., Tan, S.-H., and Lin, K. (2003). InterDom: a database of putative interacting protein domains for validating predicted protein interactions and complexes. Nucleic Acids Res. 31, 251–254. doi: 10.1093/nar/gkg079
Page, L., Brin, S., Motwani, R., and Winograd, T. (1999). The PageRank Citation Ranking: Bringing Order to the Web, Technical Report, Stanford InfoLab, Stanford University, Stanford, CA.
Papadopoulos, J. S., and Agarwala, R. (2007). COBALT: constraint-based alignment tool for multiple protein sequences. Bioinformatics 23, 1073–1079. doi: 10.1093/bioinformatics/btm076
Perez-Iratxeta, C., Bork, P., and Andrade, M. A. (2002). Association of genes to genetically inherited diseases using data mining. Nat. Genet. 31, 316–319. doi: 10.1038/ng895
Raghavachari, B., Tasneem, A., Przytycka, T. M., and Jothi, R. (2008). DOMINE: a database of protein domain interactions. Nucleic Acids Res. 36, D656–D661. doi: 10.1093/nar/gkm761
Ramensky, V., Bork, P., and Sunyaev, S. (2002). Human non-synonymous SNPs: server and survey. Nucleic Acids Res. 30, 3894–3900. doi: 10.1093/nar/gkf493
Risch, N., and Merikangas, K. (1996). The future of genetic studies of complex human diseases. Science 273, 1516–1517. doi: 10.1126/science.273.5281.1516
Roberts, J. M., Taylor, R. N., Musci, T. J., Rodgers, G. M., Hubel, C. A., and McLaughlin, M. K. (1989). Preeclampsia: an endothelial cell disorder. Am. J. Obstet. Gynecol. 161, 1200–1204. doi: 10.1016/0002-9378(89)90665-0
Rui, J., and Jiaxin, W. (2011). “Integrating sequence conservation features and a domain-domain interaction network to detect disease-associated nsSNPs,” in Proceedings of the 2011 IEEE International Conference on in Bioinformatics and Biomedicine Workshops (BIBMW) (Atlanta, GA), 262–267.
Safavian, S. R., and Landgrebe, D. (1991). A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 21, 660–674. doi: 10.1109/21.97458
Schrodi, S. J., Mukherjee, S., Shan, Y., Tromp, G., Sninsky, J. J., Callear, A. P., et al. (2014). Genetic-based prediction of disease traits: prediction is very difficult, especially about the future. Front. Genet. 5:162. doi: 10.3389/fgene.2014.00162
Suravajhala, P., and Sundararajan, V. S. (2012). A classification scoring schema to validate protein interactors. Bioinformation 8:34. doi: 10.6026/97320630008034
Tranchevent, L.-C., Capdevila, F. B., Nitsch, D., De Moor, B., De Causmaecker, P., and Moreau, Y. (2010). A guide to web tools to prioritize candidate genes. Brief. Bioinform. 12, 22–32. doi: 10.1093/bib/bbq007
Vapnik, V. (1991). “Principles of risk minimization for learning theory,” in Advances in Neural Information Processing Systems 4, NIPS Conference (Denver, CO), 831–838.
Wang, S., Hauskrecht, M., and Visweswaran, S. (2009). “Gene prioritization using a probabilistic knowledge model,” in 2009 IEEE International Conference on in Bioinformatics and Biomedicine Workshops (BIBMW) (Washington, DC), 272–278.
Wu, J., Yang, S., and Jiang, R. (2014). Inferring non-synonymous single-nucleotide polymorphisms-disease associations via integration of multiple similarity networks. Systems Biol. IET 8, 33–40. doi: 10.1049/iet-syb.2013.0033
Xie, B., Agam, G., Sulakhe, D., Maltsev, N., Chitturi, B., and Gilliam, T. C. (2012). “Prediction of candidate genes for neuropsychiatric disorders using feature-based enrichment,” in Proceedings of the ACM Conference on Bioinformatics, Computational Biology and Biomedicine (Orlando, FL: ACM).
Xu, J., and Li, Y. (2006). Discovering disease-genes by topological features in human protein–protein interaction network. Bioinformatics 22, 2800–2805. doi: 10.1093/bioinformatics/btl467
Yang, H., King, I., and Lyu, M. R. (2007). “Diffusionrank: a possible penicillin for web spamming,” in Proceedings of the 30th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (Amsterdam: ACM), 431–438.
Keywords: inherited diseases, data mining, machine learning, single nucleotide polymorphism, protein-protein interaction
Citation: Iddamalgoda L, Das PS, Aponso A, Sundararajan VS, Suravajhala P and Valadi JK (2016) Data Mining and Pattern Recognition Models for Identifying Inherited Diseases: Challenges and Implications. Front. Genet. 7:136. doi: 10.3389/fgene.2016.00136
Received: 08 March 2016; Accepted: 15 July 2016;
Published: 10 August 2016.
Edited by:
Lisa J. Martin, Cincinnati Children's Hospital Medical Center, USAReviewed by:
Kenneth M. Weiss, Pennsylvania State University, USAJing Dong, National Institutes of Health, USA
Copyright © 2016 Iddamalgoda, Das, Aponso, Sundararajan, Suravajhala and Valadi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Prashanth Suravajhala, cHJhc2hAYmlvY2x1ZXMub3Jn
Jayaraman K. Valadi, dmFsYWRpQGdtYWlsLmNvbQ==
 Lahiru Iddamalgoda
Lahiru Iddamalgoda Partha S. Das
Partha S. Das Achala Aponso1
Achala Aponso1 Vijayaraghava S. Sundararajan
Vijayaraghava S. Sundararajan Prashanth Suravajhala
Prashanth Suravajhala Jayaraman K. Valadi
Jayaraman K. Valadi