- 1Plant Pathology and Plant-Microbe Biology Section, School of Integrative Plant Science, Cornell University, Geneva, NY, USA
- 2Plant Breeding and Genetics Section, School of Integrative Plant Science, Cornell University, Ithaca, NY, USA
Defining the contributions of dispersal, reproductive mode, and mating system to the population structure of a pathogenic organism is essential to estimating its evolutionary potential. After introduction of the devastating plant pathogen, Phytophthora capsici, into a grower’s field, a lack of aerial spore dispersal restricts migration. Once established, coexistence of both mating types results in formation of overwintering recombinant oospores, engendering persistent pathogen populations. To mimic these conditions, in 2008, we inoculated a field with two P. capsici isolates of opposite mating type. We analyzed pathogenic isolates collected in 2009–2013 from this experimental population, using genome-wide single-nucleotide polymorphism markers. By tracking heterozygosity across years, we show that the population underwent a generational shift; transitioning from exclusively F1 in 2009–2010, to multi-generational in 2011, and ultimately all inbred in 2012–2013. Survival of F1 oospores, characterized by heterozygosity excess, coupled with a low rate of selfing, delayed declines in heterozygosity due to inbreeding and attainment of equilibrium genotypic frequencies. Large allele and haplotype frequency changes in specific genomic regions accompanied the generational shift, representing putative signatures of selection. Finally, we identified an approximately 1.6 Mb region associated with mating type determination, constituting the first detailed genomic analysis of a mating type region (MTR) in Phytophthora. Segregation patterns in the MTR exhibited tropes of sex-linkage, where maintenance of allele frequency differences between isolates of opposite mating type was associated with elevated heterozygosity despite inbreeding. Characterizing the trajectory of this experimental system provides key insights into the processes driving persistent, sexual pathogen populations.
Introduction
Phytophthora capsici is the filamentous, soil-borne oomycete plant pathogen responsible for Phytophthora blight, a disease inflicting significant annual crops losses worldwide (Erwin and Ribeiro, 1996; Hausbeck and Lamour, 2004; Granke et al., 2012; Lamour et al., 2012). Success of P. capsici is facilitated by its widespread ability to overcome fungicides (Lamour and Hausbeck, 2000), dearth of resistant cultivars (Granke et al., 2012), and large, diverse host range (comprising >15 plant families), including widely grown, economically important vegetable crops in the Cucurbitaceae, Solanaceae, and Fabaceae plant families (Satour and Butler, 1967; Hausbeck and Lamour, 2004; Tian and Babadoost, 2004). Extreme weather events often initiate new infestations by introducing inoculum into agricultural fields via flood waters (Dunn et al., 2010). Contaminated soil and infected plant material are commonly implicated in pathogen spread (Granke et al., 2012), however, P. capsici is not aerially dispersed (Granke et al., 2009).
Once introduced into a field, the explosive asexual cycle of P. capsici catalyzes the rapid escalation of disease within a growing season. When exposed to water saturated conditions, a single sporangium can release 20–40 zoospores, each capable of inciting root, crown, or fruit rot, the characteristic symptoms of Phytophthora blight (Hausbeck and Lamour, 2004). For sexual reproduction, the heterothallic P. capsici requires two mating types, classically referred to as A1 and A2 (Erwin and Ribeiro, 1996). Exposure to mating type specific hormones (α1 and α2) stimulates production of the gametangia, subsequent outcrossing, and formation of recombinant oospores (Ko, 1988). However, both mating types produce both male and female gametangia, and thus are capable of self-fertilization (Shattock, 1986; Ko, 1988), which is thought to occur at a lower rate relative to outcrossing in P. capsici (Uchida and Aragaki, 1980; Dunn et al., 2014).
While the asexual reproductive cycle directly inflicts crop damage, sexual reproduction confers several epidemiological advantages. First, unlike asexual propagules, oospores survive exposure to cold temperatures (Hausbeck and Lamour, 2004; Babadoost and Pavon, 2013). Thus, in regions with cold winter conditions, oospores are the primary source of overwintering inoculum (Bowers, 1990; Lamour and Hausbeck, 2003; Granke et al., 2012). Second, oospores remain in the soil for years regardless of host availability, enabling the persistence of the pathogen between growing seasons and rendering eradication unfeasible. In the spring, in the presence of susceptible hosts, germinating oospores, potentially formed in distinct years, initiate the repeating, asexual reproductive cycle (Hausbeck and Lamour, 2004; Granke et al., 2012).
Where both mating types coexist, sexual reproduction is associated with persistent pathogen populations, genetic diversity, and an approximate 1:1 ratio of A1:A2 mating types (Lamour and Hausbeck, 2001; Dunn et al., 2010). While asexual reproduction can increase the prevalence of a specific genotype within a sexually reproducing population, the inability of asexual propagules to survive cold winters (Hausbeck and Lamour, 2004; Babadoost and Pavon, 2013) implies that each year meiosis disrupts linkage between the particular combination of alleles observed within a clone (Kondrashov, 1988). As a consequence, sexual reproduction mediates the effects of clonal propagation on P. capsici population structure (Lamour and Hausbeck, 2001). Furthermore, in geographic regions where sexual reproduction occurs, genetic differentiation between field populations, even within close proximity, suggests that after an initial introduction limited gene flow occurs between fields (Lamour and Hausbeck, 2001; Dunn et al., 2010), consistent with a lack of aerial dispersal (Granke et al., 2009). Rapid asexual proliferation upon colonization, in addition to formation of long-lived resting spores, likely contribute to population subdivision, consistent with the monopolization hypothesis (De Meester et al., 2002). In this framework, local adaptation by colonizing genotypes would further engender geographic patterns of differentiation (De Meester et al., 2002).
Given this infection scenario, i.e., an initial inoculation but no subsequent introductions, we would expect P. capsici populations to exhibit signatures of a bottleneck event: reductions in genetic diversity and an increase in inbreeding over time, proportional to the number of founding isolates (Kirkpatrick and Jarne, 2000). (We define inbreeding strictly as inter-mating between related isolates, and reserve selfing to refer to self-fertilization events.) In populations which undergo a so-called founder effect, inbreeding is expected to decrease mean population fitness over time due to the expression of recessive deleterious alleles, i.e., the genetic load, in the homozygous state (Charlesworth and Charlesworth, 1987; Hartl and Clark, 2007). A related phenomenon, inbreeding depression, i.e., the difference in fitness between selfed and outcrossed progeny in a population (Kirkpatrick and Jarne, 2000), is considered a major driver of obligate outcrossing, and may contribute to maintenance of self-incompatibility in hermaphroditic plant species (Charlesworth and Charlesworth, 1987). Charting the genetic trajectory of isolated populations of P. capsici in the context of these processes, is essential to understanding pathogen evolution in an agriculturally relevant scenario.
Thus, in 2008, to investigate the response of P. capsici to a severe bottleneck, we established a closed, biparental field population, by inoculating a research field once with two heterozygous strains of opposite mating types. In a preliminary study, we tracked the allele and genotypic frequencies of five microsatellite markers in the field population from 2009–2012 (Dunn et al., 2014). We demonstrated that sexual reproduction resulted in high genotypic diversity, a function of the proportion of unique isolates (Grünwald et al., 2003), in 2009–2011, with a reduction in genotypic diversity in 2012. However, five markers afforded limited statistical power to characterize population and individual level phenomena. While we observed an increase in the inbreeding coefficient (FIS) in 2012 relative to prior years, pairwise FST values comparing isolates from 2009 through 2012 were not significantly different from zero. Thus, our initial study found minimal evidence for changes in allele frequency due to drift and/or selection.
Therefore, in the present study, we analyzed isolates collected in 2009–2013 from the P. capsici field population with genotyping-by-sequencing (GBS), a multiplexed reduced-representation sequencing technique, which simultaneously identifies and scores single nucleotide polymorphism (SNP) markers distributed throughout the genome (Elshire et al., 2011). The closed experimental field design excluded introduction of new alleles via migration, providing a unique opportunity to address the influence of inbreeding on population genetic phenomena in P. capsici. In high-density SNP genotyping isolates from the biparental field population, our goal was threefold: (1) Evaluate the effects of oospore survival on population structure; (2) Quantify the genome-wide incidence of inbreeding with respect to mating type; and (3) Identify whether specific regions deviate from the rest of the genome in terms of changes in allele frequency.
Results
GBS of the Experimental Biparental Isolates
We genotyped a total of 232 isolates collected from a closed, biparental field population of P. capsici from 2009–2013, with 35–55 isolates from each year (Supplementary Table S1). Each single-zoospore field isolate was collected from a plant which exhibited symptoms of Phytophthora blight, therefore we inherently selected for pathogenic isolates. Additionally, we genotyped 46 single-oospore progeny from an in vitro cross performed in the laboratory between the same founding parents. These in vitro isolates served as a reference for the field isolates, for which generation was a priori unknown. Three of the in vitro progeny were identified as putative selfs by Dunn et al. (2014), which was confirmed by our analysis (see ‘Selfing in the lab and field’), and are hereafter referred to as in vitro selfs to distinguish them from the in vitro F1 progeny. The A1 (isolate: 0664-1) and A2 (isolate: 06180-4) founding parents were genotyped 14 and 11 times, respectively, to estimate laboratory and genotyping errors (Supplementary Table S2).
Out of the 401,035 unfiltered variant calls, initial site filters reduced the data set to 23,485 high-quality SNPs (Supplementary Figure S1), with an average SNP call rate (i.e., the percentage of individuals successfully genotyped at each SNP) of 95.93% (median of 97.64%). The 23,485 SNPs were equally distributed among 307 scaffolds (scaffold size and number of SNPs were highly correlated (r2 = 0.95)), with an average SNP density of approximately 1 SNP every 2.5 kb. There was essentially no correlation between mean individual read depth and heterozygosity per SNP among all isolates (r2 = 0.009, P-value = 0.10), indicating that heterozygous calling post-filtering was robust to differences in mean individual sequencing coverage (Supplementary Figure S2). Genotype files are available in VCF format (Supplementary Files S1, S2).
To assess SNP genotyping accuracy, we compared biological and technical replicates of the parental isolates. Replicates of the A1 parent (n = 14) and A2 parent (n = 11), representing 4–5 distinct serial cultures, shared on average 98.30% (s = 0.45%) and 98.17% (s = 0.51%) alleles identity-by-state (IBS), respectively (Supplementary Table S2). This corresponded to 3.60% (s = 0.86%) discordant sites on average among non-missing genotypes between replicates. Lower average discordance (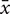 = 2.86%, s = 0.33%) between only replicates of the same parental culture (n = 54 pairwise comparisons) suggested variation associated with distinct culture time points. Therefore, our overall genotyping error rate, inclusive of variation in mycelial and DNA extractions, but not different culture time points, was approximately 3%. Among technical replicates [same DNA sample (n = 4) sequenced 3–4 times] the error rate was on average 2.95%, indicating that most of the genotype discrepancies were attributed to sequencing and genotyping errors rather than distinct mycelial harvests. When we excluded heterozygous calls in each pairwise comparison (n = 21) of the technical replicates, less than 0.0001% sites were discordant, indicating that heterozygote genotype discrepancies drove genotyping errors. As in the total data set, the association between individual sequencing coverage and heterozygosity was negligible in both sets of parental replicates (Supplementary Figure S2).
= 2.86%, s = 0.33%) between only replicates of the same parental culture (n = 54 pairwise comparisons) suggested variation associated with distinct culture time points. Therefore, our overall genotyping error rate, inclusive of variation in mycelial and DNA extractions, but not different culture time points, was approximately 3%. Among technical replicates [same DNA sample (n = 4) sequenced 3–4 times] the error rate was on average 2.95%, indicating that most of the genotype discrepancies were attributed to sequencing and genotyping errors rather than distinct mycelial harvests. When we excluded heterozygous calls in each pairwise comparison (n = 21) of the technical replicates, less than 0.0001% sites were discordant, indicating that heterozygote genotype discrepancies drove genotyping errors. As in the total data set, the association between individual sequencing coverage and heterozygosity was negligible in both sets of parental replicates (Supplementary Figure S2).
Phytophthora capsici reproduces asexually, therefore, it was theoretically possible to sample the same genotype from the field multiple times within a year. To remove the bias imparted on population genetic analyses by including clones, we retained only one isolate for each identified unique genotype (Milgroom, 1996). Pairwise identity-by-state (IBS) between replicates of the A1 and A2 parental isolates were compared to establish a maximum genetic similarity threshold to define clones (see Materials and Methods), akin to (Rogstad et al., 2002; Meirmans and van Tienderen, 2004). Applying this threshold, we identified 160 unique field isolates out of the initial 232 field isolates (Supplementary Table S1). Two in vitro isolates and one field isolate were identified as outliers with respect to deviation from the expected 1:1 ratio of allele depths at heterozygous sites (n = 2) or heterozygosity (n = 1), and subsequently removed (Supplementary Figure S3). Previous studies have shown that deviation from a 1:1 ratio of allele depths at heterozygous sites, the expectation for diploid individuals, is correlated with ploidy variation (Rosenblum et al., 2013; Yoshida et al., 2013; Li et al., 2015), therefore the two allele depth ratio outliers provide preliminary evidence for ploidy variation in P. capsici. After outlier removal, the final data set consisted of 159 field isolates, 41 in vitro F1, and three in vitro selfs.
Clones did not appear in multiple years, consistent with the inability of asexual propagules to survive the winter (Hausbeck and Lamour, 2004; Babadoost and Pavon, 2013). After clone-correction, the A2 mating type was more represented in the field (A1:A2 = 65:94; χ2 test, P-value = 0.02), a phenomenon also observed in the in vitro F1 (A1:A2 = 16:25; χ2 test, P-value = 0.16; Figure 1). The only exception was 2012, which may be explained by a smaller sample size in this year, artificially compounded by loss of several unique isolates (based on microsatellite profiles (Dunn et al., 2014) in culture prior to this study). We observed lower genotypic diversity in 2012–2013 (Supplementary Table S1), consistent with Dunn et al. (2014).
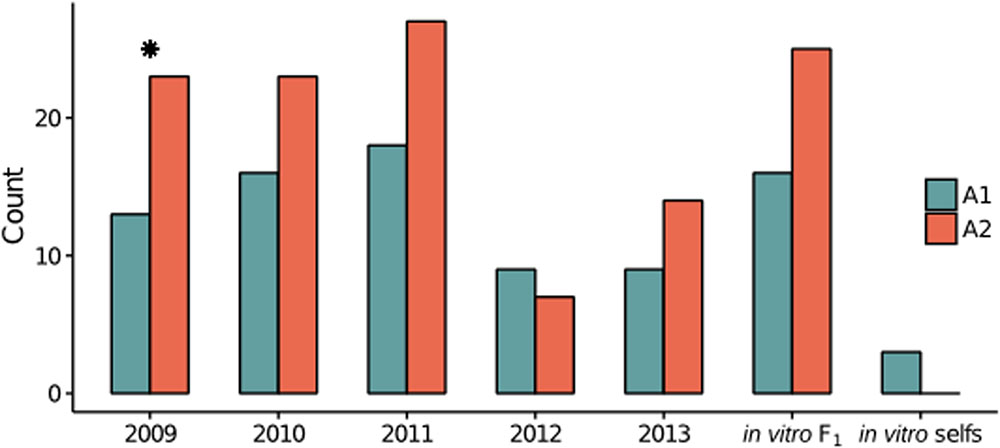
FIGURE 1. Distribution of the mating type of each isolate by year in the final, clone-corrected data set. Counts of the mating type of each isolate, A1 (teal) and A2 (reddish brown), in the in vitro F1, in vitro selfs, and clone-corrected field isolates, separated by year. The star indicates a significant difference (χ2 test; P-value < 0.1) between A1 and A2 counts.
To reduce oversampling of specific genomic regions, which can disproportionately influence population genetic inference (Price et al., 2006; Abdellaoui et al., 2013), without making assumptions about linkage disequilibrium (LD), we randomly selected one SNP within a given, non-overlapping 1 kb window. Final quality filters and including only SNPs in scaffolds containing at least 300 kb (n = 63) resulted in a data set of 6,916 SNPs (Supplementary Figure S1). Bimodal heterozygosity and minor allele frequency (MAF) distributions in this reduced SNP set were consistent with distributions in the unpruned data set (Supplementary Figure S4). The pruned data set had a median SNP call rate of 98.01% and median site depth of 18.61 (i.e., average number of reads per individual per SNP). The median sample call rate (i.e., percentage of SNPs genotyped in each sample) was 97.77%, and the median sample depth (i.e., average number of reads per SNP per individual) was 20.36. Among technical replicates (n = 4) the error rate was on average 1.52%. We utilized the pruned data set for all subsequent analyses.
Population Differentiation Increases With Year
To broadly define genetic relationships between the in vitro and field isolates relative to the founding parents, we analyzed the field, in vitro and parents (represented by consensus parental genotypes, see Materials and Methods) jointly, with principal component analysis (PCA). The PCA exhibited the expected biparental population structure, in that the majority of isolates clustered in between the parental isolates along the major axis of variation, principal component (PC) 1 (Figure 2A). Most 2009–2011 isolates clustered with the in vitro F1, whereas, many 2012–2013 isolates were dispersed along both axes, suggesting differentiation associated with year.
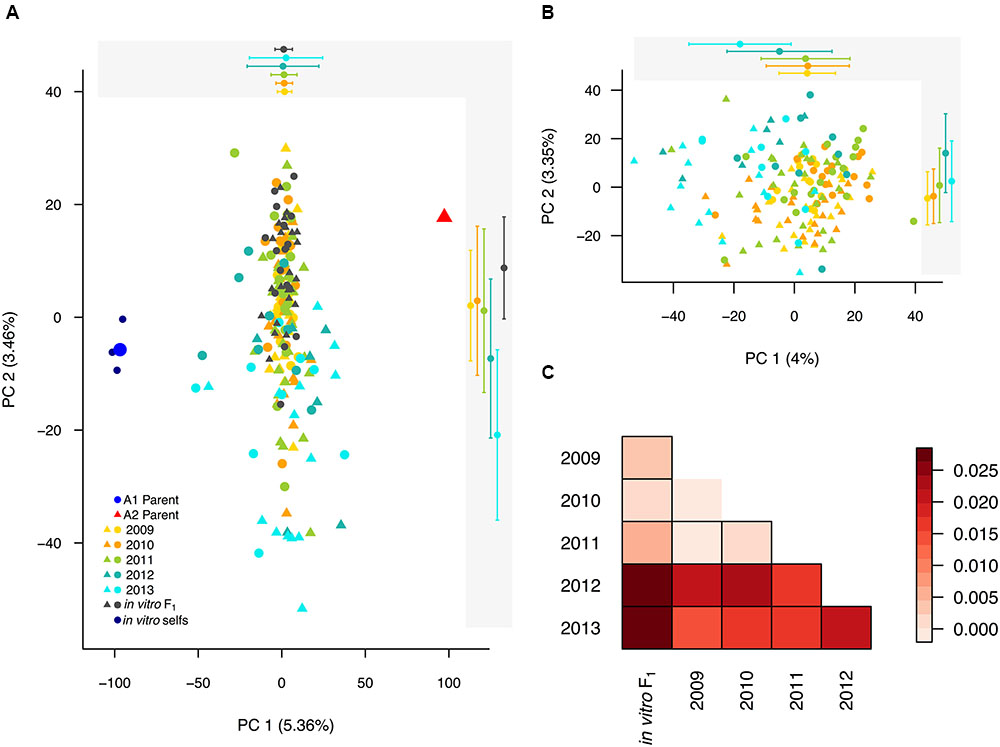
FIGURE 2. Population structure in the biparental field population relative to the in vitro F1 and founding parents. (A) Field isolates, in vitro F1, in vitro selfs, and consensus parental genotypes plotted along the first two principal components (PCs). Each year is represented by a different color, with the A1 and A2 parental isolates indicated by blue and red, respectively. Shapes indicate the mating type of each isolate, with circles (A1) and triangles (A2). For each year (2009–2013) and the in vitro F1 the means (± one standard deviation) for the first (top) and second (right) PCs are plotted in the shaded gray boxes. (B) A PCA of only the field isolates, with color and symbol scheme consistent with (A). As in (A), the means (± one standard deviation) for the first two PCs are plotted for each year. (C) Pairwise FST for comparisons between sample years and the in vitro F1 represented by a heat map, with more positive FST values increasingly red. A border indicates that the pairwise FST value was significantly different from 0, as tested by 1000 random SNP permutations.
To explore structure exclusively within the field population, we performed PCA on only the field isolates. Along PC1, isolates from 2012 to 2013 were differentiated from prior year isolates (Figure 2B). Whereas, PC2 described differentiation within and between years.
To assess the variance in allele frequencies between years, we estimated pairwise FST (Weir and Cockerham, 1984) between years, where each year was defined as a distinct population. All pairwise comparisons were significantly greater than zero, excluding pairwise FST between 2009 and 2010. Small FST estimates for comparisons between 2009, 2010, 2011 and the in vitro F1 indicated minimal variation in allele frequencies between these years. The greatest differences were observed between years 2012 and 2013 compared to 2009, 2010 and the in vitro F1 populations (Figure 2C), consistent with the PCA results. In addition, years 2012 and 2013 were also significantly differentiated from each other (FST = 0.027).
Inbreeding in the Field Population
To quantify changes in inbreeding in the closed, field population, we estimated the individual inbreeding coefficient (F) for each isolate, where F was defined as the proportion of heterozygous sites relative to expected heterozygosity in the population assuming random mating. While F does not directly measure identity-by-descent (IBD), it is highly correlated with IBD estimates in empirical and simulated data sets with relatively large numbers of markers (Kardos et al., 2015), particularly in highly subdivided, small populations (Balloux et al., 2004), such as the population under study. And, in a closed, biparental population, heterozygosity is proportional to the number of generations (Wright, 1921; Nei et al., 1975). Negative F estimates correspond to heterozygote excess relative to Hardy–Weinberg expectations for a reference population, defined here as the in vitro F1. Positive F-values indicate heterozygote deficiency.
First, to establish expectations for a known F1 population, we assessed the F distribution in the in vitro F1, after removing the three self-fertilized isolates and two additional outliers, as described above. Importantly, because allele frequencies were estimated from the population under study, F is meaningful as a relative measure in the context of this system (Wang, 2014). The in vitro F1, with a mean F of -0.366, was more heterozygous than the founding parents [average F across replicates = -0.007 (A1) and -0.183 (A2); Figure 3A]. In contrast to the unimodal in vitro F1, the field population had a bimodal F distribution, with one peak approximately centered at the in vitro F1 mean, and a second peak centered at a less negative F-value. This second peak, representing a decline in heterozygosity relative to the in vitro F1, indicated that inbreeding was occurring in the field population.
FIGURE 3. Generational shift in the field population. (A) Superimposed histograms of the individual inbreeding coefficient (F), estimated from 6,916 SNPs, in the in vitro F1 (gray) and field population (black). The in vitro F1 were more heterozygous than the founding parental isolates, corresponding to more negative F-values, indicated by a blue circle (A1 parent) and red triangle (A2 parent). In contrast, the field population exhibited a bimodal F distribution. (B) Distributions of F by year represented by violin plots, with each year shown in a distinct color and individual data points overlaid. The long upper tail of the 2011 distribution is driven by two field selfs.
To dissect the bimodal shape of the field distribution, we analyzed F for each year separately. Both for 2009 and 2010, the distributions were unimodal with F means not significantly different from the in vitro F1 mean (pairwise t-test; P-values = 1.0; Figure 3B). For years 2012 and 2013, distributions were also unimodal, but had F means significantly less negative than the in vitro F1 (P-values < 0.0001). Year 2011 had a bimodal F distribution.
To interpret the effect of changes in inbreeding on genotypic and allele frequencies with time, we analyzed both SNP heterozygosity and MAF distributions for each year. In a biparental cross, clear expectations for these quantities in the F1 generation makes them informative in distinguishing F1 from inbred generations. Specifically, in the F1 generation, sites should segregate with a MAF of either 0.25 (for a cross of Aa × AA) or 0.5 (for Aa × Aa and AA × aa), and population heterozygosity should be 50 or 100% at each SNP. In the F2 generation, i.e., a population derived from a single generation of inbreeding, MAF should remain constant, whereas heterozygosity should decline. Our results showed that the in vitro F1, 2009, and 2010 behaved in accordance with expectations for a predicted F1; the heterozygosity distributions had peaks centered at approximately 50 and 100% (Figure 4A), and the MAF distributions had peaks at 0.25 and 0.5 (Figure 4B). In contrast, MAF and heterozygosity distributions in 2012 and 2013 were not consistent with F1 expectations, in that we no longer observed obvious peaks (Figure 4). While genotypic frequency shifts in 2012 and 2013 indicated presence of inbreeding and deviation from F1 expectations, changes in the MAF distribution also denoted that these were likely not canonical F2 populations. Discrete generations are implicit in a F2, therefore deviation from F2 expectations may be attributed to violation of this assumption.
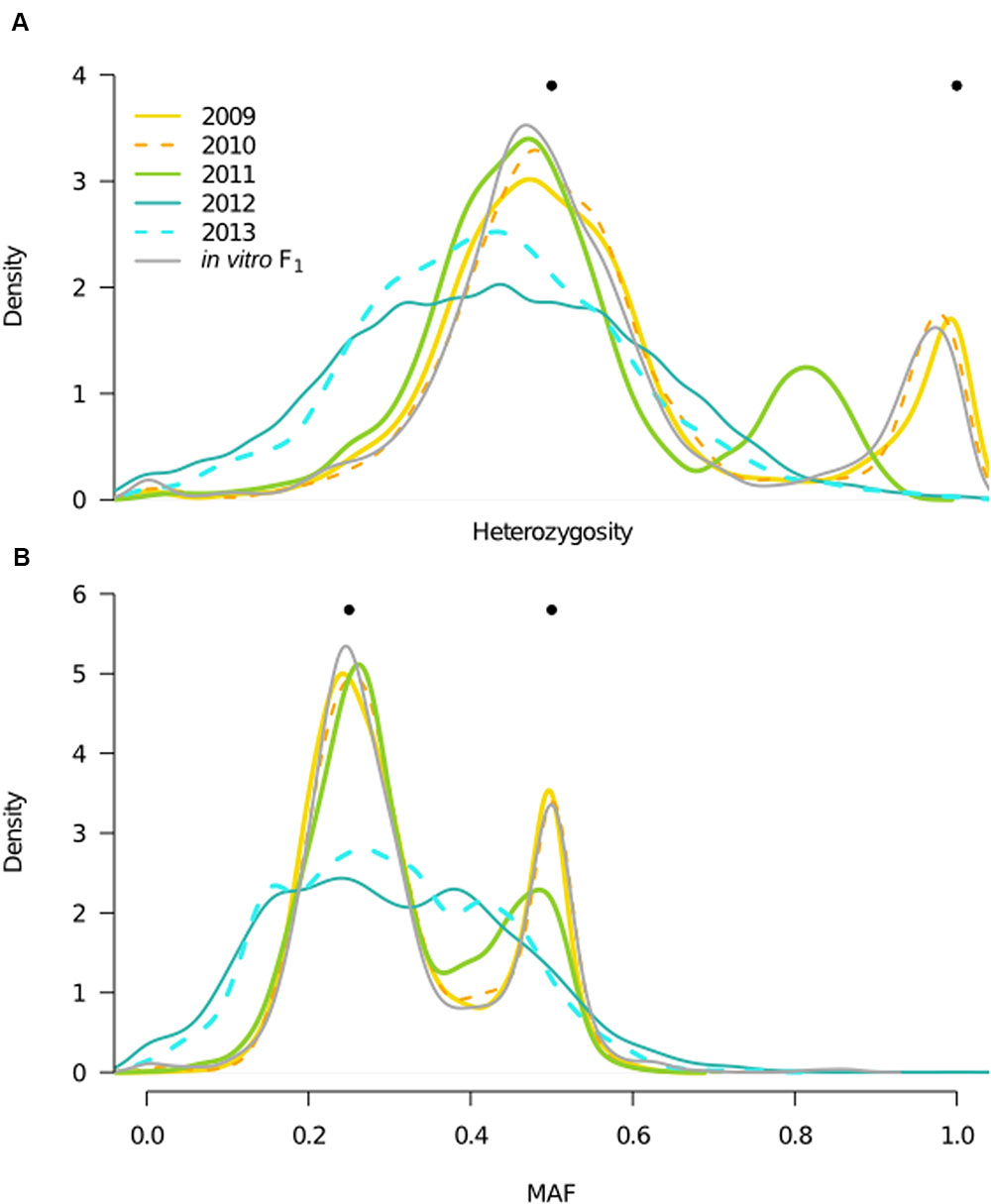
FIGURE 4. Year heterozygosity and allele frequency (MAF) distributions. Filled, black circles indicate expectations for population heterozygosity and MAF in a theoretical F1 population. (A) Distributions of the proportion of heterozygous individuals per SNP (n = 6,916) for each year and the in vitro F1, represented by kernel density estimates, with color corresponding to year, and x-axis consistent with (B). Bimodal distributions in the in vitro F1 and years 2009–2010 are consistent with expectations for the F1 generation, whereas unimodal distributions in 2012–2013 indicate presence of inbreeding. A shift in the bimodal distribution of 2011, indicates the mixed outbred and inbred composition of this year. (B) MAF distributions, where the minor allele is defined based on the frequency in the total field population, for each year and the in vitro F1, with color designations the same as in (A).
Finally, in 2011, both heterozygosity and MAF distributions were bimodal, as in an F1, but with reduced heterozygosity and deviation in allele frequencies relative to the in vitro F1 and prior years (Figure 4). These shifts in 2011 suggested coexistence of both F1 and inbred isolates (i.e., non-F1 isolates) in this year, consistent with the bimodal 2011 F distribution (Figure 3B).
Selfing in the Laboratory and Field
In addition to quantifying inbreeding (defined as inter-mating between related isolates), we also estimated the incidence of self-fertilization in the biparental, field population. The frequency at which P. capsici reproduces through self-fertilization in either field or lab conditions is unknown (Dunn et al., 2014). Given the limited prior evidence of selfing in P. capsici, we first confirmed that the three putative in vitro selfs were indeed the product of self-fertilization by the A1 parent, as hypothesized by Dunn et al. (2014). To this end, we distinguished the in vitro selfs from the in vitro F1 by four features: (1) Clustered with the A1 parent in PCA (dark blue circles in Figure 2A); (2) Alleles shared IBS disproportionately with the A1 versus A2 parent; (3) Heterozygosity approximately 50% of the A1 parent; and (4) Significantly higher inbreeding coefficients relative to the F1 [>3 standard deviations (SD) from the mean; Table 1].

TABLE 1. Selfed isolates in the in vitro and biparental field populations in terms of heterozygosity, Mendelian errors (MEs), and alleles shared identity-by-state (IBS) with either founding parent.
Having shown that generalized expectations for selfing applied to P. capsici, we utilized extreme heterozygote deficiency as an indicator of selfing in the field. As, in the field context, the first three aforementioned selfing features were inapplicable because the progenitor of a selfed isolate in the field was not a priori known. We observed that two of the 2011 field isolates were F outliers (>3 SD from the mean) with respect to the inbred field contingent distribution (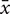 = -0.050, s = 0.12). We classified these two A1 field isolates as field selfs (Table 1). Lack of disproportionate IBS of the field selfs with either founding parent denoted that these isolates were not the product of self-fertilization by either founding parent. Therefore, we observed selfing in the in vitro and field populations at frequencies of 3/46 (6.5%) and 2/159 (1.26%), respectively, denoting minimal incidence of selfing in both lab and field scenarios.
= -0.050, s = 0.12). We classified these two A1 field isolates as field selfs (Table 1). Lack of disproportionate IBS of the field selfs with either founding parent denoted that these isolates were not the product of self-fertilization by either founding parent. Therefore, we observed selfing in the in vitro and field populations at frequencies of 3/46 (6.5%) and 2/159 (1.26%), respectively, denoting minimal incidence of selfing in both lab and field scenarios.
Classifying F1 versus Inbred Isolates in the Field Using Mendelian Errors (MEs)
Based on the above results, we hypothesized that 2009–2010 were comprised of mainly F1, 2012–2013 inbred, and 2011 a mixture of both F1 and inbred isolates. However, we had heretofore not verified that each year was homogeneous with respect to F1 and inbred composition. To quantify the number of F1 isolates, we used the fact that the genotypes of the founding parents were known to calculate an additional individual summary statistic, the proportion of Mendelian errors (MEs). A ME is defined as a genotype inconsistent with the individual being an F1 derived from specific parents (Purcell et al., 2007), here, the A1 and A2 founders. Commonly, MEs have been used to detect genotyping and experimental errors in SNP data sets where pedigree information is known (Purcell et al., 2007). The expectation is that a true F1 individual should have very few MEs, a postulate we applied to assess whether each field isolate belonged to the F1 generation.
Initial ME estimates revealed both randomly distributed and clustered ME-enriched SNPs (Supplementary Figure S6). In the Supplementary Text, we show that clustered ME-enriched SNPs corresponded to inferred mitotic loss of heterozygosity (LOH) events in the parental isolates in culture (see Supplementary Figures S6–S13 and Tables S3, S4). After removing all ME-enriched SNPs (n = 848), mean MEs per isolate for the in vitro F1 and field F1 subpopulations were 1.38 and 0.98%, below our estimated genotyping error rate of approximately 1.5%.
Akin to F, the proportion MEs per individual is a function of genotypic frequencies. Therefore, it was not surprising that year distributions of the ME statistic were consistent with F, with increased MEs in years 2012–2013 (Figure 5A). Because asexual propagules do not survive the winter (Hausbeck and Lamour, 2004; Babadoost and Pavon, 2013), it can be assumed that all F1 isolates in the field, in any year, were derived from oospores in the year of the initial field inoculation (2008). Applying a threshold of 5.58% MEs (3 SD from the in vitro F1 mean) to characterize F1 versus non-F1, we observed exclusively F1 in 2009-10, a mixture of F1 and inbred isolates in 2011 (ratio of F1 to inbred = 29:16) and all inbred isolates in 2012–2013 (Figure 5B). As such, F1 dominated in 2009–2011, demonstrating that oospores were viable and pathogenic for at least three years.
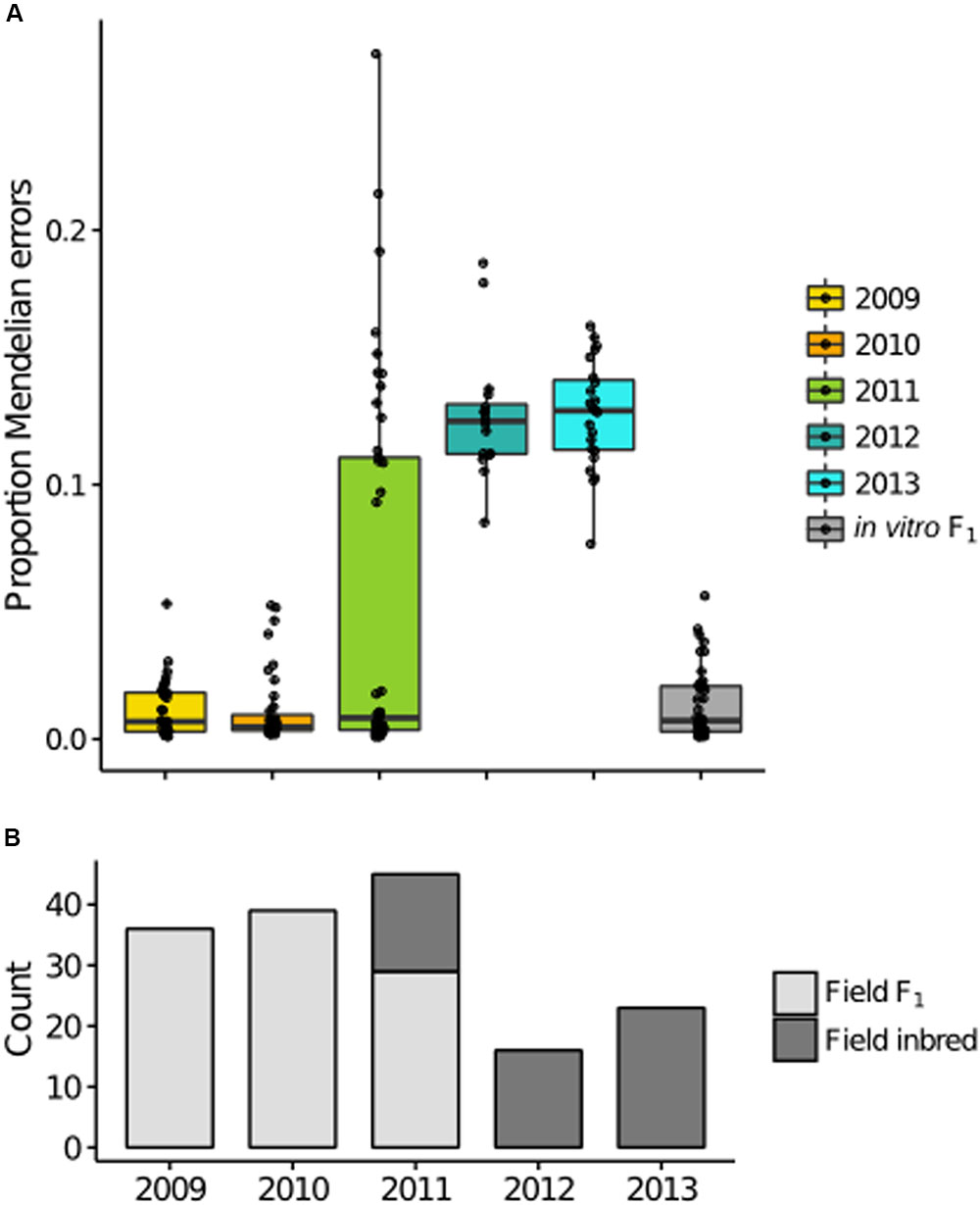
FIGURE 5. Mendelian errors (MEs) distinguish F1 and inbred isolates in the field. (A) Boxplots of the proportion of MEs per individual for each year are consistent with the inbreeding coefficient trend, with a bimodal distribution in 2011, and increased MEs in later years. (B) Classification of each isolate based on the proportion of MEs, with counts of field F1 (light gray) and field inbred (dark gray) for each sample year.
When the inbred isolates were removed from the 2011 data, the MAF distribution for 2011 was consistent with F1 expectations (Supplementary Figure S5). Concurrent observation of both F1 and inbred isolates in a single year (2011) provided direct evidence of overlapping generations in the field population, supporting overlapping generations as contributing to deviation from F2 expectations in the inbred 2012 and 2013 years.
In addition, the ME estimates allowed us to pool isolates from separate years to define subpopulations, the field F1 (n = 104) and the field inbred (n = 53; excluding the field selfs), for subsequent analyses. As in the total field population, A2 isolates were overrepresented in both the field F1 and inbred subpopulations (A1:A2 = 43:61 and 21:32, respectively).
Regions of Differentiation between Generations in the Field Population
The generational transition in the field population from F1 to inbred was accompanied by changes in the MAF distribution (Supplementary Figure S5), implying the biased transmission of alleles to generations beyond the F1. To identify which SNPs drove this allele frequency shift, we performed a genome-wide Fisher’s Exact test of allele frequency differences between the field F1 and field inbred subpopulations. We collectively analyzed these two subpopulations, rather than compare allele frequencies between years, due to the presence of overlapping generations, which complicate interpretation of temporal dynamics (Jorde and Ryman, 1995). From this analysis, we observed several regions of differentiation between these subpopulations (Figure 6; see Supplementary Table S5 for coordinates).
FIGURE 6. Regions of differentiation between the field F1 and inbred subpopulations. (A) Negative log10-transformed, false-discovery rate (FDR) adjusted P-values from the genome-wide test of allele frequency differences between the field F1 and inbred subpopulations, ordered by physical position. The gray dotted lines in (A,B) indicate the significance threshold (α = 0.10). Color alternates by scaffold. The shaded gray boxes indicate the SNPs in scaffolds 21 and 33 corresponding to regions of interest (ROIs) 2 and 1, respectively. (B) Same as (A) except that P-values are shown only for scaffolds 21 and 33. Here, gray boxes denote the sub-region within each scaffold defined as a ROI. Filled, black circles indicate SNPs within each ROI, whereas open, black circles indicate SNPs outside of the ROI. (C) Pie charts represent the haplotype frequencies found in each year [with 2011 separated into F1 and inbred (In) isolates], with the number of sampled chromosomes noted for each year. Blue corresponds to the single A1 founding parental haplotype, shades of red to the two A2 founding haplotypes, and gray to undesignated haplotypes in each ROI (see Materials and Methods).
First, we focused on the region with the most highly differentiated SNP, referred to as region of interest 1 (ROI-1; Figure 6B). Of the 94 SNPs spanned by ROI-1, 44% were among SNPs in the top 2% of loadings for PC1 in the field PCA, showing that this region was correlated with differentiation in the field population. To assess the relationship between allele frequency changes and parental haplotype frequencies, we locally phased all isolates using a deterministic approach (see Materials and Methods). Haplotypes in ROI-1 (H1, H3, and H4) were defined based on the sub-region (251,367–560,094 bp) which contained most of the significantly differentiated SNPs (44 out of 52 SNPs) and formed a LD block (Supplementary Figures S11, S14).
Segregation among the F1 isolates in each year (2009–2011) followed the F1 expectation of a 2:1:1 ratio of H1:H3:H4 haplotypes (χ2 test; P-values = 0.91, 0.99, 0.65, respectively). In contrast, in 2011 (inbred isolates only), 2012, and 2013, we observed lower frequencies of H4 and higher frequencies of H3 relative to the field F1 subpopulation (Figure 6C). The decline in H4 frequency from 22.12% in the field F1 to 4.72% (and corresponding increases in H3 and H1) in the field inbred drove allele frequency changes in ROI-1 (Supplementary Table S6). Because the H4 sequence was most distinct from the other haplotypes, the reduction in H4 frequency, along with inbreeding, resulted in declines in heterozygosity in ROI-1. Consistent reductions in H4 frequency among inbred isolates in 2011–2013 compared to F1 isolates in prior years, provided strong evidence for the influence of selection. However, absence of H4 in year 2012 is very likely an artifact of smaller sample size in this year.
We next focused on a region in scaffold 21, defined as ROI-2, with the highest density of significantly differentiated SNPs (67%; Figure 6B). In ROI-2, as in ROI-1, only three haplotypes segregated in the field population (Supplementary Table S7). While not significant (at α = 0.05), segregation among the F1 isolates in each year (2009–2011) deviated from the F1 expectation of a 2:1:1 ratio of H1:H3:H4 haplotypes (χ2 test; P-values = 0.61, 0.35, and 0.05, respectively), primarily attributed to higher H3 versus H4 haplotype frequency in the field F1 (χ2 test; P-value < 0.01). A decline in frequency of the A2 parent haplotype, H3, by 19.47% and an increase in the A1 parent haplotype, H1, by 19.81% drove allele frequency changes (Figure 6C and Supplementary Table S7). While the frequency of H3 and H4 oscillated among inbred isolates in 2011–2013, the H1 haplotype frequency was consistently higher than in the field F1. In addition, we observed a high frequency of homozygous H1 genotypes (53%), whereas the H3 and H4 haplotypes were not observed in the homozygous state in the field inbred subpopulation, contrary to expectations (Supplementary Table S7).
To posteriorly assess the significance of changes in allele frequency in ROIs 1 and 2, we compared the median FST value for significantly differentiated SNPs in each of these regions to the genome-wide SNP FST distribution, where FST was defined as in Lewontin and Krakauer (1973). Assuming that drift acts equally throughout the genome and constant Ne, extreme deviations in FST provide evidence for selection (Lewontin and Krakauer, 1973). Median observed changes in allele frequency in ROIs 1 and 2 were in the in the 97th and 98th percentiles, respectively, relative to genome-wide FST, showing that allele frequency changes in these regions vastly exceeded the genome-wide average. As violation of these assumptions can lead to false-positive detection of regions under selection (Nei et al., 1975; Bonhomme et al., 2010), we interpret our results cautiously (see Discussion).
Heterozygosity Declines Are Slower in the Mating Type Region
To investigate whether the mating system was a direct driver of differentiation in the field population, we first identified mating type associated SNPs using a Fisher’s exact test of allele frequency differences between isolates of opposite mating types in the field F1 (nA1 = 43 and nA2 = 61; Supplementary Figure S15). Most of the 184 significantly differentiated SNPs were in sub-regions of scaffolds 4 (37%) and 27 (43%), with additional differentiated SNPs in sub-regions of scaffolds 2, 34, and 40 (Figure 7 and Supplementary Table S8). All scaffolds containing significantly associated SNPs were in linkage group 10, consistent with a prior study (Lamour et al., 2012), and supporting presence of a single mating type determining region in P. capsici, as posited for P. infestans and P. parasitica (Fabritius and Judelson, 1997). SNPs in these five sub-regions comprised 20.29% of SNPs with elevated PC loadings (top 2%) in the PCA of only the field isolates, compared to 5.10% genome-wide, denoting that these SNPs were disproportionately correlated with differentiation in the field population.
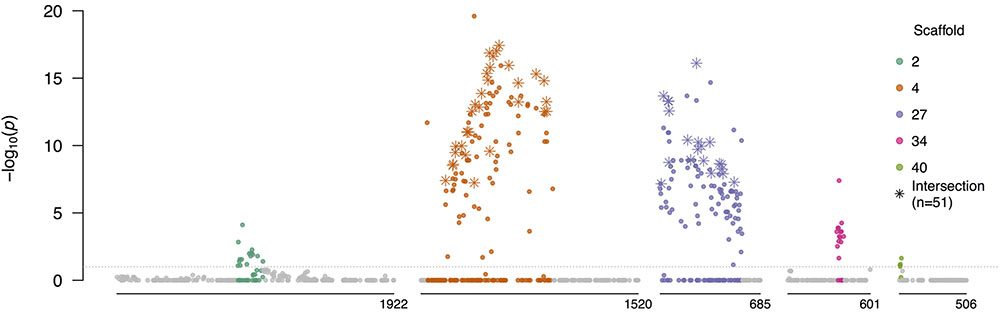
FIGURE 7. Allele frequency differences between isolates of opposite mating types. Negative log10-transformed P-values, adjusted for multiple testing, from the Fisher’s exact test of allele frequency differences between A1 and A2 isolates in the field F1, plotted against physical position, for scaffolds with significantly differentiated regions (see Supplementary Table S8 for coordinates). Colored SNPs were within the bounds of the minimum and maximum significant SNPs in each scaffold containing at least two significantly associated SNPs within 200 kb. Stars indicate the SNPs which were significant in tests of allele frequency differences between mating types in both the field F1 and inbred subpopulations (Supplementary Text). All SNPs above the gray horizontal line were significant after the FDR correction (α = 0.1).
At 98.30% of the AA × Aa SNPs associated with mating type in the field F1, the A2 parent was heterozygous (Aa) and the A1 parent was homozygous (AA). As such, heterozygosity in the field progeny at these SNPs was attributed to inheritance of the minor allele (a), descendent originally from the A2 parent. Therefore, segregation of the A2 but not A1 parental haplotypes was predominantly associated with mating type in the field F1.
We defined the mating type region (MTR) as consisting of genomic tracts encompassed by the minimum and maximum significant SNPs in scaffolds 4 and 27, which comprised 1.42 of the 1.64 Mb spanned by the five sub-regions, and contained 81% of the significantly differentiated SNPs. While we refer to a singular MTR, this was not intended to imply physical linkage between these two scaffolds. Based on the 293 SNPs in the MTR, the PCA of all isolates (in vitro and field; n = 203) showed incomplete differentiation according to mating type (Supplementary Figure S16).
To assess changes in heterozygosity in the MTR, we compared the heterozygosity distributions of the field F1 (nA1 = 43 and nA2 = 61) and inbred (nA1 = 21 and nA2 = 32) isolates in the MTR to the respective genome-wide distributions (see Materials and Methods). Observed heterozygosity in the field F1 in the MTR was not centered at a significantly greater mean than the field F1 genome-wide distribution (one-sided Wilcoxon rank-sum test, all P-values > 0.87; Supplementary Figure S17). In contrast, observed heterozygosity in the field inbreds in the MTR was shifted toward a greater mean relative to the field inbred genome-wide distribution (all P-values < 0.005; Supplementary Figure S17). Therefore, in the field inbred subpopulation, heterozygosity declines were less appreciable in the MTR compared to the rest of the genome. In addition, we found that heterozygosity in the MTR was significantly higher than the rest of the genome for both the A1 and A2 isolates in the field inbred subpopulation (all P-values < 10-4 and 0.003, respectively; Supplementary Figure S17), but not in the field F1 (all P-values > 0.99 and 0.65, respectively; Supplementary Figure S17). Yet, heterozygosity in the MTR did not significantly exceed HWE expectations for A1 inbred isolates, as observed in the A2 inbred isolates, and both mating types in the field F1 (Supplementary Figure S18). These results were replicated when the A2 inbred isolates were down-sampled to the A1 inbred sample size (data not shown).
To further dissect the genetic dynamics of mating type in the field population, we tracked the allele frequencies of markers that were heterozygous in one parent and homozygous in the other parent (AA × Aa). These markers are particularly informative because the origin of the a allele can be unambiguously assigned to the heterozygous parent. Specifically, we calculated the frequency of the parental tagging allele (pa) in the parents, the field F1, and the field inbreds at each of the AA × Aa SNPs in the MTR (nAA×Aa = 206), for each mating type separately.
For A2 tagging SNPs (n = 98), i.e., SNPs heterozygous in the A2 founding parent, we observed two classes of markers: those with pa of approximately 0.5 in the A2 and 0.0 in the A1 field F1 isolates, and the opposite scenario (Figures 8A,B; see Materials and Methods). In the first case (n = 49), differences in pa between mating types were maintained in the field inbred subpopulation (Figure 8A). Whereas, in the second case (n = 49), the difference in pa between mating types narrowed (Figure 8B). In contrast to the A2 parent tagging SNPs, markers heterozygous in the A1 parent and homozygous in the A2 parent (n = 108) predominantly followed a single pattern (Figure 8C). These markers were at approximately equal allele frequencies in both mating types in the field F1, but slightly diverged in frequency in the field inbred subpopulation. These three distinct segregation patterns were consistent with the association of presence/absence (P/A) of one of the A2 founding haplotypes in association with mating type.
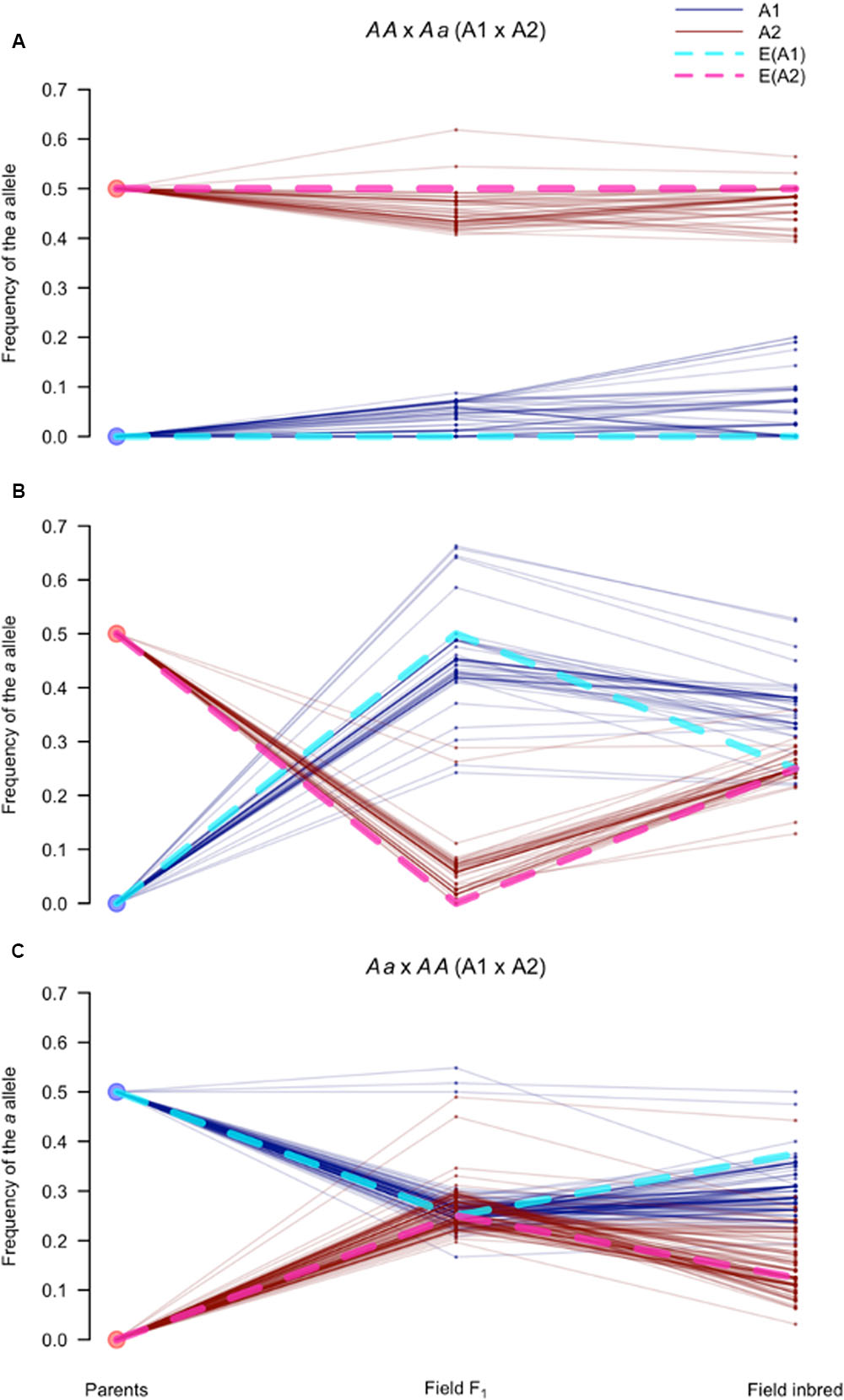
FIGURE 8. Segregation of SNPs in the mating type region follow expectations for sex-linked loci. Frequency of the a allele (pa), for AA × Aa and Aa × AA (A1 × A2) markers in the mating type associated sub-regions of scaffolds 4 and 27, defined as the mating type region (MTR). Each parallel coordinate plot (A–C) tracks pa at three time points (parents, field F1, and field inbred) in the A1 (blue solid lines) and A2 (red solid lines) isolates for: (A) AA × Aa markers (n = 49) with pa> 0.3 in the A2 and pa < 0.3 in the A1 field F1 isolates; (B) Remaining AA × Aa markers (n = 49); and (C) All Aa × AA markers. Expectations for sex-linked loci, indicated by dotted lines, assuming the A1 and A2 mating types behave like the homogametic (light blue) and heterogametic (pink) sexes, respectively, when: (A) the a allele is in the A2 determining haplotype (i.e., Y analog); (B) the a allele is in the non-A2 determining haplotype (i.e., X analog); and (C) the a allele is in either of the non-A2 determining haplotypes (i.e., X analogs).
While the structural basis of mating type determination in P. capsici is not known, observed segregation patterns in the MTR resemble those of an XY system, where P/A of the Y determines sex. Therefore, as frame of reference, we derived expectations for sex-linked loci in an XY system, i.e., loci conserved between both sex chromosomes (Clark, 1988; Allendorf et al., 1994), assuming that the A2 parent corresponded to the heterogametic sex. Using this model, expectations (blue and pink dotted lines in Figure 8) closely matched the observed pa trajectories in all three cases (Figures 8A–C), further supporting the association of one of the A2 haplotypes with mating type determination.
Discussion
To study the temporal genetic dynamics of P. capsici in response to a severe bottleneck, we SNP genotyped at high-density 232 isolates collected in years 2009–2013 from a closed, biparental field population founded in 2008, in Geneva, NY (Dunn et al., 2014). This experimental population mimics a potential infection scenario of a natural P. capsici epidemic, where a limited number of pathogen strains are thought to found a subsequently isolated population (Lamour et al., 2012; Dunn et al., 2014). Using filtered GBS data, we identified 159 unique field genotypes and obtained 6,916 high quality SNPs with high sequencing depth (∼20X coverage), low missing data, and over 97% reproducibility of genotype calls with the implemented analysis pipeline, distributed throughout the genome. With these data, we assessed temporal heterozygosity and allele frequency changes in the biparental population, representing the only controlled, multi-year genomic field study of a plant pathogen to date.
With knowledge of the parental genotypes and assuming simple Mendelian inheritance, we developed a threshold to detect F1 field isolates based on the incidence of MEs in the in vitro F1 progeny. Our results showed that both field and in vitro F1 progeny were characterized by individual heterozygosity in large excess of Hardy–Weinberg expectations, explained by the fact these isolates were descendent from only two parents. With small numbers of parents, the probability of allele frequency differences between opposite sexes (here, mating types) increases, consequently resulting in deviation from HWE among the progeny (Robertson, 1965; Pudovkin et al., 1996; Luikart and Cornuet, 1999; Balloux, 2004). In addition, discrepancies between the parental and progeny genotypes, i.e., MEs, provided evidence for mitotic LOH occurrence in lab culture. This finding indicates the need to account for mitotic LOH in genetic analyses of P. capsici, and denotes the limited utility of the parental genotypes for filtering markers used to characterize the progeny.
Over time, the field population underwent a generational shift, transitioning from F1 in 2009–2010, to multi-generational in 2011, and ultimately all inbred in 2012–2013. Presence of exclusively F1 in 2009 suggests that most of the oospores formed in the founding year (2008) were F1. As oospores require a dormancy period of approximately one month (Satour and Butler, 1968; Dunn et al., 2014), it is not surprising that there was insufficient time to produce multiple generations in the founding year. The presence of only F1 and no inbred isolates in 2010, however, cannot be similarly explained. Rather, abundant sexual reproduction in the founding year, coupled with a lower rate in 2009, may have led to disproportionate presence of F1 oospores (from 2008) surviving in the soil and germinating in 2010. Consequently, there would have been a low probability of sampling an inbred isolate in this year. Year 2011, where both inbred and F1 isolates were observed in the field, signified a generational shift in the population. The absence of F1 in the following years (2012–2013) is consistent with previous reports of oospore declines in viability over time (Bowers, 1990), and negligible oospore survival after four years in field conditions (Babadoost and Pavon, 2013). While we did not quantify disease incidence in the field, observation of predominantly F1 isolates in 2010–2011 suggests that highly productive years contributed disproportionately to population structure, in accordance with theoretical predictions for populations in which sexual propagules require a dormancy period, e.g., plant species with seed banks (Templeton and Levin, 1979; Nunney, 2002). As a consequence, heterozygosity did not immediately decline in the second year of the field population, similarly consistent with the delayed attainment of equilibrium genotypic frequencies attributed to seed bank dynamics (Templeton and Levin, 1979).
Approximate equilibrium genotypic frequencies were not observed in the field population until the fourth year (2012). Here, a single large increase in homozygosity in the total population was consistent with cycles of inbreeding beyond a theoretical F2 resulting in less appreciable declines in heterozygosity relative to the prior generation (Wright, 1921). However, two excessively homozygous field isolates, identified as field selfs, significantly deviated from this trend. Given this low frequency of selfing, we conclude that P. capsici behaved essentially as an obligate outcrossing species in the biparental field population. Occurrence of selfing in P. capsici is consistent with a previous report of oospore induction when strains of opposite mating types were separated by a membrane (Uchida and Aragaki, 1980), but contradicts previous studies which found no evidence for self-fertilization under in vitro conditions (Hurtado-Gonzales and Lamour, 2009; Lamour et al., 2012). As a single generation of self-fertilization reduces heterozygosity by approximately 50% in the progeny, minimal incidence of selfing delayed heterozygosity declines in the field population, as described for hermaphroditic plant species (Balloux, 2004).
In addition, while we observed three A1 parental selfs among the 46 in vitro progeny, we did not observe selfs derived from either founding parent in the field, despite the larger field F1 sample size. Field isolates were inherently selected for both viability and pathogenicity, as well as resilience to environmental factors, whereas, in vitro isolates were selected solely on viability in culture. Therefore, this result may reflect a fitness cost to self-fertilization, as observed in essentially all outcrossing species (Charlesworth and Charlesworth, 1987; Falconer and Mackay, 1996), manifest to a greater extent in the field versus laboratory conditions.
Given the potential fitness cost to self-fertilization in P. capsici, an increase in inbreeding may explain the allele frequency changes which accompanied the transition from an F1 to inbred population, as inbreeding presents recessive deleterious alleles in the homozygous state, rendering them subject to selection (Kirkpatrick and Jarne, 2000; Charlesworth, 2003). Simultaneously, inbreeding indirectly influences allele frequencies by decreasing the effective population size (Ne) relative to the census population size, consequently amplifying the effects of genetic drift (Charlesworth, 2009). In addition to inbreeding, many other factors likely decreased Ne, thereby increasing the influence of genetic drift: imbalanced sex (here, mating type) ratios (Charlesworth, 2009); clonal reproduction (Balloux et al., 2003); variation in reproductive success (Hartl and Clark, 2007); small population sizes (Hartl and Clark, 2007) suggested by lower genotypic diversity in 2012–2013; and overlapping generations (Felsenstein, 1971). Conversely, minimal differentiation between 2009 and 2011 denotes that oospore survival, in behaving like a seed bank, mitigates the aforementioned reductions in Ne by maintaining a reservoir of genetic variation in the soil (Templeton and Levin, 1979; Hairston and De Stasio, 1988; Nunney, 2002; Waples, 2006).
In contrast to the general trends described above, we characterized two regions (ROI-1 and ROI-2) that significantly deviated from the genome-wide distribution of allele frequency differences (median allele frequency change in the 97 percentile or greater) between the field F1 and inbred subpopulations. In these two regions, which presented only three segregating haplotypes, in contrast to the expected four, for heterozygous parents, we associated allele frequency changes with haplotype frequency shifts. Genetic drift may still explain these results, as drift has a larger effect in regions of low variation, i.e., with higher effective inbreeding coefficients corresponding to lower local Ne (Charlesworth, 2003, 2009). However, extreme changes in allele frequency are also suggestive of natural selection (Lewontin and Krakauer, 1973; Galtier et al., 2000). Here, observation of corresponding haplotype frequency shifts is consistent with hitchhiking or background selection having a large effect in inbred populations (Charlesworth, 2003), particularly those which have undergone only a few generations since founding. Alternatively, mitotic LOH, a phenomenon reported in the present study (see Supplementary Text) and in numerous Phytophthora species (Chamnanpunt et al., 2001; Grünwald et al., 2012; Lamour et al., 2012; Kasuga et al., 2016), may explain the observation of a disproportionate number of homozygous genotypes among inbred isolates in ROI-2. Evidence for mitotic LOH in numerous species, e.g., Saccharomyces cerevisiae (Magwene et al., 2011), Candida albicans (Forche et al., 2011), and the chytrid Batrachochytrium dendrobatidis (Rosenblum et al., 2013), supports the theoretical expectation that this process facilitates adaptation by interacting with selection to alter allele frequencies (Mandegar and Otto, 2007). Given the limited number of generations, we cannot unequivocally attribute these dramatic haplotype frequency shifts to selection. Furthermore, additional work is required to assess the role of these regions in pathogenicity and local adaptation.
While we observed a genome-wide increase in homozygosity in the field population due to inbreeding, reductions in heterozygosity in the identified mating type associated region were smaller relative to the genome for both A1 and A2 isolates. We show that this result is explained by persistent allele frequency differences between isolates of opposite mating types in the MTR. Maintenance of elevated heterozygosity in sex-linked regions has been attributed to differences in founding allele frequencies between sexes in several systems (Allendorf et al., 1994; Marshall et al., 2004; Waples, 2014). Further, AA × Aa SNPs associated with mating type in the field F1 were predominantly heterozygous in the A2 parent, implying that one of the A2 founding haplotypes was associated with mating type determination. Consistent with this result, segregation patterns for SNPs in the MTR resembled the behavior of loci in the pseudoautosomal (conserved) regions of heteromorphic sex chromosomes (e.g., XY or ZW; Clark, 1988), where the A2 parent corresponded to the heterogametic, male sex. These results suggest that in populations of P. capsici with few founders, heterozygosity in the MTR will be maintained despite inbreeding, proportional to LD between the mating type factor(s) and the rest of the genome. In addition, we did not detect significant temporal allele frequency changes in the MTR. This result suggests that frequency-dependent selection could play a role in maintaining polymorphism in this region (Fisher, 1930).
These findings, which represent the first detailed genomic analysis of mating type in a Phytophthora species, are consistent with the existing models of heterozygosity versus homozygosity at a single locus as determinant of mating type (Sansome, 1980; Fabritius and Judelson, 1997). However, our analysis does not demonstrate that heterozygosity per se confers the A2 mating type, nor does our analysis preclude the presence of heteromorphic mating type chromosomes in P. capsici. We applied stringent SNP filters to obtain a high-quality set of markers, likely discarding SNPs located in regions of structural variation (i.e., duplications, deletions, repeats). Indeed, early cytological work supports heterozygosity for a reciprocal translocation in association with mating type in P. capsici and numerous Phytophthora species, posited as a mechanism to suppress local recombination (Sansome, 1976). Given that chromosomal heteromorphism has arisen in diverse taxa as a consequence of suppressed recombination between sex-determining chromosomes (Bachtrog, 2013; Charlesworth, 2013), future studies will investigate the association of structural variation and recombination suppression with mating type determination in P. capsici. In addition, improved genomic resources will facilitate identification of the functional basis of mating type.
Materials and Methods
Isolate and DNA Collection
In 2008, a restricted access research field at Cornell University’s New York Agricultural Experiment Station in Geneva NY, with no prior history of Phytophthora blight, was inoculated once with two NY isolates of P. capsici, 0664-1 (A1) and 06180-4 (A2), of opposite mating types, as described in Dunn et al. (2014). From 2009 to 2013, the field was planted with susceptible crop species, and each year the pathogen was isolated from infected plant material, and cultured on PARPH medium (Dunn et al., 2014). Once in pure culture, a single zoospore isolate was obtained (Dunn et al., 2014), and species identity was confirmed with PCR using species specific primers, as previously described in Zhang et al. (2008) and Dunn et al. (2010).
Isolates collected in 2009–2012 were obtained from storage; isolates from 2013 were unique to this study and were collected from infected pumpkin plants (variety Howden Biggie). Single oospore progeny (n = 46) from an in vitro cross between the founding parents were obtained from storage (Dunn et al., 2014). To revive isolates from storage, several plugs from each storage tube were plated on PARPH media. After less than one week, actively growing cultures were transferred to new PARP or PARPH medium.
Mycelia were harvested for DNA extraction as previously described Dunn et al. (2010), except that sterile 10% clarified V8 (CV8) broth (Skidmore et al., 1984) was used instead of sterile potato dextrose broth. For each isolate, mycelia were grown in Petri plates containing CV8 broth for less than one week, vacuum filtered, and 90–110 mg of tissue were placed in 2 ml centrifuge tubes and stored at -80°C until DNA extraction. DNA was extracted using the DNeasy Plant Mini kit (Qiagen, Valencia, CA, USA) according to manufacturer’s instructions, except that mycelial tissue was ground using sterile ball bearings and a TissueLyser (Qiagen, Valencia, CA, USA) as previously described (Dunn et al., 2010).
Mating type was determined as previously described in Dunn et al. (2010). Briefly, each isolate was grown on separate unclarified V8 agar with known A1 and A2 isolates, respectively. After at least one week of growth, the plates were assessed microscopically for the presence of oospores. For each trial, the A1 and A2 tester isolates were grown in isolation and on the same plate as negative and positive controls, respectively. We obtained mating type designations for isolates from years 2009–2012 and the in vitro F1 from Dunn et al. (2014).
Genotyping
All DNA samples were submitted to the Institute of Genomic Diversity at Cornell University for 96-plex GBS (Elshire et al., 2011). In brief, each sample was digested with ApeKI, followed by adapter ligation, and samples were pooled prior to 100 bp single-end sequencing with Illumina HiSeq 2000/2500 (Elshire et al., 2011). Sequence data for samples analyzed in this study were deposited at NCBI under BioProject PRJNA376558.
To validate experimental procedures, DNA samples from the parental isolates were included with each sequencing plate (except in one instance). The parental isolates were sequenced initially at a higher sequencing depth (12-plex). Genotypes were called for all isolates simultaneously using the TASSEL 3.0.173 pipeline (Glaubitz et al., 2014). This process involves aligning unique reads, trimmed to 64bp, to the reference genome (Lamour et al., 2012) and mitochondrial (courtesy of Martin, F., USDA-ARS) assemblies, and associating sequence reads with the corresponding individual by barcode identification to call SNPs (Glaubitz et al., 2014). The Burrows–Wheeler alignment (v.0.7.8) algorithm bwa-aln with default parameters (Li and Durbin, 2009) was used to align sequence tags to the reference genome (Lamour et al., 2012). To reduce downstream SNP artifacts due to poor sequencing alignment, reads with a mapping quality <30 were removed. Default parameters were otherwise used in TASSEL, with two exceptions: (1) Only sequence tags present >10 times were used to call SNPs; and (2) SNPs were output in variant call format (VCF), with up to four alleles retained per locus, using the tbt2vcfplugin. Genotypes were assigned and genotype likelihoods were calculated as described in (Hyma et al., 2015).
Individual and SNP Quality Control
Individuals with more than 40% missing data were removed from the analysis. To mitigate heterozygote undercalling due to low sequence coverage, genotypes with read depth <5 were set to missing using a custom python script (available upon request). Subsequently, we utilized VCFtools version 1.14 (Danecek et al., 2011) to retain SNPs which met the following criteria: (1) Genomic; (2) <20% missing data; (3) Mean read depth ≥ 10; 4) Mean read depth < 50; (5) Bi-allelic; and (6) Minor allele frequency (MAF) ≥ 0.05, where MAF was defined based on the population allele frequency. We removed SNPs with high read depth (>50) as the likelihood of both heterozygote miscalling and misalignment increases at excessive read depths. Additionally, indels were removed.
To remove isolates with likely ploidy variation, we assessed allele depth ratios for each isolate, where the allele depth ratio was defined as the ratio of the major allele to the total allele depth at a heterozygous locus (Rosenblum et al., 2013; Yoshida et al., 2013; Li et al., 2015). Allele depths were extracted from the VCF file, using a custom python script (available upon request) to analyze the distribution of allele depth ratios for each individual across all SNPs.
Post clone-correction (see below) and outlier removal, SNPs were further filtered as follows. SNPs with heterozygosity rates >90% among all isolates (clone-corrected and parental replicates) were removed and/or average allele depth ratios <0.2 or >0.8. Only SNPs within scaffolds containing more than 300 kb of sequence, covering ∼48 Mb (∼75% of the sequenced genome), were retained. We defined the minor allele as the least frequent allele in the clone-corrected field population.
Multiple sequencing runs of the parental isolates were used to define consensus genotypes for each parent using the majority rule. Sites where ≥50% of calls were missing or where disparate genotype calls were equally frequent were set to missing.
All filtering and analyses, if not otherwise specified, were performed in R version 3.2.3 (R Core Team, 2015) using custom scripts (available upon request).
Identifying a Clone-Correction Threshold
To establish a maximum similarity threshold to define unique genotypes, the genetic similarity of all sequencing runs of the parental isolates were compared. Similarity was defined as IBS, the proportion of alleles shared between two isolates at non-missing SNPs. Parental replicates represented both biological (different mycelial harvests and/or independent cultures) and technical replicates (same DNA sample), thereby capturing variation associated with culture transfers, mycelial harvests, DNA extractions and sequencing runs (Supplementary Table S2). Based on the variation between parental replicates, individuals more than 95% similar to each other were considered clones, and one randomly selected individual from each clonal group was retained in the clone-corrected data set.
Population Structure
Principal component analysis was performed on a scaled and centered genotype matrix in the R package pcaMethods (Stacklies et al., 2007), using the nipalsPCA method to account for the small amount of missing data (method = ‘nipals’, center = TRUE, scale = ‘uv’). This method was used for all PCAs performed. To estimate pairwise differentiation between years, we used Weir and Cockerham’s (1984) FST measure (Weir and Cockerham, 1984), which weights allele frequency and variance estimates by population size, implemented in the R package StAMMP with the stamppFST function (Pembleton et al., 2013). We performed 1000 permutations of the SNP set to assess if FST estimates were significantly greater than zero (Weir and Cockerham, 1984; Pembleton et al., 2013).
Measures of Inbreeding
We used the canonical method-of-moments estimator of the individual inbreeding coefficient, F = 1-Ho/He, where Ho is the observed individual heterozygosity, and He is the expected heterozygosity given allele frequencies in a reference population assumed to be at HWE (Purcell et al., 2007; Keller et al., 2011). In the absence of drift and segregation distortion, allele frequencies in an F1 population should be equal to those in the parental generation. Therefore, we utilized allele frequencies in the in vitro F1 to define expected heterozygosity, as the in vitro F1 provided a more robust estimate of allele frequencies compared to the parental genotypes. For each isolate, F was calculated with respect to non-missing genotypes only. To compare average F between years, a pairwise t-test was implemented in R with pairwise.t.test (pool.sd = FALSE, paired = FALSE, p.adjust.method = ‘bonferroni’).
Heterozygosity was defined as the number of isolates with a heterozygous genotype at each SNP divided by the total number of non-missing genotype calls. Minor allele frequency (MAF) was defined as the number of minor alleles, where the minor allele was defined as the allele with the lowest frequency in the field population, present at each SNP divided by the total number of non-missing chromosomes (number of non-missing genotype calls multiplied by two). Heterozygosity and MAF distributions for each year and the in vitro F1 were graphically assessed using the density function in R.
For each individual, we calculated the proportion of MEs, defined as the ratio of MEs to the total number of non-missing tested sites, analogous to the PLINK implementation (–mendel; Purcell et al., 2007). An ME was defined as a genotype inconsistent with the individual being an F1 derived from the two founding parental isolates (Purcell et al., 2007). An isolate with a proportion MEs exceeding the in vitro F1 mean by 3 SD was classified as field inbred and otherwise as field F1.
Genome Scan for Allele Frequency Differentiation
To detect regions of differentiation between the in vitro F1, field F1, and inbred isolates, we performed a Fisher’s exact test of allele counts at each SNP for all pairwise comparisons between subpopulations, using the fisher.test function in R. P-values were adjusted for multiple testing using the Benjamini and Hochberg (1995) procedure, implemented with the p.adjust function, at a false discovery rate (FDR) of 10% (Wright, 1992; Benjamini and Hochberg, 1995). Significant SNPs were retained in further analyses only if another SNP within 200 kb also surpassed the significance threshold.
We compared the FST distribution of significantly differentiated SNPs within regions of interest (ROIs) to the genome-wide FST distribution according to Lewontin and Krakauer (1973). Here, FST was defined as, , where p0 is the frequency of the minor allele in the field F1, and Δp is the difference in allele frequency between the field F1 and field inbred subpopulations.
Haploview (Barrett et al., 2005) was used to estimate pairwise LD (r2) between SNPs in scaffolds containing ROIs.
Haplotyping
As the population was established by two parental strains, assuming no mutation, all isolates were by definition combinations of the founding parental haplotypes. Therefore, we took a deterministic approach to phasing, akin to utilizing trio information to phase parental genotypes (Browning and Browning, 2011). Haplotyping in ROIs was further facilitated by the fact that either or both parents were homozygous, with the homozygous genotype assumed to represent a founding parental haplotype. We showed that this was a valid assumption by analyzing early replicates of the parental genotypes that exhibited the “ancestral” heterozygous genotype in a specific region (Supplementary Figure S13) and by comparison to homozygous genotypes of selfed isolates (data not shown). We used the homozygous parental stretches (haplotypes) to deduce the other haplotypes from consensus genotypes for the expected genotypic classes. Progeny membership in a genotypic class was defined by k-means clustering using the kmeans function in R (centers = 8, n.iter = 1000, nstart = 100). To further refine clusters and remove recombinant isolates, we calculated local pairwise relatedness, defined as IBS, between isolates within a cluster, and removed isolates that shared on average less than 90% IBS with the respective cluster members. Next, we defined the consensus genotype based on the refined clusters utilizing the majority rule (see “Identifying a Clone-Correction Threshold”), and heterozygous genotypes within haplotypes were set to missing.
To determine the haplotype composition of each isolate, the three identified haplotypes in a region of interest were used to construct reference genotypes for all possible haplotype combinations (e.g., H1/H2, H1/H1). Then, the genotypic discordance (i.e., the number of mismatched genotypes) between each isolate genotype and reference genotype were calculated. The most similar reference genotype was assigned if genotypic discordance was less than 25%. Otherwise, the isolate genotype was deemed “Unknown.”
To create phase diagrams, haplotype tagging SNPs (SNPs which unambiguously distinguished a specific haplotype) were identified at SNPs where all haplotypes had no missing data. Individual genotypes were then classified for homozygosity or heterozygosity at each haplotype tagging SNP.
Identifying Mating Type Associated SNPs
We performed a Fisher’s exact test of allele frequency differences between isolates of opposite mating types in the field F1. Multiple test correction was performed as above (see ‘Genome Scan for Allele Frequency Differentiation’).
Heterozygosity in the Mating Type Region (MTR)
To test differences between the heterozygote frequency distribution in the MTR relative to the rest of the genome, we compared the heterozygosity of genome-wide SNPs sampled in equal proportions of marker types (e.g., AA × Aa) to the MTR using the sample function in R without replacement (replace = FALSE), excluding SNPs not polymorphic or with missing data in the parental isolates. The identified ME-enriched SNPs were excluded (see Supplementary Text). To account for an unequal ratio of A1:A2 mating type isolates, in each test, the A2s were down-sampled (without replacement) to equate with the A1 sample size in the respective subpopulation. We used the wilcox.test function in R to perform a one-sided, unpaired Wilcoxon rank sum test (alternative = ’less,’ paired = FALSE), repeated for 100 random SNP samples. Additionally, heterozygosity distributions of the A1 and A2 isolates in each subpopulation were compared to the respective genome-wide distribution, with SNP but not isolate down-sampling.
Heterozygote excess was tested at each locus in the A1 and A2 isolates for each subpopulation, using the function HWExact in the R package HardyWeinberg (Wigginton et al., 2005; Graffelman, 2015). This amounts to a one-sided test of HWE where heterozygote excess is the only evidence of deviation from HWE. We controlled for multiple testing as above.
Allele Frequency Changes in the MTR
In the MTR, the frequency of the parental tagging allele (pa) at SNPs heterozygous in one parent and homozygous in the other, was calculated for A1 and A2 isolates separately in the parental generation, the field F1 and the field inbreds, excluding missing genotypes. The A2 tagging SNPs were separated into two categories based on pa with respect to mating type in the field F1. The first case consisted of SNPs with pa ≥ 0.3 in the A2 isolates and pa ≤ 0.3 in the A1 isolates, and the second case consisted of the remaining SNPs. Expectations for pa in theoretical F1 and F2 populations, for the three cases where the a alleles is in the haplotype background of the: (1) Y in the male sex; (2) X in the male sex; and (3) X in the female sex, were derived based on the formulas in Clark (1988) and Allendorf et al. (1994).
Author Contributions
CS and MC conceived the experimental design; MC, CS, EG, and MG conceptualized the analysis; MC performed the experiments and analyses; MC and EG wrote the manuscript; CS and MG revised the manuscript.
Funding
This work was supported by the New York State Department of Agriculture and Markets (grant numbers C200780, C200818 to CS). This work was also partly funded by USDA-NIFA/DOE Biomass Research and Development Initiative (BRDI) (grant number 2011-06476 to MG) and Cornell University startup funds to MG.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Daniel C. Ilut and Amara R. Dunn for helpful conversations. We thank Holly W. Lange and Michael R. Fulcher for assistance with field and lab work.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fgene.2017.00026/full\#supplementary-material
FILE S1 | VCF file containing all sequenced clone-corrected isolates (n = 23,485 SNPs). This file includes isolates that were subsequently removed as outliers (short ids: 13PF_29A, 68_28, 68_40). The folder also contains a file with the mating type designation for each isolate.
FILE S2 | VCF file containing all sequenced non-clone-corrected isolates (n = 23,485 SNPs). This file includes isolates that were subsequently removed as outliers (short ids: 13PF_29A, 68_28, 68_40). The folder also contains a file with the mating type designation for each isolate.
References
Abdellaoui, A., Hottenga, J. J., de Knijff, P., Nivard, M. G., Xiao, X., Scheet, P., et al. (2013). Population structure, migration, and diversifying selection in the Netherlands. Eur. J. Hum. Genet. 21, 1277–1285. doi: 10.1038/ejhg.2013.48
Allendorf, F. W., Gellman, W. A., and Thorgaard, G. H. (1994). Sex-linkage of two enzyme loci in Oncorhynchus mykiss (rainbow trout). Heredity 72, 498–507. doi: 10.1038/hdy.1994.67
Babadoost, M., and Pavon, C. (2013). Survival of Oospores of Phytophthora capsici in Soil. Plant Dis. 97, 1478–1483. doi: 10.1016/j.riam.2011.01.004
Bachtrog, D. (2013). Y-chromosome evolution: emerging insights into processes of Y-chromosome degeneration. Nat. Rev. Genet. 14, 113–124. doi: 10.1038/nrg3366
Balloux, F. (2004). Heterozygote excess in small populations and the heterozygote-excess effective population size. Evolution 58, 1891–1900. doi: 10.1111/j.0014-3820.2004.tb00477.x
Balloux, F., Amos, W., and Coulson, T. (2004). Does heterozygosity estimate inbreeding in real populations? Mol. Ecol. 13, 3021–3031.
Balloux, F., Lehmann, L., and de Meeûs, T. (2003). The population genetics of clonal and partially clonal diploids. Genetics 164, 1635–1644.
Barrett, J. C., Fry, B., Maller, J., and Daly, M. J. (2005). Haploview: analysis and visualization of LD and haplotype maps. Bioinformatics 21, 263–265. doi: 10.1093/bioinformatics/bth457
Benjamini, Y., and Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Series B (Methodological) 57, 289–300.
Bonhomme, M., Chevalet, C., Servin, B., Boitard, S., Abdallah, J. M., Blott, S., et al. (2010). Detecting selection in population trees: the Lewontin and Krakauer test extended. Genetics 186, 241–262. doi: 10.1534/genetics.104.117275
Bowers, J. H. (1990). Effect of soil temperature and soil-water matric potential on the survival of Phytophthora capsici in natural soil. Plant Dis. 74, 771. doi: 10.1094/PD-74-0771
Browning, S. R., and Browning, B. L. (2011). Haplotype phasing: existing methods and new developments. Nat. Rev. Genet. 12, 703–714. doi: 10.1038/nrg3054
Chamnanpunt, J., Shan, W. X., and Tyler, B. M. (2001). High frequency mitotic gene conversion in genetic hybrids of the oomycete Phytophthora sojae. Proc. Natl. Acad. Sci. U.S.A. 98, 14530–14535. doi: 10.1073/pnas.251464498
Charlesworth, B. (2009). Fundamental concepts in genetics: effective population size and patterns of molecular evolution and variation. Nat. Rev. Genet. 10, 195–205. doi: 10.1038/nrg2526
Charlesworth, B., and Charlesworth, D. (1987). Inbreeding depression and its evolutionary consequences. Annu. Rev. Ecol. Syst. 18, 237–268. doi: 10.1146/annurev.es.18.110187.001321
Charlesworth, D. (2003). Effects of inbreeding on the genetic diversity of populations. Philos. Trans. R. Soc. B Biol. Sci. 358, 1051–1070. doi: 10.1098/rstb.2003.1296
Charlesworth, D. (2013). Plant sex chromosome evolution. J. Exp. Bot. 64, 405–420. doi: 10.1093/jxb/ers322
Clark, A. G. (1988). The evolution of the Y chromosome with X-Y recombination. Genetics 119, 711–720.
Danecek, P., Auton, A., Abecasis, G., Albers, C. A., Banks, E., DePristo, M. A., et al. (2011). The variant call format and VCFtools. Bioinformatics 27, 2156–2158. doi: 10.1093/bioinformatics/btr330
De Meester, L., Gómez, A., Okamura, B., and Schwenk, K. (2002). The Monopolization Hypothesis and the dispersal–gene flow paradox in aquatic organisms. Acta Oecol. 23, 121–135. doi: 10.1016/S1146-609X(02)01145-1
Dunn, A. R., Bruening, S. R., Grünwald, N. J., and Smart, C. D. (2014). Evolution of an experimental population of Phytophthora capsici in the field. Phytopathology 104, 1107–1117. doi: 10.1094/PHYTO-12-13-0346-R
Dunn, A. R., Milgroom, M. G., Meitz, J. C., McLeod, A., Fry, W. E., McGrath, M. T., et al. (2010). Population structure and resistance to mefenoxam of Phytophthora capsici in New York State. Plant Dis. 94, 1461–1468. doi: 10.1094/PDIS-03-10-0221
Elshire, R. J., Glaubitz, J. C., Sun, Q., Poland, J. A., Kawamoto, K., Buckler, E. S., et al. (2011). A robust, simple genotyping-by-sequencing (GBS) approach for high diversity species. PLoS ONE 6:e19379. doi: 10.1371/journal.pone.0019379
Erwin, D. C., and Ribeiro, O. K. (1996). Phytophthora Diseases Worldwide. St Paul, MN: The American Phytopathological Society.
Fabritius, A. L., and Judelson, H. S. (1997). Mating-type loci segregate aberrantly in Phytophthora infestans but normally in Phytophthora parasitica: implications for models of mating-type determination. Curr. Genet. 32, 60–65. doi: 10.1007/s002940050248
Falconer, D. S., and Mackay, T. F. C. (1996). Introduction to Quantitative Genetics, 4 Edn. Essex: Longman.
Felsenstein, J. (1971). Inbreeding and variance effective numbers in populations with overlapping generations. Genetics 68, 581–597.
Fisher, R. A. (1930). The Genetical Theory of Natural Selection: A Complete Variorum Edition. Oxford: Clarendon Press. doi: 10.5962/bhl.title.27468
Forche, A., Abbey, D., Pisithkul, T., Weinzierl, M. A., Ringstrom, T., Bruck, D., et al. (2011). Stress alters rates and types of loss of heterozygosity in Candida albicans. mBio 2, e129–e111. doi: 10.1128/mBio.00129-11
Galtier, N., Depaulis, F., and Barton, N. H. (2000). Detecting bottlenecks and selective sweeps from DNA sequence polymorphism. Genetics 155, 981–987.
Glaubitz, J. C., Casstevens, T. M., Lu, F., Harriman, J., Elshire, R. J., Sun, Q., et al. (2014). TASSEL-GBS: a high capacity genotyping by sequencing analysis pipeline. PLoS ONE 9:e90346. doi: 10.1371/journal.pone.0090346
Graffelman, J. (2015). Exploring diallelic genetic markers: the hardy weinberg package. J. Stat. Softw. 64, 1–23. doi: 10.18637/jss.v064.i03
Granke, L. L., Quesada-Ocampo, L., and Lamour, K. (2012). Advances in research on Phytophthora capsici on vegetable crops in the United States. Plant Dis. 96, 1588–1600. doi: 10.1094/PDIS-02-12-0211-FE
Granke, L. L., Windstam, S. T., Hoch, H. C., Smart, C. D., and Hausbeck, M. K. (2009). Dispersal and movement mechanisms of Phytophthora capsici sporangia. Phytopathology 99, 1258–1264. doi: 10.1094/PHYTO-99-11-1258
Grünwald, N. J., Garbelotto, M., Goss, E. M., Heungens, K., and Prospero, S. (2012). Emergence of the sudden oak death pathogen Phytophthora ramorum. Trends Microbiol. 20, 131–138. doi: 10.1016/j.tim.2011.12.006
Grünwald, N. J., Goodwin, S. B., Milgroom, M. G., and Fry, W. E. (2003). Analysis of genotypic diversity data for populations of microorganisms. Phytopathology 93, 738–746. doi: 10.1094/PHYTO.2003.93.6.738
Hairston, N. G. Jr., and De Stasio, B. T. Jr. (1988). Rate of evolution slowed by a dormant propagule pool. Nature 336, 239–242. doi: 10.1038/336239a0
Hartl, D. L., and Clark, A. G. (2007). Principles of Population Genetics. Sunderland, MA: Sinauer Associates, Inc.
Hausbeck, M. K., and Lamour, K. H. (2004). Phytophthora capsici on vegetable crops: research progress and management challenges. Plant Dis. 88, 1292–1303. doi: 10.1094/PDIS.2004.88.12.1292
Hurtado-Gonzales, O. P., and Lamour, K. H. (2009). Evidence for inbreeding and apomixis in close crosses of Phytophthora capsici. Plant Pathol. 58, 715–722. doi: 10.1111/j.1365-3059.2009.02059.x
Hyma, K. E., Barba, P., Wang, M., Londo, J. P., Acharya, C. B., Mitchell, S. E., et al. (2015). Heterozygous mapping strategy (HetMappS) for high resolution genotyping-by-sequencing markers: a case study in grapevine. PLoS ONE 10:e0134880. doi: 10.1371/journal.pone.0134880
Jorde, P. E., and Ryman, N. (1995). Temporal allele frequency change and estimation of effective size in populations with overlapping generations. Genetics 139, 1077–1090.
Kardos, M., Luikart, G., and Allendorf, F. W. (2015). Measuring individual inbreeding in the age of genomics: marker-based measures are better than pedigrees. Heredity 115, 63–72. doi: 10.1038/hdy.2015.17
Kasuga, T., Bui, M., Bernhardt, E., Swiecki, T., Aram, K., Cano, L. M., et al. (2016). Host-induced aneuploidy and phenotypic diversification in the Sudden Oak Death pathogen Phytophthora ramorum. BMC Genomics 17:385. doi: 10.1186/s12864-016-2717-z
Keller, M. C., Visscher, P. M., and Goddard, M. E. (2011). Quantification of inbreeding due to distant ancestors and its detection using dense single nucleotide polymorphism data. Genetics 189, 237–249. doi: 10.1534/genetics.111.130922
Kirkpatrick, M., and Jarne, P. (2000). The effects of a bottleneck on inbreeding depression and the genetic load. Am. Nat. 155, 154–167. doi: 10.1086/303312
Ko, W. (1988). Hormonal heterothallism and homothallism in Phytophthora. Annu. Rev. Phytopathol. 26, 57–73. doi: 10.1146/annurev.py.26.090188.000421
Kondrashov, A. S. (1988). Deleterious mutations and the evolution of sexual reproduction. Nature 336, 435–440. doi: 10.1038/336435a0
Lamour, K. H., and Hausbeck, M. K. (2000). Mefenoxam insensitivity and the sexual stage of Phytophthora capsici in michigan cucurbit fields. Phytopathology 90, 396–400. doi: 10.1094/PHYTO.2000.90.4.396
Lamour, K. H., and Hausbeck, M. K. (2001). Investigating the spatiotemporal genetic structure of Phytophthora capsici in Michigan. Phytopathology 91, 973–980. doi: 10.1094/PHYTO.2001.91.10.973
Lamour, K. H., and Hausbeck, M. K. (2003). Effect of crop rotation on the survival of Phytophthora capsici in Michigan. Plant Dis. 87, 841–845. doi: 10.1094/PDIS.2003.87.7.841
Lamour, K. H., Mudge, J., Gobena, D., Hurtado-Gonzales, O. P., Schmutz, J., Kuo, A., et al. (2012). Genome sequencing and mapping reveal loss of heterozygosity as a mechanism for rapid adaptation in the vegetable pathogen Phytophthora capsici. Mol. Plant Microbe Interact. 25, 1350–1360. doi: 10.1094/MPMI-02-12-0028-R
Lewontin, R. C., and Krakauer, J. (1973). Distribution of gene frequency as a test of the theory of the selective neutrality of polymorphisms. Genetics 74, 175–195.
Li, H., and Durbin, R. (2009). Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 25, 1754–1760. doi: 10.1093/bioinformatics/btp324
Li, Y., Zhou, Q., Qian, K., van der Lee, T., and Huang, S. (2015). Successful asexual lineages of the Irish potato Famine pathogen are triploid. bioRxiv. doi: 10.1101/024596
Luikart, G., and Cornuet, J. M. (1999). Estimating the effective number of breeders from heterozygote excess in progeny. Genetics 151, 1211–1216.
Magwene, P. M., Kayıkçı,Ö, Granek, J. A., Reininga, J. M., Scholl, Z., and Murray, D. (2011). Outcrossing, mitotic recombination, and life-history trade-offs shape genome evolution in Saccharomyces cerevisiae. Proc. Natl. Acad. Sci. U.S.A 108, 1987–1992. doi: 10.1073/pnas.1012544108
Mandegar, M. A., and Otto, S. P. (2007). Mitotic recombination counteracts the benefits of genetic segregation. Proc. R. Soc. Lond. B Biol. Sci. 274, 1301–1307. doi: 10.1098/rspb.2007.0056
Marshall, A. R., Knudsen, K. L., and Allendorf, F. W. (2004). Linkage disequilibrium between the pseudoautosomal PEPB-1 locus and the sex-determining region of chinook salmon. Heredity 93, 85–97. doi: 10.1038/sj.hdy.6800483
Meirmans, P. G., and van Tienderen, P. H. (2004). GENOTYPE and GENODIVE: two programs for the analysis of genetic diversity of asexual organisms. Mol. Ecol. Notes 4, 792–794. doi: 10.1111/j.1471-8286.2004.00770.x
Milgroom, M. G. (1996). Recombination and the multilocus structure of fungal populations. Annu. Rev. Phytopathol. 34, 457–477. doi: 10.1146/annurev.phyto.34.1.457
Nei, M., Maruyama, T., and Chakraborty, R. (1975). The bottleneck effect and genetic variability in populations. Evolution 29, 1. doi: 10.2307/2407137
Nunney, L. (2002). The effective size of annual plant populations: the interaction of a seed bank with fluctuating population size in maintaining genetic variation. Am. Nat. 160, 195–204. doi: 10.1086/341017
Pembleton, L. W., Cogan, N. O. I., and Forster, J. W. (2013). StAMPP: an R package for calculation of genetic differentiation and structure of mixed-ploidy level populations. Mol. Ecol. Resour. 13, 946–952. doi: 10.1111/1755-0998.12129
Price, A. L., Patterson, N. J., Plenge, R. M., Weinblatt, M. E., Shadick, N. A., and Reich, D. (2006). Principal components analysis corrects for stratification in genome-wide association studies. Nat. Genet. 38, 904–909. doi: 10.1038/ng1847
Pudovkin, A. I., Zaykin, D. V., and Hedgecock, D. (1996). On the potential for estimating the effective number of breeders from heterozygote-excess in progeny. Genetics 144, 383–387.
Purcell, S., Neale, B., Todd-Brown, K., Thomas, L., Ferreira, M. A. R., Bender, D., et al. (2007). PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81, 559–575. doi: 10.1086/519795
R Core Team (2015). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Robertson, A. (1965). The interpretation of genotypic ratios in domestic animal populations. Anim. Prod. 7, 319–324. doi: 10.1017/S0003356100025770
Rogstad, S. H., Keane, B., and Beresh, J. (2002). Genetic variation across VNTR loci in central North American Taraxacum surveyed at different spatial scales. Plant Ecol. 161, 111–121. doi: 10.1023/A:1020301011283
Rosenblum, E. B., James, T. Y., Zamudio, K. R., Poorten, T. J., Ilut, D., Rodriguez, D., et al. (2013). Complex history of the amphibian-killing chytrid fungus revealed with genome resequencing data. Proc. Natl. Acad. Sci. U.S.A. 110, 9385–9390. doi: 10.1073/pnas.1300130110
Sansome, E. (1976). Gametangial meiosis in Phytophthora capsici. Can. J. Bot. 54, 1535–1545. doi: 10.1139/b76-168
Sansome, E. (1980). Reciprocal translocation heterozygosity in heterothallic species of Phytophthora and its significance. Trans. Br. Mycol. Soc. 74, 175–185. doi: 10.1016/S0007-1536(80)80023-4
Satour, M. M., and Butler, E. E. (1967). A root and crown rot of tomato caused by Phytophthora capsici and P. parasitica. Phytopathology 57, 510–515.
Satour, M. M., and Butler, E. E. (1968). Comparative morphological and physiological studies of progenies from intraspecific matings of Phytophthora capsici. Phytopathology 58, 183–192.
Shattock, R. C. (1986). Genetics of Phytophthora infestans: characterization of single-oospore cultures from A1 isolates induced to self by intraspecific stimulation. Phytopathology 76:407. doi: 10.1094/Phyto-76-407
Skidmore, D. I., Shattock, R. C., and Shaw, D. S. (1984). Oospores in cultures of Phytophthora infestans resulting from selfing induced by the presence of P. drechsleri isolated from blighted potato foliage. Plant Pathol. 33, 173–183. doi: 10.1111/j.1365-3059.1984.tb02637.x
Stacklies, W., Redestig, H., Scholz, M., Walther, D., and Selbig, J. (2007). pcaMethods–a bioconductor package providing PCA methods for incomplete data. Bioinformatics 23, 1164–1167. doi: 10.1093/bioinformatics/btm069
Templeton, A. R., and Levin, D. A. (1979). Evolutionary consequences of seed pools. Am. Nat. 114, 232–249. doi: 10.1038/sdata.2015.72
Tian, D., and Babadoost, M. (2004). Host range of Phytophthora capsici from pumpkin and pathogenicity of isolates. Plant Dis. 88, 485–489. doi: 10.1094/PDIS.2004.88.5.485
Uchida, J. Y., and Aragaki, M. (1980). Chemical stimulation of oospore formation in Phytophthora capsici. Mycologia 72, 1103. doi: 10.2307/3759563
Wang, J. (2014). Marker-based estimates of relatedness and inbreeding coefficients: an assessment of current methods. J. Evol. Biol. 27, 518–530. doi: 10.1111/jeb.12315
Waples, R. S. (2006). Seed banks, salmon, and sleeping genes: effective population size in semelparous, age–structured species with fluctuating abundance. Am. Nat. 167, 118–135.
Waples, R. S. (2014). Testing for hardy-weinberg proportions: have we lost the plot? J. Hered. 106, 1–19. doi: 10.1093/jhered/esu062
Weir, B. S., and Cockerham, C. C. (1984). Estimating F-statistics for the analysis of population structure. Evolution 38, 1358. doi: 10.2307/2408641
Wigginton, J. E., Cutler, D. J., and Abecasis, G. R. (2005). A note on exact tests of hardy-weinberg equilibrium. Am. J. Hum. Genet. 76, 887–893. doi: 10.1086/429864
Wright, S. (1921). Systems of mating. II. The effects of inbreeding on the genetic composition of a population. Genetics 6, 124–143.
Wright, S. P. (1992). Adjusted p-values for simultaneous inference. Biometrics 48, 1005. doi: 10.2307/2532694
Yoshida, K., Schuenemann, V. J., Cano, L. M., Pais, M., Mishra, B., Sharma, R., et al. (2013). The rise and fall of the Phytophthora infestans lineage that triggered the Irish potato famine. Elife 2, 403–425. doi: 10.7554/eLife.00731
Keywords: Phytophthora, population genetics, inbreeding, mating system, self-fertilization, mating type, bottleneck, plant pathogen
Citation: Carlson MO, Gazave E, Gore MA and Smart CD (2017) Temporal Genetic Dynamics of an Experimental, Biparental Field Population of Phytophthora capsici. Front. Genet. 8:26. doi: 10.3389/fgene.2017.00026
Received: 12 December 2016; Accepted: 20 February 2017;
Published: 13 March 2017.
Edited by:
Norman A. Johnson, University of Massachusetts Amherst, USAReviewed by:
Stephen Wade Schaeffer, Pennsylvania State University, USACock Van Oosterhout, University of East Anglia, UK
Copyright © 2017 Carlson, Gazave, Gore and Smart. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michael A. Gore, bWFnODdAY29ybmVsbC5lZHU= Christine D. Smart, Y2RzMTRAY29ybmVsbC5lZHU=
 Maryn O. Carlson
Maryn O. Carlson Elodie Gazave
Elodie Gazave Michael A. Gore
Michael A. Gore Christine D. Smart
Christine D. Smart