- 1Quantum Systems Engineering Research Group and Department of Physics, Loughborough University, Loughborough, UK
- 2Quantum Information Science, School of Physics and Astronomy, University of Leeds, Leeds, UK
- 3Centre for Engineered Quantum Systems, School of Mathematics and Physics, The University of Queensland, St Lucia, QLD, Australia
We show that by engineering the interaction with the environment, there exists a large class of systems that can evolve irreversibly to a cat state. To be precise, we show that it is possible to engineer an irreversible process so that the steady state is close to a pure Schrödinger’s cat state by using double well systems and an environment comprising two-photon (or phonon) absorbers. We also show that it should be possible to prolong the lifetime of a Schrödinger’s cat state exposed to the destructive effects of a conventional single-photon decohering environment. In addition to our general analysis, we present a concrete circuit realization of both system and environment that should be fabricatable with current technologies. Our protocol should make it easier to prepare and maintain Schrödinger cat states, which would be useful in applications of quantum metrology and information processing as well as being of interest to those probing the quantum to classical transition.
1. Introduction
The development of many quantum technologies depends on an ability to engineer strongly non-classical states. Such states take the form of either highly entangled states of distinct degrees of freedom or a quantum coherent superposition of macroscopically distinct states in a single degree of freedom (Sanders, 2012), known as Schrödinger’s cat states [after a well known thought experiment (Schrödinger, 1935)]. It is these cat states that we consider in this paper. There has been great progress in the production of such states as well as experimentally reconstructing such states through a series of measurements in a process known as quantum state tomography (Monroe et al., 1996; Noel and Stroud, 1996; Leibfried et al., 2005; Ourjoumtsev et al., 2007; Deléglise et al., 2008; Gao et al., 2010). These developments are of great importance as, in addition to their curious nature, Schrödinger cat states can be used as a resource for developing technologies such as quantum computing (Ralph et al., 2003; Gilchrist et al., 2004), quantum communication (Jeong et al., 2001; van Enk and Hirota, 2001), and quantum metrology (Munro et al., 2002; Blatt and Wineland, 2008; Giovannetti et al., 2011). The main obstacle to deploying cat states in such applications is their fragility as they are destroyed by noise in a process termed environmental decoherence. A careful consideration of optical cat states shows that this decoherence may be interpreted as due to Poisson distributed jumps between even and odd cat states whenever a single photon is lost (Carmichael, 1993, 2003; Vitali et al., 1997). Their production and maintenance require very precise quantum control as well as low dissipation.
In this work, we present a possible realization of a protocol for double well system [in this case a Superconducting Quantum-Interference Device (SQUID)] to create Schrödinger cat states using the interaction of the system with a special kind of environment. To be specific, we engineer an environment comprising a bath of two-photon absorbers, for certain initial states, such that the system relaxes to a steady state, which is close to a pure Schrödinger cat state. The use of open systems as well as the measurement process was proposed by Yurke, Schleich, and Walls (Yurke and Stoler, 1986; Yurke et al., 1990). Gilles, Garraway, and Knight also proposed that it would be possible to engineer an environment of this kind that when paired with a parametric photon pump would exhibit many interesting effects in quantum optical systems, from the generation of Schrödinger cat states to manifestly quantum statistics (McNeil and Walls, 1974; Simaan and Loudon, 1978; Loudon and Knight, 1987; Gilles and Knight, 1993a,b; Gilles et al., 1994a,b; Guerra et al., 1997) (see also Tornau and Bach, 1974; Simaan and Loudon, 1975; Hildred and Hall, 1978; Agarwal and Hildred, 1986; Gerry, 1993; Gerry and Hach, 1993; Hach and Gerry, 1994). Two-photon absorption has also been suggested as a powerful resource for application in quantum computing (Franson et al., 2004). We note that there already exist schemes for realizing non-classical states via engineered dissipative channels (Amico et al., 2008; Diehl et al., 2008; Kraus et al., 2008; Schirmer and Wang, 2010; Ticozzi et al., 2010; Zhang et al., 2010; Busch et al., 2011; Pechen, 2011; Scully et al., 2011; Chen et al., 2012; Ticozzi and Viola, 2012; Yamamoto, 2012; Ikeda and Yamamoto, 2013) as well as a number of experimental realizations (Barreiro et al., 2011; Krauter et al., 2011; Leghtas et al., 2013). We also note that SQUIDs are an ideal candidate system for realizing this protocol as they have already been shown able to support appropriate quantum states (Nakamura et al., 1999; Friedman et al., 2000; Grajcar et al., 2004; Il’Ichev et al., 2004) and, as we shall later show, existing circuit designs can be used to engineer an environment with the suitable characteristics (Deng et al., 2010; Kumar and DiVincenzo, 2010).
We note that our scheme is simpler than and different from other driven dissipative bistable systems [for example, the coherently driven optical cavity containing a Kerr medium (Walls and Milburn, 2008), the driven Duffing mechanical resonator (Babourina-Brooks et al., 2008), tapered optical fibers (Hendrickson et al., 2010), and photon pumps (Gilles and Knight, 1993a; Gilles et al., 1994a)], as we do not include driving on either the cavity resonance or the coordinate degree of freedom. The possibility of engineering dissipative channels, such as the one that we present in this work, opens up new opportunities for exploring quantum phenomena from the micro to macroscopic level and in fields as diverse as quantum optics (Haycock et al., 2000), Bose–Einstein condensates (Andrews, 1997), quantum electronics (Friedman et al., 2000), and nano-mechanics (Badzey and Mohanty, 2005) [for which multi-phonon relaxation has already been proposed (Voje et al., 2013a,b)] or any other system in which it is possible to generate a double well potential.
2. Model System: The SQUID Ring
For the results presented in this paper, we have used as an example system a superconducting quantum-interference device (SQUID) ring. Our reason for choosing SQUIDs is that these devices are routinely fabricated and their theory is very well understood. We note that we have investigated a number of other systems (but do not include results here) and our analysis indicates that the key feature of the ring is that it can be made to form a double well potential. Moreover, non-linear systems derived from the Josephson junction in circuit QED exhibit multi photon resonance when driven by an external field (Deppe et al., 2008) and thus we expect two-photon decay to be present in such systems. The real difficulty is making it dominate over single photon effects. We will return to this in Section 4 where we propose a concrete circuit realization of a suitable and realistic environment for a SQUID. Beyond these considerations, we believe that there is nothing particularly special about the exact form of the potential needed to realize our protocol. The potential energy of the SQUID comprising a thick superconducting ring enclosing a Josephson junction weak link takes the form of a harmonic oscillator perturbed by a cosine
where the coordinate Φ is the total magnetic flux in the ring and Φ0 = h/2e is the superconducting flux quantum. We have chosen example circuit parameters that are in-line with modern fabrication techniques and suited to experimental realizations: Λ = 3 × 10−10 H for the ring’s inductance and Ic = 2 μA as the critical current of the weak link (although not in the above formula, we also chose a capacitance C = 5 × 10−15 F). We set the externally applied magnetic flux Φx = 0.5Φ0, so that the ring’s potential forms a degenerate double well. It is also convenient to introduce the bosonic annihilation a, and creation a† operators where and In Figure 1, we show the potential energy of the ring as well as the energy of the ring’s stationary states. It is worth noting that the ground state and first excited state approximate, respectively, symmetric and anti-symmetric superpositions of two coherent states centered at the bottom of each well. These two states have very nearly the same energy and the difference in their energy has been exaggerated in this plot (as have those for the second and third excited states).
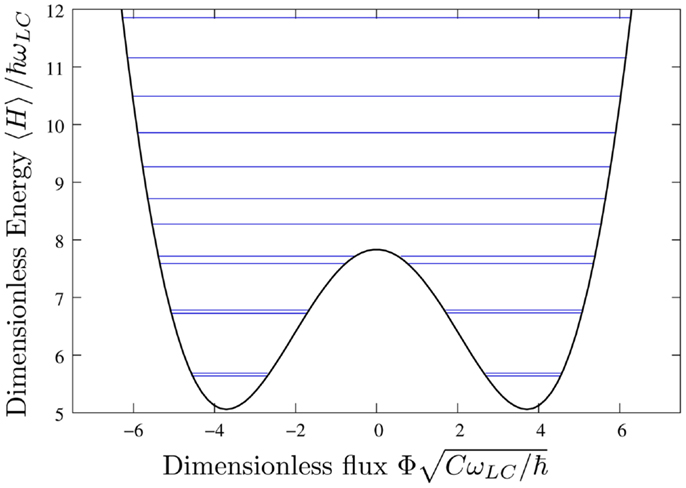
Figure 1. Stationary state energy levels: the potential energy of the ring (black) as well as the energy of the ring’s stationary states (blue). Parameters used here and throughout the paper are inductance Λ = 3 × 10−10 H, capacitance C = 5 × 10−15 F, critical current of the weak link Ic = 2 μA, and externally applied magnetic flux Φx = 0.5Φ0. Note that, we have exaggerated the energy difference between the ground and first excited states as well as stationary states two and three in order to make the different energies visible on this plot.
3. The Effect of Ideal Environments
3.1. Background
We model the effect of the environment on the system using the master equation in the Lindblad form (Viola et al., 1997)
where ρ is the density matrix describing the state of the system (initially ρ = |ψ(t = 0)〉〈ψ(t = 0)|) and H is the system’s Hamiltonian. The non-unitary effect of the environment on the system is contained in the Lindblad operators Lj with each describing a possible environment. For example, the usual Ohmic (i.e., analogous to friction proportional to velocity) or lossy bath, at zero temperature, would be described by a Lindblad operator proportional to the annihilation operator. For an undriven system, the master equation has steady state solution that, in the presence of an environment, is usually a density operator in a mixed state. In certain circumstances, at zero temperature, these solutions may be pure states such as the vacuum state of the harmonic oscillator. In general, the steady state solutions will not exhibit features such as superpositions of macroscopically distinct states and are relatively uninteresting. It is precisely this process where the environment essentially removes the system’s quantum coherence from de-localized, or more generally non-Gaussian states, that is known as environmental decoherence. The density matrix for a decohered system without these quantum correlations represents a statistical mixture of possible states of the system and, for a single quantum object, can be directly compared with classical probability density distributions (Habib et al., 1998). It should be noted, however, that there are driven dissipative systems, for example, dispersive bistability, for which the steady state is a mixed state with a considerable amount of quantum coherence in the limit of large Kerr non-linearity (Wolinsky and Carmichael, 1988; Carmichael, 1993, 2003).
We find very different behavior if one chooses a different environment comprising two-photon absorbers, described by a Lindblad operator proportional to the square of the annihilation operator. In Figure 2, we show the energy expectation values and von-Neumann entropy, S = − Tr[ρlnρ] as functions of time for solutions of the master equation for the ring in the presence of such an environment. We used as initial conditions the first twenty energy eigenstates of the ring Hamiltonian. In these plots, the energy behaves just as one would expect the energy of an undriven open quantum system to do – it settles to a single value. When one inspects the dynamics of the entropy, however, the story is quite different. One usually expects the entropy to grow from zero to some asymptotic value as the system evolves into a mixed state. While we see that this is the initial behavior, the entropy does not monotonically increase; instead it decreases until the entropy is nearly negligible. It appears that the system has to a significant extent recohered and the final density matrix is very nearly that of a pure state. While this is not the usual behavior of an open quantum system, based on previous work such as Yurke and Stoler (1986), Yurke et al. (1990), Gilles and Knight (1993a), and Gilles et al. (1994a), it is in-line with our expectations of an environment that “decoheres” a system to an almost pure state that is a very good approximation to a Schrödinger cat state.
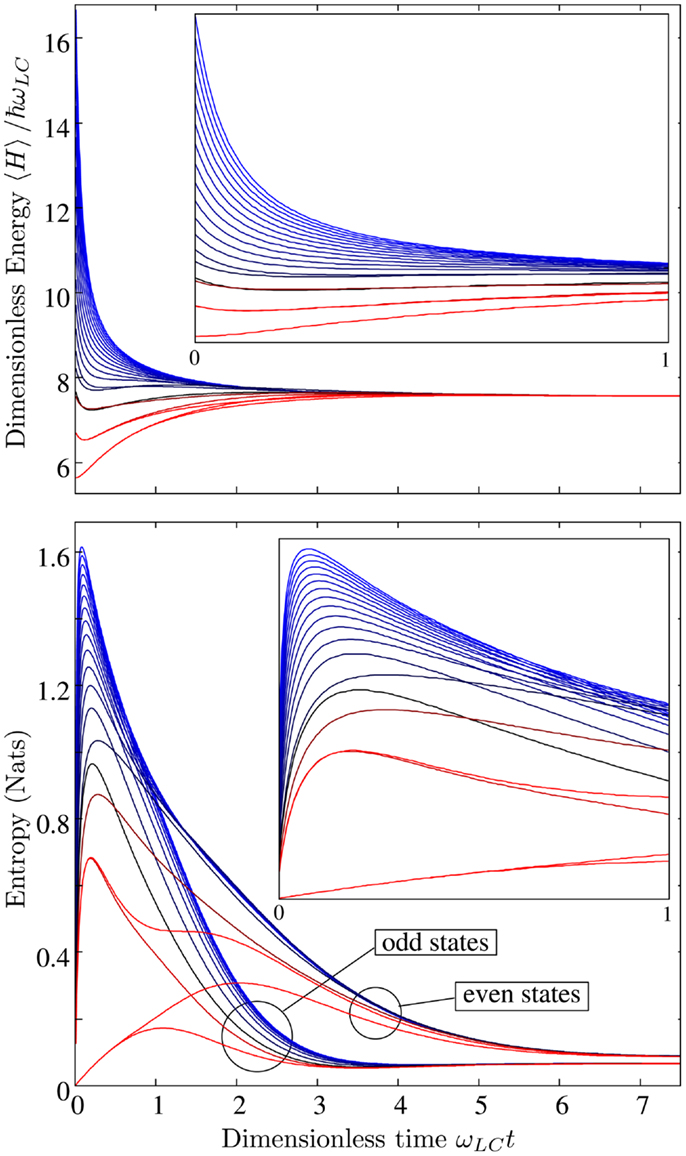
Figure 2. Effect of decoherence on energy and entropy. We show the dynamical evolution of the ring’s energy and entropy using each of its first twenty stationary states as initial conditions. The dynamics have been found by solving the master equation for the ring in the presence of a bath of two-photon absorbers (with ). We have provided insets for increased resolution of the system’s initial dynamics. The top plot shows the dynamics of the ring’s total energy. As expected for an open quantum system of this kind, the ring can be seen to decohere to one energy, a little above that of the ground state. The bottom plot shows the dynamics of the von-Neuman entropy for the ring. In each case, the initial entropy is zero as the system starts in a pure state. The entropy grows before dropping off to a low value indicating that the system’s steady state solution is very nearly a pure state.
3.2. Phase Space Method: The Wigner Function
In order to demonstrate that the system does indeed decay to a Schrödinger cat state, we will make use of the Wigner function. These pseudo probability density functions in phase space have been of great utility in demonstrating that some quantum states are Schrödinger cats (Deléglise et al., 2008). The Wigner function is
where Q is the charge variable that is conjugate to the magnetic flux Φ. In Figure 3, we show three Wigner functions. Figure 3A shows the initial state and is a coherent state centered at the origin. This is clearly recognizable as the expected Gaussian bell shape associated with coherent states. We have solved the master equation for the ring in a lossy bath, with a Lindblad of and allowed the system to reach its steady state to obtain Figure 3B. This is the Wigner function of a statistical mixture of two macroscopically distinct states and is in-line with expectations of the effect of a decohering environment on such a device (Everitt et al., 2004). In Figure 3C, we show the Wigner function that we obtain by solving the master equation, as for (Figure 3B), but replacing the damping term with a bath of two-photon absorbers, with We notice two things: firstly, the state has rotated, which we believe to be a consequence of a squeezing action associated with the bath and secondly that there are interference terms between the distinct states of the system. These interference terms, indicating quantum coherence, confirm that this state is indeed a very good approximation to a Schrödinger cat. We note that two-photon decay preserves parity, which can be easily seen if we consider the representation of the systems state vector in the harmonic oscillator basis. Here, we see that a2 will only couple even states to even states and odd states to odd states. Thus, the action of a2 on any initial state must preserve its parity. Hence, an environment comprising only two-photon absorbers would ensure that the system will relax to a steady state with same parity as the initial state. It is this symmetry property of the environment together with the symmetry in the Hamiltonian and initial condition that leads to steady state solutions that are Schrödinger cat states.
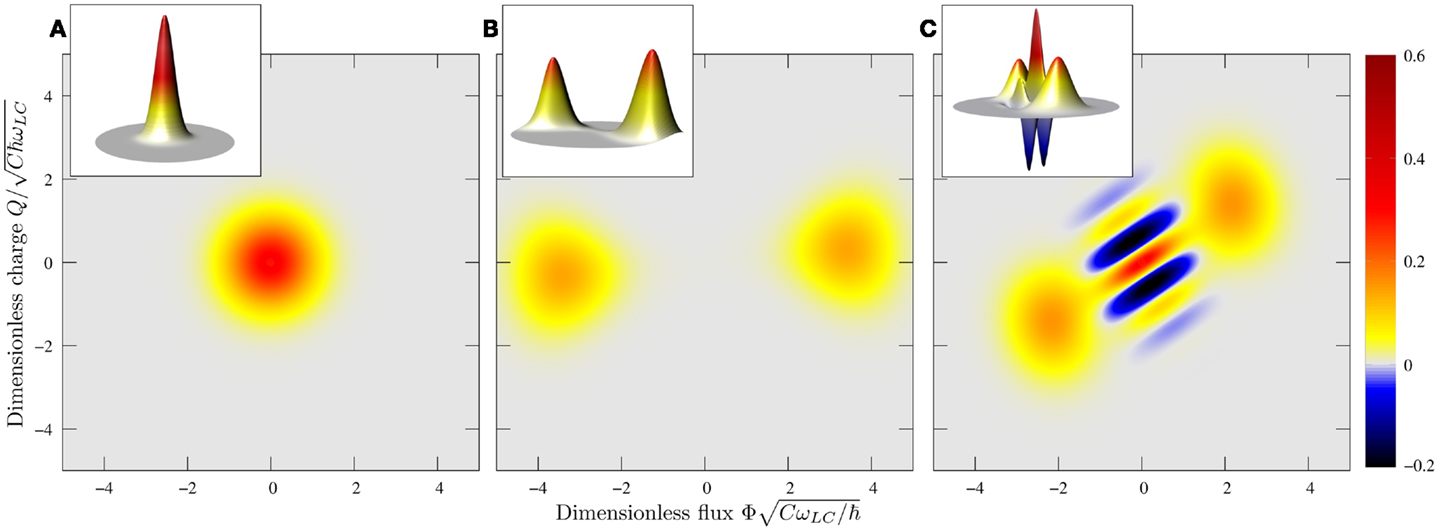
Figure 3. Cooling for a cat. In this figure we show, by making use of Wigner functions, the effect of two different environments on a ring prepared in a coherent state biased at zero flux. Each graph contains a top down view with a three dimensional plot of the function as a not to fixed scale inset. The graphs show (A), the initial state, which takes the form of a Gaussian bell. (B) The steady state solution to the master equation under the influence of a conventional decohering environment comprising a lossy bath (with a Lindblad proportional to the annihilation operator ). The ring has decohered to two distinct macroscopic states and we do not see the interference terms between them that are characteristic of a Schrödinger cat state. We have instead a statistical mixture, the usual and expected result (Everitt et al., 2004). (C) The steady state solution to the master equation for the ring coupled to a bath of two-photon absorbers (with a Lindblad proportional to the square of annihilation operator, ). In this case, the ring has decohered to a superposition of two macroscopic states but now there are interference terms between these states indicating quantum coherence – the signature of a Schrödinger cat state.
3.3. Quantifying Non-Local Correlations
In order to examine quantitatively the emergence of this cat from the initial coherent state we introduce, following (Nogues et al., 2000; Białynicki-Birula et al., 2002), a measure of how de-localized the system is in phase space that is the integral of negative parts of the Wigner function
In absolute terms, this is a useful measure, but when we know (by inspecting the Wigner function) that the states we are examining are cat-like, a more useful measure may well be a relative cattiness to some reference Schrödinger cat state.
Hence, we define:
which quantifies the ratio of the de-localization of one cat state against a reference cat and enables us to quantify if one is more [Cat(ρ, ρref) > 1], less [Cat(ρ, ρref) < 1], or just as [Cat(ρ, ρref) = 1] catty than the other. We have chosen to introduce this measure over using existing metrics such as the fidelity as it does not contain any contributions of the type that occur from, for example, correlations between a cat and its related mixed state (which might be thought of as the overlap of the “classical” like parts of the state). Computing relative measures such as the fidelity is further complicated by the fact that the final states, in terms of the size and orientation, for the different environments are very different from each other (having very little overlap). Hence, performing meaningful estimates of fidelity would be quite difficult, perhaps even impossible as we would have to provide different reference states for each environment against which to measure the fidelity. We note that while there are some limitations with the Cat measure and it should be applied with care, for the problem we study here, it suits our purposes very well. In Figure 4, we show the dynamics of this quantity for comparison with the results presented in Figure 3 using as a reference state ρref the final cat state shown in Figure 3C. Here, we can clearly see that the cattiness of the system subject to an environment of two-photon absorbers monotonically increases and asymptotically converges to a steady state.
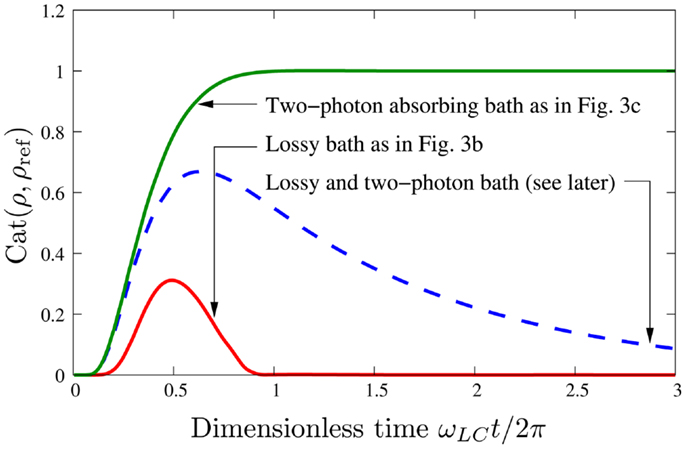
Figure 4. Relative cattiness is shown. We show the cattiness measure Cat(ρ, ρref) for the dynamics leading to Figure 3B in red and to Figure 3C in green. Here, we have used as a reference state ρref the final cat state shown in Figure 3C. For reference, later we have also included the dynamics of Cat(ρ, ρref) for an environment of two-photon absorbers and damping.
3.4. Results
It is interesting to consider what would happen to a ring that was initially in a Schrödinger cat state under the influence of a bath of two-photon absorbers. For systems with deep enough double well potentials, such as the one considered here the ground and first excited energy eigenstates are both Schrödinger cats. The ground state is, to good approximation, an even superposition of two macroscopically distinct coherent states while the first excited state is an odd superposition as can be seen from their Wigner functions in Figures 5A,C, respectively. The even and odd nature of these superpositions is reflected in the Wigner function by the phase of the interference terms between the two Gaussians of the cat. It is known that such states would decohere under the environment of a lossy bath to a statistical mixture (Everitt et al., 2004). The dynamics of the system coupled to an environment comprising a bath of two-photon absorbers are, once more, found by solving the master equation with an until an approximate steady state is reached. The Wigner function of these states is then shown with Figure 5A evolving to Figures 5B–D and Figures 5C,D. We observe that the phase in the final cat reflects that of the initial cat and the system has not simply decohered to the same steady state. The environment thus seems to preserve some of the symmetry of the initial state. We have checked the first twenty stationary states all of which decay to one of these cats or the other. Moreover, the pattern that was observed from the ground and first excited state persists and all even and odd states seem to evolve to cats of the same form as those shown in Figures 5B,D that are out of phase with each other.
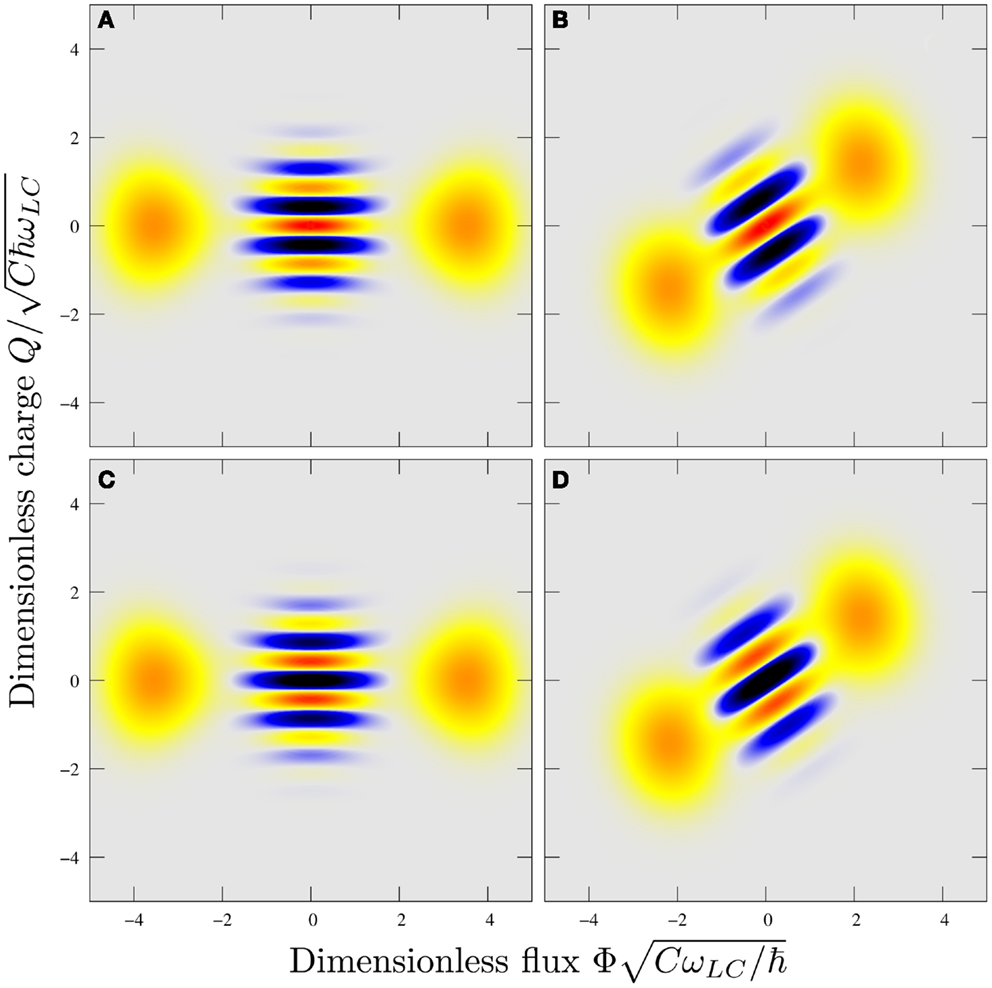
Figure 5. Preserving a cat, here we look at the ring initially in either its ground or first excited stationary state. As can be seen from their Wigner functions, plots (A,C), respectively, these take the form of Schrödinger cat states. The ground state is, to good approximation, an even superposition of two macroscopically distinct coherent states while the first excited state is an odd superposition. In terms of the Wigner functions, this is reflected in the phase of the interference terms between the two Gaussians of the cat. The effect of evolving the system in the presence of a bath of two-photon absorbers is then shown with (A,B) evolving to (C,D). We observe that the phase in the final cat reflects that of the initial cat and the system has not simply decohered to the same steady state.
This approach seems all very well and good, but an environment of two-photon absorbers is very special. It would be hard to construct such an environment without having any other source of decoherence present. We therefore need to verify that the effects of a two-photon absorbing environment cannot be completely destroyed by the presence of a more traditional environment such as a lossy bath. In Figure 6, we show the results of just such a check. For each plot, the system’s initial state was the ring’s ground state as shown in Figure 5A. In Figure 6A, we show the effect of a lossy bath. We solve the master equation with a Lindblad and allow the system to evolve until it has just decohered to a statistical mixture and we have plotted the Wigner function at this point in time. We use this run as a benchmark for computing the next two cases, which show the Wigner function solutions of the master equation computed over the same interval. In Figure 6B, we show the effect of a two-photon absorbing bath once more “decohering” to a Schrödinger cat state And in Figure 6C, we apply both the lossy bath of in Figure 6A and a two-photon absorbing environment of in Figure 6B to the ring ( and ). We see that in this figure, there remain residual Schrödinger cat state features in the Wigner function. Hence, it seems that not only does a bath of two-photon absorbers create Schrödinger cat states but also enables Schrödinger cat states to be more resilient to other forms of decoherence. In other words, the presence of an environment of two-photon absorbers seems to be prolonging the life of a damped cat. In Figure 6D, we quantify the cattiness using Cat(ρ, ρref) using the initial stationary state as shown in Figure 5A as the reference cat. For the three environments considered here, we find that for the system’s later evolution the environment of two-photon absorbers does indeed prolong the lifetime of the initial cat even in the presence of a lossy bath. We note that we obtain an almost identical set of results if we start the system off in a coherent state centered at the origin (as in Figure 3A). We chose to use the ring’s ground state as, in our view, we obtained a more instructive plot of the states cattiness from the systems dynamics. For a direct comparison of the dynamics of Cat(ρ, ρref) for these two initial conditions, we now note that the dashed line shown in Figure 4 was found for a lossy bath and a two-photon absorbing environment with and The green and blue lines of Figures 4 and 6D are directly comparable. The idea that the presence of a two-photon absorbing environment can be used to extend the lifetime (and also generate) Schrödinger cat states that holds equally well for two very different initial conditions.
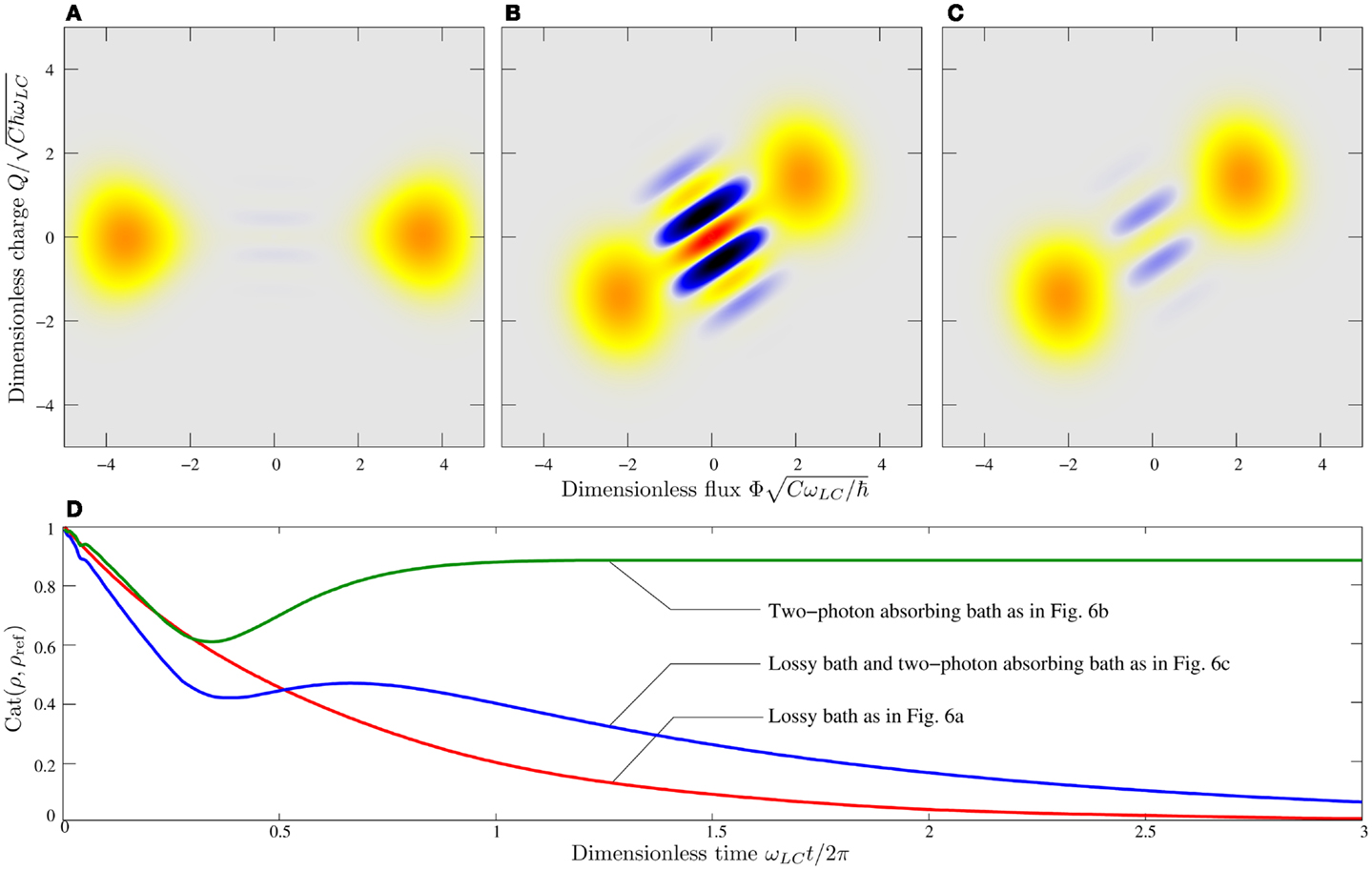
Figure 6. A stubborn cat: combatting the effect of other forms of decoherence. For each plot, the system was initialized in the ground state of the ring as in Figure 5A. In these plots, we show (A), the effect of a lossy bath on the state producing a typical plot of a cat that has just decohered to a statistical mixture – setting the time that we use to sample the other two plots of this figure (B) The effect of a two-photon absorbing bath showing decoherence to a Schrödinger cat state (C), the effect of both a lossy bath and a two-photon absorbing bath on the state. Notice that, there are still signatures of a cat state unlike for the lossy bath alone – the environment of two-photon absorbers seems to be prolonging the life of the cat ( and ) and (D), we show the cattiness Cat(ρ, ρref) for these three environments as a function of time (we have used the initial stationary state as shown in Figure 5A as the reference cat in this case). We see for the system’s later evolution the environment of two-photon absorbers does indeed prolong the lifetime of the initial cat even in the presence of a lossy bath.
4. A Realistic Model of an Environment
4.1. Overview
In order to make our above discussion a reality, we need to engineer a dissipative quantum channel that acts as a two-photon absorber. Here, we suggest a concrete realization that, whilst not perfect, still retains the key feature of environmentally induced “decoherence” to a Schrödinger cat state. Our proposal makes use of non-linearly coupled electromagnetic fields and SQUIDs. Such quantum electrodynamic circuits have already been investigated in the context of weak non-demolition measurement (Deng et al., 2010; Kumar and DiVincenzo, 2010). One example comprises two microwave superconducting resonators coupled via a SQUID, which in addition to a cross Kerr effect also manifests two-photon conversion terms if the cavities are resonant (Kumar and DiVincenzo, 2010). Such systems can be quantized (Everitt et al., 2001a,b; Stiffell et al., 2005; Wallquist et al., 2006) and with a suitable arrangement and choice of circuit parameters can be reduced (Wielinga and Milburn, 1993; Santamore et al., 2004) to the form of a double well system subject to a two-photon absorbing environment (see Section 4 for details). Unavoidably, this process also brings with it an additional dephasing term, that adds to the master equation another Lindblad operator proportional to a†a. Nevertheless, we can report that while the dephasing term smears out the Gaussian peaks in the cat the interference terms in the Wigner function representing quantum coherence between the cat states remain strong. The fact that this dephasing term preserves parity is once more the key factor in ensuring the steady state of our engineered dissipative channel is still a Schrödinger cat state. Our proposal could lead to an initial realization of a two-photon absorbing environment and concomitant interesting effects. The engineering of improved dissipative channels, without additional and unwanted decoherence effects, remains an open and interesting problem.
4.2. The Model: Derivation of the Master Equation
There are a number of models (Deng et al., 2010; Kumar and DiVincenzo, 2010) whereby two microwave superconducting cavities can be non-linearly coupled using SQUIDs. We will base our discussion on Kumar and DiVincenzo (2010). In that model, the Hamiltonian describing two microwave cavities, a probe (p) cavity and a signal (s) cavity, coupled with a SQUID is
where nα, ϕα are the standard charge and phase conjugate variables describing the collective electrical degree of freedom in each cavity and with L1 defined as the coefficient of the leading non-linear current term of the SQUID inductance. We will set cos2β = sin2β = 1/2.
The system can be quantized in the usual way in terms of the bosonic annihilation and creation operators b, b† for the probe and a, a† and for the signal cavity defined by (Wallquist et al., 2006)
The Hamiltonian may then be written as
Unlike Kumar and DiVincenzo (2010), we have not neglected the terms like b2a†2 as we will choose ωp = ωs so that these terms are resonant1.
We now include the dissipative channels for this model in the usual way. The density operator for the total system, in the interaction picture, satisfies
where and
and κa, κb are the decay rates of the photon number in the signal and probe cavity, respectively, and we have included a resonant coherent driving of the probe cavity with where |εb|2 is the photon flux of the driving field. We have also assumed that each cavity sees a zero temperature environment.
In the absence of the SQUID mediated interactions, the probe cavity will relax to a coherent state with the steady state amplitude
We will choose the phase of the probe driving as a reference phase and set β0 to be real. If we make a canonical transformation to the displaced picture by
we can linearize the Hamiltonian, Equation (9), in to obtain
where the effective Hamiltonian for the signal mode alone is
which is equivalent to a parametrically driven Kerr non-linear cavity. This model was considered by Wielinga and Milburn (1993). It is equivalent to a double well system with a hyperbolic fixed point at the origin in phase space and two elliptic fixed points symmetrically displaced from the origin. The second and third terms in equation (12) can be given a familiar interpretation. The second term is of the same form as the radiation pressure interaction between a mechanical resonator and a cavity field (a, a†). The last term is equivalent to the quantum description of sub/second harmonic generation considered by Drummond et al. (1980).
We now assume that κb, the line width of the probe cavity is large, and we adiabatically eliminate it from the dynamics. In that case from the point of view of the signal mode, the first term in equation (12) looks like a fluctuating cavity detuning while the last term looks like a two-photon loss term. This can be verified by explicit adiabatic elimination of the probe cavity field. We assume that the probe cavity, in the displaced picture, remains very close to its steady state of zero photons. The method is described in Santamore et al. (2004). The effective master equation for the signal cavity is
where the two-photon decay rate Γ2 and dephasing rate Γ⊥ are given by
4.3. Results
A peculiar feature of using SQUID coupled cavities is that the price paid for two-photon decay is an additional dephasing term on the signal cavity field. Using the strong dependence on the steady state amplitude β0 in the two-photon rate, we can make the two-photon decay term that dominate over the single photon decay of the signal cavity over the time scales of interest. In Figure 7A, we show that the dephasing term that is introduced in the above (un-damped, κa = 0) master equation has little effect on the Schrödinger cat nature of the steady state solution associated with the two-photon absorbing bath. In order to consider a worst case scenario, in Figure 7B, we go on to consider what would happen if we simultaneously weaken the effect of the two-photon environment and make the dephasing term even stronger. We have not taken these values from our model as the ratio of Γ⊥ to Γ2 has not been preserved. Our reason for presenting this data is to indicate that alternative circuit realizations, where the beneficial effects of the two-photon absorbing environment are reduced and the damaging effects of the dephasing term increased, might still be used to engineer a steady state cat. We therefore believe that the discussion in Section 3 is in-line with the behavior of realistic environments.
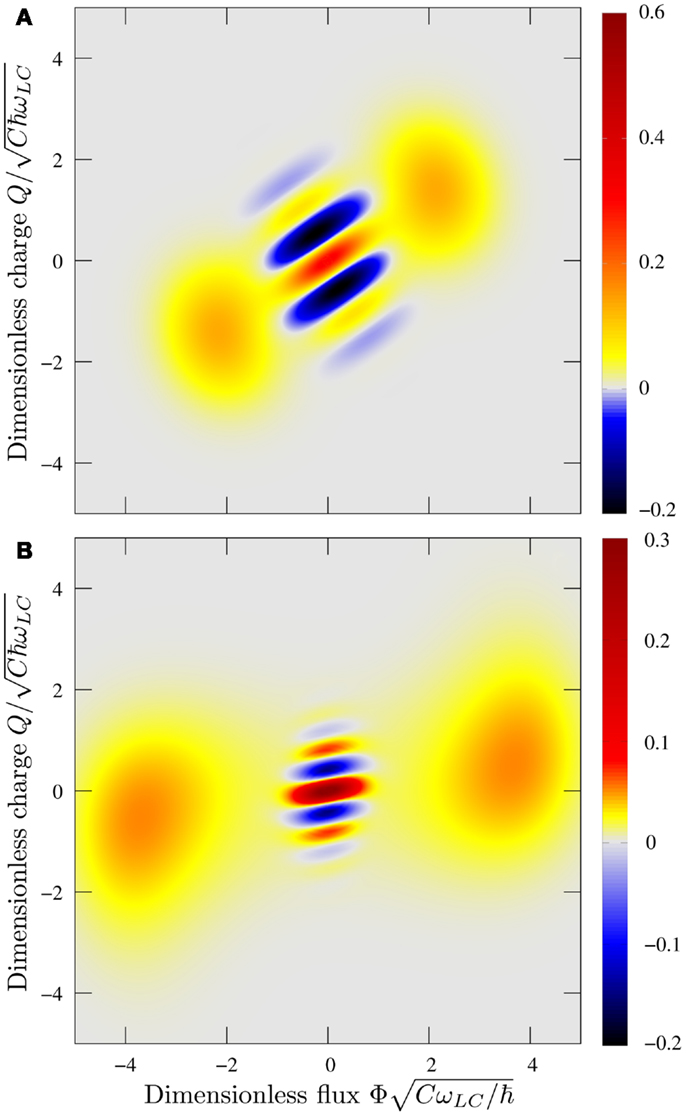
Figure 7. A persistent cat, here we look at the effect of including the dephasing term in addition to the bath of two-photon absorbers to the ring initially in its ground state. (A) The steady state solution for the environment as derived in Section 4.2 and described by master equation, equations (14) and (15) with Γ2 = 0.2 (or ) and Γ⊥ = 0.05 (or ) and we have set the damping coefficient κa = 0. (B) We show that even for an environment, other than the one considered in (A), where dephasing dominates over the two-photon absorption process ( and ), it is still possible for the steady state of the ring to be a cat.
Finally, in Figure 8 we show the cattiness [see equation (1)] of the realistic environment with two of the cases considered in Figure 6. Specifically, we consider the cases of a lossy bath a lossy bath and a two-photon absorbing ( and ) and also the full model, of equation (14), including the dephasing term ( and ). Even with the dephasing term included the environment of two-photon absorbers still prolongs the lifetime of the initial cat in the presence of a lossy bath.
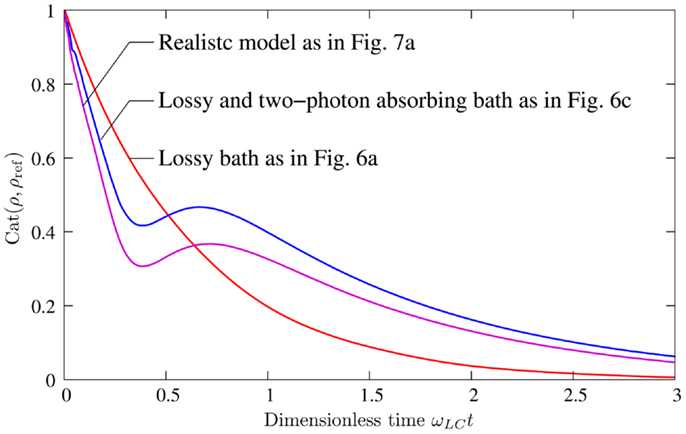
Figure 8. A stubborn cat II: the effect of a realistic environment for comparison with Figure 6, in this plot we show the cattiness for a: lossy bath ; a lossy bath and a two-photon absorbing bath ; and also the full model including the dephasing term . Even with the dephasing term included the environment of two-photon absorbers still prolongs the lifetime of the initial cat in the presence of a lossy bath.
5. Conclusion
There are two phenomena that embody quantum mechanics, namely entanglement and the Schrödinger’s cat thought experiment for making macroscopic superposition states (Schrödinger, 1935). The latter was proposed to highlight the difficulties that we have connecting quantum mechanics with everyday experience, as it neatly demonstrates the problems of understanding the emergence of the classical world from quantum theory and the measurement of quantum systems. Schrödinger’s cat has become the icon of the subject and evolved to have a well defined meaning. It is an accepted explanation within the popular literature that the reason the original thought experiment does not translate into reality (if conducted with a real cat in a box, etc.) is that the coupling of the environment to the radiation source (which included the cat itself) makes it impossible to observe the coherence between the two superposed macroscopically distinct states – a process known as decoherence. As such, environmental decoherence is something that many deem to be a crucial element in the quantum to classical transition (Bell, 1990; Habib et al., 1998; Schlosshauer, 2005; Everitt, 2009; Everitt et al., 2009). We have presented an example of an engineered environment that may be used to produce Schrödinger cat states as a steady state. It may well be that system and environment such as the one we have used here could play an interesting role in quantum mechanically enhanced metrology probing foundational aspects of quantum mechanics associated with realizing macroscopic quantum phenomena and the quantum to classical transition. In addition, the two-photon decay channel, if monitored appropriately, enables a measurement of the intensity squared of the number and may also enable novel non-linear feedback protocols. Although it is beyond the scope of the current paper, we conjecture that it may soon be possible, following (Yurke et al., 1990), to make use of an environment to create a conditional Schrödinger cat state by measurement.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Mark J. Everitt, Richard D. Wilson, and Richard D. Wilson thank the Templeton Foundation for their generous support. Gerard J. Milburn acknowledges the support of the National Science Foundation under Grant No. NSF PHY11-25915 and the Australian Research Council Centre of Excellence for Engineered Quantum Systems grant CE110001013. Mark J. Everitt would like to thank Andrew Archer, Gerry Swallowe, and Richard Giles for their help with the preparation of our manuscript.
Footnote
- ^Note that the coefficients in this equation are and
References
Agarwal, G., and Hildred, G. (1986). Time development of squeezing in two photon absorption. Opt. Commun. 58, 287–289. doi: 10.1016/0030-4018(86)90452-9
Amico, L., Fazio, R., Osterloh, A., and Vedral, V. (2008). Entanglement in many-body systems. Rev. Mod. Phys. 80, 517–576. doi:10.1103/RevModPhys.80.517
Andrews, M. R. (1997). Observation of interference between two Bose condensates. Science 275, 637–641. doi:10.1126/science.275.5300.637
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Babourina-Brooks, E., Doherty, A., and Milburn, G. J. (2008). Quantum noise in a nanomechanical duffing resonator. New J. Phys. 10, 105020. doi:10.1088/1367-2630/10/10/105020
Badzey, R. L., and Mohanty, P. (2005). Coherent signal amplification in bistable nanomechanical oscillators by stochastic resonance. Nature 437, 995–998. doi:10.1038/nature04124
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Barreiro, J. T., Müller, M., Schindler, P., Nigg, D., Monz, T., Chwalla, M., et al. (2011). An open-system quantum simulator with trapped ions. Nature 470, 486–491. doi:10.1038/nature09801
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Białynicki-Birula, I., Cirone, M., Dahl, J., Fedorov, M., and Schleich, W. (2002). In- and outbound spreading of a free-particle s-wave. Phys. Rev. Lett. 89, 060404. doi:10.1103/PhysRevLett.89.060404
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Blatt, R., and Wineland, D. (2008). Entangled states of trapped atomic ions. Nature 453, 1008–1015. doi:10.1038/nature07125
Busch, J., De, S., Ivanov, S. S., Torosov, B. T., Spiller, T. P., and Beige, A. (2011). Cooling atom-cavity systems into entangled states. Phys. Rev. A 84, 022316. doi:10.1103/PhysRevA.84.022316
Carmichael, H. (1993). An Open Systems Approach to Quantum Optics: Lectures Presented at the Université Libre de Bruxelles, October 28 – November 4, 1991 (Lecture Notes in Physics Series). Berlin: Springer-Verlag.
Carmichael, H. (2003). Statistical Methods in Quantum Optics 1: Master Equations and Fokker-Planck Equations (Statistical Methods in Quantum Optics). Berlin: Springer.
Chen, X.-Y., Shen, L.-T., Yang, Z.-B., Wu, H.-Z., and Chen, M.-F. (2012). Engineering W-type steady states for three atoms via dissipation in an optical cavity. J. Opt. Soc. Am. B 29, 1535. doi:10.1364/JOSAB.29.001535
Deléglise, S., Dotsenko, I., Sayrin, C., Bernu, J., Brune, M., Raimond, J.-M., et al. (2008). Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature 455, 510–514. doi:10.1038/nature07288
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Deng, C., Gambetta, J. M., and Lupascu, A. (2010). Quantum nondemolition measurement of microwave photons using engineered quadratic interactions. Phys. Rev. B 82, 220505. doi:10.1103/PhysRevB.82.220505
Deppe, F., Mariantoni, M., Menzel, E. P., Marx, A., Saito, S., Kakuyanagi, K., et al. (2008). Two-photon probe of the Jaynes Cummings model and controlled symmetry breaking in circuit QED. Nat. Phys. 4, 686. doi:10.1038/nphys1016
Diehl, S., Micheli, A., Kantian, A., Kraus, B., Büchler, H. P., and Zoller, P. (2008). Quantum states and phases in driven open quantum systems with cold atoms. Nat. Phys. 4, 878–883. doi:10.1038/nphys1073
Drummond, P., McNeil, K., and Walls, D. (1980). Non-equilibrium transitions in sub/second harmonic generation. Opt. Acta (Lond.) 28, 211.
Everitt, M. J. (2009). On the correspondence principle: implications from a study of the nonlinear dynamics of a macroscopic quantum device. New J. Phys. 11, 013014. doi:10.1088/1367-2630/11/1/013014
Everitt, M. J., Clark, T. D., Stiffell, P., Prance, H., Prance, R. J., Vourdas, A., et al. (2001a). Quantum statistics and entanglement of two electromagnetic field modes coupled via a mesoscopic squid ring. Phys. Rev. B 64, 184517. doi:10.1103/PhysRevB.64.184517
Everitt, M. J., Stiffell, P., Clark, T. D., Vourdas, A., Ralph, J. F., Prance, H., et al. (2001b). Fully quantum-mechanical model of a squid ring coupled to an electromagnetic field. Phys. Rev. B 63, 144530. doi:10.1103/PhysRevB.63.144530
Everitt, M. J., Clark, T. D., Stiffell, P. B., Vourdas, A., Ralph, J. F., Prance, R. J., et al. (2004). Superconducting analogs of quantum optical phenomena: macroscopic quantum superpositions and squeezing in a superconducting quantum-interference device ring. Phys. Rev. A 69, 043804. doi:10.1103/PhysRevA.69.043804
Everitt, M. J., Munro, W. J., and Spiller, T. P. (2009). Quantum-classical crossover of a field mode. Phys. Rev. A 79, 032328. doi:10.1103/PhysRevA.79.032328
Franson, J. D., Jacobs, B. C., and Pittman, T. B. (2004). Quantum computing using single photons and the Zeno effect. Phys. Rev. A 70, 062302. doi:10.1103/PhysRevA.70.062302
Friedman, J. R., Patel, V., Chen, W., Tolpygo, S. K., and Lukens, J. E. (2000). Quantum superposition of distinct macroscopic states. Nature 406, 43. doi:10.1038/35017505
Gao, W.-B., Lu, C.-Y., Yao, X.-C., Xu, P., Gühne, O., Goebel, A., et al. (2010). Experimental demonstration of a hyper-entangled ten-qubit Schrödinger cat state. Nat. Phys. 6, 331–335. doi:10.1038/nphys1603
Gerry, C. C. (1993). Non-classical properties of even and odd coherent states. J. Mod. Opt. 40, 1053–1071. doi:10.1080/09500349314551131
Gerry, C. C., and Hach, E. E. (1993). Generation of even and odd coherent states in a competitive two-photon process. Phys. Lett. A 174, 185–189. doi:10.1016/0375-9601(93)90756-P
Gilchrist, A., Nemoto, K., Munro, W. J., Ralph, T. C., Glancy, S., Braunstein, S. L., et al. (2004). Schrâšdinger cats and their power for quantum information processing. J. Opt. B Quantum Semiclassical Opt. 6, S828. doi:10.1088/1464-4266/6/8/032
Gilles, L., Garraway, B. M., and Knight, P. L. (1994a). Generation of nonclassical light by dissipative two-photon processes. Phys. Rev. A 49, 2785–2799. doi:10.1103/PhysRevA.49.2785
Gilles, L., Garraway, B., and Knight, P. (1994b). Generation of nonclassical light by dissipative two-photon processes. Phys. Rev. A 49, 2785–2799. doi:10.1103/PhysRevA.49.2785
Gilles, L., and Knight, P. (1993b). Two-photon absorption and nonclassical states of light. Phys. Rev. A 48, 1582–1593. doi:10.1103/PhysRevA.48.1582
Gilles, L., and Knight, P. L. (1993a). Two-photon absorption and nonclassical states of light. Phys. Rev. A 48, 1582–1593. doi:10.1103/PhysRevA.48.1582
Giovannetti, V., Lloyd, S., and Maccone, L. (2011). Advances in quantum metrology. Nat. Photon. 23, 222–229. doi:10.1038/nphoton.2011.35
Grajcar, M., Izmalkov, A., Il’Ichev, E., Wagner, T., Oukhanski, N., Hübner, U., et al. (2004). Low-frequency measurement of the tunneling amplitude in a flux qubit. Phys. Rev. B 69, 060501. doi:10.1103/PhysRevB.69.060501
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Guerra, E. S., Garraway, B. M., and Knight, P. L. (1997). Two-photon parametric pumping versus two-photon absorption: a quantum jump approach. Phys. Rev. A 55, 3842–3857. doi:10.1103/PhysRevA.55.3842
Habib, S., Shizume, K., and Zurek, W. H. (1998). Decoherence, chaos, and the correspondence principle. Phys. Rev. Lett. 80, 4361–4365. doi:10.1103/PhysRevLett.80.4361
Hach, E. III, and Gerry, C. (1994). Generation of mixtures of Schrödinger-cat states from a competitive two-photon process. Phys. Rev. A 49, 490–498. doi:10.1103/PhysRevA.49.490
Haycock, D. L., Alsing, P. M., Deutsch, I. H., Grondalski, J., and Jessen, P. S. (2000). Mesoscopic quantum coherence in an optical lattice. Phys. Rev. Lett. 85, 3365–3368. doi:10.1103/PhysRevLett.85.3365
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hendrickson, S. M., Lai, M. M., Pittman, T. B., and Franson, J. D. (2010). Observation of two-photon absorption at low power levels using tapered optical fibers in rubidium vapor. Phys. Rev. Lett. 105, 173602. doi:10.1103/PhysRevLett.105.173602
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hildred, G. P., and Hall, A. G. (1978). Antibunching: more than one kind in two-photon absorption. J. Phys. A Math. Gen. 11, L209. doi:10.1088/0305-4470/11/8/007
Ikeda, Y., and Yamamoto, N. (2013). Deterministic generation of Gaussian pure states in a quasilocal dissipative system. Phys. Rev. A 87, 033802. doi:10.1103/PhysRevA.87.033802
Il’Ichev, E., Smirnov, A. Y., Grajcar, M., Izmalkov, A., Born, D., Oukhanski, N., et al. (2004). Radio-frequency method for investigation of quantum properties of superconducting structures. Fiz. Nizk. Temp. 30, 823.
Jeong, H., Kim, M. S., and Lee, J. (2001). Quantum-information processing for a coherent superposition state via a mixed entangled coherent channel. Phys. Rev. A 64, 052308. doi:10.1103/PhysRevA.64.052308
Kraus, B., Büchler, H., Diehl, S., Kantian, A., Micheli, A., and Zoller, P. (2008). Preparation of entangled states by quantum Markov processes. Phys. Rev. A 78, 042307. doi:10.1103/PhysRevA.78.042307
Krauter, H., Muschik, C. A., Jensen, K., Wasilewski, W., Petersen, J. M., Cirac, J. I., et al. (2011). Entanglement generated by dissipation and steady state entanglement of two macroscopic objects. Phys. Rev. Lett. 107, 080503. doi:10.1103/PhysRevLett.107.080503
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kumar, S., and DiVincenzo, D. P. (2010). Exploiting Kerr cross nonlinearity in circuit quantum electrodynamics for nondemolition measurements. Phys. Rev. B 82, 014512. doi:10.1103/PhysRevB.82.014512
Leghtas, Z., Vool, U., Shankar, S., Hatridge, M., Girvin, S. M., Devoret, M. H., et al. (2013). Stabilizing a Bell state of two superconducting qubits by dissipation engineering. Phys. Rev. A 88, 5. doi:10.1103/PhysRevA.88.023849
Leibfried, D., Knill, E., Seidelin, S., Britton, J., Blakestad, R. B., Chiaverini, J., et al. (2005). Creation of a six-atom “Schrödinger cat” state. Nature 438, 639–642. doi:10.1038/nature04251
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Loudon, R., and Knight, P. (1987). Squeezed light. J. Mod. Opt. 34, 709–759. doi:10.1080/09500348714550721
McNeil, K. J., and Walls, D. F. (1974). A master equation approach to nonlinear optics. J. Phys. A Math. Gen. 7, 617. doi:10.1063/1.4891470
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Monroe, C., Meekhof, D. M., King, B. E., and Wineland, D. J. (1996). A “Schrödinger cat” superposition state of an atom. Science 272, 1131–1136. doi:10.1126/science.272.5265.1131
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Munro, W. J., Nemoto, K., Milburn, G. J., and Braunstein, S. L. (2002). Weak-force detection with superposed coherent states. Phys. Rev. A 66, 023819. doi:10.1103/PhysRevA.66.023819
Nakamura, Y., Pashkin, Y., and Tsai, J. (1999). Coherent control of macroscopic quantum states in a single-cooper-pair box. Nature 398, 786. doi:10.1038/19718
Noel, M., and Stroud, J. (1996). Excitation of an atomic electron to a coherent superposition of macroscopically distinct states. Phys. Rev. Lett. 77, 1913–1916. doi:10.1103/PhysRevLett.77.1913
Nogues, G., Rauschenbeutel, A., Osnaghi, S., Bertet, P., Brune, M., Raimond, J. M., et al. (2000). Measurement of a negative value for the Wigner function of radiation. Phys. Rev. A 62, 054101. doi:10.1103/PhysRevA.62.054101
Ourjoumtsev, A., Jeong, H., Tualle-Brouri, R., and Grangier, P. (2007). Generation of optical “Schrödinger cats” from photon number states. Nature 448, 784–786. doi:10.1038/nature06054
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Pechen, A. (2011). Engineering arbitrary pure and mixed quantum states. Phys. Rev. A 84, 042106. doi:10.1103/PhysRevA.84.042106
Ralph, T. C., Gilchrist, A., Milburn, G. J., Munro, W. J., and Glancy, S. (2003). Quantum computation with optical coherent states. Phys. Rev. A 68, 042319. doi:10.1103/PhysRevA.68.042319
Sanders, B. C. (2012). Review of entangled coherent states. J. Phys. A Math. Theor. 45, 244002. doi:10.1088/1751-8113/45/24/244002
Santamore, D. H., Goan, H.-S., Milburn, G. J., and Roukes, M. L. (2004). An harmonic effects on a phonon-number measurement of a quantum-mesoscopic-mechanical oscillator. Phys. Rev. A 70, 052105. doi:10.1103/PhysRevA.70.052105
Schirmer, S. G., and Wang, X. (2010). Stabilizing open quantum systems by Markovian reservoir engineering. Phys. Rev. A 81, 062306. doi:10.1103/PhysRevA.81.062306
Schlosshauer, M. (2005). Decoherence, the measurement problem, and interpretations of quantum mechanics. Rev. Mod. Phys. 76, 1267–1305. doi:10.1103/RevModPhys.76.1267
Schrödinger, E. (1935). Die gegenwärtige situation in der quantenmechanik. Naturwissenschaften 23, 807–812. doi:10.1007/BF01491891
Scully, M. O., Chapin, K. R., Dorfman, K. E., Kim, M. B., and Svidzinsky, A. (2011). Quantum heat engine power can be increased by noise-induced coherence. Proc. Natl. Acad. Sci. U.S.A. 108, 15097–15100. doi:10.1073/pnas.1110234108
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Simaan, H. D., and Loudon, R. (1975). Quantum statistics of single-beam two-photon absorption. J. Phys. A Math. Gen. 8, 539. doi:10.1088/0305-4470/8/4/016
Simaan, H. D., and Loudon, R. (1978). Off-diagonal density matrix for single-beam two-photon absorbed light. J. Phys. A Math. Gen. 11, 435. doi:10.1088/0305-4470/11/2/018
Stiffell, P. B., Everitt, M. J., Clark, T. D., Harland, C. J., and Ralph, J. F. (2005). Quantum downconversion and multipartite entanglement via a mesoscopic superconducting quantum interference device ring. Phys. Rev. B 72, 014508. doi:10.1103/PhysRevB.72.014508
Ticozzi, F., Schirmer, S. G., and Wang, X. (2010). Stabilizing quantum states by constructive design of open quantum dynamics. IEEE Trans. Automat. Contr. 55, 2901–2905. doi:10.1109/TAC.2010.2079532
Ticozzi, F., and Viola, L. (2012). Stabilizing entangled states with quasi-local quantum dynamical semigroups. Philos. Trans. A Math. Phys. Eng. Sci. 370, 5259–5269. doi:10.1098/rsta.2011.0485
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Tornau, N., and Bach, A. (1974). Quantum statistics of two-photon absorption. Opt. Commun. 11, 46–49. doi:10.1016/0030-4018(74)90330-7
van Enk, S. J., and Hirota, O. (2001). Entangled coherent states: teleportation and decoherence. Phys. Rev. A 64, 022313. doi:10.1103/PhysRevA.64.022313
Viola, L., Onofrio, R., and Calarco, T. (1997). Macroscopic quantum damping in squid rings. Phys. Lett. A 229, 23–31. doi:10.1016/S0375-9601(97)00154-0
Vitali, D., Tombesi, P., and Milburn, G. J. (1997). Controlling the decoherence of a “meter” via stroboscopic feedback. Phys. Rev. Lett. 79, 2442–2445. doi:10.1103/PhysRevLett.79.2442
Voje, A., Croy, A., and Isacsson, A. (2013a). Multi-phonon relaxation and generation of quantum states in a nonlinear mechanical oscillator. New J. Phys. 15, 053041. doi:10.1088/1367-2630/15/5/053041
Voje, A., Isacsson, A., and Croy, A. (2013b). Nonlinear-dissipation induced entanglement of coupled nonlinear oscillators. Phys. Rev. A 88, 022309. doi:10.1103/PhysRevA.88.022309
Wallquist, M., Shumeiko, V. S., and Wendin, G. (2006). Selective coupling of superconducting charge qubits mediated by a tunable stripline cavity. Phys. Rev. B 74, 224506. doi:10.1103/PhysRevB.74.224506
Wielinga, B., and Milburn, G. J. (1993). Quantum tunneling in a kerr medium with parametric pumping. Phys. Rev. A 48, 2494–2496. doi:10.1103/PhysRevA.48.2494
Wolinsky, M., and Carmichael, H. J. (1988). Quantum noise in the parametric oscillator: from squeezed states to coherent-state superpositions. Phys. Rev. Lett. 60, 1836–1839. doi:10.1103/PhysRevLett.60.1836
Yamamoto, N. (2012). Pure Gaussian state generation via dissipation: a quantum stochastic differential equation approach. Philos. Trans. A Math. Phys. Eng. Sci. 370, 5324–5337. doi:10.1098/rsta.2011.0529
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Yurke, B., Schleich, W., and Walls, D. (1990). Quantum superpositions generated by quantum nondemolition measurements. Phys. Rev. A 42, 1703–1711. doi:10.1103/PhysRevA.42.1703
Yurke, B., and Stoler, D. (1986). Generating quantum mechanical superpositions of macroscopically distinguishable states via amplitude dispersion. Phys. Rev. Lett. 57, 13–16. doi:10.1103/PhysRevLett.57.13
Zhang, W., Sun, C. P., and Nori, F. (2010). Equivalence condition for the canonical and microcanonical ensembles in coupled spin systems. Phys. Rev. E 82, 041127. doi:10.1103/PhysRevE.82.041127
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Keywords: cat state, quantum metrology, single-photon decoherence, decoherence, two-photon absorbers, quantum to classical transition, double well systems
Citation: Everitt MJ, Spiller TP, Milburn GJ, Wilson RD and Zagoskin AM (2014) Engineering dissipative channels for realizing Schrödinger cats in SQUIDs. Front. ICT 1:1. doi: 10.3389/fict.2014.00001
Received: 11 August 2014; Accepted: 04 October 2014;
Published online: 30 October 2014.
Edited by:
Andrew D. Greentree, RMIT University, AustraliaReviewed by:
Jonas Maziero, Universidade Federal de Santa Maria, BrazilZoltán Zimborás, University College London, UK
Copyright: © 2014 Everitt, Spiller, Milburn, Wilson and Zagoskin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mark J. Everitt, Quantum Systems Engineering Research Group and Department of Physics, Loughborough University, Leicestershire, Loughborough LE11 3TU, UK e-mail:bS5qLmV2ZXJpdHRAcGh5c2ljcy5vcmc=
†Present address: Richard D. Wilson, Sonobex Limited, Warwick, UK
 Mark J. Everitt
Mark J. Everitt Timothy P. Spiller
Timothy P. Spiller Gerard J. Milburn3
Gerard J. Milburn3 Alexandre M. Zagoskin
Alexandre M. Zagoskin