- Department of Electrical Engineering, University of California at Santa Cruz, Santa Cruz, CA, USA
In this paper, we propose an effective data-adaptive filtering mechanism for sharpening of noisy and moderately blurred images. We establish the connection of our proposed data-adaptive filtering procedure with the classic Difference of Gaussians (DoG) operator widely used in image processing and computer graphics. Our proposed filter renders a data adaptive and noise robust version of the classical DoG filter. We also discuss interesting special cases of our general sharpening method. Experimental results verify the effectiveness of the proposed technique for sharpening real images.
1. Introduction
With ever increasing number of images taken by digital/mobile cameras in different lighting conditions, and with various camera hardware, effective enhancement algorithms are necessary for producing higher quality images. Noise and blur are two major distortions in images taken with existing cameras. Any effective image enhancement algorithm should be equipped with appropriate mechanisms for dealing with visual degradations resulting from noise and blur. Specifically, image sharpening is a challenging task when the input image is noisy, even when the image is not severely blurred. The reason is that image sharpening is essentially a high pass filtering operation aiming at amplifying high frequency details in the input image. On the other hand, noise components in the input image exhibit high frequency attributes and any attempt to magnify fine details in the input image will naturally result in amplifying noise as well. For instance, widely used classical linear unsharp mask filters are very sensitive to the noise in the input image (Polesel et al., 2000). Another source of visual degradation is the effect of over-sharpening or the so-called overshoot/undershoot effects (Bilcu and Vehvilainen, 2008). It occurs when the sharpening algorithm tries to sharpen parts of the image which are already in focus, especially edges, which cause unpleasant artifacts in such high contrast areas of the image.
There is a vast literature on different techniques for image sharpening and contrast enhancement. There are many methods based on improving the linear unsharp masking technique. Polesel et al. (2000) are based on the idea of adaptive tuning of the sharpening parameter based on local characteristics of the input image. Kim and Allebach (2005) tried to learn the strength parameter of unsharp mask from an external set of training images. In Bilcu and Vehvilainen (2008), sigma filtering is combined with unsharp masking and a clipping process is added to control the noise and overshoot effects. Another variant of unsharp masking using an exploratory data model has been presented in Deng (2011). Also, a non-linear unsharp mask algorithm is used for mammogram enhancement in Panetta et al. (2011). Methods based on the histogram of input images constitute another category of algorithms for contrast enhancement (Pizer et al., 1987; Arici et al., 2009; Wu, 2011). Although the aforementioned methods are simple to implement, they still produce noise amplification and overshoot artifacts, which deteriorates the quality of the final results.
Anisotropic diffusion (Perona and Malik, 1990; ter Haar Romeny, 1994; Weickert, 1998) and shock filters (Osher and Rudin, 1990) are non-linear scale-space PDE-based approaches widely used for edge enhancement in different image processing applications. Alvarez and Mazorra (1994) and Gilboa et al. (2002, 2004) are among variants of those PDE-based seminal works. PDE-based methods provide a powerful mechanism for edge enhancement. However, they can lack texture and fine detail preservation in the final output images. Bilateral filter (Tomasi and Manduchi, 1998) has been used widely as an edge preserving smoothing filter for different image processing and computer vision tasks (Kornprobst and Tumblin, 2009). In Zhang and Allebach (2008) analyses, adaptive bilateral filter is proposed by introducing an offset to the range kernel definition of the original bilateral filter. This enables the filter to switch its behavior from smoothing to sharpening based on the pixel-wise adjustment of the offset parameter using a training procedure (Zhang and Allebach, 2008). Guided filtering (GF) (He et al., 2013) is another edge preserving filter that is widely used for different image processing tasks (Seo and Milanfar, 2012). In Pham et al. (2012) analyses, a variant of GF based on the same shifting idea in Zhang and Allebach (2008) is used for sharpness enhancement and noise reduction. Also, a weighted version of GF is presented in Li et al. (2015) based on a similar pixel-wise regularization parameter tuning in Farbman et al. (2008) and Min et al. (2014) for detail manipulation. In Zhu and Milanfar (2011), a restoration algorithm for noisy and weakly blurred images based on kernel regression (Takeda et al., 2007) is introduced. In Choudhury and Medioni (2011) and Talebi and Milanfar (2014), non-local multi-scale approaches have been exploited effectively for automatic sharpness enhancement and image editing, respectively. Diffusion maps for edge aware image editing are introduced in Farbman et al. (2010). Graph-based enhancement procedures have been introduced in Kheradmand and Milanfar (2014) and Liu et al. (2015). An image enhancement method based on piecewise linear directional smoothing and sharpening has been proposed in Russo (2007). Local Laplacian filters in Paris et al. (2011) reduce the halo artifacts prevalent in methods based on Laplacian pyramid. Also, a fast realization of this technique has been proposed in Aubry et al. (2014). Although these methods produce good results, there still exists room for performance improvement, especially when the input image is noisy and the goal is to simultaneously remove the noise and boost the sharpness. Also, there is a need for a more general framework to provide a better understanding of the underlying lowpass and highpass filters involved in the sharpening operation.
In this paper, we propose a new sharpening filter based on the data-adaptive Laplacian matrices for noisy and mildly blurred images. This approach is general enough to include any valid construction of smoothing and Laplacian matrices with appropriate definition of the similarity measure (Milanfar, 2013b). We establish the connection between our proposed sharpness enhancement filter and the classical DoG filters widely used in different image manipulation tasks in the literature, which provides a better understanding of the mechanism and the functionality of the underlying parameters in our proposed data-adaptive filter. Ours can be considered as a data derived and noise robust variant of the DoG filter. As such, it can be used in various tasks in which DoG operators are exploited (Marr and Hildreth, 1980; Winnemöller et al., 2006, 2012). We also discuss interesting simpler special cases of our proposed filter. Experimental results demonstrate the effectiveness of our approach in dealing with real examples, namely, the underlying structure-aware mechanism of our proposed filter enables it to enhance the sharpness in the input image while reducing noise amplification and other artifacts, such as halo and false color artifacts.
The rest of the paper is organized as follows. In Section 2, we define the mathematical model and review the classical sharpening method based on the notion of DoG operators. We also introduce our filtering matrix formulation for constructing smoothing and Laplacian matrices. Taking advantage of the spectral properties of smoothing and Laplacian matrices, we define our data-adaptive filter for sharpening. In fact, unlike the classical DoG-based sharpening operator in Winnemöller et al. (2012), we start from a filter design framework based on non-linear smoothing and Laplacian filters. Then, in Section 3, the relationship between the proposed data-adaptive filter and classical DoG operator is set up. However, we give a better understanding of the underlying filtering mechanism of the DoG-based sharpening operator and propose a data-adaptive noise robust variant of the classical DoG-based sharpening. We also discuss special cases of our general procedure for different filtering tasks. Section 4 explains an effective technique for reducing color artifacts. In Section 5, the effect of different parameters is investigated via synthetic examples. Also, experimental results for real image sharpness enhancement are presented compared to some other existing state of the art algorithms. Section 6 draws conclusions and summarizes the paper.
2. Problem Formulation and Proposed Sharpening Filter
In this section, we describe the underlying model and review the idea of classical sharpening filters based on the notion of difference of Gaussians operators. Then, we elaborate on our structure-aware sharpening filter based on data-adaptive smoothing and Laplacian matrices.
2.1. Underlying Model
The degradation process in image formation is usually mathematically modeled as
y is a lexicographically ordered vector representation of the input n × n blurred and noisy image. z is the latent image in vector form, and n is a noise vector consisting of independent and identically distributed zero mean noise with SD ε. Also, A is an n2 × n2 blurring matrix (Hansen et al., 2006). In this paper, we deal with input images that are noisy but not severely blurred. Without deblurring, the goal is to find an appropriate operator F such that is a sharpness enhanced version of the input y without amplifying noise and other edge related artifacts; and without explicitly inverting the blur operator. In fact, we do not assume knowledge of A.
2.2. Classical DoG Operator
The idea of classical DoG filter is that the difference of two Gaussian kernels is able to produce a range of different kernels with various desired frequency responses. In Marr and Hildreth (1980), the standard DoG operator is introduced as an approximation to Laplacian of Gaussian operator for edge detection1
where σ is the SD of the Gaussian function defined as . k > 1 is a positive factor. Also, x and y are spatial coordinates. An extension of the standard DoG filter in Marr and Hildreth (1980) is defined in Winnemöller et al. (2006) as
in which the parameter τ ∈ (0,1) determines the sensitivity of the edge detector (Winnemöller et al., 2006). For instance, for small values of τ, the DoG operator in equation (3) is less sensitive to noise at the expense of losing some edges in the input image. Equation (3) can be rewritten in terms of the standard DoG operator in equation (2) as
Note that the Gaussian operator preserves the average intensity of the input image whereas the average response of the standard DoG operator DoGσ,k(x,y) is zero. Therefore, changing the parameter τ in equation (4) for achieving the desired effects, inadvertently alters the average brightness of the input image2. Using a simple reparameterization, the authors in Winnemöller et al. (2012) describe the following family of sharpening filters
in which Compared to the formulation in equation (3), whereas the average brightness in the input image is retained, the level of sharpening can also be controlled by the parameter β in equation (5). This average intensity-preserving sharpening operator has been derived mostly through a heuristic approach. It is intrinsically linear and not data dependent. In the following subsections, we start from a filter design framework based on the spectral properties of the data-driven Laplacian operators. Then, in Section 3, we elaborate on its relationship with classical DoG-based sharpening operators described here in this section. This helps explain the properties of the DoG-based operators from a filtering point of view. It also provides a powerful structure-aware mechanism for dealing with more complicated real-world images where there is a need to incorporate non-linear filters for better performance.
2.3. Structure-Aware Sharpening Filter
Since any sharpening operator is inherently a highpass filter, it inadvertently leads to amplifying high frequency noise components in the input image and causes artifacts related to over-sharpening high contrast regions in the input image. Therefore, there is a need to incorporate an effective smoothing mechanism in the sharpening operator to alleviate these shortcomings while preserving image structures. Exploiting the existing self similarity in natural images tends to be an effective way to take into account the underlying structure of images when constructing such operators (Buades et al., 2005; Milanfar, 2013b), and thereby reducing the related artifacts. In the following, we first provide our matrix formulation for constructing data-adaptive smoothing and Laplacian matrices as the main building blocks for creating the final sharpening filter. Then, we introduce our data-adaptive sharpening filter.
2.3.1. Kernel Similarity, Smoothing, and Laplacian Matrices
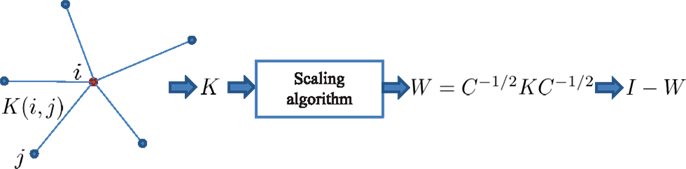
As depicted in Figure 1, the degree of correspondence between a given pixel i and any other pixel j in an image is measured using an appropriate similarity criterion K(i,j). Various definitions of K(i, j) have been used in the literature for this purpose (Tomasi and Manduchi, 1998; Buades et al., 2005; Takeda et al., 2007; Zhang and Allebach, 2008; He et al., 2013). Any symmetric, positive definite kernel is valid in our framework. So, without loss of generality, we use non-local means (NLM) definition (Buades et al., 2005) in which the structure of patches around different pixels are taken into account to compute the similarity score as
where z i and z j are patches around pixels i and j in the image z, and h is a scaling parameter. Putting all these weights together, we build the corresponding affinity (or similarity) matrix K, which is symmetric and non-negative by definition (Kheradmand and Milanfar, 2014). This matrix is then normalized using a fast symmetry-preserving matrix scaling algorithm based on Sinkhorn matrix balancing (Sinkhorn and Knopp, 1967) as
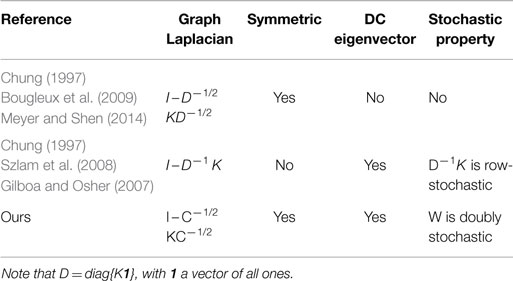
where C−1/2 is the diagonal normalizing matrix derived from matrix balancing algorithm in Knight and Ruiz (2013). The resulting smoothing filter W is a symmetric and doubly stochastic matrix3. Since W is stochastic, its largest eigenvalue would be λ1 = 1 corresponding to the constant eigenvector, which highlights its lowpass filtering properties (Kheradmand and Milanfar, 2014)4. It also preserves the average brightness when applied to an image (Milanfar, 2013b). On the other hand, the Laplacian matrix is defined as I – W with zero eigenvalue corresponding to the constant eigenvector. As such, it returns zero vector when applied to a constant signal. Therefore, it can be considered as a data-adaptive high pass operator. Note that these matrices are evaluated based on the similarity information among different parts of an image and encode the underlying structures of images in an effective manner. A spectral graph theoretic point of view of such matrices has been discussed in Gilboa and Osher (2008), Shuman et al. (2013), and Kheradmand and Milanfar (2014). Specifically, I – W is our proposed definition of graph Laplacian with advantages described in Kheradmand and Milanfar (2014)5. We have summarized the spectral properties of our definition of graph Laplacian in comparison with some other widely used normalized graph Laplacians in Table 1 (Kheradmand and Milanfar, 2014). Note that we are able to define the data-adaptive unsharp mask filter using this definition of Laplacian as I + β (I – W), which essentially adds a weighted highpass filtered version of the input image to itself to highlight the high frequency details. The problem with direct application of this filter is that it suffers from noise amplification and edge artifacts. We discuss how to improve its performance next.
2.3.2. Proposed Data-Adaptive Sharpening Filter
For any effective sharpness enhancement operator, two requirements need to be satisfied: first, noise amplification should be avoided. Second, the level of contrast in the image should be increased without introducing overshoot and gradient reversal (halo) artifacts along edges. To this end, and inspired by DoG filtering idea, we propose a three stage filtering approach as shown in Figure 2. We first apply a non-linear smoothing operator to the input noisy image. This filter is aimed to data adaptively reduce the effect of the noise in the input image while avoiding over-smoothing. The smoothing operation is followed by a data derived unsharp masking operation controlled by the parameter β > 0. Finally, the smoothing filter is applied again in order to further control the effect of amplified noise and overshoot artifacts due to the unsharp mask filter. More formally, having the lowpass smoothing and highpass Laplacian operators at our disposal, we propose the following data-adaptive sharpening filter
where W1 and W2 are constructed from similarity matrices K1 and K2 with scaling parameters h1 and h2, respectively. This provides us with the flexibility to better control the smoothing and sharpening operations. The parameters of the filter need to be tuned for the desired effects. Selection of these parameters will be discussed later. Furthermore, as will be shown in subsequent sections, our proposed filter based on the spectral properties of smoothing and Laplacian matrices exhibits nice connections to the classical DoG operator. Algorithm 1 summarizes different steps of the proposed sharpening algorithm.
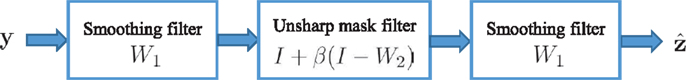
Figure 2. Block diagram of the proposed enhancement algorithm. y is the input image and is the enhanced output image.
3. Interpretation of the Proposed Filter as Data-Adaptive Difference of Smoothing Operator
In this section, we demonstrate the relationship between our proposed noise and edge aware sharpening filter and classical Difference of Gaussians filter. This analysis sheds light on the properties of the proposed filter and gives a better understanding of the underlying parameters. Specifically, we provide a data-adaptive noise and edge aware version of the classical DoG-based operators for use in different applications. Note that the proposed filtering matrix F in equation (8) can be rewritten as
If we define and H(W1, W2) = W1 W2 W1, then G can be considered as double application (diffusion operator) of the filter generated from data-adaptive Gaussian kernel in equation (6). On the other hand, H can be thought of as a cascade of data-dependent Gaussian filters with a larger bandwidth compared to that of G. The difference in bandwidth of the filters G and H is determined by the scaling parameters h1 and h2 in the NLM kernel used for defining the smoothing filters W1 and W2, respectively. In fact, our proposed sharpening filter in equation (9) can be viewed as the data-derived version of the DoG-based filter in equation (5). Here, we use the NLM kernel definition of equation (6) for producing matrices W1 and W2. However, any other edge aware kernel definition in the literature (Tomasi and Manduchi, 1998; Buades et al., 2005; Takeda et al., 2007; Zhang and Allebach, 2008; He et al., 2013) can also be exploited within the proposed filtering scheme.
3.1. Special Cases of the Proposed Sharpening Framework
There is a nice connection with other image filter design paradigms when we consider the simple case where W1 = W2 = W. In this case, the filter F in equation (9) takes the following form
Specifically, with β = 2, equation (10) boils down to F = 3W2 – 2W3. This filter is the data-adaptive version of the classical sharpened (linear) smoothing filer of Kaiser and Hamming (1977). This polynomial function of the symmetric smoothing filter W = VSVT provides a way for improving the spectral properties of the initial filter (W) by manipulating its spectrum λ with a polynomial6 function f (λ) = 3λ2 – 2λ3. This polynomial function is also well-known as the smoothstep function broadly used in computer graphics (Boreskov and Shikin, 2013). Also, note that for different values of the parameter β in equation (10) different band pass filters are generated. As an illustration, if we start from the spectrum of the lowpass symmetric filter W = VSVT constructed from a 91 × 91 image in Figure 3A, the spectral modifications due to the polynomial function f (λ) = (1 + β)λ2 – βλ3 are shown in Figure 3B for different values of the parameter β.
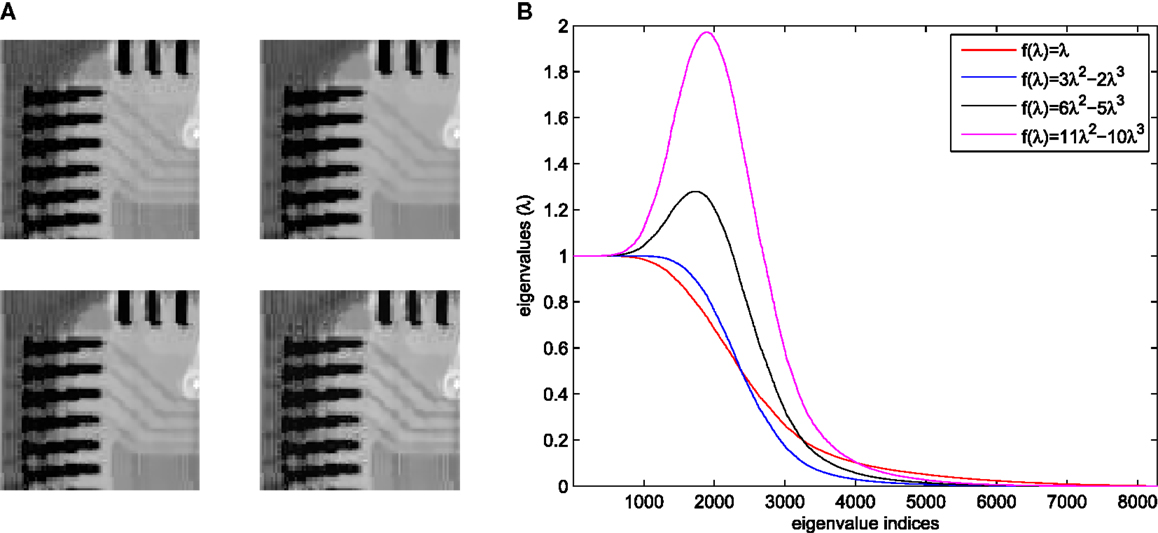
Figure 3. (A) Top left: original 91 × 91 image, (A) Top right: output with f (λ) = 3λ2 – 2λ3, (A) Bottom left: output with f (λ) = 6λ2 – 5λ3, (A) Bottom right: output with f (λ) = 11λ2−10λ3, and (B) The eigenvalues of the smoothing matrix W constructed from (A) Top left along with the eigenvalues corresponding to sharpened smoothing filter 3W2 – 2W3 and band pass filters 6W2 – 5W3 and 11W2 – 10W3.
4. Reducing Color Artifacts
Any sharpness enhancement operator intends to increase the contrast and enhance the details in the input image. Besides high frequency noise components present in the input image, there are other high contrast artifacts in color images usually called false color artifacts (Park et al., 2009; Chang et al., 2013). These sorts of color artifacts are created during the image formation process and are amplified when using a compression scheme like JPEG. Due to their high frequency, and structured nature, they might get amplified by the sharpening operation. This phenomenon causes unpleasant color artifacts in the final image which degrades the visual quality. There exist some recent works trying to alleviate such distortions mostly as post processing algorithms (Choudhury and Medioni, 2009; Rabin et al., 2011; Chang et al., 2013). We do not delve into the details of these methods. Instead, we opt for a simple mechanism within our filtering framework to avoid amplification of color artifacts. It is well-understood that human visual system is less sensitive to fine changes in chroma channels than those details in luminance channel (Chang et al., 2013). In order to reduce these artifacts in the final output, we use a similar strategy to the one in Zhu and Milanfar (2011). Strictly speaking, we convert the input RGB color image to a suitable luminance-chrominance color space, i.e., YCbCr. Then, the kernel similarity coefficients computed for the luminance channel Y can also be used for filtering the chroma channels. This prevents the false color artifacts in color channels from contributing to the filtering coefficients and is effective in reducing such distortions in the final output. However, a less aggressive sharpening is applied to color channels by choosing a smaller value of the sharpening parameter β for chroma channels. This will further avoid amplification of false color artifacts in the sharpened image. Figure 4 illustrates the input JPEG image along with its different channels in YCbCr color space and their enhanced versions using our proposed algorithm7. As can be seen, our proposed sharpening filter is able to reduce the color artifacts while avoiding noise amplification in the final output.

Figure 4. First row: (A) Input JPEG image and its different channels: (B) Luminance Y channel, (C) Chrominance Cb channel, and (D) Chrominance Cr channel. Second row: (E) Output of our sharpening filter and its different enhanced channels: (F) Enhanced luminance Y channel, (G) Enhanced chrominance Cb channel, and (H) Enhanced chrominance Cr channel.
5. Experimental Results
In this section, we demonstrate the performance of the proposed sharpening filter via a number of examples. Also, using synthetic examples the effects of different parameters are investigated. The performance of the proposed method is compared with those of Bilcu and Vehvilainen (2008), Zhu and Milanfar (2011), and He et al. (2013) for real images.
5.1. Investigating the Effect of Different Parameters via Synthetic Examples
In this subsection, we use the test images in Figure 5 to show the effect of different parameters. Slight out-of-focus blur and additive white Gaussian noise are added to test images in Figure 5. For this purpose, each image is convolved with a 3 × 3 disk function. Then, additive white Gaussian noise with SD equal to 5 is added to generate synthetic noisy and blurry examples.
The parameters h1 and h2 play an important role in the lowpass characteristics of the corresponding filters W1 and W2, respectively. These parameters control the level of sharpening and smoothing achieved by the proposed DoG-based filter in equation (9). We adopt h2 = kh1 with a positive factor k > 1 which controls the level of contrast enhancement in the output image. Also, note that the larger the parameter h1 the smoother is the resultant image. In fact, we control the level of noise reduction by the parameter h1. It also helps to avoid the unpleasing halo artifacts in the output image. On the other hand, the parameter β controls the amount of sharpening in the image as it appears in the unsharp mask part of the filter F in equation (8). In Figure 6, we fix the parameters k and β to be equal to 3 and 1.5, respectively. Then, we change the value of the scaling parameter h1. As can be seen, by increasing this parameter the level of smoothing is increased resulting in more noise reduction. On the other hand, increasing the parameter β increases the detail enhancement level of the filter, as depicted in Figure 7. The parameter k provides the algorithm with finer control over the degree of contrast enhancement, as illustrated in Figure 8 with fixed parameters β and h1.

Figure 6. Effect of the parameter h1 via synthetic examples with β = 1.5, k = 3: (A) Input noisy and blurry image, (B) Output of our sharpening algorithm with h1 = 0.8, (C) Output image with h1 = 1.2, and (D) Output image with h1 = 2.

Figure 7. Effect of the parameter β via synthetic examples with h1 = 1.4, k = 3: (A) Input noisy and blurry image, (B) Output of our sharpening algorithm with β = 1.5, (C) Output image with β = 2.5, and (D) Output image with β = 3.5.

Figure 8. Effect of the parameter k via synthetic examples with h1 = 1.4, β = 1.5: (A) Input noisy and blurry image, (B) Output of our sharpening algorithm with k = 2, (C) Output image with k = 3.5, and (D) Output image with k = 6.
In this paper, we rely on subjective evaluation to tune these parameters according to the level of noise and blur in the input image. However, any appropriate metric can be exploited to come up with automatic parameter tuning for the proposed framework. For instance, sharpness metrics in Ferzli and Karam (2009) and Zhu and Milanfar (2009) could be used for automatic parameter selection. However, this topic is outside the scope of this paper.
5.2. Real Sharpening Examples
Next, we verify the performance of our algorithm for dealing with different real scenarios. We compare the quality of images produced by our method with those of other existing algorithms for sharpness and contrast enhancement in Bilcu and Vehvilainen (2008), Zhu and Milanfar (2011), and He et al. (2013). The parameters of all algorithms are set for best subjective performance. Figure 9A depicts the input image with moderate noise and blur. Figure 9E shows the output of our sharpening algorithm compared to those of algorithms (Bilcu and Vehvilainen, 2008; Zhu and Milanfar, 2011; He et al., 2013) in Figures 9B–D. In all experiments the sharpening parameter β is selected to be equal to 0.2 for chroma channels in our proposed algorithm. As can be seen, our algorithm is better able to restore the fine details while controlling the effect of noise compared to the enhancement algorithms in Bilcu and Vehvilainen (2008) and He et al. (2013). Compared to the result of Zhu and Milanfar (2011), our method avoids noise amplification artifacts while reducing the unpleasant halo effects along edges. Figure 10 illustrates another real example with stronger noise and color artifacts. As is evident from the results, the sharpening algorithm in Bilcu and Vehvilainen (2008) produces noise amplification artifacts when the amount of noise is high in the input image. Also, the enhancement method in He et al. (2013) does not effectively perform noise reduction and sharpening operations simultaneously in this case. The sharpening method in Zhu and Milanfar (2011) produces edge artifacts as can be seen in Figure 10D. However, our proposed algorithm is able to effectively sharpen the edges while avoiding noise and edge artifacts and reducing the color distortions, as can be seen in Figure 10E. The example in Figure 11 is even more challenging as it contains more severe noise and moderate blur along with color artifacts, especially across edges. The algorithm in Bilcu and Vehvilainen (2008) does not carefully control the effect of noise in the input image and produces noise-related unpleasant artifacts. Similarly, the enhancement code in He et al. (2013) does not effectively deal with artifacts due to the noise in the input image. The algorithm in Zhu and Milanfar (2011), however, is able to provide a good level of noise reduction and contrast enhancement (Figure 11D). As regards visual quality, our result in Figure 11E is more effective in reducing the color artifacts.

Figure 9. (A) Input image, (B) Output of Bilcu and Vehvilainen (2008), (C) Output of He et al. (2013), (D) Output of Zhu and Milanfar (2011), and (E) Output of our sharpening algorithm with h1 = 0.7, k = 4, β = 1.6.

Figure 10. (A) Input image, (B) Output of Bilcu and Vehvilainen (2008), (C) Output of He et al. (2013), (D) Output of Zhu and Milanfar (2011), and (E) Output of our sharpening algorithm with h1 = 2.7, k = 4, β = 1.7.

Figure 11. (A) Input image, (B) Output of Bilcu and Vehvilainen (2008), (C) Output of He et al. (2013), (D) Output of Zhu and Milanfar (2011), and (E) Output of our sharpening algorithm with h1 = 1.4, k = 4.5, β = 1.2.
5.3. Computational Complexity
For computational efficiency, we compute the similarity coefficients for constructing filtering matrices W1 and W2 using a 9 × 9 search neighborhood around each pixel. Moreover, in equation (6) z i and z j are selected as 5 × 5 patches around pixels i and j. Also, note that our proposed sharpening algorithm is not an iterative procedure. This attribute lessens its computational demands. Table 2 summarizes the running times for un-optimized MATLAB implementations of our algorithm for the RGB color images used in this paper. We have run all the experiments on a 2.8 GHz Intel Core i7 processor. It is also possible to further reduce the computational cost of our proposed filtering algorithm by exploiting integral images (Darbon et al., 2008) for evaluating the kernel similarity coefficients in equation (6). In this paper, however, our focus is on the analysis and performance aspects of the algorithm. Speeding up the implementation will be the next step.
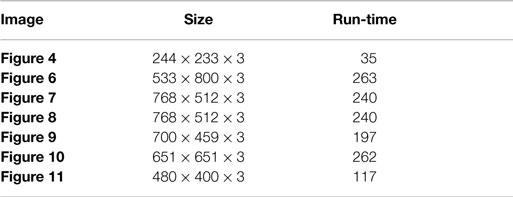
Table 2. Running times in seconds for un-optimized MATLAB implementations of our algorithm for different RGB color images.
6. Conclusion
We have proposed a new sharpening filter based on the spectral properties of data-adaptive smoothing and Laplacian matrices. We have established an analysis framework that explains the relationship between our proposed sharpening procedure and classical DoG filter. This analysis further sheds light on the underlying parameters in our proposed formulation and introduces a data dependent and noise robust version of the DoG operator for use in relevant applications. We have also shown special cases of our more general approach. We verified the effectiveness of the proposed method for sharpening real noisy and blurry images. Automatic parameter tuning and faster implementation will be considered as future works within the proposed framework.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at http://journal.frontiersin.org/article/10.3389/fict.2015.00022
Footnotes
- ^The relationship between DoG operator and the Laplacian of Gaussian has been discussed in the Supplementary Material.
- ^Preserving the average values of the input image is a desired property for filtering tasks in image processing (Milanfar, 2013b).
- ^A matrix with non-negative entries is doubly stochastic if each of its rows and each of its columns sum to 1.
- ^As discussed in Milanfar (2013a), this procedure has performance and filter analysis advantages as compared to traditional normalization D−1K with D a diagonal matrix whose ith diagonal element is the sum of the elements of the ith row in K.
- ^Also, our proposed filtering procedure is general in the sense that other graph based definitions of smoothing and Laplacian matrices can be incorporated within the same framework.
- ^λ’s are the eigenvalues of W as the diagonal elements of the diagonal matrix S. Also, the columns of the orthonormal matrix V are the eigenvectors of W which serve as a data-adaptive basis for filtering purposes (Talebi and Milanfar, 2014).
- ^The input image is from the test examples in http://www.neatimage.com/examples.html.
References
Alvarez, L., and Mazorra, L. (1994). Signal and image restoration using shock filters and anisotropic diffusion. SIAM J. Numer. Anal. 31, 590–605. doi: 10.1137/0731032
Arici, T., Dikbas, S., and Altunbasak, Y. (2009). A histogram modification framework and its application for image contrast enhancement. IEEE Trans. Image Process. 18, 1921–1935. doi:10.1109/TIP.2009.2021548
Aubry, M., Paris, S., Hasinoff, S. W., Kautz, J., and Durand, F. (2014). Fast local Laplacian filters: theory and applications. ACM Trans. Graph. 33, 167. doi:10.1145/2629645
Bilcu, R. C., and Vehvilainen, M. (2008). “Constrained unsharp masking for image enhancement,” in Image and Signal Processing, eds E. Abderrahim, L. Olivier, N. Fathallah and M. Driss (Heidelberg: Springer), 10–19.
Boreskov, A., and Shikin, E. (2013). Computer Graphics: From Pixels to Programmable Graphics Hardware. CRC Press.
Bougleux, S., Elmoataz, A., and Melkemi, M. (2009). Local and nonlocal discrete regularization on weighted graphs for image and mesh processing. Int. J. Comput. Vis. 84, 220–236. doi:10.1007/s11263-008-0159-z
Buades, A., Coll, B., and Morel, J. M. (2005). A review of image denoising algorithms, with a new one. Multiscale Model. Simul. 4, 490–530. doi:10.1137/040616024
Chang, J., Kang, H., and Kang, M. G. (2013). Correction of axial and lateral chromatic aberration with false color filtering. IEEE Trans. Image Process. 22, 1186–1198. doi:10.1109/TIP.2012.2228489
Choudhury, A., and Medioni, G. (2009). “Perceptually motivated automatic color contrast enhancement,” in Computer Vision Workshops (ICCV Workshops), 2009 IEEE 12th International Conference on, (Kyoto: IEEE), 1893–1900.
Choudhury, A., and Medioni, G. (2011). “Perceptually motivated automatic sharpness enhancement using hierarchy of non-local means,” in Computer Vision Workshops (ICCV Workshops), 2011 IEEE International Conference on, (Barcelona: IEEE), 730–737.
Darbon, J., Cunha, A., Chan, T., Osher, S., and Jensen, G. (2008). “Fast nonlocal filtering applied to electron cryomicroscopy,” in Biomedical Imaging: From Nano to Macro, 2008. ISBI 2008. 5th IEEE International Symposium on, (Paris: IEEE), 1331–1334.
Deng, G. (2011). A generalized unsharp masking algorithm. IEEE Trans. Image Process. 20, 1249–1261. doi:10.1109/TIP.2010.2092441
Farbman, Z., Fattal, R., and Lischinski, D. (2010). “Diffusion maps for edge-aware image editing,” in ACM Transactions on Graphics (TOG), Vol. 29 (New York, NY: ACM), 145.
Farbman, Z., Fattal, R., Lischinski, D., and Szeliski, R. (2008). “Edge-preserving decompositions for multi-scale tone and detail manipulation,” in ACM Transactions on Graphics (TOG), Vol. 27 (New York, NY: ACM), 67.
Ferzli, R., and Karam, L. (2009). A no-reference objective image sharpness metric based on the notion of just noticeable blur (JNB). IEEE Trans. Image Process. 18, 717–728. doi:10.1109/TIP.2008.2011760
Gilboa, G., and Osher, S. (2007). Nonlocal linear image regularization and supervised segmentation. Multiscale Model. Simul. 6, 595–630. doi:10.1137/060669358
Gilboa, G., and Osher, S. (2008). Nonlocal operators with applications to image processing. Multiscale Model. Simul. 7, 1005–1028. doi:10.1137/070698592
Gilboa, G., Sochen, N., and Zeevi, Y. (2004). Image enhancement and denoising by complex diffusion processes. IEEE Trans. Pattern Anal. Mach. Intell. 26, 1020–1036. doi:10.1109/TPAMI.2004.47
Gilboa, G., Sochen, N., and Zeevi, Y. Y. (2002). Forward-and-backward diffusion processes for adaptive image enhancement and denoising. IEEE Trans. Image Process. 11, 689–703. doi:10.1109/TIP.2002.800883
Hansen, P. C., Nagy, J. G., and O’Leary, D. P. (2006). Deblurring Images: Matrices, Spectra, and Filtering, 1 Edn. Philadelphia: SIAM.
He, K., Sun, J., and Tang, X. (2013). Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 35, 1397–1409. doi:10.1109/TPAMI.2012.213
Kaiser, J., and Hamming, R. (1977). Sharpening the response of a symmetric nonrecursive filter by multiple use of the same filter. IEEE Trans. Acoust. 25, 415–422. doi:10.1109/TASSP.1977.1162980
Kheradmand, A., and Milanfar, P. (2014). A general framework for regularized, similarity-based image restoration. IEEE Trans. Image Process. 23, 5136–5151. doi:10.1109/TIP.2014.2362059
Kim, S. H., and Allebach, J. P. (2005). Optimal unsharp mask for image sharpening and noise removal. J. Electron. Imaging 14, 023005. doi:10.1117/1.1924510
Knight, P. A., and Ruiz, D. (2013). A fast algorithm for matrix balancing. IMA J. Numer. Anal. 33, 1029–1047. doi:10.1093/imanum/drs019
Kornprobst, P., and Tumblin, J. (2009). Bilateral Filtering: Theory and Applications. Boston – Delft: Now Publishers Inc.
Li, Z., Zheng, J., Zhu, Z., Yao, W., and Wu, S. (2015). Weighted guided image filtering. IEEE Trans. Image Process. 24, 120–129. doi:10.1109/TIP.2014.2371234
Liu, X., Cheung, G., and Wu, X. (2015). Joint denoising and contrast enhancement of images using graph Laplacian operator. Proc. IEEE Int. Conf. Acoust. Speech Signal Process. (Brisbane: IEEE), 2274–2278. doi:10.1109/ICASSP.2015.7178376
Marr, D., and Hildreth, E. (1980). Theory of edge detection. Proc. R. Soc. Lond. B Biol. Sci. 207, 187–217. doi:10.1098/rspb.1980.0020
Meyer, F. G., and Shen, X. (2014). Perturbation of the eigenvectors of the graph Laplacian: application to image denoising. Appl. Comput. Harmon. Anal. 36, 326–334. doi:10.1016/j.acha.2013.06.004
Milanfar, P. (2013a). Symmetrizing smoothing filters. SIAM J. Imaging Sci. 6, 263–284. doi:10.1137/120875843
Milanfar, P. (2013b). A tour of modern image filtering: New insights and methods, both practical and theoretical. IEEE Signal Process. Mag. 30, 106–128. doi:10.1109/MSP.2011.2179329
Min, D., Choi, S., Lu, J., Ham, B., Sohn, K., and Do, M. (2014). Fast global image smoothing based on weighted least squares. IEEE Trans. Image Process. 23, 5638–5653. doi:10.1109/TIP.2014.2366600
Osher, S., and Rudin, L. I. (1990). Feature-oriented image enhancement using shock filters. SIAM J. Numer. Anal. 27, 919–940. doi:10.1137/0727053
Panetta, K., Zhou, Y., Agaian, S., and Jia, H. (2011). Nonlinear unsharp masking for mammogram enhancement. IEEE Trans. Inf. Technol. Biomed. 15, 918–928. doi:10.1109/TITB.2011.2164259
Paris, S., Hasinoff, S. W., and Kautz, J. (2011). Local Laplacian Filters: Edge-Aware Image Processing With a Laplacian Pyramid. New York, NY: ACM, 68.
Park, S. H., Kim, H. S., Lansel, S., Parmar, M., and Wandell, B. (2009). “A case for denoising before demosaicking color filter array data,” in Signals, Systems and Computers, 2009 Conference Record of the Forty-Third Asilomar Conference on, (Pacific Grove: IEEE), 860–864.
Perona, P., and Malik, J. (1990). Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 12, 629–639. doi:10.1109/34.56205
Pham, C. C., Ha, S. V. U., and Jeon, J. W. (2012). “Adaptive guided image filtering for sharpness enhancement and noise reduction,” in Advances in Image and Video Technology (Heidelberg: Springer), 323–334.
Pizer, S. M., Amburn, E. P., Austin, J. D., Cromartie, R., Geselowitz, A., Greer, T., et al. (1987). Adaptive histogram equalization and its variations. Comput. Vision Graph. Image Process. 39, 355–368. doi:10.1016/S0734-189X(87)80186-X
Polesel, A., Ramponi, G., and Mathews, V. (2000). Image enhancement via adaptive unsharp masking. IEEE Trans. Image Process. 9, 505–510. doi:10.1109/83.826787
Rabin, J., Delon, J., and Gousseau, Y. (2011). Removing artefacts from color and contrast modifications. IEEE Trans. Image Process. 20, 3073–3085. doi:10.1109/TIP.2011.2142318
Russo, F. (2007). An image-enhancement system based on noise estimation. IEEE Trans. Instrum. Meas. 56, 1435–1442. doi:10.1109/TIM.2007.899887
Seo, H.-J., and Milanfar, P. (2012). Robust flash denoising/deblurring by iterative guided filtering. EURASIP J. Adv. Signal Process. 2012, 1–19. doi:10.1186/1687-6180-2012-3
Shuman, D., Narang, S., Frossard, P., Ortega, A., and Vandergheynst, P. (2013). The emerging field of signal processing on graphs: extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 30, 83–98. doi:10.1109/MSP.2012.2235192
Sinkhorn, R., and Knopp, P. (1967). Concerning nonnegative matrices and doubly stochastic matrices. Pacific J. Math. 21, 343–348. doi:10.2140/pjm.1967.21.343
Szlam, A. D., Maggioni, M., and Coifman, R. R. (2008). Regularization on graphs with function-adapted diffusion processes. J. Mach. Learn. Res. 9, 1711–1739. doi:10.1145/1390681.1442788
Takeda, H., Farsiu, S., and Milanfar, P. (2007). Kernel regression for image processing and reconstruction. IEEE Trans. Image Process. 16, 349–366. doi:10.1109/TIP.2006.888330
Talebi, H., and Milanfar, P. (2014). Nonlocal image editing. IEEE Trans. Image Process. 23, 4460–4473. doi:10.1109/TIP.2014.2348870
ter Haar Romeny, B. M. (1994). Geometry-Driven Diffusion in Computer Vision. Norwell, MA: Kluwer Academic Publishers.
Tomasi, C., and Manduchi, R. (1998). “Bilateral filtering for gray and color images,” in Computer Vision, 1998. Sixth International Conference on, (Bombay: IEEE), 839–846.
Winnemöller, H., Kyprianidis, J. E., and Olsen, S. C. (2012). XDoG: an extended difference-of-Gaussians compendium including advanced image stylization. Comput. Graph. 36, 740–753. doi:10.1016/j.cag.2012.03.004
Winnemöller, H., Olsen, S. C., and Gooch, B. (2006). “Real-time video abstraction,” in ACM Transactions on Graphics (TOG), Vol. 25 (New York, NY: ACM), 1221–1226.
Wu, X. (2011). A linear programming approach for optimal contrast-tone mapping. IEEE Trans. Image Process. 20, 1262–1272. doi:10.1109/TIP.2010.2092438
Zhang, B., and Allebach, J. (2008). Adaptive bilateral filter for sharpness enhancement and noise removal. IEEE Trans. Image Process. 17, 664–678. doi:10.1109/TIP.2008.919949
Zhu, X., and Milanfar, P. (2009). “A no-reference sharpness metric sensitive to blur and noise,” in Quality of Multimedia Experience, 2009. QoMEx 2009. International Workshop on, (San Diego, CA: IEEE), 64–69.
Keywords: similarity matrix, sharpening, data-adaptive filtering, Laplacian matrix, DoG
Citation: Kheradmand A and Milanfar P (2015) Non-linear structure-aware image sharpening with difference of smoothing operators. Front. ICT 2:22. doi: 10.3389/fict.2015.00022
Received: 06 July 2015; Accepted: 09 October 2015;
Published: 27 October 2015
Edited by:
Kaleem Siddiqi, McGill University, CanadaReviewed by:
Stephane Coulombe, École de technologie supérieure, CanadaJing Yuan, Western University, Canada
Copyright: © 2015 Kheradmand and Milanfar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Amin Kheradmand, YW1pbmtoQHNvZS51Y3NjLmVkdQ==;
Peyman Milanfar, cGV5bWFuLm1pbGFuZmFyQGdtYWlsLmNvbQ==
 Amin Kheradmand
Amin Kheradmand Peyman Milanfar
Peyman Milanfar