Energetic Cost of Superadiabatic Quantum Computation

1. Introduction

Shortcuts to adiabatic passage (Demirplak and Rice, 2003, 2005; Berry, 2009; Torrontegui et al., 2013) provide a remarkable mechanism for speeding up quantum tasks, which can be achieved through the use of a counter-diabatic assistant driving. These techniques have been introduced to mimic the transitionless adiabatic dynamics, but with the usual constraint on the adiabatic runtime lifted. Transitionless quantum driving has been applied to a number of quantum information protocols, such as population transfer (Chen et al., 2014a; Lu et al., 2014a) and entanglement generation (Chen et al., 2014b, 2015a,b; Lu et al., 2014b). In the context of many-body systems, realizable settings have been investigated for assisted evolutions in quantum critical phenomena (del Campo et al., 2012; del Campo, 2013; Saberi et al., 2014). More recently, counter-diabatic approaches have been proposed for fast implementation of individual unitaries in quantum circuits, leading to universal superadiabatic schemes of quantum computing (QC) via local Hamiltonians (Santos and Sarandy, 2015; Santos et al., 2016). Such methods may be potentially relevant to accelerating the implementation of n-qubit controlled gates in digitized proposals of adiabatic quantum computing [see Kieferová and Wiebe (2014), Martinis and Geller (2014), Barends et al. (2015), and Hen (2015)].

The superadiabatic speedup is intrinsically connected with an increase of the energy resources demanded by the quantum computer (Santos and Sarandy, 2015; Santos et al., 2016), which in turn implies a rather versatile computational cost that is controlled by the energetic capacity available to the physical apparatus. Here, we show that this energy–time complementarity can be exploited in quantum information processing. First, we consider controlled evolutions (CE) as a mechanism to implement superadiabatic universal QC (Santos and Sarandy, 2015), which generalizes the original adiabatic approach introduced in Hen (2015). We then show that, within the superadiabatic scenario, the energetic cost can be minimized by replacing the deterministic realization of quantum gates for probabilistic implementations based on a probability distribution of a binary random variable described by an angle parameter. By doing so, the energy expense can be minimized by adjusting the probability distribution, provided the choice of the evolution time of the computational process. Second, we analyze the effects of the energy–time complementarity in analog quantum search (Grover, 1997), where the oracular approach designed by the local adiabatic Grover algorithm is known to be optimal (van Dam et al., 2001; Roland and Cerf, 2002). In this case, we show that the superadiabatic approach naturally requires an unphysical non-oracular counter-diabatic Hamiltonian, with the energy–time complexity equivalent to non-oracular adiabatic implementations.

The paper is organized as follows. In Section 2, we describe the adiabatic implementation of quantum gates via CE and several adiabatic quantum search approaches. We then provide their superadiabatic versions and introduce the metric for energetic cost used in our work. In Section 3, we investigate the energy complexity of the superadiabatic realizations of both quantum gates via CE and analog quantum search. In particular, we consider the properties of the probabilistic model of QC through CE and the consequences of the energy–time complementarity for the search problem. In Section 4, we present our conclusions and future perspectives.

2. Materials and Methods

Our aim in this Section is to discuss adiabatic implementations of QC, their superadiabatic generalizations, and the energetic cost measure adopted in this work.

2.1. Quantum Gates by Adiabatic Controlled Evolutions

Let us begin by using adiabatic CE (Hen, 2015) to implement n-controlled gates (Santos and Sarandy, 2015). To this end, we will consider the adiabatic evolution of a composite system 𝒯 𝒜 associated with a Hilbert space ℋ_𝒯 ⊗ ℋ_𝒜, where 𝒯 denotes a target subsystem containing n + 1 qubits and 𝒜 denotes an auxiliary subsystem containing a single qubit. We will use the first n qubits of 𝒯 as the control register of the n-controlled gate, while the last qubit will play the role of its target register. Then, a rotation of the target qubit of an angle ϕ around a direction $\widehat{n}$ in the Bloch sphere will be performed when the state of the control register is |11⋯ 1⟩. We will adopt here the decimal representation |11⋯ 1⟩ ≡ |N − 1⟩, with N = 2ⁿ. An n-controlled rotation over a single qubit can be adibatically implemented by preparing the auxiliary qubit in the initial state |0⟩, with the adiabatic Hamiltonian given by (Santos and Sarandy, 2015)

$H\left(s\right)=\left[\mathrm{𝟙}-P_{N-1,n_{-}}\right]\otimes H_0\left(s\right)+P_{N-1,n_{-}}\otimes H_{\mathit{\varphi }}\left(s\right),$ (1)

where $P_{k,n_{\pm }}=\mathrm{|}k\mathrm{⟩}\mathrm{⟨}k\mathrm{|}\otimes \mathrm{|}{\widehat{n}}_{\pm }\mathrm{⟩}\mathrm{⟨}{\widehat{n}}_{\pm }\mathrm{|}$ is the set of all orthogonal projectors on the subspace 𝒯 and $\mathrm{|}{\widehat{n}}_{\pm }\mathrm{⟩}\mathrm{⟨}{\widehat{n}}_{\pm }\mathrm{|}=1∕\mathrm{2(}\mathrm{𝟙}\pm \widehat{n}\cdot \overrightarrow{\mathrm{\sigma }}\mathrm{)}$, with $\overrightarrow{\mathrm{\sigma }}=\left({\mathrm{\sigma }}_x,{\mathrm{\sigma }}_y,{\mathrm{\sigma }}_z\right)$. The Hamiltonians H₀(s) and H_ϕ(s) are given by

$H_{\mathrm{\xi }}\left(s\right)=-\hslash \mathrm{\omega }\left\{{\mathrm{\sigma }}_z\cos \mathit{\theta }\left(s\right)+\sin \mathit{\theta }\left(s\right)\left[{\mathrm{\sigma }}_x\cos \mathrm{\xi }+{\mathrm{\sigma }}_y\sin \mathrm{\xi }\right]\right\},$ (2)

where θ (s) = θ₀s, θ₀ is a constant angle, ξ = {0, ϕ}, and s denotes the normalized time s = t/τ, with τ the total evolution time. The system is prepared in the initial state |Ψ(0)⟩ = |ψ_n⟩ ⊗ |0⟩, where

$\mathrm{|}{\mathrm{\psi }}_n\mathrm{⟩}={\displaystyle \sum _{m=0}^{N-1}}{\displaystyle \sum _{ϵ=\pm }}{\mathrm{\gamma }}_{m,\mathrm{ϵ}}\mathrm{|}m,{\widehat{n}}_{\mathrm{ϵ}}\mathrm{⟩}.$ (3)

Then, by adiabatic evolution, the system will evolve to the final state |Ψ(1)⟩ given by

$\begin{array}{l}\hfill \mathrm{|}\mathrm{\Psi }\left(1\right)\mathrm{⟩}=\left[\left(\mathrm{𝟙}-P_{N-1,{\widehat{n}}_{-}}\right)\left|{\mathrm{\psi }}_n\right.⟩\right]\otimes \mathrm{|}{E}_0^0\left(1\right)\mathrm{⟩}+P_{N-1,{\widehat{n}}_{-}}\left|{\mathrm{\psi }}_n\right.⟩\otimes \mathrm{|}{E}_{\mathit{\varphi }}^0\left(1\right)\mathrm{⟩},\end{array}$ (4)

where $\mathrm{|}{E}_{\mathrm{\xi }}^0\left(1\right)\mathrm{⟩}=\cos \left({\mathit{\theta }}_0∕2\right)\left|0\right.⟩+e^{i\mathrm{\xi }}\sin \left({\mathit{\theta }}_0∕2\right)\left|1\right.⟩$ is the ground state of H_ξ(1). Then, equivalently, we can write

$\mathrm{|}\text{Ψ}\left(1\right)\mathrm{⟩}=\cos \left({\mathit{\theta }}_0∕2\right)\left|{\mathrm{\psi }}_n\right.⟩\otimes \mathrm{|0}⟩+\sin \left({\mathit{\theta }}_0∕2\right)|{\mathrm{\psi }}_n^{\text{rot}}⟩\otimes \left|1\right.⟩,$ (5)

with

$\begin{array}{l}\hfill \mathrm{|}{\mathrm{\psi }}_n^{\text{rot}}\mathrm{⟩}={\displaystyle \sum _{k=0}^{N-2}}{\displaystyle \sum _{ϵ=\pm }}{\mathrm{\gamma }}_{k,\mathrm{ϵ}}\left|k,{\widehat{n}}_{\mathrm{ϵ}}\right.⟩+\left|N-1\right.⟩\otimes \mathrm{[}{\mathrm{\gamma }}_{N-1,+}\left|{\widehat{n}}_{+}\right.⟩+e^{i\mathit{\varphi }}{\mathrm{\gamma }}_{N-1,-}\left|{\widehat{n}}_{-}\right.⟩\mathrm{]}.\end{array}$ (6)

The rotated state $\mathrm{|}{\mathrm{\psi }}_n^{\text{rot}}⟩$ is the target of the n-controlled gate. However, note that |Ψ(1)⟩ in equation (5) is an entangled state. Thus, a measurement must be performed on the auxiliary system, where the action of the gate will be considered successful if 𝒜 is measured in the state |1⟩, which occurs with probability sin² (θ₀/2). On the other hand, if the outcome of a measurement on 𝒜 yields |0⟩, the adiabatic evolution should be restarted through the Hamiltonian in equation (1), as the state of the system is projected onto the initial state |Ψ(0)⟩. Naturally, by choosing θ₀ = π, we deterministically ensure the success of the computation. However, as we will show, deterministic evolutions may demand more energy resources than probabilistic processes when transitionless drivings are considered. In particular, observe also that the scheme presented here allows for the implementation of arbitrary n-controlled gates, which lead to versatile sets of universal gates, e.g., single qubit rotations and controlled-NOT operations (Nielsen and Chuang, 2000).

2.2. Adiabatic Quantum Search

Instead of adiabatic implementations of quantum circuits, we can also consider the original approach of adiabatic QC (Farhi et al., 2001), where a single annealing process is performed using energy penalties attributed to quantum states that violate the solutions of an optimization problem. Here, we employ this method to analyze three possible adiabatic implementations of quantum search over an unstructured list. An adiabatic QC approach for the quantum search through Grover’s algorithm (Grover, 1997) was first proposed in Farhi et al. (2000) and improved by using local adiabaticity (van Dam et al., 2001; Roland and Cerf, 2002), where the adiabatic evolution is required for each local time interval, instead of being globally applied as in the original proposal. In both cases, the search for a marked element in an unstructured list of N = 2ⁿ elements (labeled by n qubits) can be achieved by employing a Hamiltonian of the form

$H_0\left(s\right)=f\left(s\right)(\mathrm{𝟙}-|+⟩⟨+|)+g\left(s\right)(\mathrm{𝟙}-|m⟩⟨m|),$ (7)

where |m⟩ is the marked state, s is the normalized time (0 ≤ s ≤ 1), $\mathrm{|}+\mathrm{⟩}=1∕\sqrt{N}{\sum }_{i=0}^{N-1}\mathrm{|}i\mathrm{⟩}$, and f (0) = g(1) = 1 and f (1) = g(0) = 0. The eigenspectrum of this Hamiltonian can be exactly derived [see Das et al. (2003) and Orus and Latorre (2004)]. In particular, the two lowest eigenstates can be written as

$|E_{\pm }\left(s\right)⟩={\mathcal{N}}_{\pm }\left(s\right)\left[|m⟩+b_{\pm }\left(s\right)|\mathit{\varphi }⟩\right],$ (8)

where the normalization constant is ${\mathcal{N}}_{\pm }\left(s\right)=1∕\sqrt{1+\left(N-1\right)b_{\pm }{\left(s\right)}^2}$, $\mathrm{|}\mathit{\varphi }\mathrm{⟩}={\sum }_{i\mathrm{\ne }m}|i\mathrm{⟩}$, and

$b_{\pm }\left(s\right)=1-\frac{E_{\pm }\left(s\right)}{f\left(s\right)\overline{N}},$ (9)

with $\overline{N}=1-1∕N$, and the corresponding energies E_±(s) given by

$E_{\pm }\left(s\right)=\frac{f\left(s\right)+g\left(s\right)\pm \sqrt{{\left[f\left(s\right)+g\left(s\right)\right]}^2-4f\left(s\right)g\left(s\right)\overline{N}}}{2}.$ (10)

The other higher-energy eigenstates form an (N − 2)-fold degenerate eigenspace, whose energy is given by

$E_{\text{deg}}=\left[f\left(s\right)+g\left(s\right)\right].$ (11)

In order to explicitly provide the eigenstates $\mathrm{|}{E}_{\text{deg}}^k⟩$ (k = 1, ⋯ , N − 2) associated with the eigenenergy E_deg, we write

$\mathrm{|}{E}_{\text{deg}}^k\mathrm{⟩}={\displaystyle \sum _{n=0}^{N-1}}{c}_n^k\mathrm{|}n\mathrm{⟩}.$ (12)

Then, from the eigenvalue equation for H₀(s), it directly follows that the set $\left\{c_n^k\right\}$ is just required to satisfy the constraints ${\sum }_{n=0}^{N-1}{c}_n^k=0$ and $c_m^k=0$. As a consequence, the states $\mathrm{|}{E}_{\text{deg}}^k⟩$ can be suitably chosen as time-independent vectors.

By imposing a local adiabatic evolution (van Dam et al., 2001; Roland and Cerf, 2002), i.e., by requiring adiabaticity at each infinitesimal time interval, the runtime is minimized for the path [see also Kieferová and Wiebe (2014)]

$\begin{array}{l}\hfill \begin{array}{r}f\left(s\right)=1-g\left(s\right),g\left(s\right)=\frac{\sqrt{N-1}-\tan \left[\text{arctan}\left(\sqrt{N-1}\right)\left(1-2s\right)\right]}{2\sqrt{N-1}}.\end{array}\end{array}$ (13)

This results in a quadratic speedup over the classical search, i.e., we obtain the time complexity $O\left(\sqrt{N}\right)$ expected by the Grover quantum search (van Dam et al., 2001; Roland and Cerf, 2002).

It is possible to reduce the time complexity of the Grover quantum search by transferring the algorithmic cost to other physical resources. The second implementation of the adiabatic Grover search considered here has been introduced in Das et al. (2003) and Wen and Qiu (2008). It is also based on the Hamiltonian in equation (7) to perform the evolution, but requiring that the functions f (s) and g(s) satisfy

$\begin{array}{l}\hfill f\left(s\right)=1-s+\sqrt{N}\left(1-s\right)s,\end{array}$ (14)

$\begin{array}{l}\hfill g\left(s\right)=s+\sqrt{N}\left(1-s\right)s.\end{array}$ (15)

This implementation achieves the solution at constant time complexity O(1). As is apparent from equations (14) to (15), the original time resource has been transferred to the coupling strengths f (s) and g(s) and, as discussed in detail in the next Section, will be reflected in the energy scaling required by the system.

The two previous versions of the adiabatic Grover’s algorithm are based on oracular Hamiltonians, which we take here to be operators able to recognize the correct answer of a problem (Nielsen and Chuang, 2000). This is indeed the case if one chooses a Hamiltonian composed of an operator O_m in the form O_m = 𝟙 − |m⟩ ⟨m|. The action of O_m in the computational basis {|i⟩} is

$O_m\mathrm{|}i\mathrm{⟩}=(\mathrm{𝟙}-|m⟩⟨m|)\mathrm{|}i\mathrm{⟩}=\left\{\begin{array}{cc}0\hfill & \left(i=m\right),\hfill \\ \mathrm{|}i⟩\hfill & \left(i\ne m\right),\hfill \end{array}\right.$ (16)

so that this operator recognizes the marked state, providing no hint about its identity if acting upon any other state. Adiabatic versions of the quantum search have also been proposed via non-oracular Hamiltonians. Our third implementation of Grover’s algorithm is based on the non-linear non-oracular (NLNO) Hamiltonian proposed in Wen et al. (2009). In this work, the time-dependent Hamiltonian in equation (7) is replaced for

$\begin{array}{l}\hfill \begin{array}{r}{H}_0\left(s\right)=f\left(s\right)(\mathrm{𝟙}-|+⟩⟨+|)+g\left(s\right)(\mathrm{𝟙}-|m⟩⟨m|)+h\left(s\right)(|+⟩⟨m|+|m⟩⟨+|),\end{array}\end{array}$ (17)

where h(0) = h(1) = 0. The Hamiltonian in equation (17) contains an operator ${\overline{O}}_m=\mathrm{|}+\mathrm{⟩}⟨m|+|m⟩⟨+|$. The action of ${\overline{O}}_m$ in the computational basis {|i⟩} is

${\overline{O}}_m\mathrm{|}i\mathrm{⟩}=(|+⟩⟨m|+|m⟩⟨+\mathrm{|})\mathrm{|}i\mathrm{⟩}=\left\{\begin{array}{cc}\frac{1}{\sqrt{N}}\mathrm{|}m\mathrm{⟩}+\mathrm{|}+\mathrm{⟩}\hfill & \left(i=m\right),\hfill \\ \frac{1}{\sqrt{N}}\mathrm{|}m\mathrm{⟩}\hfill & \left(i\ne m\right).\hfill \end{array}\right.$ (18)

Observe that equation (18) implies that ${\overline{O}}_m$ cannot exactly recognize a marked element, even though it could effectively recover the marked state for N ≫ 1 with a single operation over the uniform superposition provided by the state |+⟩. Naturally, the non-oracular form of the Hamiltonian involves all the individual computational states, requiring, therefore, much more than the capacity of the Hamiltonian to recognize the marked element. This is an obviously artificial approach, whose discussion here is kept just for comparison with the superadiabatic scenario. Assuming a restricted feasibility of such a Hamiltonian, we proceed by looking at its eigenspectrum. The ground and first excited states have the same structure as in equation (8), with

$b_{\pm }\left(s\right)=\frac{\overline{N}f\left(s\right)+\frac{2h\left(s\right)}{\sqrt{N}}-E_{\pm }\left(s\right)}{\overline{N}\left[f\left(s\right)-h\left(s\right)\sqrt{N}\right]}.$ (19)

The two lowest energy levels are given by

$\begin{array}{l}{E}_{\pm }\left(s\right)=\frac{1}{2}\left\{f\left(s\right)+g\left(s\right)+\frac{2h\left(s\right)}{\sqrt{N}}\right.\hfill \\ \pm \left.\sqrt{\begin{array}{c}{\left[f\left(s\right)+g\left(s\right)\right]}^2-4f\left(s\right)g\left(s\right)\overline{N}+4h^2\left(s\right)-\frac{4h\left(s\right)}{\sqrt{N}}\left[f\left(s\right)+g\left(s\right)\right]\end{array}}\right\}.\end{array}$ (20)

As before, the higher-energy states form an (N − 2)-fold degenerate subspace, with energy given by f(s) + g(s). As shown in Wen et al. (2009), this formulation also shows constant time complexity O(1), which can be obtained by choosing a suitable interpolation, such as

$f\left(s\right)=1-s,g\left(s\right)=s,h\left(s\right)=s\left(1-s\right).$ (21)

2.3. Speeding up Adiabaticity through Superadiabatic Evolutions

The performance of adiabatic QC is dictated by a long total evolution time compared to the inverse of a power of the energy gap (Messiah, 1962; Teufel, 2003; Sarandy et al., 2004; Jansen et al., 2007). However, the adiabatic evolution can be sped up through shortcuts to adiabaticity via counter-diabatic Hamiltonians (Demirplak and Rice, 2003, 2005; Berry, 2009). The fundamental idea underlying these shortcuts to adiabaticity is to add a new contribution H_CD(t), called counter-diabatic Hamiltonian, to the original adiabatic Hamiltonian H(t). This term is constructed such that it allows the mimicking of the adiabatic evolution, however, without any constraint on the total time of evolution. The total composite Hamiltonian is

$H_{\text{SA}}\left(t\right)=H\left(t\right)+H_{\text{CD}}\left(t\right),$ (22)

which is called superadiabatic Hamiltonian. In particular, it is possible to show that the counter-diabatic term reads (Berry, 2009).

$H_{\text{CD}}\left(t\right)=\mathrm{i\hslash }{\sum }_n\left|\dot{n}\left(t\right)\right.⟩\left.⟨n\left(t\right)\right|+⟨\dot{n}\left(t\right)|n\left(t\right)⟩\left|n\left(t\right)\right.⟩\left.⟨n\left(t\right)\right|,$ (23)

where |n(t)⟩ is the eigenstate of H(t) associated with the energy E_n(t). The goal of the counter-diabatic term H_CD(t) in the Hamiltonian H_SA(t) is exactly to eliminate the diabatic contributions of H(t). Thus, if the system is initially prepared in the ground state of H(0), then the system will deterministically evolve to the instantaneous ground state of the Hamiltonian H(t) with no constraints over the evolution time. Note that, in general, one would need to be able to explicitly calculate all the eigenstates of H(t) to derive a shortcut to adiabaticity using the counter-diabatic driving. However, this may not be a hard requirement in the case of superadiabatic versions of circuit implementations, where one-qubit rotations and two-qubit entangling gates are enough to achieve QC universality (Nielsen and Chuang, 2000). In particular, as we shall see for this case, H_CD(t) can be realized through a simple time-independent operator.

2.4. Energetic Cost of Quantum Evolutions

To quantify the expense of energy in a quantum evolution driven by a Hamiltonian H(t), we adopt as the cost measure the average norm of H(t) computed for a total time of evolution τ. This yields (Kieferová and Wiebe, 2014; Santos and Sarandy, 2015; Zheng et al., 2015; Santos et al., 2016)

$\Sigma \left(\mathrm{\tau }\right)=\frac{1}{\mathrm{\tau }}{\int }_0^{\mathrm{\tau }}∥H\left(t\right)∥\mathit{dt}={\int }_0^1∥H\left(s\right)∥\mathit{ds},$ (24)

where s = t/τ is the parameterized time and the norm here is defined by the Frobenius norm (Hilbert–Schmidt norm) $∥A∥=\sqrt{\text{Tr}\left[A^{†}A\right]}$. Naturally, other norms can be adopted as, for instance, the spectral norm ${∥A∥}_2=\sqrt{{\mathrm{\lambda }}_{\text{max}}\left[A^{†}A\right]}$, where λ_max denotes the maximum eigenvalue of [A^† A]. For the Hamiltonians investigated in this work, these norms will imply into a cost simply related by a constant D^1/2, with D denoting the dimension of corresponding the Hilbert space. The Frobenius norm as well as arbitrary superadiabatic evolutions with total evolution time τ, the energetic cost can be written as

$\begin{array}{l}\hfill \begin{array}{r}{\Sigma }_{\mathit{SA}}\left(\mathrm{\tau }\right)=\frac{1}{\mathrm{\tau }}{\int }_0^{\mathrm{\tau }}\sqrt{\text{Tr}\left[H_{\mathit{SA}}^2\left(t\right)\right]}\mathit{dt}=\frac{1}{\mathrm{\tau }}{\int }_0^{\mathrm{\tau }}\sqrt{\text{Tr}\left[H^2\left(t\right)+H_{\mathit{CD}}^2\left(t\right)\right]}\mathit{dt},\end{array}\end{array}$ (25)

where we have used that Tr({H(t), H_CD(t)}) = 0 (Santos and Sarandy, 2015). This explicitly shows that a superadiabatic evolution has an energetic cost larger than its corresponding adiabatic evolution. By evaluating the trace in equation (25), we obtain

${\Sigma }_{\text{SA}}\left(\mathrm{\tau }\right)={\int }_0^1\sqrt{{\displaystyle \sum _m}\left[E_m^2\left(s\right)+{\hslash }^2\frac{{\mathrm{\mu }}_m\left(s\right)}{{\mathrm{\tau }}^2}\right]}\mathit{ds},$ (26)

where μ_m(s) = ⟨∂_sm(s)|∂_sm(s)⟩ − |⟨m(s)|∂_sm(s)⟩|² and {E_m(s)} is the energy spectrum of the adiabatic Hamiltonian H(t), with {|m(s)⟩} denoting its eigenbasis. Notice that the adiabatic limit is recovered when taking τ → ∞. Thus, the speedup obtained by the superadiabatic dynamics is limited by the energetic cost of the evolution. Indeed, this energy–time complementarity can be formally discussed through the quantum speed limit (Deffner and Lutz, 2013), which suggests that the superadiabatic evolution time is compatible with arbitrarily short time intervals (implying into corresponding arbitrarily large energies) (Santos and Sarandy, 2015), while the adiabatic evolution time obeys the lower bound τ_Ad ∝ 1/ωⁿ, with ω associated with the energy gap and n ∈ ℕ⁺ (Messiah, 1962; Teufel, 2003; Sarandy et al., 2004; Jansen et al., 2007).

3. Results

We now consider the performance of adiabatic and superadiabatic quantum computation, focusing on their time–energy complexity. This will be investigated both for the universal model of superadiabatic controlled gates and for the superadiabatic implementations of the Grover search.

3.1. Quantum Gates by Superadiabatic Controlled Evolutions

Let us begin by discussing the superadiabatic model of universal QC via CE implemented by shortcuts to adiabaticity (Santos and Sarandy, 2015). To this end, let us first write the complete set of eigenstates of H(t) as (Santos and Sarandy, 2015)

$\begin{array}{l}\hfill \mathrm{|}{E}_{0m}^{\mathrm{ϵ}k}\left(s\right)⟩=\mathrm{|}m,{\widehat{n}}_{\mathrm{ϵ}}\otimes \mathrm{|}{E}_0^k\left(s\right)⟩,\end{array}$ (27)

$\begin{array}{l}\hfill \mathrm{|}{E}_{0\left(N-1\right)}^{+k}\left(s\right)\mathrm{⟩}=\mathrm{|}N-1,{\widehat{n}}_{+}\otimes \mathrm{|}{E}_0^k\left(s\right)\mathrm{⟩},\end{array}$ (28)

$\begin{array}{l}\hfill \mathrm{|}{E}_{\mathit{\varphi }\left(N-1\right)}^{-k}\left(s\right)\mathrm{⟩}=\mathrm{|}N-1,{\widehat{n}}_{-}\otimes \mathrm{|}{E}_{\mathit{\varphi }}^k\left(s\right)\mathrm{⟩},\end{array}$ (29)

where m ∈ {0, ⋯ , N − 2}, ϵ, k ∈ { ± }, and

$\begin{array}{l}\hfill \mathrm{|}{E}_{\mathrm{\xi }}^{+}\left(s\right)\mathrm{⟩}=-\sin \frac{{\mathit{\theta }}_{0}s}{2}\left|0\right.⟩+e^{i\mathrm{\xi }}\cos \frac{{\mathit{\theta }}_{0}s}{2}\left|1\right.⟩,\end{array}$ (30)

$\begin{array}{l}\hfill \mathrm{|}{E}_{\mathrm{\xi }}^{-}\left(s\right)\mathrm{⟩}=\cos \frac{{\mathit{\theta }}_{0}s}{2}\left|0\right.⟩+e^{i\mathrm{\xi }}\sin \frac{{\mathit{\theta }}_{0}s}{2}\left|1\right.⟩,\end{array}$ (31)

with ξ ∈ {0, ϕ} and $\{\mathrm{|}{E}_{\mathrm{\xi }}^{\pm }\left(s\right)⟩\}$ denoting the set of eigenstates of each adiabatic Hamiltonian H_ξ(s), as provided by equation (2). Thus, by using the equation (22), we can show that the superadiabatic Hamiltonian is given by (Santos and Sarandy, 2015)

$H_{\text{SA}}\left(s\right)=\left[1-P_{N-1,{\widehat{n}}_{-}}\right]\otimes H_0^{\text{SA}}\left(s\right)+P_{N-1,{\widehat{n}}_{-}}\otimes H_{\mathit{\varphi }}^{\text{SA}}\left(s\right),$ (32)

where each term $H_{\mathrm{\xi }}^{\text{SA}}\left(s\right)$ corresponds to the superadiabatic Hamiltonian associated with the adiabatic Hamiltonian H_ξ(s), i.e., $H_{\mathrm{\xi }}^{\text{SA}}\left(s\right)=H_{\mathrm{\xi }}\left(s\right)+H_{\mathrm{\xi }}^{\text{CD}}$, with

$H_{\mathrm{\xi }}^{\text{CD}}=\hslash \frac{{\mathit{\theta }}_0}{2\text{τ}}\left({\mathrm{\sigma }}_y\cos \mathrm{\xi }-{\mathrm{\sigma }}_x\sin \mathrm{\xi }\right)$ (33)

being the (time-independent) counter-diabatic contribution to achieve the evolution at total time τ (Santos and Sarandy, 2015).

3.2. Energy–Time Complementarity in the CE Model of Quantum Gates

Let us now consider equation (26) to investigate the time–energy complementarity relationship in both adiabatic and superadiabatic CE models of universal quantum gates. To this end, we need the set of eigenvalues and eigenstates of the adiabatic Hamiltonian in equation (1), which are given by Eqs 27–31. The spectrum of H(s) has (2N)-degenerate levels, with $\{\mathrm{|}{E}_{0m}^{\mathrm{ϵ}+}\left(s\right)\mathrm{⟩},\mathrm{|}{E}_{0\left(N-1\right)}^{++}\left(s\right)\mathrm{⟩},\mathrm{|}{E}_{\mathit{\varphi }\left(N-1\right)}^{-+}\left(s\right)\mathrm{⟩\}}$ and $\{\mathrm{|}{E}_{0m}^{\mathrm{ϵ}-}\left(s\right)\mathrm{⟩},\mathrm{|}{E}_{0\left(N-1\right)}^{+-}\left(s\right)\mathrm{⟩},\mathrm{|}{E}_{\mathit{\varphi }\left(N-1\right)}^{--}\left(s\right)\mathrm{⟩\}}$ associated with the levels E⁺ = ℏω and E^– = −ℏω, respectively. So, by using Eqs 27–31, we can show that ${\mathrm{\mu }}_l^m\left(s\right)={\mathit{\theta }}_0^2∕4{\mathrm{\tau }}^2$. In addition, the energetic cost to implement any gate controlled by n qubits is ${\Sigma }_{\text{SA}}\left(\mathrm{\tau },n\right)=2^{n∕2}{\Sigma }_{\text{SA}}^{\mathit{sing}}\left(\mathrm{\tau }\right)$ (Santos and Sarandy, 2015), where ${\Sigma }_{\text{SA}}^{\mathit{sing}}$ is the energetic cost to implement any single qubit unitary transformation, with

${\Sigma }_{\text{SA}}^{\mathit{sing}}\left(\mathrm{\omega }\text{τ},{\mathit{\theta }}_0\right)=2\hslash \mathrm{\omega }\sqrt{1+\frac{{\mathit{\theta }}_0^2}{4{\left(\mathrm{\omega }\text{τ}\right)}^2}}.$ (34)

A similar result can be obtained from the spectral norm, with energetic cost given by ${\Sigma }_{\text{SA}}^{\mathit{sing}}\left(\mathrm{\omega }\text{τ},{\mathit{\theta }}_0\right){\mathrm{|}}_2=\left(1∕2\right){\Sigma }_{\text{SA}}^{\mathit{sing}}\left(\mathrm{\omega }\text{τ},{\mathit{\theta }}_0\right)$, since the Hilbert space has dimension D = 4 in this case. Note that the energetic cost is independent of the parameter θ₀ in the adiabatic limit ωτ → ∞. Therefore, the best computational adiabatic strategy is to set θ = π, which deterministically ensures the implementation of the gate with probability one. On the other hand, probabilistic quantum computation can be energetically favored in the superadiabatic regime. Indeed, from equation (5), we can see that, by setting 0 < θ₀ < π, the implementation of the quantum gate is achieved with a non-vanishing probability. Thus, we can investigate whether or not it is possible to find out a specific value of θ₀ such that the energetic cost is better in average than the deterministic choice θ₀ = π. To address this point, let us define the quantity

$⟨N⟩=\frac{1}{{\sin }^2\left({\mathit{\theta }}_0∕2\right)},$ (35)

which is the average number of evolutions for a successful computation. So, the average energetic cost to implement a probabilistic evolution is

$\overline{\Sigma }=⟨N⟩\Sigma ,$ (36)

where Σ is the cost of a single evolution. Without loss of generality, we will consider the cost of single gates, since similar arguments apply for the cost of n-qubit controlled gates. So, by performing superadiabatic probabilistic quantum computing, the average energetic cost is given by

$\begin{array}{l}\hfill \begin{array}{r}{\overline{\Sigma }}_{\mathit{SA}}^{\mathit{sing}}\left(\mathrm{\omega }\text{τ},{\mathit{\theta }}_0\right)=⟨N⟩{\Sigma }_{\mathit{SA}}^{\mathit{sing}}\left(\mathrm{\omega }\text{τ},{\mathit{\theta }}_0\right)=2\hslash \mathrm{\omega }{\text{csc}}^2\left(\frac{{\mathit{\theta }}_0}{2}\right)\sqrt{1+\frac{{\mathit{\theta }}_0^2}{4{\left(\mathrm{\omega }\text{τ}\right)}^2}}.\end{array}\end{array}$ (37)

The function ${\overline{\Sigma }}_{\mathit{SA}}^{\mathit{sing}}\left(\mathrm{\omega }\text{τ},{\mathit{\theta }}_0\right)\to \infty$ as θ₀ → 0 and exhibits a minimum in the interval 0 < θ₀ < π as a function of ωτ. Indeed, the angle ${\mathit{\theta }}_0^{\mathit{min}}$ that minimizes ${\overline{\Sigma }}_{\mathit{SA}}^{\mathit{sing}}\left(\mathrm{\omega }\text{τ},{\mathit{\theta }}_0\right)$ grows monotonically with ωτ, with ${\mathit{\theta }}_0^{\mathit{min}}\to \mathrm{\pi }$ as ωτ → ∞ (adiabatic limit). Then, optimizing ${\overline{\Sigma }}_{\mathit{SA}}^{\mathit{sing}}\left(\mathrm{\omega }\text{τ},{\mathit{\theta }}_0\right)$ for θ₀, we obtain

$\begin{array}{l}\hfill \frac{\partial }{\partial {\mathit{\theta }}_0}{\overline{\Sigma }}_{\mathit{SA}}^{\mathit{sing}}\left(\mathrm{\omega }\text{τ},{\mathit{\theta }}_0\right)=\mathrm{\eta }\left({\mathit{\theta }}_0,\mathrm{\omega }\text{τ}\right)\left\{{\mathit{\theta }}_0-\left[4{\left(\mathrm{\omega }\text{τ}\right)}^2+{\mathit{\theta }}_0^2\right]\text{cotan}\frac{{\mathit{\theta }}_0}{2}\right\}=0,\end{array}$ (38)

where we have defined the function

$\mathrm{\eta }\left({\mathit{\theta }}_0,\mathrm{\omega }\text{τ}\right)=\frac{{\text{csc}}^2\left({\mathit{\theta }}_0∕2\right)}{2{\left(\mathrm{\omega }\text{τ}\right)}^2\sqrt{1+{\mathit{\theta }}_0^2∕4{\left(\mathrm{\omega }\text{τ}\right)}^2}}.$ (39)

Note that η(θ₀, ωτ) is non-vanishing in the whole interval ${\mathcal{I}}_{{\mathit{\theta }}_0}\in \left[0,\mathrm{\pi }\right]$. Thus, to obtain the critical angle ${\mathit{\theta }}_0^{\text{min}}$ in ${\overline{\Sigma }}_{\mathit{SA}}^{\mathit{sing}}\left(\mathrm{\omega }\text{τ},{\mathit{\theta }}_0\right)$, we use equation (38) to note that ωτ satisfies

$\mathrm{\omega }\text{τ}=\frac{\sqrt{{\mathit{\theta }}_0^{\text{min}}}}{2}\sqrt{\tan \left(\frac{{\mathit{\theta }}_0^{\text{min}}}{2}\right)-{\mathit{\theta }}_0^{\text{min}}},$ (40)

where we can see a dependence of ${\mathit{\theta }}_0^{\text{min}}$ on the choice of ωτ. In addition, note that ${\mathit{\theta }}_0^{\text{min}}$ is such that $\tan \left(\frac{{\mathit{\theta }}_0^{\text{min}}}{2}\right)\ge {\mathit{\theta }}_0^{\text{min}}$, since the quantity ωτ is required to be real and positive. The probabilistic advantage is plotted in Figure 1, where it is shown that the optimal value for θ₀ is a continuous function of ωτ, being distinct of the deterministic implementation θ₀ = π. In the inset, we show the global minimum of the average energy for ωτ = 0.01, which occurs for θ₀ < π. In particular, ${\mathit{\theta }}_0^{\text{min}}$ moves away from π as ωτ is lowered, i.e., in the strong superadiabatic regime. As ωτ shifts toward the adiabatic limit, we find that ${\mathit{\theta }}_0^{\text{min}}\to \mathrm{\pi }$. The optimization of the energy cost is shown in the lower inset, where we define the fraction of energy required by the optimized probabilistic model as a function of ωτ as

${\Sigma }_{\text{rel}}\left(\mathrm{\omega }\text{τ}\right)=\frac{{\overline{\Sigma }}_{\mathit{SA}}^{\mathit{sing}}\left(\mathrm{\omega }\text{τ},{\mathit{\theta }}_0^{\text{min}}\right)}{{\Sigma }_{\text{SA}}^{\mathit{sing}}\left(\mathrm{\omega }\text{τ},\mathrm{\pi }\right)}.$ (41)

FIGURE 1

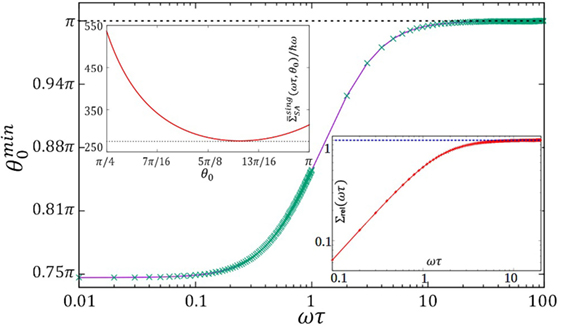
Figure 1. Optimal value ${\mathit{\theta }}_0^{\text{min}}$ for the angle parameter θ₀ as a function of ωτ, with ωτ in logarithmic scale. The points are obtained from equation (40), with the curve denoting the numerical fit. Upper inset: average energy in units of ℏω as a function of θ₀ for ωτ = 0.01. The results are obtained from equation (37). Lower inset: fraction Σ_rel(ωτ) of energy required by the optimized probabilistic model as a function of ωτ, with data in logarithmic scale. The points are obtained from equation (41), with the curve denoting the numerical fit.

Notice that Σ_rel(ωτ) decreases in the superadiabatic regime, implying into a large reduction of the energetic cost for small values of ωτ. On the other hand, Σ_rel(ωτ) →1 in the adiabatic limit, since ${\mathit{\theta }}_0^{\text{min}}\to \mathrm{\pi }$.

3.3. Superadiabatic Quantum Search

Here, we derive a superadiabatic Hamiltonian H_SA(s) for the oracular quantum search governed by the adiabatic Hamiltonian H₀(s) in equation (7). We will adopt linear interpolation, with f (s) = 1 − s and g(s) = s, as in Farhi et al. (2000) and write H_SA(s) = H₀(s) + H_CD(s). In order to determine the counter-diabatic Hamiltonian H_CD(s), we observe that, since H₀(s) has real eigenstates, we use that $⟨\dot{n}\left(s\right)|n\left(s\right)⟩=0$ in equation (23), which implies that

$H_{\mathit{CD}}\left(s\right)=\frac{\mathrm{i\hslash }}{\mathrm{\tau }}\sum _{\mathrm{\xi }=\pm }\mathrm{|}{\dot{E}}_{\mathrm{\xi }}\left(s\right)\mathrm{⟩}\mathrm{⟨}{E}_{\mathrm{\xi }}\left(s\right)\mathrm{|},$ (42)

where the energies |E_±(s)⟩ are given by equation (8) and

$\mathrm{|}{\dot{E}}_{\pm }\left(s\right)\mathrm{⟩}=-\frac{\left(N-1\right)b_{\pm }{\dot{b}}_{\pm }}{{\left(1+\left(N-1\right)b_{\pm }^2\right)}^{3∕2}}\mathrm{|}m\mathrm{⟩}+\frac{{\dot{b}}_{\pm }}{{\left(1+\left(N-1\right)b_{\pm }^2\right)}^{3∕2}}\mathrm{|}\text{ϕ}\mathrm{⟩}.$ (43)

Note that only the ground and first excited states contribute to H_CD(s), since the higher-energy degenerate sector $\{|E_{\text{deg}}^k⟩\}$ is composed by time-independent eigenvectors [see equation (12)]. Note also that the counter-diabatic Hamiltonian will naturally be non-oracular [see equation (18)], with contributions from operators, such as |ϕ⟩ ⟨m| and |m⟩ ⟨ϕ|. This is the reason behind the time complexity O(1) for the superadiabatic Hamiltonian. Naturally, such a result leads to an artificial approach. In a more physical scenario, superadiabaticity could be applied to the quantum search via the direct implementation of the Grover quantum circuit, through the controlled evolution approach discussed in Section 3.1.

3.4. Energy–Time Complementarity in the Quantum Search

Let us now analyze the time–energy complementarity relationship in the adiabatic and superadiabatic versions of the Grover search. In the adiabatic regime, the energetic cost can be computed from equation (26) and using τ → ∞. Therefore, the adiabatic cost can be written as

$\begin{array}{l}\hfill \begin{array}{r}{\Sigma }_{\text{ad}}={\int }_0^1\mathit{ds}\sqrt{\sum _m\left[E_m^2\left(s\right)\right]}={\int }_0^1\mathit{ds}\sqrt{E_{+}{\left(s\right)}^2+E_{-}{\left(s\right)}^2+\left(N-2\right)E_{\text{deg}}{\left(s\right)}^2}.\end{array}\end{array}$ (44)

Let us initially consider the oracular Hamiltonian H₀(s) in equation (7), whose eigenvalues are given by equations (10) and (11). By considering the case of local adiabatic evolution provided by the interpolation in equation (13) and by taking N ≫ 1, we obtain E_±(s) ∼ E_deg(s) ∼ O(1), which implies from equation (44) into an energetic cost ${\Sigma }_{\text{ad}}^{\mathit{LA}}$ that scales as $O\left(\sqrt{N}\right)$. On the other hand, in the superenergetic version of the quantum search, we adopt the interpolation in Eqs 14 and 15. Then, by taking N ≫ 1, we obtain now $E_{\pm }\left(s\right)\sim E_{\text{deg}}\left(s\right)\sim O\left(\sqrt{N}\right)$, which implies into an energetic cost ${\Sigma }_{\text{ad}}^{\mathit{SE}}$ that scales as O(N). This higher energetic cost is a consequence of the complementarity between energy and time, which arises to compensate the constant time complexity O(1) of the superenergetic version. Naturally, the composite energy–time complexity is kept constant for both cases. This overall complexity is reduced by taking non-oracular artificial Hamiltonians. In the case of the adiabatic NLNO model, we use the Hamiltonian in equation (17), whose ground state and first excited state energies are given now by equation (20), with the higher energies kept as in equation (11). Its energetic cost ${\Sigma }_{\text{ad}}^{\mathit{NO}}$ can also be computed from equation (44) by considering the interpolation in equation (21) and by taking N ≫ 1. Then, we obtain E_±(s) ∼ E_deg(s) ∼ O(1), which yields ${\Sigma }_{\text{ad}}^{\mathit{NO}}$ scaling as $O\left(\sqrt{N}\right)$.

For the superadiabatic algorithm, equation (26) must be used. Without loss of generality, we set energy units such that ℏ/τ = 1. We find that for N ≫ 1, the value of μ_±(s) in equation (26) evaluate to

${\mathrm{\mu }}_{\pm }\left(s\right)=⟨{\dot{E}}_{\pm }\left(s\right)\mathrm{|}{\dot{E}}_{\pm }\left(s\right)⟩=\frac{\left(N-1\right){\dot{b}}_{\pm }{\left(s\right)}^2}{{\left(1+\left(N-1\right)b_{\pm }{\left(s\right)}^2\right)}^2},$ (45)

which in turn gives the superadiabatic search energetic cost Σ_SA of order $O\left(\sqrt{N}\right)$, just reproducing the scaling of the NLNO adiabatic search. Similar results can be obtained if one chooses the spectral norm in the energetic cost, up to a common scaling factor $D^{1∕2}=\sqrt{N}$ related to the dimension of the Hilbert space. These results are summarized in Table 1.

TABLE 1

Table 1. Energy–time complexity for several versions of oracular and non-oracular Hamiltonians for the Grover quantum search.

4. Discussion

We have discussed the energetic cost of shortcuts to adiabaticity and their consequences in quantum information processing. Specifically, we considered both the superadiabatic universal gate model via CE and the superadiabatic analog quantum search. For the gate model, we have shown that, differently from the adiabatic scenario, superadiabatic probabilistic gate implementations are energetically favorable with respect to deterministic gate implementations. This implies that the additional energy resources required by superadiabatic evolutions can be minimized by a suitable probabilistic model. Indeed, probabilistic evolutions have recently been considered in similar applications for QC. In particular, they have been used to cancel errors in adiabatic processes (Kieferová and Wiebe, 2014) and as a technique to decompose unitary operations (Paetznick and Svore, 2014; Bocharov et al., 2015). Here, we have shown a new aspect of probabilistic QC, which corresponds to an advantage in the energy balance for superadiabatic dynamics while keeping its performance for a fixed evolution time. For analog quantum search, we have shown that the superadiabatic approach induces a non-oracular counter-diabatic Hamiltonian, with energy–time complexity equivalent to non-oracular adiabatic implementations. This explicitly shows that the Grover optimality is robust against transitionless drivings, which is reflected by a fixed energy–time scaling of the Hamiltonian.

Implications of probabilistic superadiabatic QC under decoherence is a further challenge of immediate interest. In a quantum open-systems scenario, there is a compromise between the time required by adiabaticity and the decoherence time of the quantum device. Therefore, a superadiabatic implementation may provide a direction to obtain an optimal running time for the quantum algorithm while keeping an inherent protection against decoherence. In this context, it is our interest to understand to what extent decoherence can affect the optimal angle ${\mathit{\theta }}_0^{\mathit{min}}$, investigating in particular if it can be robust against classes of decohering processes. Concerning specifically the Grover search, it would be interesting to understand whether superadiabatic implementations are equivalent to arbitrary non-oracular adiabatic Hamiltonians, as suggested in our present discussion. Moreover, the behavior of correlations, such as entanglement and the investigation of experimental proposals in the superadiabatic scenario are also topics under investigation.

Author Contributions

All the authors equally contributed to the conception of the work, development of the main results, and writing of the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

MS thanks Daniel Lidar for his hospitality at the University of Southern California. IC, AS, and MS acknowledge support from CNPq/Brazil and the Brazilian National Institute for Science and Technology of Quantum Information (INCT-IQ).

References

Barends, R., Shabani, A., Lamata, L., Kelly, J., Mezzacapo, A., Las Heras, U., et al. (2016). Digitized adiabatic quantum computing with a superconducting circuit. Nature 534, 222–226. doi: 10.1038/nature17658

CrossRef Full Text | Google Scholar

Berry, M. V. (2009). Transitionless quantum driving. J. Phys. A: Math. Theor. 42, 365303. doi:10.1088/1751-8113/42/36/365303

CrossRef Full Text | Google Scholar

Bocharov, A., Roetteler, M., and Svore, K. M. (2015). Efficient synthesis of universal repeat-until-success quantum circuits. Phys. Rev. Lett. 114, 080502. doi:10.1103/PhysRevLett.114.080502

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y. H., Xia, Y., Chen, Q. Q., and Song, J. (2014a). Efficient shortcuts to adiabatic passage for fast population transfer in multiparticle systems. Phys. Rev. A 89, 033856. doi:10.1103/PhysRevA.89.033856

CrossRef Full Text | Google Scholar

Chen, Y.-H., Xia, Y., Chen, Q. Q., and Song, J. (2014b). Shortcuts to adiabatic passage for multiparticles in distant cavities: applications to fast and noise-resistant quantum population transfer, entangled states preparation and transition. Laser Phys. Lett. 11, 115201. doi:10.1088/1612-2011/11/11/115201

CrossRef Full Text | Google Scholar

Chen, Y.-H., Xia, Y., Chen, Q. Q., and Song, J. (2015a). Fast and noise-resistant implementation of quantum phase gates and creation of quantum entangled states. Phys. Rev. A 91, 012325. doi:10.1103/PhysRevA.91.012325

CrossRef Full Text | Google Scholar

Chen, Y.-H., Xia, Y., Song, J., and Chen, Q.-Q. (2015b). Shortcuts to adiabatic passage for fast generation of Greenberger-Horne-Zeilinger states by transitionless quantum driving. Sci. Rep. 5, 15616. doi:10.1038/srep15616

PubMed Abstract | CrossRef Full Text | Google Scholar

Das, S., Kobes, R., and Kunstatter, G. (2003). Energy and efficiency of adiabatic quantum search algorithms. J. Phys. A: Math. Gen. 36, 2839. doi:10.1088/0305-4470/36/11/313

CrossRef Full Text | Google Scholar

Deffner, S., and Lutz, E. (2013). Energy time uncertainty relation for driven quantum systems. J. Phys. A: Math. Theor. 46, 335302. doi:10.1088/1751-8113/46/33/335302

CrossRef Full Text | Google Scholar

del Campo, A. (2013). Shortcuts to adiabaticity by counter-diabatic driving. Phys. Rev. Lett. 111, 100502. doi:10.1103/PhysRevLett.111.100502

CrossRef Full Text | Google Scholar

del Campo, A., Rams, M. M., and Zurek, W. H. (2012). Assisted finite-rate adiabatic passage across a quantum critical point: exact solution for the quantum Ising model. Phys. Rev. Lett. 109, 115703. doi:10.1103/PhysRevLett.109.115703

PubMed Abstract | CrossRef Full Text | Google Scholar

Demirplak, M., and Rice, S. A. (2003). Adiabatic population transfer with control fields. J. Phys. Chem. A 107, 9937. doi:10.1021/jp030708a

CrossRef Full Text | Google Scholar

Demirplak, M., and Rice, S. A. (2005). Assisted adiabatic passage revisited. J. Phys. Chem. B 109, 6838. doi:10.1021/jp040647w

PubMed Abstract | CrossRef Full Text | Google Scholar

Farhi, E., Goldstone, J., Gutmann, S., Lapan, J., Lundgren, A., and Preda, D. (2001). A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science 292, 472. doi:10.1126/science.1057726

PubMed Abstract | CrossRef Full Text | Google Scholar

Farhi, E., Goldstone, J., Gutmann, S., and Sipser, M. (2000). Quantum computation by adiabatic evolution. MIT-CTP-2936 (arXiv:quant-ph/0001106).

Google Scholar

Grover, L. K. (1997). Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 79, 325. doi:10.1103/PhysRevLett.79.325

CrossRef Full Text | Google Scholar

Hen, I. (2015). Quantum gates with controlled adiabatic evolutions. Phys. Rev. A 91, 022309. doi:10.1103/PhysRevA.91.022309

CrossRef Full Text | Google Scholar

Jansen, S., Ruskai, M.-B., and Seiler, R. (2007). Bounds for the adiabatic approximation with applications to quantum computation. J. Math. Phys. 48, 102111. doi:10.1063/1.2798382

CrossRef Full Text | Google Scholar

Kieferová, M., and Wiebe, N. (2014). On the power of coherently controlled quantum adiabatic evolutions. New J. Phys. 16, 123034. doi:10.1088/1367-2630/16/12/123034

CrossRef Full Text | Google Scholar

Lu, M., Xia, Y., Shen, L. T., and Song, J. (2014a). An effective shortcut to adiabatic passage for fast quantum state transfer in a cavity quantum electronic dynamics system. Laser Phys. 24, 105201. doi:10.1088/1054-660X/24/10/105201

CrossRef Full Text | Google Scholar

Lu, M., Xia, Y., Shen, L. T., Song, J., and An, N. B. (2014b). Shortcuts to adiabatic passage for population transfer and maximum entanglement creation between two atoms in a cavity. Phys. Rev. A 89, 012326. doi:10.1103/PhysRevA.89.012326

CrossRef Full Text | Google Scholar

Martinis, J. M., and Geller, M. R. (2014). Fast adiabatic qubit gates using only σ_z control. Phys. Rev. A 90, 022307. doi:10.1103/PhysRevA.90.022307

CrossRef Full Text | Google Scholar

Messiah, A. (1962). Quantum Mechanics. North-Holland, Amsterdam: North-Holland Pub. Co.

Google Scholar

Nielsen, M. A., and Chuang, I. L. (2000). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press.

Google Scholar

Orus, R., and Latorre, J. I. (2004). Universality of entanglement and quantum computation complexity. Phys. Rev. A 69, 052308. doi:10.1103/PhysRevA.69.052308

CrossRef Full Text | Google Scholar

Paetznick, A., and Svore, K. M. (2014). Repeat-until-success: non-deterministic decomposition of single-qubit unitaries. Quantum Inf. Comput. 14, 1277.

Google Scholar

Roland, J., and Cerf, N. J. (2002). Quantum search by local adiabatic evolution. Phys. Rev. A 65, 042308. doi:10.1103/PhysRevA.65.042308

CrossRef Full Text | Google Scholar

Saberi, H., Opatrny, T., Molmer, K., and del Campo, A. (2014). Adiabatic tracking of quantum many-body dynamics. Phys. Rev. A 90, 060301(R). doi:10.1103/PhysRevA.90.060301

CrossRef Full Text | Google Scholar

Santos, A. C., and Sarandy, M. S. (2015). Superadiabatic controlled evolutions and universal quantum computation. Sci. Rep. 5, 15775. doi:10.1038/srep15775

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, A. C., Silva, R. D., and Sarandy, M. S. (2016). Shortcut to adiabatic gate teleportation. Phys. Rev. A 93, 012311. doi:10.1103/PhysRevA.93.012311

CrossRef Full Text | Google Scholar

Sarandy, M. S., Wu, L.-A., and Lidar, D. (2004). Consistency of the adiabatic theorem. Quantum Inf. Process. 3, 331. doi:10.1007/s11128-004-7712-7

CrossRef Full Text | Google Scholar

Teufel, S. (2003). “Adiabatic perturbation theory in quantum dynamics,” in Lecture Notes in Mathematics, Vol. 1821 (Berlin Heidelberg: Springer-Verlag).

Google Scholar

Torrontegui, E., Ibáñez, S., Martínez-Garaot, S., Modugno, M., del Campo, A., Guéry-Odelin, D., et al. (2013). Shortcuts to adiabaticity. Adv. Atom. Mol. Opt. Phys. 62, 117. doi:10.1016/B978-0-12-408090-4.00002-5

CrossRef Full Text | Google Scholar

van Dam, W., Mosca, M., and Vazirani, U. (2001). “How powerful is adiabatic quantum computation?,” in Proceedings of the 42nd Annual Symposium on Foundations of Computer Science, Las Vegas, 279.

Google Scholar

Wen, J., Huang, Y., and Qiu, D. (2009). Entanglement proprieties of adiabatic quantum algorithms. Int. J. Quantum Inform. 7, 1531. doi:10.1142/S0219749909006000

CrossRef Full Text | Google Scholar

Wen, J., and Qiu, D. (2008). Entanglement in adiabatic quantum searching algorithms. Int. J. Quantum Inform. 6, 997. doi:10.1142/S0219749908004249

CrossRef Full Text | Google Scholar

Zheng, Y., Campbell, S., Chiara, G., and Poletti, D. (2015). Cost of transitionless driving and work output. e-print arXiv:1509.01882

Google Scholar