- 1Telefonica Research, Edificio Telefonica, Barcelona, Spain
- 2Department of Psychiatry, University of Cambridge, Cambridge, United Kingdom
- 3Departament de Fisica de la Materia Condensada, Universitat de Barcelona, Barcelona, Spain
- 4Universitat de Barcelona Institute of Complex Systems (UBICS), Universitat de Barcelona, Barcelona, Spain
In this manuscript, we propose, analyze, and discuss a possible new principle behind traditional cuisine: the Food-bridging hypothesis and its comparison with the food-pairing hypothesis using the same dataset and graphical models employed in the food-pairing study by Ahn et al. (2011). The Food-bridging hypothesis assumes that if two ingredients do not share a strong molecular or empirical affinity, they may become affine through a chain of pairwise affinities. That is, in a graphical model as employed by Ahn et al., a chain represents a path that joints the two ingredients, the shortest path represents the strongest pairwise chain of affinities between the two ingredients. Food-pairing and Food-bridging are different hypotheses that may describe possible mechanisms behind the recipes of traditional cuisines. Food-pairing intensifies flavor by mixing ingredients in a recipe with similar chemical compounds, and food-bridging smoothes contrast between ingredients. Both food-pairing and food-bridging are observed in traditional cuisines, as shown in this work. We observed four classes of cuisines according to food-pairing and food-bridging: (1) East Asian cuisines, at one extreme, tend to avoid food-pairing as well as food-bridging; and (4) Latin American cuisines, at the other extreme, follow both principles. For the two middle classes: (2) Southeastern Asian cuisines, avoid food-pairing and follow food-bridging; and (3) Western cuisines, follow food-pairing and avoid food-bridging.
1. Introduction
Since the introduction by Francois Benzi and Heston Blumenthal of the Food-pairing hypothesis, a debate on this hypothesis has been risen in gastronomy science and cuisine. Originally it states that, if two ingredients share important flavor compounds,1 there is a good chance that they will result in a tasty combination (Ahn et al., 2011; Ahn and Ahnert, 2013). In the last few years, this hypothesis attracted foodies, many chefs, and scientists. If food-pairing is one of the main principles behind our taste preferences, scientifically this would allow us to predict and build many successful new ingredient affinities based on which flavors they are composed.
Ahn et al. (2011) present a study of the food-pairing hypothesis across several regional cuisines, employing a set of tools, which derive from a new scientific field: complex networks, a sub-field of complex systems (Boccaletti et al., 2006). These mathematical techniques were applied to several regional cuisines, to encode a relation between ingredients and flavors as a network, where nodes and edges represent ingredients and flavors sharing, respectively. This network is called flavor network from now on. The authors have observed that Western cuisines show a tendency toward the food-pairing hypothesis, i.e., their flavor network contains many pairs of ingredients that share many flavor compounds, and that Eastern Asian cuisines tend to avoid compound sharing between ingredients. The study of food-pairing has lately been applied to other specific regional cuisines (Varshney et al., 2013; Jain et al., 2015; Kim et al., 2015).
The hypothesis of food-bridging stems from the combination of the theory of complex networks and gastronomy (Burdock, 2004; Ahn et al., 2011; Simas, 2012; Simas and Rocha, 2012, 2015; Vega et al., 2012; Ahn and Ahnert, 2013; Jain et al., 2015). It assumes that if two ingredients do not share a strong molecular or empirical affinity, they may become affine through a chain of pairwise affinities. That is, apricot and whiskey gum may not be affine, but if we join (or bridge) them with tomato they may become affine—assuming that tomato is affine with apricot and whiskey gum, thus creating a chain of affinities. In a graphical model of a flavor network, this corresponds to a path that joints the two ingredients, but not necessarily the shortest path. However, the shortest path represents the strongest pairwise chain of affinities between the two ingredients.
In this manuscript, we analyze and discuss the food-bridging hypothesis with a restriction to the optimal case, which corresponds to the shortest path in the graphical model. We use the same dataset and graphical models employed in the study of Ahn et al. (2011). This allows us to perform a direct comparative study between food-pairing and food-bridging.
2. Materials and Methods
2.1. Data and Ingredient Networks
The data used in this work as well as the methods employed to build ingredient networks are based on the work of Ahn et al. (2011). In short, the flavor network is a weighted graph obtained from a bipartite graph that relates 1,530 ingredients with 1,106 flavor compounds (Ahn et al., 2011). Nodes in the flavor network represent the ingredients, edge weights are the number of flavors compounds shared between pairs of ingredients (Ahn et al., 2011).
We removed some regional cuisines from the original work (Ahn et al., 2011). The reason behind is that we employed the null-model frequency-conserving described in the Ahn et al. (2011) supplementary materials, and after a permutation test and multi-comparison correction (False Discovery Rate), they show evidence of no statistical difference when compared with the null-model on the variables: food-pairing and food-bridging.
In general, the weights of a weighted network lie in a non-normalized interval Zij ∈ [a, b] ⊂ ℝ. Normalizing the network weights to the unit interval I = [0, 1] does not affect network properties, if the normalization is performed by a linear function. As shown in Simas and Rocha (2015), there is only one unique linear function that performs such normalization.
We have parameterized this function with ϵ in order to avoid merging and/or isolating vertices with weights at the boundaries of Zij ∈ [a, b]. In general, ϵ is set to 0.01.
This normalization allows us to apply the framework described in Simas and Rocha (2015), i.e., allows us to treat weighted graphs as mathematical objects defined in a specific algebra (Simas and Rocha, 2015; Simas et al., 2015a), similar to the way in which we use algebras to deal with numbers.
2.2. Food-Pairing, Food-Bridging, and Flavor Network Semi-Metricity
2.2.1. Food-Pairing
As defined in Ahn et al. (2011), food-pairing is measured by the number of flavors a pair of ingredients share. The food-pairing value of a recipe is the average number of shared flavors in the recipe, as defined in Ahn et al. (2011) and is calculated from the following equation:
where Ck corresponds to the edge weight between the pair of ingredients in the flavor network, and nR is the number of ingredients in the recipe R. Each recipe defines a sub-graph in the flavor network and Ns(R) corresponds to the average of all edges in such sub-graph.
2.2.2. Metric and Semi-Metric Edges and Paths
As defined in Simas (2012), Simas and Rocha (2012, 2015), Simas et al. (2015a,b), Kalavri et al. (2016), and Simas and Suckling (2016), an edge in a weighted graph is metric if the shortest path is equal to the edge by itself (direct connection). Otherwise, the edge is considered semi-metric, which means that there is at least one alternative path that involves other nodes. See Figure 1 for an example.
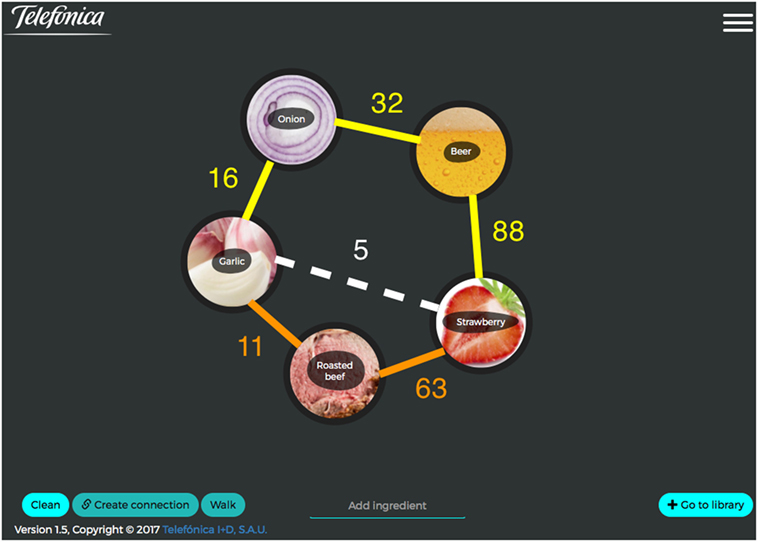
Figure 1. Semi-metric edge and paths example from the flavor network. The white edge that links “garlic + strawberry” shares 5 flavors. Therefore, it is semi-metric, because there are two alternative paths, the yellow and orange paths, that better overlap flavors or food-pairs based in a chain of other ingredients, smoothing the initial flavor contrast between these ingredients. The two semi-metric paths that connect “garlic-strawberry” are: (1) yellow path, with “garlic + roasted onion + bantu beer + strawberry,” which shares 16 + 32 + 88 = 136 flavors; and (2) orange path, with “garlic + roasted beef + strawberry,” which shares 11 + 63 = 74 flavors. The first semi-metric path may inspire a “garlic-strawberry” sauce, based on “garlic + roasted onion + bantu beer + strawberry,” and with the second semi-metric path may inspire the dish composed of “roasted beef” with garlic-strawberry sauce. This figure is an adapted print screen of the application developed by Telefonica I + D Appetit Team and available online at http://appetit.lab.tid.es—with Telefonica I + D printing permission.
We may observe in a network of ingredients that two nodes are more strongly connected by other paths (semi-metric paths), whether or not there is a direct edge between them. Figure 1 shows an example of the combination of “garlic” and “strawberry” from the flavor network, which share 5 flavors when mixed together. In this figure, we show how we may increase the poor affinity between these two ingredients by adding additional ingredients that play in the semi-metric paths of the flavor network. From the flavor network, at least two semi-metric paths are stronger than the edge that connects them. In this case, among the possible stronger paths, the optimal semi-metric path is the path that indirectly connects the two ingredients in this network; that is, the path “garlic + roasted onion + bantu beer + strawberry.” These intermediate ingredients potentiate the affinity between “garlic—strawberry.” Other semi-metric paths may exist as we show in this example: “garlic + roast beef + strawberry.”
Food-pairing is a particular case for which we only consider direct connections, if they exist. In another words, k = 0 hops (0 nodes in between). However, with semi-metric paths, we allow two ingredients to be strongly connected with k > 0 hops, whether the edge between the ingredients exists or not.
There are many ways to calculate such alternative paths between any two nodes in a weighted graph. Refer to the Figure 1 in Simas and Suckling (2016) for a summary of this calculation and, see further details in Johnson (1977), Simas and Rocha (2015), Simas et al. (2015b), Kalavri et al. (2016), and Simas and Suckling (2016).
2.2.3. Food-Bridging
Food-bridging is a hypothesis, which assumes that if two ingredients do not share a strong molecular or empirical affinity, they may become affine through a chain of pairwise affinities. That is, apricot and whiskey gum may not be affine, but if we join (or bridge) them with tomato they may become affine—assuming that tomato is affine with both apricot and whiskey gum, thus creating a chain of affinities.
Food-bridging is the ability to connect a pair of ingredients, which may or may not have a direct connection, through a path of non-repeating ingredients within a network of ingredient affinities; in the specific case of this work, the flavor network. Several paths may exist, or none. In the case that no path exists, we say that no bridge exists, otherwise, a bridge exists and all possible bridges are ranked by the strength of the path.
The notion of food-bridging is directly related to semi-metric connections between ingredients in a network of ingredients as briefly mentioned above. Semi-metricity in weighted graphs is a mathematical property of distance that measures all levels of triangle inequality violations. That is, all k − hop inequalities violations between two ingredients, where k ≥ 1 means that we have k intermediate ingredients, see Figures 1 and 3B for an example. The degree of food-bridging in a recipe is defined as an average of all semi-metric edges in a recipe, or by the average strength of all optimal semi-metric paths, respectively.
More specifically, we define the recipe optimal food-bridging strength as an average of the strengths of all the optimal paths between any pair of ingredients in the defined recipe sub-graph:
where
is the semi-metric ratio in the weighted sub-graph defined by the recipe R in the flavor network (Simas and Rocha, 2015; Simas et al., 2015b; Kalavri et al., 2016; Simas and Suckling, 2016): di,j is the direct distance and dci,j denotes the shortest path between ingredients i and j, respectively. δ is the discrete-Kronecker function, i.e., δ(condition) = 1, if the logical condition True, otherwise δ(condition) = 0—for logical condition equals False. That is, the equation numerator; , counts only the semi-metric edges.
Although we define the recipe optimal food-bridging strength , in this work we measure the degree of food-bridging in a recipe as the average of all semi-metric edges in a recipe, which represents a simpler version.
2.2.4. Network Semi-Metric Percentage
As defined in Simas and Rocha (2015), Simas et al. (2015b), Kalavri et al. (2016), and Simas and Suckling (2016), the network semi-metric percentage is given by the following equation:
where si,j is the semi-metric ratio between ingredients i and j in the flavor network. The dominator of this equation; counts all edges in the network and the numerator; , counts only the semi-metric edges.
2.2.5. Recipe Food-Bridging Percentage
Semi-metric percentage of the sub-graph representing a recipe in the ingredient network is called recipe food-bridging percentage. In other words, equation (4) above is applied to the sub-graph defined by the recipe.
2.2.6. Network Metric Backbone
As defined in Simas (2012), Simas and Rocha (2015), Simas et al. (2015b), Kalavri et al. (2016), and Simas and Suckling (2016), the metric backbone is the smallest weighted sub-graph of a weighed graph that preserves the shortest paths: sub-graph with all metric edges.
2.2.7. Network Semi-Metric Backbone
The semi-metric backbone is a sub-graph of a weighted graph with only semi-metric edges, i.e., all metric edges removed from the network (Simas et al., 2015b; Simas and Suckling, 2016).
3. Results
In Figure 2, we analyzed food-pairing and optimal food-bridging (semi-metric percentage) according to equations (2) and (4), respectively. We plotted the averages of these variables for each of the seven distinct world regions, against how they rank (Figures 2A,C), and against the number of ingredients (Figures 2B,D).
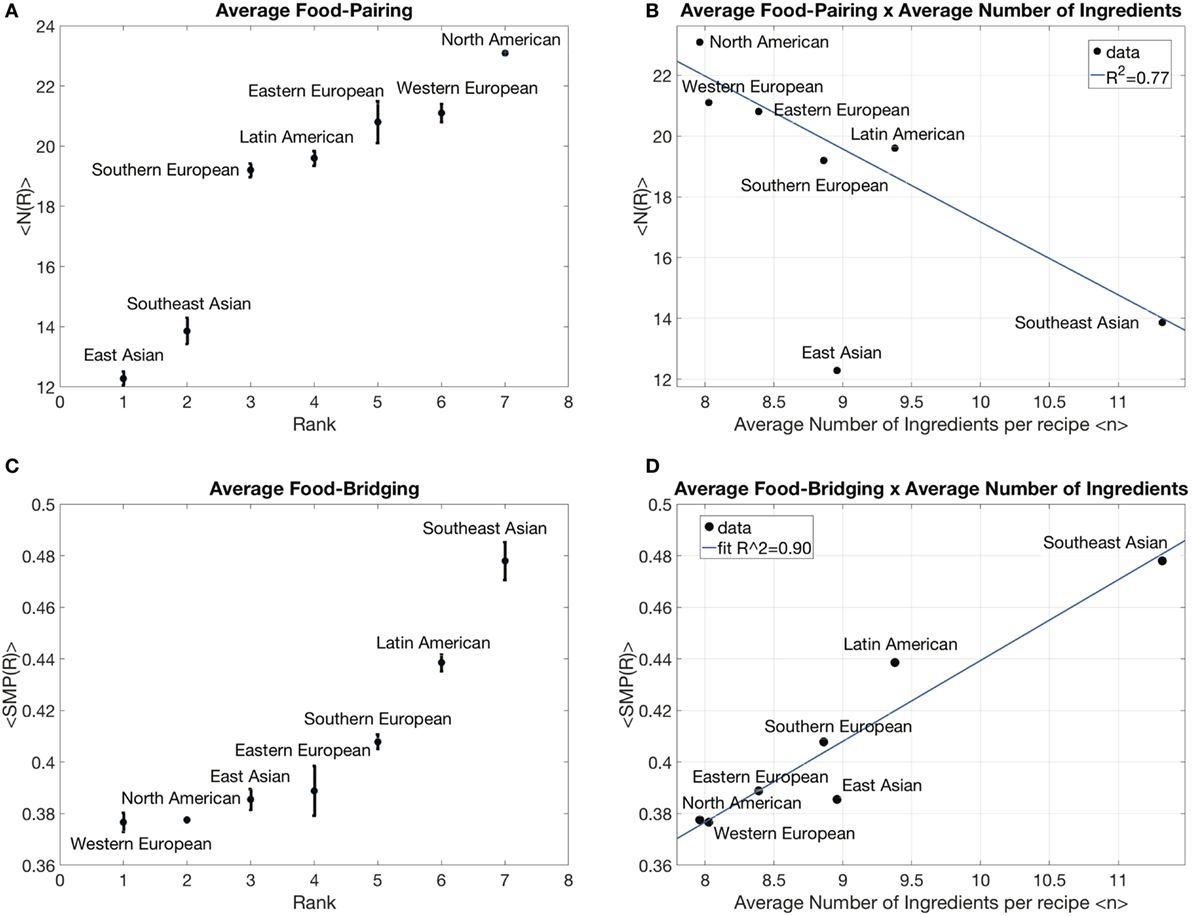
Figure 2. <N(R) > is the average over all recipes of the recipe food-pairing, <SMP(R) > is the average over all recipes of the recipe food-bridging, Rank is the sorted cuisine type by <N(R) > or <SMP(R) >, and <n > the average number of ingredients per recipe for a given cuisine type. (A) Average recipe Food-pairing (<N(R) >) vs. cuisine type Rank. (B) Average recipe Food-pairing (<N(R) >) vs. average number of ingredients per recipe (<n >). (C) Average recipe Food-bridging (<SMP(R) >) vs. cuisine type Rank. (D) Average Food-bridging (<SMP(R) >) vs. average number of ingredients per recipe (<n >).
3.1. Food-Pairing
In Figures 2A,B, we observe that there are clearly two distinct groups with respect to food-pairing: Western-based cuisines; and Eastern Asian cuisines. It corroborates with the observations in Ahn et al. (2011), Ahn and Ahnert (2013), and Jain et al. (2015) that Eastern Asian cuisines avoid food-pairing more than the Western based cuisines. Moreover, from Figure 2B, we observe that there is a negative trend of food-pairing against the average number of ingredients used in a recipe. Note that, in this case, East Asian and Southeast Asian cuisines differ mainly in the average number of ingredients used in a recipe. East Asian cuisine is a complete outlier in this trend—flagging that Southeast Asian cuisine may differ from East Asian cuisine in some other dimension. We also observe that Eastern European as well as Southeast Asian cuisines show higher variability, suggesting a richer cuisine. In fact, the source of the variability may stem from a size effect, since these two cuisines present lower volume of recipes when compared to the others, a collection of 381 and 457 recipes, respectively, with the others containing over 2,000 recipes each.
3.2. Food-Bridging
In Figures 2C,D, we observe that food-bridging ranks non-linear and depends positively and linearly on the average number of the ingredients used in recipes. From the rank, we observe that, in this case, food-bridging: East and Southeast Asian cuisines differ significantly from each other; Western cuisines cluster together at the bottom extreme; and Southeast Asian at the other extreme.
In this case, we note that food-bridging (semi-metric percentage) depends on the number of ingredients used in a recipe. This was an expected result since there are more possibilities to bridge ingredients, i.e., more degrees of freedom.
3.3. Food-Pairing and Food-Bridging
In Figure 3A, we observe the relation between food-pairing and food-bridging. We divided the group into four non-overlapping regions, which represent the following four classes.
1. Low food-pairing + low food-bridging.
2. Low food-pairing + high food-bridging.
3. High food-pairing + low food-bridging.
4. High food-pairing + high food-bridging.
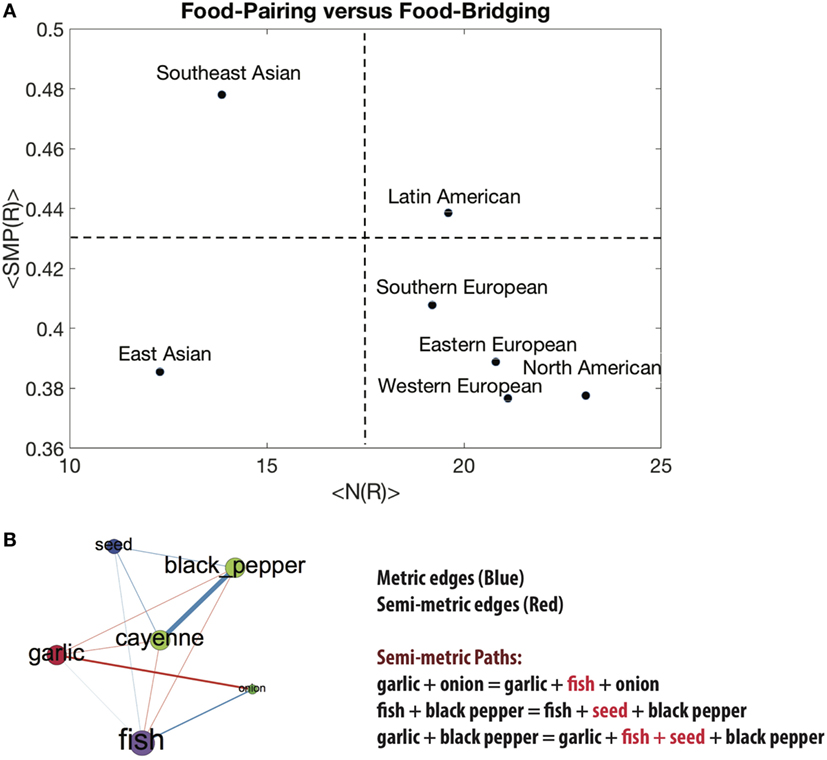
Figure 3. <N(R) > is the average over all recipes of the recipe food-pairing, and <SMP(R) > is the average over all recipes of the recipe food-bridging. (A) Classes of cooking based on average recipe Food-pairing (<N(R) >) versus average recipe Food-bridging (<SMP(R) >). We divided the space into four distinct regions or classes, as follows: (1) Low food-pairing + low food-bridging, (2) low food-pairing + high food-bridging, (3) high food-pairing + low food-bridging, (4) high food-pairing + high food-bridging. (B) An example of semi-metric analysis of a Southeast Asian cuisine with six ingredients. The semi-metric percentage of this recipe is . It shares in average 11 flavor compounds between pairs of ingredients, falling into class (2) according to (A). Moreover, this recipe has nine possible semi-metric paths or bridges, of which some are shown above.
We observe that East Asian falls into class (1), Southeast Asian into class (2), Southern, Eastern, Western European, and North American into class (3) and Latin American into class (4).
In class (1), with low food-pairing and low food-bridging, the recipe ingredients depend less on the co-occurrence of their flavor compounds, directly or indirectly (chains of pairings). Class (2) pairs flavor compounds mainly indirectly by chains or bridges between ingredients. In class (3), the ingredients mainly pair their flavor compounds without that many indirect chains or bridges. In class (4), the ingredients strongly pair and bridge their flavor compounds.
In Figure 3B, we have an example of a Southeast Asian recipe with six ingredients.2 We can observe five semi-metric edges (red) and six metric edges (blue). The semi-metric percentage of this recipe is . It shares in average 11 flavor compounds between pairs of ingredients, falling into class (2) according to Figure 3A. Moreover, this recipe has nine possible semi-metric paths or bridges, where some of them are shown in the Figure 3B.
In Figures 4 and 5, we show a sub-graph of the flavor network with the top 100 ingredients that have stronger connections or pairings (node strength). Figure 4 edges represent only metric connections (metric backbone) and Figure 5 edges show only semi-metric connections (semi-metric backbone). Node colors represent network clusters after applying a community detection algorithm, e.g., Louvain algorithm (Fortunato, 2010), and node size proportional to the node metric or semi-metric strength, respectively. The metric percentage is 27.4% of the edges from the flavor network and the semi-metric percentage is 72.6% from the flavor network, which demonstrates that there are a high number of bridge possibilities between pairs of ingredients.
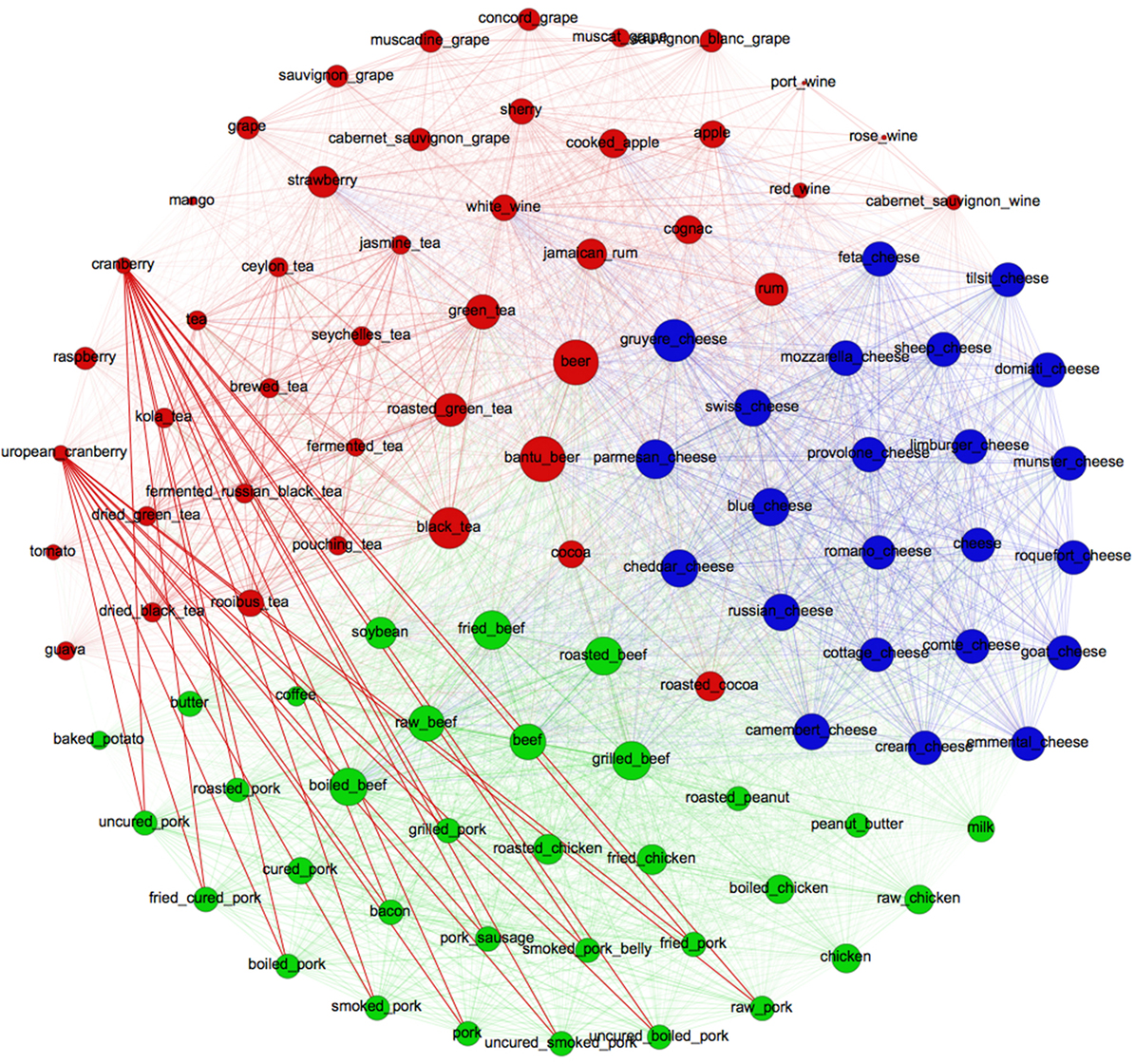
Figure 4. Metric backbone. Top 100 ingredients of flavor network with higher node strength. Edges represent metric connections and edge color the target community color (target node). Node colors represent network clusters after applying a community detection algorithm, e.g., Louvain algorithm, and size proportional to the node metric strength.
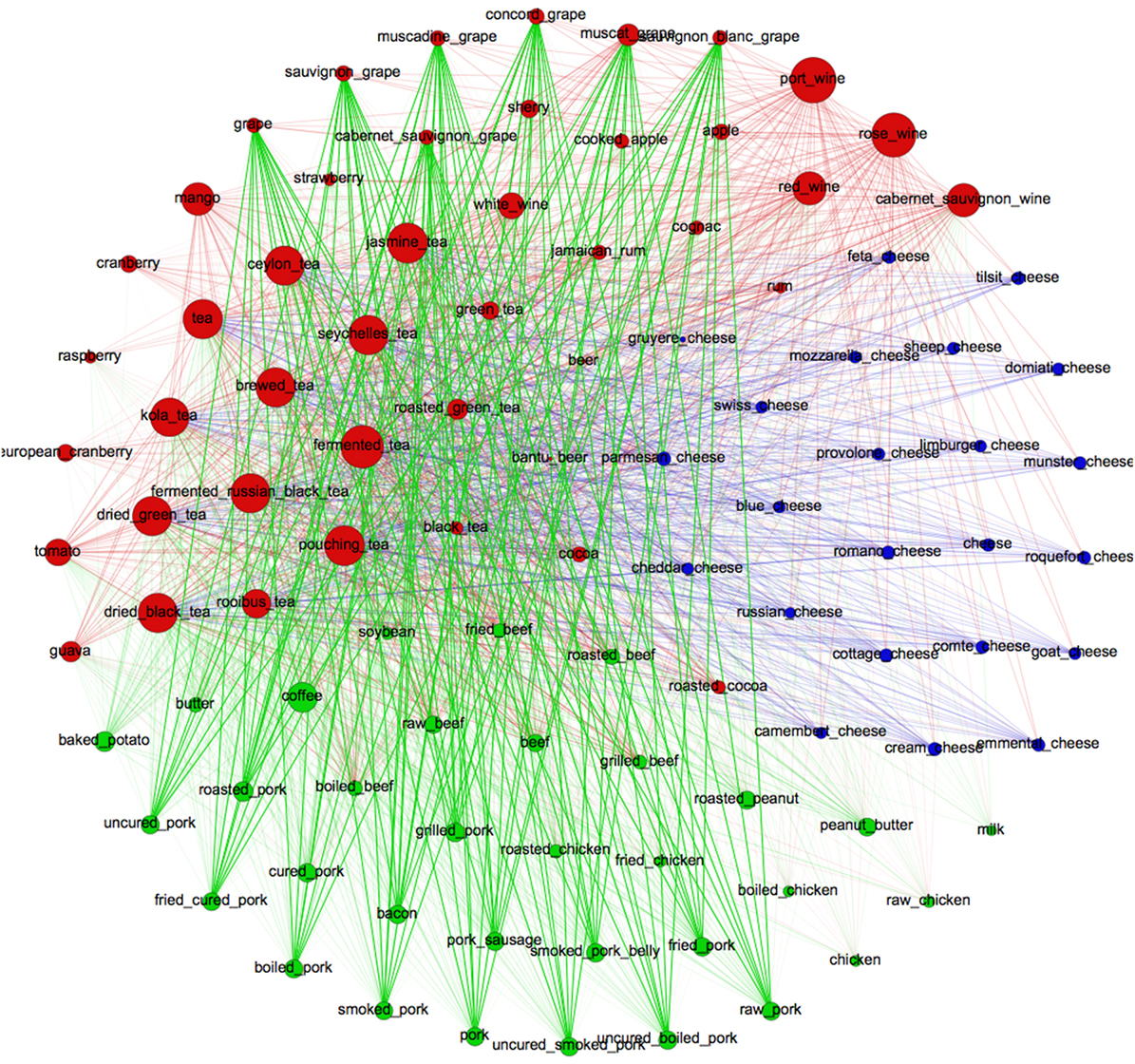
Figure 5. Semi-metric backbone. Top 100 ingredients of flavor network with higher node strength. Edges represent semi-metric connections and edge color the target community color (target node). Node colors represent network clusters after applying a community detection algorithm, e.g., Louvain algorithm, and size proportional to the node semi-metric strength.
Highly metric ingredients (node size) tend to food-pair in pairs, and highly semi-metric ingredients (node size) tend to food-pair with the addition of intermediate ingredients. For example, from Figure 4, the ingredients “beer,” “black tea,” “gruyere cheese,” etc., are good food-pairing ingredients. Figure 5 shows that “port wine,” “rose wine,” “tea,” and “tomato” are better mixed with intermediate ingredients, according to food-bridging hypothesis.
In general, we may observe from Figures 4 and 5 that there is a dichotomy; with ingredients that are less suited to food-pairing tending to use the food-bridging mechanism, and vice-versa.
4. Discussion
We have shown that the flavor network is 72.6% semi-metric, which allows food-bridging to work extensively, i.e., the number of possible semi-metric paths between ingredients is large. Food-bridging or semi-metricity, by hypothesis, may increase affinities between ingredients with or without a strong direct affinity based on chain of intermediate ingredient pairings, in this case, a chain of flavor compound affinities.
Food-pairing and food-bridging are different hypothesis that may represent possible mechanisms behind traditional cuisines. Food-pairing intensifies flavor with similar flavored ingredients and food-bridging smooths contrasted flavored ingredients in a recipe, respectively. Both hypotheses food-pairing and food-bridging are jointly observed in traditional cuisines, as shown in this work.
Regional cuisines cluster in four distinct classes defined by the possible relationship between these two mechanisms. Where East Asian cuisine is at one extreme class (1) and tends to avoid food-pairing as well as food-bridging; and Latin American cuisine is at the other extreme class (4), following both principles. Southeastern Asian and Western cuisines are in middle classes (2) and (3): class (2) avoids food-pairing and follows food-bridging; class (3) follows food-pairing and avoids food-bridging.
It is worthwhile noting from Figure 3A that the represented cuisine classes follow in some way their geopolitical distribution.
East Asia cuisine, represented by Korean, Chinese, and Japanese cuisines, tends to use contrasted ingredients with respect to flavor. This results in a cuisine that contrasts several flavors.
At the other extreme is Latin American cuisine, represented by Caribbean, Central America, South American, and Mexican cuisines. These tend to reinforce the intensity of flavor using both mechanisms, food-pairing, and food-bridging. That is, direct and indirect intensification of flavors in a recipe, reinforcing common flavors and smoothing contrasts between flavored contrasted ingredients.
In class (2), we found Southeast Asian cuisine, represented by Indonesian, Malaysian, Filipino, Thai, and Vietnamese. These cuisines are similar to East Asian cuisines with respect to food-pairing, using contrasted ingredients, but at the same time, they smooth these contrasts with other ingredients that bridge the contrast.
The other intermediate class is class (3), where we found Eastern, Southern, Western European, and North American cuisines. Eastern European cuisines are represented by Eastern Europe, in general, and Russian cuisines. Southern European cuisine is represented by Greek, Italian, Mediterranean, Spanish, and Portuguese. Western European cuisine is represented by French, Austrian, Belgian, English, Scottish, Dutch, Swiss, German, and Irish. And North American is represented by American in general, Canada, Cajun, Southern soul food, and Southwestern U.S. These cuisines tend to follow the food pairing with the direct intensification of flavors in a recipe, avoiding contrasted ingredients. Therefore, these cuisines are characterized by avoiding flavor contrasted ingredients. Moreover, in this class, at one extreme, we have Southern European, and at the other North American. The latter sub-clusters better with Western and Eastern European cuisines.
We may suggest several explanations for why, in this analysis, traditional cuisines cluster in this way across these two dimensions: food-pairing and food-bridging. The clustering aligns well with a geopolitical distribution. These cuisines may be driven by particular geographical weather and resource constrains as well as political trade in goods, which may influence the different styles of cuisine analyzed in this work.
Food-bridging, as shown, opens the possibility of better understanding possible mechanisms behind mixing ingredients in a recipe. This is a new mechanism or hypothesis, different from food-pairing, and both mechanisms are observed in traditional cuisines, in particular, in this dataset (Ahn et al., 2011).
We recognize a number of limitations in this work. We have not included, in this analysis, important features such as texture, ingredient concentrations, processes used during the recipes, such as cooking method among others (Vega et al., 2012). We restricted our analysis to the number of shared chemical flavor compounds between ingredients as in the works of Ahn et al. (Ahn et al., 2011; Ahn and Ahnert, 2013). However, for food-bridging, a contra-part of its mathematical representation—semi-metricity—is not restricted to the flavor space or more specifically to the flavor network. In general, it may be employed to other modalities: texture, color, among other empirical, or scientifically affinities.
Besides this work, semi-metricity as a topological property of weighted graphs has been shown to be a topological analysis, sensitive and specific in identifying how the flow of information propagates in the human brain (Simas et al., 2015b; Simas and Suckling, 2016), provide better recommendations in social networks (Simas and Rocha, 2012, 2015), and a better optimization of large scale graphical algorithms (Kalavri et al., 2016).
This work brings a new perspective on food-pairing and introduces food-bridging as a new principle or vector behind cooking.
Author Contributions
All authors made significant contributions to the drafting of the article.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to acknowledge Telefonica I+D for all support done in the Appetit project that have turned possible the present work. We also thank all of our colleagues involved in the Appetit project. We would like to acknowledge Oliver Smith and Emily Stott for their persistence on editing this manuscript.
Footnotes
- ^By flavor compounds, we mean molecular chemical compounds and from now on, will describe these as flavor compounds or, in short, flavors.
- ^The meaning of general ingredients products from Fenaroli’s book of Burdock (2004) is for example: fish: sweet fish, fatty fish, raw fatty fish, etc., seed: lovage seed, toasted sesame seed, angelica seed, etc.
References
Ahn, Y.-Y., and Ahnert, S. E. (2013). The flavor network. Leonardo 46, 272–273. doi:10.1162/LEON.a.00569
Ahn, Y.-Y., Ahnert, S. E., Bagrow, J. P., and Barabasi, A.-L. (2011). Flavor network and the principles of food pairing. Sci. Rep. 1, 196. doi:10.1038/srep00196
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., and Hwang, D.-U. (2006). Complex networks: structure and dynamics. Phys. Rep. 424, 175–308. doi:10.1016/j.physrep.2005.10.009
Burdock, G. A. (2004). Fenaroli’s Handbook of Flavor Ingredients, 5th Edn. Boca Raton, FL: CRC Press.
Fortunato, S. (2010). Community detection in graphs. Phys. Rep. 486, 75–174. doi:10.1016/j.physrep.2009.11.002
Jain, A., Rakhi, N. K., and Bagler, G. (2015). Analysis of food pairing in regional cuisines of India. PLoS ONE 10:e0139539. doi:10.1371/journal.pone.0139539
Johnson, D. B. (1977). Efficient algorithms for shortest paths in sparse networks. J. ACM 24, 1–13. doi:10.1145/321992.321993
Kalavri, V., Simas, T., and Logothetis, D. (2016). The shortest path is not always a straight line: leveraging semi-metricity in graph analysis. Proc. VLDB Endowment 9, 672–683. doi:10.14778/2947618.2947623
Kim, S., Sung, J., Foo, M., Jin, Y.-S., and Kim, P.-J. (2015). Uncovering the nutritional landscape of food. PLoS ONE 10:e0118697. doi:10.1371/journal.pone.0118697
Simas, T., Chavez, M., Rodriguez, P. R., and Diaz-Guilera, A. (2015a). An algebraic topological method for multimodal brain networks comparisons. Front. Psychol. 6:904. doi:10.3389/fpsyg.2015.00904
Simas, T., Chattopadhyay, S., Hagan, C., Kundu, P., Patel, A., Holt, R., et al. (2015b). Semi-metric topology of the human connectome: sensitivity and specificity to autism and major depressive disorder. PLoS ONE 10:e0136388. doi:10.1371/journal.pone.0136388
Simas, T., and Rocha, L. M. (2012). “Semi-metric networks for recommender systems,” in Proceedings of the 2012 IEEE/WIC/ACM International Joint Conferences on Web Intelligence and Intelligent Agent Technology, 4–7 December 2012, Vol. 3. Macau, 175–179.
Simas, T., and Rocha, L. M. (2015). Distance closures on complex networks. Netw. Sci. 2, 227–268. doi:10.1017/nws.2015.11
Simas, T., and Suckling, J. (2016). Commentary: semi-metric topology of the human connectome: sensitivity and specificity to autism and major depressive disorder. Front. Neurosci. 10:353. doi:10.3389/fnins.2016.00353
Simas, T. M. L. M. (2012). Stochastic Models and Transitivity in Complex Networks. Ph.D. thesis. Indiana University.
Varshney, K. R., Varshney, L. R., Wang, J., and Myers, D. (2013). Flavor pairing in medieval European cuisine: a study in cooking with dirty data. arXiv:1307.7982 [physics.soc-ph]. Available at: https://arxiv.org/abs/1307.7982
Keywords: food-pairing, food-bridging, semi-metricity, complex network theory, graph theory, metric backbone, semi-metric backbone
Citation: Simas T, Ficek M, Diaz-Guilera A, Obrador P and Rodriguez PR (2017) Food-Bridging: A New Network Construction to Unveil the Principles of Cooking. Front. ICT 4:14. doi: 10.3389/fict.2017.00014
Received: 01 February 2017; Accepted: 03 May 2017;
Published: 02 June 2017
Edited by:
Lav R. Varshney, University of Illinois at Urbana–Champaign, United StatesReviewed by:
Michael S. Vitevitch, University of Kansas, United StatesYong Yeol Ahn, Indiana University System, United States
Copyright: © 2017 Simas, Ficek, Diaz-Guilera, Obrador and Rodriguez. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tiago Simas, dGlhZ28uc2ltYXNAdGVsZWZvbmljYS5jb20=
 Tiago Simas
Tiago Simas Michal Ficek1
Michal Ficek1 Albert Diaz-Guilera
Albert Diaz-Guilera