- 1Department of Physics, School of Education, Drexel University, Philadelphia, PA, United States
- 2Department of Physics, Florida International University, Miami, FL, United States
- 3Lyman Briggs College, Department of Physics and Astronomy, Michigan State University, Lansing, MI, United States
- 4Department of Psychology, Florida International University, Miami, FL, United States
- 5Department of Psychology, Temple University, Philadelphia, PA, United States
Modeling Instruction (MI) for University Physics is a curricular and pedagogical approach to active learning in introductory physics. A basic tenet of science is that it is a model-driven endeavor that involves building models, then validating, deploying, and ultimately revising them in an iterative fashion. MI was developed to provide students a facsimile in the university classroom of this foundational scientific practice. As a curriculum, MI employs conceptual scientific models as the basis for the course content, and thus learning in a MI classroom involves students appropriating scientific models for their own use. Over the last 10 years, substantial evidence has accumulated supporting MI's efficacy, including gains in conceptual understanding, odds of success, attitudes toward learning, self-efficacy, and social networks centered around physics learning. However, we still do not fully understand the mechanisms of how students learn physics and develop mental models of physical phenomena. Herein, we explore the hypothesis that the MI curriculum and pedagogy promotes student engagement via conceptual model building. This emphasis on conceptual model building, in turn, leads to improved knowledge organization and problem solving abilities that manifest as quantifiable functional brain changes that can be assessed with functional magnetic resonance imaging (fMRI). We conducted a neuroeducation study wherein students completed a physics reasoning task while undergoing fMRI scanning before (pre) and after (post) completing a MI introductory physics course. Preliminary results indicated that performance of the physics reasoning task was linked with increased brain activity notably in lateral prefrontal and parietal cortices that previously have been associated with attention, working memory, and problem solving, and are collectively referred to as the central executive network. Critically, assessment of changes in brain activity during the physics reasoning task from pre- vs. post-instruction identified increased activity after the course notably in the posterior cingulate cortex (a brain region previously linked with episodic memory and self-referential thought) and in the frontal poles (regions linked with learning). These preliminary outcomes highlight brain regions linked with physics reasoning and, critically, suggest that brain activity during physics reasoning is modifiable by thoughtfully designed curriculum and pedagogy.
Introduction
Active learning is neither a curriculum nor a pedagogy. Active learning is a class of pedagogies and curriculum materials that strive to more fully engage students and promote critical thinking about course material. Students learn more effectively when they engage in investigations, discussions, model building, problem solving, and other active explorations (National Research Council, 2012; Kober, 2014). However, typical university instruction in physics (and other Science, Technology, Engineering, and Mathematics [STEM] fields) has been lecture-based. While lectures can be interesting, and some students clearly have been trained to become engaged during lectures (Schwartz and Bransford, 1998), for the majority of students, lectures are passive activities. This mismatch between the ways that students learn and the way many classes are taught is the primary motivation for the transformation of STEM instruction. When classrooms are transformed, the evidence is overwhelming; students learn more and are more likely to succeed in active learning settings (Freeman et al., 2014).
Multiple transformative curricula and pedagogical approaches have been developed for introductory physics to promote active learning. For example, Peer Instruction emerged to enhance standard lecture-based approaches by incorporating conceptual questions for discussion and, in turn, facilitated development of personal response systems (Crouch and Mazur, 2001). Tutorials in Physics were developed to supplement standard lectures through use in recitation sections (McDermott and Shaffer, 2001). Other materials such as Student Centered Active Learning Environment with Upside-down Pedagogies [SCALE-UP] (Beichner and Saul, 2003) and Investigative Science Learning Environments [ISLE] (Etkina et al., 2006; Etkina and Van Heuvelen, 2007) implement a studio-format that integrates lab and lecture, including greater amounts of conceptual reasoning and greater emphasis on exploration. Modeling Instruction (MI) is an active learning approach (Brewe, 2008) similar to SCALE-UP and ISLE in that it is a complete course transformation integrating lab and lecture components into one studio format class. However, MI is distinct from other reforms in that it was built around an explicit epistemological theory of science, and this foundation is one of the motivations for using functional magnetic resonance imaging (fMRI) to study how learning physics may impact brain network development.
Hestenes (1987) avers that science by its very nature is a modeling endeavor. Science proceeds by developing models that describe and ultimately predict phenomena. As a model is developed, it is validated through the interplay between the predictions generated by the model and the evidence that emerges supporting such predictions. Once a valid model has been developed, the model is deployed to new situations. This is a process which Kuhn (1970) called “normal science,” whereby scientists use existing prevalent models to explore the models' limits of applicability and search for places where the models give rise to predictions in contrast with evidence. Ultimately, models reach their limits of applicability and need to be revised or in some cases abandoned entirely, beginning what Kuhn called “revolutionary science.” When this happens, a new model is proposed, and the cycle begins anew.
The modeling theory of science is the theoretical and epistemological basis of MI. This, however, is a theory of science, not a theory of science instruction. It translates to instruction through the premise that, if modeling is how science proceeds and we believe students should be engaged in authentic scientific practices, then instruction should be designed to engage students in the process of modeling. Wells et al. (1995) describe the Modeling Cycle as the recursive process of engaging students in model development, validation, deployment, and revision.
In this paper, we first provide an overview of the theoretical background, development process and critical features behind MI as a transformative curricula and model-building endeavor. This overview serves to motivate why scientific model development in students resulting from university instruction warrants further investigation not only at the academic (e.g., grades) and social level (e.g., social networks) but also at the neurobiological level as a putatively measurable phenomena that occurs within the brain. Then, we shift focus to present results from a fMRI study in which we measured brain activity among students engaged in physics reasoning and model use before and after they completed a MI course. We subsequently discuss the results which show distinctive brain activity related to physics reasoning and that instruction consistent with a Modeling theory of science modifies brain activity from pre to post-course.
Role of Conceptual Models in Introductory Physics Curriculum
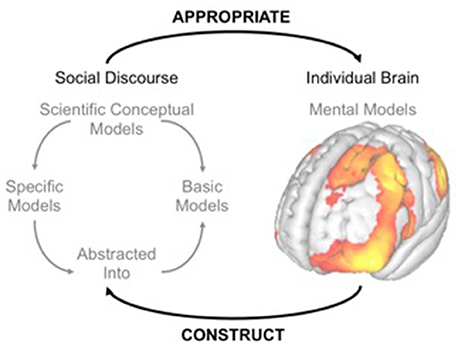
Building instruction around modeling necessitates a working understanding of models. To date, research in the MI context has focused on conceptual models, which are instructionally useful, rather than mental models, which have been difficult to directly observe. Herein, we seek to expand upon existing research by adopting neuroimaging techniques to interrogate mental models among students receiving instruction via an explicit conceptual modeling approach (i.e., MI). We operate from the following definition of a conceptual model: conceptual models are purposeful coordinated sets of representations (e.g., graphs, equations, diagrams, or written descriptions) of a particular class of phenomena that exist in the shared social domain of discourse. This definition has several features worth elaborating. First, it fits on a t-shirt. Second, this definition establishes the domain, purpose, and composition of conceptual models, which we expand upon below. Finally, this definition of conceptual models has helped us design research to look for evidence of the modeling process in classrooms. Figure 1 illustrates the relationship between conceptual and mental models.
Attempting to synthesize the many definitions and descriptions of models is not our purpose. Instead, we aim to highlight some of the features of our definition that were relevant to the development of the MI approach based on building, validating, deploying and revising models. These features (i.e., the composition, purpose, and domain of conceptual models), then will be used to structure the investigations into the nature of student's mental model formation as measured via brain-based fMRI data.
Composition
Conceptual models are composed of representations. Representations are human inventions/constructs that stand in for the phenomena (Morgan and Morrison, 1999; Giere, 2005; Frigg and Hartmann, 2006; Windschitl et al., 2008; Schwarz et al., 2009). In physics, common types of representations include graphs, vector diagrams, equations, simulations, words, and pictures (Krieger, 1987). From the MI perspective, this means that instruction should focus on helping students to identify, use, and interpret representational tools that are useful in describing physical systems. Instruction around model building necessarily focuses on what representations are common to a discipline, how they are used, and how information can be extracted from them. Further, the coordination of these representations helps to build a more robust model, and provide a variety of ways to extract information from the model (Hestenes, 1992; Halloun, 2004).
Purpose
Morgan and Morrison (1999) described mental models as mediators of thought, autonomous from, but in correspondence with the system they represent. This mediating function of models establishes the roles that models have within science as the center of thought, explanation, and prediction (Craik, 1943; Johnson-Laird, 1983). For example, Craik (1943) stated, “If the organism carries a ‘small-scale model’ of external reality and of its own possible actions within its head, it is able to try out various alternatives…” Instructionally, if models fill this role of mediators of thought, then models should structure the organization of the curriculum. Models also allow students to address new phenomena (Odenbaugh, 2005; Svoboda and Passmore, 2011; Gouvea and Passmore, 2017). This purpose is built into the instructional modeling cycle where students are encouraged to understand new phenomena by deploying existing models to extract information about and characterize the phenomena. When existing models do not work, students are expected to adapt or redevelop models that can account for these new phenomena.
Domain
We propose a distinction between scientific conceptual and mental model domains and place conceptual models in the shared social domain of discourse. This perspective differs from other conceptualizations where mental models within individuals' minds/brains are implicitly or explicitly the center of focus (Greca and Moreira, 2000, 2001). Specifically, to infer the status of a student's mental model, investigators typically assess students' actions or behaviors, such as writing, speaking, drawing, predicting, or arguing (Halloun, 1996a; Justi and Gilbert, 2000; Lehrer and Schauble, 2006). Thus, evidence of model-based reasoning exists external to the individual and is contingent on an external evaluation. Instructionally, our efforts have been to help students develop models as a distributed cognitive element. Meaning that each individual student will have an instantiation of the shared model, but the visible elements of the model exist external to individuals through writing, speaking, drawing, diagraming, predicting, and/or simulating. This notion of shared models improves team performance and the learning process (Mathieu et al., 2000). As such, the design of the MI curriculum and pedagogy focuses not on mental models per se, but on the social construction of a model. In other words, we focus students on using consistent representational tools to build models of phenomena in an interactive team environment. Models are shared among class members and agreed upon before deploying these models to analyze new situations. We provide a more detailed description of the classroom setting in section “Features of MI Learning Environment” but much of class time is spent in small groups developing models of specific phenomena on small portable whiteboards, which are then presented at larger “board meetings.” The interplay between smaller and larger groups provides a vehicle for students to use diagrams, equations, or graphs to represent elements of the model.
We do not reject that individuals have internal mental models, or that these mental models include connections between representations and concepts, or interactions between mathematics and intuition, for example. As Rogoff (1990) points out, cognitive functions are essential components of purposeful action. We are aligned with the notion that scientific conceptual models are distributed cognitive elements, which are then appropriated by individuals. During the appropriation, students construct the mental models in correspondence with the scientific conceptual models. Rather our point is that assessing external behaviors speaks to the conceptual model domain and assessing the mental model domain would benefit from directly considering the brain.
Role of Conceptual Models in Instruction
For instructional purposes, models represent an appropriate and accessible level of abstraction (Halloun, 2004). Within a larger context, models occupy the middle level of a conceptual hierarchy (Table 1; Halloun, 2004; Matthews, 2007) which is best illustrated by a representative example (Lakoff, 1987). Veterinarians are not likely to study the superordinate category of animals, which is too broad a categorization to be useful. Nor are they likely to study the subordinate category of retrievers; this is too specific to be broadly useful. Instead, dogs are likely to be the level of focus. This level is referred to as the “basic” level and is considered the ideal focus for instruction (Halloun, 2004).
In the MI classroom, building basic conceptual models begins with considering a specific phenomenon to be described. Once a target phenomenon is established, the next step is to characterize the phenomena through relevant representational tools. For example, using velocity vs. time graphs to represent the motion of a moving object. As students create representations of the object's motion, a model of this specific phenomenon is being developed, or what we call a specific model. These specific models are not generally applicable, they pertain to the specific details of the situation being considered. By necessity, specific models are predecessors to basic models. Specific models are made more robust as additional representational tools are introduced and integrated with existing ones. Introduction of representational tools and the subsequent negotiation of their use and interpretation are motivated by specific phenomena to be modeled, so the models created are always specific models.
However, a desirable scientific skill is to reason based on general models (Nersessian, 1995, 2002a,b). As such, the MI curriculum and pedagogy is specifically designed to facilitate the students' transition from specific to basic models. Basic models, which are general and represent entire classes of phenomena (such as a constant acceleration model), are abstracted from a collection of specific models (Halloun, 1996b, 2004). For example, the general features of a basic constant acceleration model can be abstracted from specific models of objects undergoing constant acceleration, such as objects in free fall, or uniformly slowing down. This is achieved in the MI classroom by having students consider a number of specific models, and then identifying the features that are similar to all such models. For example, all constant acceleration models include a linear velocity time graph. These similar features are then compiled into one model that can be used for all situations, a basic model. Basic models are useful because they are not tied to a specific phenomenon, much like the Standard Model is a basic model built up and abstracted from the specific models of atomic collisions, particle interactions, etc. Basic models are essential in science as they promote abstract reasoning about novel phenomena (Nersessian, 1995); when physicists seek to understand interactions of atomic particles they start by using the Standard Model.
Once a basic model is established, students deploy the model in a variety of settings. This deployment phase is most aligned with the standard problem solving that happens in physics classes. The purpose is to develop skill at adapting the representations that make up the model to new situations and extracting information about the situation from the representations.
The final stage in the MI instructional cycle is revision. Revision of a basic model happens when students encounter a phenomenon that does not fit with the model's assumptions. An example often encountered comes when students attempt to generate a specific model of two-dimensional motion on the basis of a one-dimensional constant acceleration model. The one-dimensional case is inadequate without modification to understand motion in two dimensions, and thus must be revised. In some cases, revision involves a simple modification of the representational tools, and in other cases, it requires starting with an entirely different model.
In summary, the modeling cycle of MI describes the progression of course content. In addition, MI also interweaves social interactions designed to facilitate discourse in the service of building conceptual models. Next, we more fully describe the precise aspects of the MI learning environment that support the development, validation, deployment, and revision of models.
Features of MI Learning Environment
Basic conceptual models are often well-developed for scientists and course instructors, yet these models are not well-developed for the students in introductory physics courses. Accordingly, the first contextual feature of the MI classroom is to support students in re-developing constituent basic models within their own learning environment. The MI instructor's role is thus to guide students through the development of these basic conceptual models by establishing activities and providing scaffolding to manage student discourse and promote model building and deployment. In this way, the MI curriculum and pedagogy can be considered a guided inquiry approach. Students are not expected to discover physical laws without strong instructor guidance who chooses activities, introduces representational tools, and guides students toward their appropriate use and interpretation. In this way, the instructor is a guide to the disciplinary norms and tools.
Student Participation in a Model-Centered Learning Environment
Accomplishing this fundamental re-development of basic conceptual models requires students to be active and engaged participants in the learning environment. Accordingly, there are specific ways MI students are expected to participate in the re-development of basic conceptual models. First, students are expected to be involved in identifying the way that tools such as pictures, diagrams, graphs, and equations are used to represent phenomena. They are not expected to invent or discover these tools, but instead to determine with instructor guidance how these tools are used and how to interpret these representations. For example, how does a vector representation of forces describe interactions the object is involved in, and what do these forces allow us to infer about the current state of the object and its future behavior? Second, students are expected to be involved in the interpretation of these representational tools and drawing inferences from them as they pertain to physical laws. Third, students are expected to then deploy these established basic conceptual models by extending them to novel situations. Finally, students are expected to communicate basic conceptual models. This promotes greater expertise with the models when presenting to others and facilitates competence in scientific communication skills.
Studio Format
MI is designed for implementation in a studio-format classroom. In studio physics classrooms students are able to flexibly engage in various types of activities, which may include labs, conceptual reasoning, or problem-solving activities. At Florida International University (FIU), the MI classroom integrates both the lecture and lab components of the introductory physics course and meets for a total of 6 h per week across 3 days. Typically, students work in small groups of three to complete in-class activities. This small group work is summarized on small portable whiteboards. These whiteboards are then presented in larger group “board meetings” where all students in the class actively participate.
Small Group Participation
During the small group component, students work on model-building activities. In these groups, students begin the process of reaching consensus by creating whiteboards for sharing or “publishing” their lab results and/or solutions to problems. The instructor's role is to circulate through the classroom, asking questions, introducing new content, and examining the whiteboards that are being prepared. This small group work allows students to work together on a model-building activity, generate conceptual models, and practice communicating scientific information in a relatively “low-stakes” setting.
Large Group Participation: The “Board Meeting”
The practice of having students first work in small groups and then present their outcomes to a larger group provides students with multiple opportunities to negotiate the use of conceptual models. The board meetings involve all students in the class gathering in a circle such that every member can see every other member and every groups' boards. During the board meeting, the instructor assumes the role of disciplinary expert and guides the discourse toward a shared conceptual model. Facilitating the discussion involves moderating the groups' whiteboard presentations, addressing student questions, and helping groups clarify their presentations and understanding. The instructor's guidance during the board meetings relies heavily on providing student groups with formative feedback. The explicit goal of these board meetings is to reach consensus regarding the conceptual models. In addition to the explicit goals, tacit goals include establishing the norms of a discourse community and encouraging students to utilize scientific argumentation strategies (Passmore and Svoboda, 2012). These strategies include supporting claims with evidence and reasoning based on the shared conceptual models.
Pairing Large and Small Group Interactions
The combined interaction structure is designed to elicit target conceptual models. The structure of these interactions also mimics the structure of science in general and physics in particular as practiced in a research setting. Students work in small research groups, building up and synthesizing the conceptual model that is subsequently ‘published’ at the board meeting, much like a scientific meeting. Both the small and large group settings rely on the pedagogical skill of the instructor. In MI-like environments (which are less “instructor-centered” than traditional classrooms), the trajectory of the learning takes varied paths based on the input of the participants. For this reason, the curriculum and pedagogy of MI are less like a script for an actor to follow, and more like a set of guidelines for an improvisational comedienne.
Impact on Student Outcomes
The combination of curriculum materials designed to recursively implement the modeling cycle and a learning environment and pedagogy that are similarly supportive have been shown to be effective at promoting learning. Like other transformed curricula in university physics, MI promotes both conceptual understanding and student success in introductory physics (Brewe et al., 2010b). A survival analysis suggests that the increased success rate in introductory physics is not a result of lowered standards, as students from MI classes showed equivalent likelihood of success in completing a major in physics as students from lecture classes (Rodriguez et al., 2016). MI students also report improved attitudes about learning physics (Brewe et al., 2009, 2013) and these attitudinal shifts are equitable in terms of ethnicity (Traxler and Brewe, 2015). The group interactions in a MI class promote more well-developed classroom networks (Brewe et al., 2010a), and these networks are known to facilitate retention in physics courses (Zwolak et al., 2017). Positive shifts in self-efficacy associated with participating in MI have been documented, (Sawtelle et al., 2010) although not consistently (Dou et al., 2016). We are in the process of studying qualitatively the construction of a conceptual model in MI (Brewe and Sawtelle, 2018) and investigating students' representational choices in problem solving (McPadden and Brewe, 2017). These studies are consistent with students constructing and using conceptual models to solve problems and analyze physical systems. The successes coming from the MI classroom motivate our current research into the neurobiological mechanisms of reasoning in physics.
Investigating Mental Model Development Using Neuroimaging
While prior assessments of MI's impact on students has typically focused on the social construction of conceptual models (Brewe, 2008, 2011; Sawtelle et al., 2012), here we consider MI's potential impact on mental models using brain imaging techniques. This study aimed to investigate brain activation during a physics reasoning task and changes in brain activation after MI course instruction relative to before such instruction. Previous neuroimaging studies have localized brain activity associated with reasoning across various modalities (e.g., mathematics, formal logic, and fluid reasoning; Prabhakaran et al., 1997; Arsalidou and Taylor, 2011; Prado et al., 2011), but no investigations have probed for such brain activity in the field of physics or across physics classroom instruction. Because of this, no standardized tasks have been adapted for the MRI environment to examine such brain activation. Therefore, as a first step, we sought to develop a novel neuroimaging paradigm to probe brain activity during physics reasoning. We focused the development of this task on mental model use during physics reasoning, as previous research has provided evidence that students' use a variety of mental models during conceptual physics reasoning (Nersessian, 1999; Hegarty, 2004). Thus, we adapted items from the well-known Force Concept Inventory (FCI; Hestenes et al., 1992) which is known to engage conceptual physics reasoning. FCI questions were modified to fit with the parameters of the MRI data collection, and to investigate physics reasoning, (see section “Physics Reasoning Task” for further details. Simultaneously, to facilitate formation of neuroanatomical hypotheses regarding the brain networks we might observe during physics reasoning, we conducted a neuroimaging meta-analysis (Bartley et al., in press) of fMRI studies that investigated problem solving across a diversity of representation modalities. Briefly, the primary outcome of that meta-analysis was that similar reasoning tasks using mathematical, verbal, and visuospatial stimuli involving attention, working memory, and cognitive control, activated dorsolateral prefrontal and parietal regions. Participants completed this physics reasoning task while undergoing functional magnetic resonance imaging (fMRI) scanning, both before (pre) and after (post) completing a physics course in order to investigate the putative impact of physics instruction on brain function. Driving this neuroeducation project were two main hypotheses: (1) This novel physics reasoning task would induce increased activity in brain regions previously associated with attention, working memory, and problem solving (e.g., lateral prefrontal and parietal regions), and (2) Activation patterns would differ from pre- to post-course, indicating that brain activity can be modified as a result of physics instruction.
A few prior studies have demonstrated that short- and long-term course instruction can impact brain function. Differences in brain function have been observed from pre- to post-course among students enrolled in a 90-day Law School Admission Test preparation course (Mackey et al., 2013). Mason and Just (2015) showed that providing information to research participants about mechanical systems while in the MRI scanner, which they called physics instruction, led to changes in knowledge representation during successive stages of learning. In a separate study, they were also able to use machine learning and factor analysis to identify neural representations of four physics concepts: motion visualization, periodicity, algebraic forms, and energy flow (Mason and Just, 2016). However, to our knowledge, this is the first neuroeducational study to consider the impact of a full, semester-long physics class on the brain.
Brief Primer on Neuroimaging Studies
This manuscript is intended for an educational research audience, with the expectation that readers have not had extensive experience with neuroimaging as a research methodology. As such, this section provides a brief overview of neuroimaging studies, particularly fMRI. In neuroimaging studies, researchers develop an experimental task to isolate mental operations of interest that participants perform lying in a MRI scanner while a series of three-dimensional brain images are acquired. Typically, these brain images are acquired approximately every 2 s and are composed of small volume elements called voxels, which in this study measured 3.4 mm3. Within each voxel, the blood's changing oxygen levels (known as the blood-oxygenation level-dependent [BOLD] signal) are measured. Task-related changes in the BOLD signal provide an indirect measure of brain activity. In one implementation of fMRI experimental design, brain images are collected in blocks. During ‘active task’ blocks, participants are presented a stimulus (e.g., a physics question) engendering cognitive processes of interest (e.g., physics reasoning) and are instructed to make a response using a MRI-compatible keypad. During carefully constructed ‘control task’ blocks, participants are also presented with stimuli and give responses; however, the stimuli presented do not engender the cognitive processes of interest. Contrasting active blocks with control blocks presumably isolates task-related brain activity associated with the cognitive processes of interest and excluding those common to both conditions (e.g., visual processing, word reading, button pressing).
Following data collection, fMRI data are processed to correct for in-scanner head movement and fitted to a standardized brain template to enable averaging over a group of participants. BOLD time series from each voxel are input into a general linear model (GLM) including distinct regressors for various task events (and other known sources of noise) to characterize the degree to which variability in the BOLD signal correlates with those task events. Resulting beta weights from active and control task blocks can then be contrasted and significant differences are interpreted as differences in brain activity between blocks. This procedure is repeated for the BOLD time series across all voxels in the entire brain. Additional multi-level modeling can be performed on these results, as was done in this study, to test for changes in brain activity across repeated measures (i.e., from pre- to post-instruction).
Methods
Participants
Participants were drawn from MI classes at FIU over the course of 3 years (academic years 2014–2017). We recruited 55 students (33 male, and 22 female) in the age range of 18–25 years old (mean ± SD: 20.1 ± 1.4). All participants were screened to be right-handed, not using psychotropic medications, and free of psychiatric conditions, cognitive or neurological impairments, and MRI contraindications. Volunteers invited to participate had not previously taken a college physics course and met either a GPA (>2.24) or SAT Math (>500) inclusion criteria. These criteria were implemented to minimize between-participant variability that could confound brain measurements associated with the experimental conditions. Written informed consent to a protocol approved by the FIU Institutional Review Board was obtained from all participants. Imaging data were collected on a General Electric 3-Tesla Healthcare Discovery 750 W MRI scanner located in the Neuroimaging Suite (NIS) of the Department of Psychology at the University of Miami (Coral Gables, FL). Each participant completed a 90-min MRI scanning session at both a pre- and post-instruction time point. The pre-session scans were scheduled within the first 4 weeks of the semester and the post-session scans were completed in the first 2 weeks following the semester. All participants were compensated for their time participating in the MRI assessment ($50 for pre- and $100 for post-scans).
Physics Reasoning Task
We adapted a set of questions from the Force Concept Inventory (FCI) for presentation in the MRI scanner (Figure 2A). The FCI was chosen given the substantial amount of extant data from students in MI at FIU on this measure (Brewe et al., 2010b), established reliability measures (Lasry et al., 2011), and known time requirements (Lasry et al., 2013). The FCI is a 30 question, multiple choice conceptual survey of students understanding of Newtonian mechanics (Hestenes et al., 1992). Each question has five multiple choice options, one correct and four distractors which were originally generated from student responses to open-ended versions of the same questions. The questions present “every-day scenarios,” do not require any mathematical calculations, and are presented as text describing the scenario accompanied by a representational diagram. To ensure that MRI data collection sessions were manageable and well-tolerated by participants, we reduced the number of FCI questions from 30 to nine (FCI 2, 3, 6, 7, 12, 14, 27, and 29). These nine questions were selected to span a range of difficulty levels that were simultaneously challenging enough to tax the mental resources of participants, but not necessarily the most difficult items in the FCI, as determined by item response curves in Morris et al. (2012) (Table 2). Additionally, because measurement of brain networks via fMRI require the repeated observations across multiple yet similar experimental trials, we sought to narrow the broad range of physics-related cognition being probed in this task and selected questions that required students to determine the trajectories and motion of objects as resulting from different scenarios and combinations of initial velocities and/or force configurations. Given technical constraints associated with the use of a four-button MRI-compatible keypad, the questions were modified by removing the least chosen of the five multiple choice options, as indicated by the item response curves of Morris et al. (2012). In the current neuroimaging task implementation, each question was parsed into three self-paced presentation phases; participants were allowed to control the timing of these phases. The first phase of the question involved presentation of the text describing the phenomena and an accompanying diagram. The second phase posed the question, and the third phase presented the multi-choice answer options. FCI responses were assessed for overall and item-specific accuracy.
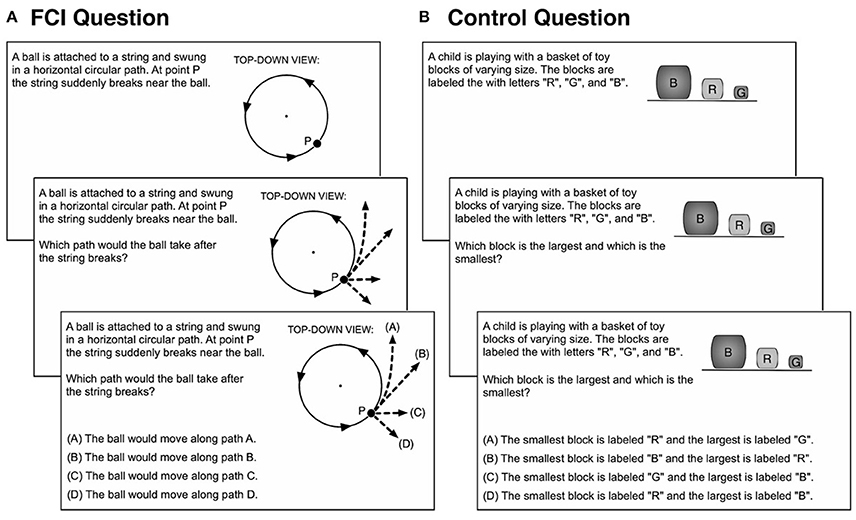
Figure 2. Example items from the physics reasoning fMRI task. (A) FCI questions described a physical scenario using pictures and words and then asked a physics question followed by four potential answers. (B) Control question shared basic visual and linguistic features with FCI questions, however control questions did not ask students to engage in physics reasoning.
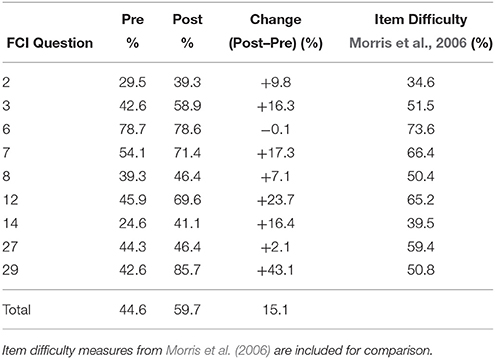
Table 2. Overall and individual item accuracy for pre and post instruction FCI questions in the scanner.
In addition to FCI questions, participants answered a series of “control questions” (Figure 2B), each of which had similar characteristics to the FCI questions in terms of reading requirements, visual complexity, and overall design. However, control questions did not inquire about physics-related content, instead these questions focused on reading comprehension and shape discrimination. Control questions allowed us to isolate cognitive processes presumably related to physics reasoning when contrasting FCI (“active task”) vs. control questions (“control task”).
FCI and control questions were presented in pseudo-random orders within three task runs. Each question was followed by 20 s of “rest,” during which participants maintained their gaze on a fixation cross centrally projected on the screen. These three runs lasted approximately 6 min each. Participants received instruction and practice on the task in a carefully managed mock scanner training session to ensure correct performance during the MRI session. In addition to acquainting participants to the task, the mock scanner also allows participants to experience what the actual MRI scan will be like.
Data Analysis
Details on fMRI data acquisition parameters can be found in the Supplementary Materials. Prior to analysis, the data were preprocessed using commonly used neuroimaging analysis software packages: FSL (FMRIB Software Library, www.fmrib.ox.ac.uk/fsl) and AFNI (Analysis of Functional NeuroImages, http://afni.nimh.nih.gov/afni). Standard fMRI preprocessing procedures involved motion correction to remove signal artifacts associated with head motion, high-pass filtering to remove low frequency trends in the signal associated with non-brain noise sources (i.e., cardiac or respiratory), and spatial smoothing to increase signal to noise ratio during analysis. The data were then mapped to a standardized brain atlas (MNI152) to allow for group-level assessments.
We conducted two primary analyses to identify: (1) brain regions linked with physics reasoning (task effect) and (2) changes in brain activity associated with physics instruction (instruction effect). To delineate brain regions linked with physics reasoning at the pre-instruction time point, each preprocessed fMRI data set was input into a voxel-level General Linear Model (GLM) including regressors for the FCI and control task conditions (and various nuisance signals). Contrast images were created for each participant by subtracting the beta weights associated with the control questions from those for the FCI questions representing the degree to which each voxel responded more during physics reasoning as compared to the control condition (FCI > Control). These participant-level contrast images were then input into a group-level, one-sample t-test and significant physics reasoning-related brain activations were defined using a threshold of Pcorrected < 0.05 (Pvoxel−level < 0.001, family-wise error [FWE] cluster correction). To delineate brain regions showing physics reasoning-related activation changes following a MI course, the participant-level FCI > Control task contrast images (described above) from the pre- and post-instruction data collection sessions were input into a group-level, paired samples t-test. Both Pre > Post and Post > Pre contrasts were computed and significant instruction-related brain activity changes were defined using a Pcorrected < 0.05 threshold (Pvoxel−level < 0.001, FWE cluster correction). Follow up correlational analyses were also conducted between the BOLD signal change across instruction (Post > Pre) in the four largest significant clusters (≥1,000 voxels) identified in the instruction effect analysis described above and accuracy post-instruction on the FCI using P < 0.0125, Bonferroni corrected,. Because the clusters probed showed significant extent across multiple brain areas, BOLD signal was extracted from spherical seeds centered at the peaks z-score of each cluster.
Results
Accuracy
Table 2 includes the accuracy results of student responses for the nine questions in the pre and post-instruction scans along with item difficulties based in classical test theory, Morris et al. (2006). A paired-samples t-test was conducted to compare post- vs. pre-instruction means. Cohen's d, was calculated to identify the magnitude of the effect, and 95% confidence intervals on the effect. The results of the t-test [t(55) = 6.31, p < 0.001] and Cohen's d (d = 0.84) with a 95% confidence interval of 0.45–1.23 indicated with a high degree of confidence that response accuracy increased after instruction. These results are consistent with prior results examining increased FCI accuracy after course instruction (Brewe et al., 2010b). Furthermore, these accuracy results from participants in the scanner are in line with the classical test theory item difficulty (outside the scanner performance), where difficulty is calculated as the average score on a particular item.
Task Effect
MI students exhibited physics reasoning-related brain activity (FCI > Control) at the pre-instruction time point in four general brain areas, the prefrontal cortex, the parietal cortex, the temporal lobes, and the right cerebellum (Figure 3, red; Supplemental Table 1). More specifically, in the prefrontal cortex (PFC), activation peaks were observed in the left superior frontal gyrus (SFG), dorsomedial PFC (dmPFC), bilateral dorsolateral PFC (dlPFC), inferior frontal gyri (IFG), and orbitofrontal cortex (OFC). Within the posterior parietal cortex, brain activity was observed bilaterally in the supramarginal gyri, intraparietal sulcus (IPS), and angular gryi (AG). Large bilateral clusters of activation during physics reasoning were also observed in middle temporal (MT) and medial superior temporal (MST) areas. These same patterns of task-related brain activity from the pre-instruction stage were also observed when performing a similar assessment at the post-instruction stage (data not shown).
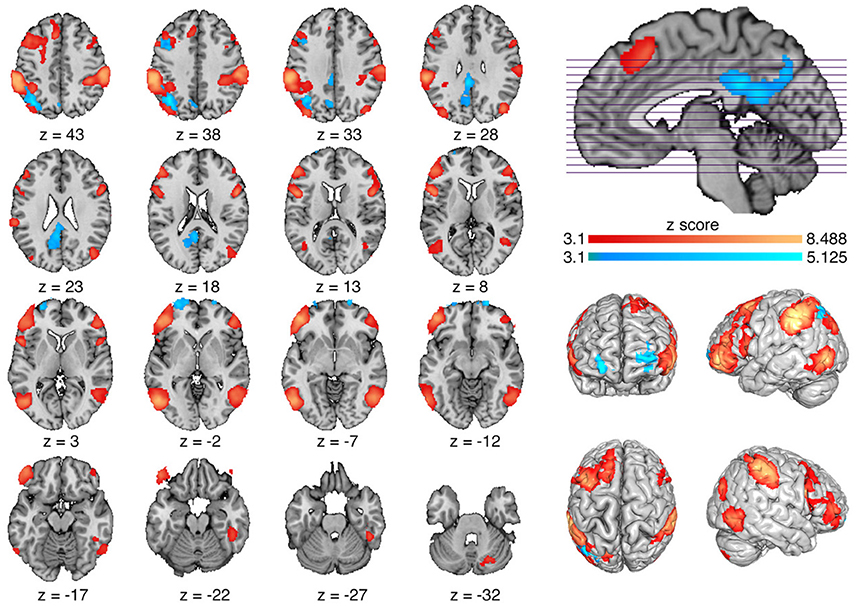
Figure 3. Group-level fMRI results. (Red) Task effect: Brain regions showing increased activity during the physics reasoning task (FCI > Control) at the pre-instruction stage. (Blue) Instruction effect: Brain regions showing increased activity at the post- relative to pre-instruction (Post > Pre) scan during the physics reasoning task.
Instruction Effect
Significant increases in brain activity following instruction (Post > Pre) were observed within prefrontal and parietal cortices (Figure 3, blue; Supplemental Table 2). In particular, three clusters of increased PFC activity were identified in the left dlPFC along the inferior precentral sulcus, and bilaterally in the frontal poles. Parietal areas demonstrating increased activation after instruction were located in the posterior cingulate cortex (PCC) extending into retrosplenial cortex and the precuneus and in the left angular gyrus. No brain regions showed significantly more task-related activity at the pre-instruction stage as compared to post-instruction (Pre > Post). Follow up correlation analysis between the left PCC, left angular gyrus, left orbital frontal pole, and left DLPFC and accuracy on the FCI yielded no significant correlation (rpcc = −0.12, pcorrected = 1; rag = −0.07, pcorrected = 1; rofc = −0.01, pcorrected = 1; rdlpfc = 0.02, pcorrected = 1).
Discussion
This neuroeducational study represents an initial effort to understand how physics reasoning may translate to the level of brain function assessed by fMRI and how instruction brings about changes in brain activity. To this end, we have provided fMRI results of brain activation from two main assessments. First, we observed that the physics reasoning task (FCI > Control questions) was associated with increased brain activity notably in lateral prefrontal and parietal regions. Second, we observed that students who completed the MI course showed increased activation during the physics reasoning task after the course in the posterior cingulate cortex and frontal pole regions.
Accuracy and Physics Reasoning
Participant responses to the FCI questions in the scanner show accuracy that is in line with published item difficulties and post course improvement in accuracy are consistent with Brewe et al. (2010b). This suggests that the MRI version of the task we developed is prompting physics reasoning that is consistent with that observed out of scanner environment. Effect sizes from pre- to post-instruction indicate similar performance on this task with modified FCI questions as on the full FCI. This improvement is indicative of a shift in physics reasoning as a result of instruction. We do not interpret these changes as recall effects for two reasons, the results of the FCI were not discussed with students, and the task itself was not identified as being derived from the FCI. Further, Henderson (2002) has shown that recall effects over the duration of a full semester are minimal. While accuracy is important for characterizing and to some degree validating the task that was developed for the fMRI environment, we did not expect accuracy to correlate with brain activity. Instead, physics reasoning, regardless of accuracy, is linked to brain activity.
Task Effect: Brain Activity Linked With Physics Reasoning
Our initial analysis identified brain activity among college students associated with physics reasoning (FCI > Control) in lateral prefrontal and parietal regions. One interpretation is that activity in these regions supports cognitive processes critical for answering physics reasoning problems such as attention, working memory, spatial reasoning, and mathematical cognition. More specifically, the lateral PFC's role in executive functions such as working memory and planning are well-characterized (Bressler and Menon, 2010) and these areas are important in manipulating representations in working memory and reasoning (Andrews-Hanna, 2012; Barbey et al., 2013). Lateral parietal regions are involved in motor functioning as well as spatial reasoning, mathematical cognition, and attention (Wendelken, 2015). Such an interpretation is reasonable in the context of the current task which likely involves generating mental simulations and representations in the service of identifying the correct answer choice. From a large-scale brain network perspective, the brain regions showing physics reasoning-related activation resemble one commonly observed functional brain network known as the central executive network (CEN). The CEN, consisting of lateral prefrontal and parietal regions (Bressler and Menon, 2010), is generally associated with externally oriented attentional and executive processes (e.g., working memory, response selection, and inhibition; Cole and Schneider, 2007; Seeley et al., 2007).
The task-related brain regions we observed were generally similar when separately considering data collected during the pre- and post-instruction scans. While speaking to the consistency of such brain activity, this analysis is not intended to determine which brain regions differ as a function of completing a MI course (see below). We suspect that such task-related brain activity would be similar among students in other instructional environments.
Instruction Effect: Changes in Brain Activity Post-instruction vs. Pre-instruction
Our second analysis identified increased brain activity among students completing the physics reasoning task after taking a MI course (Post > Pre) in the posterior cingulate cortex, frontal poles, dlPFC, and angular gyrus. These brain regions (PCC, angular gyrus) overlap with regions of another commonly observed large-scale functional brain network known as the default-mode network (DMN). The DMN, consisting of posterior cingulate cortex (PCC), angular gyri, medial PFC, and middle temporal gyri (Raichle et al., 2001; Laird et al., 2009), is generally associated with internally oriented cognitive processes (i.e., self-reflection, mind wandering, autobiographical memory, planning; Buckner et al., 2008). However, other lines of evidence also implicate DMN involvement in complex tasks such as narrative comprehension (Simony et al., 2016), semantic processing (Binder et al., 2009; Binder and Desai, 2011) or the generation and manipulation of mental images (Andrews-Hanna, 2012). In the context of the current task, one interpretation is that students may generate mental images to simulate events and formulate predictions. Additionally, post-instruction increase in DMN activity was observed during physics reasoning (which we show is supported by the CEN), and such coupling between the DMN and CEN during cognition has been hypothesized to arise during controlling attentional focus, thereby aiding in efficient cognitive function (Leech and Sharp, 2014).
Other brain regions showing greater activation during physics reasoning after the MI course included the dlPFC and the frontopolar cortex. The frontopolar cortex is a component of a decision-making network often involved with learning (Koechlin and Hyafil, 2007). The dlPFC is critically linked with the manipulation of verbal and spatial information in working memory (Barbey et al., 2013). Given previous links with, for example, mental simulation, working memory, mathematical calculations, and attention, we speculate that post-instruction increased activity in the PCC, angular gyrus, dlFPC and frontal pole may reflect enhanced mental operations and/or models involved with physics reasoning and/or generation of predictions about physical outcomes.
The PCC, left angular gyrus, left frontal pole, and left DLPFC were the four regions of greatest extent to show increased activity (Post > Pre), however, we did not see correlation between change in activity within these areas and accuracy on the FCI after instruction. The FCI is a cognitively demanding task which includes intuitive but wrong answers. Thus, it may simply be that even wrong answers on the FCI require significant mental effort. Inaccurate physics reasoning likely still involves many of the same mental operations successful physics reasoning does (i.e., mental imagery, visualization, prediction generation, and decision making, to name a few). Measures of accuracy in and of themselves may not display a simple one-to-one relationship with changes in brain activity across instruction. Rather, these changes in brain activity may be related to more complex behavioral changes in how student's reason through physics questions post- relative to pre-instruction. These might include shifts in strategy or an increased access to physics knowledge and problem solving resources.
We posit that the observed pre to post-instruction changes in brain activation during physics reasoning are consistent with what one may expect to observe as students develop refined mental models during classroom learning. Physics reasoning, regardless of an individual's familiarity with the material, is a process continually scaffolded by mental model use (Nersessian, 1995, 1999, 2002a,b; Giere, 2005; Koponen, 2006), and effective physics learning is engendered by building and deploying strategies to appropriately implement mental models during reasoning (Hestenes, 1987). In this study, we framed our exploration of learning-induced changes in brain activity in the context of the MI classroom because this pedagogical approach has been shown to effectively encourage the development and flexible implementation of models during physics reasoning (Brewe, 2008; Brewe et al., 2010b). Our experimental results do not go as far as to implicate MI as any more or less effective than other instructional strategies at supporting instructional-related changes in student's brain networks. However, if we accept that physics reasoning inherently relies on mental model use, we can begin to consider a more truly neuroeducational interpretation of physics learning in which shifts in network engagement across instruction bring about student conceptual change. Characterizing these neurobiological changes may ultimately help researchers and educators understand which instructional strategies may best support successful model development. We hold that the mental models student's deployed at the beginning of the semester during reasoning, upheld by a variety of CEN-supported attentional and executive processes, shifted after instruction, as evidenced by student's overall increased accuracy during reasoning. This instruction-induced shift in model use promoted increased involvement from key DMN and CEN regions within reasoning. This study represents an initial step in neuroeducational research demonstrating that such shifts, indicative of learning, are measurable and detectable using non-invasive brain imaging techniques. Additional work is needed to understand the relationship between external conceptual models as studied in science education, with mental models and related cognitive constructs as studied in neuroimaging literature.
This project has several limitations. First, we focused on the MI class and did not assess the brain activity of students from traditional lecture course sections or other active learning environments. Based on the data presented, we do not make claims that MI is a better or the only instructional tool capable of inducing brain network alterations. Rather, in the current study, we used MI as an exemplar case. It remains to be determined if different pedagogies differentially influence how physics reasoning-related brain networks develop. As noted above and consistent with recommendations (Freeman et al., 2014), we will explore this in the future and a future direction could investigate differences among active learning formats. Second, these analyses addressed brain activation and did not consider correlation with other behavioral measures, such as mental rotations, science anxiety, or academic performance measures which could further aid in the interpretation of these fMRI outcomes. Third, consideration of potential differences between female and male students remains for future investigations.
Notwithstanding these limitations and future direction, these preliminary outcomes implicate brain regions linked with physics reasoning and, critically, suggest that brain activity during physics reasoning is modifiable over the course of a semester of physics instruciton. Further work should investigate differences between MI and lecture instruction, as well as addressing differences among different active learning strategies across disciplines. Studying active learning broadly has the potential to more clearly elaborate how these pedagogies impact student learning and brain function.
Ethics Statement
This study was carried out in accordance with the recommendations of Florida International University's Institutional Review Board with written informed consent from all subjects. All subjects gave written informed consent in accordance with the Declaration of Helsinki. The protocol was approved by the FIU IRB.
Author Contributions
EB, JB, and AL had full access to all the data in the study and take responsibility for the integrity of the data and the accuracy of the data analysis. Study concept and design: EB, JB, MR, RL, MS, SP, and AL. Acquisition, analysis, or interpretation of data: EB, JB, MR, VS, TS, ERB, EIB, RO, AN, KB, RL, MS, SP, and AL. Drafting of the manuscript: EB and JB. Critical revision of the manuscript for important intellectual content: EB, JB, MR, VS, TS, ERB, EIB, RO, AN, KB, RL, MS, SP, and AL. Obtained funding: AL, EB, and SP. Administrative, technical, or material support: EB, RL, MS, SP, and AL. Study supervision: AL, MS, SP, MR, and EB.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Primary funding for this project was provided by NSF REAL DRL-1420627 (AL, EB, SP, and JB). Contributions from co-authors were partially provided by NSF 1631325 (AL, MR, and TS), NIH R01 DA041353 (AL, MS, and MR), NIH U01 DA041156 (AL, MS, MR, KB, and ERB), NSF CNS 1532061 (AL), NIH K01DA037819 (MS), NIH U54MD012393 (MS), and FIU Graduate School Dissertation Year Fellowships (AN and RO). Additional thanks to the FIU Instructional and Research Computing Center (IRCC, http://ircc.fiu.edu) for providing HPC and computing resources that contributed to the research results reported within this paper, and to the Department of Psychology of the University of Miami for providing access to their MRI scanner. Lastly, special thanks to the FIU undergraduate students who volunteered, participated, and contributed to this project.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fict.2018.00010/full#supplementary-material
References
Andrews-Hanna, J. R. (2012). The brain's default network and its adaptive role in internal mentation. Neuroscientist 18, 646–656. doi: 10.1177/1073858411403316
Arsalidou, M., and Taylor, M. J. (2011). Is 2+2 = 4? Meta-analyses of brain areas needed for numbers and calculations. NeuroImage 54, 2382–2393. doi: 10.1016/j.neuroimage.2010.10.009
Barbey, A. K., Koenigs, M., and Grafman, J. (2013). Dorsolateral prefrontal contributions to human working memory. Cortex 49, 1195–1205. doi: 10.1016/j.cortex.2012.05.022
Bartley, J. E., Boeving, E. R., Riedel, M. C., Bottenhorn, K. L., Salo, T., Eickhoff, S. B., et al. (in press). Meta-analytic evidence for a core problem solving network across multiple representational domains. Neurosci. Biobehav. Rev.
Beichner, R. J., and Saul, J. M. (2003). “Introduction to the SCALE-UP (student-centered activities for large enrollment undergraduate programs) project.” in Proceedings of the International School of Physics, (July), 1–17. Available online at: http://www.ncsu.edu/PER/Articles/Varenna_SCALEUP_Paper.pdf
Binder, J. R., and Desai, R. H. (2011). The neurobiology of semantic memory. Trends Cogn. Sci. 15, 527–536. doi: 10.1016/j.tics.2011.10.001
Binder, J. R., Desai, R. H., Graves, W. W., and Conant, L. L. (2009). Where is the semantic system? A critical review and meta-analysis of 120 functional neuroimaging studies. Cereb. Cortex 19, 2767–2796. doi: 10.1093/cercor/bhp055
Bressler, S. L., and Menon, V. (2010). Large-scale brain networks in cognition: emerging methods and principles. Trends Cogn. Sci. 14, 277–290. doi: 10.1016/j.tics.2010.04.004
Brewe, E. (2008). Modeling theory applied: modeling instruction in introductory physics. Am. J. Phys. 76, 1155–1160. doi: 10.1119/1.2983148
Brewe, E. (2011). Energy as a substancelike quantity that flows: theoretical considerations and pedagogical consequences. Phys. Rev. Spec. Top. Phys. Edu. Res. 7:020106 doi: 10.1103/PhysRevSTPER.7.020106
Brewe, E., Kramer, L. H., and O'Brien, G. E. (2010a). “Changing Participation Through Formation of Student Learning Communities.” in AIP Conference Proceedings. doi: 10.1063/1.3515255
Brewe, E., Kramer, L., and O'Brien, G. (2009). Modeling instruction: Positive attitudinal shifts in introductory physics measured with CLASS. Phys. Rev. Spec. Top. Phys. Edu. Res. 5:013102. doi: 10.1103/PhysRevSTPER.5.013102
Brewe, E., and Sawtelle, V. (2018). Modeling instruction for university physics: examining the theory in practice. Eur. J. Phys. doi: 10.1088/1361-6404/aac236
Brewe, E., Sawtelle, V., Kramer, L. H., O'Brien, G. E., Rodriguez, I., and Pamelá, P. (2010b). Toward equity through participation in Modeling Instruction in introductory university physics. Phys. Rev. Spec. Top. Phys. Edu. Res. 6:010106. doi: 10.1103/PhysRevSTPER.6.010106
Brewe, E., Traxler, A., de La Garza, J., and Kramer, L. H. (2013). Extending positive CLASS results across multiple instructors and multiple classes of modeling instruction. Phys. Rev. Spec. Top. Phys. Edu. Res. 9:20116. doi: 10.1103/PhysRevSTPER.9.020116
Buckner, R. L., Andrews-Hanna, J. R., and Schacter, D. L. (2008). The brain's default network: anatomy, function, and relevance to disease. Ann. N. Y. Acad. Sci. 1124, 1–38. doi: 10.1196/annals.1440.011
Cole, M. W., and Schneider, W. (2007). The cognitive control network: integrated cortical regions with dissociable functions. Neuroimage 37, 343–360. doi: 10.1016/j.neuroimage.2007.03.071
Crouch, C. H., and Mazur, E. (2001). Peer Instruction: ten years of experience and results. Am. J. Phys., 69, 970–977. doi: 10.1119/1.1374249
Dou, R., Brewe, E., Zwolak, J. P., Potvin, G., Williams, E. A., and Kramer, L. H. (2016). Beyond performance metrics : examining a decrease in students' physics self-efficacy through a social networks lens. Phys. Rev. Phys. Edu. Res. 12:20124. doi: 10.1103/PhysRevPhysEducRes.12.020124
Etkina, E. E., Murthy, S., and Zou, X. (2006). Using introductory labs to engage students in experimental design. Am. J. Phys. 74:979. doi: 10.1119/1.2238885
Etkina, E., and Van Heuvelen, A. (2007). Investigative Science Learning Environment – A Science Process Approach to Learning Physics. PER-Based Reforms in Calculus-Based Physics. Available online at: http://www.compadre.org/PER/per_reviews/media/volume1/ISLE-2007.pdf
Freeman, S., Eddy, S. L., McDonough, M., Smith, M. K., Okoroafor, N., Jordt, H., et al. (2014). Active learning increases student performance in science, engineering, and mathematics. Proc. Natl. Acad. Sci. U.S.A. 111, 8410–8415. doi: 10.1073/pnas.1319030111
Frigg, R., and Hartmann, S. (2006). “Models in science,” in Stanford Encyclopedia of Philosophy, Vol. 1, ed E. N. Zalta (Stanford, CA: Metaphysics Research Lab, Stanford University).
Giere, R. N. (2005). How models are used to represent reality. Philos. Sci. 71, 742–752. doi: 10.1086/425063
Gouvea, J., and Passmore, C. (2017). “Models of” versus “Models for”toward an agent-based conception of modeling in the science classroom. science and education, 26, 49–63. doi: 10.1007/s11191-017-9884-4
Greca, I. M. A., and Moreira, M. A. (2001). Mental, physical, and mathematical models in the teaching and learning of physics. Sci. Edu. 86, 106–121. doi: 10.1002/sce.10013
Greca, I. M., and Moreira, M. A. (2000). Mental models, conceptual models, and modelling. Int. J. Sci. Educ. 22, 1–11. doi: 10.1080/095006900289976
Halloun, I. A. (1996a). Schematic modeling for meaningful learning of physics. J. Res. Sci. Teach. 33, 1019–1041. doi: 10.1002/(SICI)1098-2736(199611)33:9<1019::AID-TEA4>3.0.CO;2-I
Halloun, I. A. (1996b). “Views About Science and physics achievement: The VASS story,” in AIP Conference Proceedings-Physics Education Research Conference, Vol. 399, (College Park, MD), 605–614.
Hegarty, M. (2004). Mechanical reasoning by mental simulation. Trends Cogn. Sci. 8, 280–285. doi: 10.1016/j.tics.2004.04.001
Henderson, C. (2002). Common concerns about the force concept inventory. Phys. Teacher 40, 542–547. doi: 10.1119/1.1534822
Hestenes, D. (1987). Toward a modeling theory of physics instruction. Am. J. Phys. 55, 440–454. doi: 10.1119/1.15129
Hestenes, D. (1992). Modeling games in the Newtonian world. Am. J. Phys. 60:732. doi: 10.1119/1.17080
Hestenes, D., Wells, M., and Swackhamer, G. (1992). Force concept inventory. Phys. Teacher 30, 141–158. doi: 10.1119/1.2343497
Johnson-Laird, P. N. (1983). Mental Models: Towards a Cognitive Science of Language, Inference, and Consciousness. Cambridge, MA: Harvard University Press.
Justi, R., and Gilbert, J. (2000). History and philosophy of science through models: some challenges in the case of'the atom'. Int. J. Sci. Educ. 22, 993–1009. doi: 10.1080/095006900416875
Kober, N. (2014). Reaching Students What Research Says about Effective Instruction in Undergraduate Science and Engineering. Washington, DC: National Academies Press.
Koechlin, E., and Hyafil, A. (2007). Anterior prefrontal function and the limits of human decision-making. Science 318, 594–598. doi: 10.1126/science.1142995
Koponen, I. T. (2006). Models and modelling in physics education: a critical re-analysis of philosophical underpinnings and suggestions for revisions. Sci. Educ. 16, 751–773. doi: 10.1007/s11191-006-9000-7
Kuhn, T. S. (1970). The Structure of Scientific Revolutions. Chicago, IL: University of Chicago Press.
Laird, A. R., Eickhoff, S. B., Li, K., Robin, D. A., Glahn, D. C., and Fox, P. T. (2009). Investigating the functional heterogeneity of the default mode network using coordinate-based meta-analytic modeling. J. Neurosci. 29, 14496–14505. doi: 10.1523/JNEUROSCI.4004-09.2009
Lakoff, G. (1987). Women, Fire, and Dangerous Things: What Categories Reveal about the Mind, Vol. 64. Chicago, IL: University of Chicago Press.
Lasry, N., Rosenfield, S., Dedic, H., Dahan, A., and Reshef, O. (2011). The puzzling reliability of the force concept inventory. Am. J. Phys. 79:909. doi: 10.1119/1.3602073
Lasry, N., Watkins, J., Mazur, E., and Ibrahim, A. (2013). Response times to conceptual questions. Am. J. Phys. 81:703. doi: 10.1119/1.4812583
Leech, R., and Sharp, D. J. (2014). The role of the posterior cingulate cortex in cognition and disease. Brain 137, 12–32. doi: 10.1093/brain/awt162
Lehrer, R., and Schauble, L. (2006). “Cultivating model-based reasoning in science education,” in The Cambridge handbook of: The learning sciences, ed R. K. Sawyer (New York, NY,: Cambridge University Press), 371–387.
Mackey, A. P., Miller Singley, A. T., and Bunge, S. A. (2013). Intensive reasoning training alters patterns of brain connectivity at rest. J. Neurosci. 33, 4796–4803. doi: 10.1523/JNEUROSCI.4141-12.2013
Mason, R. A., and Just, M. A. (2015). Physics instruction induces changes in neural knowledge representation during successive stages of learning. Neuroimage 111, 36–48. doi: 10.1016/j.neuroimage.2014.12.086
Mason, R. A., and Just, M. A. (2016). Neural representations of physics concepts. Psychol. Sci. 27, 904–913. doi: 10.1177/0956797616641941
Mathieu, J. E., Heffner, T. S., Goodwin, G. F., Salas, E., and Cannon-Bowers, J. A. (2000). The influence of shared mental models on team process and performance. J. Appl. Psychol. 85, 273–283. doi: 10.1037/0021-9010.85.2.273
Matthews, M. R. (2007). Models in science and in science education: an introduction. Sci. Educ. 16, 647–652. doi: 10.1007/s11191-007-9089-3
McDermott, L. C., and Shaffer, P. S. (2001). Tutorials in Introductory Physics. New York, NY: Pearson.
McPadden, D., and Brewe, E. (2017). Impact of the second semester university modeling instruction course on students' representation choices. Phys. Rev. Phys. Educ. Res. 13:020129 doi: 10.1103/PhysRevPhysEducRes.13.020129
Morgan, M. S., and Morrison, M. (1999). Models as Mediators: Perspectives on Natural and Social Science. New York, NY: Cambridge University Press.
Morris, G. A., Branum-Martin, L., Harshman, N., Baker, S. D., Mazur, E., Dutta, S., et al. (2006). Testing the test: Item response curves and test quality. Am. J. Phys. 74, 449–453. doi: 10.1119/1.2174053
Morris, G. A., Harshman, N., Branum-Martin, L., Mazur, E., Mzoughi, T., and Baker, S. D. (2012). An item response curves analysis of the force concept inventory. Am. J. Phys. 80:825. doi: 10.1119/1.4731618
Nersessian, N. J. (1995). Should physicists preach what they practice? Sci. Educ. 4, 203–226. doi: 10.1007/BF00486621
Nersessian, N. J. (1999). “Model-based reasoning in conceptual change,” in Model-Based Reasoning in Scientific Discovery, eds L. Magnani, N. J. Nersessian, and P. Thagard, (New York, NY: Kluwer Academic Plenum Publishers), 5–22.
Nersessian, N. J. (2002a). Abstraction via generic modeling in concept formation in science. Mind Soc. 3, 129–154. doi: 10.1007/BF02511871
Nersessian, N. J. (2002b). The Cognitive Basis of Model-Based Reasoning in Science. Cambridge: Cambridge University Press.
Odenbaugh, J. (2005). Idealized, inaccurate but successful: a pragmatic approach to evaluating models in theoretical ecology. Biol. Philos. 20, 231–255. doi: 10.1007/s10539-004-0478-6
Passmore, C. M., and Svoboda, J. (2012). Exploring opportunities for argumentation in modelling classrooms. Int. J. Sci. Educ. 34, 1535–1554. doi: 10.1080/09500693.2011.577842
Prabhakaran, V., Smith, J. A., Desmond, J. E., Glover, G. H., and Gabrieli, J. D. (1997). Neural substrates of fluid reasoning: an fMRI study of neocortical activation during performance of the Raven's Progressive Matrices Test. Cogn. Psychol. 33, 43–63. doi: 10.1006/cogp.1997.0659
Prado, J., Chadha, A., and Booth, J. R. (2011). The brain network for deductive reasoning: a quantitative meta-analysis of 28 neuroimaging studies. J. Cogn. Neurosci. 23, 3483–3497. doi: 10.1162/jocn_a_00063
Raichle, M. E., MacLeod, A. M., Snyder, A. Z., Powers, W. J., Gusnard, D. A., and Shulman, G. L. (2001). A default mode of brain function. Proc. Natl. Acad. Sci. U.S.A. 98, 676–682. doi: 10.1073/pnas.98.2.676
National Research Council (2012). “Discipline-Based Education Research: Understanding and Improving Learning in Undergraduate Science and Engineering,” in Committee on the Status, Contributions, and Future Directions of Discipline-Based Education Research; Board on Science Education; Division of Behavioral and Social Sciences and Education, eds S. R. Singer, N. R. Nielsen, and H. A. Schweingruber (National Research Council; National Academies Press). Available online at: http://download.nap.edu/cart/download.cgi?andrecord_id=13362andfree=1
Rodriguez, I., Potvin, G., and Kramer, L. H. (2016). How gender and reformed introductory physics impacts student success in advanced physics courses and continuation in the physics major. Phys. Rev. Phys. Educ. Res. 12:9. doi: 10.1103/PhysRevPhysEducRes.12.020118
Rogoff, B. (1990). “Shared thinking and guided participation: conclusions and speculation BT - Apprenticeship in thinking: cognitive development in social context,” in Apprenticeship in Thinking: Cognitive Development in Social Context (New York, NY: Oxford University Press), 189–210.
Sawtelle, V., Brewe, E., Goertzen, R. M., and Kramer, L. H. (2012). Identifying events that impact self-efficacy in physics learning. Phys. Rev. Spec. Top. Phys. Educ. Res. 8:20111. doi: 10.1103/PhysRevSTPER.8.020111
Sawtelle, V., Brewe, E., and Kramer, L. H. (2010). “Positive impacts of modeling instruction on self-efficacy,” in PERC Conference Proceedings, Vol. 1289, eds C. Singh, N. S. Rebello, and M. Sabella (Portland, OR: American Institute of Physics), 289.
Schwartz, D. L., and Bransford, J. D. (1998). A time for telling. Cogn. Instrum. 16, 475–5223. doi: 10.1207/s1532690xci1604_4
Schwarz, C. V., Reiser, B. J., Davis, E. A., Kenyon, L., Achér, A., Fortus, D., Krajcik, J., et al. (2009). Developing a learning progression for scientific modeling: making scientific modeling accessible and meaningful for learners. J. Res. Sci. Teach. 46, 632–654. doi: 10.1002/tea.20311
Seeley, W. W., Menon, V., Schatzberg, A. F., Keller, J., Glover, G. H., Kenna, H., Greicius, M. D., et al. (2007). Dissociable intrinsic connectivity networks for salience processing and executive control. J. Neurosci. 27, 2349–2356. doi: 10.1523/JNEUROSCI.5587-06.2007
Simony, E., Honey, C. J., Chen, J., Lositsky, O., Yeshurun, Y., Wiesel, A., et al. (2016). Dynamic reconfiguration of the default mode network during narrative comprehension. Nat. Commun. 7:12141. doi: 10.1038/ncomms12141
Svoboda, J., and Passmore, C. (2011). The Strategies of Modeling in Biology Education. Science and Education. Available online at: http://www.springerlink.com/index/10.1007/s11191-011-9425-5
Traxler, A., and Brewe, E. (2015). Equity investigation of attitudinal shifts in introductory physics. Phys. Rev. Spec. Top. Phys. Educ. Res. 11, 1–7. doi: 10.1103/PhysRevSTPER.11.020132
Wells, M., Hestenes, D., and Swackhamer, G. (1995). A modeling method for high school physics instruction. Am. J. Phys. 63:606. doi: 10.1119/1.17849
Wendelken, C. (2015). Meta-analysis: how does posterior parietal cortex contribute to reasoning? Front. Hum. Neurosci. 8:1042. doi: 10.3389/fnhum.2014.01042
Windschitl, M., Thompson, J., and Braaten, M. (2008). Beyond the scientific method: model-based inquiry as a new paradigm of preference for school science investigations. Sci. Educ. 92, 941–967. doi: 10.1002/sce.20259
Keywords: modeling instruction, physics reasoning, mental models, force concept inventory, fMRI, STEM learning, brain network, neuroeducation
Citation: Brewe E, Bartley JE, Riedel MC, Sawtelle V, Salo T, Boeving ER, Bravo EI, Odean R, Nazareth A, Bottenhorn KL, Laird RW, Sutherland MT, Pruden SM and Laird AR (2018) Toward a Neurobiological Basis for Understanding Learning in University Modeling Instruction Physics Courses. Front. ICT 5:10. doi: 10.3389/fict.2018.00010
Received: 29 October 2017; Accepted: 26 April 2018;
Published: 24 May 2018.
Edited by:
Nathaniel Lasry, John Abbott College, CanadaReviewed by:
Chandralekha Singh, University of Pittsburgh, United StatesRachel E. Scherr, Seattle Pacific University, United States
Copyright © 2018 Brewe, Bartley, Riedel, Sawtelle, Salo, Boeving, Bravo, Odean, Nazareth, Bottenhorn, Laird, Sutherland, Pruden and Laird. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Eric Brewe, ZXJpYy5icmV3ZUBkcmV4ZWwuZWR1
†These authors have contributed equally to this work.
‡co-first author.
 Eric Brewe
Eric Brewe Jessica E. Bartley2†‡
Jessica E. Bartley2†‡ Michael C. Riedel
Michael C. Riedel Taylor Salo
Taylor Salo Rosalie Odean
Rosalie Odean Katherine L. Bottenhorn
Katherine L. Bottenhorn Matthew T. Sutherland
Matthew T. Sutherland Shannon M. Pruden
Shannon M. Pruden Angela R. Laird
Angela R. Laird