State-dependent modulation of gap junction signaling by the persistent sodium current

Thalamic neurons fluctuate between two states: a hyperpolarized state associated with burst firing and sleep spindles, and a depolarized state associated with tonic firing and rapid, reliable information transmission between the sensory periphery and cortex. The thalamic reticular nucleus (TRN) plays a central role in thalamocortical processing by providing feed-forward and feedback inhibition to thalamic relay cells; TRN cells participate in the generation of sleep spindles, and have been suggested to focus the neural “searchlight” of attention. The mechanisms underlying synchrony in the TRN during different behavioral states are largely unknown. TRN cells are densely interconnected by electrical synapses. Here we show that activation of the persistent sodium current (I_NaP) by depolarization causes up to fourfold changes in electrical synaptic efficacy between TRN neurons. We further show that amplification of electrical synaptic responses strongly enhances tonic spike synchrony but, surprisingly, does not affect burst coordination. We use a Hodgkin–Huxley model to gain insight into the differences between the effects of burstlets, spikelets, and amplification on burst and spike times.

Introduction

In mammalian systems, electrical synapses are found in many regions throughout the brain (Connors and Long, 2004; Meier and Dermietzel, 2006) and most often couple neurons of similar functional and biochemical profiles (Galarreta and Hestrin, 2001). The thalamic reticular nucleus (TRN) is composed exclusively of inhibitory (GABAergic) neurons that express an extremely high density of strong electrical synapses composed of connexin 36 (Cx36), the protein that forms most mature mammalian neuronal gap junctions (Condorelli et al., 2000; Deans et al., 2001; Landisman et al., 2002; Long et al., 2004).

Like other thalamic neurons (Llinas and Jahnsen, 1982; Jahnsen and Llinas, 1984), TRN cells have two voltage-dependent firing modes – burst and tonic spiking – that correspond both to different voltage ranges and to different states of alertness and attention (Domich et al., 1986). During sleep spindles, TRN neurons rest at hyperpolarized potentials and, when excited, fire in rapid bursts of several sodium-mediated spikes crowning a slower calcium-mediated spike; during periods of awake attention, neurons rest at depolarized potentials and fire slower trains of spikes in tonic mode.

Relationships between gap junctional signals and voltage-dependent conductances have been previously described in other systems, with varied results. In the inferior olive, depolarization of either neuron coupled by an electrical synapse caused a reduction in coupling strength (Devor and Yarom, 2002). In molecular-layer cerebellar interneurons, one report showed amplification of electrical synaptic signals by depolarization of membrane potential, measured in the sodium-channel blocker TTX (Mann-Metzer and Yarom, 1999). Later work demonstrated that amplification of gap junction signals between coupled cerebellar Golgi interneurons is QX-314-sensitive (Dugue et al., 2009) and thus mediated by sodium currents. At the goldfish Mauthner mixed synapse, presynaptic changes in voltage also modulate gap junctional responses (Curti and Pereda, 2004).

While the influence of this amplification has been postulated to improve tonic firing synchrony amongst coupled cells (Mann-Metzer and Yarom, 1999; Dugue et al., 2009), it has never been tested. Electrical synapses have been shown to aid synchronized rhythmic firing in coupled mammalian neurons (Elson et al., 1998; Gibson et al., 1999; Galarreta and Hestrin, 2001; Landisman et al., 2002; Long et al., 2004; Hestrin and Galarreta, 2005; Pfeuty et al., 2005), but other results indicate that the influence of electrical synapses on spike coordination may be a more complex issue (Chow and Kopell, 2000; Pfeuty et al., 2005; Vervaeke et al., 2010).

We investigated modulation of gap junction-mediated synchrony during tonic and burst firing states with dual whole-cell recordings of gap junction-coupled neurons in rodent TRN in vitro. We first measured gap junction-relayed signals over different voltage ranges and subsequently tested gap junction-mediated synchrony during the two firing states; in both sets of experiments, we used 100 nM TTX to establish the contributions of I_NaP to amplification and synchrony. We also constructed a computational model to compare the efficacy of postsynaptic spikelets and burstlets in perturbing the spike times of TRN cells and to provide insight into the dynamics underlying our results.

Materials and Methods

Slice Preparation, Recording, and Drugs

Thalamocortical slices 400 μm thick were obtained from Sprague-Dawley rats aged P12–P14. Slices were cut and incubated in sucrose solution (in mM): 72 Sucrose, 83 NaCl, 2.5 KCl, 1 NaPO₄, 3.3 MgSO₄, 26.2 NaHCO₃, 22 Dextrose, and 0.5 CaCl₂. Slices were incubated at 33°C for 20 min and returned to room temperature thereafter. The bath solution for recording contained (in mM): 126 NaCl, 3 KCl, 1.25 NaH₂PO₄, 2 MgSO₄, 26 NaHCO₃, 10 dextrose, and 2 CaCl₂, saturated with 95% O₂/5% CO₂. The submersion recording chamber was held at 32–33°C (TC-324B, Warner Instruments). Micropipettes were filled with (in mM): 135 K-gluconate, 4 KCl, 2 NaCl, 10 HEPES, 1.1 EGTA, 4 ATP-Mg, 0.3 GTP-Tris, and 14 phosphocreatine-Tris (pH 7.25, 295 mOsm). For voltage-clamp measurements of I_NaP, 135 mM Cs-methanesulfonate was substituted for K-gluconate. Either 1 M CsOH or 1 M KOH was used to adjust pH of the internal solution. The approximate bath flow rate was 2 ml/min. Voltages are reported as corrected for the liquid junction potential. When noted, the bath also included 50 μM DL-2-amino-5-phosphopentanoic acid (AP5; Sigma, St. Louis, MO, USA) to block N-methyl-D-aspartate (NMDA) receptors and 20 μM 6,7-dinitroquinoxaline-2,3-dione (DNQX; Sigma) to block AMPA receptors. A dose of 100 nM TTX (total confirmed as 8 mls) was bath-applied for 4 min to block I_NaP without eliminating spikes; in some experiments voltage amplification was tested at the end to confirm continued blockage of I_NaP.

Coupling Coefficient (cc)

The coupling coefficient is the attenuation of signal transfer between one cell and its electrically coupled neighbor, measured as a ratio of the postsynaptic voltage deflection transmitted via the gap junction divided by the presynaptic voltage deflection, induced by direct current injection. To measure cc, we injected 100–200 pA hyperpolarizing current steps, each lasting 600 ms (1 s ISI), and measured the steady-state voltage responses of the injected cell, cell 1, and its electrically coupled neighbor, cell 2 (Figure 1A). The coupling coefficient from cell 1 to cell 2 is cc₁₂ =ΔVcell 2/ΔVcell 1, where ΔVcell 1 is the change in membrane voltage in the injected cell and ΔVcell 2 is the change in membrane voltage in the coupled cell. Reported data of cc represent the average of 10–20 measurements.

FIGURE 1

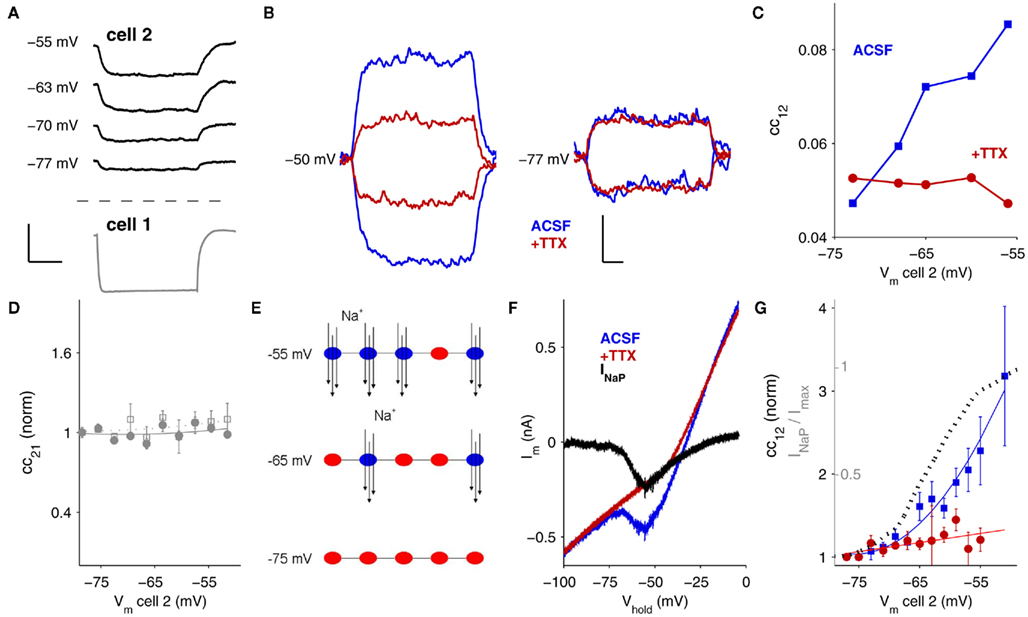
Figure 1. Signals relayed through electrical synapses are amplified by I_NaP. (A) Gap junction-relayed responses in cell 2 at different baseline membrane potentials (top) and response to hyperpolarizing current injection in cell 1 (bottom, V_m = −67 mV for all trials). Scale bar is 0.2 s, 15 mV (bottom), 5 mV (top). (B) At a baseline of V_m = −50 mV (left), both hyperpolarizing and depolarizing responses in cell 2 are amplified by I_NaP (blue traces); blockade of I_NaP by TTX eliminates the amplification (red traces). At V_m = −77 mV (right), I_NaP is inactive and does not amplify hyperpolarizing or depolarizing gap junctional responses. Scale bar is 0.1 s, 0.5 mV. (C) Coupling coefficients measured from cell 1 to cell 2 (cc₁₂ = ΔV_{cell 2}/ΔV_{cell 1}) plotted against the baseline voltage of cell 2, for a single pair. Blue data were recorded in control ACSF; red data in 100 nM TTX. (D) Coupling coefficients (filled circles) and conductance (open squares) measured from cell 2 to cell 1 (cc₂₁ = ΔV_{cell 1}/ΔV_{cell 2}) as cell 2 is depolarized, plotted against the baseline voltage of cell 2. (E) The persistent sodium current, I_NaP, is mediated by voltage-sensitive channels that flicker between open and closed states once activated. At depolarized potentials, more channels are persistently active (blue) and available to amplify responses by opening in response to depolarizing inputs or by closing in response to hyperpolarizing inputs. At hyperpolarized baseline potentials (bottom) most channels are inactive (red) and do not amplify responses. (F) I_NaP was measured by subtraction of currents from slow (10 mV/s) voltage-clamp ramps in TRN neurons. Blue trace is membrane current measured in control ACSF, red trace in 100 nM TTX, and black trace is the point-by-point subtraction, for a single TRN cell. (G) Summary plot of cc₁₂ against baseline voltage from N = 14 pairs before and after TTX. Data are normalized to most-hyperpolarized values. Dotted line is I_NaP/max(I_NaP), measured from ramps as in (C) in N = 6 neurons.

Burst coupling coefficients were calculated from the maximum amplitude of the postsynaptic burstlet divided by the amplitude of the presynaptic burst, measured from pre-burst baseline to the peak of the after-depolarizing potential following the final spike. Spike coupling coefficients were calculated from the postsynaptic spikelet amplitude divided by the height of the presynaptic spike, measured from threshold (last sharp inflection before the peak) to the spike peak.

Correlation of Tonic Spiking

Both cells were driven by simultaneous current step injections lasting 1.2 s (Figure 3A). Current values were selected for each cell separately to elicit a spiking frequency between 40–50 Hz and varied from 200–800 pA. In subsequent experiments, the current injected into one cell was held constant, while the current injected into the second cell was varied by 5–10%, in order to maximize the probability of driving an exact frequency match in both neurons. In this manner, 50–100 trials of paired firing were collected for each pair. Cells were held at the same V_m before and after TTX application. Offline, we selected the 10 pairs of tonic spiking best matched in frequency exceeding 35 Hz, then computed the average correlation coefficient for those 10 sets of spike trains.

Correlation coefficients were measured by first forming point processes from the spike times of both neurons, after discarding the first 200 ms of data to avoid spurious onset-initiated correlations. Next, we convolved each of these point processes with a 5 ms-wide Hanning window, to provide some overlap for temporally offset spikes. Finally, we cross-correlated the trains, and took the peak correlation coefficient between the two trains, within ±2 ms of delay.

Spontaneous Synaptic Events

To evaluate spontaneous synaptic events (sEPSPs), we developed custom software in Matlab. First, raw data were lightly smoothed with a 1–2.5 ms Hanning window. For each dataset, we formed a template event by averaging 5–6 hand-selected examples of temporally isolated minis. We convolved the template with the smoothed data, zero-meaned, and took the first derivative of this result, yielding the signal dc(t). Peaks in dc(t) identified locations in the data where the template’s quick rise was well-matched. We then applied a threshold to dc(t). Once candidate events were thus identified, the real start times of those events were determined by peaks in derivative in the smoothed data. This algorithm was optimized for each neuron by two parameter choices: the threshold for event detection, and the minimum amplitude for detected events. These were both taken as fractions of the SD of dc(t) or of the smoothed data, respectively. Together, these two parameters allowed us to fine-tune (a) the smallest event that could be detected, and (b) the smallest event we accepted as a miniature synaptic event. The algorithm is visually described with sample data in Figure A1 in the Appendix.

Burst Coordination

First, one cell of a pair was driven with incremental current steps lasting 1.2 s to determine the minimum threshold for burst firing, ranging from 50 to 500 pA. Threshold was considered to be the current value that elicited bursts on 100% of trials (20–30 trials). Next, both cells were driven by simultaneous steps of current injections, also lasting 1.2 s. The first cell’s current intensity was held constant at its previously determined threshold value while the second cell’s current injection was varied over five values flanking the second cell’s threshold, incrementing 2–5 pA in each successive trial. These five trials were then repeated 20–30 times. The threshold value was determined for cell 2 when stimulated with cell 1 at its threshold. All trials from this current combination, of both cells’ thresholds, were then used to determine burst jitter (SD of burst start times) and to measure time differences between burst onsets of cell 1 and 2 (absolute value of the difference between first-spike times). This procedure was then repeated following a 4 min bath application of 100 nM TTX. Cells were held at the same V_m before and after TTX application.

Properties of Single Neurons

Measurements of input resistance (R_in), spike width, spike height, burst amplitude, and spikes per burst are reported as numbers of neurons (not numbers of cell pairs) as these properties are not directly related to gap junctions. See Table A1 in Appendix.

Modeling

A single-compartment Hodgkin–Huxley model was created from the ionic current-activation equations available in NEURON (senselab.med.yale.edu) for a TRN cell (Traub et al., 2005). We used I_Na, I_Kd, I_Kt, I_K2, I_AR, I_leak, and I_T from (Traub et al., 2005) with peak conductances of 60.5, 60, 5, 0.5, 0.025, 0.1, and 0.75 μA/cm² respectively, and membrane capacitance of 1 μF/cm². Reversal potentials were 50 mV (sodium), −100 mV (potassium), 125 mV (calcium), −40 mV (AR), and −75 mV (leak). Burstlets and spikelets were modeled as synaptic inputs, dual exponentials of the form dS/dt = τ_aK(1 − S) − τ_bS with τ_a = 0.005 ms⁻¹ and τ_b = 0.02 ms⁻¹ for burstlets and τ_a = 1 ms⁻¹ and τ_b = 10 ms⁻¹ for spikelets; the electrical synaptic reversal potential used was 20 mV. Burstlets and spikelets were initiated at a user-defined time by K, a 2 ms square pulse representing a presynaptic spike. The resulting postsynaptic burstlets and spikelets matched the rise and fall times of physiological data (Figures 6A,B, insets; rise times of ∼1 ms for spikelets, ∼50 ms for burstlets). The applied current for bursts (Figure 6B) was 0.25 and 0.575 μA/cm² for tonic spiking (Figure 6A). Simulations were performed in Matlab (R2010b, Mathworks) by ode23, a second order Runge–Kutta solution with maximal time step 0.01 ms. The same set of initial conditions was used for all simulations.

Results

Amplification of Electrical Synapses by I_NaP

To measure signals across gap junctions, we delivered hyperpolarizing current steps to one neuron (cell 1) while recording voltage responses in both neurons and computed the coupling coefficient, which is the ratio of the voltage deflections (Figure 1A; cc₁₂ = ΔVcell 2/ΔVcell 1). While varying the baseline voltage of the passive, postsynaptic neuron (cell 2), we observed that the signals relayed by gap junctions are modulated by the membrane potential of the passive or postsynaptic cell: that is, at more-depolarized potentials, the postsynaptic response measured in cell 2 is larger (Figure 1A–C). Both hyperpolarizing and depolarizing postsynaptic responses are amplified (Figure 1B), indicating that a rectifying potassium current is unlikely to underlie amplification. Amplification depends solely on membrane voltage in the receiving or postsynaptic cell: coupling measured in the opposite direction, cc₂₁ remained constant even as V_m of cell 2 varies (Figure 1D). Gap junctions comprising Cx36 channels themselves are not voltage-dependent over physiological ranges of voltages across the junction (Srinivas et al., 1999; Harris, 2001), and we verified that when voltage differences across the gap junctional synapses were minimized by depolarizing both cells together, the voltage-dependent amplification persisted (data not shown), further indicating that the amplification occurs not at the gap junction itself but is postsynaptic in nature.

One possible source of amplification is an interaction between gap junction signals and voltage-gated ion channels. Voltage-dependent modulation of gap junction signals was observed in cerebellar molecular-layer interneurons in TTX (Mann-Metzer and Yarom, 1999), whereas a later study showed modulation of gap junctional signals between cerebellar Golgi cells to be QX-314-sensitive (Dugue et al., 2009). However, in inferior olive interneurons, depolarization was shown to reduce coupling (Devor and Yarom, 2002). Voltage-dependent amplification of electrical synapses by sodium currents in the presynaptic cell was also shown at the goldfish Mauthner cell synapse (Curti and Pereda, 2004). Thus, the evidence across cell types and systems has been inconsistent.

A subset of the sodium channels that normally underlie spiking can also remain persistently activated while opening and closing in a voltage-dependent manner; this is known as the persistent sodium current (I_NaP; Alzheimer et al., 1993; Crill, 1996; Taddese and Bean, 2002). As neurons depolarize, some persistently active Na⁺ channels flicker open, with the net result of further depolarizing or amplifying depolarizing events (Figure 1E). Conversely, as neurons hyperpolarize, the persistently active Na⁺ channels close, thereby removing a depolarizing influence and effectively amplifying hyperpolarizing events. Because I_NaP is voltage-dependent, a larger number of Na⁺ channels are activated and can open and close at more-depolarized baseline potentials (Figure 1E). We measured I_NaP in TRN neurons by subtracting responses to slow voltage-clamp ramps (10 mV/s; Figure 1F) with and without TTX. These results verify that the activation range of I_NaP parallels the voltage range of the observed coupling amplification (Figure 1G).

To specifically test whether I_NaP modulates electrical synaptic events between neurons of the TRN, we applied the sodium-channel blocker TTX, which can be used at low doses to selectively block I_NaP (Urbani and Belluzzi, 2000), while measuring electrical coupling and found that it eliminated the voltage-dependent amplification (Figures 1C,G). Thus we conclude that I_NaP is responsible for the voltage-dependent amplification of gap junctional signals in TRN cells.

Amplification by I_NaP occurs over a voltage range similar to the range of transition from burst to tonic spiking in TRN cells (Contreras et al., 1992; Figure 2A). The signals relayed by electrical synapses during these two firing states – burstlets and spikelets – are also amplified by depolarization (Figure 2B). In general, fast sodium spikes are transmitted quite poorly via gap junctions due to the low-pass filtering properties of gap junctions (Landisman et al., 2002; Long et al., 2004; Gibson et al., 2005). One might expect that smaller deflections in voltage would activate less I_NaP (Figure 1G) and thus amplify spikelets less than burstlets or steplets. Despite their time-course and amplitude differences, however, the normalized amplifications of burstlets and spikelets were surprisingly similar (Figure 2C): at V_m = −52 mV, burstlets were amplified by a factor of 1.5 ± 0.2 (N = 4 pairs), and spikelets were amplified by a factor of 1.4 ± 0.2 (N = 6 pairs), compared to values at V_m = −77 mV. For current steps in this set of cells, postsynaptic cc₁₂ increased by a factor of 2.6 ± 0.6 at V_m = −53 mV (N = 5 pairs) compared to values at V_m = −77 mV (N = 16 pairs).

FIGURE 2

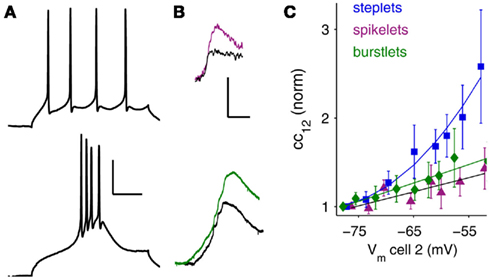
Figure 2. Bursts, spikes, and amplification. (A) From hyperpolarized baseline voltages, TRN cells emit bursts (bottom; V_m = −77 mV). At depolarized potentials, TRN cells spike regularly in tonic mode (top; V_m = −53 mV). Scale bar is 25 ms, 25 mV. (B) The corresponding postsynaptic signals at electrical synapses: spikelets (top), and burstlets (bottom), for these different spiking modes are also amplified by membrane voltage; colored traces are at depolarized potentials (spikelet V_m = −50 mV, burstlet V_m = −61 mV) and black traces are at hyperpolarized potentials (spikelet V_m = −71 mV burstlet V_m = −76 mV. Scale bar is 5 ms, 1 mV (spikelets); 4 mV, 50 ms (burstlets). (C) Summary of scaling for steplets, spikelets, and burstlets measured in N = 12 pairs of neurons, plotted against baseline voltage in the receiving cell. Data are normalized to the most-hyperpolarized voltages.

I_NaP Enhances Tonic Spiking Synchrony

Because I_NaP amplifies electrical synaptic signals over a similar voltage range to the transition from burst to tonic firing, we tested its effects on the synchrony of these two firing states. We measured effects of I_NaP on tonic spike synchrony by driving both cells of a coupled pair to fire at roughly matched frequencies, before and after TTX application (Figures 3A,B). A full blockade of sodium channels would eliminate spikes altogether; therefore we used a 4 min wash of 100 nM TTX (a total of 8 mls). This concentration effectively eliminated voltage amplification by I_NaP (Figures 1B,C,G) but reduced spike amplitude by only 17% on average (Figure 3C, inset), while its effects on spike width, mean postsynaptic spikelet height and spikelet area were insignificant (Table A1 in Appendix). Mean firing rates elicited in control and in TTX were 40.0 ± 0.9 and 41.0 ± 1.0 Hz (p = 0.47), respectively, driven by mean DC current amplitudes of 467.0 ± 57.0 and 439.8 ± 50.6 pA (p = 0.72), further demonstrating that TTX did not significantly alter baseline excitability.

FIGURE 3

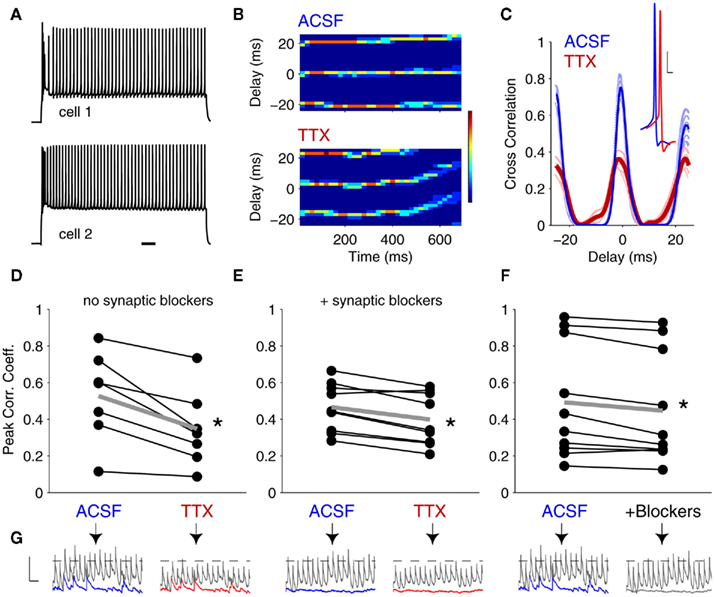
Figure 3. Tonic-spike synchrony in coupled neurons is enhanced synergistically by I_NaP and spontaneous synaptic input. (A) A pair of gap junction-coupled neurons driven to spike at similar frequencies. Scale bar 100 ms. (B) Time-course cross-correlograms for a pair of electrically coupled neurons in control (ACSF) and following 100 nM TTX application. In both conditions, spikes fired at ∼50 Hz; color bar represents 0 (navy) to 7 (dark red) correlated spikes within a given 50 ms window (y-axis); bin width = 2 ms. (C) Example cross-correlogram for paired spiking before (blue) and after (red) TTX application. Inset: spikes in a TRN cell in ACSF (blue) and in 100 nM TTX (red). Scale bar is 10 mV, 2 ms. (D) Peak correlation coefficients before and after TTX. In TTX, correlation coefficients were 34.4 ± 5.9% lower than in ACSF (mean ± SEM, N = 7 pairs, p < 0.01, one-tailed t-test). (E) Peak correlation coefficients before and after TTX application in the presence of DNQX + APV to block excitatory chemical synaptic activity. In TTX, correlation coefficients were 15.8 ± 3.2% lower than in ACSF (N = 9 pairs, p < 0.01). (F) Correlation coefficients before and after application of DNQX + APV. Here, correlation coefficients were 10.0 ± 3.3% lower than in ACSF (N = 10 pairs, p < 0.01).Thick gray lines in (D–F) represent population averages. (G) Representative spikelets (gray) and sEPSPs (blue or red) were numerically amplified and summed to demonstrate the corresponding experimental conditions of (D–F) (note the number of events crossing threshold in each case). In ACSF, spikelets and burstlets were numerically amplified by the experimentally determined factors. Scale bar is 2 mV, 50 ms.

Elimination of electrical synaptic amplification by I_NaP produced a consistent reduction in the synchrony of tonic spiking (Figures 3B–E). The average correlation coefficient between spike trains of cell pairs was reduced by 34.4 ± 5.9% following TTX application (Figure 3D; N = 7 pairs, p < 0.01, paired, one-tailed t-test). To isolate the effect of electrical synaptic amplification by I_NaP from the contribution of chemical synaptic events or their amplification (Deisz et al., 1991; Stuart and Sakmann, 1995; Pfeuty et al., 2005), we paired spiking before and after TTX while blocking excitatory chemical synaptic transmission (Figure 3E). In this case, correlation coefficients were reduced by a smaller amount, 15.8 ± 3.2% (N = 9 pairs, p < 0.01). To verify that the difference in improvement was in fact due to synaptic noise, we also tested interactions of chemical and electrical synapses (without blocking I_NaP) by measuring synchrony in pairs of neurons before and after blocking fast excitatory chemical synaptic transmission (Figure 3F). Under these conditions, we observed a surprising 10 ± 3.3% reduction in synchrony after blocking the synaptic noise (N = 10 pairs, p < 0.01). Thus, both I_NaP and the presence of synaptic noise improve synchrony of tonic spiking in TRN cells. Together, these results indicate a surprising synergy between I_NaP, electrical synapses, and chemical synaptic noise in enhancing coordination of tonic spikes, whereby depolarization toward threshold from additive spontaneous inputs, and further depolarization to threshold for tonic spiking, co-activate I_NaP, resulting in amplified spikelets and tighter synchrony of coupled neurons (Figure 3G).

Given this observed synergy from the addition of chemical synaptic noise, we tested whether the improvement of tonic spike coordination might be due to either common efferent input to coupled cells and/or robust transmission of chemical synaptic events across gap junctions. Chemical synaptic signals have been previously shown to be amplified by I_NaP (Stuart and Sakmann, 1995). To measure the effects of I_NaP on chemical synaptic events, and to examine transmission of these events across gap junctions, we recorded spontaneous excitatory postsynaptic potentials (sEPSPs) in coupled pairs before and after application of 100 nM TTX (N = 17 pairs). In both conditions, we held the membrane voltage of one cell constant and injected DC current to the other cell to hold its V_m at levels from −77 to −55 mV (Figures 4A,B).

FIGURE 4

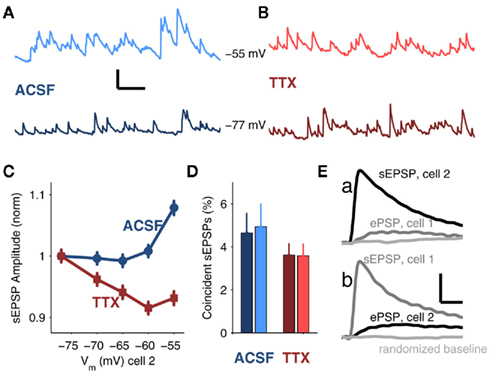
Figure 4. Spontaneous excitatory postsynaptic events (sEPSPs) in coupled neurons. (A) Sample data from a TRN cell with average V_m = −55 mV (top, light blue) and −77 (bottom, dark blue) in ACSF. Scale bar is 0.1 s, 1 mV. (B) Sample data with average V_m = −55 mV (top, light red) and −77 (bottom, dark red) in 100 nM TTX. (C) Average sEPSP amplitude (mean ± SEM) plotted against V_m for recordings in ACSF (blue, circles) and recordings in TTX (red, squares). Both data sets are normalized to their respective values at V_m = −77 mV for comparison (normalized values at V_m = −55 mV are 1.08 ± 0.01 in ACSF; 0.93 ± 0.01 in TTX). (D) Percentages of sEPSPs arriving in both cells of a coupled pair within a 1 ms window in ACSF (4.6 ± 0.93 for V_m = −77 mV, dark blue; 4.9 ± 1.1 for V_m = −55 mV, light blue) and in TTX (3.6 ± 0.54 for V_m = −77 mV, dark red; 3.6 ± 0.54 for V_m = −55 mV, light red). There were no significant effects of voltage or TTX on the data (ANOVA). (E) In a strongly coupled pair (mean cc = 0.4), average sEPSP in cell 2 (a, black trace) and corresponding trigger-averaged electrical PSP (ePSP) simultaneously recorded in cell 1 (a, gray trace); average sEPSP in cell 1 (b, gray grace) with corresponding average ePSP simultaneously recorded in cell 2 (b, black trace). Randomly selected data from the same number of samples are shown in light gray. All traces in (E) represent the average of 554 events. Scale bar is 0.1 mV, 10 ms.

When cells were depolarized to −55 mV, the distribution of sEPSP amplitudes shifted toward larger-amplitude events relative to events measured at −77 mV (p < 0.01, Kolmogorov–Smirnov test; Figures A1B,C in Appendix). Conversely, after TTX, the distribution of sEPSPs shifted toward smaller events at −55 than at −77 mV (p < 0.01, K–S test; Figures A1D,E in Appendix), due to the 22 mV reduction in synaptic driving force. To compare cases by eliminating the effects of possible changes in spontaneous release due to TTX, we normalized sEPSP amplitudes in control and TTX to their respective values at −77 mV; we found that at −55 mV, sEPSPs in ACSF were amplified by 16% relative to those measured in TTX (Figure 4C).

To determine whether synaptic inputs provide a common, synchronous, or an independent, asynchronous drive to electrically coupled neurons, we measured the temporal coincidence of sEPSPs. Overall, sEPSPs arrived at a rate of 19.4 ± 9.8 Hz in control, and 19.2 ± 8.6 Hz in TTX. We found that fewer than 5% of these sEPSPs in one cell arrived within 1 ms of an sEPSP in a coupled cell under any of the four conditions (depolarized vs. hyperpolarized, with or without TTX; Figure 4D). Additionally, the difference in coordination of sEPSPs at depolarized potentials, with or without TTX, was only slightly greater than 1% – likely too small of a difference to account for the synchrony improvement observed in the presence of synaptic noise during tonic spiking. Furthermore, the majority of sEPSPs appear to be largely electrotonically isolated from the gap junctions: only two extremely strongly coupled pairs (mean cc = 0.35 and 0.4) showed any demonstrable evidence of signal transfer of sEPSPs across gap junctions, which was evident only after averaging hundreds of events (Figure 4E). These two outlying counterexamples emphasize that for average values of coupling (∼0.1), the vast majority of sEPSPs are not shared between two coupled cells. The few inputs that are synchronous may be due to collateralization of one axon innervating a pair of coupled cells (common input), as opposed to robust propagation of sEPSPs across gap junctions. These results indicate that the majority of sEPSPs in coupled cells can be considered independent events in each cell. Overall, our data suggest that while electrical and chemical synaptic inputs synergistically enhance synchrony of tonic spikes, neither coincidences in arrival times nor the transmission of sEPSPs across gap junctions underlie that synergy.

I_NaP does not affect burst synchrony

We also tested the effects of I_NaP and sEPSPs on the coordination of burst firing in gap junction-coupled neurons. In designing stimuli, our goal was to minimally activate the calcium current (I_T), which underlies bursts, in order to allow for maximal modulation of burst timing by the burstlets conveyed through gap junctions. To accomplish this, we varied injected currents to determine burst thresholds for each cell, alone and paired, for depolarizations from ∼−70 mV (Figure 5A). We then drove both cells simultaneously with these peri-threshold stimuli. We measured burst synchrony as the difference in first-spike times before and after application of 100 nM TTX (Figure 5B). We found no significant effects of I_NaP on threshold-induced burst synchrony in either the presence or absence of chemical synaptic blockers (Figures 5C,D; p = 0.94 in normal ACSF; p = 0.99 in DNQX + APV), and in all cases, bursts were at least 10 ms apart (Figures 5C,D). Even for bursts with optimally aligned low-threshold spikes (LTS), the sodium spikes crowning the LTS remained uncorrelated (Figures A2A,B in Appendix). Surprisingly, synchrony of burst firing was also uncorrelated with the strength of electrical coupling at V_rest either in control conditions or in TTX (Figure A2C).

FIGURE 5

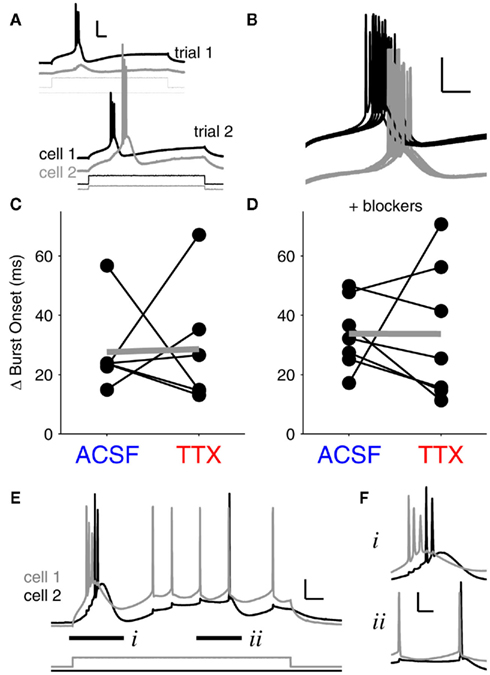
Figure 5. Bursts are unsynchronized events. (A) Demonstration of the stimulation paradigm for paired burst firing. First, current thresholds for bursts were determined independently for each cell (trial 1). Next, bursts were elicited in coupled neurons by delivering peri-threshold current injections to both neurons simultaneously (trial 2). Traces are offset for clarity. Scale bar: 25 mV, 50 ms. Burst synchrony is taken as the absolute value of the difference in burst onset times between cell 1 and cell 2. (B) Finer time-scale of 15 burst trials in a pair of coupled neurons. Bursts rarely synchronized, and individual burst onsets also varied by tens of ms. Scale bars: 25 mV, 50 ms. (C) With spontaneous synaptic activity intact, burst synchrony did not show a significant change after blocking I_NaP with 100 nM TTX. Mean difference in burst onsets in ACSF: 27.6 ± 6.0 ms (mean ± SEM, N = 6 pairs); mean difference in burst onsets in TTX: 28.6 ± 8.5 ms (p = 0.94, paired, two-tailed t-test). (D) In the presence of synaptic blockers (DNQX and APV), burst synchrony between coupled cells also showed no significant change after TTX application. Mean difference in burst onset in ACSF: 33.7 ± 4.5 ms (N = 7 pairs); mean difference in burst onset in TTX: 33.6 ± 8.7 ms (p = 0.99, paired, two-tailed t-test). Differences between values with and without blockers were insignificant (p > 0.4 for all comparisons, ANOVA). Data points in (C–F) represent average values for 20–30 trials at burst thresholds for each pair. (E) Gap junction-driven spikes in a strongly coupled pair (mean cc = 0.4) demonstrate the difference between burst and tonic spike synchrony. The burst onset difference (i) was 23 ms; the closest two spikes within the bursts were 7.4 ms apart. The tonic spikes (ii) were 1.9 ms apart. V_rest = −70 mV for both cells. Scale bar 15 mV, 50 ms. (F) Fine resolution of the paired bursts (i) and the paired tonic spikes (ii), offset for clarity. Scale bar 20 mV, 20 ms.

A case of extremely strong electrical coupling (mean cc = 0.4) illustrates the differences we found between burst and tonic spike synchrony. In this pair, cell 1 was driven to spike by current injection, and cell 2 was excited only by gap junction-relayed signals from cell 1 (Figure 5E). Both cells reached similar levels of excitation – a burst followed by a few tonic spikes. Similar to our finding that paired bursts are separated by tens of ms (Figures 5C,D), the burst onsets in this pair differed by 23 ms; even the closest spikes between the two bursts were 7.4 ms apart (Figure 5Fi. In contrast, during the subsequent tonic spikes, the closest spikes between the two cells were only 1.9 ms apart (Figure 5Fii), a separation on par with the single-millisecond precision of synchrony we observed during experiments on tonic spiking (Figure 3C). Thus, bursts are largely asynchronous amongst even the most strongly coupled neurons, while tonic spikes can be tightly synchronized.

Modeling the Effects of Burstlets and Spikelets

To gain insight into the differences between spiking synchrony in burst and tonic modes, we constructed a single-compartment model of a TRN neuron based on previous modeling work (Traub et al., 2005). After adjusting parameters of the model to generate responses to long depolarizing steps of current that matched our experimental data (Figures 6A,C; compare to Figures 3A and 5A), we applied burstlets and spikelets to the model to investigate their effects on subsequent spike times. This technique is similar to phase-response curve analysis (Ayers and Selverston, 1977; Netoff et al., 2005; Haas et al., 2010). In our case, this approach is a proxy for determining whether gap junction-relayed signals have the ability to synchronize spiking by shifting spike times in coupled neighbors. The spikelets and burstlets were modeled as synaptic inputs to the model that produced voltage responses matched in rise times to their physiological counterparts (Figures 6A,C insets; compare to Figures 2A,B).

FIGURE 6

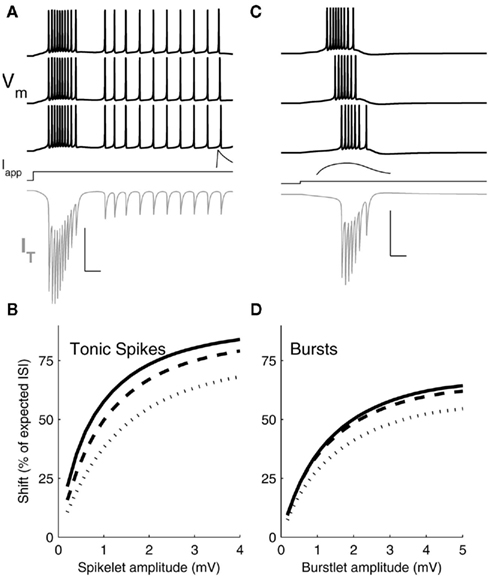
Figure 6. Simulation results. (A) Three representative voltage traces (black) from a single-compartment Hodgkin–Huxley model of a TRN cell driven to spike tonically with applied DC current (I_app) and provided with spikelet inputs of increasing amplitude (from bottom to top) preceding spikes during the regular spiking period. Spikelet shown is a response in an unstimulated TRN cell, for a spikelet arriving 10 ms before spikes in traces above. Gray trace: I_T during the first (bottom) simulation. Scale bar: 25 ms, 100 mV (V_m), 2 mV (spikelet) 15 μA/cm² (I_T). Inset: example postsynaptic spikelet. Scale bar 10 ms, 1 mV. (B) Shift in arrival time of the next spike, expressed as a percent of the interspike interval (ISI) between the input and an unperturbed spike, plotted against spikelet amplitude. Results from three sets of simulations are plotted for a spikelet applied 10 (solid), 15 (dashed), or 20 (dots) ms before the unperturbed spike. (C) Voltage traces (black) of the model driven at its burst threshold by applied DC current and provided with burstlets of increasing amplitudes (bottom to top) preceding the native burst. Burstlet shown is a response in an unstimulated TRN cell, starting 20 ms before the bursts in the traces above. I_T during the first (bottom) simulation is shown in gray. Scale bar: 25 ms, 100 mV (V_m), 2 mV (burstlet), 15 μA/cm² (I_T). Inset: example postsynaptic burstlet. Scale bar 10 ms, 1 mV. (D) Shift in subsequent spike times following burstlet inputs, plotted against postsynaptic burstlet amplitude. Results from three sets of simulations are plotted for a burstlet applied 20 (solid), 35 (dashed), or 50 (dots) ms before the first spike of the unperturbed burst.

To mimic the experiments on tonic spiking synchrony, we drove the model to spike at ∼40 Hz using a 1.2 s step of depolarizing current injection and applied a spikelet input at varying times during the spiking cycle, in order to test the effect of spikelets preceding spikes by several ms (Figure 6A). To mimic the burst-synchrony experiments, we drove the model at its burst threshold to test the effect of incoming burstlets that preceded the model neuron’s burst by tens of ms (Figure 6C). We then varied two parameters: the arrival times of the inputs, and the amplitudes of the resulting postsynaptic events.

The model revealed a major difference between burstlets and spikelets in terms of their efficacy in perturbing the next spike arrival, or in closing the temporal gaps between the presynaptic and postsynaptic spikes of the model. Presynaptic spikelets that arrive during a tonic-spike train are more effective than burstlets that arrive just before a native burst at shifting the time of the subsequent postsynaptic spike. This effect is summarized in Figures 6B,D. A 3 mV spikelet accelerated the next spike time by as much as 75% of the gap between the spikelet and the next spike (Figure 6B). In comparison, a 3 mV burstlet closed at most ∼50% of the gap between it and the next burst onset (Figure 6D).

The difference between effectiveness of spikelets and burstlets is related to the degree of activation of I_T during those inputs. During a tonic-spike train, I_T is relatively inactive (Figure 6A); the membrane is tighter and more responsive to the spikelet. During burst generation, I_T is highly activated (Figure 6C) and increases its contribution to membrane leak, shunting the incoming burstlet and increasing that shunt as the temporal gap between the input and the native burst closes. Immediately preceding the burstlet input, the model’s I_T was ∼−0.25 μA/cm² and growing; by comparison, immediately preceding the tonic spikelet input I_T was ∼−0.15 μ/cm², with transient increases during spikes (Figure 6A,C). Thus, bursts are overall less effective than spikelets at synchronizing spikes via electrical synapses in TRN cells.

Amplification of electrical synapses by I_NaP is, in turn, more effective for tonic spikes and spikelets than for bursts and burstlets in terms of synchronizing firing. For spikelets, amplification occurs for ∼1 mV events, where the gain of the spikelet efficacy (Figure 6B) is steepest and provides the most “bang for the buck” of amplification. For burstlets, which are several millivolt in size, amplification is less effective because the gain of burstlet efficacy is less steep for burstlets of several millivolt in size.

Discussion

While it has been shown that electrical synapses participate in spiking synchrony (Elson et al., 1998; Gibson et al., 1999; Galarreta and Hestrin, 2001; Landisman et al., 2002; Long et al., 2004; Hestrin and Galarreta, 2005; Pfeuty et al., 2005), and it has been anticipated that amplification of electrical synaptic signals by I_NaP would further aid synchrony (Mann-Metzer and Yarom, 1999; Dugue et al., 2009), we demonstrate here a fundamental difference in the influence of I_NaP on synchrony in tonic and burst modes of firing in electrically coupled pairs of neurons.

One might expect that because burstlets are larger and longer events than spikelets – indeed, burstlets are often several millivolt in amplitude and persist for 10 s of ms while spikelets are typically smaller and shorter (Figure 2B; Figures 6A,C) – that bursts would be more effective at promoting synchrony across gap junctions. Our results demonstrate, surprisingly, that tonic spikes synchronize much more readily than burst spikes, and that tonic spikes are modulated by I_NaP amplification of electrical synaptic signals while burst synchronization is largely unaffected. Insight into these effects is provided by our modeling study: during bursts, activation of I_T increases the leakiness of the membrane and thus adds a shunting influence to incoming burstlets. Amplification by I_NaP may also be functionally less effective for burstlets because in bursting mode, cells rest at more hyperpolarized potentials where I_NaP is less active (Figure 1). During tonic spikes, I_T is less active while I_NaP is more active; thus the membrane is both more responsive to spikelets and better able to amplify them.

Tonic Spiking

Neurons in the thalamus fire in tonic mode during wakefulness as well as certain phases of sleep (Domich et al., 1986). In this mode we found that I_NaP amplification of electrical synapses significantly enhances spiking synchrony. In addition, arrival of independent spontaneous chemical synaptic inputs and electrical synaptic spikelets synergistically activate I_NaP to coordinate tonic spikes (Figure 3D–G). Our model highlights two important details of enhanced tonic spiking coordination by amplified spikelets. First, spikelets are transmitted between neurons that are excited well above their firing threshold, thus maximizing the possible amplification by I_NaP (Figure 1). Second, at physiological ranges, small changes in spikelet amplitudes can create large changes in tonic spike synchrony. Specifically, spikelets are typically ∼1 mV in amplitude when measured at resting voltages, and the modeled effectiveness at perturbing a coupled partner’s spike time has its highest gain, or steepest slope, for ∼1–2 mV amplitude spikelets (Figure 6B). Thus, spikelets have powerful influence on tonic spiking synchrony.

In the relay thalamic regions, tightly synchronized tonic spikes in subsets of coupled TRN cells would result in tightly synchronized GABAergic inputs to thalamic relay cells, which could aid in the generation of spatially and temporally correlated rhythmic activity in downstream thalamic regions. This coordinating influence facilitates synchronization in the thalamocortical network in general; furthermore, enhanced synchrony of tonic spiking resulting from I_NaP-amplified gap junction signals may also be present in other gap junction-coupled inhibitory sub-networks in the cortex and elsewhere in the brain (Gibson et al., 1999; Mann-Metzer and Yarom, 1999; Galarreta and Hestrin, 2001; Blatow et al., 2003; Connors and Long, 2004).

Bursts in the TRN

Thalamic burst firing is a hallmark of spindle rhythms in slow wave sleep (Domich et al., 1986) and awake inattention (Bezdudnaya et al., 2006). In this state, our results indicate that bursts of neurons in the TRN rarely synchronize, similar to previous results in non-mammalian systems (Elson et al., 1998). We hypothesize that because bursts are largely shaped by low-threshold calcium currents (Parri and Crunelli, 1998; I_T), each neuron has a unique threshold and time-course of its burst, which is governed by its individual expression of CaV3.3-based channels (Huguenard and Prince, 1992). In combination with varying input resistances in any given neuron, activation of the resulting I_T results in a wide variety of burst onset times across TRN neurons (Figures A2C–F in the Appendix; Figure 5). Further, bursts in different TRN neurons vary both in terms of sub-threshold envelope shape and in the timings of the faster individual sodium spikes crowning the slower calcium depolarization. Our modeling indicates that bursts serve to decrease input resistance during those events, reinforcing the independence of each cell’s burst relative to incoming input. Burst generation in TRN neurons is thought to be compartmentalized within individual dendrites (Crandall et al., 2010); thus a burst in one dendrite may be largely unaffected by a gap junction on another dendrite. Our data indicate that even the largest possible amplification of a coupled cell’s burstlet is inadequate to overcome the internal dynamics generating an individual burst and modulate the onset or synchrony of the spikes crowning the burst.

Bursts occur and are transmitted between neurons at relatively hyperpolarized potentials, where I_NaP amplification is much less activated (Figure 1). Our model indicates that even large events of several millivolt in size, like burstlets (∼4 mV; Figure 2B and Table A1 in Appendix), are generally less effective at modulating burst times than are small-amplitude spikelets at modulating tonic spike times. Unlike amplification of spikelets, however, slight increases in burstlet amplitude have less effect on burst timing, due to the flatter slope at several-millivolt amplitudes (Figure 6D). For example, a 20% amplification of a ∼1 mV spikelet can increases the modulation of a neighbor’s spike time by 4.4% (Figure 6B); by contrast, a 20% amplification of a ∼4 mV burstlet only increases the shift in its neighbor’s spike time by 0.9% (Figure 6D).

In bursting mode, the synaptic targets of the TRN will receive independent sets of GABAergic inputs from each independent burst, which will then be subject to short-term synaptic dynamics in the thalamocortical relay neurons (Cox et al., 1996). However, because electrical synapses do not synchronize bursts in the TRN, these post-TRN bursts of inhibition are unlikely to be spatially and temporally correlated within and amongst postsynaptic targets in the thalamic relay regions. This asynchrony may provide each individual TRN neurons its own computational autonomy, and generally act to unbind activity across relay neurons and the information they transmit during these states.

Although other voltage-dependent membrane currents such as I_h or I_m may also modulate electrical synapses, we find that at least in TRN, the persistent sodium current I_NaP is the strongest modulator: amplification is flattened by 100 nM TTX (Figure 1). However, the effects of currents such as I_h or I_m on gap junctional signals will need to be established in a population of neurons with richer expressions of those currents.

Overall, these results suggest that the balance amongst intrinsic conductances, chemical synaptic drive and electrical coupling is a state-dependent and dynamic relationship.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Thomas Nowotny for helpful modeling and discussion; Judith Hirsch, Chinfei Chen, Scott Cruikshank, and Barry Connors for reading and comments on previous versions, and Bruce Bean for technical advice. This work was supported by the Milton Fund of Harvard University.

References

Alzheimer, C., Schwindt, P. C., and Crill, W. E. (1993). Modal gating of Na+ channels as a mechanism of persistent Na⁺ current in pyramidal neurons from rat and cat sensorimotor cortex. J. Neurosci. 13, 660–673.

Pubmed Abstract | Pubmed Full Text

Ayers, J. L., and Selverston, A. I. (1977). Synaptic control of an endogenous pacemaker network. J. Physiol. (Paris) 73, 453–461.

Pubmed Abstract | Pubmed Full Text

Bezdudnaya, T., Cano, M., Bereshpolova, Y., Stoelzel, C. R., Alonso, J. M., and Swadlow, H. A. (2006). Thalamic burst mode and inattention in the awake LGNd. Neuron 49, 421–432.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Blatow, M., Rozov, A., Katona, I., Hormuzdi, S. G., Meyer, A. H., Whittington, M. A., Caputi, A., and Monyer, H. (2003). A novel network of multipolar bursting interneurons generates theta frequency oscillations in neocortex. Neuron 38, 805–817.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chow, C. C., and Kopell, N. (2000). Dynamics of spiking neurons with electrical coupling. Neural Comput. 12, 1643–1678.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Condorelli, D. F., Belluardo, N., Trovato-Salinaro, A., and Mudo, G. (2000). Expression of Cx36 in mammalian neurons. Brain Res. Brain Res. Rev. 32, 72–85.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Connors, B. W., and Long, M. A. (2004). Electrical synapses in the mammalian brain. Annu. Rev. Neurosci. 27, 393–418.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Contreras, D., Curro Dossi, R., and Steriade, M. (1992). Bursting and tonic discharges in two classes of reticular thalamic neurons. J. Neurophysiol. 68, 973–977.

Pubmed Abstract | Pubmed Full Text

Cox, C. L., Huguenard, J. R., and Prince, D. A. (1996). Heterogeneous axonal arborizations of rat thalamic reticular neurons in the ventrobasal nucleus. J. Comp. Neurol. 366, 416–430.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Crandall, S. R., Govindaiah, G., and Cox, C. L. (2010). Low-threshold Ca²⁺ current amplifies distal dendritic signaling in thalamic reticular neurons. J. Neurosci. 30, 15419–15429.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Crill, W. E. (1996). Persistent sodium current in mammalian central neurons. Annu. Rev. Physiol. 58, 349–362.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Curti, S., and Pereda, A. E. (2004). Voltage-dependent enhancement of electrical coupling by a subthreshold sodium current. J. Neurosci. 24, 3999–4010.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Deans, M. R., Gibson, J. R., Sellitto, C., Connors, B. W., and Paul, D. L. (2001). Synchronous activity of inhibitory networks in neocortex requires electrical synapses containing connexin36. Neuron 31, 477–485.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Deisz, R. A., Fortin, G., and Zieglgansberger, W. (1991). Voltage dependence of excitatory postsynaptic potentials of rat neocortical neurons. J. Neurophysiol. 65, 371–382.

Pubmed Abstract | Pubmed Full Text

Devor, A., and Yarom, Y. (2002). Electrotonic coupling in the inferior olivary nucleus revealed by simultaneous double patch recordings. J. Neurophysiol. 87, 3048–3058.

Pubmed Abstract | Pubmed Full Text

Domich, L., Oakson, G., and Steriade, M. (1986). Thalamic burst patterns in the naturally sleeping cat: a comparison between cortically projecting and reticularis neurones. J. Physiol. (Lond.) 379, 429–449.

Pubmed Abstract | Pubmed Full Text

Dugue, G. P., Brunel, N., Hakim, V., Schwartz, E., Chat, M., Levesque, M., Courtemanche, R., Lena, C., and Dieudonne, S. (2009). Electrical coupling mediates tunable low-frequency oscillations and resonance in the cerebellar Golgi cell network. Neuron 61, 126–139.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Elson, R. C., Selverston, A. I., Huerta, R., Rulkov, N. F., Rabinovich, M. I., and Abarbanel, H. D. I. (1998). Synchronous behavior of two coupled biological neurons. Phys. Rev. Lett. 81, 5692.

CrossRef Full Text

Galarreta, M., and Hestrin, S. (2001). Electrical synapses between GABA-releasing interneurons. Nat. Rev. Neurosci. 2, 425–433.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gibson, J. R., Beierlein, M., and Connors, B. W. (1999). Two networks of electrically coupled inhibitory neurons in neocortex. Nature 402, 75–79.

Gibson, J. R., Beierlein, M., and Connors, B. W. (2005). Functional properties of electrical synapses between inhibitory interneurons of neocortical layer 4. J. Neurophysiol. 93, 467–480.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Haas, J. S., Kreuz, T., Torcini, A., Politi, A., and Abarbanel, H. D. (2010). Rate maintenance and resonance in the entorhinal cortex. Eur. J. Neurosci. 32, 1930–1939.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Harris, A. L. (2001). Emerging issues of connexin channels: biophysics fills the gap. Q. Rev. Biophys. 34, 325–472.

Pubmed Abstract | Pubmed Full Text

Hestrin, S., and Galarreta, M. (2005). Electrical synapses define networks of neocortical GABAergic neurons. Trends Neurosci. 28, 304–309.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Huguenard, J. R., and Prince, D. A. (1992). A novel T-type current underlies prolonged Ca(2+)-dependent burst firing in GABAergic neurons of rat thalamic reticular nucleus. J. Neurosci. 12, 3804–3817.

Pubmed Abstract | Pubmed Full Text

Jahnsen, H., and Llinas, R. (1984). Voltage-dependent burst-to-tonic switching of thalamic cell activity: an in vitro study. Arch. Ital. Biol. 122, 73–82.

Pubmed Abstract | Pubmed Full Text

Landisman, C. E., Long, M. A., Beierlein, M., Deans, M. R., Paul, D. L., and Connors, B. W. (2002). Electrical synapses in the thalamic reticular nucleus. J. Neurosci. 22, 1002–1009.

Pubmed Abstract | Pubmed Full Text

Llinas, R., and Jahnsen, H. (1982). Electrophysiology of mammalian thalamic neurones in vitro. Nature 297, 406–408.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Long, M. A., Landisman, C. E., and Connors, B. W. (2004). Small clusters of electrically coupled neurons generate synchronous rhythms in the thalamic reticular nucleus. J. Neurosci. 24, 341–349.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mann-Metzer, P., and Yarom, Y. (1999). Electrotonic coupling interacts with intrinsic properties to generate synchronized activity in cerebellar networks of inhibitory interneurons. J. Neurosci. 19, 3298–3306.

Pubmed Abstract | Pubmed Full Text

Meier, C., and Dermietzel, R. (2006). Electrical synapses – gap junctions in the brain. Results Probl. Cell Differ. 43, 99–128.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Netoff, T. I., Banks, M. I., Dorval, A. D., Acker, C. D., Haas, J. S., Kopell, N., and White, J. A. (2005). Synchronization in hybrid neuronal networks of the hippocampal formation. J. Neurophysiol. 93, 1197–1208.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Parri, H. R., and Crunelli, V. (1998). Sodium current in rat and cat thalamocortical neurons: role of a non-inactivating component in tonic and burst firing. J. Neurosci. 18, 854–867.

Pubmed Abstract | Pubmed Full Text

Pfeuty, B., Mato, G., Golomb, D., and Hansel, D. (2005). The combined effects of inhibitory and electrical synapses in synchrony. Neural Comput. 17, 633–670.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Srinivas, M., Rozental, R., Kojima, T., Dermietzel, R., Mehler, M., Condorelli, D. F., Kessler, J. A., and Spray, D. C. (1999). Functional properties of channels formed by the neuronal gap junction protein connexin36. J. Neurosci. 19, 9848–9855.

Pubmed Abstract | Pubmed Full Text

Stuart, G., and Sakmann, B. (1995). Amplification of EPSPs by axosomatic sodium channels in neocortical pyramidal neurons. Neuron 15, 1065–1076.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Taddese, A., and Bean, B. P. (2002). Subthreshold sodium current from rapidly inactivating sodium channels drives spontaneous firing of tuberomammillary neurons. Neuron 33, 587–600.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Traub, R. D., Contreras, D., Cunningham, M. O., Murray, H., Lebeau, F. E., Roopun, A., Bibbig, A., Wilent, W. B., Higley, M. J., and Whittington, M. A. (2005). Single-column thalamocortical network model exhibiting gamma oscillations, sleep spindles, and epileptogenic bursts. J. Neurophysiol. 93, 2194–2232.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Urbani, A., and Belluzzi, O. (2000). Riluzole inhibits the persistent sodium current in mammalian CNS neurons. Eur. J. Neurosci. 12, 3567–3574.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vervaeke, K., Lorincz, A., Gleeson, P., Farinella, M., Nusser, Z., and Silver, R. A. (2010). Rapid desynchronization of an electrically coupled interneuron network with sparse excitatory synaptic input. Neuron 67, 435–451.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Appendix

FIGURE A1

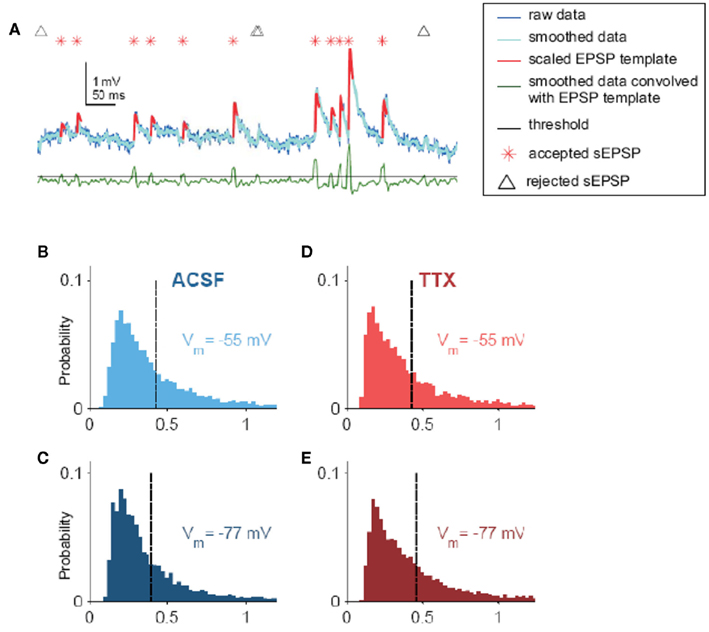
Figure A1. sEPSPs. (A) Visual description of the algorithm used to find spontaneous excitatory postsynaptic potentials (sEPSPs) in voltage traces. Raw data were smoothed lightly (dark and light blue traces, respectively) and convolved (green trace) with a template. Peaks in the convolution correspond to where the data best match the template; thus, to find candidate sEPSPs, the convolution was subjected to a threshold (black line). For each event, if the amplitude exceeded a size threshold, which was taken as a fraction of the SD of the smoothed data, it was identified as an sEPSP (red asterisk; the template, scaled to each sEPSPs individual amplitude, is superimposed on the data in red). Locations of events too small to be confirmed as sEPSPs are noted by black triangles. Convolution and amplitude thresholds were adjusted for each cell by hand. (B) Distribution of sEPSP amplitudes for V_m = −55 mV in ACSF (0.43 ± 0.004 mV, N = 5855 sEPSPs from 19 cells). (C) Distribution of sEPSP amplitudes for V_m = −77 mV in ACSF (0.40 ± 0.004 mV, N = 8145 sEPSPs from 19 cells). (D) Distribution of sEPSP amplitudes for V_m = −55 mV, in 100 nM TTX (0.43 ± 0.005 mV, N = 5598 sEPSPs from 17 cells). (E) Distribution of sEPSP amplitudes for V_m = −77 mV, in 100 nM TTX (0.46 ± 0.005 mV, N = 6592 sEPSPs from 17 cells).

FIGURE A2

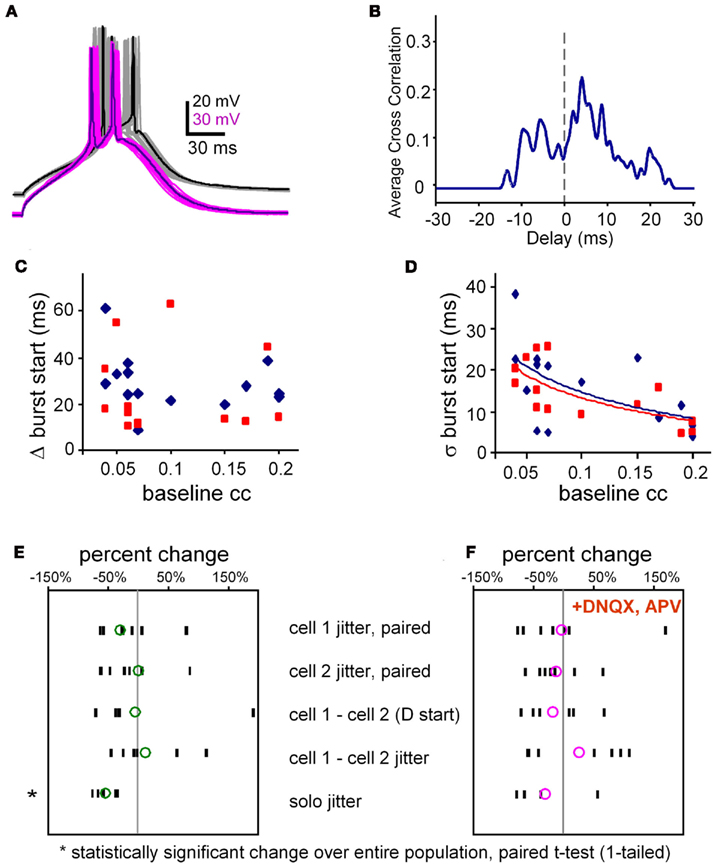
Figure A2. Burst jitter. (A) Example of 16 overlaid trials of aligned bursts from a pair of electrically coupled neurons. Note that even though their slow depolarizations (calcium spikes) are aligned, their spikes are rarely aligned. Average coupling coefficient at V_rest, was 0.14. (B) Spike cross-correlogram for data shown in (A). Spikes were represented by Hanning windows, 2 ms-wide. Cross correlation was done at the same temporal resolution as the data, 0.05 ms. (C) Burst synchrony (Δ burst start times, y-axis) is uncorrelated with electrical synaptic coupling strength (x-axis; R² = 0.06) in both ACSF (blue symbols) and in TTX (R² = 0.01, red symbols, N = 14 pairs). (D) A reduction in the jitter of burst synchrony (SD of the absolute difference in onset times) is loosely correlated with greater coupling strength (slope −83 per ms, R² = 0.29) in both ACSF (blue symbols) and in TTX (slope −78 per ms, R² = 0.48, red symbols; N = 14 pairs). Each data point in (C,D) represents the average value per pair for 20–30 trials at the two burst thresholds. (E) Changes in jitter and difference in burst arrival times. All data, except solo jitter are derived from paired burst stimulation at threshold for both neurons. Population responses of all pairs tested in normal ACSF (without blockers). Each black dash represents the average for one pair, and the green circles represent the population average derived from the individual averages. N = 7. (F) The same results as in (E) but in the presence of fast synaptic blockers. N = 7.

TABLE A1

Table A1. Action potential properties in control (ACSF) vs. TTX.