- Computational Neuroscience Unit, Okinawa Institute of Science and Technology Graduate University, Okinawa, Japan
In their seminal works on squid giant axons, Hodgkin, and Huxley approximated the membrane leak current as Ohmic, i.e., linear, since in their preparation, sub-threshold current rectification due to the influence of ionic concentration is negligible. Most studies on mammalian neurons have made the same, largely untested, assumption. Here we show that the membrane time constant and input resistance of mammalian neurons (when other major voltage-sensitive and ligand-gated ionic currents are discounted) varies non-linearly with membrane voltage, following the prediction of a Goldman-Hodgkin-Katz-based passive membrane model. The model predicts that under such conditions, the time constant/input resistance-voltage relationship will linearize if the concentration differences across the cell membrane are reduced. These properties were observed in patch-clamp recordings of cerebellar Purkinje neurons (in the presence of pharmacological blockers of other background ionic currents) and were more prominent in the sub-threshold region of the membrane potential. Model simulations showed that the non-linear leak affects voltage-clamp recordings and reduces temporal summation of excitatory synaptic input. Together, our results demonstrate the importance of trans-membrane ionic concentration in defining the functional properties of the passive membrane in mammalian neurons as well as other excitable cells.
Introduction
The non-voltage-gated component of excitable cell membranes, usually called the passive membrane, plays an important role in defining electrical properties of neurons. Passive membrane properties are controlled by the behavior of leak currents. Most leak channels in neurons are voltage-independent, 2-pore channels: the K+ permeable TASK (González et al., 2012) and Cl− permeable CIC-2 channels (Jentsch et al., 2005). There is also a small contribution from TTX-insensitive, Na+ permeable NALCN channels (Ren, 2011).
Leak channels have, by definition, a voltage-independent conductance, but leak currents do show a dependence on membrane potential, as they are driven by both electrical potentials of permeating ions and ionic concentration gradients. When a concentration gradient is taken into account, the associated electrical current rectifies with the membrane potential. The degree of rectification is dependent on the concentration gradient: the greater the concentration gradient, the greater the voltage-dependent current rectification. This phenomenon is well described by the Goldman-Hodgkin-Katz (GHK) current equation (Goldman, 1943; Hodgkin and Katz, 1949; Hodgkin and Horowicz, 1959) (Figure 1: Equation 1). Nonetheless, Ohm's law, which assumes a linear relationship with membrane potential, is routinely used to describe leak currents both in experimental measurements and in neuron models (Figure 1: Equation 2).
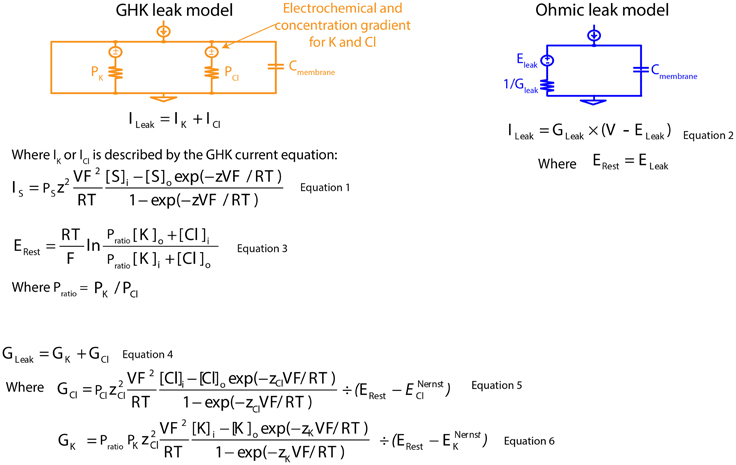
Figure 1. Mathematical descriptions of the Ohmic and Goldman-Hodgkin-Katz leak-current models. GHK, Goldman-Hodgkin-Katz; PK, absolute permeability value of K+; PCl, absolute permeability value of Cl−; Cmembrane, specific membrane capacitance; ILeak, leak current; IK, K+ component of GHK leak current; ICl, Cl− component of GHK leak current; S, permeating ion; IS, GHK-type S leak current; PS, absolute permeability value of S; z, ionic charge of S; V, membrane potential; F, Faraday's constant; R, gas constant; T, absolute temperature; Si and So, intra- and extracellular concentration of S; ERest, resting membrane potential; Pratio, permeability ratio; [K]i and [K]o, intra- and extracellular concentration of K+; [Cl]i and [Cl]o, intra- and extracellular concentration of Cl−; GLeak, membrane leak conductance; GK, K+ component of membrane leak conductance; GCl, Cl− component of membrane leak conductance; zCl, ionic charge of Cl−; ENernstCl, Nernst potential of the Cl− component of GHK leak current; zK, ionic charge of K+; ENernstK, Nernst potential of the K+ component of GHK leak current; ELeak, reversal potential of Ohmic leak current.
But is Ohm's law truly a reasonable assumption of passive membrane currents? In support of a linear leak-current model, Roth and Häusser (2001) showed, in cerebellar Purkinje neurons, that two identical current pulses of opposing sign generated voltage traces that were mirror images. Furthermore, using the dual soma-dendritic patch technique, the study showed that the soma-voltage response to a current pulse in the dendrite and the dendrite-voltage response to a current pulse in the soma were superimposable when scaled. The study then used a computational model to show that the observed electrophysiological membrane properties were well modeled using a multi-compartmental neuronal model with an Ohmic leak current. However, because these data were collected at a single holding potential, any rectification due to leak currents would have been difficult to observe.
The GHK current equation has been shown to better represent voltage-gated currents than an Ohmic model. For example, voltage-gated Ca2+ current is much better modeled using the GHK current equation because of a 10,000-fold Ca2+ concentration gradient and a divalent charge (Hille, 2001). Furthermore, kinetics of voltage-gated K+ currents in squid axon are better modeled using GHK equations despite having a much less exaggerated concentration gradient (Clay, 1991, 1998, 2009; Clay et al., 2008).
In this study, we assess the importance of a GHK-based leak current in the passive membrane properties of single- and multi-compartmental neuronal neuron models. We show that passive membrane properties [membrane time constant (tau) and input resistance (Rn)] modeled using Ohm's Law do not change with membrane potential; however, in a GHK-based leak model with identical membrane parameters, tau and Rn vary nonlinearly with both membrane potential and ionic concentration. To validate the GHK-based leak model, we investigated passive membrane properties of cerebellar Purkinje neurons in current clamp mode. We found that the relationship between tau/Rn, membrane potential and ionic concentration, were consistent with our model predictions. Through modeling, we further show that nonlinear leak current can define the kinetics of voltage-gated ion channels and the amplitude synaptic summation. Combined, our computational and experimental evidence demonstrate the importance of non-linear leak currents in neuronal excitability.
Materials and Methods
Design of the GHK Leak Model
Concentration-dependent passive membrane models are infrequently used, in part, because absolute permeability values of permeating ions (Figure 1: Equation 3) cannot be experimentally measured. We bypassed this problem by reducing the number of permeating ions modeled to two ions, and we obtained the ratio of their absolute permeability values (permeability ratio, Pratio) using the GHK voltage equation for a given resting membrane potential (Erest) (Figure 1: Equation 3). With known membrane conductance and permeability ratios, exact permeability values for both ions can be calculated (Figure 1: Equations 4–6). Modeling in this manner, allows direct comparison between linear and non-linear models, since both share the same membrane conductance and Erest for current calculation.
Modeling
All models were constructed and implemented using Python (version 2.7.5) and NEURON (version 7.4) (Carnevale and Hines, 2006; Hines, 2009) using the variable time-step method (Lytton and Hines, 2005). Unless stated otherwise, both the isopotential and compartmental models were modeled using the following membrane parameters: Erest = −85 mV, specific membrane capacitance 0.8 μFcm−2, specific membrane resistance 120,000 Ωcm2, specific intracellular resistivity 120 Ωcm2 and a total surface area of approximately 68,065 μm2, with the exception of Erest, adapted from De Schutter and Bower (1994). Both the Ohmic and GHK membrane conductances at rest were equal to the inverse of the stated membrane resistance. Furthermore, the GHK conductance was equal to the sum of the K+ and Cl− conductances at Erest.
Channel Modeling
All ion channel models were adopted from published studies. Specifically, kinetics of Kv4 and hyperpolarization-activated, non-specific cationic current were adapted from Akemann and Knöpfel (2006). Hodgkin and Huxley voltage-gated K+ channel current was simulated using the original model (Hodgkin and Huxley, 1952) with the original internal and external concentrations (Hodgkin, 1951). Both of these channel models were modified with GHK current instead of Ohmic IK, so as to investigate only the effects of non-linear leak currents. All models were created in NMODL (Hines and Carnevale, 2000) for implementation in NEURON.
Modeling Passive Membrane Voltage Response
An Ohmic, non-specific leak current was used to describe the linear voltage-current relationship, while the combined K+ and Cl− GHK currents were used to describe the non-linear voltage-current relationship. K+ and Cl− absolute permeability values were calculated from the membrane conductance, the K+/Cl− permeability ratio, and the Erest using the GHK voltage equation (Equations 1, 3, and 4).
Model Validation Using Patch clamp Electrophysiology
Mice (strain C57BL/6J 6w, Charles River) of either gender, age P17-22 and 2–4 months, were anesthetized and decapitated in accordance with the Science Council of Japan Guidelines for Proper Conduct of Animal Experiments, and with approval from the OIST Animal Resources Section.
Cerebellar sagittal slices (300 μm) were obtained at 34°C (Huang and Uusisaari, 2013; Ankri et al., 2014). Briefly, slices were obtained by dissection at 32–34°C and stored in oxygenated, artificial cerebrospinal fluid (ACSF) composed of (in mM): 125 NaCl, 2.5 KCl, 25 glucose, 25 NaHCO3, 1.25 NaH2PO4, 2 CaCl2, and 1 MgCl2. Slices were then transferred to a holding chamber filled with oxygenated ACSF at 34°C and allowed to recover for at least 30 min before use. Slices were discarded after 4 h. All chemicals were purchased from Sigma-Aldrich.
In the recording chamber, slices were perfused with oxygenated ACSF at 2 ml/min, 34°C. Neurons were visualized using infrared differential interference contrast video microscopy (Olympus BX51WI microscope) with a 40x water-immersion objective lens.
In whole-cell current clamp recordings, borosilicate glass electrodes of 5–7 MΩ were filled with an internal solution containing (in mM): 140 potassium gluconate, 10 KCl, 10 HEPES, 10 EGTA, 4 MgATP, 0.4 NaGTP, 10 phosphocreatine, 8 biocytin (pH adjusted to 7.3 with KOH). Purkinje neurons were identified by their distinctive morphology and position within the cerebellar cortex.
A resistance seal of ≥4 GΩ was required before entering whole-cell, patch-clamp configuration. Signals were amplified and low-pass filtered at 5 kHz using a Cornerstone BVC-700 A amplifier (Dagan), and were recorded at 40 kHz using a custom interface written in Labview acquisition software (National Instruments). After obtaining whole-cell configurations, Purkinje neurons were hyperpolarized to −65 mV.
Isolating the Passive Membrane Resting Potential
Cerebellar Purkinje neurons were perfused with TTX (1 μM), ZD7288 (30–50 μM), and synaptic blockers (DNQX, 10 μM and GABAzine, 10 μM) to block voltage-gated Na+, hyperpolarization-activated cationic current (Ih), and AMPA and GABAa receptor currents, respectively. High intracellular EGTA (10 mM) was used to minimize Ca2+-dependent K+ currents, which contribute to spontaneous firing of Purkinje neurons (Edgerton and Reinhart, 2003; Khaliq et al., 2003).
We observed that the Erest of cerebellar Purkinje neurons after pharmacological treatment could be permanently shifted by repeated current injections. Therefore, after each current pulse step, data were discarded if a deviation of more than 2 mV from the Erest occurred. The voltage trace of each current pulse step is the average of at least four replicates.
Analysis
Electrophysiological data were analyzed using Python 2.7, Pylab 2.7, and R 3.01. Data are given as means ± standard error and/or 95% confidence interval, and statistical significance was tested using Student's t-test. Rn was calculated from the amplitude of initial peak and steady state voltage deflection in response to a current pulse injection (−30, −15, 15 or 30 pA). Tau was estimated by a single, exponential fitting, where the fit duration was 500 ms, starting 2 ms after current pulse injection. This was done to avoid artifacts due to a voltage drop across the recording electrode (Major et al., 1994; Roth and Häusser, 2001).
Results
Passive membrane properties of an isopotential cell are conventionally measured by applying a small current pulse to produce a membrane voltage deflection from Erest. From the transient proportion of the voltage deflection, tau can be estimated using an exponential decay (see Methods); from the steady-state proportion, Rn can be calculated. We created two leak-current models, one described by a linear circuit and the other by a K+ and Cl− GHK current model, to compare the difference in passive membrane properties. These models are used to demonstrate non-linear properties of the GHK current model, they are not intended to fit the experimental data exactly.
GHK Leak Currents Make a Passive Membrane Non-linear
In the Ohmic model, membrane potential changes proportionally with injected current. As a result, injecting a positive and a negative current pulse of the same magnitude (± pulses) produces two identical voltage curves, one of which is inverted. (Figure 2A). In addition, the passive membrane properties tau and Rn, are unaffected by membrane potential change (Figure 2B). In the GHK passive membrane model, voltage deflections varied with current-clamped membrane potential. Specifically, the small current pulse that was used to produce voltage deflection in the Ohmic model, produced smaller voltage deflections at depolarizing clamped potentials and larger deflections at hyperpolarizing clamped potentials, relative to the voltage deflection at rest (Figure 2A). Notice that for any given membrane potential, the response to a positive current injection was still almost superimposable upon the response to a negative one, indicating that the response is close to linear under these conditions.
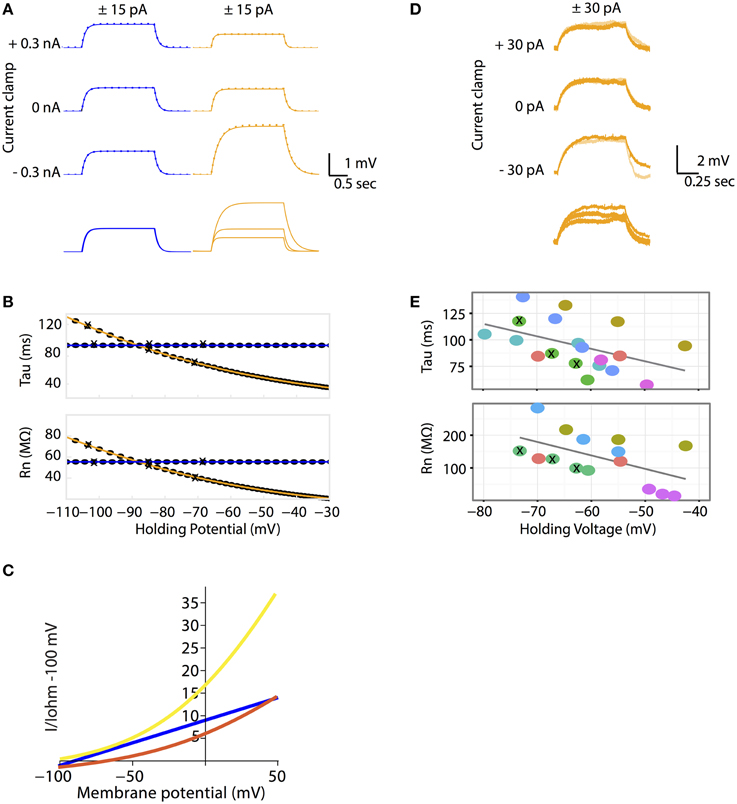
Figure 2. (A–C) The Goldman-Hodgkin-Katz leak-current model predicts non-linear voltage responses to DC current injections. (A) All Ohmic model simulations are colored in blue and all GHK model simulations are colored in orange. Voltage traces of passive membrane responses to +15 pA (solid lines) and −15 pA (inversed and superimposed, dotted lines) current injections for 2 seconds, at −0.3, 0 and +0.3 nA holding currents. Bottom traces: voltage responses to +15 pA current pulse at various holding currents superimposed. The Ohmic and GHK cell models have identical surface areas, Erest (−85 mV) and membrane resistances (120 kohm cm2). For the GHK model, ionic concentrations in mM are: [K+]in and [Cl−]in are 150 and 10 respectively, external [K+]out and [Cl−]out are 2.5 and 130, respectively. (B) Rn and tau at each holding potential calculated using the +15 nA traces. The holding potential values for the traces in (A) are marked by “X”. (C) The GHK model comprises two rectifying currents IK (yellow) and ICl (red). Ohmic current is colored blue. All currents are standardized to Ohmic current at −100 mV. All three current-voltage curves were constructed using the same Ohmic and GHK model as in (A). (D–E) Rn-voltage and tau-voltage relationships measured in cerebellar Purkinje neurons were non-linear, consistent with the GHK model prediction. (D) Voltage deflections in a Purkinje neuron (when major ionic currents are blocked) in response to +15 pA (orange) and −15 pA (pale orange) current pulse injections for 1 s at −30, 0, and +30 pA holding currents (corresponding holding potentials are −74, −67, and −63 mV, respectively). Bottom traces: voltage responses to +30 pA current pulse at various holding currents superimposed. (E) Rn-voltage and tau-voltage relationships of each recorded cell (represented by different color filled circles). Holding potentials of the traces in (D) are marked by “X”. The regression slope (β) for tau and Rn are −1.2 (p = 0.043) and −4.1 (p = 0.037) respectively. Individual cells were highlighted to show that non-linear passive membrane properties could be observed for all cells recorded (n > 5).
Why does voltage deflection decrease with depolarization and increase with hyperpolarization from Erest? In the GHK leak model, Erest lies between the reversal potentials of IK and ICl. Therefore, IK causes hyperpolarization while ICl causes depolarization. The relative proportion of the two leak currents is determined by the ratio of the degree of current rectification, determined by the concentration gradient, and their absolute permeability ratio. While in the GHK model the permeability ratio of K+ and Cl− is close to 1, the K+ gradient is significantly higher than that of Cl− (60-fold vs. 13-fold, respectively). As a result, K+ rectification is stronger than that of Cl− (Figure 2C), so the effect of K+ hyperpolarization is stronger than that of Cl− depolarization.
Experimental Verification
The crucial question addressed by this study is whether the non-linear leak model is a better fit for the passive membrane responses to electrophysiological stimulation. Using patch clamp electrophysiology in the whole-cell configuration and the current clamp protocol as described for simulations, the passive properties of cerebellar Purkinje neurons were measured. The magnitude of voltage deflections from the current injection protocol was consistent with the GHK model simulation (Figure 2D). Furthermore, tau and Rn decreased progressively with depolarizing potentials (Figure 2E). Individual cells were color-coded to highlight the presence of non-linear tau and Rn in most of the recorded cells.
Central to the GHK model prediction is that tau and Rn should be influenced by ionic concentration change. In the GHK model, changing a single ionic concentration can result in two different tau/Rn-voltage relationships depending on which property of the model is conserved. Using intracellular Cl− concentration as an example, at fixed Pratio, the tau/Rn-voltage curve shifts right, toward the Cl− reversal potential (Figure 3A black lines). Conversely, at fixed Erest, Pratio increases, which increases and decreases the K+ and Cl− leak components, respectively, and reduces the slope of the tau/Rn–voltage relationship (Figure 3A orange lines).
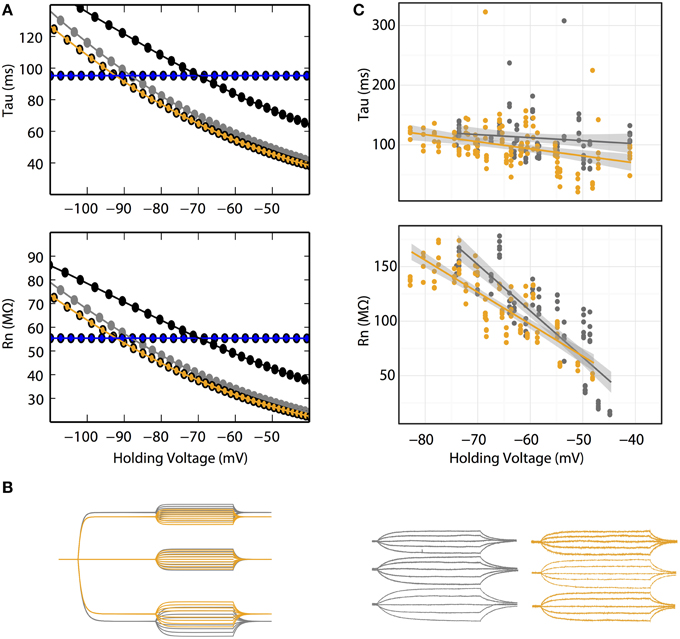
Figure 3. (A) Rn–voltage and tau-voltage relationships are concentration-dependent in the GHK model. Voltage dependence of Rn and tau of 10 (gray) and 30 (orange) mM intracellular Cl− at fixed Erest (−85 mV). Their corresponding K+ and Cl− permeability ratios are 1.34 and 7, respectively. Black: voltage dependence of Rn and tau of 30 intracellular Cl− at a K+/Cl− permeability ratio of 1.34. Ohmic simulation is shown in blue. Each data point was calculated using voltage traces from 15 pA current pulse injection. (B) Voltage responses to current pulses in cerebellar Purkinje neurons are consistent with the GHK model simulation. Left, GHK model simulation using a series of current pulses (−60 to +60 pA at 15 pA interval recorded at −30, 0, and +30 pA holding currents) for 10 and 30 mM intracellular Cl−. Right, voltage responses to current pulses (−30 to +30 pA at 15 pA interval recorded at −30, 0, and +30 pA holding currents) in cerebellar Purkinje neuron. For both simulation and experimental data, gray and orange represent 10 and 30 mM intracellular Cl−. Holding potentials for 10 mM Cl− at −30, 0, +30 pA are identical to values reported in Figure 2E; the holding potentials for 30 mM Cl− are −68, −65, and −60 mV, respectively. (C) Rn–voltage and tau-voltage relationships are concentration-dependent in cerebellar Purkinje neurons. Comparisons of tau and Rn values at each current pulse, between 10 and 30 mM intracellular Cl−. 30 mM Cl− reduced the steepness of the regression slope of Rn-voltage (β10mM = −5.6, n > 6, β30mM = −2.9, n = 6, p = 0.0002).
In Purkinje neurons patched with 30 mM Cl− -filled pipettes, smaller voltage deflections at hyperpolarizing current-clamp were observed (Figure 3B). Furthermore, the regression slope of the Rn-voltage relationship was noticeably decreased in 30 mM Cl− (β10mM = −5.6, β30mM = −2.9, p = 0.0002, n = 6, Figure 3C orange line) consistent with the simulation at fixed Erest (Figure 3A orange line).
The effect of concentration on the tau-voltage relationship was less conclusive. The slope of the higher Cl− data was steeper, contrary to our prediction (β10mM = −0.5, β30mM = −1.2, p = 0.04, n = 6). It is likely that this difference is not due to a physiological effect, but that it is an artifact of our estimate of tau. Voltage responses in extensive dendritic arbors, as in Purkinje neurons, have long been known to have more complex time courses than the single exponential fit used (Koch, 1999a,b; Rall, 1969). As the statistical difference is small, we suspect the effect of concentration change on tau was too small to allow experimental differentiation.
The resting membrane potentials measured under the 10 and 30 mM Cl− settings were −63 ± 3 and −67 ± 2 mV, respectively, while we expected that the latter would have a more depolarized potential. The underlying mechanism of this unclear, however we suspect that it is a homeostatic response trying to maintain a set point resting potential.
Non-linearity of Passive Membrane in Complex Morphology
Patch clamp recordings of passive properties of mammalian neurons are routinely conducted for neuronal excitability investigations. Why hasn't passive membrane non-linearity been observed? First, as demonstrated in our simulation and whole-cell recordings, passive non-linearity is only apparent when voltage deflections from two different holding potentials are compared. At the same holding potential, the difference between positive and negative current-induced voltage traces is minimal. Second, dendritic branching increases local input resistance (Rinzel and Rall, 1974). A current injected into a branched cell would therefore result in a larger voltage deflection than that into an isopotential cell. To demonstrate this concept, we re-ran the simulation in Figure 2 using a multi-compartmental, Purkinje neuron model of the same surface area as the isopotential cell model. This showed, indeed, a much stronger dependence of Rn on holding potential while that of tau did not change as predicted. (Figures 2B, 4). If we had performed our patch clamp recordings in a cell type with substantially less dendritic branching, we might not have observed the concentration-dependent voltage deflections in Figure 3.
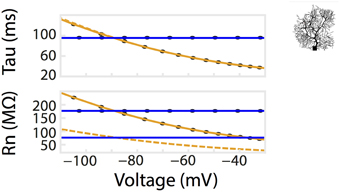
Figure 4. Dendritic branching of neurons exaggerates the non-linear relationship of Rn-voltage. A comparison of Rn/tau –voltage relationships was calculated from a multi-compartmental model with the same surface area as the isopotential model in Figure 2. Voltage responses of the model to a series of current pulses, as in Figure 2A. Corresponding values from simulation using the isopotential model are represented by dotted lines. Ohmic simulation results are shown in blue.
Physiological Consequences of Non-linear Passive Membranes
To illustrate the scale of errors caused by assuming an Ohmic leak instead of the GHK leak, we compared voltage-clamp simulations of the mammalian voltage-gated potassium current Kv4 under both settings (Figure 5A). It can be seen that the amplitude and rates of transient and steady state voltage properties of Kv4 differ substantially between the Ohmic and GHK model simulations. The underlying cause of this difference is the large K+ gradient (60-fold) in combination with the greater K+ permeability relative to that of Cl−. In contrast, in the squid axon, the K+ gradient is less steep (40-fold) and more importantly, the permeability ratio of K+/Cl− is less than 1, to achieve the reported Erest of −65 mV. So although K+ current strongly rectifies at depolarizing potentials (Clay, 2009), its contribution to the total leak is small; therefore there is little difference between the Ohmic and GHK squid axon models (Figure 5B). These examples show that, depending on the experimental preparation used, the use of Ohmic leak models may lead to significant errors in the estimate of the voltage-dependence of channel conductance from voltage clamp recordings.
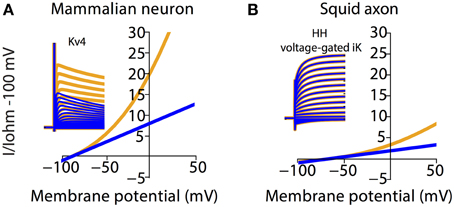
Figure 5. Channel kinetic estimation using linear (Ohmic) passive membrane kinetics can cause substantial errors in cell types with large ionic concentration gradients. Effect of GHK leak currents on simulated voltage-clamp of mammalian voltage-gated K+ current, Kv4 (A) and K+ current from the Hodgkin-Huxley model (B) The ionic concentration in (A) is the same as that in Figure 2. The ionic concentration in (B) is adapted from Table 2 in Hodgkin (1951), which listed the approximate intra- and extracellular concentration of K+, Na+, and Cl− in Loligo axons (Hodgkin, 1951). Furthermore, Erest and membrane resistance values for the squid model were set to NEURON default values. Note that both the mammalian and squid axon K+ currents were calculated by multiplying the gating variables with a GHK current component. Simulations using Ohmic and GHK leak currents are colored blue and orange, respectively. The initial fast transient is the capacitive current.
The results thus far have dealt with non-linear voltage responses due to DC current injection; however, in vivo current inputs are rarely static with varying conductances and membrane potentials. We assessed the relevance of non-linear leak in this context by modeling synaptic temporal summation in a single-compartment model. Initial EPSPs were similar between the Ohmic and GHK-based leak models; however, GHK-based temporal summation was reduced relative to the Ohmic case (Figure 6, dotted lines). We also investigated temporal summation of inhibitory potentials, but the relative difference between Ohmic and GHK models was insignificant primarily because Erest and the Cl− reversal potential were in close proximity (not shown).
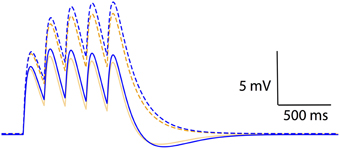
Figure 6. Non-linear passive conductances affect temporal integration of post-synpatic potentials. Temporal summation of excitatory post-synaptic potentials in an Ohmic model (blue) and a GHK model (orange) (same models as in Figure 2). Solid and dotted lines represent summation in the presence and absence of Ih respectively. The maximal conductance of Ih used in this simulation is identical to GLeak of the GHK leak current.
As a guide to the significance of the difference in temporal summation of EPSPs, we re-simulated this in the presence of a hyperpolarization-dependent, non-specific cationic current (Ih) that had the same maximal conductance as that of the leak currents (see Methods). Ih was chosen because it is known to also dampen temporal summation (Magee, 1999; Williams and Stuart, 2000; Van Welie et al., 2006; Angelo et al., 2007). The dampening effect of GHK-leak alone on temporal summation (yellow dotted line) was small relative to that of Ih and Ohmic leak combined (blue solid line); however, when combined with Ih the GHK leak still had a significant effect (orange solid line). These data suggest that the effect of GHK-leak in vivo in the presence of voltage-gated conductances is significant.
Discussion
Computational and experimental evidence presented here demonstrates that pharmacologically isolated passive membrane current is better modeled using the GHK than the Ohmic equation. The results suggest that non-linear leak currents are an important parameter for defining membrane electrical properties and that ionic concentration should be considered in neuronal modeling in general.
Our GHK model assumes that leak currents are generated solely from ion permeation through membrane pores, but physiological passive membranes are far from simplistic. As described earlier, leak currents are generated by specific channels, some of which may have more complex properties than those captured by the GHK model (Jentsch et al., 2005). Also, our model did not include several other membrane mechanisms that generate small currents. First, our model did not include active ion transporters like the ubiquitous Na+/K+ ATPase responsible for maintaining Na+ and K+ concentration gradients (Racker, 1978; Brodie et al., 1987) and K+/Cl− co-transporter 2 responsible for maintaining extracellular K+ and intracellular Cl− concentration (Payne et al., 1996; Rivera et al., 1999; Chamma et al., 2012; Seja et al., 2012). Second, the model did not take into account currents from ligand-gated ion channels, for example, tonically activated GABAa currents (Brickley et al., 1996; Semyanov et al., 2004), and glutamate-gated Cl− currents of excitatory amino acid transporters (Fairman et al., 1995; Tzingounis and Wadiche, 2007). Third, it did not consider volume-sensitive, outward-rectifying Cl− channels, which affect both excitability and Cl− flux (Inoue et al., 2005; Jentsch et al., 2005; Inoue and Okada, 2007; Zhang et al., 2011). Fourth, we did not model TTX-insensitive Na+ leak currents, which have been indicated in setting neuronal resting membrane potential (Ren, 2011). Some of the aforementioned molecular identities can be incorporated into a neuron model by changing the permeability ratio of a GHK-based leak model, for example, tonically active GABAa currents are akin to a decrease of the K+/Cl− permeability ratio. Other molecular identities, such as ion transporters, may need to be modeled in combination with intracellular and extracellular ion accumulation, separately from membrane leak current.
Limitations of the Modeling and Experimental Designs Used
The primary difficulty with the GHK model is to determine the absolute permeability value for permeating ions. In our model, two out of the three most abundant physiological ions were used in the GHK model. This is so that an exact pair of K+ and Cl− absolute permeability values could be obtained for subsequent model simulations. Ignoring the Na+ leak current may have caused an over-estimation of the effects of K+ and Cl− currents, and have rendered the Cl− current excitatory because the resting potential lies between the Nernst potential of the two ions. But the ability to simulate the effect of ionic concentration on Erest outweighed the need to have a more complete, non-linear leak-current model. Furthermore, the consistency between our experimental and simulated data suggests that a non-linear sodium leak current would not have altered the conclusion of this study.
We used the chord conductance to calculate permeability values; however, slope conductance is equally valid for the same calculation (Thompson, 1986). The chord conductance is the slope of the line drawn from a point on a current-voltage curve to the current reversal; the slope conductance is the slope of the line tangent to the same point. Either formalism is acceptable for describing conductance as long as data acquired using either formalism are not used interchangeably (Helman and Thompson, 1982). Although permeability and conductance play similar roles in describing the dependency of channel currents on channel density, they are completely unrelated parameters and it is possible to convert one into the other only at a fixed membrane potential; see Clay (2009) for a more detailed description. As a consequence, more experimental measurements of ion permeabilities in different neuron types are needed because of their importance for passive membrane properties.
It is important to note that a cocktail of drugs was perfused to isolate the passive membrane in the experimental investigation. How these drugs affect leak channel expression during the recordings, which lasted over 40 min per cell, is unknown. Therefore, values of passive membrane properties measured experimentally may not be inherently meaningful, but relative changes in them are. This also extends to Erest, which slightly hyperpolarized with increasing intracellular Cl− concentration, although we predicted the opposite. We suspect that this is due to cellular compensatory mechanisms to prevent depolarization from Erest.
Comparisons with Other Studies
The main findings of this study contradict the observation of membrane linearity in cerebellar Purkinje neurons reported by Roth and Häusser (2001). It is likely that they did not observe the nonlinear leak because their study did not compare tau and Rn across different holding potentials. Furthermore, to observe non-linearity in their investigation of membrane reciprocity, a longer duration current pulse would have been needed.
Clay (2009) demonstrated in detail the importance of using GHK equations to model voltage-gated K+ channels, including the squid delayed rectifier and A-type channels. The use of GHK instead of Ohmic equations to model the delayed rectifier suffice to change the excitability of the Hodgkin and Huxley (1952) model from type 2 to type 3, with better correspondence to experimental data (Clay et al., 2008). While Clay emphasized that the need for GHK equations applies to all types of K+ channels, he did not consider similar effects on leak channels described here.
In somato-gastric neurons, White and Hooper (2013) reported a non-linear relationship between input resistance and input capacitance with membrane potential similar to that observed here. They speculated that it is caused by various voltage-gated ionic currents (A-type K+, persistent Na+, Ca2+, Ca2+-activated K+) that activate at potentials more negative than −75 mV (Turrigiano et al., 1995; Prinz et al., 2003; White and Hooper, 2013). Although our study does not rule out this possibility, it provides a simpler explanation for the non-linear properties they reported.
Physiological Consequences of Membrane Non-linearity
The non-linearity of passive membrane differs substantially between types of preparations, for example, it is smaller in squid axons relative to mammalian neurons. This non-linearity becomes more significant as the holding potential deviates from the resting potential of the patch-clamped cell or when the K+/Cl− permeability ratio deviates from 1. Because electrophysiology recordings of neurons are routinely conducted under a range of voltages and the physiological K+/Cl− permeability ratio is commonly greater than 1, the use of Ohmic leak in passive membrane modeling is almost always inaccurate.
The non-linear relationship between Rn/tau and membrane potential, affect many routine electrophysiological measurements. If observed, they may be interpreted as evidence for the activation of voltage-gated channels by depolarization as the non-linearity has a similar potential-dependent effect on Rn and tau (Figure 2B; Rall, 1969; Koch, 1999a,b; White and Hooper, 2013). If present, the non-linearity will greatly affect voltage-clamp experiments (Figure 5A). The use of an Ohmic leak in the analysis of such data leads to an increasing overestimate of the conductance of the clamped ion channel as the holding potential further depolarizes, shifting the computed conductance-potential dependence to the right. In current clamp, non-linearity makes it more difficult to depolarize the membrane potential away from rest, which may explain why it is so strong in many neurons. Similarly, changes of tonic conductances at resting potential may cause smaller changes in membrane potential than predicted. Finally, the non-linearity affects physiologically relevant phenomena like temporal summation of EPSPs (Figure 6). Although in vivo voltage-gated channels will cause much stronger non-linearities, the effect of a GHK-based leak current is still significant.
Conclusion
We have demonstrated that under conditions where major resting ionic conductances are blocked, passive membrane properties can change with membrane potential due to their non-linear dependence on ionic concentration. This effect is usually ignored, which leads to incorrect characterization of passive and active properties of the cell. Our results suggest that, prior to investigating active properties, it is necessary to determine passive membrane properties of the cell type of interest by fully examining the effect of ion concentration via a GHK-based current model of leak currents. Our model takes into account ionic concentration at each integration time step, which can be used to model concentration-dependent neuronal computation, as well as ion homeostasis in other excitable cells.
Author Contributions
SWH constructed models, acquired data, and analyzed both simulation and experimental data. SHH, constructed models and analyzed simulation data. SWH, SHH and ED drafted and revised the article.
Funding
This work was supported by funding from the Okinawa Institute of Science and Technology Graduate University.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to Bernd Kuhn and Alexander Mikheyev for supporting this work. We also thank Marylka Y. Uusisaari, Iain Hepburn, Mario Negrello, and Minh-Son To for helpful discussions. Lastly we thank Alexander Mikheyev and Steven D. Aird for editing the manuscript.
References
Akemann, W., and Knöpfel, T. (2006). Interaction of Kv3 potassium channels and resurgent sodium current influences the rate of spontaneous firing of Purkinje neurons. J. Neurosci. 26, 4602–4612. doi: 10.1523/jneurosci.5204-05.2006
Angelo, K., London, M., Christensen, S. R., and Häusser, M. (2007). Local and global effects of I(h) distribution in dendrites of mammalian neurons. J. Neurosci. 27, 8643–8653. doi: 10.1523/jneurosci.5284-06.2007
Ankri, L., Yarom, Y., and Uusisaari, M. Y. (2014). Slice it hot: acute adult brain slicing in physiological temperature. JoVE 92:e52068. doi: 10.3791/52068
Brickley, S. G., Cull-Candy, S. G., and Farrant, M. (1996). Development of a tonic form of synaptic inhibition in rat cerebellar granule cells resulting from persistent activation of GABAA receptors. J. Physiol. 497 (Pt 3), 753–759.
Brodie, C., Bak, A., Shainberg, A., and Sampson, S. R. (1987). Role of Na-K ATPase in regulation of resting membrane potential of cultured rat skeletal myotubes. J. Cell. Physiol. 130, 191–198. doi: 10.1002/jcp.1041300204
Chamma, I., Chevy, Q., Poncer, J. C., and Lévi, S. (2012). Role of the neuronal K-Cl co-transporter KCC2 in inhibitory and excitatory neurotransmission. Front. Cell. Neurosci. 6:5. doi: 10.3389/fncel.2012.00005
Clay, D. P. D. B. F., Forger, D. B., and Paydarfar, D. (2008). A simple modification of the Hodgkin and Huxley equations explains type 3 excitability in squid giant axons. J. R. Soc. Interf. 5, 1421–1428. doi: 10.1098/rsif.2008.0166
Clay, J. R. (1991). A paradox concerning ion permeation of the delayed rectifier potassium ion channel in squid giant axons. J. Physiol. (Lond). 444, 499–511. doi: 10.1111/(ISSN)1469-7793
Clay, J. R. (2009). Determining K+ channel activation curves from K+ channel currents often requires the Goldman–Hodgkin–Katz equation. Front. Cell. Neurosci. 3:20. doi: 10.3389/neuro.03.020.2009
De Schutter, E., and Bower, J. M. (1994). An active membrane model of the cerebellar Purkinje cell. I. Simulation of current clamps in slice. J. Neurophysiol. 71, 375–400.
Edgerton, J. R., and Reinhart, P. H. (2003). Distinct contributions of small and large conductance Ca2+-activated K+ channels to rat Purkinje neuron function. J. Physiol. (Lond). 548, 53–69. doi: 10.1113/jphysiol.2002.027854
Fairman, W. A., Vandenberg, R. J., Arriza, J. L., Kavanaugh, M. P., and Amara, S. G. (1995). An excitatory amino-acid transporter with properties of a ligand-gated chloride channel. Nature 375, 599–603. doi: 10.1038/375599a0
Goldman, D. E. (1943). Potential, Impedance, and rectification in membranes. J. Gen. Physiol. 27, 37–60. doi: 10.1085/jgp.27.1.37
González, C., Baez-Nieto, D., Valencia, I., Oyarzún, I., Rojas, P., Naranjo, D., et al. (2012). K(+) channels: function-structural overview. Compr. Physiol. 2, 2087–2149. doi: 10.1002/cphy.c110047
Helman, S. I., and Thompson, S. M. (1982). Interpretation and use of electrical equivalent circuits in studies of epithelial tissues. Am. J. Physiol. 243, F519–F531.
Hines, M. L., and Carnevale, N. T. (2000). Expanding NEURON's repertoire of mechanisms with NMODL. Neural Comput. 12, 995–1007. doi: 10.1162/089976600300015475
Hodgkin, A. L. (1951). The ionic basis of electrical activity in nerve and muscle. Biol. Rev. 26, 339–409.
Hodgkin, A. L., and Horowicz, P. (1959). The influence of potassium and chloride ions on the membrane potential of single muscle fibres. J. Physiol. (Lond). 148, 127–160.
Hodgkin, A. L., and Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol 117, 500–544.
Hodgkin, A. L., and Katz, B. (1949). The effect of sodium ions on the electrical activity of giant axon of the squid. J. Physiol. (Lond). 108, 37–77.
Huang, S., and Uusisaari, M. Y. (2013). Physiological temperature during brain slicing enhances the quality of acute slice preparations. Front. Cell. Neurosci. 7:48. doi: 10.3389/fncel.2013.00048
Inoue, H., Mori, S.-I., Morishima, S., and Okada, Y. (2005). Volume-sensitive chloride channels in mouse cortical neurons: characterization and role in volume regulation. Europ. J. Neurosci. 21, 1648–1658. doi: 10.1111/j.1460-9568.2005.04006.x
Inoue, H., and Okada, Y. (2007). Roles of volume-sensitive chloride channel in excitotoxic neuronal injury. J. Neurosci. 27, 1445–1455. doi: 10.1523/jneurosci.4694-06.2007
Jentsch, T. J., Poët, M., Fuhrmann, J. C., and Zdebik, A. A. (2005). Physiological functions of CLC Cl- channels gleaned from human genetic disease and mouse models. Annu. Rev. Physiol. 67, 779–807. doi: 10.1146/annurev.physiol.67.032003.153245
Khaliq, Z. M., Gouwens, N. W., and Raman, I. M. (2003). The contribution of resurgent sodium current to high-frequency firing in Purkinje neurons: an experimental and modeling study. J. Neurosci. 23, 4899–4912. Available online at: http://www.jneurosci.org/content/23/12/4899.long
Koch, C. (ed). (1999a). “Linear cable theory,” in Biophysics of Computation Information Processing in Single Neurons (New York, NY: Oxford University Press), 25–48.
Koch, C. (ed). (1999b). “Passive dendritic tree,” in Biophysics of Computation Information Processing in Single Neurons (New York, NY: Oxford University Press), 49–84.
Lytton, W. W., and Hines, M. L. (2005). Independent variable time-step integration of individual neurons for network simulations. Neural Comput. 17, 903–921. doi: 10.1162/0899766053429453
Magee, J. (1999). Dendritic Ih normalizes temporal summation in hippocampal CA1 neurons. Nat. Neurosci. 2, 848–848. doi: 10.1038/12229
Major, G., Larkman, A. U., Jonas, P., Sakmann, B., and Jack, J. J. (1994). Detailed passive cable models of whole-cell recorded CA3 pyramidal neurons in rat hippocampal slices. J. Neurosci. 14, 4613–4638.
Payne, J. A., Stevenson, T. J., and Donaldson, L. F. (1996). Molecular characterization of a putative K-Cl cotransporter in rat brain. A neuronal-specific isoform. J. Biol. Chem. 271, 16245–16252.
Prinz, A. A., Billimoria, C. P., and Marder, E. (2003). Alternative to hand-tuning conductance-based models: construction and analysis of databases of model neurons. J. Neurophysiol. 90, 3998–4015. doi: 10.1152/jn.00641.2003
Racker, E. (1978). “Mechanisms of ion transport and ATP formation,” in Membrane Transport in Biology, eds G. Giebisch, D. C. Tosteson, and H. H. Ussing (New York, NY: Springer-Verlag), 259–287.
Rall, W. (1969). Time constants and electrotonic length of membrane cylinders and neurons. Biophys. J. 9, 1483–1508. doi: 10.1016/S0006-3495(69)86467-2
Ren, D. (2011). Sodium Leak Channels in Neuronal Excitability and Rhythmic Behaviors. Neuron 72, 899–911. doi: 10.1016/j.neuron.2011.12.007
Rinzel, J., and Rall, W. (1974). Transient response in a dendritic neuron model for current injected at one branch. Biophys. J. 14, 759–790. doi: 10.1016/S0006-3495(74)85948-5
Rivera, C., Voipio, J., Payne, J. A., Ruusuvuori, E., Lahtinen, H., Lamsa, K., et al. (1999). The K+/Cl- co-transporter KCC2 renders GABA hyperpolarizing during neuronal maturation. Nature 397, 251–255. doi: 10.1038/16697
Roth, A., and Häusser, M. (2001). Compartmental models of rat cerebellar Purkinje cells based on simultaneous somatic and dendritic patch-clamp recordings. J. Physiol. (Lond). 535, 445–472. doi: 10.1111/j.1469-7793.2001.00445.x
Seja, P., Schonewille, M., Spitzmaul, G., Badura, A., Klein, I., Rudhard, Y., et al. (2012). Raising cytosolic Cl- in cerebellar granule cells affects their excitability and vestibulo-ocular learning. EMBO J. 31, 1217–1230. doi: 10.1038/emboj.2011.488
Semyanov, A., Walker, M. C., Kullmann, D. M., and Silver, R. A. (2004). Tonically active GABA A receptors: modulating gain and maintaining the tone. Trends Neurosci. 27, 262–269. doi: 10.1016/j.tins.2004.03.005
Thompson, S. M. (1986). Relations between chord and slope conductances and equivalent electromotive forces. Am. J. Physiol. 250, C333–C339.
Turrigiano, G., LeMasson, G., and Marder, E. (1995). Selective regulation of current densities underlies spontaneous changes in the activity of cultured neurons. J. Neurosci. 15, 3640–3652.
Tzingounis, A. V., and Wadiche, J. I. (2007). Glutamate transporters: confining runaway excitation by shaping synaptic transmission. Nat. Rev. Neurosci. 8, 935–947. doi: 10.1038/nrn2274
Van Welie, I., Remme, M. W. H., van Hooft, J. A., and Wadman, W. J. (2006). Different levels of Ih determine distinct temporal integration in bursting and regular-spiking neurons in rat subiculum. J. Physiol. (Lond). 576, 203–214. doi: 10.1113/jphysiol.2006.113944
White, W. E., and Hooper, S. L. (2013). Contamination of current-clamp measurement of neuron capacitance by voltage-dependent phenomena. J. Neurophysiol. 110, 257–268. doi: 10.1152/jn.00993.2012
Williams, S. R., and Stuart, G. J. (2000). Site independence of EPSP time course is mediated by dendritic I(h) in neocortical pyramidal neurons. J. Neurophysiol. 83, 3177–3182.
Keywords: Goldman-Hodgkin-Katz equation, passive membrane properties, ionic concentration-dependence, time constant and input resistance, cerebellar Purkinje neurons
Citation: Huang S, Hong S and De Schutter E (2015) Non-linear leak currents affect mammalian neuron physiology. Front. Cell. Neurosci. 9:432. doi: 10.3389/fncel.2015.00432
Received: 09 July 2015; Accepted: 14 October 2015;
Published: 06 November 2015.
Edited by:
Andrea Nistri, Scuola Internazionale Superiore di Studi Avanzati, ItalyReviewed by:
Andrew Constanti, University College London, UKGiorgio Rispoli, University of Ferrara, Italy
Copyright © 2015 Huang, Hong and De Schutter. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shiwei Huang, c2hpd2VpaHVhbmdAb3V0bG9vay5jb20=
†Present Address: Shiwei Huang, Australian National University Medical School, The Australian National University, Canberra, ACT, Australia
 Shiwei Huang
Shiwei Huang Sungho Hong
Sungho Hong Erik De Schutter
Erik De Schutter