Dynamical Mechanism of Hyperpolarization-Activated Non-specific Cation Current Induced Resonance and Spike-Timing Precision in a Neuronal Model

Introduction

The hyperpolarization-activated current (I_h) mediated by hyperpolarization-activated cyclic nucleotide-gated (HCN) cation ion channels have been identified to contribute to many physiological and pathological functions in the nervous systems, such as neocortical spiny interneurons, cerebellar Purkinje cells, rod photoreceptors, hippocampal pyramidal neurons, inspiratory neurons, motor neurons, and thalamic relay neurons (Pape, 1996; Wahl-Schott and Biel, 2009; He et al., 2014; DiFrancesco and DiFrancesco, 2015). The functions associated with I_h include learning and memory, sleep and wakefulness, spatial reference and navigation, and circadian control (Pape, 1996; Wahl-Schott and Biel, 2009; Buzsáki and Moser, 2013; He et al., 2014; DiFrancesco and DiFrancesco, 2015). The dysregulation of HCN channels in the nervous system may lead to pathological conditions such as epilepsy (DiFrancesco et al., 2011; Reid et al., 2012), neuropathic pain (Emery et al., 2012; Schnorr et al., 2014), and Parkinsonian disease (Good et al., 2011; Masi et al., 2013). These physiological or pathological functions related to I_h are achieved by modulating the electrophysiological activities, such as the resting membrane potential, neuronal excitability, rhythmic activity, dendritic integration, and synaptic transmission (He et al., 2014; DiFrancesco and DiFrancesco, 2015).

The marked characteristics of the electrophysiological activities induced by I_h are the voltage sag and post-inhibitory rebound (spike) to hyperpolarization stimulus, due to I_h is a slow inward current activated by the hyperpolarization stimulation rather than depolarization stimulation (Ascoli et al., 2010; Engbers et al., 2011; Gastrein et al., 2011; Pavlov et al., 2011; Gonzalez et al., 2015). Furthermore, the experimental studies found that I_h can induce subthreshold membrane resonance and enhance spike-timing precision characterized by the standard deviation (STD) or coefficient variation (CV) of the interspike intervals (ISIs) (Zemankovics et al., 2010; Gastrein et al., 2011; Pavlov et al., 2011; Borel et al., 2013; Gonzalez et al., 2015). Resonance means that impedance profile of a neuron to external stimulus reaches a maximal value at a certain value corresponding to an intrinsic frequency preference (Rotstein, 2015; Vazifehkhah et al., 2015), which is an important factor related to the rhythmic oscillations (Gasparini and DiFrancesco, 1997; Hutcheon and Yarom, 2000; Giocomo et al., 2007; Moca et al., 2014; Gonzalez et al., 2015). For example, hippocampal pyramidal neurons (Hu et al., 2002; Zemankovics et al., 2010; Gastrein et al., 2011; Borel et al., 2013) exhibit subthreshold resonance to the injection of sinusoidal current, and their resonant properties contribute to the emergence of Theta oscillations (Zemankovics et al., 2010; Stark et al., 2013). Neurons in the medial superior olive and lateral superior olive exhibit different subthreshold resonance properties which influence the efficient coding of auditory spatial cues (Remme et al., 2014). Robustness of the spike-timing to physiological noise is an essential factor for neural coding (Dayan and Abbott, 2001; Butts et al., 2007). For example, precise spiking of the lateral geniculate nucleus relay neurons (Reinagel and Reid, 2002) and many other visual neurons (Buracas et al., 1998; Masuda and Aihara, 2003) carry rich information of time-varying visual stimuli such as a strong diffuse flicker. Auditory neurons in the auditory brainstem encode information based on the timing of the individual spikes (Tzounopoulos and Kraus, 2009). Precise spike-timing of neurons also influences the synchrony of oscillation (Ratté et al., 2013). Hippocampal interneurons exhibit precise firing when Theta and Gamma oscillations appear in the hippocampus and neocortex (Hájos et al., 2004; Somogyi and Klausberger, 2005; Klausberger et al., 2006; Vida et al., 2006).

In addition to these experimental studies, the roles of I_h on the modulation of the neuronal electrophysiological activities, such as the membrane subthreshold resonance and spike-timing precision, have also been simulated in the theoretical models. The influences of the types of neurons, the different resonant currents, and the factors of I_h on the subthreshold resonance have been investigated in the theoretical models (Zemankovics et al., 2010; Rotstein and Nadim, 2014; Vazifehkhah et al., 2015; Fox et al., 2017; Pena et al., 2017). For instance, some researchers suggested that the cell-type (pyramidal cells and interneurons) specificity of the impedance or resonance profiles in the hippocampal CA1 neurons maybe explained by the properties of I_h combined with the passive membrane characteristics in a conductance-based theoretical model (Zemankovics et al., 2010). Investigations on the subthreshold resonance in theoretical models of the Pyloric Dilator neurons of the crab pyloric network found that I_h and calcium current are the dominant factors to induce the resonant properties at hyperpolarized and depolarized potentials, respectively (Vazifehkhah et al., 2015; Fox et al., 2017). I_h and slow potassium current were identified to play different roles in the generation of resonance (Rotstein and Nadim, 2014). The interplay between the activation kinetics and the derivative conductance of I_h determines the resonant frequency (Pena et al., 2017). The effect of the inputs including the synaptic input, neuron type, and intrinsic properties of neuron on the spike-timing precision related to I_h have been studied in the theoretical models. For example, in a simulation study, the distributed synaptic plasticity at the cerebellum input stage can regulate spike-timing on the millisecond scale (Garrido et al., 2013). It was identified that the dendritic-targeting interneurons control the spike-timing of the hippocampal CA1 pyramidal neuron via the activation of I_h (Park and Kwag, 2012). I_h in the pyramidal cells, but not in the O-LM neurons, plays an important role in the timing of spike generation, and thus the synchronization of the pyramidal cells (Orbán et al., 2006).

Compared with many experimental and simulation results (Zemankovics et al., 2010; Gastrein et al., 2011; Pavlov et al., 2011) of the subthreshold resonance and precise spike-timing induced by I_h, there are much less theoretical investigations (Rotstein, 2015; Vazifehkhah et al., 2015) to explain the corresponding dynamical mechanism. It is well known that neuron is a nonlinear dynamical system which can be described by the differential equations, and bifurcation analysis has been identified as an effective method to identify the dynamical mechanism of the electrophysiological properties of neurons. The transition from the resting state to firing and the transition between different firing patterns can be described by the concept of bifurcation (Rinzel, 1998; Izhikevich, 2000, 2007; Tsumoto et al., 2006; Tsuji et al., 2007; Franci et al., 2012; Chen et al., 2013; Drion et al., 2015; Morozova et al., 2016; Zhao et al., 2016; Zhao and Gu, 2017). The resting states and firing patterns near the different kinds of bifurcation points exhibit different dynamics. For example, both subcritical Hopf bifurcation and saddle-node (SN) bifurcation/saddle-node on invariant circle (SNIC) bifurcation are used to characterize the transitions from the resting state to firing as the bifurcation parameter is changed. However, the resting state when perturbed and the firing pattern exhibit a fixed frequency for the subcritical Hopf bifurcation and no fixed frequency for the SN/SNIC bifurcation. The noise induced stochastic firing near the SN/SNIC bifurcation exhibits a large CV in ISIs and near the Hopf bifurcation manifests a low CV, which were used to distinguish the cortical spike trains (Gutkin and Ermentrout, 1998; Tateno et al., 2004). Although the Hopf bifurcation and SN/SNIC bifurcation have been simulated in a theoretical model to describe the activity of thalamocortical neuron, the relationships between these bifurcations and the subthreshold resonances or precise spiking-timing induced by I_h have not been built (Hindmarsh and Rose, 1994; Amarillo et al., 2015). The linear amplitude and phase resonances between two stable equilibrium, the focus and node, were compared in a linear model to describe the activity of an electrochemical cell (Rotstein, 2013; Rotstein and Nadim, 2014). As expected by our common knowledge, resonance should appear in the parameter region of the focus and non-resonance appears in the parameter region of the node. However, such an expectation was challenged by the complex or “strange” dynamical behaviors appearing in a narrow parameter region near the special equilibrium point with double zero eigenvalues. Within the narrow parameter region, the stable focus can exhibit non-resonance and the stable node exhibits resonance. In addition, the chaotic behaviors and period-doubling bifurcation cascades, which are induced by I_h, have been simulated in a conductance-based neuronal bursting model to describe the activity of cold thermoreceptors (Xu et al., 2017).

In the present paper, firstly, voltage sag/rebound (spike), resonance, and precise spike-timing induced by I_h, are simulated in a theoretical model and closely match the previous experimental observations. With increasing the conductance of I_h, g_h, the rebound (spike) and resonance become strong, and the CV of ISIs decrease, which means the enhancement of the spike-timing precision. Secondly, one-parameter bifurcation analysis and two-parameter bifurcation analysis are performed to the theoretical model. Four stable behaviors, the stable node, the stable focus, the coexistence of the resting state and firing, and the firing, locate from bottom to top in (I_app, g_h) plane. I_app is the applied current. Codimension-1 bifurcations such as Hopf, saddle-node, and saddle homoclinic orbit, and codimension-2 bifurcations such as Bogdanov-Takens (BT) related to the transition between the saddle-node and Hopf bifurcations, are acquired. Last, with help of the bifurcations, the dynamical mechanisms for I_h induced resonance, rebound (spike), and precise spike-timing are provided. Increasing g_h for the firing behavior means that it becomes far away from the bifurcation point, therefore, the capacity of resisting noisy disturbance becomes weak, which leads to the fast decrease of the standard deviation of ISIs and the decrease of CV. Increasing g_h for the resting state means that it approaches the bifurcation point, the enhancement of the rebound (spike) corresponds to the decrease of the capacity of resisting disturbance like the hyperpolarization stimulus. In addition, the “typical”-resonance and non-resonance appear in the parameter region of the stable focus and stable node far away from the bifurcation points, respectively. The “weak”-resonance appears in the parameter region of stable node near the transition point between the stable node and focus, and the non-resonance appears in the parameter region of the stable focus close to the codimension-1 and −2 bifurcation points, which are very complex or “strange”.

Materials and Methods

A Hippocampal GABAergic Neurons Model With I_h

To study the influence of I_h on cellular electrophysiological properties, a conductance-based biophysical model of Hippocampal GABAergic neuron (Wang, 2002) is used and is described as follows,

$\begin{array}{l}C\frac{dV}{dt}=-g_{Na}{m}_{\infty }^{3}h(V-E_{Na})-g_K{n}^4(V-E_K)-g_{h}H(V-E_h)\\ -g_L(V_L-E_L)+I_{app},& (1)\end{array}$

$\begin{array}{rc}\frac{dh}{dt}=\varphi ({\alpha }_h(1-h)-{\beta }_{h}h),& (2)\end{array}$

$\begin{array}{rc}\frac{dn}{dt}=\varphi ({\alpha }_n(1-n)-{\beta }_{n}n),& (3)\end{array}$

$\begin{array}{rc}\frac{dH}{dt}=(H_{\infty }(V)-H)/{\tau }_H(V).& (4)\end{array}$

where C is the membrane capacitance, and V is the membrane potential. g_Na, g_K, and g_L are the maximum conductances of the sodium current, potassium current, and leakage current, respectively. E_Na, E_K, and E_L are the reversal potentials of the sodium current, potassium current, and leakage current, respectively. g_h is the maximal conductance of I_h and E_h is the reversal potential of I_h. I_app is the applied current. m_∞ = α_m/(α_m + β_m) is the steady-state function of activation variable of the sodium current. h, n, and H are the inactivation variables of the sodium current, activation variable of the potassium current, and activation variable of I_h, respectively. The related expressions are as follows, α_m(V) = −0.1(V + 35)/(exp(−0.1(V + 35)) − 1), β_m(V) = 4exp(−(V + 60)/18), α_h(V) = 0.07exp(−(V + 58)/20), β_h(V) = 1/(exp(−0.1(V + 28)) + 1), α_n(V) = −0.01(V + 34)/(exp(−0.1(V + 34))−1), β_n(V) = 0.125exp(−(V + 44)/80), H_∞(V) = 1/(1 + exp(V + 80)/10) and τ_H(V) = 200/(exp((V + 70)/20) + exp(−(V + 70)/20)) + 5.

The parameters values are taken as C = 1 F/cm², g_Na = 35 mS/cm², E_Na = 55 mV, g_K = 9 mS/cm², E_K = −90 mV, g_L = 0.1 mS/cm², E_L = −65 mV, E_h = −30mV, and ϕ = 5.

In the experimental investigations (Gastrein et al., 2011), I_h was blocked and I_app was adjusted. In the present paper, the conductance of I_h, g_h, and I_app are chosen as the control parameters, and the equations of the theoretical model were integrated with the Euler method with a time step of 0.001 ms.

Resonance

The impedance amplitude profile method is conventionally employed to investigate the resonance property of a neuron (Hu et al., 2002; Zemankovics et al., 2010; Engbers et al., 2011; Gastrein et al., 2011; Borel et al., 2013; Gonzalez et al., 2015; Rotstein, 2015; Vazifehkhah et al., 2015). A subthreshold “ZAP” current, which is sinusoidal current with constant amplitude and linearly increasing frequency, is injected into a neuron at the resting state, and the membrane voltage response (V) of the neuron is recorded. The “ZAP” current is described as

$\begin{array}{rc}{I}_{ZAP}=I_{stim}Sin(2\pi f(t)t),& (5)\end{array}$

where $I_{stim}=0.01\mu \text{A}/\text{c}{\text{m}}^2$ and the time-depended frequency f(t) linearly increases from f_min = 0 to f_max = 20 Hz in the duration T = 20 s and is expressed as follows,

$\begin{array}{rc}f(t)=f_{min}+(f_{max}-f_{min})\frac{t}{T}.& (6)\end{array}$

The impedance profile can be obtained by calculating the ratio of the fast Fourier transforms (FFT) of the membrane voltage response to the FFT of the input “ZAP” current and is described by

$\begin{array}{rc}Z(f)=\frac{FFT(V)}{FFT(ZAP)}.& (7)\end{array}$

where Z(f) is the impedance profile and f is the frequency. Z(f) is a complex quantity and its magnitude $\left|Z(f)\right|=\sqrt{{(\left|Z_{Re}(f)\right|)}^2+{(\left|Z_{Im}(f)\right|)}^2}$ is used to quantify the strength of the subthreshold resonance. If |Z(f)| manifests a marked maximal peak at a certain frequency f, the resonance appears in the neuron. If |Z(f)| does not exhibit a marked maximal peak, no resonance appears in the neuron.

Spike-Timing Precision

Noise is ubiquitous in the nervous system (Faisal et al., 2008) and can disturb the spike-timing precision. To study the influence of noise on the spike-timing of a neuron, the white noise to simulate the current fluctuations I_noise is added to Equation and is described as follows,

$\begin{array}{rc}{I}_{noise}=DdW(t).& (8)\end{array}$

where dW(t) is a Gaussian white noise and D is the noise intensity.

For a neuron with resting state, the temporal precision of the first spike was analyzed when firing was elicited by a ramp of current that can induce membrane potential depolarization (Gastrein et al., 2011). Different ramp rates of the current induce different rates of membrane potential depolarization. For each ramp rate, multiple trials of the firings are acquired and the STD of the timing of the first spike for different trials is calculated. The faster the current ramp/membrane potential depolarization rate, the more precise the timing of the first spike.

A representative for the timing of the first spike induced by the ramp current is shown in Figure 1. When D = 0.2μA/cm², I_app = 0μA/cm², and g_h = 0.02mS/cm², the behavior of the theoretical model is resting state. When the currents with fast (1 μA/100 ms, Figure 1C) and slow (0.3 μA/100 ms, Figure 1D) ramp rates are applied, 12 trials of the first spike of the firings induced by the ramp currents are shown in Figures 1A,B, respectively. The STD of jitter timing of the first spike is 3.35 ms (mean value is 42.31 ms) for the fast ramp rate and is 8.63 ms (mean value is 80.29 ms) for the slow ramp rate. The corresponding statistics histogram calculated from 1,000 trials for the fast ramp rate is shown in Figure 1E and for the slow ramp rate in Figure 1F. The results show that the faster the current ramp, the more precise the timing of the first spike, which is consistent with the experimental observations on the stratum oriens interneurons (Gastrein et al., 2011).

FIGURE 1

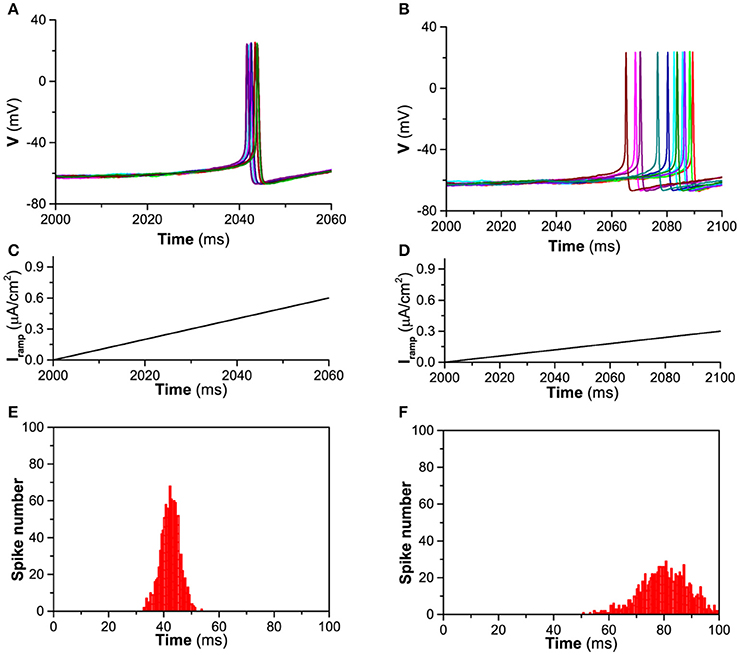
Figure 1. Timing precision of the first spike of firing induced by the ramp current when D = 0.2μA/cm², I_app = 0 μA/cm², and g_h = 0.02 mS/cm². (A) The first spike of firing induced by current with fast ramp rate (12 trials); (B) The first spike of firing induced by current with slow ramp rate (12 trials); (C) Current with fast ramp rate 1 μA/100 ms; (D) Current with slow ramp rate 0.3 μA/100 ms; (E) Number of the timing of the first spike induced by current with fast ramp rate (1000 trials); (F) Number of the timing of the first spike induced by current with slow ramp rate (1,000 trials).

For a neuron with firing, the CV of ISIs, which is the ratio of the standard deviation (STD) of ISIs to the mean value of ISIs, is used to estimate the spike-timing precision (Bacci and Huguenard, 2006; Gastrein et al., 2011; Pavlov et al., 2011), which can reflect the spike regularity. The lower the CV value, the more regular the spike trains, i.e., the more precise the spike-timing. In the present paper, CV of ISIs for firing pattern are mainly investigated and N = 2000 ISIs are used to calculate CV.

Bifurcation Analysis

In the previous experimental investigations (Gastrein et al., 2011), the resting state was considered when I_h induced rebound (spike) or subthreshold resonance was studied and the firing behavior was considered when I_h induced spike-timing precision was investigated. Therefore, the transition from the resting state to firing and the dependence of the transition on g_h and I_app is very important. The concept of nonlinear dynamics, bifurcation, describes the dynamical mechanism and presents theoretical interpretation of the transition from the resting state to firing. The transition from the resting state to the firing corresponds to the bifurcation from the stable equilibrium point to the limit cycle. The resting state corresponds to stable equilibrium point and the firing corresponds to the stable limit cycle.

The eigenvalues of the linearization of Equations. (1–4) determine the stability of the equilibrium corresponding to the resting state. There are major three types of equilibrium (Kuznetsov, 1995; Izhikevich, 2000, 2007): node, saddle, and focus. The eigenvalues of node are real and have the same sign. The eigenvalues of saddle are real and have different signs. The focus exhibits complex-conjugate eigenvalues. The resting state corresponds to a stable node with negative eigenvalues or a stable focus with eigenvalues with negative real part. When perturbed, the dynamical behavior of a focus exhibits a damped oscillation with a fixed frequency due to the imaginary part of the eigenvalues, while the behavior of node does not manifest a fixed frequency.

As a parameter is varied, the resting state can be changed to firing via a supercritical Hopf bifurcation, a subcritical Hopf (SubH) bifurcation, a SN bifurcation, or a SNIC bifurcation. The resting state corresponds to a stable focus for the Hopf bifurcation and a stable node for the SN/SNIC bifurcation. The SN/SINC bifurcation point exhibits a zero eigenvalue and the Hopf bifurcation manifests a pair of pure imaginary eigenvalues (zero real part). In addition to the Hopf and SN/SNIC bifurcation points, there are bifurcations mainly related to the limit cycle, such as the saddle homoclinic orbit (Hom) wherein a limit cycle contacted with a saddle. Except the above mentioned codim-1 bifurcations, codim-2 bifurcation such as the Bogdanov-Takens (BT) bifurcation with double zero eigenvalues, which is a transition point between the SN/SNIC bifurcation and the Hopf bifurcation, and the saddle-node homoclinic orbit bifurcation (SNHO), which is a switch point between the Hom and SNIC bifurcations, are also considered in the present paper.

Bifurcation diagrams are obtained using the dynamical software Matcont (Dhooge et al., 2003) and XPPAUT (Ermentrout, 2002).

Results

Simulations of the Experimental Observations Related to I_h

Post-inhibitory Rebound (spike) Induced by I_h

When I_app = −0.05 μA/cm², the theoretical neuron model exhibits resting state when g_h = 0.05mS/cm², 0.04 mS/cm² (in the presence of I_h), and 0.0 mS/cm² (blockage of I_h). When a hyperpolarization square current with duration 100 ms is injected to the theoretical model, the membrane potential exhibits different characteristics for different g_h levels, as shown in Figure 2.

FIGURE 2

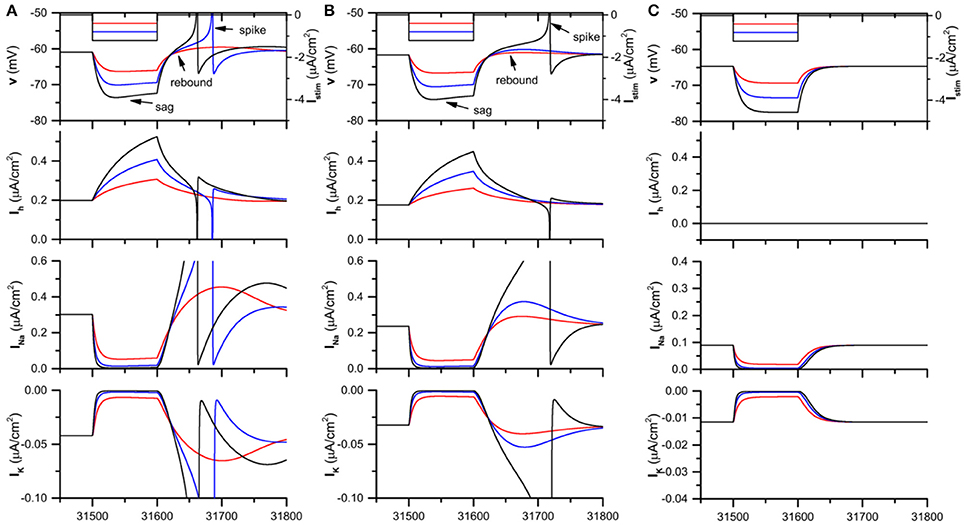
Figure 2. The I_h induced voltage sag and rebound (spike) and the evolution of the different currents in the theoretical neuron model stimulated by the hyperpolarization square current when $I_{app}=-0.05\mu \text{A}/\text{c}{\text{m}}^2$. (A) $g_h=0.05\text{mS}/\text{c}{\text{m}}^2$; (B) $g_h=0.04\text{mS}/\text{c}{\text{m}}^2$; (C) $g_h=0.0\text{mS}/\text{c}{\text{m}}^2$. The panels from top to bottom represent the hyperpolarization square current and the response of membrane potential, I_hcurrent, Na⁺ current, and K⁺ current. The amplitude of the hyperpolarization square current is −0.4 μA/cm² (black), −0.8 μA/cm² (blue), and −1.2 μA/cm² (red).

For $g_h=0.05\text{ mS}/\text{c}{\text{m}}^2$, when the strength of the hyperpolarization square current is small (−0.4μA/cm², red), both voltage sag, which appears at the initial phase of the hyperpolarization current, and post-inhibitory rebound phenomenon, which appears after the termination of the hyperpolarization current, are induced, as shown in the 1st panel of Figure 2A. When the strength increases to a middle level (−0.8μA/cm², blue), the sag and rebound become strong and the rebound spike appears. When the strength increases to a high level (−1.2μA/cm², black), both the voltage sag and rebound spike become strong, and the rebound spike appears earlier than that of the middle strength (−0.8μA/cm²).

For $g_h=0.04\text{ mS}/\text{c}{\text{m}}^2$, both voltage sag and rebound (spike) appear, and the rebound (spike) phenomenon becomes strong with increasing the current strength, which is similar to those of $g_h=0.05\text{ mS}/\text{c}{\text{m}}^2$. However, compared with $g_h=0.05\text{ mS}/\text{c}{\text{m}}^2$, both voltage sag and rebound (spike) become weak for $g_h=0.04\text{ mS}/\text{c}{\text{m}}^2$, as shown in the 1st panel of Figure 2B), which shows that the voltage sag and rebound (spike) become weak with decreasing g_h. For example, when the current strength is middle (−0.8μA/cm², blue), rebound spike appears for $g_h=0.05\text{ mS}/\text{c}{\text{m}}^2$ while not spike but rebound appears for $g_h=0.04\text{ mS}/\text{c}{\text{m}}^2$.

For $g_h=0.0\text{ mS}/\text{c}{\text{m}}^2$, which corresponds to the blockage of I_h, both voltage sag and post-inhibitory rebound spike cannot be induced by the hyperpolarization square currents with the same strengths as Figures 2A,B, as depicted in the 1st panel of Figure 2C.

The results are consistent with the previous experimental investigations of I_h, which were performed on the hippocampal pyramidal neurons and stratum oriens interneurons (Manseau et al., 2008; Ascoli et al., 2010; Zemankovics et al., 2010; Gastrein et al., 2011; Borel et al., 2013).

Enhancement of the Resting Potential and of the Firing Frequency Induced by I_h

The changes of the membrane potential for the resting state and of the firing frequency for the firing behavior in (I_app, g_h) plane are shown in Figures 3A,B, respectively. The resting state locates at down-left half and the firing at up-right half of (I_app, g_h) plane. When I_app is fixed, with increasing g_h, the membrane potential of the resting state increases, as shown in Figure 3A. The blank area corresponds to the firing behavior. When I_app is fixed, with increasing g_h, the firing frequency increases, which means that the ISIs of firing decreases, as shown in Figure 3B. The blank area corresponds to the resting state. Both results are consistent with the biological experiments (Elgueta et al., 2015). In addition, the firing threshold for I_app decreases with increasing g_h, which shows that g_h induces the decrease of the firing threshold for I_app. Both enhancement of I_h and increase of I_app play the same positive roles in evoking firing, therefore, the increase of g_h leads to the decrease of firing threshold for I_app.

FIGURE 3

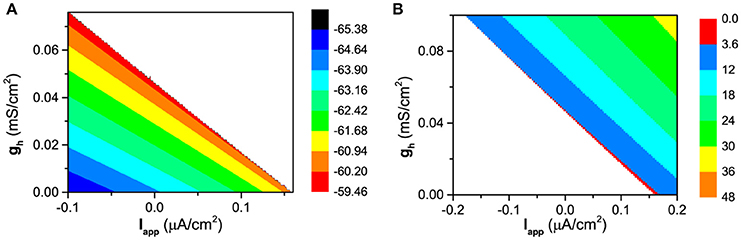
Figure 3. The changes of the dynamical behaviors of the theoretical model in (I_app, g_h) plane. (A) Membrane potential for the resting state; (B) Firing frequency for the firing behavior.

I_h Enhances the Spike-Timing Precision

When I_app = 0.17 μA/cm², the firing for both $g_h=0\text{mS}/\text{c}{\text{m}}^2$ (blockage of I_h) and $g_h=0.02\text{mS}/\text{c}{\text{m}}^2$ (in presence of I_h) in the deterministic model is period-1 and the CV of ISIs is 0.

When noise is introduced, the ISIs of the firing exhibit variability, which leads to a nonzero CV, for example, as shown in Figure 4A. With increasing noise intensity D, although CV for both $g_h=0\text{mS}/\text{c}{\text{m}}^2$ (red) and $g_h=0.02\text{mS}/\text{c}{\text{m}}^2$ (black) increases, CV for $g_h=0.02\text{mS}/\text{c}{\text{m}}^2$ is always higher than that for $g_h=0\text{mS}/\text{c}{\text{m}}^2$ in a large range of noise intensity (0 < D < 1 μA/cm²), which shows that spike-timing precision in the presence of I_h is higher than that of the blockage of I_h.

FIGURE 4

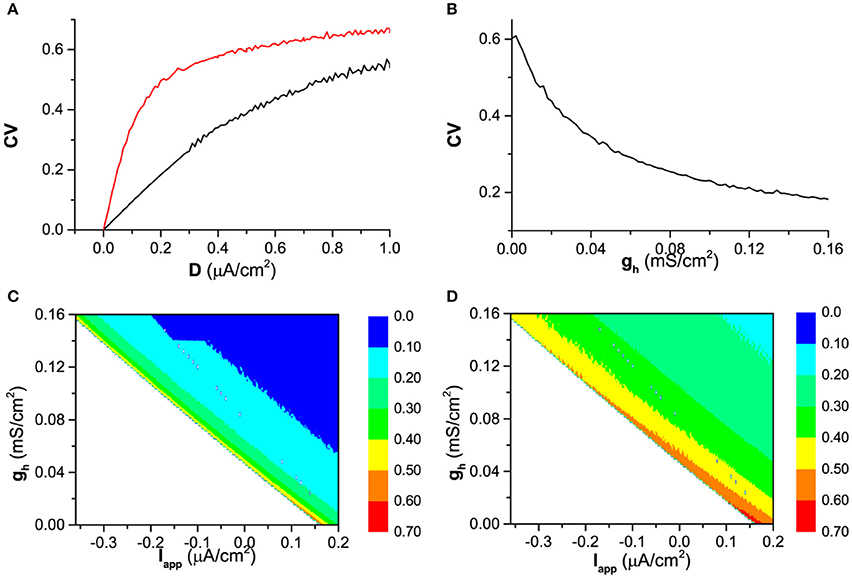
Figure 4. The spike-timing precision characterized by CV of ISIs. (A) The effect of noise intensity (D) on CV the in the presence of I_h (g_h = 0.02 mS/ cm², black) and the absence of I_h ($g_h=0\text{mS}/\text{c}{\text{m}}^2$, red) when I_app = 0.17 μA/cm²; (B) The influence of g_h on CV when noise intensity is fixed (D = 0. 6 μA/cm²) when I_app = 0.17 μA/cm²; (C) CV in (I_app, g_h) plane when D = 0.2μA/cm²; (D) CV in (I_app, g_h) when D = 0.6μA/cm².

The more spike-timing precision induced by I_h can also be found from Figure 4B. When noise intensity D is fixed, for example D = 0. 6 μA/cm²,CV decreases with increasing g_h. The dependence of CV on both I_app and g_h are shown by the color scale in (I_app, g_h) plane in Figure 4C (D = 0.2μA/cm²) and Figure 4D (D = 0.6μA/cm²). For both noise intensities, CV decrease with increasing g_h, which shows that I_h includes more spike-timing precision. No firing locates in down-left half of (I_app, g_h) plane (the blank area) and no CV is calculated.

The detailed difference of the spike-timing precision between the presence of I_h and the absence of I_h can be found from the spike trains of the firing and the ISI histogram (ISIH). For example, when I_app = 0.17 μA/cm² and D = 0.2μA/cm², the spike trains for $g_h=0\text{mS}/\text{c}{\text{m}}^2$ and $g_h=0.02\text{mS}/\text{c}{\text{m}}^2$ are shown in Figures 5A,B), respectively, and the ISIH for $g_h=0\text{mS}/\text{c}{\text{m}}^2$ and $g_h=0.02\text{mS}/\text{c}{\text{m}}^2$ is illustrated in Figures 5C,D), respectively, which closely matches the experimental observations on the hippocampal pyramidal neurons and stratum oriens interneurons (Gastrein et al., 2011). The mean value of ISIs is 208.99 ms for $g_h=0\text{mS}/\text{c}{\text{m}}^2$ and 76.98 ms for $g_h=0.02\text{mS}/\text{c}{\text{m}}^2$, respectively. The standard deviation (STD) of ISIs is 102.24 ms for $g_h=0\text{mS}/\text{c}{\text{m}}^2$ and 14.09 ms for $g_h=0.02\text{mS}/\text{c}{\text{m}}^2$, respectively. The CV of the ISIs is 0.494 for $g_h=0\text{mS}/\text{c}{\text{m}}^2$ and 0.183 for $g_h=0.02\text{mS}/\text{c}{\text{m}}^2$, respectively. The result indicates that I_h reduces the variability of ISIs, i.e., enhances the precision of the spike-timing, which can also be found from the ISIH depicted in Figures 5C,D). Compared with Figure 5D (blockage of I_h), ISIH becomes broader and lower for Figure 5C (in the presence of I_h), which also shows that I_h can enhance the spike-timing precision.

FIGURE 5

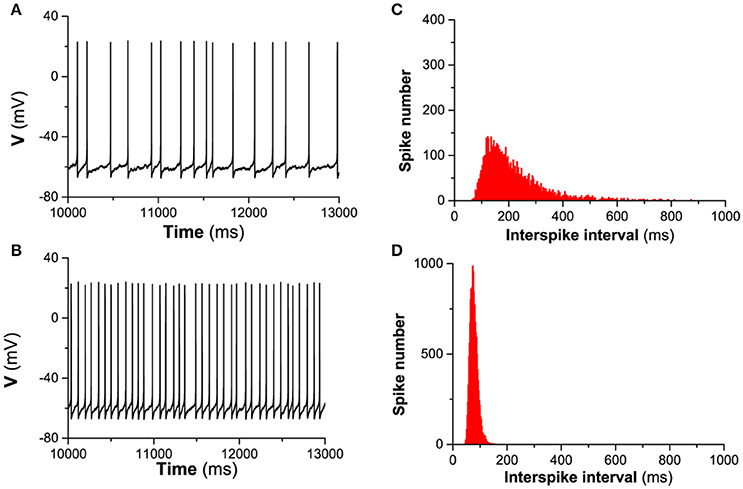
Figure 5. The influence of I_h on the spike-timing precision of the theoretical neuron model with noise (D = 0.2μA/cm²) when $I_{app}=0.17\mu \text{A}/\text{c}{\text{m}}^2$. (A,B), spike trains corresponding to $g_h=0\text{mS}/\text{c}{\text{m}}^2$ and $g_h=0.02\text{mS}/\text{c}{\text{m}}^2$, respectively. (C,D), ISIH corresponding to (A,B), respectively.

Subthreshold Resonance Induced by I_h

Two cases of the subthreshold resonance for different I_app values are simulated.

When $I_{app}=-0.05\mu \text{A}/\text{c}{\text{m}}^2$, the theoretical model exhibits resting state when g_h = 0.0 mS/cm², 0.03 mS/cm², and 0.05 mS/cm². When a subthreshold “ZAP” current (Figure 6D) is applied, the membrane potential exhibits different responses at different g_h values, as shown in Figure 6A (g_h = 0.05 mS/cm²), Figure 6B (g_h = 0.03 mS/cm²), and Figure 6C (g_h = 0.0 mS/cm²). When g_h = 0.05 mS/cm², the amplitude of the oscillation increases firstly and then decreases with respect to the increase of time/frequency, correspondingly, the impedance profile exhibits an inverse “U” shape, as shown by the first line from the top (red) in Figure 6E, showing that a “typical”-resonance appears. The resonance frequency is around 3.1 Hz. When g_h decreases to 0.03 mS/cm², the amplitude of the oscillation exhibits a slight increase at first and then a decrease with increasing time/frequency, and the height of the inverse “U” shape of the impedance profile becomes short, which shows that the resonance becomes weak, as shown by the third line (blue) from the top in Figure 6E. In the present paper, such a resonance is called as “weak”-resonance. When g_h decreases to 0.0 mS/cm², the amplitude of the oscillation decreases with increasing time/frequency and the phenomenon of resonance disappears, called as non-resonance, as shown by the last line (black) from the top in Figure 6E. With decreasing g_h from 0.05 mS/cm², to 0.04mS/cm², to 0.03 mS/cm², to 0.02 mS/cm², and to 0.0 mS/cm², the maximal impedance decreases, as shown by the black square in Figure 6E. The result is consistent with the experimental observations in many types of neurons such as the stratum oriens interneuron (Zemankovics et al., 2010; Gastrein et al., 2011; Pavlov et al., 2011; Borel et al., 2013; Gonzalez et al., 2015).

FIGURE 6

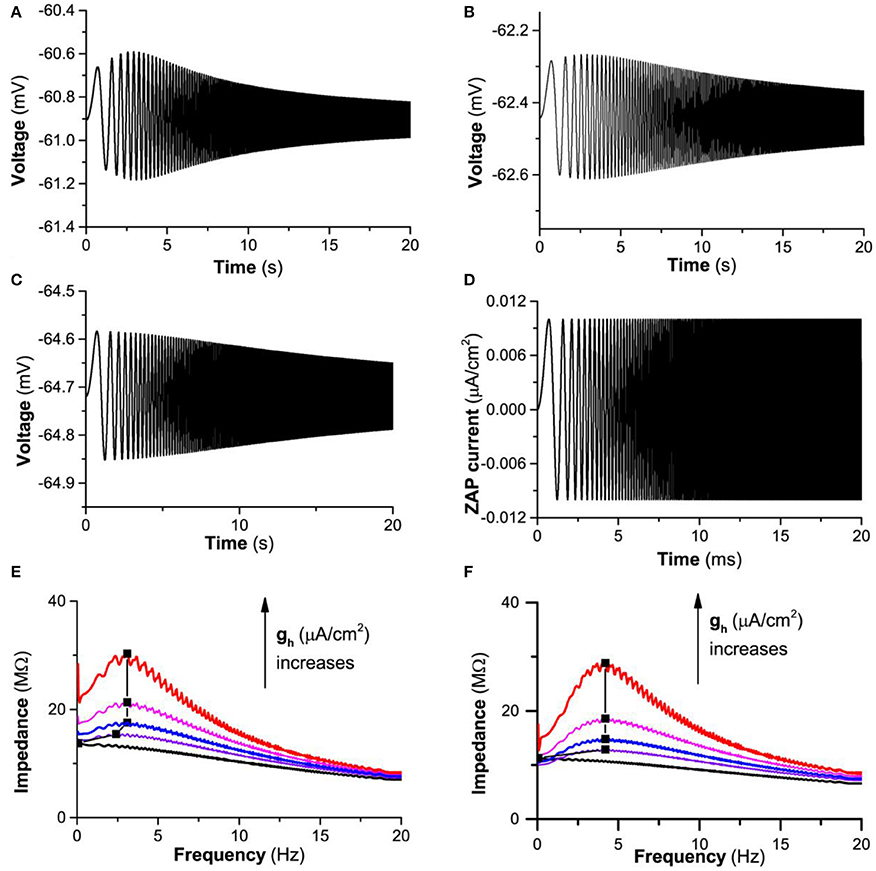
Figure 6. The influence of I_h on the subthreshold resonance of the theoretical neuron model stimulated by a subthreshold “ZAP” current. $I_{app}=-0.05\mu \text{A}/\text{c}{\text{m}}^2$. Voltage response: (A) g_h = 0.05 mS/cm²; (B) g_h = 0.03 mS/cm²; (C) g_h = 0.0 mS/cm²; (D) “ZAP” current; (E) Impedance vs. frequency at different g_h levels; From top to bottom, g_h = 0.05, 0.04, 0.03, 0.02, and 0.0 mS/cm². (F) Impedance vs. frequency at different g_h levels for $I_{app}=-0.3\mu \text{A}/\text{c}{\text{m}}^2$; From top to bottom, g_h = 0.12, 0.1, 0.08, 0.06, and 0.0 mS/cm².

Another representative similar to I_app = −0.05μA/cm² is shown in Figure 6F (I_app = −0.3 μA/cm²). The upper 2 lines (g_h = 0.12 and 0.1 mS/cm²), middle 2 lines (g_h = 0.08 and 0.06 mS/cm²), and lowest line (g_h = 0.0 mS/cm²) for impedance vs. frequency exhibit “typical”-, “weak”-, and non-resonances.

When $I_{app}=0.08\mu \text{A}/\text{c}{\text{m}}^2$, the response of the membrane potential to “ZAP” current and resonance exhibits characteristic different from $I_{app}=-0.05\mu \text{A}/\text{c}{\text{m}}^2$ and I_app = −0.3 μA/cm², as shown in Figure 7. From g_h = 0.02 mS/cm² to 0.01 mS/cm², and to 0.0 mS/cm², the responses of the membrane potential are shown in Figures 7A–C). The amplitude of the oscillation of the membrane potential decreases with increasing time/frequency, which shows that not “typical”-resonance but non- or “weak”-resonance appears, as shown by the red (g_h = 0.02 mS/cm²), blue (g_h = 0.01 mS/cm²), and black lines (g_h = 0.0 mS/cm²) in Figure 7D. With decreasing g_h, the maximal impedance decreases, as shown the black square in Figure 7D.

FIGURE 7

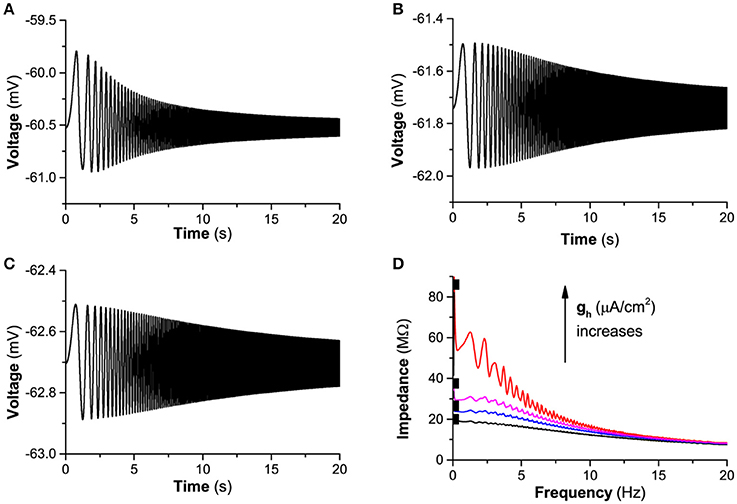
Figure 7. The influence of I_h on the subthreshold resonance of the theoretical neuron model stimulated by a subthreshold “ZAP” current when $I_{app}=0.08\mu \text{A}/\text{c}{\text{m}}^2$. Voltage response: (A) g_h = 0.02 mS/cm²; (B) g_h = 0.01 mS/cm²; (C) g_h = 0.0 mS/cm²; (D) Impedance vs. frequency at different g_h levels; From top to bottom, g_h = 0.02 (red), 0.15 (pink), g_h = 0.01 (blue), and g_h = 0.0 mS/cm² (black).

Bifurcation Analysis

One-Parameter Bifurcation

Considering that the subthreshold resonance for $I_{app}=0.08\mu \text{A}/\text{c}{\text{m}}^2$ exhibits characteristics different from that of $I_{app}=-0.05\mu \text{A}/\text{c}{\text{m}}^2$, the bifurcations with respect to g_h for $I_{app}=0.08\mu \text{A}/\text{c}{\text{m}}^2$ and I_app = −0.05 are calculated and manifest different dynamics, as shown in Figure 8.

FIGURE 8

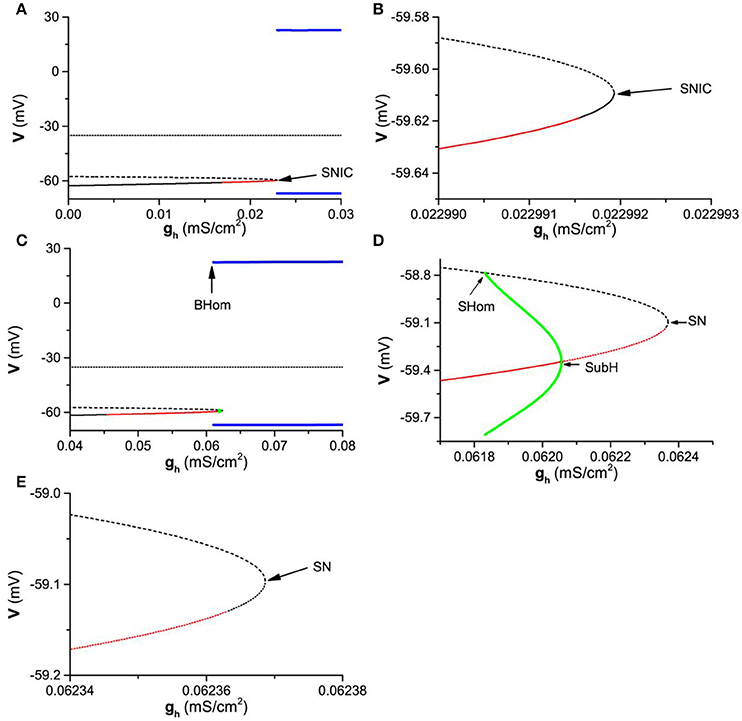
Figure 8. One-parameter bifurcations of the membrane potentials (V) with respect to g_h at different I_app levels. (A) $I_{app}=0.08\mu \text{A}/\text{c}{\text{m}}^2$; (B) Partial enlargement of the middle and lower branches of the equilibrium of (A) near SNIC; (C) $I_{app}=-0.05\mu \text{A}/\text{c}{\text{m}}^2$; (D) Partial enlargement of (C) around SN and SubH; (E) Partial enlargement of (D). The black solid, dashed, and dotted curves represent the stable node, unstable node, and saddle, respectively. The red solid and dashed curves represent the stable and unstable focus, respectively. The upper (lower) blue line represents the maximal (minimal) value of the stable limit cycle corresponding to firing. The upper (lower) green curve is the maximal (minimal) value of the membrane potential of the unstable limit cycle. SNIC and SN represent saddle-node bifurcation on invariant circle and saddle-node bifurcation, respectively. SHom and BHom are the small and big saddle homoclinic orbits, respectively. SubH represents the subcritical Hopf bifurcation.

For $I_{app}=0.08\mu \text{A}/\text{c}{\text{m}}^2$, the bifurcation of the theoretical model with respect to g_h are shown in Figures 8A,B (Figures 8B is the partial enlargement of Figures 8A). The theoretical neuron model exhibits firing/stable limit cycle (blue bold lines) when $g_h\ge 0.0229919\text{mS}/\text{c}{\text{m}}^2$. The upper and lower blue lines represent the maximal and minimal values of the membrane potential of firing. The equilibrium contains three branches (dotted, dashed, or thin solid lines). The upper branch (dotted line) and middle branch (dashed line) are unstable focus and saddle (unstable), respectively, and are not associated with the resting state. The lower branch (thin solid line) is related the resting state and composed of three parts, a stable node ($g_h<0.0169329\text{mS}/\text{c}{\text{m}}^2$, black solid line left to the red solid line), a stable focus ($0.0169329<g_h<0.0229915\text{mS}/\text{c}{\text{m}}^2$, red solid line), and a stable node ($0.0229915<g_h<0.0229919\text{mS}/\text{c}{\text{m}}^2$, black solid line right to the red solid line). Therefore, the resting state contains two dynamical behaviors, stable node and stable focus. There is a SNIC bifurcation at $g_h\approx 0.0229919\text{mS}/\text{c}{\text{m}}^2$, wherein a stable node (right part of the lower branch, black solid line right to the red line) contacts with a saddle (middle branch, dotted line) to disappear and a limit cycle (blue) appears. As g_h changes across the SNIC bifurcation point, the transition between the resting state corresponding to a stable node and the firing corresponding to a stable limit cycle happens.

Therefore, with increasing g_h, there are four stable behaviors and 3 bifurcation/transition points. The four behaviors are stable node, stable focus, stable node, and firing (stable limit cycle), and the 3 bifurcation/transition points are the transition point from the stable node to stable focus, transition point from the stable focus to stable node, and the SNIC bifurcation point.

For $I_{app}=-0.05\mu \text{A}/\text{c}{\text{m}}^2$, the bifurcations are different from those of $I_{app}=0.08\mu \text{A}/\text{c}{\text{m}}^2$, as shown in Figures 8C–E) (Figure 8D is the partial enlargement of Figure 8C, and Figure 8E is the partial enlargement of Figure 8D). Except for the firing/stable limit cycle (blue bold lines) and 3 branches of the equilibrium points (dashed or thin solid lines), a small unstable limit cycle (green) appears. The lower branch of the equilibrium point associated with the resting state is different from that of $I_{app}=0.08\mu \text{A}/\text{c}{\text{m}}^2$. With increasing g_h, the equilibrium (lower branch) is stable node ($g_h<0.0454454\text{mS}/\text{c}{\text{m}}^2$, black solid line), stable focus ($0.0454454<g_h<0.0620557\text{mS}/\text{c}{\text{m}}^2$, red solid line), unstable focus ($0.0620557<g_h<0.0623584\text{mS}/\text{c}{\text{m}}^2$, red dashed line), and unstable node ($0.0623584<g_h<0.0623686\text{mS}/\text{c}{\text{m}}^2$, black dashed line). Furthermore, there are more types of bifurcations for $I_{app}=-0.05\mu \text{A}/\text{c}{\text{m}}^2$. For example, the firing/stable limit cycle related to a big saddle homoclinic orbit (BHom) appears at $g_h\approx 0.0610595\text{mS}/\text{c}{\text{m}}^2$, wherein a stable limit cycle with large amplitude (blue) contacts with a saddle (middle branch of the equilibrium). Other three types of bifurcations are subcritical Hopf (SubH) bifurcation at $g_h\approx 0.0620557\text{mS}/\text{c}{\text{m}}^2$, saddle-node (SN) bifurcation at $g_h\approx 0.0623686\text{mS}/\text{c}{\text{m}}^2$, and small saddle homoclinic orbit (SHom) at g_h ≈ 0.061832mS/cm². The stable focus (red solid line) changes to unstable focus (red dashed line) via the SubH bifurcation and an unstable limit cycle with small amplitude (green) appears left to the SubH. The unstable limit cycle with small amplitude (green) contacts with the middle branch of the equilibrium (saddle) to form a SHom and disappears. The unstable node at the lower branch of the equilibrium contacts with the saddle (middle branch) to form a SN bifurcation and both equilibriums disappear.

As g_h increases across the SubH bifurcation point ($g_h\approx 0.0620557\text{mS}/\text{c}{\text{m}}^2$), the resting state corresponding to a focus (red solid line) changes to the firing corresponding to a stable limit cycle (blue line). As g_h decreases across the BHom bifurcation point ($g_h\approx 0.0610595\text{mS}/\text{c}{\text{m}}^2$), the firing corresponding to a stable limit cycle (blue line) changes to the resting state corresponding to a focus (red solid line). Therefore, bistability or coexistence of the resting state and firing lies between the BHom and SubH bifurcation points, which closely matches the experimental observations in the Purkinje cells (Engbers et al., 2013).

With increasing g_h, there are 6 bifurcation/transition points, the transition point from the stable node to stable focus, the BHom point, the SHom point, the SubH point, the transition point from the unstable focus to unstable node, and the SN bifurcation point related to the unstable node. There are 4 stable behaviors, the stable node, the stable focus, the coexistence of the resting state and firing, and the firing. The 3 bifurcation/transition points related to the stable dynamical behaviors, the transition point from the stable node to focus, the BHom point, and the SubH point, form the border of the parameter region between the four stable dynamical behaviors.

Two-Parameter Bifurcation

To investigate the comprehensive roles of I_h on the dynamical behaviors, bifurcations, and transitions between different kinds of bifurcations, the bifurcation diagram in (I_app, g_h) plane is acquired, as shown in Figure 9. In (I_app, g_h) plane, the codimension-1 bifurcation or transition points connect to form codimension-1 bifurcation or transition curves, which is the border of the parameter region between different dynamical behaviors. There are multiple codimension-1 bifurcation or transition curves, such as the SubH curve, BHom curve, SN curve, SNIC curve, and transition curve between node and focus which is labeled as NF curve. NF_U (dashed red line) and NF_S (solid red line) curves represent the part of the NF curve related to stable focus/node and unstable focus/node, respectively. SN_S curve is the part of the SN curve related to the stable node. The intersection point between different kinds of codimension-1 bifurcation curves is the codimension-2 bifurcation point, which is the key point to characterize the transition between different kinds of bifurcations. There are 2 codimmension-2 bifurcation points. One is Bogdanov-Takens (BT) point, which is labeled with a star and locates at $I_{app}\approx 0.0432\mu \text{A}/\text{c}{\text{m}}^2$ and $g_h\approx 0.03413\text{mS}/\text{c}{\text{m}}^2$. The other is the saddle-node homoclinic orbit (SNHO) bifurcation point, which is labeled with a black circle point and locates at $I_{app}\approx 0.07118\mu \text{A}/\text{c}{\text{m}}^2$ and $g_h\approx 0.02549\text{mS}/\text{c}{\text{m}}^2$. In addition, the NF_S curve (red line) is composed of the upper and lower branches and the connection point between two branches is called as T point (I_app ≈ 0.15751μA/cm² and g_h ≈ 0.00001mS/cm²), which is labeled with a black triangle (Figure 9D).

FIGURE 9

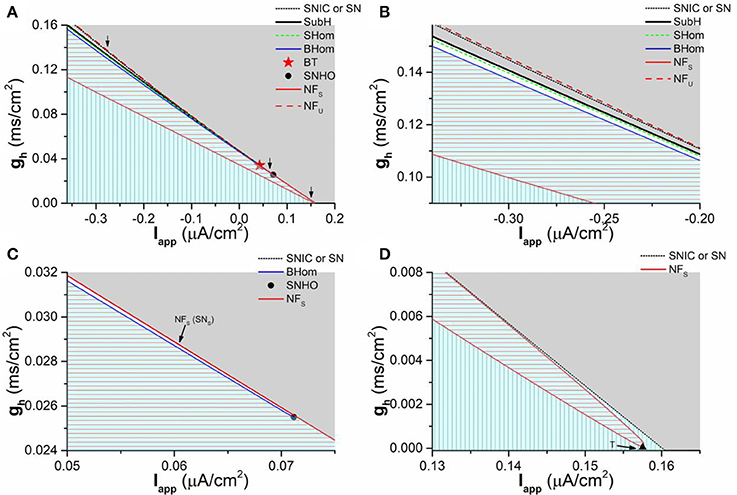
Figure 9. Two-parameter bifurcations in (g_h, I_app) plane. (A) Global view of the bifurcation diagram; (B) Partial enlargement diagram of a part of (A) around the first arrow (left to BT point); (C) Partial enlargement diagram of a part of (A) around the second arrow (between the BT point and SNHO point); (D) Partial enlargement diagram of a part of (A) around the last arrow (right to the SNHO point). SNIC and SN represent saddle-node bifurcation on invariant circle and saddle-node bifurcation, respectively. SHom and BHom are small and big saddle homoclinic orbits, respectively. SubH is the subcritical Hopf bifurcation. BT is Bogdanov-Takens bifurcation. SNHO is saddle-node homoclinic orbit bifurcation. SN_S is a part of SN curve related to the stable node. NF_U and NF_S represent the NF curve related to the stable focus/node and unstable focus/node, respectively. The stable behaviors within 4 sub-regions are firing (Gray), coexistence of firing and resting state (White area), stable focus (red horizontal lines), and stable node (vertical lines), respectively.

The enlargement of 3 part of the bifurcations from resting state to firing, which are labeled with arrows in Figure 9A, are shown in Figure 9B (Left to BT point), Figure 9C (between BT and SNHO points), and Figure 9D (right to SNHO point). The (I_app, g_h) plane is divided into 4 parts by the codimension-1 bifurcation or transition curves. From top to bottom, the stable behaviors within the 4 sub-regions are firing (gray), coexistence of firing and resting state (blank area in Figures 9B,C, too small to be seen in Figure 9A), stable focus (red horizontal lines), and stable node (vertical lines), as shown in Figure 9. The border of the parameter region of the 4 stable behaviors composed of codimension-1 bifurcation or transition curve and codimension-2 bifurcation points is shown in Table 1. From left to right, the bottom border of the firing is SubH curve (black line, Figures 9A,B), BT point, SN curve (black dashed line in Figures 9A–C, very close to the upper branch of the NF_S curve in Figure 9C), SNHO point, SNIC curve (black dashed line in Figures 9A–D). This border left to the SNHO point is the top border of the coexistence behavior, and the bottom border of the coexistence is the BHom curve (blue line in Figures 9A–C) ended at SNHO point. The top border of the stable focus region is composed of the BHom curve (blue line in Figures 9A–C) and the upper branch of the NF_S curve (red line in Figures 9C,D) between the BT point and T point, and the bottom border is the lower branch of the NF_S curve (red line in Figures 9A–D). The stable node locates in the remained area (Vertical line in Figures 9A,B,D).

TABLE 1

Table 1. The top or bottom border of the parameter region of the four stable behaviors.

The upper branch of the transition curve between the stable node and focus (NF_S curve) intersects with the codimension-1 SN bifurcation curve, SubH curve, and SHom curve at the BT point, which shows that BT point is related to both Hopf and SN/SNIC bifurcations, i.e., the transition point between Hopf and SN/SNIC bifurcations. The SNHO point is the intersection point between the bifurcation curves of SN, BHom, and SNIC. Other bifurcation (SHom and NF_U) curves not related to the stable behaviors, which are close to some of the bifurcation curves mentioned above, are not addressed in the present paper.

In summary, two obvious characteristics can be found from the bifurcation diagram. One is that the codimension-1 bifurcation curve or the border between the firing and resting state show a negative slope in the (I_app, g_h) plane, which correspond to the firing threshold shown in Figure 3. The firing behavior and the resting state locate up-right half and down-left half of (I_app, g_h) plane, respectively. The result shows that increasing g_h means far away from the bifurcation point for the firing behavior and approaching bifurcation point for the resting state corresponding to a stable focus or stable node. The other is that the distribution of the dynamical behaviors in the parameter region left and right to the BT point is different. Left to the BT point, the stable focus locates upper to the stable node. With increasing I_app, the parameter region of the stable focus becomes narrow. Down-right to the BT point, the parameter region of the resting state and stable focus becomes very narrow and at last the stable focus disappears with increasing I_app. The behavior upper, lower, and right to the stable focus is stable node (Figure 9D).

Dynamical Mechanism of I_h Induced Resonance and Spike-Timing Precision, and Rebound

Dynamical Mechanism of I_h Induced Subthreshold Resonance

Firstly, the parameter regions for the two cases of the subthreshold resonance can be identified. Two different cases of subthreshold resonance shown in subsection 3.1.4 locate at left (I_app = −0.05 μA/cm² and I_app = −0.3 μA/cm², Figure 6) and right (I_app = 0.08 μA/cm², Figure 7) to the BT point, respectively, which implies that the BT point plays very important roles in the identification of dynamical mechanism of the subthreshold resonance.

Secondly, with help of the distribution of the stable focus and node left to the BT point, the “typical” -, “weak” -, and non-resonance can be well understood. The “typical”-resonance appears at large g_h value (g_h = 0.05 mS/cm² for I_app = −0.05 μA/cm², g_h = 0.1 mS/cm² and 0.12 mS/cm² for I_app = −0.3 μA/cm²), i.e., within the parameter region of the stable focus. The non-resonance appears at g_h = 0 mS/cm² (I_app = −0.05 μA/cm² and I_app = −0.3 μA/cm²), i.e., within the parameter region of the stable node. The “weak” -resonance appears near the transition curve between the stable focus and node (g_h = 0.02, 0.03 and 0.04 mS/cm²for I_app = −0.05 μA/cm², g_h = 0.06 and 0.08 mS/cm² for I_app = −0.3 μA/cm²). The results show that the “typical”-resonance in the presence of I_h is related to the stable focus, and the non-resonance in the absence of I_h (blockage of I_h) associated with the stable node. Therefore, I_h induces a transition from the stable node to the stable focus. In nonlinear dynamics, Hopf bifurcation related to the stable focus/firing and SN/SNIC bifurcation associated with the stable node/firing. Therefore, the transition point between the Hopf bifurcation and SN/SNIC bifurcation, i.e., the BT point, exists in the neuronal system with I_h.

Thirdly, the “typical”-resonance for the stable focus or non-resonance for the stable node and the difference between them are origin from the distinction of the frequency response due to eigenvalue. The eigenvalues for the stable focus are complex numbers and for the stable node are real numbers. When disturbed, the behavior of a stable focus is a damped subthreshold oscillation with a fixed frequency which is related to the imaginary part of the complex eigenvalues, as shown in Figure 10A ($g_h=0.05\text{mS}/\text{c}{\text{m}}^2,I_{app}=-0.05\mu \text{A}/\text{c}{\text{m}}^2$). However, the behavior of a stable node after perturbed exhibits no oscillations, as shown in Figure 10B ($g_h=0.01mS/c{m}^2,I_{app}=-0.05\mu \text{A}/\text{c}{\text{m}}^2$). Such two different behaviors exhibit different frequency responses to the periodic stimulus with single frequency. For a stable focus, the oscillation amplitude of the membrane potential reaches maximal when the stimulus frequency is close to the fixed frequency of the focus. For example, when stimulus frequency is 3.1 Hz, the oscillation amplitude is higher than those of other frequencies, as shown in Figure 10C. For a stable node, the oscillation amplitude of the membrane potential remains nearly unchanged at low frequency and then decreases with increasing the stimulus frequency, as shown in Figure 10D. The periodic stimulus current is asin2πf₁t (a = 0.01μA/cm², f₁ is the frequency). The different frequency responses between the stable focus and stable node are the fundamental base of the “typical”-resonance and non-resonance phenomenon induced by the “ZAP” current.

FIGURE 10

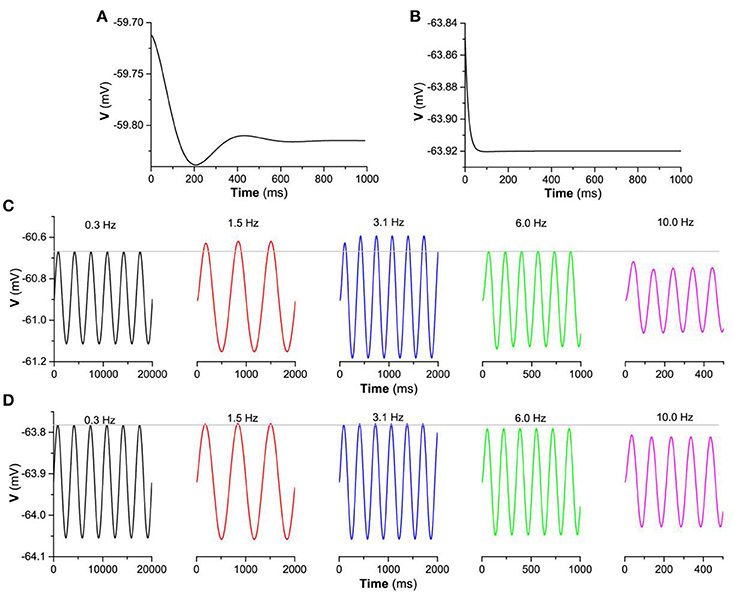
Figure 10. The membrane potential of the stable focus and stable node when perturbed and the responses to a periodic stimulus with single frequency for $I_{app}=-0.05\mu \text{A}/\text{c}{\text{m}}^2$. The membrane potential when perturbed. (A) Stable focus when g_h = 0.05 mS/cm²; (B) Stable node when; g_h = 0.01 mS/cm²; The responses of the membrane potential to periodic stimulus g_h = 0.01 mS/cm² current a sin 2π f₁t ($a=0.01\mu \text{A}/\text{c}{\text{m}}^2{f}_1$ is the frequency); Voltage response to periodic stimulus with singe frequency. (C) Stable focus when $g_h=0.05\text{mS}/\text{c}{\text{m}}^2$; (D) Stable focus when $g_h=0.01\text{mS}/\text{c}{\text{m}}^2$.

Fourthly, another important characteristic of the subthreshold resonance (Figures 6E,F,D) is that the maximal impedance increases with increasing g_h when I_app is fixed, which can be well understood with the bifurcation theory and the changes of the membrane potential shown in Figure 3A. With increasing g_h, the membrane potential increases. When I_app is fixed, increasing g_h means that approaching the bifurcation point from resting state to firing, and the oscillation amplitude of the membrane potential to a “ZAP” current stimulation increases, as shown by the difference between the maximal and minimal values of the membrane potential in Figure 11A ($I_{app}=-0.05\mu \text{A}/\text{c}{\text{m}}^2$) and Figure 11B ($I_{app}=0.08\mu \text{A}/\text{c}{\text{m}}^2$). The increase of the oscillation amplitude of the membrane potential leads to the increase of the maximal impedance with increasing g_h. Such a result is consistent with bifurcation theory wherein as a stable dynamical behavior approaches the bifurcation point, its capability of resisting disturbance such as regular stimulus becomes weaker. For the stable node or stable focus which should keep unchanged and remain at a fixed level, the weakness of the capability of resisting disturbance with increasing g_h, i.e., approaching the bifurcation point, is characterized by the increase of the oscillation amplitude of the membrane potential to the “ZAP” current stimulus.

FIGURE 11

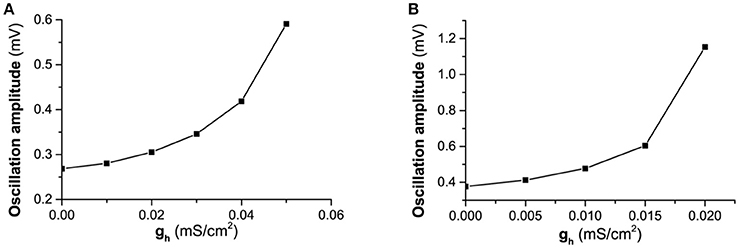
Figure 11. The changes of the difference between the maximal and minimal values of the membrane potential stimulated by a “ZAP” current with increasing g_h. (A) $I_{app}=-0.05\mu \text{A}/\text{c}{\text{m}}^2$; (B) $I_{app}=0.08\mu \text{A}/\text{c}{\text{m}}^2$.

Last, complex or “strange” phenomenon related to the subthreshold resonance appears near the bifurcation point. (1) In the small parameter region of the resting state or focus down-right to the BT point or SNHO point, not “typical”-resonance, but non-resonance or “weak”-resonance (Figure 7), appears for the stable focus, which is “strange” because a “typical”-resonance should appear. The dynamical mechanism is very complex and may be from the narrow region of focus and the close distance from the codimension-2 bifurcation point BT with double zero eigenvalues. Such a complex dynamical behavior is similar to those simulated in the parameter region near a special equilibrium with double zero eigenvalues in a linear model (Rotstein, 2013; Rotstein and Nadim, 2014). The dynamical mechanism underlying the nonlinear system used in the present paper and the difference to the linear system should be studied in future. (2) The “weak”-resonance appears for the stable node within the neighborhood of the transition curve between the stable node and focus, which is also “strange” due to a non-resonance should appear for a stable node. Such a result also shows that the complex behaviors appear near the bifurcation/transition point. Except for the bifurcation/transition point, the external stimulus signal, the “ZAP” current, may be an important factor to induce the “weak”-resonance for the stable node. (3) There is complex phenomenon in the very narrow region of the coexistence behavior. We do not address the phenomenon because the parameter region is very narrow. The complex dynamics within these three narrow parameter regions (Figure 9D) near the bifurcation/transition point should be further studied in future. Except for the three narrow regions, the “typical”-resonance and non-resonance appear in the parameter region of the stable focus and the stable node far away from the bifurcation/transition point, respectively.

Dynamical Mechanism of I_h Induced More Spike-Timing Precision

The more spike-timing precision induced by I_h can also well be understood with the bifurcation theory. For the firing behavior, the increase of g_h means that the firing becomes farther away from the bifurcation point. According to the bifurcation theory, as a stable dynamical behavior becomes farther away from the bifurcation point, its capability of resisting disturbance such as noise becomes stronger (Izhikevich, 2000, 2007; Tateno et al., 2004). For a neuronal firing, the enhancement of the capability of resisting disturbance is characterized by the further decrease of the standard deviation (STD) of ISIs than the mean value of ISIs, with increasing g_h, as shown in Figures 12, 13, which leads to the decrease of CV of ISIs, i.e., the enhancement of the spike-timing precise.

FIGURE 12

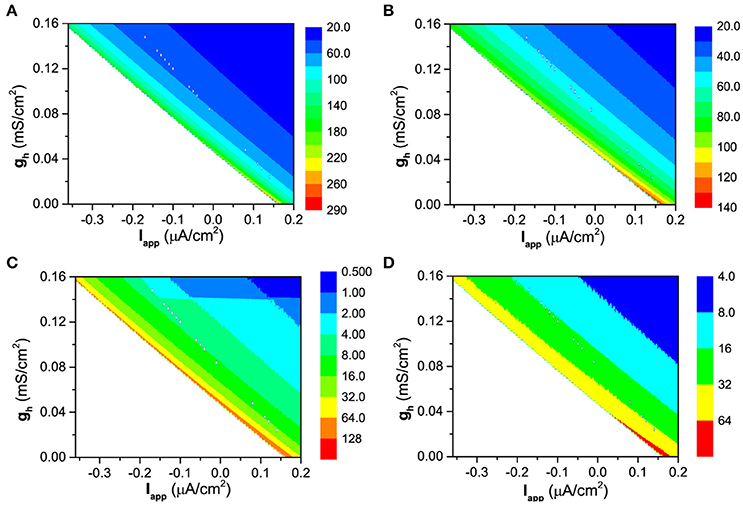
Figure 12. The dependence of the mean value and standard deviation of ISIs on both I_app and g_h at different levels of noise intensity D. Mean value of ISIs: (A) D = 0.2μA/cm²; (B) D = 0.6μA/cm²; Standard deviation of ISIs: (C) D = 0.2μA/cm²; (D) D = 0.6μA/cm².

FIGURE 13

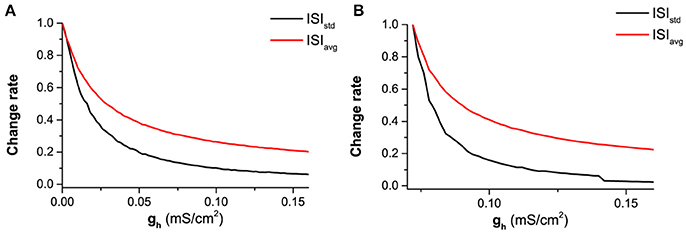
Figure 13. The decrease of normalized mean value (red) and standard deviation (black) of ISIs with increasing g_h at different levels of I_app and noise intensity D. (A) I_app = 0.17 μA/cm² and D = 0.6μA/cm²; (B) I_app = −0.08 μA/cm² and D = 0.2μA/cm². ISI_std (black) and ISI_avg (red) represent the standard deviation and mean value of ISIs.

The faster decrease of STD than the mean value can be found from Figure 12. For D = 0.2μA/cm², the mean value decreases from 290 ms to 20 ms, as shown in Figure 12A, and the STD decreases from 128 ms to 0.5 ms, as shown in Figure 12B. 290/20 (14.5) is much smaller than 128/0.5(256). For D = 0.6μA/cm², the mean value decreases from 140ms to 20ms, as depicted in Figure 12C, and the STD decreases from 64ms to 4ms, as shown in Figure 12D. 140/20 (7) is smaller than 64/4(16). The results are similar in a large noise intensity (0 < D < 1.0μA/cm²).

The faster decrease of the STD than the mean value can also be found from two representatives shown in Figure 13. If the mean value for different g_h values are normalized by the largest value corresponding to the smallest g_h, the decrease of the normalized values with increasing g_h is shown by the red line in Figure 13A (I_app = 0.17 μA/cm² and D = 0.6μA/cm²) and Figure 13B (I_app = −0.08 μA/cm² and D = 0.2μA/cm²). Similarly, the decrease of the normalized STD with increasing g_h is depicted by the black line in Figures 13A,B). For both representatives, the STD (black) decreases faster than the mean value (red).

The results show that the enhancement of the spike-timing precision is mainly caused by the fast decrease of standard deviation of ISIs with increasing g_h, which obeys the bifurcation theory wherein a stable dynamical behavior far away from the bifurcation point exhibits stronger capability of resisting disturbance such as noise.

Dynamical Mechanism of I_h Induced Rebound (Spike)

The voltage sag is mainly induced by the hyperpolarization activation of I_h, which can be found from the 2nd−4th panels of Figures 2A–C. At the initial phase of the hyperpolarization current, I_h increases with increasing time, which leads to the increase of the membrane potential, i.e., the voltage sag. If the strength of the hyperpolarization current is stronger, I_h becomes higher. Correspondingly, the voltage sag becomes stronger. If g_h is larger, I_h is higher, which also leads to the stronger voltage sag. If there is no I_h, no voltage sag appears.

The rebound (spike) is mainly induced by both I_h and Na⁺ current, as shown by the 2nd to 4th panels of Figure 2. At the termination time of the hyperpolarization current, I_h is much higher than that of the resting state, which leads to the depolarization of the membrane potential. The depolarization of the membrane potential induces the decrease of I_h and the increase of Na⁺ current which plays the dominant role and leads to further depolarization of the membrane potential. The larger the g_h, the higher the I_h; the larger the strength of the hyperpolarization square current, the higher the I_h. When g_h and/or the strength of the hyperpolarization current are lower, I_h is lower and the depolarization is not strong enough to induce a spike, which corresponds to the rebound phenomenon. When g_h and/or the strength of the hyperpolarization current are larger, I_h is higher and the depolarization is strong enough to induce a spike, which corresponds to the rebound spike phenomenon.

The rebound (spike) becomes strong with increasing g_h, which can also be well understood with the bifurcation theory. According to the bifurcation theory (Izhikevich, 2000, 2007), as a stable dynamical behavior approaches the bifurcation point, its capability of resisting disturbance such as regular stimulus becomes weaker. For the resting state, the increase of g_h means that it approaches the bifurcation point, and the weakness of the capability of resisting disturbance such as the hyperpolarization square current is characterized by the stronger rebound (spike).

For the resting state for other I_app values, the results are similar to those obtained with I_app = −0.05 μA/cm². If there is no I_h, no rebound (spike) is induced.

Discussion

Experimental studies found that I_h contributes to the voltage sag and rebound (spike) to the inhibitory square current, resonance to sinusoidal current input, and more spike-timing precision (Zemankovics et al., 2010; Engbers et al., 2011; Gastrein et al., 2011; Pavlov et al., 2011; Borel et al., 2013; Gonzalez et al., 2015), which are rarely explained theoretically. In the present paper, with increasing g_h, stronger voltage sag/rebound (spike) and resonance, and more spike-timing precision are simulated in a theoretical model. In addition, the enhancement of the membrane potential for the resting state, the increase of firing frequency for the firing behavior, and the decrease of the firing threshold for I_app induced by I_h are also simulated in the model. All results closely match those of the previous experiment, which shows that the theoretical model is suitable to investigate the dynamics of neurons with I_h.

With help of the complex bifurcations and the distribution of the stable behaviors in (I_app, g_h) plane, the dynamical mechanism that can well interpret the experimental observations is provided. With increasing g_h, the four stable behaviors are stable node, stable focus, coexistence behaviors, and the firing, which are separated by the bifurcations. For the firing behavior, the increase of g_h means that the firing becomes far away from the bifurcation point. According to the bifurcation theory, as a stable dynamical behavior becomes far away from the bifurcation point, its capability of resisting disturbance such as noise becomes strong. It is the cause that CV and standard deviation of ISIs become lower with increasing g_h, i.e., the enhancement of the spike-timing precision. For the resting state, increasing g_h means that the resting state approaches to the bifurcation point. As a stable dynamical behavior approaches to the bifurcation point, its capability of resisting disturbance such as hyperpolarization stimulus becomes strong. It is the cause that rebound (spike) becomes strong with increasing g_h.

Compared with the rebound (spike) and spike-timing precision, the dynamical mechanism for the subthreshold membrane resonance is very complex. It can be concluded that the “typical”-resonance appears in the parameter region of the stable focus far away from the bifurcation point, and non-resonance phenomenon appears in the parameter region of the stable node far away from the bifurcation point. However, complex or “strange” dynamics appear in the parameter region near the bifurcation/transition point. For example, the non-resonance phenomenon appears in the parameter region of the stable focus near a codimmenion-2 bifurcation point with double zero eigenvalues, the BT point, and “weak”-resonance appears in the parameter region of the stable node near the transition point between the stable focus and node. These results are similar to those simulated near the special point with double zero eigenvalues in a linear system (Rotstein, 2013; Rotstein and Nadim, 2014). In the experiment (Zemankovics et al., 2010; Gastrein et al., 2011; Pavlov et al., 2011; Borel et al., 2013; Gonzalez et al., 2015), the “typical”-resonance appears in the presence of I_h and non-resonance appears when I_h is blocked. According to the results of the present paper, the behavior is stable focus for the “typical”-resonance and stable node for the non-resonance phenomenon, which shows that I_h induces a transition from the stable node to stable focus. In nonlinear dynamics, the stable focus related to Hopf bifurcation and the stable node associated with SN/SNIC bifurcation. Therefore, the transition point between Hopf bifurcation and SN/SNIC bifurcation, the BT point, plays important roles in the determination of the dynamics of the neuronal system with I_h. The underlying mechanism for the complex or “strange” dynamics, which may be related to the BT point (Izhikevich, 2000, 2007; Zhao and Gu, 2017), should be studied in future.

With help of the results of the present paper, many other physiological activities observed in the experiment, such as the phase response curve (Ermentrout, 1996; Smeal et al., 2010), synchronization (Hansel et al., 1995; Ermentrout, 1996; Fink et al., 2011; Tikidji-Hamburyan et al., 2015), spike initiating dynamics (Prescott et al., 2008), and neural coding efficiency (Yi et al., 2015), can be further understood. For example, neuron with I_h exhibits resonance at a certain frequency and firing with a fixed frequency, which contributes to the formation of synchronized oscillatory (Zemankovics et al., 2010; Stark et al., 2013). It is also the cause that the synchronized oscillatory appears in the hippocampal pyramidal neurons and stratum oriens interneurons (Varga et al., 2008; Colgin, 2013). In addition, I_h can induce bistability or coexistence of the resting state and firing (Figures 6B,C). The parameter region of the bistability or coexistence of the resting state and firing, i.e., the parameter region lying between the SN/SNIC curve (black dashed line) and BHom curve (blue line), becomes wide as the conductance of I_h (g_h) increases (Figure 9), which is consistent with the previous experimental observation wherein I_h can enlarge the region of bistability or coexistence in the Purkinje cell (Engbers et al., 2013), which is a potential mechanism for the short-term memory (Durstewitz et al., 2000; Loewenstein et al., 2005; Engbers et al., 2013).

Author Contributions

ZZ, LL, and HG: conceived and designed the work; ZZ and LL: performed the simulations; ZZ, LL, and HG: analyzed and interpreted the data; ZZ and HG: wrote the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant Nos. 11572225 and 11372224.

References

Amarillo, Y., Mato, G., and Nadal, M. S. (2015). Analysis of the role of the low threshold currents I_T and I_h in intrinsic delta oscillations of thalamocortical neurons. Front. Comput. Neurosci. 9:52. doi: 10.3389/fncom.2015.00052

PubMed Abstract | CrossRef Full Text | Google Scholar

Ascoli, G. A., Gasparini, S., Medinilla, V., and Migliore, M. (2010). Local control of postinhibitory rebound spiking in CA1 pyramidal neuron dendrites. J. Neurosci. 30, 6434–6442. doi: 10.1523/JNEUROSCI.4066-09.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Bacci, A., and Huguenard, J. R. (2006). Enhancement of spike-timing precision by autaptic transmission in neocortical inhibitory interneurons. Neuron 49, 119–130. doi: 10.1016/j.neuron.2005.12.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Borel, M., Guadagna, S., Jang, H. J., Kwag, J., and Paulsen, O. (2013). Frequency dependence of CA3 spike phase response arising from h-current properties. Front. Cell. Neurosci. 7:263. doi: 10.3389/fncel.2013.00263

PubMed Abstract | CrossRef Full Text | Google Scholar

Buracas, G. T., Zador, A. M., DeWeese, M. R., and Albright, T. D. (1998). Efficient discrimination of temporal patterns by motion-sensitive neurons in primate visual cortex. Neuron 20, 959–969. doi: 10.1016/S0896-6273(00)80477-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Butts, D. A., Weng, C., Jin, J., Yeh, C. I., Lesica, N. A., Alonso, J. M., et al. (2007). Temporal precision in the neural code and the timescales of natural vision. Nature 449, 92–96. doi: 10.1038/nature06105

PubMed Abstract | CrossRef Full Text | Google Scholar

Buzsáki, G., and Moser, E. I. (2013). Memory, navigation and theta rhythm in the hippocampal-entorhinal system. Nat. Neurosci. 16, 130–138. doi: 10.1038/nn.3304

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, S. S., Cheng, C. Y., and Lin, Y. R. (2013). Application of a two-dimensional Hindmarsh-Rose type model for bifurcation analysis. Int. J. Bifurcat. Chaos. 23:50055. doi: 10.1142/S0218127413500557

CrossRef Full Text | Google Scholar

Colgin, L. L. (2013). Mechanisms and functions of Theta rhythms. Annu. Rev. Neurosci. 36, 295–312. doi: 10.1146/annurev-neuro-062012-170330

PubMed Abstract | CrossRef Full Text | Google Scholar

Dayan, P., and Abbott, L. F. (2001). Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. (London: MIT Press).

Google Scholar

Dhooge, A., Govaerts, W., and Kuznetsov, Y. A. (2003). MATCONT: a MATLAB package for numerical bifurcation analysis of ODEs. ACM Trans. Math. Softw. 29, 141–164. doi: 10.1145/779359.779362

CrossRef Full Text | Google Scholar

DiFrancesco, J. C., Barbuti, A., Milanesi, R., Coco, S., Bucchi, A., Bottelli, G., et al. (2011). Recessive loss-of-function mutation in the pacemaker HCN2 channel causing increased neuronal excitability in a patient with idiopathic generalized Epilepsy. J. Neurosci. 31, 17327–17337. doi: 10.1523/JNEUROSCI.3727-11.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

DiFrancesco, J. C., and DiFrancesco, D. (2015). Dysfunctional HCN ion channels in neurological diseases. Front. Cell. Neurosci. 9:71. doi: 10.3389/fncel.2015.00071

CrossRef Full Text | Google Scholar

Drion, G., O'Leary, T., and Marder, E. (2015). Ion channel degeneracy enables robust and tunable neuronal firing rates. Proc. Natl. Acad. Sci. U.S.A. 112, 5361–5370. doi: 10.1073/pnas.1516400112

PubMed Abstract | CrossRef Full Text | Google Scholar

Durstewitz, D., Seamans, J. K., and Sejnowski, T. J. (2000). Neurocomputational models of working memory. Nat. Neurosci. 3, 1184–1191. doi: 10.1038/81460

PubMed Abstract | CrossRef Full Text | Google Scholar

Elgueta, C., Kohler, J., and Bartos, M. (2015). Persistent discharges in dentate gyrus perisoma-inhibiting interneurons require hyperpolarization-activated cyclic nucleotide-gated channel activation. J. Neurosci. 35, 4131–4139. doi: 10.1523/JNEUROSCI.3671-14.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

Emery, E. C., Young, G. T., and McNaughton, P. A. (2012). HCN2 ion channels: an emerging role as the pacemakers of pain. Trends Pharmacol. Sci. 33, 456–463. doi: 10.1016/j.tips.2012.04.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Engbers, J. D., Anderson, D., Tadayonnejad, R., Mehaffey, W. H., Molineux, M. L., and Turner, R. W. (2011). Distinct roles for I_T and I_H in controlling the frequency and timing of rebound spike responses. J. Physiol. 589, 5391–5413. doi: 10.1113/jphysiol.2011.215632

CrossRef Full Text | Google Scholar

Engbers, J. D., Fernandez, F. R., and Turner, R. W. (2013). Bistability in Purkinje neurons: ups and downs in cerebellar research. Neural Netw. 47, 18–31. doi: 10.1016/j.neunet.2012.09.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Ermentrout, B. (1996). Type I membranes, phase resetting curves, and synchrony. Neural Comput. 8, 979–1001. doi: 10.1162/neco.1996.8.5.979

PubMed Abstract | CrossRef Full Text | Google Scholar

Ermentrout, B. (2002). Simulating, Analyzing, and Animating Dynamical Systems: A guide to XPPAUT for Researchers and Students (Philadelphia: SIAM).

Google Scholar

Faisal, A., Selen, L. P. J., and Wolpert, D. M. (2008). Noise in the nervous system. Nat. Rev. Neurosci. 9, 292–303. doi: 10.1038/nrn2258

PubMed Abstract | CrossRef Full Text | Google Scholar

Fink, C. G., Booth, V., and Zochowski, M. (2011). Cellularly-driven differences in network synchronization propensity are differentially modulated by firing frequency. PLoS Comput. Biol. 7:e1002062. doi: 10.1371/journal.pcbi.1002062

PubMed Abstract | CrossRef Full Text | Google Scholar

Fox, D. M., Tseng, H. A., Smolinski, T. G., Rotstein, H. G., and Nadim, F. (2017). Mechanisms of generation of membrane potential resonance in a neuron with multiple resonant ionic currents. PLoS Comput. Biol. 13:e1005565. doi: 10.1371/journal.pcbi.1005565

PubMed Abstract | CrossRef Full Text | Google Scholar

Franci, A., Drion, G., and Sepulchre, R. (2012). An organizing center in a planar model of neuronal excitability. SIAM J. Appl. Dyn. Syst. 11, 1698–1722. doi: 10.1137/120875016

CrossRef Full Text | Google Scholar

Garrido, J. A., Ros, E., and D'Angelo, E. (2013). Spike timing regulation on the millisecond scale by distributed synaptic plasticity at the cerebellum input stage: a simulation study. Front. Comput. Neurosci. 7:64. doi: 10.3389/fncom.2013.00064

PubMed Abstract | CrossRef Full Text | Google Scholar

Gasparini, S., and DiFrancesco, D. (1997). Action of the hyperpolarization-activated current (I_h) blocker ZD7288 in hippocampal CA1 neurons. Pflug Arch. 435, 99–106. doi: 10.1007/s004240050488

CrossRef Full Text | Google Scholar

Gastrein, P., Campanac, E., Gasselin, C., Cudmore, R. H., Bialowas, A., Carlier, E., et al. (2011). The role of hyperpolarization-activated cationic current in spike-time precision and intrinsic resonance in cortical neurons in vitro. J. Physiol. 589, 3753–3773. doi: 10.1113/jphysiol.2011.209148

PubMed Abstract | CrossRef Full Text | Google Scholar

Giocomo, L. M., Zilli, E. A., Fransen, E., and Hasselmo, M. E. (2007). Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science 315, 1719–1722. doi: 10.1126/science.1139207

PubMed Abstract | CrossRef Full Text | Google Scholar

Gonzalez, O. J. A., Mansvelder, H. D., van Pelt, J., and van Ooyen, A. (2015). H-Channels affect frequency, power and amplitude fluctuations of neuronal network oscillations. Front. Comput. Neurosci. 9:141. doi: 10.3389/fncom.2015.00141

CrossRef Full Text | Google Scholar

Good, C. H., Hoffman, A. F., Hoffer, B. J., Chefer, V. I., Shippenberg, T. S., Backman, C. M., et al. (2011). Impaired nigrostriatal function precedes behavioral deficits in a genetic mitochondrial model of Parkinson's disease. FASEB J. 25, 1333–1344. doi: 10.1096/fj.10-173625

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutkin, B. S., and Ermentrout, G. B. (1998). Dynamics of membrane excitability determine interspike interval variability: a link between spike generation mechanisms and cortical spike train statistics. Neural Comput. 10, 1047–1065. doi: 10.1162/089976698300017331

PubMed Abstract | CrossRef Full Text | Google Scholar

Hájos, N., Pálhalmi, J., Mann, E. O., Németh, B., Paulsen, O., and Freund, T. F. (2004). Spike timing of distinct types of GABAergic interneuron during hippocampal gamma oscillations in vitro. J. Neurosci. 24, 9127–9137. doi: 10.1523/JNEUROSCI.2113-04.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansel, D., Mato, G., and Meunier, C. (1995). Synchrony in excitatory neural networks. Neural Comput. 7, 307–337.

PubMed Abstract | Google Scholar

He, C., Chen, F., Li, B., and Hu, Z. (2014). Neurophysiology of HCN channels: from cellular functions to multiple regulations. Prog Neurobiol. 112, 1–23. doi: 10.1016/j.pneurobio.2013.10.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Hindmarsh, J. L., and Rose, R. M. (1994). A model of intrinsic and driven spindling in thalamocortical neurons. Philos. Trans. R Soc. Lond. B Biol. Sci. 346, 165–183. doi: 10.1098/rstb.1994.0139

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, H., Vervaeke, K., and Storm, J. F. (2002). Two forms of electrical resonance at theta frequencies, generated by M-current, h-current and persistent Na⁺ current in rat hippocampal pyramidal cells. J. Physiol. 545, 783–805. doi: 10.1113/jphysiol.2002.029249

PubMed Abstract | CrossRef Full Text | Google Scholar

Hutcheon, B., and Yarom, Y. (2000). Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends Neurosci. 23, 216–222. doi: 10.1016/S0166-2236(00)01547-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Izhikevich, E. M. (2000). Neural excitability, spiking and bursting. Int. J. Bifurcat. Chaos. 10, 1171–1266. doi: 10.1142/S0218127400000840

CrossRef Full Text | Google Scholar

Izhikevich, E. M. (2007). Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting (London: MIT press).

Klausberger, T., Magill, P. J., Márton, L. F., Roberts, J. D. B., Cobden, P. M., Buzsáki, G., et al. (2006). Brain-state- and cell-type-specific firing of hippocampal interneurons in vivo. Nature 421, 844–848. doi: 10.1038/nature01374

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuznetsov, Y. A. (1995). Elements of Applied Bifurcation Theory (New York, NY: Springer-Verlag).

Google Scholar

Loewenstein, Y., Mahon, S., Chadderton, P., Kitamura, K., Sompolinsky, H., Yarom, Y., et al. (2005). Bistability of cerebellar Purkinje cells modulated by sensory stimulation. Nat. Neurosci. 8, 202–211. doi: 10.1038/nn1393

PubMed Abstract | CrossRef Full Text | Google Scholar

Manseau, F., Goutagny, R., Danik, M., and Williams, S. (2008). The hippocamposeptal pathway generates rhythmic firing of GABAergic neurons in the medial septum and diagonal bands: an investigation using a complete septohippocampal preparation in vitro. J. Neurosci. 28, 4096–4107. doi: 10.1523/JNEUROSCI.0247-08.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Masi, A., Narducci, R., Landucci, E., Moroni, F., and Mannaioni, G. (2013). MPP(+)-dependent inhibition of I_h reduces spontaneous activity and enhances EPSP summation in nigral dopamine neurons. Br. J. Pharmacol. 169, 130–142. doi: 10.1111/bph.12104

PubMed Abstract | CrossRef Full Text | Google Scholar

Masuda, N., and Aihara, K. (2003). Ergodicity of spike trains: When does trial averaging make sense? Neural Comput. 15, 1341–1372. doi: 10.1162/089976603321780308

PubMed Abstract | CrossRef Full Text | Google Scholar

Moca, V. V., Nikolic, D., Singer, W., and Muresan, R. C. (2014). Membrane resonance enables stable and robust Gamma oscillations. Cereb. Cortex 24, 119–142. doi: 10.1093/cercor/bhs293

PubMed Abstract | CrossRef Full Text | Google Scholar

Morozova, E. O., Zakharov, D., Gutkin, B. S., Lapish, C. C., and Kuznetsov, A. (2016). Dopamine neurons change the type of excitability in response to stimuli. PLoS Comput. Biol. 12:e1005233. doi: 10.1371/journal.pcbi.1005233

PubMed Abstract | CrossRef Full Text | Google Scholar

Orbán, G., Kiss, T., and Erdi, P. (2006). Intrinsic and synaptic mechanisms determining the timing of neuron population activity during hippocampal theta oscillation. J. Neurophysiol. 96, 2889–2904. doi: 10.1152/jn.01233.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Pape, H. C. (1996). Queer current and pacemaker: the hyperpolarization-activated cation current in neurons. Annu. Rev. Physiol. 58, 299–327. doi: 10.1146/annurev.ph.58.030196.001503

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, S., and Kwag, J. (2012). Dendritic-targeting interneuron controls spike timing of hippocampal CA1 pyramidal neuron via activation of I_h. Neurosci. Lett. 523, 9–14. doi: 10.1016/j.neulet.2012.06.010

CrossRef Full Text | Google Scholar

Pavlov, I., Scimemi, A., Savtchenko, L., Kullmann, D. M., and Walker, M. C. (2011). I_h-mediated depolarization enhances the temporal precision of neuronal integration. Nat. Commun. 2:199. doi: 10.1038/ncomms1202

CrossRef Full Text | Google Scholar

Pena, R. F., Ceballos, C. C., Lima, V., and Roque, A. C. (2017). Interplay of activation kinetics and the derivative conductance determines the resonance properties of neurons. arXiv: 1712.00306. doi: 10.13140/RG.2.2.13015.98720

CrossRef Full Text | Google Scholar

Prescott, S. A., Koninck, Y. D., and Sejnowski, T. J. (2008). Biophysical basis for three distinct dynamical mechanisms of action potential initiation. PLoS Comput. Biol. 4:e1000198. doi: 10.1371/journal.pcbi.1000198

PubMed Abstract | CrossRef Full Text | Google Scholar

Ratté, S., Hong, S., De Schutter, E., and Prescott, S. A. (2013). Impact of neuronal properties on network coding: roles of spike initiation dynamics and robust synchrony transfer. Neuron 78, 758–772. doi: 10.1016/j.neuron.2013.05.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Reid, C. A., Phillips, A. M., and Petrou, S. (2012). HCN channelopathies: pathophysiology in genetic epilepsy and therapeutic implications. Br. J. Pharmacol. 165, 49–56. doi: 10.1111/j.1476-5381.2011.01507.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Reinagel, P., and Reid, R. C. (2002). Precise firing events are conserved across neurons. J. Neurosci. 22, 6837–6841. Available online at: http://www.jneurosci.org/content/22/16/6837.long

PubMed Abstract | Google Scholar

Remme, M. W., Donato, R., Mikiel-Hunter, J., Ballestero, J. A., Foster, S., Rinzel, J., et al. (2014). Subthreshold resonance properties contribute to the efficient coding of auditory spatial cues. Proc. Natl. Acad. Sci. U.S.A. 111, E2339–E2348. doi: 10.1073/pnas.1316216111

PubMed Abstract | CrossRef Full Text | Google Scholar

Rinzel, J. (1998). “Analysis of neuronal excitability and oscillations,” in Methods in Neuronal Modeling: from Synapses to Networks, eds C. Koch, and I. Segev (London: MIT Press), 135–169.

Rotstein, H. G. (2013). Preferred frequency responses to oscillatory inputs in an electrochemical cell model: linear amplitude and phase resonance. Phys. Rev. E 88:062913. doi: 10.1103/PhysRevE.88.062913

PubMed Abstract | CrossRef Full Text | Google Scholar

Rotstein, H. G. (2015). Subthreshold amplitude and phase resonance in models of quadratic type: nonlinear effects generated by the interplay of resonant and amplifying currents. J. Comput. Neurosci. 38, 325–354. doi: 10.1007/s10827-014-0544-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Rotstein, H. G., and Nadim, F. (2014). Frequency preference in two-dimensional neural models: a linear analysis of the interaction between resonant and amplifying currents. J. Comput. Neurosci. 37, 9–28. doi: 10.1007/s10827-013-0483-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Schnorr, S., Eberhardt, M., Kistner, K., Rajab, H., Kasser, J., Hess, A., et al. (2014). HCN2 channels account for mechanical (but not heat) hyperalgesia during long-standing inflammation. Pain 155, 1079–1090. doi: 10.1016/j.pain.2014.02.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Smeal, R. M., Ermentrout, G. B., and White, J. A. (2010). Phase-response curves and synchronized neural networks. Philos. Trans. R. Soc. Lond. B Biol. Sci. 365, 2407–2422. doi: 10.1098/rstb.2009.0292

PubMed Abstract | CrossRef Full Text | Google Scholar

Somogyi, P., and Klausberger, T. (2005). Defined types of cortical interneurone structure space and spike timing in the hippocampus. J. Physiol. 562, 9–26. doi: 10.1113/jphysiol.2004.078915

PubMed Abstract | CrossRef Full Text | Google Scholar

Stark, E., Eichler, R., Roux, L., Fujisawa, S., Rotstein, H. G., and Buzsáki, G. (2013). Inhibition-induced Theta resonance in cortical circuits. Neuron 80, 1263–1276. doi: 10.1016/j.neuron.2013.09.033

PubMed Abstract | CrossRef Full Text | Google Scholar

Tateno, T., Harsch, A., and Robinson, H. P. C. (2004). Threshold firing frequency-current relationships of neurons in rat somatosensory cortex: type 1 and type 2 dynamics. J. Neurophysiol. 92, 2283–2294. doi: 10.1152/jn.00109.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Tikidji-Hamburyan, R. A., Martinez, J. J., White, J. A., and Canavier, C. C. (2015). Resonant interneurons can increase robustness of Gamma oscillations. J. Neurosci. 35, 15682–15695. doi: 10.1523/JNEUROSCI.2601-15.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsuji, S., Ueta, T., Kawakami, H., Fujii, H., and Aihara, K. (2007). Bifurcations in two-dimensional Hindmarsh-Rose type model. Int. J. Bifurcat. Chaos 17, 985–998. doi: 10.1142/S0218127407017707

CrossRef Full Text | Google Scholar

Tsumoto, K., Kitajima, H., Yoshinaga, T., Aihara, K., and Kawakami, H. (2006). Bifurcations in Morris-Lecar neuron model. Neurocomputing 69, 293–316. doi: 10.1016/j.neucom.2005.03.006

CrossRef Full Text | Google Scholar

Tzounopoulos, T., and Kraus, N. (2009). Learning to encode timing: mechanisms of plasticity in the Auditory brainstem. Neuron 62, 463–469. doi: 10.1016/j.neuron.2009.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Varga, V., Hangya, B., Kranitz, K., Ludanyi, A., Zemankovics, R., Katona, I., et al. (2008). The presence of pacemaker HCN channels identifies Theta rhythmic GABAergic neurons in the medial septum. J. Physiol. 586, 3893–3915. doi: 10.1113/jphysiol.2008.155242

PubMed Abstract | CrossRef Full Text | Google Scholar

Vazifehkhah, G. B., Kouhnavard, M., Aihara, T., and Kitajima, T. (2015). Mathematical modeling of subthreshold resonant properties in Pyloric Dilator neurons. Biomed Res. Int. 2015:135787. doi: 10.1155/2015/135787

CrossRef Full Text | Google Scholar

Vida, I., Bartos, M., and Jonas, P. (2006). Shunting inhibition improves robustness of Gamma oscillations in hippocampal interneuron networks by homogenizing firing rates. Neuron 49, 107–117. doi: 10.1016/j.neuron.2005.11.036

PubMed Abstract | CrossRef Full Text | Google Scholar

Wahl-Schott, C., and Biel, M. (2009). HCN channels: structure, cellular regulation and physiological function. Cell. Mol. Life Sci. 66, 470–494. doi: 10.1007/s00018-008-8525-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X. J. (2002). Pacemaker neurons for the Theta rhythm and their synchronization in the septohippocampal reciprocal loop. J. Neurophysiol. 87, 889–900. doi: 10.1152/jn.00135.2001

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, K., Maidana, J. P., Caviedes, M., Quero, D., Aguirre, P., and Orio, P. (2017). Hyperpolarization-activated current induces period-doubling cascades and chaos in a cold thermoreceptor model. Front. Comput. Neurosci. 11:12. doi: 10.3389/fncom.2017.00012

PubMed Abstract | CrossRef Full Text | Google Scholar

Yi, G. S., Wang, J., Tsang, K. M., Wei, X. L., and Deng, B. (2015). Input-output relation and energy efficiency in the neuron with different spike threshold dynamics. Front. Comput. Neurosci. 9:62. doi: 10.3389/fncom.2015.00062

PubMed Abstract | CrossRef Full Text | Google Scholar

Zemankovics, R., Kali, S., Paulsen, O., Freund, T. F., and Hajos, N. (2010). Differences in subthreshold resonance of hippocampal pyramidal cells and interneurons: the role of h-current and passive membrane characteristics. J. Physiol. 588, 2109–2132. doi: 10.1113/jphysiol.2009.185975

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Z. G., and Gu, H. G. (2017). Transitions between classes of neuronal excitability and bifurcations induced by autapse. Sci. Rep. 7:6760. doi: 10.1038/s41598-017-07051-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Z. G., Jia, B., and Gu, H. G. (2016). Bifurcations and enhancement of neuronal firing induced by negative feedback. Nonlinear Dyn. 86, 1549–1560. doi: 10.1007/s11071-016-2976-x

CrossRef Full Text | Google Scholar