- 1Computational Neuroscience and Neural Engineering (CNET) Research Team, Intelligent Systems Research Centre, Ulster University, Derry, United Kingdom
- 2Neural Systems and Neurotechnology Research Team, Intelligent Systems Research Centre, Ulster University, Derry, United Kingdom
- 3Department of Electrical Engineering and Electronics, University of Liverpool, Liverpool, United Kingdom
- 4Reading School of Pharmacy, University of Reading, Reading, United Kingdom
- 5Faculty of Biology, Medicine and Health, University of Manchester, Manchester, United Kingdom
- 6Achucarro Center for Neuroscience, IKERBASQUE, Basque Foundation for Science, Bilbao, Spain
It has recently been proposed using a multi-compartmental mathematical model that negatively fixed charged membrane-associated sites constrain the flow of cations in perisynaptic astroglial processes. This restricted movement of ions between the perisynaptic cradle (PsC), principal astroglial processes and the astrocyte soma gives rise to potassium (K+) and sodium (Na+) microdomains at the PsC. The present paper extends the above model to demonstrate that the formation of an Na+ microdomain can reverse the Na+/Ca2+ exchanger (NCX) thus providing an additional source of calcium (Ca2+) at the PsC. Results presented clearly show that reversal of the Na+/Ca2+ exchanger is instigated by a glutamate transporter coupled increase in concentration of cytoplasmic [Na+]i at the PsC, which and instigates Ca2+ influx through the NCX. As the flow of Ca2+ along the astrocyte process and away from the PsC is also constrained by Ca2+ binding proteins, then a Ca2+ microdomain forms at the PsC. The paper also serves to demonstrate that the EAAT, NKA, and NCX represent the minimal requirement necessary and sufficient for the development of a Ca2+ microdomain and that these mechanisms directly link neuronal activity and glutamate release to the formation of localized Na+ and Ca2+ microdomains signals at the PsC. This local source of Ca2+ can provide a previously underexplored form of astroglial Ca2+ signaling.
Introduction
The concept of astroglial ionic excitability was established in 1990s following the discovery of calcium ion (Ca2+) signaling and propagating Ca2+ waves in astrocytes in vitro and in situ (Cornell-Bell et al., 1990; Cornell-Bell and Finkbeiner, 1991; Dani et al., 1992; Verkhratsky et al., 1998). Initially, astroglial excitability has been thought to be mediated by Ca2+ ions; subsequent years have demonstrated signaling roles for sodium (Na+) (Kirischuk et al., 2012; Parpura and Verkhratsky, 2012; Rose and Chatton, 2016; Rose and Verkhratsky, 2016) and chloride (Cl−) (Wilson and Mongin, 2018) while a signaling role for potassium (K+) has also begun to be considered (Breslin et al., 2018), see also (Verkhratsky and Nedergaard, 2018). Ionic signaling in astrocytes serves several physiological roles, in particular, coupling neuronal activity with astroglial homeostatic response within the confines of the astroglial cradle that enwraps at least 50% of all synapses in the central nervous system (Verkhratsky and Nedergaard, 2014, 2018; Rose and Verkhratsky, 2016). Astrocytes express elaborate molecular machinery controlling sodium (Na+) homeostasis and allowing transient intracellular Na+ increases in response to physiological activity in neuronal networks (Kirischuk et al., 2012; Rose and Verkhratsky, 2016). The Na+ signals localized to perisynaptic astroglial processes regulate the activity of numerous plasmalemmal transporters responsible for a glutamine-glutamate (GABA) astroglial-neuronal shuttle, for K+ buffering, for regulation of pH and for cellular metabolism as well as for secretion of reactive oxygen species scavengers and various neuroactive molecules (Rose and Verkhratsky, 2016; Verkhratsky and Nedergaard, 2016, 2018). Cytoplasmic Na+ dynamics are therefore directly linked to the functional activity of astrocytes and represent a mechanism for fast and local signaling at the single synapse/perisynaptic process level. Although cytosolic Na+ has emerged as a prominent ion at the interface between signaling and metabolic pathways (Chatton et al., 2016), the spatiotemporal organization of cytosolic Na+ dynamics is far from being fully characterized. Additionally, pathways that serve to trigger Na+ and K+ microdomains need to be resolved.
Computational modeling of astrocyte-neurone interaction is essential for the understanding of the transport processes between cells. However, models of ionic signaling in astrocytes still have some way to go if they are to fully capture the complex morphology of astrocytic processes seen in vivo. Some of these models focus on changes of ionic fluxes crossing the astrocyte membrane controlled by pumps and exchangers, for example Na+/K+ pump (NKA) and Na+/Ca2+ exchanger, (NCX) and K+, Na+ and Cl− channels as well as axial fluxes of ions in the intracellular space (Halnes et al., 2013). This electro-diffusive model allows channels to be distributed in different ways while gating parameters can be altered to match experimental data. Intercellular Ca2+ waves and oscillations in astrocytes (Pasti et al., 1997; Wade et al., 2011, 2012; Naeem et al., 2015) have also been modeled to identify potential mechanisms of neurone to astrocyte intracellular intercellular signaling.
Astrocytic Na+ Signaling
The major contributors to astrocyte Na+ homeostasis and signaling are the NKA, NCX and the sodium-dependent glutamate transporters (EAAT1 and EAAT2). The NKA regulates resting Na+ concentration in the cytosol ([Na+]i) and expels excess Na+ that enters astrocytes during periods of neuronal activity, whereas glutamate transporters are responsible for the bulk of Na+ influx into astrocytes accompanying glutamatergic synaptic transmission (Kirischuk et al., 2007; Rose and Karus, 2013; Rose and Verkhratsky, 2016). The NKA, NCX, and glutamate transporters co-localize in astrocytic perisynaptic processes (Minelli et al., 2007; Melone et al., 2018), suggesting their functional coupling.
All three subunits of NCX (NCX1/SLC8A1, NCX2/SLC8A2, and NCX3/SLC8A3) are expressed in astroglia, with NCX1/SLC8A1 being the predominant isoform (Pappalardo et al., 2014; Verkhratsky and Nedergaard, 2018). The stoichiometry of astroglial NCX is 3Na+:1Ca2+, and hence the equilibrium potential can be calculated from Nernst equation: ENCX = (nENa−2ECa)/(n−2) where n is a stoichiometry of Na+, and ENa and ECa are equilibrium potentials of Na+ and Ca2+, respectively. Assuming [Ca2+]i of 50–80 nM and [Na+]i of 15 mM, the ENCX could be as negative as ~−85 to −90 mV, in a similar range to measured resting membrane potential values of astrocytes (Verkhratsky and Nedergaard, 2018). As a result the NCX is prone to fluctuate between forward and reverse transport depending on actual changes in [Ca2+]i and [Na+]i and the astroglial membrane potential (Vm). Conceptually, depolarization or an increase in [Na+]i will favor NCX operation in the reverse mode, whereas an increase in [Ca2+]i promotes the forward mode of the exchanger. In this way NCX can regulate both Ca2+ and Na+ signals, being relevant in shaping ionic signals in astroglial PsCs.
Recently we presented a new hypothesis (Breslin et al., 2018), which addressed ionic dynamics in thin (<100 nm) perisynaptic processes whereby negatively charged lipids form deep potential wells near the dipole heads restricting the flow of cations along the process. The negative ion foci serve to form “traps” that attract free cytosolic cations forcing them to hop from trap to trap, thus restricting ion propagation along the process and isolating them from the soma. This “ionic retention by traps” can potentially explain the generation of the transient Na+ and K+ microdomains at PsCs. The present paper aims to further develop this model with the inclusion of Ca2+ dynamics at the PsC. We stress here that while this model is not the focus of this paper, it is necessary to include it as it replicates closely the experimentally observed Na+ microdomain in astroglial processes (Langer and Rose, 2009). Furthermore, the model allows us to test the hypothesis that reversal of the NCX, due to the Na+ microdomain, leads to Ca2+ influx and this, coupled with Ca2+ retention along the thin astrocyte process, provides for a plausible mechanism for the generation of a Ca2+ microdomain at the PsC. Moreover, as this source of Ca2+ is remote from any endoplasmic reticulum (ER) mediated Ca2+ release, we propose that this local source of Ca2+ may provide a previously under-explored form of astrocyte Ca2+ signaling.
Model
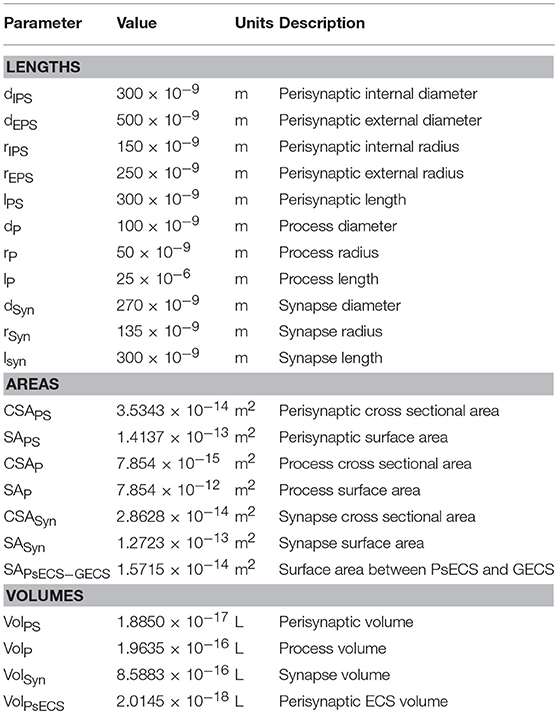
It was proposed in our earlier paper (Breslin et al., 2018) that Na+ and K+ retention occurs in thin astrocyte processes. In this paper we consider Ca2+ retention along the thin processes. This Ca2+ retention is captured using an extended form of the multi-compartmental mathematical model described in Breslin et al. (2018). The model consists of a single synapse surrounded by an astrocytic PsC. Due to the complexity of neuronal/astrocytic morphology (Xu-Friedman et al., 2001; Witcher et al., 2007; Lushnikova et al., 2009; Patrushev et al., 2013), this simplified cylindrical compartmental model (Breslin et al., 2018) simplifies the highly complex structures and the associated computational overheads, whilst retaining sufficient functionality to produce meaningful observations. All necessary dimensional details of the model can be found in Table 1. Figure 1 provides details of the multi-compartmental model described by Breslin et al. (2018).
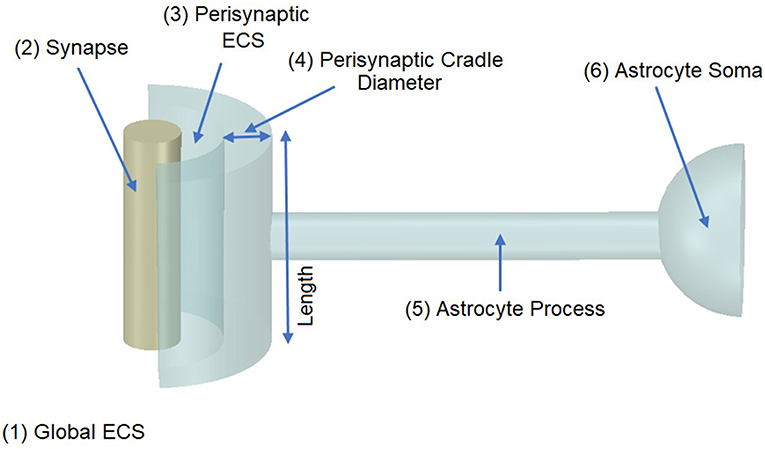
Figure 1. Model Morphology. The model consists of a single synapse enwrapped by a single astrocyte. In total there are six compartments, (1) Global Extracellular Space (GECS), (2) Synapse, (3) Perisynaptic Extracellular Space (PsECS), (4) Perisynaptic Cradle, (5) Astrocyte Process, and (6) Astrocyte Soma. Each compartment is modeled as a cylindrical structure except the GECS and soma, which are deemed dimensionless because ionic concentrations remain constant within these compartments (Breslin et al., 2018).
In the previous study (Breslin et al., 2018), K+ and Na+ were modeled to determine their influence on ion retention in the thin astrocyte process. In the current study, we adapt this model to include Ca2+ dynamics within the astrocyte PsC and extracellular space. From Figure 2, it can be seen that the synapse and PsC contain a number of ionic channels, exchangers and pumps to provide homeostasis and dynamic exchange of ions between the two cells and extracellular space.
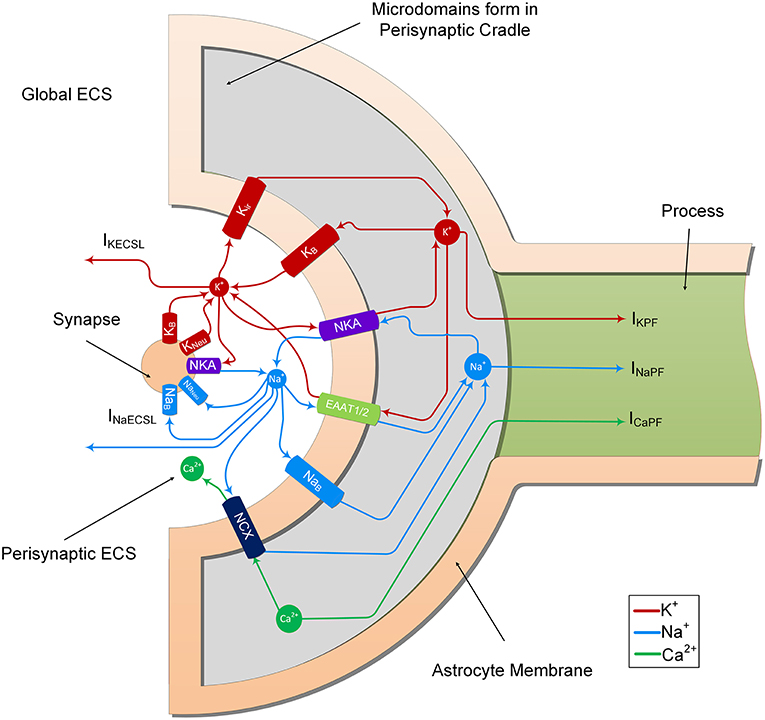
Figure 2. Ion transport machinery of the perisynaptic cradle and synapse. The model consists of 11 ionic transports. The synapse contains 5 ionic transports for Na+ and K+; NKA is the sodium/potassium pump which extrudes 3 Na+ ions for every 2 K+ ions it imports, Naneu and Kneu which are the voltage gated sodium and potassium channels of the Hodgkin and Huxley model and NaB and KB which are lump models of all the other Na+ and K+ channels. The astrocyte contains 6 channels on the inside surface area (facing the synapse) of the perisynaptic cradle; Kir is an inward rectifying K+ channel, NKA is a sodium potassium pump similar to that found on the synapse, EAAT1/2 represents the EAAT glutamate transport which is sensitive to glutamate in the synaptic cleft. This transport cotransports 3 Na+ ions with every glutamate ion and counter transports 1 K+ ion. Since this work does not consider changes in synaptic and perisynaptic glutamate changes the glutamate ion is not shown in the figure. Moreover, the EAAT dependency on H+ is also ignored. The NCX represents the sodium/calcium exchanger which exchanges 3 Na+ ions for every 1 Ca2+ ion across the membrane. At resting conditions there is a very small exchange in the forward direction as noted in the diagram. This can be reversed under physiological increase of perisynaptic Na+ concentration. Finally, the NaB and KB are lumped models of all other Na+ and K+ ionic transports, respectively. The currents IKECSL and INaECSL represent leak currents of K+ and Na+, respectively from the Perisynaptic Extracellular Space (ECS) to the global ECS. It is worth nothing that the currents IKPF, INaPF, and ICaPF represent the currents of the 3 ions under consideration from the perisynaptic cradle along the process. As described in Breslin et al. (2018), these currents model the hypothesized well-hopping mechanism which severely restricts current flow of these ions along thin processes. This results in the trapping of these ions in the perisynaptic cradle as they are imported across the membrane. Since our model assumes a well-mixed compartment, we consider these trapped ions as a microdomain formation in the perisynaptic cradle.
The neurone exchanges K+ and Na+ with the PsECS via a voltage-gated potassium channel (KNeu), voltage-gated sodium channel (NaNeu), a sodium potassium pump (NKANeu), a potassium background channel (KB on the synapse), and a sodium background channel (NaB on the synapse). The astrocyte exchanges Na+, K+, and Ca2+ with the PsECS via a background sodium transport (NaB on the astrocyte), potassium background transport (KB on the astrocyte), potassium inwardly rectifying channel (Kir), sodium-potassium-ATPase (NKA), a glutamate-sodium-potassium-proton antiporter (EAAT1/2), and the NCX. In both the astrocyte and neurone models, we define Na+ and K+ background channels; although modeled as a single transport channel for each ion, these background channels represent a lumped model for Na+ and K+ transport, taking into account a multitude of influx and efflux pathways. IKPF, INaPF, and ICaPF model the flow of K+, Na+, and Ca2+ ions along the astrocytic process to the soma. IKECSL and INaECSL models the K+ and Na+ ionic flow generated by K+ and Na+ leaking from the PsECS to the GECS. The mathematical descriptions of ionic exchanges between a neurone and astrocyte at the PsC are now presented. For a more detailed description refer to Breslin et al. (2018).
Astrocyte Model
Membrane Potential and Ion Concentrations
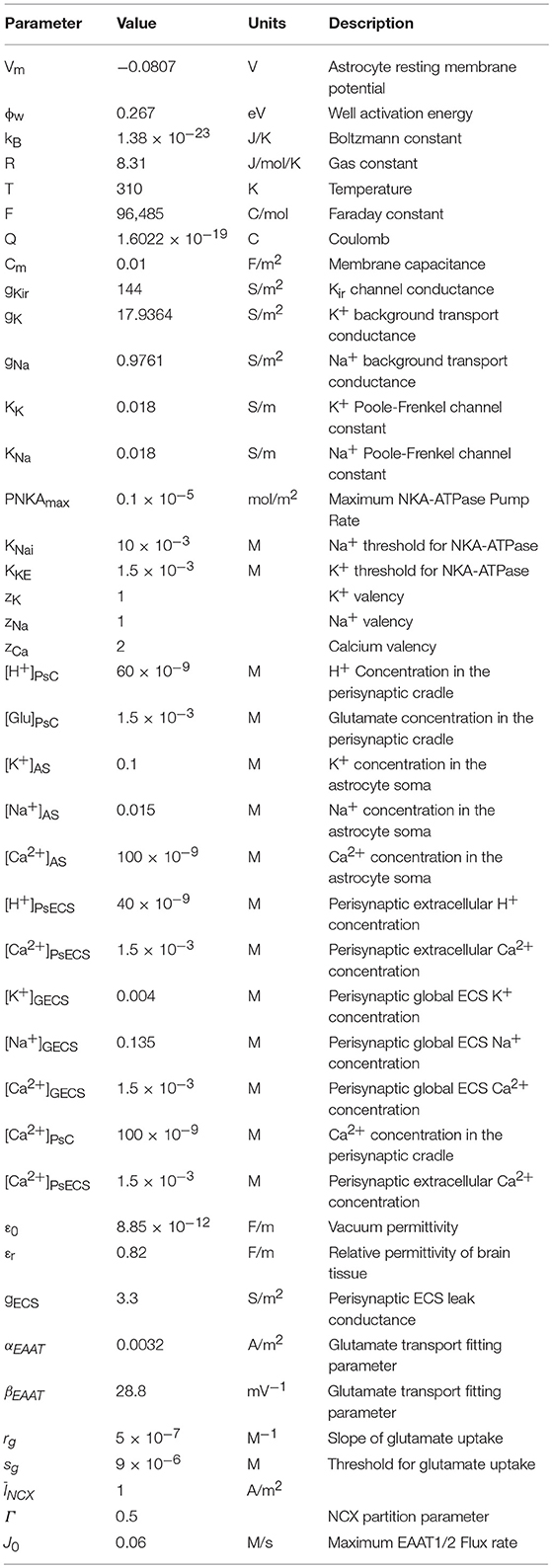
In this model the astrocyte resting membrane potential is taken as ~−80 mV, which is widely reported as the resting membrane potential for astrocytes (Verkhratsky and Nedergaard, 2018). We also assume that isopotentiality is preserved in the PsC as is the case for the astroglial syncytium (Kofuji and Newman, 2004), therefore the astrocyte membrane potential remains fixed at ~−80 mV.
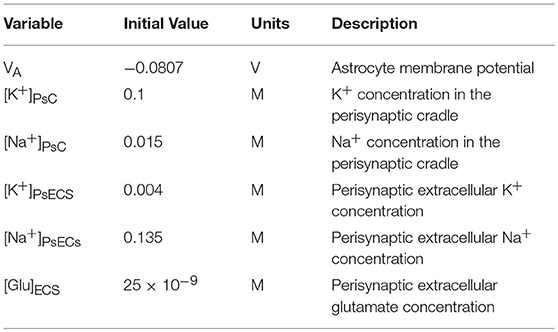
The perisynaptic model described by Breslin et al. (2018) comprises five compartments, namely PsC, PsECS, GECS, and the astrocyte process and soma. The astrocyte process is modeled as a long thin cylindrical channel that restricts the flow of cations along the process within the channel due to ion retention. In this work, each of these compartments contains three ionic concentrations, K+, Na+, and Ca2+. All channels, exchangers and transporters permeable to these ions reside on the PsC. The kinetic equations for the changes of ionic concentration of each of these ions is given below. Note: zxFVoly is used to convert the total ionic current of ion x into a concentration for the volume y, where zx is the valency of ion x, F is Faradays constant, and Voly is the volume of compartment y. All initial conditions and parameters for this model are described in Tables 2, 3, respectively. The change in PsC K+ concentration ([K+]PsC) in the PsC is given by:
where IKir is the Kir channel current, IKNKA is the K+ current through the astrocyte NKA, IKEAAT is the K+ current created by the glutamate transporter and IKPF is the K+ current flowing along the astrocyte process. K+ changes in the PsECS ([K+]PsECS) is given by:
where IKECSL is current due to K+ leakage from the PsECS to the GECS, IKNeu is the K+ current from the neurone, and IKm is the total K+ current flowing through the astrocyte membrane. K+ is held constant at baseline in the GECS and astrocyte soma compartments.
Changes in the PsC Na+ concentration ([Na+]PsC) is given by:
where INaB is a current due to Na+ influx across the membrane via Na+ permeable ion channels, this is referred to as background Na+ channel (Breslin et al., 2018), INaNKA is the Na+ dependent current component of the astrocyte NKA, INaEAAT is the Na+ current component of the glutamate transporter, INaNCX is the Na+ current component of the NCX and INaPF is the Na+ current flowing in the astrocyte process. [Na+] changes in the PsECS ([Na+]PsECS) is given by:
where INaECSL is current due to Na+ leakage from the PsECS to the GECS, INaNeu is the Na+ current from the neurone and INam is the total Na+ current flowing through the astrocyte membrane. Na+ is held constant at baseline in the GECS and astrocyte soma compartments.
Changes in the PsC Ca2+ concentration ([Ca+]PsC) is given by:
where ICaNCX is the Ca2+ dependent current component of the NCX, and ICaPF is the Ca2+ current flowing in the astrocyte process. [Ca2+] changes in all other compartments are not considered and remain constant at baseline.
Glutamate Transporter (EAAT1/2)
Glutamate released into the extracellular PsECS in the course of neurotransmission is assumed here to be entirely removed by astrocytic EAAT1/2. A transport cycle involves the co-transport of 3 Na+ and 1 H+ with 1 glutamate and counter-transport of 1 K+ (Grewer et al., 2014; Murphy-Royal et al., 2015). EAAT1/2 proteins are trafficked to the plasma membrane to facilitate the rapid removal (~3 ms) of glutamate from the cleft. Glutamate bound to these proteins is then transported to the astrocytic cytosol over a longer period: in this work a complete transport cycle is assumed to be 30 ms (Otis and Kavanaugh, 2000; Zhou and Danbolt, 2013). Existing EAAT mathematical formulations do not capture adequately this rapid binding and slow release function and therefore in this work we adopt a different approach. To model the stoichiometry and cycle rate we assume that initially a release of glutamate instantaneously binds to membrane-bound proteins and thereafter the flux of Na+ through the EAAT transporter pore follows an exponentially decaying rate given by:
where JNaEAAT is the flux rate of Na+ through the EAAT1/2, Jo is the max flux rate through the transporter, δ is the Dirac Delta function, t is time, and tsp is the previous neuronal spike time. In our model we view the membrane as a capacitor charged with bound glutamate and JNaEAAT as a discharging flux.
The Na+ current through the transporter can be calculated by:
where JNAEAAT is the Na+ flux through the EAAT co-transporter, zNa is the valency of Na+, F is the Faradays Constant, VolPsECS is the volume of the perisynaptic ECS, and SAPsC is the surface area of the PsC.
The associated K+ current through the transporter is given by:
Note that we are not considering glutamate transport to the astrocytic cytosol as we are only interested in Na+, K+, and Ca2+ dynamics. Additionally, our model for EAAT1/2 transport would need further consideration to include the dependency of fluxes on intra and extra cellular ionic concentrations.
Sodium Calcium Exchanger (NCX)
The NCX is a reversible antiporter which uses the electrochemical gradient of Na+ to exchange 3 Na+ ions for 1 Ca2+ ion across the membrane. Depending on the membrane potential and transmembrane Na+ gradient, the transporter operates either in forward mode (Na+ is transported into the cell while Ca2+ is extruded) or in the reversed mode (providing for influx of Ca2+ and efflux of Na+) (Jeffs et al., 2007).
The Na+ current component of the transporter is given by Gabbiani and Cox (2010):
where is the NCX exchanger conductance and γ is a partition parameter.
The Ca2+ current component is given by:
Leakage From Perisynaptic ECS to Global ECS
The diffusion of K+ and Na+ between the PsECS and the GECS is modeled as a simple electrochemical gradient controlled channel in which a zero extracellular potential is assumed and is given by:
where i is the ion under consideration, giECS is the conductance of the channel, SAECSL is the surface area between the PsECS and the GECS, and EiECS is the Nernst like potential of the channel given by:
Astrocyte Process Ionic Transport Model
Breslin et al. (2018) proposed that ion retention within thin astrocyte processes can give rise to the formation of K+ and Na+ microdomains at the PsC. This localization of astroglial ionic microdomains arises because in thin processes, surface conduction dominates over volume conduction, and because membrane lipids are negatively charged, deep potential wells form near the dipole heads restricting the flow of cations along the process. Therefore, cations must hop from well to well which restricts ion conduction along the membrane. This hopping effectively semi-isolates the PsC from the astrocytic main body allowing the formation of K+ and Na+ microdomains at the PsC under different conditions.
Breslin et al. (2018) proposed that the current flow IiPF (see Figure 2) through the thin process, due to ionic hopping can be represented as:
where K is a constant which represents mobility and concentration of mobile ions, Vm is the resting membrane potential of the astrocyte, ϕw is the well activation energy or potential barrier to ion flow, l is the length of the process, Q is the charge on a single ion taken as the charge on an electron, T is the absolute temperature, CSAP is the cross-sectional area of the process, ϵ is the dynamic permittivity and is given by ϵ = ϵ0 ϵr, where ϵ0 is the absolute permittivity, and ϵr is the relative permittivity of the cytoplasm, and kB is the Boltzmann constant.
The concentrations of K+, Na+, and Ca2+ in the astrocyte soma are held constant but will be continuously changing at the PsC thus establishing a dynamic concentration gradient associated with these cations. Consequently, we formulate a Nernst-like reversal potential for Na+, K+, and Ca2+ between the astrocyte soma (AS) and the PsC as:
where i is the ion under consideration. A more in-depth discussion and assumptions of the full ionic transport mechanism along thin astrocyte processes is given in Breslin et al. (2018).
Neurone Model
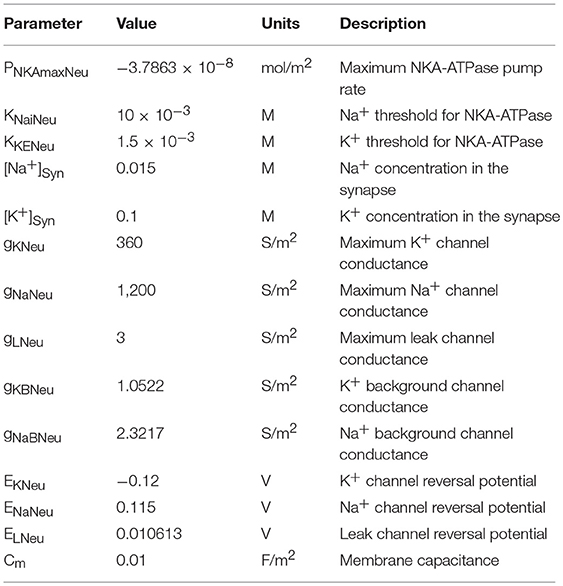
The neuronal model utilized in this work consists of the biophysical Hodgkin and Huxley (HH) type model described in Breslin et al. (2018) with the addition of a voltage-gated Na+ channel, K+ background channel and an Na+ background channel. These background channels reflect implicit influx/efflux pathways, necessary for the system to ensure dynamic equilibrium. All parameter values for the neurone model are described in Table 4. For reasons of simplicity, the internal concentrations of neurone Na+ and K+ remain constant. Whilst we recognize that the neuron NKA is driven by internal Na+ and astrocyte NKA is driven by external K+, as we are not considering internal neurone Na+ concentration change, we apply the same NKA model for each, altering the maximum pump rates accordingly.
Voltage-Gated Neuronal Sodium Channel (NaNeu)
The HH model simulates current flow of Na+ through a voltage-gated channel, therefore the current flow of Na+ from the neurone can be modeled as:
where gNaNeu is the maximum Na+ channel conductance, ENaNeu is the reversal potential of the sodium channel, VNeu is the membrane voltage of the neurone, and SAsyn is the surface area of the synapse.
Neuronal Background Ion Channels (NaB/KB)
In this model, there are two individual background ion channels for Na+ and K+. These channels use the electrochemical gradient between the PsC and ECS, resulting in an influx of Na+ and efflux of K+ under normal physiological conditions. They were modeled as a simple passive electrochemical gradient dependent channel given by Sterratt et al. (2011):
where i is the ion under consideration, giBNeu is the channel conductance. Note: the value of giNBeu is chosen in such a way that the total flux of ion i = 0 at steady state. Vneu is the neurone membrane voltage, SASyn is the surface area of the neuronal synapse, and Ei is the channel Nernst potential and is given by:
Note that the concentrations of K+ and Na+ within the neuronal synapse are held at baseline.
The complete astrocyte/neurone model was implemented using Matlab 2015b 64-bit (Windows version) by Mathworks. All simulation results presented in the results section of this paper used the forward Euler method of integration with a fixed time step of Δt = 10μs.
Results
This section reports the outcomes of a series of simulations that demonstrate the formation of a Ca2+ microdomain at the PsC. The simulations show that the Ca2+ microdomain is a direct result of ion retention along the thin astrocyte process. We have shown in a recent paper (Breslin et al., 2018) that ion retention underpins Na+ and K+ microdomain formation at the PsC during physiological neuronal excitation. In this work we show that the uptake of Na+, via EAAT channels during neuronal stimulus, creates the Na+ microdomain in the PsC thereby causing the NCX to reverse with subsequent formation of a Ca2+ microdomain in the PsC.
NCX Reversal Under Physiological Stimulation
To explore the reversal of the astrocyte NCX, a series of simulations were carried out with the presynaptic neurone stimulated using an external current to produce firing rates of 10, 20, and 30 Hz, respectively. The neuronal stimulus has a duration of ~1 min where the first 0.1 min allows the model to reach a steady state condition and the stimulus ceases after 1 min. This long stimulus period allows investigation of what effect sustained neural activity has on the intracellular/extracellular ionic concentrations. In these simulations PsECS Ca2+ is held constant at baseline, however K+ and Na+ are permitted to change via the neurone and astrocyte K+ and Na+ channels. Each time the neurone spikes, it is assumed that there is 1 mM of glutamate released into the PsC and there are enough EAAT1/2 transports which allow the instantaneous binding of all the extra glutamate. Therefore, the extracellular glutamate concentration always remains at baseline concentration. Furthermore, the maximum flux rate of EAAT1/2 (J0) is tuned such that 3 mM of Na+ is taken up from the PsECs and 1 mM of K+ is released into the PsECS by the EAAT1/2 over a period of 30 ms. Moreover, the astrocyte membrane voltage is held constant at ~-80 mV, in line with reported resting membrane potential for astrocytes, which incidentally is close to the reversal potential for the NCX. Therefore, during periods of homeostatic rest there is no net flow of Ca2+ or Na+ across the membrane associated with the NCX.
The results presented in Figure 3A show that during periods of neural stimulus, K+ ions released by the neurone, build up in the PsECS and are cleared by the astrocyte, which results in a K+ microdomain formation at the PsC (Figure 3B). At the start of the neuronal stimulation, there is a transient loss of Na+ from the PsECS (Figure 3C), due to neuronal depolarization and astrocytic EAAT transport. Furthermore, the transport of Na+ across the astrocyte membrane via Na+ background channels and EAAT transporters results in a Na+ microdomain formation (Figure 3D).
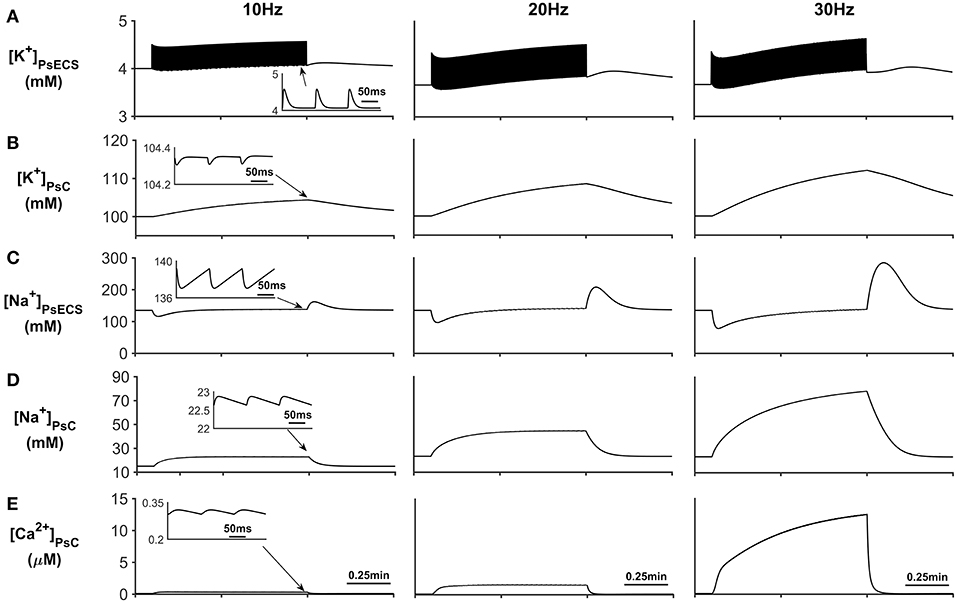
Figure 3. Astrocyte PsC ion concentrations. (A) [K+]PsECS transient. (B) [K+]PsC transient. (C) [Na+]PsECS transient. (D) [Na+]PsC transient. (E) [Ca2+]PsC transient. During periods of neuronal activity, increased [K+]PsECS is cleared by the astrocyte leading to a microdomain of K+ in the PsC. Moreover, due to the influx of Na+ predominantly via EAAT channels there is an increase in [Na+] PsC, resulting in the reversal of the NCX and Ca2+ microdomain formation. The inserts within (A–E) show the fast dynamics of the ionic concentration changes within the PsC in response to the neurone activity.
In addition to Na+ and K+ microdomain formation, it is clear from Figure 3E that a local PsC Ca2+ microdomain is also formed. This Ca2+ microdomain is formed even in the absence of an ER: the ER is widely believed to be essential for astrocyte Ca2+ dynamics (Verkhratsky et al., 2012). The microdomain of Ca2+ is caused by the reversal of the NCX causing Ca2+ influx in exchange for astrocytic Na+ efflux. This can be seen in Figure 4C where the only Ca2+ influx pathway in our model is via the NCX, the complete reversal of the NCX is due to the sudden changes in PsC Na+ during neuronal stimulation onset as the astrocyte membrane voltage is held constant.
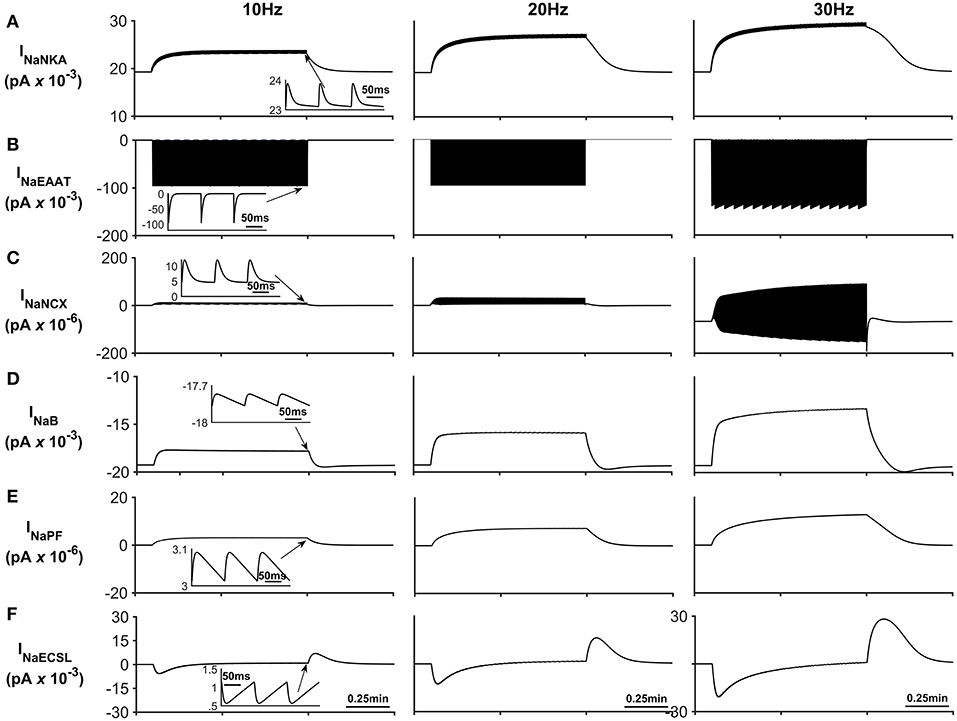
Figure 4. Astrocyte Na+ currents. (A) Na+ NKA current. This current is the main pathway for Na+ efflux from the astrocyte is the NKA while the main pathway for sodium efflux is Na+ current through the EAAT (see (B)) (C) Na+ NCX current. It can be seen that during periods of neurone stimulation, the NCX reverses which results in the efflux of Na+ from the PsC in response to the increased Na+ uptake via the EAAT. (D) Background Na+ current. This represents the uptake of Na+ through a lumped model of all other Na+ channel. The current can be seen to slow down during periods of PsC Na+ increase during neurone stimulus. (E) Na+ current along the process. The current along the process is governed by the well-hopping mechanism described by Breslin et al. (2018) which severely restricts the flow of Na+ from the PsC to the soma. This restriction results in a microdomain of Na+ forming in the PsC compartment as the Na+ cannot simply diffuse along the process. (F) Na+ current due to the leakage of Na+ from the PsECS to the GECS which is purely diffusive. The inserts within (A–F) show the fast dynamics of the currents in response to neurone activity.
Figure 4 presents the Na+ currents associated with the astrocyte. The main pathway for Na+ efflux from the astrocyte is the NKA (Figure 4A) while the main pathway responsible for Na+ uptake is the EAAT (Figure 4B).
The transient loss of Na+, observed in the PsECS (Figure 3C), is caused by the large, transient uptake by EAAT1/2 accompanying glutamate removal following neuronal stimulation, and the EAAT remains active for ~30 ms (Figure 4B). This large, transient, EAAT-derived Na+ flux, compared to the smaller, slower NKA and NaB activating transport rates, tips the transport uptake/release balance in favor of inward transportation and initiates the formation of a Na+ microdomain. As the NKA and NaB uptake increases, due to the increased Na+ concentration in the PsC, the influx/efflux, Na+ pathways tend toward a state of equilibrium and the microdomain of Na+ remains at a stable concentration. It is also noted that as Na+ increases in the PsC that the NCX works in reverse mode to remove Na+ from the PsC. Figures 4E,F show the Na+ currents along the process and between PsECS and GECS, respectively. Since the efflux of Na+ via the process is several orders of magnitude smaller than the other Na+ currents this is the main driving force for the creation of the Na+ microdomain in the PsC. Moreover, as the PsECS Na+ concentration changes, the leak current (INaECSL) between the PsECS and GECS attempts to maintain the Na+ levels in the PsECS.
Figure 5 describes the astrocytic Ca2+ currents; again, it can be seen that during neural stimulation, the influx of Na+ cause the NCX to work in reverse mode and therefore there is an influx of Ca2+ (Figure 5A). The only efflux pathway for Ca2+ considered within the model is via the thin astrocyte process, which is also governed by the well-hopping mechanism described in Breslin et al. (2018) (Figure 5B), Therefore the efflux pathway is much less dominant than the influx pathway which results in a microdomain of Ca2+ forming, as seen in Figure 3E.
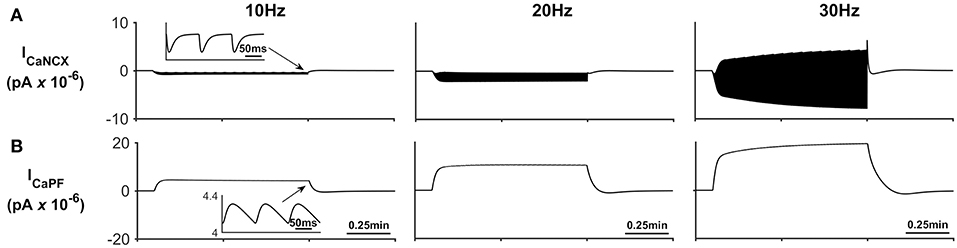
Figure 5. Astrocyte Ca2+ currents. (A) Astrocyte Ca2+ NCX current. During periods of neural stimulation an influx of Na+ via the EAAT1/2 cotransporter results in the reversal of the NCX and thus there is an influx of Ca2+ into the PsC. (B) Ca2+ current along the process. The only efflux pathway within the model is along the process. The current along the process is governed by the well-hopping mechanism described by Breslin et al. (2018) which severely restricts the flow of Ca2+ from the PsC to the soma. This restriction results in a microdomain of Ca2+ forming in the PsC compartment. The inserts within (A,B) show the fast dynamics of the currents in response to neurone activity.
The K+ currents behave in a similar manner as previously described in Breslin et al. (2018). NKA and Kir represent the dominant fluxes of K+ across the astrocytic membrane; NKA is purely responsible for K+ influx whereas Kir is in a constant state of transition between forward (K+ influx) and reverse (K+ efflux) mode during neuronal stimulus (see Figure 6). When neural stimulus ceases, the voltage-dependent reversal of Kir, along with efflux of K+ via the K+ background channel, brings the PsC levels of K+ back to the initial resting state.
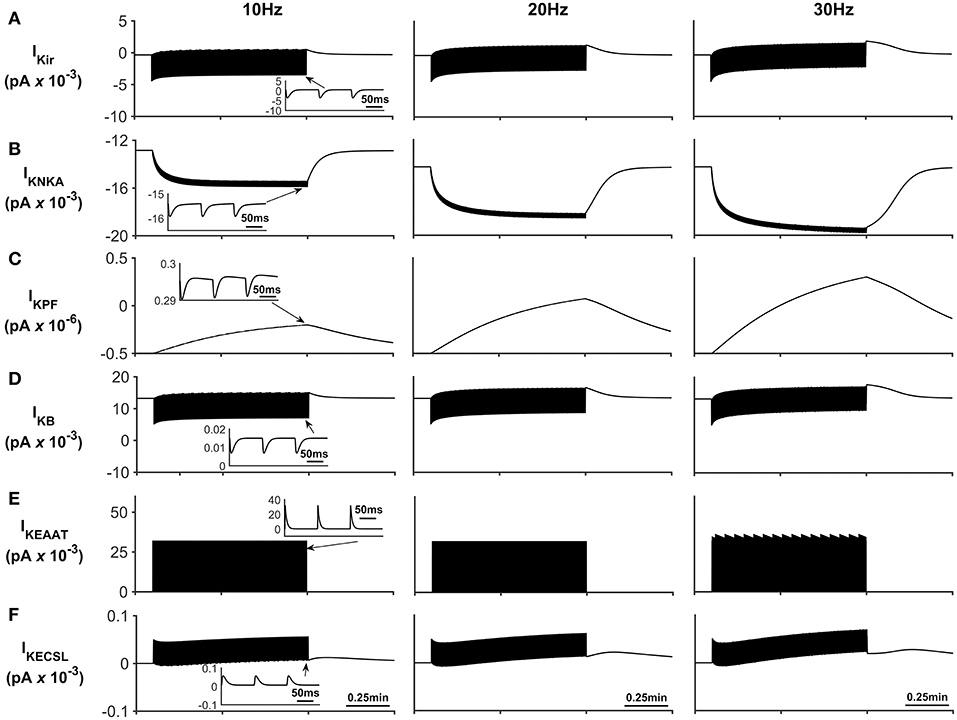
Figure 6. Astrocyte K+ currents. (A) K+ Kir Current. During periods of neurone stimulation the Kir channel will initially uptake K+ before releasing it again at a much slower rate (see insert (A)). (B) K+ NKA current. The rate of NKA increases with neurone stimulation due to the increase of PsECS K+. This current is mainly responsible for the uptake K+ in the PsC. (C) K+ current along the process. Since the current along the process is governed by the well hopping mechanism described by Breslin et al. (2018) it severely restricts the flow of K+ from the PsC to the soma. This restriction results in a microdomain of K+ forming in the PsC compartment as the K+ cannot simply diffuse along the process. Furthermore, K+ is transported across the membrane via background and EAAT K+ currents ((D,E), respectively) much more slowly as these currents are mainly driven by transient K+ fluctuations in the PsECS due to the neurone stimulation; while these currents have a higher peak magnitude, they are much more “spike like in nature” than NKA currents (See inserts (B,D,E)). (F) K+ current due to the leakage of K+ from the PsECS to the GECS which is purely diffusive.
Discussion
Intracellular ionic signaling represents the substrate for glial excitability (Verkhratsky and Nedergaard, 2018). These intracellular signaling events are mediated through spatially and temporally organized fluctuations in the concentration of major ions; there is firm evidence for physiologically relevant Ca2+ and Na+ signaling (Rose and Verkhratsky, 2016; Verkhratsky and Nedergaard, 2018; Verkhratsky et al., 2019), Cl− signaling (Wilson and Mongin, 2018; Verkhratsky et al., 2019), and K+ signaling (Rimmele and Chatton, 2014; Olsen et al., 2015). The formation of localized concentration microdomains is critical for ionic signaling spatial fidelity; while the mechanisms underlying formation of these microdomains remain under debate, a new hypothesis has already been proposed (Breslin et al., 2018). In the CNS, most excitatory synapses are tightly enwrapped by perisynaptic astroglial processes forming the synaptic cradle (Reichenbach et al., 2010; Verkhratsky and Nedergaard, 2014). This structure provides homeostatic control of the synaptic cleft and therefore requires the ability to generate relevant signals in response to neuronal activity. The perisynaptic astroglial compartment is devoid of the ER (Reichenbach et al., 2010), hence excluding the metabotropic pathway for generation of local Ca2+ microdomains. Astrocytes express glutamatergic ionotropic receptors, although the receptor-mediated current density is rather low (with whole cell currents rarely exceeding 10–100 pA), thus limiting the ionic influx (Verkhratsky and Burnstock, 2014; Rusakov, 2015). Astroglial perisynaptic membranes also express high densities of glutamate transporters (EAAT1/2), which couple glutamate transport with substantial Na+ influx (Kirischuk et al., 2007; Langer and Rose, 2009). These transporters are co-localized with NCX (Minelli et al., 2007), which couple Na+ and Ca2+ fluxes in opposite directions. Here we applied the reduced model of PsC to test the hypothesis that glutamate transporters and NCX working together are sufficient to create local Ca2+ microdomains in astroglial perisynaptic cradles.
Our model demonstrates that stimulation of astrocytes with glutamate, mimicking neuronal activity, generates substantial Na+ influx, which forms local microdomains due to the previously suggested mechanism of ion retention, where cation retention in wells dominates over conventional electrochemical diffusion (Breslin et al., 2018; Wade et al., 2018). Moreover, the generation of Ca2+ microdomains has previously been reported, albeit not at the fine process level, but the underlying ionic fluxes (and channels/transporters contributing to) have not been examined (Rusakov, 2015). This computational modeling study has identified the molecular targets and their relative contributions to the formation of a Ca2+ microdomain in the absence of an ER region. Specifically, our model predicts that the generation of a Na+ microdomain switches the NCX into reverse mode, which is sufficient to produce relevant focal Ca2+ signals; while cross-disciplinary research to test this hypothesis is beyond the scope of this paper, we envisage that this work will instigate such a project.
In essence only the EAAT, NKA, and NCX are necessary and sufficient for the development of a Ca2+ microdomain: note that to avoid rapidly increasing Ca2+ concentrations within the cradle, with increasing neuronal frequency, our model would require a Ca2+ efflux pathway, and a likely candidate is the PMCA pump. These mechanisms, which do not depend on intracellular sources for Ca2+, directly link neuronal activity and glutamate release to the formation of Na+ and Ca2+ microdomains in the perisynaptic astroglial processes, instrumental for generation of astroglial homeostatic response, which is critical for maintenance of synaptic transmission.
Author Contributions
JW, LM, AV, MD, SH, HV, BF, and AB contributed to the conception and design of the study. JW and KB developed the software for simulations. JW and BF created all graphics and data visualizations. JW, KB, LM, AV, MD, and AB wrote the first draft of the manuscript. JW, LM, AV, MD, SH, HV, BF, AB, JH, KW-L, and KB contributed to manuscript revision, read and approved the submitted version.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Breslin, K., Wade, J. J., Wong-Lin, K., Harkin, J., Flanagan, B., Van Zalinge, H., et al. (2018). Potassium and sodium microdomains in thin astroglial processes: a computational model study. PLOS Comp. Biol. 14:e1006151. doi: 10.1371/journal.pcbi.1006151
Chatton, J. Y., Magistretti, P. J., and Barros, L. F. (2016). Sodium signaling and astrocyte energy metabolism. Glia 64, 1667–1676. doi: 10.1002/glia.22971
Cornell-Bell, A. H., and Finkbeiner, S. M. (1991). Ca2+ waves in astrocytes. Cell Calcium. 12, 185–204. doi: 10.1016/0143-4160(91)90020-F
Cornell-Bell, A. H., Finkbeiner, S. M., Cooper, M. S., and Smith, S. J. (1990). Glutamate induces calcium waves in cultured astrocytes: long-range glial signaling. Science 247, 470–473. doi: 10.1126/science.1967852
Dani, J. W., Chernjavsky, A., and Smith, S. J. (1992). Neuronal activity triggers calcium waves in hippocampal astrocyte networks. Neuron 8, 429–440. doi: 10.1016/0896-6273(92)90271-E
Grewer, C., Gameiro, A., and Rauen, T. (2014). SLC1 glutamate transporters. Pflug Arch. Eur. J. Phy. 466, 3–24. doi: 10.1007/s00424-013-1397-7
Halnes, G., Østby, I., Pettersen KH Omholt, S. W., and Einevoll, G. T. (2013). Electrodiffusive model of astrocytic and neuronal ion concentration dynamics. PLoS Comput. Biol. 9:e1003386. doi: 10.1371/journal.pcbi.1003386
Jeffs, G. J., Meloni, B. P., Bakker, A. J., and Knuckey, N. W. (2007). The role of Na+/Ca2+ exchanger (NCX) in neurons following ischemia. J. Clini. Neurosci. 14, 507–514. doi: 10.1016/j.jocn.2006.07.013
Kirischuk, S., Kettenmann, H., and Verkhratsky, A. (2007). Membrane currents and cytoplasmic sodium transients generated by glutamate transport in Bergmann glial cells. Pflug Arch. Eur. J. Phy. 454, 245–252. doi: 10.1007/s00424-007-0207-5
Kirischuk, S., Parpura, V., and Verkhratsky, A. (2012). Sodium dynamics: another key to astroglial excitability? Trends Neurosci. 35, 497–506. doi: 10.1016/j.tins.2012.04.003
Kofuji, P., and Newman, E. A. (2004). Potassium buffering in the central nervous system. Neuroscience 129, 1045–1056. doi: 10.1016/j.neuroscience.2004.06.008
Langer, J., and Rose, C. R. (2009). Synaptically induced sodium signals in hippocampal astrocytes in situ. J. Physiol. 587, 5859–5877. doi: 10.1113/jphysiol.2009.182279
Lushnikova, I., Skibo, G., Muller, D., and Nikonenko, I. (2009). Synaptic potentiation induces increased glial coverage of excitatory synapses in CA1 hippocampus. Hippocampus 19, 753–762. doi: 10.1002/hipo.20551
Melone, M., Ciriachi, C., Pietrobon, D., and Conti, F. (2018). Heterogeneity of astrocytic and neuronal GLT-1 at cortical excitatory synapses, as revealed by its colocalization with Na+/K+-ATPase alpha Isoforms. Cereb Cortex. doi: 10.1093/cercor/bhy203. [Epub ahead of print].
Minelli, A., Castaldo, P., Gobbi, P., Salucci, S., Magi, S., and Amoroso, S. (2007). Cellular and subcellular localization of Na+-Ca2+ exchanger protein isoforms, NCX1, NCX2, and NCX3 in cerebral cortex and hippocampus of adult rat. Cell Calcium. 41, 221–234. doi: 10.1016/j.ceca.2006.06.004
Murphy-Royal, C., Dupuis, J. P., Varela, J. A., Panatier, A., Pinson, B., Baufreton, J., et al. (2015). Surface diffusion of astrocytic glutamate transporters shapes synaptic transmission. Nat. Neurosci. 18, 219–226. doi: 10.1038/nn.3901
Naeem, M., McDaid, L., Harkin, J., Wade, J. J., and Marsland, J. (2015). On the role of astroglial syncytia in self-repairing spiking neural networks. IEEE Trans. Neural. Netw. Learn. Syst. 26, 2370–2380. doi: 10.1109/TNNLS.2014.2382334
Olsen, M. L., Khakh, B. S., Skatchkov, S. N., Zhou, M., Lee, C. J., and Rouach, N. (2015). New insights on astrocyte ion channels: critical for homeostasis and neuron-glia signaling. J. Neurosci. 35, 13827–13835. doi: 10.1523/JNEUROSCI.2603-15.2015
Otis, T. S., and Kavanaugh, M. P. (2000). Isolation of current components and partial reaction cycles in the glial glutamate transporter EAAT2. J. Neurosci. 20, 2749–2757. doi: 10.1523/JNEUROSCI.20-08-02749.2000
Pappalardo, L. W., Liu, S., Black, J. A., and Waxman, S. G. (2014). Dynamics of sodium channel Nav1.5 expression in astrocytes in mouse models of multiple sclerosis. Neuroreport 25, 1208–1215. doi: 10.1097/WNR.0000000000000249
Parpura, V., and Verkhratsky, A. (2012). Homeostatic function of astrocytes: Ca(2+) and Na(+) signaling. Transl. Neurosci. 3, 334–344. doi: 10.2478/s13380-012-0040-y
Pasti, L., Volterra, A., Pozzan, T., and Carmignoto, G. (1997). Intracellular calcium oscillations in astrocytes: a highly plastic, bidirectional form of communication between neurons and astrocytes in situ. J. Neurosci. 17, 7817–7830. doi: 10.1523/JNEUROSCI.17-20-07817.1997
Patrushev, I., Nikolay Gavrilov, N., Turlapov, V., and Semyanov, A. (2013). Subcellular location of astrocytic calcium stores favors extrasynaptic neuron-astrocyte communication. Cell Calcium. 54, 343–349. doi: 10.1016/j.ceca.2013.08.003
Reichenbach, A., Derouiche, A., and Kirchhoff, F. (2010). Morphology and dynamics of perisynaptic glia. Brain Res. Rev. 63, 11–25. doi: 10.1016/j.brainresrev.2010.02.003
Rimmele, T. S., and Chatton, J. Y. (2014). A novel optical intracellular imaging approach for potassium dynamics in astrocytes. PLoS ONE 9:e109243. doi: 10.1371/journal.pone.0109243
Rose, C. R., and Chatton, J. Y. (2016). Astrocyte sodium signaling and neuro-metabolic coupling in the brain. Neurosci. 26, 121–134. doi: 10.1016/j.neuroscience.2015.03.002
Rose, C. R., and Karus, C. (2013). Two sides of the same coin: sodium homeostasis and signaling in astrocytes under physiological and pathophysiological conditions. Glia 61, 1191–1205. doi: 10.1002/glia.22492
Rose, C. R., and Verkhratsky, A. (2016). Principles of sodium homeostasis and sodium signaling in astroglia. Glia 64, 1611–1627. doi: 10.1002/glia.22964
Rusakov, D. A. (2015). Disentangling calcium-driven astrocyte physiology. Nat. Rev. Neurosci. 16:226. doi: 10.1038/nrn3878
Sterratt, D., Graham, B., Gillies, A., and Willshaw, D. (2011). Principles of Computational Modelling in Neuroscience, 1st ed. United Kingdom: Cambridge University Press.
Verkhratsky, A., and Burnstock, G. (2014). “Purinergic and glutamatergic receptors on astroglia,” in Glutamate and ATP at the Interface of Metabolism and Signaling in the Brain,eds P. Vladimir , A. Schousboe, and A. Verkhratsky (Cham: Springer), 55–79.
Verkhratsky, A., and Nedergaard, M. (2014). Astroglial cradle in the life of the synapse. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 369:20130595. doi: 10.1098/rstb.2013.0595
Verkhratsky, A., and Nedergaard, M. (2016). The homeostatic astroglia emerges from evolutionary specialization of neural cells. Philos. Trans. R. Soc. Lond. B Biol. Sci. 371:20150428. doi: 10.1098/rstb.2015.0428
Verkhratsky, A., and Nedergaard, M. (2018). Physiology of Astroglia. Physiol. Rev.. 98, 239–389. doi: 10.1152/physrev.00042.2016
Verkhratsky, A., Orkand, R. K., and Kettenmann, H. (1998). Glial calcium: homeostasis and signaling function. Physiol. Rev. 1198, 99–141. doi: 10.1152/physrev.1998.78.1.99
Verkhratsky, A., Rodríguez, J. J., and Parpura, V. (2012). Calcium signaling in astroglia. Mol. Cell. Endocrinol. 353, 45–56. doi: 10.1016/j.mce.2011.08.039
Verkhratsky, A., Untiet, V., and Rose, C. R. (2019). Ionic signalling in astroglia beyond calcium. J Physiol. doi: 10.1113/JP277478. [Epub ahead of print].
Wade, J., Breslin, K., McDaid, L. J., Flanagan, B., Harkin, J., Wong-Lin, K., et al. (2018). “Cation Retention in Membrane Potential Wells: Ionic Microdomain Formation at the Perisynaptic Cradle,” in Abstract from 11th FENS (Federation of European Neuroscience Societies) Forum of Neuroscience, Berlin, Germany.
Wade, J., McDaid, L., Harkin, J., Crunelli, V., and Kelso, S. (2012). Self-repair in a bidirectional coupled astrocyte-neuron (AN) system based on retrograde signaling. Front. Comput. Neurosci. 6:76. doi: 10.3389/fncom.2012.00076
Wade, J. J., McDaid, L. J., Harkin, J., Crunelli, V., and Kelso, J. S. A. (2011). Bidirectional coupling between astrocytes and neurons mediates learning and dynamic coordination in the brain: a multiple modelling approach. PLoS ONE. 6:e29445. doi: 10.1371/journal.pone.0029445
Wilson, C. S., and Mongin, A. A. (2018). The signaling role for chloride in the bidirectional communication between neurons and astrocytes. Neurosci. Lett. 689, 33–44 doi: 10.1016/j.neulet.2018.01.012
Witcher, M. R., Kirov, S. A., and Harris, K. M. (2007). Plasticity of perisynaptic astroglia during synaptogenesis in the mature rat hippocampus. Glia 55, 13–23. doi: 10.1002/glia.20415
Xu-Friedman, M. A., Harris, K. M., and Regehr, W. G. (2001). Three-dimensional comparison of ultrastructural characteristics at depressing and facilitating synapses onto cerebellar Purkinje cells. J Neurosci. 21, 6666–6667. doi: 10.1523/JNEUROSCI.21-17-06666.2001
Keywords: perisynaptic cradle, calcium microdomains, astrocytic process, Na+/Ca2+ exchange, compartment model, glutamate transport, sodium dynamics
Citation: Wade JJ, Breslin K, Wong-Lin K, Harkin J, Flanagan B, Van Zalinge H, Hall S, Dallas M, Bithell A, Verkhratsky A and McDaid L (2019) Calcium Microdomain Formation at the Perisynaptic Cradle Due to NCX Reversal: A Computational Study. Front. Cell. Neurosci. 13:185. doi: 10.3389/fncel.2019.00185
Received: 17 December 2018; Accepted: 12 April 2019;
Published: 07 May 2019.
Edited by:
Sergey M. Korogod, National Academy of Sciences of Ukraine, UkraineReviewed by:
Kalyana Srinivas Vadduri, Redpin Therapeutics Inc., New York, United StatesLeonid Savtchenko, University College London, United Kingdom
Copyright © 2019 Wade, Breslin, Wong-Lin, Harkin, Flanagan, Van Zalinge, Hall, Dallas, Bithell, Verkhratsky and McDaid. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: John Joseph Wade, amoud2FkZUB1bHN0ZXIuYWMudWs=
 John Joseph Wade
John Joseph Wade Kevin Breslin
Kevin Breslin KongFatt Wong-Lin
KongFatt Wong-Lin Jim Harkin
Jim Harkin Bronac Flanagan
Bronac Flanagan Harm Van Zalinge
Harm Van Zalinge Steve Hall
Steve Hall Mark Dallas
Mark Dallas Angela Bithell
Angela Bithell Alexei Verkhratsky
Alexei Verkhratsky Liam McDaid
Liam McDaid