1
Department of Epidemiology and Biostatistics, University of Texas Health Science Center at San Antonio, San Antonio, TX, USA
2
Research Imaging Centre, University of Texas Health Science Center at San Antonio, San Antonio, TX, USA
3
Biology Department and Neurosciences Institute, University of Texas at San Antonio, San Antonio, TX, USA
Using an electrophysiological compartmental model of a Purkinje cell we quantified the contribution of individual active dendritic currents to processing of synaptic activity from granule cells. We used mutual information as a measure to quantify the information from the total excitatory input current (IGlu) encoded in each dendritic current. In this context, each active current was considered an information channel. Our analyses showed that most of the information was encoded by the calcium (ICaP) and calcium activated potassium (IKc) currents. Mutual information between IGlu and ICaP and IKc was sensitive to different levels of excitatory and inhibitory synaptic activity that, at the same time, resulted in the same firing rate at the soma. Since dendritic excitability could be a mechanism to regulate information processing in neurons we quantified the changes in mutual information between IGlu and all Purkinje cell currents as a function of the density of dendritic Ca (gCaP) and Kca (gKc) conductances. We extended our analysis to determine the window of temporal integration of IGlu by ICaP and IKc as a function of channel density and synaptic activity. The window of information integration has a stronger dependence on increasing values of gKc than on gCaP, but at high levels of synaptic stimulation information integration is reduced to a few milliseconds. Overall, our results show that different dendritic conductances differentially encode synaptic activity and that dendritic excitability and the level of synaptic activity regulate the flow of information in dendrites.
The contribution of the passive dendritic properties of neurons on processing of synaptic activity is well established (Rall, 1962a
,b
; Marr, 1969
; Pellionisz and Szentagothai, 1973
, 1974
); however, possibly all central nervous system neurons express voltage sensitive dendritic conductances (Llinas and Yarom, 1981
; Hirst and McLachlan, 1986
; Hockberger et al., 1989
; Huguenard et al., 1989
; Masukawa et al., 1991
; Segev and London, 1999
). Active conductances can carry more current than passive conductances and, thus, have a stronger contribution to the processing and transfer of synaptic activity in dendritic trees (Gollo et al., 2009
). Furthermore, the multiple types of conductances found in dendrites could differentially filter synaptic activity depending on its temporal and spatial distribution (Poirazi and Mel, 2001
; Migliore and Shepherd, 2002
). Unfortunately, the lack of experimental access to determine the distribution and kinetics of active membrane conductances in dendrites has not allowed a thorough study of their influence on processing of synaptic activity.
In order to track the transformation of synaptic activity, and thus obtain a representation of the transfer function of the dendrite, it is necessary to determine how synaptic activity is distributed over different dendritic currents. In many cases the variability observed in dendritic currents is driven by synaptic activity and can be regulated by interactions among conductances. Quantifying the amount of variability due to synaptic activity or due to internal interactions can be done using with statistical tools derived from information theory (Shannon, 1948
; Shannon and Weaver, 1949
; Rieke, 1997
). Particularly, determining mutual information (Foffani and Priori, 2007
; Maffezzoli et al., 2008
; Quian Quiroga and Panzeri, 2009
) between synaptic activity and specific dendritic currents could result in a quantitative method to measure the contribution of individual dendritic currents on synaptic processing (Stemmler and Koch, 1999
; London et al., 2002
). Furthermore, the calculation of the entropy, conditional entropy and mutual information can help elucidate how much variability observed in the dendritic currents is due to the nature of the synaptic input or due to intrinsic properties of the dendrite.
We present the results of calculating mutual information between the net excitatory input and different dendritic currents using a detailed biophysical model of a Purkinje cell (De Schutter and Bower, 1994a
,b
). The model was stimulated with randomly distributed excitatory and inhibitory synapses that resembled granule cell and interneuron activity. We found that the calcium (CaP) and a calcium activated potassium (Kc) currents carried the largest amount of information. While the firing rate of the Purkinje cell remained constant for different combinations of synaptic input, mutual information was sensitive to such changes, thus disambiguating synaptic activity in dendrites. Our results suggest that dendritic excitability modulated by CaP and Kc channels is most effective in regulating the mutual information, and thus any possible processing of that information. Conceptually, our approach treats each dendritic conductance as an information channel that carries a certain amount of information depending on each conductance density. Since plasticity of dendritic excitability might be an important component of general learning and memory mechanisms in neurons (Xu and Kang, 2005
; Komendantov and Ascoli, 2009
), our results provide a method to quantify the effects of such changes on synaptic information processing in individual dendritic conductances.
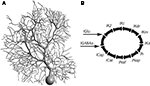
Purkinje Cell Model
We used a previously published Purkinje cell model (De Schutter and Bower, 1994b
,c
) with updated synaptic kinetics (Figure 1
A). Please refer to the cited work for kinetic details of each conductance. In brief, there is one excitatory synaptic contact made with each dendritic spine and 1,695 inhibitory GABAa-type synaptic contacts distributed at random across the dendrites. The model contains the following dendritic conductances (Figure 1
B): two types of Ca channels, a P-type, CaP (Llinas et al., 1989
) and a T-type, CaT (Kaneda et al., 1990
); two types of Ca-activated K+ channels, a BK-type (Latorre et al., 1989
) referred to here as Kc and a K2-type, K2 (Gruol et al., 1991
); and a persistent K+ channel or Km-type (Yamada et al., 1989
). The soma had two types of sodium channels, a fast current, NaF (Hirano and Hagiwara, 1989
) and a slow persistent current, NaP (French et al., 1990
); one type of calcium current T-type; and four types of potassium channels, anomalous rectifier, Ih (Spain et al., 1987
); delayed rectifier, Kdr (Yamada et al., 1989
); persistent potassium, Km; and an A-type potassium channel, KA (Hirano and Hagiwara, 1989
). In depth analysis of the model can be found elsewhere (De Shutter and Bower, 1994a
,b
,c
; Jaeger et al., 1997
; Gundappa-Sulur et al., 1999
; Santamaria et al., 2002
, 2007
Santamaria and Bower, 2005
; De Schutter and Steuber, 2009
). The updated synaptic properties are described in Santamaria et al. (2007)
.
Figure 1. (A) Morphology of the Purkinje cell model. (B) Schematic representation of the channel types incorporated into the Purkinje cell model.
Simulations
The simulations consisted in randomly activating all the excitatory and inhibitory synapses at constant Poisson firing rates. As explained in the Results we used four different combinations of excitatory and inhibitory synaptic activity that resulted in the same firing rate at the soma of the Purkinje cell. We ran simulations for up to 400 s saving the value of all dendritic and synaptic currents every 100 µs. In order to avoid initial condition effects the first 5 s of all traces were not used for the analysis. Simulations were run with a pre-release version of the new GENESIS 3 software
1
. Since each single simulation required about 25 h to complete we used a high performance computing cluster operated by the Computational Biology Initiative at UTSA
2
.
Initial Analysis
In order to simplify the analysis we monitored the total value of the synaptic or dendritic currents. This approximation to the state of dendritic currents has allowed us to analyze this model in detail in the past with testable experimental predictions (Jaeger and Bower, 1999
; Santamaria et al., 2007
). We also chose to use the total excitatory current because then the results of our study could be mapped to dynamic current clamp experiments (see Discussion). We also ran our analysis under two other conditions. In the first one we added all currents over all the dendrites except the thick smooth dendrites (primary). The second condition was adding all the current exclusively in the spiny dendrites (tertiary), without the primary and secondary. The results were practically the same as the ones reported for the summed currents over the entire dendrite, indicating that all the integration is done at the level of tertiary dendrites.
For the purposes of comparing the changes due to background activity we normalized the value of all currents from 1–100 and binned the data in 1000 equally spaced bins. All the analyses described in this paper were performed with the normalized current values.
Initial characterization of currents was done by calculating the histograms under all the different combinations of synaptic activity. Further analysis consisted in calculating the cross-correlation between the excitatory synaptic input (IGlu) and dendritic currents.
Information Theory
Since we wanted to characterize the amount of activity in dendritic currents due to synaptic stimulation we used information theory measurements. This process required calculating the entropy (H) of each current, the conditional entropy between each dendritic current and IGlu, and finally the mutual information (I).
The entropy was calculated as

where p is the probability of seeing value xi.
The conditional entropy is a number that describes the variability of a signal given that the value of a second signal is known. This is a useful measurement when trying to understand the variability of the dendritic currents as a function of the synaptic current. We calculated the conditional entropy as
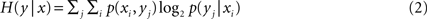
In our case, x is the input signal (IGlu) and y any of the dendritic currents. Conditional probability distributions matrices were calculated based on the binned traces. The conditional probability distributions did not result in distributions that allocated values to every matrix entry. This lack of probability space coverage was due to the biophysical restriction of the particular conductances. Coupling and long time constants also contributed to having areas in the probability density matrix that were densely populated while other remained empty.
Finally, the mutual information was calculated with eq. 3:

The mutual information is usually expressed in bits and gives the capacity of a neuron to discriminate between different stimuli that are part of the stimulus, in this case IGlu. For example, if the mutual information is equal to 5 bits, this means that a particular dendritic current is able to distinguish 25 or 32 different stimuli.
It is well known that the value of I can be biased due to the binning process and finite size of the data being analyzed (Panzeri et al., 2007
). We used a recently developed toolbox in Matlab (Natick, MA, USA) that allows the accurate calculation of the different information measurements and compensation for potential biases (Magri et al., 2009
). Independently of using such compensations we determined that a 400-s simulation was long enough by plotting the value of I for any pair of IGlu and dendritic current as a function of the time window of observation from 5–400 s. This analysis showed that after 300 s the value of I, without bias compensation, reached an asymptotic value (Figure S1 in Supplementary Material). In any case, the value of I can be biased if the joint probability distribution of the two traces being analyzed, for example IGlu and ICaP, is scattered and does not fill out the joint probability space, in our case a matrix of 1000 × 1000 entries. The ratio N/m has been shown to determine the strength of such a bias, where N is the number of non-zero entries in the joint probability distribution and m number of non-zero entries of probability distribution of the stimulus. If N/m is less than 1 then the value obtained from calculating the mutual information is biased. As shown in the supplementary materials all our simulations had an N/m > 1.
The objective of our work was to quantify the contribution of dendritic excitability on information processing in dendrites. For this purpose we used an available Purkinje cell model since this type of cell has extensive dendritic conductances and this particular model has been well validated with experimental data (Jaeger and Bower, 1994
, 1999
; Jaeger et al., 1997
; Santamaria et al., 2007
).
Calcium and Calcium Activated Potassium Channels Carry Most of the Mutual Information in the Purkinje Cell Dendrite
Information in Purkinje cells flows from synapses, to dendrites, to soma (Santamaria et al., 2007
). As opposed to cortical pyramidal cells, Purkinje cells have no backpropagating action potentials that carry somatic activity into the dendrites (Vetter et al., 2001
). Thus, Purkinje cells are ideal to quantify the incremental contribution of dendritic channels to information processing. Since excitatory synapses from parallel fibers to Purkinje cells carry the activity from outside the cerebellum (Bower, 2002
) we assumed this stimulus to be the input signal. We characterized the input signal as the total excitatory current (IGlu) because experimental techniques, such as dynamic current clamp, could be used to test modeling predictions based on this assumption (Suter and Jaeger, 2004
). Purkinje cells in vivo receive excitatory synaptic activity from parallel fiber and inhibitory activity from interneurons; we simulated these types of inputs with random input firing rates drawn from a Poissonian distribution. Firing rates at the soma can be the result of multiple combinations of excitation and inhibition in the dendrite (Santamaria et al., 2002
; Santamaria and Bower, 2005
), for that reason we selected various pairs of uncorrelated background excitatory and inhibitory activity that evoked similar firing rates at the soma. Using different combinations of excitatory and inhibitory input with the same somatic firing rate allowed us to determine information processing changes in dendrites due to different levels of synaptic activity. The background input firing rates spanned a wide range of rates 12–56 Hz and 0.5–2.0 Hz for excitation and inhibition, respectively (Santamaria and Bower, 2005
).
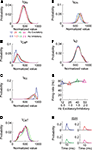
We initially quantified the effects of the random excitatory input on the histogram of values of each dendritic current. For the different combinations of background excitatory and inhibitory input we found that while the histogram of IGlu remained practically unchanged (Figure 2
A) the shape of the distribution of the CaP (ICaP, Figure 2
B) and Kc currents (IKc, Figure 2
C) varied. All other dendritic currents (ICaT, IKm, and IK2) did not show changes in the shape of their distribution as a function of background levels of synaptic stimulation (Figures 2
D–F). We did not analyze INaF, IKdr, IA, INaP, and Ih because they are only present in the soma and the thick proximal dendrite. The mean firing rate (FM), calculated as the number of spikes across the entire simulation divided by the simulation time (400 s) shows that the different combinations of synaptic activity had little influence (90.3 ± 2.4 spikes/s), Figure 2
G, similarly the distributions arising from calculating the inter-spike interval histograms for all combinations of synaptic input (Figure 2
H) differ in less than 1% in the value of their expected value and standard deviation.
Figure 2. Probability distribution of synaptic and dendritic currents. (A) The Purkinje cell model was stimulated with pairs of excitatory and inhibitory synaptic activity. The total excitatory synaptic current (IGlu) remained practically constant for all the combinations of excitatory and inhibitory activity (activity in Hz). (B) Probability distribution of the ICaP in response to the different combinations of excitatory and inhibitory activity in (A). (C) Probability distribution of IKc for the same simulations in (B). (D–F) The probability distribution of the other dendritic currents remained practically independent of level of synaptic activity. (G) The average firing rate at the soma remains constant for all combination of synaptic activity. (H) The Purkinje cell inter-spike distributions for each combination of synaptic activity in (A) have the same mean and standard deviation.
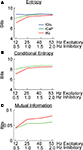
The analysis presented in Figure 2
suggests that most of the changes in background levels of synaptic activity affect the variability of ICaP and IKc. Without synaptic activity the Purkinje cell model is quiescent, thus, the source of the variability observed in the dendritic currents comes from synaptic activity and from interactions among channels. In order to quantify the amount of variability due to IGlu we made use of information theory (Victor, 2000
; Nemenman et al., 2004
; Paninski et al., 2004
; Kennel et al., 2005
). We initially calculated the entropy of IGlu, ICaP and IKc (Figure 3
A). In order to quantify the causal relationship between synaptic activity and dendritic currents we performed the information analysis with a small time lag. Thus, the conditional entropy and mutual information were calculated between the dendritic currents at time t and the glutamate input at a time t−Δt, we assumed Δt to be 1 ms. The analyses show that the entropy of dendritic currents depends on the combination of background activity. The entropy of ICaP increases and reaches the same magnitude as the entropy of IGlu as a function of the frequency of the background synaptic activity. Note that all of our calculations were biased corrected using the Panzeri and Treves method (Magri et al., 2009
). The conditional entropy quantifies the uncertainty in the value of a variable given the known value of another. Calculating the conditional entropy of ICaP and IKc with respect to IGlu shows that the variability in the currents is high (Figure 3
B), suggesting that most of the activity observed is due to intrinsic activity. However, the value of mutual information between ICaP and IKc with respect to IGlu shows an increase in information as a function of level of background level of stimulation (Figure 3
C). The value of mutual information for the other calcium channel (ICaT) was larger (Figure S2 in Supplementary Material) than for ICaP but since must of the current flows through ICaP (Santamaria et al., 2002
) we only analyzed this channel (see Discussion). Overall, the analysis presented in Figures 2 and 3
; Figure S2 in Supplementary Material show that most dendritic currents, except for CaP and KC, are not sensitive to changes in background synaptic activity. The mutual information of Kc with respect to IGlu is larger than for the same measurement done with CaP. However, the ratio of mutual information of these two currents changes as a function of the level of synaptic activity. More interestingly, this differential encoding of the background excitatory information can take place while the somatic firing rate remains constant.
Figure 3. Calculating the amount of excitatory synaptic information being carried by dendritic currents. (A) Entropy of the IGlu, ICaP, and IKc. (B) Conditional entropy of H(ICaP.IGlu) and H(IKc.IGlu). (C) Mutual information for I(ICaP,IGlu) and I(IKc, IGlu) calculated from (A) and (B); e.g. I(ICaP,IGlu) = H(ICaP)−H(ICaP.IGlu). B and C were calculated with a 1 ms time difference between IGlu and the dendritic currents. All calculations were bias corrected using the Panzeri and Treves method.
Temporal Integration Regulated by Synaptic Activity and Dendritic Excitability
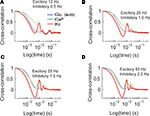
The time constants of activation and inactivation of dendritic conductances imply that information content at one point in time is influenced by past synaptic activity. We characterized these time dependent changes by calculating the cross-correlation of IGlu with ICaP and IKc for all different combinations of excitatory and inhibitory input (Figure 4
). This analysis shows that as the excitatory input frequency increases the value of ICaP (green) becomes more tightly coupled with IGlu (blue, auto-correlation), while the coupling of the ICap and IKc also increases as we have previously reported using phase plane analysis (Santamaria et al., 2002
). The amplitude of lag 0 is indicative of the amount of correlation with previous activity. The half-time auto-correlation time between IGlu–ICaP extracted from these plots ranges between 3–70 ms.
Figure 4. Cross-correlation analysis of total synaptic excitatory input and dendritic currents. The figures show the auto-correlation of the synaptic current (IGlu, blue), and the cross-correlation of IGlu with ICaP (green), and IKc (red). We repeated this analysis for all the combinations of synaptic activity (A–D).
We determined how the value of mutual information between IGlu and ICaP and IKc varied as an effect of previous activity. We calculated the mutual information between ICaP and IKc with IGlu for lag times up to 1 s. Similar to what we did in Figure 3
, at a given time lag of Δt we computed the mutual information of the value of ICaP or IKc at time t with the value of IGlu at time t−Δt. This analysis shows that the mutual information between ICaP and IGlu decays as a function of time lag (Figure 5
A). This decay is due to the leaky nature of the conductance and membrane system. However, as opposed to the cross-correlation analysis the mutual information only shows one secondary peak at around 20 ms. Similarly, the time lag analysis of IGlu and IKc show an initial decay of the mutual information and a peak at around 20 ms (Figure 5
B). Channel kinetics and level of synaptic activity generate strong correlations at lag 0 which reflect the average level of activity in the dendrite, while the second peak is the mutual information in each channel from the instantaneous value of IGlu. As is known from functional and anatomical studies of the cerebellar cortex, excitatory inputs to Purkinje cells are divided in two groups. The first group comes from parallel fibers, which are being studied in this work; the second group is the ascending segment synapses (Llinas, 1982
). The ascending segment synapses deliver a more synchronous input that forces the Purkinje cell to fire robustly (Santamaria et al., 2007
). The information analysis presented in Figure 5
suggests that paired stimulus stimulation from ascending segment synapses would then be influenced in a window of around 20 ms by previous activity. This prediction is consistent with our previous analysis of ascending segment processing in the Purkinje cell model (Santamaria and Bower, 2005
).
Figure 5. Dependence of mutual information to previous activity. (A) I[ICaP(t),IGlu(t−Δt)] for Δt between 0–1 s. (B) I[IKc(t),IGlu(t−Δt)] for Δt between 0–1 s. The different traces correspond to different combinations of synaptic activity. Mutual information was bias corrected using the Panzeri and Treves method.
Dendritic Excitability Modulates Information Content in the Dendrite
Plastic changes in the expression of active conductances affect the signal processing properties of dendritic trees (Segev and London, 1999
; Stuart and Hausser, 2001
). Each dendritic channel contributes to the encoding and transformation of synaptic input depending on channel kinetics and expression. Thus, we decided to quantify the dependence of the value of mutual information between IGlu with ICaP and IKc as a function of dendritic channel density.
We varied the excitability of the dendrite by changing the conductance of the CaP (gCaP) or Kc (gKc). The value of gCaP was varied from 25–70 S/m2, while keeping gKc at its control value (800 S/m2), and gKc ranged from 550–1000 S/m2, while keeping gCaP at the original value of 45 S/m2. This wide range of conductances resulted in changes in the somatic firing rate (Figure 6
). In the case when we varied gCaP the firing rate approached zero when gCaP < 40 S/m2. Varying gKc resulted in an almost linear dependence of the firing rate with the firing rate at each conductance level less than 10% from the collective average (Figure 6
B).
Figure 6. Somatic firing rate varies as a function of dendritic excitability. (A) Firing rate as a function of homogenously changing the conductance of CaP (gCaP). (B) Similar to A changing the conductance of Kc (gKc). The vertical lines correspond to the values of the control simulation.
The information analysis of the conductance manipulations shown in Figure 6
result in that the entropy of ICaP as a function of gCaP decreases as gCaP increased (Figure 7
A left). This dependence is robust to changes in the value of the firing rate (Figure 6
A). The conditional entropy between ICaP and IGlu had a slightly different dependence of gCaP (center). The combination of entropy and conditional entropy resulted in a relatively constant value of the mutual information that then increased as a function of background activity for increasing values of gCaP (right). We repeated the same analysis to calculate information transmission of IGlu through IKc as a function of gCaP (Figure 7
B). The functional dependence of the mutual information plots shown in Figures 7
A,B showed a similar dependence. Note that the mutual information did not reflect the firing rate behavior. Similarly, we calculated mutual information from IGlu to ICaP and IKc as a function of gKc (Figures 7
C,D). In these cases the mutual information increases as the gKc decreased, and the firing rate increased. This is due to the lower inhibitory effect of Kc over CaP. In practically all cases the ratio N/m was larger than 1 (Figures S3 and S4 in Supplementary Material).
Figure 7. Excitatory synaptic current information content in dendritic currents as a function of dendritic excitability. (A) Calculations H(ICaP), H(ICaP.IGlu) and I(ICaP,IGlu) as a function of gCaP. (B) Similar to (A) but with respect to IKc. (C,D) Identical calculations as (A) and (B) but varying gKc. Mutual information was bas corrected using the Panzeri and Treves method.
We further quantified the effect of time lags and dendritic excitability on information processing of IGlu in the dendrite. We calculated the mutual information of ICaP with IGlu as a function of gCaP and time lags up to 1 s (Figure 8
A), for all levels of background activity. This analysis shows that for high values of gCaP and low levels of background activity mutual information is maximized (Figure 8
A right). The decay of the mutual information increases as a function of the value of gCaP. A similar set of results is obtained when calculating mutual information content of IGlu–IKc (Figure 8
B). However, in this case, the effect of the background level of stimulation is not as strong as in ICaP. A more subtle influence is shown by a similar analysis of the effects on the mutual information of IGlu with ICaP and IKc while varying gKc (Figures 8
C,D, respectively). Overall, this analysis shows that the window of dendritic integration is directly modulated not only by the excitability provided by active conductances but also by the level of synaptic stimulation, especially in the case of IKc. Since both of these properties are dynamic and plastic, they allow the cell to regulate synaptic information processing.
Figure 8. Excitatory synaptic current information content in dendritic currents as a function of dendritic excitability and time lags. (A) I[ICaP(t),IGlu(t–Δt)] for Δt from 0–1 s and varying gCaP. (B) As in (A) for IKc. (C,D) Identical calculations as in (A–B) but varying gKc. The different panels correspond to different combinations of synaptic activity. Mutual information was bias corrected using the Panzeri and Treves method.
Using a Purkinje cell model we presented a statistical analysis that shows that most of the information encoded in the background excitatory input is carried by the CaP and Kc currents. We have shown that the excitability of the dendritic tree represented by the density of active dendritic conductances modulates the information content of the total excitatory input in conjunction with the amount of synaptic activity. Consequently, the time window of integration of synaptic activity is in itself dependent on the level of synaptic activity which is not necessarily reflected in the spiking activity at the soma. This dynamical range of information processing consolidates the view that Purkinje cell dendrites processes synaptic activity locally before delivering it to the soma and provide a more sophisticated function than to compensate for the electrotonic decay of synaptic signals (Segev and London, 2000
; Bekkers and Hausser, 2007
).
Information Channels in Dendrites
Neuronal response to synaptic activity is an analog-to-digital transformation that requires the integration and processing of a large number of synaptic inputs distributed across a dendrite (Segev and London, 2000
). Traditionally, information theory has been applied to determine how much of the input stimulus can be reconstructed from observing the spiking activity of a neuron (Rieke, 1997
). Under this approach, the neuron is lumped into a point source function in which dendritic processing is lost (Harris and Stark, 1972
; Sherry and Klemm, 1980
; Yamada et al., 1996
; Borst and Theunissen, 1999
; Levy and Baxter, 2002
; Schultz et al., 2009
). In this study we refined the use of mutual information and linked it to a biophysical property of dendrites. In this framework, each conductance is treated as an information channel that communicates and interacts with other information channels in the dendrite. We found that the mutual information between excitatory synaptic input and dendritic currents varies as a function of dendritic excitability and the level of synaptic activity.
Although the activity of dendritic currents is dependent on IGlu stimulation in the past our analysis shows strong mutual information at lag 0. This ‘background’ information stems from the overall level of activity in the dendrite as also shown by the cross-correlation analysis. These results are dependent on the properties of the stimulus that were meant to replicate the continuous activity arriving from parallel fibers and inhibitory synapses. This stimulation resulted in an overall level of activity of dendritic channels that is reflected at zero lag time. However, the second peak shown in the cross-correlation and mutual information is more indicative of the internal dynamics of the dendritic currents and the information content of the instantaneous value of IGlu. The differential encoding of synaptic activity underscores the modulatory property of the parallel fiber system on Purkinje cell activity (Santamaria et al., 2007
; Walter et al., 2009
).
Purkinje cells also receive synaptic activity from the ascending segment part of the granule cell axon and climbing fibers (Llinas, 1982
). Both of these synaptic inputs deliver a more instantaneous stimulus lasting a few milliseconds. Under such types of stimuli and in the absence of background parallel fiber stimulation the instantaneous mutual information would be zero and would increase to reach a maximum, possibly at 20 ms, as indicated by our cross-correlation and mutual information analyses. Thus, mutual information from different systems could be encoded differently in the Purkinje cell dendritic tree.
The time window in which we define our stimulus affects the value of the mutual information. For example, our window of analysis (1 ms) would be too slow to study information at the some where fast channels are present. However, other types of cells could have fast dendritic channels (Regehr and Tank, 1992
). Thus, caution should be taken when applying information theory to analyzing dendritic activity.
Use of Mutual Information to Tune Biophysical Models and Experimental Design
Bounding the kinetic and density parameters of dendritic current models has been difficult since present experimental techniques are limited in resolving the spatial distribution of dendritic conductances (Achard and De Schutter, 2008
; Van Geit et al., 2008
). We propose that by treating each dendritic conductance as an information channel it is possible to constrain the value and distribution of dendritic currents in encoding synaptic information. Although here we have presented data regarding encoding the total excitatory current, the same technique can be extended to total inhibitory, total synaptic current, or it can be subdivided into the different parts of the dendritic tree (primary, secondary, and tertiary dendrites). At a first iteration, traditional template matching algorithms could be used to fit a model to data. These algorithms change the density of dendritic conductances (Achard and De Schutter, 2008
). Then models could be classified due to their value of mutual information between the stimulus and each dendritic current. Using this approach we could test the hypothesis that by matching the spiking activity at the soma the information content of the synaptic activity in dendritic currents is maximized.
The simulation analysis presented in this work can be used to design experiments based on dynamic clamp technique (Sharp et al., 1993
; Kreiner and Jaeger, 2004
). A challenging experiment would consist in patching a Purkinje cell while blocking spiking activity with tetrodotoxin. The pipette could deliver artificial synaptic conductances while monitoring the resulting current in the soma. The mutual information between the synaptic input and the total dendritic current value could be calculated from this experiment. Pharmacological manipulation blocking dendritic calcium or calcium activated potassium channels in the dendrite would then uncover the contribution to information processing. Other similar experiments could be to electrically or photochemically stimulate a group of synapses while recording at the soma (Korkotian and Segal, 2006
) or to use the recently developed targeted dendrotomy technique (Bekkers and Hausser, 2007
).
Biophysical Interpretation
Dendritic excitability, in Purkinje and other cell types, is the consequence of the different concentration and distribution of active conductances over a dendritic tree (Gunay et al., 2008
; Komendantov and Ascoli, 2009
). Neuronal stimulation and development change the excitability of the cell and could be a mechanism for storing memories (Womack and Khodakhah, 2003
; Kim and Linden, 2007
). Similarly, excitability is affected by aging and illnesses that could reduce the information capacity of the dendrite (Landfield and Pitler, 1984
; Chan et al., 2007
; Kabaso et al., 2009
). It is well established that hippocampal pyramidal cells firing rate remains constant through aging (Barnes et al., 1983
; Wilson et al., 2005
) but not in Purkinje cells (Rogers et al., 1980
), however the contribution of dendritic excitability and afferent stimulation on these changes is not well understood. In any case, our analyses have shown that changes in gCaP or gKc can regulate the amount of information encoded and the time synaptic activity affects neuronal activity. As the hyperpolarizing Kc current decreases, the information contained in ICaP and IKc increases potentially allowing more information to be transmitted by the neuron (Steuber et al., 2007
).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
UTSA-TRAC and NSF HRD-0932339.
The Supplementary Material for this article can be found online at http://www.frontiersin.org/computationalneuroscience/paper/10.3389/fncom.2010.00006/