- Departments of Neurobiology and Cognitive Sciences, the Interdisciplinary Center for Neural Computation and the Center for the Study of Rationality, Hebrew University, Jerusalem, Israel
According to the theory of Melioration, organisms in repeated choice settings shift their choice preference in favor of the alternative that provides the highest return. The goal of this paper is to explain how this learning behavior can emerge from microscopic changes in the efficacies of synapses, in the context of a two-alternative repeated-choice experiment. I consider a large family of synaptic plasticity rules in which changes in synaptic efficacies are driven by the covariance between reward and neural activity. I construct a general framework that predicts the learning dynamics of any decision-making neural network that implements this synaptic plasticity rule and show that melioration naturally emerges in such networks. Moreover, the resultant learning dynamics follows the Replicator equation which is commonly used to phenomenologically describe changes in behavior in operant conditioning experiments. Several examples demonstrate how the learning rate of the network is affected by its properties and by the specifics of the plasticity rule. These results help bridge the gap between cellular physiology and learning behavior.
Introduction
According to the “law of effect” formulated by Edward Thorndike a century ago, the outcome of a behavior affects the likelihood of occurrence of this behavior in the future: a positive outcome increases the likelihood whereas a negative outcome decreases it (Thorndike, 1911 ). One quantitative formulation of this qualitative law of behavior was proposed half a century later by Richard Herrnstein, and is known as the “matching law” (Herrnstein, 1961 ). The matching law states that over a long series of repeated trials, the number of times an action is chosen is proportional to the reward accumulated from choosing that action (Davison and McCarthy, 1988 ; Herrnstein, 1997 ; Gallistel et al., 2001 ; Sugrue et al., 2004 ). In other words, the average reward per choice is equal for all chosen alternatives. To explain how matching behavior actually takes place, the “theory of Melioration” argues that organisms are sensitive to rates of reinforcement and shift their choice preference in the direction of the alternative that provides the highest return (Herrnstein and Prelec, 1991 , however, see also Gallistel et al., 2001 ). If the returns from all chosen alternatives are equal, as postulated by the matching law, then choice preference will remain unchanged. Thus, matching is a fixed point of the dynamics of melioration.
The neural basis of the law of effect has been extensively explored. It is generally believed that learning is due, at least in part, to changes in the efficacies of synapses in the brain. In particular, activity-dependent synaptic plasticity, modulated by a reward signal, is thought to underpin this form of operant conditioning (Mazzoni et al., 1991 ; Williams, 1992 ; Xie and Seung, 2004 ; Fiete and Seung, 2006 ; Baras and Meir, 2007 ; Farries and Fairhall, 2007 ; Florian, 2007 ; Izhikevich, 2007 ; Legenstein et al., 2008 , 2009 ; Law and Gold, 2009 ). In a previous study we considered the large family of reward-modulated synaptic plasticity rules in which changes in synaptic efficacies are driven by the covariance between reward and neural activity. We showed that under very general conditions, the convergence of a covariance plasticity rule to a fixed point results in matching behavior (Loewenstein and Seung, 2006 ; Loewenstein, 2008a ). This result is independent of the architecture of the decision making network, the properties of the constituting neurons or the specifics of the covariance plasticity rule.
The universality of the relation between the fixed-point solution of the covariance synaptic plasticity rule and the matching law of behavior raises the question of whether there are aspects of the dynamics of convergence to the matching law that are also universal. In this paper I study the transient learning dynamics of a general decision making network in which changes in synaptic efficacies are driven by the covariance between reward and neural activity. I examine the two-alternative repeated-choice schedule which is typically used in human and animal experiments. I show that the macroscopic behavioral learning dynamics that result from the microscopic synaptic covariance plasticity rule are also general and follow the well known Replicator equation. This result is independent of the decision-making network architecture, the properties of the neurons and the specifics of the plasticity rule. These only determine the learning rate in the behavioral learning equation. By analyzing several examples, I show that in these examples, the learning rate depends on the probabilities of choice: it is approximately proportional to the product of the probabilities of choice raised to a power, where the power depends on the specifics of the model.
Some of the findings presented here have appeared previously in abstract form (Loewenstein, 2008b ).
Results
Melioration and the Replicator Equation
One way of formalizing the theory of melioration mathematically is by assuming that subjects make choices stochastically as if tossing a biased coin. This assumption is supported by the weak temporal correlations between choices in repeated choice experiments (Barraclough et al., 2004 ; Sugrue et al., 2004 ; Glimcher, 2005 ). The bias of the coin corresponds to choice preference, and the learning process manifests itself as a change in this bias with experience toward the more rewarding alternative. Denoting the probability of choosing alternative i at time t by pi(t), the theory of Melioration posits that a change in pi(t) with time is proportional to the difference between the return from alternative i, i.e., the average reward obtained in trials in which alternative i was chosen, and the overall return. Formally,

where η > 0 is the learning rate, A denotes the action such that E[R|A = i] is the average reward obtained in trials in which alternative i was chosen and E[R] = Σi piE[R|A = i] is the average return. If the return from alternative i is larger than the average return, E[R|A = i] > E[R], then the probability that alternative i will be chosen in the future increases. If E[R|A = i] < E[R], the probability that alternative i will be chosen decreases, in accordance with the theory of Melioration. The matching law is a fixed point of Eq. 1 because it states that for all chosen alternatives (alternatives for which pi > 0), the returns, E[R|A = i] are equal. Equation 1 is known as the Replicator equation (Fudenberg and Levine, 1998 ; Hofbauer and Sigmund, 1998 ) and is widely used in learning models and in evolutionary game theory. Note that the theory of Melioration does not require η to be constant in time. Melioration will be achieved as long as η > 0.
Synaptic Plasticity and Learning
It is generally believed that choice preference is determined by the efficacies of the synapses of the decision-making neural network. Theoretically, if we were able to determine the architecture of this decision-making network and the properties of all the constituent neurons, we could determine the probability of choosing alternative i in a trial from the efficacies of all the synapses at the time of that trial. Formally,

where W = (W1,W2,…,) is the vector of the efficacies of all the synapses that are involved in the decision-making process, as schematically illustrated in Figure 1 A, and t is an index of the trial. Because choice probabilities are a function of the synaptic weights, changes in these weights due to synaptic plasticity (Figure 1 B, left) will change the choice probabilities (Figure 1 B, right), yielding the learning rule
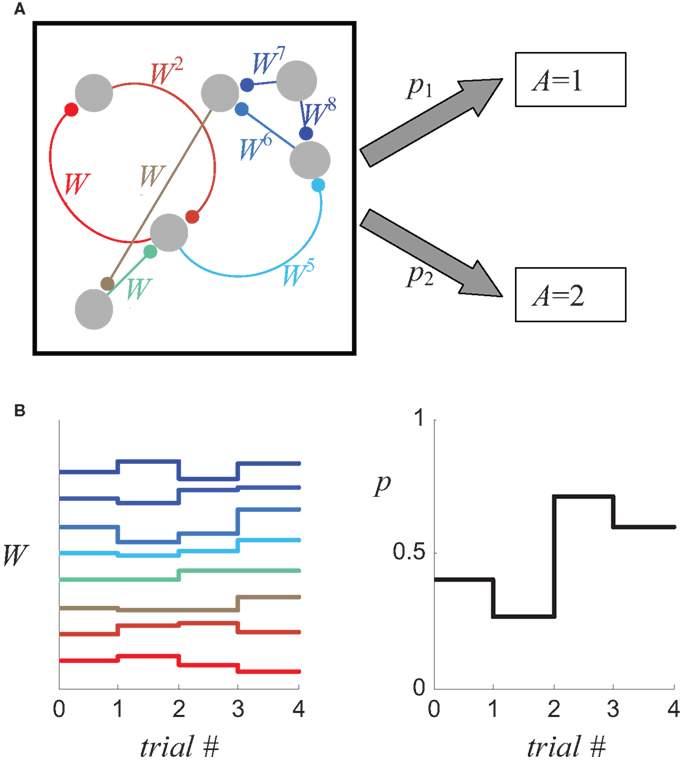
Figure 1. Relating synaptic efficacies to choice behavior. (A) A schematic description of a decision making network composed of six neurons which are connected by eight synapses. The probabilities that the network will “choose” alternative 1 and 2 (p1 and p2, respectively) depend on the efficacies of the eight synapses (denoted by Wi). (B) Changes in the efficacies of the synapses (left) result in a change of the probabilities of choice (right).
In the next section it is shown that in the context of two-alternative repeated-choice experiment, if changes in synaptic efficacies are driven by the covariance between reward and neural activity, the average velocity approximation (Heskes and Kappen, 1993 ; Kempter et al., 1999 ; Dayan and Abbott, 2001 ) of the learning rule, Eq. 3, reproduces the Replicator equation, Eq. 1.
Covariance-Based Synaptic Plasticity
In statistics, the covariance between two random variables is the mean value of the product of their fluctuations. Accordingly, covariance-based synaptic plasticity arises when changes in synaptic efficacy in a trial are driven by the product of reward and neural activity, provided that at least one of these signals is measured relative to its mean value. For example, the change in the synaptic strength W in a trial, ΔW, could be expressed by

where φ is the plasticity rate, R is the magnitude of reward delivered to the subject, N is any measure of neural activity and E[N] is the average of N. For example, N can correspond to the presynaptic activity, the postsynaptic activity or the product of presynaptic and postsynaptic activities. In the latter case, Eq. 4a can be considered Hebbian. Another example of a biologically plausible implementation of reward-modulated covariance plasticity is

where E[R] is the average of the previously harvested rewards. For both of these plasticity rules, the expectation value of the right hand side of the equation is proportional to the covariance between R and N (Loewenstein and Seung, 2006 ),

and for this reason it can be said these plasticity rules are driven by the covariance of reward and neural activity.
The biological implementation of Eqs 4a,b requires information, at the level of the synapse, about the average neural activity (in Eq. 4a) or the average reward (in Eq. 4b) (Loewenstein, 2008a ). However, covariance-based synaptic plasticity can also arise without explicit information about the averages: the average terms in Eqs 4a,b can be replaced with any unbiased estimator of the average that is not correlated with the reward. This is because such a change will not affect the average velocity approximation, Eq. 4c. For example, consider a variation of Eq. 4a, in which the average neural activity, E[N], is replaced by the neural activity τ trials ago:
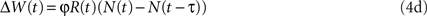
Averaging Eq. 4d yields E[ΔW(t)] = φCov[R(t), N(t)]– φCov[R(t), N(t – τ)]. If the reward delivered in trial t, R(t) is independent of the neural activity τ trials ago, N(t − τ), then the average velocity approximation of Eq. 4d yields Eq. 4c. The reward R(t) and the neural activity N(t − τ) are approximately independent if the neural activities in consecutive trials are approximately independent and if the dependence of the reward on the choice τ trials ago is weak.
Covariance Plasticity and Replicator Dynamics
In order to relate the covariance-based plasticity rules to behavior, I use the average velocity approximation in which I replace the stochastic difference equations, Eqs 4a,b,d with a differential equation in which the right hand side of the equation is replaced by its expectation value, Eq. 4c

According to the average velocity approximation, if the plasticity rate is sufficiently small, under certain stability conditions, the deviation of the stochastic realization of W from its average velocity approximation value is 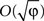 (Heskes and Kappen, 1993
). Therefore, the smaller the plasticity rate φ the better the average velocity approximation.
(Heskes and Kappen, 1993
). Therefore, the smaller the plasticity rate φ the better the average velocity approximation.
Differentiating Eq. 2 with respect to time yields

where the index k sums over all synapses that participate in the decision-making. Substituting Eq. 5 in Eq. 6 yields

where Nk and φk are the neural activity and the plasticity rate in the neuronal plasticity rule (Eq. 4) that correspond to synapse k. By definition,

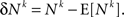
Separating the covariance term into trials in which alternative 1 was chosen (A = 1) and trials in which alternative 2 was chosen (A = 2) yields
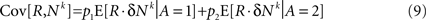
where E[δNk|A = i] is the average of ΔNk in trials in which alternative i was chosen (i∈{1,2}). The reward R is a function of the actions A and the actions are a function of the neural activities. Therefore, given an action, the reward and the neural activities are statistically independent and hence:
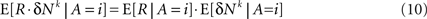
Thus, Eq. 9 becomes:
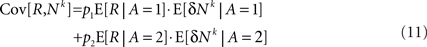
Next I separate E [δNk] into trials in which alternative 1 was chosen and trials in which alternative 2 was chosen and use the fact that by definition, E[δNk] = 0
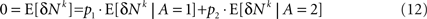
Substituting Eq. 12 in Eq. 11 yields
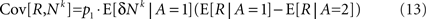
Substituting Eq. 13 in Eq. 7 results in Eq. 1 with a learning rate η that is given by
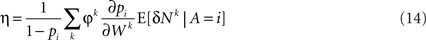
Thus, if synaptic changes are driven by the covariance of reward and neural activity, then according to the average velocity approximation, learning behavior follows the Replicator dynamics. This result is very general. The Replicator learning dynamics turns out to be a generic outcome of covariance-based synaptic plasticity implemented in any decision-making network, independently of the properties of the constituent neurons or the specifics of the covariance-based synaptic plasticity.
The Learning Rate η
The learning rate η in the Replicator equation is determined by the sum over all synapses of the product of three terms (Eq. 14): φk, ∂pi/∂Wk and E[δNk|A = i]. The first term, φk, is the plasticity rate. The second term, ∂pi/∂Wk, signifies the dependence of the probability of choice on the synaptic efficacies. In other words, it is a measure of the susceptibility of choice behavior to the synaptic efficacies. The third term, E[δNk|A = i], is the average of the fluctuations in neural activity in trials in which alternative i was chosen. This term is determined both by the plasticity rule, which determines N, and by the network properties that determine the conditional average of N. In the next sections I analyze several examples to show how the properties of the decision making network and the synaptic plasticity rule impact the effective learning rate.
The Network Architecture
An overt response in a decision making task is believed to result from competition between populations of neurons, each population representing an alternative. In this paper I implement this competition in a general decision-making network which is commonly used to study decision-making in the cortex (Wang, 2002 ). The network model consists of two populations of “sensory” neurons, each containing a large number of neurons, n, representing the two alternatives, and two populations of “premotor” neurons, which signal the chosen alternative and therefore are referred to as “premotor” (Figure 2 ). I assume that the activity of neurons in the sensory population is independent of past actions and rewards (which is why I refer to these neurons as “sensory”). Choice is determined by competition between the premotor populations. I use specific examples to analyze three general types of competition. In the first example, the decision is determined by the first population whose activity reaches a threshold; in the second example, it is the population whose activity, averaged over a particular window of time, is larger; the third example implements a dynamic competition. After the competition, the firing rate of the premotor population that corresponds to the chosen alternative is high whereas the firing rate of the other premotor population is low (Wang, 2002 ). More formally, denoting by Ma the firing rate of population a, I assume that M1 = Mwin, M2 = Mlos in trials in which alternative 1 is chosen and M1 = Mlos, M2 = Mwin in trials in which alternative 2 is chosen, where Mwin > Mlos.
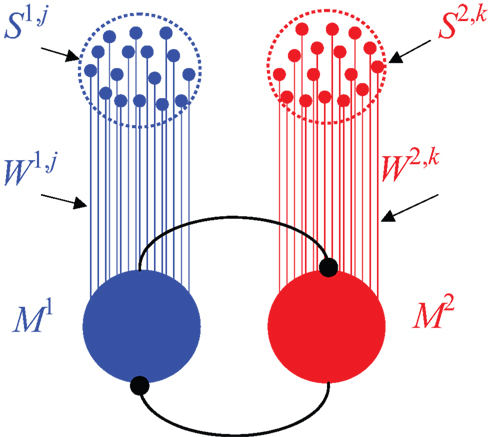
Figure 2. The decision-making network model. The network consists of two populations of sensory neurons, each denoted by Sa,i, and two populations of premotor neurons, Ma. Strength of synaptic connection between sensory neuron Sa,i and the corresponding premotor population Ma is denoted by Wa,i. Decision is mediated via competition between the premotor populations (see text).
Example 1: The Temporal Winner-Take-All Readout
A recent study has shown that the central nervous system can make accurate decisions about external stimuli in brief time frames by considering the identity of the neuron that fired the first spike (Shamir, 2009 ), a readout scheme known as temporal Winner-Take-All (tWTA). In the framework of the decision making network shown in Figure 2 , alternative 1 is chosen in trials in which the first neuron to fire a spike belongs to premotor population 1. By contrast, if the first neuron to spike belongs to population 2, alternative 2 is chosen. This readout process, which implements the Race Model for decision making in the limit of small threshold (Bogacz et al., 2006 ), can occur if the competition between the two populations of premotor neurons is mediated by strong and fast lateral inhibition. While it could be argued that it is unlikely for a single spike in a single neuron to determine choice (however see Herfst and Brecht, 2008 ), the analytical tractability of this model provides insights into how the learning rate is affected by the properties of the network. Moreover, it can be considered as the limit of a fast decision process. Finally, it can be generalized to an arbitrary threshold (n-tWTA model, Shamir, 2009 ).
In this section I study the effect of covariance-based plasticity in a decision making network characterized by a tWTA readout. I assume that during the competition, the timing of spikes of each premotor neuron in each population is determined by a Poisson process whose rate is a linear function of the input synaptic efficacy to that neuron. Formally, λa,i = Ca,i + α··Wa,i, where λa,i is the firing rate of neuron i of population a; Wa,i is the synaptic input to the neuron (a ∈ {1,2}, k∈[1,na]) 1 ;Ca,i and α > 0 are constants.
Susceptibility Because the firing of the neurons is a Poisson process and choice is determined by the identity of the first neuron to fire, it is easy to show that the probability that the first spike to fire belongs to population 1 and thus that alternative 1 is chosen in a trial, p1 is:

Differentiating Eq. 15 with respect to the synaptic efficacies yields
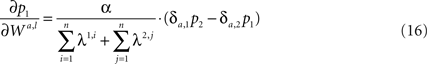
where 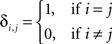 is the Kronecker delta.
is the Kronecker delta.
Plasticity rule Here I consider a synaptic plasticity rule in which the synaptic efficacies Wa,l change according to product of reward with the activity of the corresponding premotor population (after the competition), assuming that this activity is measured relative to its average value and assuming that all plasticity rates are equal φa,i = φ,

The plasticity rule of Eq. 17 is an expression of covariance because it is a product of reward and neural activity (postsynaptic activity), measured relative to its average value:

In order to compute the learning rate, I consider the term, E[δNk|A = i] in Eq. 14. The neural activity here corresponds to the activity of the premotor population following the competition. The average neural activities of the two premotor populations are

Therefore,
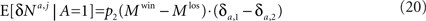
The learning rate Substituting Eqs. 16 and 20 in Eq. 14 yields

Note that the denominator in Eq. 21 is constant because:
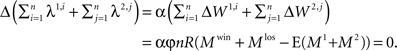
Thus, if φ > 0 then according to Eq. 21 the network model is expected to meliorate: with experience, the model will bias its choice preference in favor of the alternative that provides, on average, more reward. The rate at which this learning takes place is proportional to the product of (1) the difference between the neural activity of the premotor population in “winning” trials and “losing” trials, (2) the plasticity rate, and (3) the dependence of the firing rate on the synaptic efficacy α. It is inversely proportional to the population average firing rates of the premotor populations.
The tWTA model described above is sufficiently simple to derive the actual trial-to-trial stochastic dynamics, allowing us to better understand the resultant behavior as well as to study the quality of the average velocity approximation. Using Eqs 15 and 17, the change in probability of choice in a trial is

where a1 is an index variable that is equal to 1 in trials in which alternative 1 is chosen and to 0 otherwise. The resultant Eq. 22 is the linear reward-inaction algorithm proposed by economists as a phenomenological description of human learning behavior (Cross, 1973 ) and is commonly used in machine learning (Narendra and Thathachar, 1989 ).
Note that the dynamics of the linear reward-inaction algorithm, Eq. 22, is stochastic for two reasons. First, choice is stochastic and second, the reward schedule may be stochastic and in that case, the reward variable R is also a stochastic variable. A detailed analysis of the relation between the linear reward-inaction algorithm, Eq. 22 and its average velocity approximation, Eq. 1, appears elsewhere (Borgers and Sarin, 1997 ; Hofbauer and Sigmund, 1998 ). Here I demonstrate the relation between the stochastic dynamics and its deterministic approximation using a specific example. I simulated the stochastic dynamics, Eq. 22 in a “two-armed bandit” reward schedule in which alternatives 1 and 2 provide a binary reward with probabilities 0.75 and 0.25, respectively, and recorded the choice behavior of the model. The probability of choosing alternative 1, p1, as a function of trial number was estimated by repeating the simulation 1,000 times and counting the fraction of trials in which alternative 1 was chosen (Figure 3 A, circles). Initially, the two alternatives were chosen with equal probability. With experience, the model biased its choice preference in favor of alternative 1 that provided the reward with a higher probability, as expected from the average velocity approximation (black solid line), Eq. 1.
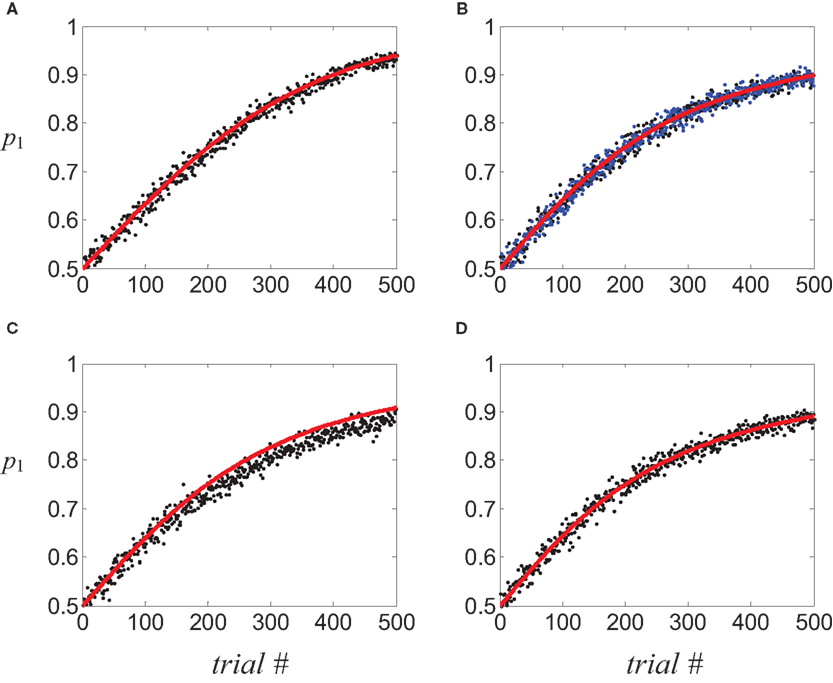
Figure 3. Covariance-based synaptic plasticity and learning. Learning behavior in a two-armed bandit reward schedule in which alternatives 1 and 2 provided a binary reward with a probability of 0.75 and 0.25, respectively.(A–D) Circles, fraction of choosing alternative 1 in 1,000 simulation of the stochastic dynamics; red line, the average velocity approximation. (A) tWTA model; (B,C) population coding model. (B) Black circles, postsynaptic activity dependent plasticity; blue circles, Hebbian plasticity. (C) Presynaptic activity-dependent plasticity. (D) Dynamic competition model. Plasticity rate in all examples was chosen such that the probability of choosing alternative 1 after 200 trials, as estimated by the average velocity approximation, is 0.75. See Section “Materials and Methods” for parameters of the simulations.
Example 2: Population Readout
The learning behavior of the neural model analyzed in the previous section follows the linear reward-inaction algorithm, a stochastic implementation of the Replicator equation with a constant learning rate. However, this result does not necessarily generalize to other neural models. In this section I present several examples in which the covariance synaptic plasticity results in a learning rate which is a function of the probabilities of choice.
In the previous section I computed the learning rate in a model in which decisions were determined by the identity of the neuron that fired the first spike. However, if the inhibition that mediates the competition between the premotor populations is weaker and slower, the decision is likely to be determined by the joint activity of many neurons, similar to the well-studied population code scheme. In this section I consider such a population readout model. I assume that the total input to each premotor population is the sum of activities of all neurons of the corresponding sensory population, each weighted by its synaptic efficacy. The chosen alternative is the one that corresponds to the larger input. Formally, denoting by Ia the synaptic input to premotor population a, alternative 1 is chosen in trials in which I1 >I2. Otherwise alternative 2 is chosen
2
. The mechanism underlying this competition is not explicitly modeled here. The synaptic input to the premotor populations, Ia, is the sum of the activities of the corresponding sensory neurons, weighted by the corresponding synaptic efficacies: denoting by Sa,k the spike count of sensory neuron k in population a in a particular temporal window, 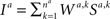 . Here I assume that the spike count of the different neurons is independently drawn, and is independent of past actions and rewards.
. Here I assume that the spike count of the different neurons is independently drawn, and is independent of past actions and rewards.
Using the central limit theorem, it can be shown that the susceptibility of the probability of choice in this model is approximately (see Materials and Methods),

The effective learning rate depends on the plasticity rule used. Here I discuss three covariance plasticity rules that differ by the neural activity term in Eq. 4c: N is (1) the postsynaptic-activity, (2) the presynaptic-activity, and (3) Hebbian (the product of presynaptic and postsynaptic activities). In Section “Materials and Methods” I show that both postsynaptic activity and Hebbian covariance rules result in a learning rate that is approximately given by

In contrast, if the neural activity in the covariance plasticity rule is presynaptic, and if this activity is drawn from a Gaussian distribution, the learning rate is approximately given by

Common to these examples and similar to the tWTA example, the population readout model is expected to meliorate. However, in contrast to the tWTA example, the rate at which this learning takes place is not constant and is proportional to (p1p2)α, where α = π/4 for postsynaptic or Hebbian covariance plasticity and α = π/2 − 1 for the presynaptic covariance plasticity. The fact that the effective learning rate is not constant and decreases as one of the probabilities of choice approaches zero has important implications for exploratory behavior: Consider a reward schedule in which the return from one of the alternatives surpasses that of the other alternative. According to Eq. 1, the probability of choosing the more profitable alternative will always increase. However, the fact that the learning rate decreased allows for continued exploration of the second alternative, albeit with an ever decreasing probability. This result is consistent with empirically observed human as well as animal behavior (Vulkan, 2000 ; Shanks et al., 2002 ; Neiman and Loewenstein, 2008 ).
In order to compare the stochastic dynamics to its average velocity approximation, I simulated the learning behavior of the decision-making model of Figure 2 , in which each sensory population in the simulations consisted of 1,000 Poisson neurons. I used the same reward schedule as in Example 1, namely, a “two-armed bandit” reward schedule in which alternatives 1 and 2 provide a binary reward with probabilities of 0.75 and 0.25. The probability of choice was estimated by repeating the simulation 1,000 times and counting the fraction of trials in which alternative 1 was chosen.
To study the consequences of a post-synaptic activity covariance rule, I simulated the network when synaptic changes are given by 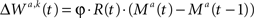 (see Eq. 4d). The simulated probability of choice is denoted by black circles in Figure 3
B. Despite the increased complexity of the network model, as well as the synaptic plasticity rule, the stochastic dynamics is remarkably similar to its average velocity approximation,
(see Eq. 4d). The simulated probability of choice is denoted by black circles in Figure 3
B. Despite the increased complexity of the network model, as well as the synaptic plasticity rule, the stochastic dynamics is remarkably similar to its average velocity approximation, 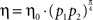 (solid line).
(solid line).
Similarly, I simulated the network using a Hebbian covariance plasticity rule, ΔWa,k(t) = φR(t)·(Sa,k(t)·Ma(t) − Sa,k(t −1)·Ma(t −1)), where Sa,k is the number of spikes fired by the presynaptic neuron at a given window of time. The results of these simulations (Figure 3 B, blue circles) are similar to those of the postsynaptic-activity dependent plasticity and are consistent with the expected average velocity approximation (solid line).
To study the consequences of a presynaptic activity covariance rule, I simulated the network dynamics with the presynaptic-activity dependent covariance plasticity rule ΔWa,k(t) = φR(t)·(Sa,k(t) − Sa,k(t−1)). The results of these numerical simulations (Figure 3
C, circles) were similar to the expected from the expected average velocity approximation 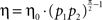 (solid line)
3
, but not exact: the learning rate of the stochastic dynamics was slightly lower than that of the deterministic dynamics. This small deviation of the stochastic dynamics from its average velocity approximation disappears when a smaller plasticity rate is used (not shown).
(solid line)
3
, but not exact: the learning rate of the stochastic dynamics was slightly lower than that of the deterministic dynamics. This small deviation of the stochastic dynamics from its average velocity approximation disappears when a smaller plasticity rate is used (not shown).
Example 3: Dynamic Competition Model
The framework used here to derive the behavioral consequences of covariance-based synaptic plasticity can also be used in more complex models, as long as the susceptibility and the conditional average of the neural fluctuations can be computed. Therefore, even if the model is too complex to solve analytically, it is possible to use a phenomenological approximation to study the effect of covariance-based synaptic plasticity on learning behavior. This is demonstrated in this section using the Soltani and Wang (2006) dynamic model for decision making. Soltani and Wang analyzed a biophysical spiking neurons model that is based on the architecture of Figure 2 . The result of their extensive numerical simulations was that the probability of choosing an alternative is, approximately, a logistic function of the difference in the overall synaptic efficacies onto the two premotor populations,
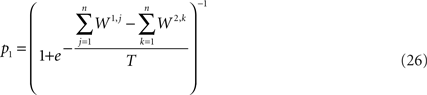
where T is a parameter that determines the sensitivity of the probability of choice to the difference in the synaptic efficacies. Equation 26 can be used to compute the susceptibility of choice behavior to the synaptic efficacies, yielding

Assuming that synaptic plasticity is postsynaptic-activity dependent, Eq. 17 4 , and substituting Eqs 27 and 20 in Eq. 14 yields

where 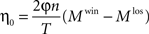
As in the previous examples, the learning rate is proportional to the product of the probabilities of choice to a power, η = η0·(p1p2)α, and in this example α = 1.
As in Example 1, this model is sufficiently simple to derive the actual trial-to-trial stochastic dynamics. Using Eqs. 17 and 26, it is easy to show that the change in probability of choice in a trial is

To study the quality of the average velocity approximation, I numerically simulated the decision making model, Eq. 29, in the same “two-armed bandit” reward schedule described in Examples 1,2 and estimated the dynamics of probability of choice by averaging over 1,000 repetitions (Figure 3 D, circles). The stochastic dynamics, Eq. 29, was remarkably similar to its average velocity approximation.
Discussion
In this paper I constructed a framework that relates the microscopic properties of neural dynamics to the macroscopic dynamics of learning behavior in the framework of a two-alternative repeated-choice experiment, assuming that synaptic changes follow a covariance rule. I showed that while the decision making network may be complex, if synaptic plasticity in the brain is driven by the covariance between reward and neural activity, the emergent learning behavior dynamics meliorates and follows the Replicator equation. The specifics of the network architecture, e.g., the properties of the neurons and the characteristics of the synaptic plasticity rule, only determine the learning rate. Thus, Replicator-like meliorating learning behavior dynamics is consistent with covariance-based synaptic plasticity.
The generality of this result raise the question of whether it is possible to infer the underlying neural dynamics from the observed learning behavior in the framework of covariance-based synaptic plasticity. The examples analyzed in this paper suggest that careful measurement of the learning rate may provide such information. In these examples, the effective learning rate is approximately η = η0·(p1p2)α, where the value of α depends on the network and the plasticity rule. For example, in the tWTA model with the postsynaptic activity-dependent covariance rule, α = 0. At the other extreme, the dynamic competition model of Soltani and Wang (2006) , with the same plasticity rule resulted in α = 1. The value of α in all the other models lies between these two values. Therefore, the value of α is a window, albeit limited, to the underlying neural dynamics. However, estimating the value of α from behavioral data is not straightforward. The main reason is that it requires the accurate estimation of the non-stationary probability of choice from the binary string of choices. Therefore, an accurate estimation of α may require a very large number of trials. Yet, despite this limitation, it is clear from previously published data on human and animal learning behavior that the learning rate decreases as the probability of choice approaches unity (Vulkan, 2000 ; Shanks et al., 2002 ; Neiman and Loewenstein, 2008 ). This result, which indicates that α > 0, refutes the naïve formulation of the Replicator equation (or its stochastic implementation, the linear reward-inaction algorithm) in which the learning rate was assumed constant, α = 0 (Cross, 1973 ; Fudenberg and Levine, 1998 ; Hofbauer and Sigmund, 1998 ). Therefore, I suggest a refinement of these models in which η = η0·(p1p2)α. However, the question of whether even careful behavioral experiments can distinguish between models with a similar value of α, for example between α = π/4 ≈ 0.8 and α = π/2 − 1 ≈ 0.6 remains open.
A learning rate that decreases as one of the probabilities of choice approaches 1 (α > 0) has important behavioral consequences. It enables a large learning rate and thus, fast learning when the probabilities of the two alternatives are approximately equal. In contrast, as one of the probabilities of choice approaches 1, learning becomes slow, allowing for continuous exploration, i.e., the choosing of both alternatives, even after a large number of trials.
Whether the theory of Melioration is a good description of the process of adaptation of choice preference is subject to debate among scholars in the field. While Replicator-like dynamics provides a good phenomenological description of choice behavior in many repeated-choice experiments, it has been argued that it is inconsistent with the rapid changes in behavior following changes in reward schedule (Gallistel et al., 2001 , however, see Neiman and Loewenstein, 2007 ). Another criticism of this theory is that it does not address the temporal credit assignment problem in more complicated behavioral experiments, generally formulated as a fully observable Markov decision process (MDP, Sutton and Barto, 1998 ). Importantly, it can be shown that other popular phenomenological behavioral models can be formulated in the Replicator framework. For example, consider an income-based model in which the income I of the two alternatives is estimated using an exponential filter and ratio of the probabilities of choosing the two alternatives is equal to the ratio of incomes:

This model has been used to describe human learning behavior in games (Erev and Roth, 1998 ) and monkeys’ learning behavior in a concurrent variable interval (VI) schedule (Sugrue et al., 2004 ). In Section “Materials and Methods” I show that Eq. 30 can be rewritten as a linear reward-inaction algorithm in which the learning rate depends on the exponentially weighted average reward.
Reinforcement learning in the brain is likely to be mediated by many different algorithms, implemented in different brain modules. These algorithms probably range from high level deliberation through temporal-difference (TD) learning and Monte Carlo methods (Sutton and Barto, 1998 ) to simple “stateless” (Loewenstein et al., 2009 ) methods such as the Replicator dynamics. Compared to these methods, the computational capabilities of covariance-based synaptic plasticity are limited. However, the implementation of the covariance rule in the neural hardware is much simpler and much more robust: network architecture and the properties of neurons can change, but as long as the synaptic rule is covariance-based the organism will meliorate.
Materials and Methods
This section provides the technical derivations supporting the text. The effective learning rates are computed for various decision-making models and the details of the numerical simulations are provided. Topics are presented in the order in which they appear in the text and equations are numbered to coincide with the equations in the text.
Choice Behavior in a Large Population of Sensory Neurons (Eq. 23)
In this section I compute the dependence of the probability of choice on the synaptic efficacies for the decision-making network in Figure 2 , assuming that (1) the number of sensory neurons is very large, (2) the different synaptic efficacies are of the same magnitude, (3) the mean activities of the sensory neurons are of the same magnitude, and (4) the activities of the sensory neurons are drawn from a distribution in which the mean and standard deviation are of the same magnitude.
Consider the decision making network in Example 2 in which alternative 1 is chosen in trials in which I1 − I2 > ze, where ze is a Gaussian noise, such that 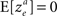 and
and 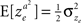 . For reasons of clarity, in the text it is assumed that
. For reasons of clarity, in the text it is assumed that 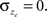
The probability that alternative 1 will be chosen is
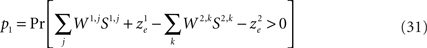
Separating Eq. 31 into deterministic and stochastic terms,

where
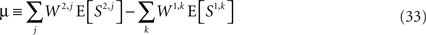
and Z is a zero-mean stochastic variable with variance
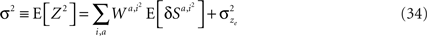
With Assumption 1–3 the central limit theorem can be applied to Eq. 32, yielding

To compute the effective learning rate, we need to compute the effect of change in the synaptic efficacies on the probability of choice, ∂p1/∂Wa,i. Using the chain rule,
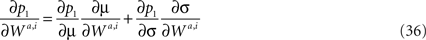
Differentiating Eq. 35 with respect to μ and σ yields

Differentiating Eqs 33 and 34 with respect to Wa,i yields
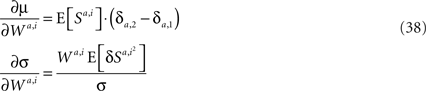
To compare the differential contribution of the two terms in Eq. 36, consider.
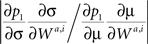
Using Eqs 37 and 38 and Assumptions 1–4,
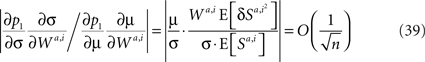
where n is the number of neurons in the sensory populations. Thus, substituting Eqs 37 and 38 in Eq. 36 and taking dominant terms yields 5
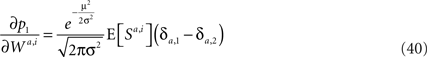
To find the dependence of susceptibility on the probability of choice, I expand Eq. 35 around μ = 0, yielding

Expanding the exponent term in Eq. 40 around μ = 0 and substituting Eq. 41 yields
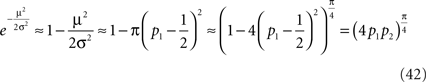
Note that the approximation of Eq. 42 is valid not only around p1 = 0.5 but also for p1 = 0 and p2 = 0 (μ → ±∞). To study the quality of this approximation for all values of pi, I numerically computed the dependence of 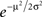 on the probability of choice and compared it to its approximation, Eq. 42. A quantitative analysis reveals that for 0.05 < p1 < 0.95, the deviations of
on the probability of choice and compared it to its approximation, Eq. 42. A quantitative analysis reveals that for 0.05 < p1 < 0.95, the deviations of 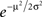 from (4p1p2)π/4 do not exceed 5%. Substituting Eq. 42 in Eq. 40 results in
from (4p1p2)π/4 do not exceed 5%. Substituting Eq. 42 in Eq. 40 results in
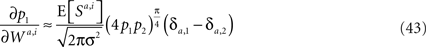
yielding Eq. 23.
Learning Rate When Syn Aptic Plasticity is Postsynaptic Activity-Dependent (Eq. 24)
In this section I compute the dependence of the effective learning rate on the probability of choice assuming the synaptic plasticity in Eq. 4c where N is the post-synaptic activity and φa,i = φ.
Substituting Eqs 20 and 43 in Eq. 14 yields

where
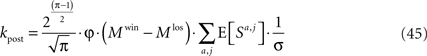
Scaling arguments show that under very general conditions, kpost hardly changes in the time relevant for the learning of p1: using Eq. 34,
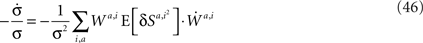
Substituting Eqs 4c and 13 in Eq. 46 yields
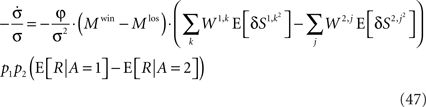
Therefore,
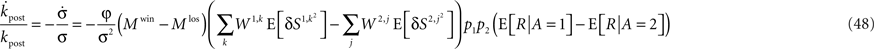
To compare the rate of change in  with the rate of change in the probability of choice, consider the ratio
with the rate of change in the probability of choice, consider the ratio  . Using Eqs 1, 44, 45, and 48,
. Using Eqs 1, 44, 45, and 48,
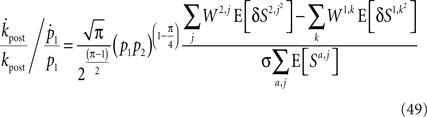
Using Assumptions 1–4,

and thus η∝(p1p2)π/4.
Learning Rate when Synaptic Plasticity is Presynaptic Activity-Dependent (Eq. 25)
In this section I compute the dependence of the effective learning rate on the probability of choice assuming the synaptic plasticity in Eq. 4c where N is the pre-synaptic activity and φa,i = φ. I further assume that this pre-synaptic activity is drawn from a Gaussian distribution.
As before, the first step is to compute the conditional fluctuations in neural activity E[δNa,j | A = 1]. For presynaptic activity-dependent plasticity, Na,j = Sa,j. Rewriting Eq. 31,

where Z′ is a zero-mean Gaussian variable with
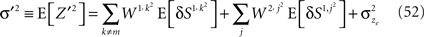
Thus,
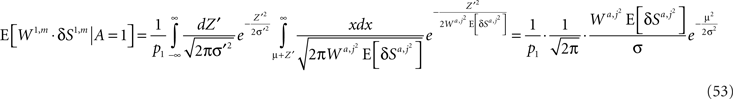
A similar calculation for E[W2,m·δS2,m | A = 1] yields
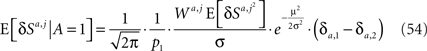
Substituting Eq. 42 in Eq. 54 yields
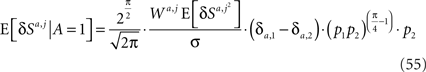
Assuming that φa,i = φ and substituting Eqs 43 and 54 in Eq. 14 yields

where
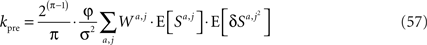
Next, I use scaling arguments to show that under very general conditions kpre hardly changes in the time relevant for the learning of p1.
Differentiating Eq. 57 with respect to time and using Eq. 34 yields
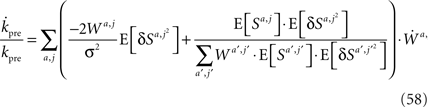
Substituting Eqs 1, 4c, 13, 41, 42, 54, 56, and 57 in Eq. 58 yields
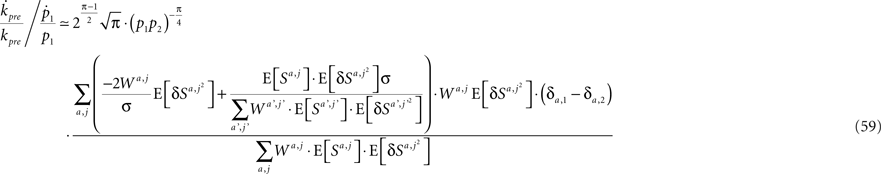
and using Assumptions 1–4,

and thus 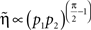 .
.
Learning Rate when Synaptic Plasticity is Hebbian
In this section I compute the dependence of the effective learning rate on the probability of choice assuming the synaptic plasticity in Eq. 4c where N is the product of presynaptic and postsynaptic neural activities and φa,i = φ. I show that the dependence of the learning rate on the probability of choice is the same as computed in the section “Learning rate when synaptic plasticity is post-synaptic activity-dependent.”
As before, to compute the learning rate we need to compute the value of E[δNa,j | A = 1] where Na,j = Sa,j·Ma.
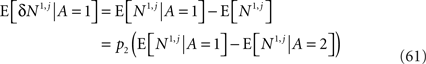
Using the assumption that E[M1|A=1]=Mwinand E[M1 | A = 2] = Mlos,
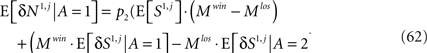
where the contributions of the average presynaptic activity and the trial-to-trial fluctuations in this activity are separated. From Eq. 54, 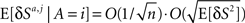 and thus the contribution of the sensory fluctuations to E[δNa,j | A = 1] is negligible, and Eq. 62 becomes
and thus the contribution of the sensory fluctuations to E[δNa,j | A = 1] is negligible, and Eq. 62 becomes
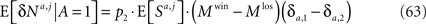
Note that Eqs 63 and 20 only differ by a constant, E[Sa,j] and therefore the dependence of the resultant learning rate on the probability of choice for the Hebbian plasticity rule is the same as in the case of postsynaptic activity-dependent plasticity.
Numerical Simulations
The reward schedule: Two-armed bandit in which alternatives 1 and 2 yielded a binary reward with a probability of 0.75 and 0.25, respectively. In Examples 1,2, the number of sensory neurons in each population was 1,000. The activity of each of these sensory neurons Sa,j in a trial was drawn from a Poisson distribution with parameter λa,i which was constant throughout all simulations. λa,i was independently drawn from a Gaussian distribution with a mean of 10 and a standard distribution of 5 truncated at λa,i = 1 (λa,i < 1 were replaced by λa,i = 1). Mwin = 12, Mlos = 2. Initial conditions in the simulations were Wa,i = λa,i/10. The synaptic plasticity rate was equal for all synapses, 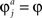 . The values of the plasticity rate in all simulations were chosen such that in the average velocity approximation, the probability of choosing alternative 1 after 200 trials would be equal to 0.75. In Figure3
A, η = 0.0110; in Figure 3
B, black circles, φ = 2.62·10−5, resulting in η0 = 0.0355; In Figure 3
B, blue circles, φ = 2.18·10−6, resulting in η0 = 0.0355; In Figure 3
C, φ = 2.90·10−3, resulting in η0 = 0.0258; In Figure 3
D, η0 = 0.0488.
. The values of the plasticity rate in all simulations were chosen such that in the average velocity approximation, the probability of choosing alternative 1 after 200 trials would be equal to 0.75. In Figure3
A, η = 0.0110; in Figure 3
B, black circles, φ = 2.62·10−5, resulting in η0 = 0.0355; In Figure 3
B, blue circles, φ = 2.18·10−6, resulting in η0 = 0.0355; In Figure 3
C, φ = 2.90·10−3, resulting in η0 = 0.0258; In Figure 3
D, η0 = 0.0488.
Income Based Model and the Linear Reward-Inaction Algorithm Rewriting (Eq. 30)
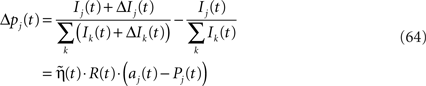
where
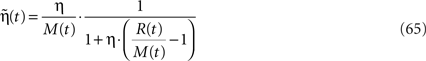
and M(t) is a an exponentially weighted average of past rewards:

If η << 1 then 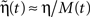 .
.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I am indebted to H. S. Seung for many fruitful discussions and encouragement. This research was supported by a grant from the Ministry of Science, Culture and Sport, Israel and the Ministry of Research, France and by THE ISRAEL SCIENCE FOUNDATION (grant No. 868/08).
Footnotes
- ^ Note that for reasons of clarity, the single index of a synapse in Eq. 14 has been replaced by two indices, the first indicating the population and the second indicating the specific synapse in that population.
- ^ In fact the example I study in Section “Materials and Methods” is slightly more general: alternative 1 is chosen in trials in which I1 − I2 > ze, where ze is a zero-mean Gaussian noise. Otherwise alternative 2 is chosen.
- ^ In the analytical derivation I assumed that the presynaptic neurons are Gaussian. However, in the numerical simulations I used Poissonian neurons. Numerical simulations reveal that the approximation is also valid for Poissonian neurons.
- ^ In the Soltani and Wang model, synaptic plasticity was not covariance-based and was restricted to the synapses that project to the “winning” population, the population that corresponded to the chosen alternative. The resultant dynamics differed from the Replicator dynamics. In particular, the fixed-point of their learning dynamics differed from the matching law in the direction of undermatching.
- ^ Note that according to Eq. 40, a cumulative normal distribution is expected to fit the numerical simulations in Soltani and Wang (2006) discussed in Example 2 better than a logistic function. In fact a careful examination of Figure 3 in that paper reveals a deviation from the fitted logistic function that is consistent with a cumulative normal distribution function.
References
Baras, D., and Meir, R. (2007). Reinforcement learning, spike-time-dependent plasticity, and the BCM rule. Neural. Comput. 19, 2245–2279.
Barraclough, D. J., Conroy, M. L., and Lee, D. (2004). Prefrontal cortex and decision making in a mixed-strategy game. Nat. Neurosci. 7, 404–410.
Bogacz, R., Brown, E., Moehlis, J., Holmes, P., and Cohen, J. D. (2006). The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced-choice tasks. Psychol. Rev. 113, 700–765.
Borgers, T., and Sarin, R. (1997). Learning through reinforcement and replicator dynamics. J. Econ. Theory 77, 1–14.
Davison, M., and McCarthy, D. (1988). The Matching Law: A Research Review.Hillsdale, NJ: Lawrence Erlbaum Assoc Inc.
Erev, I., and Roth, A. E. (1998). Predicting how people play games: reinforcement learning in experimental games with unique, mixed strategy equilibria. Am. Econ. Rev. 88, 848–881.
Farries, M. A., and Fairhall, A. L. (2007). Reinforcement learning with modulated spike timing dependent synaptic plasticity. J. Neurophysiol. 98, 3648–3665.
Fiete, I. R., and Seung, H. S. (2006). Gradient learning in spiking neural networks by dynamic perturbation of conductances. Phys. Rev. Lett. 97, 048104.
Florian, R. V. (2007). Reinforcement learning through modulation of spike-timing-dependent synaptic plasticity. Neural. Comput. 19, 1468–1502.
Gallistel, C. R., Mark, T. A., King, A. P., and Latham, P. E. (2001). The rat approximates an ideal detector of changes in rates of reward: implications for the law of effect. J. Exp. Psychol. Anim. Behav. Process. 27, 354–372.
Herfst, L. J., and Brecht, M. (2008). Whisker movements evoked by stimulation of single motor neurons in the facial nucleus of the rat. J. Neurophysiol. 99, 2821–2832.
Herrnstein, R. J. (1961). Relative and absolute strength of response as a function of frequency of reinforcement. J. Exp. Anal. Behav. 4, 267–272.
Herrnstein, R. J. (1997). The Matching Law: Papers in Psychology and Economics. Cambridge: Harvard University Press.
Herrnstein, R. J., and Prelec, D. (1991). Melioration, a theory of distributed choice. J. Econ. Perspect. 5, 137–156.
Heskes, T., and Kappen, B. (1993). “On-line learning processes in artificial neural networks,” in Mathematical Approaches to Neural Networks, Vol.51 ed. J. G. Taylor (Amsterdam: Elsevier), 199–233.
Hofbauer, J., and Sigmund, K. (1998). Evolutionary Games and Population Dynamics. Cambridge: Cambridge University Press.
Izhikevich, E. M. (2007). Solving the distal reward problem through linkage of STDP and dopamine signaling. Cereb. Cortex 17, 2443–2452.
Kempter, R., Gerstner, W., and van Hemmen, J. L. (1999). Hebbian learning and spiking neurons. Phys. Rev. E 59, 4498–4514.
Law, C. T., and Gold, J. I. (2009). Reinforcement learning can account for associative and perceptual learning on a visual-decision task. Nat. Neurosci. 12, 655–663.
Legenstein, R., Chase, S. M., Schwartz, A. B., and Maass, W. (2009). “Functional network organization in motor cortex can be explained by reward-modulated Hebbian learning,” in Advances in Neural Information Processing Systems, Vol. 22, eds Y. Bengio, D. Schuurmans, J. Lafferty, C. K. I. Williams, and A. Culotta, 1105–1113.
Legenstein, R., Pecevski, D., and Maass, W. (2008). A learning theory for reward-modulated spike-timing-dependent plasticity with application to biofeedback. PLoS Comput. Biol. 4, e1000180. doi: 10.1371/journal.pcbi.1000180.
Loewenstein, Y. (2008a). Robustness of learning that is based on covariance-driven synaptic plasticity. PLoS Comput. Biol. 4, e1000007. doi: 10.1371/journal.pcbi.1000007.
Loewenstein, Y. (2008b). Covariance-based synaptic plasticity: a model for operant conditioning. Neuroscience Meeting Planner, Washington, DC: Society for Neuroscience Abs. SFN meeting.
Loewenstein, Y., Prelec, D., and Seung, H. S. (2009). Operant matching as a Nash equilibrium of an intertemporal game. Neural. Comput. 21, 2755–2773.
Loewenstein, Y., and Seung, H. S. (2006). Operant matching is a generic outcome of synaptic plasticity based on the covariance between reward and neural activity. Proc. Natl. Acad. Sci. U.S.A. 103, 15224–15229.
Mazzoni, P., Andersen, R. A., and Jordan, M. I. (1991). A more biologically plausible learning rule for neural networks. Proc. Natl. Acad. Sci. U.S.A. 88, 4433–4437.
Narendra, K. S., and Thathachar, M. A. L. (1989). Learning Automata: An Introduction. Englewood Cliffs, NJ: Prentice-Hall.
Neiman, T., and Loewenstein, Y. (2007). A dynamic model for matching behavior that is based on the covariance of reward and action. Neural Plast. 2007, 79.
Neiman, T., and Loewenstein, Y. (2008). Adaptation to matching behavior: theory and experiments. Neuroscience Meeting Planner, Washington, DC: Society for Neuroscience Abs. SFN meeting.
Shamir, M. (2009). The temporal winner-take-all readout. PLoS Comput. Biol. 5, e1000286. doi: 10.1371/journal.pcbi.1000286.
Shanks, D. R., Tunney, R. J., and McCarthy, J. D. (2002). A re-examination of probability matching and rational choice. J. Behav. Decis. Mak. 15, 233–250.
Soltani, A., and Wang, X. J. (2006). A biophysically based neural model of matching law behavior: melioration by stochastic synapses. J. Neurosci. 26, 3731–3744.
Sugrue, L. P., Corrado, G. S., and Newsome, W. T. (2004). Matching behavior and the representation of value in the parietal cortex. Science 304, 1782–1787.
Wang, X. J. (2002). Probabilistic decision making by slow reverberation in cortical circuits. Neuron 36, 955–968.
Williams, R. J. (1992). Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 8, 229–256.
Keywords: reinforcement learning, synaptic plasticity, operant conditioning
Citation: Loewenstein Y (2010) Synaptic theory of Replicator-like melioration. Front. Comput. Neurosci. 4:17. doi: 10.3389/fncom.2010.00017
Received: 01 April 2010;
Paper pending published: 07 April 2010;
Accepted: 25 May 2010;
Published online: 17 June 2010
Edited by:
David Hansel, University of Paris, FranceReviewed by:
Maoz Shamir, Boston University, USAGianluigi Mongillo, University of Paris, France
Copyright: © 2010 Loewenstein. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Yonatan Loewenstein, Department of Neurobiology, Hebrew University, Jerusalem, 91904, Israel. e-mail:eW9uYXRhbkBodWppLmFjLmls
