A spiking neural network model of the medial superior olive using spike timing dependent plasticity for sound localization

Sound localization can be defined as the ability to identify the position of an input sound source and is considered a powerful aspect of mammalian perception. For low frequency sounds, i.e., in the range 270 Hz–1.5 KHz, the mammalian auditory pathway achieves this by extracting the Interaural Time Difference between sound signals being received by the left and right ear. This processing is performed in a region of the brain known as the Medial Superior Olive (MSO). This paper presents a Spiking Neural Network (SNN) based model of the MSO. The network model is trained using the Spike Timing Dependent Plasticity learning rule using experimentally observed Head Related Transfer Function data in an adult domestic cat. The results presented demonstrate how the proposed SNN model is able to perform sound localization with an accuracy of 91.82% when an error tolerance of ±10° is used. For angular resolutions down to 2.5°, it will be demonstrated how software based simulations of the model incur significant computation times. The paper thus also addresses preliminary implementation on a Field Programmable Gate Array based hardware platform to accelerate system performance.

Introduction

One of the key functions the ears and auditory pathways perform is that of sound localization, defined as the ability to determine from where a sound signal is generated, in relation to the position of the human head. Sound localization is considered a powerful aspect of mammalian perception, allowing an awareness of the environment and permitting mammals to locate prey, potential mates and predators (McAlpine and Grothe, 2003). In humans, sound localization depends on binaural cues which are extracted from the sound signal at each ear and compared to each other to determine from which direction the sound is traveling. The two binaural cues which play the most dominant role in sound localization are called the Interaural Time Difference (ITD), processed in the Medial Superior Olive (MSO) of the auditory system and the Interaural Intensity Difference (IID), processed in the Lateral Superior Olive (LSO). The ITD can be defined as the small difference in arrival times between a sound signal reaching each individual ear. Low frequency sound waves in the range 270 Hz–1.5 KHz have a wavelength that is greater than the diameter of the head; therefore each ear receives the sound wave at a different point in time. From this time difference, the brain can therefore calculate the angle of the originating sound source in relation to the orientation of the head (Carr, 1993; Grothe, 2003). At frequencies greater than 1.5 KHz the wavelength of the sound is similar to or smaller than the diameter of the human head, the time delay between the sound arriving at the two ears cannot be distinguished and so IID is used for localization. The combination of ITD and IID is better known as the “duplex theory of sound localization” and was first devised by Thompson and Rayleigh around the late 19th and early 20th century (Rayleigh, 1875–1876, 1907; Thompson, 1882).

An illustration of the mammalian auditory pathways involved in sound localization can be found in Figure 1. ITD processing involves the cochlea, Auditory Nerve (AN), Cochlear Nucleus (CN) and MSO. Whilst the LSO covers the wider frequency band of 1.5–20 KHz, the human MSO is calculated to be the largest of the nuclei in the Superior Olivary Complex (SOC) containing in the region of 10,000–11,000 cells (Moore, 2000) and is considered as the dominant nucleus for sound localization in humans (Kulesza, 2007). MSO cells receive excitatory innervation from both ears, and their main functionality is to work as coincidence detectors to identify the ITD and thus the azimuth sound source angle (Hancock and Delgutte, 2004). The ITDs in continuous and periodic sounds produce interaural phase differences, i.e., differences in the phase of the sound wave that approaches each ear. The fibers of the auditory nerve which respond best to low frequencies produce spike trains which are time locked to the signals’ sine curve, meaning the intervals between spikes is at the period of the curve or a multiple of that period. This occurs at both the signal onset and the ongoing signal and is important in sound localization for extracting the ITD from the sound arriving at each ear (Smith et al., 1998; Grothe, 2003; Ryugo and Parks, 2003; Joris and Yin, 2007). The stimuli at each ear which differ in phase, cause the auditory nerve fibers to produce spike trains which also exhibit a phase difference. The MSO combines the sound from the two ears; the ipsilateral inputs come directly while the contralateral inputs pass through a graded series of delays. For a sound source at a particular angle to the direction the listener is facing, an optimal delay will allow the ipsilateral and contralateral inputs to arrive coincidentally at the neuron or group of neurons, thus causing the neuron to fire. MSO neurons are organized spatially as a place map of location, i.e., a group of neurons are allocated for each particular angle on the horizontal plane (Grothe, 2003; Shi and Horiuchi, 2004). At a higher level these subgroups are subsequently also organized into frequency selective clusters as indicated in Figure 1 from Low Frequency (LF) to High Frequency (HF) regions (Kandler, 2009).

FIGURE 1

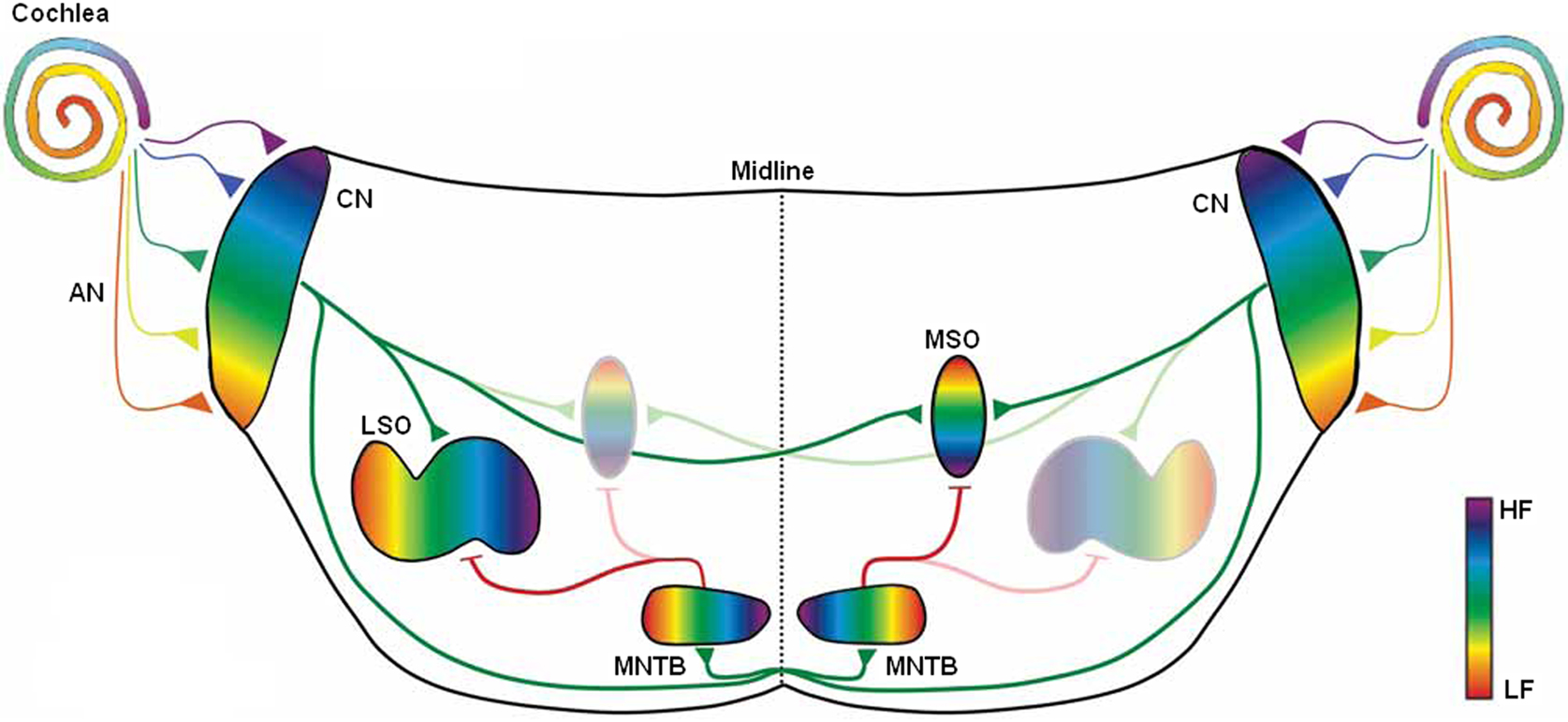
Figure 1. Spatial organization by frequency occurring in elements of the auditory system which achieve sound localization from Kandler et al. (2009).

This paper presents a Spiking Neural Network (SNN) model for sound localization. A model of the MSO based on a graded delay structure is presented which is used to perform sound localization using a biologically plausible training mechanism in the form of the Spike Timing Dependent Plasticity (STDP) learning rule (Bell et al., 1997; Markram et al., 1997; Bi and Poo, 1998; Zhang et al., 1998; Song et al., 2000). Acoustical input data, generated from an adult domestic cat is used for training and testing purposes (Tollin, 2004, 2008; Tollin et al., 2008; Tollin and Koka, 2009). Section “Models of Sound Localization” of this paper contains a review of models for sound localization previously reported in the research literature. In Section “SNN Model of the MSO”, an overview of the proposed MSO model is provided including details on the SNN architecture, neuron model and training mechanism employed. Experimental results are presented in Section “Results” including a comparison between software and hardware based implementation approaches, subsequently followed by a discussion on the most significant findings of the research in Section “Discussion”. Finally, the conclusions and a summary of future work are presented in Section “Conclusions and Future Work”.

Models of Sound Localization

The first computational model to demonstrate how ITD in mammals is used to determine the angle of origin of a sound signal was developed by Jeffress (1948). This model involved time or phase-locked inputs, facilitated via a set of delay lines, to vary the axonal path lengths arriving at the neuron and an array of coincidence detector neurons which only fire when presented with simultaneous inputs from both ears (Carr, 1993; Grothe, 2003; McAlpine and Grothe, 2003). The fundamental importance of Jeffress’ model and why it has become the prevailing model of binaural sound localization is its ability to depict auditory space with a neural representation in the form of a topological map. A graphical representation of the Jeffress model is shown in Figure 2.

FIGURE 2

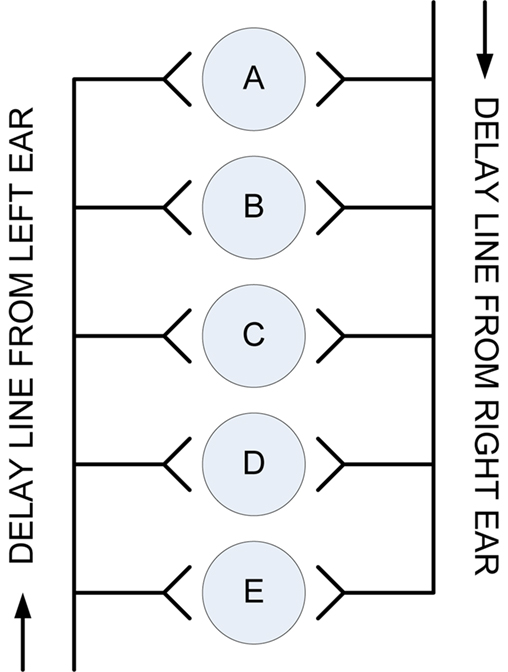
Figure 2. The Jeffress model of ITD based binaural hearing (Jeffress, 1948).

Up to the 1980s this simplistic model remained hypothetical until evidence was found which showed that the nucleus laminaris of the barn owl (homologous to the MSO in mammals) works in a similar manner (Carr and Konishi, 1990; Carr, 1993; Konishi, 2000; Burger and Rubel, 2008). However, the occurrence, structure and function of this simple delay line model in the MSO of mammals has been debated at length. Studies of the cat MSO have found evidence for differing axon lengths from the contralateral ear to the MSO where the shortest axons innervate the rostral MSO cells and the longer axons innervate caudal MSO cells, thus indicating agreement with the Jeffress model (Smith et al., 1993; Beckius et al., 1999). However, both studies also show that each axon only innervates a small portion of the MSO, unlike in the nucleus laminaris of the bird in which the entire nucleus is innervated. Less studies have been carried out on the anatomical and physiological structure and function of the mammalian MSO in comparison to the avian nucleus laminaris to determine conclusively whether the Jeffress model is an appropriate representation.

A number of computational models utilizing various mathematical techniques for sound localization have been reported in the literature (Huang et al., 1999; Handzel and Krishnaprasad, 2002; Nakashima et al., 2003; Willert et al., 2006; Keyrouz and Diepold, 2008, Li et al., 2009; Murray et al., 2009). In attempting to develop more biologically inspired approaches, a number of researchers have also proposed ANN based models (Palmieri et al., 1991; Backman and Karjalainen, 1993; Datum et al., 1996; Abdel Alim and Farag, 2000; Chung et al., 2000; Hao et al., 2007; Keyrouz and Diepold, 2008). As with their computational counterparts, it has been demonstrated that such networks can be used to localize sound sources. The neuron models used in such networks however, are highly abstracted from their biological counterparts. Inspired by neurophysiological studies on the functionalities of specific auditory neurons, a number of researchers have therefore sought to create SNN models for sound localization more closely aligned with the biological principles of auditory processing.

The first such example was proposed in 1996 by Gerstner and colleagues (Gerstner et al., 1996; Kempter et al., 1996), where Integrate-and-Fire (I&F) neurons were used to model the high precision temporal processing of the barn owl auditory pathway. Before learning, the model of the nucleus magnocellularis neuron is converged upon by many auditory input fibers with varying delays. The input to the system is a periodically modulated signal from which input spikes are generated via a stochastic process. An unsupervised Hebbian learning rule is subsequently used to strengthen the synaptic connections which enable the neuron to generate a periodic phase-locked output whilst those that are deemed unnecessary are removed. Thus, the neuron is effectively tuned to emit spiking behavior when a particular input frequency signal is applied. Whilst this technique was initially used on monaural inputs, the model was subsequently expanded to enable the ITD for binaural inputs to be determined. In this model, the neuron is stimulated simultaneously by an input signal as well as a fixed ITD time shifted signal where an unsupervised Hebbian learning rule is again used to select the optimal synaptic connections which enable a phase-locked spike output to be produced. After learning, this neuron is subsequently tuned to respond to this particular ITD for the given input frequency used during training. The authors subsequently propose that a series of these neurons may be used, each tuned to a particular interaural delay, where the overall ITD is estimated from the neural firing pattern by a population vector decoding scheme. Using this method it was estimated that approximately 100 neurons could be used to estimate the ITD with a temporal precision of 5 μs, i.e., the temporal precision of the barn owl auditory system. This work presented an efficient method for determining the ITD and was the first example of a model which accomplished this using spiking neurons. Subsequent research in this field has sought to build on this initial work through the development of models incorporating additional aspects of the auditory processing pathway which can be used to estimate azimuthal angles for sound sources across appropriate frequency ranges.

In a related approach but targeting lower latency responses, Smith (2001) employed the use of depressing synapses to detect the onsets in a phase-locked sound signal. It was observed that these onsets could be used to measure the ITDs and thus perform sound source localization. As opposed to the stochastic process used in Gerstner et al. (1996), the input audio signal was converted into a spike train by passing it through a cochlear filter, half-wave rectifier and a logistic spike generation function. Digitized sound signals were played in the presence of a model head with two microphones positioned in each ear canal. The signals covered an angular range from −70° to 30° with a resolution of 10°, at frequencies ranging from 220 Hz–3.25 KHz. This method has shown that ITDs can successfully be estimated using the approach described whilst higher accuracy was observed for lower angles at higher sound frequencies. A SNN based extensively on the Jeffress sound localization model has also been developed by Schauer et al. (2000) for implementation in a custom Very Large Scale Integration (VLSI) device. A digital delay line with AND gates was used to capture the inherent principles of the Jeffress model in an efficient manner for a hardware based implementation. Input data was recorded in an open environment with results indicating that the model was proficient at localizing single sound sources for 65 azimuthal angles. In 2007, BiSoLaNN was developed with functionality based on the ITD auditory cue (Voutsas and Adamy, 2007). The network can be described as a cross-correlation model of spiking neurons with multiple delay lines and both inhibitory and excitatory connections. Also developed was a model of the cochlea, inner hair cells and coincidence neurons. The system was subsequently tested on pure-tone sound signals between 120 Hz–1.24 KHz, which were recorded in an anechoic chamber using the Darmstadt robotic head. The localization accuracy of these frequencies was found to be 59% where it was noted that signals originating from the front of the head were localized with a higher degree of accuracy than those which originated from the two sides. In the same year, Poulsen and Moore (2007) demonstrated how SNNs could be combined with an evolutionary learning algorithm to facilitate sound localization. This work involved a simulation in a 2-dimensional environment wherein multiple agents possess an SNN which controls their movements based on binaural acoustical inputs. The evolutionary learning algorithm is employed to evolve the connectivity and weights between neurons which were based on the Spike Response Model (SRM) (Gerstner and Kistler, 2002). The evolutionary training algorithm involved updating an agents’ fitness score, i.e., increasing it if they moved closer to the sound source and decreasing it if they moved further away. After training, most agents were able to localize single sound sources, however a notable degradation in performance was observed when multiple sound sources were tested. Research on SNNs for sound localization has also led to the development of an auditory processing system to provide live sound source positions utilizing both ITD and IID to localize a broadband sound (Liu et al., 2008a). The input to the system is determined by passing the sound from two microphones through a Gamma-tone filter-bank. This process splits it into a number of frequency channels which are then encoded as phase-locking spikes. These spikes then take two routes, through the ITD and IID pathways. The ITD pathway consists of a Leaky Integrate-and-Fire (LIF) neuron which produces spikes relating to the time difference between the two inputs whilst the IID pathway uses a logarithmic ratio which computes the intensity difference and produces a spike based on this value. The network was tested on an artificial sound source covering a sweep from −90° to 90° with a relatively coarse resolution step of 30° between input locations. In the experiments conducted it was again observed that the highest localization accuracy was observed when the sound source was directly in front of the target, i.e., at the 0° position. The overall localization efficiency was determined to be 80%, which increased to 90% when a subset of input angles was used, i.e., −45° ≤ θ ≤ 45°. Further work by the same authors has involved replacing the logarithmic ratio mathematics for the IID pathway with a neuron model (Liu et al., 2008b). Experiments were performed on the network using artificial sound and real tones again with the same set of angles as before. Similar results of 80% occurred for the artificial sound across all angles whilst a localization accuracy of 95% was observed for the angles −45° ≤ θ ≤ 45°. Testing on a real sound gave 65% accuracy across all angles. In 2009, this work was again extended through the incorporation of a model of the inferior colliculus into the network where successful localization of white noise, speech and pure-tone inputs was again observed (Liu et al., 2009).

It is evident that a growing trend is emerging in the research literature towards forming a deeper understanding of how sound localization is performed in biological systems. In terms of sound localization, many researchers have based their work on the Jeffress model which, despite its relative simplicity, is generally regarded as being an appropriate representation of the MSO in mammals. Limited progress has been made however, on the development of a Jeffress inspired architecture using spiking neurons. This paper therefore, aims to address these issues by creating a Jeffress based model for the MSO using spiking neurons which is inspired by the biology of the auditory pathways to emulate the way in which mammals can localize sounds. Whilst the approaches discussed in this section have all used either simulated input data or Head Related Transfer Function (HRTF) data generated from a theoretical model of the human head, this work seeks to use real biologically observed data as input to the system. Furthermore, the network is trained to perform sound localization by means of a biologically plausible training mechanism observed in the biological brain in the form of the STDP learning rule. Whilst alternative SNN based models have typically used a resolution of θ ≥ 10°, an additional aim of this work is to determine the impact on localization accuracy when this input resolution is significantly increased, i.e., for θ ≥ 2.5°. Finally, this paper also considers that the eventual deployment environment for this model is likely to require a mobile solution such as on a robotic based platform, where powerful desktop processing is simply not available. Hence, the paper will also examine the implications and considerations for adopting a hardware based implementation strategy for the proposed model.

SNN Model of the MSO

In this section, details on the MSO model developed for performing sound localization are presented. This model is an extension of work previously presented by Wall et al. (2007, 2008). The model description commences with a high level overview of the network topology which includes a discussion on the method used to generate input data for the system. This is followed by descriptions of the spiking neuron model and the STDP learning rule used in the implementation.

Network Architecture

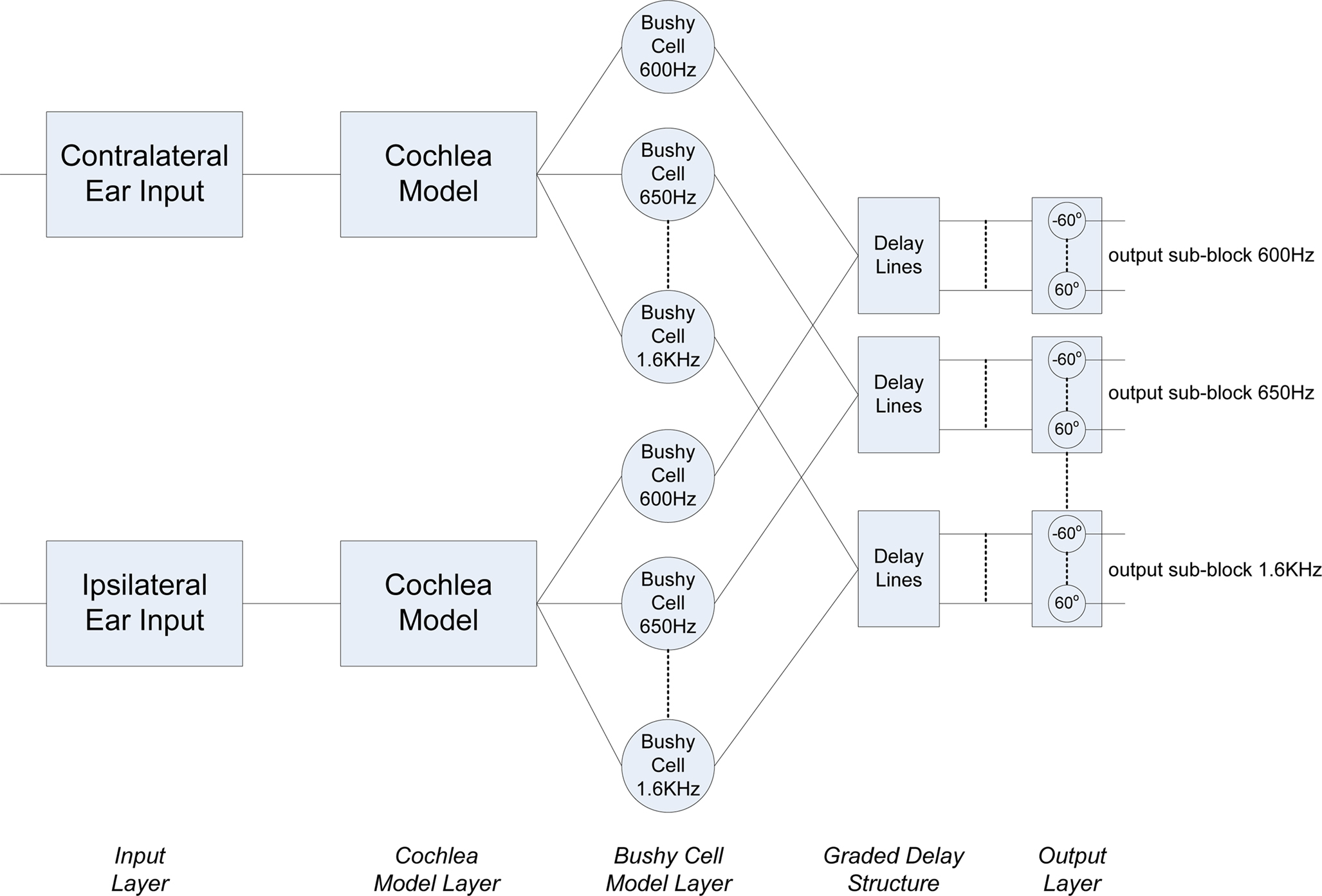
The complete network architecture for the MSO model is shown in Figure 3 and consists of a series of layers:

• Input Layer

• Cochlea Model Layer

• Bushy Cell Neurons

• Graded Delay Structure

• Output Layer

FIGURE 3

Figure 3. An overview of the proposed MSO model for sound localization.

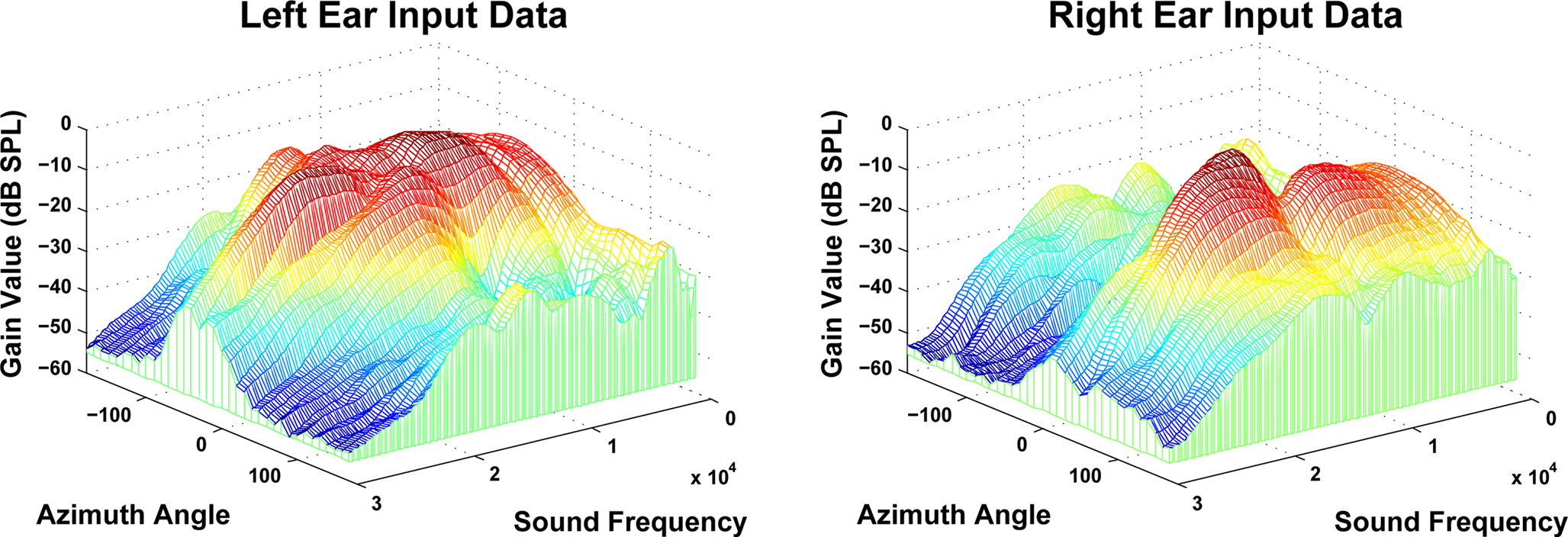
The input layer directly corresponds to the ipsilateral and contralateral ear inputs in the mammalian auditory system. As previously discussed, rather than utilize purely simulated data or HRTF generated from models of the human head, this research sought to process biologically realistic input data. To accommodate this, acoustical data generated from the adult domestic cat was supplied by Dr. Daniel J. Tollin (Tollin, 2004, 2008; Tollin et al., 2008; Tollin and Koka, 2009). This data consists of a set of HRTFs for a series of sound wave frequencies for both the left and right ears at a specific azimuthal angle. HRTF data designates the filtering of a sound before it reaches the cochlea after the diffraction and reflection properties of the head, pinna and torso have affected it. The complete data set includes ipsilateral and contralateral sample pairs for 36 different azimuthal angles (−180° to 170° in steps of 10°) at 148 distinct sound frequencies (600 Hz–30 kHz in steps of 200 Hz). As previously discussed, this research is primarily interested in developing a model of the MSO, hence the frequency range of particular interest in this regard was from 600 Hz–1.6 KHz, i.e., the upper frequency bound for which the ITD can be used for sound localization. It has also been stated however, that a further goal of this work is to ascertain the impact of increasing the azimuthal angle resolution during the training and testing phases. To facilitate this, interpolation of the input dataset was used to provide the required resolution. A 3D surface plot of the acoustical data for the left and right inputs is shown in Figure 4.

FIGURE 4

Figure 4. 3-D mesh surface plot of the acoustical input data.

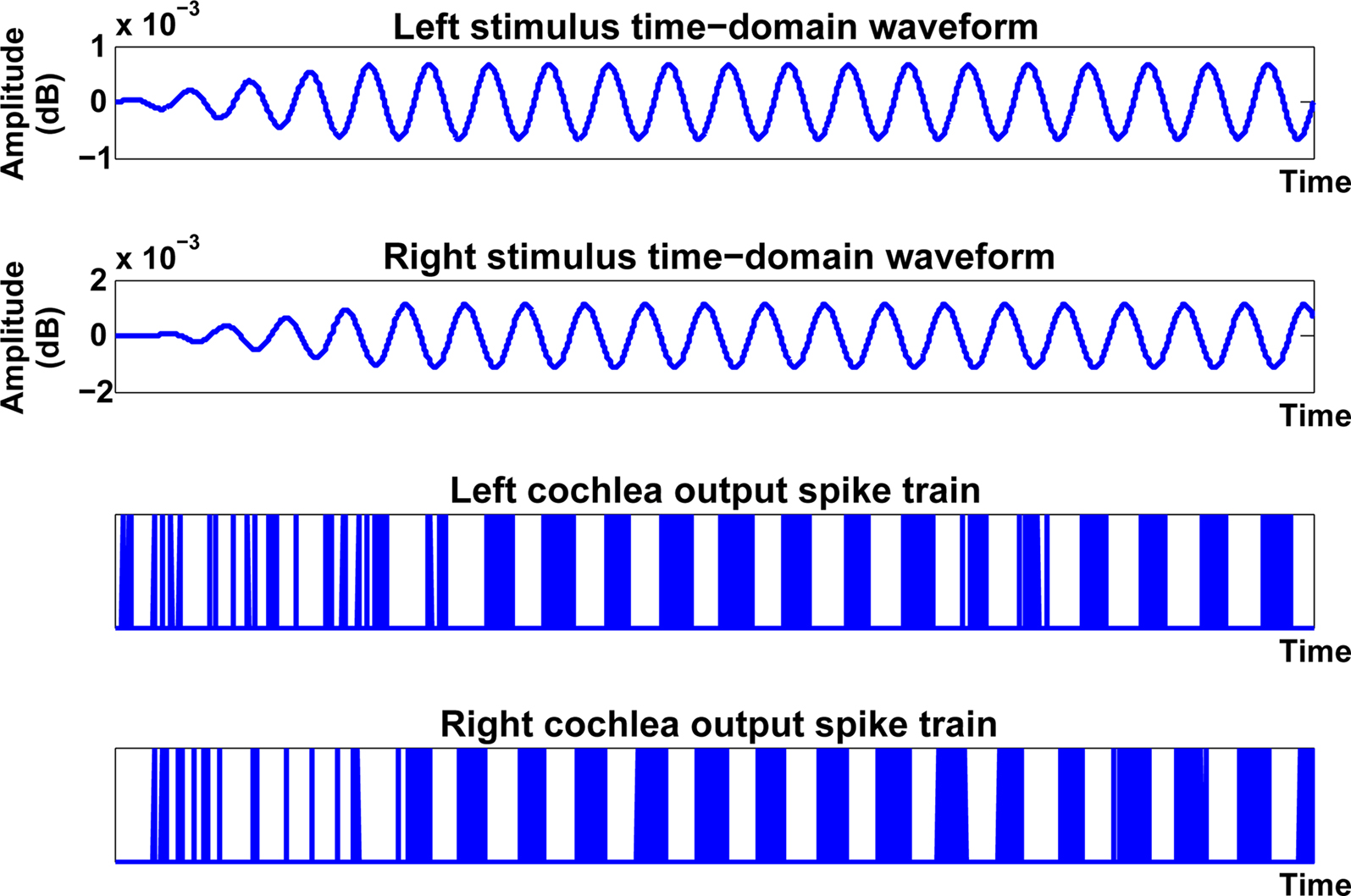
As indicated in Figure 3, the next layer in the network is the cochlea, with two instantiations of the model receiving inputs from the ipsilateral and contralateral inputs in a manner which is consistent with the mammalian auditory processing pathway. The cochlea model in this work was developed by Zilany and Bruce (2006, 2007). It is based on empirical observations in the cat and as such, is highly appropriate for post-processing the aforementioned HRTF data, which was also generated from an adult cat (Tollin and Koka, 2009). Each cochlea takes the frequency and the HRTF of a sound at a particular angle as input and produces a spike train based on and relating to that input. The input to the cochlea model initially passes through a middle-ear filter and then through three parallel filter paths; a wideband filter which depicts the filtering properties of the basilar membrane, a chirping filter which is similar to the wideband filter but does not include properties from the Outer Hair Cells (OHC), and a control path filter which models the effects of the OHC functionality. The outputs of the wideband and chirping filters then pass through models of Inner Hair Cells (IHC), after which the two outputs are summed and then low-pass filtered to produce the IHC receptor potential. This potential causes activity at a synapse model and ultimately spikes are generated through an inhomogeneous Poisson encoding process. As the spike trains generated by the cochlea model are encoded by a Poisson process, when the same data point is passed through the cochlea multiple times the spike train frequencies generated will not be identical but will be distributed around a mean frequency. Spike train frequencies generated are usually within ±30 Hz of that mean frequency, but in some cases spike trains will be generated with a frequency which is far removed from that mean frequency; these spike trains do not naturally lend themselves to being successfully classified. Thus, in the experiments conducted as part of this research, the training and testing phases were repeated several times to reduce the possibility of such anomalies distorting the results. The output of the cochlea model is characterized by bursts of spikes which are phase locked to the original sound frequency as shown in Figure 5. As indicated in Figure 3, a series of frequency selective outputs are emitted from the cochlea model (e.g., 600, 650 Hz etc.). This relates back to the auditory system presented in Figure 1, which indicates the presence of frequency selective clusters or regions in the biological MSO.

FIGURE 5

Figure 5. Plot showing sample output data from the cochlea model.

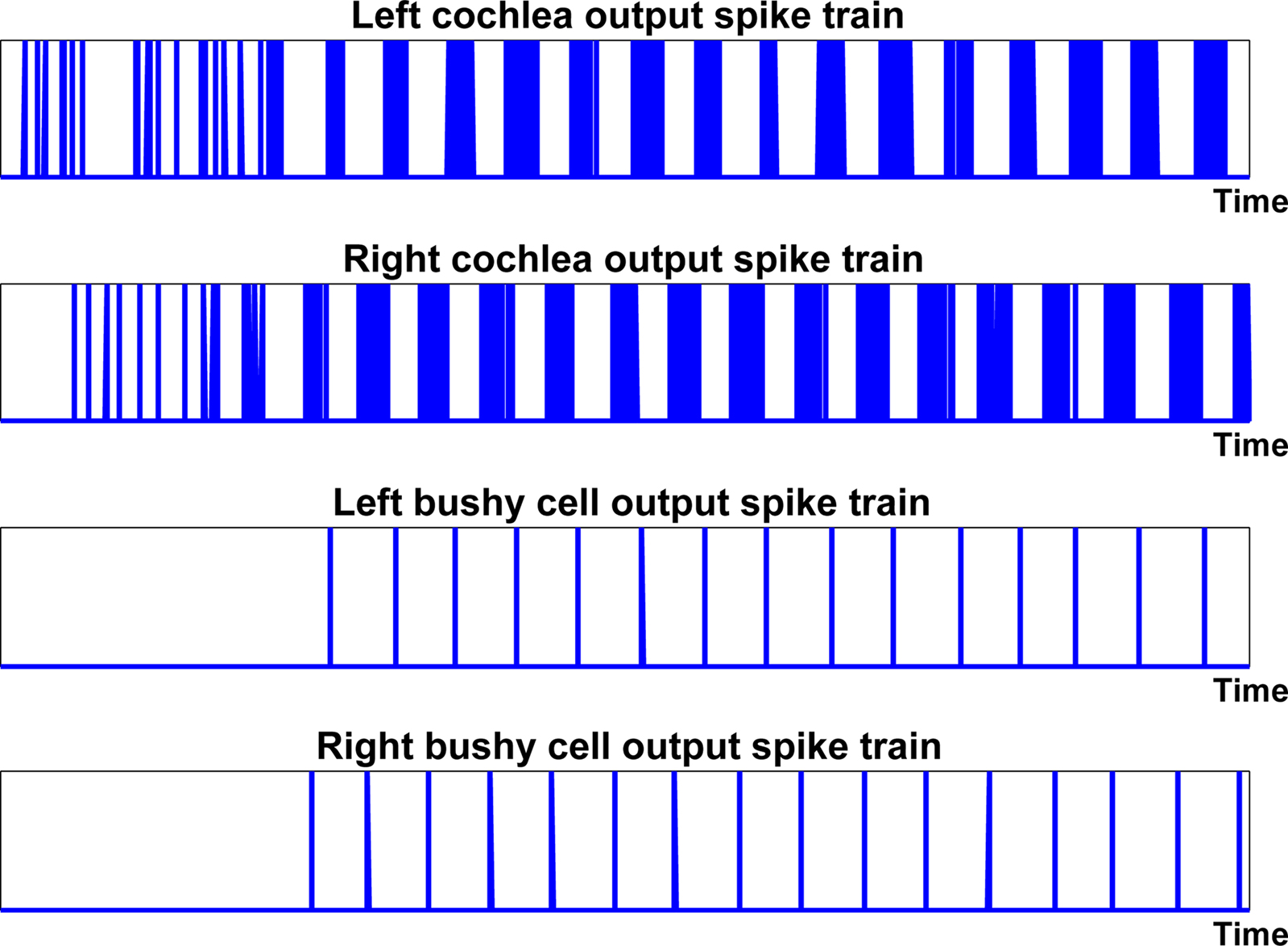
The next step in the auditory processing pathway is to process this bursting spiking activity via the bushy cell neuron layer. Knowledge of the role of bushy cells in biology remains somewhat limited but it is known that the main function of these cells in the auditory processing pathway is to maintain the phase-locked signal and to minimize the impact of noise. It is thought that bushy cells do not have a one-to-one response to auditory nerve input at low frequencies, but that a number of inputs occurring in a short space of time are required to cause the bushy cell to respond (Yin, 2002). These cells were used in the proposed network as a form of coincidence detector to convert the phase-locked bursting activity of the cochlea model to the single spike instances, as shown in Figure 6. This processing was implemented using a LIF neuron (see Appendix) where the phase-locked single spike output in place of a burst of spikes was achieved through selection of an appropriate neuron threshold and refractory period. The parameters are fixed for each bushy cell in the network, i.e., the same parameters are used for each sound frequency with which the network was trained and tested.

FIGURE 6

Figure 6. Plot showing sample output data from the bushy cell neuron.

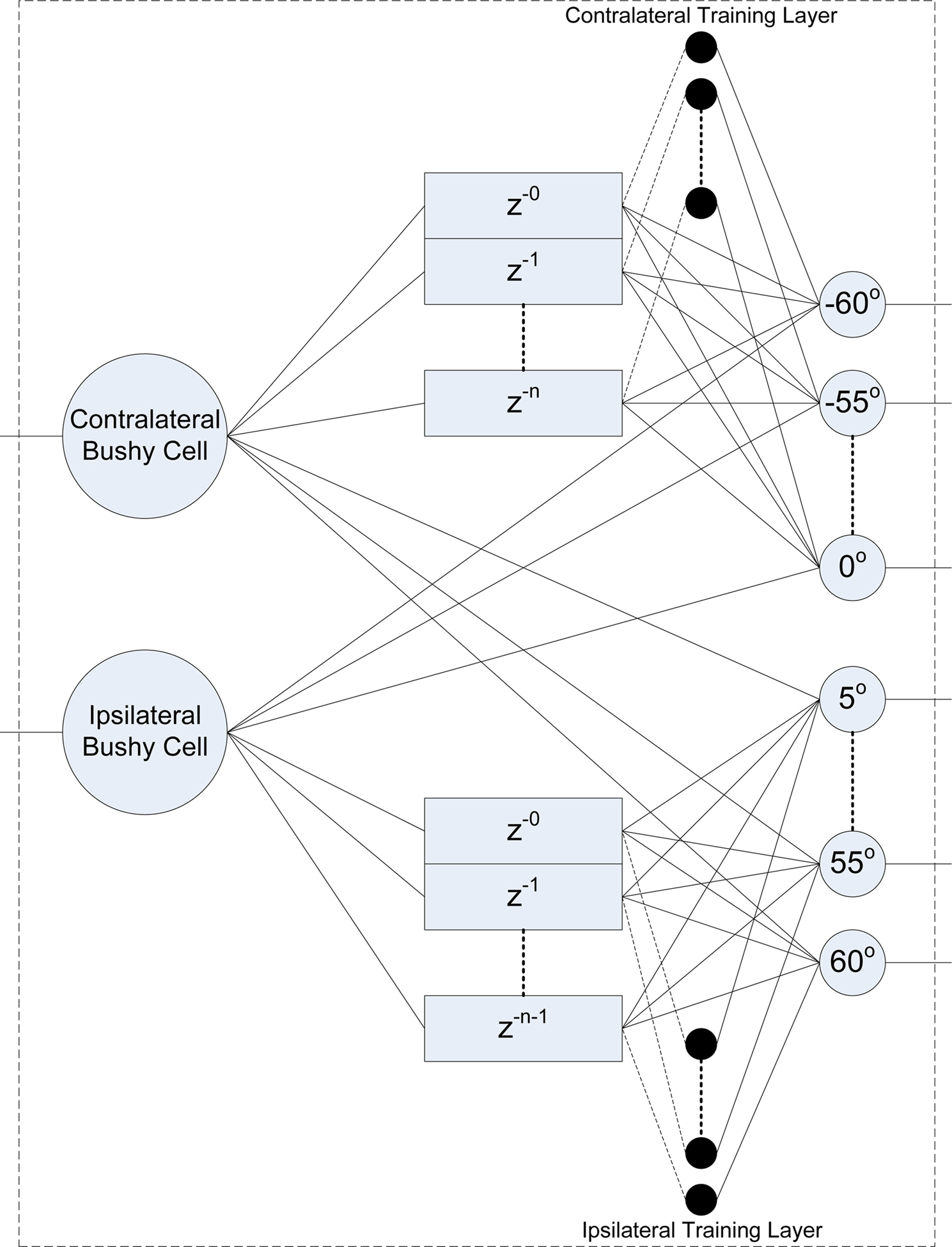
Inspired by the Jeffress model for sound localization (Jeffress, 1948), the authors propose that the multiple delay structure employed in the network model is a viable representation of the graded series of delays found in the biological MSO. In the mammalian auditory pathway, the stimuli at each ear which differ in phase, cause the auditory nerve fibers to produce spike trains which also exhibit a phase difference. The MSO combines these spike trains from each ear; the ipsilateral inputs are delivered directly while the contralateral inputs pass through a series of graded delays. For a sound source at a particular angle to the listener, only one particular delay will allow the ipsilateral and contralateral inputs to match, i.e., the original out-of-synch phase-locked spike trains come into phase. The network topology shown in Figure 7 demonstrates a method for accomplishing this functionality using spiking neurons. The neuron model used in this instance was the conductance based Integrate-and-Fire (I&F) model proposed by Destexhe (1997). This model was selected as it provides comparable behavior to more complex neuron models such as Hodgkin-Huxley (HH) (Hodgkin and Huxley, 1952) but with considerably less computational demands. Further details of the neuron model equations and parameters can be found in an Appendix.

FIGURE 7

Figure 7. The graded delay structure, an SNN based interpretation of the Jeffress model.

As shown in the Figure 7, the output of each bushy cell neuron is fully connected to the output layer, where each output neuron represents a distinct azimuthal angle. It can also be seen that the output neuron layer is organized into two groups, one for sound sources originating to the left of the head (−60° ≤ θ ≤ 0°) and the other for angles to the right of the head (0° < θ ≤ 60°). As the delay structures are fully connected to the output layer, each output neuron receives a series of delayed spikes for each single spike emitted by the corresponding bushy cell. In the proposed network model, these connections are facilitated via STDP synapses. In addition to these plastic synapses, each output neuron is also connected directly to the opposite bushy cell neuron using a fixed synapse, i.e., all left neurons (−60° ≤ θ ≤ 0°) receive direct input from the right bushy cell neuron and vise versa. Thus, when spikes from the direct and delayed inputs to the neuron coincide and the strength of the synaptic connection is of a sufficient value, an output spike or action potential is generated.

During the training phase for the network, a teaching signal in the form of a spike train is supplied to indicate which of the output neurons should be displaying spiking activity. Based on the principles first proposed by Deneve et al. (2001) the training method adopted has previously been used by the authors to facilitate co-ordinate transformation using SNNs (Wu et al., 2005, 2008). As indicated in Figure 7, each output neuron is connected to a delay line source via the training layers (contralateral and ipsilateral) where the dashed line is used to indicate a non-permanent connection. For example, if during the training process the data being supplied to the model is for a sound source located at −55°, enabling the corresponding training neuron will provide a connection between the delay line and the target output neuron. As the synaptic strength of these training layer connections are of a sufficiently high level, a single input spike will ensure that an action potential is generated for the target neuron. By nature of the STDP learning rule, any preceding input spikes to this neuron via the delay lines will result in an increase in synaptic weight for that connection. Subsequently, when the training phase is complete and the network is supplied with just the ipsilateral and contralateral input data, the corresponding output neuron representing the source azimuth angle should display spiking behavior.

The length of each delay indicated in Figure 7 was determined using a simple formula devised by Lord Rayleigh (Abdel Alim and Farag, 2000). He considered a sound wave traveling at the speed of sound, c = 343 m/s, which makes contact with a spherical head of radius r from a direction at an angle θ. The sound arrives at the first ear and then has to travel the extra distance of rθ+ rsinθ to reach the other ear as indicated in Figure 8. Dividing that distance by the speed of sound gives the simple formula:

FIGURE 8

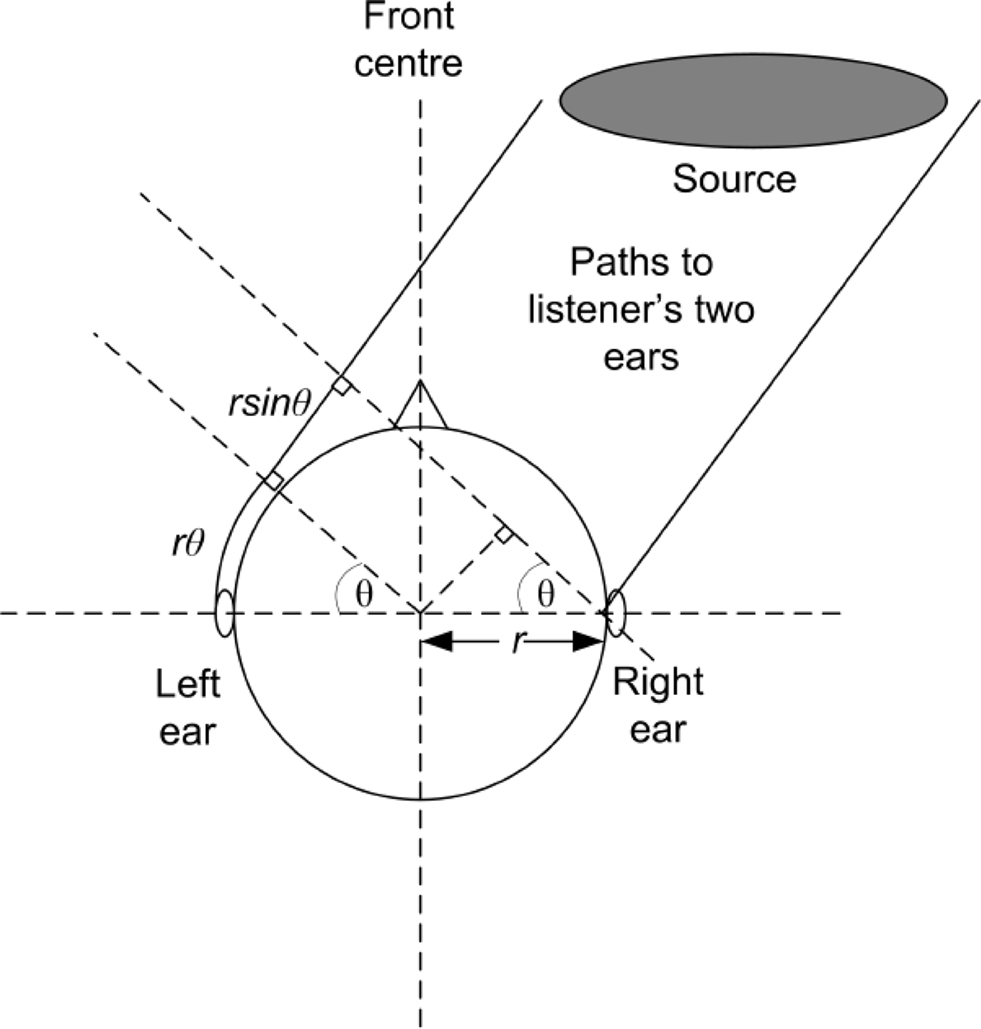
Figure 8. Diagrammatic view of Rayleigh’s simple formula for determining the ITD, adapted from Rumsey (2001).

It should be noted that this formula determines the ITD based on the assumption that the head is spherical or round. In consideration, it was decided to investigate the research of Nordlund (1962) where a series of experiments were conducted to measure the interaural time differences using a model of a true standard head. A plot of the ITD values as a function of azimuth angle for those calculated by Rayleighâ™ formula against those measured in Nordlundâ™ experiments is presented in Figure 9. It can be seen from this figure that the estimated ITDs provide an acceptable approximation with an average error of 0.0457 ms being observed across the full range of angles from 0° to 180°.

FIGURE 9

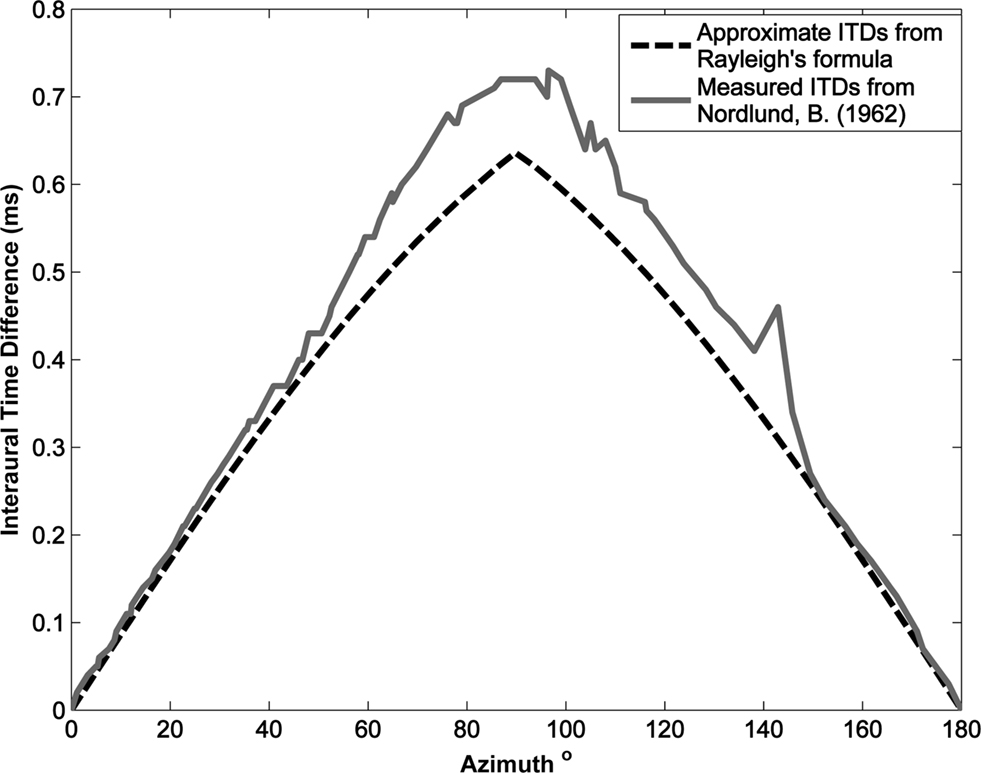
Figure 9. Interaural time difference as a function of azimuth, comparing the approximate ITD values determined by Rayleigh’s formula and those experimentally measured by Nordlund (1962).

Spike Timing Dependent Plasticity

Spike Timing Dependent Plasticity is a form of Hebbian learning that can be used to modulate synaptic weights due to temporal correlations between pre- and post-synaptic neurons. The STDP rule essentially validates Hebbs postulate dating back to 1949 (Hebb, 1949), but adds a mechanism to replicate the impact temporal information has on synaptic modifications. The first experiments that precisely measured this biological effect were presented in 1997 by Markram et al. (1997) with subsequent experimental observations being reported soon after Bell et al. (1997), Bi and Poo (1998), and Zhang et al. (1998). Examples of STDP in large scale SNNs have been reported for both software (Izhikevich et al., 2004; Hosaka et al., 2008; Masquelier et al., 2009) and hardware (Indiveri et al., 2006; Yang and Murray, 2006; Schemmel et al., 2007; Arena et al., 2009) based implementations whilst application domains of STDP have included handwritten digit recognition (Nessler et al., 2009), pattern analysis (Natschläger and Ruf, 1999) co-ordinate transformation (Wu et al., 2008) and robotic control (Northmore, 2004; Alnajjar and Murase, 2008).

The STDP learning rule is used in the proposed model to regulate the synaptic weights between the delay lines and the output neuron layer. The underlying premise of STDP is that each synapse in a SNN is characterized by a weight or peak conductance, q (the peak value of the synaptic conductance following a single pre-synaptic action potential), that is constrained to lie between 0 and a maximum value q_max. Every pair of pre- and post-synaptic spikes can potentially modify the value of q, and the changes due to each spike pair are continually summed to determine how q changes over time. As stated in Song and Abbott (2001), a pre-synaptic spike occurring at time t_pre and a post-synaptic spike at time t_post modify the corresponding synaptic conductance by q→q + q_max•F(Δt) where Δt = t_post − t_pre and F(Δt) is defined by:

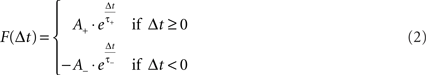
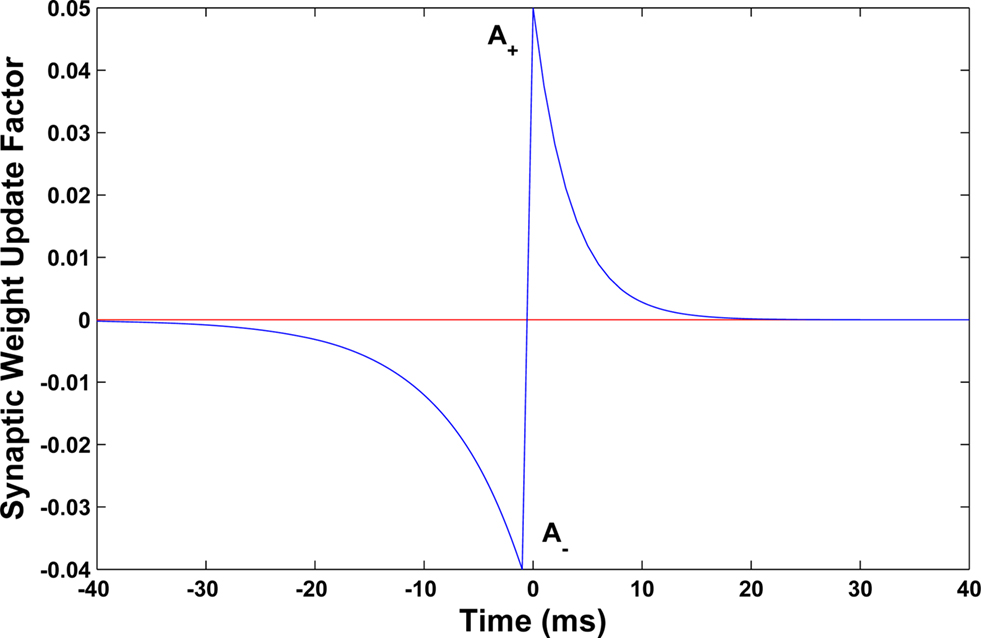
The time constants τ₊ and τ₋ determine the range of the plasticity window and A₊ and A₋ determine the maximum amount of synaptic modification in each case. The plasticity window for the MSO model implementation is presented in Figure 10 where the STDP parameter set used was (A₊ = 0.05, A₋ = 0.04, τ₊ = 4, τ₋ = 8). Whilst the temporal window for plasticity has been found to vary in different parts of the brain (Bi and Poo, 1998; Abarbanel et al., 2002; Dan and Poo, 2006), the chosen parameter set was selected based on observations by Tzounopoulos et al. (2004)which indicate that the precise timing requirements for coincident detection of pre- and post-synaptic spike events in the auditory processing pathway have resulted in plasticity windows that are shorter when compared to other mammalian synapses exhibiting STDP. This assumption is based on observations of STDP in the auditory processing pathway of mice where no synaptic plasticity updates were detected when the interval between pre and post events was longer than 20 ms (Tzounopoulos et al., 2004).

FIGURE 10

Figure 10. STDP modification function used to determine the change in synaptic weight.

The chosen implementation method is based on the Song and Abbott approach (Song et al., 2000; Song and Abbott, 2001). To enable on-line calculation of weight updates, the STDP potentiation and depression values for each synapse are determined in a similar manner to how the excitatory and inhibitory conductances are calculated. Each pre-synaptic spike causes the STDP potentiation a₊(t) to increase by an amount A₊ followed by an exponential decay in the form:

In a similar manner, each post-synaptic spike causes the STDP depression a₋(t) to increase by an amount A₋ followed by the exponential decay:

Using the forward Euler integration scheme, these equations can be solved respectively as:

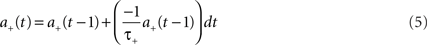
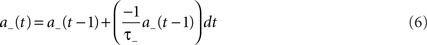
Whilst these equations are used to determine STDP potentiation and depression values, the next stage is to determine the actual changes in synaptic conductance. To achieve this, the synaptic weight is increased when a post-synaptic spike event occurs where the updated weight value is calculated as:

In a similar manner, the synaptic weight is decreased when a pre-synaptic spike event occurs where the update is calculated as:

Results

This section will discuss the results obtained when the model described in the previous section was implemented in software. Preliminary hardware results will also be presented which will indicate the potential acceleration performance that can be achieved. The cochlea model supplied by Zilany and Bruce (2006, 2007) was developed to integrate with the Matlab environment, hence the input, cochlea and bushy cell neuron layers were simulated using this tool. This Matlab model, created as outputs, a spike event list for each bushy cell neuron in the network using an Address Event Representation (AER) scheme. This data could subsequently be processed by a software or hardware based implementation of the delay layer and output layer of the MSO model.

Software Implementation

As the number of neurons and STDP synapses were expected to grow to a considerable size, particularly at the finer azimuth angular resolutions being targeted, it was decided to use a compiled language (C++) to reduce computation times. A user interface to control simulations was developed using the wxWidgets Graphical User Interface (GUI) library. Training and testing data were prepared by sweeping across the angular range of sound source signals (−60° ≤ θ ≤ 60°). The training stimulus was supplied first where the input stimulus for each angle was applied for the equivalent of 10-s real time. After the weights had stabilized, this procedure was subsequently repeated using test data to determine how well the network was able to perform sound localization.

In the first experiment, an angular resolution of θ = 5° was used where the input frequency of the sound source was also increased incrementally from 600 Hz to 1.6 KHz in steps of 50 Hz. The overall network topology to accommodate this involved 21 frequency selective clusters each containing 25 output neurons, thus giving a total of 525 neurons in the network. As indicated in Figure 7, within each cluster, the left output neurons (n = 13) were fully connected to the graded delays emanating from the left bushy cell neuron and the right neurons (n −?1 = 12) were connected in the same manner to the graded delays from the right bushy cell neuron. Thus, with 313 STDP synaptic connections in each cluster (13² + 12²), the total number of STDP synapses in the network was 6,573.

The classification accuracy of the network was evaluated using two metrics. As the spiking activity of the output layer can be distributed across multiple neurons simultaneously, the number of spikes occurring within both ±5° and ±10° of the target azimuth angle were determined and used to create an overall classification accuracy for these tolerance values. Due to the Poisson based nature of the spike data emanating from the cochlea model, the training and testing procedures were repeated four times to calculate mean values. A plot of the classification accuracies across the frequency range used in the experiments is shown in Figure 11. Overall, an average classification accuracy of 70.63% was obtained for the ±5° tolerance whilst this increased to 90.65% for the ±10° tolerance. As can be seen in the diagram, the network reports high accuracies above 90% for angles in the frequency range 600 Hz–1.25 KHz with a slight degradation being observed for higher frequencies. It should be noted however that this is consistent with the research literature which signifies the MSO as being the dominant nucleus in performing sound localization at lower frequencies whilst the LSO is used for higher frequencies. A plot illustrating the spiking activity of the output layer when an 1 KHz input signal is rotated from −60° to 60° is shown in Figure 12 whilst the weight distribution for the STDP synapses after training is complete, is shown in Figure 13 where each output neuron indicates a specific azimuth angle.

FIGURE 11

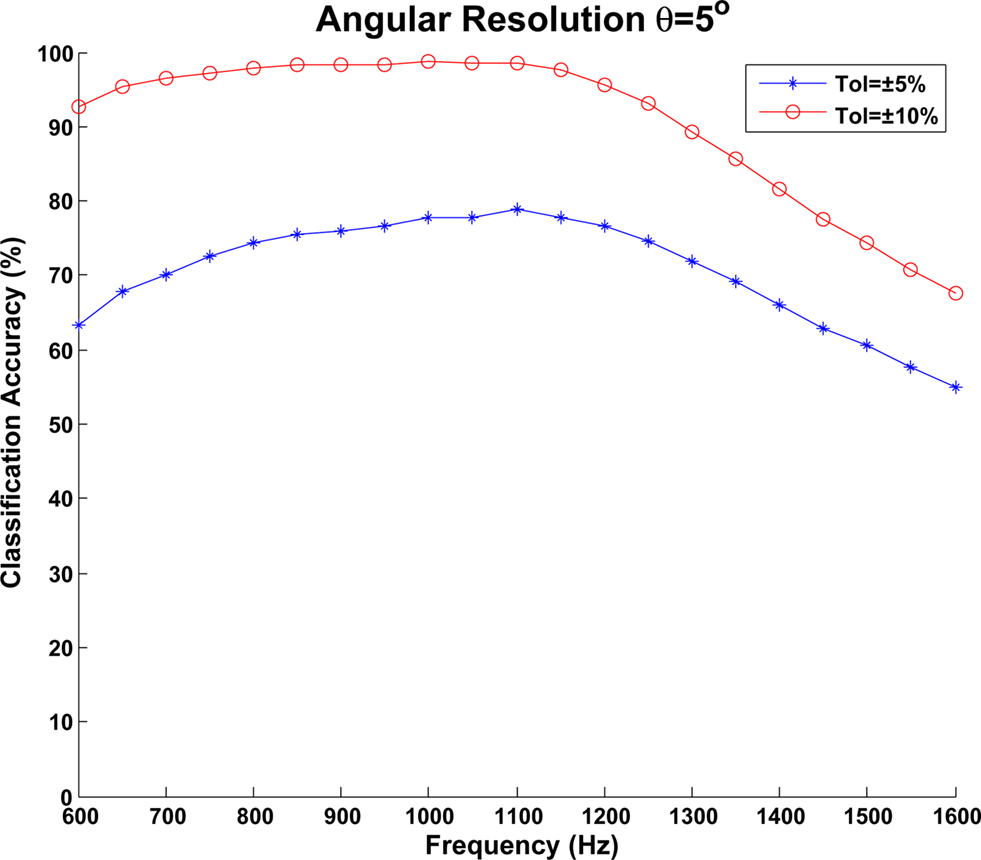
Figure 11. Classification accuracy of the MSO model when an angular resolution of θ = 5° was used. An input frequency sweep from 600 Hz to 1.6 KHz was performed in 50-Hz steps and data is shown for both ±5° and ±10° tolerances.

FIGURE 12

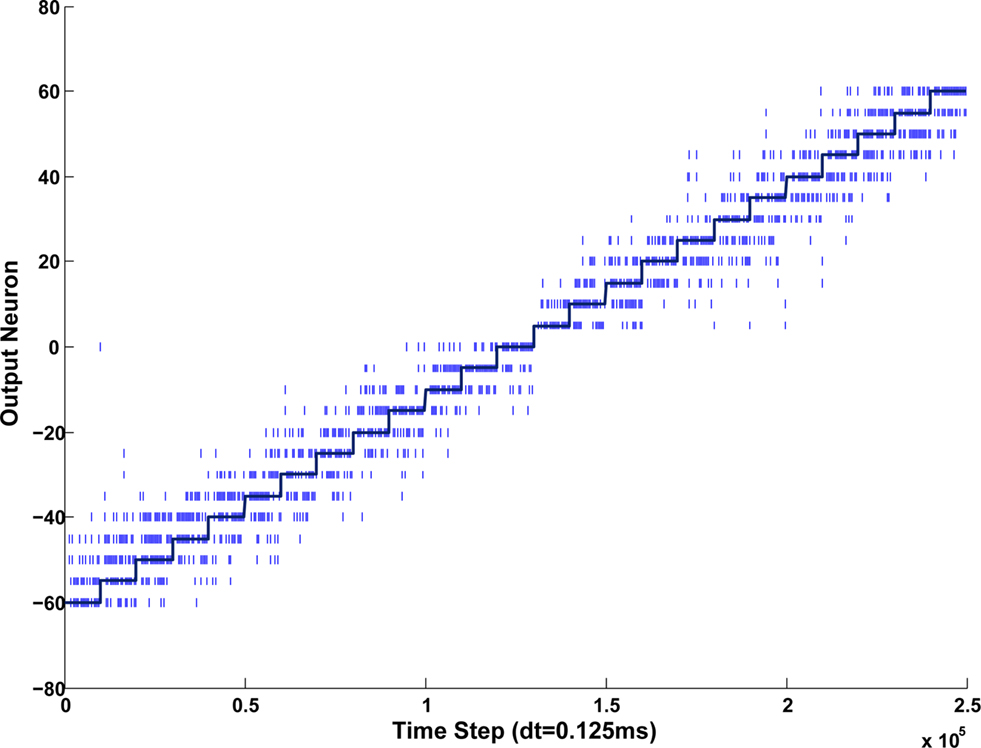
Figure 12. To illustrate typical output behavior of the model, a 1 KHz input signal was rotated from −60° to +60° and the spiking activity was recorded. These spikes are indicated as the vertical lines in the plot. The target or desired output is indicated by the stepped solid line.

FIGURE 13

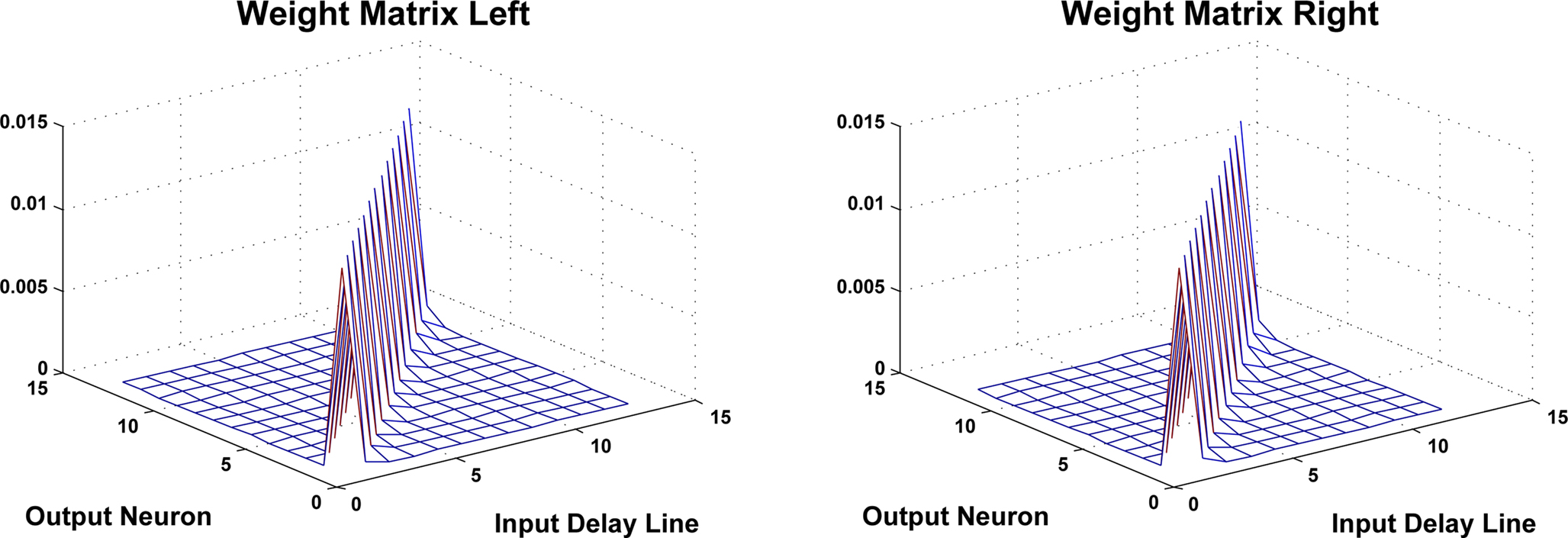
Figure 13. To indicate typical weight distributions between delay lines and output layer neurons, this figure plots the values of the left (contralateral) and right (ipsilateral) STDP weight matrices after training has been performed. The matrices shown are from the 1-KHz cluster of the network.

To further evaluate the impact of azimuth angle resolution on classification accuracy, the above experiment was repeated this time using a step size of 2.5°. This resulted in an overall increase in neuron density from 525 to 1,029 and an increase in the number of STDP synapses from 6,573 to 25,221. Once again the classification accuracies were determined for ±5° and ±10° and the results obtained are plotted in Figure 14. It can be seen from this figure that a higher classification accuracy is obtained when compared to the results for the 5° angular resolution. In this case an average classification accuracy of 78.64% was observed for a tolerance of ±5° whilst this increased to 91.82% for the ±10° tolerance.

FIGURE 14

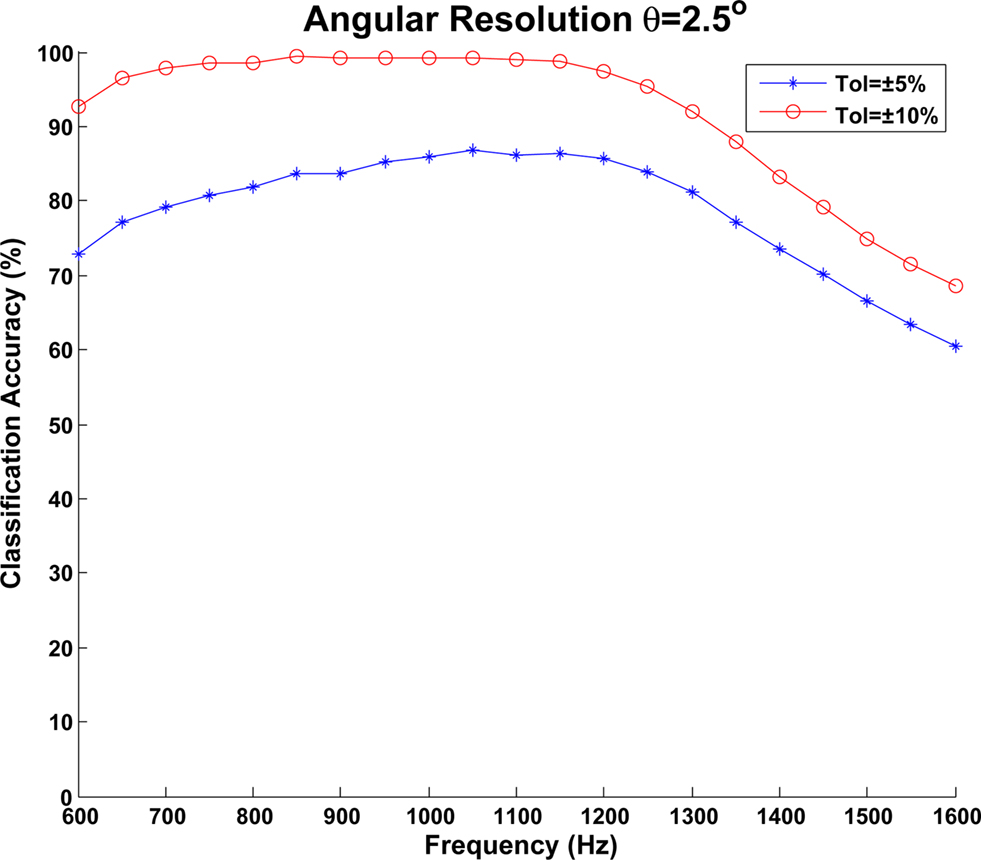
Figure 14. Classification accuracy of the MSO model when an angular resolution of θ = 2.5 was used. Again, an input frequency sweep from 600 Hz to 1.6 KHz was performed in 50-Hz steps and data is shown for both ±5° and ±10° tolerances.

Hardware Implementation

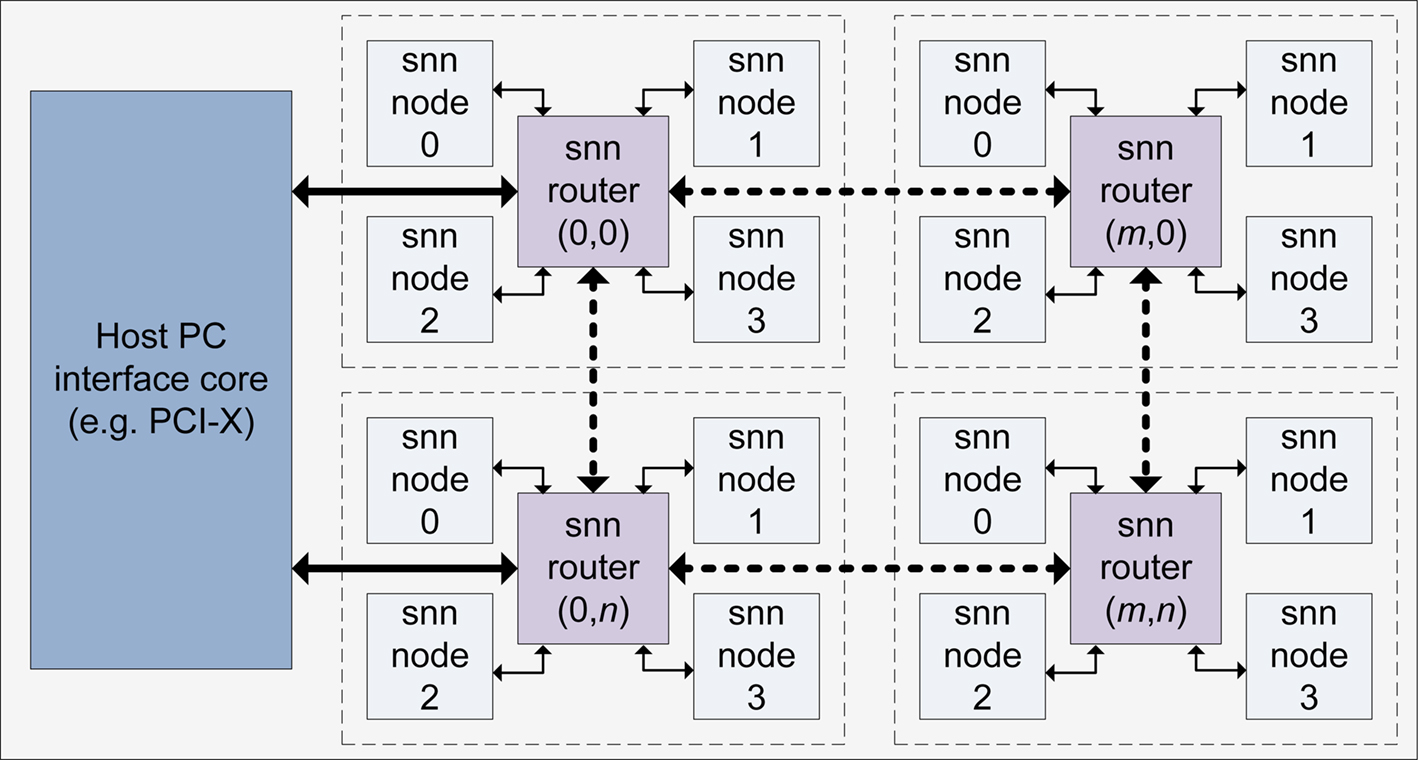
To investigate potential acceleration performance and to acknowledge the possibility of a future deployment in an embedded systems platform, a hardware based implementation of the MSO model on Field Programmable Gate Array (FPGA) hardware has also been targeted. Previous work by the authors has demonstrated the suitability of such reconfigurable devices for replicating the natural plasticity of SNNs (Glackin et al., 2009a,b) and an approach for facilitating large scale implementation of SNNs with STDP has been reported in Maguire et al. (2007). The implementation utilizes Time Division Multiplexing (TDM) to facilitate large scale network topologies whilst minimizing the logic requirements. Whilst this approach facilitates much larger networks than what would be achievable using a fully parallel implementation approach, it is important to carefully consider the speed/area trade-off and the impact this has on computational performance. If resource sharing is over utilized for instance with just one single node performing TDM control, the processing becomes almost serial in nature and no significant benefit can be obtained from the hardware implementation. Thus, for improved performance, it is necessary to maintain a level of parallelism. A degree of on-chip parallelism can be exploited by attaching a number of independent memory banks to the FPGA to allow independent TDM controllers to operate concurrently. Further parallel processing can also be achieved if a multi-FPGA platform is targeted. Thus, the proposed reconfigurable architecture is presented in Figure 15, illustrating a series of SNN routers, each connected to four SNN nodes with a communication interface to a local microprocessor host.

FIGURE 15

Figure 15. Reconfigurable hardware architecture containing multiple parallel SNN processing nodes.

In this configuration, a single SNN router attached to four SNN nodes is referred to as an SNN cluster. The SNN router within each cluster provides local communication of spike events between nodes and also supports the propagation of user data throughout the architecture. This provides an effective method of communicating data between large numbers of neurons without consuming significant on-chip routing resources. The neuron and synapse computations pertaining to an SNN network are subsequently mapped to each of the SNN nodes on the architecture providing a method of parallelizing the network. The proposed approach uses the SNN router and nodes to provide both temporal and spatial parallelism, allowing a balance between the level of speed-up and the complexity of inter-neuron routing. Moreover, it provides a configurable infrastructure whereby a number of SNN clusters can be added to allow the system to scale in performance with area.

To validate the hardware implementation approach, the SNN node processor has been developed using the VHDL language to compute a sub-cluster within the MSO model. Whilst the long term goal of this work is to fully implement the complete MSO model in hardware, to date a behavioral simulation of the SNN node processor has been completed using the ModelSim tool to perform functional verification of the design. In this instance the angular resolution used was 2.5°, hence a total of 49 neurons and 1,201 STDP synapses have been validated to perform in the desired manner. Deploying an individual snn_node for each frequency sub-cluster will allow the network to scale to the same dimensions as used in the software model, i.e., 1,029 neurons and 25,221 STDP synapses. The logic requirements for an individual snn_node implementation, as reported by the Xilinx ISE design tools, are reported in Table 1. In this instance, the target device was the Xilinx XC4VLX160 which has been previously used by the authors for implementing SNNs (Glackin et al. (2009a,b). In terms of performance, a timing constraint of 150 MHz was placed on the primary system clock and a place and route of the design performed to ensure no timing errors were reported. As such it can be deduced that for a 10-s real time simulation with STDP training enabled, the computation time for the FPGA hardware is 4.11 s. When compared to an averaged software execution time of 27.6 s which was obtained from running the same simulation on a workstation with a dual core 2.2-GHz AMD Processor, it can be seen that a speed-up factor of ×6.7 was observed. The main strength of the hardware implementation strategy however is that multiple nodes can be deployed in parallel such that while software execution times will scale linearly depending on the number of frequency selective clusters, the FPGA execution time will remain the same. Thus, it is evident that the hardware based implementation reported offers significant acceleration potential.

TABLE 1

Table 1. Device usage statistics (XC4VLX160).

Discussion

Section “Results” has presented results obtained from an implementation of an SNN based model of the MSO for performing sound localization. In attempting to evaluate these results however, it is difficult to make direct comparisons with those presented by other researchers in this field. This is due to the many different methods that are used for sound localization modeling, such as: the implementation approach which can range from purely computational to biologically inspired; the type of data from pure tones to HRTF measurements, and whether this data is simulated or experimentally derived; the resolution of angles being localized; the range of sound frequencies tested by the model; and the use of a learning algorithm to train the models. This information has been summarized for the various SNN based approaches reported in the literature and is presented in Table 2.

TABLE 2

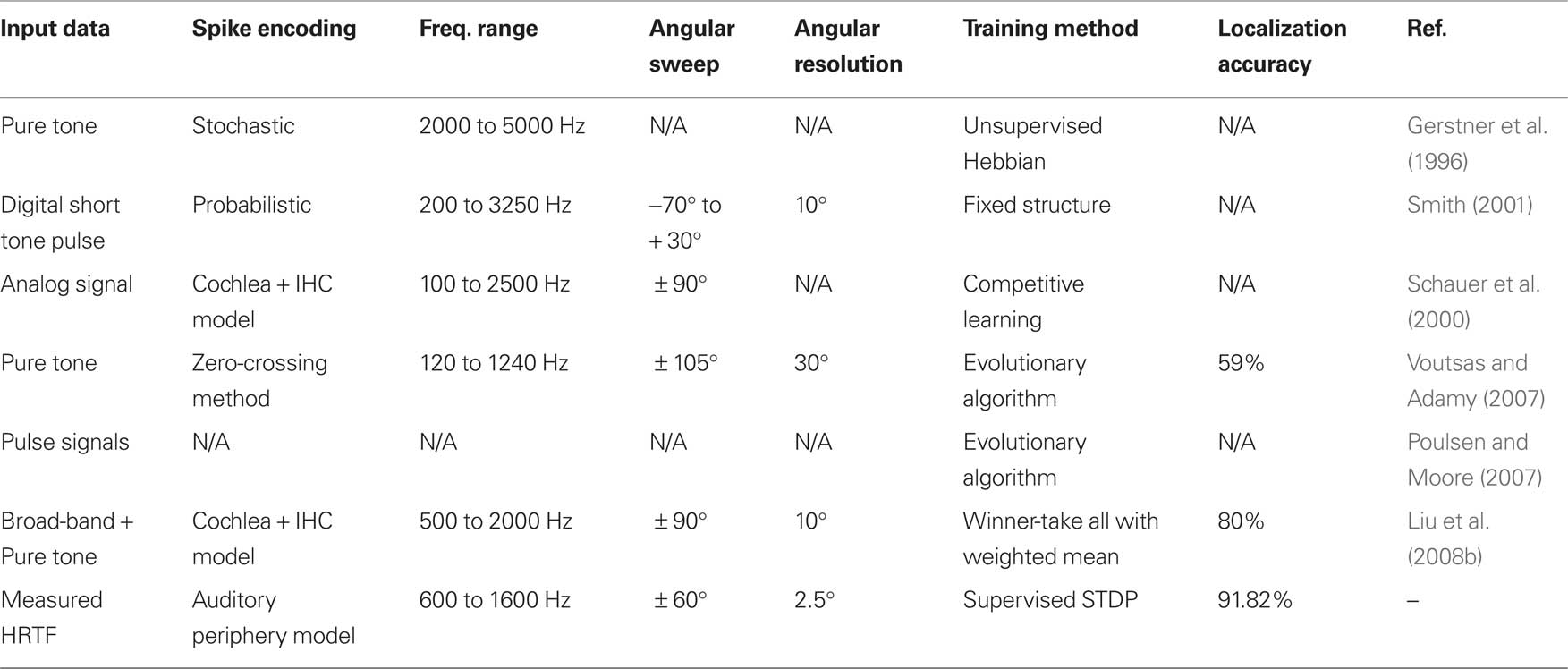
Table 2. Comparison of SNN models for sound localization as reported in the research literature, the results of the work presented in this paper are indicated in the final row.

Analysis of this table indicates a number of ways in which the work described in this paper offers advancements over the current state of the art. Whilst the early work of Gerstner et al. (1996) provided the first Jeffress inspired SNN model for sound localization, it can be seen from the table that the underlying hypothesis was not validated through experimental results to indicate how the model actually performed across relevant frequency ranges for various azimuth angles. Furthermore, the manner in which the sound source signal was converted into spike train inputs was based on a stochastic process as opposed to using biologically realistic data. In contrast, the work of Schauer et al. (2000) and Liu et al. (2008a,b) have attempted to more closely replicate the auditory processing pathway through the integration of both cochlea and IHC models. The presented work has adopted a similar approach, using a cochlea model based on empirical observations in the cat (Zilany and Bruce, 2006, 2007), but has further extended this to use experimentally measured real-world HRTF data obtained from an adult cat (Tollin and Koka, 2009). Hence, the approach described constitutes the most biologically plausible representation of the mammalian auditory processing pathway for sound localization currently reported in the literature.

The work presented has also described the incorporation of the biologically plausible STDP learning rule for network training. Whilst the nature of the teaching signal used means that the overall training approach can be considered supervised, for a task such as sound localization, some form of instruction is required to enable the model to map a particular ITD to the relevant azimuthal angle. Whilst an unsupervised Hebbian learning rule was used in Gerstner et al. (1996) to automatically determine delay line connections, each neuron was trained on an individual basis where no method was described for mapping ITDs to actual angles of sound source location. In the absence of multi-modal sensory information such as visual or tactile data to complete the required feedback loop, the authors suggest that the supervised STDP method described provides an adequate intermediate solution to this problem.

In accordance with the research literature, it has been shown that the spiking neuron model is able to localize lower sound frequencies in a more efficient manner than higher frequencies. This work also sought to investigate the impact of azimuth angular resolution on localization performance. From the results presented in the previous section it can be seen that a notable improvement in accuracy was observed, particularly for the 5° tolerance where an increase from 70.63 to 78.64% was observed. If a 10° tolerance is considered this figure increases to 91.82% when averaged over the complete frequency band. From Table 2 it can be seen that this figure compares very favorably with alternative SNN models for sound localization. Whilst a localization accuracy of 80% was reported in Liu et al. (2008b), the angular resolution of 30° was considerably lower than that used in the presented work.

The hardware implementation results, whilst preliminary, indicate the significant potential of this approach. With a ×6.7 speed-up factor observed for one processing node, increasing the scale of the hardware implementation such that each SNN processor node is responsible for an individual frequency cluster would lead to an overall acceleration of almost ×150 if the full network topology of 21 frequency clusters used for the software implementation was adopted. Whilst a software computation time of approximately 580 s is required to perform a 10-s real time simulation of this full network, the same computation can be performed on FPGA hardware in just over 4 s, thus ensuring real time performance can be maintained. As has been shown in Table 1, only a very small percentage of the FPGA device resources available have been utilized. Furthermore, the on-chip memory usage reported (RAMB16s) can be considered inflated here as the memory interface has been designed to accommodate future increases in resolution. If the angular resolution is increased to 1° and the network model extended to support a full 360° sweep of input angles, the total number of neurons required would be 7,539 whilst the number of STDP synapses would increase to 1,353,261. At this resolution, the model could be considered as approaching the biological scale as the human MSO, which is believed to contain in the region of 10,000–11,000 neurons (Moore, 2000). In terms of network data storage, this would require approximately 2.8 MB of system memory. Given that there is a total of 192 MB of external memory available on the target hardware platform it is evident that there is significant scope to accommodate this size of network and also to extend the model by incorporating additional components of the auditory processing pathway such as the LSO which is estimated to contain a further 2,500–4,000 neurons (Moore, 2000).

Conclusions and Future Work

This paper has presented a Jeffress inspired spiking based model of the MSO for sound localization. It has been shown that, when presented with biologically observed data from the adult cat, the model has been able to successfully localize the sound source. The model presented is heavily inspired by the mammalian auditory processing pathway, where the ITD was utilized to extract the azimuth angle for sounds in the frequency range of 600 Hz–1.6 KHz. A biologically plausible training mechanism in the form of the STDP rule was used to regulate the synaptic connection weights in the network and thus facilitate the desired behavior.

This paper has also evaluated the impact of increasing the angular resolution on classification performance. Here it was observed that a notable improvement was achieved when the resolution was increased from 10° to 5°. At this resolution, a classification accuracy of almost 92% was obtained from the network when an error tolerance of ±10° was allowed. It has also been shown however that this increase in resolution also results in an increase in network density from 525 to 1,029 neurons and from 6,573 to 25,221 STDP synapses. To mitigate the increased software execution times this incurs, a hardware based implementation of the model has also been proposed. It has been shown that significant acceleration performance is achievable when an FPGA based implementation platform is targeted.

In terms of future work the authors intend to investigate further refinement of the angular resolution and to extend the network architecture to localize sounds from all angles rather than the current subset of −60° ≤ θ ≤ 60°. The current single node FPGA implementation will also be extended to accommodate this extended MSO model before eventually combining it with a model of the LSO to provide a complete model for sound localization across all frequency ranges. The long term goal of this work is to create a biologically realistic model of the mammalian auditory processing pathway.

Appendix – Neuron Models

Bushy Cell: Lif Neuron Model

The spiking neuron model used to implement the bushy cell neurons was the Leaky Integrate-and-Fire (LIF) (Gerstner and Kistler, 2002). The LIF model can be implemented using the following equation:

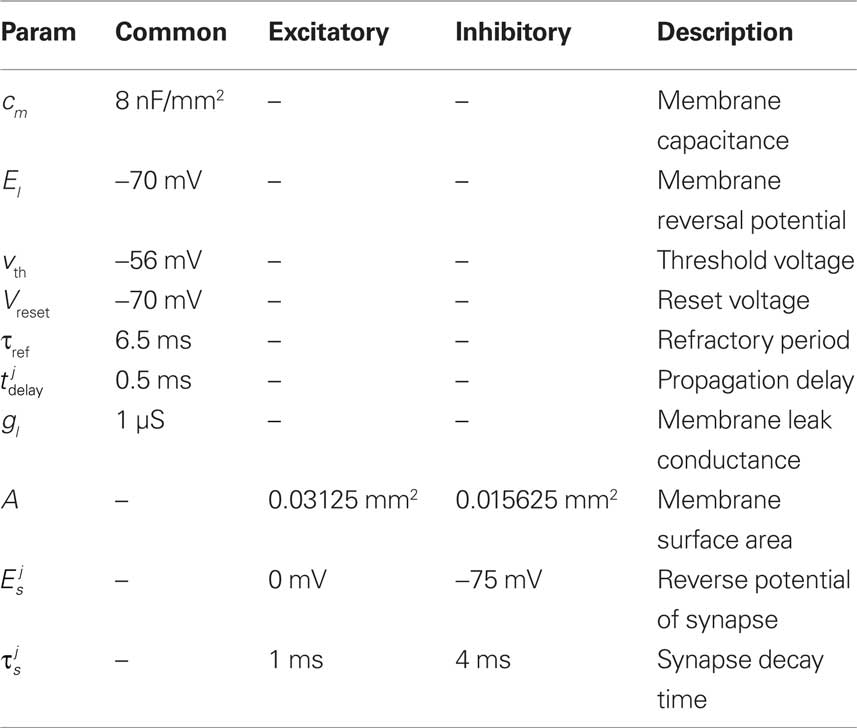
where τ_m refers to the membrane time constant of the neuron, v is the membrane potential and R_in is the membrane resistance driven by a synaptic current I_syn(t). The implementation parameters used can be found in Table 3.

TABLE 3

Table 3. LIF neuron model parameters.

MSO: Conductance Based I&F Neuron Model

For the MSO implementation, the conductance based I&F neuron model used consists of a first order differential equation where the neuron membrane potential, v, is related to the membrane currents in the form:

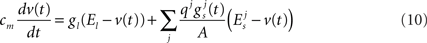
A description of the terms used can be found in Table 4. For a given synapse j, an action potential event at the pre-synaptic neuron at time t_ap triggers a synaptic release event at time 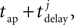causing a discontinuous increase in the synaptic conductance

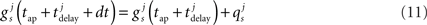
otherwise 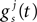is governed by

where 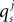refers to the weight or peak conductance of the synapse. The forward Euler integration scheme with a time step of dt = 0.125 ms can be used to solve the conductance based I&F model equations. Using this method, Eq. 10 is re-expressed as:

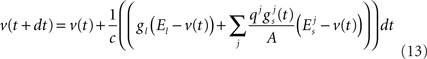
and differential equation (3) becomes,

TABLE 4

Table 4. Conductance based I&F neuron model parameters.

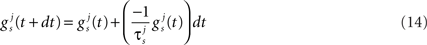
As previously discussed, an aspect of this research is to consider an eventual hardware based implementation of the network model. Hence, when selecting the neuron model parameters, a number of considerations were taken into account, For example, multiplicand and divisor parameters (e.g., 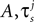) were chosen as powers of 2 such that they could be implemented using binary shift operators thus minimizing the amount of required by a full multiplier or divider. A description of the various parameters and the values used for the software and hardware implementations reported in this paper can be found in Table 4.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Our thanks go to Dr. D. J. Tollin at the University of Colorado Medical School for providing us with the HRTF data and recommending which auditory periphery models to use. Dr. Glackin is supported under the CoEIS grant from the Integrated Development Fund.

References

Abarbanel, H. D. I., Huerta, R., and Rabinovich, M. I. (2002). Dynamical model of long-term synaptic plasticity. Proc. Natl. Acad. Sci. U.S.A. 99, 10132–10137.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Abdel Alim, O., and Farag, H. (2000). “Modeling non-individualized binaural sound localization in the horizontal plane using artificial neural networks,” in Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks (IJCNN), Vol. 3. Como, 642–647.

Alnajjar, F., and Murase, K. (2008). A simple aplysia-like spiking neural network to generate adaptive behavior in autonomous robots. Adapt. Behav. 16, 306–324.

CrossRef Full Text

Arena, P., Fortuna, L., Frasca, M., and Patane, L. (2009). Learning anticipation via spiking networks: application to navigation control. IEEE Trans. Neural Netw. 20, 202–216.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Backman, J., and Karjalainen, M. (1993). “Modelling of human directional and spatial hearing using neural networks,” in 1993 IEEE International Conference on Acoustics, Speech, and Signal Processing, 1993. ICASSP-93, Vol. 1, Minneapolis.

Beckius, G. E., Batra, R., and Oliver, D. L. (1999). Axons from anteroventral cochlear nucleus that terminate in medial superior olive of cat: observations related to delay lines. J. Neurosci. 19, 3146–3161.

Pubmed Abstract | Pubmed Full Text

Bell, C. C., Han, V. Z., Sugawara, Y., and Grant, K. (1997). Synaptic plasticity in a cerebellum-like structure depends on temporal order. Nature 387, 278–281.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bi, G., and Poo, M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472.

Pubmed Abstract | Pubmed Full Text

Burger, R., and Rubel, E. (2008). “Encoding of interaural timing for binaural hearing” in The Senses: A Comprehensive Reference, Vol. 3, A. I. Basbaum, M. C. Bushnell, D. V. Smith, G. K. Beauchamp, S. J. Firestein, P. Dallos, D. Oertel, R. H. Masland, T. Albright, J. H. Kaas, and E. P. Gardner (San Diego: Academic Press), 613–630.

Carr, C. E. (1993). Delay line models of sound localization in the barn owl. Am. Zool. 33, 79–85.

Carr, C. E., and Konishi, M. (1990). A circuit for detection of interaural time differences in the brain stem of the barn owl. J. Neurosci. 10, 3227–3246.

Pubmed Abstract | Pubmed Full Text

Chung, W., Carlile, S., and Leong, P. (2000). A performance adequate computational model for auditory localization. J. Acoust. Soc. Am. 107, 432.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dan, Y., and Poo, M. (2006). Spike timing-dependent plasticity: from synapse to perception. Physiol. Rev. 86, 1033–1048.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Datum, M. S., Palmieri, F., and Moiseff, A. (1996). An artificial neural network for sound localization using binaural cues. J. Acoust. Soc. Am. 100, 372–383.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Deneve, S., Latham, P. E., and Pouget, A. (2001). Efficient computation and cue integration with noisy population codes. Nat. Neurosci. 4, 826–831.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Destexhe, A. (1997). Conductance-based integrate-and-fire models. Neural. Comput. 9, 503–514.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gerstner, W., Kempter, R., Van Hemmen, J., and Wagner, H. (1996). A neuronal learning rule for sub-millisecond temporal coding. Nature 383, 76–78.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gerstner, W., and Kistler, W. (2002). Spiking Neuron Models: Single Neurons, Populations, Plasticity. Cambridge: Cambridge University Press.

Glackin, B., Harkin, J., McGinnity, T., and Maguire, L. (2009a). “A hardware accelerated simulation environment for spiking neural networks,” in Proceedings of 5th International Workshop on Applied Reconfigurable Computing (ARC’09), Vol. 5453 of Lecture Notes in Computer Science, Prague, 336–341.

Glackin, B., Harkin, J., McGinnity, T., Maguire, L., and Wu, Q. (2009b). “Emulating spiking neural networks for edge detection on FPGA hardware,” in Proceedings of International Conference on Field Programmable Logic and Applications FPL 2009, Karlsruhe, 670–673.

Grothe, B. (2003). New roles for synaptic inhibition in sound localization. Nat. Rev. Neurosci. 4, 540–550.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hancock, K., and Delgutte, B. (2004). A physiologically based model of interaural time difference discrimination. J. Neurosci. 24, 7110–7117.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Handzel, A., and Krishnaprasad, P. (2002). Biomimetic sound-source localization. IEEE Sens. J. 2, 607–616.

CrossRef Full Text

Hao, M., Lin, Z., Hongmei, H., and Zhenyang, W. (2007). “A novel sound localization method based on head related transfer function,” in 8th International Conference on Electronic Measurement and Instruments, ICEMI, Xian, 4–428.

Hebb, D. O. (1949). The Organization of Behavior. New York: John Wiley.

Hodgkin, A., and Huxley, A. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544.

Pubmed Abstract | Pubmed Full Text

Hosaka, R., Araki, O., and Ikeguchi, T. (2008). STDP provides the substrate for igniting synfire chains by spatiotemporal input patterns. Neural. Comput. 20, 415–435.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Huang, J., Supaongprapa, T., Terakura, I., Wang, F., Ohnishi, N., and Sugie, N. (1999). A model-based sound localization system and its application to robot navigation. Rob. Auton. Syst. 27, 199–209.

CrossRef Full Text

Indiveri, G., Chicca, E., and Douglas, R. (2006). A VLSI array of low-power spiking neurons and bistable synapses with spike-timing dependent plasticity. IEEE Trans. Neural Netw. 17, 211–221.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Izhikevich, E. M., Gally, J. A., and Edelman, G. M. (2004). Spike-timing dynamics of neuronal groups. Cereb. Cortex 14, 933–944.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jeffress, L. A. (1948). A place theory of sound localization. J. Comp. Physiol. Psychol. 41, 35–39.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Joris, P., and Yin, T. C. T. (2007). A matter of time: internal delays in binaural processing. Trends Neurosci. 30, 70–78.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kempter, R., Gerstner, W., van Hemmen, J. L., and Wagner, H. (1996). Temporal coding in the submillisecond range: model of barn owl auditory pathway. Adv. Neural Inf. Process Syst. 8, 124–130.

Keyrouz, F., and Diepold, K. (2008). A novel biologically inspired neural network solution for robotic 3D sound source sensing. Soft Comput. Fusion Found. Methodologies Appl. 12, 721–729.

Konishi, M. (2000). Study of sound localization by owls and its relevance to humans. Comp. Biochem. Physiol. A 126, 459–469.

CrossRef Full Text

Kulesza, R. (2007). Cytoarchitecture of the human superior olivary complex: medial and lateral superior olive. Hear. Res. 225, 80–90.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Li, H., Lu, J., Huang, J., and Yoshiara, T. (2009). “Spatial localization of multiple sound sources in a reverberant environment,” in International Computer Symposium (ICS), 2008 ICS, Tamshui.

Liu, J., Erwin, H., Wermter, S., and Elsaid, M. (2008a). “A biologically inspired spiking neural network for sound localisation by the inferior colliculus,” in Proceedings of the 18th International Conference on Artificial Neural Networks, Part II (Nice: Springer), 396–405.

Liu, J., Erwin, H., and Wermter, S. (2008b). “Mobile robot broadband sound localisation using a biologically inspired spiking neural network,” in IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS, Heidelberg, 2191–2196.

Liu, J., Perez-Gonzalez, D., Rees, A., Erwin, H., and Wermter, S. (2009). “Multiple sound source localisation in reverberant environments inspired by the auditory midbrain,” in 19th International Conference on Artificial Neural Networks (ICANN’09), Vol. 5768 of Lecture Notes in Computer Science (Heidelberg: Springer), 208–217.

Maguire, L. P., McGinnity, T. M., Glackin, B., Ghani, A., Belatreche, A., and Harkin, J. (2007). Challenges for large-scale implementations of spiking neural networks on FPGAs. Neurocomputing 71, 13–29.

CrossRef Full Text

Markram, H., Lübke, J., Frotscher, M., and Sakmann, B. (1997). Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Masquelier, T., Hugues, E., Deco, G., and Thorpe, S. J. (2009). Oscillations, phase-of-firing coding, and spike timing-dependent plasticity: an efficient learning scheme. J. Neurosci. 29, 13484–13493.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McAlpine, D., and Grothe, B. (2003). Sound localization and delay lines – do mammals fit the model? Trends Neurosci. 26, 347–350.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Moore, J. K. (2000). Organization of the human superior olivary complex. Microsc. Res. Tech. 51, 403–412.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Murray, J. C., Erwin, H. R., and Wermter, S. (2009). Robotic sound-source localisation architecture using cross-correlation and recurrent neural networks. Neural. Netw. 22, 173–189.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nakashima, H., Chisaki, Y., Usagawa, T., and Ebata, M. (2003). Frequency domain binaural model based on interaural phase and level differences. Acoust. Sci. Technol. 24, 172–178.

CrossRef Full Text

Natschläger, T., and Ruf, B. (1999). Pattern analysis with spiking neurons using delay coding. Neurocomputing 26–27, 463–469.

CrossRef Full Text

Nessler, B., Pfeiffer, M., and Maass, W. (2009). “STDP enables spiking neurons to detect hidden causes of their inputs,” in Advances in Neural Information Processing Systems (NIPS’09) (Cambridge MA: MIT Press), 1357–1365.

Nordlund, B. (1962). Physical factors in angular localization. Acta Otolaryngol. 54, 75–93.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Northmore, D. P. M. (2004). A network of spiking neurons develops sensorimotor mechanisms while guiding behavior. Neurocomputing 58–60, 1057–1063.

CrossRef Full Text

Palmieri, F., Datum, M., Shah, A., and Moiseff, A. (1991). Sound localization with a neural network trained with the multiple extended Kalman algorithm. International Joint Conference on Neural Networks, IJCNN, Vol. 1. Seattle.

Poulsen, T. M., and Moore, R. K. (2007). “Sound localization through evolutionary learning applied to spiking neural networks,” in IEEE Symposium on Foundations of Computational Intelligence, FOCI, Honolulu, 350–356

Rayleigh, L. (1875–1876). On our perception of the direction of a source of sound. J. R. Musical Assoc. 2nd Sess., 75–84.

Rayleigh, L. (1907). On our perception of sound direction. Philos. Mag. 13, 214–232.

Rumsey, F. (2001). Spatial Audio. Oxford: Focal Press.

Ryugo, D. K., and Parks, T. N. (2003). Primary innervation of the avian and mammalian cochlear nucleus. Brain Res. Bull. 60, 435–456.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schauer, C., Zahn, T., Paschke, P., and Gross, H. M. (2000). “Binaural sound localization in an artificial neural network,” in Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP, Vol. 2, Istanbul.

Schemmel, J., Bruderle, D., Meier, K., and Ostendorf, B. (2007). “Modeling synaptic plasticity within networks of highly accelerated I&F neurons,” in IEEE International Symposium on Circuits and Systems (ISCAS’07), New Orleans, 3367–3370.

Shi, R. Z., and Horiuchi, T. K. (2004). “A VLSI model of the bat lateral superior olive for azimuthal echolocation,” in Proceedings of the International Symposium on Circuits and Systems, ISCAS, Vol. 4, Vancouver.

Smith, L. S. (2001). Using depressing synapses for phase locked auditory onset detection. Lect. Notes Comput. Sci. 2130, 1103–1108.

CrossRef Full Text

Smith, P. H., Joris, P. X., and Yin, T. C. (1993). Projections of physiologically characterized spherical bushy cell axons from the cochlear nucleus of the cat: evidence for delay lines to the medial superior olive. J. Comp. Neurol. 331, 245–260.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Smith, P. H., Joris, P. X., and Yin, T. C. T. (1998). Anatomy and physiology of principal cells of the medial nucleus of the trapezoid body (MNTB) of the cat. J. Neurophysiol. 79, 3127–3142.

Pubmed Abstract | Pubmed Full Text

Song, S., and Abbott, L. (2001). Cortical development and remapping through spike timing-dependent plasticity. Neuron 32, 339–350.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Song, S., Miller, K., and Abbott, L. (2000). Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Thompson, S. (1882). On the function of the two ears in the perception of space. Philos. Mag. 13, 406–416.

Tollin, D. J. (2004). The development of the acoustical cues to sound localization in cats. Assoc. Res. Otol. 27, 161.

Tollin, D. J. (2008). “Encoding of interaural level differences for sound localization,” in The Senses: A Comprehensive Reference Vol. 3, (San Diego: Academic Press), 631–654.

Tollin, D., and Koka, K. (2009). Postnatal development of sound pressure transformations by the head and pinnae of the cat: monaural characteristics. J. Acoust. Soc. Am. 125, 980.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tollin, D., Koka, K., and Tsai, J. (2008). Interaural level difference discrimination thresholds for single neurons in the lateral superior olive. J. Neurosci. 28, 4848.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tzounopoulos, T., Kim, Y., Oertel, D., and Trussell, L. O. (2004). Cell-specific, spike timing-dependent plasticities in the dorsal cochlear nucleus. Nat. Neurosci. 7, 719–725.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Voutsas, K., and Adamy, J. (2007). A biologically inspired spiking neural network for sound source lateralization. IEEE Trans. Neural. Netw. 18, 1785–1799.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wall, J., McDaid, L., Maguire, L., and McGinnity, T. (2008). “Spiking neuron models of the medial and lateral superior olive for sound localisation,” in IEEE International Joint Conference on Neural Networks (IJCNN’08), Hong Kong, 2641–2647.

Wall, J. A., McDaid, L. J., Maguire, L. P., and McGinnity, T. M. (2007). “A spiking neural network implementation of sound localisation,” in Proceedings of the IET Irish Signals and Systems, Derry, pp. 19–23.

Willert, V., Eggert, J., Adamy, J., Stahl, R., and Korner, E. (2006). A probabilistic model for binaural sound localization. IEEE Trans. Syst. Man Cybern. B Cybern. 36, 982.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wu, Q., McGinnity, T., Maguire, L., Belatreche, A., and Glackin, B. (2005). Adaptive co-ordinate transformation based on spike timing-dependent plasticity learning paradigm. Adv. Nat. Comput. 3610, 420–428.

CrossRef Full Text

Wu, Q., McGinnity, T., Maguire, L., Belatreche, A., and Glackin, B. (2008). 2d co-ordinate transformation based on a spike timing-dependent plasticity learning mechanism. Neural. Netw. 21, 1318–1327.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yang, Z., and Murray, A. F. (2006). An artificial early visual model adopting spike-timing-dependent plasticity. Neurocomputing 69, 1904–1911.

CrossRef Full Text

Yin, T. C. T. (2002). “Neural mechanisms of encoding binaural localization cues in the auditory brainstem,” in Integrative Functions in the Mammalian Auditory Pathway, eds D. Oertel, R. R. Fay, and A. N. Popper (New York: Springer-Verlag), 99–159.

Zhang, L. I., Tao, H. W., Holt, C. E., Harris, W. A., and Poo, M. (1998). A critical window for cooperation and competition among developing retinotectal synapses. Nature 395, 37–44.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zilany, M. S. A., and Bruce, I. C. (2006). Modeling auditory-nerve responses for high sound pressure levels in the normal and impaired auditory periphery. J. Acoust. Soc. Am. 120, 1446.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zilany, M. S. A., and Bruce, I. C. (2007). Representation of the vowel/ε/in normal and impaired auditory nerve fibers: model predictions of responses in cats. J. Acoust. Soc. Am. 122, 402.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text