- 1 Launey Research Unit for Molecular Neurocybernetics, RIKEN Brain Science Institute, Wako-shi, Saitama, Japan
- 2 School of Electrical and Electronic Engineering, The University of Adelaide, Adelaide, SA, Australia
- 3 Theoretical and Experimental Neurobiology Unit, Okinawa Institute of Science and Technology, Kunigami, Okinawa, Japan
- 4 Department of Information and Communications Engineering, The University of Electro-Communications, Chofu-shi, Japan
Synapse location, dendritic active properties and synaptic plasticity are all known to play some role in shaping the different input streams impinging onto a neuron. It remains unclear however, how the magnitude and spatial distribution of synaptic efficacies emerge from this interplay. Here, we investigate this interplay using a biophysically detailed neuron model of a reconstructed layer 2/3 pyramidal cell and spike timing-dependent plasticity (STDP). Specifically, we focus on the issue of how the efficacy of synapses contributed by different input streams are spatially represented in dendrites after STDP learning. We construct a simple feed forward network where a detailed model neuron receives synaptic inputs independently from multiple yet equally sized groups of afferent fibers with correlated activity, mimicking the spike activity from different neuronal populations encoding, for example, different sensory modalities. Interestingly, ensuing STDP learning, we observe that for all afferent groups, STDP leads to synaptic efficacies arranged into spatially segregated clusters effectively partitioning the dendritic tree. These segregated clusters possess a characteristic global organization in space, where they form a tessellation in which each group dominates mutually exclusive regions of the dendrite. Put simply, the dendritic imprint from different input streams left after STDP learning effectively forms what we term a “dendritic efficacy mosaic.” Furthermore, we show how variations of the inputs and STDP rule affect such an organization. Our model suggests that STDP may be an important mechanism for creating a clustered plasticity engram, which shapes how different input streams are spatially represented in dendrite.
Introduction
In all the cortical brain areas studied so far, neurons can modify their input/output characteristics, usually via activity-dependent modification of synaptic efficacies of the afferent axons targeting their dendrites. Experiments have shown that the pattern of synaptic inputs can trigger either long-term potentiation (LTP, Bliss and Collingridge, 1993) or long-term depression (LTD, Kirkwood and Bear, 1994) at stimulated synapses. The discovery of spike timing-dependent plasticity (STDP, Markram et al., 1997a; Bi and Poo, 1998; Debanne et al., 1998; Zhang et al., 1998) illustrated that temporal specificity and timing information plays an important role, typically characterized by a temporally asymmetric window for synaptic change, where the temporal order of pre- and postsynaptic firing determines whether a synapse is potentiated or depressed. However, for a neuron with spatial extent, not only is timing important, but also biophysical properties and the strengths and spatial arrangement of synaptic inputs across the dendrite, as these will dictate neuronal firing properties.
Whether the mechanisms underlying synaptic change also leads to the emergence of some preferred form of spatial organization of synaptic inputs across the dendrite, still requires further elucidation. Converging groups of afferent fibers form synapses which may be strong in some localized regions of the dendrite but weak or absent elsewhere. Whether such a functionally clustered spatial organization of synaptic efficacy patterning may emerge as a result of synaptic plasticity is a question that is still being actively pursued.
Notably, why would clustering be a desirable emergent property? Firstly, previous studies have illustrated non-linear summation between nearby synchronous (or near-synchronous) synaptic inputs (Koch et al., 1983; Tuckwell, 1986; Polsky et al., 2004), allowing for easier spike generation in regions with clustered inputs. Other studies have shown that altering the spatial configuration of inputs changes firing properties (Mel, 1993; Poirazi et al., 2003; Iannella et al., 2004), while correlated activity can alter the integrative properties of neurons (Destexhe and Paré, 1999; Rudolph and Destexhe, 2003). Such clusters may provide part of the scaffolding underlying the emergence of functional dendritic compartments, subregions where activity tends to be correlated and where local signal integration permits some state-dependent non-linear computation to take place, but simultaneously different to what is happening in other compartments (Polsky et al., 2004; Gasparini and Magee, 2006; Rainowitch and Segev, 2006a,b).
Importantly, various studies have indicated that plasticity may lead to arrange afferent fiber contacts into spatial clusters. Three-eyed frog experiments have shown that synapses contributed by eye-specific afferent form spatially segregated but interdigitated series of clusters across the dendrite (Katz and Constantine-Paton, 1988). In some cases, the axons are actually restricted to specific parts of the dendritic arborization as in the hippocampus, both in vivo (CA3 to CA1 connections) and in culture (Glanzman et al., 1991; Kavalali et al., 1999; Cove et al., 2006). For the neocortex, however, the rule seems to be scattered afferents (Hellwig et al., 1994; Hellwig, 2000; Anderson et al., 2002; Stepanyants et al., 2002, 2008; Binzegger et al., 2004). Little can be inferred, however, regarding functional consequences, since the presence of a synapse does not indicate strength (Somogyi et al., 1998; Megías et al., 2001; Thomson et al., 2002; Binzegger et al., 2004; Kalisman et al., 2005) and efficacies are heterogeneous (Cotrell et al., 2001; Frick et al., 2001), but see Magee and Cook (2000). Recent experiments support the clustered plasticity model (Govindarajan et al., 2006) having illustrated that LTP not only gives rise to cooperativity and coordinated regulation between nearby synapses (Harvey and Svoboda, 2007; Harvey et al., 2008), but also leads to the selection of inputs promoting spatiotemporal coincidence and thus promotes the creation of hotspots of functional synapses (De Roo et al., 2008). Taken together, these investigations suggest that the efficacy of synapses contributed by different afferent groups display a functionally clustered spatial arrangement.
Understanding how synaptic plasticity controls the strengths and spatial organization of synapses across dendrites is experimentally challenging since simultaneously tracking the formation, changes and elimination of sets of synapses remains extremely difficult. Instead, simulation provides a viable means to gain important insights. One may ask whether STDP in a compartmental model neuron can lead to some spatially heterogeneous distribution of synaptic strength akin to what has been predicted by the clustered plasticity model. For neurons receiving stimulation from several different input streams, such as layer 4 stellate cells in the visual cortex, could such a model provide insights into how plasticity maps the information contained in the activity originating from multiple input streams onto the dendrites, and whether the emergence of spatially segregated synaptic clusters form a substrate for such a mapping, such as those seen in ocular dominance formation. Our previous study is the only investigation so far to have shown that the emergence of such a spatial organization is feasible (Iannella and Tanaka, 2006). This model only incorporated sodium and delayed rectifier kdr potassium channels, lacking many other ion channels known to exist in real pyramidal cells (Stafstrom et al., 1985; Schwindt et al., 1988; Lorenzon and Foehring, 1995; Hille, 2001; Larkum et al., 2001). Our previous study, however, did not address the role of STDP in the emergence of such a spatial organization in a biophysically realistic model nor did it examine the alteration of spatial organization when multiple groups are considered. Here we investigate how STDP, admitting different degrees of competition, shapes the spatial organization of synaptic efficacies originating from multiple groups and factors which affect this organization. We show that when a neuron is stimulated by multiple independent groups of afferent fibers, spatially segregated efficacy clusters can emerge via STDP, forming a dendritic efficacy mosaic. Collectively, our results suggest that spike timing may play an important role in the mapping of information contained in multiple input streams onto dendrites.
Materials and Methods
Assessing the Degree of Segregation Between Multiple Spatial Patterns
The first systematic analysis of spatial segregation was conducted by Duncan and Duncan (1955) who introduced the spatial dissimilarity index (SDI). This index has historically been the measure of choice. However, measuring the segregation between two patterns has limited real world applications, which typically require measuring segregation between multiple spatial patterns. Since the 1980s, there have been many advances in measuring the segregation between multiple patterns along with the development of comprehensive methods and criteria with which measurements are evaluated (James and Taeuber, 1985; Massey and Denton, 1988; Reardon and Firebaugh, 2002). Recent studies have shown that the M-index, a segregation measure based upon mutual information was first proposed by Theil (1971), satisfies more quality criteria than previous measures (Frankel and Volij, 2005, 2008; Mora and Ruiz-Castillo, 2009). The M-index will be used herein to assess the degree of spatial segregation between different streams of inputs. Before we present the expression for this segregation index, we will introduce the following set of notation, subscripts j denotes dendritic location and m indexes the particular afferent group:
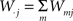 total synaptic efficiency at dendritic location j.
total synaptic efficiency at dendritic location j.
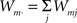 total of group m’s synaptic efficacies.
total of group m’s synaptic efficacies.
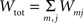 total synaptic efficacy contributed by all groups.
total synaptic efficacy contributed by all groups.
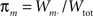 proportion of group m synaptic weights.
proportion of group m synaptic weights.
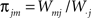 proportion of group m synaptic weights at j.
proportion of group m synaptic weights at j.
The mutual information M-index is defined as

This index can be interpreted as a likelihood-ratio measure between variables respectively indexing dendritic location j and group membership.
The Neocortical Layer 2/3 Pyramidal Cell Model
A biophysically detailed compartmental model of a reconstructed layer 2/3 pyramidal neuron receiving randomly timed excitatory and inhibitory synaptic inputs across the dendrite, was simulated using the NEURON simulation package (Hines and Carnevale, 2001). The model consisted of 119 sections with 294 segments in the dendrite. The model also included a simplified myelinated axon, similar to those used previously (Mainen et al., 1995; Iannella and Tanaka, 2006), consisting of a hillock, initial segment, five nodes and five myelin internodes, respectively. The parameters and channel types used in the simplified axon were similar to those used by others (Mainen et al., 1995; Iannella and Tanaka, 2006). A variety of synaptic receptors, voltage- and calcium-dependent ion channels experimentally found in layer 2/3 pyramidal cells were incorporated into the model. These included four types of synaptic currents; AMPA, GABAA, GABAB, and calcium permeable NMDA and various voltage-dependent currents such as, a passive leak (Ileak), a fast sodium (INa) and delayed rectifier potassium (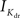 ), a transient A-type potassium current (IA), a hyperpolarization activated potassium (Ih), a muscarinic potassium (IM), a low voltage activated T-type calcium (IT), high voltage activated N- and L-type calcium current (IN) and (IHVA), three types of Ca2+-dependent potassium channels: (IC), medium AHP (ImAHP); and slow AHP (IsAHP) currents. These active channels were included throughout the axon, soma, and dendrites with densities and distributions based upon available experimental data mostly from the rat, or those used in previous studies. Passive properties used for the dendrite were similar to previous studies (Mainen et al., 1995; Iannella et al., 2004; Iannella and Tanaka, 2006): the membrane capacitance in the dendrite was Cm = 0.9 μF/cm2, the resting potential was −80 mV and the internal resistivity Ra was 200 Ωm. The effect of dendritic spines was included by correcting both the membrane capacitance and leak by a scaling factor.
), a transient A-type potassium current (IA), a hyperpolarization activated potassium (Ih), a muscarinic potassium (IM), a low voltage activated T-type calcium (IT), high voltage activated N- and L-type calcium current (IN) and (IHVA), three types of Ca2+-dependent potassium channels: (IC), medium AHP (ImAHP); and slow AHP (IsAHP) currents. These active channels were included throughout the axon, soma, and dendrites with densities and distributions based upon available experimental data mostly from the rat, or those used in previous studies. Passive properties used for the dendrite were similar to previous studies (Mainen et al., 1995; Iannella et al., 2004; Iannella and Tanaka, 2006): the membrane capacitance in the dendrite was Cm = 0.9 μF/cm2, the resting potential was −80 mV and the internal resistivity Ra was 200 Ωm. The effect of dendritic spines was included by correcting both the membrane capacitance and leak by a scaling factor.
The descriptions of the ionic currents used in the simulations were the same or similar to those used in previous modeling studies (Rhodes and Gray, 1994; Mainen et al., 1995; Rhodes and Llinás, 2001; Traub et al., 2003; Iannella et al., 2004; Iannella and Tanaka, 2006) and are given in the Supplementary Materials.
Stimulation was provided by a group of 250 inhibitory afferent fibers and typically four equally sized groups of 250 correlated excitatory afferents, unless stated otherwise. Inhibitory and excitatory afferents are not correlated with each other. Furthermore, we ascertain that any afferent from one excitatory group was not correlated with any afferent from the other excitatory group. Each fiber, either excitatory or inhibitory, forms five synaptic contacts in the model, as suggested by current anatomical data (Thomson et al., 1994, 2002; Markram et al., 1997b; Feldmeyer et al., 2002).
Simulations proceeded by initially connecting each excitatory afferent fiber to five randomly selected locations across the dendrite. Similarly, each inhibitory afferent also formed five synapses at random locations throughout the initial segment, hillock, soma, and dendrite. All synapses were activated at random times. The activity of inhibitory fibers were modeled by temporally homogeneous Poisson processes with a mean frequency of 10 Hz. The activity of excitatory afferents were modeled by a previously published realization of correlated Poisson processes where the ensemble activity of a group of fibers contains higher order statistics (Kuhn et al., 2003). The higher order interactions are mediated by synchronized activity involving only subsets of afferents belonging to a single group. The mean firing rates of all excitatory afferents used in the simulations was typically 40 Hz, with a within group correlation coefficient of C = 0.05, except where otherwise stated. A typical simulation took 500 s of simulated time, unless stated otherwise.
STDP Learning Rules
Two different STDP rules were used to change only the weights of AMPA conductances Wj(t) ∈ [0,1], (NMDA, GABAA, and GABAB conductances were not altered). The first rule is a previously described non-linear STDP rule (Gütig et al., 2003), while the remaining two are non-linear generalizations of two previously published multispike interaction based STDP rules. For clarity, we will simply call these the Gütig and Froemke STDP rules, respectively. These rules are given below.
Gütig Rule: Pair based non-linear STDP
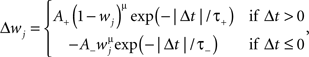
where Δt = tpost − tpre denotes the timing difference between pre- and postsynaptic events. A+ and A− are positive constants scaling the magnitude of individual weight changes, and τ+ and τ− are time constants determining the size of the temporal learning window in which potentiation and depression occurs. The presynaptic event tpre denotes the arrival time of presynaptic input to some specific dendritic location, while the postsynaptic event tpost typically denotes the time when a local dendritic spike was generated. When Δt is positive, synaptic efficacy is potentiated, and depressed otherwise; where individual changes in synaptic efficacy Wj are also weight dependent. This weight dependence has the form of a power law where the exponent μ is a positive constant. The case when μ = 0 corresponds to the additive STDP rule, where changes in synaptic efficacy are independent of Wj; while μ = 1 corresponds to the multiplicative STDP rule, where such changes are linearly dependent on the weight. For intermediate values of μ the weight dependence is non-linear. The parameters used for the non-linear STDP learning rule were A+ = 0.0025, A− = 0.001125, τ+ = 13.5 ms and τ− = 34.5 ms, in agreement with previous experiments (Froemke and Dan, 2002). Postsynaptic events were detected when the local membrane potential surpasses a pre-specified threshold θ = −20 mV.
Froemke Rule: Quadruplet spike interaction based non-linear STDP
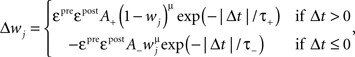
where Δt = tpost − tpre is the temporal difference between pre and postsynaptic spikes, A+ = 0.025, A− = 0.01125, 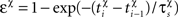 χ = {pre, post} denotes the pre-/postsynaptic suppression factor,
χ = {pre, post} denotes the pre-/postsynaptic suppression factor, 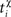 and
and 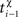 are the event times of the ith and (i − 1)th pre-/postsynaptic spikes, and
are the event times of the ith and (i − 1)th pre-/postsynaptic spikes, and 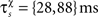 denotes the pre-/postsynaptic suppression time constants, respectively.
denotes the pre-/postsynaptic suppression time constants, respectively.
Measures of Functional Spatial Association
Developing methods for measuring how related two different entities are in space has lead to the emergence of a relatively new field, called Spatial Analysis. This field has already lead to novel yet widely used analytical and computational techniques, and whose objective sets out to provide robust methods for measuring the spatial association between events, is currently under active development. It is often assumed that entities which are close to each other share more features in common than those entities which are distant. Spatial dependencies between entities can arise via either correlation, causality or interaction, and formal measures often rely on calculating the spatial autocorrelation. Historically, Moran’s I index (Moran, 1950) is a widely used global measure of spatial association which assesses the correlation or similarities amongst the attributes of neighboring observations in a spatial pattern. Moran’s I index is a tool which measures the spatial autocorrelation of a pattern and evaluates whether the pattern is clustered, dispersed or random in space. This index is best interpreted as a weighted correlation coefficient used to detect departures from spatial randomness (Moran, 1950). It is defined as
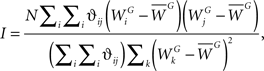
where N is the total number of dendritic locations j, ϑij is a spatial weight matrix of proximity where the simplest case is that of nearest neighbor (1 if location i is the neighbor of location j and 0 otherwise), 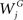 is the total synaptic weight of group G at dendritic location j, and
is the total synaptic weight of group G at dendritic location j, and 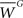 is the mean synaptic weight of a single group G. Calculated values range from −1 to 1, whose positive (negative) values indicate positive (negative) spatial autocorrelation, and where each extreme indicates either perfect dispersion or perfect correlation, respectively.
is the mean synaptic weight of a single group G. Calculated values range from −1 to 1, whose positive (negative) values indicate positive (negative) spatial autocorrelation, and where each extreme indicates either perfect dispersion or perfect correlation, respectively.
Alternatively, another index which has been used for assessing spatial autocorrelation is the Geary C index (Geary, 1954). Despite being inversely related, the Geary C index is not the inverse of Moran’s I index. Furthermore, while Moran’s I index is a global measure of spatial functional association, the Geary C index is sensitive to local autocorrelations and can be regarded as local indicator of functional association. The Geary C index is defined as follows,
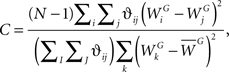
where the meanings of the symbols N, ϑij, WG, and 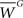 are the same as those defined for Moran’s I index. Calculated values range between 0 and 2, where numbers smaller or larger than one indicate positive or negative autocorrelation, respectively. Note that a Geary C index of 1 means that there is no spatial autocorrelation present.
are the same as those defined for Moran’s I index. Calculated values range between 0 and 2, where numbers smaller or larger than one indicate positive or negative autocorrelation, respectively. Note that a Geary C index of 1 means that there is no spatial autocorrelation present.
Results
Validation of a Detailed Model of a Layer 2/3 Pyramidal Cell
Biophysically detailed models typically try to embrace the full complexity of real cells, by incorporating as much of the morphology and known biophysical details as is feasibly possible, so that the model can replicate as much of the behavior of the cell under consideration. To investigate the emergence of spatially heterogeneous patterns of synaptic strengths in dendrites, a biophysically detailed model is required since STDP depends locally on the postsynaptic depolarization and calcium, thus the description and distribution of voltage-dependent conductances should be accurate. Note however, that the adopted STDP rule (see Materials and Methods) used in this paper does not have an explicit calcium dependence.
In constructing our biophysical model of a layer 2/3 pyramidal cell, detailed in the appendix, emphasis was placed on reproducing a variety of dendritic responses, including the frequency dependence of dendritic spike generation and distance-dependent calcium accumulation, similar to those seen in recent experiments (Kampa et al., 2006; Larkum et al., 2007). Figure 1 summaries model responses to a variety of experimental stimulus protocols. First, a short train of six simulated current pulses was injected into the soma to produce six somatic action potentials (APs). Figure 1A illustrates the dendritic voltage responses from six different locations in the dendrite to the somatically injected pulses delivered at a frequencies of 130 and 200 Hz, respectively. Dendritic spikes are clearly present but do not occur at every location in the dendritic tree. The position of dendritic responses are color-coded for clarity. Dendritic spike generation is caused by electrogenesis occurring at various locations and at different critical frequencies in the dendrite. Figure 1B indicates how the peak dendritic voltage amplitude varies non-linearly as a function of input pulse frequency for two different color-coded dendritic locations (as indicated in Figure 1A). One begins to see the generation of dendritic spikes in the model at a critical frequency of 130 Hz. This is in excellent agreement with recent experimental data from layer 2/3 pyramidal cells indicating that a critical frequency of 128 Hz is required for dendritic spike generation (Larkum et al., 2007). Figure 1C shows the corresponding peak calcium concentration as a function of frequency for the same color-coded locations (see Figure 1A). Figure 1D depicts the normalized peak calcium transient amplitudes (dF/Fpeak) during trains of six APs at increasing input frequencies for proximal and distal positions as indicated in Figure 1A. For increasing input frequencies, these trains lead to similar increases in calcium at proximal dendritic locations, however peak calcium transients (dF/Fpeak) at distal dendritic locations, were significantly larger during AP trains at and above the critical frequency for triggering a dendritic spike when compared with trains evoked at 100 Hz. This behavior is in agreement with recent experimental observations (Kampa et al., 2006). Figure 1E shows the normalized ratio of peak calcium transients evoked by three somatic APs relative to one AP at different distances from the soma along the indicated path and depicts a non-linear distance-dependent increase similar to the one observed experimentally (Kampa et al., 2006). Finally, Figure 1F shows how pairing a dendritic injection of EPSP-shaped current with a back-propagating action potential (BPAP) gives rise to a facilitatory effect where the threshold for dendritic spike generation was reduced by 25%, when a somatic spike was evoked by a brief current pulse 10 ms before dendritic current injection. The magnitude of this effect is again in excellent agreement with experimental observations from layer 2/3 pyramidal cells (compare to Figure 6C in Larkum et al., 2007).
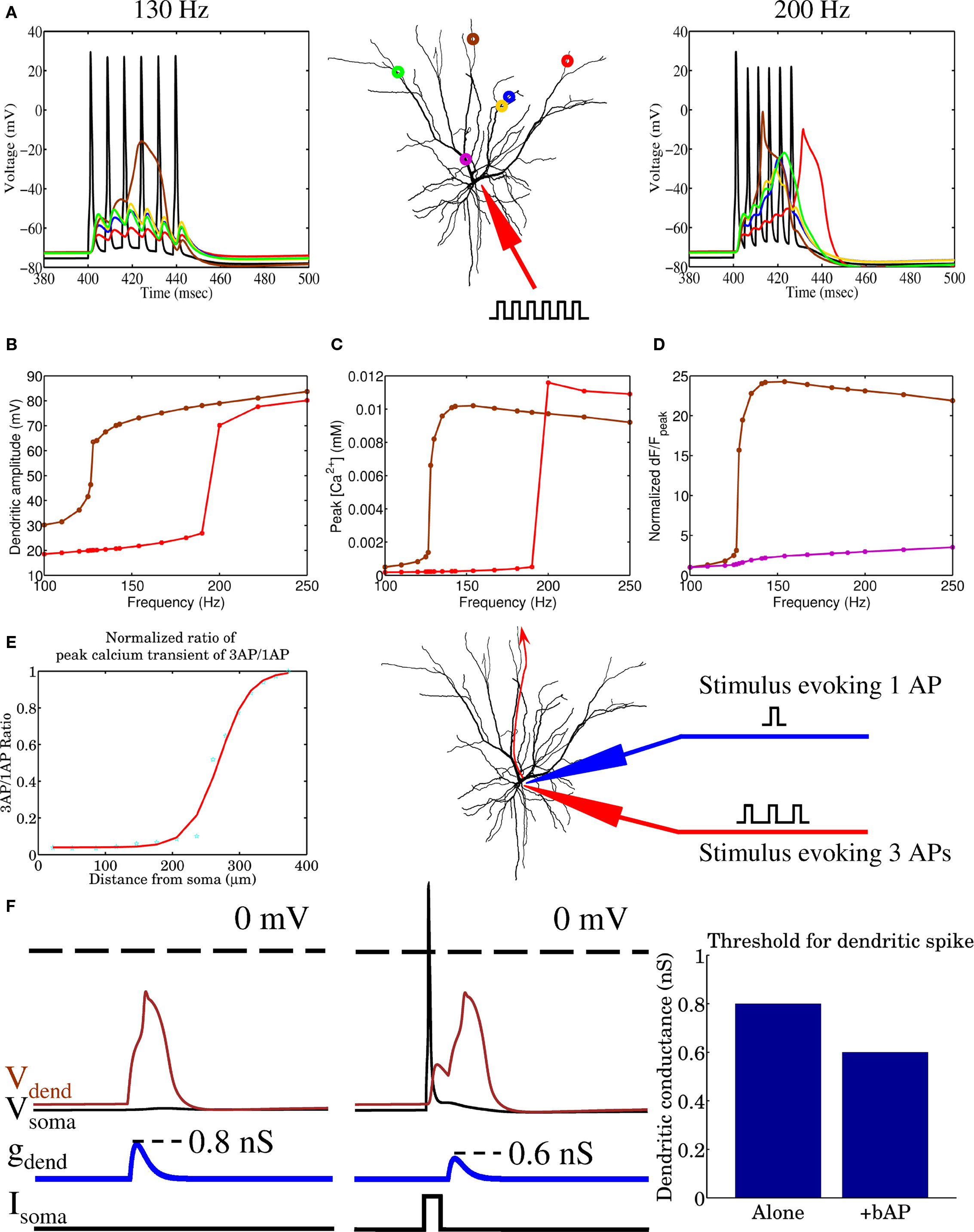
Figure 1. The biophysical model of a layer 2/3 pyramidal cell is shown to reproduce several experimentally observed properties, (A,B) including frequency dependent dendritic spike generation, a non-linear distance-dependent increase in (C) peak calcium and (D,E) the normalized ratio of peak calcium transients, and (F) a 25% reduction in the threshold for generating dendritic spikes when somatically generated spikes precede dendritic current injection by 10 ms.
The Dendritic Efficacy Mosaic and Functional Consequences
Prior to applying any learning rule, a decision needs to be made regarding how the model neuron is to be simulated. Past studies have investigated the temporal evolution and outcome of STDP in models where stimulation is primarily driven by two neural populations (Gerstner et al., 1996; Song et al., 2000; Song and Abbott, 2001; Gütig et al., 2003). More recently, multispike interactions have also been explored (Froemke and Dan, 2002; Izhikevich and Desai, 2003; Burkitt and Grayden, 2004; Appleby and Elliott, 2005, 2006, 2007; Pfister and Gerstner, 2006). In order to better understand the impact of plasticity and spike timing in cortical circuits, recent studies have focused on network-level simulations and the outcome of stimulations driven by the activity of multiple afferent groups, mimicking different neuronal populations that may, for example, encode different sensory modalities (Meffin et al., 2004; Wenisch et al., 2005; Burkitt et al., 2007; Masquelier and Thorpe, 2007; Gilson et al., 2009a,b,c,d; Masquelier et al., 2009). Here, we will adopt this multiple stream approach and compare the outcome of both spike-pair and multispike interaction based STDP. Stimulation to our spatially extended model neuron is provided by multiple equally sized groups of afferent fibers where the spike activity within a single group was correlated, but was independent of the activity in other groups. This stimulation paradigm is similar to previous STDP studies (Gerstner et al., 1996; Song et al., 2000; Gütig et al., 2003) where STDP leads to the activity-dependent formation of heterogeneous spatiotemporal patterns of synaptic efficacy. Similar to our previous study (Iannella and Tanaka, 2006), when the biophysical model receives inputs from multiple independent groups of afferent fibers with correlated activity, STDP, in conjunction with strong competition between synapses, leads to synaptic efficacies being arranged into spatially segregated clusters which effectively forms a partitioning of the dendritic tree. The resulting dendritic imprint effectively forms a tessellated spatial pattern of synaptic strength across the dendrite, as seen in Figure 2, which we will simply call a dendritic efficacy mosaic hereafter. When stimulating with four groups, Figure 2 shows the spatial organization of synaptic efficacies, before and after STDP, for each respective group. These plots display the relative dominance of a single groups compared to the total, defined as the ratio between the total efficacy by a single group and total efficacy of all groups for each location on the dendrite. Figure 2B shows the corresponding dendritic efficacy mosaic by color-coding the strongest group at each dendritic location after STDP. Before analyzing how synaptic competition affects such a dendritic partitioning, it is instructive to observe how voltage responses have changed before and after STDP. Figures 3A,B provides an example of the voltage response to stimulation from a single group of afferents, taken from the soma before and after STDP learning. Note that before STDP (Figure 3A), the somatic voltage trace contains no clear APs and is depolarized to an unusually high level. After STDP however, spikes are readily observed and the mean baseline depolarization is about −60 mV. These somatic spikes occurred since STDP led to an overall reduction in the total synaptic currents being generated throughout the neuron. The high level of depolarization observed in Figure 3A is simply attributed to the synaptic weight for the AMPA conductance initialized to wj(t) = 0.5. Starting from a lower initialization does not disrupt the emergence of either spatially segregated clusters or the dendritic mosaic (data not shown). The main difference is a reduction in the firing rate of the pyramidal cell after STDP. Figures S1A,B in the Supplementary Materials is one such example where the weights were initialized to wj(t) = 0.1; before STDP the somatic membrane recording shows that many spikes are present, but after STDP there are clearly fewer APs present. Figures 3C–F shows the voltage traces from two different (color-coded) dendritic locations (blue and green as shown in Figure 3) when stimulation is provided by a single afferent group before and after STDP. Note the presence of dendritic spikes in both Figures 3D,F, which have emerged, where STDP has led to clear changes to both somatic and dendritic voltage responses.

Figure 2. (A) STDP learning changes the initial spatial organization of synaptic strength and leads to emergence of regions dominated by a single group of afferent fibers. (B) After STDP learning the four competing groups form spatially segregated efficacy clusters. Here only the winning group is color-coded at each dendritic location.
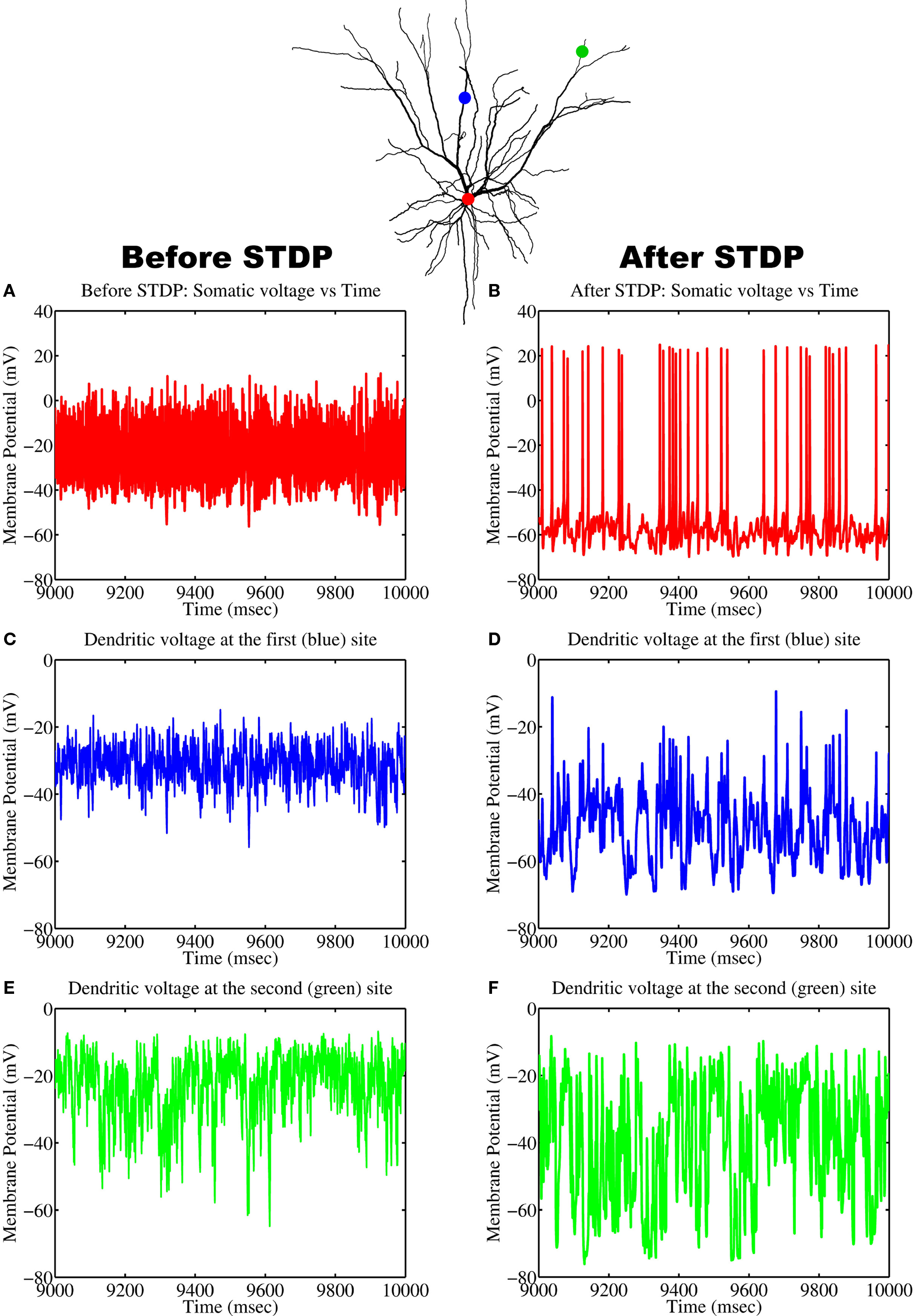
Figure 3. Changes to the voltage responses recorded at the soma and two different locations on the dendrite before and after STDP to stimulation from a single group of afferent fibers. Recording positions have been color-coded: (A,B) soma (red), (C,D) first dendritic position (blue), and (E,F) the second location (green).
Formation of the Dendritic Efficacy Mosaic Depends on Competition
The formation of spatial patterns displaying a clustered spatial organization typically emerge by competing for some limited resource (Murray, 2003). In the case of our biophysical neuron model, the processes by which STDP leads to the emergence of a dendritic efficacy mosaic was implemented using Gütig’s non-linear rule (see Materials and Methods for details), where synapses compete both spatially and temporally to control the timing of somatic and/or dendritic spike generation. Therefore it is important to determine how and under what conditions such an efficacy mosaic emerges. A key feature of Gütig’s rule is the presence of the exponent μ. This parameter controls the weight dependence of the rule and thus the degree of competition, since for μ = 0 the rule corresponds to the original additive STDP used by Abbott and Song (Song et al., 2000) and exhibits strong competition (Song et al., 2000; Song and Abbott, 2001); while for μ = 1 recovers the multiplicative STDP rule, a rule known to display stable yet weak competition between synapses (van Rossum et al., 2000). For intermediate values of μ the weight dependence is non-linear. We can now assess how the formation of such a dendritic efficacy mosaic is affected by changing the degree of synaptic competition, through the parameter μ of the STDP rule (Gütig et al., 2003). Figure 4 illustrates how the M-index, which quantifies the degree of spatial segregation between the spatial arrangements of synaptic strengths, contributed by four independent groups of correlated afferent fibers, changes as a function of the exponent μ. Note that the index is high for small μ, indicating that efficacy clusters are spatially segregated while for μ > 0.25 this segregation is poor. Spatial segregation occurs for small μ since STDP implementing strong competition between synapses, along with an active membrane, is seen to implement a winner-take-all self-organization process in space, where a single group can dominate some dendritic regions at the expense of others, while surrendering the remainder of the dendrite.
Figure 4. A plot of the M-index as a function of μ. Notice the high value of the M-index occurs when the non-linear STDP rule admits strong competition, but its value is small when synaptic competition is weak.
The Effect of Frequency on Spatially Segregated Clusters
The frequency of input spikes has previously been shown to influence the outcome of STDP via changes to the final distribution of synaptic weights (Song et al., 2000). For the case of spatially extended excitable neurons stimulated by various independent groups of fibers with correlated activity, we examine the impact of altering input frequency on the degree of spatial segregation and overall spatial organization. For the case when non-linear STDP admits strong competition, one expectation is that spatial segregation should be adversely affected for low frequencies when compared to higher input frequencies, primarily due to a reduction in the amount of potentiation; while for the weak competition case, there should be little change between the initial and final spatial distributions of synaptic efficacies across the dendritic tree, irrespective of the mean frequency of input spike activity. Figure 5 shows how the M-index changes as a function of mean input frequency when non-linear STDP admits both strong and weak competition. In the case of strong competition, for A− = 0.001125 and frequencies less than 20 Hz, the small values for the M-index indicates that spatial segregation and hence the degree of spatial partitioning between the efficacies contributed by all four afferent groups is poor. As mean afferent input frequencies are increased, the magnitude of the M-index, which measures the degree of spatial segregation, increases. For frequencies higher than 30 Hz, spatial segregation is good (indicated by the high M-index values) where maximal spatial segregation between efficacy patterns occurring for a mean input frequency of 35 Hz. In contrast, when synaptic competition is weak, the magnitude of the M-index remains low even when the mean frequencies of afferent inputs to the dendrite is increased. For the A− = 0.001125 case, high mean input frequencies of 30 Hz or more are needed to produce a high degree of spatial partitioning. This suggests that bursts may have a role to play, however for comparison, simply increasing A− by 10% to A− = 0.0012375 leads to higher M-index values over the range of selected mean input frequencies. Importantly for this specific case, we observe that a mean input frequency of 20 Hz is sufficient for a dendritic mosaic to emerge. Note that the selected values for A− were chosen so that the ratio A−/A+ lies within the experimentally observed range for this ratio (Froemke and Dan, 2002).
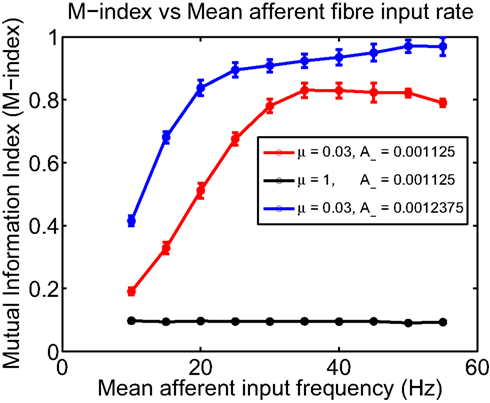
Figure 5. Plot of the M-index as a function of the mean frequency of input afferent fiber activity for two different values of μ; μ = 0. 03 (representing strong competition) and μ = 1 for weak competition between synapses. When synaptic competition is strong, for frequencies less than 20 Hz, the indices indicate that the degree of spatial segregation and the degree of partitioning is poor but improves as input frequency is increased. Computation times for the μ = 0.03 and μ = 1 were 4000 and 500 s of simulated time, respectively.
We have observed that the mean input frequency of afferent fibers alters the M-index, however, what are the consequences of these frequency effects on the response properties of the model neuron? Figure 6 shows how the firing rate of the pyramidal cell changes as a function of mean input frequency. Interestingly, the firing rate displays a dip, initially decreasing from 51.1 to 31.1 Hz for a mean input rate of 20 Hz and then rising almost linearly to 45.7 Hz for higher (mean) input rates. There are likely to be any number of contributing reasons for such non-linear behavior, including a reduction in firing rate via sodium inactivation and the non-trivial effects of noise in Hodgkin–Huxley based neuron models (Gutkin et al., 2009). Although the non-linear behavior of the somatic firing rate initially falls and then rises, we want to stress that the monotonous increase of the M-index suggests that what happens in the dendrite is more important than the activity in the soma, which is critical for STDP models based upon BPAPs. Also displayed are the corresponding changes to the probability density function (PDF), and the coefficient of variation (CV) as a function of mean input frequency. Raw interspike interval histograms are presented in Figure S2 in Supplementary Materials.
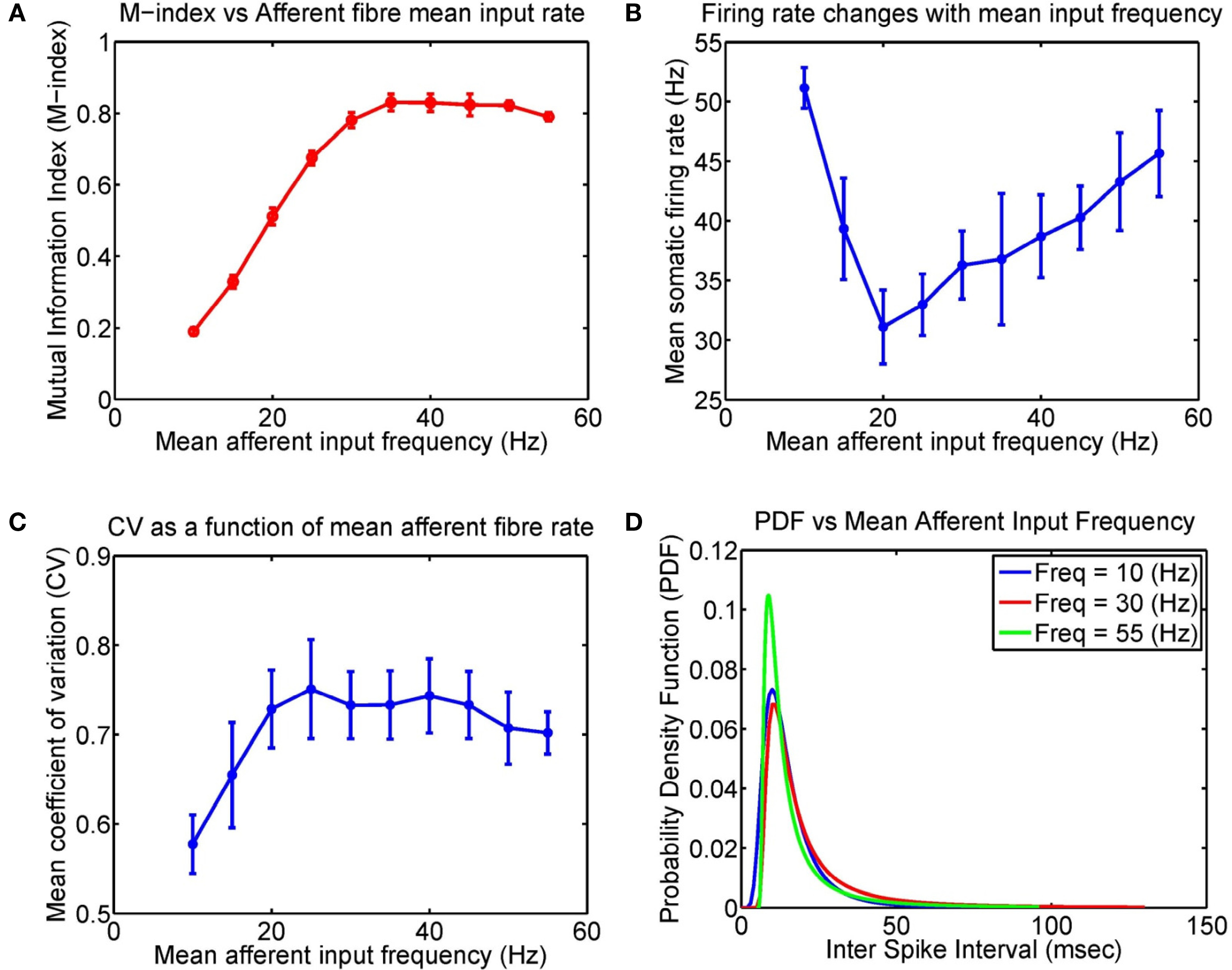
Figure 6. Input frequency affects the firing properties of the model layer 2/3 pyramidal cell after STDP learning. Here four groups of excitatory fibers and one group of inhibitory fibers were active. (A) Plot of the M-index as a function of the afferent fiber mean input frequency for μ = 0.03 (repeated from Figure 5, after 4000 s). (B) The corresponding changes to the somatic firing rates, (C), Coefficient of variation (CV), and (D) Probability density function (PDF) as a function of mean input frequency of afferent inputs, respectively. Note that the initial decrease in the firing rate may be attributed to several factors including sodium inactivation and the non-trivial effects of noise in neuron models (see Figure 1A of Gutkin et al., 2009).
Emergence of Spatially Segregated Clusters Via Multispike STDP Rules
So far spatially segregated efficacy clusters have emerged through spike-pair based STDP rules, however, previous STDP experiments have shown that changes to synaptic efficacy depends upon several factors including multiple spike interactions (Froemke and Dan, 2002; Froemke et al., 2006) and the frequency of presynaptic inputs (Sjöström et al., 2001). Pair based STDP rules are inadequate for reproducing observed changes in synaptic efficacy induced by either varying the frequency of presynaptic inputs or when triplets or more spikes are used in experimental protocols. STDP rules based upon multiple spike interactions, such as a recent rule based upon triplets of spikes (Pfister and Gerstner, 2006), are important to explain both the changes in efficacy when driven by multiple spike based stimulation and frequency effects observed during classical pairing protocol experiments (Sjöström et al., 2001). We next examine the impact of such type of rule (Froemke rule – see Materials and Methods) on the final spatial organization of synaptic efficacies after the learning process.
Figure 7 illustrates how varying the degree of synaptic competition affects the M-index. There are clear differences between spike-pair (Figure 4) and multispike interaction (Figure 7) based rules for small values of μ. By comparing Figures 4 and 7, we observe that the M-index was larger for STDP based upon multispike interactions (Froemke rule) rather than spike-pair based rules (Gütig rule). Explaining why these differences occur for small values of μ is difficult because a theoretical framework for studying changes in synaptic efficacy in realistic neuron models, as used here, is still lacking.
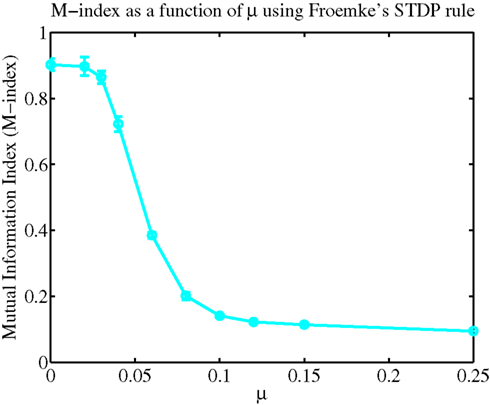
Figure 7. Spatially segregated efficacy clusters can emerge from multispike based STDP rules. To quantify how competition influences the final spatial organization of synaptic weights, again the M-index are displayed as a function of μ.
Robustness of Dendritic Efficacy Mosaic and Spatially Segregated Clusters
So far, we have seen that four independent groups of correlated afferent fibers each gives rise to spatially segregated synaptic efficacy clusters. Being contributed by each respective afferent group, these segregated clusters possess a unique global organization in space, where they form a tessellation or a mosaic which partitions the dendritic tree whereby each group dominates mutually exclusive regions of the dendrite. This leads to the question of how robust is this type of spatial patterning when the number of groups is increased. This indirectly permits one to explore the spatial scale for information storage and representation that is preferred after STDP. In particular, recent studies have emphasized that information may be stored over several nearby synapses, rather than at a single synapse (Govindarajan et al., 2006; Harvey and Svoboda, 2007; De Roo et al., 2008; Harvey et al., 2008; Larkum and Nevian, 2008; Yoshihara et al., 2009). Since information storage over several nearby synapses is indeed the main mode of information storage, one would expect that only a finite number of independent afferent groups, less than the number of synapses, can be represented throughout the dendrite. The key questions are therefore, how input representation as efficacy clusters changes and, more importantly, whether the degree of functional association between synapses degrades as the number of groups increases.
Functional association between synapses from a single group of afferent fibers is created on the postsynaptic side by STDP, resulting in local and stable potentiation of a group of synapses receiving correlated activity. Stability results because the group of synapses mutually re-enforce each other (association), where they all become more resistant to spurious changes of synaptic weight triggered random events, permitting them to maintain their function. Put simply, function is improved by the fact that they are locally associated, leading to a more robust system. In order to quantify the association between synapses, we have adopted two indices extensively used in spatial analysis. Both Moran’s I and Geary C indices were adopted as these (as previously stated in Section “Materials and Methods”) are essentially measures of spatial autocorrelation, widely used for testing the presence of spatial dependencies.
To sample more finely the effect of increasing the number of groups but keeping the total number of axons close to 1000, we selected groups so that the integer number of axons per group multiplied by the number of groups was 1000 ± 1. Figure 8A illustrates how the M-index changes as a function of increasing number of independent afferent fiber groups. Significantly, Figure 8B depicts both the Moran’s and Geary C indices, being respective global and local indicators of functional association, showing that there is a decrease in the degree of functional clustering when the number of groups increases. Note that there is a clear reduction in the rate of loss of functional clustering, where both indices are respectively expected to eventually asymptote to some finite non-zero values, keeping some degree of functional clustering between neighboring synapses. This suggests that only a finite number of afferent groups are represented in a manner where nearby synapses are functionally related and a high degree of spatial segregation can be maintained.
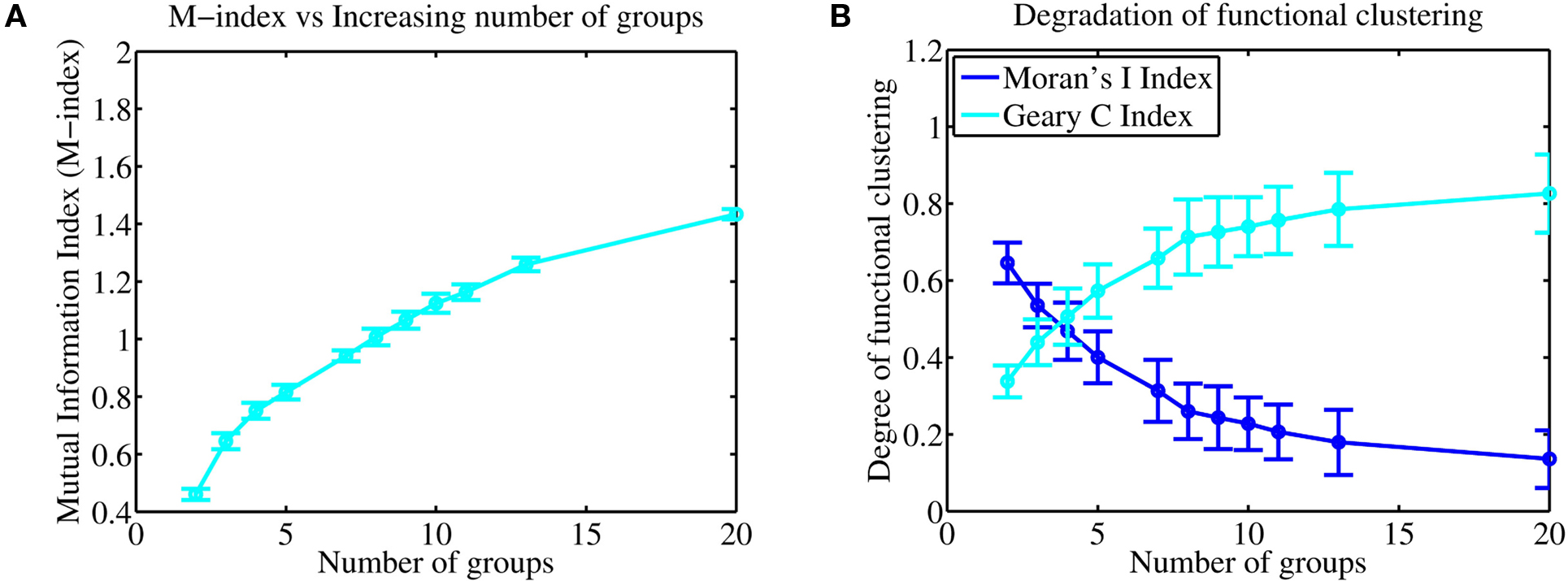
Figure 8. (A) Increasing the number of independent afferent fiber groups leads to an increase in the M-index indicating that there may be an increase in the degree of spatial segregation. (B) Interestingly, both the Moran and Geary indices show that there is a loss in the degree of functional clustering and association between nearby synapses, however, the rate of loss slows and is eventually seen to reduce to 0 where both indices are expected to asymptote to finite values, suggesting that functional clustering, both globally and locally between neighboring synapses persists. This suggests that smallest spatial scale for information storage (and representation) in the dendrite is likely to be distributed over several nearby synapses.
Discussion
Synaptic Competition and STDP Jointly Regulate Clustered Efficacy Engram Formation
In this current study, we have extended our original study (Iannella and Tanaka, 2006) by further investigating the issue of forming clustered synaptic efficacy engrams within the dendritic tree via STDP, subject to multiple input streams. A biophysical model, whose channel types and distributions are based upon available experimental findings, was used suggesting that the phenomena may exist in vivo. Specifically, when stimulation to the model was provided by four groups of correlated afferent fibers with no inter-group correlation, STDP allowed each respective group to dominate mutually exclusive regions of the dendrite, resulting in the emergence of spatially segregated clusters. These emergent clusters possess a unique spatial organization where they form a tessellated pattern which effectively partitions the dendritic tree, a patterning which we have termed a dendritic mosaic. This organization was stable in both space and time.
Significantly, we further showed that this spatial organization was robust to variations in the type of STDP (either spike-pair or multispike interaction based) rule used in the simulations. The emergence of the dendritic mosaic was prevented only when the number of independent input streams exceeded a critical value.
Functional Consequences of Clustered Synaptic Efficacy Engrams
The presence of a clustered spatial organization of synaptic efficacy within the dendrite can play important functional roles. One immediate consequence is clear; for inputs originating from a single group of afferents, activating potentiated synapses within efficacy clusters will favorably take part in neuronal firing. Specifically, activating such synapses will typically result in a larger dendritic depolarization when compared to the activation of synapses distributed diffusely in the dendritic tree, therefore making a bigger contribution toward spike generation. Previous experimental and theoretical studies support this, having shown that near synchronous activation of nearby synapses within a dendritic branch can lead to supralinear summation of their synaptic inputs. However, only linear summation was observed when synapses were activated on different dendritic branches (Poirazi et al., 2003; Gasparini et al., 2004; Polsky et al., 2004; Gasparini and Magee, 2006; Losonczy and Magee, 2006).
Local vs Global Postsynaptic Timing Information: The Case for Dendritic Spikes
In classical STDP models, synaptic weights are modified according to the timing difference between presynaptic input tpre and a postsynaptic spike tpost. Such studies assume a somatic spike can reliably back propagate to all regions of the dendritic tree, where this BPAP “tells” synapses about when the neuron fired a spike. In real pyramidal cells, however, spike generation is not restricted to the soma/axon initial segment region, but can be generated almost anywhere in the dendrite. This raises an important question as what signal conveys postsynaptic timing information and whether it should be local or global in nature. There is now mounting evidence from numerous experiments showing that the BPAP is an unreliable global signal since its known that it cannot fully invade the entire dendrite (Larkum et al., 2001; Stuart and Häusser, 2001). The extent of back-propagation varies depending upon various influences including potassium channel activation (Kampa and Stuart, 2006), synaptic background activity (Paré et al., 1998; Mickus et al., 1999), and inhibitory inputs (Larkum et al., 1999). Importantly, experimental studies have shown that synaptic efficacy can change without the need of a BPAP. Specifically, these studies illustrated that generating a local dendritic spike, by spatially clustered and near synchronous synaptic inputs, can lead to changes in synaptic strength (Schiller et al., 2000; Golding et al., 2002; Holthoff et al., 2004). For models, assuming that local dendritic spikes carry postsynaptic timing information are detected locally at each synapse is true, then the results of this paper and our previous work (Iannella and Tanaka, 2006) suggest that spatially segregated clusters emerge as a consequence.
It is now pertinent to ask what would happen if only the BPAP was used to convey postsynaptic timing information? A single theoretical study using a reconstructed CA1 pyramidal cell has shown that by assuming somatic spikes in two different models of dendritic excitability, one with a high capacity and the other with a low capacity to generate dendritic spikes, stimulated by a single group of afferents led to a large portion of highly potentiated synapses (Rumsey and Abbott, 2006). For the low capacity model potentiated synapses were typically located closer to the soma than depressed synapses (see Figure 10 in Rumsey and Abbott, 2006). Now if one considers the case when stimulation is provided by multiple groups of afferents, the results of Rumsey and Abbott (2004) seems to indicate that most synapses close to the soma, irrespective of the contributing group, would be potentiated, suggesting that the dendritic mosaic would not emerge.
Allowing the synapse to detect spikes locally has the advantage that different dendritic regions will have different sequences of postsynaptic times, and these different times essentially provides a “seed or scaffold” for clusters to emerge. This can be simply understood by the following intuitive example. When an afferent group begins to dominate some dendritic location(s) then the strength of its contributed synapses to neighboring locations are also like to be strengthened since dendritic spike generation at locations where the group dominates will also strongly depolarize adjacent locations. Synaptic inputs to these adjacent locations are likely to generate dendritic spikes and this eventually strengthens some of the synapses contributed by the dominant group, while weakening those of other groups, leading to the formation of a cluster.
Although the current STDP model provides useful insights into cluster formation, it is inadequate for understanding the biophysical mechanisms responsible such processes. Given that calcium signaling is known to be an important factor, not only for STDP (Nevian and Sakmann, 2006), but also for synaptic plasticity in general (Bliss and Lomo, 1973; Bienenstock et al., 1982; Brown et al., 1988; Dudek and Bear, 1992; Hille, 2001), we would argue that a biophysical model of STDP, based upon calcium and known (and/or yet to be discovered) biochemical signaling cascades is required (see Larkum and Nevian, 2008 for an excellent review). This model may provide useful insights for understanding the basis of synaptic plasticity and potential biophysical mechanisms, such as synaptic cross-talk, underlying cluster formation. Such a study, including the development of such a new calcium based model of STDP, is currently being pursued and whose results will be presented in a future publication.
Relationship to Previous Models
Standard theoretical STDP studies are typically conducted using simplified point or single compartment models having mainly focused on computational approaches toward the evolution of synaptic weights or the development of selective functional properties (Song et al., 2000; Song and Abbott, 2001; Gütig et al., 2003). Such investigations have provided useful insights into the role of spike timing in neuronal circuit formation or the emergence of some functional property.
However, to investigate how plasticity and active dendritic properties influences synaptic strength, the use of an elaborated compartmental model with active dendrites is gaining popularity (Rumsey and Abbott, 2004, 2006; Rainowitch and Segev, 2006a,b). To date, few studies have addressed the formation of spatial patterns of synaptic efficacies. The model presented here improves upon our previous model (Iannella and Tanaka, 2006). This previous study provided some indication that STDP may be an important mechanism involved in the development of spatially segregated efficacy clusters. Significantly, the model presented here is fundamentally different to the previous one since it not only includes several types of postsynaptic receptors, but also various voltage- and calcium-dependent ion channels, with their densities and distributions based upon data from the rat neocortex. Such biophysical detail was previously not included. The model response to high frequency stimulation patterns is now in good agreement with experimental findings.
The model presented here addresses a potentially important role for STDP in the development of spatially patterned functional synaptic inputs across the dendritic arbor. Previous models have proposed different plasticity mechanisms underlying the emergence of distance-dependent scaling in synaptic strength associated with location independent synapses (Rumsey and Abbott, 2004, 2006). In other studies, different homoeostatic plasticity mechanisms (Rabinowitch and Segev, 2006a,b) were used to examine the emergence of functional compartments within the dendrite. The current model complements these earlier studies by employing a biophysically realistic model neuron to not only illustrate a connection between the degree of clustering in the resulting arrangement of synaptic efficacies and the level of competition associated with STDP, but also the robustness of this emergent mode of spatial organization.
Predictions of the Model
Our biophysical model predicts that competition between synapses in both space and time underlies the emerging spatial arrangement of functional synaptic inputs. For neurons innervated by independent groups of afferent fibers with correlated activity, strong spatiotemporal competition may be essential for developing a dendritic efficacy mosaic, as observed in ocular dominance patterns (Katz and Constantine-Paton, 1988). Our biophysical model supports this hypothesis but shows that the segregation appears only when spatiotemporal competition was strong. When competition was weak, the dendritic efficacy mosaic fails to emerge. In this case both clustering and spatial segregation was severely degraded.
Our model also predicts that the spatial organization of synaptic efficacies along the dendrite is not random, but ordered, despite being heterogeneously distributed (Cotrell et al., 2001; Frick et al., 2001). It may reflect the nature and occurrence of correlations embedded in the spiking activity originating from different afferent groups. Support for this comes from previous studies illustrating supralinear summation of near synchronous inputs between neighboring synapses (Gasparini et al., 2004; Polsky et al., 2004; Gasparini and Magee, 2006; Losonczy and Magee, 2006); and coupling this form of electrical cooperativity with STDP then leads to the selective potentiation of those correlated inputs which led to dendritic spike generation. However, the most compelling supporting evidence comes from two recent studies by Harvey and Svoboda (2007) and De Roo et al. (2008). Harvey and Svoboda illustrated that inducing LTP at a synapse with suprathreshold stimuli, reduces the threshold of LTP induction in neighboring synapses on the same dendritic branch, allowing such synapses to be potentiated using subthreshold stimuli. This cooperativity between groups of nearby synapses (within a dendritic neighborhood) clearly leads to their coordinated regulation (Harvey and Svoboda, 2007). While the second study by De Roo et al. (2008) showed that LTP leads to the selection of inputs promoting spatiotemporal coincidence, thus promoting the creation of hotspots of functional synapses Indicating that any information or features embedded within a stimulus, such as correlations, are likely to be stored across several neighboring synapses forming a clustered engram. Using natural stimulation in vivo (such as visual), combined with recent advances in optical imaging of dendritic voltage using either organic dyes (Bradley et al., 2009) or red-shifted genetically encoded voltage sensitive proteins (Perron et al., 2009) in vivo would enable to directly test the presence of a dendritic efficacy mosaic.
Limitations of the Model
The present model was designed to test the hypothesis that STDP could serve as a mechanism involved in the formation of synaptic efficacy clusters within the dendritic tree. Despite the biophysical detail of the current neuron model, no effort was made to embed the neuron into a realistic network. The current study only considered a simple feed forward network structure, where the biophysically detailed model received feed forward inputs from neurons modeled as simple stochastic processes. Non-linear membrane dynamics and more appropriate model representations of these constituent neurons should be considered in future models.
An important issue is to elucidate both the molecular mechanisms and the role of calcium influx underlying the induction of STDP (as well as other forms of synaptic plasticity). Current STDP learning rules possess no dependence on calcium or any other molecular factors, and are exclusively parameterized by the precise timing of presynaptic inputs and postsynaptic spike generation (Zhang et al., 1998; Froemke and Dan, 2002; Froemke et al., 2005, 2006; Pfister and Gerstner, 2006). Experiments have shown that the induction of synaptic plasticity, including STDP, relies upon calcium entry into the cytoplasm of the neuron typically through NMDA receptors, voltage-dependent calcium channels and/or IP3-gated calcium release from the endoplasmic reticulum (ER). A key question here is how calcium influx via NMDA receptor activation leads to either potentiation or depression. Also experimentally verified is the consistency of LTP and LTD induction in synapses with the BCM theory of synaptic plasticity (Bienenstock et al., 1982; Dudek and Bear, 1992; Kirkwood et al., 1996; Philpot et al., 2001a,b, 2007).
Another limitation of the model is that other forms of plasticity, such as structural plasticity, were not considered. Previous experiments have shown that synaptic plasticity and learning are associated with changes to cortical/dendritic structure. One example is that the alteration of synapse morphology depends upon changing the structure of cytoskeletal filaments (Matus, 2000) through actin polymerization (Fischer et al., 1998; Dunaevsky et al., 1999) and another is the involvement of adhesion molecules in the formation of new synapses (Benson et al., 2000). Theoretical studies have also investigated the impact of structural plasticity on the memory capacity of information storage (Poirazi et al., 2001; Stepanyants et al., 2002). Here however, incorporating the biophysical details of structural plasticity, through the creation, modification and removal of synapses/spines via activity-dependent remodeling of afferent connectivity onto the dendrite was not included due to the extra complexity and computational load this would have imposed.
Ideally one should test the role of STDP (as well as other forms of plasticity) in a network composed of entirely biophysically realistic spatial model neurons specifically aimed at simulating some cortical region, like the primary visual cortex, the area corresponding to the early stage of signal processing of visual information, incorporating details of both cell type and spatial morphology of such constituent neurons. The complexity and computational resources required to conduct such simulations are enormous, only possible on the most powerful supercomputers. Despite this current obstacle, intermediate levels of model representation should be considered and are currently under investigation.
We believe that the current study provides useful insights toward understanding how the interplay between synapse location, active dendritic properties and synaptic plasticity shapes the strengths and spatial arrangements of synapses. Our study suggests that “clustering” may be the favored outcome of synaptic plasticity. More importantly, this model proposes that STDP, driven by timing differences between synaptic inputs and dendritic spike generation, may be an important mechanism contributing to the efficacy and spatial arrangements of synapses within the dendrite.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank the support of RIKEN BSI and the Advanced Center for Computing and Communication for their technical assistance.
Supplementary Material
The Supplementary Material for this article can be found online at http://www.frontiersin.org/neuroscience/frontiersincomputationalneuroscience/paper/10.3389/fncom.2010.00021/
References
Anderson, J. C., Binzegger, T., Douglas, R. J., and Martin, K. A. C. (2002). Chance or design? Some specific considerations concerning synaptic boutons in cat visual cortex. J. Neurocytol. 31, 211–229.
Appleby, P. A., and Elliott, T. (2005). Synaptic and temporal ensemble interpretation of spike-timing-dependent plasticity. Neural Comput. 17, 2316–2336.
Appleby, P. A., and Elliott, T. (2006). Stable competitive dynamics emerge from multispike interactions in a stochastic model of spike-timing-dependent plasticity, Neural Comput. 18, 2414–2464.
Appleby, P. A., and Elliott, T. (2007). Multispike interactions in a stochastic model of spike-timing-dependent plasticity. Neural Comput. 19, 1362–1399.
Benson, D., Schnapp, L., Shapiro, L., and Huntley, G. (2000). Making memories stick: cell-adhesion molecules in synaptic plasticity. Trends Cell Biol. 10, 473–482.
Bi, G.-Q., and Poo, M.-M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472.
Bienenstock, E. L., Cooper, L. N., and Munro, P. W. (1982). Theory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex. J. Neurosci. 2, 32–48.
Binzegger, T., Douglas, R. J., and Martin, K. A. C. (2004). A quantitative map of the circuit of cat primary visual cortex. J. Neurosci. 24, 8441–8453.
Bliss, T. V., and Lomo, T. (1973). Long-lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit following stimulation of the perforant path. J. Physiol. 232, 331–356.
Bliss, T. V. P., and Collingridge, G. L. (1993). A synaptic model of memory: long-term potentiation in the hippocampus. Nature 361, 31–39.
Bradley, J., Luo, R., Otis, T. S., and DiGregorio, D. A. (2009). Submillisecond optical reporting of membrane potential in situ using a neuronal tracer dye. J. Neurosci. 29, 9197–9209.
Brown, T. H., Chapman, P. F., Kairiss, E. W., and Keenan, C. L. (1988). Long-term synaptic potentiation. Science 242, 724.
Burkitt, A. N., Gilson, M., and Leo van Hemmen, J. (2007). Spike-timing-dependent plasticity for neurons with recurrent connections. Biol. Cybern. 96, 533–546.
Burkitt, A. N., and Grayden, D. B. (2004). Spike-timing-dependent plasticity: the relationship to rate-based learning for models with weight dynamics determined by a stable fixed point. Neural Comput. 16, 885–940.
Cotrell, J. R., Dubé, G. R., Egles, C., and Liu, G. (2001). Distribution, density, and clustering of functional glutamate receptors before and after synaptogenesis in hippocampal neurons. J. Neurophysiol. 84, 1573–1587.
Cove, J., Blinder, P., Abi-Jaoude, E., Lafrenière-Roula, M., Devroye, L., and Baranes, D. (2006). Growth of neurites toward neurite–neurite contact sites increases synaptic clustering and secretion and is regulated by synaptic activity. Cereb. Cortex 16, 83–92.
Debanne, D., Gähwiler, B. H., and Thompson, S. M. (1998). Long-term synaptic plasticity between pairs of individual CA3 pyramidal cells in rat hippocampal slice cultures. J. Physiol. 507, 237–247.
De Roo, M., Klauser, P., and Muller, D. (2008). LTP promotes a selective long-term stabilization and clustering of dendritic spines. PLoS Biol. 6, e219. doi: 10.1371/journal.pbio.0060219.
Destexhe, A., and Paré, D. (1999). Impact of network activity on the integrative properties of neocortical pyramidal neurons in vivo. J. Neurophysiol. 81, 1531–1547.
Dudek, S. M., and Bear, M. F. (1992). Homosynaptic long-term depression in area ca1 of hippocampus and the effects of N-methyl-D-aspartate receptor blockade. Proc. Natl. Acad. Sci. U.S.A. 89, 4363–4367.
Dunaevsky, A., Tashiro, A., Majewska, A., Mason, C., and Yuste, R. (1999). Developmental regulation of spine motility in the mammalian central nervous system. Proc. Natl. Acad. Sci. U.S.A. 96, 13438–13443.
Duncan, O., and Duncan, B. (1955). A methodological analysis of segregation indexes. Am. Sociol. Rev. 20, 210–217.
Feldmeyer, D., Lubke, J., Silver, R. A., and Sakmann, B. (2002). Synaptic connections between layer 4 spiny neurone-layer 2/3 pyramidal cell pairs in juvenile rat barrel cortex: physiology and anatomy of interlaminar signalling within a cortical column. J. Physiol. 538(Pt 3), 803–822.
Fischer, M., Kaech, S., Knutti, D., and Matus, A. (1998). Rapid actin-based plasticity in dendritic spines. Neuron 20, 847–854.
Frankel, D., and Volij, O. (2005). Scale Invariant Measures of Segregation. Econ. Theory and Game Theory, 18.
Frick, A., Zieglgänsberger, W., and Dodt, H.-U. (2001). Glutamate receptors form hot spots on apical dendrites of neocortical pyramidal neurons. J. Neurophysiol. 86, 1412–1421.
Froemke, R. C., and Dan, Y. (2002). Spike-timing dependent synaptic modification induced by natural spike trains. Nature 416, 433–438.
Froemke, R. C., Poo, M.-M., and Dan, Y. (2005). Spike-timing-dependent synaptic plasticity depends on dendritic location. Nature 434, 221–225.
Froemke, R. C., Tsay, I. A., Raad, M., Long, J. D., and Dan, Y. (2006). Contribution of individual spikes in burst-induced long-term synaptic modification. J. Neurophysiol. 95, 1620–1629.
Gasparini, S., and Magee, J. C. (2006). State-dependent dendritic computation in hippocampal ca1 pyramidal neurons. J. Neurosci. 26, 2088–2100.
Gasparini, S., Migliore, M., and Magee, J. C. (2004). On the initiation and propagation of dendritic spikes in ca1 pyramidal neurons. J. Neurosci. 24, 11046–11056.
Gerstner, W., Kempter, R., Leo van Hemmen, J., and Wagner, H. (1996). A neuronal learning rule for sub-millisecond temporal coding. Nature 383, 76–78.
Gilson, M., Burkitt, A., Grayden, D., Thomas, D., and van Hemmen, J. (2009a). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. I. Input selectivity–strengthening correlated input pathways. Biol. Cybern. 101, 81–102.
Gilson, M., Burkitt, A., Grayden, D., Thomas, D., and van Hemmen, J. (2009b). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. II. Input selectivity–symmetry breaking. Biol. Cybern. 101, 103–114.
Gilson, M., Burkitt, A., Grayden, D., Thomas, D., and van Hemmen, J. (2009c). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. III: Partially connected neurons driven by spontaneous activity. Biol. Cybern. 101, 411–426.
Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2009d). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks IV: structuring synaptic pathways among recurrent connections. Biol. Cybern. 101, 427–444.
Glanzman, D. L., Kandel, E. R., and Schacher, S. (1991). Target-dependent morphological segregation of Aplysia sensory outgrowth in vitro. Neuron 7, 903–913.
Golding, N. L., Staff, N. P., and Spruston, N. (2002). Dendritic spikes as a mechanism for cooperative long-term potentiation. Nature 418, 326–331.
Govindarajan, A., Kelleher, R., and Tonegawa, S. (2006). A clustered plasticity model of long-term memory engrams. Nat. Rev. Neurosci. 7, 575–583.
Gütig, R., Aharonov, R., Rotter, S., and Sompolinsky, H. (2003). Learning input correlations through nonlinear temporally asymmetric Hebbian plasticity. J. Neurosci. 23, 3697–3714.
Gutkin, B., Jost, J., and Tuckwell, H. (2009). Inhibition of rhythmic neural spiking by noise: the occurrence of a minimum in activity with increasing noise. Naturwissenschaften 96, 1091–1097.
Harvey, C. D., and Svoboda, K. (2007). Locally dynamic synaptic learning rules in pyramidal neuron dendrites. Nature 450, 1195–1202.
Harvey, C. D., Yasuda, R., Zhong, H., and Svoboda, K. (2008). The spread of Ras activity triggered by activation of a single dendritic spine. Science 321, 136–140.
Hellwig, B. (2000). A quantitative analysis of the local connectivity between pyramidal neurons in layers 2/3 of the rat visual cortex. Biol. Cybern. 82, 111–121.
Hellwig, B., Schuez, A., and Aertsen, A. (1994). Synapses on axon collaterals of pyramidal cells are spaced at random intervals: a Golgi study in the mouse cerebral cortex. Biol. Cybern. 71, 1–12.
Hines, M. L., and Carnevale, N. T. (2001). neuron: a tool for neuroscientists. Neuroscientist 7, 123–135.
Holthoff, K., Kovalchuk, Y., Yuste, R., and Konnerth, A. (2004). Single-shock ltd by local dendritic spikes. J. Physiol. 560, 27–36.
Iannella, N., and Tanaka, S. (2006). Synaptic efficacy cluster formation across the dendrite via stdp. Neurosci. Lett. 403, 24–29.
Iannella, N., Tuckwell, H., and Tanaka, S. (2004). Firing properties of a stochastic pde model of a rat sensory cortex layer 2/3 pyramidal cell. Math. Biosci. 188, 117–132.
Kalisman, N., Silberberg, G., and Markram, H. (2005). The neocortical microcircuit as a tabula rasa. Proc. Natl. Acad. Sci. U.S.A. 102, 880–885.
Kampa, B. M., Letzkus, J. J., and Stuart, G. J. (2006). Requirement of dendritic calcium spikes for induction of spike-timing-dependent synaptic plasticity. J. Physiol. 574(Pt 1) 283–290.
Kampa, B. M., and Stuart, G. J. (2006). Calcium spikes in basal dendrites of layer 5 pyramidal neurons during action potential bursts. J. Neurosci. 26, 7424–7432.
Katz, L. C., and Constantine-Paton, M. (1988). Relationships between segregated afferents and postsynaptic neurons in the optic tectum of three-eyed frogs. J. Neurosci. 8, 3160–3180.
Kavalali, E. T., Klingauf, J., and Tsien, R. W. (1999). Activity dependent regulation of synaptic clustering in a hippocampal culture system. Proc. Natl. Acad. Sci. U.S.A. 96, 12893–12900.
Kirkwood, A., and Bear, M. F. (1994). Homosynaptic long-term depression in the visual cortex. J. Neurosci. 14, 3404–3412.
Kirkwood, A., Rioult, M. C., and Bear, M. F. (1996). Experience-dependent modification of synaptic plasticity in visual cortex. Nature 381, 526–528.
Koch, C., Poggio, T., and Torre, V. (1983). Nonlinear interactions in a dendritic tree: localization, timing and role in information processing. Proc. Natl. Acad. Sci. U.S.A. 80, 2799–2802.
Kuhn, A., Aertsen, A., and Rotter, S. (2003). Higher-order statistics of input ensembles and the response of simple model neurons. Neural Comput. 15, 67–101.
Larkum, M. E., Kaiser, K. M. M., and Sakmann, B. (1999). Calcium electrogenesis in distal apical dendrites of layer 5 pyramidal cells at a critical frequency of back-propagating action potentials. Proc. Natl. Acad. Sci. U.S.A. 96, 14600–14604.
Larkum, M. E., Kaiser, K. M. M., and Sakmann, B. (2001). Dendritic mechanisms underlying the coupling of the dendritic with the axonal action potential initiation zone of adult layer 5 pyramidal neurons. J. Physiol. 533, 447–466.
Larkum, M. E., and Nevian, T. (2008). Synaptic clustering by dendritic signalling mechanisms. Curr. Opin. Neurobiol. 18, 321–331.
Larkum, M. E., Waters, J., Sakmann, B., and Helmchen, F. (2007). Dendritic spikes in apical dendrites of neocortical layer 2/3 pyramidal neurons. J. Neurosci. 27, 8999–9008.
Lorenzon, N. M., and Foehring, R. C. (1995). Characterization of pharmacologically identified voltage-gated calcium channel currents in acutely isolated rat neocortical neurons. i. adult neurons. J. Neurophysiol. 73, 1430–1442.
Losonczy, A., and Magee, J. C. (2006). Integrative properties of radial oblique dendrites in hippocampal ca1 pyramidal neurons. Neuron 50, 291–307.
Magee, J. C., and Cook, E. P. (2000). Somatic epsp amplitude is independent of synapse location in hippocampal pyramidal neurons. Nat. Neurosci. 3, 895–903.
Mainen, Z. F., Joerges, J., Huguenard, J. R., and Sejnowski, T. J. (1995). A model of spike initiation in neocortical pyramidal cells. Neuron 15, 1427–1439.
Markram, H., Lübke, J., Frotscher, M., and Sakmann, B. (1997a). Regulation of synaptic efficacy by coincidence of postsynaptic ap and epsp. Science 275, 213–215.
Markram, H., Lubke, J., Frotscher, M., Roth, A., and Sakmann, B. (1997b). Physiology and anatomy of synaptic connections between thick tufted pyramidal neurones in the developing rat neocortex. J. Physiol. 500(Pt 2), 409–440.
Masquelier, T., Guyonneau, R., and Thorpe, S. J. (2009). Competitive STDP-based spike pattern learning. Neural Comput. 21, 1259–1276.
Masquelier, T., and Thorpe, S. J. (2007). Unsupervised learning of visual features through spike timing dependent plasticity. PLoS Comput. Biol. 3, 0247–0257. doi: 10.1371/journal.pcbi.0030031.
Massey, D. S., and Denton, N. A. (1988). The dimensions of residential segregation. Soc. Forces 67, 281–315.
Meffin, H., Besson, J., Burkitt, A. N., and Grayden, D. B. (2004). Learning the structure of correlated synaptic subgroups using stable and competitive spike-timing-dependent plasticity. Neural Comput. 16, 885–940.
Megías, M., Emri, Z. S., Freund, T. F., and Gulyás, I. A. (2001). Total number and distribution of inhibitory and excitatory synapses on hippocampal ca1 pyramidal cells. Neuroscience 102, 527–540.
Mel, B. W. (1993). Synaptic integration in an excitable dendritic tree. J. Neurophysiol. 70, 1086–1101.
Mickus, T., Jung, H.-Y., and Spruston, N. (1999). Properties of slow, cumulative sodium channel inactivation in rat hippocampal ca1 pyramidal cells. Biophys. J. 76, 846–860.
Mora, R., and Ruiz-Castillo, J. (2009). “The invariance properties of the Mutual Information Index of multigroup segregation,” in Occupational and Residential Segregation, Vol. 17, eds Y. Flückiger, S. F. Reardon, and J. Silber (London: Emerald), 33–54.
Nevian, T., and Sakmann, B. (2006). Spine Ca2+ signaling in spike-timing-dependent plasticity. J. Neurosci. 26, 11001–11013.
Paré, D., Shink, E., Gaudreau, H., Destexhe, A., and Lang, E. J. (1998). Impact of spontaneous synaptic activity on the resting properties of cat neocortical pyramidal neurons in vivo. J. Neurophysiol. 79, 1450–1460.
Perron, A., Mutoh, H., Launey, T., and Knöpfel, T. (2009). Red-shifted voltage-sensitive fluorescent proteins. Chem. Biol. 16, 1268–1277.
Pfister, J.-P., and Gerstner, W. (2006). Triplets of spikes in a model of spike timing-dependent plasticity. J. Neurosci. 26, 9673–9682.
Philpot, B. D., Cho, K. K. A., and Bear, M. F. (2007). Obligatory role of nr2a for metaplasticity in visual cortex. Neuron 53, 495–502.
Philpot, B. D., Sekhar, A. K., Shouval, H. Z., Bear, M. F., and Cooper, L. N. (2001a). Visual experience and deprivation bidirectionally modify the composition and function of nmda receptors in visual cortex. Neuron 29, 157–169.
Philpot, B. D., Espinosa, J. S., and Bear, M. F. (2001b). Evidence for altered nmda receptor function as a basis for metaplasticity in visual cortex. J. Neurosci. 23, 5583–5588.
Poirazi, P., Brannon, T., and Mel, B. W. (2001). Impact of active dendrites and structural plasticity on the memory capacity of neural tissue. Neuron 29, 779–796.
Poirazi, P., Brannon, T., and Mel, B. W. (2003). Arithmetic of subthreshold synaptic summation in a model ca1 pyramidal cell. Neuron 37, 977–987.
Polsky, A., Mel, B. W., and Schiller, J. (2004). Computational subunits in thin dendrites of pyramidal cells. Nat. Neurosci. 7, 621–627.
Rabinowitch, I., and Segev, I. (2006a). The interplay between homeostatic synaptic plasticity and functional dendritic compartments. J. Neurophysiol. 96, 276–283.
Rabinowitch, I., and Segev, I. (2006b). The endurance and selectivity of spatial patterns of long-term potentiation/depression in dendrites under homeostatic synaptic plasticity. J. Neurosci. 26, 13474–13484.
Reardon, S. F., and Firebaugh, G. (2002). Measures of multigroup segregation. Sociol. Methodol. 32, 33–67.
Rhodes, P. A., and Gray, C. M. (1994). Simulations of intrinsically bursting neocortical pyramidal neurons. Neural Comput. 6, 1086–1110.
Rhodes, P. A., and Llinás, R. R. (2001). Apical tuft input efficacy in layer 5 pyramidal cells from rat visual cortex. J. Physiol. 6, 1086–1110.
Rudolph, M., and Destexhe, A. (2003). A fast-conducting stochastic integrative mode for neocortical neurons in vivo. J. Neurosci. 23, 2466–2476.
Rumsey, C. C., and Abbott, L. F. (2004). Equalization of synaptic efficacy by activity and timing-dependent synaptic plasticity. J. Neurophysiol. 91, 2273–2280.
Rumsey, C. C., and Abbott, L. F. (2006). Synaptic democracy in active dendrites. J. Neurophysiol. 96, 2307–2318.
Schiller, J., Major, G., Koester, H. J., and Schiller, Y. (2000). nmda spikes in basal dendrites of cortical pyramidal cells. Nature 404, 285–289.
Schwindt, P. C., Spain, W. J., Foehring, R. C., Stafstrom, C. E., Chubb, W. E., and Crill, M. C. (1988). Multiple potassium conductances and their functions in neurons from cat sensorimotor cortex in vitro. J. Neurophysiol. 59, 424–449.
Sjöström, P. J., Turrigiano, G. G., and Nelson, S. B. (2001). Rate, timing, and cooperativity jointly determine cortical synaptic plasticity. Neuron 32, 1149–1164.
Somogyi, P., Tamás, G., Lujan, R., and Buhl, E. H. (1998). Salient features of synaptic organisation in the cerebral cortex. Brain Res. Rev. 26, 113–135.
Song, S., and Abbott, L. F. (2001). Cortical development and remapping through spike timing-dependent plasticity. Neuron 32, 339–350.
Song, S., Miller, K. D., and Abbott, L. F. (2000). Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926.
Stafstrom, C. E., Schwindt, P. C., Chubb, M. C., and Crill, W. E. (1985). Properties of persistent sodium conductance and calcium conductance of layer v neurons from cat sensorimotor cortex in vitro. J. Neurophys. 53, 153–170.
Stepanyants, A., Hirsch, J. A., Martinez, L. M., Kisvarday, Z. F., Ferecsko, A. S., and Chklovskii, D. B. (2008). Local potential connectivity in cat primary visual cortex. Cereb. Cortex 18, 13–28.
Stepanyants, A., Hof, P. R., and Chklovskii, D. B. (2002). Geometry and structural plasticity of synaptic connectivity. Neuron 34, 275–288.
Stuart, G. J., and Häusser, M. (2001). Dendritic coincidence detection of epsps and action potentials. Nat. Neurosci. 4, 63–71.
Thomson, A. M., Deuchars, J., and West, D. C. (1994). Relationships between morphology and physiology of pyramid–pyramid single axon connections in rat neocortex in vitro. J. Physiol. 478(Pt 3), 423–435.
Thomson, A. M., West, D. C., Wang, Y., and Bannister, A. P. (2002). Synaptic connections and small circuits involving excitatory and inhibitory neurons in layers 2–5 of adult rat and cat neocortex: triple intracellular recordings and biocytin labelling in vitro. Cereb. Cortex 12, 936–953.
Traub, R. D., Buhl, E. H., Gloveli, T., and Whittington, M. A. (2003). Fast rhythmic bursting can be induced in a layer 2/3 cortical neurons by enhancing persistent na+ conductance or by blocking BK channels. J. Neurophysiol. 89, 909–921.
van Rossum, M. C. W., Bi, G.-Q., and Turrigiano, G. G. (2000). Stable Hebbian learning from spike timing-dependent plasticity. J. Neurosci. 20, 8812–8821.
Wenisch, O. G., Noll, J., and Leo van Hemmen, J. (2005). Spontaneously emerging direction selectivity maps in the visual cortex through stdp. Biol. Cybern. 93, 239–247.
Yoshihara, Y., De Roo, M., and Muller, D. (2009). Dendritic spine formation and stabilization, Curr. Opin. Neurobiol. 19, 146–153.
Keywords: STDP, dendrite, spatial patterning, mutual information index, dendritic efficacy mosaic
Citation: Iannella NL, Launey T and Tanaka S (2010) Spike timing-dependent plasticity as the origin of the formation of clustered synaptic efficacy engrams. Front. Comput. Neurosci. 4:21. doi: 10.3389/fncom.2010.00021
Received: 08 March 2010;
Paper pending published: 01 April 2010;
Accepted: 14 June 2010;
Published online: 14 July 2010
Edited by:
Wulfram Gerstner, Ecole Polytechnique Fédérale de Lausanne, SwitzerlandReviewed by:
Claudia Clopath, Ecole Polytechnique Fédérale de Lausanne, SwitzerlandRobert Legenstein, Graz University of Technology, Austria
Copyright: © 2010 Iannella, Launey and Tanaka. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Nicolangelo Libero Iannella, Launey Research Unit for Molecular Neurocybernetics, RIKEN Brain Science Institute, 2-1 Hirosawa, Wako-shi, Saitama 351-0198, Japan. e-mail:bmljb2xhbmdAYnJhaW4ucmlrZW4uanA=
