- 1 Department of Psychology, University of Sheffield, Western Bank, Sheffield, UK
- 2 Department of Anatomy and Developmental Biology, University College London, London, UK
Marr–Albus adaptive filter models of the cerebellum have been applied successfully to a range of sensory and motor control problems. Here we analyze their properties when applied to classical conditioning of the nictitating membrane response in rabbits. We consider a system-level model of eyeblink conditioning based on the anatomy of the eyeblink circuitry, comprising an adaptive filter model of the cerebellum, a comparator model of the inferior olive and a linear dynamic model of the nictitating membrane plant. To our knowledge, this is the first model that explicitly includes all these principal components, in particular the motor plant that is vital for shaping and timing the behavioral response. Model assumptions and parameters were systematically investigated to disambiguate basic computational capacities of the model from features requiring tuning of properties and parameter values. Without such tuning, the model robustly reproduced a range of behaviors related to sensory prediction, by displaying appropriate trial-level associative learning effects for both single and multiple stimuli, including blocking and conditioned inhibition. In contrast, successful reproduction of the real-time motor behavior depended on appropriate specification of the plant, cerebellum and comparator models. Although some of these properties appear consistent with the system biology, fundamental questions remain about how the biological parameters are chosen if the cerebellar microcircuit applies a common computation to many distinct behavioral tasks. It is possible that the response profiles in classical conditioning of the eyeblink depend upon operant contingencies that have previously prevailed, for example in naturally occurring avoidance movements.
Introduction
A striking feature of cerebellar physiology is that the cortical, nuclear and olivary territories are connected in register to form a basic microcircuit that is repeated many-fold across the cerebellum to reveal, at the cortical level, a “crystalline” array of processing elements. Numerous studies have shown that small sets of these microcircuits are fundamental for fast and accurate control of various individual motor tasks—for example, smooth pursuit eye movements (Zee et al., 1981), ocular following (Shidara et al., 1993), saccades (Optican and Robinson, 1980) the vestibulo-ocular reflex (VOR) (Ito, 1982) and limb movements (Gilbert and Thach, 1977). This combination of uniformity and general applicability suggests that the cerebellar microcircuit implements a common algorithm that is useful for a wide range of sensory and motor control tasks (Ito, 1984, 2006).
A conceptual framework that is widely used in characterizing this cerebellar algorithm is based on the models of Marr (1969) and Albus (1971). In the Marr–Albus framework, the cerebellum learns to construct appropriate outputs from input “contexts,” which are represented by those afferent sensory or motor signals on the mossy fiber inputs that occur reliably before the required output (Albus, 1971; Gilbert, 1974; Marr, 1969). Learning is driven by a second type of input, a “teaching” signal carried by climbing fibers. A simple yet general implementation of this conceptual framework is the adaptive filter, a generic signal-processing device that has wide utility in control theory and other applications (Widrow, 1985), and was first formally applied to the cerebellum by Fujita (1982). Because the cerebellum has such a homogeneous structure, it can be hypothesized that each microcircuit implements the same basic algorithm and that a particular behavioral task is specified by the information content of its climbing fiber input and by the target of its output. Adaptive filter models have been used successfully for many of the cerebellum-dependent tasks referred to above (references given in Dean et al., 2010).
Classical conditioning of eyeblink and skeletal muscle reflexes has been shown to be dependent on the cerebellum (see review by Yeo and Hesslow, 1998) and experimental analysis of the neural circuitry underlying eyeblink conditioning suggests mechanisms that fit well within the Marr–Albus framework. It appears that the conditioned stimulus (CS) is a “context” delivered to the cerebellum by the mossy fiber system, the unconditioned stimulus (US) is a “teaching” signal borne by the climbing fiber input from the inferior olive, and the resultant cerebellar output drives the conditioned response (CR) as a motor output (Hesslow and Yeo, 2002; Yeo and Hesslow, 1998). If the cerebellar microcircuit implements a single basic algorithm, as has been suggested, then this cerebellum-dependent associative learning task should have an adaptive filter implementation consistent with that of other cerebellar tasks.
However, we propose here that there is a fundamental difficulty in applying the Marr–Albus framework to classical conditioning. All Marr–Albus based models of the cerebellar role in motor control recognize that the olivary signal conveys a sensory or motor error related to movement inaccuracy, and that by reducing this signal the cerebellum learns accurate commands. But in classical conditioning of a movement there is apparently no signal related to movement inaccuracy, because by definition the US is delivered independently of the subject’s response. In a carefully controlled classical conditioning study, the US is not ameliorated and there appears no a priori reason why the system produces an accurately-timed, amplitude-scaled conditioned response. Moreover, a teaching signal that cannot diminish presents severe theoretical problems for models of the Marr–Albus type, because a meaningful endpoint to learning can never be reached. The only way to achieve stable learning is for the system itself to construct an internal estimate of movement inaccuracy, for example by comparing the US with the CR motor drive. To date, all other Marr–Albus type models of classical conditioning have used this comparator hypothesis (e.g., Grossberg and Schmajuk, 1989; Medina and Mauk, 2000; Moore et al., 1989), and yet the implications for motor learning have not been investigated systematically.
We raise this concern in the particular context of classical conditioning of the nictitating membrane (third eyelid) response in rabbits. This experimental system is well-suited for studying cerebellar function because learning is robust and tractable, the behavioral response is well-characterized and significant parts of the essential neuronal circuitry have been identified (Thompson, 1983; Yeo and Hesslow, 1998). In addition, there is strong evidence that the error signal driving the learning results from a comparison of the US and CR drive. For example, US-driven olivary responses, recorded as climbing fiber field potentials in the cerebellar cortex, and which drive learning in the cerebellar cortex, do diminish during CR acquisition (Hesslow and Ivarsson, 1996; Rasmussen et al., 2008). Finally, we have recently characterized the dynamics of the nictitating membrane response and its motor drive (Lepora et al., 2007b, 2009). Two relations were evident from this analysis: (1) the temporal profile of the motor drive (from retractor bulbi EMG spike-rate profiles) was well-approximated by a Gaussian function, whose peak amplitude was linearly related to the peak amplitude of the conditioned response; (2) the NM response profiles could be generated from this drive by passing the latter through a first-order linear differential equation equivalent to a first-order filter with time constant of the order of 100–200 ms.
Based on these principles, we construct a system-level model of NM conditioning (Figure 1) in which the cerebellum is modeled as an appropriate adaptive filter, the motor plant as a first-order filter, and the inferior olive as a comparator of the US signal and cerebellar output (as conveyed by the nucleo-olivary pathway). Then we vary the model assumptions and parameters to examine systematically how the resulting conditioned response depends on the interaction between the comparator architecture and the other principal components of the system-level neuroanatomy, in order to disambiguate the general properties of the model’s behavior from its specific dependence on parameter values. In consequence, we identify the computational consequences of a having a comparator for the inferior olive, and how these relate to the absence of sensory or motor error in a cerebellar model of classical conditioning.
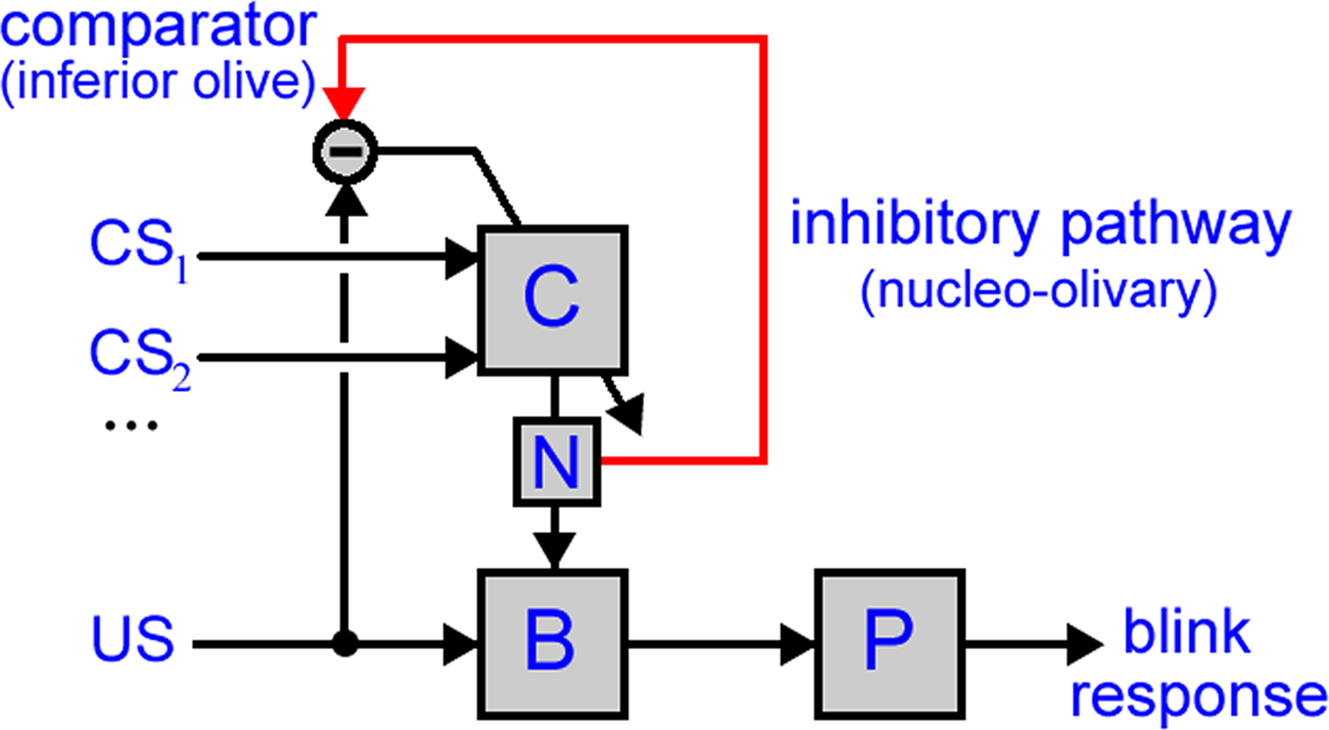
Figure 1. Model of cerebellar role in classical conditioning. The model used in this paper has two anatomical pathways: (i) the direct pathway, with the US driving premotor sites in the brainstem (B) that then drive the eyeblink motor plant (P) to produce the UR and (ii) the indirect pathway, with one or more CSs conveyed to the cerebellar cortex (C), the output of which is routed by the deep cerebellar nucleus (N) to converge with the direct pathway. Cerebellar learning is driven by a comparison in the inferior olive between the US-drive and cerebellar output. Note that this diagram shows only the projections utilized in the model, and so does not include some anatomical connectivity, for example the climbing fiber pathway from the inferior olive to deep cerebellar nucleus (which is apparently not required for the functionality examined here).
We show that: (1) Trial-level features, such as acquisition, extinction and blocking, are emergent properties of the classical conditioning model and largely independent of parameterization details; (2) Real-time features of classical conditioning, such as the CR amplitude and timing, could be accurately reproduced by appropriate tuning of the model parameters in the plant, inferior olive and cerebellum. The tuning required for (2) is a direct consequence of the olive not conveying motor error to the cerebellum, but rather an error signal from a comparison between the US and cerebellar output. We suggest that all previous models of classical conditioning employing a comparator architecture suffer from this same “fine-tuning” problem. A possible solution to this problem is that CR profiles in classical conditioning of the NM are acquired through operant contingencies that have previously prevailed, for example in naturally occurring avoidance movements. In principle, a Marr–Albus model utilizing sensory or motor error could learn these operant relationships prior to classical conditioning.
Parts of this work have been submitted previously in abstract form Lepora et al. (2007a).
Methods
Neuronal signals traveling down the “wires” in Figure 1 represent mean firing rates for the associated neuron or population of neurons, so that all information is assumed rate-coded. The systems corresponding to the “boxes” in Figure 1 are each represented by a filter transformation, which is a mathematical tool for describing the transformation of time-varying functions that is equivalent to a differential equation relating input and output signals. Most systems in Figure 1 are modeled as non-adaptive, fixed transformations. Only the (cerebellar) system C is adaptive, with its transformation continually updating according to a separate “teaching” signal.
For computational purposes, all signals are discrete over time at intervals of Δt = 1 ms. Simulations are set up over a number of trials, typically 100, each lasting for 1 s and starting at time zero. Model inputs are one CS or more, each labeled by their subscripts 1,…,n, and a single US. These stimuli are of constant intensity between their onset and offset times

where the stimulus intensities are initially normalized to Ii = IUS = 1. Accordingly, the inter-stimulus interval (ISI) equals USonset–CSonset, the time difference between CS- and US-onset times, which is here set to a standard value of 500 ms common in experimental eyeblink conditioning. The US duration USoffset–USonset is set to 10 ms, and CSonset is set to occur at t = 0 ms.
The cerebellar cortex system C represents the processes that transform the neuronal drive from the CS into the (Purkinje cell) output of the cerebellar cortex c(t). A Marr–Albus adaptive filter model of the cerebellum is used to represent this transformation (Figure 2 and see Introduction). The input expansion-recoding layer of the adaptive filter represents the transformation from the input signals (corresponding to the CS neuronal drive) into an expanded distribution of parallel signals (corresponding to parallel fiber activity):
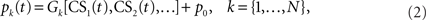
where each basis filter G1 to GN transforms the input CS signal into a parallel fiber signal p1(t),…,pN(t) and p0 is a constant offset (representing the background firing rate of granule cells). Our initial choice of basis filters is designed to transform a square-wave CS into a set of Gaussians beginning from CS-onset (Figure 3A) that have some similarity with the spectral basis functions used by Bullock et al. (1994) in their model of eyeblink conditioning. Later in this paper we will also consider other recoding strategies (Figure 3). The mathematical definition of these basis filters is covered in the Appendix. The output layer of the adaptive filter is the site of adaptation in this model, corresponding to weight multiplication and summation:
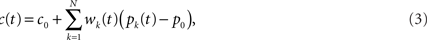
where wk are a set of adjustable weights, representing synaptic efficacies, and c0 is a constant offset (representing the background firing rate of the cerebellar output).
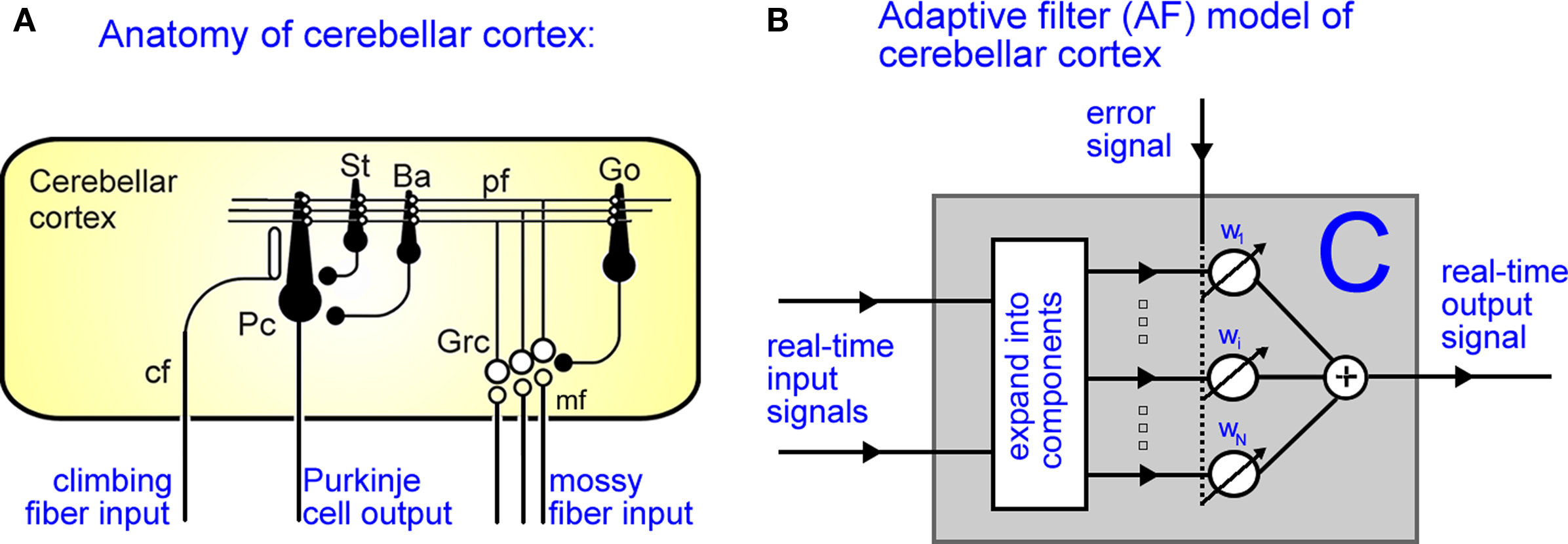
Figure 2. Adaptive filter model of cerebellar cortex. (A) Anatomy of cerebellar cortex: Mossy fiber inputs (mf) pass through the granule-Golgi cell layer (Grc-Go) to be distributed along parallel fibers (pf), which synapse directly on the Purkinje cells (Pc). (Note also the indirect pathway onto Pcs via inhibitory stellate (St) and basket cell (Ba) interneurons, with the filled and open circles denoting inhibitory and excitatory synapses respectively.) The strengths of the pf-Pc synapses change via LTD/LTP according to conjunctive activation of the parallel and climbing fibers (cf). (B) The adaptive filter model of cerebellar cortex. Real-time input signals pass through an expansion-recoding layer to be distributed in parallel, which are weighted and summed to make the output signal. The strength of these weights adapt according to the correlation between the recoded parallel signal and the error signal.
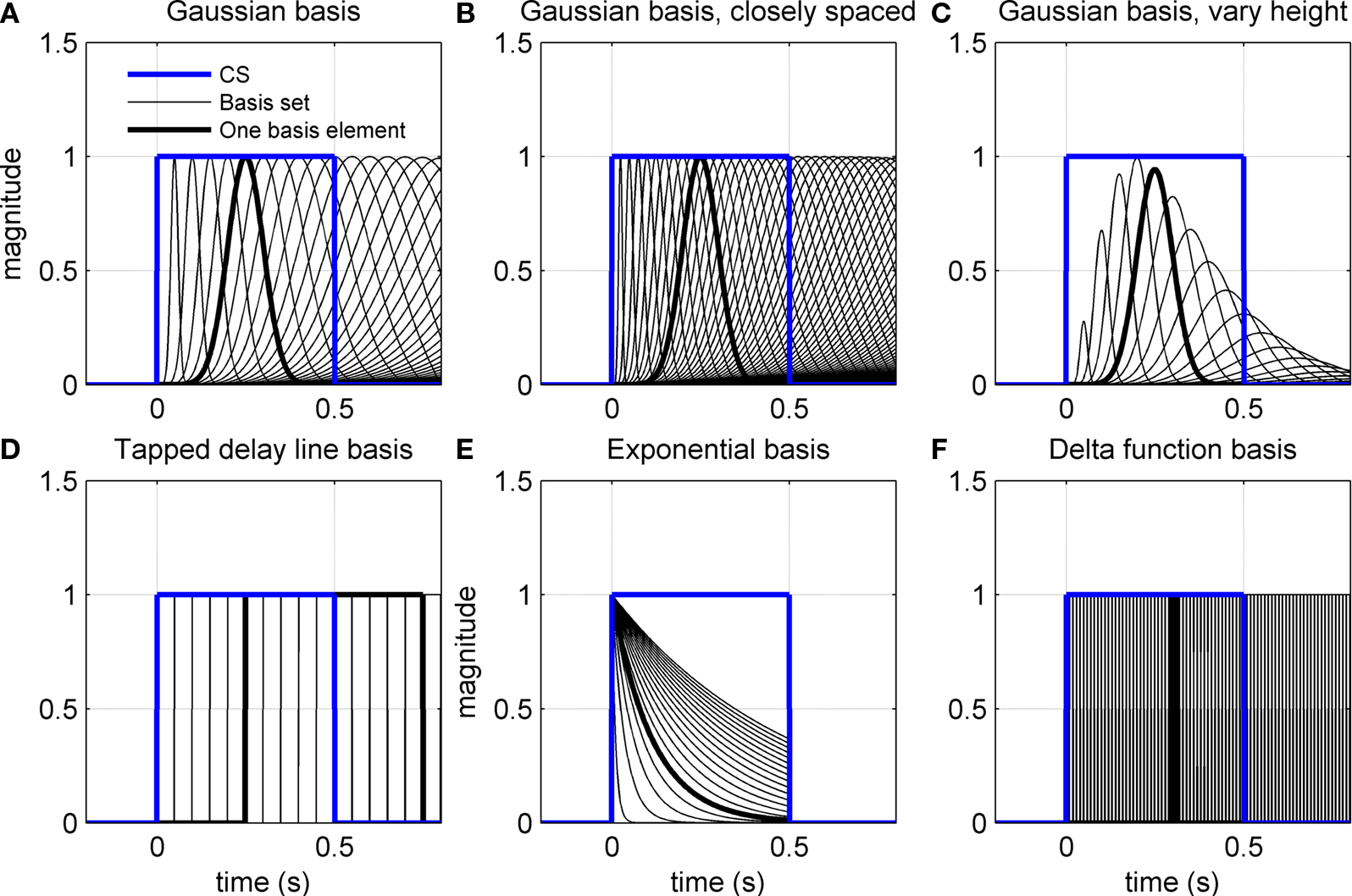
Figure 3. Various adaptive filter bases applied to CS input. (A–C) CS-onset triggered Gaussians of varying width. In (B) the widths are spaced closer together. In (C) the peak amplitudes are modulated by an envelope function. (D) Exponential basis gives a set of exponential functions truncated at US-offset. (E) Tapped delay line for basis filters gives a series of delayed CS profiles. (F) Delta function basis gives a set of narrow square-wave function from CS-onset.
Climbing fiber activity e(t) originating in the inferior olive is assumed to drive learning in accordance with the covariance learning rule in which weight changes are proportional to the temporal correlation between parallel fiber and climbing fiber signals,
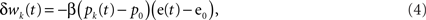
where β is the learning rate (set to a nominal value of 10−4 in the simulations) and the weights update at each time step wk(t + Δt) = wk(t) + Δwj(t). Weight changes may be positive or negative, representing long-term depression (LTD) or long-term potentiation (LTP) respectively at the parallel fiber/Purkinje cell synapse, although other sites of plasticity could be included in the same formalism if they are modified by the same error signal. Note that the learning rule depends only on the change of its inputs from their mean firing rates to ensure that the system is stable in the absence of a change of drive from the parallel and climbing fibers.
The result of conditioning is generally accepted to be a pause in Purkinje cell output (Jirenhed et al., 2007). With the sign conventions chosen here, this requires some weights wk(t) to become negative. Although parallel fiber/Purkinje cell synapses are excitatory, parallel fibers also modulate Purkinje cell output via inhibitory interneurons. Effective negative weights can thus be obtained either by allowing learning in this indirect pathway (Ekerot and Jorntell, 2003) or by assuming a constant weight on this pathway that is modulated by the excitatory input. Yet another alternative is to have parallel fibers carry both bursts and pauses generated by CS activity in Eq. 2 above. All these schemes are computationally equivalent to allowing both positive and negative weights in Eq. 3.
The deep cerebellar nucleus system N receives inhibitory input from the cerebellar cortex and is activated by a pause in cortical firing to excite sites outside the cerebellum. The simplest representation of this process is sign inversion relative to a threshold:
n(t) = n0 − c(t),
where n0 is the threshold firing rate. As we will show, this assumption leads to unobserved oscillations in the deep cerebellar nucleus output which can only be corrected by introducing a threshold non-linearity into the system. This can be achieved in various ways, but the simplest choice is to allow the deep cerebellar nucleus to activate only if the cerebellar cortical drive falls below a threshold:

This threshold non-linearity allows only a pause from the cerebellar output to activate the deep nucleus. The implications of this assumption are discussed later (see Results).
The inferior olive system O is assumed to construct its output signal e(t) by comparing the US input signal with a copy of the cerebellar nucleus output, interpreted as modulation of the excitatory US-drive by inhibitory nucleo-olivary feedback (Andersson et al., 1988). The most basic representation of this comparison is signal subtraction:
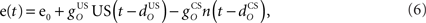
where  and
and 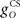 are gains and
are gains and 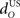 and
and 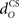 are time delays of the US and cerebellar components respectively, and e0 is a constant offset (representing the background firing rate of neurons in the inferior olive). Both gains are initially set to unity and time delays initially set to zero. The brainstem system B transforms the US input and cerebellar output signals into the motor command m(t) that drives the output (eyeblink) system, interpreted as the convergence of these two neuronal drives at the premotor sites in the brainstem. The simplest representation of this combination is a linear sum of the two signals:
are time delays of the US and cerebellar components respectively, and e0 is a constant offset (representing the background firing rate of neurons in the inferior olive). Both gains are initially set to unity and time delays initially set to zero. The brainstem system B transforms the US input and cerebellar output signals into the motor command m(t) that drives the output (eyeblink) system, interpreted as the convergence of these two neuronal drives at the premotor sites in the brainstem. The simplest representation of this combination is a linear sum of the two signals:
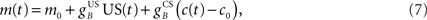
where 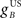 and
and 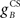 are the gains of the US and cerebellar components, which are initially set to unity. The constant offset m0 represents the background firing rate of premotor neurons, which is assumed to produce zero initial displacement of the eyeblink plant described below. Its value does not affect model performance, and is set to zero.
are the gains of the US and cerebellar components, which are initially set to unity. The constant offset m0 represents the background firing rate of premotor neurons, which is assumed to produce zero initial displacement of the eyeblink plant described below. Its value does not affect model performance, and is set to zero.
The eyeblink plant system P transforms the motor command m(t) into the output (blink) response r(t), and represents the dynamics of the blink-related muscles and peripheral tissues. A simple, experimentally verified model of this system for the nictitating membrane (third eyelid) response in rabbit is a first-order linear filter (Lepora et al., 2007b):
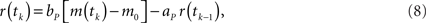
where ap = exp(−Δt/tp), bp = gp are the filter parameters defined by the gain gp = 1 and time constant tP = 100 ms that is typical from studies of this plant. Note that unlike the external eyelids the nictitating membrane in rabbit has no antagonist muscle, and thus can only move passively as it re-opens on the return phase of the blink.
Model Variants
The main aim of this paper is to investigate systematically how the performance of the above system-level model of eyeblink conditioning depends on its parameters and underlying assumptions. In particular, this approach will allow us to disambiguate features of the model performance that depend on the model’s basic computational capacity from those requiring hand-tuning of parameter values. For the sensitivity analysis, we generally take three parameter values, consisting of the default with higher and lower values. Because most CR properties change monotonically with parameter value, this is enough to qualitatively describe the model sensitivity. The variants of the eyeblink conditioning model that we consider are as follows.
Changes to eyeblink plant
The plant gain is fixed at gp = 1 to give a peak UR amplitude of ∼10 mm that gives a standard baseline for changes to the CR profile. The plant time constant is varied across values tp of 50, 100, and 200 ms to span the range observed in behavioral studies (Lepora et al., 2007b).
Changes to inferior olive comparator
It is useful to define a relative scale 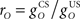 between the gains of the US-driven and cerebellar-driven components. Then the effect of the two drives can be compared with values rO of 0.5, 1, and 2, and the gain of the US component (with rO = 1) is a measure of the overall comparator gain. In addition we also varied time delays in the US-driven and cerebellar-driven components by 0, 50, and 100 ms. Values from 20 to 90 ms are compatible with the physiologically identified delays in nucleo-olivary modulation of climbing fiber responses (see Discussion).
between the gains of the US-driven and cerebellar-driven components. Then the effect of the two drives can be compared with values rO of 0.5, 1, and 2, and the gain of the US component (with rO = 1) is a measure of the overall comparator gain. In addition we also varied time delays in the US-driven and cerebellar-driven components by 0, 50, and 100 ms. Values from 20 to 90 ms are compatible with the physiologically identified delays in nucleo-olivary modulation of climbing fiber responses (see Discussion).
Changes to brainstem
The gain of the US-driven component 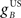 is fixed at one to keep the peak UR amplitude fixed at ∼10 mm, which provides a standard baseline to compare changes in the CR amplitude with. The gain of the cerebellar-driven component
is fixed at one to keep the peak UR amplitude fixed at ∼10 mm, which provides a standard baseline to compare changes in the CR amplitude with. The gain of the cerebellar-driven component 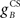 is varied around its initial value of one.
is varied around its initial value of one.
Changes to cerebellum
The basis filters used initially in our simulations are designed to give a set of Gaussians from a square-wave CS input (Figure 3A). The first two variants of the adaptive filter model consider changes to this initial set of basis filters: (i) a more closely spaced set of widths for the Gaussians (Figure 3B) and (ii) a set of Gaussians that also vary in peak amplitude (Figure 3C). The other variants consider completely different basis filters: (iii) a tapped delay line (Figure 3D), as considered in early models of eyeblink conditioning (Barto and Sutton, 1982; Moore et al., 1989); (iv) a set of decaying exponential profiles (Figure 3E); and (v) a delta function basis (Figure 3F). Mathematical details of how these basis filters are defined are given in the Appendix.
Rescorla–Wagner Trial-Level Model
To give a standard measure of trial-level behavior in classical conditioning, we implemented the Rescorla–Wagner (RW) model (Rescorla and Wagner, 1972), as it is generally regarded as a good overall account of trial-level effects in classical conditioning (e.g., Brandon et al., 2002). The RW model describes how US reinforcement of one or more CSs (as occurs in various contingency learning situations, such as blocking and conditioned inhibition) changes the CS–US association strengths V of the set S of CSs present on that trial, with learning rule:

where 0 < αi ≤ 1 is the salience for the ith CS, λ is the asymptotic value of the associations, and β1 and β2 are learning rates when the US is present/absent respectively. Our simulations typically considered 100 trials with learning rates β1 = β2 = 0.1, salience αi = 0.05 and asymptotic acquisition strength fixed to λ = 4.5.
Results
The first set of simulations was of delay conditioning with CS-onset preceding US-onset by 500 ms and CS-offset concurrent with US-offset. Behavioral experiments typically consider blocks of several acquisition trials interspersed with single CS-alone test trials. These test trials are inserted to view CR topography that is otherwise hidden by the UR (although they cannot be too frequent, otherwise CR acquisition is affected). Because a simulation can use test trials for which the system is artificially set to not learn, we followed every CS–US paired trial with a CS-only test trial to track acquisition over the entire learning process.
Simulations were considered first for trial-level features of the model where only the CR peak amplitude is examined for each trial. The more detailed real-time features of the CR topography within a trial were then considered. Dependency upon the modeling parameters was considered for both trial-level and real-time studies.
Trial-Level Acquisition and Extinction Learning is Stable and Robust
To test the basic model for appropriate acquisition of a CR, we simulated 100 CS + US paired trials with ISI of 500 ms. Appropriate extinction was tested by following these 100 acquisition trials with 100 unpaired CS-alone extinction trials. As in behavioral experiments, with CS and US intensities fixed, the amplitude of the CR peak gives a measure of CS–US associative strength. We considered first the adaptive filter model described for the basic real-time model (see Methods).
Acquisition training caused the model CR peak to increase from 0 mm on the first trial to a stable maximum of ∼4.5 mm (blue curve in Figure 4A). This maximum value was a consequence of parameter choices described in Section “Methods,” and is typical of conditioned eyeblink responses in the rabbit. Extinction training then caused the model CR peak to decrease steadily to zero response (blue curve in Figure 4B). Both the acquisition and extinction learning curves approximated exponential functions that asymptote to a stable endpoint of learning, which is the fully acquired CR in acquisition learning and the absence of a CR in extinction learning. This learning stability is an important feature that follows directly from the inferior olive comparator model in Eq. 6: as the nucleo-olivary inhibition becomes sufficiently intense to cancel the US excitation to the olive, the climbing fiber error signal approaches zero and learning ends. For comparison, the acquisition learning curve was considered when the nucleo-olivary pathway is removed from the model. CR acquisition then became unstable because there is then no inhibitory feedback to drive down climbing fiber activity as learning proceeds (red line in Figure 4A).
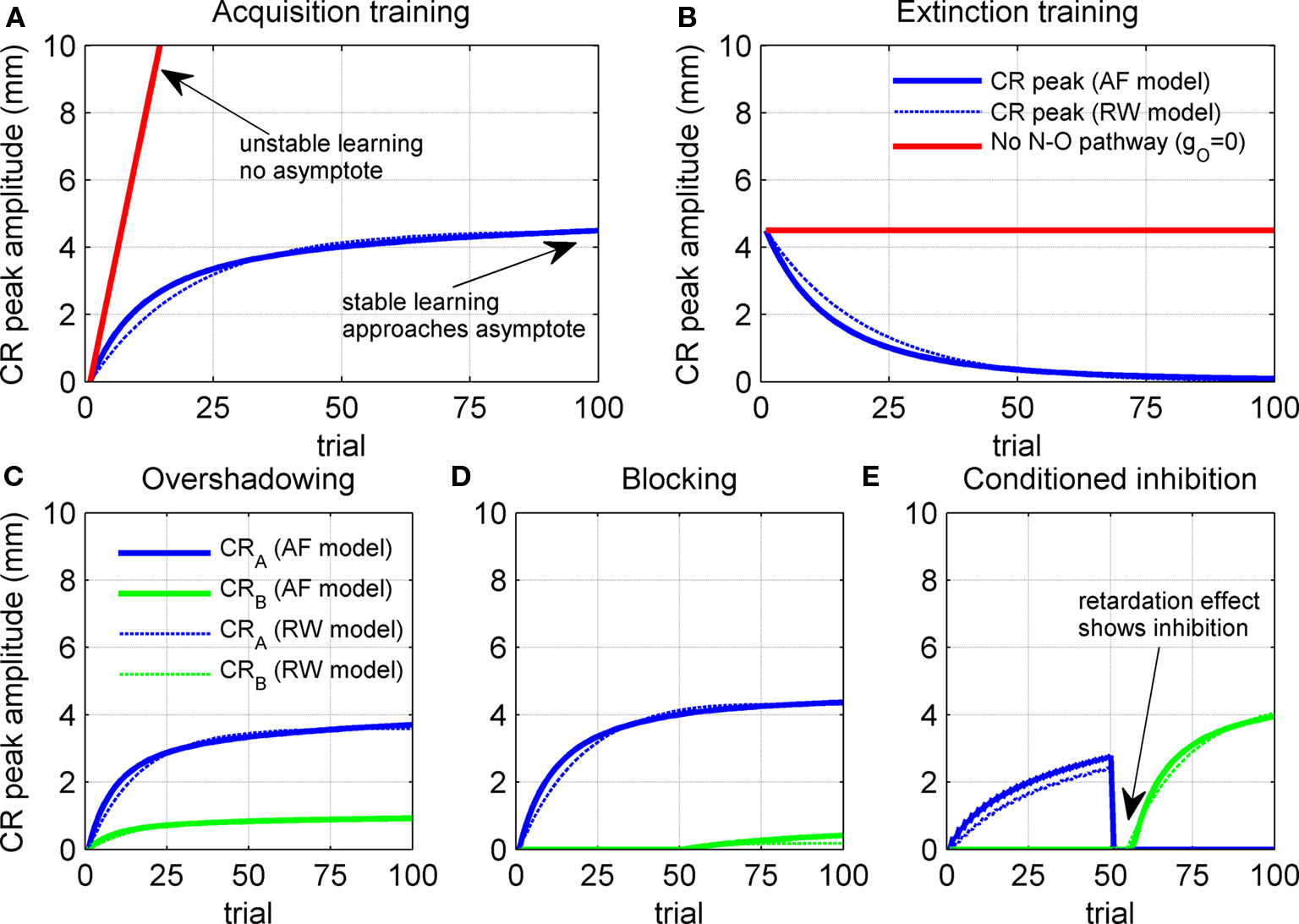
Figure 4. Trial-level model behavior. (A) Acquisition curve for model CR peak amplitude over 100 paired CS + US trials. Results shown both with and without the nucleo-olivary pathway. (B) Extinction curve for model CR peak amplitude over 100 unpaired CS-alone trials after the acquisition training in (A). (C) Overshadowing of learning to CSB by CSA over 100 compound CSA + CSB + US paired trials when CSB has twice the salience of CSA, as defined by setting IA = 2 and IB = 1 in Eq. 1. (D) Blocking of learning to CSB by 50 trials of prior CSA + US training, as tested over 50 compound CSA + CSB + US paired trials. (E) Conditioned inhibition of CSB after 50 trials of prior inhibitory training (interspersing paired CSA + US trials with unpaired CSA + CSB trials), as tested by retarded acquisition training over 50 CSB + US paired trials. Results of the Rescorla–Wagner model are shown for comparison (thin dashed lines).
Robustness of the NM conditioning model over acquisition and extinction was tested with alternatives that incorporated changes to the plant, olive comparator and cerebellar model (see Figure 6). All of the adaptive filter models that we considered approached a stable endpoint to learning in a manner qualitatively similar to that of the initial model. Features that varied included the overall learning rate, as measured by the number of trials to approach the final state, and the amplitude at full acquisition. Thus the basic acquisition and extinction behavior of the model was robust to changes in model specifics. Moreover, in all cases considered here, the acquisition and extinction learning curves had exponential profiles that approached stable asymptotes after many trials. Such learning curves are typical of models that use a supervised learning algorithm based on a covariance learning rule, of which a well-known example is the RW model (Rescorla and Wagner, 1972) of classical conditioning (dashed blue lines on Figure 4).
Trial-Level Contingency Learning Displays Blocking, Overshadowing and Conditioned Inhibition
Important examples of contingency learning are overshadowing, blocking and conditioned inhibition effects with respect to the presentation of two conditioned stimuli, CSA and CSB (assumed here to be of equal onset and duration, with ISI of 500 ms). These effects were examined firstly in the system-level model (see Methods) and then robustness to the changes in parameters was considered (see Methods for parameter details). One hundred training trials were typically used, with the training broken into two stages of 50 trials if necessary.
Overshadowing was tested by first training with compound CSA + CSB + US paired trials and then looking for a diminished CR to independent presentation of CSA and CSB (compared with CRs to each stimulus had each been trained alone) with the more salient CS dominating. In our model, salience corresponded to the amplitude of the CS drive to the cerebellum, with CSA here considered to have twice the salience of CSB. Model results were consistent with overshadowing: CR peak amplitudes of ∼3.7 and ∼0.9 mm for the individual stimuli CSA and CSB were diminished relative to the ∼4.5-mm peak amplitude for training a single CS (c.f. Figures 4A,C). Hence, with compound conditioning, the more salient CSA elicited a CR that is greater, or overshadows, that of CSB.
Blocking was tested by training a CR to the first stimulus over CSA + US paired trials, and then looking for blocked acquisition to a second stimulus CSB when training with the compound CSA + CSB + US in paired trials. Model results exhibited a clear blocking effect with the CR peak to the pre-trained stimulus CSA reaching a maximum of ∼4.5 mm, while that of the second stimulus CSB reached only ∼0.5 mm after compound training (Figure 4D).
Conditioned inhibition was tested by training the first stimulus CSA to reliably predict the US and the compound CSA + CSB to reliably predict no US (e.g., by interspersing paired CSA + US trials with unpaired CSA + CSB trials (Pavlov, 1927)). Inhibition was then manifest by, for example, requiring an extended training period to acquire an overt CR to the second stimulus CSB. Model results exhibited two aspects of conditioned inhibition: (i) inhibitory training led the first stimulus CSA to reliably predict the US and the compound CSA + CSB to reliably predict no US; (ii) acquisition training to CSB was then retarded by ∼5 trials relative to a naive CS (Figure 4E).
Robustness of contingency learning for the adaptive filter model was tested with the alternative models described in Model Variants (see Methods). All models displayed qualitatively similar trial-level behavior to the initial model, showing that the contingency learning phenomena of blocking, overshadowing and conditioned inhibition are robust features of this class of models. In addition, trial-level results were qualitatively similar to those of the RW model of classical conditioning (dashed lines on Figure 4).
Real-Time Model Results can Give Realistic CR Profiles
The previous results revealed how the NM conditioning model performs at the trial-level, where only information about the CR peak amplitude is used to describe the learning process. The following simulations examined the real-time behavior of the adaptive filter model, such as the shape of the learnt CR profile and how this profile changed during learning.
For an overall illustration of the real-time behavior during learning, consider the cascade diagram of the evolving CR profile (Figure 5A) during the acquisition training represented at the trial-level in Figure 4A. The behavior agreed qualitatively with experimental studies (Figure 5B): during acquisition training, the CR rose from an initial zero response, with the peak response occurring near the time of US-onset. However, the model CR peak was delayed by ∼75 ms after US-onset, a delay rather greater than those seen in the behavioral responses that contributed to our model of the nictitating membrane plant (Lepora et al., 2007b; see Figure 5B). The CR peak delays observed in other behavioral studies are considered in the discussion, but for the time we note that this model delay is closer to the values described in some other reports (see Hardiman and Yeo, 1992; Kehoe et al., 2009). In terms of response duration, the simulated and experimental responses were very similar, with both taking approximately 500 ms to rise and fall. Adjustments to the basic model for timing the peak CR are addressed later.
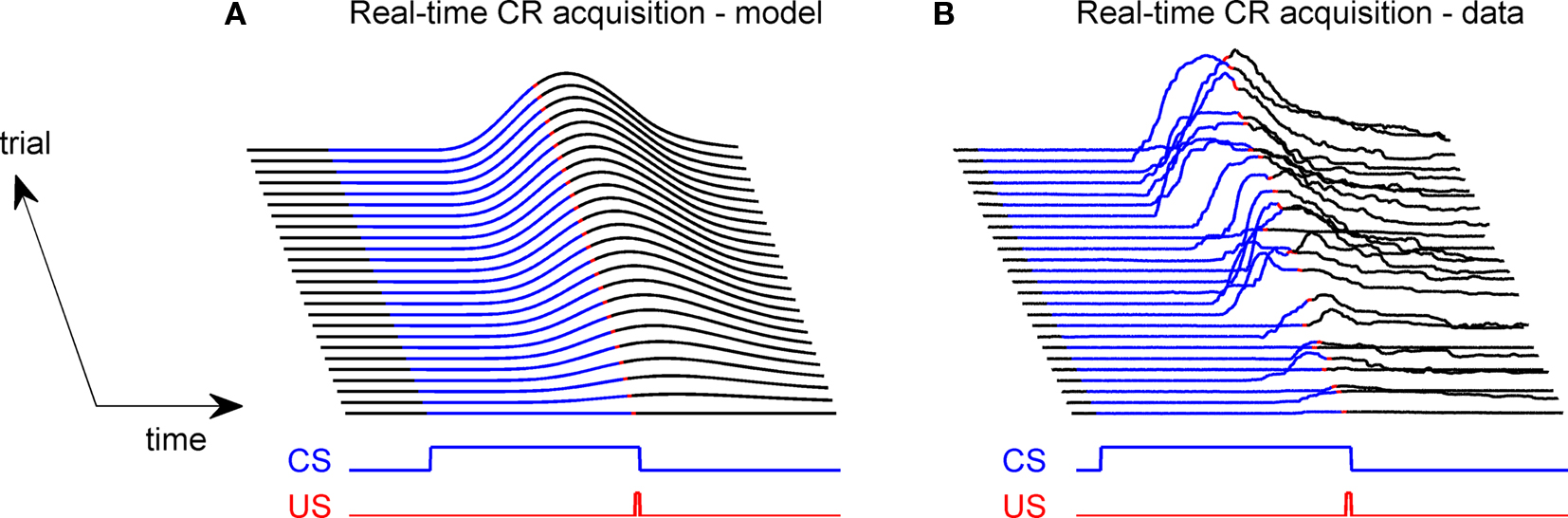
Figure 5. Real-time model behavior and comparison with data. (A) Model acquires a CR profile across 100 CS + US paired trials. US of 10 ms durations with onset 500 ms; CS of 510 ms duration CS with onset 0 ms. (B) Experimental data from classical conditioning the NM response (subject RB1; Lepora et al., 2007b).
CR Profiles Depend on Eyeblink Plant Characteristics
Firstly, we examined how the CR profile was affected by changing the parameter values of the eyeblink plant (Eq. 8). For the basic model, we used a first-order linear filter with gain gp = 1 and time constant tp = 100 ms, consistent with nictitating membrane (third eyelid) response data in rabbit (Lepora et al., 2007b). Our simulations considered the effect on the CR of varying these two parameters, the results of which are shown in Figure 6. The other default parameters in the basic model were: relative olive gain rO = 1; nucleo-olivary delay, 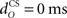 ; and CS–US ISI, tISI = 500 ms.
; and CS–US ISI, tISI = 500 ms.
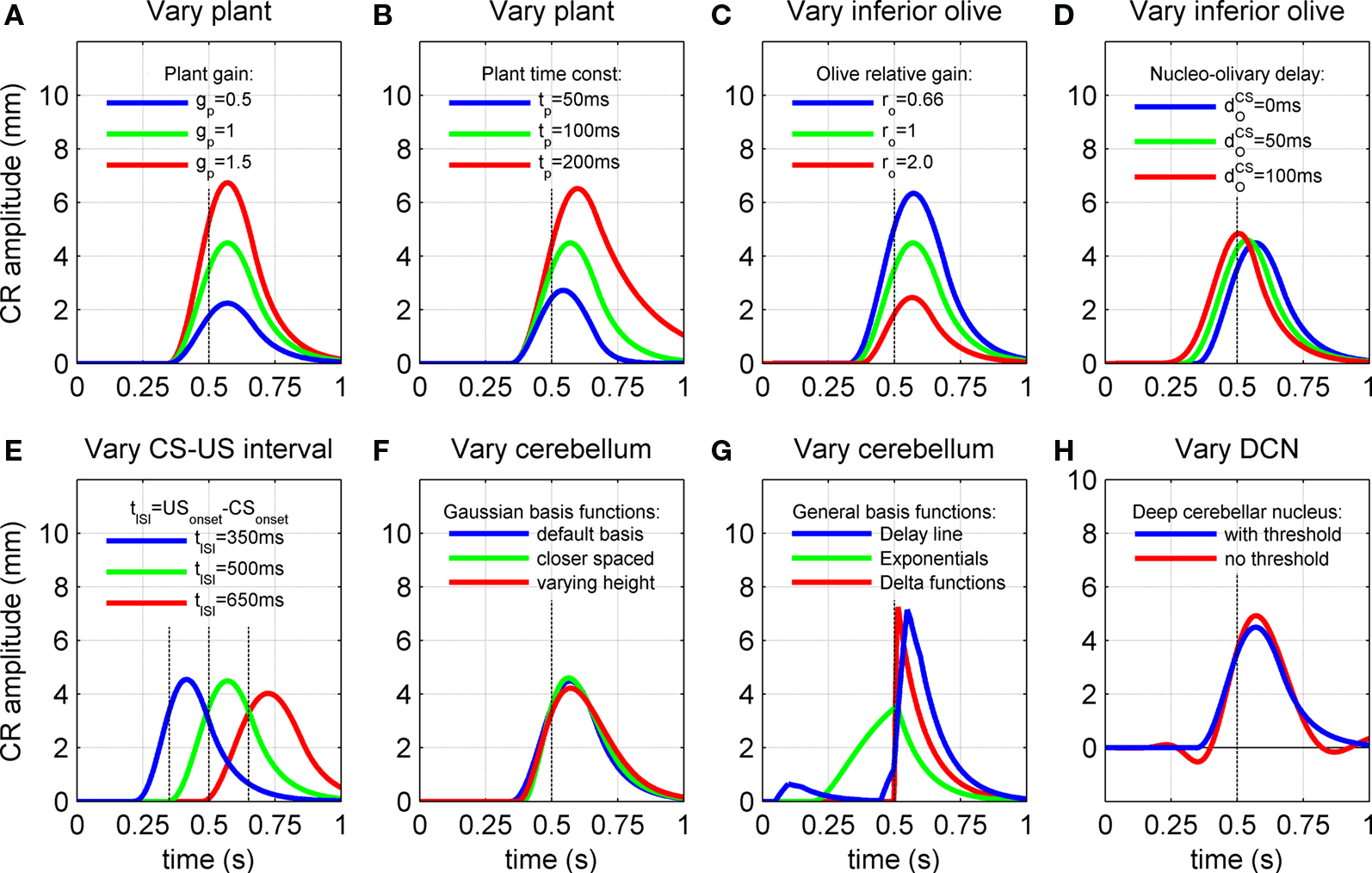
Figure 6. Effect of model characteristics on the CR profile. Examples for three parameter values are shown to illustrate the general dependence of the CR profiles on model characteristics relative to the default parameter values. The default parameters were a plant time constant, tP = 100 ms; a plant gain gP = 1; an olive relative gain, rO = 1; a nucleo-olivary delay, 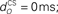 and a CS–US interval, tISI = 500 ms. CS-onset is at time zero and US-onset is marked by the vertical dashed line. Acquisition training is the same as Figure 4. (A,B) CR profile with variations in eyeblink plant gain and time constant. (C,D) CR profile with variations in inferior olive relative gain and cerebellar delay. (E) CR profile with various choices of inter-stimulus interval from CS-onset to US-onset. Gray vertical lines indicate US-onset in CS–US paired trials. (F,G) CR profile with various choices of basis filter for the adaptive filter model. (H) Effect of removing deep cerebellar nucleus (DCN) threshold on CR profile.
and a CS–US interval, tISI = 500 ms. CS-onset is at time zero and US-onset is marked by the vertical dashed line. Acquisition training is the same as Figure 4. (A,B) CR profile with variations in eyeblink plant gain and time constant. (C,D) CR profile with variations in inferior olive relative gain and cerebellar delay. (E) CR profile with various choices of inter-stimulus interval from CS-onset to US-onset. Gray vertical lines indicate US-onset in CS–US paired trials. (F,G) CR profile with various choices of basis filter for the adaptive filter model. (H) Effect of removing deep cerebellar nucleus (DCN) threshold on CR profile.
The gain of the eyeblink plant determined the linear scale between the motor drive and eyelid displacement for both the CR and UR. Therefore, varying this gain simply scaled the CR amplitude (Figure 6A) and the UR amplitude equally (figure not shown). Note that in our model the plant gain has no effect on the ratio of CR to UR peak amplitude. In the remaining simulations the plant gain was fixed at gP = 1, which gives a peak UR amplitude of ∼10 mm. Variations in the CR profile were then examined relative to this fixed UR.
The plant time constant determined the time-course of the passive return to rest of the CR after the motor drive has terminated, which relates to the visco-elastic properties of the eyeblink plant. As expected, increasing the time constant across the range of physiologically observed values (Lepora et al., 2007b) of tp = 50, 100, and 200 ms led to progressively longer return times (Figure 6B). Note also that the peak CR amplitude became larger with longer time constants, because of a corresponding decrease in elasticity or increase in viscosity of the plant. In addition, the CR peak was delayed for longer time constants, with latencies from US-onset to peak CR of 43, 70, and 98 ms for the three time constant values above. This increase in delay occurs because the plant becomes slower to react to its input as its time constant increases, resulting in a progressively longer lag between the peak drive and peak response. Note that the lag also increases with the time taken for the input drive to peak (from zero lag for an instantaneous delta function drive).
CR Profiles Depend on Inferior Olive Characteristics
CR profiles were also affected by changing the inferior olive model. The effect of changing gain parameters in the inferior olive model in Eq. 6 was more easily seen by considering an overall gain 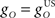 and a relative gain
and a relative gain 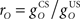 of the cerebellar output and US-drive. Varying the overall gain simply scaled the climbing fiber signal e(t) and hence the learning rate β in Eq. 4; therefore, it does not affect directly the CR profile. However, the relative gain determined the cancellation of the US-drive and cerebellar drive at learning completion, so that scaling the relative gain changed the CR amplitude proportionally to 1/rO (Figure 6C). Therefore, increasing the plant gain was equivalent to decreasing the relative olive gain (Figures 6A,C), even though they were caused by different mechanisms (the first fixed the cerebellar output and changed the plant, while the second fixed the plant and changed the cerebellar output).
of the cerebellar output and US-drive. Varying the overall gain simply scaled the climbing fiber signal e(t) and hence the learning rate β in Eq. 4; therefore, it does not affect directly the CR profile. However, the relative gain determined the cancellation of the US-drive and cerebellar drive at learning completion, so that scaling the relative gain changed the CR amplitude proportionally to 1/rO (Figure 6C). Therefore, increasing the plant gain was equivalent to decreasing the relative olive gain (Figures 6A,C), even though they were caused by different mechanisms (the first fixed the cerebellar output and changed the plant, while the second fixed the plant and changed the cerebellar output).
Increasing the time delay 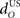 for the US-drive was equivalent to delaying US occurrence, which delayed CR occurrence by the same duration (Figure not shown). Biologically, this delay is only a few milliseconds. A more important parameter was the delay
for the US-drive was equivalent to delaying US occurrence, which delayed CR occurrence by the same duration (Figure not shown). Biologically, this delay is only a few milliseconds. A more important parameter was the delay 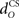 in nucleo-olivary inhibition. A key feature of the model is that the olive functions as a comparator of the CR drive and the US signal to control learning rates. Without any delays in the nucleo-olivary pathway, olivary output would only be small when the CR drive peaks at US-onset (or a few ms later to allow for neural conduction delays in the US pathway). However, as we have shown (Lepora et al., 2007b), the peak CR drive, measured as the EMG response in the retractor bulbi muscle, reliably preceded US-onset by 50–100 ms (Figure 4 of Lepora et al., 2007b). Consistent with these previous results, here we find that introducing a delay
in nucleo-olivary inhibition. A key feature of the model is that the olive functions as a comparator of the CR drive and the US signal to control learning rates. Without any delays in the nucleo-olivary pathway, olivary output would only be small when the CR drive peaks at US-onset (or a few ms later to allow for neural conduction delays in the US pathway). However, as we have shown (Lepora et al., 2007b), the peak CR drive, measured as the EMG response in the retractor bulbi muscle, reliably preceded US-onset by 50–100 ms (Figure 4 of Lepora et al., 2007b). Consistent with these previous results, here we find that introducing a delay 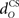 in the nucleo-olivary pathway causes the Gaussian CR drive to reliably precede the US-onset. Then due to the visco-elastic properties of the NM plant (see previous section), the peak CR lags the peak drive by a time that depends upon both the width of the Gaussian and the plant time constant (c.f. Figure 6B) and which can produce CR peaks around the US-onset or later.
in the nucleo-olivary pathway causes the Gaussian CR drive to reliably precede the US-onset. Then due to the visco-elastic properties of the NM plant (see previous section), the peak CR lags the peak drive by a time that depends upon both the width of the Gaussian and the plant time constant (c.f. Figure 6B) and which can produce CR peaks around the US-onset or later.
The actual nucleo-olivary delay 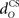 in the model is a free parameter, with values of 0, 50, and 100 ms leading to latencies from US-onset to CR peak of 70, 37, and 6 ms, respectively (Figure 6D) for a plant time constant tp of 100 ms. Note that these latencies depend on the plant dynamics, with a larger plant time constant tp of 200 ms giving longer CR peak latencies of 98, 61, and 27 ms, respectively (Figure not shown). In setting a realistic value for the nucleo-olivary delay, it should be noted that electrophysiological evidence has revealed delays of 25–90 ms in nucleo-olivary inhibition for eyeblink-related climbing fiber responses (Hesslow, 1986; Hesslow and Ivarsson, 1996).
in the model is a free parameter, with values of 0, 50, and 100 ms leading to latencies from US-onset to CR peak of 70, 37, and 6 ms, respectively (Figure 6D) for a plant time constant tp of 100 ms. Note that these latencies depend on the plant dynamics, with a larger plant time constant tp of 200 ms giving longer CR peak latencies of 98, 61, and 27 ms, respectively (Figure not shown). In setting a realistic value for the nucleo-olivary delay, it should be noted that electrophysiological evidence has revealed delays of 25–90 ms in nucleo-olivary inhibition for eyeblink-related climbing fiber responses (Hesslow, 1986; Hesslow and Ivarsson, 1996).
CR Profiles Depend on the Inter-Stimulus Interval
Next we examined how the CR profile is affected by changing the ISI from CS-onset to US-onset, while keeping the US duration fixed at 10 ms. An important aspect of this dependence in the model is that the adaptive filter basis elements were Gaussian, with widths that increased according to their time-to-peak after CS-onset (Figures 3A–C). This model feature was included to simulate a broadening of the CR profile as the ISI became longer, which is fully in accord with experimental evidence across a range of studies on both the width of the EMG drive and the shape of the CR (Lepora et al., 2007b, Figure 11).
The model results are that at three different ISIs (350, 500, 650 ms) the CR peak shifted in time relative to US-onset (Figure 6E). These finding are broadly in accord with experimental manipulations of the CS–US interval, which also reveal longer delays of CR peak with longer ISIs (Kehoe et al., 2009). Note that the profiles in Figure 6E are considered independently of nucleo-olivary delay which is set here to zero. For Gaussian basis functions of constant peak amplitude (Figure 3A), the resulting CRs showed little variation in peak amplitude (Figure 6E). However, if Gaussian basis functions of varying peak amplitude (Figure 3C) were considered, then the amplitude of the CR peak varied with ISI (Figure not shown). This effect was most pronounced over a fixed number of acquisition trials, because the model then had a slower rate of CR acquisition at longer ISIs. Details of the response latencies and other timing aspects were otherwise little affected.
Peak CR latency increases with ISI because the CR drive becomes broader at longer ISI, and this effect interacts with the plant kinetics to give a longer latency between the peak drive and response. For a plant time constant tp of 100 ms, as in Figure 6E, the CR peak latencies were 65, 70, and 74 ms for ISI of 350, 500, and 650 ms, respectively. These values were longer for a larger plant time constant tp of 200 ms, with corresponding latencies of 88, 98, and 107 ms consistent with our previous results on the plant dynamics.
CR Profiles Depend on Brainstem Characteristics
Next we examined how the CR profile is affected by changing the brainstem model in Eq. 7. The brainstem model used here linearly combines the drive from the US and cerebellar output, with a gain 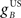 for the US-drive and a gain
for the US-drive and a gain 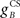 for the cerebellar drive. The effect of these two parameters was to scale the plant gain for the UR and CR respectively, which simply scaled the response amplitude by the same amount. We set the gain for the US-drive to unity to keep the UR fixed. Then the gain for the cerebellar drive scaled the CR amplitude relative to the UR (results identical to Figure 6A).
for the cerebellar drive. The effect of these two parameters was to scale the plant gain for the UR and CR respectively, which simply scaled the response amplitude by the same amount. We set the gain for the US-drive to unity to keep the UR fixed. Then the gain for the cerebellar drive scaled the CR amplitude relative to the UR (results identical to Figure 6A).
CRs Depend on Cerebellum Characteristics
The CR profile was also affected by changing the adaptive filter model of the cerebellum in Eqs 2 and 3. In particular, we considered the effect on the CR of different sets of basis elements, corresponding to sets of parallel fiber activity activated by the neuronal drive from the CS (see Figure 3).
All of the simulations considered thus far used basis elements that were Gaussian functions of varying width (Figure 3A). One simple change is to decrease the differences in width of the Gaussian functions to give more basis elements across the CS duration (Figure 3B). Another simple change is to modify the peak amplitude of the Gaussian, for example with an alpha function envelope (Figure 3C). Neither of these changes appreciably affected the profile of the fully acquired CR (Figure 6F), as might be expected because the range of possible CR motor drives that can be constructed from these elements is the same in each case.
More drastic changes to the basis elements did affect the CR profiles. A tapped delay line gives a set of basis elements that are delayed versions of the CS drive (Figure 3D) – these basis elements led to an unrealistic profile with an early onset artifact for the CR (Figure 6G, blue curve), which occurred because the broad profile with sharp onset of these basis functions led to a large initial contribution that could not be canceled in combination with later elements. Decaying exponential basis elements have earlier onsets than the Gaussians (Figure 3E) – these led to a CR with a very gradual rise to peak amplitude (Figure 6G, green curve) because more of the CR drive is happening earlier in the response. Delta function basis elements (Figure 3F) also generated unrealistic profiles (Figure 6G, red curve), with the sharp onset of the element giving a sharp onset to the CR. Our initial choice of Gaussian basis elements was motivated from their production of realistic CR profiles that do not have the artifacts described above.
CRs Depend on Thresholding in the Deep Cerebellar Nucleus
Finally, we examined the effect on CRs of removing the threshold non-linearity introduced in the model of the deep cerebellar nucleus. This threshold ensured only pauses in cortical firing can activate extra-cerebellar sites (Eq. 5).
Removing the DCN non-linearity resulted in small oscillations of the conditioned response profile, which produced early and late response artifacts (Figure 6H). For the simulations we assumed these oscillations are not realistic and included the deep cerebellar nucleus threshold in the basic model. However, it is possible such small oscillations are difficult to identify behaviorally because of their small amplitude compared to noise. In the simulations these disturbances were most evident just after CS-onset and in the response tail. The reason for the wave-like artifacts is that the cerebellar output and US-representation did not cancel perfectly in the inferior olive, because the parallel fiber activity to the cerebellar cortex contained components wider than the US. This non-cancellation interacted with the covariance learning rule to produce a wave-like disturbance spreading out from the US. Introducing the above threshold stopped the non-cancellation from being communicated to the learning rule, which prevented the oscillations.
Discussion
A widely used conceptual framework for understanding cerebellar function is that the cerebellum learns to construct accurate motor commands from input “contexts,” using a teaching signal provided by a second input (Albus, 1971; Marr, 1969). A simple yet general implementation of this conceptual framework is the adaptive filter (Widrow, 1985), which was first formally applied to the cerebellum by Fujita (1982), and used subsequently to model many cerebellar tasks. Since classical eyeblink conditioning is a preparation that has been used extensively to investigate cerebellar function (Hesslow and Yeo, 2002; Thompson, 2005; Yeo and Hesslow, 1998), it is natural to ask whether the adaptive filter formalism can be applied to this paradigm also. As we have indicated, there is a serious problem with this application. Other Marr–Albus based models recognize that the inferior olive conveys sensory or motor signals related to movement inaccuracy, and that the cerebellum reduces this signal to learn accurate commands. However, in classical conditioning of a movement there are no such signals, but instead the inferior olive is interpreted as a comparator of the US signal and cerebellar output (e.g., Andersson et al., 1988; Jirenhed et al., 2007; Kim et al., 1998; Medina et al., 2002; Rasmussen , 2008; Sears and Steinmetz, 1991).
To investigate the implications of this difference in error signal we constructed a system-level model of classical conditioning consistent with the anatomy of the eyeblink/NM response circuitry, an adaptive filter for the cerebellum coupled to a comparator signal from the inferior olive, and a linear dynamic model representing the NM motor plant (Figure 1). The plant model and drive followed from our recent study of this motor system (Lepora et al., 2007b, 2009). Thus, to our knowledge, this is the first model to explicitly include all of these components, in particular the motor plant that is vital for shaping and timing the CR profile. A number of previous classical conditioning models are also based on adaptive filter and comparator architectures (Table 1), but these components have often been implicit, rather than explicit, in the model structure (Bartha et al., 1991; Bullock et al., 1994; Grossberg and Schmajuk, 1989; Medina and Mauk, 2000; Moore et al., 1989).
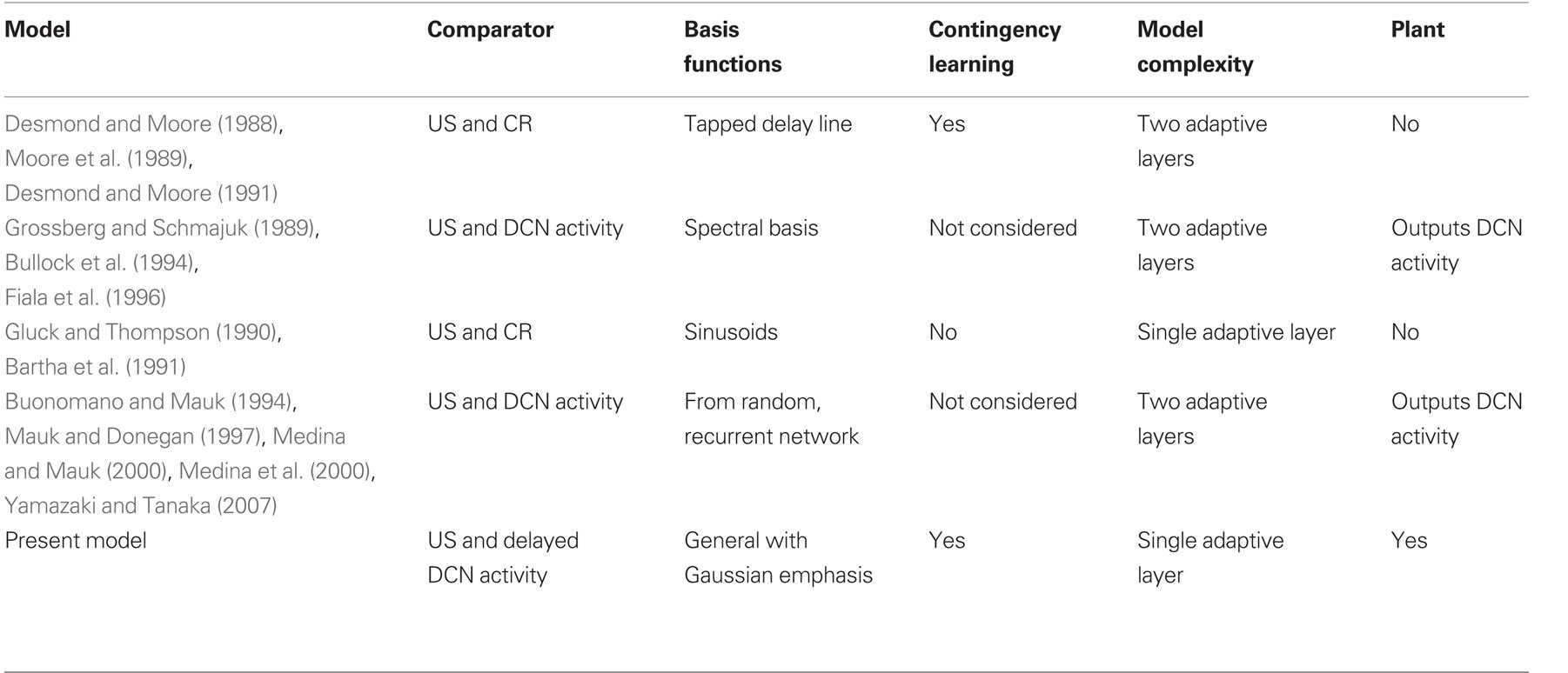
Table 1. Models of eyeblink conditioning based on an adaptive filter architecture. Models classified according to: (a) comparator inputs that provide the error signal to the adaptive filter; (b) choice of basis functions for the adaptive filter; (c) whether contingency learning was considered; (d) whether additional adaptive layers were considered; and (e) whether a plant was considered.
Given the explicit separation of our model into the plant, adaptive filter and comparator components, and the relatively few parameters of our system-level model, we were then able to investigate systematically the model assumptions and parameters to uncover the implications of using a comparator error signal in a Marr–Albus type model. This investigation gave two main results:
(1) Trial-level model behavior displayed appropriate CR acquisition and extinction effects, together with the contingency learning effects of blocking, overshadowing and conditioned inhibition. These results are compatible with the RW model of classical conditioning. Importantly, these trial-level properties were an emergent and robust feature of the basic model structure, and did not depend upon any particular parameterization (Figure 4).
(2) Real-time model behavior was able to give realistic CR profiles (Figure 6), but in this case details of the conditioned response, such as the amplitude and timing of its peak, and the overall temporal profile, were dependent upon model parameters for the inferior olive, cerebellum and eyeblink plant.
The implications of these results for understanding the cerebellar role in classical conditioning are as follows.
Implications of a Comparator Architecture for Classical Conditioning
The central feature of classical conditioning is that by definition the relation of the CS to the US is totally unaffected by the subject’s response (Gormezano et al., 1983; Pavlov, 1927). Delivery of the US is entirely outside the subject’s control, in contrast to operant conditioning where reward is contingent on the subject’s behavior (e.g., Mackintosh, 1974). In the particular case of eyeblink conditioning, the use of an airpuff CS can potentially allow lid closure to partially avoid the airpuff effects if precautions are not taken. But classical conditioning of the eyeblink/NM develops robustly with a periocular electrical US that presents no opportunity for response-related amelioration of the US, and all of the empirical data used in our modeling is from such experiments. This special feature of classical conditioning means that if the US were to be interpreted as the teaching signal there would be an immediate problem: the teaching signal continues to be delivered even when the CR is fully acquired, which would either drive the CR ever larger without limit or imply that asymptotic learning is governed by synaptic saturation, against which there is substantial evidence. This problem is reflected in the unstable behavior of the adaptive filter model when the US alone is used as a teaching signal (Figure 4A, red trace). The teaching signal continues to be delivered whatever response the model makes, so weight change continues without limit and the learning becomes unstable.
A widely accepted proposal is that the teaching signal conveyed to the cerebellum from the inferior olive is the result of a comparison between the US and CR drive (e.g., Andersson et al., 1988; Jirenhed et al., 2007; Kim et al., 1998; Medina et al., 2002; Rasmussen et al., 2008; Sears and Steinmetz, 1991). Then a copy of the CR command is subtracted from the US signal in a comparator. Thus, as learning proceeds, the CR command becomes larger until it reaches a value at which the US signal is canceled, after which learning ceases. The problem of unstable learning is therefore solved. Consistent with this suggestion, experimental evidence indicates that the signal conveyed from inferior olive to cerebellar cortex does not remain constant, but rather declines in step with the acquisition of the CR. Multiunit olivary activity (Sears and Steinmetz, 1991), cortical climbing fiber field potentials (Hesslow and Ivarsson, 1996) and complex-spike activity (Rasmussen et al., 2008) all decline with conditioning and within each trial. The temporal profile of olivary suppression is correlated with CR amplitude but with a phase shift of around 90 ms (Hesslow and Ivarsson, 1986), which is consistent with the inferior olive firing in the model discussed here.
Evidence suggests that this comparator signal could account not only for stable acquisition, but also for classical conditioning phenomena such as extinction (Bengtsson et al., 2007; Medina et al., 2002), blocking (Andersson et al., 1988; Kim et al., 1998; Rasmussen et al., 2008), and indeed all the contingencies learnt by the RW trial-level model (Sears and Steinmetz, 1991). Therefore, the classical conditioning paradigm provides information about the predictive relation between the CS and US, which can be used to modulate the representation of the US within the nervous system itself. This is the information exploited by the comparator architecture, so that by subtracting a CS-derived internal signal from the internal representation of the US, an error signal is generated that in effect represents the extent to which the US is not predicted. The performance of the system is thus driven by the intrinsic characteristics of the learning rule and error signal, so that parameterization details of the other model components are not crucial to the outcome.
This reasoning explains why models of classical conditioning based on a comparator architecture account for the trial-level performance, but real-time features of the CR profile need to be supplied by alternative means, such as tuning the model components.
Conditioned Response Timing and Comparator Properties
In eyeblink conditioning, the timing of the CR peak is governed by the ISI. In well-conditioned subjects, the CR peak on a CS-alone trial is seen to have reasonably constant latencies from the normal onset of US delivery. For an ISI of 500 ms, average reported values in well-trained subjects include about 0 ms (Lepora et al., 2007b; see Figure 5B), about 75 ms (Hardiman and Yeo, 1992) and Kehoe et al. (2009) reported an average CR peak latency lag of 114 ms when all responses are considered. Responses <0.5 mm are often excluded from analysis in NMR conditioning studies because the frequency of non-associative responses (non-CRs) increases somewhere below this value (e.g., Hardiman and Yeo, 1992). If these smaller responses were excluded, consistent with other studies, the average peak CR lag at 500 ms reported by Kehoe et al. (2009) would shorten toward 75 ms. For an ISI of 350 ms, CR peak lags are reported between 0 ms (Lepora et al., 2007b) and 50 ms (Kellett et al., 2010). The cerebellum is widely considered to play a crucial role in this CR timing but, as discussed above, classical conditioning neither provides nor requires sensory information from the periphery about the actual CR and its coincidence with the US. We now discuss how this lack of timing information implies that classical conditioning models based on a comparator architecture require tuned model parameters to achieve the observed behavior.
A key point is that in the comparator the critical timing relationship is between two internal signals, one derived by the cerebellum from the CS and the other representing the US. However, if the internal CS-derived signal is also the CR motor command, then the nature of the internal timing relationship creates a problem. For accurate timing of the CR peak to US-onset, the motor drive must peak before the US to compensate for the visco-elastic plant dynamics. Though individual subjects appear to time their CR peaks fairly consistently, the common assertion that nictitating membrane CR peaks are always timed very closely to US-onset appears to apply only to some experimental subjects. Here, the basic model produced delays in CR peak from US-onset of 70–98 ms for an ISI of 500 ms and of 65–88 ms for ISI 350 ms with realistic plant dynamics (Figure 6B). Thus the basic model does not account for the shorter CR peak lags of 0–75 ms and 0–50 ms respectively, which are seen behaviorally with these two ISIs. In previously reported cases where the US to CR peak lags were close to zero, the peak CR drive, measured as the EMG response in the retractor bulbi muscle, reliably preceded US-onset by 50–100 ms (Figure 4 of Lepora et al., 2007b). Thus, evidence from behavioral and electrophysiological analyses suggests that a realistic model should provide a mechanism for advancing the CR drive and response by approximately 50 ms.
We simulated this feature by inserting a delay in the pathway conveying a copy of the CR command to the comparator. This can be understood by first considering the system with zero delay in the pathway from cerebellum to comparator, so that the learnt cerebellar activity coincides with the US-related activity. If the delay is turned on, the signal from cerebellum to comparator then occurs after the US-related activity in the comparator, which would cause Purkinje cell activity in cerebellar cortex, and hence cerebellar output, to adapt to give a new peak of activity that occurs before the old peak activity. The general idea that a delay in the cerebellar-comparator pathway would improve CR timing is consistent with the results of recent experimental studies (Bengtsson and Hesslow, 2006; Svensson et al., 2006).
To first approximation, CR latencies for a given plant time constant are roughly equal for ISIs above about 300 ms, so that a delay in the nucleo-olivary pathway of 50 ms (near the middle of the 25–90 ms observed range of Hesslow, 1986; Hesslow and Ivarsson, 1996) will function effectively to reduce the 65–98 ms CR peak latencies in the basic model to the range of 32–61 ms that is closer to the range of behavioral data (Hardiman and Yeo, 1992; Kehoe et al., 2009; Lepora et al., 2007b). Thus, by incorporating realistic plant dynamics, the model naturally reproduces the findings that nictitating membrane CR peaks are usually delayed beyond US-onset and the magnitude of this delay correlates with the ISI, a feature of conditioning that has escaped attention until relatively recently (see Kehoe et al., 2009). The implications of these empirical and computational findings are discussed below.
Neural Basis of Comparator
A wide variety of evidence suggests that, as reflected in Figure 1, the nucleo-olivary pathway is part of the comparator (Andersson and Hesslow, 1987; Andersson et al., 1988; Bengtsson and Hesslow, 2006; Bengtsson et al., 2007; Hesslow and Ivarsson, 1996; Nicholson and Freeman, 2003; Svensson et al., 2006). However, a number of other functions have been proposed for this pathway (Bengtsson and Hesslow, 2006), including control of electrotonic coupling between inferior olive neurons (Lang et al., 1996) and feedback regulation of tonic simple-spike firing rates in Purkinje cells (Bengtsson et al., 2004). These rates are depressed by tonic increases in climbing fiber firing, but this depression in turn disinhibits cells in the deep cerebellar nuclei, whose increased activity then acts via the nucleo-olivary pathway to reduce olivary firing to a suitable value. Such a feedback mechanism could act to maintain stable baseline firing rates throughout the olivo-cerebellar circuit (Attwell et al., 2001). It is currently unclear to what extent a feedback mechanism of this kind would be compatible with a comparator function. Certainly its tonic feedback effects have complicated the interpretation of experiments designed to investigate the effects of olivary manipulations upon learning in eyeblink conditioning (Kim et al., 1998; Medina et al., 2002; Yeo et al., 1986; Zbarska et al., 2007, 2008). Note that the present model, in common with many others (Table 1), consider in effect only variations about an unchanging, tonic olivary firing rate. Therefore, it does not encompass these other functions of the nucleo-olivary pathway and does not deal with the severe effects of reducing the inferior olivary firing rate to zero by anesthesia (Cerminara and Lawson, 2004).
It has also been proposed that pathways other than the direct nucleo-olivary projection play a role in the comparator, for example the pathway from deep cerebellar nucleus to inferior olive via the red nucleus, and possibly also the trigeminal complex (Davis and Dostrovsky, 1986; Horn et al., 1998; Liu et al., 2000; Sears and Steinmetz, 1991). Furthermore, cerebellar modulation of sensory inputs to the olive could enable comparator function without direct modulation at the olive itself. For eyeblink conditioning, the excitatory and inhibitory influences on the trigeminal complex from the red nucleus (Davis and Dostrovsky, 1986), may be highly influential. However, from a computational perspective, the important features of the pathway that conveys cerebellar output (directly or indirectly) to the olive are its signal-processing capabilities. For example, the nucleo-olivary projection appears to have a hard-wired delay: brief (20 ms, 200 Hz) stimulation in appropriate regions of the brainstem produces a long-lasting inhibition which peaks 25–50 ms after stimulation onset (Hesslow and Ivarsson, 1996; Svensson et al., 2006) and nucleo-olivary inhibition during the production of a conditioned response peaks with a delay of 90 ms from CS-onset (Hesslow, 1986). These response characteristics appear qualitatively similar to those observed in vitro (Best and Regehr, 2009) and are attributed to the very unusual properties of the nucleo-olivary synapse. This delay could help with the accuracy of CR timing, as suggested previously (Svensson et al., 2006), shown explicitly here, and discussed above. However, a fixed delay could also have computational disadvantages, since the desired value of the delay would depend upon which particular part of the body (motor plant) was being controlled by any given cerebellar microzone. In addition, the eyeblink plant dynamics underlying CR production are known to vary across subjects, leading to questions about how the delay in the nucleo-olivary pathway is tuned for each particular animal. Some remarks on the information required for such tuning are discussed in the final section on avoidance learning.
Relation to Previous Models
Models of Pavlovian conditioning have been under development for many years (see, e.g., Brandon et al., 2002). For comparison with the model discussed here, we consider only those models of eyeblink conditioning based on adaptive filter architectures. For clarity, the properties of these models are summarized in tabular form (Table 1), from which we make several observations.
The first three observations relate to the computational consequences of having an adaptive filter structure with a comparator error signal.
First, all previous models based on adaptive filters use comparator error signals, in common with the model analyzed here. As explained in the Section “Introduction,” this is because a comparator allows stable learning in Marr–Albus type models of classical conditioning.
Second, their outputs are then also not fully specified by the teaching signal, so that CR profiles depend on the choice of model parameters. Real-time CR profiles can be obtained with a wide range of different assumptions, with particular focus on the signals in parallel fibers that correspond to the choice of basis function for the adaptive filter (Table 1). The reason for this richness is that CR profiles can be approximated with few parameters, whereas the details of processing in cerebellar cortex require very many parameters for their description, many of which are unspecified because the relevant evidence is not yet available. Thus, when the properties of the system output are constrained not by the requirements of the motor task, but solely by the properties of the modeled cerebellar microcircuit, there are many ways to achieve realistic-looking outputs.
Third, the principal computational properties of these models (namely acquisition/extinction of a timed response to the US) in fact follow from any adaptive filter model of the cerebellum coupled to an appropriate comparator signal. One other group of adaptive filter models (Desmond and Moore, 1988, 1991; Moore et al., 1989) has considered training with multiple stimuli, and as here found the model exhibited overshadowing, blocking and conditioned inhibition effects. However, a main finding of the present study is that any adaptive filter model of eyeblink conditioning that uses a comparator error signal will also lead to these types of contingency learning. Therefore, we expect that all models in Table 1 can learn these contingencies if they are extended to admit inputs from multiple conditioned stimuli.
The final two observations relate to how the adaptive filter architecture has been embedded within previous models.
First, the fact that some of the models in Table 1 consider a second adaptive layer in addition to the principal adaptive filter layer, either to represent deep cerebellar nuclear plasticity (e.g., Grossberg and Schmajuk, 1989; Medina and Mauk, 2000) or cerebellar granule layer plasticity (Desmond and Moore, 1988, 1991; Moore et al., 1989) does not help with the problem of principled specification of CR profiles since the additional layer provides an additional source of free parameters. We find these extra layers of plasticity are not required to model the basic trial-level and real-time aspects of eyeblink conditioning, but do not rule out that they could be necessary for other aspects of the motor task not considered here.
Second, none of the other models of eyeblink conditioning have considered the adaptive filter model of the cerebellum to control a model of the motor plant. In principle, a plant model of the type considered here could be included in these models, but those models that do not give Gaussian outputs would not give realistic CRs. For example, in Figure 9 of Grossberg and Schmajuk (1989) the model output is tuned to resemble the actual CR, and in Desmond and Moore (1988) the model outputs do not have a smooth Gaussian profile. Furthermore, none of the other models has a delay in the nucleo-olivary component of the comparator and hence all would result in a CR peak that is significantly delayed after the US-onset.
Cerebellar Role in Eyeblink Conditioning and Avoidance Learning
The above results emphasize that the central difficulty of modeling CR production in eyeblink conditioning arises because Pavlovian conditioning does not allow a response to the CS to affect the actual US, and therefore there is no information to precisely specify the CR profile.
One solution to the problem of learning the real-time features of the CR could lie in the relation between classically conditioned eyeblinks and those learned as a result of avoidance training through operant conditioning (such as occur naturally in responding to aversive stimuli and thus would have occurred previously). Because the conditioned response ameliorates the US in avoidance learning, comparison of the CR and US can take place outside the brain rather than inside it as in the comparator architecture. Such an external comparison would retain the contingency learning capacities of comparator-based models and, in addition, provide genuine “error” information from corneal sensors and other periorbital receptors to specify the CR profile. Comparison of avoidance and classically conditioned eyeblinks from this perspective raises two important questions.
First, little is known about the computational requirements of protective responses. For eyeblinks, there should be a trade-off between protecting the eye (long blink) and maintaining vision (short blink), but the precise relation is unclear. Experimental evidence concerning the effects of eyelid restraint indicates that the amplitude of unconditioned blinks is under adaptive control by the cerebellum (Chen and Evinger, 2006; Pellegrini and Evinger, 1997), and further investigation of this control may help to clarify its computational basis.
The second question concerns similarities between the temporal profiles of eyeblinks produced by classical conditioning and those resulting from avoidance training. There appears to have been little systematic investigation of this issue, but one report compares conditioned responses obtained using periocular electrical US with those obtained using an airpuff US that was directed to the unrestrained eyelids and so permitted a degree of US avoidance. The two response types were very similar (Mauk and Ruiz, 1992). If there were some avoidance component in the airpuff condition, as the authors suggest, then it would appear that the performance of the eyeblink control system is little affected when the internal comparator is substituted for external comparison, which in turn suggests that the comparator architecture is accurately tuned to mimic the external world.
A key feature of simulating these features with a future Marr–Albus type model of the cerebellum is that it should also be able to permit accurate performance on other motor control tasks, such as VOR calibration. Accumulating evidence suggests that even for precise motor control, the relevant “error” signal is not the difference between desired and actual motor outputs, not least because the desired motor commands are usually unknown. Instead, the cerebellum appears to use sensory indicators of inaccurate motor commands as teaching signals (e.g., retinal slip for the VOR). Then adaptive filter models of the cerebellum can learn to reduce motor error indirectly, by decorrelating their inputs from the sensory-derived teaching signal (Dean et al., 2002; Dean and Porrill, 2008; Porrill and Dean, 2007; Porrill et al., 2004).
One unexpected outcome of modeling the neural substrate of NM conditioning relevant to this issue is that it became increasingly evident the widely-held view that NM CR peaks are precisely timed to US-onset is inconsistent with the literature. It is much more common for NM CRs to lag the US by a delay, consistent in individual subjects, of up to 50 ms at ISIs around 350 ms, with longer lags for extended ISIs. In advancing arguments for a calibration of the NM response system under normally-occurring operant conditions, it would appear that such calibration is only partly successful if the resultant behavior has consistent timing lags. However, it should be recognized that the NM response is only one part of the eyeblink defensive system that importantly includes the external eyelid system too. For rabbits, extensive experimental evidence (e.g., Ruiz and Mauk, 1992; Zbarska et al., 2007) suggests this response system has a very similar dependence upon the cerebellum but CR peak latencies have much shorter lags from US-onset at 10–20 ms at an ISI of 250 ms even with an airpuff US (Gruart et al., 2000). Thus, if there is common drive for eyeblink and NM conditioned responses (see van Ham and Yeo, 1996) the optimization of a response system with fast (eyelid) and slower (NM) time constants might lead to the NM CR peak delays seen in the experimental literature and revealed here in our model.
In considering how the system matches CR peak to delivery of the US it should be noted that trains of electrical pulses are used as the US in behavioral experiments with typical durations of 60 ms (e.g., Kehoe et al., 2009; Kellett et al., 2010) and an airpuff US is typically longer at 100 ms (e.g., Welsh, 1992). Thus, CR peak delays similar to the US duration may reflect strategies that better optimize US cancellation through peripheral and central mechanisms. To advance our understanding of these problems, further studies with very short US durations, with detailed electrophysiological analysis of Purkinje cell activity in the critical cerebellar control regions during conditioning and with careful monitoring of eyelid and nictitating membrane responses will be needed.
Whatever the details, a marked similarity between classically conditioned blinks and those produced by avoidance training would suggest the comparator architecture illustrated in Figure 1 lacks a crucial adaptive ingredient. Understanding the nature of this adaptation would shed light not only on the prediction of sensory signals in classical conditioning, but also on the nature of cerebellar control in general.
Conclusion
(1) All Marr–Albus based models of the cerebellar role in motor control recognize that the olivary signal conveys an estimate of motor error, or sensory consequences of motor error, and that by reducing this signal the cerebellum learns accurate commands. But in classical conditioning of a movement there is no appropriate error signal. The US drives a UR and the CR emerges. The US is not ameliorated and there appears to be no reason why the system produces an accurately-timed, amplitude-scaled conditioned response.
(2) Even though a pure classical conditioning protocol ensures the CR does not ameliorate the US, the complex-spike firing thought to represent the error signal in eyeblink/NM conditioning does diminish during acquisition. The standard modeling procedure for reproducing this reduction is to subtract CR motor command from the internal representation of the US. We show that although this procedure solves problems connected with the predictability of US occurrence, it does not specify CR profiles. Their specification can only be achieved by constraining model parameters, which will necessarily compromise performance on general motor control tasks.
(3) Although previous models have employed a comparator, its computational properties have not been well characterized. Our analysis of these properties allows an understanding of the performance of previous models, and, crucially, offers a possible solution to the problem of under-specified CR profiles: we suggest that these profiles in classical conditioning of the NM could arise through operant contingencies that have previously prevailed in the subject’s experience.
(4) This solution would in principle allow a Marr–Albus model to learn both aspects of the learning, corresponding to the motor control and sensory prediction aspects of classical conditioning.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by the United Kingdom Biotechnology and Biological Research Council (Grant BBS/B/17026 under the Integrative Analysis of Brain and Behaviour Initiative) and the Wellcome Trust (VIP award to N. Lepora).
References
Andersson, G., Garwicz, M., and Hesslow, G. (1988). Evidence for a GABA-mediated cerebellar inhibition of the inferior olive in the cat. Exp. Brain. Res. 72, 450–456.
Andersson, G., and Hesslow, G. (1987). Inferior olive excitability after high-frequency climbing fiber activation in the cat. Exp. Brain. Res. 67, 523–532.
Attwell, P. J. E., Rahman, S., and Yeo, C. H. (2001). Acquisition of eyeblink conditioning is critically dependent on normal function in cerebellar cortical lobule HVI. J. Neurosci. 21, 5715–5722.
Bartha, G. T., Thompson, R. F., and Gluck, M. A. (1991). “Sensorimotor learning and the cerebellum,” in Visual Structures and Integrated Functions, Vol. 3, eds M. Arbib and J.-P. Ewert (Berlin: Springer-Verlag), 381–396.
Bengtsson, F., and Hesslow, G. (2006). Cerebellar control of the inferior olive. Cerebellum 5, 7–14.
Bengtsson, F., Jirenhed, D. A., Svensson, P., and Hesslow, G. (2007). Extinction of conditioned blink responses by cerebello-olivary pathway stimulation. Neuroreport 18, 1479–1482.
Bengtsson, F., Svensson, P., and Hesslow, G. (2004). Feedback control of purkinje cell activity by the cerebello-olivary pathway. Eur. J. Neurosci. 20, 2999–3005.
Best, A. R., and Regehr, W. G. (2009). Inhibitory regulation of electrically coupled neurons in the inferior olive is mediated asynchronous release of GABA. Neuron 62, 555–565.
Brandon, S. E., Vogel, E. H., and Wagner, A. R. (2002). Computational Theories of Classical Conditioning. A neuroscientist’s guide to classical conditioning, 1st Edn. New York: Springer-Verlag, 232–310.
Bullock, D., Fiala, J. C., and Grossberg, S. (1994). A neural model of timed response learning in the cerebellum. Neural Netw. 7, 1101–1114.
Buonomano, D. V., and Mauk, M. D. (1994). Neural-network model of the cerebellum – temporal discrimination and the timing of motor-responses. Neural. Comput. 6, 38–55.
Cerminara, N. L, and Rawson, J. A (2004). Evidence that climbing fibres control an intrinsic spike generator in cerebellar purkinje cell. J. Neurosci. 24, 4510–4517.
Chen, F. P., and Evinger, C. (2006). Cerebellar modulation of trigeminal reflex blinks: interpositus neurons. J. Neurosci. 26, 10569–10576.
Davis, K. D., and Dostrovsky, J. O. (1986). Modulatory influences of red nucleus stimulation on the somatosensory responses of cat trigeminal subnucleus oralis neurons. Exp. Neurol. 91, 80–101.
Dean, P., and Porrill, J. (2008). Adaptive-filter models of the cerebellum: computational analysis. Cerebellum 7, 567–571.
Dean, P., Porrill, J., Ekerot, C. F., and Jörntell, H. (2010). The cerebellar microcircuit as an adaptive filter: experimental and computational evidence. Nat. Rev. Neurosci. 11, 30–43. [Epub 2009 Dec 9].
Dean, P., Porrill, J., and Stone, J. V. (2002). Decorrelation control by the cerebellum achieves oculomotor plant compensation in simulated vestibulo-ocular refle. Proc. R. Soc. Lond. B, Biol. Sci. 269, 1895–1904.
Dean, P., Porrill, J., Yeo, C., and Lepora, N. (2007). A computational model of adaptive blink modification by the cerebellum. Soc Neurosci Abstr. 33, 636.611.
Desmond, J. E., and Moore, J. W. (1988). Adaptive timing in neural networks – the conditioned-response. Biol. Cybern. 58, 405–415.
Desmond, J. E., and Moore, J. W. (1991). Altering the synchrony of stimulus trace processes – tests of a neural-network model. Biol. Cybern. 65, 161–169.
Ekerot, C. F., and Jorntell, H. (2003). Parallel fiber receptive fields: a key to understanding cerebellar operation and learning. Cerebellum 2, 101–109.
Fiala, J. C., Grossberg, S., and Bullock, D. (1996). Metabotropic glutamate receptor activation in cerebellar purkinje cells as substrate for adaptive timing of the classically conditioned eye-blink response. J. Neurosci. 16, 3760–3774.
Gilbert, P. F. C. (1974). Theory of memory that explains function and structure of cerebellum. Brain Res. 70, 1–18.
Gilbert, P. F. C., and Thach, W. T. (1977). Purkinje-cell activity during motor learning. Brain Res. 128, 309–328.
Gluck, M. A., Reifsnider, E. S., and Thompson, R. F. (1990). “Adaptive signal processing and the cerebellum: models of classical conditioning and VOR adaptation,” in Neuroscience and Connectionist Theory, eds M. A. Gluck and D. E. Rumelhart (Hillsdale, NJ: Lawrence Erlbaum), 131–185.
Gormezano, I., Kehoe, E. J., and Marshall, B. S. (1983). 20 Years of classical-conditioning research with the rabbit. Prog. Psychobiol. Physiol. Psychol. 10, 197–275.
Grossberg, S., and Schmajuk, N. A. (1989). Neural dynamics of adaptive timing and temporal discrimination during associative learning. Neural Netw. 2, 79–102.
Gruart, A., Schreurs, B. G., Del-Toro, E. D., and Delgado-Garcia, J. M. (2000). Kinetic and frequency-domain properties of reflex and conditioned eyelid responses in the rabbit. J. Neurophysiol. 83, 836–852.
Hardiman, M. J., and Yeo, C. H. (1992). The effect of kainic acid lesions of the cerebellar cortex on the conditioned nictitating membrane response in the rabbit. Eur. J. Neurosci. 4, 966–980.
Hesslow, G. (1986). Inhibition of Inferior olivary transmission by mesencephalic stimulation in the cat. Neurosci. Lett. 63, 76–80.
Hesslow, G., and Ivarsson, M. (1996). Inhibition of the inferior olive during conditioned responses in the decerebrate ferret. Exp. Brain Res. 110, 36–46.
Hesslow, G., and Yeo, C. H. (2002). The Functional Anatomy of Skeletal Conditioning. A neuroscientist’s guide to classical conditioning, 1st Edn. ed. J.W. Moore, New York: Springer-Verlag, 86–146.
Horn, K. M., Hamm, T. M., and Gibson, A. R. (1998). Red nucleus stimulation inhibits within the inferior olive. J. Neurophysiol. 80, 3127–3136.
Ito, M. (1982). Cerebellar control of the vestibulo-ocular reflex: around the flocculus hypothesis. Annu. Rev. Neurosci. 5, 275–296.
Jirenhed, D. A., Bengtsson, F., and Hesslow, G. (2007). Acquisition, extinction, and reacquisition of a cerebellar cortical memory trace. J. Neurosci. 27, 2493–2502.
Kehoe, E. J., Olsen, K. N., Ludvig, E. A., and Sutton, R. S. (2009). Scalar timing varies with response magnitude in classical conditioning of the nictitating membrane response of the rabbit. Behav. Neurosci. 123, 212–217.
Kellett, D. O., Fukunaga, I., Chen-Kubota, E., and Yeo, C. H. (2010). Memory consolidation in the cerebellar cortex. PLoS ONE 5, e11737. doi: 10.1371/journal.pone.0011737.
Kim, J. J., Krupa, D. J., and Thompson, R. F. (1998). Inhibitory cerebello-olivary projections and blocking effect in classical conditioning. Science 279, 570–573.
Lang, E. J., Sugihara, I., and Llinas, R. (1996). GABAergic modulation of complex spike activity by the cerebellar nucleoolivary pathway in rat. J. Neurophysiol. 76, 255–275.
Lepora, N., Porrill, J., Yeo, C. H., and Dean, P. (2007a). Contingency learning by an adaptive filter model of cerebellum in simulated eyeblink conditioning. Soc. Neurosci. Abstr. 33, 636.11.
Lepora, N. F., Mavritsaki, E., Porrill, J., Yeo, C. H., Evinger, C., and Dean, P. (2007b). Evidence from retractor bulbi EMG for linearized motor control of conditioned nictitating membrane responses. J. Neurophysiol. 98, 2074–2088.
Lepora, N. F., Porrill, J., Yeo, C. H., Evinger, C., and Dean, P. (2009). Recruitment in retractor bulbi muscle during eyeblink conditioning: EMG analysis and common-drive model. J. Neurophysiol. 102, 2498–2513.
Liu, Y. J., Pu, Y. L., Gao, J. H., Parsons, L. M., and Xiong, J. H., Liotti, M., Bower, J. M., and Fo, P. T. (2000). The human red nucleus and lateral cerebellum in supporting roles for sensory information processing. Hum. Brain Mapp. 10, 147–159.
Mauk, M. D., and Donegan, N. H. (1997). A model of pavlovian eyelid conditioning based on the synaptic organization of the cerebellum. Learn. Mem. 4, 130–158.
Mauk, M. D., and Ruiz, B. P. (1992). Learning-dependent timing of pavlovian eyelid responses – differential conditioning using multiple interstimulus intervals. Behav. Neurosci. 106, 666–681.
Medina, J. F., Garcia, K. S., Nores, W. L., Taylor, N. M., and Mauk, M. D. (2000). Timing mechanisms in the cerebellum: testing predictions of a large-scale computer simulation. J. Neurosci. 20, 5516–5525.
Medina, J. F., and Mauk, M. D. (2000). Computer simulation of cerebellar information processing. Nat. Neurosci. Suppl. 3, 1205.
Medina, J. F., Nores, W. L., and Mauk, M. D. (2002). Inhibition of climbing fibres is a signal for the extinction of conditioned eyelid responses. Nature 416, 330–333.
Moore, J. W., Desmond, J. E., and Berthier, N. E. (1989). Adaptively timed conditioned-responses and the cerebellum – a neural network approach. Biol. Cybern. 62, 17–28.
Moore, J. W., Desmond, J. E., Berthier, N. E., Blazis, D. E. J., and Sutton, R. S., and Barto, A. G. (1986). Simulation of the classically-conditioned nictitating membrane response by a neuron-like adaptive element – response topography, neuronal firing, and interstimulus intervals. Behav. Brain Res. 21, 143–154.
Nicholson, D. A., and Freeman, J. H. (2003). Addition of inhibition in the olivocerebellar system and the ontogeny of a motor memory. Nat. Neurosci. 6, 532–537.
Optican, L. M., and Robinson, D. A. (1980). Cerebellar-dependent adaptive-control of primate saccadic system. J. Neurophysiol. 44, 1058–1076.
Pavlov, L. P. (1927). Conditioned Reflexes: An Investigation of the Physiological Activity of the Cerebral Cortex. G.V. Anrep, trans. London: Oxford University Press.
Pellegrini, J. J., and Evinger, C. (1997). Role of cerebellum in adaptive modification of reflex blinks. Learn. Mem. 4, 77–87.
Porrill, J., and Dean, P. (2007). Recurrent cerebellar loops simplify adaptive control of redundant and nonlinear motor systems. Neural. Comput. 19, 170–193.
Porrill, J., Dean, P., and Stone, J. V. (2004). Recurrent cerebellar architecture solves the motor-error problem. Proc. R. Soc. Lond. B. Biol. Sci. 271, 789–796.
Rasmussen, A., Jirenhed, D. A., and Hesslow, G. (2008). Simple and complex spike firing patterns in purkinje cells during classical conditioning. Cerebellum 7, 563–566.
Rescorla, R. W., and Wagner, A. R. (1972). “A theory of Pavlovian conditioning: variations in the effectiveness of reinforcement and nonreinforcement,” in Classical Conditioning II, eds A. H. Black and W. F. Prokasy (New York: Appleton-Century-Crofts), 64–99.
Sears, L. L., and Steinmetz, J. E. (1991). Dorsal accessory inferior olive activity diminishes during acquisition of the rabbit classically-conditioned eyelid response. Brain Res. 545, 114–122.
Shidara, M., Kawano, K., Gomi, H., and Kawato, M. (1993). Inverse-dynamics model eye-movement control by Purkinje-cells in the cerebellum. Nature 365, 50–52.
Svensson, P., Bengtsson, F., and Hesslow, G. (2006). Cerebellar inhibition of inferior olivary transmission in the decerebrate ferret. Exp. Brain Res. 168, 241–253.
Thompson, R. F. (1983). Neuronal substrates of simple associative learning – classical-conditioning. Trends Neurosci. 6, 270–275.
van Ham, J. J., and Yeo, C. H. (1996). Trigeminal inputs to eyeblink motoneurons in the rabbit. Exp. Neurol. 142, 244–257.
Welsh, J. P. (1992). Changes in the motor pattern of learned and unlearned responses following cerebellar lesions: a kinematic analysis of the nictitating membrane reflex. Neuroscience 47, 1–19.
Widrow, B. S., and Stearns, S. D. (1985). Adaptive Signal Processing. Engelwood Cliffs, NJ: Prentice-Hall Inc.
Yamazaki, T., and Tanaka, S. (2007). A spiking network model for passage-of-time representation in the cerebellum. Eur. J. Neurosci. 26, 2279–2292.
Yeo, C. H., Hardiman, M. J., and Glickstein, M. (1986). Classical-conditioning of the nictitating-membrane response of the rabbit.4. Lesions of the inferior olive. Exp. Brain Res. 63, 81–92.
Yeo, C. H., and Hesslow, G. (1998). Cerebellum and conditioned reflexes. Trends Cogn. Sci. (Regul. Ed.) 2, 322–330.
Zbarska, S., Bloedel, J. R., and Bracha, V. (2008). Cerebellar dysfunction explains the extinction-like abolition of conditioned eyeblinks after NBQX injections in the inferior olive. J. Neurosci. 28, 10–20.
Zbarska, S., Holland, E. A., Bloedel, J. R., and Bracha, V. (2007). Inferior olivary inactivation abolishes conditioned eyeblinks: extinction or cerebellar malfunction? Behav. Brain. Res. 178, 128–138.
Keywords: classical conditioning, cerebellum, eyeblink conditioning, adaptive filter, Marr–Albus, motor learning, inferior olive
Citation: Lepora NF, Porrill J, Yeo CH and Dean P (2010) Sensory prediction or motor control? Application of Marr–Albus type models of cerebellar function to classical conditioning. Front. Comput. Neurosci. 4:140. doi: 10.3389/fncom.2010.00140
Received: 23 December 2009;
Paper pending published: 30 April 2010;
Accepted: 12 September 2010;
Published online: 04 October 2010.
Edited by:
Peter Dayan, University College London, UKReviewed by:
Chris Miall, University of Birmingham, UKJim Kehoe, The University of New South Wales, Australia
Copyright: © 2010 Lepora, Porrill, Yeo and Dean. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Nathan F. Lepora and Paul Dean, Department of Psychology, University of Sheffield, Western Bank, Sheffield S10 2TP, UK. e-mail:bi5sZXBvcmFAc2hlZmZpZWxkLmFjLnVrandcC5kZWFuQHNoZWZmaWVsZC5hYy51aw==



