Limits to the development of feed-forward structures in large recurrent neuronal networks

Spike-timing dependent plasticity (STDP) has traditionally been of great interest to theoreticians, as it seems to provide an answer to the question of how the brain can develop functional structure in response to repeated stimuli. However, despite this high level of interest, convincing demonstrations of this capacity in large, initially random networks have not been forthcoming. Such demonstrations as there are typically rely on constraining the problem artificially. Techniques include employing additional pruning mechanisms or STDP rules that enhance symmetry breaking, simulating networks with low connectivity that magnify competition between synapses, or combinations of the above. In this paper, we first review modeling choices that carry particularly high risks of producing non-generalizable results in the context of STDP in recurrent networks. We then develop a theory for the development of feed-forward structure in random networks and conclude that an unstable fixed point in the dynamics prevents the stable propagation of structure in recurrent networks with weight-dependent STDP. We demonstrate that the key predictions of the theory hold in large-scale simulations. The theory provides insight into the reasons why such development does not take place in unconstrained systems and enables us to identify biologically motivated candidate adaptations to the balanced random network model that might enable it.

1 Introduction

For several decades now it has been commonly assumed that functional structures in the brain develop by strengthening synapses between neurons that fire in a correlated fashion (Hebb, 1949). In particular, feed-forward structures in which neural activity is propagated as a wave from one pool to the next (Abeles, 1991) would seem to be favored by a synaptic plasticity dynamics which strengthens causally correlated connections and weakens acausally correlated connections. This key property of spike-timing dependent plasticity (STDP) was postulated theoretically (Gerstner et al., 1993) before it was observed experimentally on the timescale of 10 ms (Markram and Sakmann, 1995; Markram et al., 1997; Bi and Poo, 1998), although strengthening of causal correlations on the timescale of 100 ms had already been found (Gustafsson et al., 1987).

Such feed-forward structures, also known as synfire chains or braids, have been postulated to underlie experimentally observed precise spike-timing, for example in mammalian cortex (Eckhorn et al., 1988; Gray and Singer, 1989; Abeles et al., 1993; Prut et al., 1998; Ikegaya et al., 2004; Pulvermüller and Shtyrov, 2009) or songbird HVC (Hahnloser et al., 2002; Kozhevnikov and Fee, 2007). The propagation of waves of activity along synfire chains has been shown to be stable under quite general conditions (Diesmann et al., 1999; Gewaltig et al., 2001). Apart from being a natural candidate for the representation of serial activities, such as the sequential activation of muscles to generate a movement, Bienenstock (1995) conjectured that all cortical computation is carried out by the action and interaction of such structures. It has since been shown that co-ordinated activity between synfire chains can realize the phenomenon of compositionality (Hayon et al., 2004).

Given the great degree of interest in feed-forward structures, the experimentally confirmed existence of a plasticity rule that is apparently predestined to generate them, and the growing availability of both tools suitable for large-scale neuronal network simulations (e.g., Morrison et al., 2005; Migliore et al., 2006; Gewaltig and Diesmann, 2007; Pecevski et al., 2009) and the high-performance computers on which to run them, it seems curious that there have been no truly convincing studies demonstrating their development.

It is in the nature of numerical studies that they use simplified models and therefore run the risk of generating artifacts, i.e., behavior that does not occur if a simplified model is replaced with a more realistic one. When investigating STDP in recurrent networks, there are at least two commonly chosen model simplifications that run a high risk of yielding such non-generalizable behavior. So far, all reports of structure development in a recurrent network have been based on network models which represent only a small fraction of the number of synaptic inputs a neuron typically receives (Hertz and Prügel-Bennet, 1996; Levy et al., 2001; Izhikevich et al., 2004; Iglesias et al., 2005; Doursat and Bienenstock, 2006; Jun and Jin, 2007; Masuda and Kori, 2007; Hosaka et al., 2008; Liu and Buonomano, 2009; Fiete et al., 2010). This is a serious issue, as STDP is driven by correlation between pre- and post-synaptic neurons. Scaling down the network size and increasing the strength of individual synapses increases the correlation between pre- and post-synaptic neurons. This leads to a strong competition effect between the inputs which can result in a very small number of inputs driving the post-synaptic neuron in a non-biological winner-takes-all manner. This is particularly so if, as for the majority of previous studies, an additive model for STDP is assumed, which has a strong symmetry breaking tendency leading to a bimodal distribution of synaptic strengths (Song et al., 2000). However, even very early experimental findings on STDP revealed that the strength of potentiation and depression is dependent on the initial strength of the synapse (Bi and Poo, 1998, but see also Debanne et al., 1996, 1999; Montgomery et al., 2001; Wang et al., 2005). Theoretical studies have revealed that even quite a small dependence on the weight leads to a qualitatively different behavior and a unimodal distribution of synaptic strengths (van Rossum et al., 2000; Rubin et al., 2001; Gütig et al., 2003; see also Morrison et al., 2008) which is more similar to the distributions observed experimentally (Turrigiano et al., 1998; Sjöström et al., 2001; Song et al., 2005). Moreover, weight-dependent “soft-bounded” rules can be more plausibly generated with a kinetic modeling approach than an additive “hard-bounded” rule (Zou and Destexhe, 2007). It is therefore not clear, and should not be assumed, that behavior observed in networks with low numbers of synapses per neuron and/or additive STDP are representative for networks with biologically realistic numbers of synapses and weight-dependent STDP. Indeed, a network exhibiting cortical connectivity levels and using a model for STDP with weight dependence fitted to experimental findings did not develop structure either spontaneously or as a result of repeated synchronous stimuli to a subset of neurons (Morrison et al., 2007).

One reason for this may have been that a critical additional mechanism is required. Many of the above mentioned studies include homeostatic regulating mechanisms such as normalization of weights on the axon and dendrite (Doursat and Bienenstock, 2006; Fiete et al., 2010), pre-synaptic activity dependent weight dynamics to maintain a given post-synaptic rate (Liu and Buonomano, 2009) or axonal pruning of weak synapses once a certain number of very strong synapses have been created (Jun and Jin, 2007). Additionally, STDP has been supplemented with plasticity dynamics on other time scales: Izhikevich et al. (2004) employ both short-term plasticity and slow long-term potentiation, whereas Jun and Jin (2007) implement slow long-term depression and a reversible activation and silencing of synapses. Clearly, some of these mechanisms are more biologically plausible than others and it may well turn out that one or more of them is necessary for the development of structure in networks with realistic connectivity.

In this article, we develop a theory for the recruitment into a structure of neurons in a recurrent network in response to repeated external synchronous input. We show that recruitment is characterized by an unstable fixed point that cannot be stabilized by simply introducing pre- or post-synaptic homeostatic mechanisms such as those proposed in previous studies (Doursat and Bienenstock, 2006; Fiete et al., 2010). We demonstrate that the key predictions of the theory can be reproduced by a large-scale neuronal network model. Finally, we consider what biologically plausible adaptations to the network model could allow the stable propagation of feed-forward structure.

2 Materials and Methods

2.1 Network Model

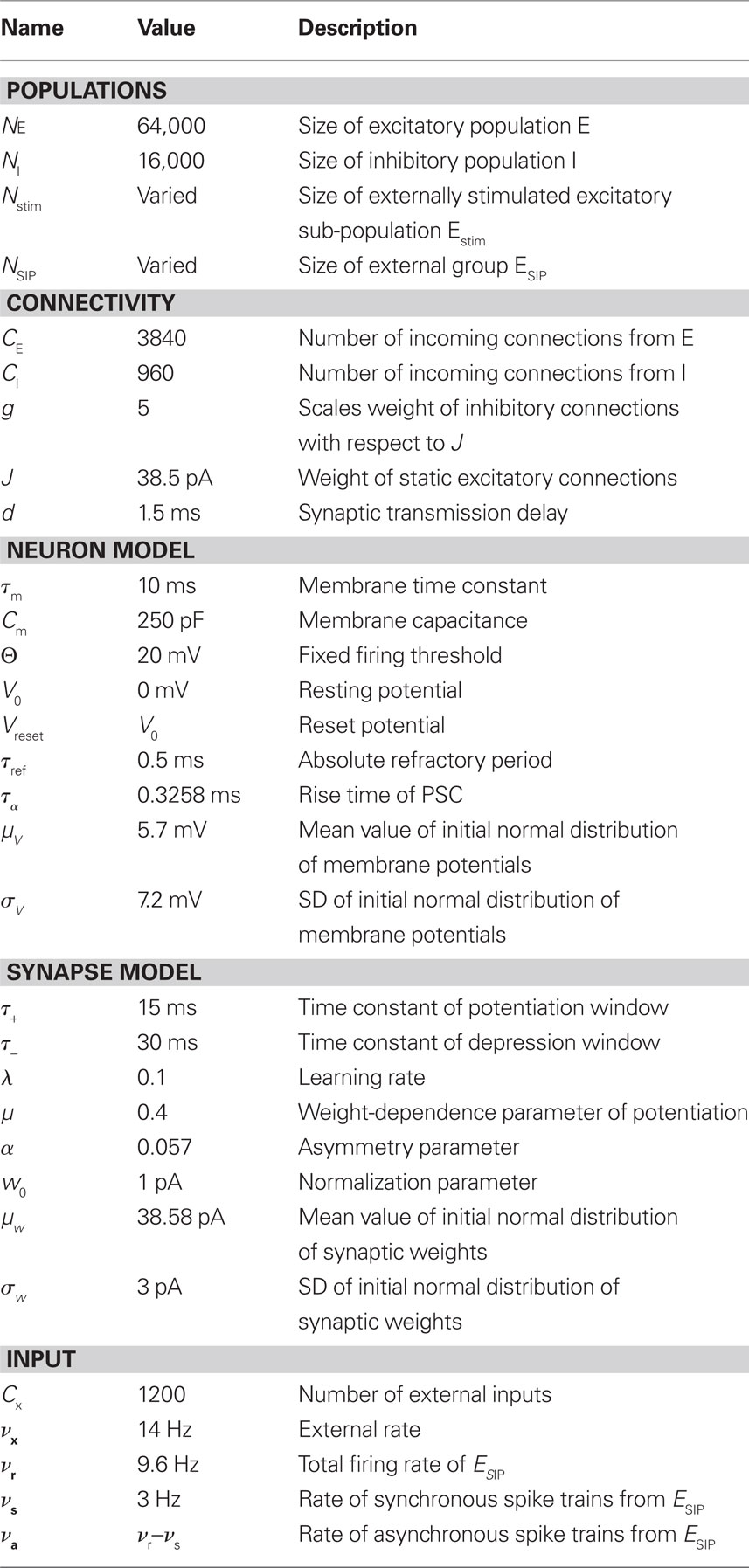
Our network model is based on the balanced random network model of Brunel (2000), see Figure 1A. The neurons are 80% excitatory and 20% inhibitory and randomly connected; excitatory–excitatory connections are subject to weight-dependent STDP, all other connections are static. The network activity is presumed to be in the asynchronous irregular regime with an average firing rate of ν_r.

FIGURE 1

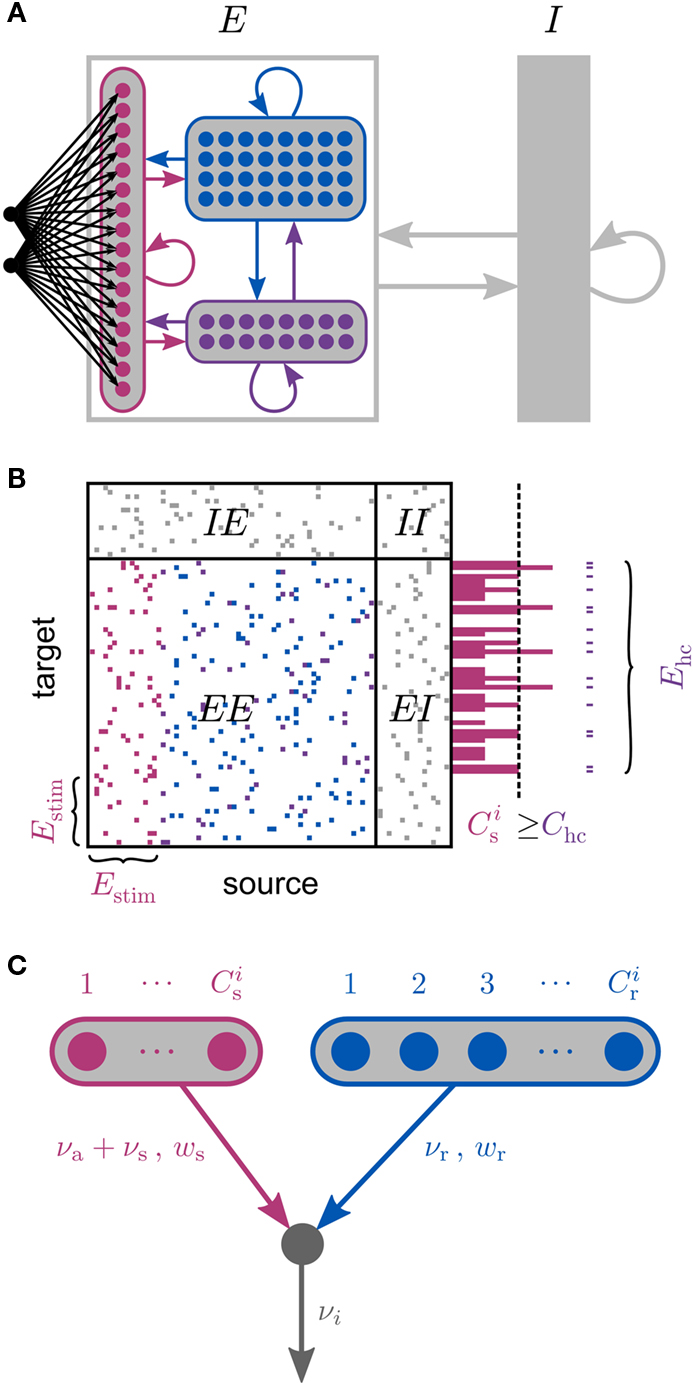
Figure 1. Network and single neuron model. (A) Balanced recurrent network model based on Brunel (2000). A subset of the excitatory population (E_stim, pink disks) receives feed-forward input from each member of an external group of size N_SIP (black disks). The external group fires synchronously with rate ν_s and asynchronously with rate ν_a. The externally stimulated population E_stim makes recurrent connections to the rest of the excitatory population. N_hc neurons receive a number of connections from E_stim above a given threshold C_hc (high-connectivity group, purple disks) whereas all other neurons receive fewer connections from E_stim (blue disks). All neurons also receive external excitatory Poisson input (not shown). (B) Determination of the high-connectivity group from the connectivity matrix (shown here in diluted form). The subdivisions of the connectivity matrix indicate the source and target populations, e.g., EI contains the connections from the inhibitory population I to the excitatory population E. The entries in row i of the connectivity matrix indicate the sources of the synaptic inputs of neuron i according to the color scheme in (A). The histogram gives the number of connections 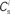each neuron receives from E_stim. If neuron i receives a number of connections from E_stim greater than or equal to the arbitrary threshold C_hc (vertical dashed line) it is considered a member of the high-connectivity group E_hc. (C) Simplified input structure of a neuron in a recurrent network: the post-synaptic neuron i (gray disk) receives input from 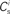neurons from E_stim (pink disks) that fire asynchronously with rate ν_a and synchronously with rate ν_s and from 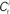neurons selected from the rest of the network (blue disks) that fire asynchronously with rate ν_r. The mean synaptic weights from these populations are w_s and w_r, respectively.

A subset E_stim of the excitatory population receives feed-forward input from each element of an external group of size N_SIP; these connections are also subject to STDP. Each neuron in the external group spikes independently as a Poisson process of rate ν_a and synchronously with the rest of the group as a Poisson process of rate ν_s, thus implementing a single interaction process (SIP, see Kuhn et al., 2003). The total rate of a neuron in the external group is the same as the network firing rate, i.e., ν_a + ν_s = ν_r. All neurons in the network receive additional excitatory independent Poisson spike trains; the neurons in the externally stimulated group receive Poisson spike trains at a slightly reduced rate to compensate for their additional external stimulus.

Due to the random connectivity, the number of connections neurons receive from E_stim is binomially distributed. For a given connectivity threshold C_hc, a high-connectivity group E_hc can be located within the excitatory population (not including E_stim). Each neuron in E_hc receives at least C_hc connections from E_stim, whereas all other excitatory neurons receive fewer than C_hc connections from E_stim. This is illustrated in Figure 1B. In general, N_SIP, N_stim, and C_hc can all be chosen independently. For a given binomial distribution of connections from E_stim, the choice of N_stim and C_hc completely determines N_hc, the number of neurons in the high-connectivity group E_hc. As we are investigating the development of feed-forward structures in this article, we are interested in the case that successive groups have similar sizes. We therefore link the independent variables such that C_hc = N_SIP and require N_hc ≈ N_stim. In other words, for a given value of N_SIP, we select the size of the externally stimulated population N_stim such that the binomial distribution of connections results in N_hc ≈ N_stim neurons that receive at least N_SIP connections from E_stim and all other excitatory neurons in the network receive fewer than N_SIP connections from E_stim.

2.2 Fixed Point Analysis of Structural Development

If pre- and post-synaptic spike trains are stochastic, the weight updates of a synapse can be described as a random walk. Using Fokker–Planck mean field theory, the drift of the random walk corresponds to the average rate of change of synaptic strength. The drift can be calculated as a function of the correlation of the pre- and post-synaptic spike trains. Assuming stationarity, the raw cross-correlation function of the pre-synaptic spike train 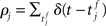and the post-synaptic spike train 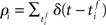with mean firing rates of ν_i/j = 〈ρ_i/j〉 is given by:

Γ_ji (Δt) = 〈ρ_j (t)ρ_i (t + Δt)〉_t

This results in the following expression for the mean synaptic drift:

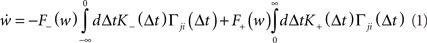
where F_± (w) describe the weight-dependent potentiation/depression of a synapse due to a single spike pair and K_± (Δt) = exp (−|Δt|/τ_±) is the window function of STDP. A more thorough derivation of (1) can be found in Kempter et al. (1999) and Kistler and van Hemmen (2000; but see also Kempter et al., 2001; Rubin et al., 2001; Gütig et al., 2003; Morrison et al., 2008; Gilson et al., 2009a).

To investigate the fixed point behavior of STDP in the context of a large recurrent network in which structure development is being induced by synchronous stimulation of a subset of neurons, we make the following assumptions, abstracted from the network model displayed in Figure 1A. Each neuron i receives 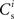excitatory connections from neurons selected from the subset of neurons E_stim receiving synchronous stimulation and 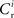connections from neurons selected from the rest of the network. Synchronous spikes from the stimulated subset occur irregularly and are governed by a Poisson process with a rate of ν_s. Each neuron in the stimulated subset also fires independently as a Poisson process with rate ν_a; the composite activity for a neuron from the stimulated subset is therefore a Poisson process with rate ν_a + ν_s. The activity of a neuron in the rest of the network can be described as a Poisson process with rate ν_r. The input structure of an excitatory neuron in the recurrent network is illustrated in Figure 1C. We further assume that the post-synaptic spike rate is generated by an inhomogeneous Poisson process 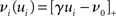with scaling factor γ, threshold ν₀ and membrane potential u_i, where [·]₊ denotes a piecewise linear function that is defined as 0 for negative values, i.e., [x]₊ = (x + |x|)/2. In the following, we will assume the function is positive and omit the square brackets. The membrane potential is given by 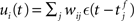where w_ij is the weight of the synapse between neuron j and neuron i, and ∊(t) describes the time course of the response of the membrane potential to the arrival of an excitatory event, i.e., w_ij∊(t) is the post-synaptic potential. Finally, we assume that the dynamics of the system is sufficiently well captured by considering the changes to the mean values of the synapses between the two input populations and the output neuron, 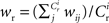and 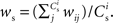The expected rate of the output neuron is therefore:

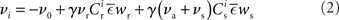
where 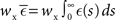is the total area under the respective post-synaptic potential. The conditional firing rate after a spike at 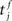from a neuron in the unstimulated input population is:

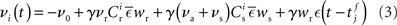
Similarly, the conditional firing rate after a spike at 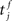from a neuron in the population receiving synchronous stimulus is:

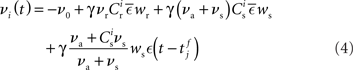
Inserting these pre- and post-synaptic spike trains into the expression for the synaptic drift given in (1) results in a coupled system of differential equations for the evolution of the mean weights:

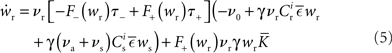
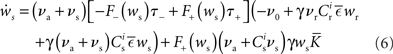
where 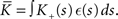The nullclines for w_r and w_s can be found by setting the left hand side of these equations to zero and solving for w_r and w_s respectively. The crossing points of the nullclines (if any) represent the fixed points of the system and can be found numerically.

To do this, appropriate values must be determined for the model parameters. For the numerical simulations in this study (see Section 2.3) we use a current-based integrate-and-fire neuron model with α-shaped post-synaptic currents, i.e., the dynamics of the membrane potential is given by:

where τ_m is the time constant of the membrane potential, C is the membrane capacitance and I is the input current. The time course of a post-synaptic current with peak amplitude w is given by:

We can therefore calculate the time course of the post-synaptic potential as:

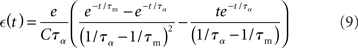
and determine the model parameters.

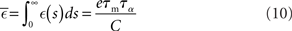
and

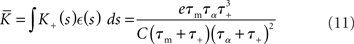
in terms of the parameters of the integrate-and-fire neuron model and the STDP update rule.

2.3 Numerical Simulations

We perform numerical simulations of the network model described in Section 2.1. Our realization of the abstract model consists of 80,000 leaky integrate-and-fire neurons with α-shaped post-synaptic currents. The neurons are 80% excitatory and 20% inhibitory, each receiving 3840 excitatory and 960 inhibitory recurrent connections. Excitatory–excitatory connections are drawn from an initial normal distribution and are subject to weight-dependent power-law STDP (Morrison et al., 2007; Standage et al., 2007).

Each neuron except the externally stimulated group E_stim receives an additional independent Poisson spike train equivalent to 1200 excitatory inputs each spiking at ν_x. When no external synchronous stimulation is provided (N_stim = 0), a choice for the rate of the independent Poisson input to each neuron of ν_x = 14 Hz results in network activity in the asynchronous irregular regime (Brunel, 2000) with an average firing rate of ν_r and a unimodal distribution of the plastic recurrent weights with mean 38.6 pA and SD 3 pA (data not shown). In the absence of homeostasis, ν_r = 9.6 Hz; in the presence of weight normalizing pre-synaptic homeostasis applied every 3 s, ν_r = 9.5 Hz; in the presence of pre- and post-synaptic homeostasis applied alternately every 1.5 s, ν_r = 9.2 Hz.

When external synchronous stimulation is provided (N_stim > 0), each neuron in E_stim receives additional external stimulus at a total rate of ν_r from each of the N_SIP neurons in the external group E_SIP. Consequently, the total rate of the independent Poisson spike trains received by neurons in E_stim is reduced to 1200·ν_x − N_SIP ν_r to compensate for the additional external stimulus. We draw the initial weights of the recurrent plastic synapses in the stimulated network from a normal distribution with the same mean and SD as the equilibrium weight distribution of the unstimulated network. The initial weights of the connections from the external group E_SIP to the stimulated group E_stim are set to the mean of the equilibrium weight distribution of the unstimulated network.

During an initial equilibration period of 100 s the external group E_SIP generates independent Poisson spike trains at rate ν_a = ν_r with no synchronous events, i.e., ν_s = 0 Hz. After this period, the external group E_SIP provides partially synchronous stimulus to the stimulated group E_stim with a synchronous rate of ν_s = 3 Hz and an asynchronous rate of ν_a = ν_r − ν_s.

We perform simulations with different values for the size N_SIP of the external group. The threshold C_hc for membership of the high-connectivity group E_hc is set equal to N_SIP. For each value of N_SIP, we examine the connectivity of the network to determine empirically the value of N_stim that results in a high-connectivity group of approximately equal size, i.e., N_hc ≈ N_stim.

Following the standards suggested by Nordlie et al. (2009), the network model details are provided in tabular form in Table 1. Table 2 contains the values for the parameters used in the network simulations.

TABLE 1

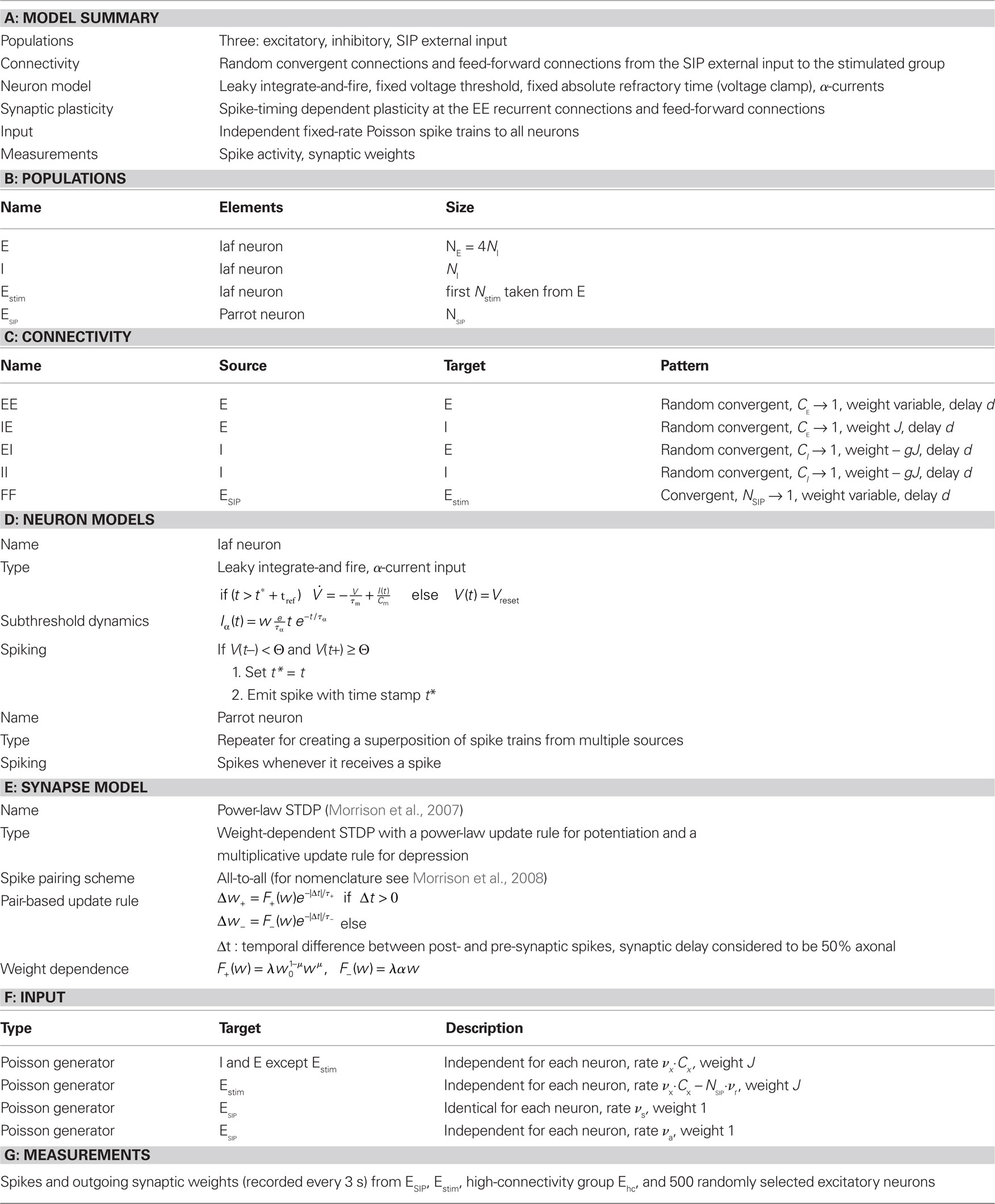
Table 1. Tabular description of network model after Nordlie et al. (2009).

TABLE 2

Table 2. Simulation parameters.

The network simulations were carried out with a computation time step of 0.1 ms on the Stallo Linux cluster (Notur, UiT) and the JUGENE BlueGene/P supercomputer using the simulation software NEST (Gewaltig and Diesmann, 2007) at revision 8611. Simulation scripts are available from the authors on request.

2.4 Data Analysis

Spike times are recorded from the stimulated group, the high-connectivity group, and from 500 neurons randomly chosen from the excitatory population (random group). The times of the synchronous spikes of the external group are also recorded. Weights of all outgoing connections were recorded in intervals of 3 s from the external group, the stimulated group, the high-connectivity group and the random group.

The development of the mean weights shown in Figure 5 is determined from the outgoing weights of the external group and the weights of the connections from the stimulated group to the high-connectivity group. The weight distributions in Figures 6D,H are histograms (bin size 1 pA) of the weights of the connections between the specific neuronal groups recorded at 25 min.

To create the histograms in Figures 6A,C,E,G we record the number of spikes in each group in each 1 ms time bin within the 10 ms directly after a synchronous event over a period of 10 s and normalize by the number of neurons and the number of synchronous input events. Figures 6B,F and 7A–D show the development of the peri-stimulus spiking activity of the specific neuronal groups, which is the number of spikes within the 10 ms before (control) and within the 10 ms after each synchronous input event. Data is normalized with respect to the number of neurons in a group and the number of synchronous input events within successive periods of 10 s.

The scatter plots in Figure 7E are generated by recording the time-to-first-spike following each synchronous event in a 1 min period for all excitatory neurons in the network. Each marker in the plot shows the mean and SD ofthe response times for a specific neuron; the color of the markers indicates the likelihood of the neuron to respond to a synchronous stimulus within 10 ms.

3 Results

3.1 Fixed Point Analysis of Weight Dynamics

To investigate the dynamics of STDP in a recurrent network undergoing synchronous stimulation, we select the update rule proposed by van Rossum et al. (2000), which is additive for potentiation (F₊(w) = λ) and multiplicative for depression (F₋(w) = αλw). This rule is a good fit to the experimental data on the dependence of the magnitude of synaptic strength change on the initial synaptic strength (Bi and Poo, 1998). Furthermore, this choice has the advantage that the rule exhibits the same qualitative behavior as other weight-dependent rules (see Morrison et al., 2008), yet is more tractable than many other weight-dependent rules such as the partially multiplicative model proposed by Gütig et al. (2003) or the power-law formulation (Morrison et al., 2007; Standage et al., 2007).

Inserting F_±(w) into the equation system for the synaptic drifts given in (5) and (6) and setting the left hand sides to zero results in the following quadratic expressions for the nullclines of w_r and w_s:

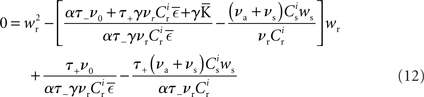
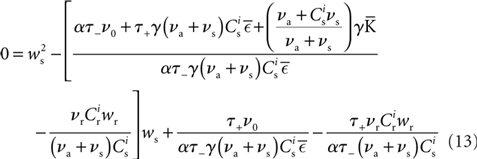
The nullclines can be determined analytically; the crossing of the nullclines can be found numerically. To this end we assume input to the neuron analogous to that received by a neuron in the recurrent network simulation described in Section 2.3. The rate of the asynchronous background population is ν_r = 9.6 Hz, and the asynchronous and synchronous rates of the SIP input are ν_a = 6.6 Hz and ν_s = 3 Hz. The total number of incoming recurrent excitatory synapses is 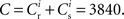We set STDP parameters α = 0.0132 pA⁻¹, λ = 0.03 pA, τ₊ = 15 ms and τ₋ = 30 ms and neuronal parameters γ = 3.66 × 10³(Vs)⁻¹ and ν₀ = 176.1 Hz. In the absence of synchronous stimulation 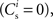this choice of synaptic and neuronal parameters results in a self-consistent output rate ν_i = ν_r and a stable fixed point 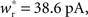thus reproducing the corresponding values of the unstimulated network simulation. The parameters 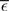and 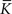are calculated from the neuronal and STDP parameters as described in Section 2.2. The nullclines for 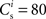are illustrated in Figure 2A. Note that as 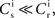the nullcline for w_s is much more sensitive to the value of w_r than vice versa. The value of 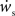is negative for values of w_s above the w_s-nullcline and positive for values of w_s below it. Similarly, 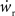is positive for values of w_r to the left of the w_r-nullcline and negative for values to the right of it. Consequently, the fixed point indicated by the intersection of the nullclines is a stable attractor. Figure 2B shows the location of the fixed point as a function of the number of synchronous inputs 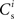. Again, w_s is the more sensitive variable.

FIGURE 2

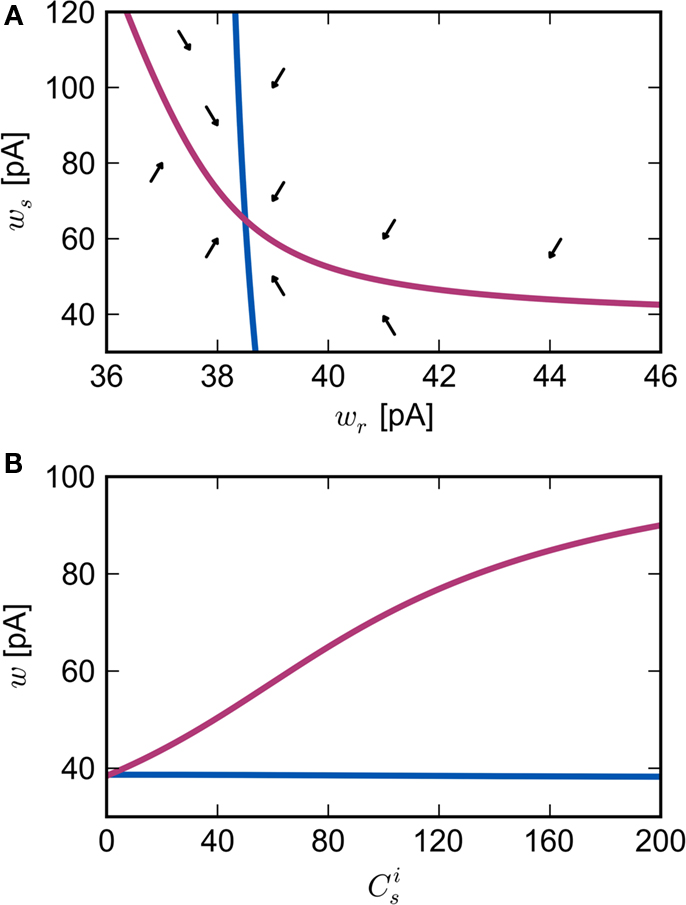
Figure 2. Fixed point of the synaptic drift equations. (A) Nullcline for w_s as a function of w_r (red curve) and for w_r as a function of w_s (blue curve) for 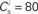. The crossing point of the nullclines determines the fixed point 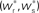of the coupled equations. Arrows show the sign of the derivatives of w_r and w_s; arrows pointing up (down) indicate 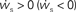arrows pointing right (left) indicate 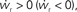for the values of w_r and w_s at the base of the arrows. (B) Location of fixed point (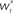; blue, 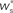; red) as a function of the number of synchronous inputs .

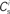We can now exploit our knowledge of the network connectivity to determine the distribution of 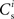and thus the distribution of fixed points. Each neuron receives C_E connections drawn randomly from the N_E excitatory neurons in the network, so the number of connections drawn from the E_stim population receiving synchronous stimulus is distributed binomially; the number of trials is C_E and the probability of success in an individual trial is p =N_stim/N_E, where N_stim is the number of neurons in E_stim. Multiplying the probability of drawing C_s connections P_P (C_s, C_E) with the number of excitatory neurons N_E gives the expected number of neurons in the network that have C_s connections from E_stim. Let us now consider an idealized network model in which the number of neurons with C_s connections from E_stim is indeed ⌊N_E · P_p (C_s, C_E)⌋ and assign each neuron a connectivity rank Rⁱ, where R^j < R^k entails 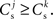Figure 3A shows the equilibrium average strength of the synapses from the stimulated neurons 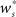as a function of the size of the stimulated group N_stim and the connectivity rank of the post-synaptic neuron in the idealized network. Only the neurons with the highest connectivity are displayed (Rⁱ ≤ 1000), as these are the neurons that will most easily be recruited into a structure. However, Figure 3A suggests that this is unlikely to occur, as 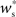increases slowly with decreasing R, i.e., neurons which receive similar numbers of connections from the stimulated group will tend to develop similar synaptic strengths. Consequently, there will be no development of clearly defined groups that respond in a qualitatively different fashion to a synchronous event in the stimulated group. The increase of 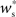with increasing N_stim is more rapid; small variations in the size of a synchronously firing group can have a large effect on the outgoing weight distribution.

FIGURE 3

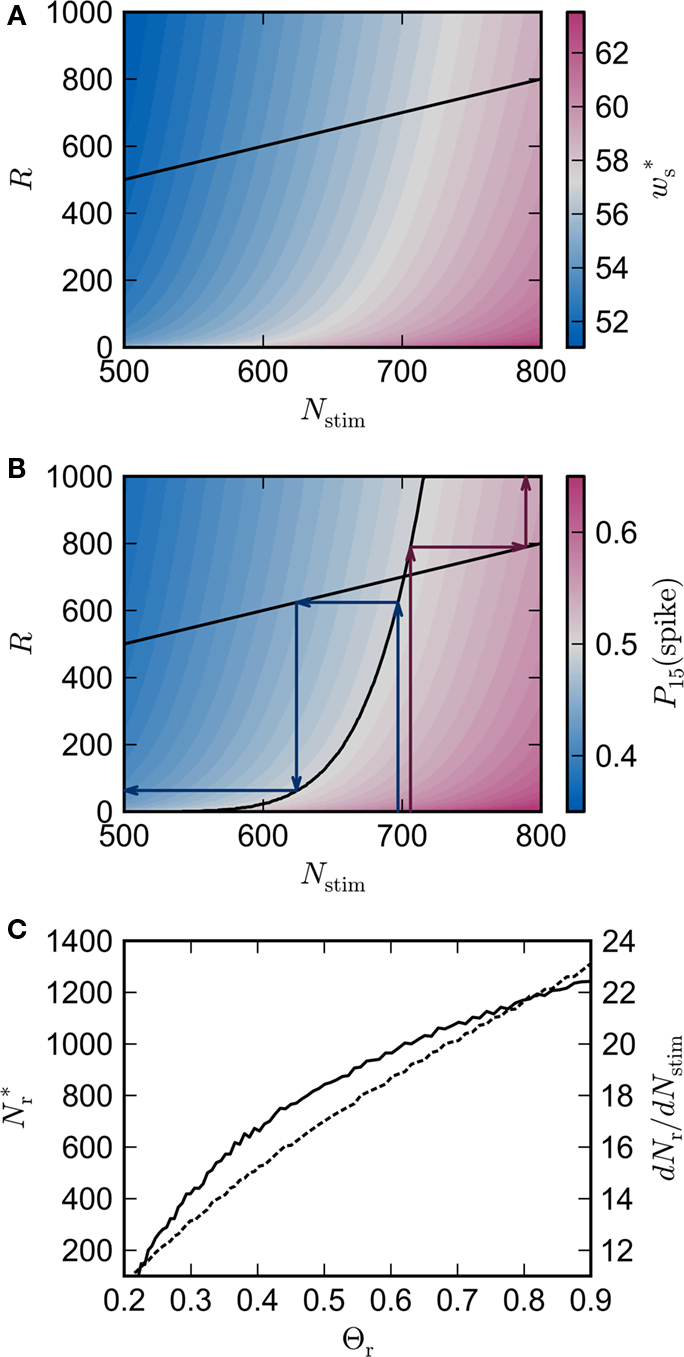
Figure 3. Distribution of fixed points and likelihood of responding to synchronous stimulus. (A) Average strength of synapse from the stimulated group 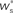as a function of the size of the stimulated group (horizontal axis) and the connectivity rank of the post-synaptic neuron (vertical axis). The black line indicates the group of highest connectivity equal in size to the stimulated group (R = N_stim). (B) Expected number of spikes emitted by the post-synaptic neuron in the 15 ms following a synchronous spike in the stimulated group; axes and black line as in (A); the black curve indicates the number of neurons which respond to a synchronous event with a spike with probability greater than or equal to the recruitment threshold Θ_r = 0.5. The black line and curve represent a return map for the development of feed-forward structure in a network with an unstable fixed point at N_stim = 701. The blue arrows show two iterations of the return map for an initial stimulated population of size N_stim = 697; the pink arrows show one iteration for N_stim = 706. (C) Location and nature of the fixed point as functions of the recruitment threshold Θ_r. Dashed curve: fixed point 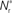, solid curve: slope of the tangent to the N_r (N_stim) curve at .

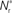This insight can be further clarified by calculating the number of spikes a post-synaptic neuron is expected to produce within a given time t after a synchronous event in the stimulated input group. This can be found by integrating the conditional firing rate:

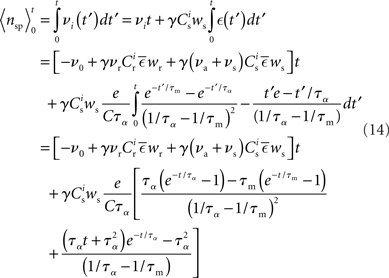
Figure 3B shows the number of spikes expected within 15 ms after a synchronous event for every fixed point calculated in Figure 3A. To determine the development of functional structure, we introduce a recruitment threshold Θ_r. All neurons that have a probability of responding to a synchronous event in E_stim of at least Θ_r are considered to have been recruited into the structure, neurons for which P₁₅ (spike) < Θ_r are considered to be outside the structure. The black curve indicates the number of neurons recruited N_r as a function of the size of the stimulated group N_stim for an arbitrary choice of recruitment threshold Θ_r = 0.5, i.e., for a choice of N_stim, the height of the black curve gives the number of neurons that are recruited by this stimulus such that each neuron has at least a 50% probability of firing immediately after a synchronous event in E_stim.

The black diagonal line indicates a connectivity rank equal to the size of the stimulated group, i.e., the N_stim neurons in the network that receive the most input from the synchronously stimulated group. The two lines represent an approximation of a return map for groups of synchronously firing neurons: the curve indicates N_r (N_stim) and the diagonal indicates N_stim, therefore their intersection reveals the fixed point at which the number of neurons recruited is equal to the number of neurons stimulated, 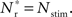If the fixed point were stable, the 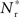recruited neurons would recruit another group of 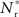neurons, which would in turn recruit another such group, thus stably propagating structure through the network. However, the fixed point is unstable, since the slope of the N_r (N_stim) curve is positive at the intersection. If N_stim is initially below the crossing point, the number of neurons recruited is smaller than N_stim. These neurons will in turn recruit even fewer neurons, and so the structure will decay to nothing within a few iterations. Conversely, if the number of stimulated neurons is larger than the crossing point, the number of neurons recruited will be greater than N_stim. These neurons will in turn recruit an even greater number of neurons, until the entire network is recruited within a few iterations. This is illustrated by the map iterations shown as arrows in Figure 3B. Note that the iterations are approximative, as the composition of pre- and post-synaptic rates is in general not constant over iterations.

Figure 3C shows the dependence of the fixed point on the choice of the recruitment threshold Θ_r. As the requirement on the reliability of spiking following a synchronous event increases, the fixed point shifts to greater values of N_stim. The slope of the tangent of the N_r (N_stim) curve is positive across the whole range of Θ_r, demonstrating that the fixed point is always unstable.

The main factors influencing the shape of Figure 3 are the random wiring of the network and the smooth change of the fixed point of the weight distribution 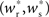with increasing number of synchronous connections (Figure 2B). The number of connections a neuron receives from a given group is binomially distributed. This causes a “fan-out” structure – if we can find a group of neurons which receives at least k inputs from a synchronously active group, we can also find an even larger group which receives slightly fewer than k connections. Due to the smooth change of the fixed point of the weight distribution with k, the equilibrium weight distribution and thus the equilibrium response to a synchronous event of a neuron receiving k − 1 or k − 2 synchronous connections is very similar to the equilibrium distribution and response of a neuron receiving k connections.

It is therefore worthwhile to determine to what extent the smooth shift of the weight distribution shown in Figure 2B is robust to parameter changes. Figure 4A shows the development of fixed points as a function of the number of synchronous connections for four different scenarios. In the top left panel we consider the case of lower input rates: ν_r = 5 Hz, ν_a = 3.5 Hz and ν_s = 1.5 Hz, corresponding to a lower recurrent network rate and a lower synchronous stimulus rate. We set ν₀ = 190 Hz and γ 7.02 × 10³ (Vs)⁻¹, which corresponds to a reduced external Poisson rate and results in a self-consistent rate ν_i = ν_r when there is no synchronous stimulus 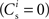. The top right panel reproduces the standard input scenario (ν_r = 9.6 Hz, ν₀ = 175 Hz) except the rate of synchronous events is a greater proportion of the total rate of the synchronous population: ν_a = 2.6 Hz and ν_s = 7 Hz. The bottom left panel reproduces the standard input scenario (ν_r = 9.6 Hz, ν_a = 6.6 Hz, ν_s = 3 Hz, ν₀ = 175 Hz) for the multiplicative STDP model introduced by Rubin et al. (2001): F₊ (w) = λ (w_max − w) and F₋ (w) = αλw. The synaptic parameters are chosen as for the additive/multiplicative model of van Rossum et al. (2000) investigated above, but with α = 2.13 and w_max = 200 pA. Finally, the bottom right panel shows the results for the standard input scenario in combination with the power-law STDP developed in Morrison et al. (2007) and investigated numerically in Section 3.2: 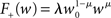and F₋ (w) = λαw. Synaptic parameters are set as above, but with α = 0.057, w₀ = 1 pA and μ = 0.4. In this example, the nullclines cannot be calculated analytically. For both the alternative STDP models investigated, the deviating parameters are chosen to give the same results for the standard input scenario with no synchronous input 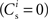as the additive/multiplicative model of van Rossum et al. (2000) investigated above: a self-consistent rate 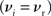and a stable fixed point .

FIGURE 4

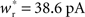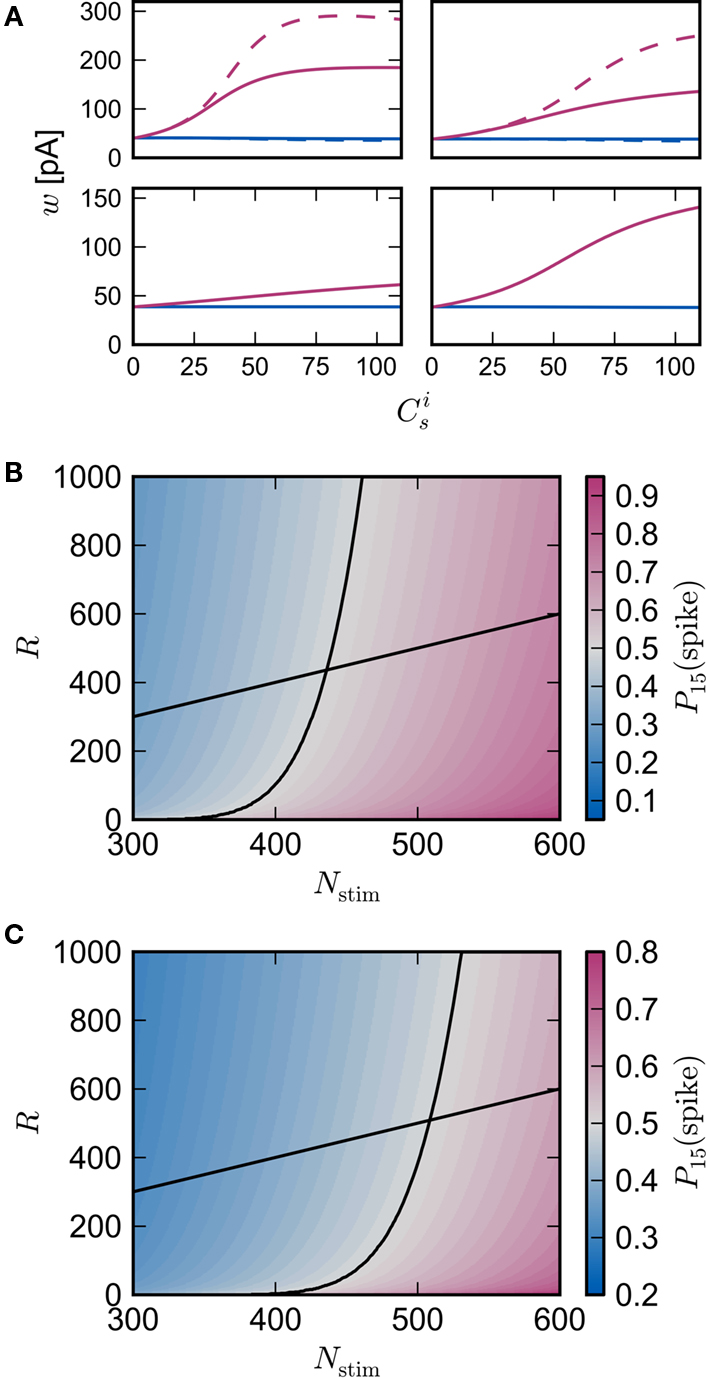
Figure 4. Robustness of results with respect to input rate, STDP model and post-synaptic homeostasis. (A) Location of fixed point (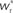; blue, 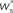; red) as a function of the number of synchronous inputs 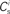for different scenarios, see text for details. Top left: low recurrent and external rates (solid curves) with additional homeostatic regulation of the post-synaptic rate (dashed curves). Top right: high synchronous rate (solid curves) with additional homeostatic regulation of the incoming synaptic weights of the post-synaptic neuron. Bottom left: standard input rates and multiplicative STDP model. Bottom right: standard input rates and power-law STDP model. (B) Expected number of spikes emitted by the post-synaptic neuron in the 15 ms following a synchronous spike in the stimulated group in the low rate scenario; axes and black curves as in Figure 3. (C) As in (B) for the standard input rate scenario with the power-law STDP model.

It has previously been suggested that homeostatic regulatory mechanisms are crucial for the development of structure (Doursat and Bienenstock, 2006; Liu and Buonomano, 2009; Fiete et al., 2010). The equation system for the synaptic drifts given in (5) and (6) can easily be extended to incorporate post-synaptic homeostatic mechanisms. A term −λ_ν (ν_i − ν_h) acts to increase the synaptic weights if the rate of the post-synaptic neuron is less than a desired rate ν_h and to decrease them if the post-synaptic rate exceeds ν_h. A natural choice for ν_h is the self-consistent rate of the unstimulated network, ν_r. 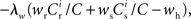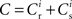Similarly, a homeostatic mechanism to conserve the sum of a neuron’s incoming synaptic weights can be modeled by an additional term where is the total number of incoming synapses and w_h is a desired mean synaptic weight. A natural choice for w_h is the fixed point of the one-dimensional system in the case that the neuron receives no synchronous input 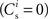. For both models of post-synaptic homeostasis, the expressions for the nullclines of w_r and w_s given in (12) and (13) acquire additional contributions to the linear and constant coefficients but maintain their quadratic form. In Figure 4A, the development of the fixed point assuming post-synaptic rate homeostasis is shown for the low rate scenario with λ_ν = 3 × 10⁻⁴ pA. Similarly, the fixed point development assuming post-synaptic weight homeostasis is shown for the high synchronous rate scenario with λ_w = 5 × 10⁻⁶ s⁻¹. In both cases, the presence of post-synaptic homeostasis causes a greater separation to develop between the mean weights of the unsynchronized inputs and the synchronized inputs.

In all scenarios, a smooth shift of the fixed point of the weight distribution 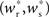with increasing number of synchronous connections can be observed. When combined with the assumption of random connectivity, all scenarios result in a qualitatively similar return map to that shown in Figure 3 with an unstable fixed point. This is demonstrated in Figures 4B,C with a recruitment threshold of Θ_r = 0.5 for the low rate scenario (without homeostasis) and the power-law STDP scenario, respectively. As the theoretical model is developed from the point of view of the post-synaptic neuron, it is not easily extensible to account for pre-synaptic homeostatic mechanisms such as the normalization of outgoing weights. However, due to the similarity in behavior between neurons with similar numbers of synchronous inputs, implementing a pre-synaptic mechanism to regulate the total strength of outgoing synapses will not result in symmetry breaking for some specific value of 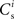. These results lead us to conclude that stable development of structure as a response to synchronous stimulation cannot occur in randomly connected networks incorporating weight-dependent STDP without additional network, cellular or sub-cellular assumptions.

3.2 Simulation Results

To check the predictions of the theoretical model we simulate a large-scale neuronal network with biologically realistic numbers of incoming synapses per neuron and weight-dependent STDP, see Section 2.3 for details. An excitatory sub-population of the network E_stim of size N_stim is stimulated by an external group E_SIP of size N_SIP in which the neurons fire mostly independently but with synchronous events at 3 Hz. Figure 5 shows the development of the mean synaptic weight between the external synchronous group and the stimulated group (top panel) and between the stimulated group and the high-connectivity group (bottom panel) for different sizes of the external group N_SIP. The size of the stimulated group N_stim is chosen such that a high-connectivity group E_hc can be found of similar size (N_hc ≈ N_stim) where each neuron in the high-connectivity group receives at least N_SIP connections from the stimulated group whereas all other excitatory neurons in the network receive fewer than N_SIP connections from the stimulated group. For low values of N_SIP, the mean synaptic weight between E_SIP and E_stim saturates within 10 min. As predicted by the theoretical model derived above, the downstream effect is much weaker; little change can be seen in the mean synaptic weight between E_stim and E_hc, even though each neuron in the E_hc receives at least as many inputs from E_stim as each neuron in E_stim receives from E_SIP. For higher values of N_SIP, the network is still evolving at 10 min, but the substantially greater effect on the mean synaptic weights between E_SIP and E_stim, and between E_stim and E_hc can be clearly seen.

FIGURE 5

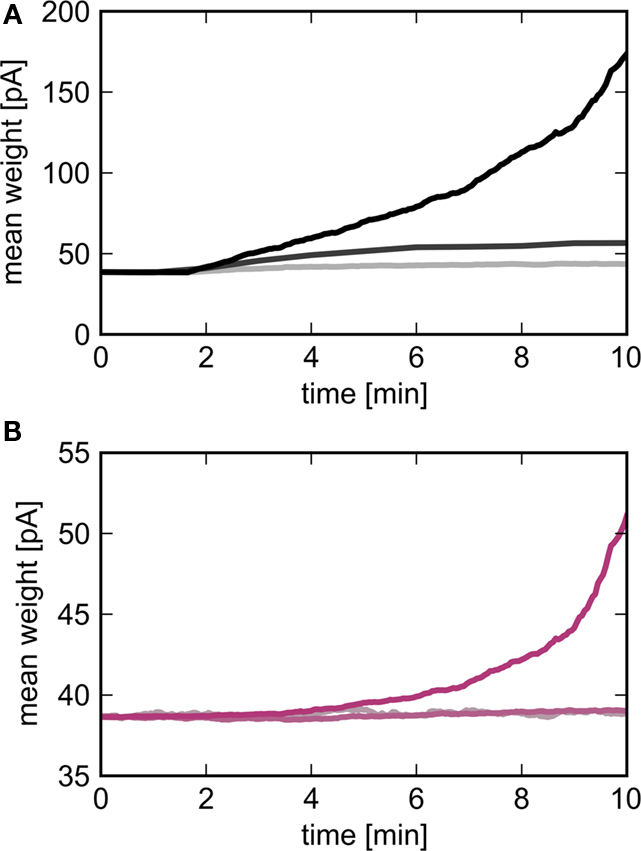
Figure 5. Evolution of the mean synaptic weights as a function of the size of the external group N_SIP. Light to dark curves correspond to N_SIP = 10, 20, 30 resulting in a size for the stimulated group N_stim = 46, 164, 295 respectively. (A) Mean weight of synapses between the external group E_SIP and the stimulated group E_stim as a function of time. (B) Mean weight of synapses between the stimulated group and the high-connectivity group receiving at least N_SIP connections from it (N_hc = 44, 158, 291).

The rapid change in network behavior as the number of synchronous inputs increases can be seen in Figure 6, see Section 2.4 for the data analysis details. In the upper panel, N_SIP = 20 and N_stim = 164. Each neuron in the stimulated group E_stim receives input from each of the 20 neurons in the external stimulating group E_SIP. Each neuron in the corresponding high-connectivity group E_hc of a similar size (N_hc = 158) receives at least 20 synaptic inputs from E_stim. All other excitatory neurons in the network receive 19 or fewer synaptic inputs from E_stim and on average 10. The probability that neurons in the stimulated group fire in response (i.e., within 10 ms) to a synchronous stimulation event increases slightly in the first 10 min and then saturates. The probability that neurons in E_hc fire in response to a synchronous stimulation event mediated by E_stim remains at base level (i.e., determined by the network firing rate of ≈10 Hz) throughout the simulation. The weight distributions between all groups are very similar (see Figure 6D).

FIGURE 6

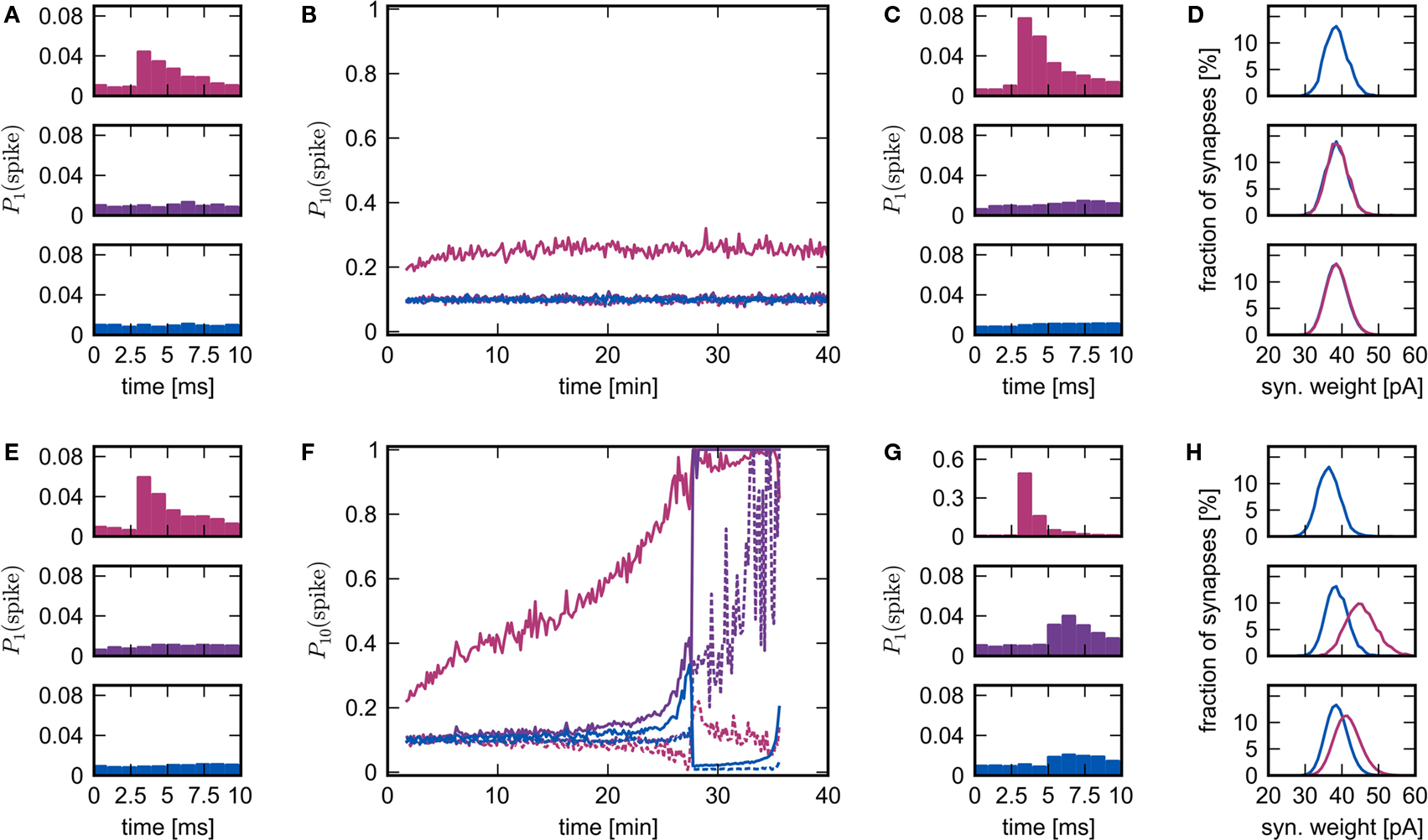
Figure 6. Evolution of network response to synchronous stimulus. (A) Probability of emitting a spike after a synchronous event in the first 10 s of stimulation for the stimulated group (top), the high-connectivity group (middle) and the random group (bottom) for N_SIP = 20 and N_stim = 164. (B) Evolution of the probability of emitting a spike in the 10 ms immediately before (dashed lines) or immediately after a synchronous event (solid lines) in successive 10 s periods. Colors as in (A). (C) As in (A) but for the 10 s period following 25 min of simulation. (D) Distribution of incoming synaptic weights at 25 min for the stimulated group (top) from the random group (blue), the synaptic weight distribution from the external group (mean 56.9 pA) is not shown; for the high-connectivity group (middle) from the random group (blue) and the stimulated group (pink); for the random group (bottom) from the random group (blue) and the stimulated group (pink). (E–H): As for (A–D) but for N_SIP = 25 and N_stim = 228. The synaptic weight distribution from the external group to the stimulated group (mean 161.4 pA) is not shown in the top panel of (H).

In the lower panel, N_SIP = 25, N_stim = 228 and N_hc = 228. Each neuron in E_hc receives 25 or more synaptic inputs from E_stim, whereas all other excitatory neurons in the network receive 24 or fewer inputs from E_stim and on average 14. The probability that neurons in E_stim fire in response to a synchronous stimulation event increases steadily over the course of the simulation until almost all neurons are firing in response to every synchronous event. The probability that neurons in E_hc fire in response to a synchronous stimulation event, mediated by E_stim, remains at approximately base level for the first 20 min. Between 20 and 25 min, the probability of response increases sharply. However, the probability that neurons randomly selected from the rest of the network fire in response to a synchronous stimulation event also increases sharply during this period. This is reflected in the weight distributions. The middle panel of Figure 6H shows the distribution of incoming synaptic weights to the high-connectivity group E_hc. The mean of the distribution of weights between E_stim and E_hc shifts to a higher value than that between randomly selected neurons and E_hc, as seen in Figure 2B. However, the same is true to a lesser extent for the distributions of the incoming weights to the random group (bottom panel of Figure 6H). Note that the mean of the distribution of the incoming synaptic weights to the stimulated group from the rest of the network has shifted to a lower value (top panel of Figure 6H) due to the acausal correlation between activity in the network and activity in the stimulated group. If the synapses from E_SIP to E_stim are clipped to an upper bound, this drift eventually leads to a decoupling of the stimulated group, as was reported in Morrison et al. (2007). However, the insight that STDP reduces the strength of recurrent connections was originally described by Abbott and Nelson (2000), and more recently proved for polysynaptic loops of arbitrary length by Kozloski and Cecchi (2010).

Between 27 and 28 min the increasing response of the network to synchronous events causes it to enter a pathological state in which some neurons are firing very rapidly all the time and some are almost silent. The theoretical model developed in Section 3.1 does not predict the occurrence or the characteristics of the pathological state, as it does not take into account the interactions between neurons in the network, only the interactions between a synchronously firing group and its post-synaptic targets.

To test the conclusion that the introduction of homeostatic mechanisms do not alter the nature of the fixed point, we repeat the above experiments with pre-synaptic homeostasis. Every 3 s the outgoing synapses of every excitatory neuron in the recurrent network are adjusted by a multiplicative factor such that the total sum of its plastic synapses is reset. Similarly to the results obtained without homeostasis, synchronous stimulation from a group of N_SIP = 20 external neurons is neither enough to produce a reliable response of the stimulated group (N_stim = 164) nor any substantial changes in the high-connectivity group (N_hc = 158), whereas a slightly stronger stimulus (N_SIP = 25, N_stim = 228, N_hc = 228) causes a network to enter a pathological state (see Figures 7A,B). The transition occurs much later, at around 90 min rather than 28 min in the absence of homeostasis, demonstrating the stabilizing effect of the weight normalization. Unlike the results shown in Figure 6F for pure STDP, as soon as the stimulated group reflects the stimulus with sufficient reliability, a clear difference between the response likelihood of the high-connectivity group and the network as a whole can be observed. The high response likelihood of the high-connectivity group breaks down rapidly when the network starts responding more strongly to the synchronous stimulation at around 60 min. This is another example of the decoupling of a synchronously active group from its embedding network as described above and in Morrison et al. (2007). As the response to the synchronous stimulus of the network generally lags behind the response in the high-connectivity group, acausal correlations are generated in the incoming synapses of the high-connectivity group. As the synaptic weights decrease, so does the mean membrane potential, thus diminishing the response of the neurons to the synchronous stimulus events. The stimulated group E_stim does not decouple in this fashion because the increasing strength of the connections from the external input can compensate for the loss of input from the recurrent network.

FIGURE 7

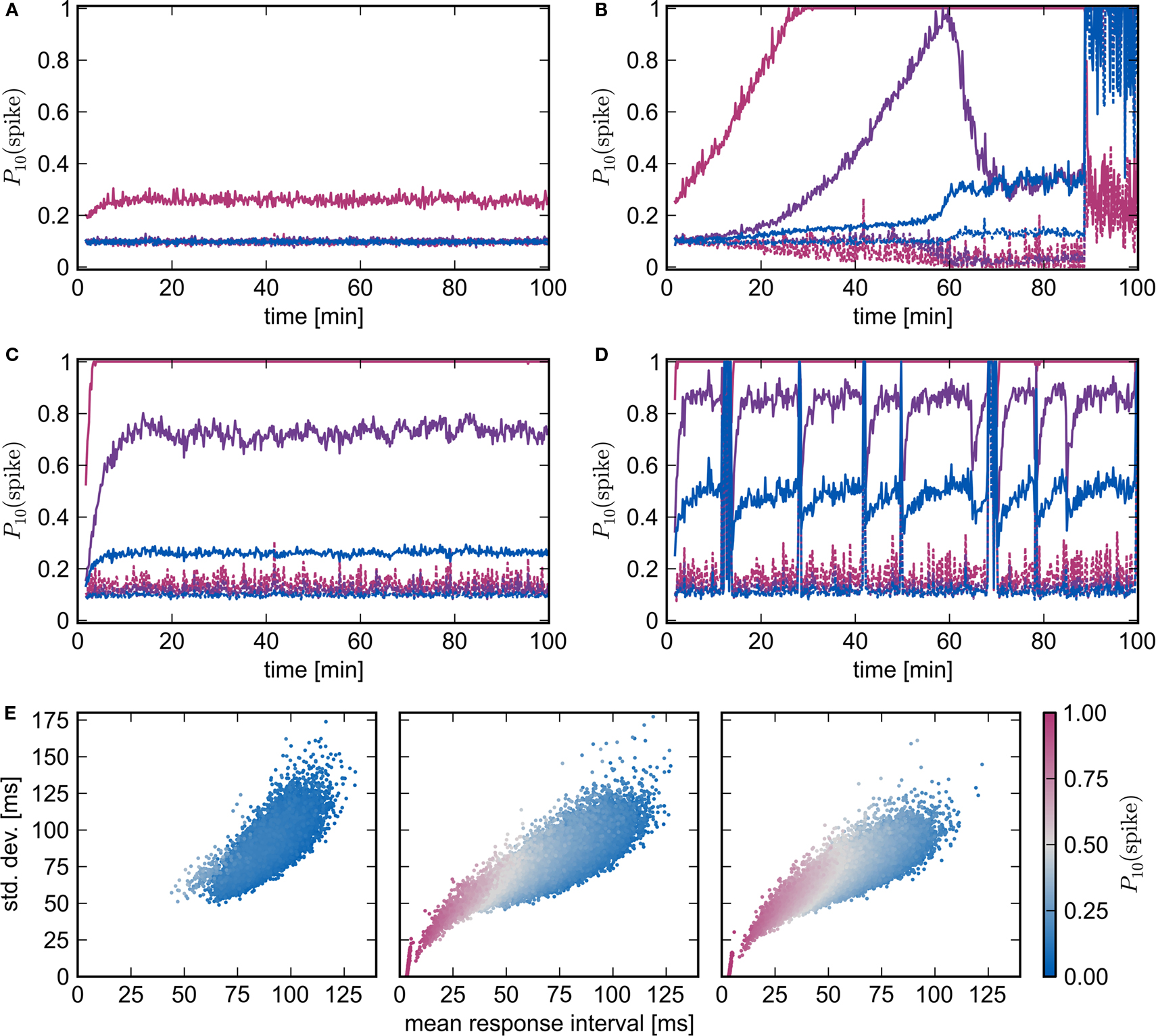
Figure 7. Spike-timing dependent plasticity and homeostasis. (A,B) Evolution of network response to synchronous stimulus where STDP synapses in the recurrent network are subject to weight normalizing pre-synaptic homeostasis for N_SIP = 20, N_stim = 164, N_hc = 158 and N_SIP = 25, N_stim = 228, N_hc = 228, respectively. Probability of emitting a spike in the 10 ms immediately before (dashed lines) or immediately after a synchronous event (solid lines) in successive 10 s periods for the stimulated group (pink), the high-connectivity group (purple) and the random group (blue). (C,D) As in (A,B) but for pre- and post-synaptic homeostasis; N_SIP = 50, N_stim = 584, N_hc = 576 and N_SIP = 75, N_stim = 961, N_hc = 963, respectively. (E) Response latency and reliability for a network with STDP, pre- and post-synaptic homeostasis. Mean and SD of the response interval for each excitatory neuron to each synchronous event in the 26th minute (left, middle) or 21st minute (right). Marker color indicates the likelihood of the neuron to fire within 10 ms of a synchronous event. From left to right the panels correspond to N_SIP = 20, 50, 75 and N_stim = 164, 584, 961.

Figures 7C,D show the development of the response likelihood when post-synaptic homeostasis is also applied, such that the total strength of incoming and outgoing synapses are normalized alternately every 1.5 s. The network behavior is much more stable. The network remains in a stable asynchronous irregular activity regime even when an external group of size N_SIP = 50 stimulates a group of N_stim = 584 excitatory neurons (Figure 7C). However, the response probability of the high-connectivity group (N_hc = 576) saturates at a lower level than the maximum response likelihood reached in Figure 7B with purely pre-synaptic homeostasis. Although increasing N_SIP increases the number of neurons in E_stim available to drive a potential high-connectivity group E_hc, it also increases the size of E_hc. In the presence of pre-synaptic homeostasis, this reduces the mean strength of the connections between E_stim and E_hc.

Synchronous stimulation from an external group of size N_SIP = 75 drives the network into a pathological state despite the homeostasis as can be seen in Figure 7D. The interaction between the homeostasis and the strong stimulus sets up an oscillatory behavior in which the network repeatedly enters a pathological state but is reset by the application of homeostasis. Between pathological interludes, all neurons have a high probability of responding to a synchronous stimulus. The absence of clearly defined neuronal groups can be seen in Figure 7E. In the left panel, the network with STDP, pre- and post-synaptic homeostasis shows little response to synchronous stimulation by a small group of N_SIP = 20 external neurons: the average latency is approximately the inter-spike interval of the network background rate. The middle and the left panel correspond to Figures 7C,D, i.e., synchronous stimulation by much larger external groups of N_SIP = 50 and N_SIP = 75 neurons, respectively. The neurons of the stimulated group (N_stim = 584 and N_stim = 961) can be seen to have separated themselves and respond quickly and reliably to the synchronous stimulus. The mean response latency shifts to an earlier value and the mean SD of the latency is reduced, demonstrating that the network as a whole responds earlier and more reliably to the stronger stimulus. Those neurons that respond earliest also have the lowest SD and are thus most likely to respond within 10 ms of a synchronous stimulus. However, there is no separation of a second group from the mass. We therefore conclude that no development of feed-forward structure can be observed, even in the presence of pre- and post-synaptic homeostasis and strong synchronous stimulus.

4 Discussion

We have developed a simple model using a mean field approach and a linear neuron model to investigate the propagation of feed-forward structure in plastic recurrent networks. The key prediction of the model is that the number of neurons recruited by a repeated synchronous stimulus protocol is subject to an unstable fixed point. A synchronously firing group of neurons of a size below that of the fixed point recruits a smaller group, leading to a failure of the structure to propagate, whereas a synchronously firing group of a size above that of the fixed point recruits a larger group, causing the whole network to be recruited. In other words, a repeated synchronous stimulus is always either not enough or too much. We demonstrated by simulation that a large-scale network behaves as predicted by the mean field theory.

The existence of the unstable fixed point is robust. Employing a different weight-dependent STDP model, altering the input rates or introducing homeostatic mechanisms, e.g., regulating incoming synapses so as to maintain the total synaptic strength or post-synaptic rate, only influences the dynamics quantitatively. The unstable fixed point can be shifted to a larger or smaller group size, but it cannot be turned into a stable fixed point. The instability arises through the combination of a binomial distribution of connections from a given synchronously active group with the smooth change of the stable fixed point in the synaptic weight distribution as a function of the number of synchronous connections. Thus, any change to the model assumptions which does not produce a qualitative change in at least one of these factors will produce similar results, e.g., distributing the conduction delays or defining the conduction delay to be largely axonal, although such adaptations of the network model may well suppress or alter the pathological state the network enters when the amount of stimulation is too high (see Lubenov and Siapas, 2008). As an example, we demonstrated that the introduction of pre- and post-synaptic homeostatic mechanisms that maintain the total strength of outgoing and incoming recurrent synapses makes the network more stable, but does not enable the development of feed-forward structures.

Stable propagation of feed-forward structure is only possible if one or more of our assumptions are false. Other simulation studies have previously reported structure development (Hertz and Prügel-Bennet, 1996; Levy et al., 2001; Izhikevich et al., 2004; Doursat and Bienenstock, 2006; Jun and Jin, 2007; Masuda and Kori, 2007; Hosaka et al., 2008; Liu and Buonomano, 2009; Fiete et al., 2010). However, it is our contention that the risk of non-generalizable results is high when studying networks that are small, have few incoming synapses per neuron, or assume STDP rules that are independent of the synaptic weight. Each neuron in our network model receives a biologically realistic number of inputs (6000) and the network exhibits a biologically realistic degree of sparseness (connection probability of 0.06), while our model of STDP reproduces the experimentally found weight dependence of the amount of potentiation and depression a synapse undergoes (Bi and Poo, 1998; Morrison et al., 2007). We therefore suggest that the previously reported development of structure be considered artifactual until a greater degree of validation can be obtained. In our view, a weak proof of principle would be the demonstration of bounded structural growth in a network model with at least as great a degree of biological realism as in our study with respect to connectivity and plasticity, with additional assumptions that at least do not contradict experimental findings. A stronger, more convincing, proof would be provided by such a network model in which the additional assumptions are experimentally motivated.

Given that the brain does develop stable signal pathways, there is every reason to expect that a network model can be developed that fulfills these criteria for a strong proof of principle. One indication that the model we have investigated is overly simplified is that the combination of network structure, neuronal dynamics and plasticity leads to a symmetrical distribution of synaptic weights, rather than the skewed distribution observed experimentally (Sjöström et al., 2001). Therefore, a promising candidate adaptation that might result in a stable fixed point and thus stable propagation of feed-forward structure is the initial connectivity of the network. Here, we assume a random graph; however, the cortical network consists of several layers with layer-specific connectivity and exhibits long range patchy connections (Lewis et al., 2002; Schüz and Braitenberg, 2002; Thomson and Bannister, 2003; Binzegger et al., 2004). A more realistic graph structure might eliminate the “fan-out” tendency that underlies the instability of the fixed point. Such adaptations may also entail the use of a more complex neuron model than assumed here. Kumar et al. (2008) demonstrated that the regime enabling stable propagation activity in a feed-forward sub-network embedded in a locally connected random network is much greater for a conductance-based neuron model than previously found for a current-based model (Mehring et al., 2003). Moreover, a more sophisticated neuron model, particularly with respect to the dendritic integration of inputs, might exhibit greater symmetry breaking properties.

Another candidate is the formulation of the STDP rule. Although we have shown that our results are robust to the choice of update rule, we have only considered extremely simplified models of STDP exclusively at excitatory–excitatory synapses; the role of plasticity at inhibitory synapses is neglected. We addressed models in which the STDP window is fitted by two exponential functions, which is easy to analyze but may be too simplistic. Further, we have so far only considered rules based on pairs of spikes. Pfister and Gerstner (2006) introduced a rule based on triplets of spikes which accounts for experimental findings on the dependence of the weight change on the frequency of the pairing protocols (Sjöström et al., 2001). The triplet model has been shown to map to the BCM rule (Bienenstock et al., 1982) and to give near-optimal information transmission when combined with spike-frequency adaptation in the post-synaptic neuron (Hennequin et al., 2010). The triplet interaction could well also prove to be important for the development of structure. Moreover, recent experimental findings reveal that neuromodulation can influence STDP. Seol et al. (2007) showed that the polarity of the STDP window depends on the activation of receptors sensitive to cholinergic and adrenergic activity. A recent study by Kozloski and Cecchi (2010) demonstrated that polysynaptic loops eliminated by standard STDP can be restored by such a reversed rule. This finding suggests that the interaction of causal and anti-causal windows may indeed result in the kind of symmetry breaking that would enable groups of neurons to develop a qualitatively different response to a given synchronous stimulus. Neuromodulation can also be essential either for inducing STDP or for altering the threshold for induction, see Pawlak et al. (2010) in this special issue for a review. Finally, our theoretical approach does not take into account interactions of STDP with other forms of plasticity except post-synaptic homeostasis. Although no development of feed-forward structure occurs in our homeostatically regulated network models, the presence of homeostasis certainly has a strong stabilizing effect on the network dynamics. Therefore, homeostasis may be a crucial element that enables network dynamics to be maintained during stimulus-driven development of structure. Short-term plasticity is another feature overlooked in the current study. The interaction of STDP with depression and facilitation could result in different network dynamics that would be more favorable to symmetry breaking, as could the incorporation of tagging processes to stabilize the developed structures (Frey and Morris, 1997; Reymann and Frey, 2007; Clopath et al., 2008). We therefore conclude that the development and investigation of more sophisticated models of STDP that interact with other forms of plasticity on different time scales would be a useful future extension of this research.

A third area in which the model presented here could be adapted is the stimulus protocol. Here, we investigated whether structure can develop from the seed of a single correlated group. Several forms of synaptic pathway organization have been identified and mathematically analyzed for recurrent networks under the assumption that they receive input from more than one pool of correlated inputs (e.g., Gilson et al., 2009b,c; see Gilson et al., 2010 for a thorough review). However, the majority of the findings assume STDP that is independent of the synaptic weight or only very weakly dependent. Moreover, only small networks are considered in which each neuron receives external correlated input. It will therefore be interesting to discover how these results scale up to the large, sparsely connected networks with weight-dependent plasticity considered in this article.

These candidate adaptations are not intended to be exhaustive. There are many ways in which the theoretical approach and network model presented here could be improved and supplemented. However, we hope that the suggestions above can serve to stimulate research to reveal the necessary and sufficient conditions for the development of structure in the mammalian brain.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Partially funded by DIP F1.2, BMBF Grant 01GQ0420 to BCCN Freiburg, EU Grant 15879 (FACETS), EU Grant 269921 (BrainScaleS), Helmholtz Alliance on Systems Biology (Germany), Next-Generation Supercomputer Project of MEXT (Japan), Neurex, and the Junior Professor Program of Baden-Württemberg. High-performance computing facilities were made available through the Norwegian Metacenter for Computational Science (Notur) and JUGENE Grant JINB33 at the Research Center Jülich. We gratefully acknowledge T. Potjans for his help in determining appropriate connectivity levels for our network model and S. Jahnke for his comments on an earlier version of the manuscript.

References

Abbott, L. F., and Nelson, S. B. (2000). Synaptic plasticity: taming the beast. Nat. Neurosci. 3(Suppl.), 1178–1183.

Abeles, M. (1991). Corticonics: Neural Circuits of the Cerebral Cortex, 1st Edn. Cambridge: Cambridge University Press.

Abeles, M., Bergman, H., Margalit, E., and Vaadia, E. (1993). Spatiotemporal firing patterns in the frontal cortex of behaving monkeys. J. Neurophysiol. 70, 1629–1638.

Pubmed Abstract | Pubmed Full Text

Bi, G.-Q., and Poo, M.-M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472.

Pubmed Abstract | Pubmed Full Text

Bienenstock, E. (1995). A model of neocortex. Network 6, 179–224.

CrossRef Full Text

Bienenstock, E. L., Cooper, L. N., and Munro, P. W. (1982). Theory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex. J. Neurosci. 2, 32–48.

Pubmed Abstract | Pubmed Full Text

Binzegger, T., Douglas, R. J., and Martin, K. A. C. (2004). A quantitative map of the circuit of cat primary visual cortex. J. Neurosci. 39, 8441–8453.

Brunel, N. (2000). Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 8, 183–208.

Pubmed Abstract | Pubmed Full Text

Clopath, C., Ziegler, L., Vasilaki, E., Büsing, L., and Gerstner, W. (2008). Tag-trigger-consolidation: a model of early and late long-term-potentiation and depression. PLoS Comput. Biol. 4, e1000248. doi: 10.1371/journal.pcbi.1000248

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Debanne, D., Gähwiler, B. H., and Thompson, S. M. (1996). Cooperative interactions in the induction of long-term potentiation and depression of synaptic excitation between hippocampal CA3-CA1 cell pairs in vitro. Proc. Natl. Acad. Sci. U.S.A. 93, 11225–11230.

Pubmed Abstract | Pubmed Full Text

Debanne, D., Gähwiler, B. H., and Thompson, S. M. (1999). Heterogeneity of synaptic plasticity at unitary CA1-CA3 and CA3-CA3 connections in rat hippocampal slice cultures. J. Neurosci. 19, 10664–10671.

Pubmed Abstract | Pubmed Full Text

Diesmann, M., Gewaltig, M.-O., and Aertsen, A. (1999). Stable propagation of synchronous spiking in cortical neural networks. Nature 402, 529–533.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Doursat, R., and Bienenstock, E. (2006). “Neocortical self-structuration as a basis for learning,” in 5th International Conference on Development and Learning (ICDL 2006), Indiana University, Bloomington, IN.

Eckhorn, R., Bauer, R., Jordan, W., Brosch, M., Kruse, W., Munk, M., and Reitböck, H. J. (1988). Coherent oscillations: a mechanism of feature linking in the visual cortex? Biol. Cybern. 60, 121–130.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fiete, I. R., Senn, W., Wang, C. Z. H., and Hahnloser, R. H. R. (2010). Spike-time-dependent plasticity and heterosynaptic competition organize networks to produce long scale-free sequences of neural activity. Neuron 65, 563–576.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Frey, U., and Morris, R. (1997). Synaptic tagging and long-term potentiation. Nature 385, 533–536.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gerstner, W., Ritz, R., and van Hemmen, J. (1993). Why spikes? Hebbian learning and retrieval of time-resolved excitation patterns. Biol. Cybern. 69, 503–515.

Pubmed Abstract | Pubmed Full Text

Gewaltig, M.-O., and Diesmann, M. (2007). NEST (Neural Simulation Tool). Scholarpedia 2, 1430.

Gewaltig, M.-O., Diesmann, M., and Aertsen, A. (2001). Propagation of cortical synfire activity: survival probability in single trials and stability in the mean. Neural Netw. 657–673.

Pubmed Abstract | Pubmed Full Text

Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2009a). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. I. Input selectivity – strengthening correlated input pathways. Biol. Cybern. 101, 81–102.

CrossRef Full Text

Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2009b). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. II. Input selectivity – symmetry breaking. Biol. Cybern. 101, 103–114.

CrossRef Full Text

Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A., and van Hemmen, J. L. (2009c). Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks IV. Structuring synaptic pathways among recurrent connections. Biol. Cybern. 101, 427–444.

CrossRef Full Text

Gilson, M., Burkitt, A. N., and van Hemmen, J. L. (2010). STDP in recurrent neuronal networks. Front. Comput. Neurosci. 4:23. doi: 10.3389/fncom.2010.00023

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gray, C. M., and Singer, W. (1989). Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc. Natl. Acad. Sci. U.S.A. 86, 1698–1702.

Pubmed Abstract | Pubmed Full Text

Gustafsson, B., Wigstrom, H., Abraham, W. C., and Huang, Y.-Y. (1987). Long-term potentiation in the hippocampus using depolarizing current pulses as the conditioning stimulus to single volley synaptic potentials. J. Neurosci. 7, 774–780.

Pubmed Abstract | Pubmed Full Text

Gütig, R., Aharonov, R., Rotter, S., and Sompolinsky, H. (2003). Learning input correlations through nonlinear temporally asymmetric Hebbian plasticity. J. Neurosci. 23, 3697–3714.

Pubmed Abstract | Pubmed Full Text

Hahnloser, R. H., Kozhevnikov, A. A., and Fee, M. S. (2002). An ultra-sparse code underlies the generation of neural sequences in a songbird. Nature 419, 65–70.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hayon, G., Abeles, M., and Lehmann, D. (2004). Modeling compositionality by dynamic binding of synfire chains. J. Comput. Neurosci. 17, 179–201.

Pubmed Abstract | Pubmed Full Text

Hebb, D. O. (1949). The Organization of Behavior: A Neuropsychological Theory. New York: John Wiley and Sons.

Hennequin, G., Gerstner, W., and Pfister, J.-P. (2010). STDP in adaptive neurons gives close-to-optimal information transmission. Front. Comput. Neurosci. 4:143. doi: 10.3389/fncom.2010.00143

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hertz, J., and Prügel-Bennet, A. (1996). Learning synfire-chains by self-organization. Network 7, 357–363.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hosaka, R., Araki, O., and Ikeguchi, T. (2008). STDP provides the substrate for igniting synfire chains by spatiotemporal input patterns. Neural Comput. 20, 415–435.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Iglesias, J., Eriksson, J., Grize, F., Tomassini, M., and Villa, A. (2005). Dynamics of pruning in simulated large-scale spiking neural networks. Biosystems 79, 11–20.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ikegaya, Y., Aaron, G., Cossart, R., Aronov, D., Lampl, I., Ferster, D., and Yuste, R. (2004). Synfire chains and cortical songs: temporal modules of cortical activity. Science 5670, 559–564.

CrossRef Full Text

Izhikevich, E. M., Gally, J. A., and Edelman, G. M. (2004). Spike-timing dynamics of neuronal groups. Cereb. Cortex 14, 933–944.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jun, J. K., and Jin, D. Z. (2007). Development of neural circuitry for precise temporal sequences through spontaneous activity, axon remodeling, and synaptic plasticity. PLoS ONE 2, e723. doi: 10.1371/journal.pone.0000723

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kempter, R., Gerstner, W., and van Hemmen, J. L. (1999). Hebbian learning and spiking neurons. Phys. Rev. E 59, 4498–4514.

Kempter, R., Gerstner, W., and van Hemmen, J. L. (2001). Intrinsic stabilization of output rates by spike-based Hebbian learning. Neural Comput. 12, 2709–2742.

CrossRef Full Text

Kistler, W. M., and van Hemmen, J. L. (2000). Modeling synaptic plasticity in conjunction with the timing of pre- and postsynaptic action potentials. Neural Comput. 12, 385–405.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kozhevnikov, A., and Fee, M. S. (2007). Singing-related activity of identified HVC neurons in the zebra finch. J. Neurophysiol. 97, 4271–4283.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kozloski, J., and Cecchi, G. A. (2010). A theory of loop formation and elimination by spike timing-dependent plasticity. Front. Neural Circuits 4:7. doi: 10.3389/fncir.2010.00007

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kuhn, A., Aertsen, A., and Rotter, S. (2003). Higher-order statistics of input ensembles and the response of simple model neurons. Neural Comput. 1, 67–101.

CrossRef Full Text

Kumar, A., Rotter, S., and Aertsen, A. (2008). Conditions for propagating synchronous spiking and asynchronous firing rates in a cortical network model. J. Neurosci. 28, 5268–5280.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Levy, N., Horn, D., Meilijson, I., and Ruppin, E. (2001). Distributed synchrony in a cell assembly of spiking neurons. Neural Netw. 14, 815–824.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lewis, D., Melchitzky, D., and Burgos, G.-G. (2002). Specificity in the functional architecture of primate prefontal cortex. J. Neurocytol. 31, 265–276.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Liu, J. K., and Buonomano, D. V. (2009). Embedding multiple trajectories in simulated recurrent neural networks in a self-organizing manner. J. Neurosci. 29, 13172–13181.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lubenov, E. V., and Siapas, A. G. (2008). Decoupling through synchrony in neuronal circuits with propagation delays. Neuron 58, 118–131.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Markram, H., Lübke, J., Frotscher, M., and Sakmann, B. (1997). Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Markram, H., and Sakmann, B. (1995). Action potentials propagating back into dendrites trigger changes in efficacy of single-axon synapses between layer V pyramidal neurons. Soc. Neurosci. Abstr. 21, 2007.

Masuda, N., and Kori, H. (2007). Formation of feedforward networks and frequency synchrony by spike-timing-dependent plasticity. J. Comput. Neurosci. 22, 327–345.

Pubmed Abstract | Pubmed Full Text

Mehring, C., Hehl, U., Kubo, M., Diesmann, M., and Aertsen, A. (2003). Activity dynamics and propagation of synchronous spiking in locally connected random networks. Biol. Cybern. 88, 395–408.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Migliore, M., Cannia, C., Lytton, W. W., Markram, H., and Hines, M. (2006). Parallel network simulations with neuron. J. Comput. Neurosci. 21, 119–223.

Pubmed Abstract | Pubmed Full Text

Montgomery, J., Pavlidis, P., and Madison, D. (2001). Pair recordings reveal all-silent synaptic connections and the postsynaptic expression of long-term potentiation. Neuron 29, 691–701.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Morrison, A., Aertsen, A., and Diesmann, M. (2007). Spike-timing dependent plasticity in balanced random networks. Neural Comput. 19, 1437–1467.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Morrison, A., Diesmann, M., and Gerstner, W. (2008). Phenomenological models of synaptic plasticity based on spike-timing. Biol. Cybern. 98, 459–478.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Morrison, A., Mehring, C., Geisel, T., Aertsen, A., and Diesmann, M. (2005). Advancing the boundaries of high connectivity network simulation with distributed computing. Neural Comput. 17, 1776–1801.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nordlie, E., Plesser, H. E., and Gewaltig, M.-O. (2009). Towards reproducible descriptions of neuronal network models. PLoS Comput. Biol. 5, e1000456. doi: 10.1371/journal.pcbi.1000456

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pawlak, V., Wickens, J. R., Kirkwood, A., and Kerr, J. N. D. (2010). Timing is not everything: neuromodulation opens the STDP gate. Front. Syn. Neurosci. 2:146. doi: 10.3389/fnsyn.2010.00146

CrossRef Full Text

Pecevski, D., Natschläger, T., and Schuch, K. (2009). PCSIM: a parallel simulation environment for neural circuits fully integrated with python. Front. Neuroinform. 3:11. doi: 10.3389/neuro.11.011.2009

CrossRef Full Text

Pfister, J.-P., and Gerstner, W. (2006). Triplets of spikes in a model of spike timing-dependent plasticity. J. Neurosci. 26, 9673–9682.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Prut, Y., Vaadia, E., Bergman, H., Haalman, I., Hamutal, S., and Abeles, M. (1998). Spatiotemporal structure of cortical activity: Properties and behavioral relevance. J. Neurophysiol. 79, 2857–2874.

Pubmed Abstract | Pubmed Full Text

Pulvermüller, F., and Shtyrov, Y. (2009). Spatiotemporal signatures of large-scale synfire chains for speech processing as revealed by MEG. Cereb. Cortex 19, 79–88.

Pubmed Abstract | Pubmed Full Text

Reymann, K. G., and Frey, J. U. (2007). The late maintenance of hippocampal LTP: Requirements, phases, “synaptic tagging,” “late-associativity” and implications. Neuropharmacology 52, 24–40.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rubin, J., Lee, D., and Sompolinsky, H. (2001). Equilibrium properties of temporally asymmetric Hebbian plasticity. Phys. Rev. Lett. 86, 364–367.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schüz, A., and Braitenberg, V. (2002). “The human cortical white matter: quantitative aspects of cortico-cortical long-range connectivity,” in Cortical Areas: Unity and Diversity, Chapter 16, eds A. Schüz and R. Miller (London: Taylor and Francis), 377–385.

Pubmed Abstract | Pubmed Full Text

Seol, G., Ziburkus, J., Huang, S., Song, L., Kim, I., Takamiya, K., Huganir, R., Lee, H.-K., and Kirkwood, A. (2007). Neuromodulators control the polarity of spike-timing-dependent plasticity. Neuron 55, 919–929.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sjöström, P., Turrigiano, G., and Nelson, S. (2001). Rate, timing, and cooperativity jointly determine cortical synaptic plasticity. Neuron 32, 1149–1164.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Song, S., Miller, K. D., and Abbott, L. F. (2000). Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926.

Pubmed Abstract | Pubmed Full Text

Song, S., Sjöström, P. J., Reigl, M., Nelson, S., and Chklovskii, D. B. (2005). Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 3, e350. doi: 10.1371/journal.pbio.0030350

CrossRef Full Text

Standage, D., Jalil, S., and Trappenberg, T. (2007). Computational consequences of experimentally derived spike-time and weight dependent plasticity rules. Biol. Cybern. 96, 615–623.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Thomson, A. M., and Bannister, P. (2003). Interlaminar connections in the neocortex. Cereb. Cortex 13, 5–14.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Turrigiano, G. G., Leslie, K. R., Desai, N. S., Rutherford, L. C., and Nelson, S. B. (1998). Activity-dependent scaling of quantal amplitude in neocortical neurons. Nature 391, 892–896.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van Rossum, M. C. W., Bi, G.-Q., and Turrigiano, G. G. (2000). Stable Hebbian learning from spike timing-dependent plasticity. J. Neurosci. 20, 8812–8821.

Pubmed Abstract | Pubmed Full Text

Wang, H.-X., Gerkin, R. C., Nauen, D. W., and Bi, G.-Q. (2005). Coactivation and timing-dependent integration of synaptic potentiation and depression. Nat. Neurosci. 8, 187–193.

Pubmed Abstract | Pubmed Full Text

Zou, Q., and Destexhe, A. (2007). Kinetic models of spike-timing dependent plasticity and their functional consequences in detecting correlations. Biol. Cybern. 97, 81–97.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text