Inferring synaptic connectivity from spatio-temporal spike patterns

1 Introduction

Reconstructing or reverse-engineering the exact interaction topology of coupled dynamical units has become an active area of research in different fields of biology, including genetics, ecology, and neuroscience (see Yeung et al., 2002; Makarov et al., 2005; Cadenasso et al., 2006, for recent theoretical results). In neuroscience, such efforts generally focus on establishing the functional or effective connectivity between individual neurons and different regions of the brain using methods based on correlations in the activity between the constituent parts of the network (Aertsen and Gerstein, 1985; Aertsen et al., 1989). This research has yielded many valuable results, commonly on a scale larger than the individual elements such as nerve cells and synaptic connections that make up the networks involved (Jirsa and McIntosh, 2007).

Explicit approaches that reconstruct actual connections between individual elements are more difficult in general, but where feasible they offer exact, fine-grained results, for instance by establishing the presence or absence of individual synapses. These more detailed approaches have attracted serious attention recently, triggered by the availability of large high-resolution data sets and the computational power to handle them. Noteworthy from a theoretical point of view is a method of stochastic optimization (Makarov et al., 2005) that fits a network model of spiking leaky integrate-and-fire (LIF) neurons to an oncoming data stream and thus avoids estimating parameters beforehand. The performance of this reconstruction method has been addressed for simulated, as well as real, extracellular multiunit array (MUA) recordings. The computational requirements seem however somewhat prohibitive as the largest network which Makarov et al. report having reconstructed consists of N = 5 neurons.

Other studies have focused on networks of smoothly coupled units. One of the earlier results in this regard is a synchronization method presented by Yu et al. (2006). Assuming pre-knowledge of all model parameters, a second network of the same units is set up as a model, and its interaction topology is varied via continual error minimization until it synchronizes with the original system. Via a thresholding process, the resulting topology is identified as that of the original network. This approach has been shown to perform well for networks of up to N = 16 nodes. Yu and Parlitz (2008) combine the basic idea of error minimization with an intricate mechanism for driving the network to a steady state, at which point the connectivity can be recovered from the individual node dynamics. Since this technique dispenses with the need to explicitly model the connectivity of the network they are able to achieve reconstructions of significantly larger networks (N = 50).

An alternative approach for smoothly coupled systems close to steady states (Timme, 2007) uses measurements of the collective response–dynamics under different external driving conditions. As the collective dynamics depends on both the (known) driving signals and the (unknown) interaction topology, an increasing number of driving–response experiments yields more and more restrictions on the topology. Worked out explicitly for phase-locking oscillators, the method is insensitive to details of the units’ dynamics and their coupling function and a linear approximation is often sufficient to infer the topology. Hence, the experiments yield a system of linear equations that restrict the topology consistent with all experiments that is then solved to obtain the incoming connections for each unit. This approach has been successfully applied to Kuramoto oscillators, where networks of many hundreds of units were reconstructed. Assuming sparsity of the network connectivity, such reconstructions may be supplemented by an optimization step (Timme, 2007) that reduces the number of experiments needed to reconstruct up to a desired accuracy (cf. also Yeung et al., 2002; Napoletani and Sauer, 2008). Since all experimental approaches in practice have to deal with a systematic undersampling with regard to finite measurement times and the number of neurons that can be reliably recorded, such optimization methods are likely a necessary step in any potentially useful algorithm.

Here, we present a method to explicitly reconstruct both topology and connection weights for networks of LIF neurons. LIF neurons with current-based synapses incorporate two key features of biological neurons: they integrate the input currents of their presynaptic neurons and send spikes whenever this accumulated and filtered input sufficiently depolarizes the membrane potential V(t). Though this class of LIF neurons lacks a lot of biophysical detail such as the spike dynamics itself, voltage-dependent integration properties, or neuronal morphology, their study can help to understand biologically relevant collective dynamic states of neuronal networks, such as population rate oscillations (Brunel and Hakim, 1999; Brunel, 2000), propagation of synchronous activity volleys (Diesmann et al., 1999), or asynchronous irregular activity states (Brunel, 2000; Jahnke et al., 2009). Moreover, they are simple enough to be amenable to analytical methods and thus reveal principle insights regarding relations between network interactions and dynamics. In general, the collective dynamics of even simple networks of LIF neurons can be highly complex, depending not only on interaction topology but also on synaptic coupling strengths, local neuron parameters, and initial conditions (van Vreeswijk and Sompolinsky, 1996; Timme et al., 2002; Denker et al., 2004; Zillmer et al., 2009).

The method presented here is in part an extension to pulse-coupled, spiking units of the driving–response approach for smoothly coupled phase-oscillators given by Timme (2007). In particular, it uses the information provided by spike times and model parameters only. Moreover, the method developed here does not require steady states as in Timme (2007) or Yu and Parlitz (2008), but works as well for complex spatio-temporal activity, such as irregular or even chaotic spiking, given that certain technical conditions are met. The robust optimization technique (Yeung et al., 2002; Timme, 2007; Napoletani and Sauer, 2008) can be applied here as well, to reconstruct networks of several hundred nodes from a comparably small number of experiments with only a small loss of accuracy.

Biological neuronal networks naturally present much more challenging problems for reconstruction than moderately sized networks of model neurons. The technique presented here should hence not be considered as a substitute to current approaches that work with spiking data from experiments, but as a theoretical complement. This notwithstanding, it has the advantage that it does not depend on continual access to the actual membrane potentials. Since in practice intracellular recordings from a large group of neurons are still beyond technical feasibility, in general any method that restricts itself to spike time data has strong merits. In this sense it presents a necessary first step toward a robust explicit method that could be used in tandem with larger-scale statistical methods.

In Section 2 we will provide necessary definitions and derivations for the LIF neuron, and then outline the basic method as it applies to exact data and known model parameters. In Section 3 we will discuss implementation and performance of the method in several contexts such as algorithmic efficiency, data requirements, and the effect of noise and uncertainty on reconstruction accuracy. In Section 4 possible extensions and applications of the method will be noted.

2 Neuron Model and Reconstruction Theory

2.1 Dynamics and Collective Solution between Subsequent Spikes

The subthreshold dynamics of the membrane potential V_i(t) of a LIF neuron i is given by the linear ordinary differential equation

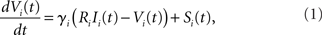
where γ_i is the inverse of the membrane time constant, R_i is the membrane resistance, I_i(t) is a temporally constant, externally applied stimulation current, and S_i(t) represents recurrent network interactions. Whenever V_i(t) crosses the threshold value V_T,i neuron i sends a spike to its postsynaptic neighbors and V_i reverts to the neuron’s reset potential V_R,i < V_T,i. The interaction between neurons within the network is hence represented by the weighted δ-pulse function

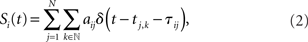
in which t_j,k denotes the k-th spike time of neuron j, and a_ij and 𝝉_ij are the synaptic coupling strength and the synaptic transmission delay of the connection j → i, respectively.

If there are no recurrent interactions (S_i(t) ≡ 0) and I_i is constant the solution of (1) for initial condition V_i(0) = V_R,i is given by

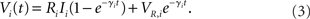
This implies that for R_iI_i > V_T,i (suprathreshold external current) the membrane potential is oscillating such that V_i(t + T_i) = V_i(t) with period

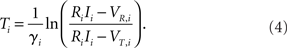
The general solution of the non-autonomous inhomogeneous linear differential equation (1) for times t > t₀ with initial condition V_i(t₀) is given by (cf. Arnol’d, 1992)

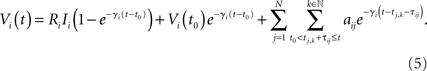
This solution, which holds for all times t > t₀ until neuron i next experiences a threshold crossing, provides the basis for the reconstruction method described below.

It should be noted that the tractable nature of this model means that simulating networks of LIF neurons is straightforward. In particular, it can be efficiently and exactly done using standard event-based simulation techniques (Mattia and Giudice, 2000; Timme et al., 2003).

2.2 General Reconstruction Methodology

How can we obtain the interaction strengths a_ij for a particular neuron i and thus the network topology? The aim is to assemble multiple linearly independent instances of (5) into a linear system of rank N and solve for the unknown a_ij values. If the model parameters R_i, V_R,i, V_T,i, γ_i, and 𝝉_ij are known and the dynamical quantities t₀, t, V_i(t₀), and V_i(t) are specified, equation (5) provides a restriction on the N input coupling strengths a_ij for a given neuron i. Choosing sufficiently many different values of the pairs t and t₀ so as to provide linearly independent instances of (5) will therefore give N restrictions that fully determine all coupling strengths a_ij, j ∈ {1,…,N}. Repeated for each i this yields the entire network topology.

Acceptable inter-spike intervals

We can use subsequent spike times t₀ = t_i,ℓ−1 and t = t_i,ℓ to fix the dynamical quantities if they are chosen in an appropriate way. We first note that we can safely use any spike time to determine an initial condition, since post-spike the LIF neuron always immediately resets to voltage V_R,i. Hence our criterion for choosing an interval depends only on the way threshold crossings are induced, either by an incoming excitatory spike (spike-induced spiking) or by passive propagation due to sufficiently large driving I_i (current-induced spiking). For current-induced spiking the membrane potential 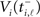of neuron i is known to be exactly at the threshold value V_T,i, while spike-induced spiking will generally supply excess depolarization such that the actual membrane potential will be at some unknown value 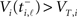. Hence if we restrict our choice of intervals (t_{i,ℓ −1}, t_i,ℓ) to those terminating with current-induced spikes the following substitutions are valid in (5):

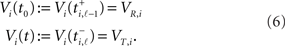
In order to find these intervals we must compare the spike times t_i,ℓ of neuron i with all possible arrival times t_j,k + 𝝉_ij of all neurons j. To exclude intervals with potentially spike-induced spikes, we restrict the analysis to intervals where no t_j,k + 𝝉_ij coincides with the respective t_i,ℓ and hence define the inter-spike interval (t_{i,ℓ − 1}, t_i,ℓ) as acceptable for neuron i if

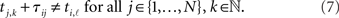
It is important to note two things: first, that we often have at our disposal many more than N acceptable intervals; and second, that not every set of N acceptable intervals will provide N linearly independent instances of (5). In particular, consecutive acceptable intervals might contain very similar arrival patterns, resulting in badly conditioned or even low-rank systems. Of course, there is no constraint to select only N intervals; if we use M > N intervals then the system will be formally overdetermined but solvable, though M ≫ N is not favorable for efficiency reasons. Usually, selecting a subset of N or more intervals distributed across the respective incoming spike trains will be sufficient if the spiking is asynchronous and irregular (meaning that inter-spike interval correlations decrease quickly with time), the mean firing rate for all neurons is positive, and the spike recording is long-enough to find sufficiently many uncorrelated acceptable inter-spike intervals to derive N linearly independent instances of (5). In Section 3.1 various strategies for selecting subsets of acceptable intervals will be discussed. Note that we are not constrained to use spike train segments obtained under a single driving condition.

Assuming there are M ≥ N acceptable intervals that will ensure linear independence, all presynaptic connections for neuron i, A_i = (a_i1,…,a_iN) are obtained in the following way: let 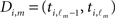be the m-th member of our subset of acceptable inter-spike intervals, and 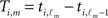be the respective inter-spike interval of neuron i. We then define the M × N matrix Θ⁽ⁱ⁾ and the column vector B⁽ⁱ⁾ by

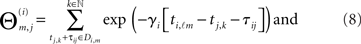
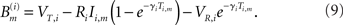
The incoming connectivity for neuron i is obtained by solving the linear system

for A_i. Repeating the procedure for each neuron i ∈ {1,…, N} separately yields all N rows of the coupling matrix A, and thus the entire synaptic connectivity of the network.

2.3 Reconstruction in the Presence of Simple Periodic Spiking

The method described above can be applied to a broad range of spiking patterns and does not rely on network synchronization, phase-locking, or other steady state requirements. Since repeated spike patterns within the inter-spike intervals will lead to linear dependent rows in the derived Θ matrix (8), systems that do exhibit phase-locked dynamics may require special handling. For excitatory and mixed systems it is usually sufficient to use heterogeneous driving currents I_i, e.g., randomly drawn from some distribution ℙ(I), with a variance large enough to perturb the system out of any phase-locked state. Certain inhibition dominated LIF networks exhibit stable dynamics even under a wide range of heterogeneous drivings. Inhibitory networks where a_i ≡ Σ_j a_ij < 0 and 0 < (max_i a_i − min_i a_i) < 𝝉i_ij will generate stable phase-locked states with common period T when stimulated with a homogeneous current I_i = I (Denker et al., 2004). When a_i = a < 0 for each i the system will also be able to consistently achieve stability under heterogeneous driving conditions, since the spread of the spike pattern is solely caused by the spread ΔI_i,m ≡ max_i I_i,m − min_i I_i,m of the driving currents. This last subclass of networks we will denote as homogeneous inhibitory.

Homogeneous inhibitory LIF networks typically exhibit simple periodic spike patterns, i.e., all neurons fire exactly once before the same spike pattern repeats. If the neurons fire in a simple periodic pattern such that for any given inter-spike interval t_{i,ℓ − 1}, t_i,ℓ each neuron j ≠ i spikes exactly once within (t_{i,ℓ − 1} − 𝝉_ij, t_i,ℓ − 𝝉_ij), each acceptable interval contains a complete set of representative arrivals, and (5) simplifies to

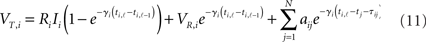
for all i ∈ {1,…, N}.

In order to guarantee linear independence it is necessary to gather data from multiple, relatively short spike trains obtained under varied driving conditions I_i,m, m ∈ {1,…, N} (cf. Timme, 2007) which additionally satisfy ∀_i,ji ≠ j ⇒ I_i,m ≠ I_j,m. If a network is able to achieve periodic simple spike patterns under each of these drivings then all intervals after the initial transient period are acceptable with identical or close to identical arrival patterns, hence we can always choose the last intervals recorded to solve the N linear systems (5). This means that although this type of network dynamics makes it mandatory to repetitively drive the system with independent sets of currents, it spares us the necessity of scanning the spike data for acceptable intervals and so allows for fast reconstruction. We will refer to this case as the specialized method for homogeneous inhibitory networks.

3 Implementation and Performance

3.1 Acceptable Interval Searches

For LIF networks other than the homogeneous inhibitory networks described in Section 2.3, spike patterns will almost always be asynchronous rather than simple periodic; hence we must actively search through spike trains for acceptable intervals.

In principle, if a full-rank system is embedded in the data then only N intervals are required, some of which may contain zero or more than one representative t_j,k + 𝝉_ij value. One alternative to trying to identify such a minimum set of intervals would be to select M > N intervals according to some criterion which either guarantees or at least maximizes the chance that we have a full-rank subset; we could, for example, select all available acceptable intervals. Similarly, if we have M > N intervals we have the choice of solving the overdetermined M × N system by, e.g., a least-squares method, or aggregating instances of (5) to patch together an N × N system.

In our implementation we used independent partial scans of spike train segments to collect M ≥ N intervals; the scans use the heuristic described below to construct a full-rank system if possible while reducing search time and keeping M reasonably close to N. Multiple intervals found in close proximity are combined to create exactly solvable N × N systems, since they are preferable to overdetermined systems in terms of both time requirements and numerical stability.

Within segments, our search strategy is based on a minimum-scan-length policy. Given data segments S_m, m ∈ {1,…,N}, then for each neuron i each segment S_m is scanned only as far as needed to obtain representative t_j,k + 𝝉_ij values for all neurons j, and intervals are only chosen if they contributed a new member to the representative set. Instances of (5) for the intervals are then summed to become the m-th row of the solution matrix Θ⁽ⁱ⁾ and m-th element of the vector B⁽ⁱ⁾. When particular representatives are not present in particular segments then corresponding elements are set to zero. Balancing representatives by requiring a full set for each row and excluding redundancies is more than we technically require, but in practice this results in better conditioned Θ⁽ⁱ⁾ matrices and hence more accurate results.

3.2 Accuracy of the Basic Method

We first analyze the performance of the method for full-rank systems without additional noise or uncertainty. As shown in Figure 1, the reconstruction error is negligible, both for networks with phase-locked spike patterns as well as those with irregular spiking. The numerical error that appears in the reconstructions is solely the result of small truncation errors in the derived data being propagated through global operations such as matrix inversion. When the specialized version of the method is used on phase-locking networks, this error level is as well directly and linearly dependent on the degree of synchronization experienced by the network (see Figure 3). As the exit tolerance is decreased this tunable error meets a hard limit where the truncation is no longer caused by early termination of the simulation, but instead by the fixed-precision numbers used by the machine the calculations are performed on. It should be noted that (apart from their influence on the network’s ability to synchronize) the magnitude of simulation parameters does not affect the accuracy of the results in any noticeable way.

FIGURE 1

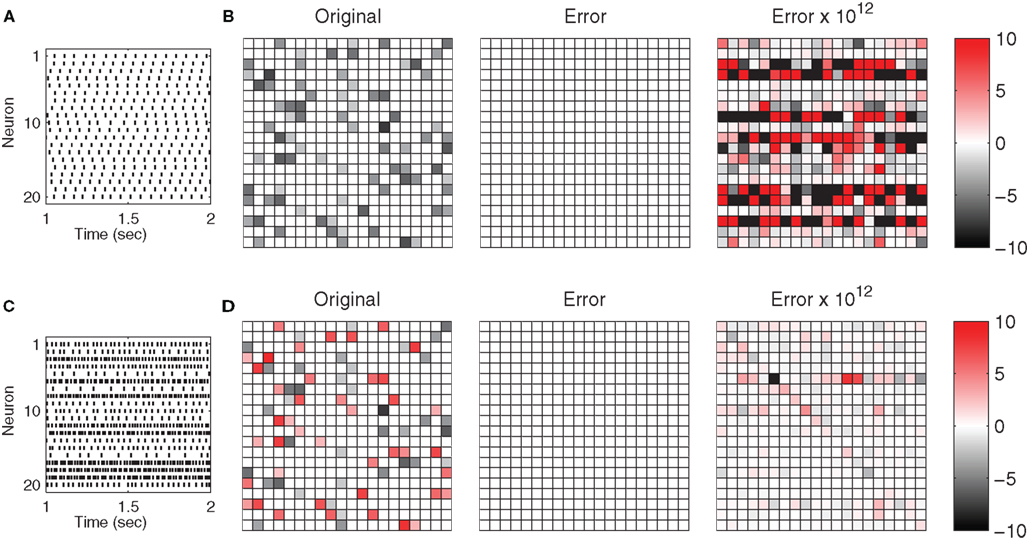
Figure 1. Topology reconstruction from simple periodic and complex aperiodic spike patterns. (A) Simple periodic spike pattern of an inhibitory network. (B) Connection weights of the same network, with full rank reconstruction error 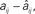and its magnification; strengths and errors are color coded on same scale. Error is on the level of numerical accuracy. (C) Complex spatio-temporal spike pattern of a heterogeneous network with both inhibitory and excitatory connections. (D) Connection weights and error for the heterogeneous network. Both networks share the same underlying adjacency structure; the heterogeneous network was obtained from the inhibitory network by randomly changing the signs of connections with probability p = 0.5. Simulation parameters for both systems (uniform for all neurons): external driving γ_iR_iI_i = 1 mV/ms with uniform random variation ΔI/I = 5%, 1/γ_i = 31.64 ms, V_R,i = 0 mV, V_T,i = 20 mV, 𝝉_ij = 5 ms.

Since the general reconstruction method does not depend on synchronization, for data characterized by sustained irregular or chaotic spiking the entire error can be attributed to fixed-precision effects. A necessary precondition for achieving this level of accuracy is of course that enough data be made available. As Figure 2A shows, the minimum number of intervals required to achieve full accuracy is not large; roughly 7 or 8 per segment (≈160 total) for a 20-neuron network, for example. Whether data is obtained from N independent drivings or from a single run does not as well seem to have a large effect; sampling out of a very long run does reduce the minimum requirement by an interval or two, but the amount of data that must be generated in the first place to achieve this effect is appreciably greater. Compare also the specialized method featured in Figure 3, where the data requirement is exactly one interval per segment, but to achieve, e.g., 10⁻¹⁰ accuracy each segment needs to be ≈60 intervals long.

FIGURE 2

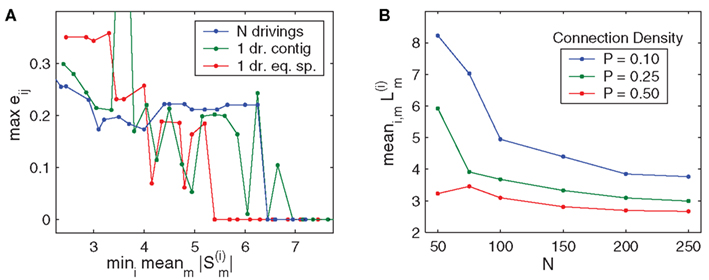
Figure 2. Reconstruction accuracy for complex spatio-temporal patterns as affected by search requirements. (A) Maximum reconstruction error 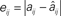vs. data availability as measured by segment length (in spikes) for slowest neuron. Different curves compare effect of data source: (blue) segments obtained under N different drivings, (green) contiguous segments taken from one run of moderate length, or (red) segments taken at equally spaced intervals from a long run (roughly 1000 spikes per neuron in this case). Runs use the same sample network and parameters as shown in Figures 1C,D. (B) Interval search length L using min-scan-length strategy vs. size of network N for different connection densities P. Note: all reconstructions here achieved the numerical limit of accuracy. Simulation parameters: balanced networks (Σ_j a_ij = 0) with no other restriction on pre- or postsynaptic connectivity, data obtained under N uniformly randomized driving conditions, base driving γ_iR_iI_i = 1.5 mV/ms, ΔI/I = 1%; 𝝉_ij = 2 ms, 1/γ_i = 20 ms, V_R,i = 0 mV, V_T,i = 20 mV (uniform for all neurons).

FIGURE 3

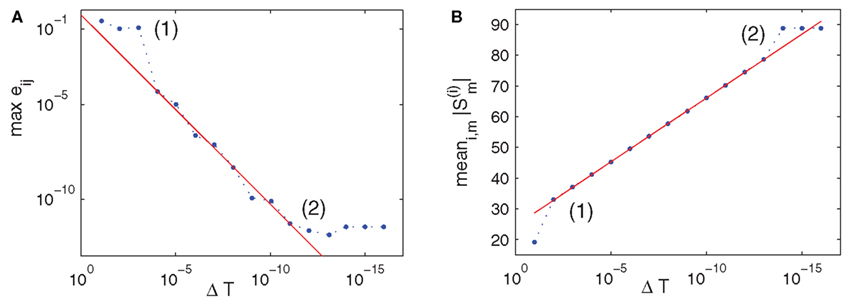
Figure 3. Reconstruction accuracy for phase-locking networks as affected by periodicity. (A) Maximum reconstruction error 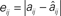vs. phase-locking as measured by exit tolerance ΔT, the maximum difference between final period lengths of different neurons. (B) Length of simulation runs S_m (given as number of spikes emitted by neuron i, 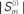) needed to achieve a specified ΔT. Annotations: (1) indicates non-full-rank solutions due to insufficient synchronization; (2) indicates numerical saturation. Data is from sample network used for Figures 1A,B.

Independent of the driving conditions applied, there is no prior constraint on network configurations solvable by the methodology, aside from the assumption that a_ij < V_T,i − V_R,i, i.e., that no single spike can move the membrane potential from reset to threshold. In particular there are no other restrictions on the synaptic coupling strengths a_ij, or whether they are zero (no synapse present), positive (excitatory), or negative (inhibitory).

There is on the other hand no prior guarantee that any particular driving will give good results. In practice, randomly varied driving which satisfies R_iI_i > V_T,i almost always gave us fully accurate reconstructions. There are two situations that can cause problems for the general method when otherwise long-enough data streams are made available: (i) quiescent neurons (no recoverable incoming or outgoing connections), and (ii) neurons for which all spiking throughout entire segments is spike-induced (outgoing connections recoverable, incoming connections not). Only (i) arose in our testing on random networks with random drivings, and never with networks subject to any kind of balance conditions, e.g., |Σ_j,inhib a_ij| ≃ |Σ_j,excit a_ij|. It should be noted that with respect to both situation (i) and situation (ii) the accuracy of reconstruction of the remainder of the network is not affected, and if needed both situations can be prevented by adjusting the driving to the relevant neurons.

3.3 Efficiency

To check the speed of the methods we reconstructed networks of N = 50 to N = 500 neurons. As the range of N here implies, moderately sized networks (several hundred neurons) are still feasible for both the specialized and the general method; using the specialized method reconstruction of 250 neuron networks took about 1 min on a single node of a 4-CPU 2 GHz machine, while general reconstruction of the same network took about 20 min.

As these time ranges imply, the general method’s reliance on data acquired from directly searching spike trains makes it noticeably slower than the specialized method in the size range tested here. This is in part due to the length of searches, but fixed costs for setting up the searches and computational platform were also factors (implementations were done in MATLAB, which is optimized for matrix operations but not generic search routines).

The worst case running time for the search phase of the general method is 𝒪(S_maxN³), where S_max is the length of the longest spike train. In practice most searches are not worst case; for the network of Figure 1D, for example, the mean segment length was 92 spikes, while the mean search length was 12 intervals and the mean number of acceptable intervals selected was around 3. As Figure 2B shows, the search length does not seem to increase as N grows but rather converges to a constant value; a similar effect is seen with the connection density (and hence the number of connections). We note that if situation (ii) mentioned in Section 3.2 occurs, the search time will in fact revert to the theoretical worst case.

After the search phase is completed, the algebraic operations require solving N individual N × N linear systems, so they have a time complexity of O(N⁴) using conventional matrix inversion or Gaussian elimination. Hence, if the length of each neuron’s spike train is bounded within O(N) (i.e., each neuron spikes a fixed number of times for each neighbor) the worst case running time for the method as a whole is as well O(N⁴). The numerical results shown in Figure 1 suggest that this amount of data should generally be quite sufficient for accurate reconstruction. The implication is that the computational effort of reconstructing the structural connectivity of spiking neural networks scales polynomially, and not exponentially, with network size. This is a significant finding concerning network reconstruction, since many other problems in bioinformatics are known or conjectured to be NP-complete, that is, for all intents and purposes intractable (cf. Foulds and Graham, 1982; Ngo et al., 1994).

3.4 Exploiting Sparsity – Solutions for Underdetermined Systems

Recent studies (Yeung et al., 2002; Timme, 2007) used singular value decomposition USV^T = Θ⁽ⁱ⁾ and optimization for sparsity to reconstruct with M ≪ N distinct driving conditions. In general, this yields the underdetermined system 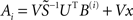where 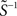is the pseudoinverse of S and x is any vector. Setting 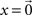gives us the usual least-squares solution, but on the naturalistic assumption that neuronal network connectivity matrices A are sparse we can choose x so as to maximize the number of zeros in each A_i. To do this we use the heuristic of solving the overdetermined system 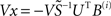for x so as to minimize the L₁-norm of the difference; our implementation uses the fast L₁-norm solver of Barrowdale and Roberts (1974).

Our primary interest is the lowest M < N we require to obtain sufficiently many reconstructed couplings 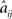close enough to the corresponding elements of the original connectivity matrix a_ij, so that 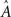(after appropriate rounding) can be used as a plausible estimate for A in any hypothetical analysis. Hence along with the usual error measurements we also use a custom quality-of-fit metric, 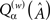, that essentially yields the proportion of sufficiently close element-to-element matches, in this case for a given M:

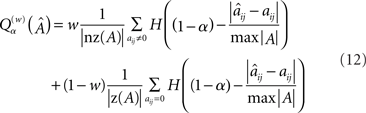
The parameter a is a value between 0 and 1 governing the desired per-element accuracy, e.g., an a value of 0.80 means we want the proportion of elements in the reconstructed matrix that are within (roughly) 80% to 120% of the target value. nz(A) and z(A) are the sets of all non-zero and all zero elements of A, respectively, and H is the Heaviside step function. The weighting is incorporated to prevent false high scores when M is low and the target A is very sparse (cf. the original version of the quality measure in Timme, 2007). We exclusively used 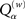with w = 0.5, which in the following we simply denote by Q_α. Figure 4A shows a sampling of Q_α values vs. M.

FIGURE 4

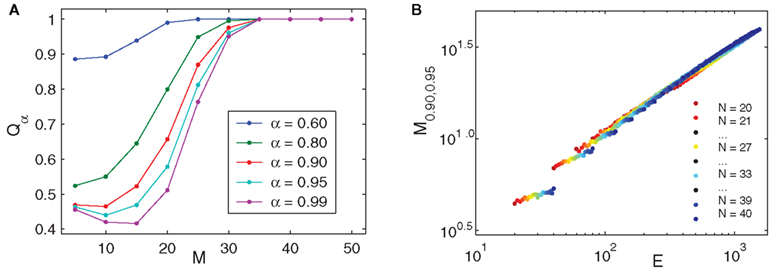
Figure 4. Quality of rank-deficient reconstruction. (A) Various Q_α values vs. M [N = 50, mean number of presynaptic connections K = 12; model parameters (uniform for all neurons) 𝝉_ij = 2 ms, 1/γ_i = 20 ms, V_R,i = 0 mV, V_T,i = 20 mV, base driving γ_iR_iI_i = 1.5 mV/ms, ΔI/I = 1%]. (B) Log-log plot of M_0.90,0.95 vs. E for networks with N = 20–40 neurons and average presynaptic connections K∈{1,2,…,N − 1} (over 600 points in total). Q_α values for (B) were obtained from averages of 20 trials for each N, K combination over each M from 1 to N; simulation parameters (unitless, uniform for all neurons) are 𝝉_ij = 0.25, γ_i = 1 − e⁻¹, V_R,i = 0, V_T,i = 1, base driving γ_iR_iI_i = 1, 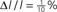. For both panels, all networks are random homogeneous inhibitory with normally distributed random connection weights.

Networks with simple phase-locked spike pattern dynamics are solvable using the faster specialized method, so since a great many reconstruction computations were required these were used as our testbed. Comparison of interpolated values of Q_a across different values of N, M, the number of connections E, and other simulation parameters confirmed that the quality of reconstruction for M < N depends almost entirely on M/N and the edge density P = E/N². To determine the minimum M necessary to achieve a desired quality-of-fit we define

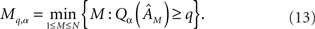
The Q_α profiles in Figure 4A show that there will be values of q for which Q_α does not exist or is not unique. When both q, α ≥ 0.75, however, M_q,α is well-defined and we consistently obtained relations of the form

where scaling exponent 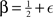, with |∈| ≪ 1/2 and c ≪ E. A simple log-log fit of the data used for Figure 4B, for example, gives a scaling exponent of 0.504, with c below one. The overall result implies that we can expect M_q,α to grow linearly with N when P is fixed, and roughly as 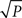when N is fixed.

For general spatio-temporal patterns we obtain similar results, though they are not as pronounced or consistent, and there seems to be a greater dependence on factors other than M, N, and E, such as actual network parameters and specific spike pattern. The particular interval search strategy used has an influence as well. These intermingled technical issues require further theoretical and computational studies.

3.5 Spike Timing Variability Due to Noise and Uncertainty

In the previous subsections we have described the performance of the reconstruction method for exactly known model parameters and spike times. In such cases, when there is sufficient data available for a full-rank solution the accuracy is limited only by machine precision, demonstrating that reconstruction of large pulse-coupled networks from spike time data is in principle feasible.

For real world data one must deal with limitations in our knowledge of neuron parameters, and also uncertainties due to the noisiness of the system. Even if spike times themselves are accurately measured and correctly assigned to their respective source neurons, spike timing is an inherently noisy process with intrinsic contributions from, e.g., fluctuations in ion channel dynamics and dendritic integration, as well as extrinsic contributions from, e.g., synaptic failure and dependence on the network state itself (Gerstner and Kistler, 2002). This leads to variability in both spike times as well as transmission delays, even under identical external conditions (Mainen and Sejnowski, 1995; van Steveninck et al., 1997; Destexhe et al., 2003).

In this section we present some preliminary results concerning the performance of the reconstruction method when spike reception times are subject to additive random jitter bounded by an upper amplitude δ_S. The presence of temporal jitter induces an uncertainty in comparison of spike times and estimated arrival times, and hence the identification of acceptable intervals [cf. (7)]. Given a spike by neuron i at time t_i,ℓ induced by a spike from neuron j at t_j,k, if we naively try to apply the acceptable interval criterion in Section 2.2 to the jittered times 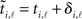and 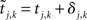, then the interval as measured 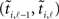will very likely be erroneously accepted. Note that the measured/estimated time between the simultaneous arrival and spiking events is |δ_j,k − δ_i,ℓ| ≤ 2max{|δ_j,k|, |δ_i,ℓ|} ≤ 2δ_S. As well, even if the interval is actually acceptable, arrivals close to both the initial spike time t_{i,l − 1} and the terminal spike time t_i,l can cause inaccuracy by being wrongly assigned (or not assigned) to it. In order to exclude either case a new condition for the interval to be acceptable for neuron i has to be defined:

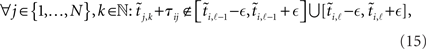
with the uncertainty ∈ depending on the noise amplitude δ_S.

Without explicit knowledge of δ_S, deciding on which ∈ to choose is problematic: if too small there will be too many false positives, leading to large errors in the reconstruction; if too large many false negatives may lead to long interval searches, and in the worst case no acceptable intervals will be identified at all. As well, for fixed δ_S and ∈ simple probability dictates that increasing the network size will also increase the number of false negatives. This issue is a subject of future research.

Figure 5A shows how reconstruction accuracy (as given by the maximum absolute error) grows with uncertainty in the data, here implemented as jitter of amplitude δ_S applied after the fact to exact simulation data. The ∈ used = 2 max δ_S. Figure 5B shows how our custom quality-of-fit metric Q_α scales with applied noise as it approaches the model parameter values in magnitude. The a value of 0.95 means that we are only considering a reconstructed element a hit when its value deviates from the target’s by 5% or less. What may not be apparent from the log-log plot is that the decline in accuracy scales in a roughly linear way with the noise level, until the last point at 1.0 (this jog is an artifact of the 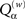weighting used: the method can detect insufficient data and suppress untrustworthy results, but this feature was turned off for the error level tests; without the self-diagnostics, when there is no usable data whatsoever the method will return a uniformly zero matrix, which will generate correct matches for every non-connection in the original network).

FIGURE 5

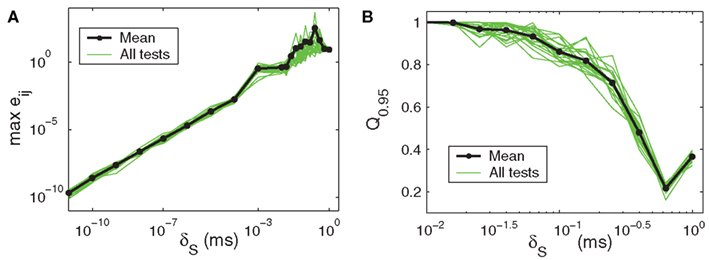
Figure 5. Reconstruction accuracy as affected by noisy data. (A) Maximum reconstruction error 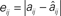vs. noise level, here given as upper bound δ_S on the displacement applied after the fact to exact times from the original simulation data. (B) Quality of reconstruction metric Q_α vs. added noise level, for α = 0.95 and maximum added noise ranging from 0.01 to 1. Data sets for both panels were obtained from the same sample network and parameters as shown in Figures 1C,D.

Rank-deficient reconstruction as discussed in the previous subsection could be used to improve the accuracy of results for noisy systems. In our testing we have found that when M is close to but strictly less than N, application of SVD plus the L₁-norm solver acts as a numerical filter by forcing spurious low-grade connections toward zero strength. The optimal value for M in this case has yet to be determined (using M = N − 1 usually gives very similar results to full-rank reconstruction). A potential application of the same principle is removing real but marginal connections from reconstruction results in order to obtain simpler connectivity patterns.

4 Discussion

Understanding the relationship between structure and function of neuronal circuits lies at the very core of neuroscience. Modern recording devices, such as MUA that record the extracellular spike activity of tens to hundreds of neurons, provide time series whose interpretation can aid the understanding of the relevant functional connectivity and its spatial structure (cf. Aertsen and Gerstein, 1985; Aertsen et al., 1989; Berger et al., 2007, 2010, and others). Yet, to reconstruct the detailed connectivity of a neuronal network from recorded spike data is beyond recent data analysis techniques due to the complexities introduced by both individual neuron dynamics and network effects.

Here we have developed an explicit method for the reconstruction of network connectivity of LIF neurons from spike time information that is fast, accurate, and robust. The method works natively on networks exhibiting non-stationary complex spatio-temporal dynamics (i.e., “plain” irregular spiking, Section 2.2); to solve networks with strong synchronizing tendencies it can, for example, make use of multiple randomized external driving conditions. A specialization of the method allows it to very efficiently reconstruct networks exhibiting simple spike patterns (Section 2.3), a dynamics that is reliably generated by a large subset of uniformly inhibitory LIF networks. This class is often used as a stand-in for inhibition dominated cortical networks (cf. Brunel and Hakim, 1999; Denker et al., 2004; Jahnke et al., 2009).

The general method is capable of reconstructing networks with several hundred neurons and arbitrary connectivity in a reasonable time given standard computational resources. In this regard the methodology compares favorably with reconstruction methods previously put forward for neuron networks (Makarov et al., 2005) and oscillator networks (Yu et al., 2006). Furthermore, the method is amenable to an optimization used earlier with reconstruction techniques for networks with fixed point dynamics (Yeung et al., 2002) and periodic dynamics (Timme (2007), cf. also Napoletani and Sauer (2008)) that substantially reduces the amount of data required.

The method introduced here is one of the first to achieve synapse-level reconstructions working from spike-based data, and it extends recoverability of pulse-based networks far beyond previously accessible sizes. However, as it currently stands, it does have its limitations that need to be addressed by future research if it is to be applied to biologically realistic data. To begin with, it is model dependent, and has to be given fixed known parameter values, even though these values need not be the same for every neuron in the network. As well, the method requires injection of external currents to individual neurons with a precision not yet generally achievable in an experimental setting (Houweling et al., 2010), nor will it work with externally undriven or weakly driven systems. While with some modification it can handle bounded amounts of noise and/or uncertainty, it is sensitive to errors with respect to, e.g., spike sorting.

Neuron models with more realistic spike generation mechanisms are worth further analysis within the response–dynamics idea that underlies our methodology. Possible extensions include: the spike-response model, a modification of the LIF neuron that incorporates refractoriness (Gerstner and Kistler, 2002); the two variable adaptive exponential integrate-and-fire neuron, which is capable of a much wider range of individual neural behavior (bursting, fast, and slow mode, etc., cf. Brette and Gerstner, 2005); and further non-linear models such as the quadratic integrate-and-fire neuron (Izhikevich, 2007). Ultimately, the general aim is that a single algorithm contains the specifications for a repertoire of different models, which can be adapted to particular self-contained networks or also parts of networks, given an input model that mimics the residual large-scale network or upstream input areas. Since all available recording techniques have to deal with the general problem of undersampling, both with regard to the number of neurons as well as with regard to the finite time a stable recording is possible, minimizing the data required for desired accuracy is an important feature of any potentially useful reconstruction algorithm.

The method presented here is not designed to replace large-scale correlation-based methods, as functional connectivity continues to be the main approach to reconstruction problems in neuroscience. However, to determine the details within the regions of interest that functional connectivity studies identify will require methods that can provide data on the scale of individual synaptic connections. The complexity analysis provided in Section 3.3 shows for the first time that reconstruction based on spike pattern information is computationally feasible. If explicit methods such as the one presented here can be developed to work on large-scale networks with appropriate biophysical neuron models, they may become invaluable in these studies. Thus we see our methodology as an eventual complement to techniques currently in use, providing a promising starting point for future research of neural circuit inference from spiking activity.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Sara Solla and Fred Wolf for helpful comments. We also thank Christian Henrich for his contributions in the early stages of this work, and Zeina S. Khan for her careful reading of the manuscript. We acknowledge funding by the Federal Ministry of Education and Research (BMBF) Germany for partial support under Grant No. 01GQ1005B.

References

Aertsen, A., and Gerstein, G. L. (1985). Evaluation of neuronal connectivity: sensitivity of cross-correlation. Brain Res. 340, 341–354.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Aertsen, A., Gerstein, G. L., Habib, M. K., and Palm, G. (1989). Dynamics of neuronal firing correlation: modulation of “effective connectivity.” J. Neurophysiol. 61, 900–917.

Pubmed Abstract | Pubmed Full Text

Arnol’d, V. I. (1992). Ordinary Differential Equations (R. Cooke, trans.). Berlin: Springer-Verlag.

Barrowdale, I., and Roberts, F. D. K. (1974). Algorithm 478: solution of an overdetermined system of equations in the l₁ norm [F4]. Commun. ACM 17, 319–320.

Berger, D., Borgelt, C., Louis, S., Morrison, A., and Grün, S. (2010). Efficient identification of assembly neurons within massively parallel spike trains. Comput. Intell. Neurosci. 2010, 439648.

Berger, D., Warren, D., Normann, R., Arieli, A., and Grün, S. (2007). Spatially organized spike correlation in cat visual cortex. Neurocomputing 70, 2112–2116.

CrossRef Full Text

Brette, R., and Gerstner, W. (2005). Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J. Neurophysiol. 94, 3637–3642.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brunel, N. (2000). Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 8, 183–208.

Pubmed Abstract | Pubmed Full Text

Brunel, N., and Hakim, V. (1999). Fast global oscillations in networks of integrate-and-fire neurons with low firing rates. Neural Comput. 11, 1621–1671.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cadenasso, M. L., Pickett, S. T. A., and Grove, J. M. (2006). Dimensions of ecosystem complexity: heterogeneity, connectivity, and history. Ecol. Complex. 3, 1–12.

CrossRef Full Text

Denker, M., Timme, M., Diesmann, M., Wolf, F., and Geisel, T. (2004). Breaking synchrony by heterogeneity in complex networks. Phys. Rev. Lett. 92, 074103.

Pubmed Abstract | Pubmed Full Text

Destexhe, A., Rudolph, M., and Pare, D. (2003). The high-conductance state of neocortical neurons in vivo. Nat. Rev. Neurosci. 4, 739–751.

Pubmed Abstract | Pubmed Full Text

Diesmann, M., Gewaltig, M.-O., and Aertsen, A. (1999). Stable propagation of synchronous spiking in cortical neural networks. Nature 402, 529–533.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Foulds, L., and Graham, R. (1982). The Steiner problem in phylogeny is NP-complete. Adv. Appl. Math. 3, 43–49.

Gerstner, W., and Kistler, W. (2002). Spiking Neuron Models: Single Neurons, Populations, Plasticity. Cambridge, UK: Cambridge University Press.

Houweling, A., Doron, G., Voigt, B., Herfst, L., and Brecht, M. (2010). Nanostimulation: manipulation of single neuron activity by juxtacellular current injection. J. Neurophysiol. 103, 1696–1704.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Izhikevich, E. (2007). Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. Cambridge, MA: The MIT Press.

Jahnke, S., Memmesheimer, R.-M., and Timme, M. (2009). How chaotic is the balanced state? Front. Comput. Neurosci. 3:13. doi: 10.3389/neuro.10.013.2009

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jirsa, V. K., and McIntosh, A. R. (eds). (2007). Handbook of Brain Connectivity. Berlin: Springer.

Mainen, Z., and Sejnowski, T. (1995). Reliability of spike timing in neocortical neurons. Science 268, 1503–1506.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Makarov, V. A., Panetsos, F., and de Feo, O. (2005). A method for determining neural connectivity and inferring the underlying network dynamics using extracellular spike recordings. J. Neurosci. Methods 144, 265–279.

Pubmed Abstract | Pubmed Full Text

Mattia, M., and Giudice, P. (2000). Efficient event-driven simulation of large networks of spiking neurons and dynamical synapses. Neural Comput. 12, 2305–2329.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Napoletani, D., and Sauer, T. (2008). Reconstructing the topology of sparsely connected dynamical networks. Phys. Rev. E 77, 026103.

Ngo, J., Marks, J., and Karplus, M. (1994). “Computational complexity, protein structure prediction, and the Levinthal paradox,” in The Protein Folding Problem and Tertiary Structure Prediction, eds K. Merz and S. Le Grand (Boston: Birkhauser), 433–506.

Timme, M. (2007). Revealing network connectivity from response dynamics. Phys. Rev. Lett. 98, 224101.

Pubmed Abstract | Pubmed Full Text

Timme, M., Wolf, F., and Geisel, T. (2002). Coexistence of regular and irregular dynamics in complex networks of pulse-coupled oscillators. Phys. Rev. Lett. 89, 258701.

Pubmed Abstract | Pubmed Full Text

Timme, M., Wolf, F., and Geisel, T. (2003). Unstable attractors induce perpetual synchronization and desynchronization. Chaos 13, 377–387.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van Steveninck, R., Lewen, G., Strong, S., Koberle, R., and Bialek, W. (1997). Reproducibility and variability in neural spike trains. Science 275, 1805–1808.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van Vreeswijk, C., and Sompolinsky, H. (1996). Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274, 1724–1726.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yeung, M. K. S., Tegnér, J., and Collins, J. J. (2002). Reverse engineering gene networks using singular value decomposition and robust regression. Proc. Natl. Acad. Sci. U.S.A. 99, 6163–6168.

Pubmed Abstract | Pubmed Full Text

Yu, D., and Parlitz, U. (2008). Driving a network to steady states reveals its cooperative architecture. Europhys. Lett. 81, 48007.

Yu, D., Righero, M., and Kocarev, L. (2006). Estimating topology of networks. Phys. Rev. Lett. 97, 188701.

Pubmed Abstract | Pubmed Full Text

Zillmer, R., Brunel, N., and Hansel, D. (2009). Very long transients, irregular firing, and chaotic dynamics in networks of randomly connected inhibitory integrate-and-fire neurons. Phys. Rev. E 79, 031909.