Extraction of network topology from multi-electrode recordings: is there a small-world effect?

The simultaneous recording of the activity of many neurons poses challenges for multivariate data analysis. Here, we propose a general scheme of reconstruction of the functional network from spike train recordings. Effective, causal interactions are estimated by fitting generalized linear models on the neural responses, incorporating effects of the neurons’ self-history, of input from other neurons in the recorded network and of modulation by an external stimulus. The coupling terms arising from synaptic input can be transformed by thresholding into a binary connectivity matrix which is directed. Each link between two neurons represents a causal influence from one neuron to the other, given the observation of all other neurons from the population. The resulting graph is analyzed with respect to small-world and scale-free properties using quantitative measures for directed networks. Such graph-theoretic analyses have been performed on many complex dynamic networks, including the connectivity structure between different brain areas. Only few studies have attempted to look at the structure of cortical neural networks on the level of individual neurons. Here, using multi-electrode recordings from the visual system of the awake monkey, we find that cortical networks lack scale-free behavior, but show a small, but significant small-world structure. Assuming a simple distance-dependent probabilistic wiring between neurons, we find that this connectivity structure can account for all of the networks’ observed small-world-ness. Moreover, for multi-electrode recordings the sampling of neurons is not uniform across the population. We show that the small-world-ness obtained by such a localized sub-sampling overestimates the strength of the true small-world structure of the network. This bias is likely to be present in all previous experiments based on multi-electrode recordings.

1 Introduction

In recent years, techniques in systems neuroscience and electrophysiology to record from many neurons in parallel became widely available (see, e.g., Georgopoulos et al., 1986; Nicolelis et al., 1997, 2003; Santhanam et al., 2006; Jarosiewicz et al., 2008). While in the beginning, this was seen merely as a way to perform many single-neuron experiments simultaneously, the full potential of such parallel recordings was soon realized and led to a paradigm shift in the analysis from single-spike statistics (Perkel et al., 1967a; Brillinger, 1988; Bialek et al., 1991; Rieke et al., 1999; Gerstner and Kistler, 2002) toward the analysis of neural population activity and interactions between neurons. Early attempts focused on pair-wise cross-correlation analysis (Perkel et al., 1967b; Aertsen et al., 1989), but recent statistical models have tried to capture the global network activity (Iyengar, 2001; Brown et al., 2004; Truccolo et al., 2005; Schneidman et al., 2006; Pillow et al., 2008; Paninski et al., 2010) in an attempt to understand how neurons collectively encode and process information. The access to this high- dimensional type of data has also triggered a challenge for statistical data analysis and modeling (Kass et al., 2005): What is an adequate low- dimensional description of the structure in the spiking activity of neural populations?

One possible solution is to extract the dynamic coupling (or effective connectivity) structure based on the recorded spike trains. The effective coupling between two neurons quantifies how the spiking activity of one neuron enhances or reduces the spiking probability of the second one and should in general be directed and causal. After thresholding, such a coupling structure reduces to a binary, directed connectivity matrix in which a non-zero entry indicates a directed coupling between two neurons. The connectivity matrix defines a graph and its structural properties can be further quantified. Using this analysis scheme, the overall network activity can be summarized in a few quantitative parameters of the inferred network topology (Figure 1).

FIGURE 1

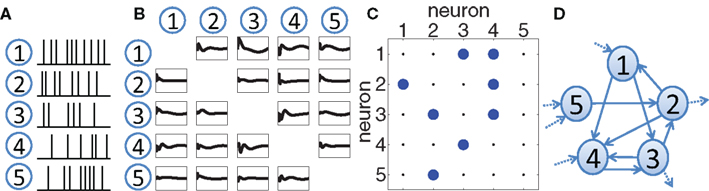
Figure 1. Schematic overview of our approach. (A) The activity of a number of neurons has been recorded in the form of a set of spike trains, e.g., using extracellular electrodes. (B) A statistical framework is applied to extract effective coupling filters between the neurons, based on the spike train recordings. These couplings will in general be causal and asymmetric. (C) By thresholding, a binary coupling matrix A_ij is obtained where a non-zero entry represents a directed influence from neuron i to neuron j. (D) An equivalent visualization of the matrix is a graph in which the nodes correspond to neurons and directed edges represent the significant causal influences. This graph can then be quantified using graph-theoretic measures.

The construction of the network graph proceeds therefore in three steps. First, we need to extract couplings from time-series observations. Several statistical methods have been proposed that extend beyond simple cross-correlation analysis. A particularly interesting statistical model is the generalized linear model (GLM; McCullagh and Nelder, 1989). GLMs allow the extraction of directed, i.e., causal coupling filters that are conditioned on the whole population response (Figure 1B). This is in contrast to many other proposed schemes that are based only on pair-wise measures or very crude approximations to the overall population activity.

As a second step, each coupling can be further reduced to a binary entry in a connectivity matrix by thresholding (Figure 1C). Since GLMs are set up on the basis of maximum-likelihood estimation, the threshold can be chosen by cross-validation and is therefore not a free parameter of the estimation procedure.

Third, once a graph of the effective connectivity is estimated (Figure 1D), its structural properties can be studied (Bullmore and Sporns, 2009; Rubinov and Sporns, 2010). Two notions have been influential in the analysis of biological networks: small-world (Watts and Strogatz, 1998) and scale-free networks (Barabási and Albert, 1999). The latter are characterized by the fact that their degree distribution, i.e., the distribution of the number of incoming or outgoing links at each node, can be described by a power-law.

Small-world networks show a highly clustered structure while retaining an overall low average path length between any two nodes (see Section 2.4 for a formal definition). In simulation studies, it has been shown that small-world topology can evolve from certain optimality considerations (Sporns et al., 2000) and synaptic plasticity rules (Cho and Choi, 2010). A functional role of small-world structures has been hypothesized for improved memory recall in associative networks (Morelli et al., 2004) and faster and more reliable synchronizability (Lago Fernández et al., 2000).

Both concepts of scale-free and small-world networks have been empirically studied in the context of neuroscience, especially in systems neuroscience where connectivity between different brain areas was studied using coarse-grained signals such as fMRI, EEG, or MEG (see, e.g., Reijneveld et al., 2007; Bullmore and Sporns, 2009; Chavez et al., 2010; Sepulcre et al., 2010). Only very few studies have attempted to quantify small-world properties of neural networks on the level of individually recorded neurons (Bettencourt et al., 2007; Yu et al., 2008). These studies suffer from a number of flaws: First, they consider only networks that were obtained from in vitro preparations or anesthetized animals. Furthermore, their estimates of the connectivity matrix were either based on pair-wise measures (Bettencourt et al., 2007) or used very crude approximations to the population activity (Yu et al., 2008). Both studies used undirected (i.e., correlative) measures that did not offer any notion of causality.

In this paper, we attempt to overcome most of these limitations by using multi-electrode recordings from the awake monkey on a larger data set than in previous approaches. The monkey was exposed to naturalistic video sequences while activity was recorded from a set of neurons in the visual cortex, using multiple electrodes. We investigate scale-free and small-world properties of neuronal networks using directed couplings estimated by GLMs. For this, the quantity proposed by Humphries and Gurney (2008) for quantifying small-world-ness has to be generalized to directed networks. We find that the networks under consideration lack scale-free behavior, but show a small, but significant small-world structure.

We show that the design of typical electrophysiological experiments imposes a particular sampling scheme that can have a considerate impact on how the small-world structure of the network is evaluated (Bialonski et al., 2010). Random graphs that take the geometry of the experiment into account can serve as a more refined null model than the homogeneous random graphs that are usually proposed as reference models to evaluate small-world properties. Using such refined reference models, we find that most of the small-world structure can be attributed to a simple distance-dependent connection probability between neurons. Finally, typical experimental methods are based on sub-sampling from a larger network. We investigate how this sub-sampling is likely to affect the estimation of small-world properties by simulating multi-electrode experiments in a virtual network of neurons that are coupled in a physiologically plausible way.

2 Materials and Methods

The general approach taken in this paper can be split into an analysis of experimental recordings, followed by several computational steps and a simulation to model the impact of sampling effects on the reconstructed topology of neural networks. The methods used in each step are outlined below.

2.1 Experimental Setup

All experimental procedures were approved by local authorities (Regierungspraesidium Hessen, Darmstadt, Germany) and were in accord with the guidelines of the European Community for the care and use of laboratory animals (European Union directive 86/609/EEC).

Data was obtained with one rhesus monkey (Macaca mulatta). The monkey had to perform a fixation task. During fixation, short excerpts from natural movies were shown. The gray-scaled movies were recorded indoors in the lab and outdoors on the fields and contain global movement patterns that resemble those generated by natural head-movements. A trial consisted of a baseline of 2.2 s and the visual stimulation of 2.8 s length. For the present analysis, we restricted analysis to the time windows in which the stimulus was presented.

Recordings were made from the opercular region of V1 (receptive fields centers, 2.0–3.0° eccentricity) and from the superior bank of the calcarine sulcus (10.0–13.0° eccentricity). Electrodes were inserted independently into the cortex via guide tubes positioned above the dura (diameter, 300 μm; Ehrhardt Söhne, Germany), assembled in a customized recording device. Quartz-insulated tungsten–platinum electrodes (Thomas Recording, Germany; diameter, 80 μm) with impedances ranging from 0.3 to 1.0 MΩ were used to record simultaneously the extracellular activity from several sites in both superficial and deep layers of the cortex.

Spiking activity of small groups of neurons (MUA) were obtained by amplifying (1000×) and band-pass filtering (0.7–6.0 kHz) the recorded signals with a customized 32 channels Plexon pre-amplifier connected to a HST16o25 headset (Plexon Inc., USA). Additional 10× signal amplification was done by on-board amplifiers (E-series acquisition boards, National Instruments, USA). The signals were digitized and stored using a LabVIEW-based acquisition system. Spikes were detected by amplitude thresholding, which was set interactively after on-line visualization of the spike waveforms (typically, 2–3 SDs above noise level). Spike events and corresponding waveforms were sampled at 32 kS/s (spike waveform length, 1.2 ms).

Off-line spike-sorting was performed using a dynamic template matching method implemented in a custom software package (SpikeOne, developed by Nan-Hui Chen). Sorting was initiated by an automatic procedure which defined up to 12 different clusters. Afterward, various displays, such as tuning curves, autocorrelograms, and measurements of recording stability were used to guide interactively which cluster to merge or delete. Only clusters well-separated in 2D and 3D plots of spike principal-component-analysis scores were assigned to single-units (SUA) if a refractory period was confirmed in inter-spike interval distributions (Figure 2B). Only trials for which fixation was maintained over the stimulus presentation were included in the analysis. For neurons with low firing rates (<4 Hz), the responsiveness to the stimulus can hardly be detected, so we restricted analysis to cells with an average firing rate of more than 4 Hz. Sorted cells with very high firing rates (>100 Hz) seem unphysiological and were excluded from the data set, too.

FIGURE 2

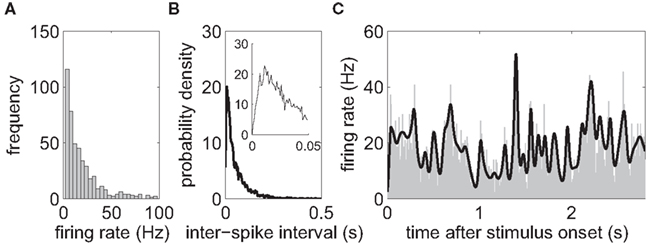
Figure 2. Basic data analysis. (A) Histogram of the average firing rate of each neuron during the stimulus presentation (N = 455 neurons). The neural firing rates have a mean of 20.9 Hz with SD of 18.6 Hz. Sorted cells with average rates below 4 Hz and above 100 Hz were excluded from the analysis. (B) Histogram of the inter-spike interval distribution of a single neuron, pooled over all trials. For better visibility, only inter-spike intervals shorter than 500 ms are shown. The neuron had an average firing rate of 17.6 Hz. The inlet zooms into the range of intervals up to 50 ms. The distribution is unimodal and a relative refractory period is visible. (C) Peri-stimulus-time histogram (PSTH) for a single neuron, obtained by averaging over 92 trials (gray area). The prediction of the firing rate based on the stimulus-dependent component g_stimulus(t) only (black line, see Section 2.2 for a definition) closely follows the shape of the PSTH.

The number of electrodes used in each recording varied from session to session, ranging between 3 and 10 electrodes. In most recordings, five electrodes were used. Due to the results of spike-sorting and the position of the electrodes, the number of identified cells varied, too. On average, there were 27 individual neurons identified (SD = 9, min. = 16, max. = 44). Each data set contained on average 71 trials (SD = 33, min. = 32, max. = 147; see Figure 2C for a typical PSTH). In total, there were 455 neurons. The neural firing rates had a mean of 20.9 Hz with SD of 18.6 Hz (Figure 2A).

2.2 Generalized Linear Models

Since all spikes of a given neuron have roughly the same shape, spikes can be treated as stereotypical events in time and are mathematically represented as a point process. When the spike train is divided into bins, this allows the representation of the spike train as a time series of discrete counts. If the bin width is chosen small enough, the spike train is approximated by a binary time series, indicating the presence of a single spike inside a given time bin (Brillinger, 1988).

For GLMs (McCullagh and Nelder, 1989), the probability of spiking is a function of a stimulus, the neuron’s own past activity, and the activity of the other neurons in the recorded network (Okatan et al., 2005; Truccolo et al., 2005). The coupling to the past activity of the neurons is mediated by temporally filtering the spike trains with self- and cross-history kernels. It has been shown that this type of neuron model is equivalent to a spike response model with a particular noise term using the escape-rate approximation (Gerstner and Kistler, 2002; Paninski, 2003). Moreover, these models can predict not only the spike times, but also the subthreshold membrane potential during patch recordings (Jolivet et al., 2004).

To describe multi-neuron data, the network of neurons is modeled as a Markov dynamical network, as the spiking process is intrinsically stochastic. It consists of a directed graph in which the N vertices correspond to neurons and M directed edges represent causal interactions between the neurons. We restrict ourselves to simple directed graphs, i.e., there is no more than one edge between an ordered pair of vertices. Note that two neurons i and j can be connected by up to two edges, one from i to j and another one from j to i. Additionally, there are no self-loops. In other words, the adjacency matrix is binary with zeros on the diagonal. Moreover, we consider the graph topology as static, i.e., the structure of edges and vertices does not vary over time.

For the dynamics at each vertex, we used Bernoulli-GLMs. These are time-discretized models of the conditional intensity function λ(t | H_t) that generalizes the concept of an instantaneous firing rate, conditioned on the history H_t of the point process (Daley and Vere-Jones, 2002):

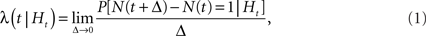
where N(t) denotes the number of events inside the time interval [0, t] (counting function). The benefit of using the conditional intensity for point processes is that it is closely related to the log-likelihood of a point process:

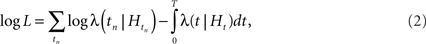
where {t_n} denotes the set of spike times in the interval [0, T]. Hence, maximum-likelihood estimates can be easily obtained with parametric models of the conditional intensity (Pawitan, 2001).

The spiking intensity is a function of the effective drive h of the neuron that contains the stimulus and the neurons’ past spiking activities: h = β₀ + g_history(t) + g_ensemble(t) + g_stimulus(t), where g_history(t) summarizes the effect of the neuron’s own past spikes, g_ensemble(t) the effect of the spikes of other neurons in the recorded ensemble, and g_stimulus(t) is the modulation by the stimulus. The bias term β₀ adjusts the overall excitability of the neuron, i.e., its baseline firing rate.

For Bernoulli-GLMs, the spiking probability λ(t | H_t)Δ within a small time bin of width Δ is related to the effective drive h through a static non-linearity:

Rewriting and taking the logarithm, we get:

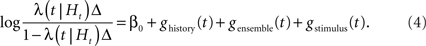
Here we used Δ = 1 ms. Because of an absolute refractoriness, this is sufficient to constrain the number of spikes in each time bin to either 0 or 1.

The history-dependent part depends on the neuron’s own previous spikes and describes the relative refractoriness and adaptation effects. The filters are represented with a set of spline functions (Kass and Ventura, 2001; Koyama and Kass, 2008). Each spline function is a piece-wise polynomial of degree 3, where additionally the polynomials are joined at knot points such that the resulting function is twice continuously differentiable. Splines allow a smooth filter approximation using only a small number of free parameters. Here, we chose m_h = 7 basis splines (B-splines of order 3) with non-uniform knot spacings (De Boor, 2001). Knot points are spaced on a roughly logarithmic scale up to 64 ms (Figure 3A). This temporal range was chosen after the observation that the magnitude of most estimated filters decline back to zero well within the first 20–40 ms (Figure 3B). Let the jth spline be of shape B_j(Δt), then the history term on the right-hand side of Equation 4 for neuron i is:

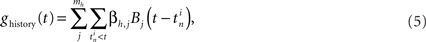
where denotes the set of spike times of neuron i and β_h,j are the model coefficients to be estimated from the data. The auto-regressive component g_history(t) will model longer-lasting refractory effects (negative coefficients) or rebound-like oscillatory behavior (positive weight coefficients).

FIGURE 3

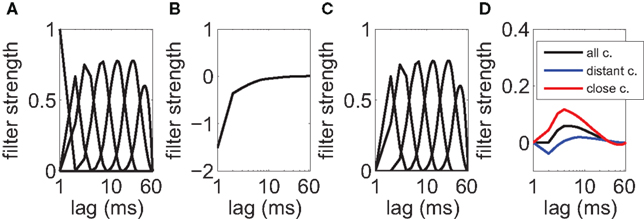
Figure 3. Coupling filters in the generalized linear model. (A) Spline basis functions that are used for the spike-history kernel. Note the logarithmic scale on the x-axis. (B) Mean filter that was obtained for the self-history dependencies (auto-regressive component) after fitting. A refractory period with a time constant of around 10 ms is visible. (C) Spline basis functions that are used for the cross-history kernels. (D) The mean filter for cross-dependencies fitted from the data shows a slight excitatory impact from other neurons (black line). The average over pairs of neurons at the same electrode (red line) shows that most close couplings are effectively excitatory. The mean coupling between distant pairs (blue line) shows a biphasic response in time.

The ensemble contribution is the past activity of the other recorded cells. It describes the effect of all excitatory or inhibitory postsynaptic potentials on the current drive of neuron i. The term g_ensemble(t) is mathematically similar to the self-history term, but sums over all the past histories of the other neurons:

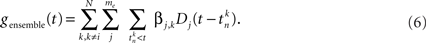
In the above, the m_e = 6 spline basis functions D_j(Δt) are similar to the self-history basis with the modification that instantaneous couplings (within the same time bin and up to 2 ms into the past) are excluded to prevent that any spurious correlations that remain despite careful spike-sorting show up in the coupling matrix (Figure 3C). The combination of six basis functions enables us to describe a wide range of potential time courses of excitatory and inhibitory interactions between pairs of neurons over a large temporal range (Figure 3D).

The stimulus term is modeled using basis splines so that the firing rate can vary as a function of the time since stimulus onset. m_s = 74 basis splines C_j(t) splines with uniform spacing over the trial length of 2.8 s were used. The stimulus term is thus given by:

Modeling the external input g_stimulus(t) to each neuron requires careful attention. This term describes the modulatory impact of the presented visual stimulus to the firing response of the neuron over time (Figure 2C). Hence, we assume that this modulatory response is the same for all trials in which the same stimulus was presented. It is important to explicitly describe the influence of the stimulus on the neural responses in order to account for spike correlations that are purely stimulus-induced and not due to effective connectivity.

All model coefficients 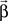and their significance values are estimated using standard maximum-likelihood methods (McCullagh and Nelder, 1989; Pawitan, 2001).

2.3 Inferring Effective Connectivity

The vertices of the graph are associated with the neurons and the edges are representing significant effective connections – effective as opposed to anatomical connection, because the interactions are inferred only based on the observed spiking activity (Aertsen et al., 1989). Functional connectivity is used in the literature as a term for symmetric measures that do not infer a causal direction of interaction (Bullmore and Sporns, 2009).

Since the estimation procedure of Section 2.2 will typically give non-zero parameters to all connections, the network graph will initially contain connections between each pair of neurons. However, not all of these interactions contribute significantly to the activity of a neuron. The maximum-likelihood estimation also yields p-values for each parameter to estimate its significance. Coefficients of stimulus modulation and self-history turn out to be highly significant and are therefore always included. Directed cross-couplings are kept if at least one of the coefficients of the filter is significant, i.e., its p-value is smaller than the Bonferroni-corrected significance level α (p < α/m_e). All other connections are removed. The remaining vertices form a graph whose structure is further analyzed.

The threshold α for binarizing the coupling matrix is determined using split-sample validation: The full model with all-to-all connections is fitted on 80% of the data (training set). Then, for a wide range of thresholds α, pruned models are generated by removing non-significant filters that do not satisfy the threshold criterion. The constant coefficient β₀, i.e., the bias in Equation 4, of the reduced models is then re-estimated on the training data to correct for changes in global excitability due to the removal of connections. The performance of these models is then evaluated on the 20% of the data that was not used for fitting (test set). The model with optimal threshold is the one with maximum likelihood on the test data.

2.4 Graph-Theoretical Analysis

The graph of the inferred coupling structure consists of N vertices and M directed edges. This corresponds to an edge density of ρ = M/(N² − N). We use three different measures to quantify the topology of the graph.

First, basic measures of the graph topology are the in- and out-degree distributions and the average degree 〈k〉. The in-degree denotes the number of incoming links at each vertex while the out-degree counts the number of outgoing edges.

Second, the characteristic path length L of a network is the average of the shortest paths lengths between any connected pair of nodes. To evaluate small-world properties, surrogate random networks (Erdös–Renyi random graphs) are considered that preserve the number of vertices N and the average density ρ. The characteristic path length of the equivalent random network is denoted L_r. Here, L_r is calculated by averaging over 500 realizations of random networks. For small-world networks, the characteristic path length scales only logarithmically with the network size (Albert and Barabási, 2002). The same scaling is observed in random networks (Fronczak et al., 2004). In other words, for small-world networks the average distance between any two nodes should be approximately equal to the one of a random network with the same size and connection density:

Third, the clustering coefficient for a vertex i has been defined for undirected graphs as the fraction of pairs of neighbors of vertex i who are themselves neighbors. The cluster coefficient of the complete network is taken as the average of the local coefficients. This notion has been generalized to directed networks (Fagiolo, 2007): Given a vertex i and two of its neighbors, there are potentially eight different directed triangles. The cluster coefficient is calculated as the number of realized triangles divided by the possible number of triangles (i.e., eight) with each pair of neighbors. Let the adjacency matrix be denoted by A with elements (a_ij), then the clustering coefficient C_i at vertex i can be written as (Fagiolo, 2007):

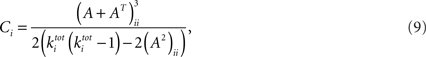
where 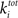is the sum of incoming and outgoing edges at vertex i. The clustering coefficient for the whole network is given by:

This generalized clustering coefficient has two important properties: First, it reduces to the classical clustering coefficient in case of undirected graphs. Secondly, for a directed Erdös–Renyi random graph with wiring probability ρ, 〈C〉 = ρ, just as in the undirected case.

To evaluate the small-world property, we are interested in the clustering coefficient of the network compared to that of a random network. Let C_r denote the clustering coefficient of an equivalent random network (matched size and connection density, averaged over 500 random realizations), then we can define for small-world networks:

We have discussed three different topological measures. The first one, the degree distribution, is used as a measure for the scale-freeness of a network: A graph is said to be scale-free if its degree distribution follows a power-law (or at least a truncated power-law for large degrees; Fronczak et al., 2004). The second (characteristic path length) and third (clustering coefficient) both relate to the concept of small-world networks. It was proposed to measure “small-world-ness” Sw in a single number as the fraction of γ and λ (Humphries et al., 2006; Humphries and Gurney, 2008):

Though the original definition was based on undirected networks, we propose here to use the γ and λ defined for directed networks. From a combination of Equations 8 and 11 we get a measure of small-world-ness for directed graphs:

To assess the statistical significance of an observed Sw, surrogate Sw values are calculated from random networks. Based on this distribution (that scatters around 〈Sw〉 = 1), a z-score and a corresponding p-value (one-sided test) can be calculated.

3 Results

3.1 Basic Results

The complete data set has been collected in 20 recording sessions, each with a different electrode placement (see Section 2.1 for details). For all population models, a goodness-of-fit test that is commonly used for point process models was applied (Brown et al., 2002; Haslinger et al., 2010). Only data sets, for which at least 80% of the neurons passed the test, were kept. This excluded 3 data sets from the analysis so that the following analysis was performed on the remaining 17 data sets. Figure 3 shows typical filters that were estimated for the auto-regressive and cross-regressive components. Some of the cross-interactions had a biphasic time course with a fast excitatory component and a slower inhibitory interaction. These could potentially be interpreted as a direct excitatory feed-forward component combined with an indirect interaction via inhibitory interneurons that were not picked up by the electrodes (see also Kriener et al., 2009 for a discussion on effective inhibitory couplings between neurons).

Only significant couplings between neurons were considered to construct the connectivity matrix with binary links between neurons (one example is shown in Figure 4). The significance of a coupling is indicated by the p-values that are assigned to each model parameter by the estimation procedure. The threshold to convert the coupling filters into a binary estimate of the effective connectivity was set to α = 0.05 after performing the validation scheme (see Section 2.3; Figure 5). A region of optimal values for the threshold was found to be between α = 0.02 and 0.08. The qualitative results of the following analysis do not depend on the exact choice of a within this region (data not shown).

FIGURE 4

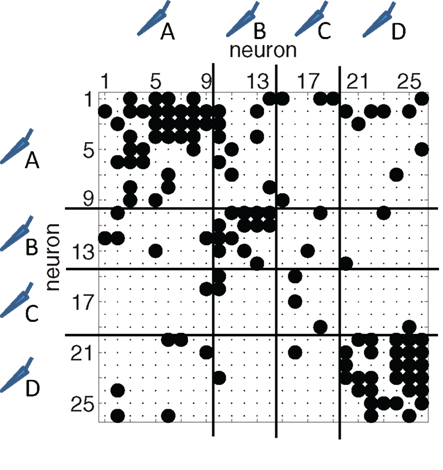
Figure 4. Typical binary connectivity matrix from one reconstructed network with N = 26 neurons. A non-zero entry at row i and column j indicates a directed link from neuron i to neuron j. Neurons are sorted according to the electrode from which they were recorded from. In this example, four electrodes were used (A–D, the separation is indicated with the horizontal and vertical lines). Connections between neurons at the same electrode show up in blocks along the diagonal.

FIGURE 5

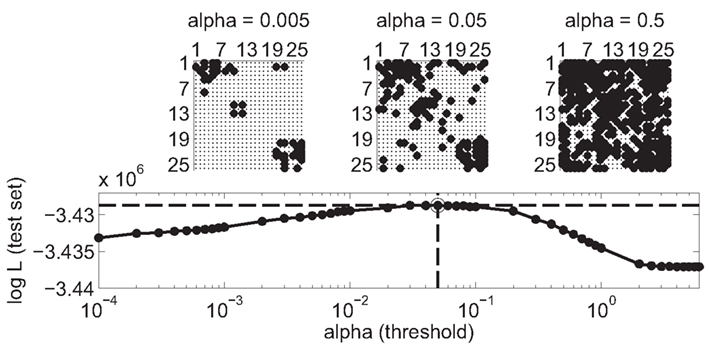
Figure 5. Choice of threshold for binary connectivity matrix. The model is fitted on 80% of the data set (training set). Reduced models are created by applying a threshold a on the significance value of estimated coefficients for the cross-coupling terms. The performance of the models is evaluated on the 20% remaining data (test set). Performance is measured with the log-likelihood of the data (larger value indicates a better model). A broad regime from 0.02 ≤ α ≤ 0.08 of optimal threshold is visible. In the study, α was set to 0.05 (circle and dashed lines). The choice of threshold directly influences the edge density of the reconstructed graph. Examples of connectivity matrices are shown for different choices of threshold (α = 0.005, 0.05, and 0.5). A non-zero entry at row i and column j indicates a directed link from neuron i to neuron j. Neurons are sorted according to the electrode from which they were recorded from.

Note that the choice of the threshold has a direct influence on the inferred edge density (the probability to find a directed link between neurons i and j if they are randomly picked; see Figure 5): For the given threshold of α = 0.05, the edge density ρ of the reconstructed coupling matrix varied across the 17 data sets between ρ = 0.07 and 0.19 (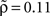). Thus, the values of ρ are consistent with estimates of cortical connectivity from paired whole-cell recordings (Song et al., 2005).

3.2 Cortical Networks do not Show Scale-Free Structure

In each of the 17 connectivity graphs, we count the number of incoming links converging onto a neuron (in-degree) as well as the number of outgoing links (out-degree). Across recording sessions, the mean in- and out-degrees vary between 1.6 and 4.9 with an average of 2.9. The distributions are peaked around their mean value with a slight skew to the right (Figure 6).

FIGURE 6

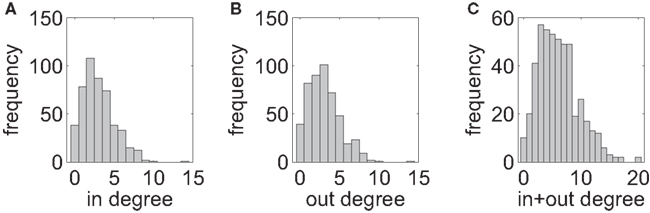
Figure 6. Degree distributions, summed over all 17 data sets. (A) In-degree. (B) Out-degree. (C) Summed in- and out-degrees per vertex. There is no indication of a power-law for any of the three distributions as it would be required for scale-free networks.

A scale-free network requires a degree distribution that can be described by a power-law with negative exponent. The distributions are not even monotonically decreasing, so there is no indication for a power-law behavior. Even if the distribution were monotonic, the limited size of the networks would not allow to faithfully confirm a scale-free-like behavior. This is because the range of possible values for the degree barely span two orders of magnitude that are not sufficient for sound statistical tests of power-laws (Clauset et al., 2009; De Lomana et al., 2010).

3.3 Cortical Networks Show a Small, but Significant Small-World Structure

To assess the extent of small-world structure present in the recordings, we need to evaluate the typical distance between any two neurons within the network. The average characteristic path length (see Section 2.4) of the networks is L = 2.7 ± 0.4 (mean ± SD). A comparison with the path lengths L_r expected in a random network of the same size yields λ = L/L_r = 0.97 ± 0.10 (see Figure 7 for summary statistics). Hence, the characteristic path lengths are in the range expected from equivalent random networks.

FIGURE 7

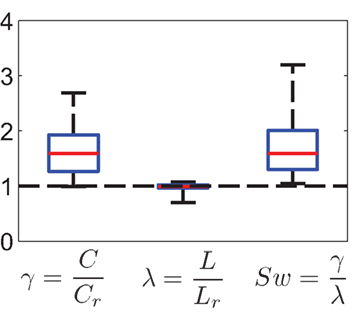
Figure 7. Summary statistics of small-world property (N = 17 networks). The left box plot represents the distribution of γ = C/C_rand, the middle box plot shows λ = L/L_rand, and the small-world-ness measure Sw = γ/λ is shown on the right plot. All Sw were larger than 1. The baseline for random networks corresponds to the dashed line. Red line denotes median, boxes represent 25 and 75% quantiles. Whiskers extend to the extremal values.

Next, we asked whether neighboring neurons are more likely to have a common joint neighbor than expected from an equivalent randomized network: The average clustering coefficient C is 0.18 ± 0.08, with γ = C/C_r = 1.62 ± 0.44. The small-world coefficient Sw varies between 1.05 and 3.19 with a mean of Sw = 1.71 (SD = 0.57; Figure 7). In fact, 7 out of the 17 data sets with Sw > 1 have a highly significant small-world-ness (p-values <0.001).

3.4 Distance-Dependent Connectivity Accounts for Observed Small-World Structure

In the present study, as well as in most previous approaches (Bettencourt et al., 2007; Yu et al., 2008), multiple electrodes were used to obtain the multi-neuron signals. This imposes certain constraints on how the neurons of the whole network are sampled: Each electrode picks up the neural activity from a few cells that are close to the electrode tip. Typically, these neurons are only a few micrometer apart. In contrast, the different electrodes are placed in most experiments with a distance of several hundreds of micrometers. It is known that the probability for two neurons to form a synaptic connection is strongly dependent on their physical distance (Hellwig, 2000; Holmgren et al., 2003; Matsuzaki et al., 2008; Stepanyants et al., 2009).

The high connection probability between near-by neurons manifests itself in a high local clustering coefficient, while sparse long-range connections between neurons from different electrodes introduce the shortcuts necessary to create a significant small-world effect (Bialonski et al., 2010). For many of the reconstructed networks, the small-world structure is clearly visible in the binary connectivity matrix (Figure 4). The clustering structure of the network coincides with the spatial constraints that are imposed by the use of multiple electrodes (Figure 8A). We wondered whether the assumption of a simple distance-dependent wiring probability could account for the observed small-world structure obtained by this kind of multi-electrode recordings.

FIGURE 8

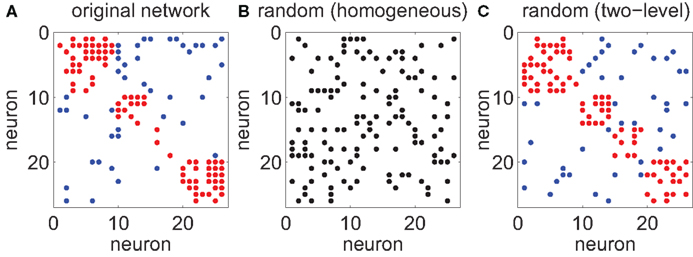
Figure 8. Refined null models to account for multi-electrode setup. (A) The original connectivity structure inferred from a multi-electrode experiment. A non-zero entry at row i and column j indicates a directed link from neuron i to neuron j. Neurons are sorted according to the electrode from which they were recorded from. Links between neurons at the same electrode are represented as blocks along the diagonal (red dots). All other links are between neurons from different electrodes (blue dots). (B) Small-world-ness Sw is defined against a reference network. For the classical measure, the reference network is a homogeneous Erdös–Renyi random graph of the same size as the original network and the same connection density ρ, i.e., each link between any two neurons is present with the same probability. (C) For multi-electrode recordings, there are two principal length scales: distances between neurons at the same electrode and distances across electrodes. Pairs of neurons at the same electrode (red dots) are assumed to have a different connection density ρ₁ than pairs of neurons from different electrodes (blue dots, ρ₂). Empirically we find ρ₁ > ρ₂ which is consistent with a monotonically decreasing distance-dependent wiring probability.

The classical small-world-ness (Equation 13) is defined with respect to a reference network, i.e., a homogeneous Erdös–Renyi random graph of the same size and average connection density ρ as the original network (Figure 8B). Here, we propose to measure small-world-ness against a refined null model in which there are two regimes of connection probabilities: ρ₁ corresponds to a wiring probability between neurons that share the same electrode tip, while ρ₂ is the probability of a directed connection between two neurons from different electrodes (typically ρ₂ < ρ < ρ₁; Figure 8C). Surrogate networks can now be constructed that use the same number of electrodes and neurons per electrode and estimated ρ₁ and ρ₂ from the data set.

Normalizing the empirically observed clustering coefficients and path lengths to these networks yields a modified small-world-measure Sw* (analogously to Equation 13). Any value of Sw* higher than 1 now indicates small-world structure that goes beyond the structure expected from multi-electrode recordings and a simple two-layered distance-dependency.

In fact, taking the simple distance-dependent wiring probability into account, we find that the modified small-world-ness Sw* has a mean of 1.37 with SD 0.49. The individual small-world-ness of each network is reduced by more than 60% with respect to the baseline condition Sw = 1 (Figure 9). More importantly, none of the 17 values is now highly significantly different from one (p < 0.001). Hence, a simple two-stage distance-dependent connection probability can account for most of the observed small-world structure.

FIGURE 9

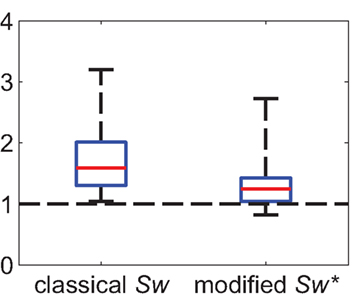
Figure 9. Summary statistics of modified small-world-ness (N = 17 networks). The left box plot shows the distribution of the classical small-world-ness parameter Sw with homogeneous random graphs as reference networks. The right box plot shows the distribution of the modified small-world-ness, taking into account two different connection probabilities. The individual small-world-ness of each network is reduced by more than 60% compared to the baseline of Sw = 1 (dashed line). Red line denotes median, boxes represent 25 and 75% quantiles. Whiskers extend to the extremal values.

3.5 Localized Sub-Sampling Overestimates True Small-World-Ness

Any electrophysiological recording constitutes a sub-sample of the true network activity. It is known that sub-sampling can severely affect how structural properties of the network are estimated (Stumpf et al., 2005; Lee et al., 2006). Moreover, recordings with multiple electrodes give a biased picture of the overall connectivity: Neurons are either very close in space (at the same electrode) or distant (in the range of millimeters) so that only two characteristic length scales are sampled.

To study the effect of sub-sampling on the estimation of small-world-ness, we performed a simulation study by placing neurons in a virtual volume, wiring them according to a distance- dependent probability distribution and inserting virtual electrodes that sub-sample the global connectivity graph. As we are interested in the topological properties of the network, we did not explicitly model the neural spiking activity, but assumed that all connections between the sampled neurons can be perfectly recovered. When mimicking a multi-electrode experiment, a neuron is included in the sub-graph if it is close to one of the virtual electrode positions. In the control condition, the same number of neurons is randomly chosen across the overall network.

More specifically, N = 1000 point neurons were placed in a 3D volume and directed edges were inserted with a distance-dependent probability law p(d) which we assumed to be a power-law with a baseline p₀:

where a is the power-law exponent and the amplitude k ensures that the values of p(d) can be interpreted as a probability over the range of distances in our simulated graph. We chose a power-law because it is a monotonically decreasing function and its heavy tail ensures a finite amount of long-range connections. Its qualitative shape is consistent with experimental evidence on cortical connectivity (Hellwig, 2000; Holmgren et al., 2003; Matsuzaki et al., 2008), although we note that other functions, such as an exponentially decaying profile or constant local connectivity with global rewiring could be used as well (Voges et al., 2007, 2010). To ensure that the results are independent of the exact shape of p(d), we varied the exponent of the power-law a between 1 and 3. This range of exponents covers the values found empirically for both neural and non-biological, as well as generative models for growing networks (Barabási and Albert, 1999; Humphries et al., 2006).

The small-world-ness Sw (Equation 12) can be computed for the overall network. We then mimicked a multi-electrode experiment by placing N_e = 6 electrodes randomly in the volume and assumed that each neuron that is within a certain radius around the electrode tip is included in the sub-sampled connectivity graph (Figure 10A). The radius relates to the average number of neurons per electrode and was matched to the experimental conditions. The coefficients of the connection density (Equation 14) were chosen so as to match the typical densities ρ₁ and ρ₂ of connections at the two characteristic length scales (Figure 10B, boxes). We assume that all connections between the sub-sampled neurons can be perfectly recovered and estimated the small-world-ness.

FIGURE 10

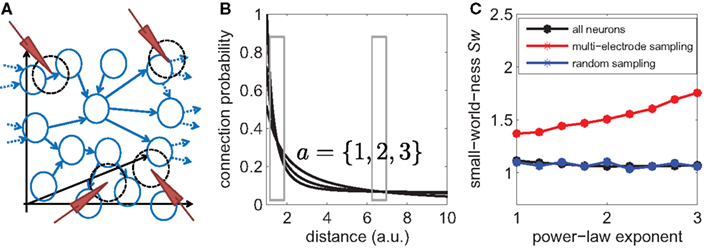
Figure 10. Localized sub-sampling overestimates true small-world-ness. (A) Scheme of the simulation of the network topology. Neurons were placed in a 3D volume and linked with a distance-dependent wiring probability. Virtual electrodes were placed in the volume assuming that each electrode can pick up the neurons and their connections within a certain radius around the electrode tip. This represents the typical sampling geometry of multi-electrode recordings. (B) The distance-dependent probability was assumed to be a power-law with a constant baseline p(d) = p_o + kd^−a. The simulations were repeated for different exponents a. The distributions are shown here for a = 1, 2, and 3. The parameters were matched in each case to obtain the same average densities as found in the experiments for the two principal length scales (gray boxes). (C) The small-world-ness of the big network is shown as a function of the power-law exponent (black line). There is a small, but non-trivial small-world structure visible. The small-world-ness that is obtained by sub-sampling using a localized sampling scheme (“multi-electrode sampling,” red line) shows that the small-world-ness is generally overestimated, independent of the exact shape of the connectivity distribution. Random sub-sampling using the same degree of sparsity, however, has little effect on the estimate of small-world-ness (blue line).

To distinguish this particular type of localized sampling from the general effect of sparse sub-sampling, we simulated a second condition in which the same number of neurons as for the multi-electrode sampling were selected, but in a completely random manner across the whole network.

The results of the simulation show that such networks composed of a large number of neurons have a rather small, but non-trivial small-world structure (Sw ∼ 1.1 over a wide range of power-law exponents; Figure 10C, black line).

We now discuss the effects of the two sampling schemes. First, for the localized sub-sampling, we find that the estimated small-world-ness is much higher than the true small-world-ness of the whole network: If measured as Sw − 1, the alleged small-world-ness is higher by a factor of up to 8 compared to the true value. This results holds independently of the exact shape of the probability law (power-law exponents varied between 1 and 3; see Figure 10C, red line).

Using the sampling geometry of typical multi-electrode experiments, only a small sub-sample of N_sub = 26 neurons out of the total N = 1000 neurons were selected. To rule out that the observed bias is merely because of this sparse sub-sampling, we estimated small-world-ness using a second simulated sampling scheme, using the same number of 26 neurons but chosen completely randomly from the network. As can be seen in Figure 10C (blue line, “random sampling”), sparse random sub-sampling has only little effect on the estimated value of the small-world-ness.

We conclude that it is the special locality constraint that typical multi-electrode experiments impose on the measured connectivity and not the sub-sampling per se that gives rise to an overestimation of the true small-world-ness.

4 Discussion

4.1 Effective Connectivity Using Generalized Linear Models

We have presented a graph analysis on a network of individually recorded neurons whose effective connectivity was estimated using a regression framework. Extracting connectivity structure from large-scale recordings is a topic of ongoing investigations (Okatan et al., 2005; Gürel et al., 2009; Stevenson et al., 2009; Eldawlatly et al., 2010). Typically, such analyses use the raw pair-wise correlation coefficient (see, e.g., Marre et al., 2009 for a discussion) or, more recently, pair-wise Ising models fitted to population data (Schneidman et al., 2006; Roudi et al., 2009). None of these methods infers the direction of the interaction, hence, they always produce symmetric connectivity matrices. The GLM framework permits to estimate causal, i.e., directed interactions and will, in general, result in asymmetric connectivity matrices.

The estimation procedure of GLMs leads to temporal coupling filters for each directed link between two neurons that can be interpreted as the effective excitatory or inhibitory interaction. Here, we used a spline basis function representation of the filter. There are several ways to reduce the shape of the filter into a single number that represents the strength of the interaction: In principle, one can use the raw coefficient magnitudes or features of the temporal filter, such as its amplitude or net integral (Rebesco et al., 2010). However, for complex temporal interactions, such as biphasic responses, the net surface below the filter will not be a good measure of interaction strength. In this study, we used the smallest p-value (or equivalently the highest surprise value) of the spline coefficients to apply the threshold. The significance value measures whether the spiking activity can be better predicted by including the particular covariate and hence is a measure that reflects the importance of a causal interaction better than, e.g., the peak amplitude of the cross-coupling filter.

Since GLMs are based on a likelihood framework, they allow to choose the threshold for binarizing the coupling matrix in a principled manner. Here, we proposed to find a global threshold that would maximize the likelihood of the model on a novel test set. Although this scheme suggests an optimal threshold region (see Section 3.1), the procedure is not guaranteed to be consistent and more sophisticated selection schemes have been proposed (Quinn et al., 2010). Moreover, when going to larger networks, it might become necessary to use regularized GLMs where a sparse prior is assumed on the coefficients of the cross-couplings (Gerwinn et al., 2009, 2010; Rebesco et al., 2010). In addition, performance should be evaluated on artificial data sets where the true connectivity is known (for GLMs, see, e.g., Rebesco et al., 2010). Unfortunately, such a comprehensive comparison of different algorithms and statistical models is still missing.

4.2 Biased Estimation of Small-World-Ness for Experiments with Multiple Electrodes

There have been attempts to use graph theory in analyzing neuroscientific data (see Sporns and Zwi, 2004; Reijneveld et al., 2007; Cho and Choi, 2010 for recent reviews), but typically it is used to study large-scale connectivity, e.g., between different brain regions (Bullmore and Sporns, 2009). Only very few studies address the properties of connections between single neurons. This might be due to technical limitations which prevented the recording from a large number of neurons until a few years ago (Brown et al., 2004).

The number of neurons used in this study is low, but comparable to previous studies: Bettencourt et al. (2007) study three networks between N = 20 and N = 62; Yu et al. (2008) consider three networks between N = 17 and N = 24. Here, we provided evidence on a larger data set with 17 different recordings with the largest network having N = 44 neurons. The limited number of neurons prohibits a detailed analysis of the degree distribution with respect to scale-free properties as the data barely span two orders of magnitude. Still it is visible that the degree distribution is not a monotonically decreasing function so that a strict power-law behavior can be excluded based on the available data.

Based on the generalization of the clustering coefficient to directed, binary networks (Fagiolo, 2007), we proposed a small-world measure for directed networks analogously to Humphries and Gurney (2008). All data sets showed a small-world behavior, although not all values Sw > 1 were statistically significant. However, a large fraction of the networks showed indeed a highly significant small-world behavior. One has to note, that the absolute scale of Sw is still rather low compared to what has been observed in other networks. It was shown in Humphries and Gurney (2008) that Sw scales approximately linear with the network size N for real-world networks which suggests that the order of magnitude that we observe is reasonable for the networks considered here. Also, our results are in general agreement with previous studies on small-world properties of networks of individually recorded neurons (Bettencourt et al., 2007; Yu et al., 2008).

The small-world property of the networks should not come as a surprise. It has been found that neural connectivity is a function of distance between the neurons. Hence, it is expected to find a high, local connectivity and sparser long-range connections. This geometry naturally leads to networks satisfying the small-world criterion (see Section 3.4; Bialonski et al., 2010).

It is known that sub-sampling has an effect on the estimation of basically any network parameter. Stumpf et al. (2005) have shown that randomly sub-sampled networks of scale-free networks are not scale-free themselves. Other empirical studies have found that properties like the clustering coefficient and average distances can dramatically change when the network is only sparsely sampled (Lee et al., 2006). Thus, we cannot expect to be able to extract small-world properties from a massive neural network when we only have access to the activity of a few neurons. Going beyond these earlier studies on random sub-sampling, we have shown here in a simulated network with physiological topology, that using multiple electrodes to sample neurons from the network will generally overestimate the true small-world-ness (Section 3.5). Here, we used a power-law to model the connection probability as a function of physical distance. The results are robust with regard to the exact shape of function, so we expect the same conclusions to hold for other decreasing functions with heavy tails.

The overestimation of small-world-ness arises because each electrode picks up many neurons at the small length scale, but the sampling on the larger scale is limited by the number of electrodes. Since this bias is based on rather general assumptions, it is likely to affect not only the estimations of small-world-ness in this study, but also in previous published reports on small-world structure that are based on multiple-electrode recordings (Bettencourt et al., 2007; Yu et al., 2008).

4.3 Future Directions

We now briefly discuss some solutions to prevent the biases in estimating small-world structure: First, densely packed multi- electrode arrays together with a reliable detection of single-unit activity would remove the bias of a localized, clustered sampling scheme. Secondly, advances in recording techniques have made it possible to record from a large number of neurons of a local population using calcium-imaging and two photon microscopy (Grewe and Helmchen, 2009). This allows the recording of a complete local population of around 50–200 neurons with a temporal precision to resolve single action potentials (Grewe et al., 2010). This strategy therefore creates a sampling from the network that is more uniform than in the case of multiple electrodes. As an alternative to our quantitative approach, Kriener et al. (2009) suggested that small-world signatures can be found in the shape of the distribution of pair-wise cross-correlations.

A second suggestion for future work is to extend the concepts to directed, weighted networks. Instead of thresholding to a binary matrix, it should be possible to work directly with the absolute strength of the inferred connectivity (Boccaletti et al., 2006; Bullmore and Sporns, 2009). The reference or null networks would then not only be of the same size and keep the average degree, but would also conserve the empirical weight distribution. However, the interpretation of the graph-topological quantities would not be straightforward in the context of neural networks (for example, the path length from one node to another would now depend on the coupling strength between the pairs of neurons on the path). In addition, other graph properties could be studied, such as centrality measures (Boccaletti et al., 2006) or network motifs (Sporns and Kötter, 2004; Song et al., 2005).

A final proposal is to look at relative changes of graph topology of the same network, but under different conditions, e.g., different global brain states or stimulation (Bialonski et al., 2010). We expect the effective coupling in a neural network to be task-dependent (Hasson et al., 2009) and altered by the induction of plasticity (Rebesco et al., 2010). Since the biases enter both reconstructed connectivity estimates, relative changes in different conditions should be unaffected. We want to emphasize that other studies looking at large-scale brain connectivity have not just established the presence of small-world structure but have also found changes in the prevalence of this structure depending on clinical conditions, e.g., in neurodegenerative diseases (Reijneveld et al., 2007; Buckner et al., 2009; Chavez et al., 2010). We expect that the same statistical procedures could be applied in the case of networks composed of individually recorded neurons.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Part of the results appeared in abstract form in Gerhard et al. (2010). Felipe Gerhard thanks Martin Hasler for helpful comments on an earlier version of this manuscript. Felipe Gerhard is supported by the Swiss National Science Foundation (SNSF) under the grant number 200020-117975. Gordon Pipa is partially supported by EU project PHOCUS, 240763, FP7-ICT-2009-C.

References

Aertsen, A. M., Gerstein, G. L., Habib, M. K., and Palm, G. (1989). Dynamics of neuronal firing correlation: modulation of “effective connectivity.” J. Neurophysiol. 61, 900–917.

Pubmed Abstract | Pubmed Full Text

Albert, R., and Barabási, A. L. (2002). Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97.

Barabási, A.-L., and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512.

CrossRef Full Text

Bettencourt, L. M. A., Stephens, G. J., Ham, M. I., and Gross, G. W. (2007). Functional structure of cortical neuronal networks grown in vitro. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 75, 021915.

Pubmed Abstract | Pubmed Full Text

Bialek, W., Rieke, F., de Ruyter van Steveninck, R. R., and Warland, D. (1991). Reading a neural code. Science 252, 1854–1857.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bialonski, S., Horstmann, M. T., and Lehnertz, K. (2010). From brain to earth and climate systems: small-world interaction networks or not? Chaos 20, 013134.

Pubmed Abstract | Pubmed Full Text

Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., and Hwang, D. (2006). Complex networks: structure and dynamics. Phys. Rep. 424, 175–308.

Brillinger, D. (1988). Maximum likelihood analysis of spike trains of interacting nerve cells. Biol. Cybern. 59, 189–200.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brown, E. N., Barbieri, R., Ventura, V., Kass, R. E., and Frank, L. M. (2002). The time-rescaling theorem and its application to neural spike train data analysis. Neural. Comput. 14, 325–346.

Pubmed Abstract | Pubmed Full Text

Brown, E. N., Kass, R. E., and Mitra, P. P. (2004). Multiple neural spike train data analysis: state-of-the-art and future challenges. Nat. Neurosci. 7, 456–461.

Pubmed Abstract | Pubmed Full Text

Buckner, R. L., Sepulcre, J., Talukdar, T., Krienen, F. M., Liu, H., Hedden, T., Andrews-Hanna, J. R., Sperling, R. A., and Johnson, K. A. (2009). Cortical hubs revealed by intrinsic functional connectivity: mapping, assessment of stability, and relation to Alzheimer’s disease. J. Neurosci. 29, 1860–1873.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bullmore, E., and Sporns, O. (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198.

Pubmed Abstract | Pubmed Full Text

Chavez, M., Valencia, M., Navarro, V., Latora, V., and Martinerie, J. (2010). Functional modularity of background activities in normal and epileptic brain networks. Phys. Rev. Lett. 104, 118701.

Pubmed Abstract | Pubmed Full Text

Cho, M. W., and Choi, M. Y. (2010). Brain networks: graph theoretical analysis and development models. Int. J. Imaging Syst. Technol. 20, 108–116.

Clauset, A., Shalizi, C. R., and Newman, M. E. J. (2009). Power-law distributions in empirical data. SIAM Rev. 51, 661–703.

CrossRef Full Text

Daley, D. J., and Vere-Jones, D. (2002). An Introduction to the Theory of Point Processes, Vol. 1, 2nd Edn. New York: Springer.

De Boor, C. (2001). A Practical Guide to Splines (Rev. Edn.). New York: Springer.

De Lomana, A. L., Beg, Q. K., De Fabritiis, G., and Villà-Freixa, J. (2010). Statistical analysis of global connectivity and activity distributions in cellular networks. J. Comput. Biol. 17, 869–878.

Pubmed Abstract | Pubmed Full Text

Eldawlatly, S., Zhou, Y., Jin, R., and Oweiss, K. G. (2010). On the use of dynamic Bayesian networks in reconstructing functional neuronal networks from spike train ensembles. Neural. Comput. 22, 158–189.

Pubmed Abstract | Pubmed Full Text

Fagiolo, G. (2007). Clustering in complex directed networks. Phys. Rev. E 76, 026107.

Fronczak, A., Fronczak, P., and Holyst, J. A. (2004). Average path length in random networks. Phys. Rev. E 70, 056110.

Georgopoulos, A. P., Schwartz, A. B., and Kettner, R. E. (1986). Neuronal population coding of movement direction. Science 233, 1416–1419.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gerhard, F., Pipa, G., and Gerstner, W. (2010). Estimating small-world topology of neural networks from multi-electrode recordings. Front. Comput. Neurosci. Conference Abstract Bernstein Conference on Computational Neuroscience. doi: 10.3389/conf.fncom.2010.51.00088.

CrossRef Full Text

Gerstner, W., and Kistler, W. M. (2002). Mathematical formulations of Hebbian learning. Biol. Cybern. 87, 404–415.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gerwinn, S., Macke, J., and Bethge, M. (2009). Bayesian population decoding of spiking neurons. Front. Comput. Neurosci. 3:21. doi: 10.3389/neuro.10.021.2009

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gerwinn, S., Macke, J. H., and Bethge, M. (2010). Bayesian inference for generalized linear models for spiking neurons. Front. Comput. Neurosci. 4:12. doi: 10.3389/fncom.2010.00012

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Grewe, B. F., and Helmchen, F. (2009). Optical probing of neuronal ensemble activity. Curr. Opin. Neurobiol. 19, 520–529.

Pubmed Abstract | Pubmed Full Text

Grewe, B. F., Langer, D., Kasper, H., Kampa, B. M., and Helmchen, F. (2010). High-speed in vivo calcium imaging reveals neuronal network activity with near-millisecond precision. Nat. Methods 7, 399–405.

Pubmed Abstract | Pubmed Full Text

Gürel, T., Rotter, S., and Egert, U. (2009). Functional identification of biological neural networks using reservoir adaptation for point processes. J. Comput. Neurosci. 29, 279–299.

Pubmed Abstract | Pubmed Full Text

Haslinger, R., Pipa, G., and Brown, E. (2010). Discrete time rescaling theorem: determining goodness of fit for discrete time statistical models of neural spiking. Neural. Comput. 22, 2477–2506.

Pubmed Abstract | Pubmed Full Text

Hasson, U., Nusbaum, H. C., and Small, S. L. (2009). Task-dependent organization of brain regions active during rest. Proc. Natl. Acad. Sci. U.S.A. 106, 10841–10846.

Pubmed Abstract | Pubmed Full Text

Hellwig, B. (2000). A quantitative analysis of the local connectivity between pyramidal neurons in layers 2/3 of the rat visual cortex. Biol. Cybern. 82, 111–121.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Holmgren, C., Harkany, T., Svennenfors, B., and Zilberter, Y. (2003). Pyramidal cell communication within local networks in layer 2/3 of rat neocortex. J. Physiol. 551(Pt 1), 139–153.

Pubmed Abstract | Pubmed Full Text

Humphries, M. D., and Gurney, K. (2008). Network ‘small-world-ness’: a quantitative method for determining canonical network equivalence. PLoS ONE 3, e0002051. doi: 10.1371/journal.pone.0002051

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Humphries, M. D., Gurney, K., and Prescott, T. J. (2006). The brainstem reticular formation is a small-world, not scale-free, network. Proc. R. Soc. B Biol. Sci. 273, 503–511.

Iyengar, S. (2001). “The analysis of multiple neural spike trains,” in Advances in Methodological and Applied Aspects of Probability and Statistics, ed. N. Balakrishnan (New York: Taylor and Francis), 507–524.

Jarosiewicz, B., Chase, S. M., Fraser, G. W., Velliste, M., Kass, R. E., and Schwartz, A. B. (2008). Functional network reorganization during learning in a brain-computer interface paradigm. Proc. Natl. Acad. Sci. U.S.A. 105, 19486–19491.

Pubmed Abstract | Pubmed Full Text

Jolivet, R., Lewis, T. J., and Gerstner, W. (2004). Generalized integrate-and-fire models of neuronal activity approximate spike trains of a detailed model to a high degree of accuracy. J. Neurophysiol. 92, 959–976.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kass, R. E., and Ventura, V. (2001). A spike-train probability model. Neural. Comput. 13, 1713–1720.

Pubmed Abstract | Pubmed Full Text

Kass, R. E., Ventura, V., and Brown, E. N. (2005). Statistical issues in the analysis of neuronal data. J. Neurophysiol. 94, 8–25.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Koyama, S., and Kass, R. E. (2008). Spike train probability models for stimulus-driven leaky integrate-and-fire neurons. Neural. Comput. 20, 1776–1795.

Pubmed Abstract | Pubmed Full Text

Kriener, B., Helias, M., Aertsen, A., and Rotter, S. (2009). Correlations in spiking neuronal networks with distance dependent connections. J. Comput. Neurosci. 27, 177–200.

Pubmed Abstract | Pubmed Full Text

Lago Fernández, L. F., Huerta, R., Corbacho, F., and Sigüenza, J. A. (2000). Fast response and temporal coherent oscillations in small-world networks. Phys. Rev. Lett. 84, 2758–2761.

CrossRef Full Text

Lee, S. H., Kim, P. J., and Jeong, H. (2006). Statistical properties of sampled networks. Phys. Rev. E 73, 16102.

Marre, O., Boustani, S. E., Frégnac, Y., and Destexhe, A. (2009). Prediction of spatiotemporal patterns of neural activity from pairwise correlations. Phys. Rev. Lett. 102, 138101.

Pubmed Abstract | Pubmed Full Text

Matsuzaki, M., Ellis-Davies, G. C. R., and Kasai, H. (2008). Three-dimensional mapping of unitary synaptic connections by two-photon macro photolysis of caged glutamate. J. Neurophysiol. 99, 1535–1544.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McCullagh, P., and Nelder, J. A. (1989). Generalized Linear Models. Boca Raton: Chapman and Hall/CRC.

Morelli, L. G., Abramson, G., and Kuperman, M. N. (2004). Associative memory on a small-world neural network. Eur. Phys. J. B 38, 495–500.

Nicolelis, M. A., Ghazanfar, A. A., Faggin, B. M., Votaw, S., and Oliveira, L. M. (1997). Reconstructing the engram: simultaneous, multisite, many single neuron recordings. Neuron 18, 529–537.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nicolelis, M. A. L., Dimitrov, D., Carmena, J. M., Crist, R., Lehew, G., Kralik, J. D., and Wise, S. P. (2003). Chronic, multisite, multielectrode recordings in macaque monkeys. Proc. Natl. Acad. Sci. U.S.A. 100, 11041–11046.

Pubmed Abstract | Pubmed Full Text

Okatan, M., Wilson, M. A., and Brown, E. N. (2005). Analyzing functional connectivity using a network likelihood model of ensemble neural spiking activity. Neural. Comput. 17, 1927–1961.

Pubmed Abstract | Pubmed Full Text

Paninski, L. (2003). Estimation of entropy and mutual information. Neural. Comput. 15, 1191–1253.

Paninski, L., Ahmadian, Y., Ferreira, D. G., Koyama, S., Rahnama Rad, K., Vidne, M., Vogelstein, J., and Wu, W. (2010). A new look at state-space models for neural data. J. Comput. Neurosci. 29, 107–126.

Pubmed Abstract | Pubmed Full Text

Pawitan, Y. (2001). In All Likelihood: Statistical Modelling and Inference Using Likelihood. Oxford: Oxford University Press.

Perkel, D. H., Gerstein, G. L., and Moore, G. P. (1967a). Neuronal spike trains and stochastic point processes. I. The single spike train. Biophys. J. 7, 391–418.

CrossRef Full Text

Perkel, D. H., Gerstein, G. L., and Moore, G. P. (1967b). Neuronal spike trains and stochastic point processes. II. Simultaneous spike trains. Biophys. J. 7, 419–440.

CrossRef Full Text

Pillow, J. W., Shlens, J., Paninski, L., Sher, A., Litke, A. M., Chichilnisky, E. J., and Simoncelli, E. P. (2008). Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature 454, 995–999.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Quinn, C. J., Coleman, T. P., Kiyavash, N., and Hatsopoulos, N. G. (2010). Estimating the directed information to infer causal relationships in ensemble neural spike train recordings. J. Comput. Neurosci. doi: 10.1007/s10827-010-0247-2. [Epub ahead of print].

CrossRef Full Text

Rebesco, J. M., Stevenson, I. H., Koerding, K., Solla, S. A., and Miller, L. E. (2010). Rewiring neural interactions by micro-stimulation. Front. Syst. Neurosci. 4:39. doi: 10.3389/fnsys.2010.00039

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Reijneveld, J. C., Ponten, S. C., Berendse, H. W., and Stam, C. J. (2007). The application of graph theoretical analysis to complex networks in the brain. Clin. Neurophysiol. 118, 2317–2331.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rieke, F., Warland, D., de Ruyter Van Steveninck, R., and Bialek, W. (1999). Spikes: Exploring the Neural Code. Cambridge, MA: The MIT Press.

Roudi, Y., Nirenberg, S., and Latham, P. E. (2009). Pairwise maximum entropy models for studying large biological systems: when they can work and when they can’t. PLoS Comput. Biol. 5, e1000380. doi: 10.1371/journal.pcbi.1000380

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rubinov, M., and Sporns, O. (2010). Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52, 1059–1069.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Santhanam, G., Ryu, S. I., Yu, B. M., Afshar, A., and Shenoy, K. V. (2006). A high-performance brain-computer interface. Nature 442, 195–198.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schneidman, E., Berry, M. J., Segev, R., and Bialek, W. (2006). Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 440, 1007–1012.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sepulcre, J., Liu, H., Talukdar, T., Martincorena, I., Yeo, B. T. T., and Buckner, R. L. (2010). The organization of local and distant functional connectivity in the human brain. PLoS Comput. Biol. 6, e1000808. doi: 10.1371/journal.pcbi.1000808

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Song, S., Sjöström, P. J. J., Reigl, M., Nelson, S., and Chklovskii, D. B. (2005). Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 3, e68. doi: 10.1371/journal.pbio.0030068

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sporns, O., and Kötter, R. (2004). Motifs in brain networks. PLoS Biol. 2, e369. doi: 10.1371/journal.pbio.0020369

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sporns, O., Tononi, G., and Edelman, G. M. (2000). Theoretical neuroanatomy: relating anatomical and functional connectivity in graphs and cortical connection matrices. Cereb. Cortex 10, 127–141.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sporns, O., and Zwi, J. D. (2004). The small world of the cerebral cortex. Neuroinformatics 2, 145–162.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stepanyants, A., Martinez, L. M., Ferecskó, A. S., and Kisvárday, Z. F. (2009). The fractions of short- and long-range connections in the visual cortex. Proc. Natl. Acad. Sci. U.S.A. 106, 3555–3560.

Pubmed Abstract | Pubmed Full Text

Stevenson, I., Rebesco, J., Hatsopoulos, N., Haga, Z., Miller, L., and Körding, K. (2009). Bayesian inference of functional connectivity and network structure from spikes. IEEE Trans. Neural Syst. Rehabil. Eng. 17, 203–213.

Pubmed Abstract | Pubmed Full Text

Stumpf, M. P. H., Wiuf, C., and May, R. M. (2005). Subnets of scale-free networks are not scale-free: sampling properties of networks. Proc. Natl. Acad. Sci. U.S.A. 102, 4221–4224.

Pubmed Abstract | Pubmed Full Text

Truccolo, W., Eden, U. T., Fellows, M. R., Donoghue, J. P., and Brown, E. N. (2005). A point process framework for relating neural spiking activity to spiking history, neural ensemble, and extrinsic covariate effects. J. Neurophysiol. 93, 1074–1089.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Voges, N., Aertsen, A., and Rotter, S. (2007). Statistical analysis of spatially embedded networks: from grid to random node positions. Neurocomputing 70, 1833–1837.

CrossRef Full Text

Voges, N., Guijarro, C., Aertsen, A., and Rotter, S. (2010). Models of cortical networks with long-range patchy projections. J. Comput. Neurosci. 28, 137–154.

Pubmed Abstract | Pubmed Full Text

Watts, D. J., and Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature 393, 440–442.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yu, S., Huang, D., Singer, W., and Nikolic, D. (2008). A small world of neuronal synchrony. Cereb. Cortex 18, 2891–2901.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text