- 1 Department of Computational Biology, Royal Institute of Technology, Stockholm, Sweden
- 2 Stockholm Brain Institute, Karolinska Institute, Stockholm, Sweden
- 3 Department of Numerical Analysis and Computer Science, Stockholm University, Stockholm, Sweden
This study proposes a computational model for attentional blink or “blink of the mind,” a phenomenon where a human subject misses perception of a later expected visual pattern as two expected visual patterns are presented less than 500 ms apart. A neocortical patch modeled as an attractor network is stimulated with a sequence of 14 patterns 100 ms apart, two of which are expected targets. Patterns that become active attractors are considered recognized. A neocortical patch is represented as a square matrix of hypercolumns, each containing a set of minicolumns with synaptic connections within and across both minicolumns and hypercolumns. Each minicolumn consists of locally connected layer 2/3 pyramidal cells with interacting basket cells and layer 4 pyramidal cells for input stimulation. All neurons are implemented using the Hodgkin–Huxley multi-compartmental cell formalism and include calcium dynamics, and they interact via saturating and depressing AMPA/NMDA and GABAA synapses. Stored patterns are encoded with global connectivity of minicolumns across hypercolumns and active patterns compete as the result of lateral inhibition in the network. Stored patterns were stimulated over time intervals to create attractor interference measurable with synthetic spike traces. This setup corresponds with item presentations in human visual attentional blink studies. Stored target patterns were depolarized while distractor patterns where hyperpolarized to represent expectation of items in working memory. Simulations replicated the basic attentional blink phenomena and showed a reduced blink when targets were more salient. Studies on the inhibitory effect of benzodiazepines on attentional blink in human subjects were compared with neocortical simulations where the GABAA receptor conductance and decay time were increased. Simulations showed increases in the attentional blink duration, agreeing with observations in human studies. In addition, sensitivity analysis was performed on key parameters of the model, including Ca2+-gated K+ channel conductance, synaptic depression, GABAA channel conductance and the NMDA/AMPA ratio of charge entry.
Introduction
The phenomenon of attentional blink (AB) was first observed by Broadbent and Broadbent (1987) and later reported as an attentional limit by Raymond et al. (1992). It occurs when two expected stimulus items are presented less than 500 ms apart. A standard experimental method for studying AB is known as the rapid serial visual presentation (RSVP) test. During experimental trials, sequences of symbolic items such as characters or numbers are presented on a computer screen. Individual items are presented approximately every 100 ms (lag) with an exposure time of about 60 ms, although this varies. The subject is told to attend to specific target items and to report verbally or press a button after a trial indicating what was seen. In the dual-task experiment, the subject is told to report on two targets T1 followed by T2 presented serially each trial, if they occur. T2 is likely to be missed if it is presented 200–500 ms after T1. A single-task experiment is often used as a control and entails only reporting T2, if it occurs. AB has been observed in both vision and audition (Tremblay et al., 2005) and is a factor in reaction time (Zuvic et al., 2000). Two common psychological hypotheses for AB are the two-stage model which has capacity limits and the interference model which may not. According to the two-stage model, a stimulus is perceived during a first stage and then processed during a second stage, which takes longer (Chun and Potter, 1995). If T2 is presented before an attended T1 has finished processing the second stage, recognition of T2 can be lost and will not reach working memory. In the interference model, T1, T2 and distractors immediately following T1 and T2 compete for attention in working memory and T2 can be lost due to interference with T1 and distractors (Kranczioch et al., 2003). An alternative hypothesis for AB is known as the locus coeruleus (LC)–norepinephrine (NE) hypothesis (Nieuwenhuis et al., 2005). After a salient stimulus, NE is released from neurons in the LC which project across the neocortex and normally up-regulates attention. The theory asserts that AB results from a refractory period of NE release which lasts about 500 ms.
A phenomenon known as lag 1 sparing occurs when T1 is followed about 100 ms later by T2 and the AB occurrence is reduced. This typically happens only when the items appear in the same spatial location (Visser et al., 1999b). According to Hommel and Akyurek (2005), two common psychological hypotheses for lag 1 sparing are the sluggish gate hypothesis and the competition hypothesis. The sluggish gate hypothesis suggests that during the time attention is focused on T1, T2 can slip in (Chun and Potter, 1995). The competition hypothesis suggests that competition exists for attention of T1 and T2, and the accuracy of recalling T1 and T2 are negatively correlated with each other. If both items are recognized, temporal order is often lost (Chun and Potter, 1995). Kesseler et al. (2005) suggests that lag 1 sparing cannot be explained by competition alone and found evidence that two items recognized with lag 1 consolidate in the left temporo-parieto-frontal (TPF) area but not the right TPF or frontal areas.
This computational study investigates a hypothesis that AB is due to competition and interference between active neocortical memory patterns. Neural memory patterns are collections of interconnected pyramidal neurons that represent external stimuli or internal abstract representations. Presentation of a stimulus can activate a neural attractor corresponding with a stored memory pattern. Because memory patterns typically compete with winner-take-all dynamics, an active attractor can prevent other attractors corresponding with subsequent stimuli from becoming active until the initial active attractor decays due to neural adaptation and synaptic depression. The computational model of the neocortex used in our simulations is based on earlier work on attractor memory networks in neocortex (Fransén and Lansner, 1998), later work adding structural hypercolumns and minicolumns to the model (Lundqvist et al., 2006) and further work showing how modular networks of hypercolumns increase the stability of active memory patterns and decrease sensitivity to parameter variations (Lundqvist et al., 2010). We suggest that AB is due to interference of neural attractors in parietal association and/or prefrontal cortex. The T1 attractor is initially aided by item expectation in working memory, which provides more salience than distractors. Thus, since recognition of sensory perception cannot be achieved without the activation of an attractor, and an attractor initiated from T1 has not decayed sufficiently for another attractor to fire from T2, then recognition of the sensory stimulus from T2 is lost and AB occurs.
Studies have been performed on the effects of drugs on AB using the RSVP test and all drugs studied thus far appear to show unchanged or increasing AB. Perhaps the brain is normally optimizing for a minimal AB window and some drugs throw it off that optimum. Findings indicate benzodiazepines administered to human subjects will impair some cognitive processes and cause an increase of AB (Boucart et al., 2000), with diazepam the most active. Boucart concluded that benzodiazepines impair visual integration in the temporal domain, complementing earlier studies which found benzodiazepines impaired visual integration in the spatial domain as well. Several studies have also shown that both adult and child subjects with attention deficit hyperactivity disorder (ADHD) have a longer AB. Neurodegenerative diseases such as Alzheimer’s and Parkinson’s also have been found to increase the duration of AB, as does the natural aging process. However, a study of action video games has found that human gamers reduce both the amplitude and length of their AB (Green and Bavlier, 2003). In addition, a study on mental training found that meditation can reduce the AB (Slagter et al., 2007).
Materials and Methods
The Network Model
The subsampled neocortical model used in this investigation represents a patch of neocortex in the parietal area with a square topology of 4 × 4 hypercolumns (or macrocolumns) each separated by 500 μm. It is similar to the neocortical model used in Lundqvist et al. (2006). Hypercolumns in human neocortex are 300–600 μm in diameter (Mountcastle, 1997) with primary sensory cortex generally smaller and higher associative cortex on the larger end. It is believed that human hypercolumns have ∼80–100 minicolumns each (Mountcastle, 1997). Our model is subsampled with 16 minicolumns within a hypercolumn, clustered into an area of 200 μm in diameter while hypercolumnar separation distances of 500 μm are maintained. Minicolumns are 50 μm in diameter. To compensate for subsampling and to maintain biologically plausible synaptic connection counts, the model has neuronal connectivity more dense than actual cortex. Each minicolumn contains 25 cells, consisting of 20 pyramidal cells in layer 2/3 (L2/3), and 5 input pyramidal cells in a rudimentary layer 4 (L4). The number of L2/3 pyramidal cells in minicolumns varies considerably across different areas of human cortex and even more so across species, but 20 appears to be a reasonable number for human association cortex. Each hypercolumn has 32 inhibitory basket cells or 10% of the number of L2/3 pyramidal cells, which is two cells for every minicolumn. The basket cells are important for lateral inhibition between minicolumns. According to Markram et al. (2004), L2/3 of neocortex has 20–25% interneurons, half of which are basket cells. Other interneurons were not included in this model for simplicity. Unlike Lundqvist et al. (2006), regular spiking non-pyramidal (RSNP) interneurons were not included in the model since they did not significantly effect the attractor dynamics and behavior in this case. In terms of model connectivity, basket cells within a hypercolumn horizontally innervate minicolumns but lie outside them. Basket cells have reciprocal connections between L2/3 pyramidal cells within a hypercolumn. Figure 1 shows a two-dimensional representation of the minicolumns and basket cells in the simulated neocortical patch. A third dimension is introduced with the vertical placement of pyramidal cells in the minicolumns.
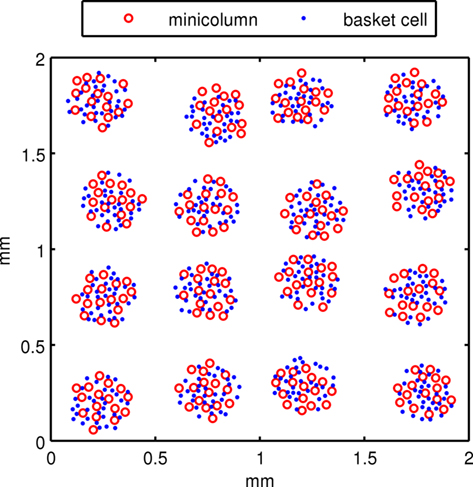
Figure 1. The view of a subsampled neocortical patch with 4 × 4 hypercolumns. Each hypercolumn contains 16 minicolumns. Pyramidal cells are instantiated within minicolumns and basket cells are instantiated outside of them.
Positions of hypercolumns in the neocortical patch were laid out on a square grid 500 μm apart with a 7% standard deviation in the x and y directions. At each hypercolumn location, minicolumns and basket cells were randomly assigned within a set radius and with a minimum distance from each other. From this 2D geometry of minicolumns, L2/3 pyramidal cells were populated by randomly assigning them a z location at each minicolumn coordinate with a range for L2/3. L4 pyramidal cells were randomly assigned a z location below this. The geometric distance between neurons was used to determine propagation delays, assuming a neural propagation speed of 0.5 m/S.
Synaptic connections between types of neurons were assigned a synaptic type with fixed weights having 10% standard deviation for AMPA, NMDA, and GABAA conductance. Synapses were randomly generated based on the connection probabilities of each synaptic type. Within a minicolumn, each L4 pyramidal cell has a 25% probability of a feedforward connection to each L2/3 pyramidal cell. L2/3 pyramidal cells are connected to each other’s basal dendrites locally within minicolumns having a 25% connection probability. They are also connected globally to apical dendrites across hypercolumns, storing 16 orthogonal patterns, each with one minicolumn in every hypercolumn. Pyramidal cells within such an orthogonal pattern have a connection probability of 28.4% between them. These stored patterns represent previously learned memories, as long-term plasticity is not implemented in the model. They are also simplified, because in reality pairs of stored patterns may not have lateral inhibition between them or may have excitatory connections. In such cases, attractors in different memory patterns can be active simultaneously and not be restricted to winner-take-all dynamics. This is an area we intend to explore in future work. L2/3 pyramidal cells have excitatory connections with a 50% probability to the 16 closest basket cells within a hypercolumn, while basket cells have inhibitory connections with a 50% probability to all L2/3 pyramidal within a hypercolumn. An attractor is activated by stimulating a randomly selected range of 4–6 minicolumns within an orthogonal memory pattern. Within these selected minicolumns, the L4 pyramidal cells were stimulated with four spikes at partially random intervals (67 Hz for 60 ms), delivered to an excitatory synapse on the soma. This can cause the L4 pyramidal cells to fire, in turn stimulating the basal dendrite of connected L2/3 pyramidal cells in the same minicolumn. If there is enough stimulation and recurrent activity, an attractor will emerge first in the L2/3 of the minicolumn, potentially spreading globally across to other minicolumns in the memory pattern. Figure 2 shows the neocortical microcircuit used.
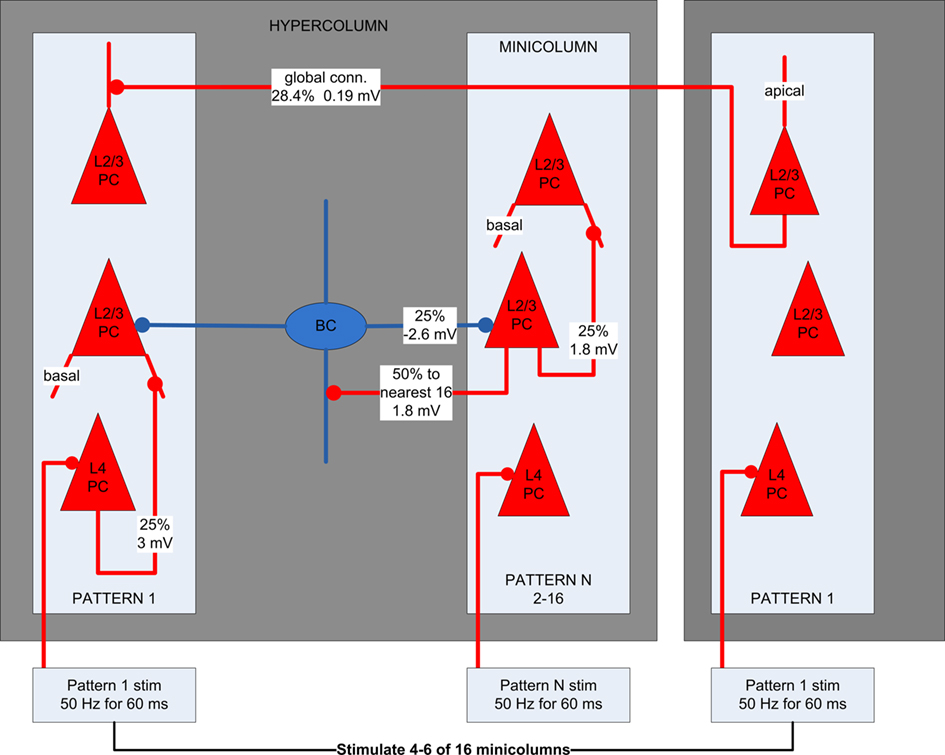
Figure 2. The neocortical microcircuit used in the simulations. Pyramidal cells are red and basket cells are blue. Each synaptic connection type has an assigned probability and EPSP/IPSP amplitude. Each hypercolumn has 16 minicolumns, each of which is part of one of 16 orthogonal patterns. L2/3 pyramidal cells in minicolumns within the same pattern have a 28.4% probability for global connections between them and 0% probability with pyramidal cells in other patterns.
Cell Models
The neocortical model contains pyramidal and basket cells that utilize Hodgkin–Huxley type equations and include calcium dynamics based on Ekeberg et al. (1991) and Fransén and Lansner (1995). For the cell membrane, voltage-dependent ion channels for Na+, K+, and Ca2+ are explicitly represented by the Hodgkin–Huxley equations. The Na+ channels have an equilibrium potential of 50 mV, the K+ channels have an equilibrium potential of −80 mV and the Ca2+ channels have an equilibrium potential of 150 mV. Additional channels exist in the membrane for Ca2+-gated K+ (KCa) and Ca2+ leakage. The KCa channels exhibit properties of both BK and SK type channels (Sah, 1996) are voltage sensitive and produce after-hyperpolarization (AHP) and spike frequency adaptation (SFA). The pyramidal cell is a regular spiking excitatory neuron with compartments for the soma, initial segment, basal dendrite and an apical dendrite with three segments. The soma diameter is 21 μm, the basal dendrite is 63-μm long and 5-μm thick and the apical dendrite is 210-μm long and 5-μm thick. All compartmental sizes had a standard deviation of 10%. The soma and initial segment are active compartments while the dendrites are passive only. The soma and dendritic compartments have synaptic connections, Ca2+ pools and KCa channels. Only the soma has a fast Ca2+ pool which is computed from extended Hodgkin–Huxley equations, but both the soma and dendrites have slow Ca2+ pools supplied by NMDA channels when open. The time constant of the fast Ca2+ pool is 160 ms and the slow Ca2+ pool is 2000 ms. The resting potential is −65 mV and Poisson noise provides a positive bias on the apical dendrite. The basket cells are inhibitory and have compartments for a soma, initial segment and a single dendrite. The soma diameter is 7 μm with a standard deviation of 10% and the dendrite is 20-μm long. The soma and initial segment are active while the dendrite is passive only. The resting potential is −65 mV while Poisson noise provides a positive bias on the dendrite. The basket cell does not have Ca2+ channels or Ca2+ pools and is fast spiking and non-adapting. All cell temperatures were set to 37 C. Cell equations are found in the Appendix with parameters in Tables A1–A3. It is likely that integrate-and-fire neurons would produce behavior similar to the multi-compartmental Hodgkin–Huxley type neurons we implemented and this is an area for further study. However, there are some advantages to using multi-compartmental Hodgkin–Huxley neurons, besides being more biologically plausible. Multi-compartmental models can separate the dynamics for short-range and long-range connections with more diverse dendritic targeting and calcium dynamics, as we did. It also allows modulatory and psychotropic drug effects on ion and channels and receptors to be more readily explored, as we did as well.
Synapse Models
All neurons have excitatory synaptic channels for glutamergic Kainate/AMPA. The L2/3 pyramidal cells also have excitatory NMDA channels and inhibitory GABAA channels. The NMDA channels include dynamics for the Mg2+ ion block and Ca2+ pools and have a 4 ms latency with respect to Kainate/AMPA channels in the same synapse. NMDA to AMPA ratios in cortical pyramidal cells vary across the experimental studies (Myme et al., 2003), but a reasonable representation seemed to be an NMDA/AMPA ratio of 6 for charge entry per unitary EPSP, at −60 mV. All synapses are saturating and aggregated by type and compartment (Lytton, 1996). Synaptic depression of EPSCs and IPSCs as described in Varela et al. (1999) are included on all synaptic channels. Kainate/AMPA and NMDA channels have a fast depression factor of 0.78 with a decay time constant of 634 ms and a slow depression factor of 0.97 with a time constant of 9300 ms. The GABAA synapse has a single depression factor of 0.94 and a decay constant of 1900 ms. These constants are based on slices of rat visual cortex randomly stimulated at mean rate of 4 Hz (Varela et al., 1999). Although these depression factors may appear weak, effective depression factors based on differences between foreground and background firing activity are considerably lower than absolute depression factors from foreground activity alone, particularly in cortical slice measurements which likely have less background activity than in vivo measurements.
Simulation Methods
The neocortical model was implemented with version 7.1 of the parallel NEURON simulator (Carnevale and Hines, 2006) using the hoc and mod programming languages. Simulations were performed on the IBM Blue Gene/L supercomputer with a 128 node partition in virtual node mode, providing 256 processors, each which ran one MPI process simulating a single minicolumn (25 neurons) and two basket cells. The entire model had exactly 6912 neurons and about 596,800 total synapses having a standard deviation of 463 across the generated synaptic connection matrices. Each cortical simulation was for 5 s of cortical activity with a fixed simulator time step of 50 μs. Noise is required for the cortical dynamics to function. While it is not required to activate an attractor with stimulation, it is required to sustain activity. Poisson processes with a rate of 300 Hz provided background EPSP noise to the L2/3 pyramidal and basket cells. The noise conductance was proportional to the cell area, but four times higher in pyramidal cells as compared to the basket cells.
Simulated RSVP
A random seed was used to generate a unique connection matrix, each of which represented a cortical patch in a single human subject. Each connection matrix was used for a group of simulated RSVP trials, as an individual subject would be. Random number generators providing parameter variance and noise for each cell were assigned a seed of unique primes multiplied by a common global seed, which changed with each trial set. A trial set consisted of simulated RSVP trials from lag 1 to lag 9. Each simulated trial consisted of a random sequence of 14 items, each presented for a duration of 65 and 100 ms apart, as shown in Figure 3. In the dual-task condition, T1 was always presented as the third item of the 14, with T2 presented at lag 1 through lag 9. Distractors were presented for the first two items in the sequence, the intervening items between T1 and T2, and items following T2. T1 and T2 were potentiated for the entire trial by depolarizing pyramidal cells in the corresponding stored patterns 0.75 mV and hyperpolarizing all other stored patterns 0.75 mV by current injection into the soma. This is hypothesized to be similar to a gating bias when expected items are held in working memory. For presentation of both expected and distraction items, a random range of 4–6 minicolumns out of 16 were stimulated within a stored pattern.
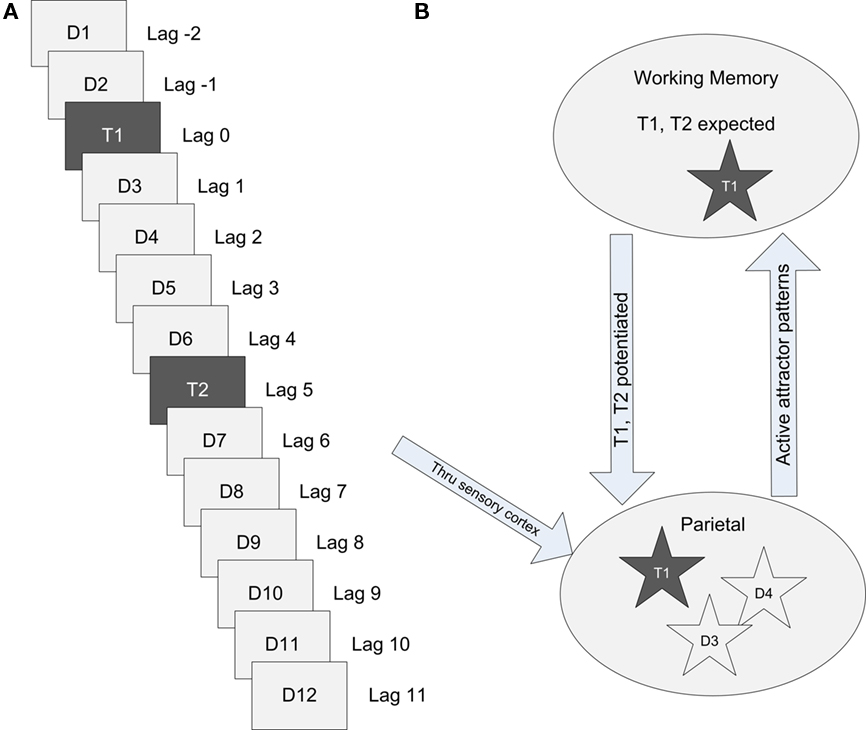
Figure 3. Simulated RSVP with targets T1, T2, and distractor patterns D1–D12. (A) A stream of items presented every 100 ms or lag during an RSVP task. Two distractors precede T1 which is followed by a varying number of interleaving distractors before the target T2 is presented. (B) Conceptual model of the cortical information flow during an RSVP task at lag 3.
Visual stimuli propagates through sensory cortex and into parietal cortex before entering working memory. Targets are expected in working memory and potentiated to favor activation. If an attractor in the cortical patch completes its pattern across hypercolumns and enters the foreground, it enters working memory and is recognized. In the example illustrated in Figure 3, target T1 has been recognized.
Detecting Active Attractors
Targets in the RSVP stream that become active attractors are considered to be consciously recognized if those patterns complete across hypercolumns and the attractor dwell time is longer than 100 ms after input stimulation stops. The threshold used for detection is a cumulative total of greater than 1000 spikes across the 320 L2/3 pyramidal cells in minicolumns of an active memory pattern. Figure 4 shows the analysis of spiking activity in the cortical patch, using example lag 2 and lag 5 trials. Figures 4A,B show the occurrence of AB while Figures 4C,D show the absence of one. Figures 4A,C show the spiking activity of pyramidal and basket cells within the network and ordered by hypercolumns, each consisting of 432 cells. Within a hypercolumn, cell types are grouped together and ordered by L4 Pyramidal, L2/3 Pyramidal and basket cells. During each lag, L4 pyramidal cells were stimulated in 4–6 randomly selected minicolumns within a memory pattern. This can be seen in Figures 4A,C, along with the triggered activation of L2/3 pyramidal and basket cells in the same hypercolumn. Lines of spiking L2/3 pyramidal cells indicate active minicolumns. The same minicolumn number in each hypercolumn is part of the same memory pattern, so when active minicolumns are equally separated, they are likely to be in the same pattern. Figures 4B,D show mean spiking activity within memory patterns. This was calculated by averaging the inter-spike interval within a 40-ms window across all L2/3 pyramidal cells in the same memory pattern. Figure 4B shows only T1 entering the foreground state at lag 0 while distractor patterns remain in the background state. T2 at lag 2 does not become active enough to be sustained or recognized. In Figure 4D, T1 at lag 0 and T2 at lag 5 both become active, sustained and recognized. Figures 4B,D use nearly identical sequences of trial stimuli, but diverge in behavior at lag 2 when the trial shown in Figure 4B is presented with a target and the trial shown in Figure 4D is not.
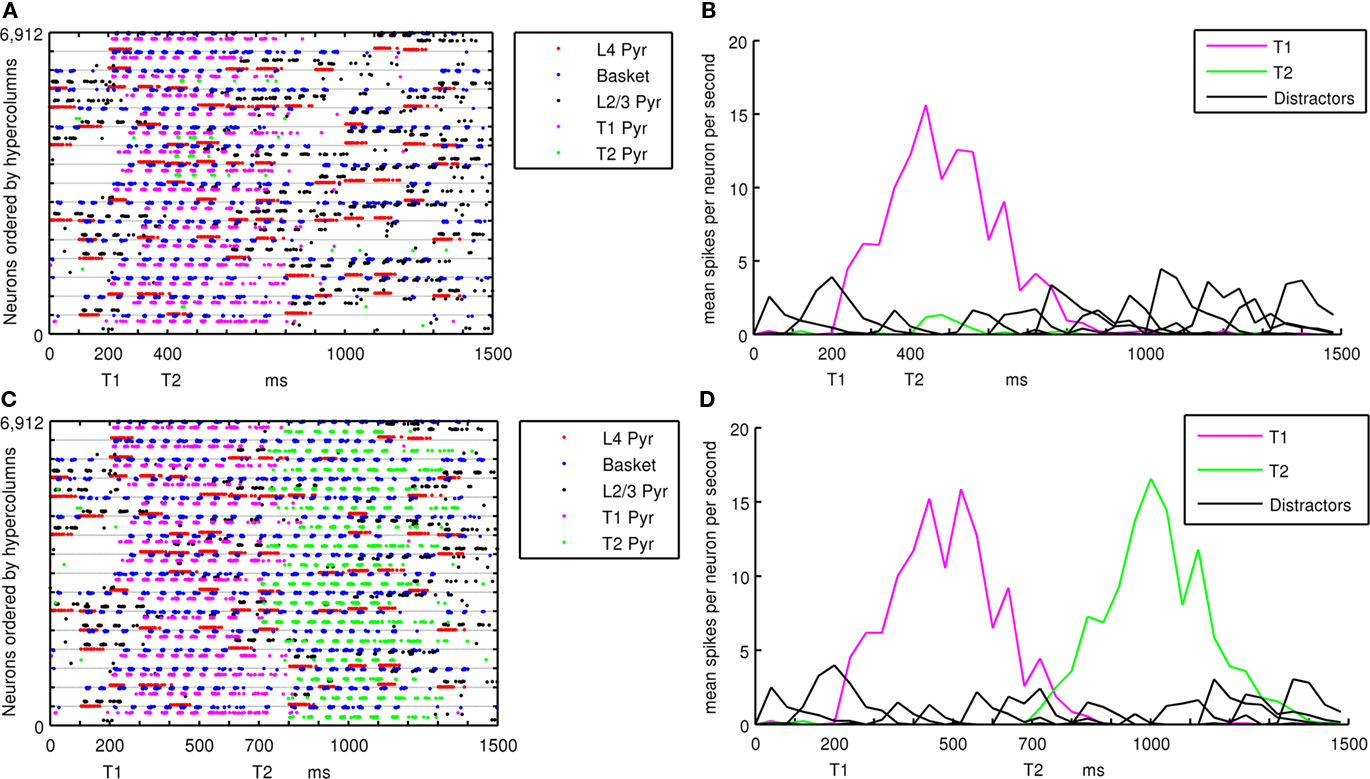
Figure 4. Spiking activity during a simulated RSVP with L4 pyramidal cells in red, basket cells in blue and L2/3 pyramidal cells in black for distractor patterns, magenta for T1 and green for T2. (A) Plot of all spiking activity in the cortical patch during an AB. (B) Shows mean activity within stored patterns during an AB. (C) Plot of all spiking activity in the cortical patch when AB does not occur. (D) Shows mean activity within stored patterns when AB does not occur. Figure A1 in the Appendix shows spiking activity of (A) and (C) from a different view.
Results
Simulating Attentional Blink
In the first experiment, five synaptic connection matrices for the cortical patch were generated to represent five individuals. From each of these, 10 trial sets were run for both the dual-task and single-task control. Each trial set consisted of trials for lag 1 to lag 9. In all, 900 trials were run for both the dual and single tasks. The percentage of active attractors is hypothesized to be equivalent to the percentage of correctly reported items during an AB RSVP experiment. Figure 5C summarizes the simulation results and Figure 5A shows a typical human AB experimental result (Chun and Potter, 1995). The simulation results reproduce the basic AB but do not produce lag 1 sparing, as can happen when items in the RSVP stream are spatially shifted (Visser et al., 1999b) or due to attentional switching (Visser et al., 1999a). This suggests that the lag 1 sparing phenomenon represents a separate mechanism to the AB effect, which is not represented by our model. Figure 5B decomposes the dual-task data in Figure 5A into separate components for AB and lag 1 sparing. If an exponentially decaying component for lag 1 sparing is removed leaving just the AB component, the human and simulated curves have very similar shapes. As compared to human experimental AB curves, our model produces a dual-task result with a lower initial detection rate.
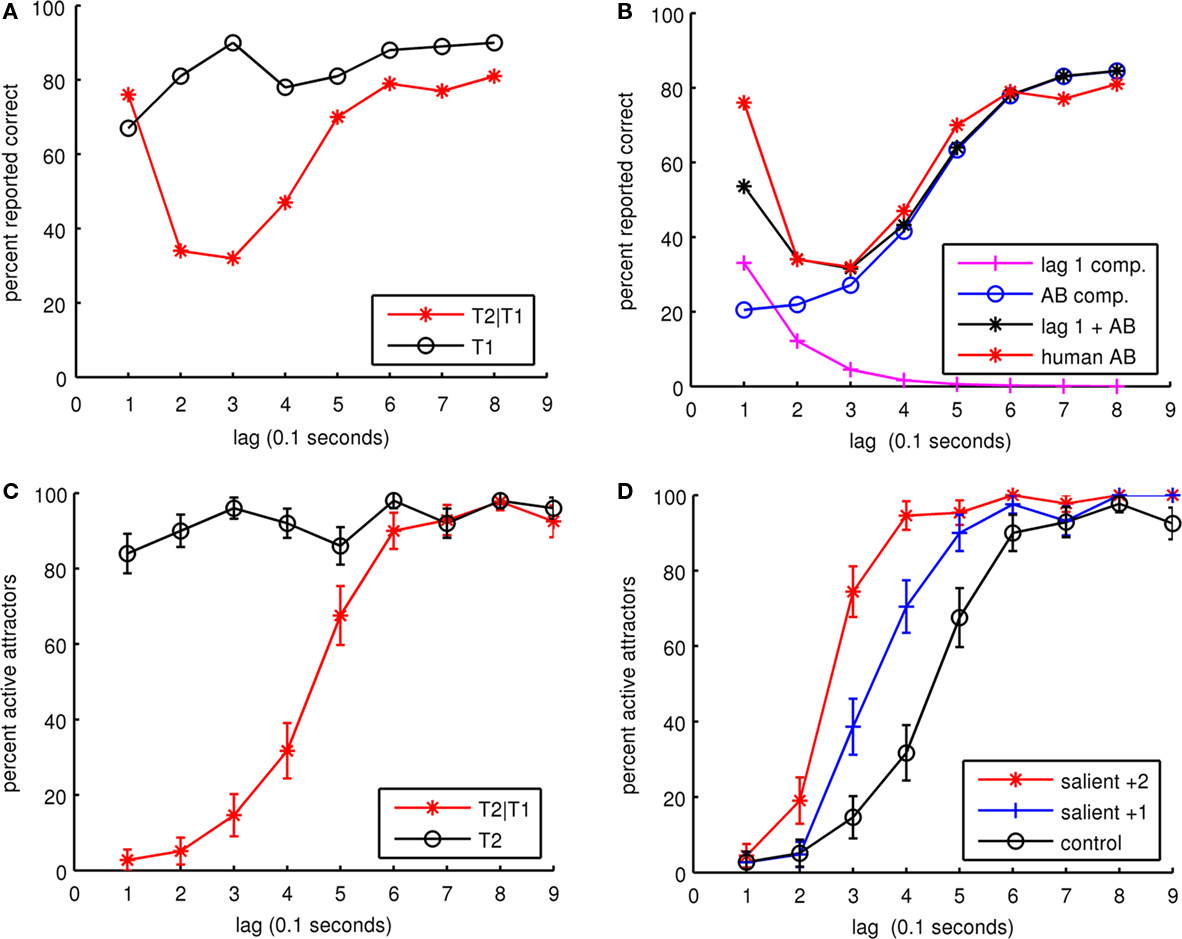
Figure 5. (A) Human experimental results for AB. The dual-task experiment (T2|T1) is shown in red and the single-task control (T1) is shown in black. Here T1 recognized represents the trials where T1 was recognized alone and along with T2. The dual task shows lag 1 sparing. Data from Chun and Potter(1995; p. 112, Table 1). Copyright 1995 by the American Psychological Association. Adapted with permission. (B) Decomposition of dual-task human experimental AB results in (A) into two separate components. The first component represents lag 1 sparing with an exponential decay of 100 ms, starting at the beginning of T1 presentation. The second component represents AB with a sigmoid like hyperbolic tangent function. (C) Simulation of five individuals showing the dual task in red (T2|T1) and a single-task control in black (T2). (D) The effect of more salient target stimuli on the AB.
Attentional Blink with Higher Target Salience
In the second experiment, target stimuli were made more salient by increasing the target stimulus strength. As in the first experiment, the same five simulated individuals were used and each individual was run for 10 trial sets at two levels of salience and a control. In the salient +1 condition, stimulus was increased by an average of one minicolumn for a randomly selected range of 5–7 minicolumns within the target pattern. In the salient +2 condition, the stimulus was increased by an average of two minicolumns for a range of 6–8 minicolumns within the target pattern. In the control condition, all targets were stimulated with a randomly selected range of 4–6 minicolumns within the target patterns. In all cases, distractors were stimulated with 4–6 minicolumns within a distractor pattern. As can be seen in Figure 5D, increasing stimuli by one minicolumn reduced the AB by roughly 1 lag, showing that more salient target stimuli reduces the AB. These results can be compared with an experiment in Chun and Potter (1995), where target letters were followed by either distractor digits or keyboard symbols. The keyboard symbols were designed to be more discriminable from the letter targets than the digit distractors were. The experiment showed that the more discriminable keyboard symbols resulted in reduced AB.
Attentional Blink with Benzodiazepine
In the third experiment, the GABAA conductance and decay time constant were modified to simulate the experimental effects on humans of the benzodiazepine family of drugs (Boucart et al., 2000, 2007). Again, the same five connection matrices from the first experiment were used, with the same number of trials. Because benzodiazepines such as diazepam, lorazempam, and flurazepam are GABA agonists, the drug effects can be simulated by changing the conductance and decay time constant of the GABAA synapses in the simulation. It is difficult to quantitatively associate a benzodiazepine dosage given to human beings during AB experiments with the parameters in the neocortical model. Human AB drug studies typically administer one drug dosage orally with a placebo control. The efficiency of drug digestion and transport into the blood stream, across the blood–brain barrier, diffusion rates into synapses and drug decay rates are all unknowns. However, it is possible to determine qualitative monotonic relationships between simulated drug concentrations and human behavior. Both the GABAA synaptic conductance and decay time constant were increased by 20%, which corresponds with findings on the effects of 1 μM of flurazepam on rat hippocampal slices (Mozrzymas et al., 2007). Figure 6 compares AB simulations of normal and modified GABAA parameters with a human AB benzodiazepine drug study (Boucart et al., 2000). The increased GABAA conductance and decay time constant increased the AB by about 1 lag and is qualitatively similar to the human study. One difference between the simulation and the Boucart et al. (2000) study is that the differences between normal and elevated GABAA eventually disappear in the simulation. The difference in perceptual performance in the human study between the placebo and the drugs change less over time, so it is possible the drugs are impeding general cognitive performance as well as increasing AB.
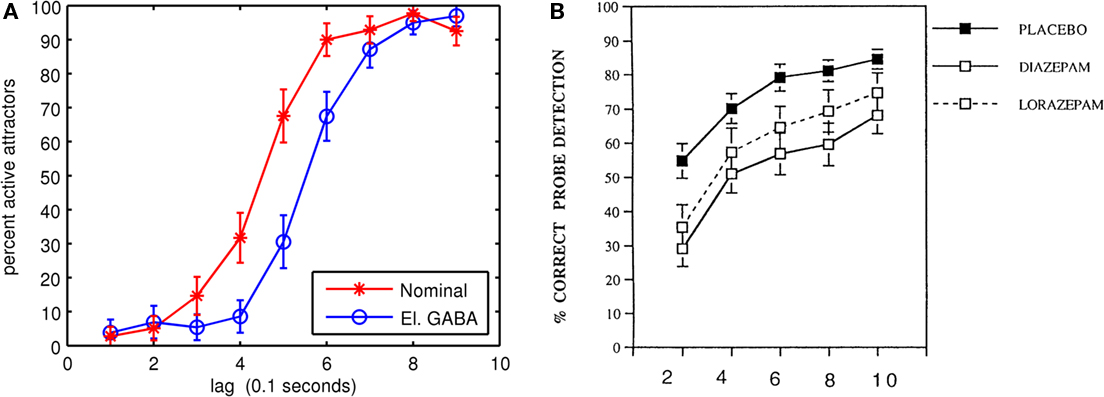
Figure 6. Simulated and experimental effects of benzodiazepines. (A) Simulated dual task (T2|T1) AB under a nominal control condition and with GABAA channel conductance and decay time constant elevated by 20%. (B) AB human study showing the effects of benzodiazepines on dual-task performance. Reproduced with kind permission from Boucart et al. (2000; Figure 2).
Sensitivity Analysis
Since the neocortical model utilizes biophysical Hodgkin–Huxley type spiking neurons, it has a number of cell parameters, some of which effect the network dynamics more than others. Sensitivity analysis was preformed individually on four key parameters of the model, which are the conductance of the KCa channel, synaptic depression on the glutamatergic synapses, the synaptic GABAA conductance and time constant and the ratio of NMDA to AMPA charge entry per unitary EPSP at −60 mV. These parameters were important when tuning the model for correct behavior. All analyzed parameters were in the L2/3 pyramidal cells except the NMDA/AMPA ratio, which affected both the L2/3 pyramidals and the AMPA channels on basket cells. For each parameter, five trials were run using one memory pattern from each of the five simulated individuals. The memory pattern was neither depolarized nor hyperpolarized. Each parameter spanned a range of 30 incremental steps while other parameters were fixed at the experimental simulation settings. To measure attractor frequency, an average inter-spike interval was calculated within a 40-ms window across active L2/3 pyramidal cells within an active memory pattern. To determine dwell time, an attractor was considered to be terminated when the average firing rate within a pattern dropped below 14 spikes or 1.1 Hz within a 40-ms window.
In Figure 7A, a significantly lower KCa conductance increased the attractor dwell time and lowered the average firing rate over attractor activity. When the KCa conductance was low enough, an attractor persisted and achieved a steady state with synaptic depression, but at a lower firing rate. A relatively high KCa results in short attractors with higher variability in dwell time and firing rate. Figure 7B shows synaptic depression, where a depression factor of one is an absence of depression. Generally, as synaptic depression increases, both attractor dwell time and firing rates drop. In Figure 7C, an increasing GABAA conductance extended dwell time and decreased the mean firing rate, effectively slowing down cortical processing. However, if the GABAA conductance and synaptic time constant was high enough, the attractors became unstable, until finally they could no longer become active at all. In Figure 7D, the NMDA/AMPA ratio analysis shows a stable plateau for both dwell time and firing rate. The flat dwell time curve was intentional, and was achieved by selecting pairs of NMDA and AMPA conductance values based on a reference attractor at the selected model parameters. The sampled NMDA/AMPA pairs determined a linear relationship used to select simulated ratios over the range. The attractors became unstable with ratios at the low end, when the NMDA contribution is perhaps too low to maintain recurrence and at the high end when perhaps there is an insufficient AMPA contribution to remove the Mg+ block and boost the NMDA current. When AMPA conductance was fixed instead, the range of this plateau was reduced to between ratios of 5.1 and 7.7.
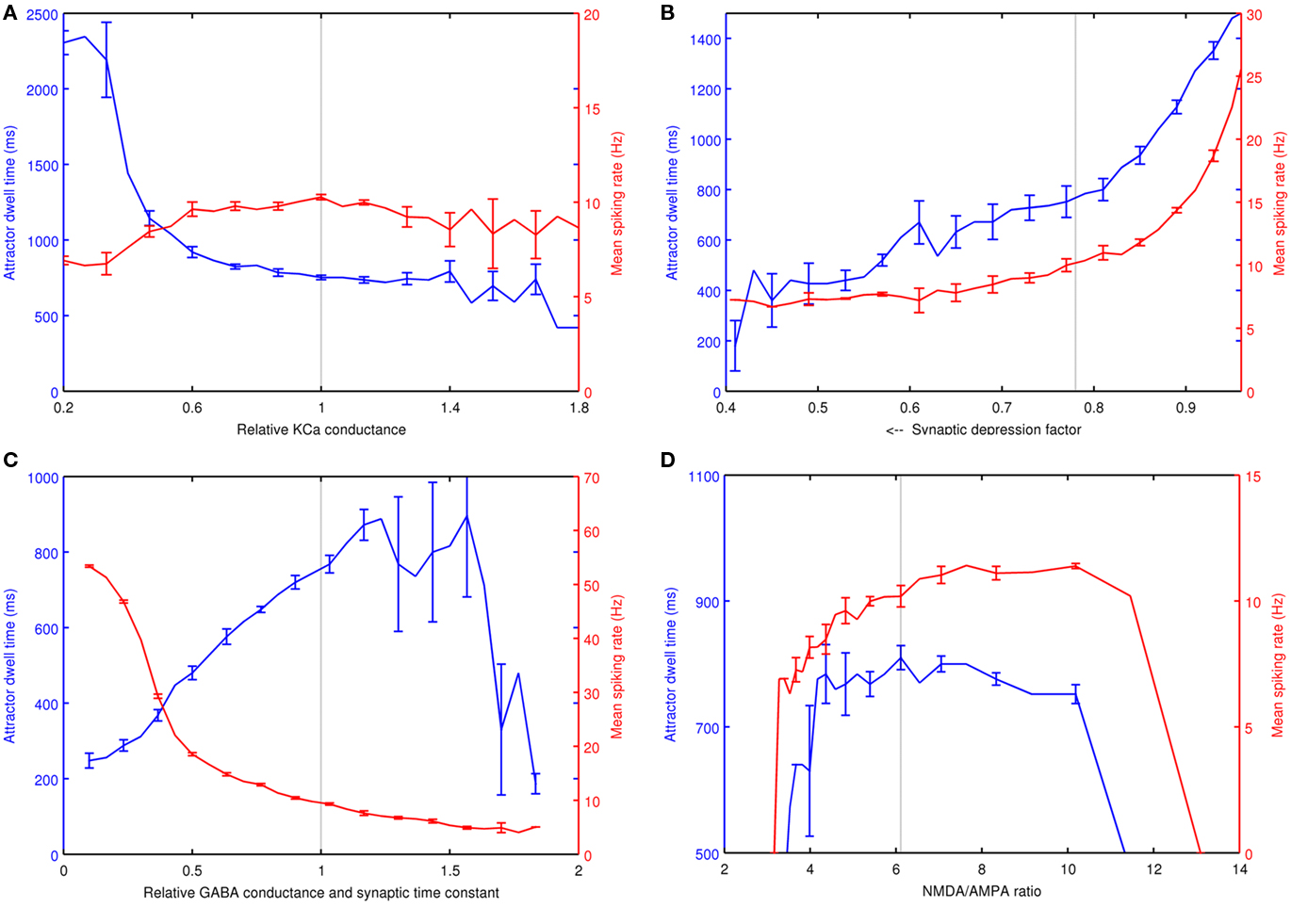
Figure 7. Sensitivity analysis of four variables on attractor dwell time and mean spiking rate. These are (A) the relative KCa conductance in L2/3 pyramidal cells, (B) the synaptic depression factor in L2/3 pyramidal cells, (C) the relative GABA conductance and time constant in L2/3 pyramidal cells and (D) the NMDA/AMPA ratio of charge entry per unitary EPSP at −60 mV. The dashed line in each plot represents the parameter settings used in AB simulations.
In our presented results, the stored memory patterns in our model were all orthogonal. In real cortex, patterns can be overlapping, but it is not known exactly how this occurs. For example, patterns might have shared minicolumns or have diffuse, random connections between them. We ran simulations with random and diffuse overlapping connections, but this did not show a significant difference in behavior. In this case, the same number of global connections within a pattern were also added across all patterns, resulting in a 1.7% overlap between patterns. If the patterns had shared minicolumns or were not randomly diffuse but instead represented encoded hierarchies, the results may have been different. This is an area for further study. Neural transmission speeds did effect pattern completion times, but the effect was gradual.
Discussion
The cortical simulations of AB produced main results similar to human experimental data, except for the effects of lag-1 sparing. Additionally, the simulations with an increased GABAA conductance and time constant showed qualitative and monotonic correlations with human AB benzodiazepine studies. This is encouraging, considering that the model of the neocortex as simulated is dramatically simplified compared to real neocortex. The large variability in human data on AB as illustrated by comparing Figure 5B with Figure 6B (placebo) makes the validation of models challenging. The attentional circuitry in the brain is known to involve several cortical and non-cortical subsystems with both hierarchical and lateral cross connections. The implemented model is a flat cortical patch of 16 hypercolumns representing part of the parietal and/or prefrontal cortex, without feedforward, feedback, or lateral connections from other areas of cortex. Additionally, only a small subset of known neuronal types in the human cortex was modeled and of those only a small subset of known ion channels was included in the model. Still, important aspects of neural machinery at the minicolumn and hypercolumn levels were captured by the model. While many parameters were chosen based on electrophysiological data across species, several were chosen somewhat arbitrarily due to lack of experimental data.
Attractor states in neocortical slices have been observed with active durations between 60 ms and 30 s, although 55% of active states lasted approx. 600 ms on average (Cossart et al., 2003). Attractor duration in the computational model was tuned to be between 500 ms and 1 s by adjusting adaptation of the L2/3 pyramidal cells with synaptic depression and calcium dynamics, particularly the conductance of KCa channels. Inhibition from basket cells contributed to the production of attractor spiking frequency and duration. The spiking rate of the L2/3 pyramidal cells were regulated by inhibition from proximal basket cells and produced a mean spiking rate of 14 Hz at the nominal GABAA levels and about 13 Hz with the higher GABAA channel conductance and decay rate. The higher GABAA levels reduced the oscillation frequency between L2/3 pyramidal and basket cells by about 7%, generally reduced cortical activity and had the effect of extending the attractor dwell time and the duration of attractor interference. Our simulations thus establish interesting relations between synaptic properties and macroscopic neural dynamics. Simulations showed that while increasing the GABAA conductance and time constant increased the AB, decreasing this also causes the AB to shrink. Sensitivity analysis also showed a shorter dwell time for decreased GABAA conductance. From this, we can predict that other GABAA agonists such as pentobarbital or alcohol should cause the AB to increase and GABAA antagonists such Metrazol or Flumazenil should cause the AB to decrease. With less inhibition, active memory patterns should adapt faster, causing T1 to be active for a shorter amount of time and allowing T2 to become active sooner.
In addition to a long-range excitatory effect of expected targets in working memory, we assume unexpected patterns are inhibited indirectly. A long-range excitatory connection from a pyramidal cell can excite an inhibitory interneuron which in turn can inhibit another pyramidal cell close to it. Disynaptic inhibition (Silberberg and Markram, 2007) is an example of this. As mentioned in the network model description, RSNP cells were excluded in this version of the model. They received long-range connections from pyramidal cells and locally inhibited pyramidal cells in the same minicolumn. It was interesting to observe that powerful attentional gating was possible with a difference of only 1.5 mV between expected (facilitated) and unexpected (inhibited) memory patterns.
The most significant limitation of this computational model is the absence of lag 1 sparing. This is likely due to insufficient complexity in the current model structure rather than limitations of attractor dynamics. Attractors for both expected patterns were seen to arise at lag 0, but competition typically caused one to dominate by lag 1. Our analysis indicates that lag 1 sparing may be due to another neural component initiated by T1 which decays exponentially with a time constant of about 100 ms. One possibility for enabling lag 1 sparing in the model is to include different types of interneurons and behaviors in the cortical microcircuit. For example, basket cells are part of a fast inhibitory sub-circuit with depressing synapses while some other interneurons are part of a slow inhibitory sub-circuit with facilitating synapses (Silberberg, 2008). By including them both to provide lateral inhibition, the difference in response times may provide a window of about 100 ms where attractors may coexist and persist, instead of the present winner-take-all dynamics normally leaving a single attractor active. Another possible source for lag 1 sparing is the temporal dynamics of a globally activated attractor between the parietal cortex and the dorso-lateral prefrontal cortex.
There are other AB phenomena which we do not reproduce in this model, such as increased processing of the T1 + 1 slot, blink attenuation with T1 + 1 blank and T2 + 1 blank; delayed consolidation for T2s seen during the blink; spatial specificity of the lag 1 enhancement; T1–T2 costs at lag 1; late stage bottleneck; and spreading the sparing (Bowman et al., 2008). Most of these phenomena require processing of lag 1 sparing, which our model does not yet support. However, we did demonstrate that more salient stimuli attenuates AB, which is phenomenologically related to blink attenuation with T1 + 1 blank. Regarding the late stage bottleneck, evidence from ERP studies (Sergent et al., 2005) show that even when T2 is missed, it is still partially processed, showing activity in sensory cortex. While our model represents a single area of cortex, a more complete model can represent a network of areas. This would allow memory patterns to become both locally and globally activated, with expectation providing top-down facilitation and sensory input providing bottom-up stimulation. Attractors in sensory or parietal cortex alone may not be enough to globally activate working memory, producing a late stage bottleneck. Preliminary work modeling two cortical areas show this behavior.
Comparison to Other Computational Models
Several other computational connectionist or neural models have been developed for AB. The LC–NE hypothesis was implemented as a computational model (Nieuwenhuis et al., 2005). This approach seems to require that recognition of an expected target occur before NE release from the LC. Visual stimuli via the low road pathway can reach the superior colliculus (SC) and LC before the high road of cortical visual processing. However, while the SC might recognize low-resolution fearful stimuli like spiders or snakes (Öhman et al. 2007), the SC is probably unlikely to recognize an abstract weakly conditioned but expected item presented during a RSVP task. This is likely to require the stimulus to propagate through visual, parietal, and prefrontal cortex to generate a neural correlate such as the P300 with a significant latency. Thus, if recognition of T1 did not need NE release, it is not clear why T2 would need it. Then again, if recognition of T1 is not required for NE release, any distractor would also trigger NE release and the NE refractory period would propagate throughout the RSVP stream. The NE–LC hypothesis can partially explain lag 1 sparing, assuming T1 is recognized by the SC. Although NE decays rapidly, the NE-LC hypothesis explains lag 1 sparing to be the result of NE release from T1 which is still active preceding up to T2 when it occurs only 100 ms later. This hypothesis appears to correspond closely with the sluggish gate hypothesis for lag 1 sparing (Chun and Potter, 1995). However, since lag 1 sparing is lost with a moderate spatial shift between T1 and T2 in the visual field, it is not clear how NE release from the LC can be sufficiently localized in visual cortex, even if informed by the SC. Still, it does not appear that the LC–NE hypothesis and the AB attractor hypothesis proposed here are necessarily mutually exclusive.
The boost and bounce theory (Olivers and Meeter, 2008) is also implemented as a computational connectionist model. In this model of an RSVP trial, a target T1 follows a stream of distractors and evokes recurrent feedback from gating neurons in working memory, boosting the target stimulus and allowing it to enter working memory to be consciously perceived. If a distractor immediately follows the target, it is initially enhanced due to temporal proximity. However, gating neurons detect a mismatch in expectation and generate a strong inhibitory response, causing a bounce of subsequent stimuli and the AB. In the case of lag 1, there is no distractor between targets and the target T2 is allowed to pass into working memory by the gating neurons. The computational model is able to reproduce the AB and lag 1 sparing, although it is not clear how it was implemented. Both the boost and bounce theory and the model presented here have excitatory recurrent networks with an attentional gate to boost a target into working memory. However, instead of an inhibitory response to a mismatch of expectation, our model uses lateral inhibition through attractor interference to reject subsequent targets and distractors while the attractor for T1 is still active.
The episodic simultaneous type serial token (eSTST) model (Wyble et al., 2009) and the earlier simultaneous type, serial token (ST22) model (Bowman and Wyble, 2007) are both implemented as a connectionist model and are similar to the two stage theory of AB. The models encode a visual stimulus by type during the first stage and bind the stimulus to tokens in working memory during the second stage. In order to bind a stimulus to a token and enter the second stage, attention must be boosted with a blaster, which is triggered by a target in the RSVP stream. A blaster is somewhat similar to NE release in the LC–NE hypothesis. To regulate attention, excitatory connections from target input compete with inhibitory connections from working memory encoding. While the first target is being encoded in working memory, the blaster is suppressed between lag 2 and 4. Like the two stage theory, there are capacity limits including a binding pool of available episodic tokens and a binding limit of one stimulus to a single episodic token for any given moment in time. In eSTST, a sequence of bound tokens also encode temporal order. Both models are able to reproduce the basic AB and lag 1 sparing. Our model is similar to this one with respect to competition between an active target in working memory and incoming stimuli. However, our model is based in generic attractor models of perception and memory and thus does not have tokens or a blaster.
Zylberberg et al. (2010) recently implemented a cortical spiking network model for reproducing the psychological refractory period (PRP) and AB. It includes multiple excitatory and inhibitory neural populations for two sensory cortices, a task setting network, router and two motor cortices. The router processes input from the sensory cortices in the context of a set task. When task relevant input is processed, spikes are generated in the motor cortex. The neural populations have lateral inhibition and recurrence which allows active neural populations to dominate. The task setting network provides excitatory input to task relevant neurons in the router. When T1 is selected as a task and T1 is presented to a sensory cortex, the task setting and router networks become active for T1 and generate recurrence with NMDA receptors. This recurrence can block activation of T2 when subsequently set as the task, causing the PRP and AB. Because the task setting network was encoded for just T1 and T2, distractors were implemented by simulating non-specific neurons in sensory cortex, after T2. This indeed sometimes prevented activation of T2 in the motor output, when the interval between T1 and T2 was less than 500 ms. However, distractors are not presented between T1 and T2 as in most RSVP experiments. A network task-set encodes two patterns, whereas ours encodes 16 stored patterns. Having just two patterns is the reason why distractors cannot be represented. We create several simulated individuals with different synaptic connection matrices and in each trial randomly choose the targets from the 16 possible patterns. However, we have an association cortex but do not have sensory or motor cortices represented in our model. While both models have excitatory and inhibitory neurons, ours has a modular structure with minicolumns and hypercolumns. Although Zylberberg et al. (2010) lacks distractors, their model is able to reproduce a human like AB curve, but without lag 1 sparing. In some respects, this implementation is closest to our model among the ones discussed because it includes attractor dynamics and is implemented at the neural level, using populations of integrate-and-fire excitatory pyramidal cells and inhibitory interneurons with AMPA, NMDA, and GABA receptors.
Conclusion
The AB attractor hypothesis described here provides an explanation for competition between various stimuli and the attentional lag that can occur when one of those stimuli becomes dominant. It is based in the attractor network theory of perception and memory and our study provides an additional connection between this theory and experimental data on human perceptual processing. While other models can reproduce AB and some lag 1 sparing as well, each model has its own limitations and assumptions. Thus, a consensus approach has not yet emerged. Our hope is that attractor dynamics with neural populations can add to this debate. Our approach also facilitates building models at the neuron and channel level, which enables the investigation of the effects of psychotropic drugs.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by grants from the Swedish Foundation for Strategic Research (through the Stockholm Brain Institute; www.stockholmbrain.se), the Swedish Science Council (Vetenskapsradet, VR-621-2004-3807; www.vr.se), and the European Union (FACETS project, FP6-2004-IST-FETPI-015879; http://facets.kip.uni-heidelberg.de).
References
Boucart, M., de Visme, P., and Wagemans, J. (2000). Effect of benzodiazepine on temporal integration in object perception. Psychopharmacology (Berl.) 152, 249–255.
Boucart, M., Waucquier, N., Micheal, G. A., and Libersa, C. (2007). Diazepam impairs temporal dynamics of visual attention. Exp. Clin. Psychopharmacol. 15, 115–122.
Bowman, H., and Wyble, B. (2007). The simultaneous type, serial token model of temporal attention and working memory. Psychol. Rev. 114, 38–70.
Bowman, H., Wyble, B., Chennu, S., and Craston, P. (2008). A reciprocal relationship between bottom-up trace strength and the attentional blink bottleneck: relating the LC-NE and ST(2) models. Brain Res. 1202, 25–42.
Broadbent, D. E., and Broadbent, M. H. P. (1987). From detection to identification: response to multiple targets in rapid serial visual presentation. Percept. Psychophys. 42, 105–113.
Chun, M., and Potter, M. (1995). A two-stage model for multiple target detection in rapid serial visual presentation. J. Exp. Psychol. Hum. Percept. Perform. 21, 109–127.
Cossart, R., Aronov, D., and Yuste, R. (2003). Attractor dynamics of network UP states in the neocortex. Nature 423, 283–288.
Ekeberg, Ö., Wallén, P., Lansner, A., Tråvén, H., Brodin, L., and Grillner, S. (1991). A computer based model for realistic simulations of neural networks. Biol. Cybern. 65, 81–90.
Fransén, E., and Lansner, A. (1995). Low spiking rates in a population of mutually exciting pyramidal cells. Netw. Comput. Neural Sys. 6, 271–288.
Fransén, E., and Lansner, A. (1998). A model of cortical associative memory based on a horizontal network of connected columns. Netw. Comput. Neural Sys. 9, 235–264.
Green, C.S., and Bavelier, D. (2003). Action video game modifies visual selective attention. Nature 423, 534–537.
Hodgkin, A. L., and Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544.
Hommel, B., and Akyurek, E. (2005). Lag-1 sparing in the attentional blink: benefits and costs integrating two events into a single episode. Q. J. Exp. Psychol. A. 58, 1415–1433.
Kesseler, K., Schmitz, F., Gross, J., Hommel, B., Shapiro, K., and Schnitzler, A. (2005). Cortical mechanisms of attention in time: neural correlates of the Lag-1-sparing phenomenon. Eur. J. Neurosci. 21, 2563–2574.
Kranczioch, C., Debener, S., and Engel, A. (2003). Event-related potential correlates of the attentional blink phenomenon. Brain Res. Cogn. Brain Res. 17, 177–187.
Lundqvist, M., Compte, A., and Lansner, A. (2010). Bistable, irregular firing and population oscillations in a modular attractor memory network. PLoS Comput. Biol. 6, e1000803. doi: 10.1371/journal.pcbi.1000803
Lundqvist, M., Rehn, M., Djurfeldt, M., and Lansner, A. (2006). Attractor dynamics in a modular network model of the neocortex. Netw. Comput. Neural Sys. 17, 253–276.
Lytton, W. (1996). Optimizing synaptic conductance calculation for network simulations. Neural Comput. 8, 501–509.
Markram, H., Toledo-Rodriguez, M., Wang, Y., Gupta, A., Silberberg, G., and Wu, C. (2004). Interneurons of the neocortical inhibitory system. Nat. Rev. Neurosci. 5, 793–807.
Mozrzymas, J., Wójtowicz, T., Piast, M., Lebida, K., Wyrembek, P., and Mercik, K. (2007). GABA transient sets the susceptibility of mlPSCs to modulation by benzodiazepine receptor agonists in rat hippocampal neurons. J. Physiol. 585, 29–46.
Myme, C., Sugino, K., Turrigiano, G., and Nelson, S. (2003). The NMDA-to-AMPA ratio at synapses onto layer 2/3 pyramidal neurons is conserved across prefrontal and visual corticies. J. Neurophysiol. 90, 771–779.
Nieuwenhuis, S., Gilzenrat, M. S., Holms, B. D., and Cohen, J. D. (2005). The role of the locus coeruleus in mediating the attentional blink: a neurocomputational theory. J. Exp. Psychol. Gen. 134, 291–307.
Öhman, A., Carlsson, K., Lundqvist, D., and Ingvar, M. (2007). On the unconscious subcortical origin of human fear. Physiol. Behav. 92, 180–185.
Olivers, C., and Meeter, M. (2008). A boost and bounce theory of temporal attention. Psychol. Rev. 115, 836–863.
Raymond, J. E., Shapiro, K. L., and Arnell, K. M. (1992). Temporary suppression of visual processing in an RSVP task: an attentional blink? J. Exp. Psychol. 18, 849–860.
Sah, P. (1996). Ca2+-activated K+ currents in neurones: types, physiological roles and modulation. Trends Neurosci. 19, 150–154.
Sergent, C., Baillet, S., and Dehaene, S. (2005). Timing of the brain events underlying access to consciousness during the attentional blink. Nat. Neurosci. 10, 1391–1400.
Silberberg, G. (2008). Polysynaptic subcircuits in the neocortex: spatial and temporal diversity. Curr. Opin. Neurobiol. 18, 332–337.
Silberberg, G., and Markram, H. (2007). Disynaptic inhibition between neocortical pyramidal cells mediated by Martinotti cells. Neuron 53, 735–746.
Slagter, H. A., Lutz, A., Greischar, L. L., Francis, A. D., Nieuwenhuis, S., Davis, J. M., and Davidson, R. J. (2007). Mental training affects distribution of limited brain resources. PLoS Biol. 5, e138. doi: 10.1371/journal.pbio.0050138
Tremblay, S., Vachon, F., and Jones, D.M. (2005). Attentional and perceptual sources of the auditory attentional blink. Percept. Psychophys. 67, 195–208.
Varela, J., Sen, K., Gibson, J., Fost, J., Abbott, L., and Nelson, S. (1997). A qualitative description of short-term plasticity at excitatory synapses in layer 2/3 of rat primary visual cortex. J. Neurosci. 17, 7926–7940.
Varela, J., Song, S., Turrigiano, G., and Nelson, S. (1999). Differential depression at excitatory and inhibitory synapses in visual cortex. J. Neurosci. 19, 4293–4304.
Visser, T. A., Bischof, W. F., and Di Lollo, V. (1999a). Attentional switching in spatial and nonspatial domains: Evidence from the attentional blink. Psychol. Bull. 125, 458–469.
Visser, T. A., Zuvic, S. M., Bischof, W. F., and Di Lollo, V. (1999b). The attentional blink with targets in different spatial locations. Psychon. Bull. Rev. 6, 432–436.
Wyble, B., Bowman, H., and Nieuwenstein, M. (2009). The attentional blink provides episodic distinctiveness: sparing at a cost. J. Exp. Psychol. Hum. Percept. Perform. 35, 787–807.
Zuvic, S. M., Visser, T. A., and Di Lollo, V. (2000). Direct estimates of processing delays in the attentional blink. Psychol. Res. 63, 192–198.
Keywords: attentional blink, attention, neocortex, cortical dynamics, Hodgkin–Huxley model, attractor networks
Citation: Silverstein DN and Lansner A (2011) Is attentional blink a byproduct of neocortical attractors?. Front. Comput. Neurosci. 5:13. doi: 10.3389/fncom.2011.00013
Received: 29 July 2010; Accepted: 15 March 2011;
Published online: 03 May 2011.
Edited by:
Hava T. Siegelmann, Rutgers University, USAReviewed by:
Paolo Del Giudice, Italian National Institute of Health, ItalyAndrey Olypher, Emory University, USA
Copyright: © 2011 Silverstein and Lansner. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Anders Lansner, Department of Computational Biology, School of Computer Science and Communication, Royal Institute of Technology, Albanova University Centre, Roslagstullsbacken 35A, 114 21 Stockholm, Sweden. e-mail:YWxhQGNzYy5rdGguc2U=

