- 1 Laboratory for Behavior and Dynamic Cognition, RIKEN Brain Science Institute, Saitama, Japan
- 2 Faculty of Comprehensive Informatics, Shizuoka Institute of Science and Technology, Shizuoka, Japan
- 3 Laboratory for Biolinguistics, RIKEN Brain Science Institute, Saitama, Japan
- 4 Department of Cognitive and Behavioral Sciences, Graduate School of Arts and Sciences, The University of Tokyo, Tokyo, Japan
How the brain learns and generates temporal sequences is a fundamental issue in neuroscience. The production of birdsongs, a process which involves complex learned sequences, provides researchers with an excellent biological model for this topic. The Bengalese finch in particular learns a highly complex song with syntactical structure. The nucleus HVC (HVC), a premotor nucleus within the avian song system, plays a key role in generating the temporal structures of their songs. From lesion studies, the nucleus interfacialis (NIf) projecting to the HVC is considered one of the essential regions that contribute to the complexity of their songs. However, the types of interaction between the HVC and the NIf that can produce complex syntactical songs remain unclear. In order to investigate the function of interactions between the HVC and NIf, we have proposed a neural network model based on previous biological evidence. The HVC is modeled by a recurrent neural network (RNN) that learns to generate temporal patterns of songs. The NIf is modeled as a mechanism that provides auditory feedback to the HVC and generates random noise that feeds into the HVC. The model showed that complex syntactical songs can be replicated by simple interactions between deterministic dynamics of the RNN and random noise. In the current study, the plausibility of the model is tested by the comparison between the changes in the songs of actual birds induced by pharmacological inhibition of the NIf and the changes in the songs produced by the model resulting from modification of parameters representing NIf functions. The efficacy of the model demonstrates that the changes of songs induced by pharmacological inhibition of the NIf can be interpreted as a trade-off between the effects of noise and the effects of feedback on the dynamics of the RNN of the HVC. These facts suggest that the current model provides a convincing hypothesis for the functional role of NIf–HVC interaction.
Introduction
Due to its similarity to human speech in being a learned complex sequential behavior, birdsong has come to be a widely studied topic in neuroscience. The Bengalese finch in particular learns highly complex songs that have syntactical structure, providing researchers with an excellent biological model for studying this phenomenon (e.g., Okanoya, 2004; Sakata and Brainard, 2006, 2009). Figure 1 shows a typical sound spectrogram of the song sequences of the Bengalese finch. The song consists of several varieties of “syllables,” the smallest units of a birdsong. Each syllable can be identified as a discrete element on a sound spectrogram and is denoted by a letter of the alphabet, for example “a,” “b,” and “c.”

Figure 1. Sound spectrogram of the song syllable sequence of the Bengalese finch. A song consists of several repetitions of an introductory syllable followed by a syllable sequence. Each syllable is identified as a discrete element in the sound spectrogram and is denoted by a letter of the alphabet. Songs are described in terms of sequences of syllables. The syllable “a” is the introductory syllable of this song.
Syllable-to-syllable transitions follow rules that can be described using a finite state automaton which we refer to as “syntax.” Normally, the automaton describing a Bengalese finch’s song has probabilistic branching and recursive connections (Honda and Okanoya, 1999; Okanoya, 2004; Sakata and Brainard, 2006). A series of syllables without branching constitutes what is referred to as a “chunk,” and sequences of chunks generate diverse “motifs.” Owing to the recursive structure and branching of the automaton describing their songs, the Bengalese finch is considered to generate an almost infinite number of different motifs. The complexity of this song structure is in contrast to the linearity of the songs produced by the Zebra finch, which is nonetheless a close relative of the Bengalese finch (Zann, 1996).
The acquisition and production of songs is made possible by a group of discrete brain nuclei and their connecting pathways, referred to as the song system (Figure 2; Nottebohm et al., 1976; Nottebohm, 2005). Within the song system, the HVC (used as a proper name, not as an abbreviation) plays a key part as a premotor nucleus generating temporal patterns of songs. In electrophysiological studies of the Zebra finch, the activation pattern of each HVC neuron was found to be highly context-dependent, corresponding to a particular moment in a song motif (Fee et al., 2004). Moreover, a recent study showed that cooling the HVC results in slowing song speed with preserved acoustic structure, whereas cooling the RA, a downstream motor nucleus, does not affect temporal structure of song (Long and Fee, 2008). This evidence strongly suggests that the HVC is a temporal pattern generator for song syllable sequences.
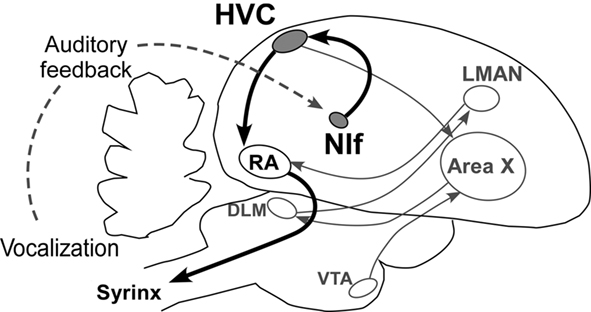
Figure 2. Neural basis of birdsong. The NIf–HVC–RA pathway acts as the song production pathway (for clarity, the pathway responsible for song learning is not highlighted). LMAN, lateral magnocellular nucleus of anterior nidopallium; DLM, medial nucleus of the dorsolateral thalamus; VTA, ventral tegmental area.
Due to its strong premotor activity, the nucleus interfacialis (NIf), one of the upstream inputs to the HVC, has been considered to play an important role in the generation of birdsong (Okanoya, 2004). One common belief regarding its function is that the NIf is a major source of auditory input to the HVC (Nottebohm et al., 1976; Coleman et al., 2007; Roy and Mooney, 2009).
Although lesions in the NIf do not affect generation of songs in the Zebra finch (Cardin et al., 2005), in the Bengalese finch the NIf is considered to be one of the essential regions that generate complexity in songs. While lesions of the NIf in the Bengalese finch reduce the branching of syllable-to-syllable transitions, syllable sequences still correspond to paths on the original diagram (Hosino and Okanoya, 2000). The reduction of complexity occurs only in birds that sing songs that are complex, and not in birds that sing simple songs. Based on this observation, it is inferred that the NIf, in cooperation with the HVC, provides complexity for the generation of songs.
However, it remains unclear what types of interactions between the HVC and the NIf have the potential to produce complex syntactical songs. That these questions have not yet been answered is a consequence of the technical difficulties associated with investigating the actual interactions between brain regions of singing birds. In order to overcome these difficulties, computational modeling has been used in several studies of neural mechanisms in songbirds. For example, Fee et al. (2004) proposed a model in which the HVC generates temporal patterns of songs through cooperation with the RA. In this model, it is assumed that temporal patterns of songs are represented as feedforward activities of the HVC, the role of which is analogous to a recording “tape.” Doya and Sejnowski (1995), Fiete et al. (2004, 2007), and Jin et al. (2007) also developed models based on a similar assumption. Although the design of these models is sufficient for explaining the song generation of the Zebra finch, the songs of which are very linear, they are not sufficient to explain the song generation of the complex syntactical song of the Bengalese finch.
In order to investigate the mechanism of song production in the Bengalese finch, Katahira et al. (2007) recently proposed a computational model, in which complex syntactical sequences with probabilistic branching can be produced by simple interactions between deterministic spike propagations and random noise. Jin (2009) also proposed a model based on the similar idea of a “branching chain” with random noise. These models mainly focused on the microcircuit level of the HVC, and successfully showed that spikes can stably propagate through branching chains of neurons in cooperation with inhibitory interneuron and random noise (Katahira et al., 2007; Jin, 2009).
Based on a similar idea of the interaction between deterministic dynamics and random noise, but using firing rate level abstraction, we also developed a macro level neural network model of HVC–NIf interaction of the song production in the Bengalese finch (Yamashita et al., 2008). In this system, the HVC was modeled by a recurrent neural network (RNN) that learns to generate temporal patterns of song sequences and the NIf was modeled as a random noise generator which provides stochasticity for branching of song sequences. The model successfully reproduced song sequences obtained from real Bengalese finches and mimicked developmental learning process of real young birds (Yamashita et al., 2008).
In the current study, we test our previously proposed idea of the functional role of NIf–HVC interaction, through a comparison between a biological experiment and a computational model simulation. The focus of the current model is on how complex syntactical songs of the Bengalese finch can arise from dynamics of neural connections representing groups of neurons in discrete brain nuclei. The model of neurons is a conventional firing rate model, in which each unit’s activity represents the average firing rate over a group of neurons. Due to its level of abstraction, consistency in physiological details, such as features of neural activity at the level of individual neurons and characteristics of individual synapses, were not considered. However, the level of abstraction used in our model could be suitable for investigating macro level dynamics of brain regions through direct comparison with behavior of actual animals.
Data of the biological experiment was obtained from a distinct study conducted by the same authors (Okumura et al., 2007a). In this biological experiment, activity of the NIf is reversibly inhibited and changes of songs induced by this pharmacological inhibition were observed. The plausibility of the model is tested by the comparison between the changes in the songs of actual birds that are induced by pharmacological inhibition of the NIf and the changes in the songs produced by the model that result from modification of parameters representing NIf functions.
Materials and Methods
Summary of Biological Experiment and Analysis of Song Sequence
In order to characterize the changes of song sequences in actual songbirds, we first briefly introduce the methods and the findings of the biological experiment (Okumura et al., 2007a). All experimental procedures were undertaken in accordance with the animal experimentation guidelines of RIKEN (RIKEN-BSI) approved by the institute’s animal ethics committee. Subjects of the experiments were five adult male Bengalese finches (body weight 12.7–15.5 g). The birds were obtained from the breeding colony of the Laboratory of Biolinguistics, RIKEN-BSI and a commercial supplier (Komiyama pet shop, Tokyo, Japan). These birds were at least 180 days old and their adult songs were crystallized. The number of notes in their songs varies from 8 to 14, and entropies of their songs vary between 1.41 and 1.63.
Activity of the NIf was reversibly inhibited by muscimol (GABA agonist) through reverse microdialysis technique (Höcht et al., 2007). Details of the experimental equipment and surgical procedure for guide cannula implantation are described in Okumura et al. (2007b). The tips of the guide cannulae were located 2.00 mm anterior, 1.50 mm lateral from the Y point (Lambda), and 1.85 mm deep from the surface of the dura mater. This coordination is approximately 0.30 mm above the center of the NIf. The position of the guide cannula was verified through histological experiment (Figure 3B). The range of minimum distance from active surface membranes of the probes to the border of the NIf was 0–150 μm and its average was approximately 60 μm. It is thus inferred that the observed changes in songs resulted from the chemical effects on the NIf.
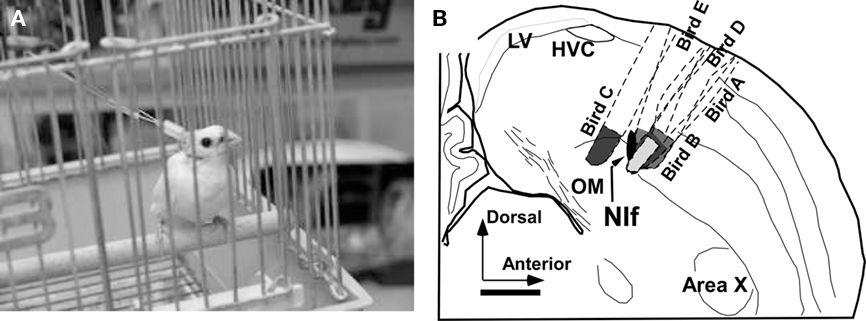
Figure 3. Subject of biological experiment with the experimental equipment (A) and summary of probe positions confirmed by histological experiment (B). LV, lateral ventricle; OM, tractus occipitomesencephalicus.
Through the microdialysis cannula, muscimol was perfused for 30 min followed by 6-h recording of songs. The concentration of muscimol in perfusion fluid (avian artificial cerebrospinal fluid) was 50 mM, and the perfusion rate was 1.0 μl/min. Following the perfusions of muscimol, we did not observe any abnormal behavior. The birds were able to fly, rest, jump to the other perch, eat, and sing as usual in their cage (Figure 3A). After chemical perfusion, all songs were recorded over time in a sound attenuated chamber using a PC-based multi-channel triggering hard disk recording system (Avisoft Recorder; Avisoft Bioacoustics, Berlin, Germany). Acoustic features of each song (syllables) were preserved. Observed changes were limited to their song syntax, which is the target of the current analysis.
Recorded songs were described by sequences of letters through sound spectrogram analysis. Changes in song syntax were analyzed by counting the occurrence frequencies of letter blocks in each song sequence. We use the term “letter block” to refer to strings of syllables, for example a three letter block “abc,” four letter block “abcd” and so on. The distribution of letter block occurrence probabilities reflects distinguishing features of each song. In a previous study, it was found that the songs of the Bengalese finch can usually be satisfactorily reproduced using a third-order Markov model (Hosino and Okanoya, 2000). Although a third-order Markov process corresponds to the probability distribution of four letter blocks, results for letter blocks of length between three and five did not show any qualitative difference. Due as well to the limited amount of actual birdsong data, the longer the length of letter block is, the less reliable the calculated statistics are. Therefore, in the present study, the length of the letter block was set at 3.
In order to evaluate the similarity between two song sequences, the Kullback–Leibler-divergence (KL-divergence), a well-known distance measure of probabilistic distributions, is used (Cover and Thomas, 1991). The KL-divergence is determined by the following formula:
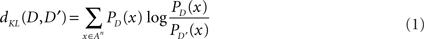
where A corresponds to the component syllables of a particular song, An is the set of all strings of length n that can be built from D and D′ correspond to a particular song syntax with a probabilistic distribution of strings, and PD(x) is the occurrence probability of string x under distribution D. Specifically, in the current study, D and D′ correspond to probability distributions of the songs in the normal condition and songs altered by chemical perfusion, respectively. As is standard, we set 0log0 = 0 and 0/0 = 1. In cases where there is a string with a null probability in D′, but not in D, PD′(x) is set to a small value (1.0 × 10−6) to avoid division by zero.
In order to evaluate the diversity of songs, we use the block entropy, determined by the following formula

in both cases, n is set to 3.
After chemical perfusion, recorded songs were grouped into 30 min intervals. Analyses were conducted for each interval using measures described earlier. The birds were considered to have recovered from the effects of chemical perfusion at the moment at which the KL-divergence stabilizes to the control level (point of recovery). Data for each bird was shifted such that their points of recovery were aligned on the time axis (Figure 4).
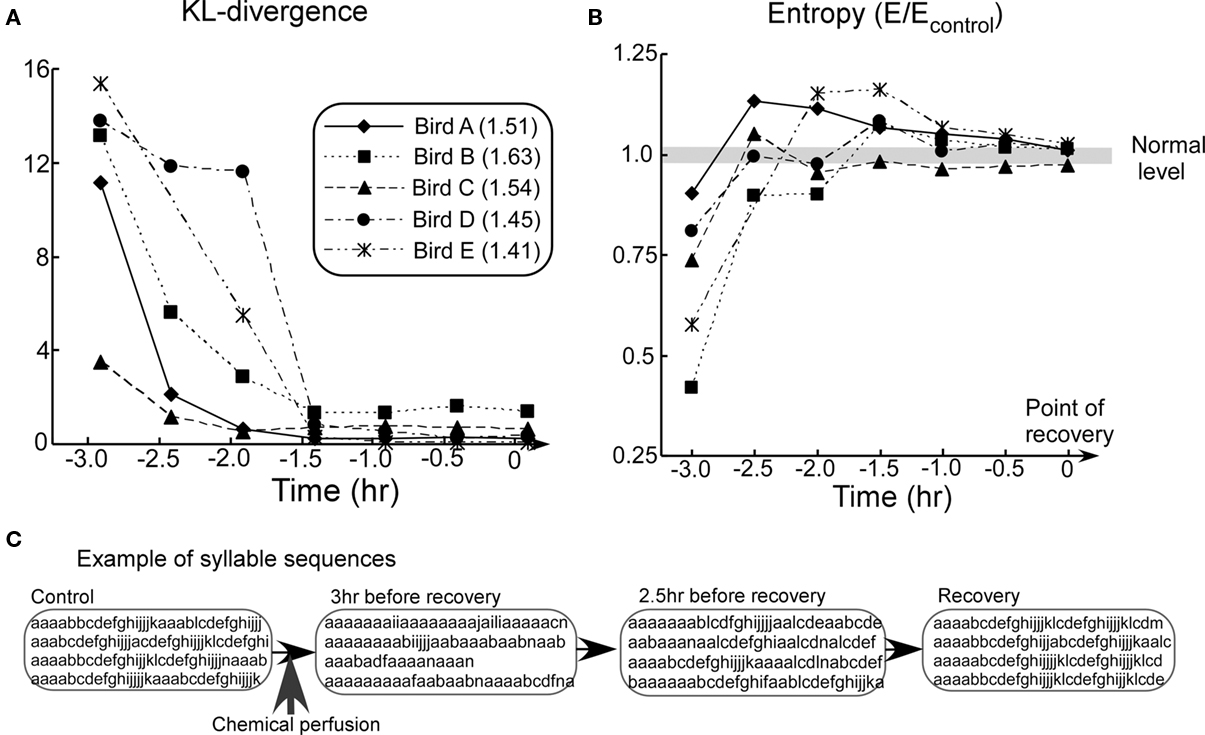
Figure 4. Summary of biological findings. (A) KL-divergence from the animal experiment. (B) Block entropy from the animal experiment. (C) Examples of song sequences in the recovery process (Bird A). In the graphs (A,B), time 0 correspond to the point of recovery. In graphs (B), the entropy values E are divided by the values of the control. Thus, the value 1.0 corresponds to normal level for all subjects (gray line). Values in the figure legend indicate the mean block entropies of each animal subject.
In all the subjects, KL-divergence monotonically decreased to a level of the fluctuations typical of the Bengalese finch’s songs (Figure 4A). This indicates that activity of the NIf recovered to its normal level. Block entropies, on the other hand, first showed very low values, then rose to a level higher than the control, and finally settled down to the control level (Figure 4B). This trend, which is found to be consistent among all birds, represents the distinctive result of this experiment.
Figure 4C shows examples of song sequences from the pharmacological experiment. At the early stage of recovery process, extension of the introductory repeated syllable sequences and decrease in length of the subsequent normal syllable sequence were observed. Extension of the introductory repeated syllable sequences resulted in a low entropy value. In the middle stage of recovery, extension of the introductory repeated syllable sequences continued to be observed. In addition, normal song sequences interspersed with extended repetition of the introductory syllable were also observed. These interruptions introduce syllable-to-syllable transitions which did not appear in song sequences under normal conditions. This variability of syllable-to-syllable transitions resulted in relatively high entropy. In the last stage, however, these abnormal syllable sequences disappeared. As a result, KL-divergence and entropy of the song sequences eventually recovered to normal levels. These results confirm that NIf activity is essential for the Bengalese finch to produce complex syntactical songs.
Model
Model overview
The architecture of the model used in the current study is shown in Figure 5. The model was developed based on the following three assumptions, each of which is supported by established biological evidence: (1) Temporal patterns of songs are represented as network dynamics in the HVC. (2) The NIf provides auditory feedback to the HVC. (3) The NIf generates random noise that feeds into the HVC. Assumption (3) is the simplest possible assumption consistent with the fact that simple interactions between the HVC and the NIf generate complexity of syntax in temporal birdsong sequences.
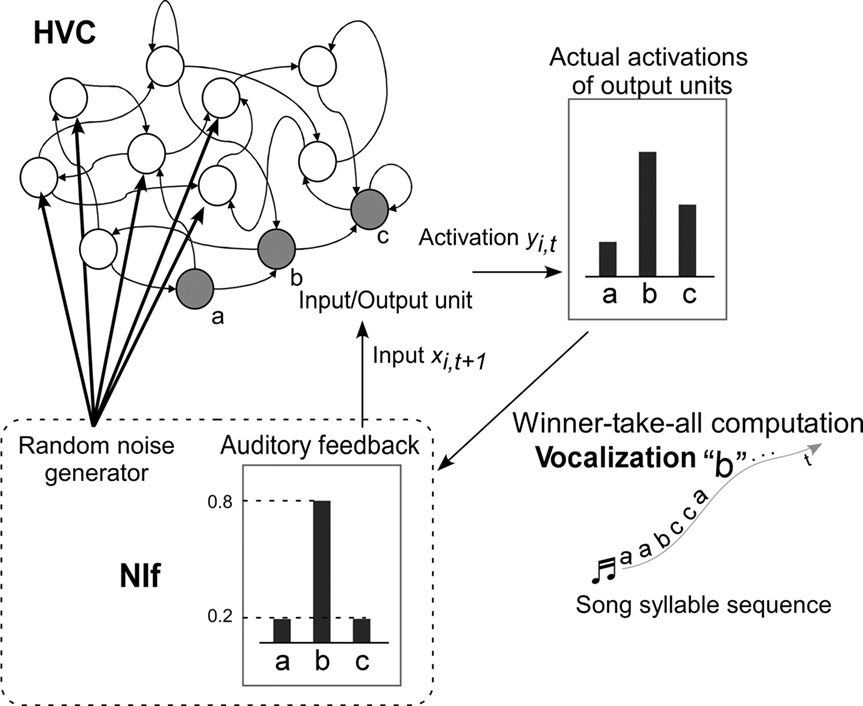
Figure 5. Model overview. Shaded circles are the input–output units of the RNN. Each input–output unit corresponds to a song syllable. Bars on the top right of the diagram indicate activation of output units at time t. Syllable “b” with the highest activation is selected to be the vocalized syllable sound at time t (WTA computation). The bars on the bottom of the diagram indicate the values of the auditory feedback input at time t + 1. The level of noise added to the non-input–output units and the level of feedback are assumed to correspond to the activity of the NIf.
The HVC is modeled by a fully connected RNN that learns to generate temporal patterns of song syllable sequences. Every unit of the RNN is connected to every other unit, including itself. This connectivity allows the RNN to preserve internal states and to generate temporal sequences of birdsongs. The number of RNN units, including input–output units, is 35. This is the minimum value large enough to successfully allow the network to learn songs with a maximum number of syllables. The number of input–output units is the same as the number of syllables in the song that the model learns. Each of the input–output units corresponds to a syllable sound.
The input to the RNN is a vocalized syllable sound at the current time step, and the output of the system is a syllable sound for the next time step. The discrete time step of the RNN is incremented with each syllable output of the song sequence. The level of auditory feedback sent back through the NIf is assumed to be modified according to the level of NIf activity. The NIf is also assumed to generate random noise which is fed to the RNN units of the HVC. This noise provides stochasticity for branching of syllable sequences, in cooperation with the RNN of the HVC.
Model dynamics
The model of neurons is a conventional firing rate model, in which the output of each unit is determined by applying a sigmoid function to the sum of all its inputs. The membrane potential (ui,t) and the activation (yi,t) of the ith unit at time t are determined by following formula
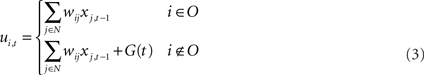

where O is the set of indices corresponding to the input–output units, xi,t is the neural state of the ith unit at time t, N is the total number of units, θi is the threshold of the ith unit, f is the sigmoid function f(x) = 1/1 + e−x, and G(t) is the noise added to the membrane potential of non-input–output units. This noise provides stochasticity for branching of syllable sequences, in cooperation with the RNN of the HVC. The level of noise is defined in terms of the interval of a uniform distribution. For example, if the noise level is set to 0.5 then the noise follows a uniform distribution on the interval [−0.5, 0.5]. Noise is added only during the generation of sequences, not during model learning. Even if noise is added during training, results do not show any difference. Therefore, to reduce the number of arbitrarily set parameters, additive noise G(t) was set to 0 during training. In the previous study, we showed that there is an optimal noise range within which the model generates syllable sequences that have branching probability distributions very similar to the template (Yamashita et al., 2008). For the normal condition, during testing, G(t) is set at this optimal level of noise.
The output syllable of the model at each time step is selected by winner-take-all (WTA) computation: the output unit with the highest activation is selected as the output syllable of the network. The selection of output syllables by the WTA computation resembles the vocalization process of songbirds in the sense that real birds, like the output of the WTA computation, only generate whole syllables like “a” or “b,” not mixed sounds like “a + b.” In real birds, vocalized syllable sounds are sent back to the HVC via the NIf as auditory feedback. To implement this feedback process, vocalized sound outputs from the current time step are fed back as auditory inputs at the next time step. For example, if “b” was the vocalized sound at time t then at time t + 1, the input unit corresponding to syllable “b” is only set as “active” and other input units are set as “inactive.” On the other hand, activation values of the non-input–output (context) units yi,t are simply copied to the neural states of next time step xi,t + 1. These calculations including selection of an output sound and external feedback inputs are described as follows.
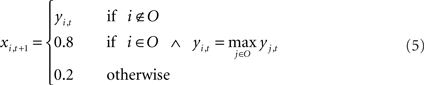
In the process of training, synaptic weights values sometimes grow too large, resulting from the sigmoid used in the activation function. To avoid this problem in learning, for the normal condition, the activation values of an active unit and those of inactive units are set to 0.8 and 0.2, instead of using 1.0 and 0.0 respectively. This limitation of the activation range of input–output units is commonly used to avoid divergence of weight values during learning process. Both in training and in generation, initial states of the network are set to their neutral value, i.e., the internal state of each neuron is set to 0.
Training
In the song learning of real birds, template song sequences are considered to be stored somewhere in the brain; the bird modifies its vocal output until the auditory feedback it receives matches the memorized template (Funabiki and Konishi, 2003). In the proposed model, a network is trained by means of supervised learning using template song sequences obtained from real birds. The conventional back-propagation through time (BPTT) algorithm is used for learning of the model network (Rumelhart and McClelland, 1986). Interested readers could find details of the learning algorithms as described in our previous work (Yamashita et al., 2008). In the current study, the BPTT is used not for mimicking the song learning process of the actual Bengalese finch but as a general learning rule. Therefore obtained results reflect the characteristic feature of the proposed network architecture, not the learning algorithm.
Simulation of pharmacological experiment
In simulating the effects of chemicals, the model is first trained to imitate the song sequences of the Bengalese finch taken from the biological experiment (Figure 6). In order to examine the effect of chemicals on the NIf, two parameters, corresponding to the level of activity of the NIf, are modified, one defining the level of added noise and the other defining the level of auditory feedback. The recovery process from the chemical effects over the course of time is simulated using a model described in the following formula,

where R(t)is the recovery rate at time t, K is a parameter which determines the slope of the curve. Since the absorption of chemicals is ignored in this calculation, the recovery rate monotonically increases from 0 to 1. The level of noise in the recovery process, G(t), which is added to the internal value of non-input–output units at time t, is determined as follows,

where G* is the optimal level of noise at which the model generates syllable sequences that have branching probability distributions very similar to the template. For each individual model that learns its respective song, this optimal value of noise is set as the value of the normal condition. In the process of recovery, noise level increases monotonically from 0 to the optimal level G*.
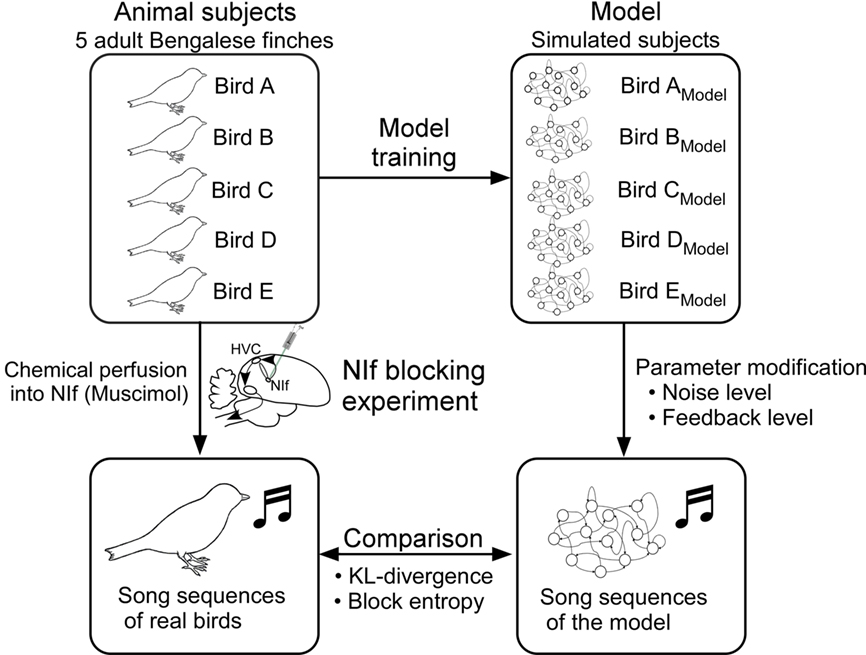
Figure 6. Experimental procedure. Each of the five model networks is trained using the song of a different Bengalese finch subject. Once each model learns to generate the song sequence of its respective animal subject sufficiently well, values of the synapse weights are fixed and the model network is considered to reproduce the behavior of its subject. Performance of the trained model is evaluated using the similarity measure described earlier.
The level of feedback is determined as the activation value of the input unit at the next time step based on a vocalized syllable at the current time step. In simulation of the recovery process, Eq. 5 is modified as follows,
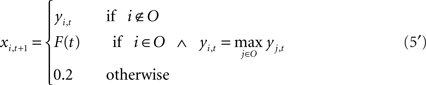

The level of feedback in the process of recovery, F(t), is determined as a linear function of the recovery rate R(t). Thus, the level of feedback increases monotonically from 0.2 (inactive level) to 0.8 (normal level). RG(t) and RF(t) are the recovery rates of noise and feedback defined by Eq. 6 using the parameters KG and KF, respectively. The point at which the recovery rate reaches 0 corresponds to the point of recovery in the biological experiment.
Results
Reproduction of Animal Subjects’ Songs
Performance of the model was evaluated by calculating the KL-divergence between template songs and learner’s songs. Through the learning process, KL-divergence decreases until it reaches a level that corresponds to the fluctuations typical of the Bengalese finch’s songs (Figure 7). This indicates that the current model successfully learned to generate complex syntactical songs nearly identical to those of the subject birds in the biological experiment. A model that manages to learn to generate the song sequence of its respective animal subject is considered to have reproduced the behavior of its subject.
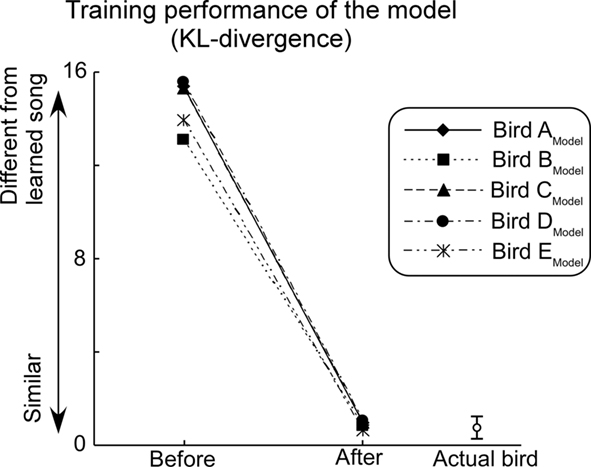
Figure 7. Performance of the model. The level of noise added is set to the optimal level for each learning trial and feedback is set to a normal level. Bar on the right bottom of the graph indicates the mean and degree of SD of KL-divergence among control songs (i.e., daily fluctuations of the subjects’ songs).
Simulation of Chemical Effects on the NIf
In order to examine the effects of changes in the levels of noise and feedback, KL-divergence and entropy are calculated from sequences generated with various levels of noise and feedback. Figure 8 shows an example of the relationship between noise, feedback, KL-divergence and block entropy. KL-divergence is minimal when the noise and feedback are at normal levels. The values of KL-divergence increase as noise and feedback levels decrease, contours of constant divergence taking the shape of concentric circles (Figure 8A). When both noise and feedback are at their minimum level, KL-divergence reaches a maximum value. Entropy, on the other hand, reaches a maximum with the highest level of noise and lowest level of feedback (Figure 8B). From the maximal entropy point, values decrease as noise decrease and feedback increase, contours again taking the shape of concentric circles. These features are consistent among all five model networks, each model bird learning songs of their respective animal subject counterparts.
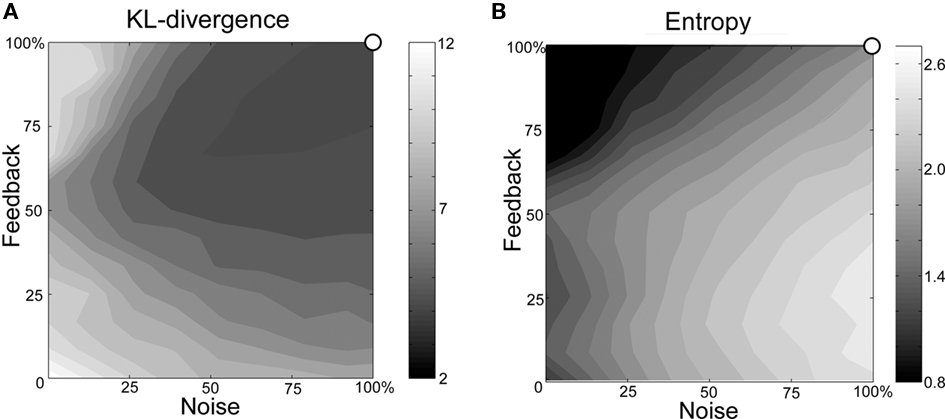
Figure 8. Example of the relationship between noise, feedback and (A) KL-divergence and (B) block entropy (Bird BModel). The origin of the axes corresponds to the condition in which both functions are set to minimal levels. The upper-right corner of each graph corresponds to the normal state.
Temporal changes in the effect of chemicals on the NIf were simulated using the model of recovery process described earlier (Eqs 6–8). In order to investigate the relationship between the auditory feedback and noise in the recovery process, changes of songs were observed while changing the value of the parameter K which determines the slope of the curve for recovery rates. The value of KF for auditory feedback was held fixed at 0.05. Difference in conditions was described in terms of the ratio of KG and KF (KG/KF).
Kullback–Leibler-divergence consistently decreases monotonically and stabilizes to the control level among all five model networks (Figures 9A,C,E). On the other hand, under the condition of KG/KF = 1.0, in three out of five model birds, changes in entropies resulting from the simulated pharmacological effects exhibited trends that are similar to those observed with the animal subjects (Figure 9D). That is, block entropies first show very low values, then rise to a level higher than the control, and finally settle down again to the control level. Under the condition of KG/KF = 1.5, overshoot of entropy values in the recovery process is exaggerated due to an increase in the relative effect of noise. This trend is consistently observed among all five model networks (Figure 9B). On the other hand, under the condition that KG/KF = 0.5, this effect is reduced, and it disappeared in most of the cases (Figure 9F).
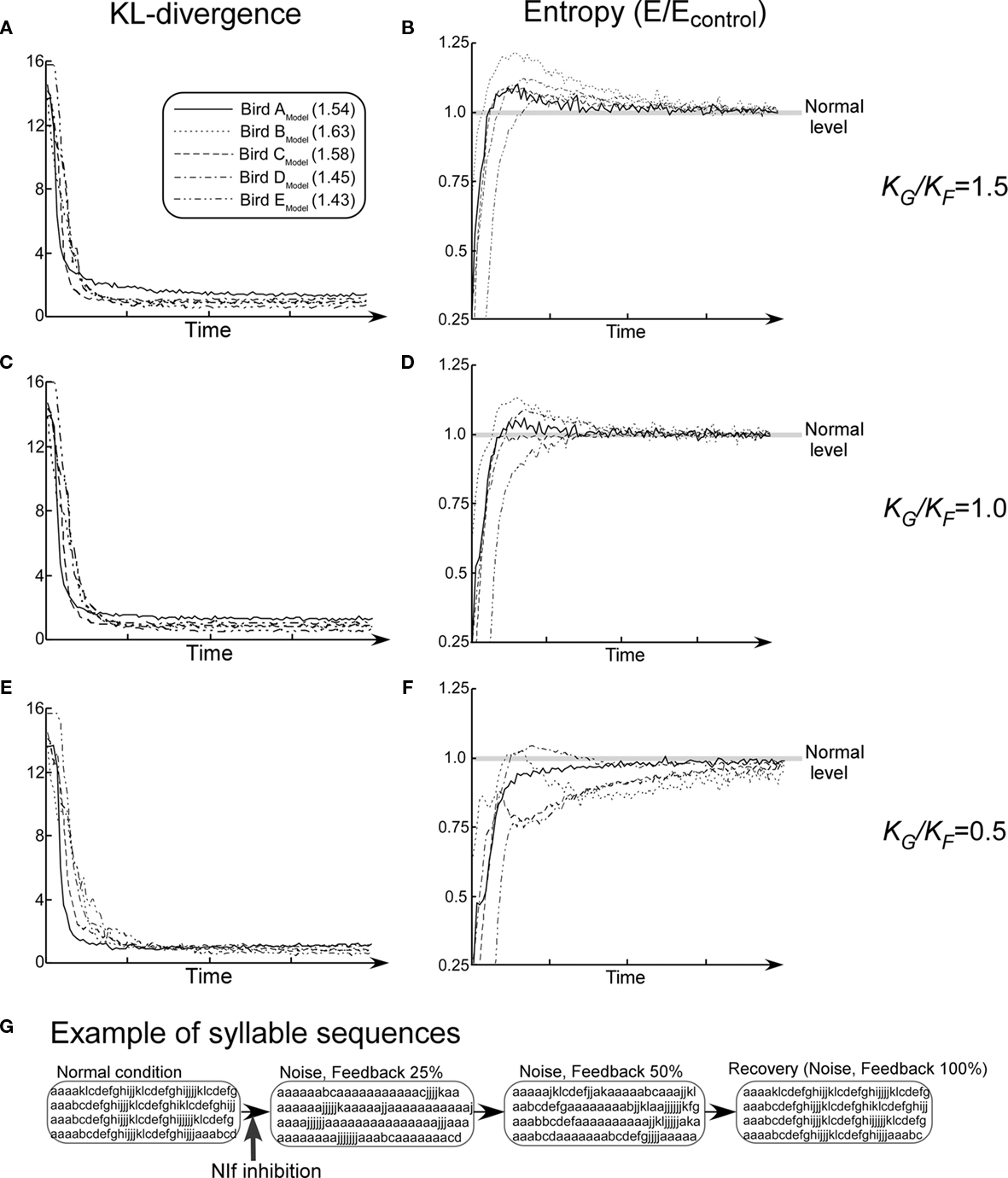
Figure 9. Summary of the simulation of recovery process from the NIf inhibition while changing the value of KG/KF. (A,C,E) KL-divergence from the simulation. (B,D,F) Block entropy from the simulation. (G) Examples of song sequences in the recovery process (Bird AModel, KG/KF = 1.0). Values in the figure legend indicate the mean block entropies of each model bird.
Figure 9G shows examples of song sequences generated by the model in the recovery process. Changes in songs resulting from the simulated pharmacological effects exhibit trends that are similar to those observed with the animal subjects. At an early stage of the recovery process, extension of the introductory repeated syllable sequences and decrease in length the subsequent normal syllable sequence are observed. In the middle stage of recovery, extension of the introductory repeated syllable sequences continue to be observed. In addition, normal sequences are interspersed with extended repetition of the introductory syllable. In the last stage, however, these abnormal syllable sequences completely disappear. A similar development is observed in the case of animal subjects (Figure 4C).
These observations strongly suggest that the distribution of entropy values results from a trade-off between the effects of noise and the effects of feedback on the dynamics of the RNN of the HVC. As a general rule, decrease of the noise level diminishes randomness of RNN dynamics. Therefore, decrease in the level of noise results in low entropy values. On the other hand, decreases in the level of feedback have an opposite effect, diminishing the difference between the maximum and minimal values of output activity (activation range; Figure 10A). Reduction of the activation range raises the relative effect of noise, resulting in the identity of the selected output unit switching more easily Figure 10B. For this reason, decreases in the level of feedback result in higher entropy values.
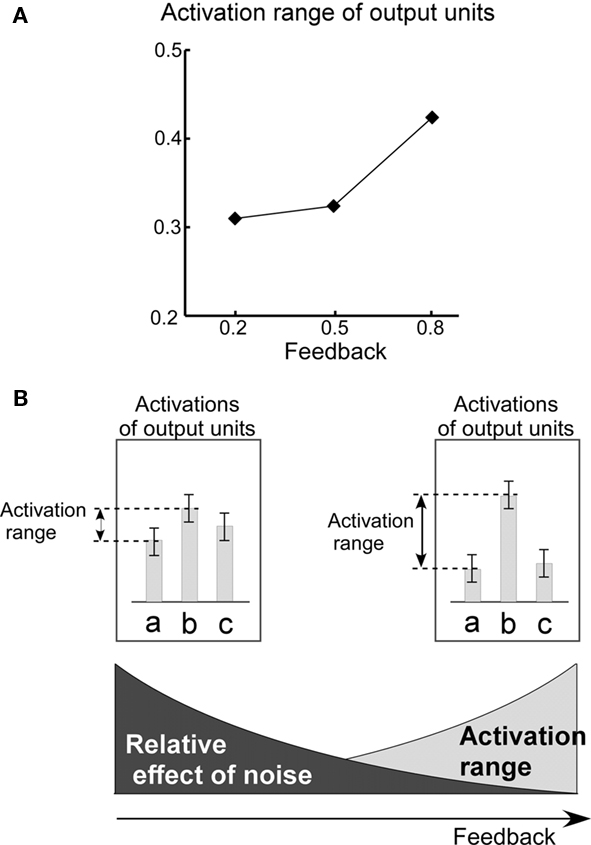
Figure 10. Activation range. (A) Relationship between the level of feedback and the activation range. The activation range is calculated from the formula, 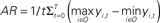 , where yi,t is the activation value of output units “before” application of the WTA computation. The graph shows mean values of activation ranges calculated from all five model networks learning their respective songs. (B) A schematic drawing of the relative effect of noise, which corresponds to the level of feedback. The bars in the diagram indicate the activation of the output units corresponding to syllables “a,” “b,” and “c.” Error bars indicate the range of possible fluctuation values resulting from noise. For the case of low level feedback, the activation range is so small that the effects of noise can easily switch which syllable it is that gets outputted.
, where yi,t is the activation value of output units “before” application of the WTA computation. The graph shows mean values of activation ranges calculated from all five model networks learning their respective songs. (B) A schematic drawing of the relative effect of noise, which corresponds to the level of feedback. The bars in the diagram indicate the activation of the output units corresponding to syllables “a,” “b,” and “c.” Error bars indicate the range of possible fluctuation values resulting from noise. For the case of low level feedback, the activation range is so small that the effects of noise can easily switch which syllable it is that gets outputted.
In the recovery process, entropies of song sequences reflect competing effects of the two parameters. At early stages of the recovery process, both noise and feedback are at a low level. Although the activation range is low, the absolute level of noise is also low. Thus, entropy of the sequences is lower than the level sustained under normal conditions. In the middle stage of the recovery process, subject to certain ranges of noise and feedback, the relative effect of noise reaches a level so high that entropy values rise to higher than normal values. Within this range, seemingly random syllable transitions not present in the normal sequences begin to appear. In the last stage of the recovery process, the level of feedback reaches a high enough level to reduce the relative effects of noise. As a result, entropy returns to its normal level, a condition in which noise affects the dynamics of the RNN only at the branching points of song sequences.
Discussion
Model Mechanism
It is known that deterministic dynamics of the RNN is able to represent multiple temporal sequences with probabilistic branching through associations between various initial states and internal dynamics of context units (“initial sensitivity”; Nishimoto et al., 2004; Namikawa and Tani, 2010). However, in the current study, initial states of the network were set to their neutral value, both in training and in generation. This setting of the neutral initial states corresponds to a plausible assumption that a path of branching which would be selected in the production of song sequences is not determined before a bird starts to sing. This assumption leads to the requirement of two additional mechanisms that enable the RNN to generate complex song syllable sequences with probabilistic branching: additive noise and an auditory feedback process.
As a result of learning from the song sequences of real birds, activation patterns of the RNN used to model the HVC converge to the probabilities of syllable-to-syllable transitions in learned song sequences. In other words, at non-branching points (within chunk), only one output unit, corresponding to the next syllable, is active, and other output units are inactive. At branching points (chunk-to-chunk connection), on the other hand, the activity of output units is distributed according to the occurrence probability of each branch. However, this activation is not enough to generate complex sequences with probabilistic branching. Due to the completely deterministic dynamics of the RNN, in the absence of noise, the model network is only capable of generating one song sequence made up of a set of branches corresponding to the most frequent path in the learned song. This is despite the fact that syllable sequences learned from the template contain some branching, and despite the fact that activation of the RNN of the HVC represents branching that is probabilistically distributed. In the current model, additive noise, which is assumed to be provided in a way that is context independent, is essential to reproduce stochasticity of branching in song syllable sequences.
In addition to noise, in the current model, the auditory feedback process plays an important role in maintaining dynamics of the RNN of the HVC. As shown in Figure 10A, reduction of the auditory feedback level diminishes the range of RNN activation. In particular, the effect of feedback reduction on RNN dynamics is large at branching points in song syllable sequences. This is due to the fact that at branching points, the activation of output units, which correspond to the occurrence probabilities of each branch, competes with each other. At non-branching points, in contrast, at which competition of the output activations does not occur, the effect of feedback reduction is low.
The importance of the feedback input at the branching point of a song sequence is related to the assumption that WTA-like dynamics occur outside of the HVC. Specifically, in the current model, it was assumed that WTA computation corresponds to the vocalization which occurs at downstream parts of the HVC such as RA and other motor nuclei, whereas auditory feedback corresponds to external inputs to the HVC. As described earlier, owing to the stochastic nature of the Bengalese finch song, the activation of output units of the RNN is distributed at branching points. Due to such distributed activity, the dynamics of the RNN of the HVC needs to be maintained by the external feedback inputs which reflect the result of WTA computation.
An alternative to the above assumption is that WTA-like dynamics occur within the HVC. For example, Katahira et al. (2007) and Jin (2009) proposed models in which distributed activity of the HVC at song branching is maintained using WTA-like dynamics (lateral inhibition of interneurons) within the HVC. These models showed that, through the WTA-like dynamics within the HVC, stochastic song sequence can be reproduced without any feedback inputs (Katahira et al., 2007; Jin, 2009). Therefore, the role of the auditory feedback process was deferred as outside the scope of these studies. However, if external feedback inputs are not necessary to produce stochastic sequence of the Bengalese finch song, the assumption is inconsistent with the fact that reduction of auditory feedback strongly affects song structure in the Bengalese finch, whose songs exhibit probabilistic branching (Okanoya and Yamaguchi, 1997; Sakata and Brainard, 2006), but does not affect song structure in the case of the Zebra finch, whose songs exhibit no branching (Bottjer and Arnold, 1984).
Due to the level of modeling, discussing correspondences between the proposed model and an actual brain is possible only at a macro level of abstraction. However, our hypothesis that auditory feedback contributes to maintaining the dynamics of the HVC provides a possible explanation for the question of how auditory information is integrated into premotor activity of the HVC.
In the simulation of the pharmacological experiment, the model showed that complex features of changes in entropy values can be interpreted as a trade-off between the effects of noise and the effects of feedback on the dynamics of the RNN. Parameter studies of the current model also demonstrated that overshoot of entropy values is enhanced under the condition that the noise-like activity recovers more quickly than does the feedback level (KG/KF > 1.0). Although the current implementation is extremely simple, in the sense that both noise and feedback levels are linear function of R(t), this dissociation of timescale could be interpreted as the difference in sensitivity to excitatory–inhibitory interaction in the NIf. Noise-like activity may originate in the intrinsic activity of the NIf. Theoretical studies have proposed a hypothesis that the noise-like activity of neurons results from interaction between excitatory and inhibitory activation (Vreeswijk and Sompolinskyref, 1996; Amit and Brunelm, 1997). Moreover, the studies have shown that such noise-like activity is robustly generated over a wide range of activation levels. On the other hand, there exists a hypothesis claiming that precise balance between excitation and inhibition is important for gating and transmitting signals (Vogels and Abbott, 2009). In the pharmacological experiment, transmission of auditory information may be disturbed by the imbalance of excitation and inhibition (i.e., enhanced inhibition induced by GABA agonist). Given that noise generation occurs over a wide range of excitatory–inhibitory interaction, and transmission of auditory information is sensitive to specific excitatory–inhibitory interaction, it is likely that noise generating function would recover first. Auditory feedback function would recover after excitatory–inhibitory interaction has returned to within a specific range.
Correspondence to Previous Biological Findings
Auditory feedback
In addition to NIf–HVC pathway, other auditory–vocal integration pathways have been heavily investigated recently. For example, it was shown that the nucleus Uvaeformis (Uva), which is a thalamic input to the HVC and NIf, may gate the auditory inputs to the HVC and the NIf from the auditory brainstem (Coleman et al., 2007). The same research group subsequently showed that the nucleus caudal mesopallium (CM), a source of cortical auditory input to the NIf, also projects directly to the HVC (Bauer et al., 2008). These observations suggest that some pathways other than NIf–HVC pathway may also be involved in auditory–vocal integration in song production.
However, in spite of wide agreement on the importance of auditory–vocal integration in song production, how auditory information is integrated into premotor activities of the HVC remains as of yet unclear. In the current study, rather than attempt to fully implement details of auditory information pathways, we instead investigated, in an abstract manner, how auditory information affects the dynamics of HVC activity in the song production process.
One of the key findings of the biological portion of this study (Okumura et al., 2007a) is that extended repetition of the introductory syllable sequences is induced by NIf inhibition (Figure 4C). In the simulation portion of this experiment, extended repetition of the introductory syllable sequences is reproduced (Figure 9G). This phenomenon is similar to stuttering in humans (Lee, 1950) and songbirds (Leonardo and Konishi, 1999) induced by auditory feedback modification.
These facts suggest that the changes of songs induced by pharmacological inhibition of the NIf in our biological study may be interpreted as the modification of HVC dynamics resulting from reduction of auditory-related activities in the NIf. Our observations also suggest that the NIf may contribute to real time control mechanisms governing complex vocal behavior, and that studying the function of the NIf in the Bengalese finch could help contribute to a better understanding of human vocal behavior.
Another possible function
In the current model, the NIf is also assumed to generate random noises, which are fed into the HVC. The model showed that additive noise, in cooperation with deterministic dynamics of the HVC, is enough to reproduce occurrence probabilities of branching in song syllable sequences, even though noise is provided from the NIf independent of the syllable sequence context. In order to confirm the hypothesis that noise-like activity of the NIf is enough to generate complex syntactical songs, it would be useful to perform tests in which electrical stimulation (microstimulation) is applied to the NIf while the level of auditory feedback is assumed to be maintained at a normal level. In the Bengalese finch, the diversity of songs would be expected to increase as a result of such electrical stimulation; in particular, stimulation at the branching points of song sequences would be expected to show increased effects. To test this prediction, we are preparing to perform experiments in which electric stimulation is applied to the NIf.
The proposed model suggests that the production mechanism generating simple songs in the Zebra finch, and the mechanism generating complex syntactical songs in the Bengalese finch, are in essence the same, but with the exception that, in latter case, noise is added. The model also suggests that the NIf may not require a very complex representation. Our hypothesis is consistent with the fact that the NIf is a very small nucleus consisting of a small number of neurons and the fact that the activation pattern of the NIf is less context-dependent than that of the HVC or that of the RA (McCasland, 1987; Cardin and Schmidt, 2004). This is also consistent with the fact that the Bengalese finch and the Zebra finch, the songs of which are simple, are closely related and may indicate that there are no major functional differences between these species.
The proposed hypothesis that the NIf performs a noise-like function also provides a possible connection between NIf activity and developmental learning of song syllable sequences, although the training algorithm that is currently used (back-propagation) is not considered biologically plausible. We hypothesize that the noise-like activity of the NIf, by generating fluctuations at each transition, could assist in exploration during the learning of syllable-to-syllable transition rules. This is similar to the hypothesis stating that the random activity of the lateral magnocellular nucleus of anterior nidopallium (LMAN) supports exploration in syllable learning by fluctuating each individual sound (Doya and Sejnowski, 1995; Kao et al., 2005; ölveczky et al., 2005; Fiete et al., 2007). From this point of view, another testable prediction is proposed. If the noise-like activity of the NIf provides the random fluctuations necessary for exploration in the learning of syllable-to-syllable transition rules, then at the early stage of learning, one would expect higher activity of the NIf (for exploration), whereas high activity would not be necessary at the end of the learning process. In the Bengalese finch, however, NIf activity might be relatively high even at the end of the learning process, allowing the Bengalese finch to produce complex songs with syntactical structure. To confirm the predictions, changes of NIf activity during development and differences in NIf activity between the Bengalese finch and the Zebra finch must be examined.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Jun Namikawa for technical assistance. We also thank Chris Salzberg and Stephen Paul McKibbin for help with manuscript. Finally, we wish to express our gratitude to Jun Nishikawa and Kentaro Katahira for many stimulating discussions and comments on the early version of this manuscript. This research was partially supported by the Ministry of Education, Culture, Sports, Science and Technology, Grants-in-Aid for for Scientific Research on Innovative Areas (No. 22120523, 2010-2011).
References
Amit, D. J., and Brunelm, N. (1997). Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb. Cortex 7, 237–252.
Bauer, E. E., Coleman, M. J., Roberts, T. F., Roy, A., Prather, J. F., and Mooney, R. (2008). A synaptic basis for auditory-vocal integration in the songbird. J. Neurosci. 28, 1509–1522.
Bottjer, S. W., and Arnold, A. P. (1984). The role of feedback from the vocal organ. I. Maintenance of stereotypical vocalizations by adult zebra finches. J. Neurosci. 4, 2387–2396.
Cardin, J. A., Raksin, J. N., and Schmidt, M. F. (2005). Sensorimotor nucleus NIf is necessary for auditory processing but not vocal motor output in the avian song system. J. Neurophysiol. 93, 2157–2166.
Cardin, J. A., and Schmidt, M. F. (2004). Auditory responses in multiple sensorimotor song system nuclei are co-modulated by behavioral state. J. Neurophysiol. 91, 2148–2163.
Coleman, M. J., Roy, A., Wild, J. M., and Mooney, R. (2007). Thalamic gating of auditory responses in telencephalic song control nuclei. J. Neurosci. 27, 10024–100036.
Doya, K., and Sejnowski, T. J. (1995). A novel reinforcement model of birdsong vocalization learning. Adv. Neural Inf. Process. Syst. 7, 101–108.
Fee, M. S., Kozhevnikov, A. A., and Hahnloser, R. H. (2004). Neural mechanisms of vocal sequence generation in the songbird. Ann. N. Y. Acad. Sci. 1016, 153–170.
Fiete, I. R., Fee, M. S., and Seung, H. S. (2007). Model of birdsong learning based on gradient estimation by dynamic perturbation of neural conductances. J. Neurophysiol. 98, 2038–2057.
Fiete, I. R., Hahnloser, R. H., Fee, M. S., and Seung, H. S. (2004). Temporal sparseness of the premotor drive is important for rapid learning in a neural network model of birdsong. J. Neurophysiol. 92, 2274–2282.
Funabiki, Y., and Konishi, M. (2003). Long memory in song learning by zebra finches. J. Neurosci. 23, 6928–6935.
Höcht, C., Opezzo, J. A., and Taira, C. A. (2007). Applicability of reverse microdialysis in pharmacological and toxicological studies. J. Pharmacol. Toxicol. Methods 55, 3–15.
Honda, E., and Okanoya, K. (1999). Acoustical and syntactical comparison between songs of the white-backed Munia (Lonchura striata) and its domesticated strain, the Bengalese finch (Lonchura striata var.domestica). Zoolog. Sci. 16, 319–326.
Hosino, T., and Okanoya, K. (2000). Lesion of a higher-order song nucleus disrupts phrase level complexity in Bengalese finches. Neuroreport 11, 2091–2095.
Jin, D. Z. (2009). Generating variable birdsong syllable sequences with branching chain networks in avian premotor nucleus HVC. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 80, 051902.
Jin, D. Z., Ramazanoğlu, F. M., and Seung, S. H. (2007). Intrinsic bursting enhances the robustness of a neural network model of sequence generation by avian brain area HVC. J. Comput. Neurosci. 23, 283–299.
Kao, M. H., Doupe, A. J., and Brainard, M. S. (2005). Contributions of an avian basal ganglia-forebrain circuit to real-time modulation of song. Nature 433, 638–643.
Katahira, K., Okanoya, K., and Okada, M. (2007). A neural network model for generating complex birdsong syntax. Biol. Cybern. 97, 441–448.
Leonardo, A., and Konishi, M. (1999). Decrystallization of adult birdsong by perturbation of auditory feedback. Nature 399, 466–470.
Long, M. A., and Fee, M. S. (2008). Using temperature to analyse temporal dynamics in the songbird motor pathway. Nature 456, 189–194.
Namikawa, J., and Tani, J. (2010). Learning to imitate stochastic time series in a compositional way by chaos. Neural Netw. 23, 625–638.
Nishimoto, R., and Tani, J. (2004). Learning to generate combinatorial action sequences utilizing the initial sensitivity of deterministic dynamical systems. Neural Netw. 17, 925–933.
Nottebohm, F. (2005). The neural basis of birdsong. PLoS Biol. 3, e164. doi: 10.1371/journal.pbio.0030164
Nottebohm, F., Stokes, T. M., and Leonard, C. M. (1976). Central control of song in the canary, Serinus canaries. J. Comp. Neurol. 165, 457–486.
Okanoya, K. (2004). The Bengalese finch: a window on the behavioral neurobiology of birdsong syntax. Ann. N. Y. Acad. Sci. 1016, 724–735.
Okanoya, K., and Yamaguchi, A. (1997). Adult Bengalese finches (Lonchura striata var. domestica) require real-time auditory feedback to produce normal song syntax. J. Neurobiol. 33, 343–356.
Okumura, T., Yamashita, Y., Okanoya, K., and Tani, J. (2007a). Function of the sensori-motor nucleus NIf in generation of complex syntactical song in the Bengalese finch I. A biological study. Soc. Neurosci. Abstr. 33, 646.2.
Okumura, T., Okanoya, K., and Tani, J. (2007b). Application of light-cured dental adhesive resin for mounting electrodes or microdialysis probes in chronic experiments. J. Vis. Exp. 6, e249.
ölveczky, B. P., Andalman, A. S., and Fee, M. S. (2005). Vocal experimentation in the juvenile songbird requires a basal ganglia circuit. PLoS Biol. 3, e153. doi: 10.1371/journal. pbio.0030153
Roy, A., and Mooney, R. (2009). Song decrystallization in adult zebra finches does not require the song nucleus NIf. J. Neurophysiol. 102, 979–991.
Rumelhart, D. E., and McClelland, J. L. (1986). Parallel Distributed Processing. Cambridge: MIT Press.
Sakata, J. T., and Brainard, M. S. (2006). Real-time contributions of auditory feedback to avian vocal motor control. J. Neurosci. 26, 9619–9628.
Sakata, J. T., and Brainard, M. S. (2009). Social context rapidly modulates the influence of auditory feedback on avian vocal motor control. J. Neurophysiol. 102, 2485–2497.
Vogels, T. P., and Abbott, L. F. (2009). Gating multiple signals through detailed balance of excitation and inhibition in spiking networks. Nat. Neurosci. 12, 483–491.
van Vreeswijk, C., and Sompolinsky, H. (1996). Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science 274, 1724–1726.
Keywords: recurrent neural network, HVC, NIf, Bengalese finch, zebra finch
Citation: Yamashita Y, Okumura T, Okanoya K and Tani J (2011) Cooperation of deterministic dynamics and random noise in production of complex syntactical avian song sequences: a neural network model. Front. Comput. Neurosci. 5:18. doi: 10.3389/fncom.2011.00018
Received: 26 November 2010;
Accepted: 30 March 2011;
Published online: 18 April 2011.
Edited by:
David Hansel, University of Paris, FranceCopyright: © 2011 Yamashita, Okumura, Okanoya and Tani. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Yuichi Yamashita, Laboratory for Behavior and Dynamic Cognition, RIKEN Brain Science Institute, 2-1 Hirosawa, Wako-shi, Saitama 351-0198, Japan. e-mail:eWFtYXlAYnJhaW4ucmlrZW4uanA=


 Kazuo Okanoya3,4 and Jun Tani1
Kazuo Okanoya3,4 and Jun Tani1