Higher Order Spike Synchrony in Prefrontal Cortex during Visual Memory

Pipa, Gordon; Munk, Matthias H J

doi:10.3389/fncom.2011.00023

ORIGINAL RESEARCH article

Front. Comput. Neurosci., 08 June 2011
volume 5 - 2011 | https://doi.org/10.3389/fncom.2011.00023

Higher order spike synchrony in prefrontal cortex during visual memory

Gordon Pipa^1,2,3 Matthias H. J. Munk⁴*

¹ Department of Neurophysiology, Max-Planck-Institute for Brain Research, Frankfurt/Main, Germany
² Institute of Cognitive Science, University of Osnabrueck, Osnabrueck, Germany
³ Frankfurt Institute for Advanced Studies, Frankfurt, Germany
⁴ Department of Physiology of Cognitive Processes, Max-Planck-Institute for Biological Cybernetics, Tübingen, Germany

Precise temporal synchrony of spike firing has been postulated as an important neuronal mechanism for signal integration and the induction of plasticity in neocortex. As prefrontal cortex plays an important role in organizing memory and executive functions, the convergence of multiple visual pathways onto PFC predicts that neurons should preferentially synchronize their spiking when stimulus information is processed. Furthermore, synchronous spike firing should intensify if memory processes require the induction of neuronal plasticity, even if this is only for short-term. Here we show with multiple simultaneously recorded units in ventral prefrontal cortex that neurons participate in 3 ms precise synchronous discharges distributed across multiple sites separated by at least 500 μm. The frequency of synchronous firing is modulated by behavioral performance and is specific for the memorized visual stimuli. In particular, during the memory period in which activity is not stimulus driven, larger groups of up to seven sites exhibit performance dependent modulation of their spike synchronization.

Introduction

Synchrony of neuronal spike firing has originally been proposed as a fundamental property of neocortical function (Delage, 1919; Hebb, 1949; Abeles, 1982, 1991) and has been observed under various conditions in numerous areas of the cerebral cortex. Early evidence was provided by studies of primary visual cortex (Gray et al., 1989; reviewed in Singer and Gray, 1995), later synchrony was observed in extrastriate (Kreiter and Singer, 1996) and other sensory areas like A1 (Ahissar et al., 1992; deCharms and Merzenich, 1996) and executive areas including frontal cortex (Vaadia et al., 1995), primary motor cortex (Murthy and Fetz, 1996; Riehle et al., 1997; Pipa et al., 2007). However, the nature of synchronous firing has nurtured a long standing debate whether synchrony serves the integration of signals distributed over large neuronal populations (Singer, 1999 versus Shadlen and Movshon, 1999). One interesting problem in this discussion was that studies in which attention was explicitly or implicitly modulated, synchrony could either change as predicted by properties of the sensory stimuli (Kreiter and Singer, 1996; Maldonado et al., 2000; Steinmetz et al., 2000) or in a counterintuitive way, which was not related to properties of the stimuli (de Oliveira et al., 1997; Thiele and Stoner, 2003). Two recent studies (Dong et al., 2008; Lima et al., 2010) have once more investigated whether the “binding-by-synchronization” hypothesis can predict spike synchrony in area V1 of behaving macaques. Both studies found synchrony which did show some degree of stimulus dependence, but reflected more spatial properties of the underlying connectivity as had been shown before for correlated firing of neurons in V1 and V2 (Nowak et al., 1999; Kohn and Smith, 2005) rather than direct evidence for figural binding. In higher cortical areas like inferotemporal cortex, neurons can synchronize their spiking when monkeys successfully solve visual recognition tasks (Gochin et al., 1994; Anderson et al., 2006) or processes features of faces (Hirabayashi and Miyashita, 2005), but evidence for stimulus dependent or even object-specific synchronized firing in higher visual areas remains sparse. Despite of this unresolved issues, cortical areas beyond sensory pathways express temporally precise spike firing which has been related to prediction of go signals (Riehle et al., 1997), decision making (Dudkin et al., 1995; Thiele and Hoffmann, 2008), spatial (Constantinidis and Goldman-Rakic, 2002), as well as working memory for temporal intervals and color (Sakurai and Takahashi, 2006).

Does millisecond precise neuronal firing have any relevance for cortical information processing? Evidence for the behavioral relevance of precise neuronal timing beyond mere covariation with behavior was recently provided by electrical stimulation experiments in auditory cortex which showed that rats can detect inter-stimulus-intervals of 3 ms (Yang et al., 2008). However, there is growing evidence that precise neuronal activity patterns across different spatiotemporal scales are highly relevant for information coding in sensory and associational areas of the cortex (Kayser et al., 2009). Another piece of evidence that points to the relevance of precise neuronal timing is the observation that during attention, the variance of spike responses is reduced (Mitchell et al., 2007), which may be related to the occurrence of stabilizing gamma oscillations (Rodriguez et al., 2010).

However, there are other observations of cortical synchrony which suggest that precise spike timing is a much more general principle of cortical function than serving the encoding of behaviorally relevant information provided by sensory input. One of the prominent properties of corticocortical networks is their massive divergence and convergence (Salin and Bullier, 1995) and the very low number of synaptic contacts between individual cells (Douglas and Martin, 2004) combined with small unitary synaptic potentials (Sjöström et al., 2008). As a consequence, signal propagation along cortical pathways depends on cooperativity of a large number of converging presynaptic neurons (Sjöström et al., 2008). But, beyond feed-forward processing of sensory information, cortical networks are continuously active (Arieli et al., 1996; De Luca et al., 2006), which may be the consequence of reverberating synfire chains (Abeles et al., 1993; Prut et al., 1998) and is most likely the basis for ongoing brain processes like thinking and dreaming. Regulating the general fluidity of neuronal interactions on large spatial scales are likely to reflect general capabilities of the cortical network which can be addressed more empirically as general factor of intelligence (van den Heuvel et al., 2009). Beyond these putative cognitive functions of precise neuronal timing, synchronous cortical activity is involved in the organization of cortical circuits as abundant evidence for spike timing dependent plasticity suggests (Caporale and Dan, 2008).

Why could synchronous spiking be useful for in the organization of short-term memory in prefrontal cortex? (1) Synchrony might sustain endogenous activity during the memory delay for maintaining stimulus information without depending on further sensory drive, (2) Synchrony may support sensory coding of feature conjunctions as hypothesized in the binding hypothesis (see however Dong et al., 2008), (3) Synchronous activity could drive downstream neurons in premotor cortex to prepare and execute the behavioral responses, (4) Synchrony may reconnect more abstract representations to sensory representations during rehearsal as has been shown for locking of theta oscillations across areas with dual micro electrode recordings in ventral PFC and V4 (Liebe et al., 2009; Hoerzer et al., 2010), (5) Synchrony might structure executive processes underlying task performance by driving circuits that serve different subtasks in the memory process. We set out to determine whether we can find synchronous spiking in our multi-site prefrontal recordings and if confirmed, to test whether this synchrony is task and/or stimulus dependent.

Materials and Methods

We therefore trained two female monkeys (M. mulatta) to perform a visual short-term memory task which consisted of a 0.5-s sample presentation, followed by a 3-s delay and a 2-s test presentation (Figure 1). Sample stimuli were randomly drawn from a set of 20 familiar stimuli and test stimuli were drawn from the same set excluding the sample of this trial in half of the trials in which non-matching test stimuli were used. Match and Non-match trials were presented in random order. When the test stimulus was shown, the monkey had to decide whether the stimulus was matching the sample and respond by pressing the left of two buttons while in case of a non-match, the monkey had to press the right button. By requiring behavioral responses for both types of test stimuli we made sure that all trials are homogenous with respect to response preparation and motor activity. Stimulus presentation and behavioral control were provided by a custom-made program. The monkeys did not have to fixate, but we measured eye movements at high resolution with the double magnetic induction method (Bour et al., 1984). The percentage of correct behavioral responses ranged between 71 and 87% across sessions. Anatomical MRI scans (T1-flash, 1 mm³ isovoxel, 1.5 T) were used to guide implantation of recording chambers and to reconstruct recording positions. All procedures were approved by the local authorities (Regierungspräsidium) and are in full compliance with the guidelines of the European Community (EUVD 86/609/EEC) for the care and use of laboratory animals.

FIGURE 1

Figure 1. Time structure of the visual memory task.

Simultaneous recording of multi-unit activity was performed with up to 16 platinum–tungsten-in-quartz fiber microelectrodes (Thomas RECORDING, Giessen, Germany) from ventral PFC. Electrodes had been arranged in a square shaped 4 × 4 grid with a distance between nearest neighbors of 500 μm. Signals were filtered (0.5–5 kHz, 3 dB/octave), digitized at 32 kHz, and saved as time stamp with attached waveform. Preprocessing included the rejection of artifacts (movements, licking) and removing line noise at 50 ± 0.5 Hz. Spike pattern analyses were performed for sets of trials constructed from the stimulus and behavioral protocol using the NeuronMeter software package (http://neuronmeter.convis.info). Data will become available online at the German Neuroinformatics Node (http://www.neuroinf.de/).

Analysis of Synchronous Firing

To identify differences in neuronal coupling expressed by modulation of spike synchrony we used a bivariate and multivariate extension of NeuroXidence (Pipa et al., 2008; Wu et al., submitted; see also http://www.NeuroXidence.com). In the present article, each incidence of a synchronized firing event is referred to as a joint-spike event (JSE), while the identity of a JSE is referred to as a joint-spike pattern (JS-pattern). Or, with other words JSE are realizations of a JS-pattern.

In a first step, the frequency 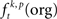yes of JSEs of a certain JS-pattern (p) was determined by the bivariate and multivariate extension of NeuroXidence for each trial (t) and for each factor (k) of an experiment. To account for the stochasticity of spike times, a JS-pattern is defined by a millisecond wide temporal window, which accounts for the maximal uncertainty of synchronous firing (Figure 2A). In this paper, this uncertainty (t_c) was set to 3 ms. Note that the detection of a JSE is not based on binned spike trains, but uses the exact experimental spike times which were sampled at a precision of 32 kHz, i.e., times of threshold crossing were initially recorded as multiples of 31.25 μs. For illustrative purposes, Figures 2B,C demonstrate how significant JS-patterns (Figure 2B) are destroyed when spike trains are randomly jittered by t_r = 15 ms (Figure 2C). In the original data, the total number of significant joint-spike patterns consisted of patterns with complexities 2–6, 59% of JSP with complexity 2, 13% complexity 3, 17% complexity 4, 10% complexity 5 and 1% complexity 6. After jitter the number of significant patterns was reduced for all complexities. Compared to the frequency of significant joint-spike pattern in the original data, the percentage in respect to the complexity dropped from 59 to 54% (c2), from 13 to 3% (c3), from 17 to 4%, from 10 and 1 to 0% for complexity 5 and 6. This effect is summarized in Figure 2D as frequency distribution of JS-patterns as a function of their complexity and a Cumulative Distribution Function based on a two sample KS-test is plotted in Figure 2E.

FIGURE 2

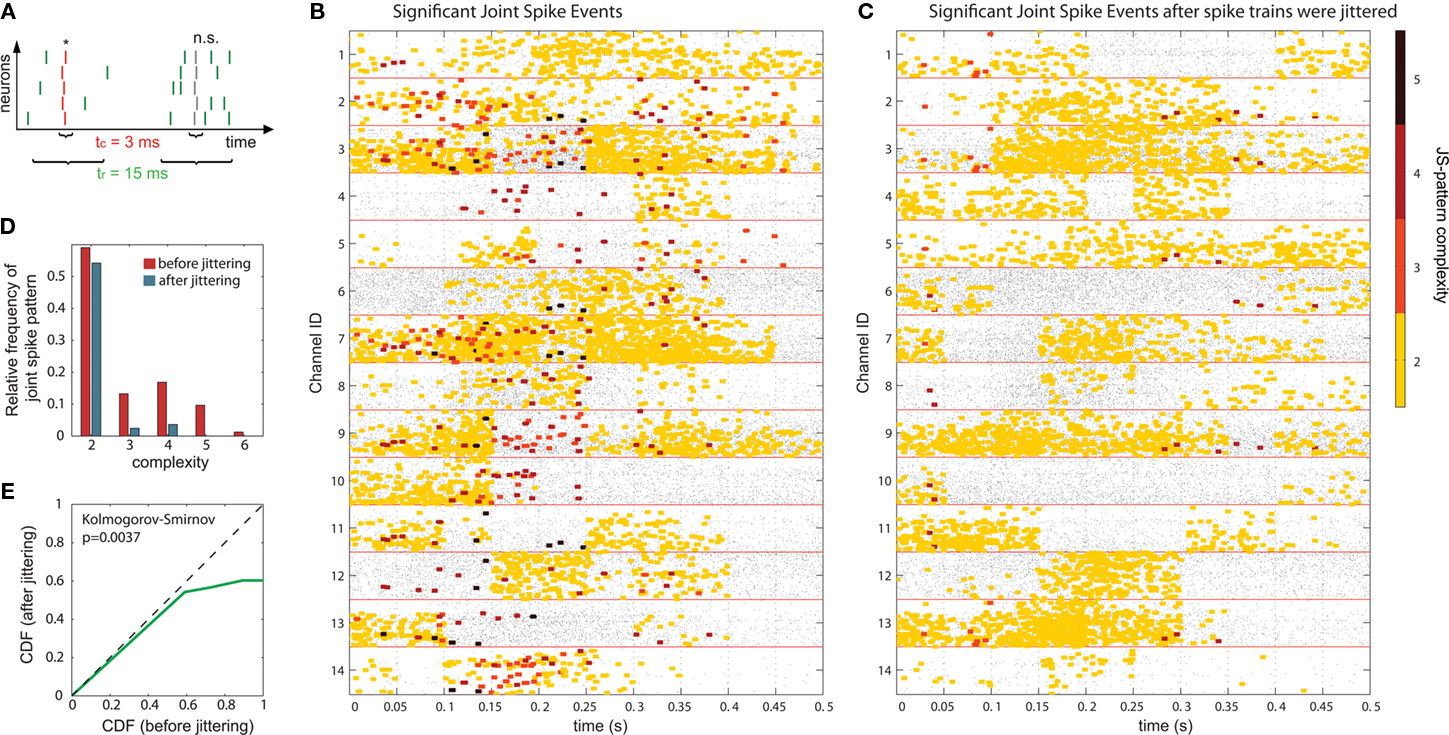
Figure 2. Demonstration of time windows, coincidences before and after significance estimation and after introducing artificial jitter. (A) Sketch to illustrate the idea of testing joint-spike events (JSE) by comparing time scales. Joint-spike patterns (JSP) are considered significant if there are more or less JSE than in a dataset in which spike timing of neurons is synchronized and spike rate covariations are slower than t_r = 15 ms. To define this criterion, two time scales were introduced. The first time scale (t_c) defines the temporal precision with which spikes have to coincide in order to be detected as JSE. The second time scale (t_r) defines the maximum speed of rate covariation. Using these two time scales, JSEs are considered as significant if there are significantly more JSEs, i.e., coincidence firing with an uncertainty less than t_c, in the original data than in a surrogate data set obtained by jittering the original spike trains with ±7.5 ms. (B) Raster plot of all significant synchronous patterns in 14 sites after correction with t_r. (C) Raster plot of the same data after destroying JSPs: In order to demonstrate that the JSPs shown in (B) are real, we performed a control for which both – original and surrogate – data were jittered with the same t_r = 15 ms. This control corresponds to a data set that does not have any fine temporal spike synchronization across neurons, but may have spike rate covariation slower than t_r. (D) Quantitative comparison of the number of significant JSPs in original and control data set, shown in (B,C), respectively. Red bars are normalized to 1, and the blue bars are normalized to the total numbers of non-jittered patterns (red = number of patterns of complexity c in non-jittered data / number of patterns for all complexities in non-jittered data; blue = number of patterns of complexity c in jittered data / number of patterns for all complexities in non-jittered data). (E) Cumulative Distribution Function of a two sample KS-test. The p-value of 0.0037 reflects that the number of JSPs is highly significantly decreased.

In a second step, the frequencies 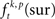yes of chance JSEs were estimated for JS-pattern (p), trial (t), and experimental factor (k) from surrogate data which were derived from the original data by jittering each individual spike train under the assumption that neuronal spike discharge is not coupled on a fine temporal scale. We generated exactly one surrogate trial for each original trial to prevent a sampling bias. For setting the amount of jitter applied to the original data when generating the surrogates, a second slower time scale t_r was defined which was set to t_r = 15 ms. The slower time scale t_r sets the minimal interval during which rate covariation may explain coincident firing. Therefore, t_r defines the maximal extent of the jittering, which is applied to destroy any fine temporal cross-structure that may exist between different spike trains. Because spike trains are shifted as a whole against each other within t_r, the auto-structure, rate covariations across neurons as well as rate variation and other features of each individual spike train, which are slower than the time scale t_r, are preserved.

In a third step, we determined for each trial (t), each experimental factor (k), and each JS-pattern (p), the difference 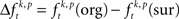yes of JSE frequencies in original and surrogate data sets. Ultimately, this difference 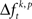yes is used to test whether the strength of synchrony of a certain JS-pattern differs across experimental conditions. To this end, the bi- and multivariate versions of NeuroXidence test whether the mean or median of the delta frequencies 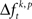yes of JSEs is significantly different across experimental factors. For the bivariate case, mean and median were compared by unpaired t-test and Mann–Whitney U-test, respectively. For the multivariate case, an ANOVA or a Kruskal–Wallis test were used. This comparison yields exactly one p-value per JS-pattern tested across experimental factors and trials. To prevent any sampling bias, only those JS-patterns were tested for which JSEs occurred at least once for every individual factor. For each experiment between hundreds and many thousands of JSE patterns were tested.

In order to summarize the results across all tested JS-patterns detected in each experiment, we grouped JS-patterns based on their complexity (c), which is given by the number of sites participating in a synchronous event. JS-complexity ranges from c = 2 (pairs), in which at least two sites have fired in synchrony during a temporal window of t_c= 3 ms. If c = 3, at least three sites fired synchronously, and so on. We analyzed JS-patterns with a complexity of up to c = 8. To summarize results for each complexity we derived the frequency σ of JS-patterns that each expressed a significant difference in 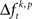yes across the factors k.

In order to account for dynamic modulations of spike coupling throughout the different periods of each trial, we performed the joint-spike analysis outlined above by using sliding windows. The sliding window length was chosen to fit the assumed time scale of changes of neuronal coupling given the underlying processes that encode, maintain, or decode information. Given the sometimes very transient rate responses we used a sliding window of 100 ms length during the sample and test stimulus presentation periods. The delay period could be analyzed with longer windows of 400 ms because of much slower rate modulations. Note that this choice of the sliding window length is independent of the spike rate modulation per se. NeuroXidence allows for an unconstrained choice of sliding window length, because it accounts for auto-structure and rate covariation slower than t_r. This distinguishes NeuroXidence from other methods like for example the unitary event method (Grün et al., 1999, 2002, 2003) which all require stationary data.

Behavioral and Stimulus Specific Modulation of Spike Synchronization

First we used the bivariate NeuroXidence method to detect modulation of spike synchronization depending on the behavioral success of the monkeys, comparing trials with correct or incorrect behavioral responses. On average, performance was ∼80%, trials with correct responses were four times more frequent than trials with behavioral errors. To prevent any bias, we balanced the number of correct and incorrect trials for each session by selecting subsets of correct trials which were close in time to the error trials. With the bivariate version of NeuroXidence we tested whether synchrony was modulated by the performance of the monkey and derived the direction of modulation, i.e., tested whether synchronous firing compared to chance occurred more often in correct trials than in incorrect (relative increase for correct), or whether synchronous firing occurred more often in incorrect trials than in correct (relative increase for incorrect). In a second step we derived the frequency ρ of JS-patterns of complexity c that expressed a significant increase of spike synchrony for correct responses 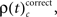yes and the frequency of JS-patterns of complexity c that expressed a significant increase of spike synchrony for incorrect responses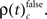 yes

The multivariate version of NeuroXidence was used to detect stimulus specific modulations of spike synchronization. Here, the k-experimental factors were all the 20 different visual stimuli presented during the sample period. These were tested for significant differences 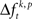yes across stimuli. A significant difference indicates that the strength of spike synchrony is modulated in a stimulus specific manner. As for changes related to behavioral performance, we next summarized results by computing the frequency of JS-patterns for each complexity c that expressed a stimulus specific modulation of spike synchrony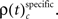 yes

Temporal Modulation of JS-Pattern Complexity

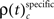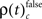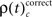The frequencies yes for stimulus specific as well as yes and yes for performance related modulations of spike synchrony had been computed for each JS-pattern complexity and each sliding window. Note that each JS-pattern that contributes to any of the three frequencies ρ(t)_c can be considered as significant. To test whether the frequency of JS-patterns also has been significantly modulated over time, we compared 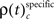yes and the difference 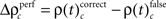yes to analogous results obtained from analyses of the same data, but based on permuted trials. Trial permutation exchanged trials between experimental factors while the simultaneity and the auto-structure of all recorded spike trains was preserved. This way we could destroy any performance or stimulus specific modulations, while keeping all other properties of the joint-spike trains intact so that the analysis of spike synchrony and temporal modulation of neuronal coupling is not compromised (Figure 3A). Therefore trial permutation serves as an ideal estimate of the frequency ρ(t)_c and its variability under the null hypothesis that synchrony is unchanged between experimental factors. Trial permutation was performed independently for each sliding window, giving exactly one p-value per JS-pattern for the original trial structure and for the trial permuted data (Figure 3B). 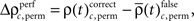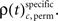As for the original data, we then computed the frequencies yes and yes Using the average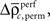 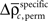yes yes and the SD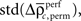 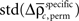yes yes of both frequencies over time for the same complexity, we expressed the modulations of JS-pattern frequency as time course of the trial for each complexity as a z-scores: 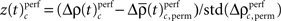yes for behavioral performance (Figure 3C), and 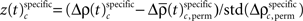yes for stimulus specificity (not shown). In a last step, we compared the modulation of z-scores for performance and stimulus specific modulations of spike synchrony based on a critical z-score accounting for multiple comparisons of all sliding windows and all complexities. Note that the distribution of 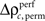yes is not expected to be normal given that 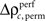yes is a difference of counts which are rather low. Therefore using the z-score may not be appropriate. We validate the modulation of z-scores for performance and stimulus specific modulations based on a rank order statistic. To this end we performed the permutation analysis three times, yielding in total 1368 estimates of 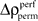yes (three times 97 estimates across time and 8 pattern complexities). We then determined the largest absolute value Δρ_crit out of all 1368 estimates and used this as the critical value for a minimal significant difference from zero (corresponding test level is p < 0.001). This latter rank test is independent of the underlying distribution of chance deviations from zero. Using both methods we found mostly the same time complexity pattern to be significant.

FIGURE 3

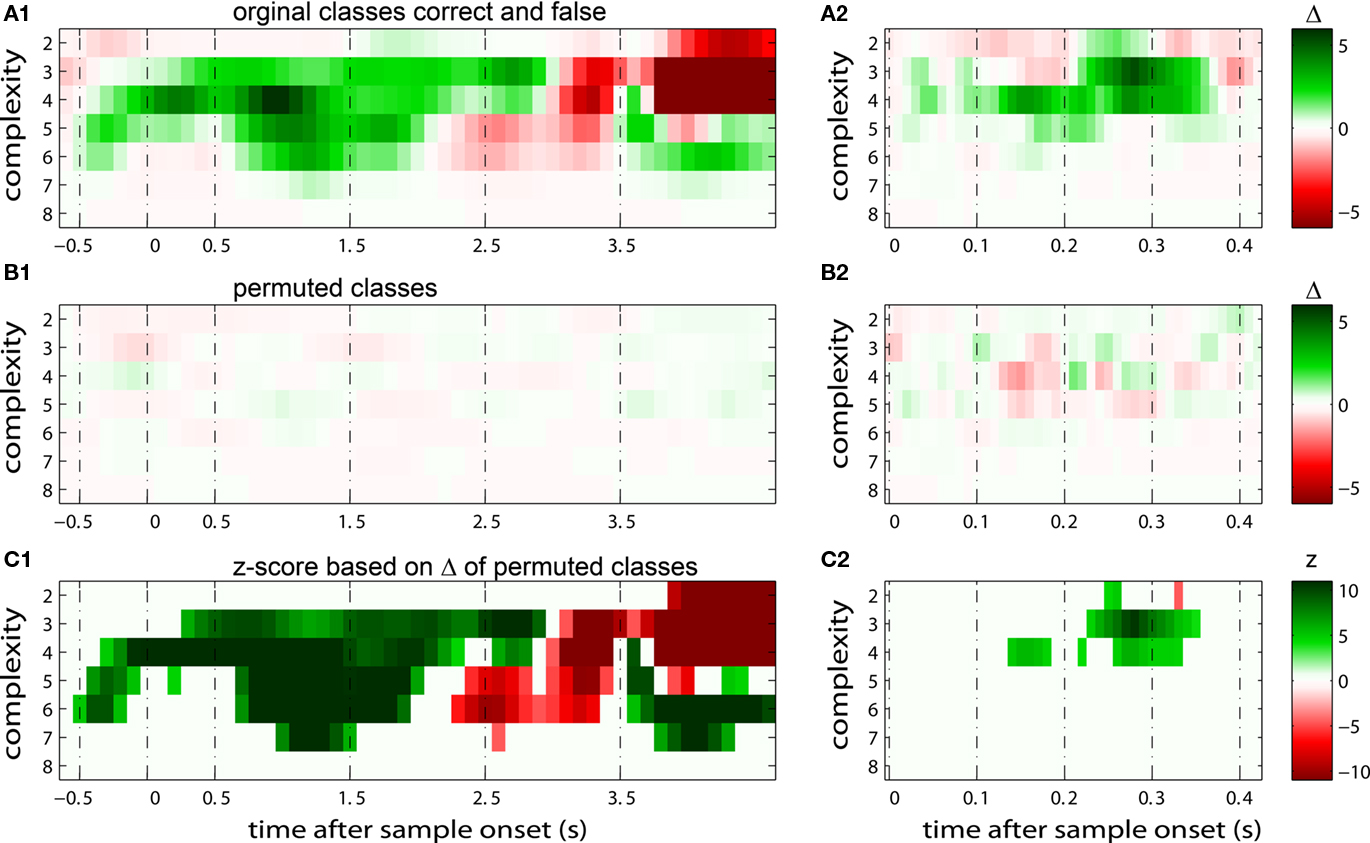
Figure 3. Effects of permuting trials on pattern incidence and as basis of a significance estimate. The x-axis represents time after sample stimulus onset in seconds. The y-axis shows pattern complexity and the z-axis (color) is explained for each figure below. Sliding windows span 400 ms in (A1–C1), while they are 100 ms long in (A2–C2). (A) Shows the difference between the frequencies of JS-patterns with increases of synchrony for trials with correct and false behavioral responses. (B) Shows the results for the identical dataset, but with randomly permuted trials across the classes “correct” and “false.” Based on the average level of differences in (B) and the SD of these differences, differences in (A) were expressed as z-scores in (C). We subtracted the average difference per complexity, but evaluated significance across the entire time course of the trial, starting at −0.5 and ending at 4.3 s after sample stimulus onset. (C) We then divided this difference, derived for each sliding window and complexity, by the SD of the respective measurement in the case that classes are permuted [shown in (B)].

Median Versus Mean

The entire analysis was performed for both, mean pattern frequency, based on t-test and ANOVA, as well as for median pattern frequency based on Mann–Whitney U-test and Kruskal–Wallis test. ANOVA and Kruskal–Wallis test were used for multivariate analyses. For both tests we obtained qualitatively and quantitatively very similar results. In particular, comparison of z-scores yielded the same significant modulation across time and for the same complexities. However, the results based on evaluation of means revealed slightly higher values. Therefore we present the more conservative results based on median testing in this paper.

Number of Surrogates

In the presented approach we derived exactly one surrogate trial from each original trial by shifting all spike trains individually by a random time smaller t_r. A small number of surrogates prevents a sampling bias, because if original and surrogate data have exactly the same number of samples, they also have the same degrees of freedom. Increasing the number of samples of the surrogates could be achieved by more than one jitter configuration of the same original trial. This, however, would have two effects. First, the number of different patterns would be larger in the surrogate data, since the probability for individual patterns to occur – at least once – scales with the number of samples. The second effect is that computing the difference 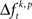yes of spike pattern frequencies is non-trivial: in order to compute this difference one can use the average 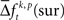yes computed across surrogates for the same trial. This again gives as many surrogate samples as original frequencies such that the same paired test 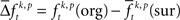yes can be used. However, using more than one surrogate causes the distribution of the difference to approach a normal distribution. This in turn changes the median compared to the mean. Since this change is stronger for skewed distributions, the amount of change is also a function of the frequency of patterns. A true null hypothesis implies that the amount of change of the median compared to the mean, which is induced by using more than one surrogate, is a function of the firing rate. Using more than one surrogate per trial can falsify the significance estimation (a detailed discussion on these effects and the choice of number of surrogates per trial including numerical calibrations can be found in Pipa et al., 2008 and Wu et al., submitted). Thus, using only one surrogate per trial is the most conservative approach. Since our results indicate that the test power with just one surrogate is still sufficiently high, we decided to use a single surrogate per trial.

Null Hypothesis

The null hypothesis (HØ) of this study assumes that synchronization of spike discharge is not different across different conditions of the experiment. Synchronization of spiking activity across sites is measured by comparing the frequency of a certain JS-pattern with the expected frequency if neurons are not synchronized. More specifically, here synchronization is defined as coordinated firing on a time scale faster than t_c. Slower effects on a time scale larger t_r such as rate covariation across neurons, are not considered as synchronization. Testing HØ is therefore based on, first, a spike rate and spike train auto-structure corrected measure of synchronization, and second, a test that checks whether an experimental excess or deficit of spike synchrony compared to chance levels is the same or different across conditions. The latter test is based on a mean or median test for each JS-pattern (p) and uses the spike rate and spike train auto-structure corrected measure of synchronization 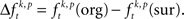yes HØ is rejected, in case of testing the mean, if the average of 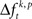yes across trials for a certain JS-pattern (p) is different across the factors k. The median testing rejects HØ, if the median of 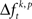yes across trials for a certain JS-pattern (p) is different across the factors k. The median test is more strict, because HØ is only rejected if the difference of 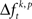yes is consistent across trials. Due to the rate and auto-structure correction, based on surrogate data, any source of changes of 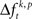yes other than fine temporal changes on a time scale faster than t_c can be excluded (analytical and numerical demonstration for this can be found in Pipa et al., 2008 and Wu et al., submitted).

Pattern Complexity

We investigated JS-pattern complexity ranging from 2 to 8. In order to estimate the impact of JS-pattern complexity on global cortical cooperativity, we distinguish between sub- and supra-patterns. A sub-pattern is a pattern that is embedded in a more complex JS-pattern. Thus, the complexity of a sub-pattern is always smaller than the complexity of the embedding JS-pattern. As an example, any complexity 3 pattern contains three sub-patterns of complexity 2. The more complex embedding pattern is called supra-pattern. It is not straight forward to predict the significance of a given JS-pattern, i.e., whether its sub- and supra-patterns are significantly different from chance level. For a sub-pattern, we know that it occurs at least as often as its supra-pattern. This, however, is not sufficient for qualifying a sub-pattern as significant JSE, even if the embedding supra-pattern has been proven to be significant. The reason is that the expected frequency of chance occurrences of a pattern usually increases with decreasing complexity. Thus, the frequency of a supra-pattern may be larger than the critical minimal frequency of patterns of large complexity, but below the critical frequency for low complexity patterns. In this case, significant high complexity JS-patterns occur, while sub-patterns may not be significant, as can be observed in the data presented here (e.g., Figures 3C1,C2). In the opposite case, low complexity JS-patterns are significant, but not their embedding supra-patterns. The simplest explanation is that the supra-pattern does not occur often enough.

Results

We report results based on the analysis of neuronal spiking of 133 multi-units recorded during 12 experimental sessions of a visual memory task (Figure 1). The two monkeys performed a total of 9830 trials with on average 80% correct responses. In these data we identified differences in neuronal coupling expressed by modulation of spike synchrony by using a bivariate and multivariate extension of the NeuroXidence method. As detailed in the method section, we first identified synchronous firing on a time scale of 3 ms and corrected for rate modulation on a time scale of 15 ms and slower (Figure 2). To test whether joint-spike events were modulated for different experimental factors, we tested whether the rate and spike train auto-structure corrected synchrony differed across experimental conditions. The 3803 JS-patterns visible in Figure 4C were composed of 329 JS-pattern with complexity c = 2, 1455 with c = 3, 1581 with c = 4, 407 with c = 5, 30 with c = 6, and 1 JS-pattern of complexity c = 7. For each JS-pattern we determined whether spike synchrony was stronger in correct or in error trials. The highest number of significant JS-patterns was found between 150 and 250 ms after sample onset (Figures 4A2,B2). During this period, 808 JS-patterns were significant (c2: 91, c3: 308, c4: 325, c5: 73, c6:10, c7:1). This amounts to 21.2% of the identified JS-patterns and is therefore much higher than the expected number of false positives given by the test level of 1%. As shown in Figure 4D, the firing rates as determined in 20 ms intervals cannot explain the difference in JS-patterns. However, the incidence and temporal profile is different for different sites. Some sites participated only in low complexity JS-patterns, while others started with strong modulation of high complexity JS-patterns, which were particularly pronounced during the later phase of the sample presentation (see units 1, 6, and 12 in Figure 4A2 and units 3, 7, and 10 in Figure 4B2).

FIGURE 4

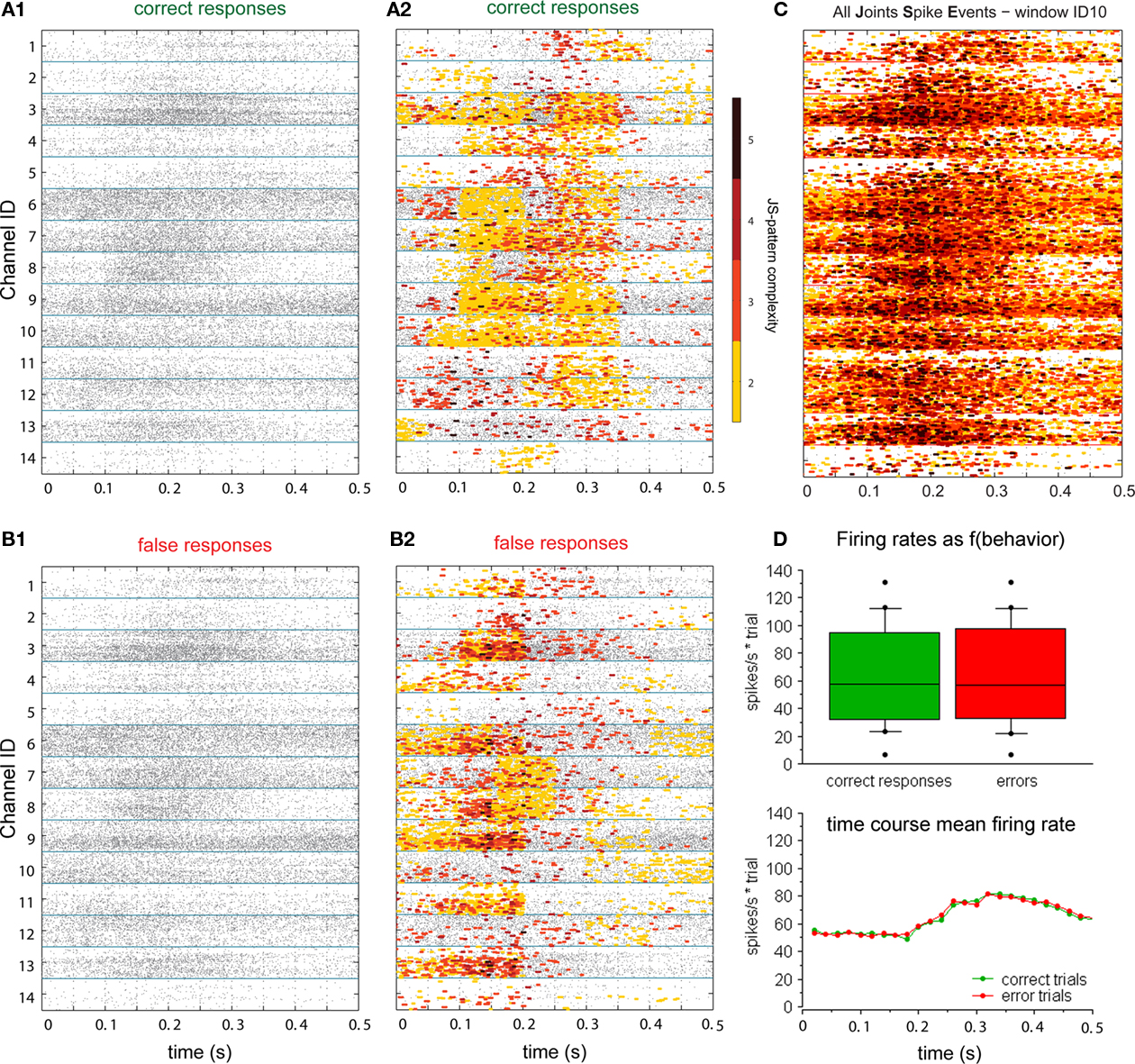
Figure 4. Millisecond precise joint spike events (JSE) in prefrontal multi-units. (A1, B1) Raster plots of 14 simultaneously recorded multi-unit signals (dots) for the sample stimulus period in trials with correct (A1) and erroneous behavioral responses (B1). (A2, B2) The same raster plots with superimposed JSEs marked by colored squares, each covering an interval of maximal 3 milliseconds; colors reflect JSE complexity, i.e. how many units participated in a pattern. Yellow indicates JSE of pairs of units (c = 2), red and darker colors represent higher complexities ranging from c = 3 to 5. (A2) shows only JSEs which occurred in sets of sites that synchronized more often during trials with correct behavioral responses, while (B2) shows those JSE that occurred more often during error trials. (C) All JS-patterns combined from (B2, C2), irrespective of their modulation by behavioural performance. (D) Distributions of firing rates across all units, split for trials with correct and erroneous behavioral responses and below as average time course.

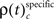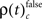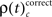Integrating across all experiments, we obtained a total of 18150 different JS-patterns (Table 1) that changed the level of synchrony in a performance related way (all test levels 1%) and which involved up to 8 units (corresponds to complexity = 7) simultaneously (Figure 5). To summarize the results, we determined the frequencies yes for stimulus specific, or yes and yes for performance related modulations of spike synchrony per complexity and per sliding window, and expressed this as a rate (s⁻¹). Note that each JS-pattern that contributes to any of the three frequencies ρ(t)_c is in excess of all patterns sampled across all experimental conditions and thus can be considered significant. Figure 5A shows 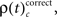yes which is the rate of JS-patterns in sliding windows of 400 ms duration for each complexity, reflecting more synchrony during trials with correct compared to incorrect responses. While Figure 5A1 represents the entire time course starting 700 ms before sample stimulus presentation and ending after test stimulus processing, Figure 5A2 features the sample response epoch with higher temporal resolution (sliding window of 100 ms duration). In analogy, Figure 5B1,B2 show the rate of 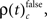yes that is the rate per second of JS-patterns which reflect more synchrony during trials with incorrect compared to correct responses. These analyses show that across all experiments, the highest rate of performance dependent JS-patterns can reach up to 120 patterns per second which was observed for complexity 4 and during error trials also 3, but not in pairs. 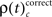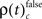High rates of yes and yes occurred during all behaviorally relevant epochs: during sample stimulus processing, during early delay and during test stimulus processing. Remarkably, rates 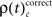yes were particularly high during the delay period of correct trials during which visual memory was required to generate an appropriate response.

TABLE 1

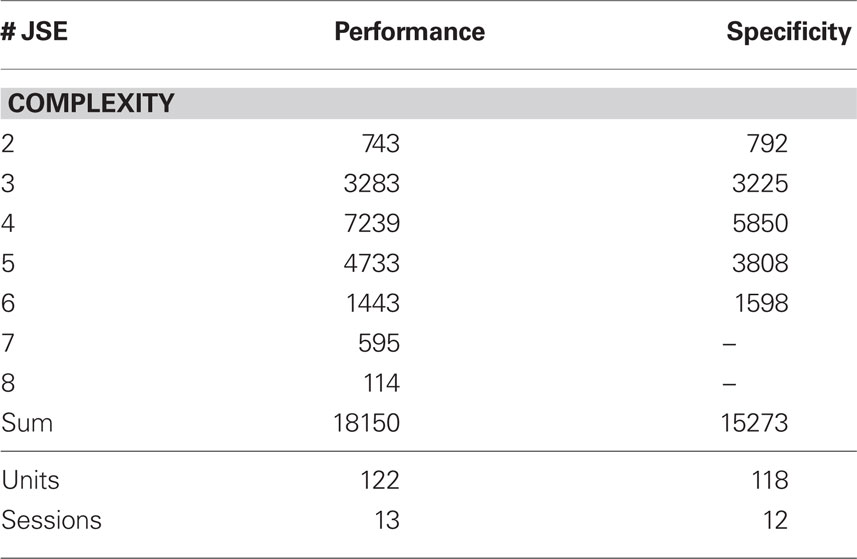
Table 1. Number of joint-spike events (JSE) detected to be modulated by behavioral performance and stimulus specificity.

FIGURE 5

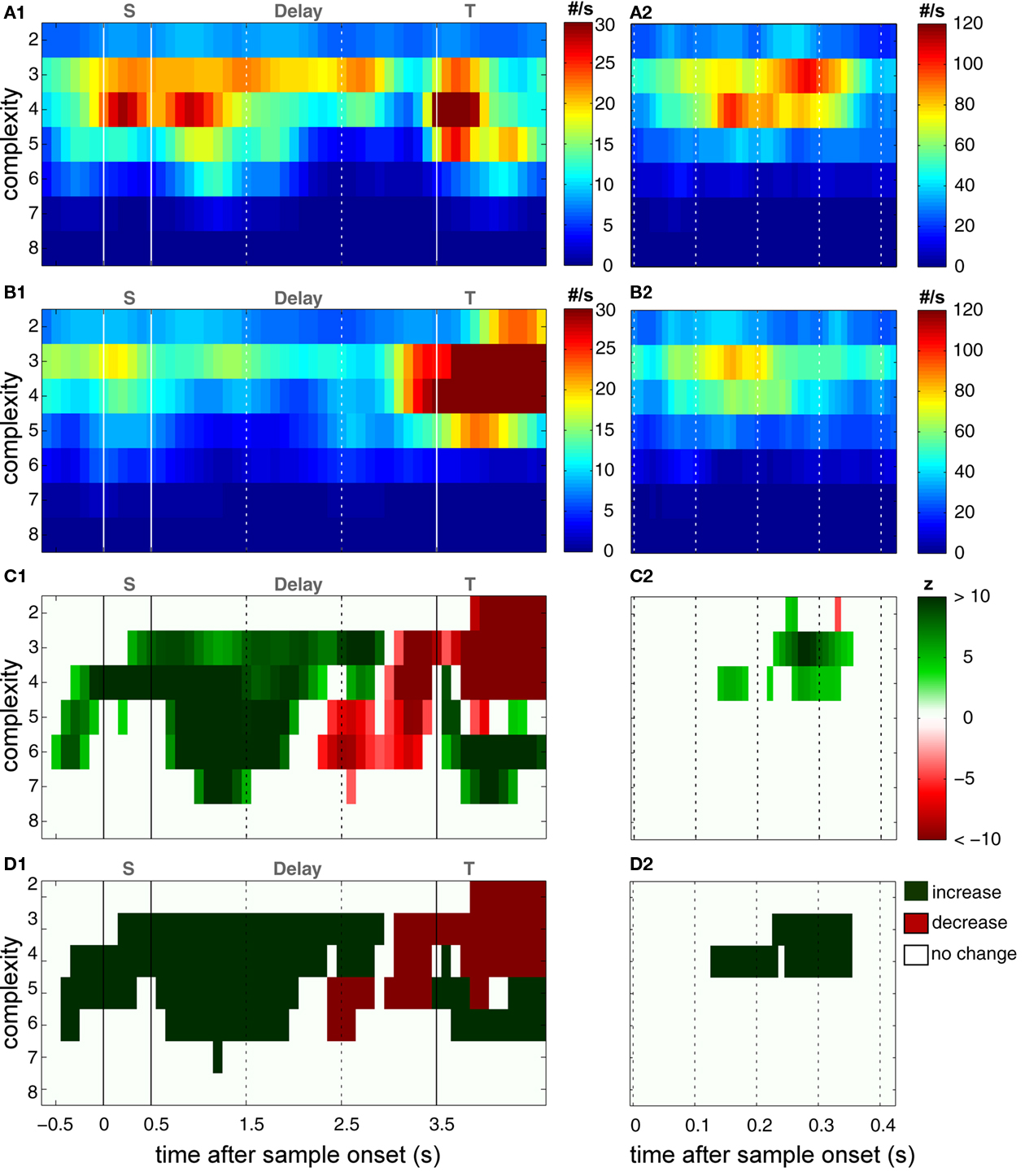
Figure 5. Time course and performance dependence of joint-spike event complexity. Rate of JSE (z-axis/color scale) with complexity (y-axis) ranging from 2 to 8 which was significantly modulated by behavioral performance, displayed as a function of time with respect to the onset of sample stimuli (x-axis). (A,B) JSE rate plotted for sets of recoding sites which expressed more JSE during trials with correct behavioral responses (A) and during error trials (B). (C) Time resolved contrast of the rates plotted in (A,B) after z-transformation. z-scores were computed by taking the absolute difference between values in (A,B), divided by the SD of values obtained in permuted trials with correct and erroneous behavioral responses, thus referencing to the variance of the same experiment. The critical z-value was 4.2, given a test level of 1% and a Bonferroni correction for 48 sliding windows and 7 complexities. (D) Colored time complexity bins mark periods of significant differences of performance dependent joint-spike events at a test level of 0.1%. Significance was evaluated using a rank order test of the original differences shown in (C1,C2) compared with results obtained based on permuted trials (compare to Figures 3B1,B2). On the left (A1–D1), pattern incidence is shown for the entire duration of the task based on analyses with sliding windows of 400 ms duration, while on the right (A2–D2), pattern incidence was analyzed with sliding windows of 100 ms duration and plotted exclusively for the first 400 ms of sample stimulus presentation.

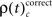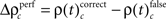To compare changes of frequencies yes and yes we computed yes and derived a z-score 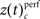yes based on a permutation test, that randomized class labels for correct and incorrect trials, to test whether observed differences can be explained by chance. Based on critical z-scores, which were corrected for multiple comparison across different complexities and different sliding windows, we identified periods and complexities (“time complexity bins”) with significant modulations of the frequency of JS-patterns that each showed a significant and performance related modulation of spike synchrony (Figure 5C1). In other words, Figure 5C measures how significant the overall increase of spike synchrony was in correct compared to error trials. Strongest modulation of spike synchrony was observed for JS-patterns of higher complexities and during the delay period. While the maximum complexity with significant modulations of 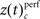yes reached 4 during the sample presentation (Figure 5C2), the complexity reached up to 7 during the delay. Surprisingly, pairwise synchrony measured by 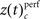yes was not significantly modulated. In general, behaviorally relevant periods are dominated by increases of synchronous activity in correct trials. Only during late delay and test stimulus presentation, spike synchrony of low complexities was stronger during error trials (Figure 5C1).

In stark contrast to the results for trials with correct behavioral responses, lower numbers of JSE were observed during error trials (Figure 5B). Most notably, this observation is not caused by some scaling or signal-to-noise problem, because during test stimulus processing, when the monkey had to retrieve memory content and compare this to the test stimulus, an increase of JSE frequency was observed which is compatible with the JSE frequency observed during sample stimulus processing and the early delay in correct trials (compare Figures 5A1,B1). An interesting feature of JSE increases during test stimulus processing is that complexity during correct trials is higher (4–6) compared to the complexity of JSE during error trials (2–5). Finally, we computed a contrast for JSE modulation in trials with correct and incorrect behavioral responses after z-transformation using the variance obtained from permuted data in each experiment (Figure 5C). The main finding of this analysis is that during the first half of the delay, JSE increases during successful trials outbalance JSE during error trials while during late delay the converse is true. This is not a shaky effect, because these effects hold for many hundred milliseconds and are consistent across numerous adjacent complexities (Figure 5D).

We then also tested whether the occurrence of synchronous spike patterns was stimulus specific (Figure 6). Stimulus specific modulation of synchrony could be identified in 15273 patterns involving up to six units (Table 1). When comparing Figures 5 and 6, it is evident that stimulus specific modulation of synchronous firing is much more confined to stimulus response epochs than performance dependent modulation with two interesting exceptions: during early and mid delay. First, during early delay, JSE of complexity 3 occurred in a stimulus specific fashion for 800 ms, supporting the idea that synchronous neuronal activity during early delay is involved in encoding and stabilizing memory related activity. Second, well over a second into the delay, a short burst of JSE of complexity 5 discharged highly significant stimulus specific synchronous spikes (Figure 6B) which is reminiscent of the elevated rate of JSE c = 5 observed during correct trials in the performance analysis (Figure 5A1). Another interesting relation between performance dependent synchrony increases and stimulus specific synchrony increases can be observed during test stimulus processing when the monkey has to perform a comparison between arriving sensory information and memory content: First, the time complexity pattern of stimulus specific JSE peaks at around 300 ms after test stimulus onset at complexity 4 which matches the peak of performance dependent JSE modulation in correct trials. This is, of course, expected, because the analysis of stimulus specific JSE was exclusively performed on trials with correct behavioral responses. Note the different JSE pattern during error trials. Second, stimulus specific JSE modulation during test stimulus processing was more than twice as strong as during sample stimulus processing (compare, e.g., JSE of complexity 4 during “S” and “T” periods in Figure 6A), which was not the case for correct trials in the performance dependent modulation (Figure 5A1).

FIGURE 6

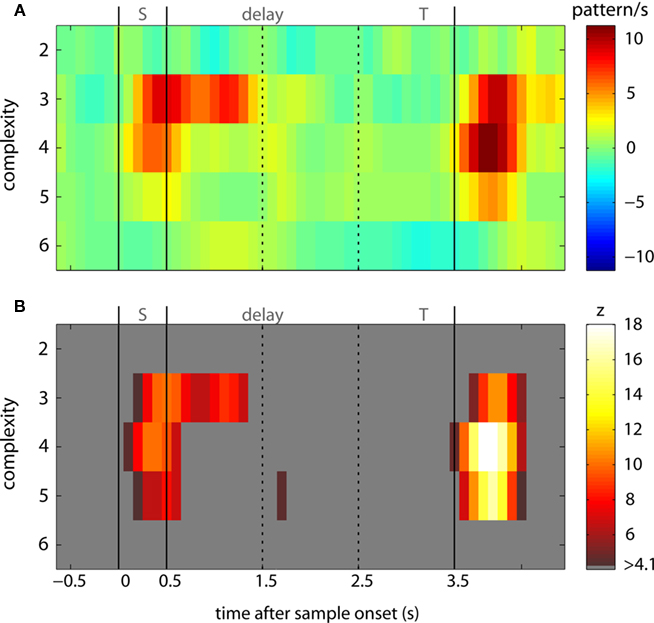
Figure 6. Time course of stimulus specific joint-spike events. (A) Incidence of JSE of complexities 2–6 which exhibited a stimulus specific modulation during 3 ms short intervals in patterns per second. (B) Statistical evaluation of stimulus specific JSE incidence was performed in analogy to the analysis of performance dependent JSE incidence. z-sores were computed by dividing the number of JSE in trials in which a specific visual object was memorized divided by the SD of JSE in trials from the same recording session, but after permutation for memorized stimuli. To this end we used the identical data and the identical number of trails per stimulus, but permuted stimuli randomly across all trails. z-transforms were performed for each individual complexity and based on the SD derived from the entire time course starting at the beginning of the baseline and including all other epochs until after button press of the monkey. The critical z-value was 4.08 given a test level of 1% and a Bonferroni correction for 48 sliding windows and 5 complexities.

The temporal precision of JS-patterns is an important parameter of this study. We have chosen t_c to be 3 ms. Other studies used less precise patterns that may extend from 5 ms to even more imprecise recurrences. To select the appropriate temporal scale for our analysis, we performed the same analysis procedure for four different t_c windows with (t_c = 2, 3, 5, and 7 ms). The lower bound of rate responses were scaled in the same way with t_r = α* t_c, and α = 3 leading to t_r values of 6, 9, 15, and 21 ms. We found that effects across the four scales were compatible, but strongest modulation of performance and stimulus related modulations of spike synchrony were observed for t_c= 3 ms. This finding suggests that the experimental data reported here were dominated by JS-patterns with a temporal precision of 3 ms. For smaller t_c, i.e., t_c= 2 ms, much less JSE were detected since most of the observed JSEs had an imprecision larger than 2 ms. For longer t_c, i.e., 5 and 7 ms, the rate correction was effectively stronger because the model imprecision t_c was too large for the dominating imprecision in the data.

Discussion

The main finding of this study is that patterns of precise spike synchrony (≤3 ms), here referred to as joint-spike events (JSE), change their frequency of occurrence and their complexity in a dynamic way which depends on the behavioral success of the monkey and the stimuli in the memory task. These JSE are no rare events, nor do they occur by chance. JSE with performance related changes occur more than 20 times more often than expected by chance. This raises the question how relevant synchronous firing may be for cortical processing (Herrmann et al., 2004; Uhlhaas et al., 2009).

Analysis Approach

Synchronous patterns of higher complexity had been observed in behaving monkeys before, but there have been and still are intensive discussions about whether such events might occur just by chance (Baker and Lemon, 2000). First and foremost, complex and usually time varying structures of spike trains caused the fear that model based analyses, which assume either stationary firing rates or idealized spike density distributions like following a Poisson distribution or reflecting a renewal process, cause false positive findings. To avoid such assumptions, we have chosen a non-parametric approach that estimates the amount of chance JSE per trial based on permuted data from the exact same experiment thus preserving the auto-structure. Therefore any kind of complex structure, but also any kind of rate modulation slower than t_r, the time scale for rate changes considered by NeuroXidence. At the same time the method stays very sensitive, on a level that is compatible to other methods, like standard pairwise cross correlation, factorial recoding of synchronous spike trains derived from data compression algorithms (Schnitzer and Meister, 2003) or the Unitary Event method (Pipa et al., 2008).

A complication that arises when dealing with the activity of a large number of neurons is that the number of JS-patterns grows so large that standard approaches based on single JS-patterns are no longer applicable and the amount of information is overwhelming and may even become confusing. To overcome this problem, we chose a simple strategy which consists of computing the frequency of JS-patterns that have before been shown to be significantly modulated by experimental factors. Using this simplification, we lost the identity of JS-patterns, but we were able to condense observations to a very handy low dimensional set of numbers: frequency and pattern complexity for each time window. However, this reduction requires a second level of hypothesis testing, since, even though each JS-pattern that is included in the statistics is significant, the expected level of significant JS-patterns is unknown. Therefore we used another robust non-parametrical test, based on permutations. This test compares the frequency of patterns observed in trials selected for original experimental factors (i.e., trials with correct versus incorrect behavioral responses, or the different stimuli the monkey had to memorize) and, a second set of JS-pattern frequencies derived from permuted class labels. This test preserved the simultaneity of recorded neuronal activity, but swapped trials between different experimental conditions in order to destroy any differences in neuronal synchrony between conditions. Using this, we derived a z-sore and applied a Bonferroni correction. This second step is robust against changes of rates and particular auto-structures of neuronal activity across conditions, because NeuroXidence uses surrogate data which maintain this structure. Since a permutation test is used, no assumption is made regarding the distribution of any parameter. Last, but not least, testing median and mean JSE frequency at the level of individual JS-patterns provided very similar results for the modulation of spike synchrony.

To avoid that synchronous activity could have escaped our attention due to shallow significance levels we set the criteria for detecting JS-patterns as conservative as possible. We chose the required temporal precision t_c of a synchronous firing pattern to be equal or less than 3 ms (see also Pipa et al., 2007 for further discussion on time scale separation). This parameter confines the analysis to very precise patterns, in particular if more than two multi-units were involved. On the one hand, the interval t_c can also be seen as a necessary upper bound of time scales which define a very fast increase of firing rate covariation across all units participating in a JS-pattern. On the other hand, the second interval t_r is important to contrast synchrony to all other kinds of rate covariation, in particular, on slower time scales. We chose t_r = 15 ms which implies that any covariation of firing rates occurring within more than 15 ms (or slower as 66 Hz) is considered as rate. Any covariation of firing rates occurring within less than 3 ms (or faster than 333 Hz) is considered to be a JS-pattern. It is important to note that 15 ms as an upper bound of rate covariations is very conservative given that firing rate changes are typically observed with bin sizes of several tens of milliseconds.

Methodological Limitations

A first limitation of the current approach is that the analysis does not consider the nature of the analyzed JS-patterns, e.g., their spatial structure. This implies that for example information about the similarity of patterns accounted for different experimental conditions could not be analyzed. The spatial structure, however, might be very relevant for the neuronal processes. Furthermore, this limitation implies that similarity and stability of JS-patterns over time across different sliding windows were not analyzed. This might be very relevant, as a stable increase of JSE during the delay period which lasted for more than 2 s, may have been composed of very different sets of JS-patterns over time. Knowledge of this stability might allow to distinguish between the two hypotheses which either assume that information is encoded in stable and rather small subpopulations, or, that information is encoded on the sequences of many and very rich transitions of different neuronal states. However, technically this tracking of stability seems very demanding if not even impossible at the time.

A second limitation of the current analysis is that we cannot determine the actual size of neuronal assemblies which are involved in the encoding and maintenance of behaviorally relevant information. Given our finding that up to 8 multi-units out of a population of 10–24 can be involved in behaviorally relevant JS-patterns, one may conclude that assemblies can be very large, maybe involving a third or even half of the neurons. From a theoretical perspective, such a code may appear very attractive, because the coding space becomes really large, if on average a third or half of the neurons in a population engage in JS-patterns.

A third limitation of the current approach being restricted to multi-unit signals implies that we have investigated JS-patterns among several small, spatially separated neuronal populations and not single, well isolated units which are generally considered to reflect the activity of a single neuron. As we have recorded all wave forms at sufficient spectrotemporal resolution we have tried to sort spikes, but with limited success, the major obstacle being that most of the signals recorded for this study were not recorded with tetrodes, but with single-ended fiber microelectrodes. Therefore, despite good S/N, synchronous spikes occurring at individual sites were most of the time misclassified as deformed rare spike waveforms, which were discarded. Thus we restricted the analysis and interpretation of this study to multi-unit signals. As a consequence, estimates of the assembly size as discussed above are even further hampered by concluding about synchronous firing only for several groups of neurons. However, this is a conservative approach for answering the question whether synchronous firing exists above chance, because each individual locally observed spike might already represent a synchronous event. Since we do not rely on any statistical assumption for the distribution of JS-patterns occurring by chance, but simply permute the existing time series, there is no trivial explanation for false positive events.

Our finding that JS-patterns with a precision of 3 ms and rate corrected at a time scale of 9 ms were more modulated by experimental variables like behavioral performance than patterns at more precise or less precise scales suggests that the precision of 3 ms is biologically meaningful. Compared to other studies, which reported JS-patterns of 5 ms precision, these time scales appear to be too short (Riehle et al., 1997). This difference, however, can be partly attributed to the chosen analysis techniques. For example in the paper by Riehle et al. (1997) the unitary event method was used. This method detects JSE based on binned spike trains with a bin size corresponding to the assumed temporal precision of the JS-pattern. Binning however requires that the window must be larger than the actual precision of the pattern, because JS-patterns close to the boarder of two bins have an effectively much smaller window than JS-patterns which are centered on a bin. Therefore, the detectability of a JS-pattern with methods using binning depends on the relative position of JS-patterns within the bins. In contrast, NeuroXidence describes a JS-pattern by the exact preset imprecision, given by t_c. Results presented in Pipa et al. (2007) demonstrate this link between two time scales for exactly the same data as presented in Riehle et al. (1997). By applying NeuroXidence to these data, the authors confirmed the previous results based on the binning UE method to contain JSEs on the same time scale of 5 ms. However, reducing the preset time scale from 5 to 3 ms for the NeuroXidence method, resulted in an even stronger deviation from the chance level, while the number of patterns detected by binning decreased significantly. This indicates that the NeuroXidence method is more sensitive to find the lower bound of spiking precision of JS-patterns.

An earlier study that has successfully dealt with higher order spike patterns extracted from simultaneous recordings of retinal ganglion cells has used a factorial recoding of synchronous spike trains that was derived from data compression algorithms (Schnitzer and Meister, 2003). This method is also very efficient in detecting and storing synchronous spike trains, but unfortunately also involved time binning which has been shown to miss coincidences (Pipa et al., 2007). The advantage of this method is that one can preserve the identity of each unit and of all groups of units involved in synchronous firing which is certainly a feature we want to include in future versions of our analysis technique.

Functional Implications

For the analysis of synchronous firing patterns one can distinguish the complexity from the order of a JS-pattern. While the complexity just gives the number of neurons or sites involved in a JS-pattern, the order determines the real underlying correlation structure. The latter is necessary to distinguish between the chance level and the occurrence of sub-patterns of a more complex JS-pattern (Martignon et al., 2000; Nakahara and Amari, 2002; Schneider and Grün, 2003). However, the latter is also more of theoretical nature than of any practical relevance. It had been demonstrated that the amount of data necessary to distinguish between a certain set of orders is gigantic compared to the amount of data which is usually available in real experiments, but also with respect to the amount of information a neuron in the cortex would have to decode if sub-patterns would be able to carry relevant information. Both arguments are in favor of using the much simpler JS-pattern complexity. Pattern complexity can be simply interpreted as a kind of input saliency for downstream neurons. The higher the complexity, the more neurons participate, the more salient the input pattern is, because the more numerous simultaneous or nearly simultaneous inputs are, the more they can draw from spatial summation properties of postsynaptic membranes resulting in more rapid depolarization or even non-linear amplification of the postsynaptic membrane potential.

What precisely synchronous spike firing of distributed populations of cortical neurons really means for information processing and generating appropriate behavior is not yet well understood. The observation that JSE incidence was massively increased even before the predictable end of the memory delay is reminiscent of JSE in motor cortex due to sensorimotor expectancy (Riehle et al., 1997), suggesting that spike synchrony in PFC could reflect a mechanism for the temporal organization of executive processes. However, the finding that synchronous spiking is modulated by, both, behavioral performance and the memorized visual stimuli, suggests that synchrony is a very fundamental processing mechanism of the cortex. How well synchronous spike signals can be used in the future to actually decode information processed and maintained in distributed cortical circuits remains to be seen. The well established fact that coincident neuronal activity is a potent trigger for synaptic plasticity suggests that synchronous activity may be a better predictor for what cortical circuits need to be adapted for rather than an expression of their current performance.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are grateful to Hanka Klon-Lipok, Michaela Klinkmann, Urda Franzius and Ellen Städtler for their enduring long-term efforts to train our animals, prepare recording equipment and help us during experiments, Thomas Maurer for excellent technical support, Christiane Kiefert and Clemens Sommer for dedicated animal care. Funding: VolkswagenStiftung I/77 142 (Matthias H. J. Munk), EU NEST-Pathfinder GABA Project 043309. In part financed by the EC Project PHOCUS Grant 240763 (Gordon Pipa).

References

Abeles, M. (1982). Local Cortical Circuits, An Electrophysiological Study. Heidelberg: Springer.

Abeles, M. (1991). Corticonics, Neural Circuits of the Cerebral Cortex. New york: Cambridge University Press.

Abeles, M., Bergman, H., Margalit, E., and Vaadia, E. (1993). Spatiotemporal firing patterns in the frontal cortex of behaving monkeys. J. Neurophysiol. 70, 1629–1638.