- 1 Bernstein Center Freiburg, Freiburg, Germany
- 2 Faculty of Biology, University of Freiburg, Freiburg, Germany
- 3 Department of Neurobiology, Weizmann Institute of Science, Rehovot, Israel
- 4 Department of Medical Neurobiology, Institute for Medical Research Israel-Canada, Faculty of Medicine, The Hebrew University of Jerusalem, Jerusalem, Israel
- 5 Interdisciplinary Center for Neural Computation, The Hebrew University of Jerusalem, Jerusalem, Israel
- 6 Edmond and Lily Safra Center for Brain Sciences, The Hebrew University of Jerusalem, Jerusalem, Israel
- 7 Department of Bioengineering, Imperial College London, London, UK
- 8 Department of Electrical and Electronic Engineering, Imperial College London, London, UK
When faced with unpredictable environments, the human motor system has been shown to develop optimized adaptation strategies that allow for online adaptation during the control process. Such online adaptation is to be contrasted to slower over-trial learning that corresponds to a trial-by-trial update of the movement plan. Here we investigate the interplay of both processes, i.e., online adaptation and over-trial learning, in a visuomotor experiment performed by macaques. We show that simple non-adaptive control schemes fail to perform in this task, but that a previously suggested adaptive optimal feedback control model can explain the observed behavior. We also show that over-trial learning as seen in learning and aftereffect curves can be explained by learning in a radial basis function network. Our results suggest that both the process of over-trial learning and the process of online adaptation are crucial to understand visuomotor learning.
Introduction
In the recent past, a number of neurophysiological studies have examined sensorimotor learning in primates using multi-electrode recording techniques in order to gain insight into the biological mechanisms of such learning on a cellular level (Shen and Alexander, 1997; Wise et al., 1998; Li et al., 2001; Gribble and Scott, 2002; Padoa-Schioppa et al., 2002; Paz et al., 2003). The general paradigm in these experiments has been to introduce kinematic or dynamic perturbations during reaching movements and to observe neuronal changes while the animal is learning the new sensorimotor mappings. Learning such mappings can be conceptualized as the acquisition and retention of internal models (Wolpert et al., 1995; Kawato, 1999), and neurophysiological studies of learning have focused on the question of how the neuronal representations of these internal models evolve over the course of many trials. Importantly, in these studies a trial is a repetitive episode in an experiment, where the same motor task is performed again and again so that a changing behavioral response can be identified with a learning process.
However, many tasks require adaptation within a single trial (Braun et al., 2009). For example, a number of studies have examined adaptive behavior in reaching tasks under visuomotor rotations, where a rotation is introduced between the hand movement and a cursor that is controlled on a screen (Paz et al., 2003). In early trials where the occurrence of the rotation is unexpected, the control process has to adapt online to the new visuomotor mapping during the movement (Braun et al., 2009). Such online adaptation can be distinguished conceptually from online error correction that has been investigated more extensively, see e.g., (Diedrichsen et al., 2005). Online error correction takes place, for example, if in a reaching task the target jumps suddenly to another position, and we need to correct our movement trajectory. However, there is no adaptation of the visuomotor mapping involved, since the rules of the control process – i.e., the “control policy” that maps sensory inputs to motor outputs – do not change. We just need to update the current target position and continue to run the same control process. Previous studies have either focused on over-trial learning of visuomotor mappings (Krakauer et al., 2000), that is the gradual update of a motor plan over the course of many trials, or on online adaptation in tasks where the visuomotor mapping changed on a trial-by-trial basis (Braun et al., 2009). Here we investigate both over-trial learning and online adaptation in a single visuomotor learning experiment performed by macaques.
Results
We investigated a visuomotor learning experiment performed by macaques (Paz et al., 2003). Two rhesus monkeys were exposed to visuomotor rotations with rotation angles ±45° and ±90° within the classical center-out reaching paradigm (Figure 1). The experiment was structured in three epochs distinguished by trial type: pre-learning standard center-out to eight targets, learning a randomly chosen visuomotor rotation to one target, and post-learning standard center-out to eight targets. During the learning epoch monkeys required between 10 and 15 trials to learn the transformation (Paz et al., 2003) and thus, in the first few learning trials adaptive behavior had to be produced online during movement execution. After target appearance each trial began with a variable hold period (“preparatory phase”), whereupon a GO signal prompted the monkey to move the cursor to the target (“movement phase”). The two phases correspond to the two types of learning that we investigate: over-trial learning of a movement plan during the preparatory phase and online adaptation during the movement phase.
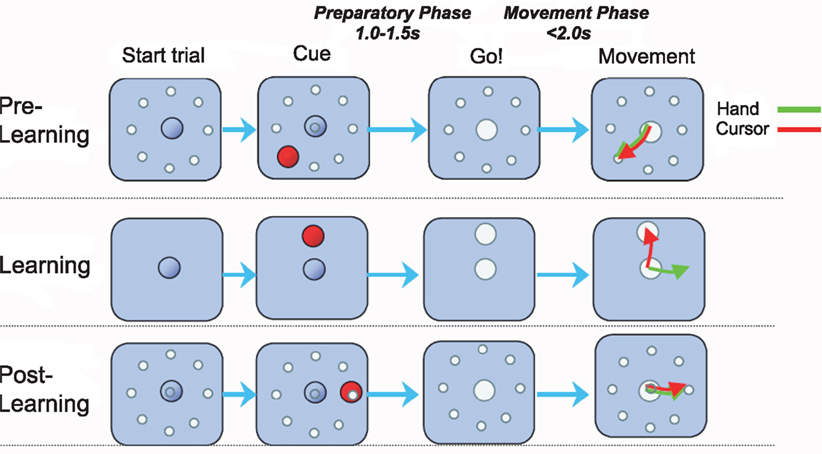
Figure 1. Visuomotor learning task. Each trial began when the monkey centered the cursor on the origin for at least 1 s. After a variable hold period a target appeared at one of eight possible positions 4 cm from the origin. The monkey had to keep the cursor in the origin for an additional 1.0–1.5 s (“preparatory phase”) until the origin disappeared, corresponding to the GO signal. In the ensuing movement the target had to be reached within 2 s (“movement phase”). The trials were blocked in epochs. In the pre-learning epoch the monkey performed center-out reaching movements with veridical feedback. In the learning epoch a visuomotor rotation between hand and cursor movement was introduced – the rotation angle was randomly chosen to be one of four possibilities (−90°, −45°, +45°, +90°). In the post-learning epoch the standard mapping was re-established.
Over-trial learning of movement plans has been extensively investigated in various computational frameworks, such as feedback-error learning (Kawato et al., 1987) – for reviews see (Wolpert and Ghahramani, 2000; Tin and Poon, 2005). In this framework over-trial learning is conceptualized as a trial-by-trial update of a movement plan that aims to reproduce a given desired or reference trajectory. The process of planning is then followed by a process of movement execution that consists of tracking the pre-programmed desired trajectory (DT) in the face of unforeseen perturbations (Figure 2A). In an alternative control scheme, the controller does not only adapt across trials to adjust its movement plan but also online within each trial during movement execution (Figure 2B). This scheme has been previously investigated within the framework of adaptive optimal feedback control (Braun et al., 2009). In an adaptive optimal feedback controller, a predictive model of the environment is used in conjunction with an optimal controller that employs these model predictions to compute its control commands in a continuous fashion. The processes of model prediction and motor execution are both adaptive and closely intertwined without the need of a reference trajectory. Instead, the controller optimizes a given performance criterion that specifies the task goal.
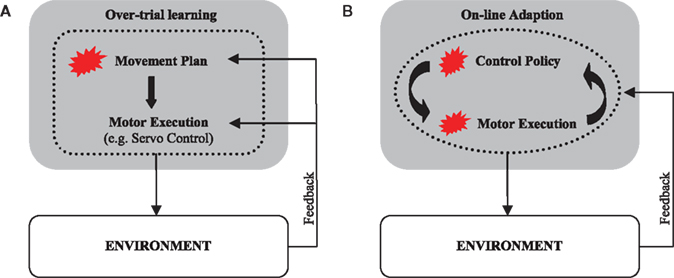
Figure 2. Sensorimotor learning schemes. (A) In a desired trajectory controller, the movement plan is adapted during sensorimotor learning. The correct movement plan produces a movement along the desired trajectory when executed. The process of motor execution itself is not adaptive and consists of tracking the given desired trajectory. (B) An online adaptive controller employs an adaptive predictive model of the environment to compute an adaptive motor response. The process of motor execution generates adaptive optimal policies online. Both movement planning and execution are adaptive. Red blots designate adaptive modules.
When treating the above visuomotor learning experiment in the framework of feedback-error learning two control components have to be distinguished: an inverse internal model 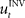 that computes a pre-specified sequence of control commands producing the DT in the absence of disturbances, and a hard-wired feedback-error controller
that computes a pre-specified sequence of control commands producing the DT in the absence of disturbances, and a hard-wired feedback-error controller 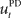 that compensates for deviation errors from the DT in the presence of noise and disturbances during movement execution or in the presence of a wrong inverse internal model about the environment (Figure 3A). The total control signal is the sum of the two individual control commands, such that
that compensates for deviation errors from the DT in the presence of noise and disturbances during movement execution or in the presence of a wrong inverse internal model about the environment (Figure 3A). The total control signal is the sum of the two individual control commands, such that 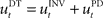 . The inverse internal model stores a pre-specified sequence of control signals producing the desired cursor trajectory
. The inverse internal model stores a pre-specified sequence of control signals producing the desired cursor trajectory 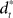 in the absence of perturbation. The DT to a specific target can be thought of as the mean experimental trajectory to that target under undisturbed conditions. The inverse model
in the absence of perturbation. The DT to a specific target can be thought of as the mean experimental trajectory to that target under undisturbed conditions. The inverse model 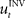 can then be determined by running the inverse dynamics on the experimentally recorded DT. The error-feedback controller
can then be determined by running the inverse dynamics on the experimentally recorded DT. The error-feedback controller 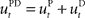 is often designed as a proportional–derivative (PD) controller that compensates deviations from the DT by counteracting the error signal
is often designed as a proportional–derivative (PD) controller that compensates deviations from the DT by counteracting the error signal 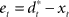 , where xt corresponds to the actual trajectory. The PD controller consists of two terms: a proportional part
, where xt corresponds to the actual trajectory. The PD controller consists of two terms: a proportional part 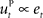 and a derivative part
and a derivative part 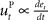 , that is
, that is 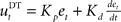 . If the environmental dynamics change over time, the inverse internal model
. If the environmental dynamics change over time, the inverse internal model 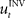 needs to be modified (Bhushan and Shadmehr, 1999). However, this modification becomes only effective in subsequent trials, because the inverse model is like a movement tape that has to be played from the start. As the inverse internal model generates consistently wrong control commands during early transformation trials when it has not fully adapted, the error-feedback controller has to take over during such trials. This means that performance in such trials critically depends on the error-feedback gains Kp and Kd (Figure 3B). Especially, for large rotation angles the error-feedback gains have to be very low, because a naive controller under these conditions will produce a circling movement into the target, which requires low movement speed. In a quantitative analysis we found that PD control gains that allow for stable performance are too low to explain experimental speed profiles for transformation angles ≥70° (Figure 3C). Moreover, it can be shown mathematically that for transformation angles ≥90° a PD controller cannot be stabilized anymore (see Methods). Therefore, feedback-error learning with a non-adaptive PD controller in its feedback loop cannot explain successful target reaches in the first learning trials as they are observed experimentally for monkeys (Figure 4) and humans (Braun et al., 2009). Consequently, the feedback-error learning scheme must be modified to allow for online adaptation, for example, by applying the estimated inverse transformation to the error-feedback controller (Nakanishi and Schaal, 2004).
needs to be modified (Bhushan and Shadmehr, 1999). However, this modification becomes only effective in subsequent trials, because the inverse model is like a movement tape that has to be played from the start. As the inverse internal model generates consistently wrong control commands during early transformation trials when it has not fully adapted, the error-feedback controller has to take over during such trials. This means that performance in such trials critically depends on the error-feedback gains Kp and Kd (Figure 3B). Especially, for large rotation angles the error-feedback gains have to be very low, because a naive controller under these conditions will produce a circling movement into the target, which requires low movement speed. In a quantitative analysis we found that PD control gains that allow for stable performance are too low to explain experimental speed profiles for transformation angles ≥70° (Figure 3C). Moreover, it can be shown mathematically that for transformation angles ≥90° a PD controller cannot be stabilized anymore (see Methods). Therefore, feedback-error learning with a non-adaptive PD controller in its feedback loop cannot explain successful target reaches in the first learning trials as they are observed experimentally for monkeys (Figure 4) and humans (Braun et al., 2009). Consequently, the feedback-error learning scheme must be modified to allow for online adaptation, for example, by applying the estimated inverse transformation to the error-feedback controller (Nakanishi and Schaal, 2004).
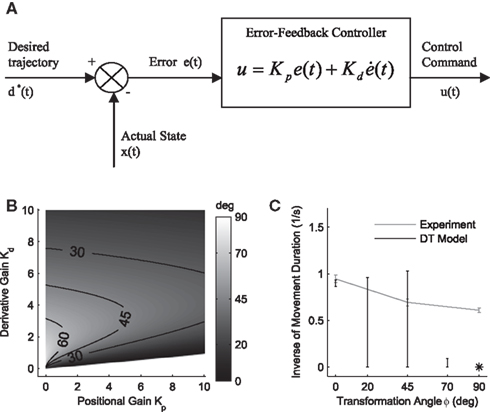
Figure 3. Desired trajectory model with non-adaptive PD controller. (A) For unexpected transformation trials, motor execution in the desired trajectory framework relies completely on the presumed error-feedback controller to correct for deviations from the desired trajectory. To this end, a movement error e(t) is calculated at every point in time as the difference between the desired state d*(t) and the actual state x(t). A corrective control command is computed, proportional to this error e(t) with proportionality constant Kp. To ensure stable performance, it is also important to consider the temporal change of the error by means of another proportionality constant Kd. This PD controller works as a general tracker. (B) Feedback gains Kp and Kd of the hard-wired error-feedback controller that allow for stable control for the different transformation angles. As the transformation angle increases, the zone of stable control shrinks to low feedback gains, i.e., slow control (the light-colored area). (C) Movement durations for a controller with the feedback gains from (A) for the monkey experiment. Stable control with a desired trajectory controller requires extremely slow movements when confronted with high transformation angles. The gains are too low and therefore the movement times are too long to explain the experimental movement durations for transformation angles ≥70°. For 90° transformations, the error-feedback controller cannot be stabilized anymore.
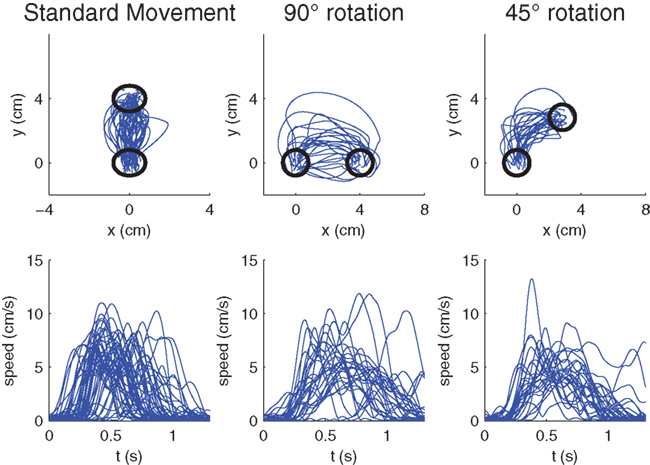
Figure 4. Raw hand-movement data (100 ms after the GO signal) from the monkey experiments. (Left) Randomly sampled trajectories from pre-learning trials to the 90° target with veridical feedback. (Middle) First learning trials of ±90°-transformations. The −90° rotations have been mirrored to the other side. (Right) First learning trials of ±45°-transformations. Again the −45° rotations have been mirrored to the other side. The lower panels show the respective speed profiles.
Another possibility for a control framework that is capable of online adaptation and control is provided by the framework of adaptive optimal feedback control (Todorov and Jordan, 2002; Braun et al., 2009). The basic idea is that an adaptive optimal feedback controller employs the best available estimate of the relevant task variables at every instant of time (in our case the estimate of the rotation angle 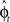 ) for generating a control signal which minimizes the expected cost, while the estimates of the task variables are simultaneously tuned online during movement execution to fit sensory observations (Figure 5). Thus, the adaptive optimal control problem breaks down into an estimation problem and a control problem. The estimator tries to fit a predictive forward model to the observations and the controller utilizes this estimated forward model to produce an optimal control command (Braun et al., 2009). We implemented such an adaptive optimal feedback controller in a modified linear quadratic Gaussian (LQG) setting with a linear arm model and control-dependent noise (see Methods). The linear arm model (a point mass model) was primarily chosen for mathematical tractability and because of previous successes in describing human movements (Todorov and Jordan, 2002; Braun et al., 2009). To test the model quantitatively on the experimental data from our visuomotor experiment, we adjusted the free parameters of the model to fit the mean trajectory and variance of the 90°-transformation trials and used this parameter set for predictions on the 45°-transformation trials and standard trials. We found that the adaptive optimal feedback control model is able to consistently capture the main characteristics of the mean trajectories, speed profiles, angular momentum, and trial to trial variability of movements during early transformations (Figure 6). The variability pattern of the 45° transformations trials deviates somewhat from the model predictions, which can be attributed to the simplicity of the point mass model and the relatively small number of highly variable trials. The predictions for the 45° transformations trials yielded r2 > 0.77 for all kinematic variables.
) for generating a control signal which minimizes the expected cost, while the estimates of the task variables are simultaneously tuned online during movement execution to fit sensory observations (Figure 5). Thus, the adaptive optimal control problem breaks down into an estimation problem and a control problem. The estimator tries to fit a predictive forward model to the observations and the controller utilizes this estimated forward model to produce an optimal control command (Braun et al., 2009). We implemented such an adaptive optimal feedback controller in a modified linear quadratic Gaussian (LQG) setting with a linear arm model and control-dependent noise (see Methods). The linear arm model (a point mass model) was primarily chosen for mathematical tractability and because of previous successes in describing human movements (Todorov and Jordan, 2002; Braun et al., 2009). To test the model quantitatively on the experimental data from our visuomotor experiment, we adjusted the free parameters of the model to fit the mean trajectory and variance of the 90°-transformation trials and used this parameter set for predictions on the 45°-transformation trials and standard trials. We found that the adaptive optimal feedback control model is able to consistently capture the main characteristics of the mean trajectories, speed profiles, angular momentum, and trial to trial variability of movements during early transformations (Figure 6). The variability pattern of the 45° transformations trials deviates somewhat from the model predictions, which can be attributed to the simplicity of the point mass model and the relatively small number of highly variable trials. The predictions for the 45° transformations trials yielded r2 > 0.77 for all kinematic variables.
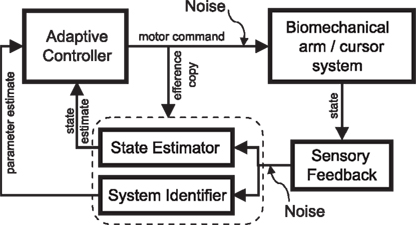
Figure 5. Block diagram of adaptive motor control in the closed loop. For successful motor learning to take place, the brain has to tackle three problems simultaneously: it has to issue a control command in the face of uncertainty, it has to estimate the current state of the biomechanical system, and it has to identify this system. The adaptive controller is adjusted according to ongoing system identification (“parameter estimate”). The adaptive controller translates the task goal (cost function), the adjustable forward model and the current state estimate into an optimal control command. The forward model is identical to the one that is used during the estimation process and optimal control computations are carried out depending on the latest model update.
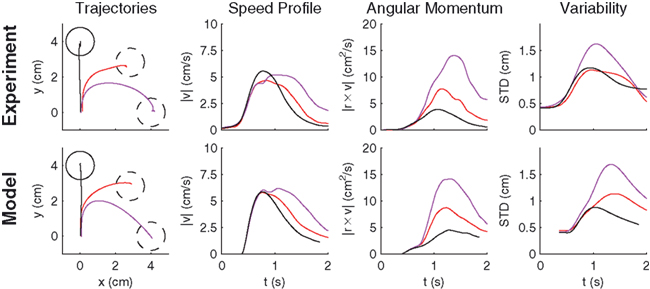
Figure 6. Predictions of the adaptive optimal control model compared to monkey movement data. Averaged experimental hand trajectories (left column), speed profiles (middle left column), angular momenta (middle right column), and trajectory variability (right column) for standard trials (black) and different transformation angles [±45° (red), ±90° (magenta)]. The peak in the angular deviation profile reflects the corrective movement. Higher rotation angles are associated with higher variability in the movement trajectories. All trajectories were rotated to the same standard target, since model predictions were isotropic. The model consistently reproduces the characteristic features of the experimentally observed behavior.
In our visuomotor learning task, the adaptive optimal control model has to continuously estimate the rotation angle 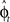 . In each trial this estimate evolves from an initial estimate
. In each trial this estimate evolves from an initial estimate 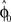 that represents the prior over the expected visuomotor rotation. Thus, over-trial learning corresponds to updating the prior
that represents the prior over the expected visuomotor rotation. Thus, over-trial learning corresponds to updating the prior 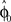 from trial to trial. In the absence of any learning experiences the initialization reflecting the standard mapping would be
from trial to trial. In the absence of any learning experiences the initialization reflecting the standard mapping would be 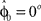 . In a block of identical transformation trials the initial parameter estimate should successively approximate the true rotation angle, thus reflecting over-trial learning. The initial parameter estimate
. In a block of identical transformation trials the initial parameter estimate should successively approximate the true rotation angle, thus reflecting over-trial learning. The initial parameter estimate 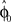 in each trial corresponds to the assumed association between target direction
in each trial corresponds to the assumed association between target direction 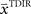 and the required movement direction
and the required movement direction 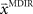 . This belief association can be estimated from the experiment by examining initial movement directions before sensory feedback sets in. Mathematically, this mapping can be expressed by a function approximator that is sequentially adapting to the presented learning pairs. One of the simplest and most generic function approximators are radial basis function networks (Moody and Darken, 1989). Such an approximator would retain initial estimates
. This belief association can be estimated from the experiment by examining initial movement directions before sensory feedback sets in. Mathematically, this mapping can be expressed by a function approximator that is sequentially adapting to the presented learning pairs. One of the simplest and most generic function approximators are radial basis function networks (Moody and Darken, 1989). Such an approximator would retain initial estimates 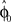 over trials in dependence of the target direction, such that
over trials in dependence of the target direction, such that 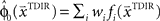 . The basis functions fi(°) are often chosen as bell shaped functions with a center
. The basis functions fi(°) are often chosen as bell shaped functions with a center 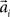 and a width bi, for example von Mises functions in case of a circular variable, i.e.,
and a width bi, for example von Mises functions in case of a circular variable, i.e., 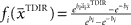 with
with 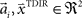 and
and 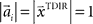 , where the centers
, where the centers 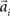 have to be scattered (more or less) uniformly over the unit circle. The over-trial weight update can then be accomplished by standard gradient-based methods like the Widrow–Hoff rule,
have to be scattered (more or less) uniformly over the unit circle. The over-trial weight update can then be accomplished by standard gradient-based methods like the Widrow–Hoff rule, 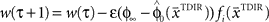 , where τ represents the trial number and ɸ∞ corresponds to the final plateau value in the learning curve. While ɸ∞ is introduced here ad hoc, the residual error might be explicable in terms of the two learning mechanisms, since for small angular deviations online adaptation is not necessary anymore for stable control, so updating of the prior
, where τ represents the trial number and ɸ∞ corresponds to the final plateau value in the learning curve. While ɸ∞ is introduced here ad hoc, the residual error might be explicable in terms of the two learning mechanisms, since for small angular deviations online adaptation is not necessary anymore for stable control, so updating of the prior 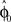 might cease when major online adaptations terminate. The time course of over-trial learning would be determined by the learning constant ε in this model. The learning constant can be adjusted to fit the experimental learning curve of initial movement directions (Figure 7).
might cease when major online adaptations terminate. The time course of over-trial learning would be determined by the learning constant ε in this model. The learning constant can be adjusted to fit the experimental learning curve of initial movement directions (Figure 7).
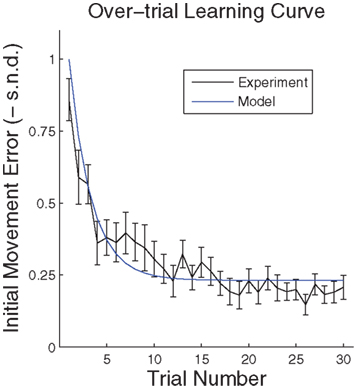
Figure 7. Over-trial learning curve. Performance error was assessed by signed normalized deviation (SND) from a straight line, calculated as a directional deviation – the required hand direction minus the actual hand direction (taken when the speed crossed a 2-cm/s threshold), normalized by the transformation in the session (±45° or ±90°). The learning curve reflects changes in initial movement direction. The model curve is computed by applying the Widrow–Hoff rule to the basis function network described in the text.
When the transformation is switched off unexpectedly during the learning epoch, behavioral studies have documented characteristic deviations in direction of the learned target (Krakauer et al., 2000; Paz et al., 2003). These aftereffects indicate the formation of an internal model during learning. As the initial movement is largely devoid of corrective feedback, this deviation error can be predicted by the prior that has been retained in the radial basis function network during the learning epoch, because the weights wi have adapted to the transformation. Thus, the function 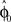 predicts the generalization of the learned transformation across the workspace by virtue of its dependence on target direction. Importantly, there is a relation between this pattern of generalization and the underlying basis functions. In our case, this implies a relation between the width of the von Mises tuning functions in the radial basis function network and the broadness of the aftereffect (Figure 8). Due to the bias-variance trade-off, however, the best fit of the aftereffect will in general not allow determining the optimal tuning width uniquely, since the goodness of fit also depends on the number of basis functions and the noise of the fitted data. However, if the number of basis functions is high enough and homogeneously distributed, the goodness of fit becomes essentially independent from this number (see for example, Tanaka et al., 2009). For our data and number of basis functions (n = 100) the best fitting basis function width is b ≈ 7, which would correspond to a SD of σ ≈ 15° in a Gaussian basis function. Compared to broad cosine-tuning functions (σ ≈ 50°) often reported to be prevalent in motor systems (Todorov, 2002), this comparatively narrow width is qualitatively much more consistent with the basis function width of σ ≈ 23° that is typically assumed for parietal neurons and was recently reported in a behavioral study on learning visuomotor rotations (Tanaka et al., 2009).
predicts the generalization of the learned transformation across the workspace by virtue of its dependence on target direction. Importantly, there is a relation between this pattern of generalization and the underlying basis functions. In our case, this implies a relation between the width of the von Mises tuning functions in the radial basis function network and the broadness of the aftereffect (Figure 8). Due to the bias-variance trade-off, however, the best fit of the aftereffect will in general not allow determining the optimal tuning width uniquely, since the goodness of fit also depends on the number of basis functions and the noise of the fitted data. However, if the number of basis functions is high enough and homogeneously distributed, the goodness of fit becomes essentially independent from this number (see for example, Tanaka et al., 2009). For our data and number of basis functions (n = 100) the best fitting basis function width is b ≈ 7, which would correspond to a SD of σ ≈ 15° in a Gaussian basis function. Compared to broad cosine-tuning functions (σ ≈ 50°) often reported to be prevalent in motor systems (Todorov, 2002), this comparatively narrow width is qualitatively much more consistent with the basis function width of σ ≈ 23° that is typically assumed for parietal neurons and was recently reported in a behavioral study on learning visuomotor rotations (Tanaka et al., 2009).
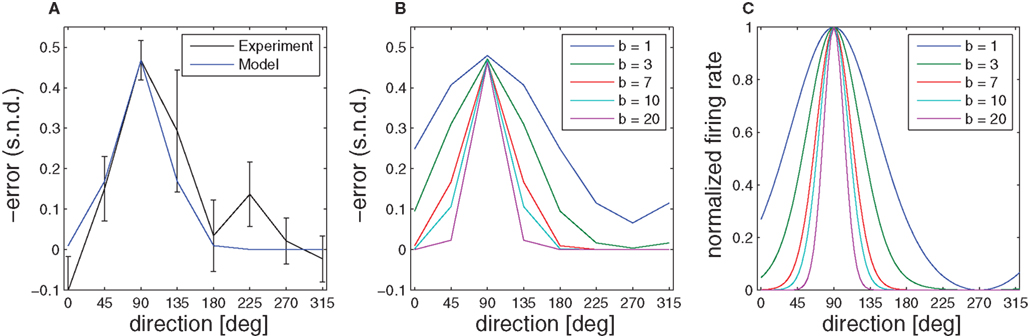
Figure 8. Aftereffect. (A) Initial directional error (taken when the speed crossed a 2-cm/s threshold) in standard center-out movements of monkeys after the visuomotor rotation was switched off. The error is most pronounced in the direction of the target that was used during the learning phase. (B) Given a simple radial basis function network, the broadness of the aftereffect curve depends on the width of the underlying basis functions, which is denoted by the parameter b. (C) Model basis functions that correspond to different aftereffect curves.
Discussion
In this study we have examined evidence for over-trial learning and online adaptation in a visuomotor learning experiment performed by macaque monkeys. Crucially, online adaptive behavior cannot be explained by DT controllers that rely on a non-adaptive feedback-error controller. When we used an adaptive optimal feedback control model (Braun et al., 2009) instead, we were able to reproduce adaptive behavior in early learning trials that reflect online adaptation. However, it should be noted that feedback-error learning would still be possible with an adaptive error-feedback controller in the feedback loop that is specific for the tool in use (in our case the computer cursor). In total, this would add up to three controller types that have to be learned for each tool under error-feedback control: an inverse internal model, an online adaptive error-feedback controller, and a forward internal model that is required for estimation purposes to stabilize the feedback loop. In contrast, the framework of adaptive optimal feedback control only requires learning a forward model (Todorov and Jordan, 2002). The additional difficulty in the optimal control framework is the computation of the optimal policy based on the assumed forward model.
Moreover, there are other interesting features of the error-feedback controller: (1) the error-feedback controller has to track the DT in extrinsic cursor coordinates, and (2) some kind of temporal alignment mechanism with regard to the reference trajectory needs to be postulated due to the excess movement time in the face of unexpected perturbations. Often, it is assumed that a DT is first selected in task-oriented coordinates and then translated via an inverse kinematic transformation, for example, into joint angles (Kawato et al., 1987; Mussa-Ivaldi and Bizzi, 2000). Thereby, the problem of motor redundancy is solved explicitly. Subsequently, a motor command (e.g., muscle torques) is generated via an inverse dynamic transformation by translating the DT in muscle coordinates. Importantly, though, tracking a DT in muscle coordinates in the case of learning a visuomotor rotation does not help, because this trajectory would presume knowing the relationship between desired cursor state and desired muscle state. Consequently, the error-feedback controller would have to operate in extrinsic cursor coordinates as a function of the desired and actual cursor state. This leads to the consequence that there should be an immense repository of extrinsic desired trajectories for all tools that require adaptive control and that these desired trajectories are tracked in “tool space.” Accordingly, the central nervous system would have to pre-compute detailed extrinsic trajectories for complex tool use in advance – for an extended discussion see also (Shadmehr and Wise, 2005). Additionally, a temporal alignment mechanism with regard to the computation of the DT needs to be postulated whenever an unpredicted perturbation thwarts the original movement plan to an extent that changes the total movement duration. As feedback-error corrections are based on the comparison of actual and desired limb position at a certain moment of time, it is not clear how the reference values for the surplus time should be calculated. Somehow the DT would need to be re-evaluated and re-aligned, requiring an additional alignment mechanism. The nature of such a mechanism is however not necessarily trivial.
In our study we have also investigated over-trial learning. Such over-trial learning corresponds to the trial-by-trial update of the prior belief over expected transformations. We used a radial basis function network to model this trial-by-trial update by fitting both the over-trial learning curve and an aftereffect curve that reveals learned movement directions when the transformation is switched off unexpectedly. Previous studies have used aftereffect errors to make inferences with respect to the underlying basis functions (Donchin et al., 2003; Tanaka et al., 2009). In particular, the recent study by Tanaka et al. (2009) investigated over-trial learning of visuomotor rotations by using a population-coding model (Salinas and Abbott, 1995) that was based on a radial basis function network, where the input layer consisted of narrow Gaussian-tuned visual units and the output was given by a weighted sum of preferred hand-movement directions. Their results suggested that post-adaptation generalization could be reproduced by narrow directional tuning widths (σ ≈ 23°) in the input layer, whereas broad tuning functions such as cosine tuning or bimodal Gaussian tuning curves could not reproduce the observed generalization pattern. In the literature basis functions are often interpreted in terms of neuronal tuning functions (Pouget and Snyder, 2000), where different types of tuning functions have been reported for different parts of the brain. For example, narrow Gaussian tuning functions have been previously reported for the parietal cortex area (Andersen et al., 1985; Brotchie et al., 1995; Graziano et al., 1997), whereas cosine tuning has been reported for motor cortical areas (Georgopoulos et al., 1982) and bimodal tuning curves have been reported for the cerebellum (Coltz et al., 1999). Tanaka et al. (2009) therefore concluded that their model was consistent with the notion that adaptive processes with respect to visuomotor rotation learning could be instantiated by changes in synaptic weights between neurons in posterior parietal cortex and motor cortex. The results in our study are consistent with this interpretation, in that we also found that comparatively narrow basis functions could explain the observed generalization pattern. Of course, this hypothesis can ultimately only be tested by simultaneously studying neuronal activity changes both in the motor cortical and parietal brain areas.
In previous studies different time scales of motor learning have roughly been differentiated as “within-session” and “across-session” learning (Karni et al., 1998; Costa et al., 2004). Within-session learning has further been associated with two different interacting learning mechanisms that act again on different time scales (Smith et al., 2006). Moreover, such “within-session” learning has been associated with establishing optimal control routines and corresponds roughly to over-trial learning in our experiment. Here we want to add the notion of “within-trial” adaptation and to denote optimal adaptive real-time sensorimotor integration occurring on an even shorter time scale. This is in line with previous studies which have provided evidence that online sensorimotor integration can be described by optimality principles (Baddeley et al., 2003; Kording and Wolpert, 2004; Braun et al., 2009). Our results are in line with these previous studies that suggest that motor learning occurs on multiple timescales.
Methods
Animals and Data Acquisition
Two female rhesus monkeys (Macaca mulatta, ~4.5 kg) operated two manipulanda that recorded the two-dimensional movements of their two arms. Animal care complied with the NIH Guidelines for the Care and Use of Laboratory Animals (1996) and with guidelines supervised by the Institutional Committee for Animal Care and Use at Hebrew University.
Experimental Design
The monkeys controlled two cursors on a video screen 50 cm away by operating the two manipulanda in the horizontal plane. At the beginning of each trial, both cursors had to be centered at a circular starting position, then a laterality cue indicated the hand to be used and one out of eight possible concentrically arranged targets (radius 0.8 cm, center-target distance 4 cm) lit up, while the monkey was waiting for the go signal to move, which appeared after a variable hold period of 1.0−1.5 s. In a successful trial, the target had to be reached in less than 2 s (movement period), whereupon a liquid reward was delivered. The experiment was structured in a pre-learning epoch, a learning epoch, and a post-learning epoch. During the pre-learning epoch, a standard eight-target center-out task was performed to randomly chosen targets. During the learning epoch, only the upward target was presented in every trial and one out of four possible rotations (±45°, ±90°) was applied. In one session it was always the same transformation in all learning trials, but different transformations were used on different days. During the post-learning epoch veridical cursor feedback was re-established. See (Paz et al., 2003) for further details.
Proof of Instability of a PD Controller Exposed to 90° Transformations
In the following we perform a linear stability analysis of the system given by 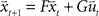 , where
, where  corresponds to the state vector and
corresponds to the state vector and  corresponds to the control signal. If we assume a point mass model for the dynamics, the state vector
corresponds to the control signal. If we assume a point mass model for the dynamics, the state vector 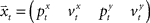 is defined by position pt and velocity vt, and the matrices F and G are given by
is defined by position pt and velocity vt, and the matrices F and G are given by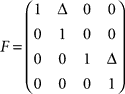 and
and 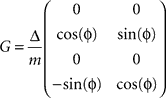 with the time discretization constant Δ and the point mass m. The PD controller can then be written as
with the time discretization constant Δ and the point mass m. The PD controller can then be written as 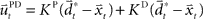 with the DT
with the DT 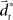 and control gain matrices
and control gain matrices 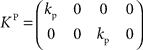 and
and 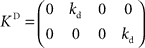 . In order to determine the stability of this closed-loop system, we have to compute the following closed-loop transfer function by taking the z-transform:
. In order to determine the stability of this closed-loop system, we have to compute the following closed-loop transfer function by taking the z-transform: 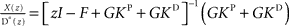 . Stability of the closed loop can be examined by checking whether all poles of the transfer function lie within the unit circle. To this end, we need to compute the denominator of the matrix inverse and find the roots of the expression
. Stability of the closed loop can be examined by checking whether all poles of the transfer function lie within the unit circle. To this end, we need to compute the denominator of the matrix inverse and find the roots of the expression
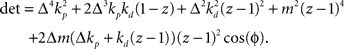
If we set ɸ = 90° and solve for z, we get four solutions given by 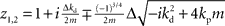 and
and 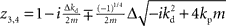 .
.
If stable closed-loop control should be possible, we have to assume that there are constants kp, kd ∈ ℜ such that |zi| < 1, ∀i with i = 1,2,3,4 under the constraint m, Δ > 0. Computing the absolute values one finds that 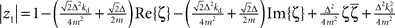 and
and 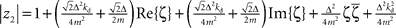 with the substitution
with the substitution 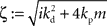 and Re{ζ}and Im{ζ} denoting the real and imaginary parts of zrespectively. Similarly, one finds |z3| = |z2| and |z4| = |z1|. From the requirement |z1| < 1∧|z2| < 1 it follows that |z1| + |z2| < 2. For this to be true it must be also true that
and Re{ζ}and Im{ζ} denoting the real and imaginary parts of zrespectively. Similarly, one finds |z3| = |z2| and |z4| = |z1|. From the requirement |z1| < 1∧|z2| < 1 it follows that |z1| + |z2| < 2. For this to be true it must be also true that 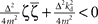 , which is a contradiction. Therefore, there are no constants kp, kd ∈ ℜ to stabilize the feedback loop.
, which is a contradiction. Therefore, there are no constants kp, kd ∈ ℜ to stabilize the feedback loop.
Computational Model: Online Adaptation
The adaptive optimal feedback controller that was used to model online adaptation in Figure 6 was taken from (Braun et al., 2009). We assumed a linear arm model, where the control signal ut is contaminated by signal-dependent noise (with scalar magnitude ∑u) and smoothed by a second-order muscle-like low-pass filter with time constants τ1 = τ2 = 40 ms (Todorov and Jordan, 2002). The resulting force vector ft acts on the point mass (m = 0.5 kg) representing the hand that has position 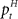 and velocity vt. In turn, the hand position is translated into a cursor position pt by a rotation matrix Dɸ, such that
and velocity vt. In turn, the hand position is translated into a cursor position pt by a rotation matrix Dɸ, such that 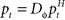 . The aim of the control process is to bring the cursor position pt to the target position ptarget. Sensory feedback of the cursor position, speed, and force is provided with a time delay of 150 ms and the feedback was contaminated by additive Gaussian noise with a covariance of 0.04 cm2 for position, 4 cm2/s2 for speed, and 400 cN2 for force. We also assumed a quadratic infinite horizon cost function
. The aim of the control process is to bring the cursor position pt to the target position ptarget. Sensory feedback of the cursor position, speed, and force is provided with a time delay of 150 ms and the feedback was contaminated by additive Gaussian noise with a covariance of 0.04 cm2 for position, 4 cm2/s2 for speed, and 400 cN2 for force. We also assumed a quadratic infinite horizon cost function 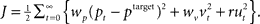 The weights wp and wv punish positional error between cursor and target and high velocities, the parameter r punishes excessive control signals. Since the absolute value of the cost function does not matter, we set wp = 1. Since the system dynamics are linear and the cost is quadratic, the adaptive controller can be described by a linear state-feedback control law that is updated in every time step with the current estimate of ɸ (Braun et al., 2009). Estimating the rotation parameter ɸ during the movement constitutes the process of online adaptation. The speed of this adaptation process (modeled as a random walk) is determined by a scalar covariance Ωv. Details of the model can be found in (Braun et al., 2009).
The weights wp and wv punish positional error between cursor and target and high velocities, the parameter r punishes excessive control signals. Since the absolute value of the cost function does not matter, we set wp = 1. Since the system dynamics are linear and the cost is quadratic, the adaptive controller can be described by a linear state-feedback control law that is updated in every time step with the current estimate of ɸ (Braun et al., 2009). Estimating the rotation parameter ɸ during the movement constitutes the process of online adaptation. The speed of this adaptation process (modeled as a random walk) is determined by a scalar covariance Ωv. Details of the model can be found in (Braun et al., 2009).
Computational Model: Over-Trial Learning
We assumed a radial basis function network for learning and retaining the parameter estimate 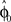 that initializes the belief about the assumed association between target direction
that initializes the belief about the assumed association between target direction 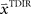 and the required movement direction
and the required movement direction 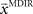 in each trial. The estimate
in each trial. The estimate 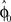 is used by the online adaptation process as the mean of a Gaussian distribution representing the initial belief at the beginning of the trial. The radial basis function network had the form
is used by the online adaptation process as the mean of a Gaussian distribution representing the initial belief at the beginning of the trial. The radial basis function network had the form 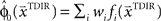 , where the basis functions fi (o) were given by von Mises functions
, where the basis functions fi (o) were given by von Mises functions 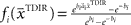 with preferred direction
with preferred direction 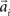 and width bi. The centers
and width bi. The centers 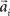 have to be scattered (more or less) uniformly over the unit circle, i.e.,
have to be scattered (more or less) uniformly over the unit circle, i.e., 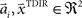 and
and 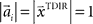 . The over-trial update of the weights wi was accomplished by gradient descent, yielding
. The over-trial update of the weights wi was accomplished by gradient descent, yielding 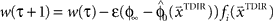 , where τ represents the trial number and ɸ∞ corresponds to the final plateau value in the learning curve.
, where τ represents the trial number and ɸ∞ corresponds to the final plateau value in the learning curve.
Model Fit: Online Adaptation
There were four free scalar parameters in the adaptive optimal control model that were fit to the data: the cost parameters wv and r, the adaptation rate Ωv, and the signal-dependent noise level ∑u. We adjusted these parameters to fit the mean trajectory of the 90°-rotation trials (by collapsing the + and −90° trials into one angle). These parameter settings were then used to extrapolate behavior to both the standard trials and the 45° rotation trials. The fitted parameter values were wv = 0.1, r = 0.03, Ωv = 0.0001, and ∑u = 1.5.
Model Fit: Over-Trial Learning
The performance error in the over-trial learning process was assessed by signed normalized deviation (SND) from a straight line, calculated as an angular deviation – the required hand direction minus the actual hand direction (taken when the speed crossed a 2-cm/s threshold), normalized by the transformation in the session (±45° or ±90°). The learning parameter ε and the steady-state estimate ɸ∞ of the over-trial estimator were fitted to the over-trial measure of the performance error obtained from the initial movement (taken when the speed crossed a 2-cm/s threshold). To predict the performance error after adaptation, we also fitted the aftereffect error for different widths of the basis functions (b = 1,3,7,10,20).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This study was supported in parts by the German Federal Ministry of Education and Research (BMBF grant 01GQ0420 to BCCN Freiburg), the German-Israeli Project Coordination (DIP), the Israel Science Foundation (ISF), and the Böhringer-Ingelheim Fonds (BIF).
References
Andersen, R. A., Essick, G. K., and Siegel, R. M. (1985). Encoding of spatial location by posterior parietal neurons. Science 230, 456–458.
Baddeley, R. J., Ingram, H. A., and Miall, R. C. (2003). System identification applied to a visuomotor task: near-optimal human performance in a noisy changing task. J. Neurosci. 23 3066–3075.
Bhushan, N., and Shadmehr, R. (1999). Computational nature of human adaptive control during learning of reaching movements in force fields. Biol. Cybern. 81 39–60.
Braun, D. A., Aertsen, A., Wolpert, D. M., and Mehring, C. (2009). Learning optimal adaptation strategies in unpredictable motor tasks. J. Neurosci. 29 6472–6480.
Brotchie, P. R., Andersen, R. A., Snyder, L. H., and Goodman, S. J. (1995). Head position signals used by parietal neurons to encode locations of visual stimuli. Nature 375 232–235.
Coltz, J. D., Johnson, M. T., and Ebner, T. J. (1999). Cerebellar Purkinje cell simple spike discharge encodes movement velocity in primates during visuomotor arm tracking. J. Neurosci. 19 1782–1803.
Costa, R. M., Cohen, D., and Nicolelis, M. A. (2004). Differential corticostriatal plasticity during fast and slow motor skill learning in mice. Curr. Biol. 14 1124–1134.
Diedrichsen, J., Hashambhoy, Y., Rane, T., and Shadmehr, R. (2005). Neural correlates of reach errors. J. Neurosci. 25 9919–9931.
Donchin, O., Francis, J. T., and Shadmehr, R. (2003). Quantifying generalization from trial-by-trial behavior of adaptive systems that learn with basis functions: theory and experiments in human motor control. J. Neurosci. 23 9032–9045.
Georgopoulos, A. P., Kalaska, J. F., Caminiti, R., and Massey, J. T. (1982). On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. J. Neurosci. 2 1527–1537.
Graziano, M. S. A., Hu, X. T., and Gross, C. G. (1997). Visuospatial properties of ventral premotor cortex. J. Neurophysiol. 77 2268–2292.
Gribble, P. L., and Scott, S. H. (2002). Overlap of internal models in motor cortex for mechanical loads during reaching. Nature 417 938–941.
Karni, A., Meyer, G., Rey-Hipolito, C., Jezzard, P., Adams, M. M., Turner, R., and Ungerleider, L. G. (1998). The acquisition of skilled motor performance: fast and slow experience-driven changes in primary motor cortex. Proc. Natl. Acad. Sci. U.S.A. 95 861–868.
Kawato, M. (1999). Internal models for motor control and trajectory planning. Curr. Opin. Neurobiol. 9 718–727.
Kawato, M., Furukawa, K., and Suzuki, R. (1987). A hierarchical neural-network model for control and learning of voluntary movement. Biol. Cybern. 57 169–185.
Kording, K. P., and Wolpert, D. M. (2004). Bayesian integration in sensorimotor learning. Nature 427 244–247.
Krakauer, J. W., Pine, Z. M., Ghilardi, M. F., and Ghez, C. (2000). Learning of visuomotor transformations for vectorial planning of reaching trajectories. J. Neurosci. 20 8916–8924.
Li, C. S., Padoa-Schioppa, C., and Bizzi, E. (2001). Neuronal correlates of motor performance and motor learning in the primary motor cortex of monkeys adapting to an external force field. Neuron 30 593–607.
Moody, J., and Darken, C. D. (1989). Fast learning in networks of locally-tuned processing units. Neural Comput. 1 281–294.
Mussa-Ivaldi, F. A., and Bizzi, E. (2000). Motor learning through the combination of primitives. Philos. Trans. R. Soc. Lond. B Biol. Sci. 355 1755–1769.
Nakanishi, J., and Schaal, S. (2004). Feedback error learning and nonlinear adaptive control. Neural Netw. 17 1453–1465.
Padoa-Schioppa, C., Li, C. S., and Bizzi, E. (2002). Neuronal correlates of kinematics-to-dynamics transformation in the supplementary motor area. Neuron 36 751–765.
Paz, R., Boraud, T., Natan, C., Bergman, H., and Vaadia, E. (2003). Preparatory activity in motor cortex reflects learning of local visuomotor skills. Nat. Neurosci. 6 882–890.
Pouget, A., and Snyder, L. H. (2000). Computational approaches to sensorimotor transformations. Nat. Neurosci. 3(Suppl.), 1192–1198.
Salinas, E., and Abbott, L. F. (1995). Transfer of coded information from sensory to motor networks. J. Neurosci. 15 6461–6474.
Shadmehr, R., and Wise, S. P. (2005). The Computational Neurobiology of Reaching and Pointing: A Foundation For Motor Learning. Cambridge, MA: MIT Press.
Shen, L., and Alexander, G. E. (1997). Neural correlates of a spatial sensory-to-motor transformation in primary motor cortex. J. Neurophysiol. 77 1171–1194.
Smith, M. A., Ghazizadeh, A., and Shadmehr, R. (2006). Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol. 4:e179. doi: 10.1371/journal.pbio.0040179
Tanaka, H., Sejnowski, T. J., and Krakauer, J. W. (2009). Adaptation to visuomotor rotation through interaction between posterior parietal and motor cortical areas. J. Neurophysiol. 102 2921–2932.
Tin, C., and Poon, C. S. (2005). Internal models in sensorimotor integration: perspectives from adaptive control theory. J. Neural Eng. 2 S147–S163.
Todorov, E., and Jordan, M. I. (2002). Optimal feedback control as a theory of motor coordination. Nat. Neurosci. 5 1226–1235.
Wise, S. P., Moody, S. L., Blomstrom, K. J., and Mitz, A. R. (1998). Changes in motor cortical activity during visuomotor adaptation. Exp. Brain Res. 121 285–299.
Wolpert, D. M., and Ghahramani, Z. (2000). Computational principles of movement neuroscience. Nat. Neurosci. 3(Suppl.), 1212–1217.
Keywords: visuomotor learning, motor control, online adaptation, over-trial learning
Citation: Braun DA, Aertsen A, Paz R, Vaadia E, Rotter S and Mehring C (2011) Online adaptation and over-trial learning in macaque visuomotor control. Front. Comput. Neurosci. 5:27. doi: 10.3389/fncom.2011.00027
Received: 06 October 2010;
Accepted: 22 May 2011;
Published online: 14 June 2011.
Edited by:
Xiao-Jing Wang, Yale University School of Medicine, USAReviewed by:
Emilio Salinas, Wake Forest University, USAThomas Trappenberg, Dalhousie University, Canada
Copyright: © 2011 Braun, Aertsen, Paz, Vaadia, Rotter and Mehring. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Daniel A. Braun, Computational and Biological Learning Lab, Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK. e-mail:ZGFiNTRAY2FtLmFjLnVr


 Rony Paz3
Rony Paz3
