Gait modulation in C. elegans: an integrated neuromechanical model

Equipped with its 302-cell nervous system, the nematode Caenorhabditis elegans adapts its locomotion in different environments, exhibiting so-called swimming in liquids and crawling on dense gels. Recent experiments have demonstrated that the worm displays the full range of intermediate behaviors when placed in intermediate environments. The continuous nature of this transition strongly suggests that these behaviors all stem from modulation of a single underlying mechanism. We present a model of C. elegans forward locomotion that includes a neuromuscular control system that relies on a sensory feedback mechanism to generate undulations and is integrated with a physical model of the body and environment. We find that the model reproduces the entire swim-crawl transition, as well as locomotion in complex and heterogeneous environments. This is achieved with no modulatory mechanism, except via the proprioceptive response to the physical environment. Manipulations of the model are used to dissect the proposed pattern generation mechanism and its modulation. The model suggests a possible role for GABAergic D-class neurons in forward locomotion and makes a number of experimental predictions, in particular with respect to non-linearities in the model and to symmetry breaking between the neuromuscular systems on the ventral and dorsal sides of the body.

1. Introduction

One essential requirement for the survival of most animals is the ability to move around in a world characterized by complex, unpredictable, and variable environments. Adapting to different environments often involves the use of qualitatively distinct patterns of locomotion, called gaits. The animal’s nervous system is responsible for generating the rhythmic neuromuscular activity associated with each of these gaits and must coordinate the task of switching seamlessly between them. Furthermore, the animal must be able to reliably adapt any of these patterns in response to external perturbations. Understanding the neural basis of animal locomotion is an important challenge that has received considerable attention (Kiehn et al., 1998; Grillner and Wallén, 2002; Hill et al., 2003; Borgmann et al., 2009).

The popular model organism Caenorhabditis elegans is a tiny (≈1 mm long) nematode worm with a largely invariant nervous system, consisting of exactly 302 neurons with known connectivity (White et al., 1986; Chen et al., 2006). Moreover, the behavioral roles of many of these neurons have been uncovered using experimental techniques including targeted cell killing (Chalfie et al., 1985; McIntire et al., 1993b) and genetic mutations (Brenner, 1974; McIntire et al., 1993a). The result is an organism in which the nervous system is mapped at cellular resolution. Despite its small size and the apparent simplicity of the underlying nervous system, the worm is capable of a surprisingly rich repertoire of behaviors including navigation and foraging, mating, learning, and even rudimentary social behavior (aggregation).

Central to all of these behaviors, the worm’s locomotion is remarkably adaptive and changes in response to its environment. Specifically, the body undulations used by the worm when swimming in liquid or crawling on a firm gel substrate like agar are kinematically different (see Movie S1 in Supplementary Material), and have generally been thought to represent two distinct gaits (White et al., 1986; Pierce-Shimomura et al., 2008). In line with this two gait hypothesis, previous models of the worm’s locomotion (Niebur and Erdös, 1991; Bryden and Cohen, 2004, 2008; Karbowski et al., 2008) have mostly addressed crawling on agar. Recent results, however, demonstrated that forward swimming and crawling are two extremes in a spectrum of behaviors. Indeed the intermediate waveforms can be revealed by placing worms in appropriate intermediate media (Berri et al., 2009; Fang-Yen et al., 2010; Sznitman et al., 2010; Boyle et al., 2011). The continuity of the swim-crawl transition strongly suggests that the entire range of behaviors are produced through modulation of a single neural mechanism. This discovery sets an exciting new challenge to develop a model of the worm that is capable of reproducing the entire range of locomotor behaviors.

Here we present an integrated neuromechanical model of C. elegans forward locomotion, grounded in the neurobiology, anatomy, and physics of the real worm, that successfully accounts for locomotion across a range of media from water to agar, as well as in more complex inhomogeneous environments. This model suggests that sensory feedback mechanisms are sufficient to account for the observed modulation of the locomotion behavior in different environments. Analysis of the model sheds further light on the mechanisms that generate and modulate the oscillations and leads to a number of experimental predictions.

2. Materials and Methods

We begin with the premise, grounded in the C. elegans circuitry that a single neural circuit is responsible for all of the worm’s forward locomotion, from slow (0.5 Hz), short wavelength, sinuous crawling patterns to fast (2 Hz), long wavelength, thrashing, or swimming patterns. With this in mind, we set out to develop a model of this neural circuit and its modulation that can account for the entire range of behaviors.

A large body of previous work (Niebur and Erdös, 1991; Sauvage, 2007; Berri et al., 2009; Boyle, 2010; Fang-Yen et al., 2010; Sznitman et al., 2010; Petzold et al., 2011; Shen and Arratia, 2011) has found that the physics of the worm’s body and environment are important components of the locomotion system. In particular, any model that is meant to account for motor behavior across different physical environments must incorporate the corresponding physics in some manner. In our model, as explained below, it is also important to capture the detailed shape of the body, as it may impact on any proprioceptive feedback mechanisms.

Stretch-receptor-mediated proprioception has long been postulated to exist in C. elegans motoneurons and has recently been reported experimentally (Li et al., 2006; Schafer, 2006). Specifically, proprioceptive mechanisms are thought to channel information to the motoneurons about the bending of the body (posteriorly and possibly locally). In differing physical environments, the response to identical muscle activation patterns would produce different body shapes, thus constituting completely passive environment-mediated modulation of the locomotion. Under such conditions, one would also expect the proprioceptive signal to differ, providing closed-loop neural control and adaptation of the neuromuscular pattern of activity to variable environments. Indeed, in our model, such sensory feedback is the primary driving force behind the oscillation mechanism.

The model description that follows is consistent with the order in which the model was developed and parameters fixed. Specifically, the physical parameters of the environment should be independent from the choice of model of the worm, and so were fixed first. Following similar logic, the behavior of the passive body (lacking neuromuscular control) was modeled second and all corresponding parameters were fixed. The muscles were modeled next, and the neural control was incorporated last, without any modifications to already set parameters of the muscles, body, or environment. The model software is available as supporting information (S14).

2.1. Properties of the Environment

Small size and relatively slow speeds mean that the worm’s motion is well described by low Reynolds number physics, in which inertial forces can be neglected. As previously demonstrated (Berri et al., 2009), the resistive forces applied by the worm’s physical environment can be well represented by local drag coefficients resisting motion tangential (C_||) and normal (C_⊥) to the local body surface. In Newtonian fluids of known viscosity, values of drag coefficients can be determined from slender body theory, using equations due to Lighthill (1976)

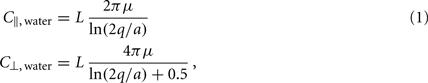
where μ is the dynamic viscosity (≈1 MPa·s for water); q is proportional to the wavelength (λ) of the body wave (typically about 1.5 mm in water, giving q = 0.09λ = 1.35 × 10⁻⁴ m); and L = 1 mm and a = 40 μm are the length and radius of the body, respectively.

Note that the values above are for the whole worm, so the drag coefficient experienced locally along the worm is proportionately smaller. Importantly, in Newtonian environments, the ratio of drag coefficients is fully specified by the geometry of the object, and for the worm is roughly K = C_⊥/C_|| ≈ 1.5.

For agar, Wallace estimated the tangential drag coefficients C_||,agar by directly measuring the force required to pull glass fibers of similar dimension to C. elegans across the surface (Wallace, 1969). Based on this measurement, Niebur and Erdös (1991) estimated C_||,agar = 3.2 × 10⁻³ kg·s⁻¹. We previously estimated the normal drag coefficient C_⊥,agar from recordings of wild type worms using our motion simulator (Berri et al., 2009). Briefly, we found the ratio of drag coefficients to be in the range K_agar ≈ 30–40; taking a value of K_agar = 40 and Niebur and Erdös’ estimate for C_||,agar gives C_⊥,agar = 128 × 10⁻³ kg·s⁻¹, which will be used in what follows.

For generality in our simulations, we allow all combinations of drag coefficients C_|| and C_⊥, such that (i) the minimum drag coefficients correspond to a water environment; (ii) the maximum drag coefficients correspond to estimates of agar properties; and (iii) the ratio of drag coefficients falls within the range 1.5 ≤ K ≤ 40. The specific combinations used are shown in Figure 4C.

2.2. The Physical Model

In line with previous work (Niebur and Erdös, 1991; Boyle et al., 2008), we model the worm’s body as a 2D outline. The 2D representation is justifiable as the C. elegans body (with the exception of the head) only bends in the dorso-ventral plane. The passive body is modeled as a lightly damped elastic beam. The model body is divided into repeating “segments” and articulated by pairs of (D)orsal and (V)entral muscles, with each muscle located in the gap between two points of the physical model (see Figures 1A,B). The hydrostatic skeleton and muscles are represented by a combination of damped springs and solid rods connecting these points. Each resulting set of four points and two muscles is referred to as a segment. The number of segments thus corresponds to the number of muscle pairs in the model. We have chosen M = 48 to provide a good approximation of a smooth (biologically unsegmented) body without being excessively computationally expensive. This number also approximates closely the number of muscles along the body (C. elegans has 48 dorsal and 47 ventral muscle cells). Note, however, that the term “segments” is used for convenience to denote repeating structures, and does not imply biological segmentation. The muscles are modeled as damped springs whose spring “constant,” rest length, and damping “constant” are functions of the level of activation. This implementation endows the muscles with simplified Hill-like length-force and speed-force relations (Hill, 1938), as illustrated in Figures 2A,B respectively.

FIGURE 1

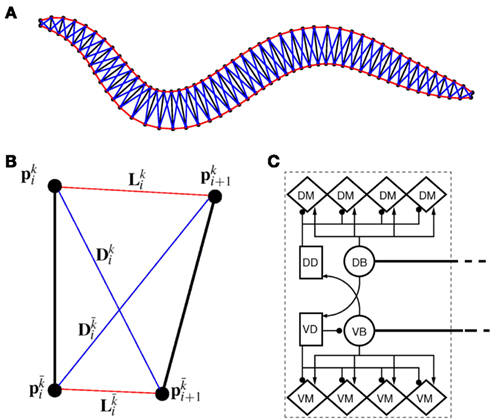
Figure 1. (A) Structure of the physical model. The worm is represented by 49 solid rods (black lines) whose end points (filled black circles) are connected by lateral (red) and diagonal (blue) elements. (B) Detailed schematic diagram of a single segment of the physical model illustrating nomenclature. Solid rods maintain equal width, diagonal elements (blue) preserve internal pressure and active muscles line the lateral elements (red). k and 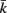denote opposite ventral and dorsal sides, or vice versa. (C) Schematic of the neuromuscular model, showing one of 12 repeating units making up a symmetrized circuit for forward locomotion control. The circuit includes a pair of B-class excitatory neurons (circles), a pair of D-class inhibitory neurons (squares), and four muscles (diamonds) on each side (dorsal and ventral). Synapses are labeled either as excitatory (arrowhead) or inhibitory (circlehead). Posteriorly directed lines from B-class neurons denote the stretch receptor inputs. AVB also forms gap junctional connections with VB and DB (not shown).

FIGURE 2

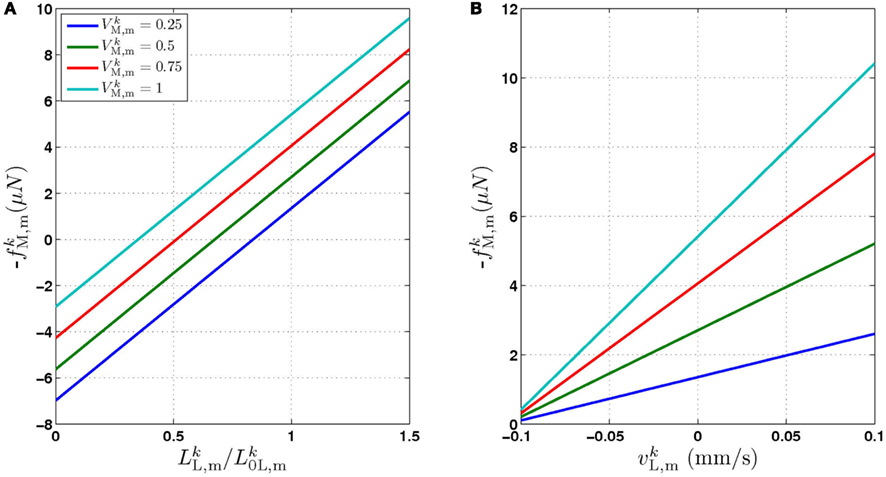
Figure 2. The force generated by model muscles is a function of their activation, length, and rate of contraction. (A) Force/length relationship obtained by holding the muscle at a specific length. (B) Force/velocity relationship obtained by allowing the muscle to contract at a specified rate and measuring the force it exerts at the moment it reaches its rest length L_0L. The model therefore provides a simple linear approximation of these properties of biological muscles. Note that in both cases − f is plotted for simplicity, because contractile forces are defined as negative in the model.

Structure

In the model, a worm of length L and radius R is represented by P = 2(M + 1) = 98 discrete points 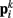, where i = 1, …, M + 1 and k = {D, V}. In other words 49 dorso-ventral point pairs i = 1, …, M + 1 form the boundaries of the M = 48 segments. The model approximates the tapered shape of the worm as a prolate ellipse. To avoid zero-valued radii at the ends, the major radius is taken to be slightly greater than L/2. For a minor radius R, the radii along the body are given by

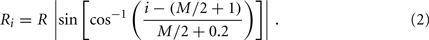
Neglecting the worm’s radial elasticity implies the body will maintain a fixed diameter over time. This allows opposite points and 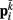to be connected by a solid rod of length 2R_i (with 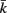denoting the opposite side to k, i.e., 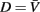and 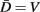). Lateral elements representing passive cuticle forces and active muscle forces connect each point 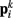to adjacent points 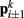. The volume-preserving effect of internal pressure is approximated by diagonal elements that connect 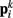to 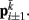Together, these elements yield a net force 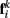on each point. The forces acting on 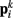and 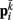combine into a net force and torque acting on the midpoint of the ith rod.

Passive body forces

In the absence of muscle activation, passive body forces capture the combined effect of the cuticle and internal pressure. In the interest of numerical stability, diagonal elements that strongly resist compression are used to represent the effect of pressure.

For the model to work in a highly resistive environment such as agar, spring forces suffice (Niebur and Erdös, 1991; Boyle et al., 2008). However, to model motion in liquid, damping terms must also be included. We therefore model each lateral and diagonal element as a spring in parallel with a damper. Forces applied by the passive lateral elements are given by

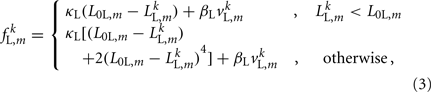
where κ_L, β_L, and L_0L,m denote the lateral spring constant, damping constant, and rest length, respectively. The length of lateral element is 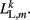while 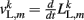. Note that, due to the non-constant radius, the rest lengths vary along the worm according to 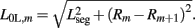Similarly, the forces exerted by diagonal elements are given by

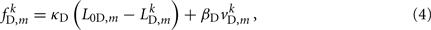
where κ_D, β_D, and L_0D,m denote the diagonal spring constant, damping constant, and rest length, respectively, the latter given by 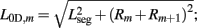the length of the diagonal element is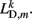

The parameters for the passive body were chosen by comparing the behavior of the passive physical model embedded in virtual water and agar environments to that of a flaccid C. elegans in water or on agar (Sauvage, 2007). Accordingly, a model worm initiated in a bent position will straighten almost instantaneously in water but will straighten only very slowly on agar. These parameters are given in Table 1.

TABLE 1

Table 1. Parameters of the physical model.

Active muscle forces

The worm’s longitudinal body wall muscles are anchored to the inside of the cuticle and are effectively grouped into dorsal and ventral sets. In the model, muscles connect adjacent points on the same side of the body, and therefore act in parallel with the passive lateral elements representing the cuticle (Figure 1B). Thus, the muscle length and cuticle length for a given section of the body are assumed to be identical, consistent with recent experimental findings (Petzold et al., 2011). Qualitatively following Hill’s relations (Hill, 1938), muscle forces are modeled as a function of the muscle activation and mechanical state (Figure 2), such that (i) as a muscle shortens the maximum force it can develop will decrease, eventually reaching saturation, and (ii) the force it generates varies inversely with the speed of contraction. Accordingly, muscles are implemented as a variable lateral element (again consisting of a spring acting in parallel with a damper), whose spring parameter 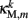(equivalent to the spring “constant” in an ideal Hooke’s Law spring), spring rest length 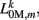and damping coefficient 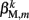all depend on the muscle activation. An anterior-posterior gradient in the maximum muscle efficacies is implemented by a linearly (posteriorly) decreasing factor F_max,m. This gradient makes the shape of the worm more biologically realistic (see Figure 3). Finally, the most anterior muscles receive somewhat weaker innervation to prevent the tip of the head from displaying unrealistically strong bending. Muscle forces are therefore given by

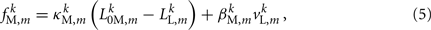
where

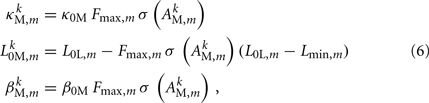
and where κ_0M and β_0M are constants. The function σ is a piecewise linear approximation of a sigmoid that binds the muscle’s electromechanical response to the allowable range

FIGURE 3

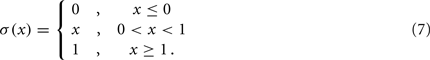
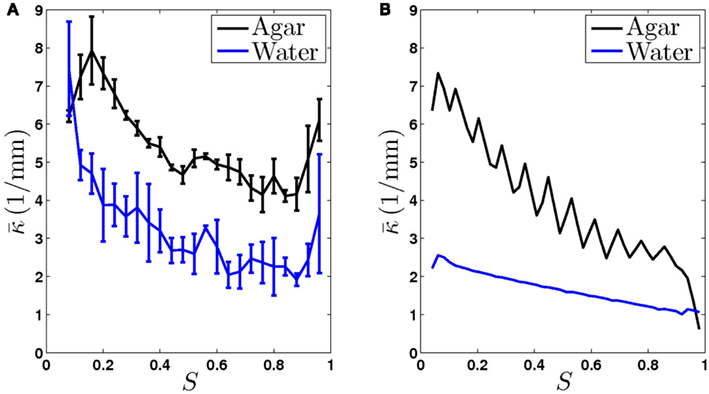
Figure 3. The worm’s locomotion wave exhibits a posteriorly decreasing gradient in curvature, averaged over time 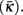S is a measure of the position along the worm’s body, with S = 0 corresponding to the head and S = 1 corresponding to the tail. (A) Experimentally observed curvature gradient obtained by averaging the curvature at each point along the body, first over time (≈10 s) and then over several worms (n = 3 for agar and n = 5 for water). Bars indicate the standard deviation over the n worms. (B) Qualitatively similar curvature gradients exhibited by the model, due to the gradients in muscle efficacy and stretch receptor weighting.

A minimum muscle length L_min,m prevents the muscles from contracting unrealistically. To allow the same curvatures to be attained for all segments along the worm, L_min,m is modulated according to the shape of the worm (see Table 1). Muscle parameters were chosen such that the worm was strong enough to bend its body on agar, but could not generate unrealistically tight curvature (Table 1).

2.3. The Neuromuscular System

C. elegans forward locomotion is controlled by head and ventral nerve cord circuits. The ventral cord subcircuit associated with forward locomotion contains four main classes of motoneurons (11 VB, 7 DB, 13 VD, and 6 DD neurons) and one key pair of interneurons (class AVB). Longitudinal body wall muscles line the body. These muscles contract and relax in the dorso-ventral plane. The individual members of each motoneuron class are arranged sequentially along the body such that their motor output regions do not overlap (White et al., 1986). In line with previous models (Niebur and Erdös, 1991; Bryden and Cohen, 2004, 2008; Karbowski et al., 2008), we consider a simplified, symmetrized neural circuit, disregarding the asymmetry in neuron numbers, and thus allowing us to create the model as a series of repeating units. In a rough correspondence with muscle and neuron numbers (on the ventral side), we chose to model N = 12 neural units, with each controlling M/N = 4 muscle segments. These neural units are identical, except for changes in certain parameters. These simplifications are designed to aid the analysis of the circuit and its dynamics and to reduce the number of free parameters. While this approximation is reasonable for a model that is restricted to generating sinuous undulations, it may need revisiting for models to capture a richer set of behaviors, in particular where additional classes of neurons are included.

The neural circuit

In the worm, VB and DB neurons receive input from AVB interneurons via electrical synapses and excite muscles on the (V)entral and (D)orsal sides. DD (VD) neurons receive input from VB (DB) motoneurons and inhibit the opposing dorsal (ventral) muscles. Thus excitation of muscles on one side of the body is likely to result in inhibition of muscles on the opposite side. Chen et al. (2006) have also reported some inhibitory connections from VD to VB neurons which provide motoneuron-to-motoneuron inhibition on the ventral side. These connections do not feature in the connectivity diagrams of White et al. (1986) and are seldom discussed. In addition to these chemical synaptic connections, electrical synapses exist between adjacent VB (DB) neurons and between adjacent muscle cells (White et al., 1986; Chen et al., 2006).

In the model, the ventral cord circuit (White et al., 1976, 1986; Chen et al., 2006) is simplified to a single AVB command neuron that drives a series of N = 12 repeating units, each containing one motor neuron of each class DBn, VBn, DDn, and VDn, with n = 1, …, N (see Figure 1C). Note the inclusion of neural inhibition from VD to VB, that is partially consistent with the connectivity data (Chen et al., 2006). Within each unit, B-class neurons receive a constant-current input from AVB, switching the entire circuit on and off. D-class neurons are modeled as passive (linear) elements. Postulated stretch-receptor-mediated proprioception in B-class neurons forms the fundamental oscillatory mechanism of the model. Each DB (VB) neuron integrates stretch-receptor currents from the dorsal (ventral) side, both locally and posteriorly, along its axon. Finally, all electrical synapses except those between AVB and VB/DB are neglected in our model. Indeed, a modeling study on the role of inter-muscle coupling (Boyle and Cohen, 2008) suggested that the coupling may be too weak to have any observable effect and our simulation experiments found that electrical coupling among adjacent motoneurons was similarly insignificant in the present model (data not shown).

Motor neurons

Motivated by electrophysiological recordings of RMD motor neurons in the head (Mellem et al., 2008), we model B-class neurons as binary bistable elements. For simplicity, a binary variable S = {0, 1} denotes off and on states (and abstractly represents polarized and depolarized membrane potentials). Each B-neuron turns on in response to a supra-threshold input signal which includes internal activation from stretch receptors (see below) and synaptic inputs. B-neurons turn off when this signal falls below some threshold. Hysteresis is implemented by making the activation/deactivation threshold state dependent (see arrows in Figure 7A). Given the short time scale of RMD neurons, which we estimate to be ≤10 ms (see Figure 2 of Mellem et al., 2008), it is reasonable to model these neurons as instantaneous.

The state variables for model B-class neurons are given by

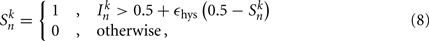
where 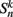is the neuronal state variable for the nth neuron on side k; ∈_hys sets the width of the hysteresis band; and 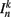is the total input (or “electrical current”) into the neuron in question. Hysteresis is achieved by introducing state-dependent activation and deactivation thresholds 0.5(1 ± ∈_hys). This prevents oscillations of arbitrarily small amplitude and, in conjunction with the stretch receptor weight, controls the extent of body bending. Each D-class neuron is excited by a single B-class neuron and assumed to respond instantaneously (with state ).

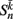The input term 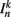for B-class neurons is given by

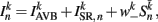
where 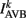(a constant input current from forward locomotion command interneurons AVB) differs for dorsal and ventral neurons; 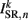is the stretch receptor (SR) current; and 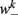sets the inhibitory (GABAergic) synaptic weight. Note that only ventral neurons receive inhibitory synaptic inputs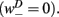

Stretch receptors

Mechanosensory feedback and its importance in the regulation of locomotion has been reported in C. elegans interneurons (Li et al., 2006). While direct evidence for proprioception is still lacking in the motoneurons themselves, mechanosensitive stretch receptor channels have long been postulated to exist in B (and A) class motoneurons. This suggestion was originally motivated by the morphology of these neurons, specifically their long, posteriorly directed undifferentiated processes on which no synapses are found (White et al., 1986). Indeed, the stretch receptor hypothesis is widely recognized as an attractive and plausible conjecture (Riddle et al., 1997; Tavernarakis et al., 1997; Bryden and Cohen, 2004, 2008; O’Hagan and Chalfie, 2005; Karbowski et al., 2008) and forms the basis of our model. The proposed mechanosensitive channels in these processes would respond to the changes in length associated with body bending. In our model, stretch receptors integrate over local and posterior body segments, in line with the anatomy.

The stretch receptor current

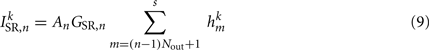
sums over contributions from a number of segments m of the physical model, where s = min{M; N_SR + (n − 1) N_out} sets the number of segments sensed to either N_SR or to the number of remaining posterior segments. A prefactor

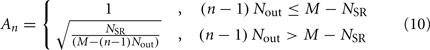
compensates for the variable number of contributing segments. The conductance parameter G_SR,n increases linearly from head to tail to compensate for the decreasing curvature of undulations down the worm, imposed by the gradient in muscle efficacy. Finally, 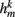is the effective stretch receptor activation function. We allow the stretch receptor conductance to generate a depolarizing response to stretch and a polarizing response to compression, relative to the local segment resting length. (A similar effect could be achieved in the worm with stretch sensitive channels that are partially open at the rest length.) For simplicity, we take this function to be linear (bilinear) on the ventral (dorsal) sides:

where L_0L,m is the segment rest length and 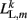is the current length of the kth side of the mth segment. Here,

is required due to the elliptical shape (and variable radius) of the body, and

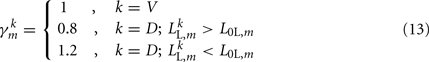
modifies the dorsal stretch receptors to ensure that the worm will move straight despite the asymmetry in the neural circuit.

Conductance-based neurons

The neural model presented above makes use of two key simplifications, namely treating the neurons as binary and instantaneous. However, it could certainly be argued that a mechanism that works with simple binary neurons would not necessarily work with more realistic continuous-valued (and non-instantaneous) neurons. To validate the binary model, we developed a conductance-based model of the B-class neurons based on the RMD dynamics presented in Mellem et al. (2008).

We begin by replacing the binary neural states 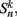which were updated according to equation (8), with continuous-valued membrane potentials 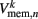which evolve according to

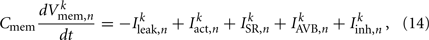
where C_mem is the membrane capacitance, and the individual terms in these equations are as follows:

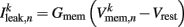
is the leak current, where G_mem and 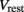are the membrane leak conductance and reversal potential respectively.

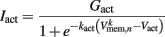
is a state dependent self-exciting current responsible for the bistability, with a maximum conductance G_act and activation function parameters k_act and .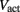

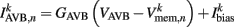
is the external AVB input, where G_AVB is the corresponding gap junction conductance, V_AVB is the AVB membrane potential; the bias current 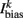is responsible for breaking symmetry between dorsal and ventral neurons (and is set to 0 dorsally). The inhibitory input is set to 0 dorsally and is given by

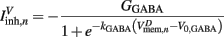
on the ventral side, where G_GABA is the maximum synaptic conductance for neural inhibition and k_GABA and 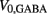are the corresponding activation parameters. Finally, the muscle inputs that would otherwise be given by equation (16) are replaced by

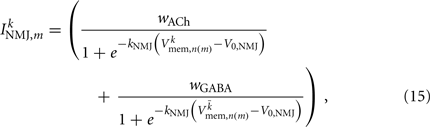
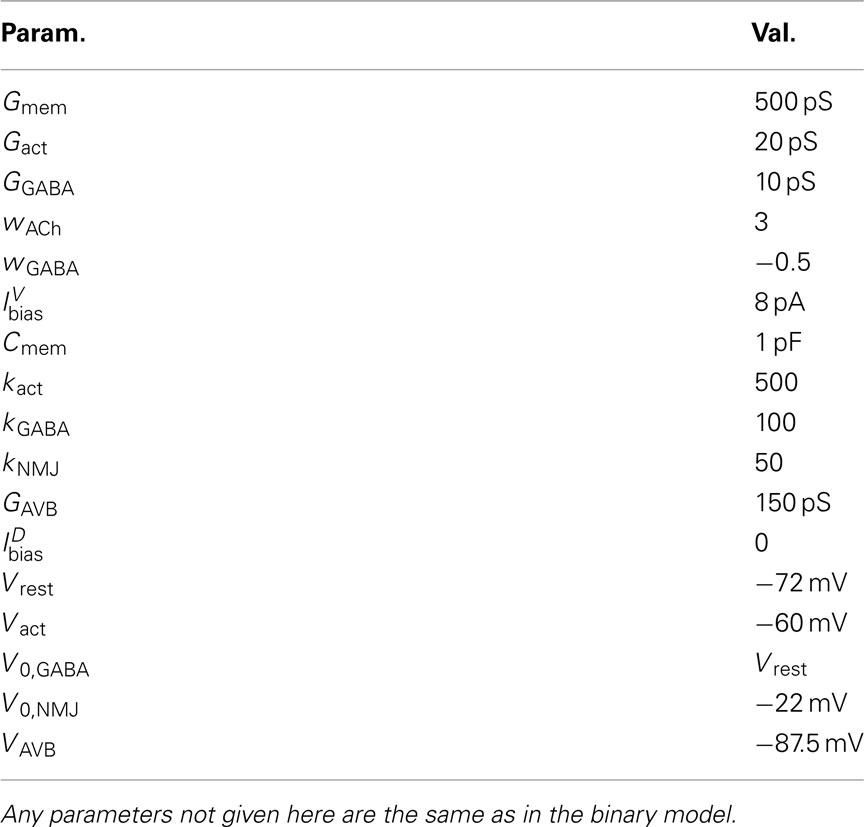
where the w_ACh and w_GABA set the weights of the excitatory (ACh) and inhibitory (GABA) neuromuscular junctions, and the parameters V_0,NMJ and k_NMJ determine the NMJ activation function. Parameter values for the conductance-based model are given in Table 2.

TABLE 2

Table 2. Continuous model parameters.

Muscle electrophysiology

Ventral (dorsal) muscle cells m receive both excitatory and inhibitory current inputs from the local VBn (DBn) and VDn (DDn) motor neurons n(m) = ceil[m/N_out] (with each neuron outputting to N_out = 4 muscles). The total input “current” to the muscles is therefore given by

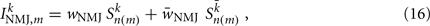
where w_NMJ are the excitatory neuromuscular junction (NMJ) weights and 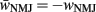denote the strength of GABAergic muscle inhibition by D-class neurons (Table 3).

TABLE 3

Table 3. Parameters of the neuromuscular model.

Muscles respond as leaky integrators with a characteristic time scale of τ_M = 100 ms, which crudely agrees with response times of obliquely striated muscle (Milligan et al., 1997). The muscle activation is represented by the unitless variable 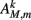that evolves according to

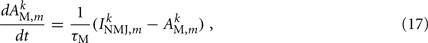
where 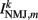is the total current driving the muscle.

2.4. Numerical Methods

The model was implemented in C++ and uses a freely available implicit solver (SUNDIALS IDA 2.3.0; Hindmarsh et al., 2005) as a physics engine. The neuromuscular system was solved by Euler integration (with a 1 ms step); the Sundials physics solver used adaptive time steps with a base relative error tolerance of 10⁻¹² and absolute spatial tolerances of 10⁻⁹ for the coordinates and 10⁻⁵ for rod angles. For less resistive media C_|| ≤ 27.3 × 10⁻⁶ kg·s⁻¹ or C_⊥ ≤ 51.2 × 10⁻⁶ kg·s⁻¹, all tolerances were reduced by a factor of 10.

3. Results

Having developed our neuromechanical model of C. elegans forward locomotion, the first key question is to what extent this model can capture swimming and crawling behaviors in different physical environments. In particular, one would expect that placing model worms in different virtual environments would result in different motor behaviors, but it is not clear a priori what range of motor behaviors can be obtained in this way. For example, what would a model that was optimized for replicating crawling behavior yield when placed in virtual water, or vice versa? And are two different parameter sets needed to generate crawling and swimming patterns? If so, some form of neural or muscular modulation mechanism may need to be conjectured to account for parameter changes.

3.1. A Single Neural Mechanism Accounts for Swimming and Crawling

We find that a single model with a single set of parameters is able to reproduce both crawling and swimming with realistic undulation frequencies and waveforms (Figures 4B and 5A,C; Movie S2 in Supplementary Material). Crucially, this is accomplished without any explicit modulatory mechanism (beyond proprioceptive feedback). Indeed, the only changes necessary to obtain these different behaviors are to the effective drag coefficients that define the model environment. We conclude that a single, fixed neural circuit is sufficient to model both behaviors, without recourse to neuromodulation, additional sensory input to head neurons, or variations in proprioceptive fields or properties.

FIGURE 4

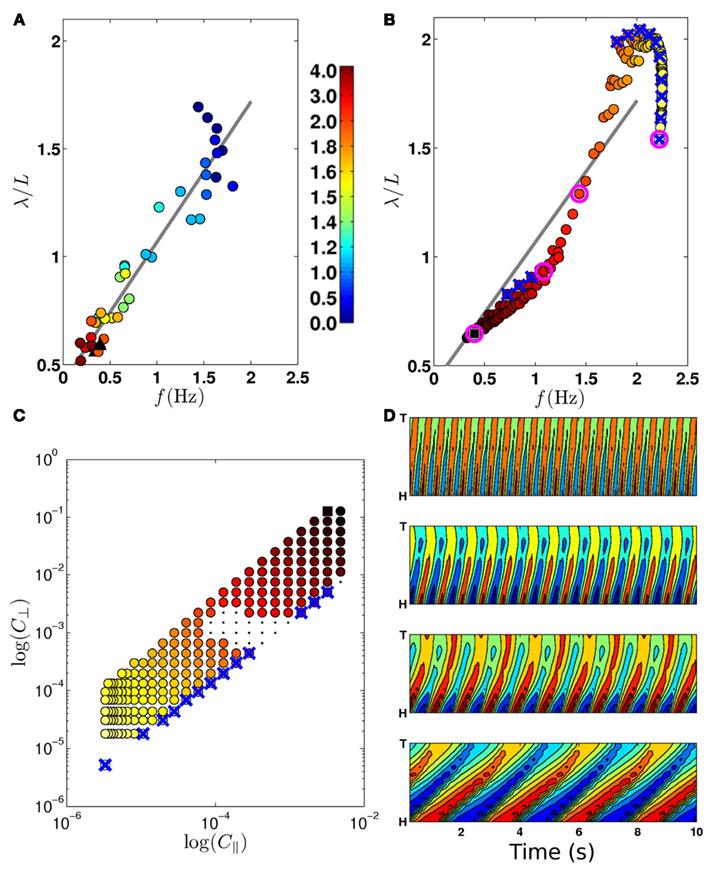
Figure 4. (A) Experimentally observed transition from swimming to crawling, from Berri et al. (2009), showing locomotion in gelatin (circles; color bar indicates percent gelatin concentrations) and agar (black triangles). (B) The swim-crawl transition. The model reproduces the smooth regulation of undulation frequencies and wavelengths with good quantitative agreement [colors as in (C)]. Selected points used in (D) are highlighted with pink circles. Wave properties are extracted as described in Berri et al. (2009). (C) Values of C_|| and C_⊥ used to evaluate the swim-crawl transition (1.5 ≤ K ≤ 40). Colors denote the product C_|| × C_⊥, ranging from light yellow (virtual water) to dark red (virtual agar). Newtonian environments (K = 1.5) are marked with blue crosses, as are the corresponding points in (B). A few combinations of drag coefficients yielded uncoordinated behavior (black dots), and were omitted from (B). (D) Contour plots for locomotion in (from top) water, two intermediate environments and agar. The plots show the local curvature (color) along the worm (vertical axis) and in time (horizontal axis).

FIGURE 5

Figure 5. Selected stills showing behavior of the integrated model in, virtual water (A), intermediate gelatin (B), and agar (C). The corresponding movie clips are available in Supporting Information (Movie S2 in Supplementary Material). The time (in seconds) for each frame is given in the top right hand corner. Note the different time intervals between stills in (A) versus (B) and (C).

How does the same model generate both crawling and swimming patterns? To understand the common oscillatory mechanism underpinning these behaviors, it is helpful to follow an oscillation in a single neural unit connected to a section of body. Consider such a system that is initialized with both DB and VB states off, with the body shape completely straight. Switching the AVB input on drives VB above its activation threshold, and causes the ventral muscles to contract, stretching the dorsal side. At some point the dorsal stretch will be sufficient to activate DB and VD. Ventral inhibition resets VB (switching it off). At this stage bending will reverse, with the dorsal side contracting and the ventral side stretching, until the dorsal contraction drops the input to DB below the deactivation threshold, turning it off and indirectly releasing VB from inhibition. Note the importance of dorso-ventral asymmetry that allows the ventral side to be activated first and to de-activate only in response to ventral inhibition (with AVB on).

For the oscillation to propagate down the length of the body, some form of coupling among units is required. In our model, the neural units are indirectly coupled through the shape of the body (i.e., through posterior stretch receptors) and through the physical properties of the body and environment. The relative importance of these contributions depends on the properties of the medium (Boyle, 2010; Fang-Yen et al., 2010). First let us consider highly resistive environments, such as agar. With the body initialized along a straight line, as above, all VB neurons are on. During forward motion, the worm’s body exhibits a decreasing undulation amplitude from head to tail. Accordingly, in the model, ventral muscles exert a contractile force with a decreasing gradient toward the tail. Thus the head is the most strongly activated and will bend first, pulling the worm forward slightly and allowing more of the body to bend. Sufficient bending of the head will eventually activate dorsal neurons and bending will reverse. It is the delay in bending (rather than in actuation) imposed by strong lateral drag forces that gives rise to the crawling wavelength. In less resistive media such as water, neural units cannot rely on physical coupling via the environment for entrainment, so the synchronizing effect of non-local stretch receptor signals must determine the spatial wavelength.

To test the above reasoning we used the model to experiment with variable length stretch receptor fields in B-class motor neurons. Comparison of Figure 6 to Figure 4D confirms that forward crawling (but not swimming) can be generated by a model with exclusively local proprioceptive feedback. Thus the model predicts that shortening the distal processes of B-class neurons through laser axotomy or mutation would lead to a locomotion defect that is significantly more pronounced in less resistive media like water.

FIGURE 6

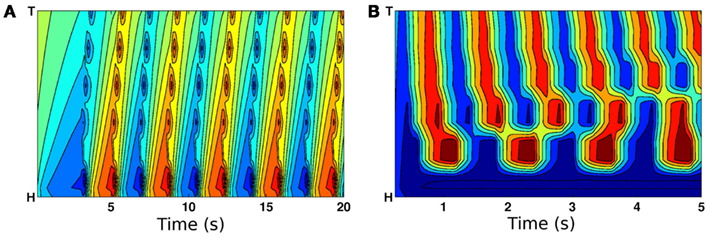
Figure 6. Curvature plots showing the effect of eliminating posterior stretch receptor input such that feedback is from local segments only. (A) On virtual agar, model worms still propagate coordinated waves from head to tail. (B) In contrast, locomotion in water is highly uncoordinated.

3.2. Increasing Fluid Viscosity or Viscoelasticity is Sufficient to Account for the Swim-crawl Transition

Having developed a model that can swim and crawl, we performed simulations of the same model in a range of additional model environments and compared our results with experimental data. In the model, fluid environments are represented by local drag coefficients resisting motion tangential (C_||) and normal (C_⊥) to the local body surface. In Newtonian environments, the ratio K = C_⊥/C_|| is constant. More general, viscoelastic environments (like gels), are also well described by a pair of drag coefficients, but the ratio K can vary. We tested our model in a range of viscous and viscoelastic model environments.

First, we sought to test the model’s swim-crawl transition. This transition has been experimentally mapped in gelatin solutions with different concentrations (Berri et al., 2009), and is characterized by a smooth and monotonic frequency-wavelength relation (Figure 4A). Our model is also capable of intermediate behaviors (Figures 4D and 5; Movie S2 in Supplementary Material) and follows a similar frequency-wavelength relation (Figure 4B) across a large class of intermediate environments, qualitatively reproducing the smooth swim-crawl transition. Thus, we find that the entire swim-crawl transition can be modeled by a single (fixed parameter) neuromechanical system that is being modulated purely by modifying the drag coefficients of the fluid environment.

A waveform modulation similar to that reported by Berri et al. (2009) for viscoelastic media was consequently reported also for increasing viscosities (Fang-Yen et al., 2010; Shen and Arratia, 2011). It is therefore natural to ask whether the model could also generate a swim-crawl transition in Newtonian media of increasing viscosity. Figures 4B,C confirm that, in the model, Newtonian media can modulate the waveform and kinematics of the locomotion, similarly to the modulation observed in viscoelastic media.

Combined, these results suggest that it is the resistivity of the medium, rather than the ratio of drag coefficients that modulates the waveform and kinematics of locomotion. Such a conclusion would be consistent with our previous observation (Berri et al., 2009) that the worm can generate crawling-like undulations even in isotropic environments with K ≈ 1.

3.3. The Model Reproduces Observed Locomotion Dynamics in Artificial Dirt Environments

While in the lab C. elegans is studied mostly on agar environments, its natural habitat is far more heterogeneous and likely to include many solid obstacles. Studying locomotion in complex environments can inform our understanding of the worm’s behavior in more natural environments. Furthermore, studying the worm’s response to solid obstacles can shed light on its proprioceptive mechanisms and closed-loop motor control. In particular, arrays of microfluidic posts (“artificial dirt”) have recently been developed specifically for this purpose (Lockery et al., 2008; Park et al., 2008). We recreated model microfluidic chambers with the same quasi-2D hexagonal arrays as in Lockery et al. (2008) and cubic arrays as in Park et al. (2008) and used these to perform simulations of our integrated model. We find that the model copes well with these environments, producing remarkably realistic locomotion when compared to the reported behavior (Lockery et al., 2008; Park et al., 2008). Specifically, as in the experiments, the model yields crawling behavior in the hexagonal post configuration (Movies S3–S5 in Supplementary Material; Lockery et al., 2008) and swimming like motion in the cubic configuration (Movie S6 in Supplementary Material; Park et al., 2008).

To investigate whether the difference in behavior can be attributed to the layout of the posts or increased resistance, we performed simulations with variable post sizes and inter-post separations; with either water- or agar-filled chambers; and with or without an effective ceiling (Lockery et al., 2008). We found that both the post layout and the properties of the filler medium can affect the locomotion behavior. When the filler medium has low resistance (i.e., water) the undulation frequency is high, but the amplitude and wavelength depend on the post layout (Movies S7–S9 in Supplementary Material). In contrast, when the filler medium is highly resistive (i.e., agar) the behavior tends to be crawling-like. In cases where the post layout is roughly compatible with crawling, the locomotion waveform adapts to these constraints (Movie S10 in Supplementary Material). However, when the layout is not compatible, the posts essentially become obstacles (Movie S11 in Supplementary Material).

3.4. The Model Reproduces Contact Forces

One advantage of a fully integrated neuromechanical model is its physical grounding that can be tested against measurable properties or even actual force measurements. Indeed, the force exerted by C. elegans as it moves against a microfluidic pillar was recently reported to be 2.5 ± 2.5 μN (Doll et al., 2009). Recreating the same setup in our model, we obtain a value of F = 0.84 ± 0.22 μN for the mean peak contact force when the worm touches a pillar in model simulations. This value is totally consistent with the experimentally reported value, which is particularly remarkable when considering that parameters in our physical model were chosen purely on the basis of estimates of environmental properties and behavioral observations (Sauvage, 2007).

3.5. Bistable Neuromuscular Control is Essential for Sustaining Proprioceptively Driven Undulations across the Range of Observed Behaviors

Previous models of locomotion have typically assumed graded potential neurons (Niebur and Erdös, 1991; Karbowski et al., 2006; Bryden and Cohen, 2008), in line with available data at the time (Goodman et al., 1998; Nickell et al., 2002; Francis et al., 2003; O’Hagan et al., 2005). In fact, the richness of neuronal dynamics has only recently come to light (Mathews et al., 2003; Suzuki et al., 2003; Mellem et al., 2008). In particular, the finding of bistable motoneurons with discrete membrane potential states (Mellem et al., 2008) suggests that motor control circuits may be modeled as a network of binary motoneurons with hysteresis.

Bistability introduces memory into the system, allowing neurons to respond differently to inputs when the body is bending one way or the other. This allows the system to generate robust oscillations with a broad range of frequencies (here, ≈0.5–2 Hz) that depend on the physical load. Indeed, in the absence of such bistability (or explicit modulation of the neuronal properties), one would expect oscillations to occur only over a relatively narrow range, determined by the interplay between relevant neuronal time constants.

In our model bistability is implemented by modeling B-class neurons as binary entities with bistable activation functions (see Figure 7). This simplification approximates the behavior of RMD neurons as reported in Mellem et al. (2008). The strong non-linearity imposed by binary threshold elements (even without bistability) turns the B-neurons into on-off elements and ensures on-off switching of inputs to the muscles, and hence anti-phase (dorso-ventral) muscle contractions that are entrained to the neurons. Interestingly, previous models of locomotion have introduced non-linearities elsewhere in the locomotion circuit. In the case of Bryden and Cohen (2008) for example, stretch receptor conductances have strong non-linearity that effectively leads to “on-off” neuronal states, even though the underlying equations were of a graded potential neuron. The introduction of bistability into the stretch receptor conductances, or indeed into any of a number of components of the model, may lead to similar network dynamics that can robustly adapt to a range of physical environments.

FIGURE 7

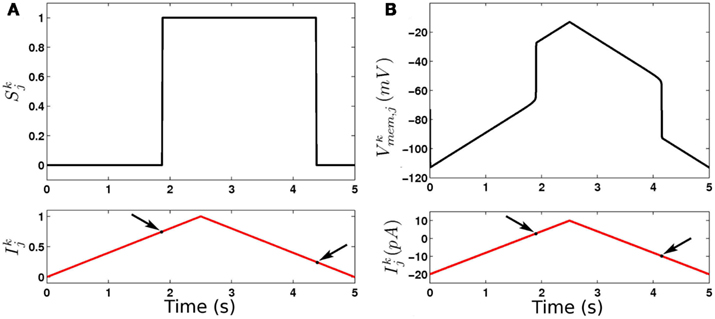
Figure 7. Dynamics of binary (A) and continuous (B) model B-class neurons. Note the different thresholds for activation and deactivation (arrows).

3.6. Bistable Neural Dynamics Are Consistent with Recent Recordings of NMJ Currents

While the relative simplicity of the binary model makes it preferable to use for most of our simulations, certain questions remain outside its scope. Specifically, the simplified dynamics of the binary neurons, with discrete on and off states, makes it impossible to evaluate their behavior against electrophysiological data in a meaningful way. A recent publication by Liu et al. (2009) provides the first characterization of the C. elegans body wall neuromuscular junction (NMJ) response to optogenetic activation and inhibition of B-class neurons.

In their experiments, Liu et al. used channelrhodopsin, a light activated depolarizing ion channel, to stimulate the presynaptic B-class neuron with light of increasing intensity, and recording the response current in the muscle cells. They found that the postsynaptic current increases smoothly as shown in Figure 8A. Liu et al. also used halorhodopsin, a light activated hyperpolarizing ion channel, to inhibit the presynaptic neuron, finding that the postsynaptic current is reduced. Looking at these results, the obvious interpretation is that the cholinergic motor neurons exhibit tonic, graded release of neurotransmitter at resting membrane potential that can be up- and down-regulated by membrane potential. This elegant result is an important contribution to understanding (and modeling of) this and other neural circuits in C. elegans. Moreover, the results might be taken to suggest that the motor neuron membrane dynamics are similarly graded. Indeed, had the neurons fired classical all-or-nothing action potentials then one might expect the postsynaptic currents to be similarly binary, or at least strongly non-linear. It might appear, therefore, that the findings of Liu et al. (2009) do not support the model proposed here.

FIGURE 8

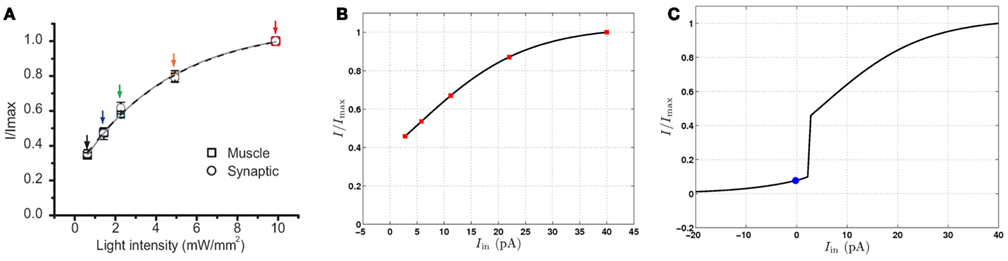
Figure 8. Postsynaptic currents in response to excitation of motor neurons, normalized by the maximum current. (A) Postsynaptic currents in response to light stimuli (reproduced with permission from Liu et al., 2009). Symbols indicate experimental data points and the solid lines are the best single exponent fits. (B) Postsynaptic currents at the conductance-based model NMJ in response to depolarizing current injection to a VB motor neuron. Red squares highlight specific points for comparison with (A). (C) Postsynaptic response of the conductance-based model to hyperpolarizing and depolarizing currents. The blue circle indicates the postsynaptic current at the neuron’s rest potential. Limited up- and down-regulation of the membrane potential in either the “on” or “off” state will result in smooth modulation of the postsynaptic current.

To examine this apparent inconsistency, we developed a conductance-based model of B-class neurons (see Section 2.3). Using this neural model and a simpler, rectangular body model, we were able to demonstrate reasonably realistic locomotion in water and on agar (Boyle, 2010), confirming that the locomotion mechanism presented here does not depend on the binary approximation.

Like the binary model, here too B-class neurons exhibit rapid (though not instantaneous) switching between low and high membrane potentials. However, the binary discrete “on”/“off” states are replaced by continuous-valued ranges of membrane potentials (Figure 7).

Using this conductance-based model, we compared the behavior of our continuous neural model (Figure 8B) to the data (Liu et al., 2009; Figure 8A). Specifically, we compared the postsynaptic current in the real and virtual muscles, measured as a function of the presynaptic current stimulus or light intensity. We find that, despite the strongly non-linear response in the B-class model neurons, there exists good quantitative agreement with the reported experimental currents. Figure 8C shows that the postsynaptic current in the model also decreases significantly in response to presynaptic hyperpolarization, in line with the experimental finding of tonic neurotransmitter release. While this model cannot be used conclusively to infer a single model of B-class neurons (or even to rule out passive behavior of these neurons), we can conclude that the data of Liu et al. (2009) are consistent with the bistable B-class neuron dynamics.

3.7. The Model Predicts a Role for GABAergic D-Class Neurons in Forward Locomotion

In the worm’s ventral cord locomotion circuit, cholinergic neurons of class B and A mediate forward and backward locomotion respectively. The only inhibition in this circuit is mediated by D-class GABAergic neurons. Individual D-class neurons receive input from both A- and B-class neurons. They inhibit muscles, and in some cases also motoneurons of class D, on either side, and of classes A and B, on the ventral side only (Chen et al., 2006; Boyle, 2010). The connectivity diagram of these inhibitory D-class neurons suggests involvement in both forward and backward locomotion (White et al., 1986; Chen et al., 2006). The function of D-class neurons can be knocked out through mutation of genes required in the GABA pathway (McIntire et al., 1993b), by targeted killing of D-class neurons (Walthall et al., 1993) and by laser axotomy (Yanik et al., 2004), yielding essentially the same so-called shrinker phenotype (Hodgkin, 1983) in all cases: When touched on the head, wild type worms will back up, whereas worms whose GABA pathway is defective will contract muscles along both sides of their bodies. Thus, D-class neurons are implicated in backward motion, or at least its initiation. In contrast, forward locomotion in these mutants or D-ablated worms is described either as wild type (Walthall et al., 1993; Yanik et al., 2004), or nearly wild type with a reduction in amplitude (McIntire et al., 1993b). This leads to the commonly held conclusion that D-class neurons are not essential for forward locomotion.

We therefore investigated the effect of removing inhibition from our model. We find that removing all inhibition in our model leads to grossly normal crawling behavior on model agar, but a total inability to swim in water (Movies S12 and S13 in Supplementary Material). At first sight, this model result may appear in stark contradiction to experimental data. In fact, in every case where forward locomotion of GABA pathway defective worms was reported (McIntire et al., 1993b; Walthall et al., 1993; Yanik et al., 2004), the assay was performed on agar. Our model therefore makes a novel prediction that these worms are forward swim-defective.

Further analysis of the swim-defective model phenotype suggests that in the model, it is neural inhibition (of VB by VD neurons) that is responsible for the swim-defective phenotype. This effect is consistent with our description of the oscillation mechanism which requires inhibition of VB neurons to switch them off when the dorsal side is activated. Recall that in our model, we have introduced asymmetries in the parameters of the ventral and dorsal neurons that allow ventral (VBn) but not dorsal (DBn) neurons to switch on even when the worm is completely straight. During crawling, the delay imposed by the physical interactions between the body and environment allows the ventral side of the body to contract sufficiently to switch the VB neurons off, even in the absence of neural inhibition. However, during swimming, the low resistivity of water no longer allows VB to reset except via neural inhibition. Interestingly, muscle inhibition does not appear to offer an appropriate resetting mechanism in the context of a sensory feedback based oscillatory mechanism in which B-class neurons are depolarized in response to local stretch (Boyle, 2010). The role of a resetting mechanism is to ensure that when a given neuron becomes depolarized, its opposite counterpart is immediately repolarized – something that is easily achieved through direct neural inhibition. In contrast, if the opposite muscle is inhibited instead, the resulting relaxation would indirectly depolarize the opposite neuron (via stretch receptors) thus delaying, rather than accelerating, its repolarization.

4. Discussion

We have presented a fully integrated, biologically and physically grounded model that accounts for C. elegans locomotion in a variety of media ranging from water to agar, and in complex environments such as artificial dirt. The model was motivated by the recent finding that swimming, crawling, and a continuum of intermediate locomotion waveforms represent different manifestations of the same fundamental behavior in different physical environments (Berri et al., 2009; Fang-Yen et al., 2010; Boyle et al., 2011). These findings strongly suggested that a single underlying neural mechanism is at work, and posed a clear challenge to generate a model of the neural control of locomotion that is valid across more than a single environment.

Mechanisms of gait modulation in other model systems can include gradual recruitment of neurons into an active pool (Li et al., 2007) and local modulation of the appropriate pattern generating circuits (Harris-Warrick, 1993). In C. elegans, the sparsity of motoneurons along the ventral cord of the animal appears to preclude the former possibility, suggesting that the range of observed behaviors results from the modulation of a single circuit.

Here, we have demonstrated that a model with ascending proprioceptive control is sufficient to generate most of the observed behaviors. In this model, the worm’s forward locomotion requires neither central pattern generated control nor additional head circuitry. Nor does our model require any modulation of the neuronal or circuit parameters. Rather, the adaptation of the waveform in different media requires only indirect modulation via the physical response of the body to the environment. The modulation of the neural control circuit is then accomplished solely via proprioceptive integration of the different body shapes.

This novel mechanism is neurally economical and produces robust locomotion in extremely varied environments. Thus, the model here highlights the added insight that can be gained by studying the worm’s locomotion nervous system in the context of its physical embodiment. Of course, the sufficiency of this circuit and circuit mechanism in no way rules out a range of other likely contributions to the locomotion system, including participation of other ventral cord motor neurons (e.g., of classes AS and VC), effects due to the largely independent head motor circuit, and indeed contributions from neuromodulation (Sawin et al., 2000). That said, this model points to the power of proprioceptive modulation in this system and predicts that the worm’s forward locomotion should be robust to defects in these other circuit mechanisms.

Our model contains a number of essential ingredients. First, to adapt the neural activity patterns to the different media, the proprioceptive (or stretch receptor) signal must span a sufficient length of the body. Previously, the necessary extent of proprioceptive receptive fields has been considered only for crawling-like motor patterns (Niebur and Erdös, 1991; Bryden and Cohen, 2008), but we find that our model requires integration of proprioceptive inputs over up to half a body length. Indeed, our model suggests that the length of this receptive field should be determined by the longest (i.e., swimming) wavelength of undulations. That said, B-class axons in C. elegans do not extend to half a body length, suggesting additional mechanisms may be at play. For example, modifications to body properties, different stretch receptor distributions and (possibly non-linear) conductances, and additional proprioceptive pathways (other than via B-neurons) may all contribute to reducing the minimum required receptive field.

Secondly, some bistability is essential in our model to support the dynamic range of undulation frequencies. In line with data on RMD neurons, we have chosen to implement such bistability via state-dependent activation and deactivation of the B-class motor neurons. In addition, some form of strong non-linearity is likely to be needed somewhere along the neuromuscular pathway to avoid muscle co-activation on the two sides of the body. In other words, for wild type worms performing forward locomotion it is reasonable to expect that when one side is contracting, the other side should relax. In fact, RMD neurons exhibit such strong non-linearities, and we conjecture that B-class neurons may exhibit similar behavior. Thus, we have implemented bistability by defining binary activation states of B-class motor neurons. To validate these assumptions against available data (Liu et al., 2009), we also presented a complementary conductance-based model of B-class neurons. The ability to fine tune the activation of motor neurons within effective bands of “off” and “on” activation states may confer important advantages to the worm in richer, more realistic forms of motor pattern generation. However further experiments would be needed to ascertain whether B-class neurons exhibit any bistable behavior.

Finally, our model achieves robust proprioceptively driven pattern generation that is not reliant on independent head oscillations and can initiate locomotion from any initial worm conformation. To do so requires some asymmetry between the ventral and dorsal sides. In our model, we have chosen to instantiate that asymmetry by a lower activation threshold of the ventral side. Consequently, an additional mechanism must be invoked in order to reset the activation of the ventral side. Perhaps surprisingly, muscle inhibition by D-class neurons is not likely to perform this role (Boyle, 2010). By contrast, neural inhibition could in principle provide a suitable mechanism and would be interesting to investigate further experimentally. Specifically, if neural inhibition is responsible for VB resetting then our model predicts that GABA-null worms should experience strong defects in forward swimming, but not necessarily in crawling. Alternatively a range of other mechanisms could be involved in resetting neuronal states on one or both sides of the body. Of those, perhaps the most likely involves activity dependent changes in neuronal excitability or in neurotransmitter release (Liu et al., 2009). Other mechanisms, involving other inhibitory pathways (other than VD to VB inhibition) or even modified body properties may contribute to the predicted asymmetry.

Our model prediction that the extent of uncoordinated locomotion is medium dependent suggests that certain defects (such as removal of inhibition) should lead to very little or no phenotype on agar and to severe defects in water. This discrepancy arises from a purely mechanical perspective, which leads to qualitatively different views of swimming and crawling (Fang-Yen et al., 2010). During crawling, mechanical load by the external medium helps to support the body shape and facilitates the generation of thrust. Thus, sufficiently minor defects in the locomotion nervous system may be masked or disguised. During swimming, external load is insufficient, suggesting that defects in mechanisms that contribute to locomotion may be more apparent.

The generation and propagation of sinuous undulations along the body axis is arguably one of the simpler motor behaviors orchestrated by C. elegans, and yet even this behavior is not yet fully understood. Our integrated neuromechanical model proposes a possible circuit mechanism that accounts for the worm’s forward locomotion in a range of uniform and heterogeneous physical environments. The model highlights the ability of biological systems to exploit their physical environments in order to achieve effective and robust locomotion and sheds light on the neural mechanisms that would be needed to achieve this. Further work will build on our understanding of forward locomotion control to study more complex motor pattern generation that may require additional neural mechanisms as well as contributions from other neural subcircuits.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank Ian Hope and Sophie Bamps for extensive discussions that were of great benefit to this work. Our research was made possible with funding from the EPSRC (EP/C011953/1 and EP/C011961/1) and BBSRC (BB/E008038/1).

Supplementary Material

The Movies S1–S13 for this article, along with the model source code S14, can be found online at http://www.frontiersin.org/computational_neuroscience/10.3389/fncom.2012.00010/abstract

References

Berri, S., Boyle, J. H., Tassieri, M., Hope, I. A., and Cohen, N. (2009). Forward locomotion of the nematode C. elegans is achieved through modulation of a single gait. HFSP J. 3, 186–193.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Borgmann, A., Hooper, S. L., and Biüschges, A. (2009). Sensory feedback induced by front-leg stepping entrains the activity of central pattern generators in caudal segments of the stick insect walking system. J. Neurosci. 29, 2972–2983.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Boyle, J. H. (2010). C. elegans Locomotion: and Integrated Approach. Ph.D. thesis, School of Computing, University of Leeds, Leeds.

Boyle, J. H., Berri, S., Tassieri, M., Hope, I. A., and Cohen, N. (2011). Gait modulation in C. elegans: it’s not a choice, it’s a reflex! Front. Behav. Neurosci. 5:10. doi: 10.3389/fnbeh.2011.00010

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Boyle, J. H., Bryden, J. A., and Cohen, N. (2008). “An integrated neuro-mechanical model of C. elegans forward locomotion,” in LNCS: Neural Information Processing, Part 1, Vol. 4984, eds M. Ishikawa, K. Doya, H. Miyamoto, and T. Yamakawa (Berlin: Springer-Verlag), 37–47.

Boyle, J. H., and Cohen, N. (2008). C. elegans body wall muscles are simple actuators. Biosystems 94, 170–181.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brenner, S. (1974). The genetics of Caenorhabditis elegans. Genetics 77, 71–94.

Pubmed Abstract | Pubmed Full Text

Bryden, J. A., and Cohen, N. (2004). “A simulation model of the locomotion controllers for the nematode Caenorhabditis elegans,” in From Animals to Animats 8: Proceedings of the Eighth International Conference on the Simulation of Adaptive Behavior, eds S. Schaal, A. J. Ijspeert, A. Billard, S. Vijayakumar, J. Hallam, and J.-A. Meyer (Cambridge: MIT Press/Bradford Books), 183–192.

Bryden, J. A., and Cohen, N. (2008). Neural control of Caenorhabditis elegans forward locomotion: the role of sensory feedback. Biol. Cybern. 98, 339–351.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chalfie, M., Sulston, J. E., White, J. G., Southgate, E., Thomson, J. N., and Brenner, S. (1985). The neural circuit for touch sensitivity in Caenorhabditis elegans. J. Neurosci. 5, 956–964.

Pubmed Abstract | Pubmed Full Text

Chen, B., Hall, D., and Chklovskii, D. (2006). Wiring optimization can relate neuronal structure and function. Proc. Natl. Acad. Sci. U.S.A. 103, 4723–4728.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Doll, J. C., Harjee, N., Klejwa, N., Kwon, R., Coulthard, S. M., Petzold, B., Goodman, M. B., and Pruitt, B. L. (2009). SU-8 force sensing pillar arrays for biological measurements. Lab Chip 9, 1449–1454.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fang-Yen, C., Wyart, M., Xie, J., Kawai, R., Kodger, T., Chen, S., Wen, Q., and Samuel, A. D. T. (2010). Biomechanical analysis of gait adaptation in the nematode Caenorhabditis elegans. Proc. Natl. Acad. Sci. U.S.A. 107, 20323–20328.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Francis, M. M., Mellem, J. E., and Maricq, A. V. (2003). Bridging the gap between genes and behavior: recent advances in the electrophysiological analysis of neural function in Caenorhabditis elegans. Trends Neurosci. 26, 90–99.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Goodman, M. B., Hall, D. H., Avery, L., and Lockery, S. R. (1998). Active currents regulate sensitivity and dynamic range in C. elegans neurons. Neuron 20, 763–772.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Grillner, S., and Wallén, P. (2002). Cellular bases of a vertebrate locomotor system-steering, intersegmental and segmental co-ordination and sensory control. Brain Res. Rev. 40, 92–106.

CrossRef Full Text

Harris-Warrick, R. M. (1993). Pattern generation. Curr. Opin. Neurobiol. 3, 982–988.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hill, A. A., Masino, M. A., and Calabrese, R. L. (2003). Intersegmental coordination of rhythmic motor patterns. J. Neurophysiol. 90, 531–538.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hill, A. V. (1938). The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. B Biol. Sci. 126, 136–195.

CrossRef Full Text

Hindmarsh, A., Taylor, A., and Serban, R. (2005). Sundials. Available at: http://www.llnl.gov/CASC/sundials/

Hodgkin, J. (1983). Male phenotypes and mating efficiency in Caenorhabditis elegans. Genetics 103, 43–64.

Pubmed Abstract | Pubmed Full Text

Karbowski, J., Cronin, C. J., Seah, A., Mendel, J. E., Cleary, D., and Sternberg, P. W. (2006). Conservation rules, their breakdown, and optimality in Caenorhabditis sinusoidal locomotion. J. Theor. Biol. 242, 652–669.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Karbowski, J., Schindelman, G., Cronin, C., Seah, A., and Sternberg, P. (2008). Systems level circuit model of C. elegans undulatory locomotion: mathematical modeling and molecular genetics. J. Comput. Neurosci. 24, 253–276.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kiehn, O., Harris-Warrick, R. M., Jordan, L. M., Hultborn, H., and Kudo, N. (1998). Neuronal Mechanisms for Generating Locomotor Activity, 1st Edn. New York: New York Academy of Sciences.

Li, W., Feng, Z., Sternberg, P. W., and Xu, X. Z. S. (2006). A C. elegans stretch receptor neuron revealed by a mechanosensitive TRP channel homologue. Nature 440, 684–687.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Li, W. C., Sautois, B., Roberts, A., and Soffe, S. R. (2007). Reconfiguration of a vertebrate motor network: specific neuron recruitment and context-dependent synaptic plasticity. J. Neurosci. 27, 12267–12276.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lighthill, J. (1976). Flagellar hydrodynamics. SIAM Rev. Soc. Ind. Appl. Math. 18, 161–230.

Liu, Q., Hollopeter, G., and Jorgensen, E. M. (2009). Graded synaptic transmission at the Caenorhabditis elegans neuromuscular junction. Proc. Natl. Acad. Sci. U.S.A. 106, 10823–10828.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lockery, S. R., Lawton, K. J., Doll, J. C., Faumont, S., Coulthard, S. M., Thiele, T. R., Chronis, N., McCormick, K. E., Goodman, M. B., and Pruitt, B. L. (2008). Artificial dirt: microfluidic substrates for nematode neurobiology and behavior. J. Neurophysiol. 99, 3136–3143.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mathews, E. A., García, E., Santi, C. M., Mullen, G. P., Thacker, C., Moerman, D. G., and Snutch, T. P. (2003). Critical residues of the Caenorhabditis elegans unc-2 voltage-gated calcium channel that affect behavioral and physiological properties. J. Neurosci. 23, 6537–6545.

Pubmed Abstract | Pubmed Full Text

McIntire, S. L., Jorgensen, E., and Horvitz, H. R. (1993a). Genes required for GABA function in Caenorhabditis elegans. Nature 364, 334–337.

CrossRef Full Text

McIntire, S. L., Jorgensen, E., Kaplan, J., and Horvitz, H. R. (1993b). The GABAergic nervous system of Caenorhabditis elegans. Nature 364, 337–341.

CrossRef Full Text

Mellem, J. E., Brockie, P. J., Madsen, D. M., and Maricq, A. V. (2008). Action potentials contribute to neuronal signaling in C. elegans. Nat. Neurosci. 11, 865–867.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Milligan, B. J., Curtin, N. A., and Bone, Q. (1997). Contractile properties of obliquely striated muscle from the mantle of squid (Alloteuthis subulata) and cuttlefish (Sepia officinalis). J. Exp. Biol. 200, 2425–2436.

Pubmed Abstract | Pubmed Full Text

Nickell, W. T., Pun, R. Y., Bargmann, C. I., and Kleene, S. J. (2002). Single ionic channels of two Caenorhabditis elegans chemosensory neurons in native membrane. J. Membr. Biol. 189, 55–66.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Niebur, E., and Erdös, P. (1991). Theory of the locomotion of nematodes: dynamics of undulatory progression on a surface. Biophys. J. 60, 1132–1146.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

O’Hagan, R., and Chalfie, M. (2005). Mechanosensation in Caenorhabditis elegans. Int. Rev. Neurobiol. 69, 169–203.

CrossRef Full Text

O’Hagan, R., Chalfie, M., and Goodman, M. B. (2005). The MEC-4 DEG/ENaC channel of Caenorhabditis elegans touch receptor neurons transduces mechanical signals. Nat. Neurosci. 8, 43–50.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Park, S., Hwang, H., Nam, S. W., Martinez, F., Austin, R. H., and Ryu, W. S. (2008). Enhanced Caenorhabditis elegans locomotion in a structured microfluidic environment. PLoS ONE 3, e2550. doi: 10.1371/journal.pone.0002550

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Petzold, B. C., Park, S. J., Ponce, P., Roozeboom, C., Powell, C., and Goodman, M. B. (2011). Caenorhabditis elegans body mechanics are regulated by body wall muscle. Biophys. J. 100, 1977–1985.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pierce-Shimomura, J. T., Chen, B. L., Mun, J. J., Ho, R., Sarkis, R., and McIntire, S. L. (2008). Genetic analysis of crawling and swimming locomotory patterns in C. elegans. Proc. Natl. Acad. Sci. U.S.A. 105, 20982–20987.

CrossRef Full Text

Riddle, D. L., Blumenthal, T., Meyer, B. J., and Priess, J. R. (eds). (1997). C. elegans II, 2nd Edn. New York: Cold Spring Harbour Laboratory Press.

Sauvage, P. (2007). Etude de la locomotion chez C. elegans et perturbations mecaniques du mouvement. Ph.D. thesis, Universite Paris, Paris.

Sawin, E. R., Ranganathan, R., and Horvitz, H. R. (2000). C. elegans locomotory rate is modulated by the environment through a dopaminergic pathway and by experience through a serotonergic pathway. Neuron 26, 619–631.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schafer, W. R. (2006). Proprioception: a channel for body sense in the worm. Curr. Biol. 16, R509–R511.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shen, X. N., and Arratia, P. E. (2011). Undulatory swimming in viscoelastic fluids. Phys. Rev. Lett. 106, 208101.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Suzuki, H., Kerr, R., Bianchi, L., Frokjaer-Jensen, C., Slone, D., Xue, J., Gerstbrein, B., Driscoll, M., and Schafer, W. R. (2003). In vivo imaging of C. elegans mechanosensory neurons demonstrates a specific role for the MEC-4 channel in the process of gentle touch sensation. Neuron 39, 1005–1017.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sznitman, J., Shen, X., Sznitman, R., and Arratia, P. E. (2010). Propulsive force measurements and flow behavior of undulatory swimmers at low Reynolds number. Phys. Fluids 22, 121901.

CrossRef Full Text

Tavernarakis, N., Shreffler, W., Wang, S., and Driscoll, M. (1997). unc-8, a DEG/ENaC family member, encodes a subunit of a candidate mechanically gated channel that modulates C. elegans locomotion. Neuron 18, 107–119.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wallace, H. R. (1969). Wave formation by infective larvae of the plant parasitic nematode Meloidogyne javanica. Nematologica 15, 65–75.

CrossRef Full Text

Walthall, W. W., Li, L., Plunkett, J. A., and Hsu, C. Y. (1993). Changing synaptic specificities in the nervous system of Caenorhabditis elegans: differentiation of the DD motoneurons. J. Neurobiol. 24, 1589–1599.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

White, J., Southgate, E., Thomson, J., and Brenner, S. (1976). The structure of the ventral nerve cord of Caenorhabditis elegans. Philos. Trans. R. Soc. Lond. B Biol. Sci. 275, 327–348.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

White, J., Southgate, E., Thomson, J., and Brenner, S. (1986). The structure of the nervous system of the nematode Caenorhabditis elegans. Philos. Trans. R. Soc. Lond. B Biol. Sci. 314, 1–340.

CrossRef Full Text

Yanik, M. F., Cinarm, H., Cinarm, H. N., Chisholm, A. D., Jin, Y., and Ben-Yakar, A. (2004). Neurosurgery: functional regeneration after laser axotomy. Nature 432, 822.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text