- IBM T. J. Watson Research Center, Yorktown Heights, NY, USA
High-frequency oscillations (HFOs) are an important part of brain activity in health and disease. However, their origins remain obscure and controversial. One possible mechanism depends on the presence of sparsely distributed gap junctions that electrically couple the axons of principal cells. A plexus of electrically coupled axons is modeled as a random network with bi-directional connections between its nodes. Under certain conditions the network can demonstrate one of two types of oscillatory activity. Type I oscillations (100–200 Hz) are predicted to be caused by spontaneously spiking axons in a network with strong (high conductance) gap junctions. Type II oscillations (200–300 Hz) require no spontaneous spiking and relatively weak (low-conductance) gap junctions, across which spike propagation failures occur. The type II oscillations are reentrant and self-sustained. Here we examine what determines the frequency of type II oscillations. Using simulations we show that the distribution of loop lengths is the key factor for determining frequency in type II network oscillations. We first analyze spike failure between two electrically coupled cells using a model of anatomically reconstructed CA1 pyramidal neuron. Then network oscillations are studied by a cellular automaton model with random network connectivity, in which we control loop statistics. We show that oscillation periods can be predicted from the network’s loop statistics. The shortest loop, around which a spike can travel, is the most likely pacemaker candidate. The principle of one loop as a pacemaker is remarkable, because random networks contain a large number of loops juxtaposed and superimposed, and their number rapidly grows with network size. This principle allows us to predict the frequency of oscillations from network connectivity and visa versa. We finally propose that type I oscillations may correspond to ripples, while type II oscillations correspond to so-called fast ripples.
Introduction
High-frequency oscillations (HFO) are ubiquitous in mammalian hippocampus in both physiological and pathological conditions (Engel et al., 2009; Bragin et al., 2010; Girardeau and Zugaro, 2011). HFO in the range of 80–200 Hz (ripples) are readily recorded in normal hippocampus of rodents and non-human primates, in vivo and in vitro (Buzsaki et al., 1992; Ylinen et al., 1995; Chrobak and Buzsáki, 1996; Maier et al., 2003; Skaggs et al., 2007). High-frequency ripples occur on top of sharp waves and they may be important for episodic memory consolidation in animals and humans (Buzsáki, 1998; Axmacher et al., 2008).
Pathological HFO in the range of 250–600 Hz (fast ripples) occur in hippocampus and parahippocampal structures in patients with mesial temporal lobe epilepsy (Bragin et al., 1999, 2002, 2010). These pHFO are recorded in dentate gyrus, hippocampus proper, and entorhinal cortex, and are used as biomarkers of foci of epileptic seizures.
The neuronal generators of normal and pathologic HFOs remain obscure (see Discussion). Coupling of axons by gap junctions can be the origin of hippocampal high-frequency oscillations, as suggested by experiments and simulations (Draguhn et al., 1998; Traub et al., 1999, 2001, 2002, 2010; Traub and Bibbig, 2000; Roopun et al., 2010, see reviews in Traub et al., 2011, and Traub and Whittington, 2010).
Gap junctions are ubiquitous in the nervous system (Söhl et al., 2005; Dere and Zlomuzica, 2011). In general, non-rectifying gap junctions are bi-directional and symmetric in their electrical conductance, although rectifying gap junctions are found, too (Phelan et al., 2008). In our model we assume that axons of pyramidal cells are sparsely coupled by non-rectifying gap junctions to form a random network (axonal plexus). Connections are strong, which means that a spike in one axon elicits a spike in another connected axon, without the need of multiple spike summation.
The model of axonal plexus can demonstrate rich patterns composed of growing and coalescing spatial waves (Traub et al., 1999, 2010; Lewis and Rinzel, 2000; Vladimirov et al., 2011). Under certain conditions the system oscillates, although the units (axons) are non-oscillatory intrinsically: only after their neighbor fires, they fire, too.
Oscillations in the network can be elicited in several ways. When units are connected by strong gap junctions, spontaneous spiking of random units generates externally driven oscillations due to birth and coalescence of multiple excitatory waves, similar to rain drops falling onto a still pond and making circular waves that grow in diameters with time. Essentially, spontaneous random inputs are multiplied in the network by creating waves of excitation. Wave dynamics determines the characteristic time scale, which sets the preferred oscillation period of the network. When waves meet, they coalesce (Traub et al., 2010). At sufficiently frequent spontaneous spiking of units, the system oscillates with frequency about 150 Hz (Traub et al., 1999). In the present paper, we call this oscillation mode “type I”; it requires highly conductive gap junctions (implying no spike propagation failures), and spontaneous random activations or external stimulation.
Alternatively, oscillations can be reentrant and self-sustained (type II). This can occur in a network containing a mixture of strong and weak gap junctions, if some axons elicit spike doublets. We further refer to gap junctions that fail to pass the second spike in a spike doublet as “weak” gap junctions. Failures on weak gap junctions break the symmetry of spike propagation: spike doublets remain doublets when they pass through strong gap junctions, but reduce to single spikes when they cross a weak gap junction. Propagation of a spike doublet in one direction and a single spike in another direction results in a single spike in the end, after 2 + 1 collision due to Hodgkin-Huxley properties of an axon. The surviving spike continues to travel and reenter around the loop if it is sufficiently long.
Reentrant oscillations due to symmetry breaking were predicted in networks of electrically connected axons (Lewis and Rinzel, 2000; Munro and Boergers, 2010) and were shown experimentally in crayfish axons in (Tseng et al., 2008). In their experiments, Tseng and co-authors stimulated an axon in an electrically coupled LG (lateral giant) network by paired spikes, and observed network oscillations with periods ranging from 2.99 ms (334 Hz) to 1.45 ms (686 Hz), corresponding to loops from 14 to 4 neurons, respectively. The effect of gap junction failure was also studied in simulations where neurons have hyperpolarized somatic voltage, lowered gap junction conductance, or both (Munro and Boergers, 2010). The axons which are highly connected to other axons (hubs) are more prone to gap junction failures, because they are more strongly shunted by their neighbors, and thus have longer refractory times.
Spikes can fail at weak gap junctions because of electrotonic properties of the latter. When spike doublet with short interspike interval (1–3 ms) is elicited in an axon, the second spike lies in the relative refractory period of the first, and it is affected by first spike’s remaining activation of K+ channels. This makes the second spike harder to elicit (more current required), lower in amplitude and propagation speed, and more prone to failure at gap junctions (Tseng et al., 2008). Effectively, an axon with a weak gap junction has a longer refractory time, if the spike comes through a weak gap junction.
In our model, heterogeneity in gap junction conductances introduces heterogeneity in axonal refractory times, which in turn leads to self-sustained reentrant activity around loops. If a network contains some weak gap junctions, a pair (or burst) of spikes at one axon can elicit self-sustained oscillations.
Frequency prediction for such oscillations is challenging, because large networks contain multiple loops juxtaposed and superimposed, and how the loop interactions contribute to the frequency of total network activity is non-trivial. We have analyzed several basic configurations of loops, and found that in most cases the smallest loop with a weak gap junction becomes the pacemaker which drives oscillations in longer loops by “injecting” spikes into them. This suggested the principle “smallest loop is the pacemaker”: the smallest loop that contains a weak gap junction drives the rest of the network. To prove the concept, we simulated random networks of electrically coupled axons where a fraction of gap junctions is weak. We used a cellular automaton model which simulates second spike failures by imposing longer refractoriness of axons with weak gap junctions. In those networks, we monitored the periods of self-sustained oscillations and the statistics of loop length distribution. To control the loop lengths, we designed an algorithm to break loops of defined lengths, and monitored the resulting periods of reentrant oscillations in networks altered in this way. In agreement with the proposed principle, the periods are set by the smallest available loops, confirming their role as the pacemakers of network oscillations.
Our work shows that the shortest loops of random networks determine the most likely period of reentrant network oscillations. The pacemaker loop must contain one weak gap junction or other kind of symmetry breaking, and it drives the rest of connected network. The period of oscillation around the pacemaker loop must, however, be longer than the refractory time of its slowest axon, which sets the minimum length of possible pacemaker loops.
Materials and Methods
Model of Anatomically Reconstructed Pyramidal Neuron
We used one of few available pyramidal neurons with anatomically reconstructed axonal (and dendritic) arbors, rat hippocampal CA1 neuron from NeuroMorpho database1. This cell was reconstructed from serial sections originally traced in (Tamamaki and Nojyo, 1991), using an automated procedure developed in (Scorcioni and Ascoli, 2005). The neuron morphology was imported by NEURON Import 3D tool and saved as template. The soma size was changed to L = 15, diam = 15 μm, axonal diam = 0.5 μm, dendritic diam = 1 μm. The neuron has 271 axonal and 195 dendritic sections, with total length of 51.5 and 13.5 mm, respectively. Originally the axon stemmed out from basal dendrite, which we changed to somatic attachment for simplicity.
Ionic conductances were inserted with parameters shown in Table 1, based on the thalamocortical column model described in Traub et al. (2005). Passive electrotonic properties were: membrane capacitance Cm = 0.9 μF/cm2, axonal membrane conductance gpas = 0.001 S/cm2 (Rm = 1000 Ωcm2), soma/dendritic membrane conductance gpas = 2 × 10−5 S/cm2 (Rm = 5 × 104 Ωcm2). Cytoplasmic resistivity for the axon was Ra = 100 Ωcm, for soma Ra = 200 Ωcm, dendrites Ra = 200 Ωcm. Reversal potentials Epas = −70, ENa = 50, EK = −95, ECa = 125 mV. A steady hyperpolarizing current of −0.1 nA was applied to the soma to prevent spontaneous spikes. Simulations were performed on NEURON 7.22 (Carnevale and Hines, 2006). The model is available from ModelDB database (accession number 144401). Plotting of the detailed neuron was made using TREES tool in Matlab (Cuntz et al., 2010).
Cellular Automaton Model
The CA model was used in a modified version from (Traub et al., 1999). A unit (axon) can be in one of three basic states: resting (excitable, E), firing (F), or refractory (R1, …, 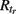 ). A unit in the excitable state becomes firing if one or more of its neighbors are firing. After one time step the firing unit becomes refractory for period tr, after which it becomes excitable again. Thus each node rests in (E) or undergoes a sequence of states (E, F, R1, …,
). A unit in the excitable state becomes firing if one or more of its neighbors are firing. After one time step the firing unit becomes refractory for period tr, after which it becomes excitable again. Thus each node rests in (E) or undergoes a sequence of states (E, F, R1, …, 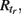 E) if activated by a neighbor. The formal rules of the CA are as follows
E) if activated by a neighbor. The formal rules of the CA are as follows
1. excitable (E) → firing (F) if any neighbor is (F) and gap junction between them is strong,
2. excitable (E) → firing (F) if any neighbor is (F), gap junction is weak, but previous spike was more than tr + 2 times steps ago,
3. F → refractory (R1),
4. Ri → R(i + 1), i < tr,
5. 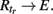
The states of all nodes are updated simultaneously every time step. Initially all units are in excitable state, except one random unit which fires 2 successive spikes: at time 1 and at t = tr + 3.
In network simulations we chose tr = 1 to avoid long periods and the searching of long loops. Therefore, units can fire again after tr + 2 = 3 time steps (1 time step for firing, tr being refractory, 1 being excitable). Weak gap junctions produce an effective refractory time tr + 1 = 2. Therefore, a unit with a weak gap junction can fire again only after 4 time steps (1 time step for firing, tr + 1 being refractory, 1 being excitable), making 4 the shortest loop length which can sustain reentrant oscillations. This is why loops of length 3 are not used by reentrant oscillations in our network simulations (Figures 5A and 6A).
Random Networks
In this work we changed from Erdős-Rényi-type networks used earlier (Traub et al., 1999; Lewis and Rinzel, 2000; Vladimirov et al., 2011) to scale-free networks which are more often found in natural systems (Strogatz, 2001). However, our main results are likely to hold for any degree distribution, provided that network has multiple loops of various lengths.
We simulated scale-free networks of 30 × 30 units with power-law degree distribution and exponential cutoff: P(k) = Ck-τe−k/λ, τ = 2, λ = 10. Weak gap junctions were 10% of the total gap junction population, positioned randomly at initialization, and remained unchanged during the simulation. Networks were constructed with local connectivity: connections were randomly chosen within radius rc = 5 from a node (distance 1 is the grid interval). Our main results did not change qualitatively when connectivity was instead global, because a neighborhood of radius 5 is large enough to represent a random network. However, local connectivity has the advantage of producing spatial effects (waves), as studied in earlier works (Lewis and Rinzel, 2000; Vladimirov et al., 2011). The results were similar in networks with Poisson degree distribution (〈k〉 = 2), and in scale-free networks with different power and cutoff τ = 2…2.4, λ = 10…20.
Period of oscillations was determined from auto-correlograms of summed network activity.
Loop Distribution
The distribution of loop lengths in uncorrelated undirected random network is given by
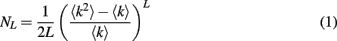
which is valid for sufficiently short loops, where L is the loop length, 〈k〉 and 〈k2〉 are the first and second moments of network’s degree distribution: 〈k〉 = ∑kP(k), 〈k2〉 = ∑k2P(k) (Dorogovtsev et al., 2008). The expression in brackets is greater than 1, therefore NL grows nearly exponentially with L.
Finding all loops in a random network is a computationally expensive task (NP-complete), and there are numerous algorithms aimed at minimizing the computational costs. In our simulations we used Matlab code kindly provided by J. Jeffry Howbert, which is essentially equivalent to an algorithm suggested in Johnson (1975), but implemented for undirected graphs. The daunting task of finding loops in our large networks was simplified by the constraint of finding all loops not exceeding a threshold (Lmax = 16, 30).
Breaking of Loops
To break all loops of specific length in a network (for example, from 3 to 10), we first searched for all loops in the appropriate length range, with some reserve toward longer loops (3–20). In each loop we picked a random link and eliminated its entry from the network’s adjacency matrix. The operation was repeated for all loops in the given length range (3–10), and the modified adjacency matrix was used to build lists of gap junctions and the units’ neighbors, which were used in each actual cellular automaton simulation. Matlab code is available from NV upon request.
Results
Weak Gap Junctions
We start by modeling propagation of spike doublets between two pyramidal neurons whose axons are connected by a gap junction. We simulate two pyramidal neurons each based on an anatomically reconstructed CA1 neuron from Neuromorpho database (neuron ca1a, NMO_00927). The soma of neuron 1 was stimulated by a depolarizing current pulse (1 nA, 1 ms) which elicited two full spikes in axon 1. The two axons are electrically coupled by a gap junction, each at distance of 370 μm from its soma. Higher gap junction conductance (g ≥ 3 nS) lets both spikes propagate successfully, while lower conductance (1–2 nS) blocks propagation of a second spike (Figure 1). Thus, a difference in g from 2 to 3 nS makes a qualitative change in the recipient axon spiking, allowing the second successive spike to propagate or not. We will refer to a gap junction which passes only one spike out of two as “weak,” in contrast to “strong” ones that pass both spikes.
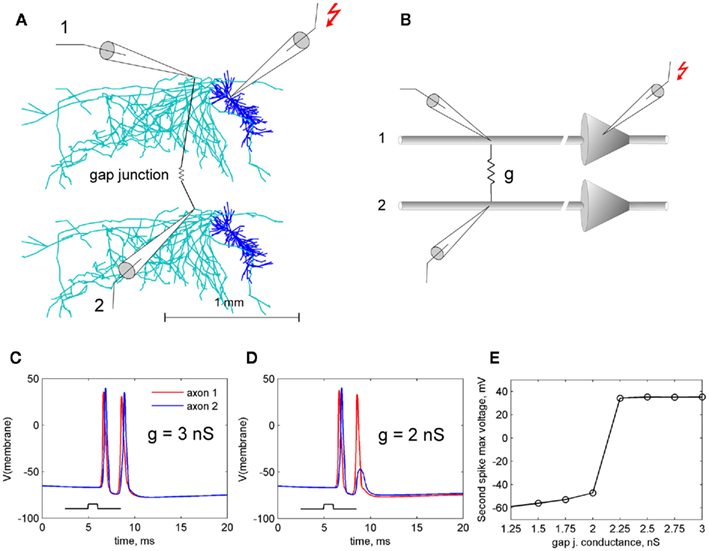
Figure 1. Simulation of spike propagation failure at axo-axonal gap junction. (A). Two pyramidal cells with anatomically reconstructed axonal arbors are coupled by a gap junction. Axons are gray, dendrites are blue. Soma 1 is stimulated by current injection [1 nA, 1 ms, shown on bottom in (C,D)] which results in doublet of axonal spikes. (B). Schematic circuit of the cells and virtual electrodes. Depending on gap junction conductance, second spike may pass the gap junction and become a full spike (C) or fail and become a spikelet (D), because firing threshold is not reached. (E) The second spike passes in all-or-none fashion, depending on gap junction conductance. The transition occurs sharply at a critical gap junction conductance of about 2.1 nS.
Oscillations in One Loop
When axons of pyramidal cells are connected by gap junctions in a loop, a weak gap junction creates dynamic asymmetry in the loop, which leads to reentrant spike propagation. Indeed, when two spikes meet one approaching from the opposite direction, the leading spikes annihilate each other and the trailing spike continues its propagation around the loop (Figure 2). When the spike travel time around the loop is longer than refractory period of an axon, the spike reenters the loop and continues this reentrant activity in self-sustained mode.
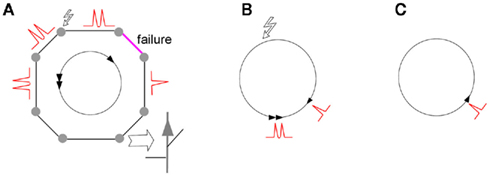
Figure 2. Initiation of reentrant oscillations in a loop of electrically coupled axons. Filled circles are pyramidal neurons which have axons electrically coupled into a loop. Stimulus in one cell (zigzag arrow) initiates doublets of spikes in both directions (A). Failure in one direction at a weak gap junction (magenta) passes only one spike propagating one way against two spikes propagating the other way. Two spikes meeting one spike at the end of the loop (B) leave one spike that keeps traveling around the loop (C). Arrowheads show individual spikes. Note that the time of spike travel around the loop must be greater than refractory time of axon, for spike reentry.
In a random network, each loop is embedded in the network structure, with possibly multiple connected neighbors. Therefore, reentrant activity leads to global network oscillations, where the loop acts as a pacemaker. However, even in small random networks, many loops can be superimposed and interconnected, and the presence of randomly occurring weak gap junctions poses a challenging task to determine which of the many possible loops will be the pacemaker.
Oscillations in Two Connected Loops
We further examine what determines the oscillations in the case of two loops of different size, with weak gap junctions in each, connected by sharing several strong gap junctions (one of the possible 2-loop systems is shown in Figure 3). A manual tracing of spike coordinates in the loops suggests that once reentrant activity starts in the smaller loop, it continues, and makes the smaller loop a pacemaker for the larger loop. We examined 10 different 2-loop configurations, by varying the number of shared gap junctions, presence of weak gap junction in either loop, and initial position of the spike doublet, and found them all consistent with the concept of smallest loop as a pacemaker. Examination of several 3-loop system also supported this rule (drawings not shown). However, manual examination is slow, while the number of possible combinations of loop lengths, the way they are connected, positions of weak gap junctions and initial stimulus create a large multi-dimensional space which can be only explored computationally, in the context of random networks.
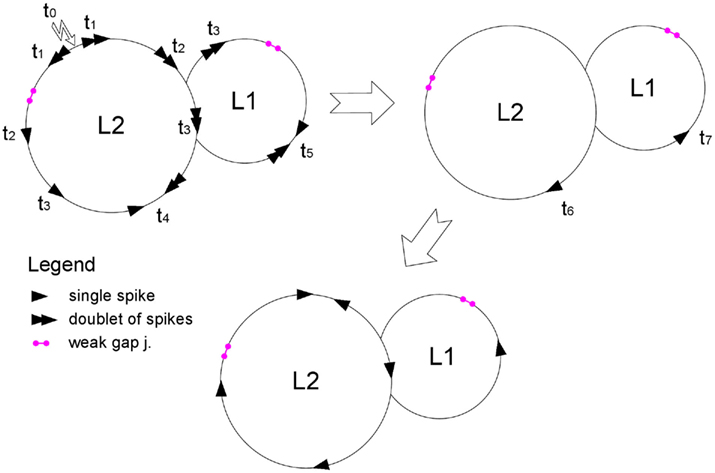
Figure 3. Scheme of spike reentrant oscillation in two connected loops. After an axon in loop L2 is stimulated (zigzag arrow) and fires two successive spikes, the doublets propagate in both directions around the loop. Weak gap junctions in each loop are shown by magenta segments; other gap junctions are not shown. The spikes are shown as snapshots at successive time steps ti. First scheme shows spike propagation before collision in each loop (at t4 and t5, respectively). Second scheme shows the two spikes remaining after each collision. A spike in the small loop reenters with shorter period L1 and proceeds to the large loop at the two junction points, creating two counter-propagating spikes in the larger loop, which annihilate each other (third scheme). Period of spike entering (L1) is the same in both loops, so that the smaller loop is the pacemaker and the larger loop is the follower. The loops contain L1 and L2 neurons, respectively; time units are non-dimensional.
Oscillations in Random Networks
In order to explore various loop configurations and initial conditions, we simulated random networks where neurons were represented by cellular automata with memory. In an earlier cellular automaton model of axonal spiking, the unit responded according to its present state and states of its connected neighbors (Traub et al., 1999; Munro and Boergers, 2010). Here we modified the model to account for second spike failure. A weak gap junction now has memory of its recent spikes, and does not pass a second spike if the time passed since the previous spike is not sufficiently long. This is not meant to imply that real gap junctions have memory. It only reflects the non-linearity in trans-junctional spike propagation in the case of two spikes coming in rapid succession. Effectively, cellular automaton units and gap junctions have their own refractory times: normal gap junctions have the same refractory time as axonal units (tr), while weak gap junctions have a longer refractory time (tr + 1).
Our results do not depend much on any particular network degree distribution, provided that there are multiple loops of different length in a network. For our simulations we chose scale-free networks which are often found in natural systems (Strogatz, 2001). We simulated a randomly connected network of 40 × 40 units with power-law degree distribution and exponential cutoff: P(k) = Ck-τe−k/λ, τ = 2, 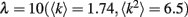 . Weak gap junctions were 10% of total gap junction population, were assigned randomly at the initiation step, and remained unchanged during simulation. The percentage of weak gap junctions can be within 5–20% to ensure their sparse but representative distribution in a network.
. Weak gap junctions were 10% of total gap junction population, were assigned randomly at the initiation step, and remained unchanged during simulation. The percentage of weak gap junctions can be within 5–20% to ensure their sparse but representative distribution in a network.
To initialize network activity, a single randomly chosen unit was stimulated by two successive spikes. If activity did not vanish to zero due to connectivity mishaps, the network demonstrated self-sustained reentrant oscillations with clearly defined frequency (Figure 4).
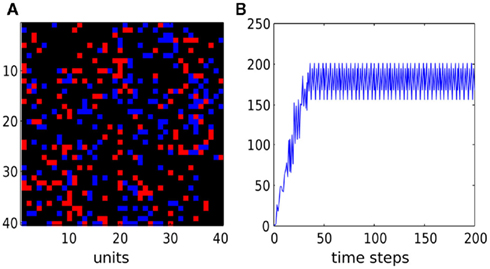
Figure 4. Activity in a random network with weak gap junctions. (A) Snapshot of network state at the end of simulation (red for active, blue for refractory, black for resting units). (B) Sum of active cells as a function of time. After a short initial period, the network starts to oscillate with frequency of 4 and oscillates in self-sustained mode without any external stimulus. Initially all cells were resting except one which emitted two successive spikes. Time units are non-dimensional. The network has power-law degree distribution (gap junctions per node), with power τ = 2, cutoff λ = 10.
Simulations of a single representative network are shown in Figure 5A. Network wiring and hence the loop distribution are fixed, while oscillation periods depend on the choice of which gap junctions are weak, and which cell fires a doublet initially. The network was simulated 500 times with a random choice of weak gap junctions (10%) and random initially spiking cell. Periods sharply peak above the lowest possible value of 4 (refractory time of a weak gap junction, non-dimensional, see Methods). The period of 4 is the shortest possible period of reentrant oscillation around a loop. Note that there are numerous loops of length 3 but they are unused by reentrant oscillations because they are too short for reentry. Loops in a network were searched using a backtracking algorithm (Johnson, 1975).
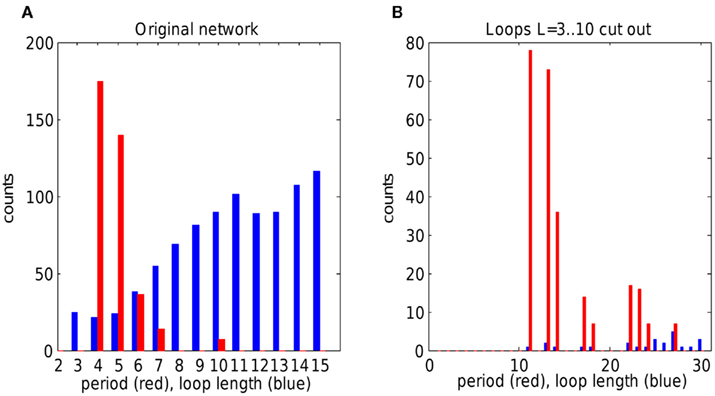
Figure 5. The effect of loop distribution on oscillation periods in single random network. (A) Loop length distribution (blue) and oscillation periods (red) in a single network of size 40 × 40, simulated 500 times, with random choice both of weak gap junctions and of initially spiking unit. Oscillations sharply peak at lowest possible loop length. Note that oscillations of period 3 are not allowed because effective refractory time is 4. (B) Simulations of a random network made up from network in (A) by cutting out loops with length between 3 and 10. Oscillations show peak at period 11, that is from one of the smallest available loops. Note the change in overall loop distribution, because disruption of short loops affects other loops.
To check how altered loop distribution affects oscillation periods, we designed an algorithm that cuts out all loops in a defined length range. When the network was devoid of loops with length in the range 3–10, the new network demonstrated reentrant oscillations with periods starting from 11, that is from the shortest available loops (Figure 5B). Note the overall drop of loop number, because cutting short loops affects all other loops, too.
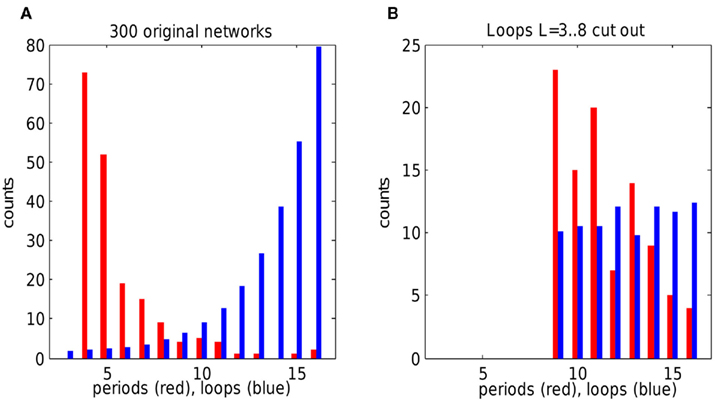
Figure 6. Oscillation periods versus loop distribution in random networks. (A) Oscillation periods (red) and loop length distribution (blue) in 300 scale-free networks. Oscillations sharply peak at lowest possible loop length (4). Note that oscillations of period 3 are not allowed because effective refractory time is 4. Each network of size 30 × 30 was simulated once with random choice of weak gap junctions and of initially spiking unit. (B) Same networks with loops of length from 3 to 8 cut out. Oscillations in modified networks show peak at period 9, corresponding to the smallest available loops. Note the change in overall loop distribution, because disruption of short loops affects other loops and the overall degree distribution. Loop counts are scaled by 1/1000 in (A) and 1/10 in (B) for display purposes. Networks which had no self-sustained activity were excluded from analysis.
To take into account network variability, we simulated 300 scale-free networks with random connectivity and initial conditions, and plotted their total loop distribution against total oscillation period distribution. Again, oscillation periods were sharply peaked around effective refractory time 4 when all loops were intact (Figure 6A). When loops with length in range 3–8 were eliminated, the periods in the resulting new set of networks peaked around the minimal loop length of 9 (Figure 6B), confirming the principle of shortest loop as a pacemaker. The number of 9-periods was not much higher than 10- and 11-periods because many networks did not contain 9-loops (or had very few of them). Thus the preference of oscillations for a shortest loop is less striking in the modified networks. However, in both cases of the original networks and those with loops 3–8 cut out, the change of loop distribution makes a predictable change in oscillation periods, according to the suggested rule of shortest loop as the pacemaker.
The short loop which became the pacemaker injects its reentrant spike into other loops through common connections, in such a way that spikes traverse the longer loops, with the result that individual neurons fire at the same rate in all loops (see also Discussion and Figure 8).
Maximum Frequency in Network of Anatomically Detailed Neurons
The results shown above predict that oscillations in axonal networks will likely converge to the maximum possible frequency allowed by refractoriness of axons and the distribution of loops. In the cellular automaton model we used a very short refractory time tr = 1 for simplicity, with non-dimensional time units. In a somewhat more realistic cellular automaton model, the time unit is 0.25 ms and refractory time tr = 10–15 time units (2.5–3.75 ms; Traub et al., 1999). Assuming that the axonal plexus has a loop distribution as in a random network, loops of length 10–15 can be very abundant. So the period for reentrant oscillations will likely be determined by the refractory time of axons. In this section we quantitatively estimate the effective refractory time of a detailed axonal model such as shown in Figure 1.
We couple model axons of anatomically reconstructed neurons by gap junctions into a loop of n cells, with 45 μm distance between the two gap junctions on each axon (Figure 7, n = 5). Among a total of n gap junctions in the loop, one was weak (1.5 nS) and the rest were normal (3 nS). By stimulating one soma and adjusting the number of cells in the loop, we find a loop containing a minimal number of cells in which reentrant activity emerges.
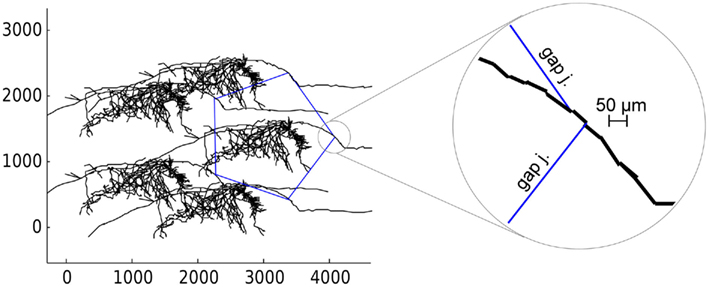
Figure 7. Loop of 5 anatomically detailed neurons axonally coupled by gap junctions. Gap junctions are shown by blue lines. Axes are spatial coordinates in micrometers. Circle on right shows the zoomed position of two gap junctions on the axon. Axon is represented by discrete line segments due to simplifications of anatomical reconstruction.
Depending on the properties of ionic channels in the axons, the size of the smallest loop that could sustain reentrant oscillations varied. With axonal potassium K(M) conductance present, the shortest loop required as many as 40 cells, giving a minimum period of oscillations 13 ms (77 Hz). This happens because K(M) significantly increases axonal refractory time due to the channel’s slow kinetics. Without K(M) conductance (leaving Na(F), K(DR), and K(A)) the effective refractory time was much shorter, allowing minimum loop size of only 10 cells and minimum period 3.5 ms (285 Hz). With minimal conductances (Na(F) and K(DR) only) the shortest loop was 9 cells, period 3.2 ms (312 Hz). It is unclear how abundant are K(M) and K(A) channels in axonal collaterals; therefore our rough estimate for reentrant oscillations varies from 77 to 312 Hz, corresponding to frequencies of gamma, ripples and fast ripples range (Table 2). These data suggest that reentrant oscillations at fast ripple frequency might be most likely to occur when K(M) is suppressed, as for example by high cholinergic “tone.”
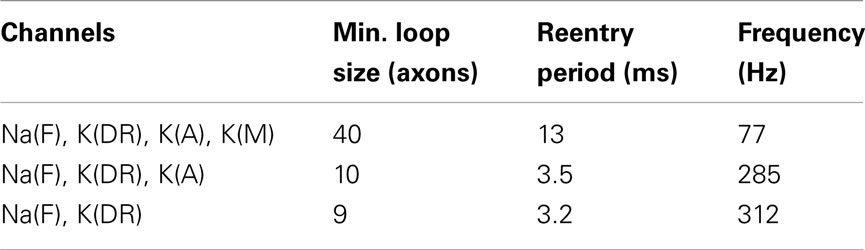
Table 2. Ionic channel composition, minimal loop with sustained reentry, period, and frequency of reentrant oscillation in loops of axonally coupled pyramidal cells.
In our simulations, a strong depolarizing current pulse (1 nA) injected into the soma elicited axonal spikes at 2 ms interval (500 Hz). This time is consistent with the axonal refractory time obtained in experiments (2.5 ms, 400 Hz; Raastad and Shepherd, 2003; Popovic et al., 2011). In our model, 2 ms is the minimum refractory time at which an axon can spike a second time under a strong somatic stimulus. However, current entering an axon via a weak gap junction is smaller and can not make the axon spike again so rapidly; therefore, the axonal effective refractory time is longer, about 3.5 ms. Effective axonal refractory time is difficult to define precisely. It depends on ionic channel composition, number of gap junctions on the axon and the distances between them, and local electrotonic properties of the axon, as well as the strength of stimulus. Importantly, the reentrant oscillation period of a loop is determined in part by the effective refractory time of its slowest axon. Therefore, modulation of the properties of a few specific axons may potentially modulate the oscillation frequency of a network containing thousands of neurons.
Discussion
In this paper we adopt the notation type I and type II oscillations to distinguish between two possible mechanisms of high-frequency synchronous activity of pyramidal neurons sparsely coupled by axonal gap junctions. Type I implies rare spontaneous spiking of axons and strong gap junctions, and type II requires a doublet of spikes in one of the axons and the presence of some weak gap junctions.
We use two computational models to study the problem of type II oscillations in axonal arbors of hippocampal pyramidal cells. We start with a model of anatomically reconstructed neuron from rat CA1 and show that different gap junction conductance may or may not pass the second spike in a spike doublet. A moderate difference in gap junction conductance makes a large difference when pyramidal cells are connected in random networks which inherently contain loops. Failures of second spikes on weak gap junctions create dynamic asymmetry in loops, remaining spikes reverberate in loops, and some loops become pacemakers.
The frequency of spike reentrant oscillations is studied in scale-free random networks by applying a reduced model of axonal plexus. The model uses three-state cellular automata of Greenberg-Hastings type to imitate axonal spiking. A new feature of the model is the presence of “weak” gap junctions. The weak gap junctions constitute a small fraction of total gap junction population, but they are essential for reentrant oscillations because they do not pass the second successive spike (at short interspike interval), due to “memory.” Memory here is used in an algorithmic sense to simulate the junction’s ability to block the second successive spike by using memory about the time passed since a previous spike.
The main result of this work is the tight connection between the period of network oscillation and the distribution of short loops. By using loop searching and loop-cutting algorithms in random networks, we show that network oscillations choose the shortest available loops, a principle we call “shortest loop is the pacemaker.” This gives a strong predictive conclusion: by knowing the network connectivity (distribution of loops) we can infer its likely oscillation frequency, and vise versa. The third factor to take into account is, of course, the refractory time of an axon, since oscillation period can not be shorter than that.
A necessary condition for a short loop to be a pacemaker, under the conditions we have examined, is that it must contain one, and only one, weak gap junction. If the loop contains no weak gap junction, spike doublets travel through the loop symmetrically and annihilate each other. If the loop contains more than one weak gap junction, pairs of spikes become single spikes in both directions, and also annihilate each other. Therefore, there is inherent variation in the choice of the pacemaker loop among available loops – it must be short and contain only one weak gap junction.
In our simulations of anatomically reconstructed neurons connected in a loop of n cells, each neuron has 2 gap junctions separated by a distance of about 50 μm. Gap junctions were separated along an axon rather than concentrated in a hub (Traub et al., 1999; Munro and Boergers, 2010), since we suspect that separation is more likely, assuming that gap junctions occur at random along axonal collaterals.
Throughout the paper we have assumed that gap junctions are non-rectifying, that is conductance is the same in both directions of current flow. If gap junctions are rectifying, they might produce reentrant oscillations more easily than non-rectifying, from single initial spike and without the need for weak gap junctions. It is not clear, however, whether a shortest loop will serve as a pacemaker in a network of rectifying gap junctions.
Even if gap junctions have high conductance, gap junctions close to the soma could have compromised ability to pass the second spike, due to perisomatic synaptic inhibition and the impedance load of the soma and dendrites (Traub et al., 2000; Munro and Boergers, 2010, this work, data not shown). Variability in “effective” gap junction conductance might be inherent if some gap junctions are close to the soma, or neighbored by other gap junctions and shunted by them. In the present model, we changed neuron geometry so that axon comes out from soma rather than from basal dendrite as in original anatomical reconstruction. This can compromise ability of some proximal gap junctions to pass spikes, but does not alter our general conclusions about the axonal network.
In large (100 × 100) networks with fixed weak gap junctions, reentrant activity has a spatial form of target and/or spiral waves. For example, Figure 8 shows the network activity with single weak gap junction in a loop which becomes the pacemaker. The reentrant activity emerging from pacemaker loop has a local form of spiral wave, and activity spreads to broader areas as target (arc) waves. Note that, despite complex connectivity, the total network activity oscillates precisely with the period equal to the length of pacemaker loop.
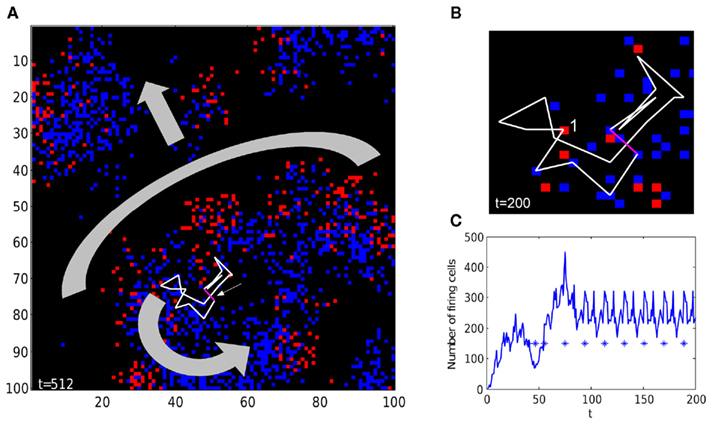
Figure 8. Spiral and target-like waves in a random network. (A) The 100 × 100 network contains a single weak gap junction (magenta segment, pointed to by small arrow), in a loop of 19 units connected by gap junctions (white lines). Once reentrant activity starts, the loop becomes a pacemaker, and produces a spiral wave (shown by thick curved arrow), and a target-like (arc) wave (shape and direction are shown by thick gray arc and arrow). See Movie S1 in Supplementary Material for time-lapse activity. (B) Zoom-in of the pacemaker loop. The cell marked by 1 is currently firing, followed by a tail of five refractory cells (refractory time tr = 5). See Movie S2 in Supplementary Material for time-lapse activity. (C) Once reentrant activity has started at around t = 100, the total number of firing units oscillates with a period of 19, which precisely matches the length of the pacemaker loop. Stars are spikes of a randomly chosen unit, showing that individual axons fire with the same period as network activity. The network has a power-law degree distribution (gap junctions per node), with power τ = 2, cutoff λ = 10.
Firing of single units has the same period as the total network activity (but different phase), as shown in Figure 8C for a randomly chosen unit (asterisks). Generally, units have different phases, thus total network amplitude decreases with larger network size due to unit phase averaging. However, in a network of finite size (104 in our simulations), variations of axonal phase and connectivity do not allow smoothing network activity completely. Some axons may have more neighbors connected by gap junctions, and in actual tissue more projections to local interneurons, both effectively increasing role of the axon in LFP. In line with these predictions, in vivo LFPs have relatively small amplitude (ca 0.1 mV) superimposed on large, slower signal, and units fire phase-locked with LFP (Engel et al., 2009).
We do not find a clear distinction between target and spiral waves in the reentrant network activity – the oscillation core may have spiral, target, or mixed wave shape, depending on the geometry of pacemaker loop and its connections to the rest of network. Target and/or spiral waves can be also obtained in the cellular automaton model when the probability of spike propagation via gap junctions changes with time (N. Vladimirov, unpublished), or when spike propagation time varies among gap junctions (A. Cuevas, personal communication).
Spiral and ring waves were reported in experiments on rat cortex visualized by voltage-sensitive dye imaging, induced by application of carbachol and bicuculline (Huang et al., 2004, 2010). A use of foldable high-density electrodes in vivo (Viventi et al., 2011) demonstrated the presence of plain and spiral waves in cat visual cortex, when a seizure was induced by administration of picrotoxin. Although primary frequencies of measured spiral waves were slow (∼10 Hz), both methods demonstrate the existence of spiral waves in the induced cortical seizures. If applied to epileptogenic cortex, these methods can give insights into spatio-temporal structure of HFOs and possibly demonstrate reentrant spiral waves during epileptic seizures. One should note, however, that the above-mentioned experimental spiral waves were probably the result of chemical synaptic excitation rather than gap junctions.
In essence, our network of axons connected by gap junctions is strikingly similar to excitable cardiac cell tissue, where adjacent myocytes are also connected by gap junctions (Weingart and Maurer, 1988; Sheikh et al., 2009), and demonstrate target and spiral reentrant waves. Regular target waves change to spiral when cell-to-cell coupling is reduced (Bub et al., 2005), because potentials fail at weak gap junctions, wave symmetry breaks, which allows spiral reentrant waves to occur.
One signature of reentrant activity is a presence of spiral waves or target waves in networks with local spatial connections. In our simulations we assumed that the radius of connectivity does not exceed rc = 5, in units of grid step between cells. However, this may not be the case in CA1 because of great span of axonal arbor which extends millimeters away from the soma. Therefore, the maximum length of connection may be of the same order as the network dimensions (millimeters), and spiral or target waves may be difficult to observe as an evidence of reentrant activity.
How can the presence of reentrant oscillations be tested experimentally? It might be possible to start ripples in CA1 mini-slice by eliciting 2 axonal spikes (but not 1) in a pyramidal neuron’s axon, at least in some pyramidal cells. Pharmacological blockade of K(A) and K(M) channels might increase the oscillation frequency of ripples due to shortening of axonal refractory time. A hole cut in CA1 mini-slice stratum oriens might shape the underlying axonal loops and alter the oscillation frequency in that slice. This indirect evidence, together with a specific gap junction blocker, might reveal the role of reentrant oscillations in hippocampus.
A more convincing experiment might demonstrate transition between type I (noise-induced) and type II (reentrant) oscillations by pharmacologically reducing electrical coupling between gap junctions. A gradual adding of gap junction blocker such as carbenoxolone into the bath around a hippocampal slice could transiently reduce the ripple frequency from 150 down to less than 100 Hz, because it takes more time for spike to pass through gap junction with lower conductance (Traub et al., submitted). A further increase of gap junction blocker concentration could transiently put the network into fast ripple frequency of about 300 Hz (due to emergence of reentrant oscillation because of gap junction failures).
If conditions for both type I and type II oscillations are met (strong gap junctions, noise, and weak gap junctions), the type II oscillations take over because of their higher frequency (simulations not shown).
In our simulations, once the reentrant mode is established it does not terminate and continues in seizure-like mode. In a real network, there may be several possible mechanisms of reentry termination. Temporal variations in gap junction conductance, long-term depression of gap junctions, or inhibition of axonal activity by some external mechanism are possible terminators of otherwise uncontrolled and pathological reentrant activity.
Models of Ripples
It has been suggested that type I oscillations are the core mechanism of ripples in sharp wave-ripple complexes (Traub et al., 1999, 2010; Traub and Bibbig, 2000).
There are at least two alternative models for ripples. The first model suggests that ripples emerge from synchronization of inhibitory interneurons, which are excited by strong but transient depolarization (Buzsaki et al., 1992; Ylinen et al., 1995). In particular, ripples have been attributed to synchronous GABAergic inhibition of pyramidal cells by basket cells, the latter being excited by CA3 pyramidal neurons during sharp waves.
Indeed, network of inhibitory interneurons can demonstrate oscillations due to mutual IPSPs when cells reach sufficient depolarization (Whittington et al., 1995; Traub et al., 1996). However, this type of oscillations is shown in gamma range (30–70 Hz) but has not been demonstrated in ripples range.
Some experimental evidence argues against the interneuron-based model as well. Ripples persist and even increase in amplitude with GABAA receptors blocked (Draguhn et al., 1998; Jones and Barth, 2002; Maier et al., 2003; Nimmrich et al., 2005), during pharmacological blockade of all chemical transmission in vitro (AMPA/kainate, NMDA, and GABAA, GABAB receptors blocked) and even in Ca-free medium which blocks chemical synaptic transmission (Draguhn et al., 1998). Furthermore, CA1 pyramidal neurons during ripples receive phase-locked excitatory postsynaptic currents (EPSC; Maier et al., 2011).
On the other hand, gap junction blockers (octanol, halothane, carbenoxolone) reversibly suppress high-frequency activity in vitro (Draguhn et al., 1998; Maier et al., 2003). A probable gap junction between hippocampal mossy fiber axons was shown in Hamzei-Sichani et al. (2007) by using freeze-fracture replica immunogold labeling (FRIL). As further evidence, dye coupling occurs between CA1 pyramidal cells through structures which lack spines and have collaterals emerging at approximately right angles, so that the coupling structures appear to be axons (Schmitz et al., 2001).
The second alternative model suggests that transient activity in ripple frequency can occur in recurrent networks of pyramidal neurons with dendrites that supra-linearly enhance synchronous excitatory synaptic inputs (Memmesheimer, 2010). This mechanism is plausible in highly recurrent CA3, but it remains unclear how this model can possibly explain ripples in CA1 which lacks strong recurrent connections, or how ripples persist in non-synaptic conditions, where they are suppressible by gap junction blockers.
Models of Fast Ripples
Simulations and experiments with axonal networks show that they can oscillate by reentrant mechanism (Lewis and Rinzel, 2000; Tseng et al., 2008; Munro and Boergers, 2010), which we call type II and explore through this paper in detail. We suggest that type II oscillations may be the driving mechanism of fast ripples in CA1.
There are alternative models of fast ripples as well. Foffani et al. (2007) have shown that fast ripple frequency appear as harmonic of ripples in epileptic rat CA3 slices. In their experiments, the authors demonstrated that fast ripples can emerge from disorganized ripples because of jitter in interspike intervals (ISI) of pyramidal cells. Jitter in ISIs is suggested to be the result of elevated synaptic excitation of cells in epileptic hippocampus. However, Engel et al. (2009) have argued that fast ripples are not harmonics of ripples.
Ibarz et al. (2010) have shown by simulations and experiments that fast ripples might be generated by bursting pyramidal neurons in either of two regimes: in-phase synchronous firing, when LFP coincides with bursting frequency of individual cells, and out-of-phase firing, when phases of individual neurons are temporally shifted by propagation delays and LFP shows high-frequency harmonics of cellular intraburst frequency. To evaluate this model, it would help to test whether fast ripples, in an in vitro model, are dependent on AMPA/Kainate receptors.
Both gap junctions and chemical synapses can contribute to neural network synchronization, including sharp wave ripples in normal brain and epileptic seizures in pathology. In this work we have tried to bridge the scales of gap junction, axonal electrotonic properties, neural network topology and frequency of network oscillations. Reentry may be a critical one of several possible mechanisms of pathological high-frequency oscillations observed clinically and experimentally in vivo.
Conflict of Interest Statement
All authors are employed by the IBM T. J. Watson Research Center and contributed to all aspects of the study. The research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to J. Jeffry Howbert for sharing his Matlab code for loop searching algorithm, and to Ted Carnevale for his advice about NEURON programming. We thank Armando Cuevas for helpful discussions. We also thank both reviewers for their valuable feedback. The work was supported by grants NIH/NINDS (http://nih.gov) R01NS062955 to Nikita Vladimirov and Roger D. Traub, R01NS44133 to Roger D. Traub, R01GM081747 to Yuhai Tu, and Alexander von Humboldt Stiftung (www.humboldt-foundation.de) and Einstein Stiftung Berlin to Roger D. Traub.
Supplementary Materials
The Supplementary Material for this article can be found online at http://www.frontiersin.org/Computational_Neuroscience/10.3389/fncom.2012.00017/abstract
Footnotes
- ^http://neuromorpho.org, ID: NMO_00927, name ca1a
- ^www.neuron.yale.edu
References
Axmacher, N., Elger, C., and Fell, J. (2008). Ripples in the medial temporal lobe are relevant for human memory consolidation. Brain 131, 1806.
Bragin, A., Engel, J. Jr., and Staba, R. (2010). High-frequency oscillations in epileptic brain. Curr. Opin. Neurol. 23, 151.
Bragin, A., Engel, J., Wilson, C. L., Fried, I., and Buzsáki, G. (1999). High-frequency oscillations in human brain. Hippocampus 9, 137–142.
Bragin, A., Mody, I., Wilson, C. L., and Engel, J. (2002). Local generation of fast ripples in epileptic brain. J. Neurosci. 22, 2012–2021.
Bub, G., Shrier, A., and Glass, L. (2005). Global organization of dynamics in oscillatory heterogeneous excitable media. Phys. Rev. Lett. 94, 28105.
Buzsáki, G. (1998). Memory consolidation during sleep: a neurophysiological perspective. J. Sleep Res. 7, 17–23.
Buzsaki, G., Horvath, Z., Urioste, R., Hetke, J., and Wise, K. (1992). High-frequency network oscillation in the hippocampus. Science 256, 1025.
Chrobak, J., and Buzsáki, G. (1996). High-frequency oscillations in the output networks of the hippocampal–entorhinal axis of the freely behaving rat. J. Neurosci. 16, 3056–3066.
Cuntz, H., Forstner, F., Borst, A., and Häusser, M. (2010). One rule to grow them all: a general theory of neuronal branching and its practical application. PLoS Comput. Biol. 6, e1000877. doi:10.1371/journal.pcbi.1000877
Dere, E., and Zlomuzica, A. (2011). The role of gap junctions in the brain in health and disease. Neurosci. Biobehav. Rev. 36, 206–217.
Dorogovtsev, S. N., Goltsev, A. V., and Mendes, J. F. F. (2008). Critical phenomena in complex networks. Rev. Mod. Phys. 80, 1275–1335.
Draguhn, A., Traub, R., Schmitz, D., and Jefferys, J. (1998). Electrical coupling underlies high-frequency oscillations in the hippocampus in vitro. Nature 394, 189–192.
Engel, J. Jr, Bragin, A., Staba, R., and Mody, I. (2009). High-frequency oscillations: what is normal and what is not? Epilepsia 50, 598–604.
Foffani, G., Uzcategui, Y., Gal, B., and Menendez de la Prida, L. (2007). Reduced spike-timing reliability correlates with the emergence of fast ripples in the rat epileptic hippocampus. Neuron 55, 930–941.
Girardeau, G., and Zugaro, M. (2011). Hippocampal ripples and memory consolidation. Curr. Opin. Neurobiol. 21, 452–459.
Hamzei-Sichani, F., Kamasawa, N., Janssen, W., Yasumura, T., Davidson, K., Hof, P., Wearne, S., Stewart, M., Young, S., Whittington, M., Rash, J. E., and Traub, R. D. (2007). Gap junctions on hippocampal mossy fiber axons demonstrated by thin-section electron microscopy and freeze–fracture replica immunogold labeling. Proc. Natl. Acad. Sci. U.SA. 104, 12548.
Huang, X., Troy, W., Yang, Q., Ma, H., Laing, C., Schiff, S., and Wu, J. (2004). Spiral waves in disinhibited mammalian neocortex. J. Neurosci. 24, 9897.
Huang, X., Xu, W., Liang, J., Takagaki, K., Gao, X., and Wu, J. (2010). Spiral wave dynamics in neocortex. Neuron 68, 978–990.
Ibarz, J., Foffani, G., Cid, E., Inostroza, M., and de la Prida, L. (2010). Emergent dynamics of fast ripples in the epileptic hippocampus. J. Neurosci. 30, 16249–16261.
Johnson, D. (1975). Finding all the elementary circuits of a directed graph. SIAM J. Sci. Comput. 4, 77–84.
Jones, M., and Barth, D. (2002). Effects of bicuculline methiodide on fast (200 Hz) electrical oscillations in rat somatosensory cortex. J. Neurophysiol. 88, 1016.
Lewis, T. J., and Rinzel, J. (2000). Self-organized synchronous oscillations in a network of excitable cells coupled by gap junctions. Network 11, 299–320.
Maier, N., Nimmrich, V., and Draguhn, A. (2003). Cellular and network mechanisms underlying spontaneous sharp wave–ripple complexes in mouse hippocampal slices. J. Physiol. (Lond.) 550, 873–887.
Maier, N., Tejero-Cantero, Á., Dorrn, A., Winterer, J., Beed, P., Morris, G., Kempter, R., Poulet, J., Leibold, C., and Schmitz, D. (2011). Coherent phasic excitation during hippocampal ripples. Neuron 72, 137–152.
Memmesheimer, R. (2010). Quantitative prediction of intermittent high-frequency oscillations in neural networks with supralinear dendritic interactions. Proc. Natl. Acad. Sci. U.SA. 107, 11092.
Munro, E., and Boergers, C. (2010). Mechanisms of very fast oscillations in networks of axons coupled by gap junctions. J. Comput. Neurosci. 28, 539–555.
Nimmrich, V., Maier, N., Schmitz, D., and Draguhn, A. (2005). Induced sharp wave-ripple complexes in the absence of synaptic inhibition in mouse hippocampal slices. J. Physiol. (Lond.) 563, 663–670.
Phelan, P., Goulding, L., Tam, J., Allen, M., Dawber, R., Davies, J., and Bacon, J. (2008). Molecular mechanism of rectification at identified electrical synapses in the Drosophila giant fiber system. Curr. Biol. 18, 1955–1960.
Popovic, M., Foust, A., McCormick, D., and Zecevic, D. (2011). The spatio-temporal characteristics of action potential initiation in layer 5 pyramidal neurons: a voltage imaging study. J. Physiol. (Lond.) 589, 4167–4187.
Raastad, M., and Shepherd, G. M. G. (2003). Single-axon action potentials in the rat hippocampal cortex. J. Physiol. (Lond.) 548, 745–752.
Roopun, A. K., Simonotto, J. D., Pierce, M. L., Jenkins, A., Nicholson, C., Schofield, I. S., Whittaker, R. G., Kaiser, M., Whittington, M. A., Traub, R. D., and Cunningham, M. O. (2010). A nonsynaptic mechanism underlying interictal discharges in human epileptic neocortex. Proc. Natl. Acad. Sci. U.S.A. 107, 338–343.
Schmitz, D., Schuchmann, S., Fisahn, A., Draguhn, A., Buhl, E., Petrasch-Parwez, E., Dermietzel, R., Heinemann, U., and Traub, R. (2001). Axo-axonal coupling: a novel mechanism for ultrafast neuronal communication. Neuron 31, 831–840.
Scorcioni, R., and Ascoli, G. (2005). Algorithmic reconstruction of complete axonal arborizations in rat hippocampal neurons. Neurocomputing 65, 15–22.
Sheikh, F., Ross, R., and Chen, J. (2009). Cell-cell connection to cardiac disease. Trends Cardiovasc. Med. 19, 182–190.
Skaggs, W., McNaughton, B., Permenter, M., Archibeque, M., Vogt, J., Amaral, D., and Barnes, C. (2007). EEG sharp waves and sparse ensemble unit activity in the macaque hippocampus. J. Neurophysiol. 98, 898–910.
Söhl, G., Maxeiner, S., and Willecke, K. (2005). Expression and functions of neuronal gap junctions. Nat. Rev. Neurosci. 6, 191–200.
Tamamaki, N., and Nojyo, Y. (1991). Crossing fiber arrays in the rat hippocampus as demonstrated by three-dimensional reconstruction. J. Comp. Neurol. 303, 435–442.
Traub, R., and Bibbig, A. (2000). A model of high-frequency ripples in the hippocampus based on synaptic coupling plus axon–axon gap junctions between pyramidal neurons. J. Neurosci. 20, 2086.
Traub, R., Bibbig, A., Fisahn, A., LeBeau, F., Whittington, M., and Buhl, E. (2000). A model of gamma-frequency network oscillations induced in the rat CA3 region by carbachol in vitro. Eur. J. Neurosci. 12, 4093–4106.
Traub, R., Contreras, D., Cunningham, M., Murray, H., LeBeau, F., Roopun, A., Bibbig, A., Wilent, W., Higley, M., and Whittington, M. (2005). Single-column thalamocortical network model exhibiting gamma oscillations, sleep spindles, and epileptogenic bursts. J. Neurophysiol. 93, 2194.
Traub, R., Cunningham, M., and Whittington, M. (2011). Chemical synaptic and gap junctional interactions between principal neurons: partners in epileptogenesis. Neural Netw. 24, 515–525.
Traub, R., Draguhn, A., Whittington, M., Baldeweg, T., Bibbig, A., Buhl, E., and Schmitz, D. (2002). Axonal gap junctions between principal neurons: a novel source of network oscillations, and perhaps epileptogenesis. Rev. Neurosci. 13, 1–30.
Traub, R., Duncan, R., Russell, A., Baldeweg, T., Tu, Y., Cunningham, M., and Whittington, M. (2010). Spatiotemporal patterns of electrocorticographic very fast oscillations (>80 Hz) consistent with a network model based on electrical coupling between principal neurons. Epilepsia 51, 1587–1597.
Traub, R., and Whittington, M. (2010). Cortical Oscillations in Health and Disease. New York: Oxford University Press.
Traub, R., Whittington, M., Buhl, E., LeBeau, F., Bibbig, A., Boyd, S., Cross, H., and Baldeweg, T. (2001). A possible role for gap junctions in generation of very fast EEG oscillations preceding the onset of, and perhaps initiating, seizures. Epilepsia 42, 153–170.
Traub, R., Whittington, M., Stanfords, I., and Jefferys, J. (1996). A mechanism for generation of long-range synchronous fast oscillations in the cortex. Nature 383, 17.
Traub, R. D., Schmitz, D., Jefferys, J. G. R., and Draguhn, A. (1999). High-frequency population oscillations are predicted to occur in hippocampal pyramidal neuronal networks interconnected by axoaxonal gap junctions. Neuroscience 92, 407–426.
Tseng, S., Tsai, L., and Yeh, S. (2008). Induction of high-frequency oscillations in a junction-coupled network. J. Neurosci. 28, 7165.
Viventi, J., Kim, D. H., Vigeland, L., Frechette, E. S., Blanco, J. A., Kim, Y. S., Avrin, A. E., Tiruvadi, V. R., Hwang, S. W., Vanleer, A. C., Wulsin, D. F., Davis, K., Gelber, C. E., Palmer, L., Van der Spiegel, J., Wu, J., Xiao, J., Huang, Y., Contreras, D., Rogers, J. A., and Litt, B. (2011). Flexible, foldable, actively multiplexed, high-density electrode array for mapping brain activity in vivo. Nat. Neurosci. 1599–1605.
Vladimirov, N., Traub, R., and Tu, Y. (2011). Wave speed in excitable random networks with spatially constrained connections. PLoS ONE 6, e20536. doi:10.1371/journal.pone.0020536
Weingart, R., and Maurer, P. (1988). Action potential transfer in cell pairs isolated from adult rat and guinea pig ventricles. Circ. Res. 63, 72–80.
Whittington, M., Traub, R., and Jefferys, J. (1995). Synchronized oscillations in interneuron networks driven by metabotropic glutamate receptor activation. Nature 373, 612–615.
Keywords: network, loop, pacemaker, gap junction, axon, pyramidal neuron
Citation: Vladimirov N, Tu Y and Traub RD (2012) Shortest loops are pacemakers in random networks of electrically coupled axons. Front. Comput. Neurosci. 6:17. doi: 10.3389/fncom.2012.00017
Received: 07 February 2012; Accepted: 16 March 2012;
Published online: 03 April 2012.
Edited by:
David Hansel, University of Paris, FranceReviewed by:
Carmen Canavier, LSU Health Sciences Center, USAChristian Leibold, Ludwig Maximilians University, Germany
Copyright: © 2012 Vladimirov, Tu and Traub. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Nikita Vladimirov, IBM T. J. Watson Research Center, P.O. Box 218, Yorktown Heights, NY 10598, USA. e-mail:bmlraXRhLnZsYWRpbWlyb3ZAZ21haWwuY29t