Population coding in sparsely connected networks of noisy neurons

1. Introduction

In order to understand cortical function, it is important to know how populations of neurons work together to encode and process information. A fundamental question about the cortical spike code is the approximate number of degrees of freedom in cortical activity. Many neurons' spike rates vary with a given external variable, such as reach direction (Schwartz et al., 1988), suggesting that there may be far fewer dimensions to cortical activity than there are neurons. As an example, there are millions of neurons in the primate middle temporal area (MT), but they may encode only a few thousand variables. Specifically, the activity of MT neurons varies markedly with fields of motion direction and speed (Maunsell and van Essen, 1983), binocular disparity (Zeki, 1974; DeAngelis and Uka, 2003), and to some extent orientation and spatial frequency (Maunsell and Newsome, 1987). Moreover, receptive fields are much larger in MT than in V1 (Gattass and Gross, 1981). If we suppose, for the sake of argument, that each receptive field encodes 10 motion-related variables, and if there are about 1000 distinct receptive fields in MT, then perhaps only about 10,000 distinct variables are encoded by the activity of millions of neurons.

One potential advantage of such redundancy is that it enables accurate reconstruction of stimuli or motor commands (Georgopoulos et al., 1986) from the relatively noisy spiking activity of individual neurons. The collective activity of a population of many neurons conveys more information to perceptual decision processes than the activity of individual neurons (Cook and Maunsell, 2002; Cohen and Newsome, 2009), despite early indications to the contrary (Britten et al., 1992). Overlapping tuning of many neurons may also facilitate information processing, e.g., function approximation in support of sensori-motor transformations (Pouget et al., 2000; Deneve et al., 2001).

Overlapping neural tuning (sometimes called signal correlations) may arise from inputs that are shared between neurons. Neighboring neurons typically receive many common inputs (Perin et al., 2011; Yoshimura et al., 2005). However, this does not guarantee correlated responses, because shared inputs could in principle be weighted differently by each neuron, resulting in varied tuning (analogous to multiple distinct outputs of a feedforward artificial neural network). Correlated activity would, however, arise from shared inputs if synaptic weights were correlated across neurons. This assumption is made in the population-coding models of Eliasmith and Anderson (Eliasmith and Anderson, 1999, 2003; Eliasmith et al., 2002). In these models, matrices of synaptic weights have a rank much lower than the number of neurons in the pre-synaptic and post-synaptic populations. The low rank of the weight matrix constrains the responses of post-synaptic neurons to encode a low-dimensional vector. For example, Singh and Eliasmith (2006) modeled two-dimensional (2-D) working-memory in a population of 500 neurons with recurrent connections. (The same assumption is implicit in neural network models with small numbers of high-fidelity neurons that are each meant to approximate a group of low-fidelity neurons, e.g., O'Reilly and Munakata, 2000). These models have assumed dense recurrent connections, in contrast with the sparse connections of the cortex.

In the present study, we address the question of whether the low-dimensional neural spike codes that appear to exist in the cortex are actually consistent with cortex-like spatial connection patterns. In particular, we study recurrent networks with sparse, mainly local connections, modeled after the intrinsic connections within superficial cortical layers. In superficial layers, most of the synapses onto each neuron originate from nearby neurons (Nicoll and Blakemore, 1993). Adjacent neurons have the highest probability of connection—about 20% if only functional connections are considered (Perin et al., 2011) or as high as 50–80% considering physical contacts estimated by microscopy (Hellwig, 2000)—and the probability falls off with distance over a few hundred micrometers (Hellwig, 2000; Perin et al., 2011). We construct network models by connecting nodes at random according to such probability functions, and find that these connection matrices typically have a rank roughly equal to the number neurons. We show that high rank is consistent with a high-dimensional neural activity manifold, and a high-noise spike code. This suggests that network structure is a potential contributor to the observed high variability of cortical activity. However, we also show that it is possible to construct networks with very similar spatial connection probabilities that nonetheless have low-dimensional dynamics and low noise. The connections in these low-dimensional networks have additional structure and higher cluster factors than random connections that are sampled directly from spatial connection probabilites.

2. Materials and Methods

Note that vectors are in bold and matrices are in capitals throughout.

2.1. Simulations

Our network models consist of leaky integrate-and-fire (LIF) spiking point neurons (Koch, 1999). Post-synaptic current at a synapse decays exponentially (with a single time constant) after each spike. The net synaptic current I_i(t) that drives the ith neuron's spike generator is a weighted sum of post-synaptic currents, i.e.,

$\begin{array}{cc}{I}_i\left(t\right)=\frac{{\alpha }_i}{\tau }{e}^{-t/\tau }\ast {\displaystyle \sum }_j{W}_{ij}{\displaystyle \sum }_P\delta (t-t_{jp}),& \left(1\right)\end{array}$

where α_i is a scaling factor, τ is the time constant of post-synaptic current decay, W_ij is the weight of the synapse from the jth to the ith neuron, δ(t−t_jp) is an impulse at the time of the pth spike of the jth neuron, and * denotes convolution.

The neurons have cosine tuning curves, as in the data e.g., of Georgopoulos et al. (1986), and Dubner and Zeki (1971). Specifically, the spike rate of the ith neuron is:

$\begin{array}{cc}{r}_i=G[{\alpha }_i{\tilde{\varphi }}^T{}_{i}x+{\beta }_i],& \left(2\right)\end{array}$

where α_i and β_i are constants, x is the vector variable to which neurons are responsive, ${\tilde{\varphi }}_i$ is the neuron's preferred direction in the corresponding vector space, and G[·] is the LIF spike rate function,

$\begin{array}{cc}G[J]=\{\begin{array}{l}\frac{1}{{\tau }_{ref}-{\tau }_{m}In(1-\frac{J_{th}}{J})}ifJ>J_{th}\hfill \\ 0otherwise\hfill \end{array},& \left(3\right)\end{array}$

in which τ_ref is the neuron refractory period, τ_m is the membrane time constant, and J_th is the lower threshold for activity.

Cosine tuning is a consequence of linear synaptic integration (as in Equation 1). This can be seen by noting that the synaptic weights W can be decomposed [e.g., through singular value decomposition (SVD)] into a product,

$\begin{array}{cc}W=\tilde{\Phi }\Phi .& \left(4\right)\end{array}$

Φ maps the spiking activity of n neurons onto a new vector $x\in {ℝ}^k$, where k ≤ n is the rank of W. The synaptic input to each neuron can be viewed as a function of x, specifically $\tilde{\Phi }x$. The dimension k of x, therefore, corresponds to the number of degrees of freedom in the firing rates of all neurons in the network. The spiking activity of the neurons can be said to encode x, which we call the “state” of the network, or the “encoded variable,” and similarly x can be reconstructed from the neurons' firing rates through various means. (In a more elaborate model in which some nodes provide sensory input, x might correspond to identifiable stimulus properties). The ith row of $\tilde{\Phi }$ is the preferred direction of the ith neuron. The jth column of Φ is called the decoding vector of the jth neuron.

Network dynamics depend on synaptic weights W, and W can be adjusted to approximate desired dynamics. We were particularly interested in networks that exhibit k-dimensional dynamics, with k much less than the number of neurons. For some simulations we chose decoding weights so that network dynamics approximated a differential equation,

$\begin{array}{cc}dx/dt=f\left(x\right).& \left(5\right)\end{array}$

Here f(x) is a feedback function that defines the dynamics of x. In combination with exponential post-synaptic current dynamics, this required that Φ reconstruct a linear estimate of τf(x) + x, i.e.,

$\begin{array}{cc}\tau f\left(x\right)+x\approx \Phi [\begin{array}{c}\frac{1}{\tau }{e}^{-t/\tau }\ast {\displaystyle \sum }_p\delta (t-t_{1p})\\ \frac{1}{\tau }{e}^{-t/\tau }\ast {\displaystyle \sum }_p\delta (t-t_{2p})\\ \dots \end{array}].& \left(6\right)\end{array}$

This modeling approach is based on the work of Eliasmith and Anderson (Eliasmith and Anderson, 2003; Eliasmith, 2005).

The input to the LIF spiking models was biased so that each neuron's firing rate intercepted zero at some point between −1 and 1 along the neuron's preferred direction. The intercepts were chosen at random with uniform density in this range. The input was also scaled so that the ith neuron's firing rate was between 80 and 120 spikes/s (again randomly chosen with uniform density) at $x={\tilde{\Phi }}_i$.

2.2. Sparse Local Connections

Our networks had random, sparse, primarily local connections. The notion of locality means that the neurons exist in a topological space; the neurons were placed in a 2-D grid. Connections were randomly chosen according to the Euclidean distance between neurons. The probability of a synapse from the jth onto the ith neuron was:

$\begin{array}{cc}{\Omega }_{ij}=P_{max}exp\left(\frac{-D_{ij}^2}{2{\sigma }^2}\right),& \left(7\right)\end{array}$

where D_ij is the distance between the neurons and P_max is the maximum connection probability. Unless otherwise specified, we chose a P_max of 1/3 for our experiments. Throughout the paper, Ω are matrices of spatial connection probabilities, C are Boolean matrices of connections (often these were simply samples of Ω), with a 1 or true indicating a connection, and 0 or false indicating no connection. Matrices of synaptic connection weights are denoted by W, where non-zero elements correspond to elements of C containing 1 (true).

2.3. Optimization of Network Dynamics

Synaptic weights can be generated according to Equation 4, by choosing diverse preferred direction vectors at random, and optimal decoders (Eliasmith and Anderson, 2003). However, the resulting connections are invariably dense, and therefore, physiologically unrealistic. We searched instead for synaptic weights that optimally approximated certain feedback dynamics under various sparseness constraints. We compared two approaches in particular. In Method A, we generated sparse connection structures C by sampling from the connection probability matrix Ω. We then optimized the synaptic weights W of these connections to approximate predefined network dynamics as closely as possible (details below). This method produced very poor approximations, in which network activity was dominated by noise. In Method B, we created new connection matrices that were guaranteed to have a low rank, and which approximated the spatial connection probabilities Ω as closely as possible (details below). This method produced high-fidelity networks with interesting higher-order connection statistics.

2.3.1. Method A: optimization of sparse connections

In this approach, we began by generating an n × n connection matrix C by sampling randomly according to connection probabilities Ω. We then weighted these connections to minimize two cost functions, which we called decoding error and encoding error (associated with Φ and $\tilde{\Phi }$, respectively). We defined the decoding error in the approximation of a function f(x) as,

$\begin{array}{cc}{ϵ}_d=\frac{1}{2}\underset{x}{{\displaystyle \int }}\Vert \Phi r\left(x\right)-f\left(x\right){\Vert }_2^{2}dx,& \left(8\right)\end{array}$

where r(x) are the firing rates of the neurons. We used a Monte-Carlo integration method, sampling x from a Gaussian distribution with mean zero and covariance matrix I. This produced a simplified estimate of decoding error,

$\begin{array}{cc}{ϵ}_d=\frac{1}{2m}\Vert \Phi R-F{\Vert }_F^2,& \left(9\right)\end{array}$

where R and F are matrices of firing rates and f(x), respectively, at each sample of x, m is the number of samples, and || · ||_F is the Frobenius norm. The gradient of this error with respect to W_ij is,

$\begin{array}{cc}\frac{\partial {ϵ}_d}{\partial W_{ij}}={\displaystyle \sum _l\frac{\partial {ϵ}_d}{\partial {\Phi }_{lj}}\frac{\partial {\Phi }_{lj}}{\partial W_{ij}},}& (10)\end{array}$

where,

$\begin{array}{cc}\frac{\partial {ϵ}_d}{\partial {\Phi }_{lj}}=\frac{1}{m}{\displaystyle \sum _q{\left[\Phi R-F\right]}_{lq}{R}_{jq}}& (11)\end{array}$

and

$\begin{array}{cc}\frac{\partial {\Phi }_{lj}}{\partial W_{ij}}={\left({\tilde{\Phi }}^{-1}\right)}_{li}& \left(12\right)\end{array}$

Ideally, all the neurons in the model would have tuning curves over the same few variables (e.g., reach directions), because k such variables can be accurately reconstructed from the firing rates of n neurons if k « n (as discussed in the Introduction and elaborated further in the Results; see Section 3.1). However, in principle, population activity could have as many degrees of freedom as there are neurons (k ≈ n), preventing accurate reconstruction from noisy spiking. We defined encoding error in terms of the extent to which the neurons' firing rates vary in more than k dimensions. Specifically, without loss of generality, we defined the encoding error as the fraction of the squared length of the preferred direction vectors that was orthogonal to the first k dimensions, i.e.,

$\begin{array}{cc}{ϵ}_e=\frac{1}{2}\frac{{\displaystyle \sum }_i{\displaystyle \sum }_{l=k+1}^n{\left({\tilde{\Phi }}_{il}\right)}^2}{{\displaystyle \sum }_i{\displaystyle \sum }_{l=1}^n{\left({\tilde{\Phi }}_{il}\right)}^2},& \left(13\right)\end{array}$

where k is the dimension of the lower-dimensional subspace to which we tried to constrain network activity. (Other lists of preferred direction vectors with the same rank are related to $\tilde{\Phi }$ by a change of basis). The gradient of this error with respect to W_ij is,

$\begin{array}{cc}\frac{\partial {ϵ}_e}{\partial W_{ij}}=\underset{l}{{{\displaystyle \sum }}^{}}\frac{\partial {ϵ}_e}{\partial {\tilde{\Phi }}_{il}}\frac{\partial {\tilde{\Phi }}_{il}}{\partial W_{ij}}.& (14)\end{array}$

where,

$\begin{array}{cc}\frac{\partial {\tilde{\Phi }}_{il}}{\partial W_{ij}}={\left({\Phi }^{-1}\right)}_{jl}& \left(15\right)\end{array}$

and

$\begin{array}{cc}\frac{\partial {ϵ}_e}{\partial {\tilde{\Phi }}_{il>k}}=\frac{\sigma -{\sigma }_k}{{\sigma }^2}{\tilde{\Phi }}_{il},& \left(16\right)\end{array}$

$\begin{array}{cc}\frac{\partial {ϵ}_e}{\partial {\tilde{\Phi }}_{il\le k}}=\frac{-{\sigma }_k}{{\sigma }^2}{\tilde{\Phi }}_{il},& \left(17\right)\end{array}$

where $\sigma ={\displaystyle {\sum }_i{\displaystyle {\sum }_{l=1}^n{\left({\tilde{\Phi }}_{il}\right)}^2}}$ and ${\sigma }_k={\displaystyle {\sum }_i{\displaystyle {\sum }_{l=k+1}^n{\left({\tilde{\Phi }}_{il}\right)}^2}}$.

To minimize these costs for a sparse connection matrix, we first drew the synaptic weight of each connection (corresponding to C_i = true) from a zero-mean Gaussian distribution. These initial weights were scaled to give neurons realistic ranges of firing rates (typically <120 spikes/s). We performed SVD to obtain W = USV^T, and set $\tilde{\Phi }$ = US, and Φ = V^T. We then divided $\tilde{\Phi }$ by the average length of preferred direction vectors (rows of $\tilde{\Phi }$), and multiplied Φ by the same factor. This made the preferred direction vectors unit-length on average without changing W (the preferred directions were later scaled to have exactly unit length).

We then performed 20,000 gradient-descent steps. In each step, we first adjusted W according to $\partial {ϵ}_e/\partial W_{ij}$, changing only the elements that corresponded to true entries in the connection matrix C. We then rescaled rows of $\tilde{\Phi }$ to have unit length, and recalculated the weights as $w=\tilde{\Phi }\Phi$. The latter change did not introduce new connections, because it did not affect whether pairs of encoding and decoding vectors were orthogonal. We then updated W according to $\partial {ϵ}_d/\partial W_{ij}$. The step size along the $\partial {ϵ}_e/\partial W_{ij}$ gradient was 1/1000 of the change predicted by the gradient to eliminate the error. We encountered stability problems related to the step size along the $\partial {ϵ}_d/\partial W_{ij}$ gradient, so at each iteration we began with a step of 1/100 of the change predicted to eliminate the cost, and repeatedly halved the step size and retried if changes did not decrease the decoding error (up to 10 step-size reductions in each iteration).

2.3.2. Method B: generation of low-rank sparse connections

Method A was ineffective in producing high-fidelity, low-dimensional feedback dynamics (see Results). We, therefore, sought a way to introduce additional structure into the connections to reduce the rank of W with minimal changes to connection probabilities. In particular, given an n × n matrix Ω of connection probabilities, we wanted to find n × k and k × n matrices of probabilities, denoted Ω^L and Ω^R, such that samples C^L and C^R from these matrices would yield C = C^LC^R, with P(C_ij) ≈ Ω_ij. Given such a decomposition, we could then draw samples C^L and C^R to obtain Boolean connection matrices with realistic spatial connection probabilities. We could also replace the non-zero elements of C^L and C^R with any choice of real numbers. In particular, we could replace elements of C^R with decoding weights that were optimized to produce various feedback dynamics. This method resulted in networks with low-dimensional dynamics and a much better signal-to-noise ratio than Method A (see Results).

Note that P(C_ij) = 1 − ∏_l(1 − C^L_ilC^R_lj) and that P(C_ij) ≤ 1/3 in our models. For low probabilities, P(C_ij) ≈ ∑_lC^L_ilC^R_lj. Therefore, we first performed non-negative matrix factorization (Lee and Seung, 2001) of Ω to obtain a rough approximation of Ω^L and Ω^R, and then adjusted these factors using gradient descent to obtain a better approximation of Ω. The gradient of P(C_ij) with respect to C^L_il is:

$\begin{array}{cc}\frac{\partial P(C_{ij})}{\partial C_{il}^L}=C_{lj}^R{\displaystyle \prod _{k\ne l}[1-C_{ik}^L{C}_{kj}^R].}& (18)\end{array}$

At each step, we updated C^L according to:

$\begin{array}{cc}{C}_{il}^L=C_{il}^L-\kappa {\displaystyle \sum _j\frac{\partial P(C_{ij})}{\partial C_{il}^L}(P(C_{ij})-{\Omega }_{ij}),}& (19)\end{array}$

where κ is a learning rate, and performed the analogous update for C^R. As shown in the Results, the accuracy with which Ω was approximated depended mildly on k.

2.4. Factors of Boolean Matrices

To further examine the failure of Method A, we investigated whether connection matrices C that were directly sampled from connection probabilities Ω had a low-rank decomposition (see Section 3.3), like the C matrices created using Method B. Our goal was to confirm that these C were inherently high-rank, and that the gradient descent procedure of Method A had not simply missed a low-dimensional decomposition. We drew sparse, local connection matrices C from Ω and tried to decompose them into low-rank products. As in Method B, we sought Boolean matrices C^L and C^R so that C_ij of the connection matrix is true if some pair of corresponding entries in the left and right factor matrices C^L and C^R are both true, i.e., C_ij = (C^L_i1&C^R_1j) ∨ (C^L_i2&C^R_2j) ∨ … ∨ (C^L_ik&C^R_kj).

For an n × n Boolean matrix C and rank k, there are 2^2nk different potential combinations of Boolean C^L and C^R, so it is not feasible to check whether each of them produces a given C. Therefore, we iteratively inspected larger and larger submatrices. We first found all submatrices of C^L_1,1:k and C^R_1:k,1 (where the subscript 1:k denotes elements between 1 and k, inclusive) that had product C_1,1, and all submatrices C^L_2,1:k and C^R_1:k,2 that had product C_2,2. We then combined these lists to find combinations of submatrices C^L_1:2,1:k and C^R_1:k,1:2 that were consistent with both C_1,1 and C_2,2, and eliminated from the list any combinations that were inconsistent with either C_2,1 or C_1,2. We then expanded the search to include C_3,3, etc. Once we encountered a submatrix that could not be represented as a rank-k product, we knew that the full connection matrix also could not be factored into a rank-k product.

2.5. Sparsely Connected Integrator

To verify that Method B (above) resulted in high-fidelity feedback dynamics, we used this method to model multi-dimensional neural integrators (Section 3.5). These models consisted of 30 × 30 square grids of neurons (edge length = 1). We used Method B to produce sparse connections with connection probabilities $P\left(C_{ij}\right)\approx \frac{1}{3}\exp \left(\frac{-D_{ij}^2}{2{\sigma }^2}\right)$ where D_ij is the distance between nodes i and j, and σ = 9. We simulated two networks, one with rank-9 and one with rank-90. Synaptic weights W were defined as a product $W=\tilde{\Phi }\Phi$, where the ith row of $\tilde{\Phi }$ is the preferred direction vector of the ith neuron and the lth row of Φ contains weights of the optimal linear estimator (OLE) (Salinas and Abbott, 1994) of the variable x_l. The resulting integrator models were similar to those of Eliasmith and Anderson (2003) except that $\tilde{\Phi }$ and Φ were sparse. Non-zero entries corresponded to non-zero (true) values of the left and right factors C^L and C^R. The non-zero elements of each preferred direction vector were drawn at random from a hypersphere, with $\left|\right|{\tilde{\Phi }}_i|{|}_2=1$. For each row of Φ, an OLE (Salinas and Abbott, 1994) was constructed from only the non-zero entries. Feeding the decoded estimates of the encoded vector x back to the neurons in this manner caused the network to act as an integrator of x, similarly to the densely connected networks of Eliasmith and Anderson (2003).

3. Results

3.1. Signal-to-Noise Ratio and the Dimension of Feedback Dynamics

This section presents introductory simulations that are meant to clarify the context of the later results. The key points are that (1) dense recurrent networks can exhibit low-dimensional dynamics with a high signal-to-noise ratio, and in contrast (2) high-dimensional neural network dynamics are noisy.

We begin with an example of 2-D dynamics in a densely connected network. Past work (Eliasmith and Anderson, 2003) has shown that neuron populations with all-to-all recurrent connections can encode small numbers of state variables with high fidelity, and can express a wide variety of dynamics. Matrices of recurrent synaptic weights have a low rank in this situation, relative to the number of neurons. To illustrate this point, we implemented the van der Pol oscillator using the feedback dynamics of a neural network of LIF nodes. The van der Pol oscillator has two state variables, x = [x₁x₂]^T, with dynamics dictated by,

$\begin{array}{cc}\begin{array}{l}{\dot{x}}_1=\mu (x_1-\frac{1}{3}{x}_1^3-x_2),\hfill \\ {\dot{x}}_2=\frac{1}{\mu }{x}_1.\hfill \end{array}& \left(20\right)\end{array}$

Its solution follows a periodic trajectory in a 2-D space, as indicated in Figure 1A. Each neuron in the simulation was connected to all the other neurons. Using the approach outlined in Section 2.1, we assigned random preferred directions to each neuron (uniformly distributed around the unit circle), and used a pseudoinverse (based on SVD) to find the linear decoding weights that optimally approximated τf(x) + x, where f(x) is in this case the right hand side of Equation 20. The (dense) synaptic weights were then $W=\tilde{\Phi }\Phi$, where rows of $\tilde{\Phi }\in {ℝ}^{300\times 2}$ are the preferred direction vectors and $\tilde{\Phi }\in {ℝ}^{2\times 300}$ are the optimal linear decoding weights. Even though the network is fully connected, and thus the synaptic weight matrix is 300 × 300, it has a rank of only 2, and (equivalently) two non-zero singular values (Figure 1C). The solution of this system is a limit-cycle in the x₁x₂-plane, revealing that the neural network has 2-D dynamics.

FIGURE 1

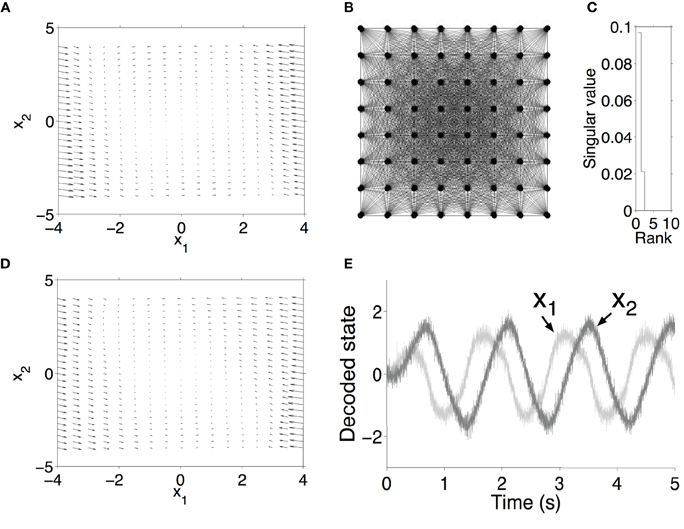
Figure 1. Neuron approximation of a van der Pol oscillator using 300 leaky-integrate-and-fire neurons with all-to-all connections. (A) Flow field of the ideal system. (B) Illustration of a fully connected network. (C) Singular values of recurrent weights in neural model. (D) Flow field of neural model. (E) State variables decoded from spiking activity in a simulation of the network.

It is also possible to create all-to-all recurrent neural networks that encode high-dimensional dynamics. Their encoding fidelity suffers, however. Figure 2 illustrates how the dimension of the encoding space influences the accuracy with which a finite number of noisy neurons can encode variables. If the encoding space is only 2-D, then the activity of the 200 neurons is focussed on representing these dimensions, yielding an accurate representation as shown in Figure 2D. However, if the activity of the 200 neurons is spread over a 200-dimensional (200-D) encoding space, then each neuron's firing rate typically does not vary much along any one dimension. These subtle variations in firing rate are more easily lost within the noise, so that estimates of higher-dimensional state variables are less accurate. This is exemplified by the highly noisy state estimate shown in Figure 2E, and the very highly noisy estimate in Figure 2F, compared to the more accurate low-dimensional state estimate in Figure 2D. Note that the LIF parameters, maximum firing rates, and intercepts along the preferred direction vectors are identical in panels A, B, and C of Figure 2. Only the dimension of the preferred direction vectors differs across these panels. The tuning curves appear less steep on average in panel B than in panel A because in a higher dimensional space, the neurons' preferred directions tend to have a smaller projection onto x₁.

FIGURE 2

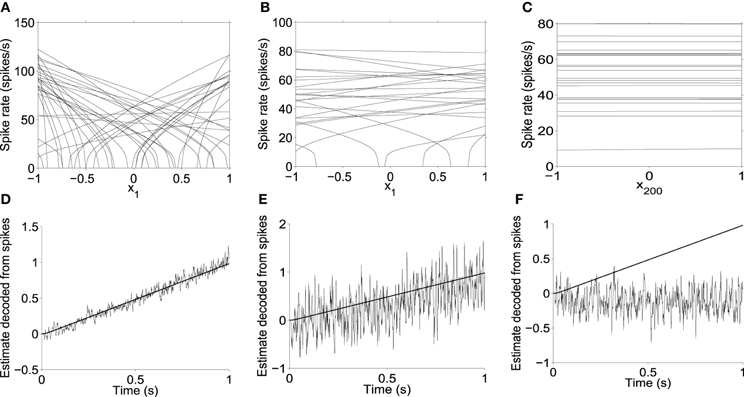
Figure 2. Multidimensional encoding using all-to-all networks. (A) Slice through tuning curves along a single dimension x₁ in a 2-dimensional (2-D) population (x_{i\ne 1} = 0). (B) Slice through tuning curves along x₁ in a 200-D population in which the singular values of the weight matrix decrease linearly from the highest value to zero, similar to those of random matrices discussed later. (C) Slice through tuning curves along x₂₀₀ in the 200-D population (i.e., the dimension associated with the smallest singular value). (D,E,F) Optimal linear estimate [Salinas and Abbott (1994)] of represented variables, from spikes of the populations shown in the top panels. (D) Estimate of x₁ in the 2-D population shown in A. (E) Estimate of x₁ in the 200-D population, different projections of which are shown in B and C. (F) Estimate of x₂₀₀ in the same 200-D population.

3.2. Optimizing Sparsely Connected Networks for Low-Dimensional Dynamics (Method A)

As illustrated in the previous section, networks with all-to-all recurrent connections support low-dimensional, high-fidelity population codes. However, connections in the cortex are sparse, and dominantly between nearby neurons (Hellwig, 2000; Stepanyants and Chklovskii, 2005). We wanted to see if such biological constraints were consistent with the low-dimensional, high-fidelity population coding that we know to be possible in densely connected networks.

Random, sparse, locally connected networks typically have full rank. Panels A and B of Figure 3 show a sketch of an example network of neurons in an 8 × 8 grid with sparse, local connections, and the corresponding connection matrix. If synaptic weights are drawn randomly from a Gaussian distribution, these connection matrices typically have full rank with a wide range of singular values (Figure 3C). There is little variation in magnitudes of these singular values (see error bars Figure 3C), so low rank is very unlikely in these networks.

FIGURE 3

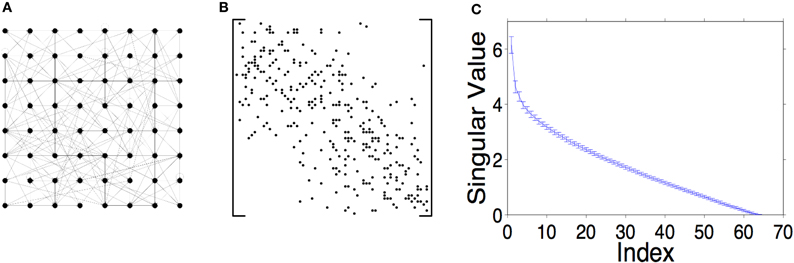
Figure 3. Random, sparse, locally connected networks, like the one sketched in A, have connection matrices with high rank. (B) Example of a sparse, local connection matrix. A black dot in the i th row and j th column indicates a connection from the j th to the i th neuron. (C) The distribution of singular values is very regular. The graph shows the mean and one standard deviation over 100 trials. The networks were generated using a P_max = 0.3 and a σ = 2 (see Section 2.2).

We wondered if the synaptic weights in these networks could be modified to reduce the rank, or at least to concentrate the network dynamics into a small number of dimensions. Figure 4 shows a sparsely connected network that was optimized for low-dimensional feedback dynamics using Method A (Section 2.3.1). This model consisted of a 10 × 10 grid of neurons with P_max = 1/3 and σ = 2.5, and was optimized for 2-D dynamics. The optimization procedure reduced both encoding and decoding error (panel A). However, optimal performance was still very poor. Panel C shows a scatter plot of reconstructions ${\widehat{x}}_1={\Phi }_{1}r\left(x\right)$ vs x₁. There was some correlation between x₁ and its reconstruction, but errors were large (this is a typical example).

FIGURE 4

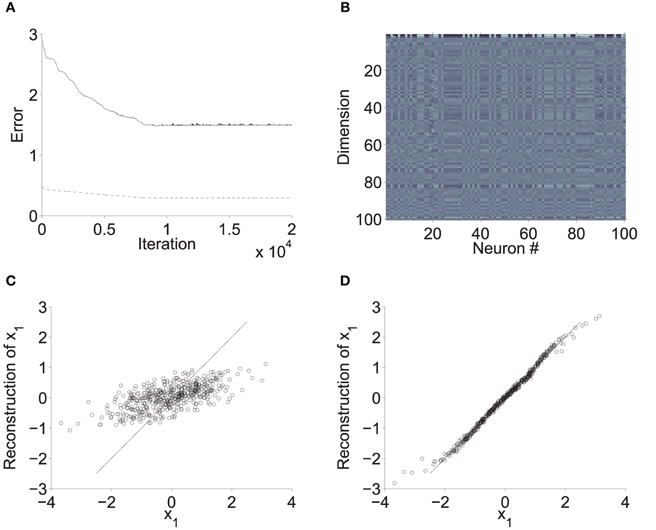
Figure 4. Optimization of sparse connection weights. The network in this example consisted of a 10 × 10 grid of neurons, with P_max = 1/3 and σ = 2.5. Optimization was performed as described in 2.3.1 to approximate 2-D dynamics (specifically a 2-D integrator). (A) Decoding error (solid) and encoding error (dashed) decreased over 20 K gradient descent iterations, but did not improve beyond about half the values associated with random weights (this example was typical). (B) Final $\tilde{\Phi }$, with the preferred directions of different neurons in columns (light = high value; dark = low value). The final preferred direction vectors have larger amplitudes in the first two dimensions than in all other dimensions. (C) Linear reconstruction of x₁ from firing rates at 500 random values of x, as ${\widehat{x}}_1={\Phi }_1\left[r\left(x\right)+\epsilon \right]$, where ε is Gaussian noise with standard deviation of of 10 spikes/s. The reconstruction is very poor. (D) Reconstruction by an alternative Φ associated with dense connections (with the same neurons) is much more accurate.

We also experimented with various other methods of reducing the rank of a sparse weight matrix, without regard to decoding error. For example, we took the SVD of the synaptic weight matrix and iteratively scaled down the smaller singular values and reconstructed the modified weight matrix, throwing away any new connections that were not in the original network. This method concentrated variations in the synaptic weights along a small number of dimensions. However, this resulted in a small number of large weights. Typically, k (with k « n) neurons had many large input or output weights, while the rest had near zero input or output (not shown).

In general, we were unable to find a way to set the synaptic weights in such a network (i.e., with connections sampled from spatial connection probabilities Ω) so that the network exhibited both low-dimensional dynamics and accurate linear reconstruction of a feedback function. These results suggest that sparse, random, diagonally dominant connections may be inconsistent with high-fidelity dynamics. The inherently high rank of these weight matrices is related to the limited overlap between inputs to different neurons. In the extreme, if there were no overlap at all (as in a diagonal feedback matrix) then the weights could only be rank-deficient if some neurons lacked input.

3.3. Decomposition of Boolean Connection Matrices

As discussed above, various optimization methods failed to find synaptic weights that could impart low-dimensional dynamics to the sparse connection matrices C ∈ {true, false}^{n × n} sampled from Ω. This was an intuitive outcome, but failure of the optimization methods does not guarantee that such weights do not exist. Therefore, we examined a related question that could be tested conclusively. Specifically, we tested whether various instances of C could be decomposed into lower-dimensional Boolean factors, as C = C^LC^R, with C^L ∈ {true, false}^{n × k} and C^R ∈ {true, false}^{k × n}. If this were possible, the connection structure itself would have inherently low rank, independent of a specific choice of synaptic weights. Replacing the true elements of C^L and C^R with real numbers would then create low-rank weight matrices with corresponding k-dimensional dynamics. This approach, therefore, tests whether a given connection matrix has an associated family of low-dimensional recurrent dynamics, similar to an all-to-all connection matrix.

To test this possibility, we first generated connection matrices C by sampling connections from probabilities Ω. For an n × n Boolean matrix C and rank k, we sought the largest submatrix of C that could be represented as a product of rank-k Boolean matrices (for details see Section 2.4). Our approach allowed us to test whether 400 × 400 Boolean connection matrices were consistent with any product of Boolean matrices up to rank 4. As shown in Figure 5C, none of the connection matrices we generated could be decomposed into low-rank products. In fact, typically only a small fraction of each connection matrix (of dimension less than 10 × 10) was consistent with any product of rank four or less. This is an intuitive result because for k « n, the factor matrices contain many fewer degrees of freedom than the connection matrix. These results suggest that—in contrast to densely connected networks—random, sparse, localized networks do not typically have a connection structure that is consistent with flexible low-dimensional dynamics (unless low-dimensional dynamics are due to a small number of large synapses).

FIGURE 5

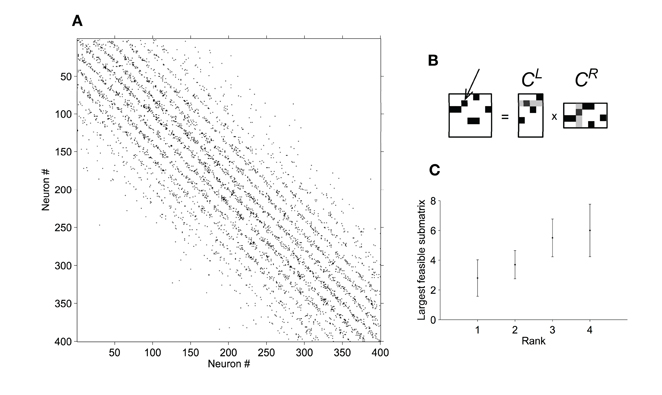
Figure 5. Boolean matrices (black = connection; white = no connection). (A) Sparse, localized connections in a random example network of 20 × 20 neurons. (B) The largest sub-matrix starting from (1,1) that can be expressed as a product of two rank-4 Boolean matrices. (C) Mean ± SD dimension of largest submatrices that can be expressed as a product of Boolean matrices of various ranks, tabulated over 10 random connection matrices per dimension. Low-rank products are typically inconsistent even with very small fractions of random connection matrices.

3.4. Low-Rank Approximation of Spatial Connection Probabilities (Method B)

It is straightforward to create an n × n synaptic weight matrix $W\in {ℝ}^{n\times n}$ of reduced rank k, as a product W^LW^R, where $W^L\in {ℝ}^{n\times k}$ and $W^R\in {ℝ}^{k\times n}$. For example, multiplying a 7 × 4 matrix by a 4 × 7 matrix yields a 7 × 7 matrix with rank at most 4. Indeed, every rank-defficient matrix can be represented as such a product. Furthermore, one may construct sparse low-rank weight matrices by choosing sparse enough W^L and W^R ; Figure 6 shows an example. However, it was not immediately obvious to us whether a low-rank matrix product could generate a sparse weight matrix with realistic spatial connection statistics. To address this question as directly as possible, therefore, we attempted to factor matrices Ω of spatial connection probabilities into left and right matrices that could be sampled to give a low-rank product (see Section 2.3.2, Method B).

FIGURE 6

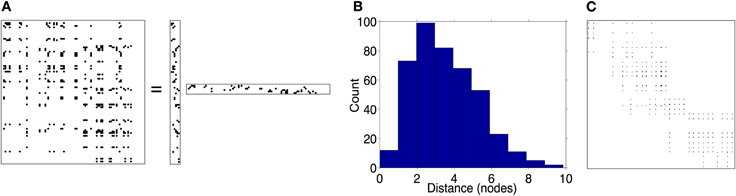
Figure 6. Low-rank connection matrices (see Material and Methods section), (P_max = 0.3, σ = 3). (A) illustrates a product of two rank-6 matrices creating a 100 × 100 rank-6 matrix. (B) distribution of connections over different lengths. (C) a rank-6 connection matrix for a 30 × 30 network; one can plainly see the 6 different clusters of neurons.

Figure 7 shows an example of a 100-neuron network that was constructed according to Method B (Section 2.3.2). In contrast with the results of Method A (above) this network has exactly 4-D dynamics, by construction. Furthermore, the decoding weights Φ reconstruct x much more accurately than those of Method A (Figure 7B), although not as accurately as dense Φ (Figure 7D).

FIGURE 7

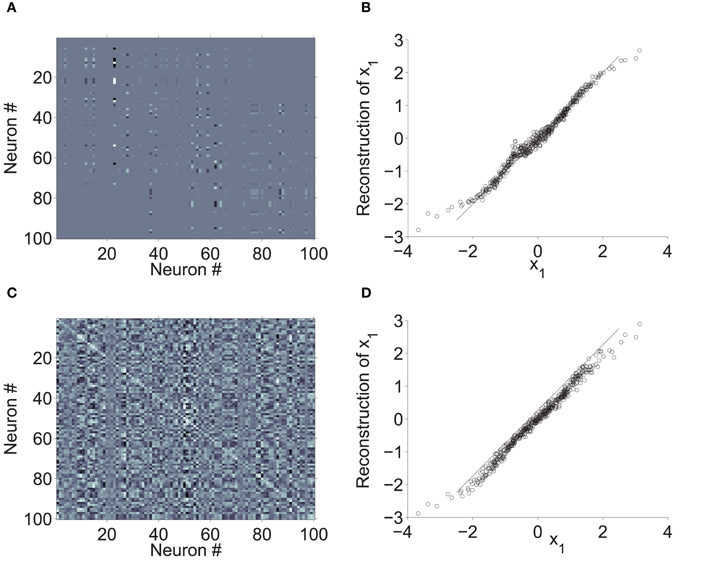
Figure 7. A sparse, low-rank network. The neurons and spatial connection probabilities in this example are the same as those in 3. Connections were structured according to Method B (2.3.2) to approximate a 4-D integrator. (A) Synaptic weights of the sparse network (white = highest; black = lowest; gray = zero). (B) Linear reconstruction of x₁ from noisy firing rates, based on the Φ associated with the synaptic weights in A. (C) Synaptic weights of dense connections between the same neurons, in a network that approximates a 4-D integrator. (D) Reconstruction error associated with the dense decoding weights.

In this example network, some columns of the sparse weight matrix have many large values while others only have small values, so that some neurons have a much larger impact on network activity than others. We suspected that this was related to the small network size and low absolute number of dimensions. Therefore, we investigated connection statistics in much larger networks (on the scale of a cortical column) with a wide range of ranks, in order to estimate the range of ranks that correspond to realistic connectivity in large networks.

Figure 8A shows an example Ω for a 10,000-neuron network with sparse, primarily local connections. The top panel of Figure 8B zooms in on a small sub-matrix of the spatial connection probabilities Ω. To illustrate how the rank k affects the approximation of spatial connection statistics, the remaining panels in Figure 8B show (for the same sub-matrix) the empirical connection probabilities P(C_ij), generated over 1000 samples. P(C_ij) is shown for networks with rank 1, 10, 100, and 1000 (progressing from the top down). In these networks, rank k ≥ 10 (up to three orders of magnitude lower than the number of neurons) yielded good approximations of the ideal spatial connection probabilities. This suggests that subtle changes in connection structure (with minimal effect on spatial connection probability) allow a network to support very low-rank population codes.

FIGURE 8

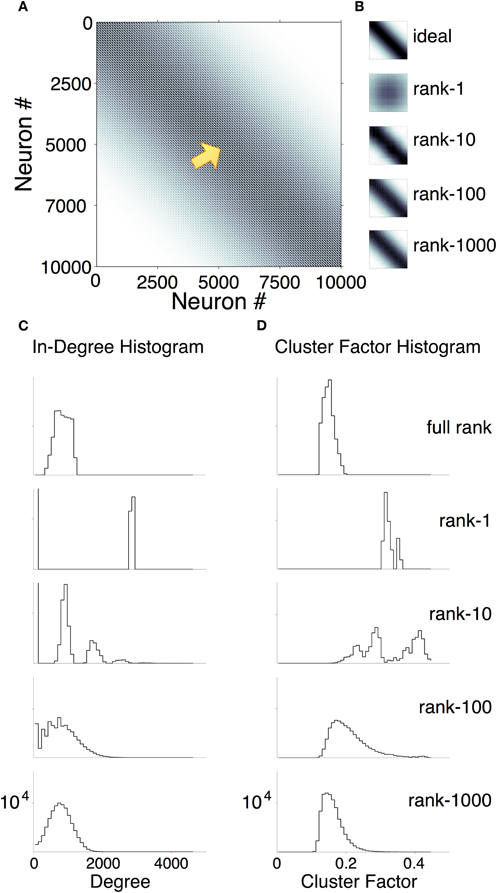
Figure 8. Factorization of a 10,000 node probability matrix and associated network statistics. (A) Ideal connection probability matrix Ω (white = 0; black = 1/3). (B) Close-up of a sub-matrix of Ω (top panel) showing more detail from neuron 5000 to neuron 5100 (at the location of the arrow in A). The remaining panels are empirical probabilities P(C) of the same connections from factorizations of various ranks (1000 samples each; rank = 1, 10, 100, and 1000 from top to bottom). (C and D) In-degree histogram (out-degree was almost identical) and cluster factor histogram. (Both over nine networks.) Top: connections sampled directly from probability matrix. Second from top: connections sampled from rank-1 factors. Third: rank-10 factors. Fourth: rank-100. Fifth: rank-1000.

We then examined various statistics of the low-rank networks and compared them to those of high-rank networks with approximately the same spatial connection probabilities. Figure 8C plots the distribution of in-degree over 10,000-node networks of various ranks. The out-degree distributions were nearly identical. Networks of rank k ≥ 100 had qualitatively similar degree distributions. Figure 8D plots distributions of cluster factors (Watts and Strogatz, 1998) for various ranks. In networks with k = 100 (but not k = 1000), cluster factors were substantially higher than those of full-rank networks. In k = 10 networks, the degree distribition was multi-modal, because a minority of neurons received dense connections from one or more clusters other than their own.

3.5. A Sparsely Connected, Low-Dimensional Integrator

We performed example simulations in order to verify that our sparse, low-rank networks (Section 3.4) could in fact be configured to exhibit chosen dynamics, and that their activity has a much better signal-to-noise ratio than high-rank networks with the similar spatial connection probabilities. Figure 9 shows simulations of 9-D and 90-D neural integrators (Aksay et al., 2007). In each case, the network consisted of a 30 × 30 grid of neurons with random, sparse, and local connections, and similar spatial connection probabilities. The ideal connection probabilities Ω are shown in Figure 9A, and the empirical connection probabilities P(C_ij) are shown in B (rank-9) and C (rank-90).

FIGURE 9

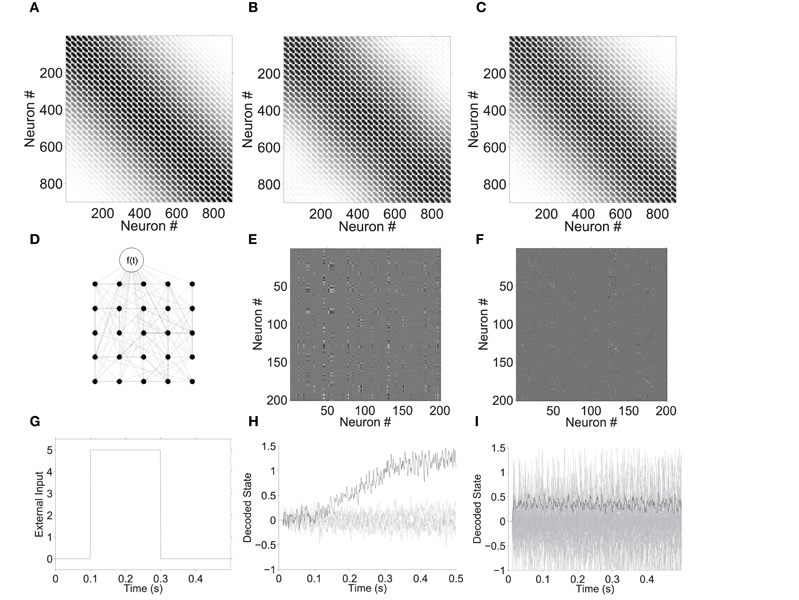
Figure 9. Neural integrator example with 900 sparsely connected neurons in a 30 × 30 grid. (A) Matrix Ω of ideal spatial connection probabilities (white = 0; black = 1/3). (B) Actual connection probabilities P(C) with rank-9 factors. (C) Connection probabilities P(C) with rank-90 factors. (D) Illustrative sketch of a small integrator network, with external input node. An example of the weight matrices for the rank-9 and rank-90 networks is shown in E and F, respectively. For the input function shown in G, plots H and I show the linear reconstruction of x₁ (dark), and other dimensions of x (light) from network spiking activity. The decoding vectors Φ of each network were used for these reconstructions (rank-9 and rank-90, respectively).

An integrator network should ideally maintain a constant encoded value when there is no external input, and gradually change the encoded value at a rate proportional with non-zero input. [Neural integrators, however, exhibit non-ideal behavior such as drift toward attractors (Koulakov et al., 2002)]. The ideal behavior in these simulations, with external input shown in Figure 9G, is to hold a value of 0 for 0.1 s, then increase at a rate of 5 units per second for 0.2 s, and then hold an attained value of 1 thereafter.

Figure 9H and I plot linear reconstructions of x obtained by multiplying post-synaptic currents by Φ, for the 9-D and 90-D networks, respectively. The value of x₁ is plotted in black, and x_l>1 in gray. Panel H demonstrates that the sparsely connected 900-neuron network behaves roughly as an integrator in nine dimensions (≈100 neurons per dimension). In contrast, Figure 9I shows that a similar 90-D network (≈10 neurons per dimension) is dominated by noise and does not integrate its input.

These simulations illustrate that sparsely connected networks can exhibit low-dimensional, high-fidelity dynamics if the weight matrix has a low-rank.

4. Discussion

Low-dimensional recurrent dynamics allow noisy neurons to encode an underlying state vector with high fidelity. The main conclusion of this study is that sparse and primarily local connections are consistent with low-dimensional recurrent dynamics. However, if connections are simply instantiated at random according to spatial connection probabilities, network dynamics apparently have about as many dimensions as there are neurons. Some additional structure is needed to obtain a low-rank synaptic weight matrix and corresponding low-dimensional dynamics.

4.1. Relevance of Linear Reconstruction

We considered the fidelity of the spike code in various networks in terms of linear reconstruction (Salinas and Abbott, 1994) of the state x.

There are many other reconstruction methods. An early method, the population vector, was developed to decode activity in the primate motor cortex during reaching movements (Georgopoulos et al., 1986). The preferred reaching directions of these neurons are combined using a weighted vector sum, where the vector points in the preferred direction and has magnitude equal to the neuron's firing rate. This simple weighted vector sum is a good predictor of reaching direction (Georgopoulos et al., 1986). The population vector method works if there is a sufficient number of neurons, and if their preferred stimuli are uniformly distributed (Theunissen and Miller, 1991; Salinas and Abbott, 1994). Moreover, the population vector method is very similar in performance to maximum likelihood estimates when the neurons have broad turning curves (Seung and Sompolinsky, 1993). As another example, researchers inferred a rat's location from the activity of hippocampal neurons (so called “place cells”) (Wilson and McNaughton, 1993). First, they compiled a signature of neural activities associated with each location in the rat's environment. Later, hippocampal activities were used to estimate the rat's location by choosing the signature with “maximal correspondence.”

Other reconstruction methods have various advantages over optimal linear reconstruction. These include the centroid of preferred directions (e.g., Boyraz and Treue, 2011), which can be generalized to avoid the sensitivity of linear reconstruction to noise correlations (Tripp, 2012), maximum likelihood estimation (Seung and Sompolinsky, 1993), and others (Quian Quiroga and Panzeri, 2009). Information theory also provides a way to evaluate the content of a spike code, independently of any decoding method (Bialek et al., 1999).

We chose linear reconstruction because it is physiologically relevant in terms of its relationship with linear synaptic integration (see Section 2.1). In particular, neurons that integrate inputs linearly can be viewed as being cosine-tuned to a linear reconstruction of a state vector that is encoded by network activity. Linear reconstruction error, therefore, provides a compact index of the shared noise intrinsic in feedback dynamics, in the context of linear synaptic integration.

Linear synaptic integration is a simplification, but it is a reasonable approximation in many conditions (Poirazi et al., 2003; Araya et al., 2006), despite the complexity of neuron membranes and morphology. The computational role of various non-linearities is the subject of ongoing work (Carandini and Heeger, 2011; Gómez González et al., 2011).

4.2. Relationships with Cortical Anatomy

The network models used in this study are highly simplified and only loosely related to cortical anatomy. However, qualitative comparisons are possible. It is striking that in all but the lowest-dimensional networks, spatial connection probabilities are almost indistinguishable from those of full-rank randomly connected networks. With 10,000 neurons, networks with dimensions as low as 10 had connection probabilities that were very similar to 10,000-dimensional networks (Figure 8B). In-degree and out-degree were also similar across networks of rank 100 and higher (Figure 8C). We would, therefore, not expect a biological network's spatial connection probabilities or degree distribution to be very predictive of the network's dynamics or signal-to-noise ratio.

The clearest hallmark of our lower-rank networks was the tendency for nearby neurons to form clusters, with relatively dense inter-connections (Figure 6C). This is consistent with evidence of clustering in cortical microcircuits. Pairs of connected layer 5 neurons are more likely than random networks to have reciprocal connections (Markram, 1997). Similarly, pairs of connected layer 2/3 neurons are more likely than unconnected pairs to share input from a third layer 2/3 cell (Yoshimura et al., 2005). Dense interconnections among triplets are also more likely than expected in a random network (Song et al., 2005). In larger groups of up to eight neurons, connection probabilities diverge even more from the expectations of random networks (Perin et al., 2011). Cortical neurons, therefore, appear to form clusters with relatively dense interconnections, as did our networks with reduced rank and high signal-to-noise ratio. These clusters have been viewed as cell assemblies that encode individual memories (Perin et al., 2011). Their role in our models is slightly broader; they simply encode a state variable (which could be a scalar or vector) and govern its feedback dynamics. Feedback dynamics could potentially form an attractor (e.g., Figure 1), consistent with a content-addressable memory function, and/or an integrator (Figure 9), consistent with a working-memory function. Feedback dynamics could also conceivably underlie a non-memory-like function.

4.3. Limitations and Future Work

The limitations of this study are mainly due to the simplicity of our model compared with the immense complexity of real cortical microcircuits.

A key limitation is that we did not distinguish between different cell types, most notably between excitatory and inhibitory neurons. In realistic synaptic weight matrices, each column would contain values of only one sign, reflecting the fact that neurons are typically either excitatory or inhibitory. Some of our results (e.g., Figure 5) did not require the specification of synaptic weights, and are, therefore, not affected by this limitation. However, our method of generating a sparse weight matrix by decomposing the connection probability matrix (Method B) does not allow us to distinguish between excitatory and inhibitory neurons in a straightforward way. Such a distinction might be achieved by constraining the factor matrices, but we have not explored this approach. Alternatively, our weight matrices could be viewed as functional rather than physical connections, which are implemented by a closely related physical combination of excitatory and inhibitory connections. A matrix of functional synaptic weights can be transformed into a more realistic combination of direct excitatory connections and indirect inhibitory connections through a separate population of inhibitory neurons (Parisien et al., 2008). Previous use of this method has involved dense connections, but we experimented with this approach and found that it also works well with sparse connections.

Our model of cell-intrinsic dynamics is also highly simplified, and we have not explored the impact of more complex cell dynamics. Cell-intrinsic dynamics could potentially increase the dimension of recurrent dynamics, e.g., via spike rate adaptation or synaptic depression that varies in rate across the population (Markram, 1997).

We have modeled recurrent networks in isolation without considering the effects of external inputs (except at a very high level; Figure 9). This is a standard approach, and some dynamic properties (e.g., stability) depend only on internal dynamics and state. A relevant point for future work in this direction is that clusters of layer 2/3 neurons may receive input from distinct groups of layer 4 neurons, with less-segregated input from layer 5 (Yoshimura and Callaway, 2005).

4.3.1. Approximation of low-dimensional dynamics

In our models, neuron responses are restricted to a low-dimensional space by low-rank synaptic weight matrices. As we have shown, this leads to high-fidelity representation despite individually noisy neurons. In the simplest case, if the weight matrix has rank one, each neuron receives the same inputs with the same weights (or their negatives). In this case, each neuron is driven by the same weighted sum of spikes, S_w. Such a network would behave similarly if, in some of the neurons, the weights of two very similarly active neurons were swapped. The synaptic weight matrix would then have rank two. However, if the swapped neurons were perfectly synchronized, the network dynamics would not change at all. In general, there may be many combinations of weights S_w* ≈ S_w that approximate the original sum. In this way, a high-dimensional network might behave much like a low-dimensional network. We have not yet explored the effects in such a network of the residual dimensions that would arise from varied approximations S_w*.

5. Conclusion

In highly simplified models of superficial cortical layers, we have shown that low-dimensional, high-fidelity encoding of state variables depends on additional structure, beyond connection probabilities that depend only on distance between neurons. This additional structure involves clusters of relatively densely connected neurons, consistent with cortical microsctructure.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Murphy Berzish for feedback and assistance with the figures. We are also thankful for the support of the Natural Sciences and Engineering Research Council of Canada (NSERC).

References

Aksay, E., Olasagasti, I., Mensh, B., Goldman, M., and Tank, D. (2007). Functional dissection of circuitry in a neural integrator. Nat. Neurosci. 10, 494–504.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Araya, R., Eisenthal, K. B., and Yuste, R. (2006). Dendritic spines linearize the summation of excitatory potentials. Proc. Natl. Acad. Sci. U.S.A. 103, 18799–18804.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bialek, W., Ruyter van Steveninck, R. D., Rieke, F., and Warland, D. (1999). Spikes: Exploring the Neural Code. Cambridge, MA: MIT Press.

Boyraz, P., and Treue, S. (2011). Misperceptions of speed are accounted for by the responses of neurons in macaque cortical area MT. J. Neurophysiol. 105, 1199–1211.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Britten, K., Shadlen, M., Newsome, W., and Movshon, J. (1992). The analysis of visual motion: a comparison of neuronal and psychophysical performance. J. Neurosci. 12, 4745–4765.

Pubmed Abstract | Pubmed Full Text

Carandini, M., and Heeger, D. J. (2011). Normalization as a canonical neural computation. Nat. Rev. Neurosci. 13, 51–62.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cohen, M. R., and Newsome, W. T. (2009). Estimates of the contribution of single neurons to perception depend on timescale and noise correlation. J. Neurosci. 29, 6635–6648.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cook, E. P., and Maunsell, J. H. R. (2002). Dynamics of neuronal responses in macaque MT and VIP during motion detection. Nat. Neurosci. 5, 985–994.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

DeAngelis, G. C., and Uka, T. (2003). Coding of horizontal disparity and velocity by MT neurons in the alert macaque. J. Neurophysiol. 89, 1094–1111.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Deneve, S., Latham, P. E., and Pouget, A. (2001). Efficient computation and cue integration with noisy population codes. Nat. Neurosci. 4, 826–831.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dubner, R., and Zeki, S. M. (1971). Response properties and receptive fields of cells in an anatomically defined region of the superior temporal sulcus in the monkey. Brain Res. 35, 528–532.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eliasmith, C. (2005). A unified approach to building and controlling spiking attractor networks. Neural Comput. 17, 1276–1314.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eliasmith, C., and Anderson, C. H. (1999). Developing and applying a toolkit from a general neurocomputational framework. Neurocomputing 26–27, 1013–1018.

Eliasmith, C., and Anderson, C. H. (2003). Neural Engineering: Computation, Representation, and Dynamics in Neurobiological Systems. Cambridge, MA: MIT Press.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Eliasmith, C., Westover, M. B., and Anderson, C. H. (2002). A general framework for neurobiological modeling: an application to the vestibular system. Neurocomputing 4446, 1071–1076.

Pubmed Abstract | Pubmed Full Text

Gattass, R., and Gross, C. G. (1981). Visual topography of striate projection zone (MT) in posterior superior temporal sulcus of the Macaque. J. Neurophysiol. 46, 621–638.

Pubmed Abstract | Pubmed Full Text

Georgopoulos, A., Schwartz, A., and Kettner, R. (1986). Neuronal population coding of movement direction. Science 233, 1416–1419.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gómez González, J. F., Mel, B. W., and Poirazi, P. (2011). Distinguishing linear vs. non-linear integration in CA1 radial oblique dendrites: It's about time. Front. Comput. Neurosci. 5:44. doi: 10.3389/fncom.2011.00044

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hellwig, B. (2000). A quantitative analysis of the local connectivity between pyramidal neurons in layers 2/3 of the rat visual cortex. Biol. Cybern. 82, 111–121.

Pubmed Abstract | Pubmed Full Text

Koch, C. (1999). Biophysics of Computation. Oxford: Oxford University Press.

Pubmed Abstract | Pubmed Full Text

Koulakov, A., Raghavachari, S., Kepecs, A., and Lisman, J. (2002). Model for a robust neural integrator. Nat. Neurosci. 5, 775–782.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lee, D. D., and Seung, H. S. (2001). Algorithms for non-negative matrix factorization. Neural Info. Proc. Syst. 13, 556–562.

Markram, H. (1997). A network of tufted layer 5 pyramidal neurons. Cereb. Cortex 7, 523–533.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Maunsell, J. H. R., and Newsome, W. T. (1987). Visual processing in monkey extrastriate cortex. Annu. Rev. Neurosci. 10, 363–401.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Maunsell, J. H. R., and van Essen, D. C. (1983). Functional properties of neurons in middle temporal visual area of the Macaque monkey. I. Selectivity for stimulus direction, speed, and orientation. J. Neurophysiol. 49, 1127–1147.

Pubmed Abstract | Pubmed Full Text

Nicoll, A., and Blakemore, C. (1993). Patterns of local connectivity in the neocortex. Neural Comput. 5, 665–680.

O'Reilly, R. C., and Munakata, Y. (2000). Computational Explorations in Cognitive Neuroscience. Cambridge, MA: MIT Press.

Parisien, C., Anderson, C. H., and Eliasmith, C. (2008). Solving the problem of negative synaptic weights in cortical models. Neural Comput. 20, 1473–1494.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Perin, R., Berger, T. K., and Markram, H. (2011). A synaptic organizing principle for cortical neuronal groups. Proc. Natl. Acad. Sci. U.S.A. 108, 5419–5424.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Poirazi, P., Brannon, T., and Mel, B. W. (2003). Arithmetic of subthreshold synaptic summation in a model CA1 pyramidal cell. Neuron 37, 977–987.

Pubmed Abstract | Pubmed Full Text

Pouget, A., Dayan, P., and Zemel, R. (2000). Information processing with population codes. Nat. Rev. Neurosci. 1, 125–132.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Quian Quiroga, R., and Panzeri, S. (2009). Extracting information from neuronal populations: information theory and decoding approaches. Nat. Rev. Neurosci. 10, 173–185.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Salinas, E., and Abbott, L. F. (1994). Vector reconstruction from firing rates. J. Comput. Neurosci. 1, 89–107.

Pubmed Abstract | Pubmed Full Text

Schwartz, A. B., Kettner, R. E., and Georgopoulos, A. P. (1988). Primate motor cortex and free arm movements to visual targets in three-dimensional space. I. Relations between single cell discharge and direction of movement. J. Neurosci. 8, 2913–2927.

Pubmed Abstract | Pubmed Full Text

Seung, H. S., and Sompolinsky, H. (1993). Simple models for reading neuronal population codes. Proc. Natl. Acad. Sci. U.S.A. 90, 10749–10753.

Pubmed Abstract | Pubmed Full Text

Singh, R., and Eliasmith, C. (2006). Higher-dimensional neurons explain the tuning and dynamics of working memory cells. J. Neurosci. 26, 3667–3678.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Song, S., Sjöström, P. J., Reigl, M., Nelson, S., and Chklovskii, D. B. (2005). Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 3:e68. doi: 10.1371/journal.pbio.0030068

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stepanyants, A., and Chklovskii, D. B. (2005). Neurogeometry and potential synaptic connectivity. Trends Neurosci. 28, 387–394.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Theunissen, F. E., and Miller, J. P. (1991). Representation of sensory information in the cricket cercal sensory system. II. Information theoretic calculation of system accuracy and optimal tuning-curve widths of four primary interneurons. J. Neurophysiol. 66, 1690–1703.

Pubmed Abstract | Pubmed Full Text

Tripp, B. P. (2012). Decorrelation of spiking variability and improved information transfer through feedforward divisive normalization. Neural Comput. 24, 867–894.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Watts, D. J., and Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature 393, 440–442.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wilson, M. A., and McNaughton, B. L. (1993). Dynamics of the hippocampal ensemble code for space. Science 261, 1055–1058.

Pubmed Abstract | Pubmed Full Text

Yoshimura, Y., and Callaway, E. M. (2005). Fine-scale specificity of cortical networks depends on inhibitory cell type and connectivity. Nat. Neurosci. 8, 1552–1559.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Yoshimura, Y., Dantzker, J. L. M., and Callaway, E. M. (2005). Excitatory cortical neurons form fine-scale functional networks. Nature 433, 868–873.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zeki, S. M. (1974). Cells responding to changing image size and disparity in the cortex of the Rhesus monkey. J. Physiol. 242, 827–841.

Pubmed Abstract | Pubmed Full Text