- 1 Department of Perception, Cognition and Action, Max Planck Institute for Biological Cybernetics, Tübingen, Germany
- 2 Department of Brain and Cognitive Engineering, Korea University, Seoul, Korea
There is evidence that observers use learned object motion to recognize objects. For instance, studies have shown that reversing the learned direction in which a rigid object rotated in depth impaired recognition accuracy. This motion reversal can be achieved by playing animation sequences of moving objects in reverse frame order. In the current study, we used this sequence-reversal manipulation to investigate whether observers encode the motion of dynamic objects in visual memory, and whether such dynamic representations are encoded in a way that is dependent on the viewing conditions. Participants first learned dynamic novel objects, presented as animation sequences. Following learning, they were then tested on their ability to recognize these learned objects when their animation sequence was shown in the same sequence order as during learning or in the reverse sequence order. In Experiment 1, we found that non-rigid motion contributed to recognition performance; that is, sequence-reversal decreased sensitivity across different tasks. In subsequent experiments, we tested the recognition of non-rigidly deforming (Experiment 2) and rigidly rotating (Experiment 3) objects across novel viewpoints. Recognition performance was affected by viewpoint changes for both experiments. Learned non-rigid motion continued to contribute to recognition performance and this benefit was the same across all viewpoint changes. By comparison, learned rigid motion did not contribute to recognition performance. These results suggest that non-rigid motion provides a source of information for recognizing dynamic objects, which is not affected by changes to viewpoint.
Introduction
Object motion can play an important role in the detection and perception of three-dimensional (3D) objects. For example, the perceptual system can use translational motion to group image fragments of the same object and segregate it from a cluttered background (Fahle, 1993; Nygård et al., 2009). In addition, an object’s 3D structure and shape can be recovered from a sequence of two-dimensional (2D) images that depict its rotations in depth using structure-from-motion computations (Ullman, 1979; Grzywacz and Hildreth, 1987).
The role of object motion is not limited to shape recovery. There is evidence that object motion per se can be directly used to recognize objects (e.g., Stone, 1998, 1999; Lander and Bruce, 2000; Knappmeyer et al., 2003; Liu and Cooper, 2003; Newell et al., 2004; Vuong and Tarr, 2006; Vuong et al., 2009; Setti and Newell, 2010). For example, Johansson’s (1973) classic point-light display demonstrates that an observer can use only the motion of dots attached to the joints of an otherwise invisible human actor to recognize the actor’s action (e.g., walking or dancing), sex, or even identity if the observer is highly familiar with the actor (Cutting and Kozlowski, 1977). Other studies have shown that manipulating an object’s learned motion can affect observers’ performance on different recognition tasks (e.g., Stone, 1998, 1999; Liu and Cooper, 2003).
However, it is not clear how object motion is encoded in visual memory. To address this issue, we tested observers’ ability to recognize dynamic objects from different perspective viewpoints. When an object is seen from different viewpoints, it projects different 2D retinal images (e.g., imagine viewing a car from the side or from above). Importantly, the larger the difference between two viewpoints is, the more visually dissimilar the projected images will be. For static objects, measuring how viewpoint changes affect recognition performance has helped to reveal how static object features (e.g., edges and parts) are encoded in visual memory (e.g., Biederman, 1987; Tarr et al., 1998; Foster and Gilson, 2002). There is evidence from different recognition tasks that static features can be encoded in a view-invariant or view-dependent manner (see Peissig and Tarr, 2007, for a review). Using a similar strategy, we systematically manipulated the viewpoint to determine whether object motion is encoded in a view-invariant or view-dependent manner.
Features that are encoded in a view-invariant manner in visual memory are robust to changes in viewing conditions (e.g., viewpoint change or illumination change). In comparison, features that are encoded in a view-dependent manner are stored in visual memory as they appear to an observer under specific viewing conditions (e.g., like a template). They are thus less robust to changes to viewing conditions. One way to distinguish between these two types of features is to test recognition performance across changes in viewpoints (Peissig and Tarr, 2007). That is, one can test how observers’ recognition performance (e.g., accuracy and/or response times) varies with changes in viewpoint. Typically, recognition performance decreases with increasing differences between a familiar and a novel viewpoint (e.g., Bülthoff and Edelman, 1992; Tarr et al., 1998). This robust viewpoint effect across many stimuli and recognition tasks has motivated many computational models to adopt a view-dependent approach to understanding visual object recognition (e.g., Serre et al., 2007; Ullman, 2007; for a view-invariant approach, see Hummel and Biederman, 1992).
To date, only a few studies have investigated how object motion affected recognition performance across changes in viewpoint. For example, the recognition of non-rigid facial motion (e.g., expressions) has been shown to be less affected by viewpoint changes than the recognition of rigid (e.g., head nodding) and non-rigid facial motion combined (Watson et al., 2005). The recognition of point-light walkers has also been shown to be influenced by view-dependent information and insensitive to distortions of the human body’s 3D structure (Bülthoff et al., 1998). More recently, Vuong et al. (2009) found that observers could use the articulatory motion of novel objects to help them recognize objects across larger viewpoint changes. These articulatory motions are similar to the movements of the human body.
Stone (1998) referred to the learned motion of a dynamic object as its spatio-temporal signature. He demonstrated that observers directly used these signatures for object recognition (Stone, 1998, 1999). In his studies, observers first learned a small set of novel amoeboid objects that rotated rigidly in depth with a tumbling motion. During the learning phase, the objects always rotated in depth in the same manner (and particularly in the same direction). These objects were presented as an animation consisting of an ordered sequence of views (i.e., a video). When observers’ reached a learning criterion, Stone reversed the rotation direction of these now familiar objects, by presenting the learned animation sequence in reverse frame order (i.e., presenting videos of the learned objects backward). This sequence-reversal manipulation reduced recognition accuracy by as much as 22%. Importantly, this manipulation does not disrupt the spatial properties of the 2D images in the animation sequence nor does it disrupt structure-from-motion processes (Ullman, 1979). Therefore, sequence-reversal effects supported the claim that a moving object provides dynamic information per se for recognition, in addition to static shape information (Stone, 1998, 1999).
Sequence-reversal has been used extensively to study the role of object motion in recognition across different tasks, stimuli, and even species. The sequence-reversal effect has been demonstrated with a large set of 32 rigidly rotating objects, which were implicitly learned (Liu and Cooper, 2003). In addition, the effect has been shown to be more prominent when observers identified objects with highly similar shapes compared to those with highly distinctive 3D structures (Vuong and Tarr, 2006). In addition, Wang and Zhang (2010) showed that observers were also sensitive to local frame sequences. In their study, they took an animation sequence and divided it into shorter sub-sequences. They then reversed the frame order within these “local” sub-sequences, while preserving the “global” order of the sub-sequences themselves. They found that observers’ recognition performance was impaired in this case. The sequence-reversal effect has also been demonstrated with non-rigidly moving faces (Lander and Bruce, 2000). Finally, this effect has even been shown with pigeons, indicating that sequence-reversal disrupts a source of visual information that is not unique to human cognition (Spetch et al., 2006).
The current experiments were conducted to investigate the effect of sequence-reversal on the recognition of dynamic amoeboid objects across changes in viewpoint. These objects were chosen because they lack a distinctive geometric structure and because they do not constitute a highly familiar object class (e.g., faces). If observers rely on an object’s motion, sequence-reversal would impair recognition performance, compared to preserving the learned sequence order. On the other hand, there would be no influence of sequence-reversal if recognition depends strictly on static view-dependent information (e.g., 2D shape features) because these features are not disrupted by this manipulation. In addition, we investigated how the effect of sequence-reversal interacted with viewpoint changes for non-rigid and rigid object motion.
Materials and Methods
Three experiments were conducted to assess how participants encoded object motion learned from a specific viewpoint. In particular, the experiments were designed to determine whether object motion was encoded for recognition in a view-invariant or view-dependent manner (Watson et al., 2005; Perry et al., 2006; Vuong et al., 2009). Each experiment consisted of a familiarization phase, followed by a testing phase. In the familiarization phase, participants learned two objects that deformed non-rigidly (Experiments 1–2) or rotated rigidly in depth over time (Experiment 3). Each object’s motion was the same on every trial during this phase. In the testing phase, observers were required to discriminate the learned target objects from two new distracter objects.
To replicate previous findings (e.g., Stone, 1998, 1999; Lander and Bruce, 2000; Liu and Cooper, 2003; Vuong and Tarr, 2006), we first investigated if sequence-reversal affected the recognition of novel non-rigidly deforming objects on an old-new recognition task (Experiment 1a) and a two-interval forced-choice (2IFC) task (Experiment 1b). Following this, we investigated the effect of sequence-reversal on recognizing non-rigidly deforming (Experiment 2) or rigidly rotating (Experiment 3) objects across a range of novel viewpoints.
Participants
Seventy volunteers (age range: 18–35 years) were recruited from the Institute’s participant database – E1a: 16; E1b: 14; E2: 24; E3: 21. They were paid 8€/h for their time and provided informed consent, approved by the local ethics committee. All participants had normal or corrected-to-normal vision and did not participate in more than one experiment.
Apparatus
The experiments were conducted on a Macintosh G4 computer, which was controlled by customized MATLAB software that used the PsychToolBox extension (Brainard, 1997; Pelli, 1997). The stimuli were presented on a 21′′ CRT monitor with a resolution of 1152 × 864 pixels and a refresh rate of 75 Hz. Participants were seated 60 cm from the screen. All responses were collected from a standard keyboard.
Material
Figure 1 shows an example of the 3D amoeboid object used in the current study. All the visual stimuli were bounded by a square that was centered on the screen (diagonal ≈ 15.6°). The experimental stimuli were derived from animation sequences of 100 numerically labeled images (320 × 320 pixels) that depicted the objects moving smoothly over time (22 frames/s), either deforming non-rigidly (Experiments 1 and 2) or rotating rigidly in depth (Experiment 3). Each sequence was rendered from seven camera viewpoints (see Figure 1B).
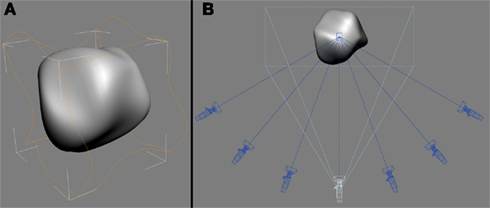
Figure 1. Amoeboid objects were creating by applying a set of sinusoidal deformation fields (orange outline) that deformed a base sphere in 3D space (A). View-sequences of the objects moving over time were rendered from seven virtual cameras (B). The white camera indicates the 0° viewpoint used during the familiarization phase.
The 3D objects and their animation sequences were produced using 3D Studio Max (v. 7; Autodesk, Montreal). For each object, the 3D coordinates of a sphere’s vertices were smoothly modulated by the application of a series of random sinusoidal deformation fields in Studio Max (see Figure 1A). By randomly shifting the phase of the sinusoidal deformation fields applied to the base sphere, we could synthesize amoeboids with different 3D shapes (Norman et al., 1995).
Non-rigid deformations could be introduced by shifting the phases of these sinusoidal deformation fields simultaneously at a rate of ∼0.16 cycles every 20th frame. This induced a smooth deformation of each object’s 3D structure over time. Alternatively, each object could be rigidly rotated about its center to a new pose every 20th frame. This produced a smooth rigid tumbling motion that did not deform the object’s 3D structure. A randomly determined sequence of poses ensured that each object had a unique rigid rotational path in depth.
Altogether, 4 non-rigidly deforming objects were created for Experiment 1, 16 non-rigidly deforming objects for Experiment 2, and 16 rigidly rotating objects for Experiment 3. For each participant, four objects were randomly selected from the set of possible objects of the relevant experiment. Two of the objects were randomly assigned to be targets and two as distracters.
A virtual camera was positioned in front of each object and focused on its center of mass. This was designated as the 0° viewpoint (the white camera in Figure 1B). This camera was rotated clockwise or counter-clockwise along the azimuth. Ordered sequences of 100 images were then rendered for each object from seven viewpoints (0°, ±20°, ±40°, ±60°; see Figure 1B). Video examples are provided as Supplementary Material. All participants learned the objects from the 0° viewpoint during the familiarization phase. In addition, a grayscale luminance noise pattern served as a mask.
Experimental Procedure
Figure 2 illustrates the trial sequence on the familiarization and testing phases for the old-new recognition task (Experiment 1) and the 2IFC task (Experiments 1b, 2, and 3).
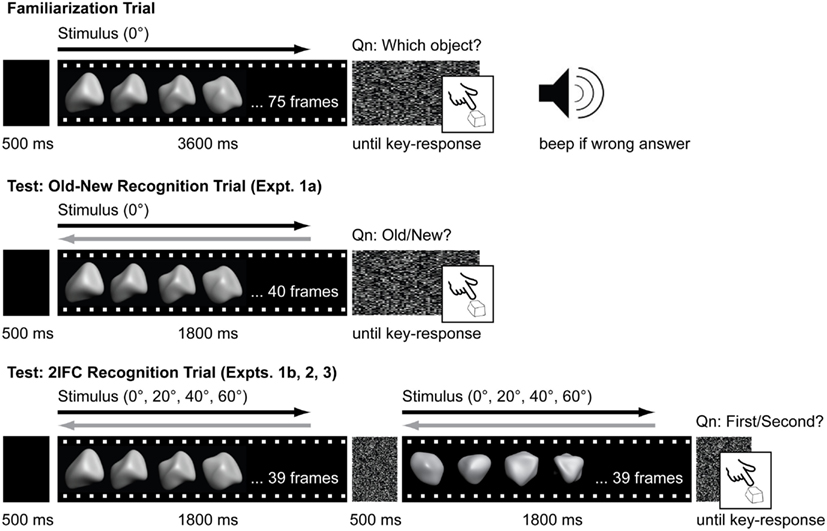
Figure 2. Timeline of familiarization and test trials. From top to bottom: Familiarization trial for all experiments, Old-new recognition test trial for Experiment 1a, 2IFC recognition test trial for Experiments 1b, 2, and 3. On familiarization trials, animations for the stimuli were always presented in ascending sequence order (black arrow) and objects were always presented from the 0°viewpoint. On test trials, animations for the stimuli could be animated in either the same sequence order as during familiarization (black arrow) or in reverse sequence order (gray arrow). With the exception of Experiment 1, objects could also be presented from a range of perspective viewpoints (0°, ±20°, ±40°, ±60°).
Familiarization phase
The familiarization phase was the same for all three experiments. During this phase, one of the two target objects was presented on each trial. The stimulus was a 75-image sequence that was sampled from the object’s full 100-image sequence. These sequences were always presented in numerically ascending-order. After the presentation of each stimulus (∼3.4 s), a noise mask appeared until participants responded with one of two keys (i.e., y or b) to indicate the object’s identity. Each target was randomly assigned a key. Participants were provided with an auditory feedback for incorrect responses. Every participant performed 104 familiarization trials.
Testing phase
During the testing phase, participants had to discriminate targets learned during the familiarization phase from distracters. In this phase, the stimuli were shorter animation sequences (i.e., 40 sequential images for Experiment 1a; and 39 sequential images for Experiments 1b, 2, and 3) of the two targets learned during the familiarization phase or two distracters. These sequences lasted ∼1.8 s each. For the old-new recognition task (Experiment 1a), participants were presented with one stimulus on each trial and had to decide whether that stimulus was old (i.e., one of the targets) or new (i.e., one of the distracters) by responding with one of two keys after the stimulus presentation ended. For the 2IFC task (Experiments 1b–3), two stimuli were presented sequentially on each trial, one of which was a target and one of which was a distracter. The target and distracter were separated by a 500 ms noise mask. There was also a noise mask presented at the end of the second interval, which stayed on the screen until participants responded. Each target object appeared equally often in the first and second interval. Participants had to decide which interval contained the target object. They were only allowed to respond after both stimuli had been presented. In all experiments, participants were encouraged to respond as quickly and as accurately as possible.
The dynamic objects could be shown in either ascending or descending-order frame sequences. For the target objects, the ascending-order sequence was the same (learned) object motion and the descending-order sequence was the reverse object motion. For Experiments 2 and 3, target objects could be presented from all seven viewpoints (i.e., 0°, ±20°, ±40°, ±60°). The distracter objects in these two experiments were presented at one of these viewpoints, which were randomly chosen. Participants were informed that the target objects’ motion could be reversed relative to their motion in the familiarization phase. They were instructed to continue to respond to these as targets.
The test stimuli were sampled only from the central range of the full 100-image sequences (i.e., images 26–75); images that comprised this range were presented equally often during the familiarization phase. The four objects (two targets and two distracters) were presented equally often. There were an equal number of trials in all test conditions (sequence order in Experiment 1; sequence order and viewpoint difference in Experiments 2 and 3). There were a total of 352 test trials for Experiment 1a, 192 trials for Experiment 1b, and 224 trials for Experiments 2 and 3.
Results
Recognition performance in the test conditions was measured by sensitivity (d′; MacMillan and Creelman, 1991). Figure 3 summarizes sensitivity scores for Experiments 1, 2, and 3, which were collapsed for the direction of the viewpoint difference in Experiments 2 and 3. In the present study, we focused on observers’ sensitivity data because we were interested in how object motion was encoded in visual memory. Nonetheless, it should be noted that response-time results were consistent with sensitivity scores and there was no evidence of any speed-accuracy trade-offs. The sensitivity data were submitted to paired-sampled t-tests or repeated-measures analyses of variance (ANOVAs). Confidence intervals were computed using the within-subjects error term from the sequence order condition (Experiment 1) or its interaction with viewpoint difference (Experiments 2 and 3), where appropriate (Loftus and Masson, 1994). An α-level of 0.05 indicated statistical significance. Greenhouse–Geisser corrections were applied when the assumption of sphericity was violated. In addition, effect sizes were computed as Cohen’s d and partial η2 for the t-tests and ANOVAs respectively (Morris and DeShon, 2002).
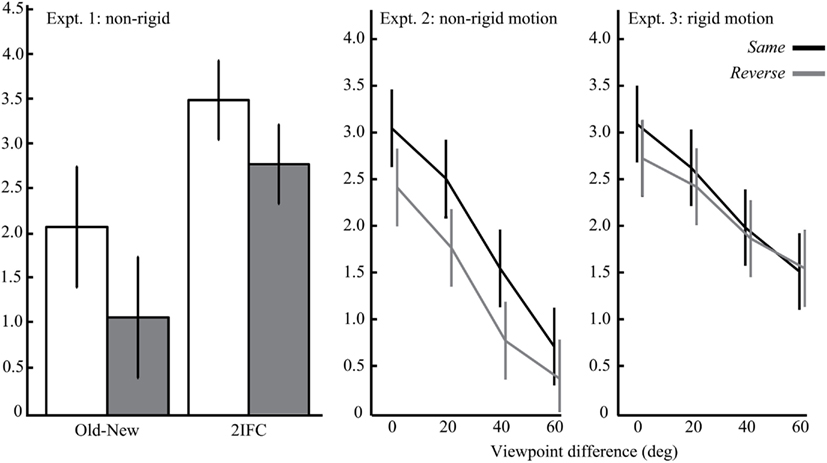
Figure 3. Mean sensitivity (d′) scores of Experiments 1 to 3 (from left to right), when animations were presented in the same (black) or reverse (gray) sequence order. Error bars represent the 95% confidence intervals.
Experiment 1
Experiment 1 tested the effect of sequence-reversal of non-rigidly deforming amoeboids on an old-new recognition (Experiment 1a) and 2IFC task (Experiment 1b). A significant main effect of sequence order was found on d′ scores (E1a: t15 = 3.19, Cohen’s d = 0.81; E1b: t13 = 3.49, Cohen’s d = 1.02). Participants were more sensitive in recognizing learned objects when they were animated in the same sequence order as during the familiarization phase than when they were animated with the reverse order. Like previous studies on rigid object motion (Stone, 1998, 1999; Liu and Cooper, 2003; Vuong and Tarr, 2006; Wang and Zhang, 2010), these results show that recognition performance is similarly sensitive to learned non-rigid motion.
Experiment 2
In Experiment 2, we tested the effect of sequence-reversal of non-rigidly deforming objects across different viewpoints using the 2IFC task. The participants’ d′ scores were submitted to a repeated-measures ANOVA for the test conditions of sequence order (same, reverse) and viewpoint difference (0°, ±20°, ±40°, ±60°).
Main effects were found for both sequence order (F1,23 = 13.0, partial η2 = 0.36) and viewpoint difference (F2,44.9 = 42.8, partial η2 = 0.65). Sequence-reversal and novel objects viewpoints produced lower d′ scores. In addition, d′ decreased linearly as a function of viewpoint difference, as revealed by a significant linear trend (F1,23 = 67.2, partial η2 = 0.75). There was no significant interaction between sequence order and viewpoint difference (F1,69 = 0.66, partial η2 = 0.03). That is, the sequence-reversal effect was constant across the different viewpoints. Taken together, these findings show that the recognition of non-rigidly deforming objects was sensitive to changes to the learned viewpoint as well as learned object motion.
Experiment 3
Experiment 3 was identical to Experiment 2 except that we tested the effect of sequence reversal with rigidly rotating objects. The d′ data from Experiment 3 were submitted to the same ANOVA as in Experiment 2. In contrast to Experiment 2, there was no significant effect of sequence order (F1,20 = 2.18, partial η2 = 0.10). However like the previous experiment, there was a significant effect of viewpoint difference (F3,60 = 13.3, partial η2 = 0.40). More specifically, d′ decreased linearly as a function of viewpoint difference (F1,20 = 22.9, partial η2 = 0.53). There was no significant interaction between sequence order and viewpoint difference in Experiment 3 (F1,60 = 0.56, partial η2 = 0.03). Thus, the recognition of rigidly rotating objects in this experiment was sensitive to changes to the learned viewpoint but not to learned object motion.
Discussion
In the current study, we used a sequence-reversal manipulation to test the extent to which observers encoded object motion per se during learning, and how robust such dynamic representations are to viewpoint changes (Stone, 1998, 1999; Liu and Cooper, 2003; Vuong and Tarr, 2006; Wang and Zhang, 2010). We found a sequence-reversal effect for non-rigidly deforming objects across a variety of tasks (Experiments 1 and 2): Observers performed more accurately (as measured by sensitivity) when target objects were shown in the same sequence order than when they were shown in the reverse sequence order, even though sequence reversal did not disrupt the objects’ 3D structure or set of available 2D images. We also found a large viewpoint effect when observers were tested with these objects (Experiment 2): Observers’ sensitivity decreased with increasing viewpoint changes from the learned viewpoint. Importantly, however, the benefit of preserving the learned object motion was constant across all magnitudes of viewpoint change. In contrast to non-rigid motion, we found a viewpoint effect but no sequence-reversal effect when the objects rotated rigidly in depth (Experiment 3). Taken together, these results provide insights into how object motion is encoded in visual memory, and provide important constraints for different models of object recognition.
Learned Non-Rigid Object Motion Provides a View-invariant Benefit to Dynamic Object Recognition
In combination with previous studies, our results suggest that the process of visual object recognition relies on both view-dependent shape information as well as motion information (Stone, 1998, 1999; Liu and Cooper, 2003; Vuong and Tarr, 2006; Wang and Zhang, 2010). This conclusion has several important implications. First, by using visually similar amoeboid objects that did not have distinctive static shape features, our results directly show that non-rigid object motion can be encoded in visual object memory. Second, learned non-rigid object motion contributes directly to the recognition process in a view-invariant manner, although dynamic objects seem to be encoded in view-dependent manner. That is, the pattern of recognition performance suggests that the contribution of learned non-rigid object motion does not deteriorate with increasing disparity between learned and novel viewpoints. Lastly, our findings extend the results from previous studies showing that non-rigid object motion can facilitate view generalization (Watson et al., 2005; Vuong et al., 2009). Importantly, our results show that this facilitation is not restricted to a highly familiar object class (i.e., faces) or restricted to only articulatory motion.
The pattern of recognition performance in Experiment 2 – namely, a consistent contribution of object motion across viewpoint differences – mirrors one that has been reported before (Foster and Gilson, 2002). Foster and Gilson observed that certain object properties, such as the number of discernible parts, led to a uniform benefit to the recognition of novel bent-wire objects, regardless of the viewpoint of the test objects. Objects that were discriminable on the basis of the number of their parts were better recognized than those that did not differ with respect to this property. Nonetheless, observers’ recognition performance with these objects also decreased with increasing differences in viewpoint.
Foster and Gilson (2002) proposed that the successful recognition of an object can depend on multiple sources of information, those that are accessible across views and those that are dependent on view-familiarity. Visual object recognition can rely on either or both contributions. Like the number of object parts, learned non-rigid motion could constitute an object property that can be accessed across a range of viewpoints and, thus, provides a view-invariant benefit to recognition. However, recognition can also continue to rely on view-dependent information such as image-based features of an object’s shape.
Interestingly, we did not find a significant benefit of learned motion for rigidly rotating objects (Experiment 3). Previous studies which demonstrated a reversal effect with rigid rotation used the same tumbling motion across all objects (Stone, 1998, 1999; Liu and Cooper, 2003; Vuong and Tarr, 2006). In our current study, each object had a unique tumbling motion. Future work will be necessary to determine if this stimulus difference could account for the contrasting results. However, it should be noted that the reversal effect is not automatic; it can be mediated by factors such as shape similarity and task difficulty (Liu and Cooper, 2003; Vuong and Tarr, 2006). For example, it has been shown to be more prominent in the recognition of blobby objects similar to the ones used here and less so with objects which have highly distinctive parts (Vuong and Tarr, 2006). In addition, it is more apparent in the recognition of objects that were learned moving fast compared to those that were learned moving slow (Balas and Sinha, 2009).
Future experiments will be needed to determine the particular spatio-temporal aspects of motion that are encoded to give rise to the view-invariant benefit we observed here. For example, optic-flow patterns could be directly represented as a dynamic object property for subsequent recognition (Casile and Giese, 2005). In the next two sections, we outline some possible mechanisms that could explain the contribution of object motion to recognition.
Temporal Associations for Learning Object Motion
In a dynamic environment, subsequent views of the same object tend to occur in close temporal proximity, even if these views are drastically different from each other. Several researchers have suggested that this temporal contingency can induce time-dependent Hebbian learning between neuronal units – possibly in the anterior inferotemporal (IT) brain regions (Miyashita, 1988) – that is sensitive to the order of view-dependent shape features present in successive images of an animation sequence (Wallis and Bülthoff, 2001; Wallis, 2002). Learning these spatio-temporal associations of a dynamic object can be reinforced with repeated exposure to that object undergoing the same motion. Thus, a learned animation sequence will lead to a larger neural response than a reversed animation sequence (Wallis, 1998).
Our results are consistent with this form of temporal-associative learning. While a temporal-associative account of dynamic object learning remains plausible, it is unlikely to fully explain the contribution of learned object motion to recognition performance. For example, a purely temporal-associative account suggests that the contribution of learned motion to object recognition is automatic, regardless of whether the motion is rigid or non-rigid. However, we did not find any benefits of rigid motion for object recognition in our study.
Hierarchical Models for the Recognition of Learned Object Motion
In addition to temporal-associative mechanisms, other researchers have proposed hierarchical-processing mechanisms that could provide insights into how object motion can be encoded in visual memory and contribute to object recognition in a view-invariant manner. Generally, these hierarchical models assume that visual features are progressively processed from simple features (e.g., edges) to more complex features that are conjunctions of simpler ones (Riesenhuber and Poggio, 1999; Serre et al., 2007).
Although these models were originally proposed for static features, they can be extended to include dynamic features. For example, Giese and Poggio (2003) introduced a motion pathway that operates in parallel with a form pathway. This motion pathway contributes to visual recognition by processing visual motion in a feed-forward and hierarchical fashion, employing principles similar to those proposed for the form pathway (Riesenhuber and Poggio, 1999). Giese and Poggio’s model proposes that visual motion is first processed in early visual cortex (V1, V2) by direction-selective neurons. The motion signals are subsequently pooled by detectors for local optic-flow patterns such as translation and expansion in the temporal lobe (e.g., hMT+). Eventually, these relatively simple optic-flow patterns are pooled by detectors that respond selectively to complex optic-flow patterns that define the individual moments of familiar movement sequences (e.g., STS). Thus, complex static and dynamic features at the end of both pathways can, in principle, encode the unique spatio-temporal patterns of an object’s learned motion.
Giese and Poggio’s (2003) model was originally intended for the recognition of biological motion. Nonetheless, it should also generalize to the recognition of novel object classes with unique spatio-temporal patterns. Indeed, our results in combination with previous studies suggest that different types of motion (rigid versus non-rigid) can lead to more accurate recognition across different viewpoint changes (see also, Watson et al., 2005; Perry et al., 2006; Vuong et al., 2009; Wallis et al., 2009). Within Giese and Poggio’s model, this would suggest that recognition performance is influenced by optic-flow patterns, in the mid- and especially the later processing stages of visual motion. Speculatively, these features could capture the motion information that our participants relied upon for object recognition (Watson et al., 2005; Perry et al., 2006; Vuong et al., 2009; Wallis et al., 2009).
Conclusion
The contribution of learned object motion to the recognition of dynamic objects is view-invariant. However, our results suggest that any such contributions of object motion are not automatic but may depend on the requirements of the recognition task instead. Computational models of object recognition should consider the contribution of motion-based information, independently from image-based information about an object’s shape. Future studies should also investigate the conditions that lead to a stronger reliance on certain types of information over others.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by the Max Planck Society and the WCU (World Class University) program through the National Research Foundation of Korea funded by the Ministry of Education, Science and Technology (R31-10008). We would like to thank Profs. Ian Thornton, Roland Fleming, Christian Wallraven, and Dr. Isabelle Bülthoff for their helpful comments.
Supplementary Material
The Movies S1–S8 for this article can be found online at http://www.frontiersin.org/Computational_Neuroscience/10.3389/fncom.2012.00026/abstract
References
Balas, B., and Sinha, P. (2009). A speed-dependent inversion effect in dynamic object matching. J. Vis. 9, 1–13.
Biederman, I. (1987). Recognition-by-components: a theory of human image understanding. Psychol. Rev. 94, 115–147.
Bülthoff, H. H., and Edelman, S. (1992). Psychophysical support for a two-dimensional view interpolation theory of object recognition. Proc. Natl. Acad. Sci. U.S.A. 89, 60–64.
Bülthoff, I., Bülthoff, H. H., and Sinha, P. (1998). Top-down influences on stereoscopic depth-perception. Nat. Neurosci. 1, 254–257.
Casile, A., and Giese, M. A. (2005). Critical features for the recognition of biological motion. J. Vis. 5, 348–360.
Cutting, J. E., and Kozlowski, L. T. (1977). Recognizing friends by their walk – gait perception without familiarity cues. Bull. Psychon. Soc. 9, 353–356.
Fahle, M. (1993). Figure-ground discrimination from temporal information. Proc. R. Soc. Lond. B Biol. Sci. 254, 199–203.
Foster, D. H., and Gilson, S. J. (2002). Recognizing novel three-dimensional objects by summing signals from parts and views. Proc. R. Soc. Lond. B Biol. Sci. 269, 1939–1947.
Giese, M. A., and Poggio, T. (2003). Neural mechanisms for the recognition of biological movements. Nat. Rev. Neurosci. 4, 179–192.
Grzywacz, N. M., and Hildreth, E. C. (1987). Incremental rigidity scheme for recovering structure from motion – position-based versus velocity-based formulations. J. Opt. Soc. Am. A 4, 503–518.
Hummel, J. E., and Biederman, I. (1992). Dynamic binding in a neural network for shape recognition. Psychol. Rev. 99, 480–517.
Johansson, G. (1973). Visual perception of biological motion and a model for its analysis. Percept. Psychophys. 14, 201–211.
Knappmeyer, B., Thornton, I. M., and Bülthoff, H. H. (2003). The use of facial motion and facial form during the processing of identity. Vision Res. 43, 1921–1936.
Lander, K., and Bruce, V. (2000). Recognizing famous faces: exploring the benefits of facial motion. Ecol. Psychol. 12, 259–272.
Liu, T., and Cooper, L. A. (2003). Explicit and implicit memory for rotating objects. J. Exp. Psychol. Learn. Mem. Cogn. 29, 554–562.
Loftus, G. R., and Masson, M. E. J. (1994). Using confidence intervals in within-subject designs. Psychon. Bull. Rev. 1, 476–490.
MacMillan, N. A., and Creelman, C. D. (1991). Detection Theory: A User’s Guide. Cambridge: Cambridge University Press.
Miyashita, Y. (1988). Neuronal correlate of visual associative long-term-memory in the primate temporal cortex. Nature 335, 817–820.
Morris, S. B., and DeShon, R. P. (2002). Combining effect size estimates in meta-analysis with repeated measures and independent-groups designs. Psychol. Methods 7, 105–125.
Newell, F. N., Wallraven, C., and Huber, S. (2004). The role of characteristic motion in object categorization. J. Vis. 4, 118–129.
Norman, J. F., Todd, J. T., and Phillips, F. (1995). The perception of surface orientation from multiple sources of optical information. Percept. Psychophys. 57, 629–636.
Nygård, G. E., Looy, T. V., and Wagemans, J. (2009). The influence of orientation jitter and motion on contour saliency and object identification. Vision Res. 49, 2475–2484.
Peissig, J. J., and Tarr, M. J. (2007). Visual object recognition: do we know more now than we did 20 years ago? Annu. Rev. Psychol. 58, 75–96.
Pelli, D. G. (1997). The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat. Vis. 10, 437–442.
Perry, G., Rolls, E. T., and Stringer, S. M. (2006). Spatial vs temporal continuity in view invariant visual object recognition learning. Vision Res. 46, 3994–4006.
Riesenhuber, M., and Poggio, T. (1999). Hierarchical models of object recognition in cortex. Nature 2, 1019–1025.
Serre, T., Wolf, L., Bileschi, S., Riesenhuber, M., and Poggio, T. (2007). Robust object recognition with cortex-like mechanisms. IEEE Trans. Pattern Anal. Mach. Intell. 29, 411–426.
Setti, A., and Newell, F. N. (2010). The effect of body and part-based motion on the recognition of unfamiliar objects. Vis. Cogn. 18, 456–480.
Spetch, M. L., Friedman, A., and Vuong, Q. C. (2006). Dynamic object recognition in pigeons and humans. Learn. Behav. 34, 215–228.
Stone, J. V. (1999). Object recognition: view-specificity and motion-specificity. Vision Res. 39, 4032–4044.
Tarr, M. J., Williams, P., Hayward, W. G., and Gauthier, I. (1998). Three-dimensional object recognition is viewpoint dependent. Nat. Neurosci. 1, 275–277.
Ullman, S. (1979). The interpretation of structure from motion. Proc. R. Soc. Lond. B. Biol. Sci. 203, 405–426.
Ullman, S. (2007). Object recognition and segmentation by a fragment-based hierarchy. Trends Cogn. Sci. (Regul. Ed.) 11, 58–64.
Vuong, Q. C., Friedman, A., and Plante, C. (2009). Modulation of viewpoint effects in object recognition by shape and two kinds of motion cues. Perception 38, 1628–2648.
Vuong, Q. C., and Tarr, M. J. (2006). Structural similarity and spatiotemporal noise effects on learning dynamic novel objects. Perception 35, 497–510.
Wallis, G. (1998). Spatio-temporal influences at the neural level of object recognition. Network 9, 265–278.
Wallis, G. (2002). The role of object motion in forging long-term representations of objects. Vis. Cogn. 9, 233–247.
Wallis, G., Backus, B. T., Langer, M., Huebner, G., and Bülthoff, H. H. (2009). Learning illumination-and orientation-invariant representations of objects through temporal association. J. Vis. 9, 1–8.
Wallis, G., and Bülthoff, H. H. (2001). Effects of temporal association on recognition memory. Proc. Natl. Acad. Sci. U.S.A. 98, 4800–4804.
Wang, Y., and Zhang, K. (2010). Decomposing the spatiotemporal signature in dynamic 3D object recognition. J. Vis. 10, 1–16.
Keywords: visual object recognition, motion, spatio-temporal signature, non-rigid motion, reversal effect, view-dependency, rigid motion, depth rotation
Citation: Chuang LL, Vuong QC and Bülthoff HH (2012) Learned non-rigid object motion is a view-invariant cue to recognizing novel objects. Front. Comput. Neurosci. 6:26. doi: 10.3389/fncom.2012.00026
Received: 17 January 2012; Accepted: 22 April 2012;
Published online: 22 May 2012.
Edited by:
Jay Hegdé, Georgia Health Sciences University, USACopyright: © 2012 Chuang, Vuong and Bülthoff. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Heinrich H. Bülthoff, Department of Perception, Cognition and Action, Max Planck Institute for Biological Cybernetics, Spemannstrasse 41, 72076 Tübingen, Germany. e-mail:aGhiQHR1ZWJpbmdlbi5tcGcuZGU=

 Quoc C. Vuong1
Quoc C. Vuong1