A single theoretical framework for circular features processing in humans: orientation and direction of motion compared

1. Introduction

When viewing a scene, it is known that perception of one element is strongly affected by the spatial context in which it is embedded (Spillmann and Werner, 1996; Albright and Stoner, 2002). These contextual modulations are used as sensitive tools for unraveling a given feature perception and relate it to the specific visual structure where it is known to be processed. Frequently studied are misperceptions and illusory effects on simple features as contour, brightness, color, orientation, or motion (Marshak and Sekuler, 1979; Reinhardt-Rutland, 1988; Lesher, 1995; Spillmann and Ehrenstein, 1996; Spillmann and Werner, 1996). On the other hand, neurophysiological studies in the last decades demonstrated common structural patterns of neuronal organization within different sensory areas (Mountcastle, 1997), and since Hubel and Wiesel (1974) seminal work a functional regular pattern of feature coding within a given visual area.

Of interest here are the early orientation and direction of motion perception. Contextual effects on small oriented stimuli are associated to the primary visual cortex organization known to be the first stage of orientation computation in primates and humans (Gilbert and Wiesel, 1990; Field et al., 1993; Polat and Sagi, 1993; Chavane et al., 2000; Kapadia et al., 2000). On the other hand, contextual effects on larger direction of motion stimuli, such as random-dot-patterns, are attributed to neuronal processing in area MT/V5 of primates and humans (Braddick, 1993; Britten, 2003; Born and Bradley, 2005). These two features have strong similarities: (1) they are circular variables, (2) they have a hyper-column organization in their respective areas with center-surround receptive field interactions, and (3) within each feature contextual modulations are well reported in psychophysical and neurophysiological studies.

In the psychophysical literature two types of behavioral measures demonstrate these contextual modulations: changes in detection of a target signal or changes in the perceived orientation or motion direction of the target. For orientation feature, strong contrast surrounds decrease the ability to detect a similarly oriented low contrast center target (surround suppression, e.g., Petrov et al., 2005) while at the same time strong oriented surrounds change the perceived orientation of high contrast center targets (tilt illusion effect, e.g., Westheimer, 1990; Solomon and Morgan, 2006; see Figures 1A,B for example of stimuli). In a similar vein, for motion direction feature, strong unidirectional motion in the surround suppresses the ability to detect center weak motion signals that have similar directions (Murakami and Shimojo, 1993; Ido et al., 2000), while at the same time change the perceived direction of a strong center motion signal (Kim and Wilson, 1997; Tzvetanov et al., 2006; Tzvetanov and Womelsdorf, 2008; see Figures 1C,D for example of stimuli). Interestingly, researchers use only one of these two psychophysical measures as experimental probe for inferring computational principles related to each feature. For instance, Gilbert and Wiesel (1990) proposed an influential population coding model for interpreting the tilt illusion, which is explained by V1 orientation-tuned neurons whose activity is modified by the presence of strong surround stimuli through inhibitory interactions. This framework was later successfully applied in the motion domain for predicting perceived direction of motion (Tzvetanov and Womelsdorf, 2008).

FIGURE 1

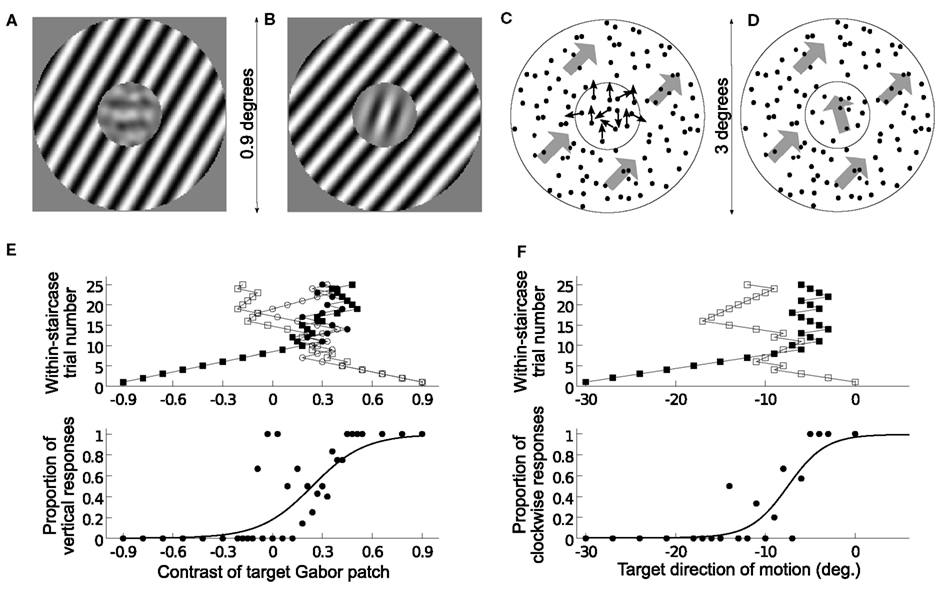
Figure 1. Stimulus design, task, and raw data analysis. (A–D) Example stimuli for orientation (A,B) and direction of motion features (C,D), and detection task (A,C) and discrimination task (B,D). (A) Horizontal target Gabor patch of contrast 0.5 with a surround orientation of +20° (0° surround is vertical orientation). (B) Target Gabor patch of contrast 0.9 has +20° orientation and surround +20° relative to center. (C) Upward target motion direction of contrast 0.5, half of the central dots move upward, with surround of +45° (0° is upward direction of motion). Thick gray arrows depict the unidirectional motion of all dots in the corresponding aperture. (D) Target motion direction of contrast 1 has −20° direction of motion and surround direction of +65° relative to center. (E) Example of measurement of one psychometric function in the orientation-detection task (subject 3; surround orientation +10°). Upper panel: the four staircases pictured as within-staircase trial number versus presented Gabor contrast. Open symbols are for convergence points of 20 and 42.8%, filled symbols for convergence points of 80 and 57.2%; negative contrasts represent horizontal target orientations (90°). Bottom panel: pooled data at each visited contrast level of the target (filled dots) and corresponding Bayesian estimate of the psychometric function (solid curve; parameters: μ = 0.24, σ = 0.26, l = 0.003). (F) Example of measurement for discrimination of motion direction (subject 4; surround motion direction of −20°). Same convention as in (E) (two staircases target the 25 and 75% convergence points; Bayesian estimates of parameters: μ = −7.5°, σ = 3.5°, l = 0.005).

Therefore, I tested whether a single modeling framework of coding and processing of circular feature in the cortex, based on the work of Gilbert and Wiesel (1990), could lead to analogous perceptual effects in both domains for both experimental probes used by researchers: weak signal perception and perceived value of strong central signal (Figure 1). For the purpose of comparison between orientation and direction of motion, stimulus, and experimental design for both features were matched as close as possible in order to allow modeling with a single computational model. Following the above presented path, it was expected that a proper stimulus design and results analyses will enhance the analogous contextual effects on both circular features and one modeling framework will explain the observations.

The paper is structured as follows. Section 2 presents psychophysical characterization of the contextual effects on both features and experimental probes, and describes the model that includes contrast coding and the resulting fits to the data, section 3 discusses the results and model in comparison to the literature, and section 4 describes the methods employed in the work.

2. Results

Based on the similarities between both visual features, stimuli were created such that they should lead to very similar contextual effects between the two features. The target size was adjusted for activating a corresponding theoretical center receptive field structure, that is, also a central hyper-columnar structure, and strong surround placed around it for eliciting mainly surround-to-center inhibitory interactions (Kapadia et al., 2000). Within a feature, two tasks were performed with identically sized stimuli (Figures 1A–D). For detection task, noise was added to the weak target signal such that the sum of their contrasts was constant. For the discrimination task, the strong target signal was presented without noise. For simplicity of comparison between features and model predictions, surround values were always created and expressed relative to the 0° center value, that is, vertical orientation or upward motion direction (see Figures 1A–D; Materials and methods, sec. 4, for details).

Six subjects performed two separate tasks on both visual features, detection or discrimination of orientation and direction of motion (Figure 1). Within each task and feature, strong surround signals were simultaneously presented and irrelevant with regard to the task on the target. Center and surround stimuli presentations were randomized from trial to trial such that no clue of next target and surround could be inferred by the person.

2.1. Signal Detection Changes

In the first task, subjects were asked to detect the orientation/direction of motion of a target signal in the center of a center-surround configuration for different surround orientations/motion directions (Figures 1A,C). The target signal was embedded in noise such that the sum of noise and target contrasts was constant. They had to respond whether the target had one of two possible values: for orientation, if a Gabor patch had horizontal or vertical orientation; for motion direction if the motion of a random-dot-pattern was in an upward or downward direction. For a given surround, the contrast of the target started with strong values and was varied with an adaptive procedure for sampling the psychometric function in the transition region between both possibilities, where subjects’ perception is less reliable (example in Figure 1E). The perceived reference point (midpoint) and detection threshold around it were extracted with Bayesian fitting (see Materials and methods, sec. 4). The former corresponds to what the subjects perceive as no signal present, that is, for a given surround they perceive the center stimulus as noise along the feature-task reference axes. The later is the amount of shift from midpoint necessary for them to reliably respond (>84%) only one target value.

In the orientation-detection task, all six subjects showed systematic modulation of their perceived reference point as a function of surround orientations (Figure 2A, open dots). For surround context of vertical orientation, they perceived vertically oriented central targets with contrast of about 0.2 as being noise, while surround horizontal orientations led to perception of horizontal target orientations with contrast of about 0.2 (−0.2 in Figure 2A) as noise. Surround orientations away from these two cardinal axes rapidly decreased this misperception and for diagonal orientations (±45°) subjects perceived noise when noise stimulus was presented (target contrast around 0). This modulation by the context was confirmed with the ANOVA test (F(17, 85) = 15.2, $\widehat{\epsilon }=0.128,$ p_adj < 0.001). The threshold for detecting the target signal orientation did not show visible systematic effects with varying surround orientations (Figure 2C), confirmed by the ANOVA test on this parameter (F(17, 85) = 1.86, $\widehat{\epsilon }=0.196,$ p_adj > 0.05).

FIGURE 2

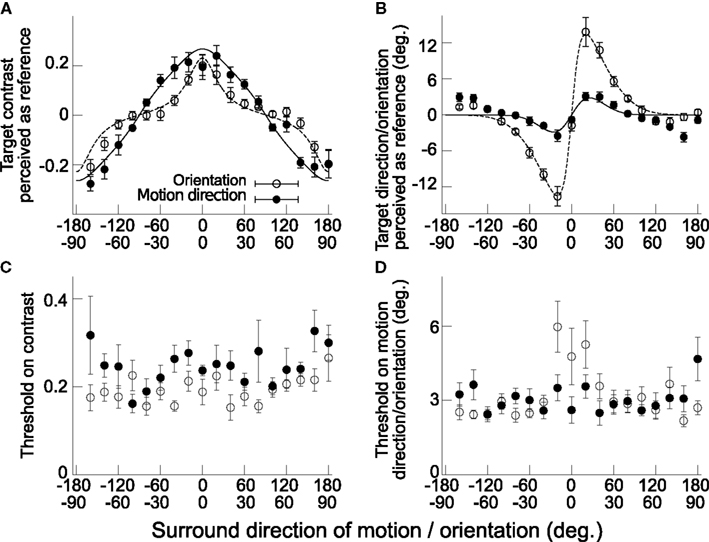
Figure 2. Surround modulates detection and discrimination of center signal similarly for orientation and direction of motion features. (A) Contrast of target signal perceived as noise, the reference, as a function of surround motion direction/orientation. Negative contrasts are for downward motion directions or horizontal orientation of target and zero contrast represent only noise in the center of the stimulus. Zero degree surround is vertical upward motion or vertical orientation and positive values are clockwise tilts relative to zero. Filled dots are for motion direction feature and open dots for orientation feature (error bars depict SEM, n = 6). (B) Target orientation/direction of motion perceived as vertical orientation/upward motion, the reference, as a function of surround orientation/motion direction. Zero degree is vertical upward motion or vertical orientation and positive values are clockwise tilts from zero. Here, surround values are expressed relative to center target value, e.g., +20° surround orientation is relative to +10° central target orientation. (C) Contrast thresholds for detection task in (A). (D) Orientation/Motion direction thresholds for discrimination task in (B). All plotting conventions as in (A). Solid and dashed lines in (A) and (B) are the best fitted model predictions respectively for motion direction and orientation (see Results, sec. 2, and Materials and methods, sec. 4).

In the direction of motion-detection task, all six subjects showed systematic modulation of their perceived reference point as a function of surround motion direction (Figure 2A, filled dots). Surround upward motion directions modified perception of weak upward target signals in opposite direction (contrast of about 0.2 of upward target motion direction perceived as noise), while surround downward motion changed perception of weak downward signals in opposite direction (contrast of −0.2 of downward target motion direction perceived as noise). Surround directions away from these two opposite directions decreased the effect and horizontal motion directions in the surround did not produce visible changes in center weak signal perception. This perceptual modulation was confirmed with the ANOVA test (F(17, 85) = 20.6, $\widehat{\epsilon }=0.127,$ p_adj < 0.001). The thresholds for detecting the target motion direction were not affected by the surround (Figure 2C; ANOVA results: F(17, 85) = 1.84, $\widehat{\epsilon }=0.156,$ p_adj > 0.05).

2.2. Perceived Value Changes

In the second task, subjects were asked to discriminate the orientation or direction of motion of a strong target signal in the center of a center-surround configuration for different surround orientations/motion directions (Figures 1B,D). They had to respond whether the orientation or direction of motion of the center target was clockwise/counterclockwise from an inner vertical reference orientation or vertical upward direction. For each surround value, the target signal orientation/motion direction started at strong deviations from perceived reference point and it was varied with an adaptive procedure for sampling the psychometric function around the perceived vertical orientation/upward motion direction of the subject (example in Figure 1F). Here, the reference point corresponds to what subjects perceive to be the vertical orientation or upward motion direction. The threshold corresponds to the necessary shift in one direction from reference point for subjects to reliably report (>84%) one deviation.

In the orientation-discrimination task, perceived verticality of the strong target signal was systematically modulated by surround orientations (confirmed with ANOVA results: F(17, 85) = 41.0, $\widehat{\epsilon }=0.150,$ p_adj < 0.00001), with misperceptions of target orientations peaking at about ±12° for ±10° surround orientations. This is the standard tilt illusion effect for center-surround configuration, with repulsive effects of surround orientation on perceived central target orientation (Georgeson, 1973). A small attraction effect is seen in the data for surround orientations of ±(60–80) degrees, also known in the literature (Wenderoth and Johnstone, 1988; Westheimer, 1990). The thresholds of discrimination around each reference point were also modulated by surround orientations, with higher thresholds for surrounds of −10, 0, and 10° (Figure 2D; ANOVA results: F(17, 85) = 5.0, $\widehat{\epsilon }=0.185,$ p_adj < 0.01).

In the direction of motion-discrimination task, perceived upward motion direction of the center strong target signal was also systematically modulated by surround motion directions (confirmed with ANOVA results: F(17, 85) = 11.2, $\widehat{\epsilon }=0.156,$ p_adj < 0.001). Misperceptions of motion direction were peaking at around ±3–4° for surround directions of ±20–40°. This is the standard motion repulsion effect for center-surround configuration (Marshak and Sekuler, 1979; Kim and Wilson, 1997; Tzvetanov and Womelsdorf, 2008). The results showed an attraction effect at surround directions of ±(140–160) degrees. It is known in the literature (Tzvetanov and Womelsdorf, 2008), but for a subset of the subjects, while here it is apparent in all six subjects data. Thresholds for motion direction discrimination did not seem to be modulated with surround directions (Figure 2D; ANOVA results: F(17, 85) = 2.0, $\widehat{\epsilon }=0.241,$ p_adj > 0.05).

2.3. Modeling with a Single Framework Within-Feature Contextual Interactions

The above results individually demonstrated how within-feature surround context modulates the perception of weak and strong center signals. While the literature discusses each feature separately for explaining these center-surround perceptual effects on only one of the psychophysical probes, here I will demonstrate how one framework for processing circular feature nicely explains all observations. I base this model on the previous influential work of Gilbert and Wiesel (1990) on orientation coding, contextual effects and perception, and later applications in the direction of motion domain (Kim and Wilson, 1997; Tzvetanov and Womelsdorf, 2008).

Briefly, it is assumed that simple circular feature perception is obtained directly through decoding of activity of the neurons coding that feature, i.e., for small orientated stimuli the neurons in area V1 and for motion direction the neurons in area MT/V5. The hyper-column model of Hubel and Wiesel on circular feature is used combined with a second dimension corresponding to stimulus contrast (that is, at a given location in the visual field neurons with different preferred values spanning all the feature space and contrast space are present, with constant neuronal density across each dimension; see Figure 3A). It is considered that center stimulus size is adjusted to activate directly a central hyper-column, and that spatially surround neurons/hyper-columns, responding to the surround stimulus, interact with the central hyper-column through inhibitory interactions. This description could be taken as an implementation of a standard receptive field with antagonistic center-surround.

FIGURE 3

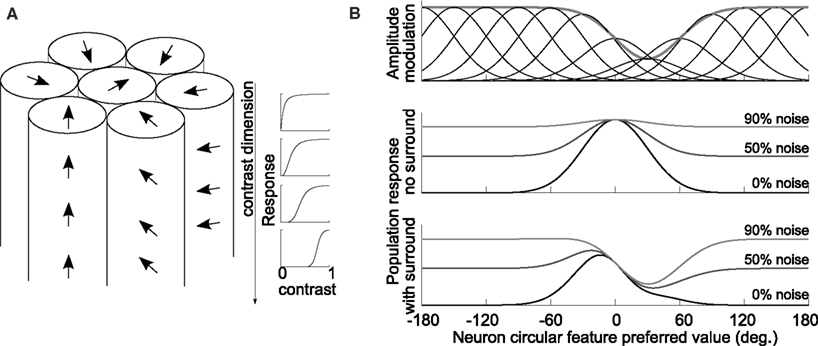
Figure 3. Model illustration. (A) Theoretical hyper-column containing neurons responding to a circular feature and contrast. Arrows depict the feature vector and one column represents neurons with identical preferred feature value but with different contrast sensitivities; four different contrast response functions are pictured rightward of the model. (B) Example of theoretical response curves to the circular feature modulated by surround context (top panel; thick gray line is the inhibitory effect of a +30° surround direction), population response to a 0° target without (middle panel) and with surround (bottom panel) for three levels of noise input.

Within this central hyper-column, the response r_i,m(θ_c, C_c) of a neuron most sensitive to input θ_i to a stimulus with circular parameter θ_c and contrast C_c is described by its tuning curve to input circular feature and contrast (corresponding indices i and m). A common mathematical model of this tuning curve is a wrapped Gaussian function for the circular variable multiplied by the contrast response function (Swindale, 1998; Busse et al., 2009):

$r_{i,m}\left({\theta }_c,C_c\right)=A_{i,m}{g}_m\left(C_c\right)\sum _{k=-1}^{k=1}exp\left(-\frac{1}{2}\frac{{\left({\theta }_i-{\theta }_c+kR\right)}^2}{{\sigma }_i^2}\right),$(1)

with A_i,m the maximum firing rate of the neuron sensitive to θ_i with contrast response function g_m(C_c) (defined between 0 and 1), and σ_i the standard deviation of the response curve along the circular variable (here wrapping with 3 terms from −1 to 1 is sufficient; R is the feature range: 180° for orientation, 360° for motion direction; further on, printed equations are limited to k = 0, assuming the two other terms being present). For simplicity, it is assumed that all hyper-column neurons have standardized maximum amplitudes A_max and identical tuning widths σ_i ≡ σ_c. Taking into account the independence of coding contrast and circular feature (Busse et al., 2009), one can represent the response to contrast with a generic contrast function g(C_c), giving a theoretical neuronal response function:

$\begin{array}{llll}{r}_i\left({\theta }_c,C_c\right)& =\frac{1}{M}\sum _{m=1}^M{r}_{i,m}\left({\theta }_c,C_c\right)& & \\ & =A_{i}g\left(C_c\right)exp\left(-\frac{1}{2}\frac{{\left({\theta }_i-{\theta }_c\right)}^2}{{\sigma }_c^2}\right),& & \text{(2)}\end{array}$

once contrast space is shrinked (see Materials and methods, sec. 4).

Response amplitudes are modulated by contextual influences through surround-to-center inhibitory interactions and thus are dependent on contextual parameters (for motion sensitive neurons in MT/V5 and orientation sensitive neurons in V1: Allman et al., 1985; Gilbert and Wiesel, 1990; Kapadia et al., 2000). For a full surround context with circular parameter θ_s as in this study, the inhibition is maximal when surround feature equals the center neuron preferred value (Allman et al., 1985; Gilbert and Wiesel, 1990), and a simple mathematical description of this inhibition effect due to context stimuli could be taken as a wrapped Gaussian (Tzvetanov and Womelsdorf, 2008):

$A_i=A_{max}\left(1-A_{inh}exp\left(-\frac{1}{2}\frac{{\left({\theta }_i-{\theta }_s\right)}^2}{{\sigma }_s^2}\right)\right),$(3)

with A_max the maximum firing rate of center neuron tuned to θ_i when no surround is present, A_inh the proportion of inhibition due to the surround with value θ_s onto central neuron i, and σ_s the width of inhibition in the feature space from surround-to-center population (examples in Figure 3B, top panel). The amplitude A_inh can be itself dependent on surround parameters others than the circular feature (e.g., surround contrast).

Using this central hyper-column activity, a simple rule for decision about the input value given the activity profile is the vector average (Seung and Sompolinsky, 1993; Dayan and Abbott, 2001), such that each neuron is considered to code a feature value (the vector direction is its preferred value θ_i) and the weight is its activity due to the input. This rule is written, in complex number notation:

$\begin{array}{llll}R{\text{e}}^{j{\theta }_{pred}^{\text{mo}}}& =\frac{1}{\mathcal{N}}\sum _{i=1}^N{r}_i{\text{e}}^{j{\theta }_i}\equiv \frac{1}{\mathcal{N}}{\int }_{-\pi }^{\pi }{r}_i{\text{e}}^{j{\theta }_i}d{\theta }_i& & \text{(4)}\\ R{\text{e}}^{j2{\theta }_{pred}^{\text{or}}}& =\frac{1}{\mathcal{N}}\sum _{i=1}^N{r}_i{\text{e}}^{j2{\theta }_i}\equiv \frac{1}{\mathcal{N}}{\int }_{-\pi ∕2}^{\pi ∕2}{r}_i{\text{e}}^{j2{\theta }_i}d{\theta }_i,& & \text{(5)}\end{array}$

respectively for motion direction and orientation prediction, and $\mathcal{N}={\sum }_{i=1}^N{r}_i$.

Based on this model, we can compute two cases of interest in this study: null target signal embedded in noise and strong signal perception. The response r_i due to signal plus noise, as experimentally presented in this study, can be described as:

$\begin{array}{llll}& r_i\left({\theta }_c,{\theta }_s,C_c\right)=A_i& & \\ & \times \left[g\left(C_c\right)exp\left(-\frac{1}{2}\frac{{\left({\theta }_i-{\theta }_c\right)}^2}{{\sigma }_c^2}\right)+g\left(1-C_c\right)\eta \right],& & \text{(6)}\end{array}$

with η being the resulting noise activity due to only input feature noise. Because of stimulus design, input noise is assumed to create constant activity across feature space and the sum of signal and noise contrasts is one (see Figure 3B). For motion direction case, including equations (3) and (6) into equation (4), one obtains:

$\begin{array}{l}R{e}^{j{\theta }_{pred}^{mo}}=\frac{1}{\mathcal{N}}{A}_{\max }[g\left(C_c\right){\displaystyle \sum _{i=1}^N{e}^{-{\left({\theta }_i-{\theta }_c\right)}^2/2{\sigma }_c^2}{e}^{j{\theta }_i}}\\ -A_{inh}g\left(C_c\right){\displaystyle \sum _{i=1}^N{e}^{-{\left({\theta }_i-{\theta }_s\right)}^2/2{\sigma }_s^2}{e}^{-{\left({\theta }_i-{\theta }_c\right)}^2/2{\sigma }_c^2}{e}^{j{\theta }_i}}\\ -A_{inh}g\left(1-C_c\right)\eta {\displaystyle \sum _{i=1}^N{e}^{-{\left({\theta }_i-{\theta }_s\right)}^2/2{\sigma }_s^2}{e}^{j{\theta }_i}}].\end{array}$(7)

For orientation prediction one replaces ${\theta }_{pred}^{\text{mo}}$ with $2{\theta }_{pred}^{\text{or}}$ and ${\text{e}}^{j{\theta }_i}$ with ${\text{e}}^{j2{\theta }_i}$. Let us consider the two cases of interest, C_c = 0 and C_c = 1. For C_c = 0, only noise input, g(Cc) = 0, and in equation (7) only the last term is not null. It gives a predicted direction θ_s + π, at the opposite to surround feature value θ_s (for orientation, orthogonal to surround orientation, at θ_s + π/2). This nicely explains the common behavioral observations in the orientation and direction of motion domains of surround suppression onto similar center signals and enhancement of opposite/orthogonal signals (Murakami and Shimojo, 1993, 1996; Ido et al., 2000; Zenger-Landolt and Heeger, 2003). For C_c = 1, no noise input, g(1 – C_c) = 0, and in equation (7) the first two terms are not null. This last case provides a good description of the direction of motion repulsion curve observed experimentally, and here additionally is demonstrated to match the orientation repulsion curve.

A nice consequence of the above described model is that, for a given theoretical population characteristics and interactions, it can be used to predict both psychophysical probes which researchers report separately in the literature: weak signal and strong signal perception in context. The target input contrast that cancels perception of signal along the feature-task axis represented by opposite/orthogonal values can be found numerically (minimizing R in equation (7) as a function of target contrast), and same for the perceived value by extracting θ_pred without noise input.

The above data on detection and discrimination of each feature within contextual modulation were fit with the corresponding model. Due to parameters entanglement in predicting the results, only three free model parameters were used: the surround-to-center inhibition strength A_inh, the center population tuning width σ_c, and the noise η created in the neuronal response due to the input feature noise (surround-to-center tuning width σ_s was set equal to σ_c, and g(C) = C), and the global chi-square minimized (see Materials and methods, sec. 4, for details). I have to point out that the discrimination data showing attractive effects are not explainable by the currently built model based on inhibitory interactions onto amplitude of firing. Consequently, discrimination data for | θ_s | > 100 for motion direction and | θ_s | > 50 for orientation were discarded from fitting and χ² statistical tests.

The resulting best fitted models for each feature are presented in Figures 2A,B (solid line for direction of motion feature, dashed line for orientation feature). Within each feature, the resulting best fit predicted correctly the overall data, that is, simultaneously detection of weak target and discrimination of strong target signal presented with surround context (motion direction model parameters: A_inh = 0.38, σ_c = 20.3, η = 0.70, χ² = 28.5, df = 26, p > 0.05; orientation model parameters: A_inh= 1.11, σ_c = 14.8, η = 0.04, χ² = 34.1, df = 26, p > 0.05).

3. Discussion

I investigated whether a single theoretical framework of coding and processing the circular features orientation and direction of motion could explain the observed similarities in their contextual modulation. The experimental results with two psychophysical probes, weak signal and strong signal perception, and good model fits to the data confirmed this hypothesis.

For both circular features, detection of weak target signals that have similar values as the surround were suppressed (e.g., vertical surround orientation with vertical center Gabor patch target) while orthogonal/opposite values enhanced the perception of weak target center. This was observed in the shift of the perceived reference point at 0 and 90/180° surround orientations/motion directions (Figure 2A). The amount of shift for both features are similar, of about 0.2 contrast units, while the shapes of the modulation as a function of surround are dissimilar. For the discrimination task, both features demonstrated a repulsive effect on perceived central strong signal for surround values close to the center target (Figure 2B), but with very different amplitude effects. Intriguingly, the orientation repulsion effect observed in the current data was far stronger than commonly reported in the literature using target line segments (reports of 2–3° repulsions, e.g., O’Toole and Wenderoth, 1977; Westheimer, 1990; Kapadia et al., 2000). But a more recent study using target Gabor patches, with a close experimental design to the one here, reported stronger repulsions (of about 6°, see Solomon and Morgan, 2006). These differences remain to be understood and it could be that different stimulus types differentially activate the hyper-columns and feature space, or involve interactions due to other features. For example, Gabor patches are specifically designed to activate oriented stimuli with a narrow range of spatial frequency tuning. On the other hand, line segments involve orientation-tuned cells with a larger span of spatial frequency tunings, which would include on top of the orientation contextual interaction also spatial scale contextual interactions - a topic of interest by itself for understanding local-global grouping and early object representations.

The feature-task similarities and dissimilarities in the current data were very well explained by the model of circular feature coding and decoding in the early visual pathway, with only three free parameters. While the surround repulsion and suppression onto similar center signal is understood through the surround-to-center inhibitory interactions, the differences in modulation between both features were very well fit with different theoretical population characteristics: the amplitude of inhibition from the surround onto the center hyper-column was total in the case of orientation while for the motion it was 0.38; the noise level created by the input noise in the orientation stimulus was low (0.04) contrary to the motion direction stimulus where it was strong (0.7); the neuronal tuning widths were of about 15° for orientation feature and of about 20° for motion direction feature.

On the other hand, for both domains, results in the discrimination task showed an attractive interaction for surrounds near the opposite of target value. These results, already known in the psychophysics literature and it seems not systematic between-subjects (at least for direction of motion domain, see Tzvetanov and Womelsdorf, 2008), are not predictable with the current model of center-surround interactions. I acknowledge that the model of Gilbert and Wiesel (1990) could be used for predicting this opposite/orthogonal effect in the orientation and motion direction domains by assuming that surround presence changes tuning width of the center neuronal population already at an early stage of stimulus coding (their Figure 8g) or through additional opposite/orthogonal inhibitory interactions. Since these effects seem not systematic across subjects, then one needs to provide a direct functional link between the final perceptual effect and local effects in the corresponding areas for subjects with and without these effects (e.g., through fMRI, EEG/MEG measures in humans, or direct neuronal measures in primates).

One issue in the current experimental design are the stimuli and their size. It is known that receptive field (RF) diameters of orientation-tuned neurons in V1 are dependent on their spatial frequency selectivity and could be described by Gabor functions, while the RF diameters of purely motion direction tuned neurons in MT/V5 are about 10 times bigger than V1 RFs at an equivalent eccentricity (Born and Bradley, 2005). The RF surround area that modulates the response of the neuron to stimuli in the classical RF has an extension that can go far beyond the RF, but generally the strongest effects are obtained at close distances peaking at about one RF distance, which is a nice counterpart of psychophysical observations (Westheimer, 1990; Kim and Wilson, 1997). Consequently, stimulus sizes in orientation and direction of motion perception need to be adjusted such that theoretically they correspond to comparable levels of excitation within the corresponding visual area, i.e., theoretically directly matching the size of a RF, and surround size selected for making the strongest effect on the center. The stimuli were: for the orientation domain, Gabor patches for their spatial frequency selectivity in exciting orientation-tuned neurons; for the motion domain, random-dot-patterns because they do not contain orientation cues and therefore are appropriate to stimulate purely motion direction sensitive neurons. For the orientation stimulus, a center diameter of 3 × σ_t= 3/f_t (see sec. 2) was fixed based on previous psychophysical observations (Solomon and Morgan, 2006; Tzvetanov and Simon, 2006), and for the direction of motion stimulus a diameter of 1°, far greater than the smallest RF in V1. The surround annulus was chosen to have one center diameter width, without gap from the center stimulus, and thus its center being at a distance of one center stimulus diameter.

Reports of similarities in functional organization and processing of different features within the cortex (Mountcastle, 1997) already led researchers to propose a common computational framework for various features. Clifford and colleagues (Clifford et al., 2000; Clifford, 2002) showed that adaptation after-effects in the orientation, motion direction, and color features could be explained by a single feature model of self-calibration and decorrelation acting into the feature space. Nevertheless, this idea is discussed for the orientation and motion direction domains because of the variety of adaptation effects on neuronal tuning in the corresponding areas and spread of adaptation effects across different areas (Georgeson, 2004). Here, I was interested in the possibility that a single computational framework, corresponding to a well defined functional organization and processing of the feature within one area, could explain the results of contextual modulation. I applied this principle to the perceptual modifications due to context of two circular features by creating as close as possible experimental stimuli in both domains for similarly activating the corresponding processing areas, and measured the effects on two behavioral probes (perception of weak and strong target signal). The model successfully predicted the data.

This study demonstrated how a single theoretical framework of circular feature processing in human cortex leads to similar behavioral outcomes for two well known features: orientation and direction of motion. It related the final perceptual outcome to the local theoretical population characteristics while the global functional organization remains identical across features. It is of interest to consider the functional implementation of the current model based on neurophysiological observations of context modulation onto neuronal activity. For the orientation domain, multiple modeling studies have proposed how local inhibitory interactions between neurons or neuronal populations create the orientation and contrast tuning together with proposing explanations of the center-surround neurophysiological observations (e.g., Stetter et al., 2000; Spratling, 2011). Other studies even successfully demonstrated how the psychophysical tilt after-effect, that is, adaptation induced tilt illusion, could be generated by a self-organizing model of V1 (Bednar and Miikkulainen, 2000) or how neurophysiological knowledge of adaptation effects on orientation tuning curves in V1 are predicted from analysis of a population coding model that explains the tilt after-effect (Jin et al., 2005). While proposing a detailed network model goes far from the original aim of this work, the common psychophysical pattern of results and the good fit of a single theoretical framework allow to propose that the implementation of both features should have a very similar structure in the two corresponding areas (V1 and MT/V5).

Further comparisons and tests on these features would allow generalization of this computational framework to other interaction patterns. For instance, the current study was concerned mainly with center-surround inhibitory interactions instantiated at strong surround values. But it is well known in psychophysical and neurophysiological studies that these center-surround modulations are contrast dependent: at low surround contrast detection of a weak center signal is improved (facilitation/assimilation for orientation/motion direction, e.g., Polat and Sagi, 1993; Ido et al., 2000) while the perception of a strong center signal changes as a function of the surround contrast (Kapadia et al., 2000). Thus, one interesting step would be to characterize psychophysically the similarities and differences of these contextual modulations for both features at low surround contrast and introduce additional excitatory effects believed to create the behavioral observations. And last, an even more ambitious project would be to perform a characterization of the spatio-circular interaction pattern by measuring, as for example in Kapadia et al. (2000), the effect of a spatially localized small surround onto the perception of the center target for broad range of feature and space values. This would provide a very nice spatio-circular map that could help to propose a much detailed model and provide a better link to neurophysiological findings.

4. Materials and Methods

4.1. Observers

Six subjects participated in the study (5 naïve paid subjects and the author, 5 males, 23–35 years old). They had normal or corrected-to-normal vision. With exception of the author, they were naïve with regard to the purpose of the experiment and gave written consent for participating in the study. The experiment was approved by the Ethic committee of the German Psychology Society.

4.2. Apparatus and Stimuli

Stimuli were displayed on a 21′′ CRT grayscale monitor (EIZO FlexScan T962; 85 Hz, resolution of 1600 × 1200 pixels) with self-written functions for Matlab (Mathworks Inc.) using the Psychophysics toolbox (Brainard, 1997; Pelli, 1997) on a Linux based Intel quadcore Q9400 (2.66 GHz processor, 4 GB) with a nVidia GeForce 9600GT (512 MB) graphic card. Subjects’ head was stabilized with a chin-rest at a distance of 2.5 m from the monitor, representing a spatial resolution of ∼175 pixels/degree of visual angle. Mean monitor background luminance was 50 cd/m², the experiment conducted in a dimly illuminated room. Stimuli were presented centered on fixation point and viewed binocularly. The screen area was delimited by a circular window of diameter 300 mm cut in a black cardboard centered on the screen in order to avoid local cues for vertical/horizontal and position. Luminance values were obtained from a 256 RGB gray levels look-up table.

Orientation stimuli – Center stimuli were the sum of a natural Gabor patch with a filtered white noise image, giving the spatial luminance profiles:

$\begin{array}{l}L\left(x,y,t\right)=L_0+L_0{C}_{t}exp\left(-\frac{\left(x^2+y^2\right)}{{\sigma }_t^2}\right)\\ \times cos\left(2\pi f_t\left(cos\left({\theta }_c\right)x+sin\left({\theta }_c\right)y\right)\right)\\ +L_0\left(C_{max}-C_t\right)N\left(x,y,t\right).\end{array}$(8)

L₀ is the background luminance of the screen, C_t is the Gabor patch contrast between 0 and 1 (σ_t, f_t) its standard deviation and spatial frequency, and θ_c the Gabor patch angle (Figures 1A,B). Because of monitor luminance limitations, the maximum achievable contrast of the Gabor patch or noise was not 1 but lower (C_max= 0.923). Therefore the noise term contains a factor (C_max – C_t) instead of (1 – C_t). N(x, y, t) was a time varying white noise image filtered through a difference of Gaussians:

$\begin{array}{llll}DOG\left(x,y\right)& =\frac{1}{2\pi {\sigma }_c^2}exp\left(-\frac{x^2+y^2}{2{\sigma }_c^2}\right)& & \\ & -\frac{1}{2\pi {\sigma }_s^2}exp\left(-\frac{x^2+y^2}{2{\sigma }_s^2}\right).& & \text{(9)}\end{array}$

DOG peak frequency f_peak in the Fourier domain is related to its parameters through the relation: $f_{peak}^2=4ln\left({\sigma }_s∕{\sigma }_c\right)∕\left({\sigma }_s^2-{\sigma }_c^2\right);$ σ_c was computed by fixing σ_s = 1.1σ_c and f_peak = f_t. For each trial and frame of Gabor patch presentation a different white noise image was created, filtered and all values divided by the absolute maximum (in practice all noise images were computed before each session for time saving during the experiment). The center stimulus had 0.15° radius. For the detection task, the target Gabor patch could take two possible orientations of 0 (vertical) or 90 (horizontal) degrees, and its contrast was varied from trial to trial around the perceived reference point corresponding to perceived noise. For procedural and experimental purposes, horizontal orientations were assigned negative values of contrast, e.g., C_t= –0.3 corresponds to a horizontal Gabor patch with contrast 0.3, while vertical Gabor patches maintained their sign. In the orientation-discrimination task, the target orientation was varied around vertical from trial to trial to measure subject’s perceived verticality and no noise was added to the Gabor patch. Context orientation stimulus was an annulus disk of cosine grating with inner/outer radius of 0.15/0.45° added to a noise (equation (8) without the exponential term and C_t replaced by C_s). For both center and surround, the cosine had a phase of 0, spatial frequency of 10 cpd, and σ_t = 1/f_t. The surround context orientation was defined relative to the center target orientation and could be one of the 18 predefined values: from −80° to 90° in steps of 10°. For detection task, 0° is vertical surround orientation; for discrimination task, surround of 0° has an orientation equal to central target orientation; positive values are clockwise from 0°.

Motion stimuli were moving random-dot-patterns (100 dots/square degree; each dot had speed of 8°/s, 0.033° diameter, and contrast of about −47 cd/m²) presented in either a 1° diameter virtual circular aperture (target) or surround annulus virtual aperture of inner/outer radius of 0.5/1.5° (context; Figures 1C,D). A proportion of dots, thereafter called contrast C of the motion, were moving at constant speed in a fixed direction and the remaining percentage of dots (1 – C) were moving at the same speed but each of these dots with a randomly assigned direction fixed for the full presentation. For the direction of motion-detection task, the target motion stimulus could take two directions, upward or downward motion, and its contrast was varied between 0 and 1. For experimental and procedural reasons, downward motion direction was defined with negative contrast, e.g., C = –0.5 indicates that 50% of the dots were moving straight downward and the remaining 50% were each assigned random directions. In the direction discrimination task, the target motion direction was varied from trial to trial near vertical upward for measuring subjects’ perceived upward direction of motion. The surround direction of motion was defined with respect to the center target direction and could be one of 18 predefined values: from −160 to +180 in steps of 20°. For detection task, 0° is a vertical upward motion surround; for discrimination task, surround of 0° has a motion direction equal to central target motion direction; positive values are clockwise from 0°.

4.3. Procedure

Each subject performed the target detection and target discrimination task for both features, orientation and motion direction, giving 4 combinations of feature-task. They were instructed to fixate a small square (∼0.024° size; dark for orientation stimuli, bright for motion stimuli) displayed at the center of the screen and that the stimulus will be presented centered at it. They started each trial by pressing a button and 17 frames (200 ms) after fixation point disappearance the whole stimulus (target + context) was presented for 3 frames (∼35 ms) for orientation feature, and 11 frames (∼130 ms) for motion feature with the fixation point remaining through all trial for this feature. Subjects had to report: (1) for orientation-detection task whether the central target orientation was more vertical or horizontal; (2) for orientation-discrimination task whether target orientation was tilted clockwise/counter-clockwise from their inner verticality reference; (3) for motion-detection task whether the target direction of motion in the center had stronger upward or downward motion direction; (4) for motion-discrimination task whether the center target direction was tilted clockwise/counterclockwise from vertical upward direction. They answered by pressing one of two predefined keys on the keyboard. No feedback was provided about response correctness.

Psychometric curves for feature detection or discrimination were measured at each context values using the weighted up-down adaptive procedure (Kaernbach, 1991). Detection Task – For each context value, e.g., a given surround orientation, four staircases were assigned that converged respectively at the 80, 20, 57.1, and 42.8% convergence points (respectively Up/Down step sizes of 4/1, 1/4, 4/3, 3/4 in contrast steps of 0.03). The starting point was set at contrast ±0.9 opposite from the convergence point (negative values correspond to horizontal Gabor patches for orientation task and vertical downward direction for motion task), and each staircase consisted of 25 trials providing 100 trials per psychometric function estimation. The 18 context values for one feature were presented in two experimental blocks, e.g., surround orientations of −80°, −60°, … 80° in one block and −70°, −50°, … 90° orientations in a second block. All 36 staircases of one block (9 context values × 4 staircases per context value) were pseudorandomly presented from trial to trial for a total of 900 trials in one block. Discrimination task – For each context value, e.g., a given surround motion direction, two staircases were assigned that converged respectively at 75 and 25% convergence points (Up/Down steps of 3/1 and 1/3 in steps of 0.75° for orientation and 1° for motion direction features; the author had 0.75° staircase step for motion direction). Previous work showed strong inter-subject differences for the repulsion effect. Therefore, the starting point was set as a function of the mean expected repulsion effect at a given surround value plus or minus fifteen staircase step sizes, such that the starting target value was opposite of the convergence point with respect to the expected midpoint of the psychometric function. It followed the equation:

${\theta }_{c,start}={\theta }_{step}\times \left[\text{round}\left(A_f\frac{{\theta }_s}{10}{e}^{1-|{\theta }_s/10|}\right)\pm 15\right].$(10)

A_f was 10 for orientation feature and 15 for motion feature, θ_s is the surround value orientation or motion direction, and θ_step the staircase minimum step size. Each staircase was assigned 25 trials providing 50 trials per psychometric function estimation. As for the detection task, the 18 context values of one feature were presented in two separate blocks. All 36 staircases were pseudorandomly presented trial to trial for a total of 450 trials in one block (see Figures 1E,F for measurements and staircase examples).

The experiment was done in four sessions, one session per day, and each feature and task were presented in separate blocks. Subjects performed one block of each task in each session and all blocks randomized between-subjects and sessions. Short pauses were allowed anytime and breaks were forced every 200 trials in the detection task and 225 trials in the discrimination task, and longer breaks for resting between the two blocks. Each subject had a short practice for a minimum of 50 trials for each feature-task before the experiment was performed.

4.4. Data Analysis and Statistics

For each task, feature and context value the data was analyzed by counting the proportion p_i = y_i/n_i at a given target value x_i (bottom panels of Figures 1E,F). For orientation-detection tasks (respectively motion direction), y_i is the count of vertical orientation responses (upward motion direction responses) at x_i target level presentation, and n_i the total number of x_i level presentation; x_i was the contrast of Gabor patch target (respectively contrast of motion direction target). For orientation-discrimination task (respectively direction of motion task) y_i is the count of clockwise responses from inner vertical orientation reference (respectively inner vertical upward direction of motion) at x_i target level; x_i was the orientation (respectively motion direction) of the central target. This experimental data set {x_i, p_i}, was modeled as a logistic function:

$p\left(x\right)=l+\frac{1-2\text{1}}{1+\exp \left(\frac{In\left(21/4\right)}{\sigma }\left(x-\mu \right)\right)}$(11)

with l being subject’s lapsing rate, μ the midpoint or perceived reference point, and σ the detection/discrimination threshold around the midpoint corresponding to the necessary shift from μ for reliably reporting (>84%) always one target value. The function was adjusted to the data through Bayesian fitting (Treutwein and Strasburger, 1999) with the simplex algorithm. The priors on the three parameters were: l – beta probability distribution with parameters Beta(1.1, 20); μ – normal probability distribution with parameters Norm(a, 10w) with a and w being the mean and standard deviation obtained from each experimental data set {x_i, p_i} (a = Σp_ix_i and $w=\sqrt{\sum p_i{\left(x_i-a\right)}^2}$); σ – gamma probability distribution with parameters Gamma(a_G, b_G) fixed at a_G = 1 + w/b_G and $b_G=\left(\sqrt{5}-1\right)w∕2$ such that the mode and variance of the Gamma distribution is w. This way the Bayesian priors on midpoint and threshold are based on the data.

The point of perceived reference (μ) and discrimination threshold (σ) are extracted for each subject, task, feature, and context value. For taking into account within-subject reference point variability, midpoints μ of a given block were adjusted by subtracting the within-block mean. From all 432 Bayesian fits, only one lapsing rate had a value above 0.05 (l = 0.08) and therefore this parameter is not reported further. Each μ and σ for a given feature-task was subjected to a one-way within-subject ANOVA test (context value with 18 levels, 6 subjects) with adjusted Greenhouse-Geisser $\widehat{\epsilon }$ statistics. All analyses and plots were performed with self-written functions and scripts using the softwares Matlab (Mathworks Inc.) and Octave (www.octave.org).

4.5. Model Implementation and Fit to the Data

For simpler model presentation in the article, equation (7) was directly implemented in a function for Matlab and Octave for computing the population vector average. For persons (as myself) interested in final mathematical equations, equation (7) can be hand-integrated (by changing the sum to an integral) with some assumptions on integrals of error function on complex numbers, and thus provide a nice mathematical, though complicated, description of the theoretical modulation by context. It is not of great importance in the current presentation of model and data fitting.

For a given population characteristics (A_inh, σ_c, η) and input stimulus, the predicted model response R and angle θ_pred were computed. Then, they were used as described in the main text for minimizing the total chi-square of detection and discrimination data:

$\begin{array}{l}{\chi }^2={\displaystyle \sum _{k=1}^{k=18}{\left({\mu }_{det}^k-{\mu }_{det,pred}^k\right)}^2/{\left(s{e}_{det}^k\right)}^2}\\ +{\displaystyle \sum _{m=1}^{m=11}{\left({\mu }_{dis}^m-{\mu }_{dis,pred}^m\right)}^2/{\left(s{e}_{dis}^m\right)}^2},\end{array}$(12)

with (se) being the between-subjects standard error on the midpoint datum, and all 18 surround detection results used but only 11 surround discrimination results are used. The discrimination results showed opposite surround attractive effects in both features, which is not explainable with this model of inhibitory surround-to-center interactions. Therefore, discrimination data for surround angles greater than 50/100° relatively to center (respectively for orientation and motion direction) were not considered for fitting and model prediction. Different or additional inhibition must be taken into account for explaining these opposite surround-to-center interactions onto perceived value (Gilbert and Wiesel, 1990; Tzvetanov and Womelsdorf, 2008).

One important mathematical step in model derivation is the passage from 2D contrast and circular feature space (equation (1)) to the 1D circular feature representation with a generic contrast response function (equation (2)). Given the independence of coding of contrast and circular variable (Busse et al., 2009), one can sum equation (1) along the contrast dimension. It results in the following:

$r_i\left({\theta }_c,C_c\right)=A_i\left(\frac{1}{M}\sum _{m=1}^{m=M}{g}_m\left(C_c\right)\right)exp\left(-\frac{1}{2}\frac{{\left({\theta }_i-{\theta }_c\right)}^2}{{\sigma }_i^2}\right)$(13)

with M the number of neurons with identical circular tuning but different contrast response functions. Taking the common Naka-Rushton equation for neuronal contrast response $r\left(c\right)=c^n∕\left(c^n+c_m^n\right)$, with the assumption that semisaturation constant c_m and power exponent n must be related such that r(1) = 1 (or at least ε close to one), the sum over contrast space gives a near linear relation on contrast, and therefore we can approximate:

$g\left(C_c\right)=\frac{1}{M}\sum _{m=1}^{m=M}{g}_m\left(C_c\right)\simeq C_C$(14)

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

During this project the author was supported by the Deutsche Forschungsgemeinschaft (grant number TZ 69/1-1).

References

Albright, T. D., and Stoner, G. R. (2002). Contextual influences on visual processing. Annu. Rev. Neurosci. 25, 339–379.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Allman, J., Miezin, F., and McGuinness, E. (1985). Stimulus specific responses from beyond the classical receptive field: neurophysiological mechanisms for local-global comparisons in visual neurons. Annu. Rev. Neurosci. 8, 407–430.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bednar, J. A., and Miikkulainen, R. (2000). Tilt aftereffect in a self-organizing model of the primary visual cortex. Neural Comput. 12, 1721–1740.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Born, R., and Bradley, D. (2005). Structure and function of visual area MT. Annu. Rev. Neurosci. 28, 157–189.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Braddick, O. (1993). Segmentation versus integration in visual motion processing. Trends Neurosci. 16, 263–268.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brainard, D. H. (1997). The psychophysics toolbox. Spat. Vis. 10, 433–436.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Britten, K. H. (2003). “The middle temporal area: motion processing and the link to perception,” in The Visual Neurosciences, Vol. 2, Chap. 81, eds L. M. Chalupa and J. S. Werner (Cambridge: MIT Press), 1203–1216.

Busse, L., Wade, A. R., and Carandini, M. (2009). Representation of concurrent stimuli by population activity in visual cortex. Neuron 64, 931–942.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chavane, F., Monier, C., Bringuier, V., Baudot, P., Borg-Graham, L., Lorenceau, J., and Frégnac, Y. (2000). The visual cortical association field: a Gestalt concept or a psychophysiological entity? J. Physiol. 94, 333–342.

Clifford, C. W. G. (2002). Perceptual adaptation: motion parallels orientation. Trends Cogn. Sci. (Regul. Ed.) 6, 136–143.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Clifford, C. W. G., Wenderoth, P., and Spehar, B. (2000). A functional angle on some after-effects in cortical vision. Proc. R. Soc. Lond. B Biol. Sci. 267, 1705–1710.

CrossRef Full Text

Dayan, P., and Abbott, L. (2001). Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Cambridge, MA: MIT Press.

Field, D. J., Hayes, A., and Hess, R. F. (1993). Contour integration by the human visual system: evidence for a local “association field.” Vision Res. 33, 173–193.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Georgeson, M. (1973). Spatial frequency selectivity of a visual tilt illusion. Nature 245, 43–45.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Georgeson, M. (2004). Visual aftereffects: cortical neurons change their tune. Curr. Biol. 14, R751–R753.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gilbert, C. D., and Wiesel, T. N. (1990). The influence of contextual stimuli on the orientation selectivity of cells in primary visual cortex of the cat. Vision Res. 30, 1689–1701.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hubel, D., and Wiesel, T. (1974). Sequence regularity and geometry of orientation columns in the monkey striate cortex. J. Comp. Neurol. 158, 267–294.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ido, K., Ohtani, Y., and Ejima, Y. (2000). Summation between nearby motion signals and facilitative/inhibitory interactions between distant motion signals. Vision Res. 40, 503–516.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jin, D. Z., Dragoi, V., Sur, M., and Seung, H. S. (2005). Tilt aftereffect and adaptation-induced changes in orientation tuning in visual cortex. J. Neurophysiol. 94, 4038–4050.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kaernbach, C. (1991). Simple adaptive testing with the weighted up-down method. Percept. Psychophys. 49, 227–229.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kapadia, M. K., Westheimer, G., and Gilbert, C. D. (2000). Spatial distribution of contextual interactions in primary visual cortex and in visual perception. J. Neurophysiol. 84, 2048–2062.

Pubmed Abstract | Pubmed Full Text

Kim, J., and Wilson, H. (1997). Motion integration over space: interaction of the center and surround motion. Vision Res. 37, 991–1005.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lesher, G. W. (1995). Illusory contours: toward a neurally based perceptual theory. Psychon. Bull. Rev. 2, 279–321.

CrossRef Full Text

Marshak, W., and Sekuler, R. (1979). Mutual repulsion between moving visual targets. Science 205, 1399–1401.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mountcastle, V. B. (1997). The columnar organization of the neocortex. Brain 120, 701–722.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Murakami, I., and Shimojo, S. (1993). Motion capture changes to induced motion at higher luminance contrasts, smaller eccentricities, and larger inducer sizes. Vision Res. 33, 2091–2107.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Murakami, I., and Shimojo, S. (1996). Assimilation-type and contrast-type bias of motion induced by the surround in a random-dot display: evidence for center-surround antagonism. Vision Res. 36, 3629–3639.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

O’Toole, B., and Wenderoth, P. (1977). The tilt illusion: repulsion and attraction effects in the oblique meridian. Vision Res. 17, 367–374.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pelli, D. G. (1997). The videotoolbox software for visual psychophysics: transforming numbers into movies. Spat. Vis. 10, 437–442.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Petrov, Y., Carandini, M., and McKee, S. P. (2005). Two distinct mechanisms of suppression in human vision. J. Neurosci. 25, 8704–8707.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Polat, U., and Sagi, D. (1993). Lateral interactions between spatial channels: suppression and facilitation revealed by lateral masking experiments. Vision Res. 33, 993–999.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Reinhardt-Rutland, A. H. (1988). Induced movement in the visual modality: an overview. Psychol. Bull. 103, 57–71.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Seung, H., and Sompolinsky, H. (1993). Simple models for reading neuronal population codes. Proc. Natl. Acad. Sci. U.S.A. 90, 10749–10753.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Solomon, J. A., and Morgan, M. (2006). Stochastic re-calibration: contextual effects on perceived tilt. Proc. R. Soc. Lond. B Biol. Sci. 273, 2681–2686.

CrossRef Full Text

Spillmann, L., and Ehrenstein, W. (1996). “From neuron to gestalt: mechanisms of visual perception,” in Comprehensive Human Physiology, Vol. 1, Chap. 43, eds U. Windhorst R. Greger (Berlin: Springer-Verlag), 861–893.

Spillmann, L., and Werner, J. (1996). Long-range interactions in visual perception. Trends Neurosci. 19, 428–434.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Spratling, M. W. (2011). A single functional model accounts for the distinct properties of suppression in cortical area V1. Vision Res. 51, 563–567.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stetter, M., Bartsch, H., and Obermayer, K. (2000). A mean-field model for orientation tuning, contrast saturation, and contextual effects in the primary visual cortex. Biol. Cybern. 82, 291–304.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Swindale, N. V. (1998). Orientation tuning curves: empirical description and estimation of parameters. Biol. Cybern. 78, 45–56.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Treutwein, N., and Strasburger, H. (1999). Fitting the psychometric function. Percept. Psychophys. 61, 87–106.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tzvetanov, T., and Simon, L. (2006). Short- and long-range spatial interactions: a redefinition. Vision Res. 46, 1302–1306.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tzvetanov, T., and Womelsdorf, T. (2008). Predicting human perceptual decisions by decoding neuronal information profiles. Biol. Cybern. 98, 397–411.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tzvetanov, T., Womelsdorf, T., Niebergall, R., and Treue, S. (2006). Feature-based attention influences contextual interactions during motion repulsion. Vision Res. 46, 3651–3658.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wenderoth, P., and Johnstone, S. (1988). The different mechanisms of the direct and indirect tilt illusions. Vision Res. 28, 301–312.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Westheimer, G. (1990). Simultaneous orientation contrast for lines in the human fovea. Vision Res. 30, 1913–1921.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Zenger-Landolt, B., and Heeger, D. (2003). Response suppression in V1 agrees with psychophysics of surround masking. J. Neurosci. 23, 6884–6893.

Pubmed Abstract | Pubmed Full Text