How adaptation shapes spike rate oscillations in recurrent neuronal networks

Introduction

A prominent characteristic of cortical activity is its rhythmicity as shown by electroencephalography or the local field potential. Dominant oscillation frequencies in these signals range from <1 to 100 Hz and reflect synchronous activity of populations of neurons. Such oscillations are linked to behavioral states (Wang, 2010) and involved in a variety of cognitive functions (Engel et al., 2001; Fries, 2001; Melloni et al., 2007; Ghazanfar et al., 2008; Wang, 2010) as well as pathological conditions (Hammond et al., 2007; Zijlmans et al., 2009; Uhlhaas and Singer, 2010). It is therefore important to understand the mechanisms of oscillations in neuronal networks, how they are initiated and terminated, and how their frequency is determined.

Fast rhythmic activity in the beta and gamma band (>20 Hz) can be generated by network-based mechanisms, such as synaptic excitation-inhibition loops or by feedback inhibition alone (Isaacson and Scanziani, 2011). In these scenarios the oscillation frequency is largely determined by the inhibitory decay time constant (Brunel and Wang, 2003; Tiesinga and Sejnowski, 2009). Low-frequency oscillations, on the other hand, could depend on slow transmembrane outward currents (Compte et al., 2003; Gigante et al., 2007b; Destexhe, 2009), which are mediated by low-threshold voltage-dependent muscarinic (M) and high-threshold calcium-gated afterhyperpolarization (AHP) K⁺ channels, respectively (Brown and Adams, 1980; Connors et al., 1982; Stocker, 2004). These currents cause spike frequency adaptation and are typically more pronounced in cortical regular spiking pyramidal (excitatory) neurons compared to fast spiking (inhibitory) interneurons (La Camera et al., 2006). Both, the M and AHP type K⁺ currents, are susceptible to cholinergic modulation (McCormick, 1992). Their kinetic time constants range from milliseconds to seconds (Abel et al., 2004; Manuel et al., 2005) and can be pharmacologically manipulated (Pedarzani et al., 2001).

Here we study the interplay of the dynamics of such adaptation currents with synaptic excitation and inhibition in recurrent networks of excitatory and inhibitory neurons. Specifically, we ask (1) how adaptation can generate slow oscillations, (2) how it modulates faster rhythms based on synaptic interaction, and (3) how adaptation affects resonance properties of the network.

In-vivo recordings from behaving animals have revealed that even when the population activity oscillates, the spike trains of the constituent neurons are rather irregular and display Poisson-like characteristics (Fries, 2001; Wang, 2010). This stochasticity in neuronal responses allows us to derive a mean-field model from a recurrent network of adaptive spiking model neurons coupled through conductance-based synapses with heterogeneous strengths and delays. Our approach is based on the Fokker–Planck (FP) formalism (Brunel, 2000; Deco et al., 2008) and efficiently describes the activity of large networks where the features of the spiking neurons (i.e., the model parameters) are retained. Using this method we analyze network responses to constant as well as rhythmic external input. In particular we describe asynchronous irregular states with constant steady-state activity as well as oscillatory states and their properties. We validate our mean-field results qualitatively by large-scale network simulations.

Methods

We first describe our network model containing two populations (excitatory and inhibitory) of adaptive spiking neurons with delayed conductance-based synaptic coupling. Based on that model we then derive mean-field model equations and solve them numerically to obtain distributions of the membrane potentials and instantaneous spike rates.

Network Model

We consider a network of N = N_ℰ + N_ℐ adaptive exponential integrate-and-fire neurons (aEIF) proposed by Brette and Gerstner (2005), where N_ℰ and N_ℐ are the numbers of excitatory and inhibitory neurons, respectively. The dynamics of the i-th neuron of population α ∈ {ℰ, ℐ} is described by

$\begin{array}{l}\begin{array}{cc}C\frac{d{V}_i^{\alpha }}{dt}=I_{\text{ion}}(V_i^{\alpha })-w_i^{\alpha }+I_{\text{syn},i}^{\alpha }(V_i^{\alpha },t)& (1)\end{array}\\ \begin{array}{cc}{\tau }_w\frac{d{w}_i^{\alpha }}{dt}=a(V_i^{\alpha }-E_L)-w_i^{\alpha }& (2)\end{array}\end{array}$

with reset condition

$\begin{array}{cc}\text{if }{V}_i^{\alpha }>V_{\text{cut}}\text{ then }\{\begin{array}{l}{V}_i^{\alpha }:=V_r\hfill \\ w_i^{\alpha }:=w_i^{\alpha }+b.\hfill \end{array}& (3)\end{array}$

The first Equation (1) is for the membrane potential V^α_i, where the capacitive current through the membrane with capacitance C equals the sum of ionic currents I_ion, the adaptation current w^α_i and the synaptic current I^α_{syn, i}. The ionic currents are given by

$\begin{array}{cc}{I}_{\text{ion}}(V):=g_L(E_L-V)+g_L{\Delta }_T{e}^{\frac{V-V_T}{{\Delta }_T}},& (4)\end{array}$

where the first term on the right-hand side describes an Ohmic leak current with conductance g_L and reversal potential E_L. The exponential term with threshold slope factor Δ_T and threshold potential V_T approximates the Na⁺-current which is responsible for the generation of spikes, assuming that the activation of Na⁺-channels is instantaneous and neglecting their inactivation (Fourcaud-Trocme et al., 2003). Equation (2) governs the dynamics of the adaptation current w^α_i, where τ_w denotes the adaptation time constant and a quantifies a conductance that mediates subthreshold adaptation. A spike is said to occur at the time when V^α_i diverges to infinity, but in practice a finite “cutoff” value V_cut is chosen. When V^α_i crosses V_cut from below, V^α_i is set to the reset potential V_r and w^α_i is incremented by b, cf. condition (3). In this way spike-triggered adaptation is included in the model. Immediately after the reset, V^α_i and w^α_i are clamped for a refractory period T_ref.

The aEIF model has been shown to reproduce a broad range of subthreshold dynamics (Touboul and Brette, 2008) and spike patterns of cortical neurons (Naud et al., 2008) and can well predict their spike times (Jolivet et al., 2008) and post-stimulus time histograms (Pospischil et al., 2011). Importantly, the subthreshold and spike-triggered adaptation components of this model have been shown to capture the effects of the M and AHP currents in a detailed biophysical neuron model, respectively (Ladenbauer et al., 2012).

Neuron i of population α receives total synaptic current

$\begin{array}{cc}{I}_{\text{syn},i}^{\alpha }(V_i^{\alpha },t):={\displaystyle \sum _j{I}_{ij}^{\alpha ,\text{ ext}}}+{\displaystyle \sum _j{I}_{ij}^{\alpha ,ℰ}}+{\displaystyle \sum _j{I}_{ij}^{\alpha ,ℐ}},& (5)\end{array}$

which is the superposition of synaptic inputs I^{α, ext}_ij from K_ext external excitatory neurons, I^{α, ℰ}_ij from K_ℰ excitatory neurons of the network and I^{α, ℰ}_ij from K_ℐ inhibitory neurons of the network. j is the index of the respective presynaptic neuron. The synaptic current I^{α, γ}_ij caused by neuron j of population γ ∈ {ext, ℰ, ℐ} is modeled using delta functions,

$\begin{array}{l}\begin{array}{cc}{I}_{ij}^{\alpha ,\text{ ext}}(V_i^{\alpha },t):=C{J}_{ij}^{\alpha ,\text{ ext}}{\displaystyle \sum _k\delta (t-t_j^k)\left(E_{ℰ}-V_i^{\alpha }\right)}& (6)\end{array}\\ \begin{array}{cc}{I}_{ij}^{\alpha ,\beta }(V_i^{\alpha },t):=C{J}_{ij}^{\alpha ,\beta }{\displaystyle \sum _k\delta (t-t_j^k-d_{ij}^{\alpha ,\beta })\left(E_{\beta }-V_i^{\alpha }\right)},& (7)\end{array}\end{array}$

where β ∈ {ℰ, ℐ} denotes the presynaptic population. J^{α, γ}_ij are dimensionless synaptic efficacies drawn from a Gaussian distribution with mean J_{α, γ} and standard deviation ΔJ_{α, γ}. Here we consider that J_{α, γ} ≡ J_γ and ΔJ_{α, γ} ≡ ΔJ_γ depend only on the presynaptic population γ. t^k_j is the k-th spike time of neuron j from the respective population. E_ℰ and E_ℐ denote the excitatory and inhibitory reversal potentials, respectively. d^{α, β}_ij is the synaptic delay, sampled using a bi-exponential probability density

$\begin{array}{cc}{p}_d^{\alpha ,\beta }(d):=\frac{1}{{\tau }_d-{\tau }_r}\left(e^{-\frac{d-d_0}{{\tau }_d}}-e^{-\frac{d-d_0}{{\tau }_r}}\right)& (8)\end{array}$

for positive delays d, where d₀ is the minimal delay and τ_r, τ_d are the rise and decay time constants, for each pair of populations. In the model we use two different delay distributions p^ℰ_d and p^ℐ_d which do not depend on the postsynaptic population as for the synaptic weights. For a schematic diagram of the network, see Figure 1.

FIGURE 1

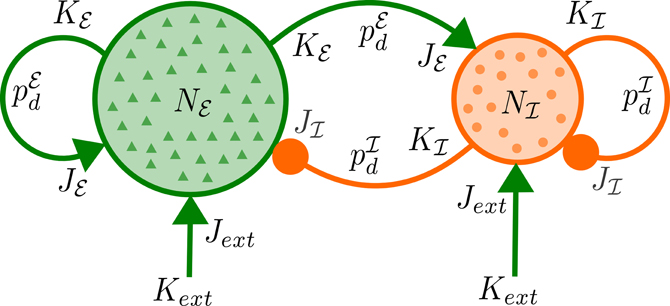
Figure 1. Network architecture. Each of N_ℰ excitatory and N_ℐ inhibitory neurons receives excitatory input from K_ext external neurons with mean synaptic strength J_ext as well as synaptic input from K_ℰ (K_ℐ) excitatory (inhibitory) neurons of the network with mean strength J_ℰ (J_ℐ) and delays distributed according to p^ℰ_d (p^ℐ_d).

We assume the neurons from the external population generate spike times according to Poisson processes with rates r^α_ext(t). The spike rate of each population α ∈ {ℰ, ℐ} at time t is given by the average number of spikes of neurons from the corresponding population in the interval [t, t + Δt],

$\begin{array}{cc}{r}_{\alpha }^{\Delta t}(t):=\frac{1}{N_{\alpha }\Delta t}{\displaystyle \sum _{j=1}^{N_{\alpha }}{\displaystyle {\int }_t^{t+\Delta t}{\displaystyle \sum _k\delta (s-t_j^k)ds}}}.& (9)\end{array}$

In the mean-field limit N → ∞, Δt → 0 we obtain a continuous population spike rate r_α(t) (see below).

We selected the following parameters for the neuron model: C = 200 pF, g_L = 10 nS, E_L = −70 mV, Δ_T = 1 mV, V_T = −50 mV, V_r = −70 mV, V_cut = −40 mV, and T_ref = 1.4 ms (Badel et al., 2008; Destexhe, 2009). For excitatory neurons the adaptation parameters were varied within reasonable ranges: τ_w ∈ [5, 1000] ms, a ∈ [0, 10] nS, b ∈ [0, 50] pA. For inhibitory neurons adaptation was neglected (a = b = 0) since it was found to be weak in fast spiking interneurons compared to pyramidal cells (La Camera et al., 2006).

The network parameter values were N_ℰ = 40,000, N_ℐ = 10,000, K_ext = 1600, K_ℰ = 1600, K_ℐ = 400, E_ℰ = 0 mV, E_ℐ = −80 mV, J_ext = 0.003, J_ℰ = 0.003, and ΔJ_γ = 0.1J_γ with γ ∈ {ext, ℰ, ℐ} (Brunel and Wang, 2003). To adjust the balance of recurrent synaptic excitation and inhibition we introduce the parameter

$\begin{array}{cc}g:=\frac{J_{ℐ}|E_L-E_{ℐ}|}{J_{ℰ}|E_L-E_{ℰ}|},& (10)\end{array}$

which is the ratio of total charges induced at rest (Kumar et al., 2008). g determines J_ℐ and thus ΔJ_ℐ for fixed J_ℰ and was varied in [0.8, 4] which yields a physiological range of inhibitory postsynaptic potential amplitudes (Tamas et al., 1997). Note that the value of g that corresponds to balanced mean recurrent excitatory and inhibitory synaptic currents depends on the mean membrane potential for each population. The effect of a spike of presynaptic neuron j on neuron i is mediated by a delayed instantaneous increment or decrement of the postsynaptic membrane potential, cf. Equations (1), (5), and (7). This implies that d^{α, β}_ij reflects the conduction delay as well as delays in the synaptic kinetics. We therefore chose the parameter values of p^ℰ_d and p^ℐ_d such that conduction delays as well as typical time courses of excitatory AMPA and inhibitory GABA_A synaptic receptors are taken into account. The values we selected were d₀ = 1 ms, τ^ℰ_r ∈ [1.25, 1.5] ms, τ^ℰ_d ∈ [1.5, 2] ms, τ^ℐ_r ∈ [0.55, 1.25] ms, and τ^ℐ_d ∈ [1.5, 5] ms. The input rate of the excitatory population r^ℰ_ext was varied in [1, 12.5] Hz. r^ℐ_ext was chosen such that r_ℰ = r_ℐ in case of uncoupled populations of neurons, i.e., J_ℰ = J_ℐ = 0.

Mean-Field Model

We reduce the two-population network of aEIF neurons to the mean-field model in three steps. First, we replace the synaptic current fluctuations by a Gaussian white noise process via the diffusion approximation. Next, we take a mean-field limit to formulate the stochastic network model in terms of two coupled deterministic scalar partial differential equations (PDE). Finally, to allow for efficient numerical computation we reduce the number of variables in these equations using an adiabatic approximation.

Diffusion approximation

We approximate the total synaptic current I^α_{syn, i} of Equation (5) by its mean plus a fluctuating Gaussian part, which is justified by the following physiologically plausible assumptions: (1) The number of synaptic inputs to a neuron is large, i.e., K_ext, K_ℰ, K_ℐ » 1 (Destexhe et al., 2003) and (2) the postsynaptic potential amplitudes elicited by individual presynaptic spikes are small, i.e., J_ext|E_ℰ − V|, J_ℰ|E_ℰ − V|, J_ℐ|E_ℐ − V| « V_cut − V_r (Williams and Stuart, 2002). We further assume that (3) the network connectivity is random and sparse, i.e., K_ℰ, K_ℐ « N, and that (4) presynaptic spike times are represented by Poisson processes which are homogeneous in each small time interval. The total synaptic current can then be written as (Brunel, 2000; Nykamp and Tranchina, 2000; Renart et al., 2004; Richardson, 2004; Gigante et al., 2007b)

$\begin{array}{cc}{I}_{\text{syn},i}^{\alpha }\approx {\mu }_{\alpha ,i}(V_i^{\alpha },t)+{\sigma }_{\alpha ,i}(V_i^{\alpha },t){\eta }_i(t),& (11)\end{array}$

where μ_{α, i} and σ_{α, i} are the infinitesimal mean and standard deviation of I^α_{syn, i}, respectively, and η_i is a Gaussian white noise process with δ-autocorrelation. The infinitesimal mean is given by

$\begin{array}{cc}\begin{array}{l}{\mu }_{\alpha ,i}:=\underset{\Delta t\to 0}{\lim }\frac{\langle {\displaystyle {\int }_t^{t+\Delta t}{I}_{\text{syn},i}^{\alpha }}(s)ds\rangle }{\Delta t}\\ ={\mu }_{\alpha ,i}^{\text{ext}}+{\mu }_{\alpha ,i}^{ℰ}+{\mu }_{\alpha ,i}^{ℐ}\end{array}& (12)\end{array}$

with

$\begin{array}{l}\begin{array}{cc}{\mu }_{\alpha ,i}^{\text{ext}}=C(E_{ℰ}-V_i^{\alpha })J_{\text{ext}}{K}_{\text{ext}}{r}_{\text{ext}}^{\alpha }(t)& (13)\end{array}\\ \begin{array}{cc}{\mu }_{\alpha ,i}^{\beta }=C(E_{\beta }-V_i^{\alpha })J_{\beta }{K}_{\beta }(r_{\beta }\ast p_{\beta })(t),& (14)\end{array}\end{array}$

where 〈·〉 denotes the expectation operator. The infinitesimal variance is

$\begin{array}{cc}\begin{array}{l}{\sigma }_{\alpha ,i}^2:=\underset{\Delta t\to 0}{\lim }\frac{\langle {\left({\displaystyle {\int }_t^{t+\Delta t}{I}_{\text{syn},i}^{\alpha }}(s)ds\right)}^2\rangle +O(\Delta t^2)}{\Delta t}\\ ={\left({\sigma }_{\alpha ,i}^{\text{ext}}\right)}^2+{\left({\sigma }_{\alpha ,i}^{ℰ}\right)}^2+{\left({\sigma }_{\alpha ,i}^{ℐ}\right)}^2\end{array}& (15)\end{array}$

with

$\begin{array}{l}\begin{array}{cc}{\sigma }_{\alpha ,i}^{\text{ext}}=C(E_{ℰ}-V_i^{\alpha })\sqrt{\left(J_{\text{ext}}^2+\Delta J_{\text{ext}}^2\right)K_{\text{ext}}{r}_{\text{ext}}(t)}& (16)\end{array}\\ \begin{array}{cc}{\sigma }_{\alpha ,i}^{\beta }=C(E_{\beta }-V_i^{\alpha })\sqrt{\left(J_{\beta }^2+\Delta J_{\beta }^2\right)K_{\beta }(r_{\beta }\ast p_{\beta })(t)},& (17)\end{array}\end{array}$

where β ∈ {ℰ, ℐ} and * denotes convolution. In Equations (13), (14), (16), and (17) we have used that the presynaptic Poisson processes, the synaptic weights and delays are independent.

Mean-field limit

We analyze networks of sparsely coupled neurons, i.e., the probability for a connection between any pair of neurons is low, cf. assumption (3) above. For large N correlations between the fluctuations of synaptic currents of different neurons become negligible, i.e., 〈 η_i(t) η_j(t) 〉 = 0 for i ≠ j. In the mean-field limit N → ∞ the network model Equations (1)–(4), Equations (11)–(17) can be described by two FP equations—one for each population α—which are delay-coupled by the population spike rates r_ℰ and r_ℐ,

$\begin{array}{cc}\frac{\partial p_{\alpha }}{\partial t}+\frac{\partial S_{\alpha }^V}{\partial V}+\frac{\partial S_{\alpha }^w}{\partial w}=0& (18)\end{array}$

with

$\begin{array}{l}\begin{array}{cc}\begin{array}{l}{S}_{\alpha }^V:=\left(\frac{I_{\text{ion}}(V)-w+{\mu }_{\alpha }}{C}-\frac{{\sigma }_{\alpha }}{2C^2}\frac{\partial {\sigma }_{\alpha }}{\partial V}\right)p_{\alpha }\\ -\frac{{\sigma }_{\alpha }^2}{2C^2}\frac{\partial p_{\alpha }}{\partial V}\end{array}& (19)\end{array}\\ \begin{array}{cc}{S}_{\alpha }^w:=\frac{a(V-E_L)-w}{{\tau }_w}{p}_{\alpha }.& (20)\end{array}\end{array}$

p_α(V, w, t) is the probability density to find a neuron of population α in the state (V, w) at time t. S^V_α(V, w, t) and S^w_α(V, w, t) are the probability fluxes in positive V and w direction, respectively. Note that we used the Stratonovich interpretation of the underlying stochastic equations (Risken, 1996; Richardson, 2004). To account for the reset condition (3) the flux through the cutoff voltage V_cut at w is re-injected after the refractory period T_ref at V_r, w + b, i.e.,

$\begin{array}{cc}\begin{array}{l}\underset{V\downarrow V_r}{\lim }{S}_{\alpha }^V(V,w+b,t)-\underset{V\uparrow V_r}{\lim }{S}_{\alpha }^V(V,w+b,t)\\ =S_{\alpha }^V(V_{\text{cut}},w,t-T_{\text{ref}})\forall w\in ℝ.\end{array}& (21)\end{array}$

This implies that in general p_α is not differentiable at the line V = V_r. The boundary conditions are reflecting for w → ±∞, V → −∞ and absorbing for V = V_cut,

$\begin{array}{l}\begin{array}{cc}\underset{w\to \pm \infty }{\lim }{S}_{\alpha }^w(V,w)=0\forall V\in (-\infty ,V_{\text{cut}}]& (22)\end{array}\\ \begin{array}{cc}\underset{V\to -\infty }{\lim }{S}_{\alpha }^V(V,w)=0\forall w\in ℝ& (23)\end{array}\\ \begin{array}{cc}{p}_{\alpha }(V_{\text{cut}},w)=0\forall w\in ℝ& (24)\end{array}\end{array}$

The spike rate of population α is given by the integral of the cutoff fluxes,

$\begin{array}{cc}{r}_{\alpha }(t)={\displaystyle {\int }_{ℝ}{S}_{\alpha }^V}(V_{\text{cut}},w,t)dw.& (25)\end{array}$

At any timepoint t the histogram of the membrane potentials of neurons in population α can be seen as a sample drawn from the probability density p_α(V, t) which is governed by the FP equation.

Adiabatic approximation

Solving the 2 + 1 dimensional PDE (Equations 18–20) with corresponding reset and boundary conditions (21)–(24) numerically is possible but computationally demanding. We therefore reduce the dimensionality of the FP system Equations (18)–(20) assuming the timescales of membrane voltage and adaptation current dynamics are separable. This is justified by the observation that the dynamics of neuronal adaptation is significantly slower than the other in the model system such as membrane time constant and average inter-spike interval (Womble and Moises, 1992; Stocker, 2004). Under this assumption, the adaptation current of each neuron can be seen as an efficient integrator that filters the fluctuations in the neuronal activity. We approximate w^α_i(t) in Equation (2) by its population average w_α(t), which evolves according to

$\begin{array}{cc}{\tau }_w\frac{d{w}_{\alpha }}{dt}=a({\langle V\rangle }_{p_{\alpha }(V,t)}-E_L)-w_{\alpha }+{\tau }_{w}b{r}_{\alpha }(t),& (26)\end{array}$

where 〈·〉_p denotes the average over the density p (Brunel et al., 2003; Gigante et al., 2007b). The probability density p_α(V, t) then satisfies the 1 + 1 dimensional FP equation

$\begin{array}{cc}\frac{\partial p_{\alpha }}{\partial t}+\frac{\partial S_{\alpha }^V}{\partial V}=0,& (27)\end{array}$

where again S^V_α is the probability flux defined in Equation (19) and w : = w_α(t) appears as a system parameter. The reset condition is

$\begin{array}{cc}\begin{array}{l}\underset{V\downarrow V_r}{\lim }{S}_{\alpha }^V(V,t)-\underset{V\uparrow V_r}{\lim }{S}_{\alpha }^V(V,t)\\ =S_{\alpha }^V(V_{\text{cut}},t-T_{\text{ref}}).\end{array}& (28)\end{array}$

and the boundary conditions (23)–(24) become

$\begin{array}{l}\begin{array}{cc}\underset{V\to -\infty }{\lim }{S}_{\alpha }^V(V)=0,& (29)\end{array}\\ \begin{array}{cc}{p}_{\alpha }(V_{\text{cut}})=0.& (30)\end{array}\end{array}$

The population spike rates are given by the corresponding fluxes through the cutoff voltage,

$\begin{array}{cc}{r}_{\alpha }(t)=S_{\alpha }^V(V_{\text{cut}},t).& (31)\end{array}$

Note that the adiabatic approximation described above could be applied repeatedly for additional slow variables.

Numerical Solution

We solved the reduced FP Equation (27) subject to conditions (28)–(30) and mean adaptation current dynamics (Equation 26) forward in time until either steady states r^∞_ℰ, r^∞_ℐ with r^∞_α : = lim_{t → ∞} r_α(t) or stable oscillatory states were reached. The probability densities p_ℰ, p_ℐ were initialized using normalized Gaussians with mean 0.5 · (V_r + V_T) and standard deviation 0.2 · (V_T − V_r). We applied a first-order finite volume method on a finite and non-uniform grid V₀ < V₁ < ··· < V_NV using upwind-fluxes to stabilize the numerical solution (LeVeque, 2002). Time was discretized using the implicit Euler method on an equidistant grid, i.e., $t_{n+1}-t_n\equiv \overline{\Delta t}$. The resulting linear equation systems were solved with a preconditioned Krylov subspace method in each time step. Specifically, BiCGSTAB (van der Vorst, 1992) was used in combination with an incomplete LU decomposition preconditioner (Saad, 2003) that strongly improved the convergence speed.

w_ℰ was initialized with values w_ℰ(0) ∈ [0, 500] pA (and w_ℐ ≡ 0). The other parameters were $\overline{\Delta t}=50\text{ μs}$, min_m ΔV_m = 1 μV with ΔV_m : = V_{m + 1}−V_m, V₀ : = −100 μV, V_NV = V_cut and N_V = 256.

We complemented the mean-field results with numerical simulations of the network model Equations (1)–(4) using a Runge–Kutta second order method implemented in Brian 1.4 (Goodman and Brette, 2009) with a time step of 50 μs.

In case of stable periodic population spike rates the oscillation frequency was determined by the dominant frequency of the Fourier spectrum of r_ℰ over the last 2 s of runtime.

Results

Adaptation Mediates Oscillations

To examine how the interplay of adaptation and recurrent synaptic input shapes network dynamics we vary the type, strength and timescale (parameters a, b, and τ_w) of adaptation for excitatory neurons as well as the strength of synaptic inhibition (parameter g) across networks. Adaptation currents are disregarded for inhibitory neurons, which is supported by experimental observations, see the section Methods. We consider constant rates r^ℰ_ext, r^ℐ_ext for the external Poisson-inputs and identical delay distributions p^ℰ_d ≡ p^ℐ_d. First, we examine steady-state spike rates, oscillation amplitudes and frequencies for networks with different values of spike-triggered adaptation b and inhibition strength g, see Figure 2A. All networks without adaptation (a = b = 0) settle into asynchronous states with constant population rates that decrease with increasing g. For networks with increased b slow oscillatory states become stable if recurrent excitation is sufficiently strong. The larger b is, the less recurrent excitation is necessary for sustained oscillations. Amplitude and period of the oscillatory rate decrease with an increase of b and g, respectively. Thus, in networks where recurrent synaptic excitation dominates inhibition at least slightly, spike-triggered adaptation b generates spike rate oscillations. The dynamics of an example network is shown in Figure 2B. The evolution of the population spike rates r_ℰ, r_ℐ, membrane potential probability densities p_ℰ, p_ℐ and adaptation current w_ℰ display periodic bursts of population activity. As a validation of the findings above using the mean-field model the activity of simulated large networks of spiking neurons is shown in Figure 2C. The raster plots reveal population bursts when b is increased and g is small. An asynchronous state with low population activity occurs if g is increased. If in addition adaptation is removed (a = b = 0) the network settles into an asynchronous state with increased spike rates.

FIGURE 2

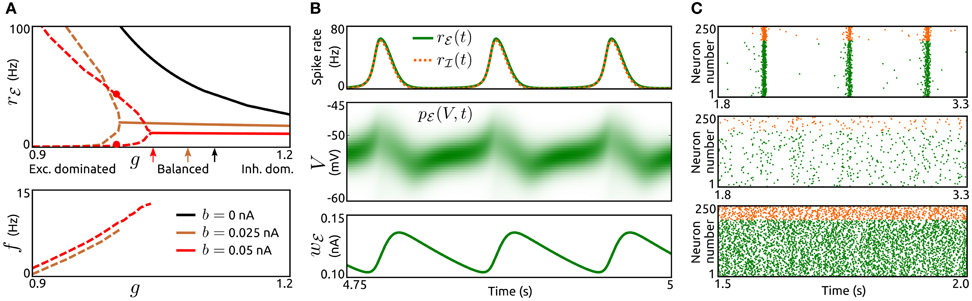
Figure 2. Population bursts caused by spike-triggered adaptation. (A) Top: Spike rate r_ℰ of the excitatory population as a function of the strength of inhibition g for networks without spike-triggered adaptation (b = 0, black) and with increased levels of b (0.025 nA, brown and 0.05 nA, red). In case of stable oscillatory states the maxima and minima of the periodic r_ℰ are shown by dashed lines. Solid lines represent asynchronous states. Arrows indicate balance of recurrent excitation and inhibition for both populations. Bottom: Corresponding oscillation frequencies f. τ_w = 200 ms, a = 0, and r^ℰ_ext = 6.25 Hz. The parameter values for both delay distributions p^ℰ_d, p^ℐ_d were τ_r = 1.5 ms and τ_d = 2 ms. For other model parameters see the section Methods. (B), Top: Time-dependent spike rates r_ℰ(t) (green) and r_ℐ(t) (orange, dashed) for the parameter values b = 0.05 nA and g = 1, as indicated in (A) by red dots. Center: Corresponding membrane potential density p_ℰ(V, t). Bottom: Corresponding mean adaptation current w_ℰ(t). (C): Raster plots of simulated networks of N = 50,000 aEIF neurons for b = 0.05 nA, g = 0.85 (top), b = 0.05 nA, g = 1.05 (center) and b = 0, g = 1 (bottom). The spike times of 200 excitatory neurons and 50 inhibitory neurons, all randomly selected, are shown by green and orange dots, respectively. τ_w = 200 ms, a = 0, and r^ℰ_ext = 3.75 Hz. Other parameter values as in (A).

The mechanism that generates these oscillations is a loop of recurrent excitation, build up and decay of adaptation current as indicated in Figure 2B. A low level of population activity is initiated by the external input r^ℰ_ext and recurrent synaptic excitation boosts the activity, thereby increasing the adaptation current w_ℰ through b in a spike rate dependent way. The adaptation current in turn acts as a negative feedback which eventually outweighs the recurrent excitation. The population activity drops rapidly and the adaptation current decays slowly. Upon recovery from the adaptation current the cycle starts again.

Next, we investigate how these oscillations are affected by the external input r^ℰ_ext, the subthreshold adaptation conductance a and the adaptation timescale τ_w, see Figure 3. The existence of adaptation-induced oscillations is quite sensitive to the level of r^ℰ_ext (Figure 3A). Periodic activity is stable for small values of r^ℰ_ext (above threshold). While oscillation frequencies increase monotonically with increasing r^ℰ_ext, oscillation amplitudes increase initially for a small interval of r^ℰ_ext values and decrease over the following interval. For larger values of r^ℰ_ext oscillatory activity is destabilized and asynchronous states occur. Interestingly, an increase in a does not lead to oscillations. On the contrary, periodic population bursts are destabilized by a. The dependence of oscillation amplitude and frequency on τ_w is shown in Figure 3B. Stable oscillations exist for a large range of values of τ_w, where the frequencies decrease with increasing τ_w. Oscillations are unstable for small adaptation timescales in the range of the membrane time constant and for very large values of τ_w.

FIGURE 3

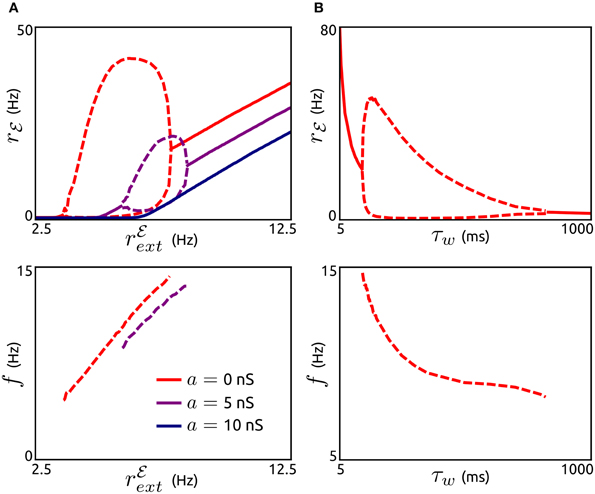
Figure 3. Effects of subthreshold adaptation, external input, and adaptation timescale on population bursts. (A), Top: Spike rate r_ℰ depending on the external input r^ℰ_ext for networks without subthreshold adaptation (a = 0, red) and with increased levels of a (5 nS, violet and 10 nS, dark blue). Maxima and minima of oscillating r_ℰ are shown by dashed lines. Bottom: Corresponding frequencies f. b = 0.05 nA, τ_w = 200 ms, g = 1, and other parameter values as in Figure 2A. (B): Maxima and minima of r_ℰ (top) and oscillation frequency as a function of the adaptation time constant τ_w. a = 0, r^ℰ_ext = 6.25 Hz, and other parameter values as in (A).

Adaptation Modulates Frequencies of Network-Based Oscillations

Here we study the influence of adaptation on oscillations generated by recurrent synaptic excitation-inhibition (ℰ−ℐ) loops. The pace of such oscillations is believed to be largely determined by the decay of inhibition. To describe their dependence on the timescale of inhibition for various recurrent network regimes (from excitation dominated to inhibition dominated) we first consider networks of neurons without an adaptation current (a = b = 0), see Figures 4A,B. By varying the decay τ^ℐ_d of inhibition and its strength (by parameter g) across networks we find that stable oscillatory states occur if inhibition is sufficiently slow in comparison to excitation. The oscillation frequencies increase with increasing external input spike rate r^ℰ_ext, increasing g and decreasing τ^ℐ_d, respectively. A low value of r^ℰ_ext leads to frequencies in the low beta band (Figure 4A), for a higher value of r^ℰ_ext the frequencies span the beta and low gamma bands (Figure 4B). Note that the network parameters can be adjusted to obtain higher oscillation frequencies. The generating mechanism underlying the oscillations is a loop of recurrent synaptic excitation and inhibition, initiated by the excitatory external input. We verified this by removing the recurrent excitatory input to the inhibitory population, which lead to a destabilization of the oscillations. For larger values of g as the ones used in Figure 4, the ℰ−ℐ-loop mechanism is replaced by an ℐ-ℐ-loop that does not depend on recurrent excitation (not shown). Since adaptation is only exhibited by excitatory neurons, we disregard the parameter space where ℐ-ℐ-loop-based rhythmic activity occurs and focus on ℰ-ℐ-loop-based oscillations instead.

FIGURE 4

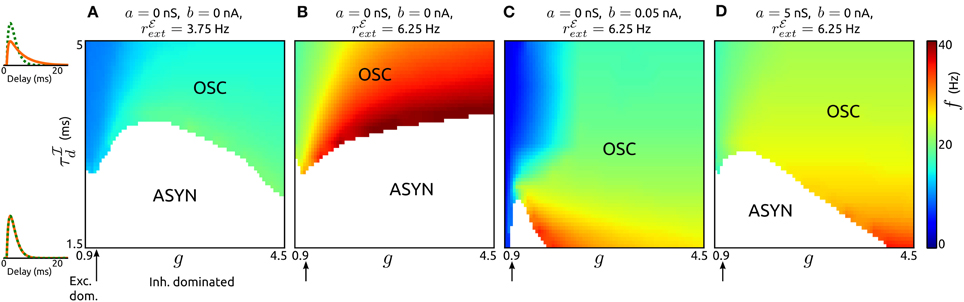
Figure 4. Influence of synaptic inhibition and adaptation on network-based oscillations. (A–D): Existence of oscillatory states (OSC) and corresponding frequencies f as a function of the strength g and timescale τ^ℐ_d of synaptic inhibition for networks with adaptation parameters and external input strengths as specified. Asynchronous states (ASYN) are indicated by white regions in the parameter space. Arrows mark balance of recurrent excitation and inhibition. On the left p^ℰ_d (green) and p^ℐ_d (orange) are shown for τ^ℐ_d = 1.5 ms, τ^ℐ_d = 5 ms. τ^ℐ_r was chosen such that the peaks of p^ℰ_d and p^ℐ_d occur at the same delay value. τ_w = 200 ms, τ^ℰ_r = 1.25 ms, and τ^ℰ_d = 1.5 ms. For other parameter values see the Methods section.

An increase of spike-triggered adaptation or subthreshold current stabilizes oscillatory states also for faster recurrent inhibition, see Figures 4C,D. This change in single neuron dynamics causes oscillations in large parts of explored (g, τ^ℐ_d)-space. In particular, for spike-triggered adaptation asynchronous states only occur in a small region of the parameter space. Interestingly, the oscillation frequencies are significantly reduced by either type of adaptation.

Next, we investigate how the timescale of adaptation τ_w affects oscillations mediated by an ℰ-ℐ-loop. In Figure 5A we show the dependence of amplitude and frequency of such oscillations on τ_w for networks with both adaptation components increased (a = 5 nS, b = 0.05 nA) and either dominant recurrent excitation (g = 1.05) or inhibition (g = 1.5). In both cases, stable oscillatory states exist for a large range of time constants. As τ_w increases the oscillation frequencies decrease while the amplitudes first increase abruptly and then decrease. The networks settle into asynchronous states for small τ_w (in the order of the membrane time constant) or large τ_w (several hundreds of milliseconds). Note that these effects of τ_w are similar if either a or b is increased individually (not shown). We validated these effects by simulations of aEIF neuron networks, see Figure 5B. The raster plots show that an increase in τ_w leads to a decrease in oscillation frequency and amplitude.

FIGURE 5

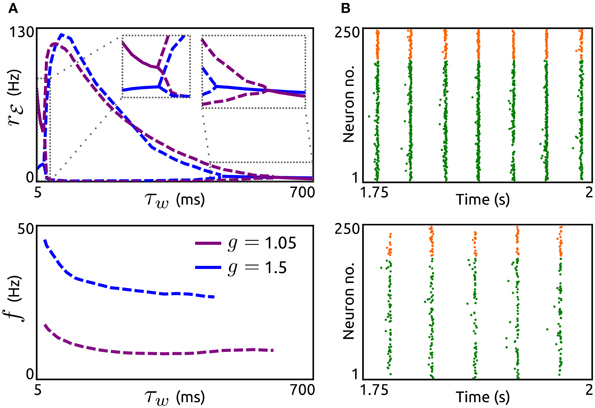
Figure 5. Effects of adaptation timescale on network-based oscillations. (A) Top: Spike rate r_ℰ as a function of the adaptation time constant τ_w for networks with dominant recurrent excitation (g = 1.05, violet) and inhibition (g = 1.5, blue). Dashed lines indicate maxima and minima of oscillating r_ℰ, solid lines represent constant r_ℰ. Bottom: Corresponding oscillation frequencies f. a = 5 nS and b = 0.05 nA. r^ℰ_ext = 7.5 Hz, τ^ℰ_r = 1.25 ms, τ^ℰ_d = 1.55 ms, τ^ℐ_r = 0.98 ms, and τ^ℐ_d = 2 ms. Other parameters as in Figure 4. (B): Raster plots of simulated networks of size N = 50,000 with g = 1.5 and τ_w = 100 ms (top) as well as τ_w = 400 ms (bottom), showing the spike times of 200 excitatory and 50 inhibitory aEIF neurons. Other parameter values as in (A).

Adaptation Promotes Periodic Signal Propagation

To analyze how the resonance properties of recurrent networks in asynchronous states are influenced by adaptation currents, we here consider external Poisson-inputs with oscillatory rates with frequency f. Gain of input spike rate and phase difference between network and input spike rates as a function of input frequency for networks without (a = b = 0) and with adaptation (a = 5 nS, b = 0.05 nA) considering two adaptation time constants are presented in Figures 6A,B. Excitation dominated networks without adaptation do not exhibit resonance at any frequency and show only phase delays. The presence of an adaptation current leads to a significant amplification of oscillations in the input which is particularly strong at lower frequencies (of the beta band). This effect is pronounced for an increased adaptation timescale. In addition, adaptation causes a phase advance for low oscillation frequencies.

FIGURE 6

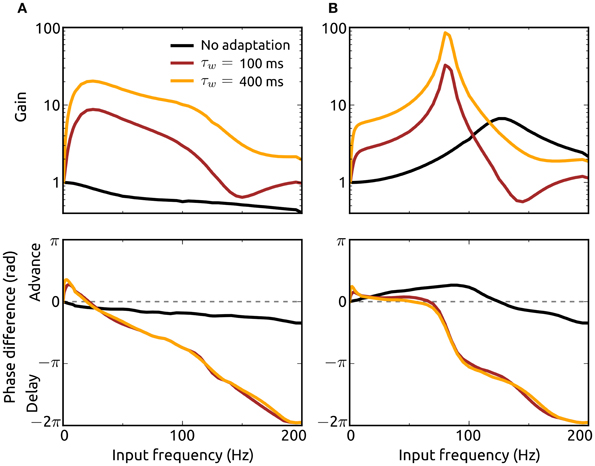
Figure 6. Effects of adaptation on resonance properties of recurrent networks. Gain (top) and phase shift (bottom) of the spike rate r_ℰ for networks with dominant recurrent excitation [g = 1.05, (A)] and inhibition [g = 1.5, (B)] as a function of the input frequency f. The gain is defined as the quotient of the oscillation amplitude in r_ℰ for the input with frequency f and the amplitude for the lowest frequency (f_min = 0.5 Hz). Adaptation parameter values are a = b = 0 (black), a = 5 nS, b = 0.05 nA, τ_w = 100 ms (dark red), and a = 5 nS, b = 0.05 nA, τ_w = 400 ms (orange). Delay distributions are identically parameterized (p^ℰ_d ≡ p^ℐ_d) with τ_r = 1.25 ms and τ_d = 1.5 ms. The Poisson-input rates r^ℰ_ext, r^ℐ_ext each consist of a baseline rate plus a sinusoidal component of small amplitude (1/1000th of the baseline) with frequency f. The baseline of r^ℰ_ext is chosen to yield a steady-state spike rate r^∞_ℰ of 50 Hz with constant input rate. The baseline rate of r^ℐ_ext is chosen as explained in the Methods section.

In networks where recurrent inhibition dominates excitation on the other hand even in the absence of adaptation currents resonance is shown for a high frequency band and phase advances for lower frequencies. Adaptation greatly enhances resonance and shifts the preferred frequency band to the high gamma range. The resonance effect is even stronger if the adaptation current is slower, i.e., τ_w increased. Although these effects of adaptation on resonance properties of recurrent networks are similar when either the subthreshold (a) or spike-triggered adaptation component (b) is increased individually, the dominant contribution to the frequency amplifications comes from b (not shown). We additionally examined the response of single neurons to oscillatory noisy inputs using our mean-field model and found that adaptation mediates resonance even in the absence of recurrent input (not shown). These results emphasize the importance of adaptation for the amplification and thus propagation of oscillatory signals in neuronal networks.

Discussion

In this work we have investigated the role of neuronal adaptation currents in shaping spike rate oscillations in large recurrent networks of excitatory and inhibitory neurons. Based on a network of aEIF model neurons sparsely coupled through conductance-based synapses with heterogeneous delays and strengths driven by noisy external input, we used a mean-field method taking advantage of the FP equation. We simplified the problem by applying an adiabatic approximation and solved the resulting equations numerically. Using this method we obtain membrane potential distributions and population averages of spike rates and adaptation currents. At the same time, the dynamical properties of single neurons, i.e., the neuron model parameters, are retained in the derived mean-field network model.

Alternative mean-field methods have been developed for conductance-based model neurons (Robinson et al., 2008) and recurrent networks thereof in asynchronous states (Shriki et al., 2003), where spike rates are obtained without having to solve a PDE. Our approach based on the FP equation on the other hand treats noise in the synaptic inputs in more detail and allows for the calculation of membrane potential distributions in addition to spike rates.

We chose the aEIF model because it provides a rich yet low-dimensional description of neuronal dynamics and includes a proper phenomenological description of the M and AHP adaptation currents. The effects of subthreshold (a) and spike-triggered adaptation (b) on response properties of aEIF neurons (measured by spike rate-input current relationships and phase response curves) match those of M and AHP adaptation currents in a Hodgkin–Huxley type neuron model, respectively (Ladenbauer et al., 2012). Furthermore, fitting the aEIF model parameters to a detailed biophysical model using standard electro-physiological paradigms revealed a clear relationship between parameter a and the conductance for the M current as well as between parameter b and the AHP current (not shown).

Our method is based on several assumptions which allow to derive the mean-field equations. The Poisson approximation of spike train statistics is justified by experimental findings (Tolhurst et al., 1983; McAdams and Maunsell, 1999) although spiking seems to be more regular in some cortical areas (Maimon and Assad, 2009). The sparse random connectivity implies vanishing noise correlations between neurons in the large network limit and an experimental study in primary visual cortex of awake monkeys has reported almost zero noise correlations (Ecker et al., 2010). However, there is an ongoing debate about the strength of correlations in experimental data (Cohen and Kohn, 2011). We have used an adiabatic approximation, which relies on separable time scales of adaptation current and membrane voltage. Although this assumption is violated for small values of τ_w, numerically solving the unreduced FP system, Equations (18)–(24), showed that our results are robust regarding the violation of this assumption. The results we obtained by simulations of aEIF networks and the mean-field results show quantitative differences. However, the presented effects described using the mean-field model are validated qualitatively by the network simulations.

We have shown that spike-triggered adaptation provides a mechanism to generate spike rate oscillations in a low frequency range (alpha band and lower) if recurrent excitation is sufficiently strong. Increased subthreshold adaptation on the other hand does not contribute to this mechanism but rather dampens such oscillations. The type of adaptation current therefore strongly determines rhythmic activity in excitation dominated networks. The importance of activity-driven adaptation for slow oscillations is consistent with results from simulations of detailed (thalamo-)cortical spiking neuron network models (Bazhenov et al., 2002; Compte et al., 2003; Destexhe, 2009), mean-field studies based on networks of excitatory neurons under the assumption sparse (Gigante et al., 2007b) and all-to-all connectivity (Nesse et al., 2008), as well as phenomenological rate models (Latham et al., 2000). We have further shown that reducing inhibitory synaptic strength leads to a reduction on oscillation frequency, which is in agreement with similar experimental findings (Sanchez-Vives et al., 2010).

The M and AHP K⁺ currents, which mediate spike frequency adaptation in pyramidal neurons, are known to be deactivated by acetylcholine (McCormick, 1992), with the AHP current showing higher sensitivity. Since the adaptation parameter b is strongly related to AHP type adaptation, our results support the hypothesis that the cholinergically induced activating transition from slow-wave oscillations to asynchronous irregular states (Lee and Dan, 2012) is mediated (at least in part) by a reduction of spike-triggered adaptation (Destexhe, 2009).

We have demonstrated that an increase of either type of adaptation current leads to a reduction in the frequency of oscillations generated by a loop of recurrent excitation and inhibition. This shows that the dynamical properties of neurons in addition to coupling characteristics strongly affect the network frequency. Also the passive (integrative) membrane properties significantly influence such networks oscillations as has been described previously (Geisler et al., 2005). Our additional finding of decreased frequencies for increased adaptation time constants is consistent with the results from a computational study on clustering effects of spike-triggered adaptation in gamma oscillations (Kilpatrick and Ermentrout, 2011).

Low input frequencies have been shown to be suppressed in the output of single excitatory neurons with increased spike-triggered (Gigante et al., 2007a) or subthreshold adaptation (Richardson et al., 2003; Prescott and Sejnowski, 2008), which we confirmed using our aEIF-based mean-field model. Such a high pass property of single neurons has also been found using a more general model of adaptation (Benda and Herz, 2003). We have demonstrated that both adaptation currents cause spike rate resonance in excitation dominated recurrent networks. Inhibition dominated networks, on the other hand, exhibit resonance without adaptation and we have shown that increased adaptation of excitatory neurons strongly amplifies this resonance. A similar effect has been described for purely inhibitory networks (Richardson, 2009). In addition, our results show that adaptation shifts the resonance frequency to lower values.

In excitation dominated networks, adaptation further leads to phase advances for low input frequencies in addition to phase delays for higher frequencies as observed in previous studies on single excitatory neurons (Fuhrmann et al., 2002; Gigante et al., 2007a). These adaptation-induced phase advances enable synchronization of periodic activity between distant neurons (and populations of neurons) in different areas of the brain if the strength of adaptation is controlled appropriately, e.g., through cholinergic neuromodulation.

Here we have considered one adaptation current for each neuron of the excitatory population. To account for the multimodal distribution of adaptation timescales found experimentally (La Camera et al., 2006) our approach can be easily extended to include multiple adaptation currents.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Timm Lochmann for helpful comments on the manuscript. This work was supported by the DFG Collaborative Research Center SFB910.

References

Abel, H. J., Lee, J. C. F., Callaway, J. C., and Foehring, R. C. (2004). Relationships between intracellular calcium and afterhyperpolarizations in neocortical pyramidal neurons. J. Neurophysiol. 91, 324–335.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Badel, L., Lefort, S., Brette, R., Petersen, C. C. H., Gerstner, W., and Richardson, M. J. E. (2008). Dynamic I-V curves are reliable predictors of naturalistic pyramidal-neuron voltage traces. J. Neurophysiol. 99, 656–666.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bazhenov, M., Timofeev, I., Steriade, M., and Sejnowski, T. J. (2002). Model of thalamocortical slow-wave sleep oscillations and transitions to activated states. J. Neurosci. 22, 8691–8704.

Pubmed Abstract | Pubmed Full Text

Benda, J., and Herz, A. V. M. (2003). A universal model for spike-frequency adaptation. Neural Comput. 15, 2523–2564.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brette, R., and Gerstner, W. (2005). Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J. Neurophysiol. 94, 3637–3642.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brown, D. A., and Adams, P. R. (1980). Muscarinic suppression of a novel voltage-sensitive K+ current in a vertebrate neurone. Nature 283, 673–676.

Pubmed Abstract | Pubmed Full Text

Brunel, N. (2000). Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 8, 183–208.

Pubmed Abstract | Pubmed Full Text

Brunel, N., Hakim, V., and Richardson, M. (2003). Firing-rate resonance in a generalized integrate-and-fire neuron with subthreshold resonance. Phys. Rev. E 67, 051916.

Pubmed Abstract | Pubmed Full Text

Brunel, N., and Wang, X.-J. (2003). What determines the frequency of fast network oscillations with irregular neural discharges? I. Synaptic dynamics and excitation-inhibition balance. J. Neurophysiol. 90, 415–430.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cohen, M. R., and Kohn, A. (2011). Measuring and interpreting neuronal correlations. Nat. Neurosci. 14, 811–819.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Compte, A., Sanchez-Vives, M. V., McCormick, D. A., and Wang, X.-J. (2003). Cellular and network mechanisms of slow oscillatory activity (<1 Hz) and wave propagations in a cortical network model. J. Neurophysiol. 89, 2707–2725.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Connors, B., Gutnick, M., and Prince, D. (1982). Electrophysiological properties of neocortical neurons in vitro. J. Neurophysiol. 48, 1302–1320.

Pubmed Abstract | Pubmed Full Text

Deco, G., Jirsa, V. K., Robinson, P. A., Breakspear, M., and Friston, K. (2008). The dynamic brain: from spiking neurons to neural masses and cortical fields. PLoS Comput. Biol. 4:e1000092. doi: 10.1371/journal.pcbi.1000092

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Destexhe, A. (2009). Self-sustained asynchronous irregular states and up-down states in thalamic, cortical and thalamocortical networks of nonlinear integrate-and-fire neurons. J. Comput. Neurosci. 27, 493–506.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Destexhe, A., Rudolph, M., and Paré, D. (2003). The high-conductance state of neocortical neurons in vivo. Nat. Rev. Neurosci. 4, 739–751.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ecker, A. S., Berens, P., Keliris, G. A., Bethge, M., Logothetis, N. K., and Tolias, A. S. (2010). Decorrelated neuronal firing in cortical microcircuits. Science 327, 584–587.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Engel, A., Fries, P., and Singer, W. (2001). Dynamic predictions: oscillations and synchrony in top-down processing. Nat. Rev. Neurosci. 2, 704–716.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fourcaud-Trocme, N., Hansel, D., van Vreeswijk, C., and Brunel, N. (2003). How spike generation mechanisms determine the neuronal response to fluctuating inputs. J. Neurosci. 23, 11628–11640.

Pubmed Abstract | Pubmed Full Text

Fries, P. (2001). Modulation of oscillatory neuronal synchronization by selective visual attention. Science 291, 1560–1563.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fuhrmann, G., Markram, H., and Tsodyks, M. (2002). Spike frequency adaptation and neocortical rhythms. J. Neurophysiol. 88, 761–770.

Pubmed Abstract | Pubmed Full Text

Geisler, C., Brunel, N., and Wang, X.-J. (2005). Contributions of intrinsic membrane dynamics to fast network oscillations with irregular neuronal discharges. J. Neurophysiol. 94, 4344–4361.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ghazanfar, A., Chandrasekaran, C., and Logothetis, N. (2008). Interactions between the superior temporal sulcus and auditory cortex mediate dynamic face/voice integration in rhesus monkeys. J. Neurosci. 28, 4457–4469.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gigante, G., Del Giudice, P., and Mattia, M. (2007a). Frequency-dependent response properties of adapting spiking neurons. Math. Biosci. 207, 336–351.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gigante, G., Mattia, M., and Del Giudice, P. (2007b). Diverse population-bursting modes of adapting spiking neurons. Phys. Rev. Lett. 98, 1–4.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Goodman, D. F. M., and Brette, R. (2009). The brian simulator. Front. Neurosci. 3, 192–197. doi: 10.3389/neuro.01.026.2009

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hammond, C., Bergman, H., and Brown, P. (2007). Pathological synchronization in Parkinson's disease: networks, models and treatments. Trends Neurosci. 30, 357–364.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Isaacson, J. S., and Scanziani, M. (2011). How inhibition shapes cortical activity. Neuron 72, 231–243.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Jolivet, R., Schürmann, F., Berger, T. K., Naud, R., Gerstner, W., and Roth, A. (2008). The quantitative single-neuron modeling competition. Biol. Cybern. 99, 417–426.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kilpatrick, Z. P., and Ermentrout, B. (2011). Sparse gamma rhythms arising through clustering in adapting neuronal networks. PLoS Comput. Biol. 7:e1002281. doi: 10.1371/journal.pcbi.1002281

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kumar, A., Schrader, S., Aertsen, A., and Rotter, S. (2008). The high-conductance state of cortical networks. Neural Comput. 20, 1–43.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

La Camera, G., Rauch, A., Thurbon, D., Lüscher, H.-R., Senn, W., and Fusi, S. (2006). Multiple time scales of temporal response in pyramidal and fast spiking cortical neurons. J. Neurophysiol. 96, 3448–3464.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ladenbauer, J., Augustin, M., Shiau, L., and Obermayer, K. (2012). Impact of adaptation currents on synchronization of coupled exponential integrate-and-fire neurons. PLoS Comput. Biol. 8:e1002478. doi: 10.1371/journal.pcbi.1002478

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Latham, P. E., Richmond, B. J., Nelson, P. G., and Nirenberg, S. (2000). Intrinsic dynamics in neuronal networks. I. Theory. J. Neurophysiol. 83, 808–827.

Pubmed Abstract | Pubmed Full Text

Lee, S.-H., and Dan, Y. (2012). Neuromodulation of brain states. Neuron 76, 209–222.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

LeVeque, R. (2002). Finite Volume Methods for Hyperbolic Problems. Cambridge: Cambridge University Press.

Maimon, G., and Assad, J. A. (2009). Beyond Poisson: increased spike-time regularity across primate parietal cortex. Neuron 62, 426–440.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Manuel, M., Meunier, C., Donnet, M., and Zytnicki, D. (2005). How much afterhyperpolarization conductance is recruited by an action potential? A dynamic-clamp study in cat lumbar motoneurons. J. Neurosci. 25, 8917–8923.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McAdams, C. J., and Maunsell, J. H. (1999). Effects of attention on the reliability of individual neurons in monkey visual cortex. Neuron 23, 765–773.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

McCormick, D. A. (1992). Neurotransmitter actions in the thalamus and cerebral cortex and their role in thalamocortical activity. Progr. Neurobiol. 39, 337–388.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Melloni, L., Molina, C., Pena, M., Torres, D., Singer, W., and Rodriguez, E. (2007). Synchronization of neural activity across cortical areas correlates with conscious perception. J. Neurosci. 27, 2858–2865.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Naud, R., Marcille, N., Clopath, C., and Gerstner, W. (2008). Firing patterns in the adaptive exponential integrate-and-fire model. Biol. Cybern. 99, 335–347.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nesse, W. H., Borisyuk, A., and Bressloff, P. C. (2008). Fluctuation-driven rhythmogenesis in an excitatory neuronal network with slow adaptation. J. Comput. Neurosci. 25, 317–333.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nykamp, D. Q., and Tranchina, D. (2000). A population density approach that facilitates large-scale modeling of neural networks: analysis and an application to orientation tuning. J. Comput. Neurosci. 8, 19–50.

Pubmed Abstract | Pubmed Full Text

Pedarzani, P., Mosbacher, J., Rivard, A., Cingolani, L. A., Oliver, D., Stocker, M., et al. (2001). Control of electrical activity in central neurons by modulating the gating of small conductance Ca(2+)-activated K+ channels. J. Biol. Chem. 276, 9762–9769.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pospischil, M., Piwkowska, Z., Bal, T., and Destexhe, A. (2011). Comparison of different neuron models to conductance-based post-stimulus time histograms obtained in cortical pyramidal cells using dynamic-clamp in vitro. Biol. Cybern. 105, 167–180.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Prescott, S. A., and Sejnowski, T. J. (2008). Spike-rate coding and spike-time coding are affected oppositely by different adaptation mechanisms. J. Neurosci. 28, 13649–13661.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Renart, A., Brunel, N., and Wang, X.-J. (2004). “Mean-field theory of irregularly spiking neuronal populations and working nemory in recurrent cortical networks,” in Computational Neuroscience: A Comprehensive Approach, ed J. Feng (Boca Raton, FL: CRC Press), 431–490.

Richardson, M. (2004). Effects of synaptic conductance on the voltage distribution and firing rate of spiking neurons. Phys. Rev. E 69, 1–8.

Pubmed Abstract | Pubmed Full Text

Richardson, M. (2009). Dynamics of populations and networks of neurons with voltage-activated and calcium-activated currents. Phys. Rev. E 80, 1–16.

Pubmed Abstract | Pubmed Full Text

Richardson, M. J. E., Brunel, N., and Hakim, V. (2003). From subthreshold to firing-rate resonance. J. Neurophysiol. 89, 2538–2554.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Risken, H. (1996). The Fokker–Planck Equation: Methods of Solutions and Applications. Berlin: Springer.

Robinson, P. A., Wu, H., and Kim, J. W. (2008). Neural rate equations for bursting dynamics derived from conductance-based equations. J. Theor. Biol. 250, 663–672.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Saad, Y. (2003). Iterative Methods for Sparse Linear Systems. Philadelphia, PA: SIAM.

Sanchez-Vives, M. V., Mattia, M., Compte, A., Perez-Zabalza, M., Winograd, M., Descalzo, V. F., et al. (2010). Inhibitory modulation of cortical up states. J. Neurophysiol. 104, 1314–1324.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shriki, O., Hansel, D., and Sompolinsky, H. (2003). Rate models for conductance-based cortical neuronal networks. Neural Comput. 15, 1809–1841.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Stocker, M. (2004). Ca(2+)-activated K+ channels: molecular determinants and function of the SK family. Nat. Rev. Neurosci. 5, 758–770.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tamas, G., Buhl, E. H., and Somogyi, P. (1997). Fast IPSPs elicited via multiple synaptic release sites by different types of GABAergic neurone in the cat visual cortex. J. Physiol. 500, 715–738.

Pubmed Abstract | Pubmed Full Text

Tiesinga, P., and Sejnowski, T. J. (2009). Cortical enlightenment: are attentional gamma oscillations driven by ING or PING? Neuron 63, 727–732.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tolhurst, D. J., Movshon, J. A., and Dean, A. F. (1983). The statistical reliability of signals in single neurons in cat and monkey visual cortex. Vision Res. 23, 775–785.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Touboul, J., and Brette, R. (2008). Dynamics and bifurcations of the adaptive exponential integrate-and-fire model. Biol. Cybern. 99, 319–334.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Uhlhaas, P. J., and Singer, W. (2010). Abnormal neural oscillations and synchrony in schizophrenia. Nat. Rev. Neurosci. 11, 100–113.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

van der Vorst, H. A. (1992). Bi-CGSTAB: a fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 13, 631–644.

Wang, X.-J. (2010). Neurophysiological and computational principles of cortical rhythms in cognition. Phyiol. Rev. 90, 1195–1268.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Williams, S. R., and Stuart, G. J. (2002). Dependence of EPSP efficacy on synapse location in neocortical pyramidal neurons. Science 295, 1907–1910.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Womble, M. D., and Moises, H. C. (1992). Muscarinic inhibition of M-current and a potassium leak conductance in neurones of the rat basolateral amygdala. J. Physiol. 457, 93–114.

Pubmed Abstract | Pubmed Full Text

Zijlmans, M., Jacobs, J., Zelmann, R., Dubeau, F., and Grotman, J. (2009). High-frequency oscillations mirror disease activity in patients with epilepsy. Neurology 72, 979–986.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text